Abstract
This study on the local stability of quaternion-valued neural networks is of great significance to the application of associative memory and pattern recognition. In the research, we study local Lagrange exponential stability of quaternion-valued neural networks with time delays. By separating the quaternion-valued neural networks into a real part and three imaginary parts, separating the quaternion field into subregions, and using the intermediate value theorem, sufficient conditions are proposed to ensure quaternion-valued neural networks have equilibrium points. According to the Halanay inequality, the conditions for the existence of local Lagrange exponentially stable equilibria of quaternion-valued neural networks are established. The obtained stability results improve and extend the existing ones. Under the same conditions, quaternion-valued neural networks have more stable equilibrium points than complex-valued neural networks and real-valued neural networks. The validity of the theoretical results were verified by an example.
Keywords:
quaternion-valued neural network; local Lagrange exponential stability; multiple equilibrium points; time delay MSC:
34D20; 65L20
1. Introduction
Because of the wide application prospect in pattern recognition, associative memory, optimization, and others, dynamic characteristics of global stability and local stability have been deeply studied for several kinds of recurrent neural networks [1,2,3,4,5,6]. Global stability can be applied to optimization problems [7,8,9,10,11,12], and local stability can be applied to pattern recognition [13,14,15,16,17]. The topological structure of activation functions has an important influence on the dynamic characteristics of recurrent neural networks. The local stability of recurrent neural networks with monotonically increasing activation functions was studied in References [18,19]. The local stability of recurrent neural networks with nonmonotonic activation functions was studied in Reference [20]. The local stability of recurrent neural networks with discontinuous activation functions was studied in Reference [21]. When applying recurrent neural networks to pattern recognition, stable equilibrium points of recurrent neural network are mapped into the ideal memory pattern. For example, in [22], the authors designed a recurrent neural network with 25 neurons to store three patterns. The more stable the equilibrium points are, the larger the memory capacity of the recurrent neural networks is. When the initial state is located in the domain of attraction of the equilibrium point corresponding to the pattern that is retrieved, the initial state will converge into the stable equilibrium point. That is, the desired output pattern can be derived. Each stable equilibrium point has a certain domain of attraction. The larger the domain of attraction of the equilibrium point is, stronger the fault tolerance of the memory pattern is. Therefore, it is very meaningful to study how to increase the number of stable equilibrium points and expand the domain of attraction of stable equilibrium points. By studying the multiple stability of complex-valued recurrent neural networks, the number of stable equilibrium points was increased [23]. By studying the multistability of recurrent neural networks with multi-order activation functions, the number of stable equilibrium points was increased [24].
In the practical application of recurrent neural networks, time delay is inevitable. Because time delay is often the origin of system instability and oscillation, a large number of researchers have discussed neural networks with time delay [25,26,27]. The research on the multiple stability of recurrent neural networks with time delay is very significant.
In recent decades, due to the development of algebra, the quaternion has gradually become a research hotspot and has successfully been applied to signal processing. As a special generalization of complex-valued neural network, a quaternion-valued neural network has a quaternion state, a quaternion link matrix, and a quaternion activation function, which are based on the non-commutation of the quaternion product. Due to the fact that complex-valued recurrent neural networks can increase the number of stable equilibrium points, quaternion-valued recurrent neural networks have more stable equilibrium points. Because of the quaternion state, one-dimensional quaternion-valued neural network can be separated into four dynamic equations. Therefore, under the same activation function, a one-dimensional quaternion-valued neural network, two-dimensional complex-valued neural network, and four-dimensional real-valued neural network have the same number of equilibrium points. That is to say, in the case of the same dimension, a quaternion-valued neural network has more stable equilibrium points than a complex-valued neural network and a real-valued neural network. However, the non-commutativity makes the research on quaternion-valued neural networks more difficult. Recently, the dynamic characteristics of quaternion-valued neural networks have been deeply studied for their applications in information processing, optimization, and automatic control [28,29,30,31].
This paper makes two contributions. (1) By separating the quaternion-valued neural network into a real part and three imaginary parts, we obtain sufficient conditions of existence of equilibrium points. (2) Some criteria are established to ensure larger storage capacity than the existing multistability results.
In this paper, we study local Lagrange exponential stability of quaternion-valued neural networks with time delays. In Section 2, we describe the neural network model, the definitions, and the lemma used in this paper. Multistability results of the quaternion-valued neural networks are described in Section 3. An example is given to verify the effectiveness of the results in Section 4. Furthermore, the conclusion is presented in Section 5.
2. Problem Formulation and Some Preliminaries
Consider the quaternion-valued neural networks with delays described by
for System (1) is equivalent to the following vector form:
where is the state vector, represents the self-feedback connection weight matrix, represent the connection weight,
represents the activation function, is the time delay,
is the external input vector, denotes the set of real numbers, denotes the set of quaternion numbers, and for
in which and the imaginary units obey the following rules:
Denote
Let
Denote
Then, can be divided into subsets. Denote
It is easy to see that have subsets, respectively. We divide into two parts: and . In this paper, we mainly discuss the stability of the equilibrium point in . In the following, one lemma and one definition used in this paper are given.
Lemma 1
(Halanay Inequality [32,33]). Assume constant numbers , satisfy is a nonnegative continuous function on , and as , the following inequality is satisfied:
where is the Dini derivative. is constant. Then as we have
in which λ is the unique positive solution of the equation .
Suppose the continuous initial condition associated with system (1) or (2) is for any . Based on the definition of global exponential stability in the Lagrange sense for recurrent neural networks in [34,35], we give the definition of locally exponentially stability in the Lagrange sense of an equilibrium point for system (1) or system (2).
Definition 1
As a special case of asymptotic stability, exponential stability has a faster convergence rate. This will be conducive to efficient pattern recognition applications.
3. Existence and Stability of Multiple Equilibrium Points
In this section, we will study the existence and stability of multiple equilibrium points for system (1). We can separate system (1) into a real part and three imaginary parts. System (1) can be rewritten as follows for
Denote the following functions for
Define the following continuous functions
We can derive the following results from the previous definitions for i = 1, 2, …, n,
Based on the above inequality, the following results can be obtained.
Theorem 1.
Proof.
According to the definition of , we can obtain the fact that
From condition (11), we have
Let be an arbitrary subregion located in . Denote as the closure of . Without loss of generality, assume
where the value of is or or , is a very small constant. According to intermediate value theorems (12) and (13), we can derive that
Therefore, there exists such that Denote a mapping with
G is continuous. By Brouwer’s fixed point theorem, there exists one fixed point in . So is also an equilibrium point of system (1). has subregions, and is an arbitrary subregion in . Therefore, there exist equilibrium points for system (1). □
Remark 1.
By dividing the quaternion field into multiple local regions, as well as the boundary value principle and Brouwer’s fixed point principle, sufficient conditions for the existence of local equilibrium points of system (1) are established. Ref. [15] established sufficient conditions for the existence of multiple equilibrium points of fractional-order competitive neural networks by using the concave-convex characteristics of activation functions. Compared with Ref. [15], the boundary value principle in this paper is simpler and easier to understand.
Theorem 2.
Assume condition (11) holds; then, is positively invariant.
Proof.
By means of reduction to absurdity, we suppose is not positively invariant. Then there exist such that escapes from . Therefore, there are two cases as follows,
Case A.
Case B.
From Case A, we can derive . From Case B, we can derive . However, for Case A,
where the definitions of are as follows,
It can be seen that inequality (14) is in contradiction with Case A. Similarly, for Case B,
where the definitions of are the same as Case A. Inequality (15) is in contradiction with Case B. Therefore, is positively invariant. □
Remark 2.
In Theorem 2, we have analyzed the invariant property of . This property means that initial states of system (1) in will not escape from , which is conducive to the discussion of the stability of the equilibrium point later.
Now, we will investigate the stability of multiple equilibrium points for system (1).
Theorem 3.
Proof.
Let be an arbitrary subregion located in . From Theorem 1 and Theorem 2, there exist an equilibrium point in . Let be the equilibrium point in , and . Suppose is an arbitrary neuron state in . Denote . Denote the following function,
where
Then
Similarly,
It follows from (17)–(20) that
Therefore,
where . According Lemma 1, we can derive that,
where is the unique positive solution of equation of . Denote From (21), we have
So,
It can be known from Definition 1 that is a locally exponentially state equilibrium point in the Lagrange sense. Therefore, there exist at least locally exponentially stable equilibrium points in the Lagrange sense for system (1). □
Remark 3.
According to Lemma 1 and Definition 1, Theorem 3 is derived. Equation (21) guarantees local exponential stability in the Lagrange sense of equilibrium points. In order to obtain Equation (21), it is necessary to assume that (16) holds. By defining functional and mathematical analysis, it is concluded that there exist at least locally exponentially stable equilibrium points in thes Lagrange sense for system (1).
Remark 4.
In this paper, we discuss the stability of equilibrium points in , which has subsets. Under conditions (11) and (16), it can be derived from Theorem 3 that the equilibrium points of these subsets are locally exponentially stable in theLagrange sense. Moreover, there are equilibrium points in . Due to the existence of the high dimension and the time delay for system (1), it is difficult to discuss the stability of equilibrium points in . We will discuss it further in follow-up research.
Remark 5.
Because a one-dimensional quaternion-valued neural network can be separated into four dynamic equations, under the same activation function, the one-dimensional quaternion-valued neural network, the two-dimensional complex-valued neural network, and the four-dimensional real-valued neural network have the same number of equilibrium points. That is to say, in the case of the same dimension, the quaternion-valued neural network has more stable equilibrium points than the complex-valued neural network [23] and the real-valued neural network [19]. The stable equilibrium points of the neural network are designed as the ideal patterns of pattern recognition, so a quaternion-valued neural network has larger storage capacity than the existing complex-valued neural network and the real-valued neural network in the same conditions.
Remark 6.
Unlike the application of pattern recognition based on a deep learning algorithm, the quaternion-valued neural network determines the weight of a neural network according to the sufficient conditions in the theorem. When the initial state of the neural network is in the invariant domain, the state of the neural network will converge to the equilibrium point corresponding to the invariant domain. The equilibrium point is designed as an ideal pattern in pattern recognition applications.
4. Simulation Results
In this section, we will give an example to verify the validity of the theoretical results. Consider the following one-dimensional quaternion-valued neural network,
where the activation function is defined as follows, , and
According to the correspondence of real parts and imaginary parts, system (22) can be transformed into four formulas,
According to the definition of (3)–(10), it can be concluded that, , . Let , then . Meanwhile, conditions (11) and (16) hold. That is to say, all conditions of Theorem 3 are satisfied. According to Theorem 3, system (22) has 16 locally exponentially stable equilibrium points in the Lagrange sense. In fact, we can verify the conclusion through simulation experiments. We simulate the running tracks of the neuron states of system (22) through the function of ode45 in Matlab software. The simulation results with 64 initial states show that system (22) has 16 locally exponentially stable equilibrium points, which are as follows,
The theoretical results are verified to be valid. Because the four-dimensional state cannot be displayed in the same figure, transient behaviors of states , , , and with 64 initial states are depicted in four separate figures. Please see Figure 1, Figure 2, Figure 3 and Figure 4. Because stable states of , , and are all located in [1.825, 2.425] and [−1.925, −1.325], the four figures look very similar. In fact, these 16 stable equilibrium points are different. It can be seen from Figure 1, Figure 2, Figure 3 and Figure 4 that each initial state converges exponentially to the stable equilibrium state. As a special case of asymptotic stability, exponential stability has a faster convergence rate.
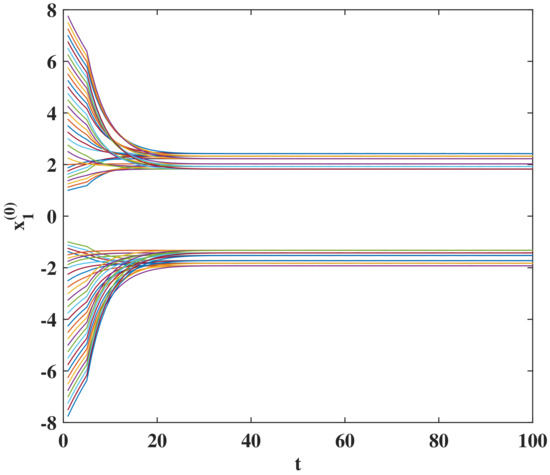
Figure 1.
Transient states of for system (22).
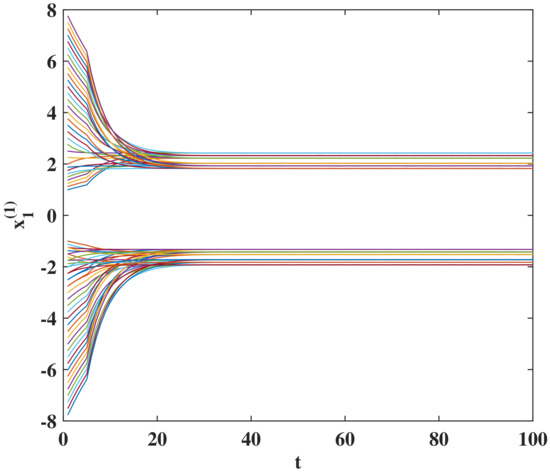
Figure 2.
Transient states of for system (22).
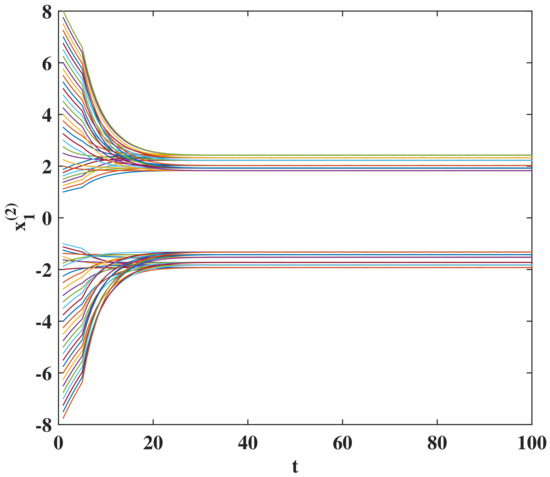
Figure 3.
Transient states of for system (22).
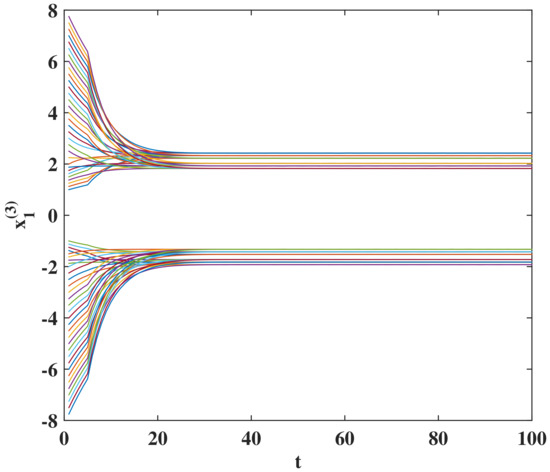
Figure 4.
Transient states of for system (22).
5. Conclusions
This paper has studied local Lagrange exponential stability of quaternion-valued neural networks with delays. By separating the quaternion-valued neural network into a real part and three imaginary parts, some sufficient conditions have been established to ensure that equilibrium points exist. By using Halanay inequality, the conditions have been established to ensure equilibria were local Lagrange exponentially stable. One example has been given to verify the validity of the theoretical results. Through analysis, it was shown that, under the same conditions, quaternion-valued neural networks have more stable equilibrium points than complex-valued neural networks and real-valued neural networks. That is, quaternion-valued neural networks have greater storage capacity in pattern-recognition applications.
Author Contributions
Conceptualization, W.D. and Y.H.; software, W.D. and T.C.; validation, W.D. and T.C.; project management, W.D. and H.L.; preparation of the original draft, W.D., Y.H. and T.C. visualization, W.D. and T.C.; methodology, Y.H. and H.L.; investigation, Y.H. and H.L.; revision, X.F. and H.L.; supervision, X.F. and H.L.; funding acquisition, X.F. and H.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (Grant No. 62106225), Natural Science Foundation of Zhejiang Province (Grant No. LY20F020024).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
Sincere thanks to everyone who suggested revisions and improved this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zheng, Y.; Sheng, W.; Sun, X.; Chen, S. Airline passenger profiling based on fuzzy deep machine learning. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 2911–2923. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Chen, S.; Xue, Y.; Xue, J. A Pythagorean-Type Fuzzy Deep Denoising Autoencoder for Industrial Accident Early Warning. IEEE Trans. Fuzzy Syst. 2017, 25, 1561–1575. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhou, X.; Sheng, W.; Xue, Y.; Chen, S. Generative adversarial network based telecom fraud detection at the receiving bank. Neural Netw. 2018, 102, 78–86. [Google Scholar] [CrossRef] [PubMed]
- Cao, J.; Wang, J. Global asymptotic stability of a general class of recurrent neural networks with time-varying delays. IEEE Trans. Circuits Syst. I 2003, 50, 34–44. [Google Scholar]
- Cao, J.; Wang, J. Global asymptotic stability of recurrent neural networks with multiple time-varying delays. IEEE Trans. Neural Netw. 2008, 19, 855–873. [Google Scholar]
- Zhang, H.; Liu, Z.; Huang, G.; Liu, Z.; Wang, Z. Novel weighting-delay-based stability criteria for recurrent neural networks with time-varying delay. IEEE Trans. Neural Netw. 2010, 21, 91–106. [Google Scholar] [CrossRef]
- Wu, A.; Zeng, Z. Exponential stabilization of memristive neural networks with time delays. IEEE Trans. Neural Netw. Learn. Syst. 2012, 12, 1919–1929. [Google Scholar]
- Wu, A.; Zeng, Z. Dynamic behaviors of memristor-based recurrent neural networks with time-varying delays. Neural Netw. 2012, 36, 1–10. [Google Scholar] [CrossRef]
- Wu, A.; Zeng, Z. Lagrange stability of memristive neural networks with discrete and distributed delays. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 690–703. [Google Scholar] [CrossRef]
- Wen, S.; Huang, T.; Yu, X.; Chen, M.; Zeng, Z. Aperiodic sampled-data sliding-mode control of fuzzy systems with communication delays via the event-triggered method. IEEE Trans. Fuzzy Syst. 2016, 24, 1048–1057. [Google Scholar] [CrossRef]
- Lakshmanan, S.; Prakash, M.; Lim, C.P.; Rakkiyappan, R.; Balasubramaniam, P.; Nahavandi, S. Synchronization of an inertial neural network with time-varying delays and its application to secure communication. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 195–207. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Guo, R.; Liu, X.; Lin, C. Lagrange Exponential Stability of Complex-Valued BAM Neural Networks with Time-Varying Delays. IEEE Trans. Syst. 2020, 50, 3072–3085. [Google Scholar] [CrossRef]
- Liu, P.; Zeng, Z.; Wang, J. Multistability of recurrent neural networks with nonmonotonic activation functions and mixed time delays. IEEE Trans. Syst. 2016, 46, 512–523. [Google Scholar] [CrossRef]
- Song, Q.; Chen, X. Multistability Analysis of Quaternion-Valued Neural Networks With Time Delays. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 5430–5440. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Zeng, Z. Multistability and Stabilization of Fractional-Order Competitive Neural Networks With Unbounded Time-Varying Delays. IEEE Trans. Neural Netw. Learn. Syst. 2021, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Huang, T.; Feng, D.; Zeng, Z. Multistability and robustness of complex-valued neural networks with delays and input perturbation. Neurocomputing 2021, 447, 319–328. [Google Scholar] [CrossRef]
- Zhang, F.; Huang, T.; Feng, D.; Zeng, Z. Multistability of delayed fractional-order competitive neural networks. Neural Netw. 2021, 140, 325–335. [Google Scholar] [CrossRef]
- Cheng, C.Y.; Lin, K.H.; Shih, C.W. Multistability and convergence in delayed neural networks. Phys. D Nonlin. Phenom. 2007, 225, 61–74. [Google Scholar] [CrossRef]
- Zeng, Z.; Huang, T.; Zheng, W. Multistability of recurrent neural networks with time-varying delays and the piecewise linear activation function. IEEE Trans. Neural Netw. 2010, 21, 1371–1377. [Google Scholar] [CrossRef]
- Wang, L.L.; Chen, T.P. Multistability of neural networks with Mexican-hat-type activation functions. IEEE Trans. Neural Netw. Learn. Syst. 2012, 23, 1816–1826. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, H.; Wang, Z. Multistability and multiperiodicity of delayed bidirectional associative memory neural networks with discontinuous activation functions. Appl. Math. Comput. 2012, 219, 899–910. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, H.; Wang, Z. Dynamical stability analysis of multiple equilibrium points in time-varying delayed recurrent neural networks with discontinuous activation functions. Neurocomputing 2012, 91, 21–28. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, H.; Wang, Z. Multistability of complex-valued recurrent neural networks with real-imaginary-type activation functions. Appl. Math. Comput. 2014, 229, 187–200. [Google Scholar] [CrossRef]
- Zhang, F.; Zeng, Z. Multiple ψ-Type Stability of Cohen-Grossberg Neural Networks With Both Time-Varying Discrete Delays and Distributed Delays. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 566–579. [Google Scholar] [CrossRef]
- Cai, Z.; Huang, L.; Zhang, L. Finite-time synchronization of master-slave neural networks with time-delays and discontinuous activations. Appl. Math. Model. 2017, 47, 208–226. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, Z.; Lin, C.; Chen, J. Fixed-time synchronization for complex-valued BAM neural networks with time-varying delays via pinning control and adaptive pinning control. Chaos Solitons Fractals 2021, 153, 111583. [Google Scholar] [CrossRef]
- Wei, X.; Zhang, Z.; Lin, C.; Chen, J. Synchronization and anti-synchronization for complex-valued inertial neural networks with time-varying delays. Appl. Math. Comput. 2021, 403, 126194. [Google Scholar] [CrossRef]
- Wei, R.; Cao, J.; Huang, C. Lagrange exponential stability of quaternion-valued memristive neural networks with time delays. Math. Methods Appl. Sci. 2020, 43, 7269–7291. [Google Scholar] [CrossRef]
- Xiao, J.; Cao, J.; Zhong, S.; Wen, S. Novel methods to finite-time Mittag-Leffler synchronization problem of fractional-order quaternion-valued neural networks. Inf. Sci. 2020, 526, 221–244. [Google Scholar] [CrossRef]
- Wu, Z. Multiple asymptotic stability of fractional-order quaternion-valued neural networks with time-varying delays. Neurocomputing 2021, 448, 301–312. [Google Scholar] [CrossRef]
- Udhayakumar, K.; Rakkiyappan, R.; Liu, X.; Cao, J. Mutiple psi-type stability of fractional-order quaternion-valued neural networks. Appl. Math. Comput. 2021, 401, 126092. [Google Scholar]
- Gopalsamy, K. Stability and Oscillations in Delay Differential Equations of Population Dynamics; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1992. [Google Scholar]
- Cao, J.; Wang, J. Absolute exponential stability of recurrent neural networks with Lipschitz-continuous activation functions and time delays. Neural Netw. 2004, 17, 379–390. [Google Scholar] [CrossRef]
- Liao, X.; Luo, Q.; Zeng, Z.; Guo, Y. Global exponential stability in Lagrange sense for recurrent neural networks with time delays. Nonlinear Anal. Real World Appl. 2008, 9, 1535–1557. [Google Scholar] [CrossRef]
- Aladdin, A.M.; Rashid, T.A. A New Lagrangian Problem Crossover: A Systematic Review and Meta-Analysis of Crossover Standards. arXiv 2022, arXiv:2204.10890. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).