Abstract
This paper explores statistical inferences when the lifetime of product follows the inverse Nakagami distribution using progressive Type-II censored data. Likelihood-based and maximum product of spacing (MPS)-based methods are considered for estimating the parameters of the model. In addition, approximate confidence intervals are constructed via the asymptotic theory using both likelihood and product spacing functions. Based on traditional likelihood and the product of spacing functions, Bayesian estimates are also considered under a squared error loss function using non-informative priors, and Gibbs sampling based on the MCMC algorithm is proposed to approximate the Bayes estimates, where the highest posterior density credible intervals of the parameters are obtained. Numerical studies are presented to compare the proposed estimators using Monte Carlo simulations. To demonstrate the proposed methodology in a real-life scenario, a well-known data set on agricultural machine elevators with high defect rates is also analyzed for illustration.
Keywords:
inverse Nakagami model; progressively censored data; maximum likelihood estimation; maximum product of spacing approach; Bayesian inference MSC:
62F10; 62F15
1. Introduction
Due to non availability of information/data, experiments are often conducted with censoring schemes where the testing is ceased before the failure of all units. Generally speaking, censoring means that there is only a portion of exact failure times of observed units are known under studies. Two common censoring schemes are Type-I censoring and Type-II censoring. In Type-I censoring, the test is terminated at a predetermined time, whereas in Type-II censoring experiment stops at a predetermined number of failures. However, such conventional censoring schemes sometimes may take a longer time due to the product characteristic of being highly reliable with a long lifetime.
Therefore, in order to find a more efficient way to collect failure information in lifetime studies, many other censoring schemes have been proposed, and progressive Type-II censoring is the most popular in practice. In this scheme, the detailed scenarios can be described as follows. Suppose that n independent identical components are placed in a life test, and only m(≤n) failures are observed with a prefixed censoring scheme . When the first failure time, say , has occurred, survival components are randomly removed from the test.
When the second failure time, say , has occurred, survival components are randomly removed from the test. Following a similar procedure until the mth failure, say , has occurred, the remaining survival components are removed from the test, and the experiment stops. Therefore, are called progressive Type-II censored samples with the censored scheme . It is noted that and that many censoring schemes are its special cases, including Type-II censoring and the complete sample.
The conventional Type-I censoring, Type-II censoring and various progressive censoring scenarios have been extensively implemented and discussed in wide practical situations. See, for example, some recent works of Ducros and Pamphile [1], Zhao et al. [2], Jia [3], Kohansal and Shoaee [4], Mahto et al. [5], Luo et al. [6], Han and Kundu [7] and the references therein. For more details about conventional and progressive censoring schemes, one may refer to the monographs of Lawless [8], Balakrishnan and Aggarwala [9].
Let be a progressive Type-II censored data with censoring scheme from the population with cumulative distribution function (CDF) and probability density function (PDF) , then the joint density function can be written as
with being regular constants.
The Nakagami distribution is a well-known model in communications engineering, medical image processing, hydrologic engineering and seismological analysis (see, e.g., Wang et al. [10], Tsui et al. [11], Sarkar [12], Nakahara and Carcole [13]). As an extension and application of existing lifetime models, the corresponding inverse distributions have provided a potential comprehension of common models in data fitting (see, Basheer [14], Punzo [15], Ghitany et al. [16]). The inverse Nakagami distribution (IND) was introduced by Louzada [17] as an extension of the Nakagami distribution proposed by Nakagami [18]. A random variable X is said to have IND with the CDF
and the PDF as expressed as follows
where is the complete gamma function.
In statistical inference, the maximum product of spacing estimation (MPS) technique was initially proposed by Cheng and Amin [19] and then further discussed by Ranneby [20] where the MPS method is treated as an alternative approach to traditional maximum likelihood estimation (MLE) for inferential studies. Recently, the MPS technique has attracted great attention in data analysis due to its potential advantage over the classical ML procedure. For instance, Singh et al. [21,22], Shao [23], El-Sherpieny et al. [24], Volovskiy and Kamps [25], Kawanishi [26] have discussed the MPS method under various data types when the lifetime distributions were the Weibull, power Lomax, generalized inverted exponential, generalized power Weibull, Lindley and generalized Rayleigh models, respectively. Anatolyev and Kosenok [27] studied the invariance property of the MPS and stated that the MPSEs have more efficient properties than the MLEs for skewed distributions or in small sample cases for heavy-tailed distributions.
Due to the IND’s importance and practicability, our aim in this paper is to develop an estimation procedure for IND parameters when progressive Type-II censored data is available. The MLEs and maximum product spacing estimates (MPSEs) as well as the approximate confidence intervals (ACIs) for both cases are obtained. In addition, Bayesian point and interval estimates are obtained based on likelihood functions from MLE and MPSE scenarios, respectively. As far as we know, no attempt has been made on estimation of IND parameters based on progressive Type-II censored data using the considered methods of estimation.
The rest of article is organized as follows. Classical likelihood based estimations, including MLE and ACI, are discussed in Section 2. Section 3 presented parameter estimation as well as ACI using the MPS technique. Bayesian inference is proposed in Section 4 based on likelihood and maximum product spacing functions, respectively, and associated Monte Carlo algorithms are proposed for complex posterior computation. Simulation studies and a real data example are presented in Section 5 for illustration. Our concluding remarks are presented in Section 6.
2. Classical Likelihood Estimation
In this section, the MLEs and ACIs of the parameters and are obtained based on the classical likelihood function.
Suppose are progressive Type-II censored variables from IND with censoring scheme , the likelihood function can be written from (1)–(3) as
where is the lower incomplete gamma function. Ignoring the constant term, the log-likelihood function of and is given by
2.1. Point Estimation Based on MLE Approach
Upon differentiating (5) with respect to and , the MLEs of and can be obtained from the following equations
where is the digamma function, and
It is noted that there are no closed forms for the MLEs and of and ; thus, numerical techniques, such as the Newton–Raphson method, could be implemented for computation.
2.2. ACIs Based on MLEs
The second derivatives of can be obtained directly as follows
and
where is the trigamma function, and
The approximate asymptotic variance–covariance matrix of the MLEs and can be obtained through the inverse of the observed Fisher information matrix as
Under mild regularity conditions, the asymptotic distribution of the MLE is known that . Thus, for arbitrary , the ACIs of the parameters and can be obtained as follows
where is the upper th percentile point of the standard normal distribution.
3. Maximum Product of Spacing Estimation
In this section, MPSEs are constructed for the IND parameters and under progressively censored data.
3.1. Point Estimation Based on MPS Approach
Following Ng et al. [28], the product spacings under the progressive Type-II censoring scheme can be constructed as
with
where with being the parameter vector of the lifetime distribution of the considered population. Therefore, for the progressively Type-II censored data from IND (2), the MPS function can be expressed as follows
and the associated logarithm of MPS function can be written as
By taking derivaties of (9), the MPSEs of and can be obtained from following non-linear equations, such as
where and
Similarly, the MPSEs and could be also obtained by using a numerical approach.
3.2. ACIs Based on MPSEs
In this subsection, the ACIs are constructed for the model parameters and based on MPSEs.
Following similar line as conventional ACIs in Section 2.2, the asymptotic variance–covariance matrix of and under MPS scenario can be written as
Therefore, based on the asymptotic properties of the MPSEs as in the case of the MLEs, it follows that . Therefore, the ACIs of and are given, respectively, by
4. Bayesian Inference
Modern products may exhibit high reliable and long life-cycles, which sometimes yield limited availability of data in lifetime experiments where a limited sample size may heavily affect the accuracy of the inferential results. Therefore, the Bayesian inference is provided as an alternative to the traditional likelihood method due to its ability to integrate extra information into the inferential approach.
In this section, Bayesian inference is discussed for the unknown parameters based on the conventional likelihood function and MSP function, respectively. In this paper, an objective prior is considered for as follows (see Louzada et al. [17])
4.1. Posterior Density Using the Likelihood Function
Based on the traditional likelihood function (5), the posterior density of and can be written as
For an arbitrary function of parameters and , the Bayes estimator under squared error loss function is given by
Clearly, the corresponding Bayes estimator of is expressed as the ratio of two integrals, which does not have a specific form. To solve that problem, we utilize the MCMC method to obtain the Bayesian point estimates and the highest posterior density (HPD) credible intervals.
From the joint posterior density function (13), the conditional posterior distributions of and can be expressed, respectively, as
and
Since the conditional posterior distribution of and cannot be reduced analytically to some well-known distributions, therefore, in order to find the Bayes estimates, the Gibbs sampling based on MCMC algorithm is used to generate random samples from these posterior distributions. The following Algorithm 1 is provided below.
| Algorithm 1: Bayesian estimation via Gibbs sampling. |
|
4.2. Posterior Density Using Maximum Product Spacing Function
Similarly, based on the MPS function (8), the MPS-based posterior density function of and is given by
and the MPS-based conditional posterior distributions of and , respectively, are
and
Further, following the similar line as Algorithm 1, the MPS-based Bayesian point and interval estimates could be obtained for arbitrary parameter ; the details are omitted here to save space.
5. Numerical Analysis
5.1. Simulation Studies
In this section, extensive simulation studies are conducted for investigating the performance of the proposed methods. For comparing the accuracy of different results, the performance of different point and interval estimates are evaluated based on the following criteria quantities:
- (a)
- The mean square error (MSE) for point estimate of and , respectively, computed by .
- (b)
- The average bias (AB) for point estimate defined by .
- (c)
- The average width (AW) of intervals of .
Moreover, for different sample size , following types of censoring scheme (CSs) are considered in this part as
- CS I:
- and ;
- CS II:
- and ;
- CS III:
Since the closed form of the inverse function of IND CDF does not exist, to generate the progressively Type-II censored data from IND, one could use the principle of progressive Type-II censoring scheme and the variable transformation, the manner proposed by Louzada et al. [17] and Balakrishnan and Kundu [29]. For different choices of sample sizes and the values of the parameters , the numerical analysis are conducted based on 1000 repeats.
In addition, the simulation work was conducted in R software where the maximum likelihood and maximum product of spacing estimates are obtained by using the global optimization search algorithm in R software, and interested readers can ask for the program on request. All the results of the criteria quantities are listed in Table 1, Table 2, Table 3 and Table 4, where significance level for all interval estimates. Moreover, for Bayesian estimation, the Gibbs sampling size N is taken to be 10,000 with a burn-in time of 5000. In addition, for showing the performance of different results in a visual representation, the associated numerical results are shown in Figure 1 and Figure 2.

Table 1.
The ABs and MSEs (within bracket) for the model parameters at .

Table 2.
The AWs for the model parameters at .

Table 3.
The ABs and MSEs (within bracket) for the model parameters at .

Table 4.
The AWs for the model parameters at .
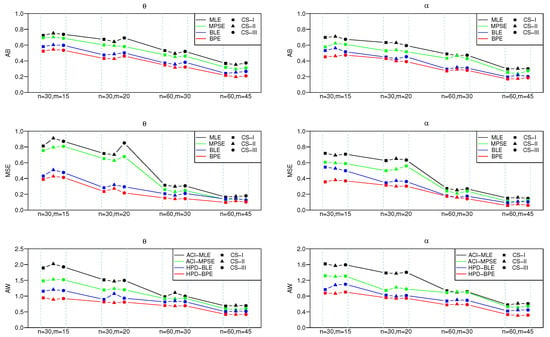
Figure 1.
Plots of AB, MSE and AW for the model parameters at .
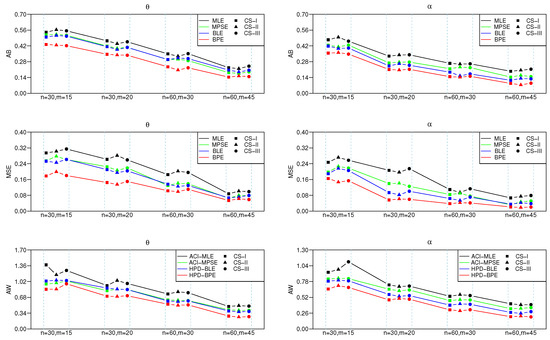
Figure 2.
Plots of AB, MSE and AW for the model parameters at .
- As the effective sample size n or m or their combination increases, ABs and MSEs of the MLEs and MPSEs as well as Bayesian estimates become smaller, which indicates the consistency property of the proposed estimates.
- Under fixed schemes, MPSEs outperform the method of MLEs in terms of ABs and MSEs. A similar phenomenon also appears for the MPSE using the Bayesian method, and these are superior to traditional MLE under various CSs I, II and III, respectively.
- The Bayesian estimates perform better as compared to the method of MLE in terms of the criteria quantities in general.
- The AWs of all likelihood and MPSE-based ACIs and the Bayesian HPD credible intervals decrease when the effective sample sizes increase.
- The MPSE-based ACIs perform better comparing with traditional likelihood-based ACIs; whereas similar superiority also appeared between Bayes HPD credible interval estimates based on likelihood and MPS functions in terms of AW.
- The AW of the intervals obtained from the Bayesian approach are generally shorter than those of the ACIs.
To sum up, from the listed simulation results, the efficiency of the MPS method is superior to traditional likelihood-based point and interval estimates under classical and Bayesian analysis, respectively. This further indicates that the MPSEs provide potential good alternatives to likelihood estimation under progressive censoring when the latent lifetime of items follows IND.
5.2. Real Life Example
To demonstrate the adaptability of the proposed methodologies to real phenomena, in this section, we re-analyze one real data set presented in Table 5 related to agricultural machine elevators showing high defect rates after a short repair time, which compromises the cost of production. For this data set, Louzada et al. [17] illustrated that compared with traditional Weibull, Gamma and log-normal distributions, the IND provides a best fit in terms of various goodness-of-fit criteria quantities with MLEs and under complete data.

Table 5.
Complete agricultural data of machine motors.
From the complete real data from Table 5, two sets of progressively Type-II censored data are provided in Table 6 with traditional Type-II scenarios. The associated point and interval estimates are listed in Table 7 with the significance level for interval estimates. The bias between the point estimates and the MLEs of and obtained under complete samples are also provided and are shown in square brackets in Table 7.

Table 6.
Progressively Type-II censored samples from agricultural machine motor data.

Table 7.
Point and interval estimates of and under real-world data.
From the tabulated results in Table 7, it is observed the MLE and MPSE performed similar in terms of the bias, and the Bayes results appear similar under the data sets (i) and (ii). Further, if we consider the corresponding estimated CDFs, respectively, via all the estimated results, it is also noted that they match quite well under each data cases; see Figure 3 for illustration.
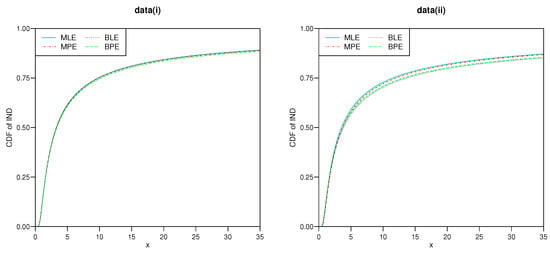
Figure 3.
Plots of CDF of the IND using different estimates under data sets (i) and (ii).
In addition, the complicated forms of the traditional and MPS likelihood equations make them difficult to establish the existence and uniqueness of the associated MLEs and MPSEs. However, with modern computing technology, two variables could be solved numerically. For illustration, the contour maps of are presented in Figure 4 and Figure 5 for the likelihood and MPS likelihood functions, respectively.
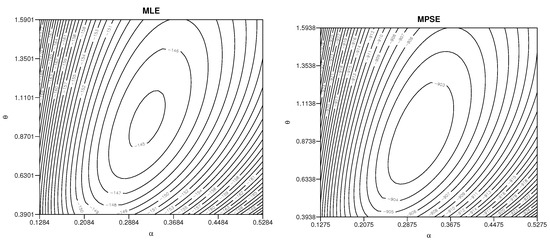
Figure 4.
Contour plots of and using the likelihood function (left) and MPE function (right) based on data set (i).
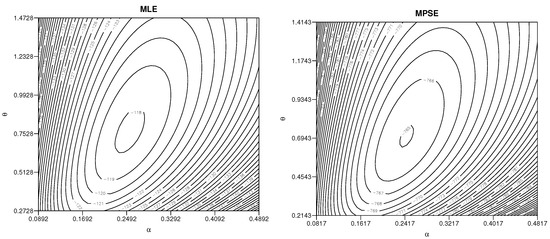
Figure 5.
Contour plots of and using the likelihood function (left) and MPE function (right) based on data set (ii).
In addition, for the Bayesian MCMC approach, trace plots with their sample mean and credible intervals and corresponding histograms of the associated chain values for and are listed in Figure 6, Figure 7, Figure 8 and Figure 9 based on the data sets (i) and (ii), respectively. The plots indicate good mixing performance.
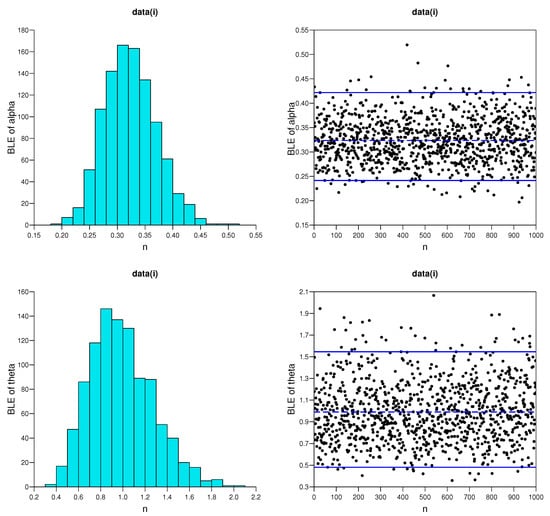
Figure 6.
Trace plots (the posterior mean (dashed line) with credible intervals (solid lines)) and corresponding histograms of BLEs of and for data set I.
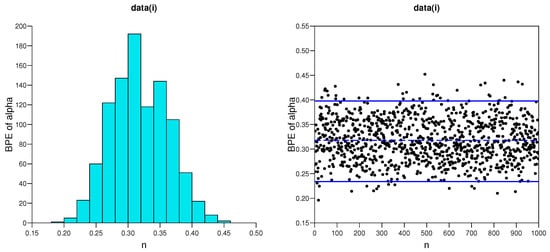
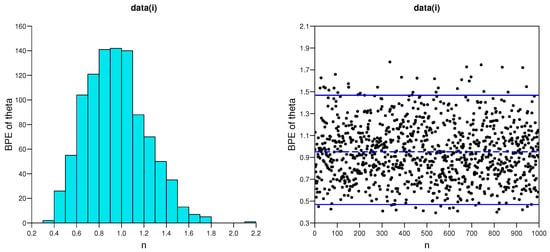
Figure 7.
Trace plots (the posterior mean (dashed line) with credible intervals (solid lines)) and corresponding histograms of BPEs of and for data set I.
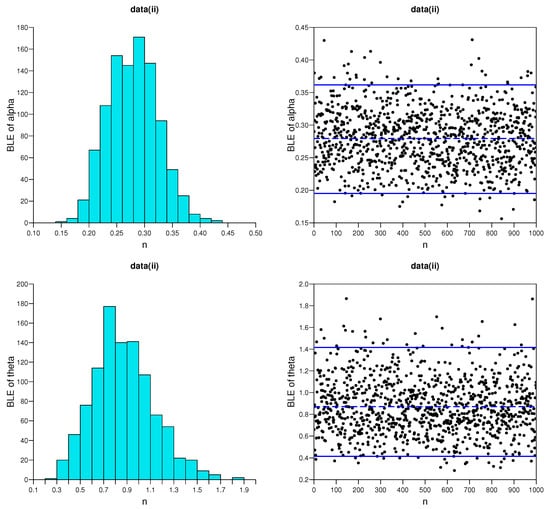
Figure 8.
Trace plots (the posterior mean (dashed line) with credible intervals (solid lines)) and corresponding histograms of BLEs of and for data set II.
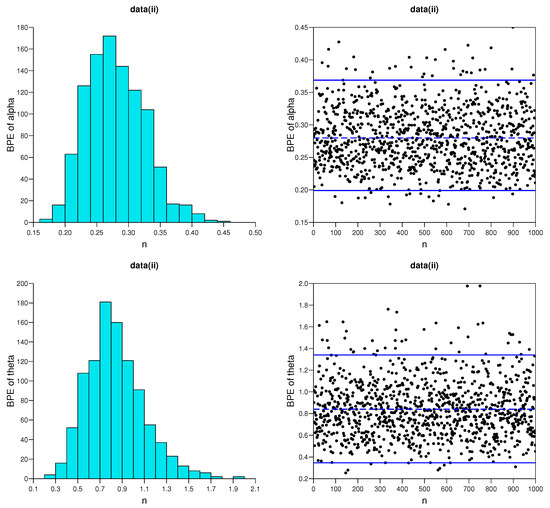
Figure 9.
Trace plots (the posterior mean (dashed line) with credible intervals (solid lines)) and corresponding histograms of BPEs of and for data set II.
6. Conclusions
In this paper, we discussed statistical inference of the inverse Nakagami distribution when the failure times are progressively censored. In addition, the traditional maximum likelihood estimation and MPS approaches were introduced for the IND parameters. Extensive simulations and real-world examples were performed to investigate the performance of different methods. The numerical results demonstrated that the MPS method outperformed the ML method in terms of the criteria quantities under both classical and Bayesian perspectives. We concluded that the MPSEs provide a reasonable alternative for estimating IND parameters compared with the usual likelihood approach. Due to the scenario of the MPS method, although the inferential work was discussed for IND progressively censored data, the work could be extended to other types of censoring schemes, such as Type-I censoring, Type-II censoring and progressive (hybrid) censoring as well as interval censoring, which will be explored in the future.
Author Contributions
Data curation, S.D.; Formal analysis, L.W.; Methodology, Y.M.T. All authors equally contributed in writing this manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Natural Science Foundation of China (No. 12061091), the Yunnan Fundamental Research Projects (No. 202101AT070103) and the Doctoral Research Foundation of Yunnan Normal University (No. 00800205020503129).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank reviewers for their valuable comments and suggestions, which improved this paper significantly.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ducros, F.; Pamphile, P. Bayesian estimation of Weibull mixture in heavily censored data setting. Reliab. Eng. Syst. Saf. 2018, 180, 453–462. [Google Scholar] [CrossRef] [Green Version]
- Zhao, H.; Wu, Q.; Li, G.; Sun, J. Simultaneous Estimation and Variable Selection for Interval-Censored Data with Broken Adaptive Ridge Regression. J. Am. Stat. Assoc. 2020, 115, 204–216. [Google Scholar] [CrossRef]
- Jia, X. Reliability analysis for Weibull distribution with homogeneous heavily censored data based on Bayesian and least-squares methods. Appl. Math. Modell. 2020, 83, 169–188. [Google Scholar] [CrossRef]
- Kohansal, A.; Shoaee, S. Bayesian and classical estimation of reliability in a multicomponent stress-strength model under adaptive hybrid progressive censored data. Stat. Pap. 2021, 62, 309–359. [Google Scholar] [CrossRef]
- Mahto, A.K.; Tripathi, Y.M.; Wu, S.-J. Statistical inference based on progressively type-II censored data from the Burr X distribution under progressive-stress accelerated life test. J. Stat. Comput. Sim. 2021, 19, 368–382. [Google Scholar] [CrossRef]
- Luo, C.; Shen, L.; Xu, A. Modelling and estimation of system reliability under dynamic operating environments and life ordering constraints. Reliab. Eng. Syst. Saf. 2022, 218, 108136. [Google Scholar] [CrossRef]
- Han, D.; Kundu, D. Inference for a step-stress model with competing risks for failure from the generalized exponential distribution under type-I censoring. IEEE Trans. Reliab. 2015, 64, 31–43. [Google Scholar] [CrossRef]
- Lawless, J.L. Statistical Models and Methods for Life Time Data, 2nd ed.; Wiley: New York, NY, USA, 2003. [Google Scholar]
- Balakrishnan, N.; Aggarwala, R. Progressive Censoring: Theory, Methods, and Applications; Berkhauser: Boston, MA, USA, 2000. [Google Scholar]
- Wang, N.; Song, X.; Cheng, J. Generalized method of moments estimation of the Nakagami-m fading parameter. IEEE Trans. Wire Commun. 2012, 11, 3316–3325. [Google Scholar] [CrossRef]
- Tsui, P.; Huang, C.; Wang, S. Use of Nakagami distribution and logarithmic compression in ultrasonic tissue characterization. J. Med. Biol. Eng. 2006, 26, 69–73. [Google Scholar]
- Sarkar, S.; Goel, N.; Mathur, B. Performance investigation of Nakagami-m distribution to derive flood hydrograph by genetic algorithm optimization approach. J. Hydrol. Eng. 2010, 15, 658–666. [Google Scholar] [CrossRef]
- Nakahara, H.; Carcole, E. Maximum-likelihood method for estimating Coda Q and the Nakagami-m parameter. Bull. Seismol. Soc. Amer. 2010, 100, 3174–3182. [Google Scholar] [CrossRef]
- Basheer, A.M. Alpha power inverse Weibull distribution with reliability application. J. Taibah. Uni. Sci. 2019, 13, 423–432. [Google Scholar] [CrossRef] [Green Version]
- Punzo, A. A new look at the inverse Gaussian distribution with applications to insurance and economic data. J. Appl. Stat. 2019, 46, 1260–1287. [Google Scholar] [CrossRef]
- Ghitany, M.E.; Mazucheli, J.; Menezes, A.F.B.; Alqallaf, F. The unit-inverse Gaussian distribution: A new alternative to two-parameter distributions on the unit interval. Commun. Stat. Theory M 2019, 48, 3423–3438. [Google Scholar] [CrossRef]
- Louzada, F.; Ramos, P.L.; Nascimento, D. The Inverse Nakagami-m Distribution: A Novel Approach in Reliability. IEEE Trans. Reliab. 2018, 67, 1030–1042. [Google Scholar] [CrossRef]
- Nakagami, N. The m-distribution a general formulation of intensity distribution of rapid fading. In Statistical Methods in Radio Wave Propagation; Pergamon: New York, NY, USA, 1960; pp. 3–36. [Google Scholar]
- Cheng, R.C.H.; Amin, N.A.K. Estimating parameters in continuous univariate distributions with a shifted origin. J. R. Stat. Soc. Ser. B 1983, 45, 394–403. [Google Scholar] [CrossRef]
- Ranneby, B. The maximum spacing method. An estimation method related to the maximum likelihood method. Scand J. Stat. 1984, 9, 103–112. [Google Scholar]
- Singh, R.K.; Singh, S.K.; Singh, U. Maximum product spacings method for the estimation of parameters of generalized inverted exponential distribution under Progressive Type II Censoring. J. Stat. Manag. Sys. 2016, 19, 219–245. [Google Scholar]
- Singh, R.K.; Singh, S.K.; Singh, R.K. A Comparative Study of Traditional Estimation Methods and Maximum Product Spacings Method in Generalized Inverted Exponential Distribution. J. Stat. Appl. Prob. 2014, 3, 153–169. [Google Scholar] [CrossRef]
- Shao, Y. Consistency of the maximum product of spacings method and estimation of a unimodal distribution. Stat. Sin. 2001, 11, 1125–1140. [Google Scholar]
- El-Sherpieny, E.A.; Almetwally, E.M.; Muhammed, H.Z. Progressive Type-II hybrid censored schemes based on maximum product spacing with application to Power Lomax distribution. Phys. A 2020, 553, 124251. [Google Scholar] [CrossRef]
- Volovskiy, G.; Kamps, U. Maximum product of spacings prediction of future record values. Metrika 2020, 83, 853–868. [Google Scholar] [CrossRef] [Green Version]
- Kawanishi, T. Maximum likelihood and the maximum product of spacings from the viewpoint of the method of weighted residuals. Comput. Appl. Math. 2020, 156, 1–18. [Google Scholar] [CrossRef]
- Anatolyev, S.; Kosenok, G. An alternative to maximum likelihood based on spacings. Econ. Theory 2005, 21, 472–476. [Google Scholar] [CrossRef] [Green Version]
- Ng, H.K.T.; Luo, L.; Hu, Y.; Duan, F. Parameter estimation of three parameter Weibull distribution based on progressively Type-II censored samples. J. Stat. Comput. Sim. 2012, 82, 1661–1678. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Kundu, D. A simple simulational algorithm for generating progressive Type-II censored samples. Am. Stat. 1995, 49, 229–230. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).