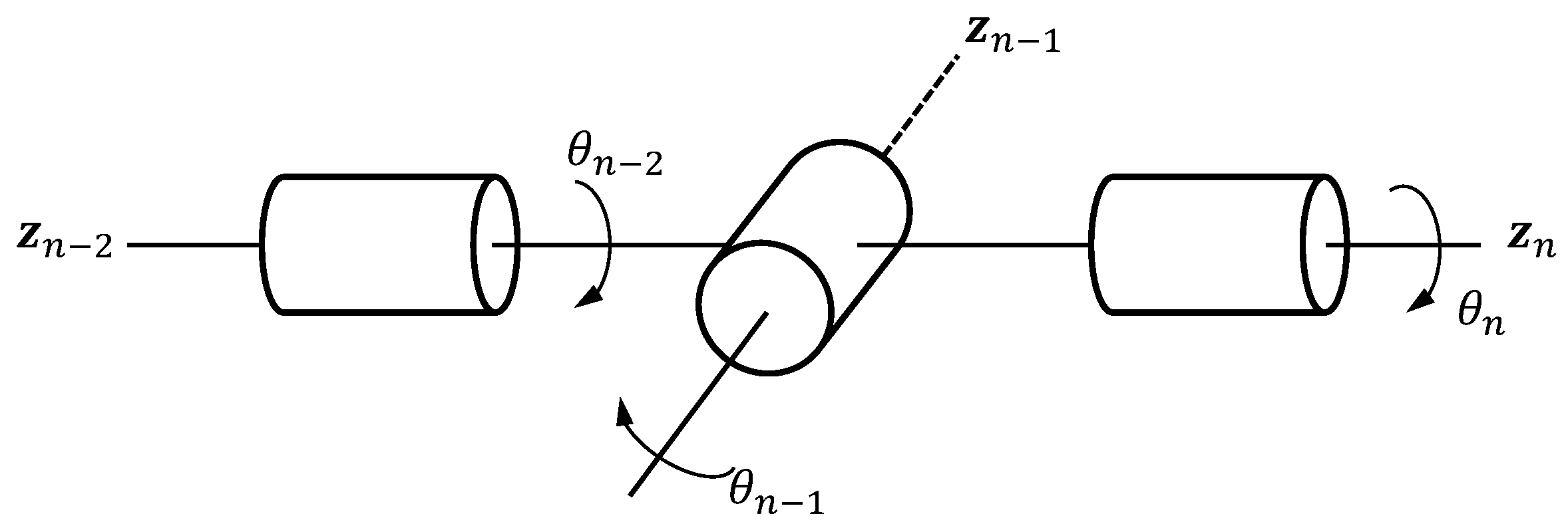1. Introduction
A serial robot manipulator is an open kinematic chain made up of a sequence of rigid bodies, called links, connected by means of actuated kinematic pairs, called joints, that provide relative motion between consecutive links. At the end of the last link, there is a tool or device known as the end-effector. Only two types of joints are considered throughout this work: revolute joints, which only perform rotations, and prismatic joints, which only perform translations. If joint i is revolute (prismatic), the amount it rotates (translates) is encoded by an angle (a displacement ). These scalars are known as the joint variables of the robot.
From a kinematic point of view, the end-effector position and orientation (also known as the pose) can be expressed as a differentiable function , where denotes the space of joint variables, called the configuration space of the robot, and X is the space of all positions and orientations of the end-effector with respect to a reference frame, which is usually called the operational space. A serial robot is said to have n degrees of freedom (DoF) if its configuration can be minimally specified by n variables. For a serial robot, the number and nature of the joints determine the number of the DoF. For the task of positioning and orientating its end-effector in the three-dimensional space, the manipulators with more than six DoF are called redundant while the rest are non-redundant.
In order to describe its relative position and orientation, a frame
is attached to each joint (
Figure 1). The relations between consecutive joint frames are conventionally described by homogeneous transformation matrices. In particular,
relates frame
to frame
(the first joint frame is related to a fixed reference frame, known as the world frame). Therefore, the end-effector pose
of a robot with
n DoF with respect to the world frame can be represented as:
with
where
R is a rotation matrix that describes the end-effector orientation with respect to the world frame, while
is a position vector describing the end-effector position with respect to the world frame. This description is equivalent to the one provided by
f, known as the kinematic function of the serial robot. Thus,
, where
denotes the vector describing the end-effector pose and
denotes the vector whose components are the joint variables, also known as the configuration of the robot. Clearly, either
if joint
i is revolute or
if joint
i is prismatic.
Deriving the kinematic relation defined by
f with respect to time, we obtain another relation:
where
denotes the end-effector velocity vector,
; the vector of the joint velocities; and
J, the Jacobian matrix of
f. If
, then each column
can also be computed as:
Definition 1. Given a serial robot with n DoF, a singularity or kinematic singularity is a configuration satisfying , where denotes the rank of the matrix argument. The set of all singular configurations is a subset of that is usually denoted by and known as the singular set.
Using the relation (
3), it is easy to see that if
is a singularity of a given serial robot, then the following two statements hold:
The robot loses at least one degree of freedom or, equivalently, its end-effector cannot be translated along or rotated around at least one Cartesian direction.
Finite linear and angular velocities of the end-effector may require infinite joint velocities.
In addition, Gottlieb [
1] and Hollerbach [
2] have independently proven that any serial manipulator with
DoF has singularities. The identification of such singularities is achieved by solving the following non-linear equation:
if the robot is non-redundant and
if it is redundant.
In general, if the serial robot possesses at least one revolute joint, several coefficients of the Jacobian matrix are non-linear expressions, and thus, neither Equation (
5) nor Equation (
6) are easy to formulate and solve. However, for manipulators with a spherical wrist, a simplification can be made. For these robots, the axes of their last three joints intersect at a common point, known as the wrist center point, or are parallel (the intersection point and, hence, the wrist center point, is the point at the infinity). Since the origin of the frame attached to the end-effector can be placed at the wrist center point, a zero block appears in
by definition (see Equation (
4)). Hence:
where
are blocks of order
,
is a block of order
and 0 denotes a block of order
, whose entries are all zero. Now, Equation (
5) is simplified to:
from which the singularities can be obtained as solutions of either
or
. These two equations allow us to decouple the singularities into position and orientation singularities as follows:
Similarly, we can make the same decoupling for redundant robots:
Remark 1. The Jacobian matrix is represented with respect to the world frame (usually located at the base of the robot). However, sometimes it is useful to represent in a different frame . To do so, the following identity is used: where:with and where denotes the rotation matrix that relates the orientation of with respect to the orientation of the world frame. Singularity identification is one of the fundamental research fields in robot kinematics since, as stated before, it affects the motion of the robot and its performance when executing different tasks. Therefore, such identification is fundamental to enhancing the performance of current control and motion planning strategies by designing approaches to handle them. For instance, current applications of the subject include the handling of singularities for a robust control architecture in human–robot collaboration [
3], the planning of singularity-free trajectories [
4,
5] and the smooth trajectory generation for rotating extensible manipulators or painting robots [
6,
7]. However, such identification is still problematic. The majority of the current approaches are based on the computation of either
or
or on the manipulation of the singular values of
[
8,
9,
10]; hence, they are not computationally efficient. In addition, there is no efficient way of computing how close an arbitrary configuration is to a given singularity (which is fundamental for defining a threshold from where the strategies to handle them start to work). In this context, geometric algebra turns out to be very useful. In addition, it is currently applied to several problems in robot kinematics and geometry [
11,
12,
13,
14,
15].
There is not much literature regarding the identification of singularities using geometric algebra, and the majority of the contributions focus on parallel mechanisms. For serial robots, Corrochano & Sobczyk [
16] extend the Lie bracket of two vectors defined in any Lie algebra to what they call the superbracket of the lines
,
, where the line
denotes the axis of joint
i. For serial robots with six DoF, the main idea is to split the superbracket into smaller superbrackets, called bracket monomials, that are equated to zero. The singularities are the solutions of these monomial bracket equations. Following the same idea, Kanaan et al. [
17] define the superbracket in a Grassmann–Caley algebra. Since the Lie bracket is well defined in every Grassmann–Caley algebra, the superbracket is also well defined. However, splitting the superbracket into the bracket monomials in this context is not intuitive and, as a consequence, is not always realizable. In addition, there is no standard procedure for computing these brackets’ monomials.
For parallel mechanisms, the majority of works [
18,
19,
20,
21,
22] focus on approaches developed for some particular parallel robots. The main idea consists of computing, for each leg of the mechanism, the exterior product of the twists defined by its joints and equating it to zero. For those legs with less than six actuated joints, combinations of two, three or more legs are considered. The main problem with these approaches is their lack of generalisability. Each approach is designed for the specific parallel robot the authors work with.
Huo et al. [
23] present a mobility analysis applying conformal geometric algebra and a singularity analysis using an idea similar to the ones presented in the above-mentioned contributions. A mobility analysis of overconstrained parallel mechanisms is performed using Grassmann–Cayley algebra by Chai et al. [
24], while Yang and Li [
25] propose a novel identification method for the constraint singularities of parallel robots based on differential manifolds. Finally, Kim et al. [
26] apply conformal geometric algebra to the identification of the singularities of a particular type of parallel manipulator, the SPS-parallel manipulator. Several lines and planes are defined using the different joint axes. Then, the relative positions of different combinations of these geometric entities are studied to geometrically find the singularities. However, this method cannot be extended to other classes of parallel or serial robots, nor can it be implemented as an algorithm due to its complex geometrical nature.
In this paper, a novel approach for singularity identification based on the six-dimensional and three-dimensional geometric algebras is introduced. It extends the works developed for parallel robots and reviewed above. In particular, one of the novelties of this method is that it can be applied to both redundant and non-redundant serial robots of any geometry. We first model the twists defined by the joint axes as vectors of the six-dimensional geometric algebra. Then, we manipulate the exterior product of these twists. In addition, this method can be simplified for serial robots with a spherical wrist using, instead of the six-dimensional geometric algebra
, the three-dimensional geometric algebra
. Once the singularities have been identified and since rotors describe the transformations between arbitrary multivectors in geometric algebra, a distance function
D can be defined in the configuration space
that can be used to determine the distance of any arbitrary configuration
to a given singularity
. This is the first time, to the best of the authors’ knowledge, that such a distance function has been defined. It is well-known that there are several indices that can be used to check whether a given configuration is close to a singularity or not. For instance, the Jacobian matrix
allows us to define the manipulability index
as:
where
are the singular values of
. Alternatively, we can also define the condition number of
,
. Clearly, the former is close to zero when the configuration is close to a singularity, while the value of the latter increases as the robot approaches to a singular configuration. Although there are several approaches based on the use of such indices [
27,
28], none of them define a distance function, and as stated in [
29], they do not provide a realistic measure of how close a singularity is, only whether it is close or not. On the other hand, Yao et al. [
30] propose a different index of closeness to singularities for planar parallel robots based on the volume of the workspace. Although interesting, it is still not a distance function, and it cannot be easily applied to serial robots. Similarly, Nawratil [
31] defines a distance function for parallel manipulators of the Stewart–Gough type. However, it measures how close a given pose of the end-effector is to a singular pose (i.e., the pose associated with a singular configuration). Hence, such a distance function is not defined in the configuration space
but in the operational space
X. Finally, Bu [
32] defines an angle between the velocity vector associated with one of the joints and the manifold generated by the others. Again, such an angle acts as a measure of closeness but not as a distance function, and thus, it does not provide a realistic measure of how close a singularity is.
The rest of the paper is organized as follows:
Section 2 presents an overview of geometric algebra that will be useful for understanding the proposed contribution. In
Section 3, the novel singularity identification approach and the simplification for serial robots with a spherical wrist are fully developed, while the novel distance function is constructed in
Section 4. The application of these results to the Kuka LWR 4+, a redundant serial robot with a spherical wrist, is given in
Section 5.
Section 6 lists three different applications where both the singularity identification and the novel distance function can be applied in order to illustrate their utility. Finally, the conclusions are given in
Section 7.
2. Mathematical Preliminaries: Geometric Algebra
One of the main problems of vector spaces is that linear transformations between them are represented through matrices, which entails a high computational cost when implemented. To overcome these and related problems, geometric algebra provides an excellent framework. It was first introduced by W. K. Clifford [
33], whom based his own work on the previous works of H. Grassmann [
34] and W. R. Hamilton [
35]. Throughout this section, a brief overview of geometric algebra is presented. More detailed treatments of the subject can be found in [
36,
37,
38,
39].
Definition 2. Given two vectors , the outer or exterior product of and , , is a new element that can be seen as the oriented area of the parallelogram obtained by sweeping the vector along . The exterior product is bilinear, associative and anticommutative. In particular, for every .
The new element defined by the exterior product is called a bivector, and it is defined to have grade two. By extension, the outer product of a bivector with a vector is known as a trivector, is denoted by and is defined to have grade three. Trivectors can be seen as the oriented volume obtained by sweeping the bivector along .
This can be generalized to an arbitrary dimension. Thus,
denotes a
k-blade, i.e., an element of grade
k. Linear combinations of
k-blades are known as
k-vectors, while linear combinations of
k-vectors (for different
k) are known as multivectors.
In his work [
33], Clifford extends the exterior product by adding a scalar product between vectors, the inner product. He defines the geometric product (also known as the Clifford product) as follows:
Thus, the geometric product between two vectors has two components: the scalar component given by the inner product and the bivector component given by the exterior product. Clearly, it also inherits the associativity and bilinearity of the exterior product.
When applied to an orthonormal basis
of
, the geometric product acts as follows:
Thus, for each , the set of k-vectors is spanned by:
(scalars).
(vectors).
(bivectors).
(trivectors).
⋮
(r-vectors).
⋮
(pseudoscalar).
Then, for each , there are exactly generators for the set of k-vectors, and thus, the set of k-vectors defines a vector space with basis and dimension .
Definition 3. Let denote the real vector space of dimension n. Then, the vector space spanned by the basisendowed with the geometric product defined in (13) is an algebra over known as the geometric algebra (GA) of . Such an algebra is denoted by and has the dimension . Remark 2. Since the grading structure of multivectors is a property associated with the exterior product, the elements of can still be called k-blades, k-vectors and multivectors.
An important family of linear operators in are the grade-k projection operators, denoted by for . Applied to an arbitrary multivector A, projects onto the grade-k components in A, i.e., it returns the components of A that can be expressed as a linear combination of . Obviously, if denotes a k-vector, then .
Using these operators, general multivectors
can be expressed as:
Hence, the set of all k-vectors for a given is a vector subspace of denoted by and spanned by .
The multivector representation (
16) is very useful in defining another important operator in
. This linear operator is known as the reversion operator and is denoted by the superscript ∼. The reversion is defined over the geometric product of
m vectors as:
Applied to
k-vectors, we have that:
due to the anticommutativity of the exterior product. Finally, since reversion is a linear operator, the reverse of an arbitrary multivector is:
Notice that the reversion operator corresponds simply to matrix transposition when a matrix representation of the n-dimensional algebra is considered.
Finally, another operator of great interest is the dual operator. Every grade-
n element of
is of the form
for a scalar
. For each
,
is known as the volume element
of
, while the generator
is known as the pseudoscalar of
and is usually denoted by
I. Pseudoscalars allow us to define the dual operator, whose action over a
k-vector
is:
where
is an
-vector.
Now, let us go back to the bivectors of
since they will be fundamental in the modelling of the rotations in
. An important property of these bivectors is that they always square to a scalar. Therefore, given a bivector
B, the unit bivector associated with
B is
. Unit bivectors of
always square to -1. This allows us to compute the following series:
where
. Expanding Equation (
21), we have that:
Equation (
22) indicates that
could be related to rotations. Indeed, we have the following result.
Proposition 1. Let B be a unit bivector and ; then, defines a rotation by an angle θ with a rotation plane represented by B. It acts over an element through the sandwiching product:Such an element R is termed a rotor. Rotors satisfy the following properties:
- (1)
;
- (2)
for ;
- (3)
for ;
- (4)
Given two frames
and
, there always exists a rotor
R that transforms one into the other, i.e., there exists a rotor
R such that
for
. This rotor is computed as [
36,
40]:
where
denotes the reciprocal frame of
.
The first property is the analogous version of the property defining the orthogonal matrices with determinant equal to 1, which are known to represent rotations. The second property proves that both R and encode the same rotation, while the third property is known as the geometric covariance of rotors.
In general, rotors define a group
with the geometric product as the group product:
Therefore, the product of two different rotors and also encodes a rotation. In particular, it is the rotation resulting from the composition of the rotations encoded by and , respectively. In addition, the second property states that provides a double covering of the rotation group.
Finally, one of the most important geometric algebras is the spatial geometric algebra
, whose basis is:
where
is an orthonormal basis of
and
.
3. Identification of Singularities Using Geometric Algebra
Since six degrees of freedom are required to describe the position and orientation of a rigid body in the three-dimensional space, the more natural way of formulating the singularity problem is through the six-dimensional geometric algebra
, which extends naturally the three-dimensional algebra
introduced in
Section 2. Screw theory [
41,
42] provides an intuitive and geometrical description of the differential kinematics of serial and parallel manipulators using six-dimensional vectors. Because of this, throughout this chapter, some concepts taken from this theory will be employed. This will provide the initial framework to completely understand the approach introduced in this section.
As stated in the introduction, we are going to work with three-dimensional rigid motions, i.e., three-dimensional orientation-preserving isometries. They form a Lie group, called the special Euclidean group, denoted by
. Its associated Lie algebra is:
where
is a skew-symmetric matrix of order 3,
, and
denotes the vector space of order 4 square matrices with real entries. Since every skew-symmetric matrix
can be represented as a vector
, we can express an element
as a six-dimensional vector
, termed a twist. Therefore, twists are the infinitesimal generators of rigid motions via the exponential map, i.e.,
with
. The next theorem is a fundamental result in screw theory.
Theorem 1 (Chasles, 1830 [
43])
. Every rigid motion can be realized as a rotation around an axis followed (preceded) by a translation along the same axis. Definition 4. A screw motion consists of a rotation around an axis followed (preceded) by a translation along the same axis, the screw axis ℓ. The ratio between the translational and the rotational parts of the motion is known as the pitch and is denoted by h. In particular, if a point is rotated around ℓ by an angle and translated along ℓ by an amount d, then . By convention, if , .
Remark 3. For infinitesimal motions, if , then the pitch is defined as .
Hence, every rigid motion is a screw motion. Particular cases of screw motions are pure rotations (pure translations) where the translation (rotation) is the identity or, equivalently, (). In addition, every screw motion can be characterized by the triple , where q denotes the magnitude of the motion. If , then and , while if , then and . We call this triple the screw associated with the screw motion, and we denote it using $.
Proposition 2. Given a screw with screw axis ℓ, pitch h and magnitude q, there exists a twist ξ such that the rigid motion it generates is the screw motion associated with $.
Proposition 2 states a correspondence between twists and screws that is useful for our purposes. In particular, if
is a point on
ℓ and
is its direction unit vector, then
and we have that:
A twist
associated with a magnitude 1 screw
$ is said to be a unit twist. Hence, any twist
can be seen as a unit twist multiplied by the magnitude of the associated screw axis:
where
is a unit twist. Clearly,
is associated with
, while
is associated with
.
Proposition 3. Let us consider a rigid body performing a screw motion represented by the screw , where the magnitude is a time-dependent variable. Its velocity during the screw motion is given by the associated twist ξ, where, now, the pitch is defined as in Remark 3. In particular:where, here, () is known as the twist amplitude. Now, let us consider a serial robot with
n DoF, where
denote the angular and linear velocity vectors of its end-effector. If Equation (
3) is expanded, the following is obtained:
where
denotes the
i-th column of the Jacobian matrix
J. Notice that the right side of Equation (
31) can be seen as the addition of the twists associated with the joints of the robot, where
plays the role of the twist amplitude and where the linear and angular parts are interchanged. However, for the sake of formality, let us consider the unit twist
associated with the
i-th joint of the robot (Since, from now on, we are going to work exclusively with unit twists, the subindex
U is omitted for simplicity). Then:
where, as stated in the introduction,
is the direction vector of the joint axis,
(
) is the origin of the frame attached to the end-effector (
i-th joint) and
if joint
i is revolute and
if joint
i is prismatic.
Remark 4. The unit twists defined in Equation (32) are represented with respect to the world frame, not with respect to the local frame attached to the previous joint. If the unit twists are defined with respect to a local frame, we need to use the adjoint transformation to represent them with respect to the world frame. In particular, , where is the adjoint transformation associated with the rigid motion f, i.e., the rigid motion transforming the reference frame to the local frame in which the twist is initially represented. The following is a key result:
Theorem 2 (Tsai, 1999 [
44])
. Given a serial robot with n DoF:where, again, denote the angular and linear velocity vectors of the robot’s end-effector and . The main advantage of the screw-based Jacobian matrix defined in Equation (
33) is that it allows a geometrical identification of the singularities. Moreover, if an approach based on geometric algebra is used, an intuitive geometrical and computer-friendly algebraic identification of the singularities is possible. For that purpose, let us consider the geometric algebra
, where, for every
, the unit twist
can be modelled as a vector. Indeed, we make the identification
with the vector
, where
are the basis vectors of
.
The following gives the main result of this section.
Theorem 3. Let denote the unit twist defined by the i-th joint expressed as a vector of . Then: Theorem 3 can be seen as a particular case of a more general result:
Theorem 4. Let be a set of n vectors of . Then: Theorem 4 can be easily deduced from Equation (4.143) in [
36] (p. 108):
where
F is a linear transformation in
,
, and, as stated in
Section 2,
I denotes the pseudoscalar of
.
In particular, Theorem 4 is true for any set of six vectors of , which proves Theorem 3. Now, the following corollary of Theorem 3 allows us to characterize the singularities of any serial robot of 6 DoF.
Corollary 1. Given a serial robot with 6 DoF and associated unit twists , then if, and only if, .
Proof. Taking the dual of Equation (
34), the following identity is obtained:
and, therefore, the singularities of the serial robot are those configurations
verifying that:
Now, since for a given non-zero multivector
,
if, and only if,
, Equation (
38) can be simplified to:
Thus, if, and only if, . □
Remark 5. Notice that what has also been proven in Corollary 1 is that the outer product of n vectors of is zero if, and only if, the n vectors are linearly dependent.
In addition, Corollary 1 allows us to re-define the singular set as:
Remark 6. What Theorem 3 states is that, for instance, if two unit twists and satisfy , then they represent the same twist, and hence, they generate the same screw motion. This means that if such a screw motion is a pure translation, then the translational axes are either parallel or coincident, while if the screw motion is a pure rotation, the rotational axes are coincident (Since the twists contain the term for , they cannot be parallel). Regarding the kinematic singularities of serial robots, this implies that two prismatic joints whose axes are either parallel or coincident give rise to a singularity and, equivalently, that two revolute joints whose axes are coincident give rise to a singularity. This is, in fact, in agreement with what is known about kinematic singularities since two parallel revolute joint axes do not give rise to a singularity. Obviously, the same geometrical interpretation can be made for three, four or more unit twists satisfying that their outer product is zero.
With respect to redundant serial robots, it is clear that, for , for any . Hence, Corollary 1 on its own does not allow us to characterize the singularities of redundant robots. However, this problem can be easily overcome by studying all the possible combinations of six unit twists in . We denote the set of all combinations of six elements that can be drawn from by S. Clearly, S has elements of the form , where and .
Theorem 5. Given a serial robot with n DoF and associated unit twists , then if, and only if, for each :where is the i-th element of S. Proof. It follows that, for
:
where
uses Equations (
37) and
uses the fact that all the minors of order 6 of the matrix
have null determinants. Clearly,
if, and only if,
, which, in turn, is equivalent to
(by Definition 1). □
The computation of either Equation (
39) for non-redundant robots or Equation (
41) for redundant ones is computationally more efficient than the computation of either
or
. The main reason for this lies in the computational complexity of the operations needed to obtain the expressions (
39) or (
41) with respect to the complexity of the operations needed for obtaining
or
. It is clear that the outer product of
n vectors of
behaves like the addition and product of real numbers, and hence, it has complexity
, while the determinant has complexity
or
depending on the algorithm used. In addition, for redundant robots, there are two main operations: the product between
and
and the determinant of the product matrix. This implies that, for this case, the complexity increases to
.
Special Case: Serial Robots with a Spherical Wrist
Similarly to what happens with the Jacobian matrix
J, a simplification can be achieved for robots that have a spherical wrist. As stated in
Section 1, the singularities of these robots can be decoupled into position and orientation singularities. Position singularities involve the first
joints and are computed by studying the rank of the following matrix:
where
if joint
i is revolute and
if joint
i is prismatic. On the other hand, orientation singularities involve the last three joints and are computed through the determinant of the following matrix:
Now, let us consider the three-dimensional geometric algebra . As proven in Theorem 4 for , for any three vectors . Hence, analogously to what has been performed before, the following characterization for the position and orientation singularities can be deduced.
Theorem 6. Given a serial robot with n DoF and a spherical wrist, if either or are denoted by for , then:
is a position singularity if, and only if, for each , where is the i-th combination of three elements drawn from .
is an orientation singularity if, and only if,
Proof. The proof is completely analogous to the proof of Corollary 1 and Theorem 5. □
Remark 7. Since the last three joint axes either intersect at a single point or are parallel, there is only one orientation singularity, namely, when these three joint axes are coplanar. This can also be easily deduced from Equation (45). A schematic representation of such singularity, also called wrist singularity, is depicted in Figure 2. 4. Distance to Singularities
Let
be two arbitrary configurations of a serial robot with
n DoF and let
be the unit twists associated with its joints. Then, there exist
, where, for each
,
is a configuration-dependent rotor in the six-dimensional geometric algebra
such that (
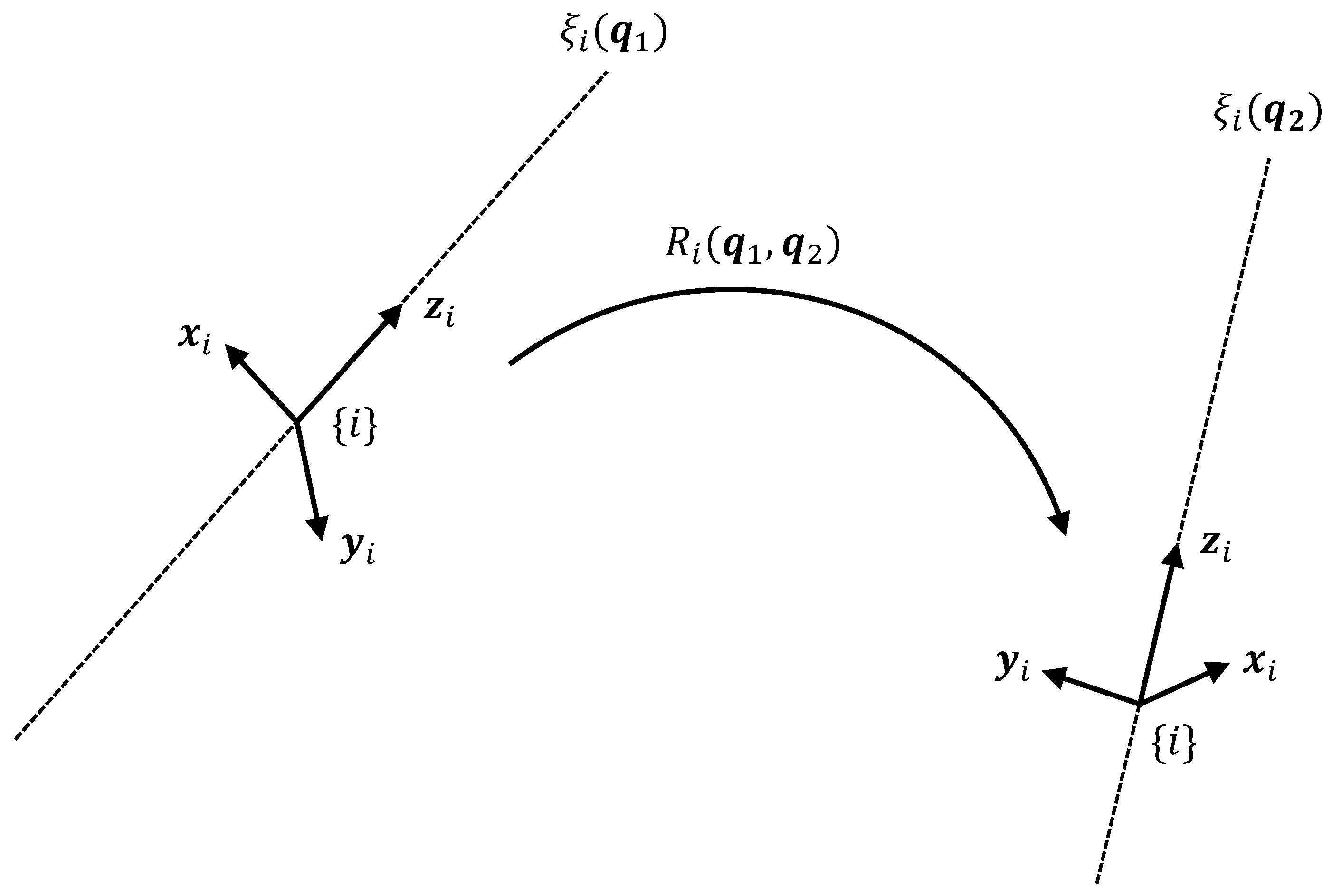
Figure 3):
The reason why these rotors exist is simple: unit twists are modelled as vectors in and there always exists a rotor relating any pair of vectors in any geometric algebra . In particular, there is always a rotor relating the same unit twist in two different configurations .
Now, let
denote a singularity of a serial robot. As explained in the previous section, if the serial robot has a spherical wrist, then
only involves a maximum of two or three joints and, therefore, two or three unit twists. If, conversely, the robot has no spherical wrist, then it can involve a maximum of six joints. Let us suppose, without loss of generality, that a given singularity
involves the joints
with associated unit twists
for
. Then, for any configuration
, there exist
such that:
The notation chosen for these rotors expresses a configuration dependence that is not a functional dependency, i.e., there is no analytical expression for these rotors with as a variable.
Now, it is clear that
if, and only if,
for every
. However, since for each
j,
does not define a function on
, a distance function cannot be defined. However, the measure of how close a given configuration
is to a singularity can be set as:
Example 1. Let be a singularity of a serial robot that only involves the second and third joints. Then, for any configuration , there exist and such that: Therefore, is close to if, and only if:and is singular if, and only if:where, in general, . These rotors can be constructed in many different ways. The easiest way consists of considering, for each
, the frame
attached to joint
i and constructed from
. This three-dimensional frame varies with the configuration
. Hence, for two different configurations
and
, there are two frames
attached to joint
i. As shown in
Section 2, we can recover the three-dimensional rotor that transforms one of the frames into the other. Since each frame
depends continuously on the configuration
, the rotor
is a continuous function defined as follows:
Thus, these configuration-dependent rotors exhibit a functional dependency on the configuration, which allows us to define a distance function. Such distance is based on the norm of a multivector
, defined by the relation:
To prove that is a norm, the following two lemmas are necessary.
Lemma 1. For any given multivector , .
Proof. According to Equation (
19), it follows that:
Now, note that, for each
,
is a
i-vector, i.e., it only contains terms of grade
i. The geometric product of two
k-vectors (with different
k) is stated as follows [
36] (p. 103):
Therefore, it is clear that
for
. Thus:
Now, each
can be expanded as follows:
where, for every
,
and
are the base elements of
. Therefore:
and, thus:
where, clearly,
with
the Kronecker delta. Then:
which, for every
, is a positive scalar. This implies that the sum of Equation (
57) is also a positive scalar. □
Lemma 2. Given three strictly positive real numbers , the following properties hold:
;
if, and only if, .
Proof. Both properties can be obtained by a straightforward computation. □
Proposition 4. The function defined by the identity is a norm in , i.e.,
- (i)
for all . In particular, if, and only if, .
- (ii)
for all and .
- (iii)
for all (usually known as the triangle inequality).
Proof. - (i)
Given a multivector
X, identity
is equivalent to:
Thus, it is clear by Lemma 1 that the positive branch of Equation (
62) is well defined and that
. In particular, if
, then:
where all the terms of the last equation are positive by Lemma 1 and, thus, all of them are equal to zero. Now, note that each addend is the geometric product of an
i-vector with its reverse. Therefore, if such product is zero, the corresponding
i-vector must be zero. Since all the terms are zero, all the
i-vectors that form
X are zero, and thus,
X is zero.
- (ii)
If
and
, then:
where
uses the linearity of the grade-0 projection operator (as stated in
Section 2).
- (iii)
Given two different multivectors
X and
Y, they can be expanded as linear combinations of the basis elements of
as follows:
Now, it follows that:
and hence:
where
uses Lemma 1, while
and
C are just notations given to simplify the different manipulations. Since
(If either
are equal to zero, then either
or
, which will make the condition
trivial):
where
uses the first or second property of Lemma 2 depending on whether
or
. It only remains to check if
,
. Indeed, the previous inequality is equivalent to that
. Now:
and, thus,
turns to:
which is equivalent to:
which, in turn, is equivalent to:
Since this last inequality is always true, the triangle inequality is also true.
□
Now, a distance function D can be defined for rotors.
Theorem 7. The function defined by the identity is a distance in , i.e.,
- (i)
for all . In particular, if, and only if, ;
- (ii)
for all ;
- (iii)
for all .
Proof. The proof is straightforward and uses the fact that is a norm. Given two different rotors and :
- (i)
. In particular:
where
uses the first property of a norm.
- (ii)
- (iii)
Given a third rotor
, we have that:
where
uses the third property of a norm.
□
As stated before, the end-effector pose of a serial robot and the pose of each one of its joints are described by the configuration-dependent rotors
and
, respectively. Thus, one can be tempted to extend the distance function
D to
as follows:
This function verifies all the requirements of a distance function with the exception of:
The reason is simple: a given pose of the end-effector can be associated with up to 16 different configurations if the serial robot is non-redundant and an infinite number if it is redundant. In particular, this means that with . However, this problem can be overcome as follows:
For each joint
i, denote by
the configuration space of the subchain formed by the first
i joints. It is clear that, if the robot has
n degrees of freedom,
for every
. Then, the following set of functions can be defined:
where, as stated before,
is the rotor that describes the pose of joint
i. Again, these functions are not distance functions for the same reason as
D (Equation (
76)) is not a distance function.
The function:
where
(
) denotes the first
i coordinates of the configuration vector
(
), defines a distance function in
.
Proof. Since, for each
,
satisfies the requirements
and
of a distance function, it is clear that
D also satisfies them. In addition,
for each
and
. Therefore,
for arbitrary
. Finally, if
, then, since any term of Equation (
79) is a positive scalar, it can be deduced that
for every
. Thus,
and
not only have the same end-effector pose, but the same pose for of each of its joints, which clearly implies that
. □
This distance function can be restricted to just by considering the joints involved in a given singularity .
Definition 5. Let be a singularity of a serial robot that involves joints . Then, the function is defined by the expression:where, for each , is the function defined in (78) and is a distance function in . 5. Application to the Serial Robot Kuka Lwr 4+
To show the advantages of the proposed method, an illustrative example is developed in this section, making use of the Kuka LWR 4+, an anthropomorphic robotic arm with seven degrees of freedom and a spherical wrist. It is schematically depicted in
Figure 4. Since it has a spherical wrist, its singularities can be decoupled into position and orientation singularities. Hence, Theorem 6 can be applied in order to find out such singularities. The computations with the vectors of
have been carried out using the Clifford Multivector Toolbox of MATLAB [
45].
With respect to the position singularities, the following system of
equations should be solved:
where, as computed in [
46], we have that:
where
and where
and
. However, in order to simplify these expressions, the system of Equation (
81) is expressed with respect to the frame attached to the fourth joint of the Kuka LWR 4+. To do so, a relation analogous of relation (
9) is applied. Here, instead of pre-multiplying by the corresponding rotation matrix, the system of Equation (
81) is multiplied by the three-dimensional rotor
R that performs the rotation between the frame attached to the end-effector and the frame attached to the fourth joint. For instance, the first equation of the system (
81) becomes:
which, using the geometric covariance property for rotors introduced in
Section 2, becomes:
Therefore, the system of Equation (
81) becomes:
where
Now, the system of Equation (
85) becomes:
which clearly has two different solutions:
or, equivalently, .
or, equivalently, and .
These two solutions correspond to the position singularities of the Kuka LWR 4+.
With respect to the orientation singularities, there is only one equation to solve:
Again, the expression of each
for
can be simplified by expressing those vectors with respect to the frame attached to the fourth joint. Thus, Equation (
88) becomes:
where
uses the anticommutativity of the outer product. Clearly, the last expression of Equation (
89) is zero if, and only if,
or, equivalently, if, and only if,
. Thus, the Kuka LWR 4+ only has one orientation singularity (the wrist singularity, as explained in Remark 7).
Finally, the distance function defined in Definition 5 can be applied to any of the already obtained singular configurations. Let us consider, for instance, the position singularity
. Then, the distance between an arbitrary configuration
and this singularity is given by the expression:
where
denotes the singular configuration
and
is the rotor defining the pose of the fourth joint of the Kuka LWR 4+.
In particular,
can be found as explained in
Section 2. Indeed, if
denotes the orthogonal basis defined by the world frame and
(respectively,
), the orthogonal basis defined by the frame attached to the fourth joint under the effect of configuration
(respectively, singular configuration
), then:
where
is the reciprocal frame of
. Since
is also an orthonormal set of vectors, such a reciprocal frame is:
Thus, Equation (
91) turns to:
Evaluating Equation (
93) for the KUKA LWR 4+, we obtain:
where
are the basic bivectors of
and
Therefore, by Proposition 4 and the decomposition used in the Proof of Lemma 1, the distance of an arbitrary configuration
to the position singularity
is given by:
where
7. Conclusions
This paper proposes a novel singularity identification method for arbitrary serial robots based on the six-dimensional geometric algebra . For non-redundant serial robots, we take the six unit twists associated with the joints, and we model them as vectors of . Hence, the problem reduces to find the configurations causing the exterior product to vanish since, as proven in Corollary 1, if, and only if, . Analogously, for a redundant robot with n DoF, we consider the different combinations of six unit twists taken from , and we find the configurations causing all the exterior products of the form for to vanish.
For serial robots with a spherical wrist, a simplification is possible. For these manipulators, the singularities are of two types: position singularities and orientation singularities. The former are identified as the configurations causing the exterior products to vanish for , where is the linear velocity component of the unit twist and is modelled as a vector of , while the latter are identified as the configuration causing the exterior product to vanish, where is the i-th joint axis and, again, is modelled as a vector of . Thus, the simplification consists of evaluating the exterior product of three vectors in instead of six vectors in .
Once the singularities are identified, a distance function is defined such as its restriction to the singular set , defined in Definition 5, is also a distance function that allows us to check how far an arbitrary configuration is to a singularity. This distance function exploits the fact that between any two vectors , there always exists a rotor R such that .
The advantages of the strategy introduced in this work are clear. First, it is a computer-friendly approach that avoids the computation of the determinant of an order (for non-redundant robots) or (for redundant robots) matrix and the Jacobian matrix J. In addition, the novel distance function defined in Definition 5 can be used to improve the performance of current control schemes or motion planning algorithms, which, as seen in the introduction, is still a hot research topic in robotics.