Insight in Thermally Radiative Cilia-Driven Flow of Electrically Conducting Non-Newtonian Jeffrey Fluid under the Influence of Induced Magnetic Field

Abstract

This paper investigates the mobility of cilia in a non-uniform tapered channel in the presence of an induced magnetic field and heat transfer. Thermal radiation effects are included in the heat transfer analysis. The Jeffrey model is a simpler linear model that uses time derivatives rather than convected derivatives as the Oldroyd-B model does; it depicts rheology other than Newtonian. The Jeffrey fluid model is used to investigate the rheology of a fluid with cilia motion. The proposed model examines the behavior of physiological fluids passing through non-uniform channels, which is responsible for symmetrical wave propagation and is commonly perceived between the contraction and expansion of concentric muscles. To formulate the mathematical modeling, the lubrication approach is used for momentum, energy, and magnetic field equations. The formulated linear but coupled differential equations have been solved analytically. Graphs for velocity profile, magnetic force function, induced magnetic field, current density, pressure rise, and heat profile are presented to describe the physical mechanisms of significant parameters. It is found that the eccentricity parameter of the cilia equations opposes the velocity and the magnetic force functions. The thermal radiation decreases the temperature profile while it increases for Prandtl and Eckert numbers. A promising impact of the magnetic Reynolds number and electric field on the current density profile is also observed.

1. Introduction

Cilia structures are highly complex, resembling flexible rods or fine hairs, and are found in all major animal species except nematodes. Immotile and motile cilia have two primary functions: detection and fluid flow generation. Sleigh [1] described the structure of flagella and cilia in 1962. He discussed the four main patterns of metachronal waves in detail, which are symplectic, antiplectic, dexioplectic, and laeoplectic metachronal waves. The combined movement of the cilia tips systematically degenerates in a wave-like manner causing a metachronal wave.

Each cilium has a diameter of around 250 nm and a typical length of 2 to 15 µm. They are often classified into two types: motile and immotile. The existence of a 9 + 0 arrangement of axonemes with nine doublet microtubules in immotile cilia and a 9 + 2 structure of axonemes with nine doublet microtubules with a center microtubule pair in motile cilia. Motile cilia travel back and forth in a concentrated way. They are particularly effective in creating flow, and due to their tiny dimensions, they function in a low Reynolds number hydrodynamic regime [2]. Motile cilia include ependymal cilia in the brain [3], which move cerebrospinal fluid in the brain ventricle system to nourish and support brain homeostasis, and respiratory cilia [4], which can also aid in the flow of mucus and dust particles breathed up and out of the lungs. Large embedded particles are picked up by the mucus layer and moved in an integrated ciliary action. Mucociliary clearance, based on the continuous flow of fluid through the airway lumens, prevents the buildup of inhaled pollutants and bacteria in the respiratory tract. Similarly, cilia are present in female fallopian tubes, which aid in transporting fertilized ovum from the ovary to the uterus [5]. Lardner and Shak [6] addressed the motions of cilia in general and carefully explained the role of cilia movement in fluid transportation through the efferent of the male reproductive tract. Sher Akbar [7] studied nanoparticles in the symmetric ciliated channel for the biomathematical analysis of carbon nanotubes. Several researchers have recently addressed cilia motion in various geometrical configurations, which are listed in the studies [8,9,10].

The most essential component regulating ciliary function is temperature. Temperature fluctuations affect the amounts of moisture and humidity required in ciliated cells to sustain normal physiological conditions. In particular, heat affects the ciliary circulation in a way that is comparable to its influence on many biological processes; as the temperature rises, the cilia beat faster until they are damaged by high temperatures [11,12]. Many human disorders are caused by ciliary motility defects, including male and female infertility, lung and renal disease, mental illness, and developmental abnormalities. These conditions are classified as motile ciliopathies [13,14]. As heat transport occurs due to temperature differences, the three primary mechanisms of heat transfer are conduction, convection, and radiation. Improving heat transport is important in a ciliated movement [15,16,17,18,19]. Akbar and Butt [20] investigated the viscoelastic fluid model under the impact of heat transfer to better understand the role of cilia in the respiratory system and its essential roles associated with fluid transport in the human body. Butt et al. [21] investigated heat transport effects in a ciliated circular tube using the PTT (Phan–Thien–Tanner) fluid model. Abdou Al-Zubaidi et al. [22] studied the heat analysis of blood flow by taking into account the cilia movement of Newtonian, dilatant, and pseudo-plastic fluids in a horizontal inclined channel in front of metachronal waves and achieved the analytical solution. McCash et al. [23] studied the effects of a heated viscous Newtonian fluid on peristaltic flow through a ciliated elliptic conduit. It was mentioned that elliptic cross-sections had a longer circular length, which allowed for better estimation of finer colling effects, heat transport analyses, etc.

The diverse functions of living cilia, on the other hand, have inspired many researchers. They have been studying artificial cilia’s properties in microfluidic applications such as microsensors, microrobots, light, particle manipulation, droplet antifouling surfaces, self-cleaning microfluidic mixing, and microfluidic pumping. The microfluidic channel was used by Mayne and Toonder [24] to test the ability of magnetic cilia in fluid mixing and bacterium collection.

Magnetohydrodynamics (MHD) is a growing topic of study in medical sciences and advanced biomedical engineering. It has several medicinal uses, including cancer therapy, preventing bleeding in time surgery, cell departure, magnetic endoscopy, and drug delivery targeting using magnetic particles as drug movers. Many problems inside the human body are addressed using various diagnostic techniques such as magnetic resonance imaging. Rashidi et al. [25] presented a detailed analysis of the applications of an effective magnetic field in simple flow, pulsatile flow, peristaltic flow, and drug delivery. Farooq et al. [26] investigated the combined effects of magnetic fields and heat transfer on ciliary-generated flows in the human body. Akbar et al. [27] studied the effects of magnetic induction and electrical fields on the dissipative flow of ciliary-produced MHD copper-water nanofluid. Sadaf and Nadeem [28] investigated fluid flow in the presence of heat transfer and a magnetic field with cilia beating along a curved ciliated channel. Few core investigations relevant to the topic can be found in references [29,30,31,32,33,34].

In the current study, we used the Jeffrey fluid model to analyze cilia motion. The Jeffrey model is a simpler linear model that uses time derivatives rather than convected derivatives as the Oldroyd-B model does; it depicts rheology other than Newtonian. The proposed study focuses on the convected Jeffrey’s model, which extends the original Maxwell convected viscoelastic model. The presented formulation (see Equation (10)) does not account for the stress time derivative (valid for steady flows). In comparison to other viscoelastic flow models, the proposed Jeffrey fluid is simpler (such as see the refs. [35,36,37]). Since its equations could be reduced to those of Newtonian models as a particular case, the Jeffrey model is regarded as a generalization of the frequently used Newtonian fluid model. The Jeffrey fluid model can characterize the stress relaxation feature of non-Newtonian fluids, whereas the standard viscous fluid model cannot. The Jeffrey fluid model accurately describes a class of non-Newtonian fluids with a distinctive memory time scale, also referred to as the relaxation time. Azaiez and Homsy [38] addressed other Jeffrey fluid models, such as the co-rotational variant. Similarly, the Jeffrey fluid model was addressed for polymeric flows [39,40], steady blood flows [41,42], steady boundary layer flows [43,44], etc.

Following the above literature review, it is seen that cilia-driven flow in the tapered channel is still unavailable. As a result, the Jeffrey fluid model was used to explain the cilia-induced flow through the asymmetric ciliated tapered channel. By using the Jeffrey fluid model, it is possible to analyze both Magnetohydrodynamic Newtonian and non-Newtonian phenomena with long wavelengths and low Reynolds numbers. The implications of induced magnetohydrodynamics on the heat transfer rate are also discussed. The governing equations are modeled and simplified using the lubrication hypothesis. The computational software Mathematica is used to find the analytical solution to the corresponding differential equations. Similarly, the impacts of different physical variables on the velocity profile, magnetic force function, induced magnetic field, current density, and temperature profile were graphically shown. In addition, streamlines are used to explain the trapping phenomena of cilia-driven flow.

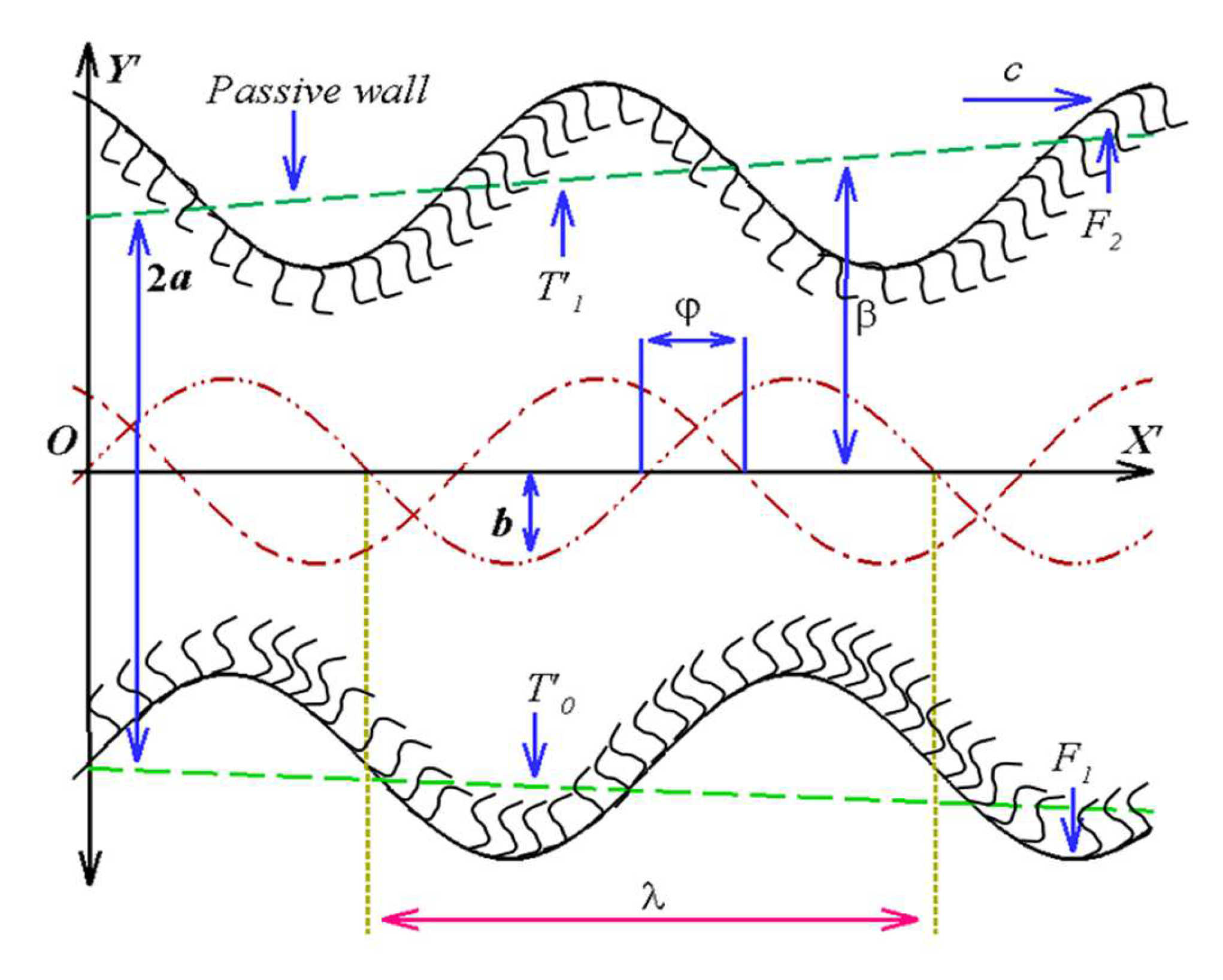
2. Viscoelastic Fluid in a Ciliated Tapered Channel: Mathematical Modeling

We consider the Jeffrey fluid model under the effects of a magnetic field in a tapered channel whose inner wall is ciliated in the form of an asymmetric metachronal wave moving towards the right with wave speed c. The lower wall of the tapered channel is maintained at a temperature of $T_0^{\prime }$ and the upper wall at $T_1^{\prime }$. A Cartesian coordinate system is taken for the tapered channel in which $X^{\prime }$ axis is across the axial direction and $Y^{\prime }$ axis lies along the transverse direction as shown in Figure 1.

The envelope of cilia tips for the tapered channel is presumed to be written as [45]:

$$\left.\begin{array}{c}{Y}^{\prime }=F_1\left(X^{\prime },t^{\prime }\right)=-X^{\prime }\mathit{tan}\beta -a-aϵ\mathit{cos}\left[-\frac{\phi }{2}+\frac{2\pi }{\lambda }\left(X^{\prime }-c{t}^{\prime }\right)\right]=H_1,\\ Y^{\prime }=F_2\left(X^{\prime },t^{\prime }\right)=X^{\prime }\mathit{tan}\beta +a+aϵ\mathit{cos}\left[\frac{\phi }{2}+\frac{2\pi }{\lambda }\left(X^{\prime }-c{t}^{\prime }\right)\right]=H_2, \end{array}\right\}$$

(1)

where $H_1$ is the lower wall of the ciliated tapered channel, $H_2$ is the upper wall of the ciliated tapered channel, $X^{\prime }$ is the axial dimensional coordinate, $t^{\prime }$ is the dimensional time, $\beta$ is the inclined angle of unperturbed walls, $a$ is the channel half-width, $\lambda$ is the wavelength, $ϵ$ is a non-dimensional measure with respect to any of the cilia length, and $\phi$ is the phase difference, which may be in the range 0$\le \phi \le$ $\pi$ for symmetric contractions of wave $\phi =\pi$. According to the sleigh, the cilia tips are assumed to move in elliptic paths so that the horizontal locus of the cilia tip is specified as

$$X^{\prime }=F_3\left(X_0,X^{\prime },t^{\prime }\right)=X_0+ϵ\omega a\sin \left[\frac{2\pi }{\lambda }\left(X^{\prime }-c{t}^{\prime }\right)\right],$$

(2)

where $X_0$ is a reference position of the cilia and $\omega$ is a measure of the eccentricity of the elliptic path. To determine the horizontal and vertical position of the velocities of the cilia, we have

$$U^{\prime }=\frac{\partial F_3}{\partial t^{\prime }}{|}_{X_0}=\frac{\partial F_3}{\partial t^{\prime }}+\frac{\partial F_3}{\partial X^{\prime }}\frac{\partial X^{\prime }}{\partial t^{\prime }}=\frac{\partial F_3}{\partial t^{\prime }}+\frac{\partial F_3}{\partial X^{\prime }}{U}^{\prime },$$

(3)

$$\left.\begin{array}{c}{V}^{\prime }=\frac{\partial F_1}{\partial t^{\prime }}{|}_{X_0}=\frac{\partial F_1}{\partial t^{\prime }}+\frac{\partial F_1}{\partial X^{\prime }}\frac{\partial X^{\prime }}{\partial t^{\prime }}=\frac{\partial F_1}{\partial t^{\prime }}+\frac{\partial F_1}{\partial X^{\prime }}{U}^{\prime },\\ V^{\prime } =\frac{\partial F_2}{\partial t^{\prime }}{|}_{X_0}=\frac{\partial F_2}{\partial t^{\prime }}+\frac{\partial F_2}{\partial X^{\prime }}\frac{\partial X^{\prime }}{\partial t^{\prime }}=\frac{\partial F_2}{\partial t^{\prime }}+\frac{\partial F_2}{\partial X^{\prime }}{U}^{\prime }.\end{array}\right\}$$

(4)

The alternate form of the velocity components is provided below by invoking Equation (2) in (3) and (1) in (4), respectively:

$$U^{\prime }=\frac{2ac\omega ϵ\pi \cos \left[\frac{2\pi }{\lambda }\left(X^{\prime }-c{t}^{\prime }\right)\right]}{-\lambda +2a\omega ϵ\pi \cos \left[\frac{2\pi }{\lambda }\left(X^{\prime }-c{t}^{\prime }\right)\right]},$$

(5)

$$V^{\prime }=\pm \frac{2acϵ\pi \left(\sin \left[\frac{\phi }{2}\pm \frac{2\pi }{\lambda }\left(X^{\prime }-c{t}^{\prime }\right)\right]+\omega \cos \left[\frac{2\pi }{\lambda }\left(X^{\prime }-c{t}^{\prime }\right)\right]\tan \beta \right)}{-\lambda +2a\omega ϵ\pi \cos \left[\frac{2\pi }{\lambda }\left(X^{\prime }-c{t}^{\prime }\right)\right]}.$$

(6)

The equations governing the flow of a Jeffrey fluid in the presence of an induced magnetic field are as follows [46,47]:

• The continuity equation

$$\mathbf{\nabla }·{\mathit{V}}^{\prime }=0.$$

(7)

2.

Maxwell’s equation

$$\left.\begin{array}{c}\mathbf{\nabla }·{\mathit{B}}^{\prime }=0,\mathbf{\nabla }\times {\mathit{B}}^{\prime }={\mu }^{\prime }{\mathit{J}}^{\prime },\\ \mathbf{\nabla }\times {\mathit{E}}^{\prime }=-\frac{\partial {\mathit{B}}^{\prime }}{\partial t^{\prime }}, {\mathit{J}}^{\prime }={\sigma }^{\prime }\left({\mathit{E}}^{\prime }+{\mathit{V}}^{\prime }\times {\mathit{B}}^{\prime }\right).\end{array}\right\}$$

(8)

3.

The equation of motion

$$\rho \left(\frac{\partial {\mathit{V}}^{\prime }}{\partial t^{\prime }}+\left({\mathit{V}}^{\prime }·\mathbf{\nabla }\right)V^{\prime }\right)=\mathbf{\nabla }·{\mathit{T}}^{\prime }+{\mathit{J}}^{\prime }\times {\mathit{B}}^{\prime },$$

(9)

where ${\mathit{T}}^{\prime }=-{\mathit{p}}^{\prime }\mathit{I}+{\mathit{S}}^{\prime }$ in which the extra stress tensor ${\mathit{S}}^{\prime }$ for the Jeffrey fluid model is defined as [48,49]

$${\mathit{S}}^{\prime }=\frac{\mu }{1+{\vartheta }_1}\left(\dot{\mathsf{\Omega }}+{\vartheta }_2\ddot{\mathsf{\Omega }}\right),$$

(10)

4.

The energy equation

$$\rho {\xi }^{\prime }\frac{d\mathit{T}}{d{t}^{\prime }}=\tau ·\mathit{L}-\mathbf{\nabla }·\mathit{q}-\mathbf{\nabla }·{\mathit{q}}_r^{\prime },$$

(11)

In the above equations, ${\mathit{V}}^{\prime }$ is the velocity vector, ${\mu }^{\prime }$ is the magnetic permeability, ${\sigma }^{\prime }$ is the electric conductivity, $\rho$ is the density of the fluid, ${\mathit{p}}^{\prime }$ is the pressure, ${\vartheta }_1$ is the ratio of relaxation to retardation times, ${\vartheta }_2$ is the retardation time, $\dot{\mathsf{\Omega }}$ is the shear rate where dots show the differentiation with respect to time, ${\mathit{J}}^{\prime }={\mathit{J}}_0^{\prime }+{\mathit{J}}_1^{\prime }$ is the current density in which ${\mathit{J}}_1^{\prime }$ is the induced current density, ${\mathit{B}}^{\prime }={\mathit{B}}_0^{\prime }+{\mathit{B}}_1^{\prime }$ is the magnetic field in which ${\mathit{B}}_1^{\prime }$ is the induced magnetic field and ${\mathit{B}}_0^{\prime }$ is the constant applied magnetic field, ${\mathit{E}}^{\prime }={\mathit{E}}_0^{\prime }+{\mathit{E}}_1^{\prime }$ is the electric field (${\mathit{E}}_0^{\prime }$ is the constant applied electric field and ${\mathit{E}}_1^{\prime }$ is the induced electric field), ${\xi }^{\prime }$ is the specific heat, $\mathit{q}=(-k^{\prime }\frac{dT}{d{t}^{\prime }}, k^{\prime }$ being the thermal conductivity) is the heat flux vector, and ${\mathit{q}}_r^{\prime }$ is the radiative heat flux.

Here we consider the effects of an induced magnetic field, for this low magnetic Reynolds number approximation must be dropped, and thus ${\mathit{E}}_1^{\prime }={\mathit{B}}_1^{\prime }={\mathit{J}}_1^{\prime }\ne 0$, and from Maxwell’s Equation (8), we obtain the induction equation as follows [50]:

$$\mathbf{\nabla }\times \left({\mathit{V}}^{\prime }\times {\mathit{B}}^{\prime }\right)+\zeta {\mathbf{\nabla }}^2{\mathit{B}}^{\prime }=\frac{\partial {\mathit{B}}^{\prime }}{\partial t^{\prime }},$$

(12)

where $\zeta =\frac{1}{{\mu }^{\prime }{\sigma }^{\prime }}$ is the magnetic diffusivity. A two-dimensional flow including an applied transverse constant magnetic field is represented by the equations:

$${\mathit{V}}^{\prime }=\left[U^{\prime }\left(X^{\prime },Y^{\prime },t^{\prime }\right),V^{\prime }\left(X^{\prime },Y^{\prime },t^{\prime }\right),0\right],{\mathit{B}}_0^{\prime }=\left[0,B_0^{\prime },0\right]$$

(13)

$${\mathit{B}}_1^{\prime }=\left[B_1^{\prime }\left(X^{\prime },Y^{\prime },t^{\prime }\right),B_2^{\prime }\left(X^{\prime },Y^{\prime },t^{\prime }\right),0\right],{\mathit{E}}_0^{\prime }=\left[0,0,E^{\prime }\right],$$

(14)

$${\mathit{E}}_1^{\prime }=\left[0,0,E_3^{\prime }\left(X^{\prime },Y^{\prime },t^{\prime }\right)\right],$$

(15)

and thus, we received the following expression [39]:

$${\mathit{J}}^{\prime }\times {\mathit{B}}^{\prime }=\left[\begin{array}{c}-\left\{{\sigma }^{\prime }\left(E^{\prime }+U^{\prime }{B}_0^{\prime }\right)+\frac{1}{{\mu }^{\prime }}\left(\frac{\partial B_2^{\prime }}{\partial X^{\prime }}-\frac{\partial B_1^{\prime }}{\partial Y^{\prime }}\right)\right\}\left(B_0^{\prime }+B_2^{\prime }\right),\\ +\left\{{\sigma }^{\prime }\left(E^{\prime }+U^{\prime }{B}_0^{\prime }\right)+\frac{1}{{\mu }^{\prime }}\left(\frac{\partial B_2^{\prime }}{\partial X^{\prime }}-\frac{\partial B_1^{\prime }}{\partial Y^{\prime }}\right)\right\}{B}_1^{\prime }\end{array}\right].$$

(16)

In the above Equation (16) we utilized the value of ${\mathit{J}}_1^{\prime }$ from Ampere’s law instead of Ohm’s law, i.e., (${\mathit{J}}^{\prime }={\sigma }^{\prime }({\mathit{E}}_0^{\prime }+{\mathit{V}}^{\prime }\times {\mathit{B}}_0^{\prime })+\frac{1}{{\mu }^{\prime }}\left(\mathbf{\nabla }\times {\mathit{B}}_1^{\prime }\right))$. Also, we deduced the expression of Lorentz force for the applied magnetic field by ignoring the terms of the induced magnetic field, i.e., (${\mathit{J}}^{\prime }\times {\mathit{B}}^{\prime }=\left[{\sigma }^{\prime }{U}^{\prime }{B}_0^{\prime }{}^2,0\right]$). The governing equations are now in a flowing form:

$$\frac{\partial U^{\prime }}{\partial X^{\prime }}+\frac{\partial V^{\prime }}{\partial Y^{\prime }}=0,$$

(17)

$$\begin{array}{l}\rho \left(\frac{\partial U^{\prime }}{\partial t^{\prime }}+U^{\prime }\frac{\partial U^{\prime }}{\partial X^{\prime }}+V^{\prime }\frac{\partial V^{\prime }}{\partial Y^{\prime }}\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=-\frac{\partial p_m^{\prime }}{\partial X^{\prime }}+\frac{\partial S_{X^{\prime }{X}^{\prime }}^{\prime }}{\partial X^{\prime }}+\frac{\partial S_{X^{\prime }{Y}^{\prime }}^{\prime }}{\partial Y^{\prime }}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\left\{{\sigma }^{\prime }\left(E^{\prime }+U^{\prime }{B}_0^{\prime }\right)+\frac{1}{{\mu }^{\prime }}\left(\frac{\partial B_2^{\prime }}{\partial X^{\prime }}-\frac{\partial B_1^{\prime }}{\partial Y^{\prime }}\right)\right\}\left(B_0^{\prime }+B_2^{\prime }\right),\end{array}$$

(18)

$$\begin{array}{l}\rho \left(\frac{\partial V^{\prime }}{\partial t^{\prime }}+U^{\prime }\frac{\partial V^{\prime }}{\partial X^{\prime }}+V^{\prime }\frac{\partial V^{\prime }}{\partial Y^{\prime }}\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=-\frac{\partial p_m^{\prime }}{\partial Y^{\prime }}+\frac{\partial S_{Y^{\prime }{X}^{\prime }}^{\prime }}{\partial X^{\prime }}+\frac{\partial S_{Y^{\prime }{Y}^{\prime }}^{\prime }}{\partial Y^{\prime }}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\left\{{\sigma }^{\prime }\left(E^{\prime }+U^{\prime }{B}_0^{\prime }\right)+\frac{1}{{\mu }^{\prime }}\left(\frac{\partial B_2^{\prime }}{\partial X^{\prime }}-\frac{\partial B_1^{\prime }}{\partial Y^{\prime }}\right)\right\}{B}_1^{\prime }\end{array}$$

(19)

$$\begin{array}{l}\rho {\xi }^{\prime }\left(\frac{\partial T}{\partial t^{\prime }}+U^{\prime }\frac{\partial T}{\partial X^{\prime }}+V^{\prime }\frac{\partial T}{\partial Y^{\prime }}\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=k^{\prime }\left(\frac{{\partial }^{2}T}{\partial {X^{\prime }}^2}+\frac{{\partial }^{2}T}{\partial {Y^{\prime }}^2}\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\frac{\mu }{{\vartheta }_1+1}\left(1+{\vartheta }_2\left\{U^{\prime }\frac{\partial }{\partial X^{\prime }}+V^{\prime }\frac{\partial }{\partial Y^{\prime }}\right\}\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\times \left(2\left\{{\left(\frac{\partial U^{\prime }}{\partial X^{\prime }}\right)}^2+{\left(\frac{\partial V^{\prime }}{\partial Y^{\prime }}\right)}^2\right\}+{\left(\frac{\partial U^{\prime }}{\partial Y^{\prime }}+\frac{\partial V^{\prime }}{\partial X^{\prime }}\right)}^2\right)-\frac{\partial q_r^{\prime }}{\partial Y^{\prime }}\end{array}$$

(20)

$$\frac{\partial B_1^{\prime }}{\partial X^{\prime }}+\frac{\partial B_2^{\prime }}{\partial Y^{\prime }}=0,$$

(21)

$$\frac{\partial B_1^{\prime }}{\partial t^{\prime }}=\zeta \left(\frac{{\partial }^2{B}_1^{\prime }}{\partial {X^{\prime }}^2}+\frac{{\partial }^2{B}_1^{\prime }}{\partial {Y^{\prime }}^2}\right)+\frac{\partial }{\partial Y^{\prime }}\left(U^{\prime }{B}_2^{\prime }+U^{\prime }{B}_0^{\prime }-V^{\prime }{B}_1^{\prime }\right),$$

(22)

$$\frac{\partial B_2^{\prime }}{\partial t^{\prime }}=\zeta \left(\frac{{\partial }^2{B}_2^{\prime }}{\partial {X^{\prime }}^2}+\frac{{\partial }^2{B}_2^{\prime }}{\partial {Y^{\prime }}^2}\right)+\frac{\partial }{\partial X^{\prime }}\left(U^{\prime }{B}_2^{\prime }+U^{\prime }{B}_0^{\prime }-V^{\prime }{B}_1^{\prime }\right),$$

(23)

$$\frac{\partial E_3^{\prime }}{\partial Y^{\prime }}=-\frac{\partial B_1^{\prime }}{\partial t^{\prime }},$$

(24)

$$\frac{\partial E_3^{\prime }}{\partial X^{\prime }}=-\frac{\partial B_2^{\prime }}{\partial t^{\prime }},$$

(25)

in which $p_m^{\prime }=p^{\prime }+\left\{{\left(B_1^{\prime }\right)}^2+{\left(B_2^{\prime }\right)}^2\right\}/2{\mu }^{\prime }$. The associated boundary conditions are

$$\left.\begin{array}{c}{U}^{\prime }{|}_{Y^{\prime }=H_1}=U^{\prime }{|}_{Y^{\prime }=H_2}=\frac{2ac\omega ϵ\pi \mathit{cos}[\frac{2\pi }{\lambda }\left(X^{\prime }-c{t}^{\prime }\right)]}{-\lambda +2a\omega ϵ\pi \mathit{cos}[\frac{2\pi }{\lambda }\left(X^{\prime }-c{t}^{\prime }\right)]},\\ V^{\prime }{|}_{Y^{\prime }=H_1}=\frac{\partial H_1}{\partial t^{\prime }},V^{\prime }{|}_{Y^{\prime }=H_2}=\frac{\partial H_2}{\partial t^{\prime }},\\ T{|}_{Y^{\prime }=H_1}=T_0^{\prime },T{|}_{Y^{\prime }=H_2}=T_1^{\prime }\end{array}\right\},$$

(26)

The $q_r^{\prime }$ is the radiative heat flux which is defined as [51]

$$q_r^{\prime }=-\frac{4{\sigma }^{*}}{3k^{*}}\frac{\partial T^4}{\partial Y^{\prime }},$$

(27)

where $k^{*}$ and ${\sigma }^{*}$ are the mean absorption coefficient and the Stefan-Boltzmann constant. We assume the temperature differences within the flow are sufficiently small such that $T^4$ may be expressed as a linear function of temperature.

$$T^4\approx T^{*3}\left(4T-3T^{*}\right).$$

(28)

In view of above Equation (28), Equation (27) becomes

$$q_r^{\prime }=-\frac{16{\sigma }^{*}{T}^{*3}}{3k^{*}}\frac{\partial T}{\partial Y^{\prime }},$$

(29)

Incorporating the non-dimensional quantities mentioned below:

$$\left.\begin{array}{c}x=\frac{X^{\prime }}{\lambda },y=\frac{Y^{\prime }}{a},t=\frac{{\mathit{ct}}^{\prime }}{\lambda },u=\frac{U^{\prime }}{c},v=\frac{V^{\prime }}{\delta c},h_1=\frac{H_1^{\prime }}{a},\delta =\frac{a}{\lambda },\mathit{Rd}=\frac{16{\sigma }^{*}{T}^{*3}}{3k^{*}\mu {\xi }^{\prime }}\\ h_x=\frac{B_1^{\prime }}{B_0^{\prime }},h_y=\frac{B_2^{\prime }}{B_0^{\prime }},E^{\prime }=\frac{E^{\prime }}{B_0^{\prime }c},R_m={\sigma }^{\prime }{\mu }^{\prime }ac,p_m=\frac{a^2{p}_m^{\prime }}{\lambda \mu c},S=\frac{a}{\mu c}{S}^{\prime },\\ Re=\frac{\rho ac}{\mu },M=a{B}_0^{\prime }\sqrt{\frac{{\sigma }^{\prime }}{\mu }},Pr=\frac{\mu {\xi }^{\prime }}{k^{\prime }},Ec=\frac{c^2}{{\xi }^{\prime }(T_0^{\prime }-T_S)},\theta =\frac{(T-T_S)}{(T_0^{\prime }-T_S)},\end{array}\right\},$$

(30)

Now, using the aforesaid non-dimensional parameters, the dimensionless governing Equations (17)–(25) are described below:

$$\begin{array}{l}\delta Re\left(\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}\right)\\ =-\frac{\partial p_m}{\partial x}+\delta \frac{\partial }{\partial x}{S}_{xx}+\frac{\partial }{\partial y}{S}_{xy}-M^2\left(E+u\right)\left(1+h_y\right)\\ -\frac{M^2}{R_m}\left(\delta \frac{\partial h_y}{\partial x}-\frac{\partial h_x}{\partial y}\right)\left(1+h_y\right),\end{array}$$

(31)

$$\begin{array}{l}{\delta }^{2}Re\left(\frac{\partial u}{\partial t}+\delta u\frac{\partial v}{\partial x}+\delta v\frac{\partial v}{\partial y}\right)\\ =-\frac{\partial p_m}{\partial y}+{\delta }^2\frac{\partial }{\partial x}{S}_{yx}+\delta \frac{\partial }{\partial y}{S}_{yy}+\delta M^2\left(E+u\right)h_x\\ +\delta \frac{M^2}{R_m}{h}_x\left(\delta \frac{\partial h_y}{\partial x}-\frac{\partial h_x}{\partial y}\right),\end{array}$$

(32)

$$\begin{array}{l}RePr\delta \left(\frac{\partial \theta }{\partial t}+u\frac{\partial \theta }{\partial x}+v\frac{\partial \theta }{\partial y}\right)\\ ={\delta }^2\frac{{\partial }^2\theta }{\partial x^2}+\left(1+PrRd\right)\frac{{\partial }^2\theta }{\partial y^2}\\ +\frac{1}{{\vartheta }_1+1} PrEcRePr\delta \left(\frac{\partial \theta }{\partial t}+u\frac{\partial \theta }{\partial x}+v\frac{\partial \theta }{\partial y}\right)\\ ={\delta }^2\frac{{\partial }^2\theta }{\partial x^2}+\left(1+PrRd\right)\frac{{\partial }^2\theta }{\partial y^2}\\ +\frac{1}{{\vartheta }_1+1} PrEc\\ \times \left[\left\{1+{\vartheta }_2\delta \left(u\frac{\partial }{\partial x}-v\frac{\partial }{\partial y}\right)\right\}\left\{2{\delta }^2\left({\left(\frac{\partial u}{\partial x}\right)}^2+{\left(\frac{\partial v}{\partial y}\right)}^2\right)\right\}\right],\\ +{\left(\frac{\partial u}{\partial y}+{\delta }^2\frac{\partial v}{\partial x}\right)}^2\end{array}$$

(33)

$$\frac{\partial }{\partial y}\left(u{h}_y+u-\delta v{h}_x\right)+\frac{1}{R_m}\left({\delta }^2\frac{{\partial }^2{h}_x}{\partial x^2}+\frac{{\partial }^2{h}_x}{\partial y^2}\right)=\delta \frac{\partial h_x}{\partial t},$$

(34)

$$\frac{\partial }{\partial x}\left(u{h}_y+u-\delta v{h}_x\right)-\frac{1}{R_m}\left({\delta }^2\frac{{\partial }^2{h}_y}{\partial x^2}+\frac{{\partial }^2{h}_y}{\partial y^2}\right)=-\frac{\partial h_y}{\partial t},$$

(35)

wherein the above Equations (31)–(35) magnetic force functions are defined as: $h_x=\frac{\partial \varphi }{\partial y}$, $h_y=-\delta \frac{\partial \varphi }{\partial x}$, and the extra stress tensor in components form are defined as:

$$S_{xx}=\frac{2\delta }{{\vartheta }_1+1}\left(1+{\vartheta }_2\delta \left(\frac{\partial }{\partial t}+u\frac{\partial }{\partial x}+v\frac{\partial }{\partial y}\right)\right)\frac{\partial u}{\partial x},$$

(36)

$$S_{xy}=S_{yx}=\frac{1}{{\vartheta }_1+1}\left(1+{\vartheta }_2\delta \left(\frac{\partial }{\partial t}+u\frac{\partial }{\partial x}+v\frac{\partial }{\partial y}\right)\right)\left({\delta }^2\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}\right),$$

(37)

$$S_{yy}=\frac{2\delta }{{\vartheta }_1+1}\left(1+{\vartheta }_2\delta \left(\frac{\partial }{\partial t}+u\frac{\partial }{\partial x}+v\frac{\partial }{\partial y}\right)\right)\frac{\partial v}{\partial y}.$$

(38)

However, under the conditions of a long wavelength and a low Reynolds number, the dimensionless equations that describe the system have the following form:

$$-\frac{\partial p_m}{\partial x}+\frac{1}{{\vartheta }_1+1}\frac{{\partial }^{2}u}{\partial y^2}-M^2\left(E+u\right)+\frac{M^2}{R_m}\frac{\partial h_x}{\partial y}=0,$$

(39)

$$\frac{\partial p_m}{\partial y}=0,$$

(40)

$$u+\frac{1}{R_m}\frac{\partial h_x}{\partial y}=0,$$

(41)

$$\left(1+PrRd\right)\frac{{\partial }^2\theta }{\partial y^2}+\frac{1}{1+{\vartheta }_1}PrEc{\left(\frac{\partial u}{\partial y}\right)}^2=0.$$

(42)

The corresponding boundary conditions are

$$\left.\begin{array}{c}u{|}_{y=h_1}=u{|}_{y=h_2}=\frac{2a\omega ϵ\pi \delta \cos [2\pi \left(x-t\right)]}{-1+2a\omega ϵ\pi \delta \cos [2\pi \left(x-t\right)]}\\ v{|}_{ y=h_1}=\frac{\partial h_1}{\partial t},v{|}_{ y=h_2}=\frac{\partial h_2}{\partial t}\end{array}\right\},$$

(43)

$$\theta {|}_{y=h_1}=1,\theta {|}_{y=h_2}=m,$$

(44)

where m is the wall temperature ratio.

3. Analytical Solutions

With the help of computational software “Mathematica” the exact solution Equation (38) which satisfies the corresponding boundary conditions (Equations (43) and (44)) is obtained and we receive the axial velocity of the fluid in a ciliated tapered channel that is

$$\begin{gathered} u=\frac{\left(\left(E{M}^2+\frac{\partial p_m}{\partial x}\right)\cosh \left(\frac{\left(h_1-h_2\right)\sqrt{M^2\left(1+{\vartheta }_1\right)}}{\sqrt{2}}\right)-\left(E{M}^2+2M^{2}A+\frac{\partial p_m}{\partial x}\right)\cosh \left(\frac{\left(h_1+h_2-2y\right)\sqrt{M^2\left(1+{\vartheta }_1\right)}}{\sqrt{2}}\right)\times \\ \left(\cosh \left(\frac{\left(h_1+h_2\right)\sqrt{M^2\left(1+{\vartheta }_1\right)}}{\sqrt{2}}\right)+\sinh \left(\frac{\left(h_1+h_2\right)\sqrt{M^2\left(1+{\vartheta }_1\right)}}{\sqrt{2}}\right)\right)\right)}{M_2\left(\cosh \left(\sqrt{2}{h}_1\sqrt{M^2\left(1+{\vartheta }_1\right)}\right)+\cosh \left(\sqrt{2}{h}_2\sqrt{M^2\left(1+{\vartheta }_1\right)}\right)\right) \\ +M_2\left(\sinh \left(\sqrt{2}{h}_1\sqrt{M^2\left(1+{\vartheta }_1\right)}\right)+\sinh \left(\sqrt{2}{h}_2\sqrt{M^2\left(1+{\vartheta }_1\right)}\right)\right)} \end{gathered}$$

(45)

wherein above equation $A=\frac{2a\omega ϵ\pi \delta \cos [2\pi \left(x-t\right)]}{-1+2a\omega ϵ\pi \delta \cos [2\pi \left(x-t\right)]}$. The solution of Equation (42) can be written as:

$$\begin{gathered} \theta =\frac{\mathrm{sech}{\left(\frac{\left(h_1-h_2\right)\sqrt{M^2\left(1+{\vartheta }_1\right)}}{\sqrt{2}}\right)}^2}{32\left(h_1-h_2\right)M^4\left(1+PrRd\right)\left(1+{\vartheta }_1\right)} \\ \times \left(\begin{array}{c}-4M^2\left[\begin{array}{c}Ec{\left\{h_2\right)}^2{\left(M^2\left(E+2A\right)+\frac{\partial p_m}{\partial x}\right)}^{2}Pr\left(h_1-y\right)+Ec{h}_1{M}^4{\left(E+2A\right)}^{2}Pr\left(h_1-y\right)y+\\ Ec{h}_1{\left(\frac{\partial p_m}{\partial x}\right)}^{2}Pr\left(h_1-y\right)y+\\ h_2\left\{\begin{array}{c}-Ec{M}^4{\left(E+2A\right)}^{2}Pr\left(h_1-y\right)\left(h_1+y\right)+\\ Ec{\left(\frac{\partial p_m}{\partial x}\right)}^{2}Pr\left(-{\left\{h_1\right)}^2-y^2\right)+M^2\left(\begin{array}{c}4+4PrRd-2Ec\\ \left(E+2A\right)\frac{\partial p_m}{\partial x}Pr\\ \left(h_1-y\right)\left(h_1+y\right)\end{array}\right)\end{array}\right)-2M^2\\ \left(\left(2+2PrRd-2Ec{h}_1\left(E+2A\right)\frac{\partial p_m}{\partial x}Pr\left(h_1-y\right)\right)y+2\left(1+PrRd\right)\left(h_1-y\right)m\right)\end{array}\right)\\ \left(1+{\vartheta }_1\right)+\left\{\begin{array}{c}Ec{h}_1{\left(M^2\left(E+2A\right)+\frac{\partial p_m}{\partial x}\right)}^{2}Pr-\\ 16M^4\left(1+PrRd\right)\left(y\left(-1+m\right)-h_{1}m\right)\left(1+{\vartheta }_1\right)\\ -h_2\left(2Ec{M}^2\left(E+2A\right)\frac{\partial p_m}{\partial x}Pr+\frac{\partial p_m}{\partial x}Pr+EcPr{\left(\frac{\partial p_m}{\partial x}\right)}^2+M^4\left(\begin{array}{c}Ec{\left(E+2A\right)}_{2}Pr+16\\ \left(1+PrRd\right)\left(1+{\vartheta }_1\right)\end{array}\right)\right)\end{array}\right)\\ \times \cosh \left(\left(h_1-h_2\right)\sqrt{M^2\left(1+{\vartheta }_1\right)}\right)-Ec\left(h_1-h_2\right){\left(M^2\left(E+2A\right)+\frac{\partial p_m}{\partial x}\right)}^{2}Pr\times \\ \cosh \left(\sqrt{2}M\left(h_1+h_2-2y\right)\sqrt{1+{\vartheta }_1}\right)\end{array}\right), \end{gathered}$$

(46)

In the fixed frame, the instantaneous flow rate is defined as

$$Q=\underset{h_1}{\overset{h_2}{{\displaystyle \int }}}u\left(x,y,t\right)dx.$$

(47)

The equation for pressure gradient is defined using Equations (45) and (47), and we have

$$\begin{gathered} \frac{\partial p_m}{\partial x}=-\left(M^2\left(\cos \mathrm{h}\left(\frac{\left(h_1+h_2\right)\sqrt{M^2\left(1+{\vartheta }_1\right)}}{\sqrt{2}}\right)-\sin \mathrm{h}\left(\frac{\left(h_1+h_2\right)\sqrt{M^2\left(1+{\vartheta }_1\right)}}{\sqrt{2}}\right)\right)\times \left(M\left(-E{h}_1+E{h}_2+ \\ 2Q\right)\sqrt{\left(1+{\vartheta }_1\right)}\cos \mathrm{h}\left(\sqrt{2}M{h}_1\sqrt{1+{\vartheta }_1}\right)+M\left(-E{h}_1+E{h}_2+ \\ 2Q\right)\sqrt{1+{\vartheta }_1}\cos \mathrm{h}\left(\sqrt{2}{h}_{2}M{h}_1\sqrt{1+{\vartheta }_1}\right)\right)-E{h}_1\sqrt{M^2\left(1+{\vartheta }_1\right)}\sin \mathrm{h}\left(\sqrt{2}{h}_{1}M\sqrt{1+{\vartheta }_1}\right)+ \\ E{h}_2\sqrt{M^2\left(1+{\vartheta }_1\right)}\sin \mathrm{h}\left(\sqrt{2}{h}_{1}M\sqrt{1+{\vartheta }_1}\right)+2Q\sqrt{M^2\left(1+{\vartheta }_1\right)}\sin \mathrm{h}\left(\sqrt{2}{h}_{1}M\sqrt{1+{\vartheta }_1}\right)- \\ E{h}_1\sqrt{M^2\left(1+{\vartheta }_1\right)}\sin \mathrm{h}\left(\sqrt{2}{h}_{2}M\sqrt{1+{\vartheta }_1}\right)+E{h}_2\sqrt{M^2\left(1+{\vartheta }_1\right)}\sin \mathrm{h}\left(\sqrt{2}{h}_{2}M\sqrt{1+{\vartheta }_1}\right)+ \\ 2Q\sqrt{M^2\left(1+{\vartheta }_1\right)}\sin \mathrm{h}\left(\sqrt{2}{h}_{2}M\sqrt{1+{\vartheta }_1}\right)+2\sqrt{2}\left(E+ \\ 2A\right)\sin \mathrm{h}\left(\frac{\left(h_1+h_2\right)\sqrt{M^2\left(1+{\vartheta }_1\right)}}{\sqrt{2}}\right)\left(\cos \mathrm{h}\left(\frac{\left(h_1+h_2\right)\sqrt{M^2\left(1+{\vartheta }_1\right)}}{\sqrt{2}}\right)+\sin \mathrm{h}\left(\frac{\left(h_1+h_2\right)\sqrt{M^2\left(1+{\vartheta }_1\right)}}{\sqrt{2}}\right)\right)\right)/ \\ \left(\left(2\left(-h_{1}M\sqrt{\left(1+{\vartheta }_1\right)}\cos \mathrm{h}\left(\frac{\left(h_1+h_2\right)\sqrt{M^2\left(1+{\vartheta }_1\right)}}{\sqrt{2}}\right)+h_{2}M\left(1+{\vartheta }_1\right)\cos \mathrm{h}\left(\frac{\left(h_1+h_2\right)\sqrt{M^2\left(1+{\vartheta }_1\right)}}{\sqrt{2}}\right)+ \\ \sqrt{2}\sin \mathrm{h}\left(\frac{\left(h_1+h_2\right)\sqrt{M^2\left(1+{\vartheta }_1\right)}}{\sqrt{2}}\right)\right)\right)\right). \end{gathered}$$

(48)

The expression for magnetic force function from Equation (41) can be written as

$$u+\frac{1}{R_m}\frac{{\partial }^2\varphi }{\partial y^2}=0,$$

(49)

and the associated boundary conditions are

$$\varphi {|}_{y=h_1}=0,\varphi {|}_{y=h_2}=0,$$

(50)

Now, the solution of Equation (49) will take the form

$$\varphi =\frac{\begin{array}{c}{R}_m\left(\frac{\partial p_m}{\partial x}+M^2\left(2A+\frac{\partial p_m}{\partial x}\left(h_1-y\right)\left(h_2-y\right)\left(1+{\vartheta }_1\right)+E\left(1+M^2\left(h_1-y\right)\left(h_2-y\right)\left(1+{\vartheta }_1\right)\right)\right)\right.\\ \left.-M^2\left(E+2A\right)+\frac{\partial p_m}{\partial x}\left(\cosh \left(\frac{M\left(h_1+h_2-2y\right)\sqrt{\left(1+{\vartheta }_1\right)}}{\sqrt{2}}\right)\sec \mathrm{h}\left(\frac{M\left(h_1+h_2\right)\sqrt{\left(1+{\vartheta }_1\right)}}{\sqrt{2}}\right)\right)\right)\end{array}}{4M^2\left(1+{\vartheta }_1\right)},$$

(51)

and the axial induced magnetic field $h_x\left(x,y\right)$ is obtained by taking the derivative of Equation (51) w.r.t $“y”$, and the expression of non-dimensional current density in the fixed frame is given as

$$J_z\left(x,y\right)=R_m\left(E+u-\frac{{\partial }^2\varphi }{\partial y^2}\right).$$

(52)

The expression for pressure rise can be written as

$$\Delta p_m={{\displaystyle \int }}_0^1\frac{d{p}_m}{dx}dx.$$

(53)

4. Graphical Results and Discussion

This section comprises seven subsections. The effects of various parameters on the velocity component $\left(u\right)$, magnetic force function $\left(\varphi \right)$, induced magnetic field $(h_x)$, current density $(J_z),$ pressure rise $\left(\mathsf{\Delta }p\right)$, temperature profile $\left(\theta \right)$ and trapping mechanism are presented.

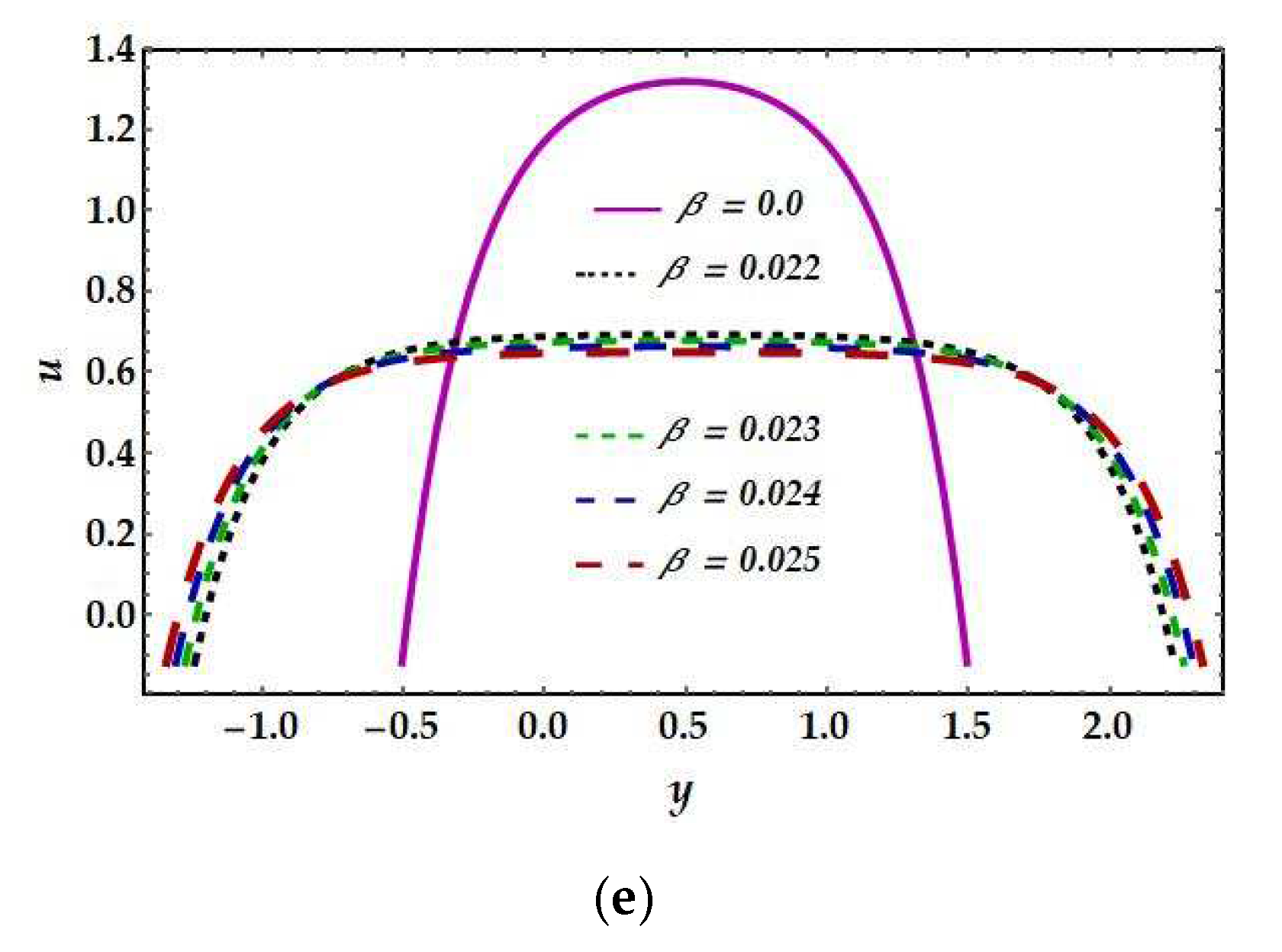
4.1. Velocity Profiles

Figure 2a–e shows the behavior of axial velocity versus the different physical parameters. In Figure 2a, we observe that by increasing the values of the Hartmann number $\left(M\right)$, the velocity of fluid gradually decreases in the center of the ciliated tapered channel because the Hartmann number is the ratio of electromagnetic forces to viscous forces. Therefore, large values of the Hartmann number create a resistance in the opposite direction of fluid movement as compared to the very small values of the Hartmann number, which cause a decline in the velocity field. Additionally, we can see the Lorentz force is less dominating closer to the walls of the channel. However, in Figure 2b, a similar type of behavior is noticed for the Jeffrey parameter (${\vartheta }_1$) on the velocity profile. Further, when the Jeffrey fluid parameter ${\vartheta }_1\to 0$ the behavior of the fluid becomes Newtonian, which ensures that present results are valid for both Newtonian and non-Newtonian models. In Figure 2c, we observe that the velocity of the fluid is maximum at the center and gradually decreases at the wall for large values of eccentricity parameter $\left(\omega \right)$. Figure 2d depicts that as we increase the cilia length parameter $\left(ϵ\right)$ the velocity of fluid is maximal at the center of the channel but behaves differently at the walls of the channel. From Figure 2e it is noticed that when the values of inclined angle $(\beta$) of the unperturbed walls increases, then the velocity profile significantly increases closer to the wall but decreases in the middle of the channel. This shows that the inclination angle is also responsible and plays an efficient role to control the flow.

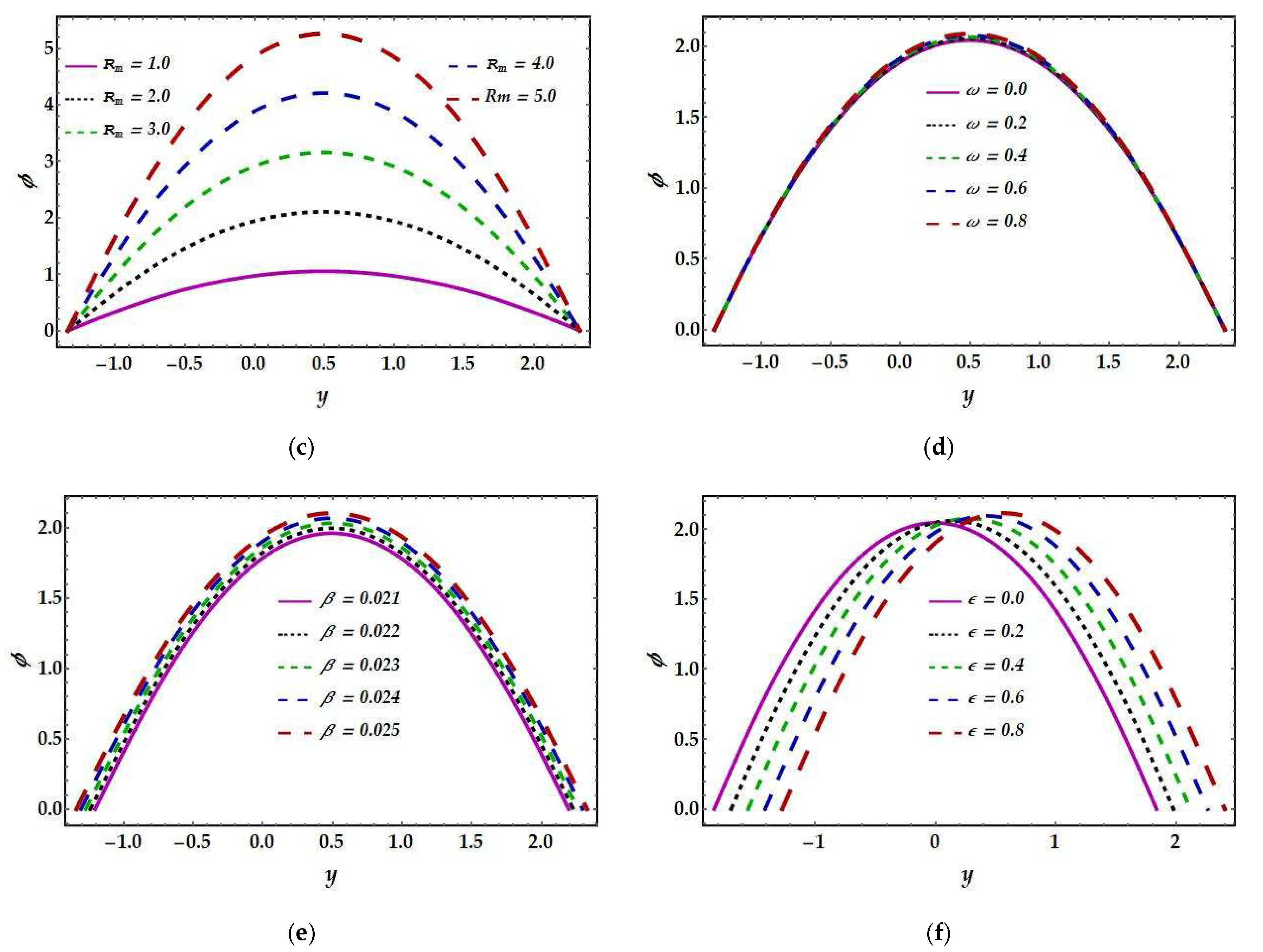
4.2. Magnetic Force Function

The magnetic force function for different values of the Hartmann number $\left(M\right)$ and Jeffrey fluid parameter $({\vartheta }_1)$ is plotted in Figure 3a,b. It is noticed that the magnitude of magnetic force function shows a significant decline when $\left(M\right)$ and $({\vartheta }_1)$ increases. The Lorentz force dominates the magnetic force function, as seen in Figure 3a. However, in Figure 3b, it can be seen that the Jeffrey fluid parameter has little or no influence on the magnetic force function but is decreasing. In Figure 3c, we see that increasing the magnetic Reynolds number ($R_m$) strengthens the magnetic force function. The magnetic Reynolds number is directly proportional to magnetic permeability and electromagnetic forces, as shown by Equation (31). Higher magnetic Reynolds numbers increase magnetic permeability, which helps in improving the magnetic force function. In Figure 3d, it is seen that increasing the eccentricity of the elliptic path ($\omega$) optimizes the magnetic force function, although the changes are minor. Figure 3e shows that a change in the inclination angle ($\beta$) influences the behavior of the magnetic force component over the whole domain. Higher inclination values indicate an increasing trend in the velocity characteristic along the entire channel. Figure 3f illustrates that the magnitude of the magnetic force function at the wall of the channel is opposite to each other for different values of cilia length parameter ($ϵ$).

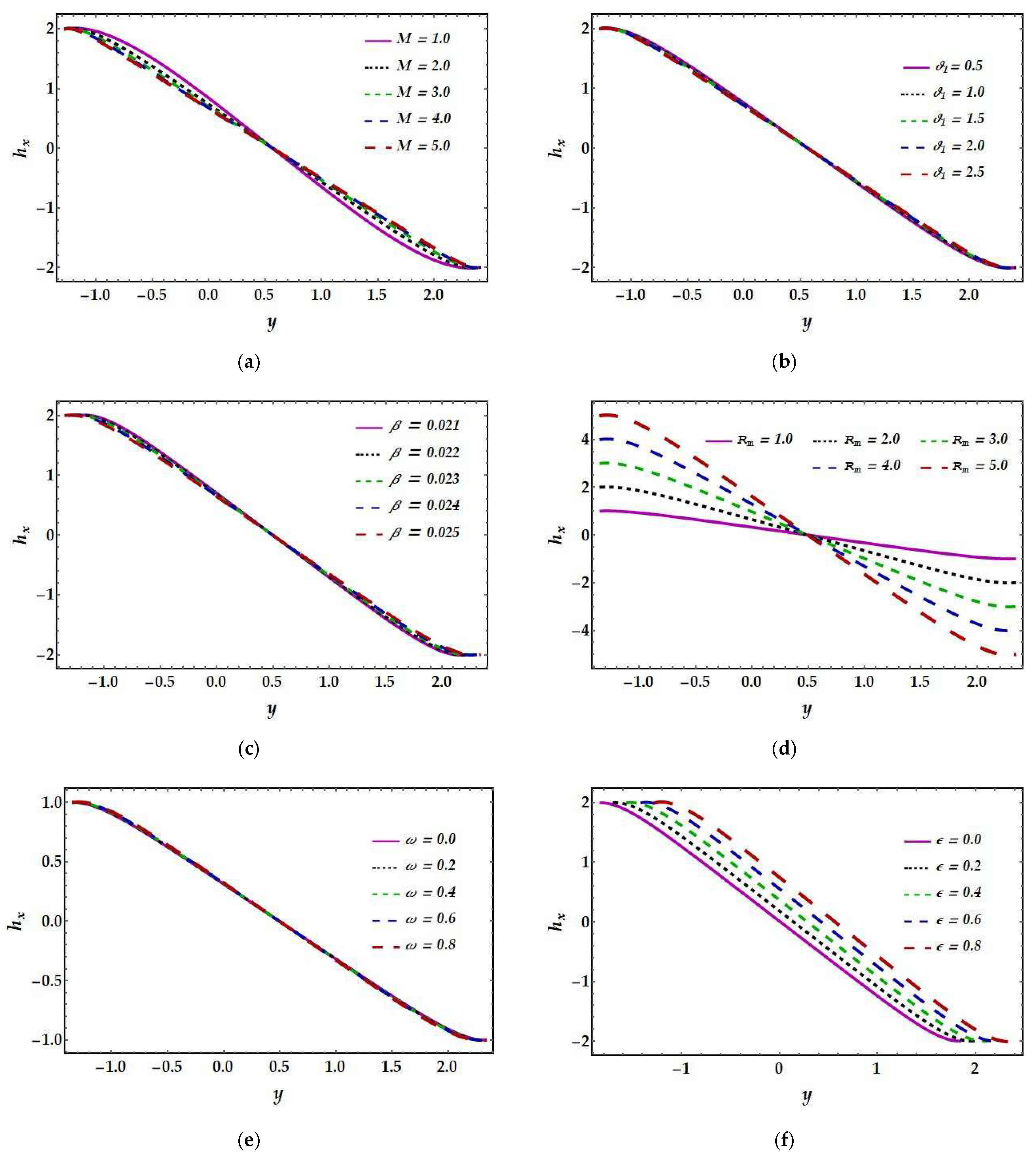
4.3. Magnetic Field Characteristics

Figure 4a–f depicts the findings for the induced magnetic field h_x across several important parameters. As seen in Figure 4a, when the Hartmann number (M) increases, the induced magnetic displays dual behavior, such as a reducing mechanism in the bottom part of the channel and a growing mechanism in the upper boundary. The Jeffrey fluid parameter (${\vartheta }_1$) and inclination angle ($\beta$) exhibit comparable effects on the induced magnetic field in Figure 4b,c; however, the effects from both variables on the induced magnetic field are insignificant. In the presence of a magnetic field Reynolds number (R_m), the induced magnetic field accumulates in the bottom half of the channel and decreases in the upper section, as illustrated in Figure 4d. In Figure 4e, a similar kind of pattern is observed for the eccentricity parameter ($\omega$), although the impacts are essentially minor. The induced magnetic field increases over the entire domain under the significant effect of the cilia length parameter, as seen in Figure 4f.

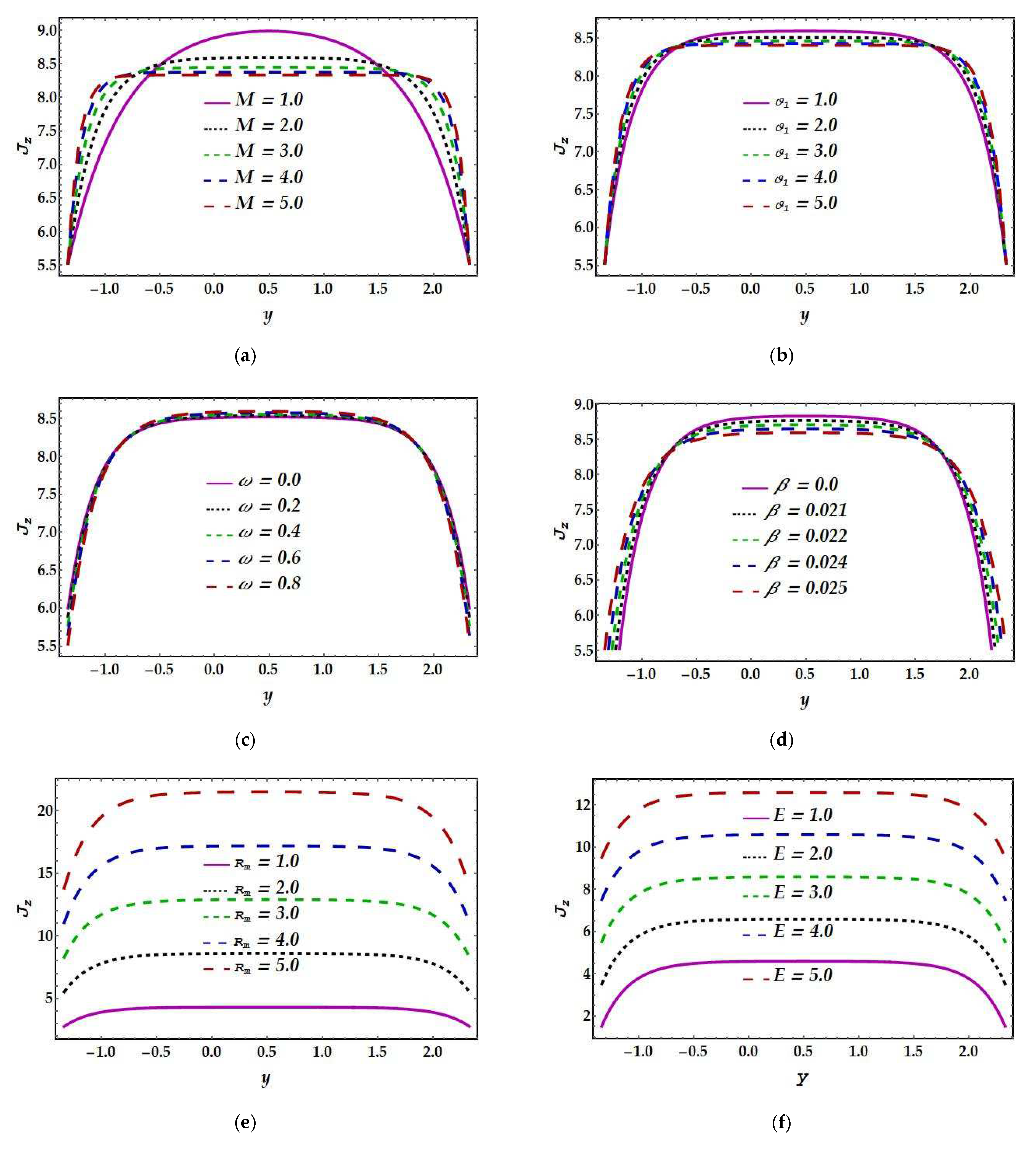
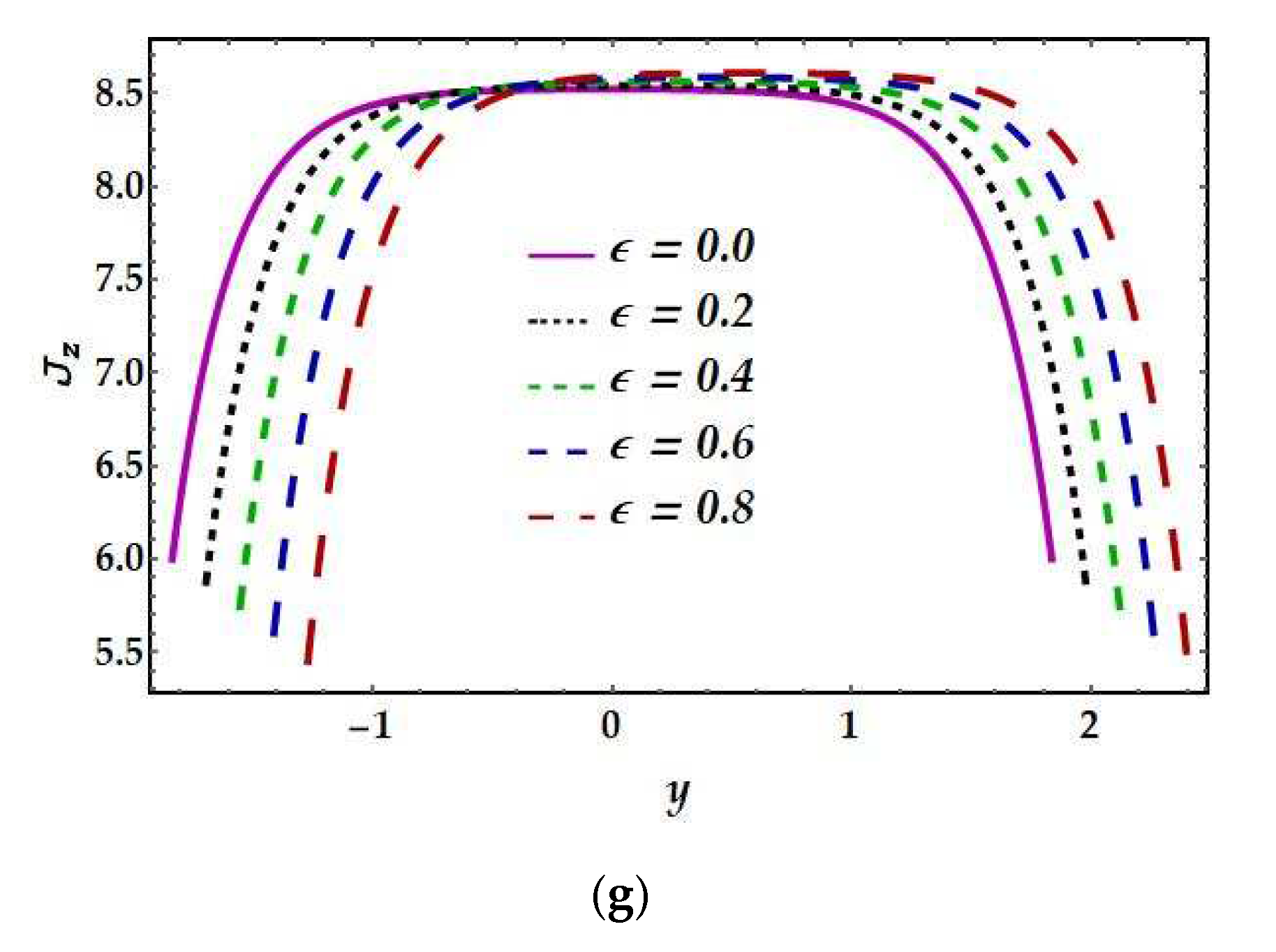
4.4. Current Density

Figure 5a–g depicts the variance in current density characteristics for all emerging parameters, and all graphs are parabolic in shape. It is also noticed that towards the middle of the channel and along the channel walls, the current density behaves in the opposite direction, as seen in Figure 5a–d for different values of the Hartmann number (M), Jeffrey parameter (${\vartheta }_1$), eccentricity parameter ($\omega$), and inclined angle ($\beta$). Figure 5a,b shows that the Hartmann number and Jeffrey fluid parameter oppose the increase in current density in the streamwise direction, but adjacent to the boundaries, the response is entirely reversed. The eccentricity parameter shows negligible effects on the current density profile as shown in Figure 4c. The consequences of the inclined angle tend to reduce the current density profile in the channel’s center, while it increases closer to the walls as illustrated in Figure 4d. The existence of a magnetic Reynolds number (R_m) and an electric field (E) helps in optimizing the current density profile dramatically, as seen in Figure 4e,f. As the cilia length rises, the current density grows in the upper portion of the channel while declining in the lower half. However, we identified a major point in this graph at $y\approx 0.2$.

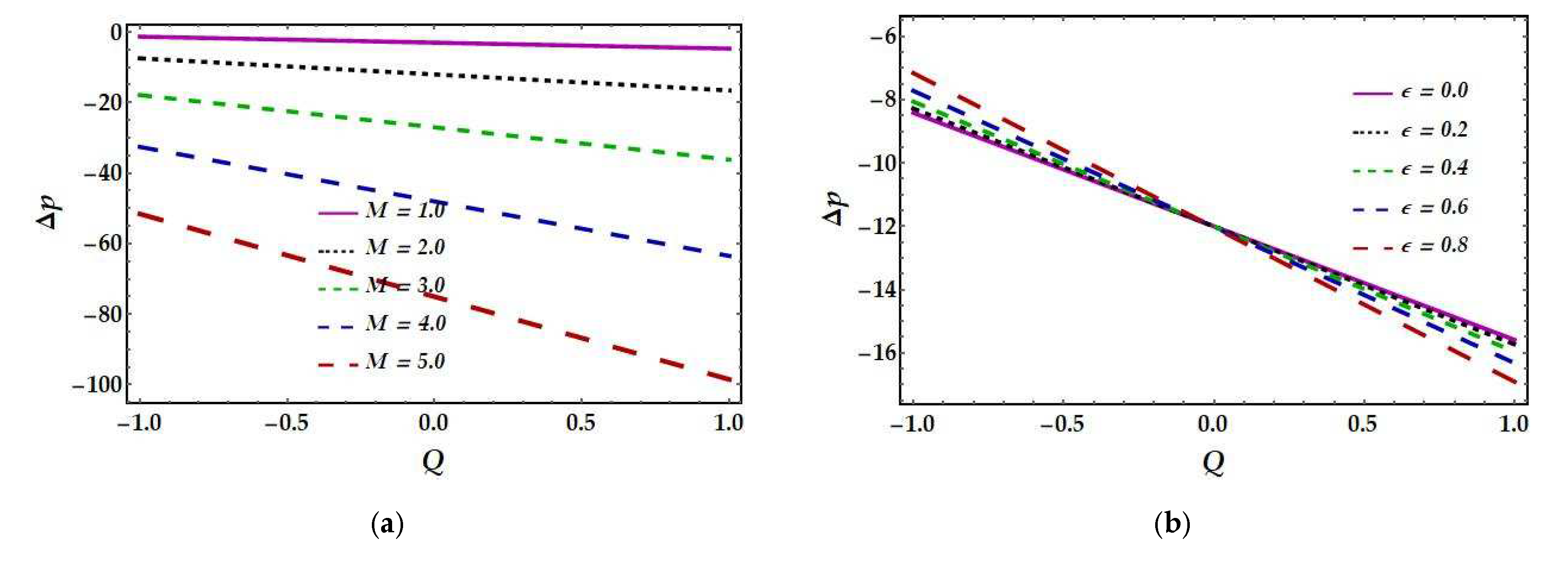
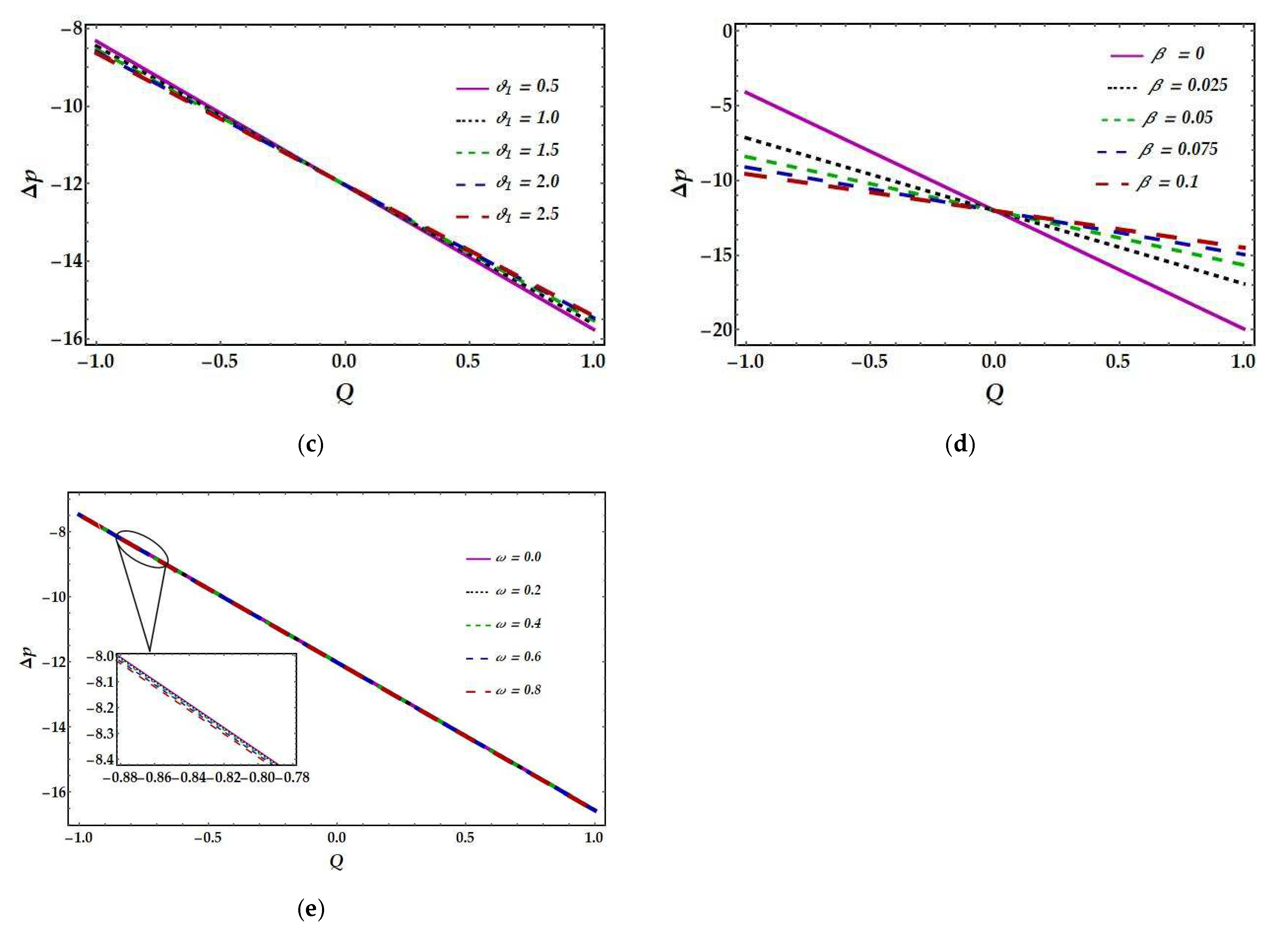
4.5. Pressure Rise

The main purpose of this part is to discuss the pumping characteristics along the whole flow region. Therefore, Figure 6a–e demonstrates the effects of the Hartmann number ($M$), Jeffrey parameter (${\vartheta }_1$), cilia length parameter ($ϵ$), the inclined angle of the unperturbed wall, and the eccentricity of an elliptical path ($\omega$) on the pressure rise profile. It can be seen in Figure 6a that as the influence of Hartmann number (M) increases, the pressure rise phenomenon is observed to decrease equally throughout the pumping region. On the other hand, the large values of the cilia length parameter ($ϵ$) show that the pumping rate increases in the region ($-1\le Q<0$) but decreases in the remaining region ($0<Q\le 1$) as illustrated in Figure 6b. Figure 6c,d shows the pumping rate rises in the region ($0<Q\le 1$) but decreases in the other region ($-1\le Q<0$) for higher values of the Jeffrey parameter (${\vartheta }_1)$ and inclined angle $\left(\beta \right)$, respectively. Figure 6e represents the decreasing behavior of the pressure rise throughout the pumping region for larger values of eccentricity parameter ($\omega$).

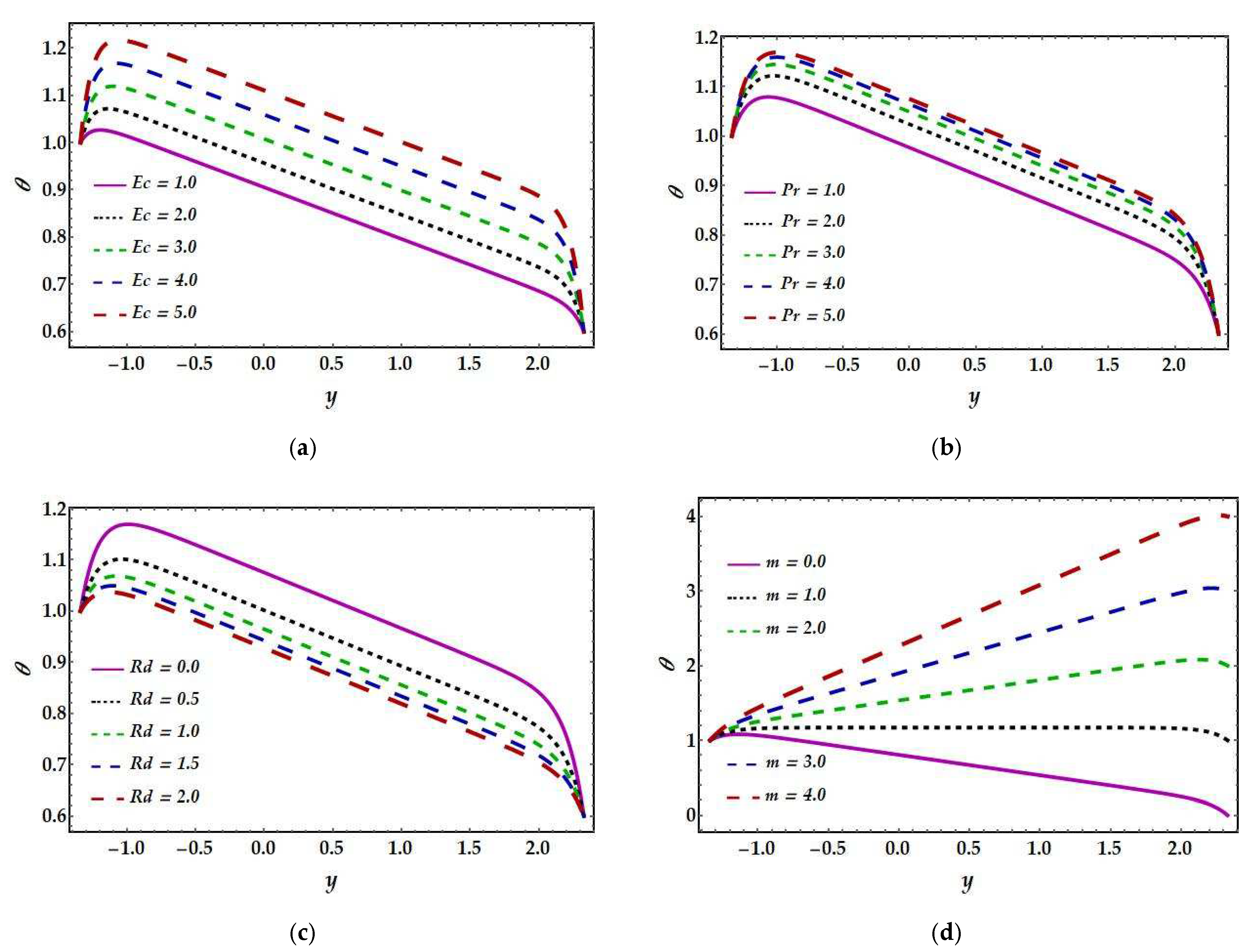
4.6. Temperature Profile

Figure 7a,b demonstrates the effects of the Prandtl number (Pr) and the Eckert number (Ec). It is observed that the nature of temperature profiles exhibits an increasing tendency concerning both parameters. As a result, we may conclude that momentum diffusivity and advective transport contribute significantly to the enhancement of temperature profiles. Figure 7c shows the behavior of thermal radiation (Rd) on the temperature profile. Thermal radiation replicates the function of radiative heat transmission compared to thermal conduction heat transfer. When $Rd=0$, the temperature profile reveals that radiation effects are absent. It can be seen that higher amounts of radiation reduce the temperature profile. Figure 7d illustrates that as the temperature ratio (m) values are increased, the temperature profile rises.

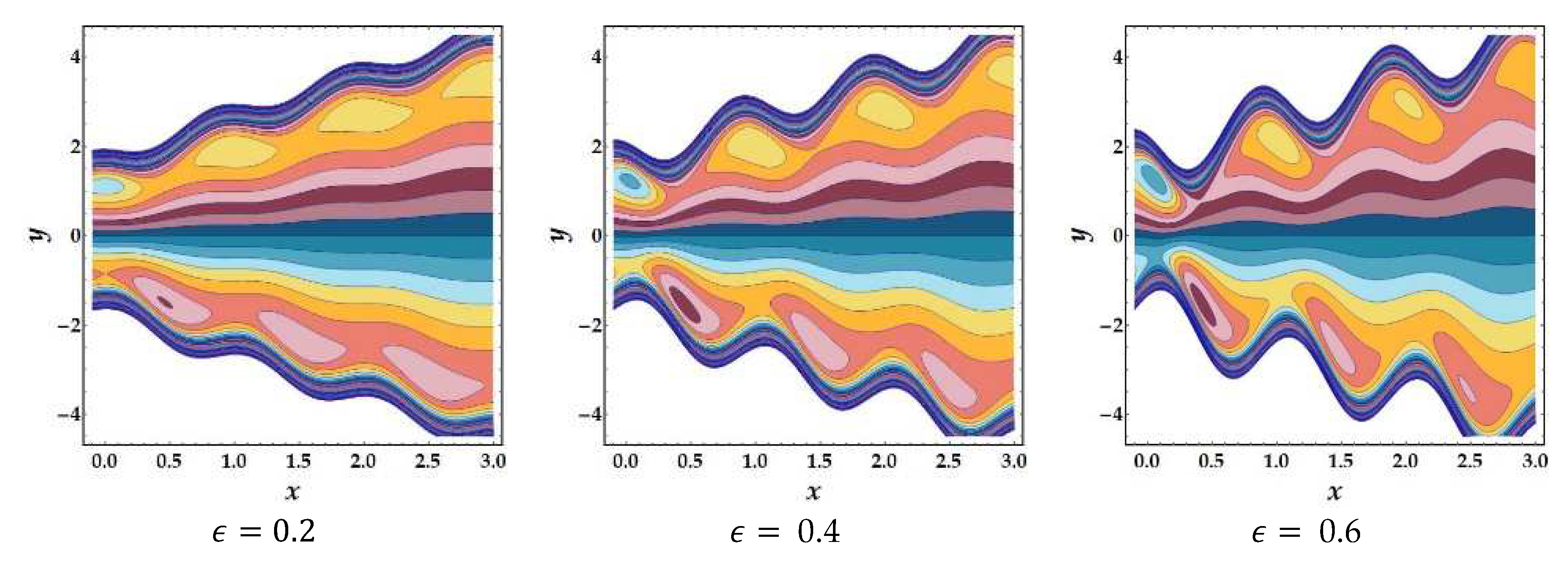
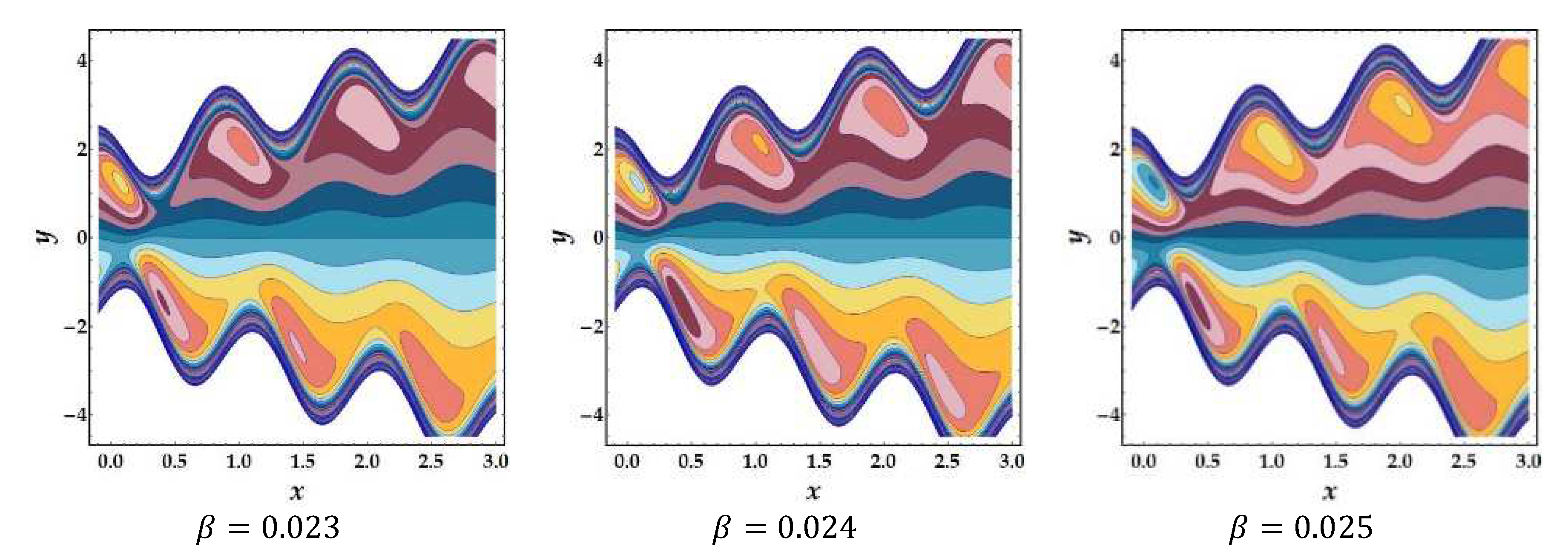
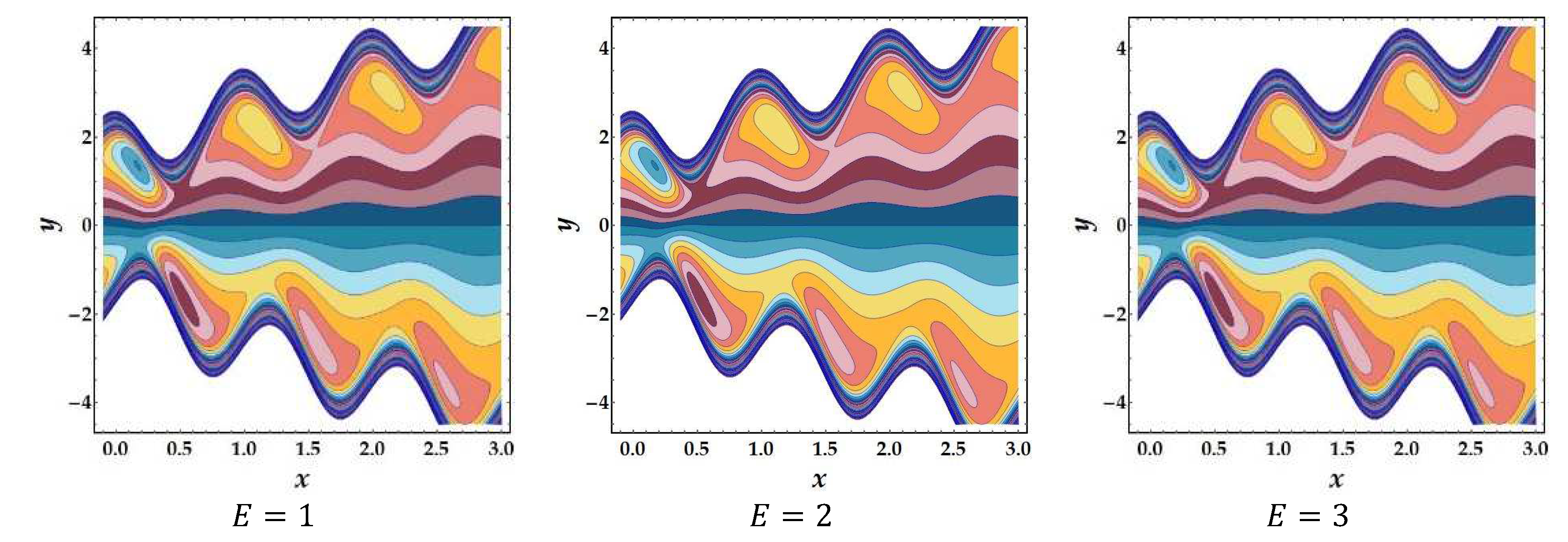
4.7. Trapping Phenomena

Trapping is another essential peristaltic transport mechanism. Trapping is the production of an inwardly flowing bolus of fluid by enclosed streamlines, which is propelled as a head together with the peristaltic wave. This physical phenomenon may be responsible for regulating blood thrombus creation and food bolus motility in the gastrointestinal system. Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13 show streamlines for all of the emerging parameters for the ciliated tapering channel. These images represent the trapping phenomena, in which a trapped bolus of fluid enveloped by streamlines moves along a metachronal wave. Figure 8 shows that as the Hartmann number (M) is increased, the number of trapped boluses diminishes. Figure 9 depicts similar results for the Jeffrey parameter (${\vartheta }_1$). The non-Newtonian effects inhibited the development of the trapping bolus, while in Figure 10 and Figure 11, the opposite behavior is noticed for cilia length $\left(ϵ\right)$ and inclined angle ($\beta$), respectively. Increased values in these parameters improve the volume and frequency of trapping boluses. Figure 12 and Figure 13 show that the number of boluses reduces initially for smaller values of electric field $\left(E\right)$ and eccentricity parameter $\left(\omega \right)$, whereas when ($E>1$) and ($\omega >0$) the effects are negligible, and no change occurs.

5. Concluding Remarks

In this study, the Jeffrey fluid model is used to evaluate cilia-driven flow through a ciliated, asymmetric tapering channel with thermally radiative heat transfer and magnetic phenomena. The suggested problem’s mathematical formulation is simplified using lubrication theory. Since the finalized differential equations are coupled and linear, we employed computer tools to find analytical solutions. The most important findings are listed below:

i.

The velocity profile decreases for large values of the Hartmann number and Jeffrey fluid parameter, while the eccentricity parameter exhibits the opposite trend.

ii.

For the velocity profile and magnetic force function, large values of the cilia length parameter exhibit an opposing tendency closer to the walls.

iii.

For a higher magnetic Reynolds number, inclined angle, and for higher eccentricity parameter values, the magnetic force function acts as an increasing function. However, for the Hartmann number and the Jeffrey parameter, the opposite result has been noticed.

iv.

The effects of the Hartmann number, Jeffrey fluid, and inclined angle on induced magnetic exhibit similar behavior, although the effects of eccentricity parameter and magnetic Reynolds number are opposite.

v.

The magnetic Reynolds number and electric field have had a considerable influence on current density, whereas the Hartmann number and Jeffrey fluid parameter have shown identical behavior.

vi.

Temperature profiles reveal rising behavior for the Eckert and Prandtl numbers but decreasing behavior for the radiation parameter.

vii.

The number of trapped boluses falls as the influence of the Hartmann number and Jeffrey fluid parameter improves but increases in the presence of the cilia length parameter and inclination angle.

viii.

For large values of the electric field and eccentricity variable, the number of trapped boluses functions similarly.