Towards the Sign Function Best Approximation for Secure Outsourced Computations and Control

Abstract

Homomorphic encryption with the ability to compute over encrypted data without access to the secret key provides benefits for the secure and powerful computation, storage, and communication of resources in the cloud. One of its important applications is fast-growing robot control systems for building lightweight, low-cost, smarter robots with intelligent brains consisting of data centers, knowledge bases, task planners, deep learning, information processing, environment models, communication support, synchronous map construction and positioning, etc. It enables robots to be endowed with secure, powerful capabilities while reducing sizes and costs. Processing encrypted information using homomorphic ciphers uses the sign function polynomial approximation, which is a widely studied research field with many practical results. State-of-the-art works are mainly focused on finding the polynomial of best approximation of the sign function (PBAS) with the improved errors on the union of the intervals $\left[-1,-ϵ\right]{{\displaystyle \cup }}^{}\left[ϵ,1\right]$. However, even though the existence of the single PBAS with the minimum deviation is well known, its construction method on the complete interval $\left[-1,1\right]$ is still an open problem. In this paper, we provide the PBAS construction method on the interval $\left[-1,1\right]$, using as a norm the area between the sign function and the polynomial and showing that for a polynomial degree $n\ge 1$, there is (1) unique PBAS of the odd sign function, (2) no PBAS of the general form sign function if $n$ is odd, and (3) an uncountable set of PBAS, if $n$ is even.

1. Introduction

Comparing numbers in a homomorphic cipher causes the problem of finding the polynomial of best approximation of the sign function (PBAS). To approximate it, various approaches are used: rational functions [1], Bernstein polynomials [2], Chebyshev polynomials of the first kind [3,4], Fourier series expansions, artificial neural networks [5], least-squares [6,7,8,9], Newton–Raphson [10], etc. In these approaches, the noncontinuous sign function is replaced by a continuous function $s\left(x\right)$ equal to:

$$s\left(x\right)=\{\begin{array}{c}1 if x>ϵ, \\ \frac{x}{ϵ}, if x\in \left[-ϵ,ϵ\right].\\ -1 otherwise \end{array}$$

The main issue is that the approximation is considered on the union of two intervals $\left[-1,-ϵ\right]{{\displaystyle \cup }}^{}\left[ϵ,1\right]$. The smallest deviation of a polynomial from the sign function is used as a measure of quality. However, this measure has a maximum error close to 0.5 in the zero neighborhood regardless of the degree of the polynomial, which makes it inapplicable for approximating a polynomial on the complete interval $\left[-1,1\right]$.

According to Chebyshev theory, there exists a single polynomial $f\left(x\right)$ for continuous function $s\left(x\right)$ with the minimum deviation $\min \underset{x\in \left[-1,1\right]}{\max }\left|s\left(x\right)-f\left(x\right)\right|$ [11], also known as minimax approximate polynomial or polynomial of best approximation.

The form of the minimax polynomial for the sign function approximation depends on $ϵ$. Various strategies for choosing $ϵ$ for polynomial approximate $s\left(x\right)$ are proposed. However, the problem of constructing PBAS remains open.

In this paper, we consider the classical definition of the sign function:

$$sign\left(x\right)=\{\begin{array}{c} 1 if x>0,\\ 0 if x=0,\\ -1 if x<0.\end{array}$$

To construct the PBAS, we use the norm as the area between the sign function and the polynomial $f\left(x\right)$, determined by the following formula.

$$\Vert f\left(x\right)\Vert ={{\displaystyle \int }}_{-1}^0\left|-1-f\left(x\right)\right|dx+{{\displaystyle \int }}_0^1\left|1-f\left(x\right)\right|dx={{\displaystyle \int }}_{-1}^0\left|1+f\left(x\right)\right|dx+{{\displaystyle \int }}_0^1\left|1-f\left(x\right)\right|dx$$

This norm allows us to avoid dramatically increasing the least deviation of the polynomial from the sign function as a result in the zero neighborhood.

Let us formulate the problem of the PBAS construction.

It is required to find the polynomial $Q_n\left(x\right)={\displaystyle \sum }_{i=0}^n{a}_i{x}^i$, where $\forall i=\overline{0,n}:a_i{x}^i$ is the $i$-th term, $a_i\in ℝ$ is a coefficient, $x$ is a variable, and $\mathrm{deg}{Q}_n\left(x\right)\le n$.

It is formally defined as follows:

$$\Vert {\displaystyle \sum }_{i=0}^n{a}_i^{\left(0\right)}{x}^i\Vert =\Delta =\underset{a_0,a_1,\dots ,a_n}{\inf }\Vert {\displaystyle \sum }_{i=0}^n{a}_i{x}^i\Vert$$

If $Q_n\left(x\right)$ exists, it is called the PBAS. In [11], p. 160, the theorem is proved that the PBAS exists. However, the number of PBAS and their form remains open. In this paper, we study these two problems.

The rest of the paper is organized as follows: Section 2 discusses the properties of the norm, which are then used in the proof. Section 3 discusses approximation of the sign function by Bernstein polynomials. It is shown that if $n\ge 1$ and $Q_n\left(x\right)$ is the PBAS, then $\Vert Q_n\left(x\right)\Vert \le 1$. Section 4 discusses the PBAS properties. Section 5 discusses the number of the PBAS odd functions. Section 6 investigates the problem of the existence of the PBAS of general form. Section 7 contains a conclusion.

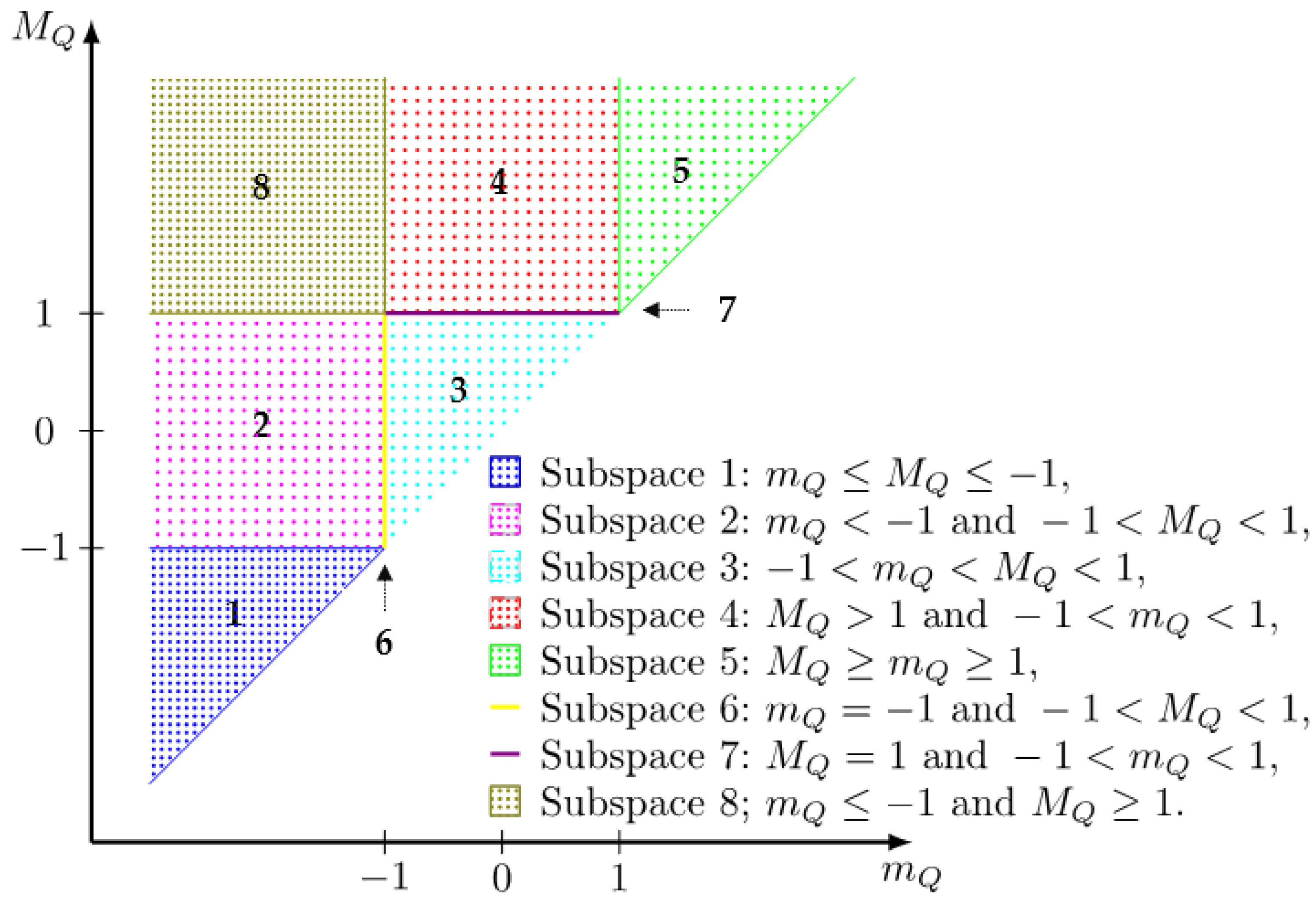
2. Norm and Its Properties

The section discusses the main properties of the norm used for the proof.

Property 1.

If$f\left(x\right)$is an even function, then$\Vert f\left(x\right)\Vert \ge 2$.

Proof. 

Since $f\left(x\right)$ is an even function, then ${{\displaystyle \int }}_{-1}^0\left|1+f\left(x\right)\right|dx={{\displaystyle \int }}_0^1\left|1+f\left(x\right)\right|dx$; therefore:

$$\begin{array}{ll}\Vert f\left(x\right)\Vert & ={{\displaystyle \int }}_0^1\left|1+f\left(x\right)\right|dx+{{\displaystyle \int }}_0^1\left|1-f\left(x\right)\right|dx\\ & ={{\displaystyle \int }}_0^1\left|1+f\left(x\right)\right|+\left|1-f\left(x\right)\right|dx\end{array}$$

considering that $\forall x\in ℝ: \left|1+f\left(x\right)\right|+\left|1-f\left(x\right)\right|\ge 2$, then

$$\Vert f\left(x\right)\Vert \ge {{\displaystyle \int }}_0^{1}2dx=2$$

The property is proven. □

Let us consider an example of calculating the norm for $n=0$.

Example 1.

(a) 

Calculate$\Vert a_0\Vert$; if$\left|a_0\right|\le 1$, then${{\displaystyle \int }}_0^1\left|1+a_0\right|+\left|1-a_0\right|dx=2$.

(b) 

Calculate$\Vert a_0\Vert$; if$\left|a_0\right|>1$, then${{\displaystyle \int }}_0^1\left|1+a_0\right|+\left|1-a_0\right|dx=2\left|a_0\right|>2$.

From the data presented in Example 1, we can conclude that for$n=0$, there is an uncountable number of PBAS, and they are given by$f\left(x\right)=a_0$, where$\left|a_0\right|\le 1$.

Property 2.

If$f\left(x\right)$is an odd function, then$\Vert f\left(x\right)\Vert =2{{\displaystyle \int }}_0^1\left|1-f\left(x\right)\right|dx$.

Proof. 

Since $f\left(x\right)$ is an odd function, then ${{\displaystyle \int }}_{-1}^0\left|1+f\left(x\right)\right|dx={{\displaystyle \int }}_0^1\left|1-f\left(x\right)\right|dx$; therefore:

$$\Vert f\left(x\right)\Vert =2{{\displaystyle \int }}_0^1\left|1-f\left(x\right)\right|dx$$

The property is proven. □

Property 3.

If$f\left(x\right)=e\left(x\right)+o\left(x\right)$is a general function, then$\Vert f\left(x\right)\Vert \ge \Vert o\left(x\right)\Vert$

, where$e\left(x\right)$is an even function and$o\left(x\right)$is an odd function.

Proof. 

$$\Vert f\left(x\right)\Vert ={{\displaystyle \int }}_{-1}^0\left|1+e\left(x\right)+o\left(x\right)\right|dx+{{\displaystyle \int }}_0^1\left|1-e\left(x\right)-o\left(x\right)\right|dx$$

Let $x=-t$, then:

$$\begin{array}{c}{{\displaystyle \int }}_{-1}^0\left|1+e\left(x\right)+o\left(x\right)\right|dx=-{{\displaystyle \int }}_1^0\left|1+e\left(-t\right)+o\left(-t\right)\right|dt\\ ={{\displaystyle \int }}_0^1\left|1+e\left(t\right)-o\left(t\right)\right|dt\end{array}$$

Therefore,

$$\begin{gathered} \Vert f\left(x\right)\Vert ={{\displaystyle \int }}_0^1\left|1-e\left(x\right)-o\left(x\right)\right|+\left|1+e\left(x\right)-o\left(x\right)\right|dx \\ \ge {{\displaystyle \int }}_0^1\left|2-2\cdot o\left(x\right)\right|dx=2{{\displaystyle \int }}_0^1\left|1-o\left(x\right)\right|dx \end{gathered}$$

According to Property 2 $\Vert o\left(x\right)\Vert =2{{\displaystyle \int }}_0^1\left|1-o\left(x\right)\right|dx$, we find:

$$\Vert f\left(x\right)\Vert \ge \Vert o\left(x\right)\Vert$$

The property is proven. □

Property 4.

$\forall \varphi \in \left(0,\frac{\pi }{2}\right):$

$$\Vert f\left(x\right)+g\left(x\right)\Vert \le {\sin }^2\varphi \Vert \frac{1}{{\sin }^2\varphi }\cdot f\left(x\right)\Vert +{\cos }^2\varphi \Vert \frac{1}{{\cos }^2\varphi }\cdot g\left(x\right)\Vert .$$

Proof. 

By the definition,

$$\Vert f\left(x\right)+g\left(x\right)\Vert ={{\displaystyle \int }}_{-1}^0\left|1+f\left(x\right)+g\left(x\right)\right|dx+{{\displaystyle \int }}_0^1\left|1-f\left(x\right)-g\left(x\right)\right|dx$$

According to the basic trigonometric identity ${\sin }^2\varphi +{\cos }^2\varphi =1$, then

$$\begin{gathered} \left|1+f\left(x\right)+g\left(x\right)\right|=\left|{\sin }^2\varphi +f\left(x\right)+{\cos }^2\varphi +g\left(x\right)\right|\le \left|{\sin }^2\varphi +f\left(x\right)\right|+\left|{\cos }^2\varphi +g\left(x\right)\right| \\ ={\sin }^2\varphi \left|1+\frac{1}{{\sin }^2\varphi }\cdot f\left(x\right)\right|+{\cos }^2\varphi \left|1+\frac{1}{{\cos }^2\varphi }\cdot g\left(x\right)\right| \end{gathered}$$

$$\begin{gathered} \left|1-f\left(x\right)-g\left(x\right)\right|=\left|{\sin }^2\varphi -f\left(x\right)+{\cos }^2\varphi -g\left(x\right)\right|\le \left|{\sin }^2\varphi -f\left(x\right)\right|+\left|{\cos }^2\varphi -g\left(x\right)\right| \\ ={\sin }^2\varphi \left|1-\frac{1}{{\sin }^2\varphi }\cdot f\left(x\right)\right|+{\cos }^2\varphi \left|1-\frac{1}{{\cos }^2\varphi }\cdot g\left(x\right)\right|. \end{gathered}$$

Therefore:

$$\Vert f\left(x\right)+g\left(x\right)\Vert \le {\sin }^2\varphi \Vert \frac{1}{{\sin }^2\varphi }\cdot f\left(x\right)\Vert +{\cos }^2\varphi \Vert \frac{1}{{\cos }^2\varphi }\cdot g\left(x\right)\Vert$$

The property is proven. □

Corollary 1.

$\forall \varphi \in \left[0,\frac{\pi }{2}\right]:$

$$\Vert {\sin }^2\varphi \cdot f\left(x\right)+{\cos }^2\varphi \cdot g\left(x\right)\Vert \le {\sin }^2\varphi \Vert f\left(x\right)\Vert +{\cos }^2\varphi \Vert g\left(x\right)\Vert .$$

Proof. 

According to Property 4 $\forall \varphi \in \left(0,\frac{\pi }{2}\right): \Vert {\sin }^2\varphi \cdot f\left(x\right)+{\cos }^2\varphi \cdot g\left(x\right)\Vert \le {\sin }^2\varphi \Vert f\left(x\right)\Vert +{\cos }^2\varphi \Vert g\left(x\right)\Vert$. Let us show that the inequality holds in the case $\varphi =0$, then $\Vert g\left(x\right)\Vert \le \Vert g\left(x\right)\Vert$ in the case $\varphi =\frac{\pi }{2}$, then $\Vert f\left(x\right)\Vert \le \Vert f\left(x\right)\Vert$.

The corollary is proven. □

Corollary 2.

If $\Vert f\left(x\right)\Vert =\Vert g\left(x\right)\Vert =a$, then $\forall \varphi \in \left[0,\frac{\pi }{2}\right]:$

$$\Vert {\sin }^2\varphi \cdot f\left(x\right)+{\cos }^2\varphi \cdot g\left(x\right)\Vert \le a$$

Proof. 

According to Corollary 1, we get:

$$\begin{gathered} \Vert {\sin }^2\varphi \cdot f\left(x\right)+{\cos }^2\varphi \cdot g\left(x\right)\Vert \le {\sin }^2\varphi \Vert f\left(x\right)\Vert +{\cos }^2\varphi \Vert g\left(x\right)\Vert \\ =a\cdot {\sin }^2\varphi +a\cdot {\cos }^2\varphi =a \end{gathered}$$

The corollary is proven. □

From Example 1, it follows that if $n=0,$ then there are infinitely many PBAS of the zero degree. If $f\left(x\right)=-1$ and $g\left(x\right)=1$, then $Q_0\left(x\right)={\sin }^2\varphi \cdot f\left(x\right)+{\cos }^2\varphi \cdot g\left(x\right)=\cos 2\varphi$ defines every PBAS of degree zero.

Let us investigate the problem of the number of PBAS of degrees greater than or equal to one.

3. Approximation of the Sign Function by Bernstein Polynomials

Let us apply the Bernstein polynomials for an approximation of the sign function $f_n\left(x\right)$.

$$f_n\left(x\right)=\frac{2n+1}{4^n}\left(\begin{array}{c}2n\\ n\end{array}\right){\displaystyle \sum }_{i=0}^n{\left(-1\right)}^i\cdot \frac{1}{2i+1}\cdot \left(\begin{array}{c}n\\ i\end{array}\right)\cdot x^{2i+1}$$

(1)

Since the function $f_n\left(x\right)$ is odd, using Property 2, we can calculate $\Vert f_n\left(x\right)\Vert$ using $\Vert f_n\left(x\right)\Vert =2{{\displaystyle \int }}_0^1\left|1-f_n\left(x\right)\right|dx$. Let us calculate the value ${{\displaystyle \int }}_0^1\left|1-f_n\left(x\right)\right|dx$, proving the following statement.

Statement 1.

$\forall n\in {\mathbb{Z}}_{+}:{{\displaystyle \int }}_0^1\left|1-f_n\left(x\right)\right|dx=\frac{2n+1}{\left(2n+2\right)4^n}\left(\begin{array}{c}2n\\ n\end{array}\right)$

Proof. 

Since the Bernstein polynomials on the interval $\left[-1,1\right]$ have the property that $\forall n\in {\mathbb{Z}}_{+},x\in \left[-1,1\right]:\left|f_n\left(x\right)\right|\le 1$,

$${{\displaystyle \int }}_0^1\left|1-f_n\left(x\right)\right|dx={{\displaystyle \int }}_0^{1}1-f_n\left(x\right)dx$$

Substituting—instead of $f_n\left(x\right)$—expression (1), we find

$$\begin{gathered} {{\displaystyle \int }}_0^1\left|1-f_n\left(x\right)\right|dx={{\displaystyle \int }}_0^{1}1-\frac{2n+1}{4^n}\left(\begin{array}{c}2n\\ n\end{array}\right){\displaystyle \sum }_{i=0}^n{\left(-1\right)}^i\cdot \frac{1}{2i+1}\cdot \left(\begin{array}{c}n\\ i\end{array}\right)\cdot x^{2i+1}dx \\ {=\left(x-\frac{2n+1}{4^n}\left(\begin{array}{c}2n\\ n\end{array}\right){\displaystyle \sum }_{i=0}^n{\left(-1\right)}^i\cdot \frac{1}{\left(2i+1\right)\left(2i+2\right)}\cdot \left(\begin{array}{c}n\\ i\end{array}\right)\cdot x^{2i+2}\right)|}_0^1 \\ =1-\frac{2n+1}{4^n}\left(\begin{array}{c}2n\\ n\end{array}\right){\displaystyle \sum }_{i=0}^n{\left(-1\right)}^i\cdot \frac{1}{\left(2i+1\right)\left(2i+2\right)}\cdot \left(\begin{array}{c}n\\ i\end{array}\right) \end{gathered}$$

We represent $\frac{1}{\left(2i+1\right)\left(2i+2\right)}$ in the form $\frac{1}{\left(2i+1\right)\left(2i+2\right)}=\frac{1}{2 i+1}-\frac{1}{2i+2}$, and we find:

$$\begin{gathered} {{\displaystyle \int }}_0^1\left|1-f_n\left(x\right)\right|dx=1-\frac{2n+1}{4^n}\left(\begin{array}{c}2n\\ n\end{array}\right){\displaystyle \sum }_{i=0}^n{\left(-1\right)}^i\cdot \frac{1}{2i+1}\cdot \left(\begin{array}{c}n\\ i\end{array}\right) \\ +\frac{2n+1}{4^n}\left(\begin{array}{c}2n\\ n\end{array}\right){\displaystyle \sum }_{i=0}^n{\left(-1\right)}^i\cdot \frac{1}{2i+2}\cdot \left(\begin{array}{c}n\\ i\end{array}\right) \end{gathered}$$

Substitute

$$\begin{gathered} {\displaystyle \sum }_{i=0}^n{\left(-1\right)}^i\cdot \frac{1}{2i+1}\cdot \left(\begin{array}{c}n\\ i\end{array}\right)=\frac{4^n}{\left(2n+1\right)\left(\begin{array}{c}2n\\ n\end{array}\right)} \\ {\displaystyle \sum }_{i=0}^n{\left(-1\right)}^i\cdot \frac{1}{2i+2}\cdot \left(\begin{array}{c}n\\ i\end{array}\right)=\frac{1}{2n+2} \end{gathered}$$

Hence,

$${{\displaystyle \int }}_0^1\left|1-f_n\left(x\right)\right|dx=\frac{2n+1}{\left(2n+2\right)4^n}\left(\begin{array}{c}2n\\ n\end{array}\right)$$

The statement is proven. □

Corollary 3.

$\forall n\in {\mathbb{Z}}_{+}:\Vert f_n\left(x\right)\Vert \le \min \left(1, \frac{2}{\sqrt{3n+1}}\right)$

Proof. 

Since $f_n\left(x\right)$ is an odd function, according to Property 2:

$$\Vert f\left(x\right)\Vert =2{{\displaystyle \int }}_0^1\left|1-f\left(x\right)\right|dx$$

Let $n\ge 1:$

$$\Vert f_n\left(x\right)\Vert =2\cdot \frac{2n+1}{\left(2n+2\right)4^n}\left(\begin{array}{c}2n\\ n\end{array}\right)<\frac{2}{4^n}\left(\begin{array}{c}2n\\ n\end{array}\right)\le \frac{2}{\sqrt{3n+1}}\le 1$$

if $n=0$, then $\Vert x\Vert =1$; therefore $\forall n\in {\mathbb{Z}}_{+}$: $\Vert f_n\left(x\right)\Vert \le 1$.

The corollary is proven. □

From Property 1 and Corollary 3, we can conclude that if $n\ge 1$, the PBAS is not an even function.

4. Properties of the PBAS

Since the polynomial $Q_n\left(x\right)$ is a continuous function on the interval $\left[-1,1\right]$, according to the Weierstrass theorem, it is bounded by this in interval and reaches the minimum and maximum values—that is, there are $x_m,x_M\in \left[-1,1\right]$ such that $\forall x\in \left[-1,1\right]:Q_n\left(x_m\right)\le Q_n\left(x\right)\le Q_n\left(x_M\right)$. Let us denote $m_Q=Q_n\left(x_m\right)$ and $M_Q=Q_n\left(x_M\right)$, and $m_Q\le M_Q$. Let us investigate the values of $m_Q$ and $M_Q$ for the PBAS $Q_n\left(x\right)$. The result is presented in the form of the following lemma.

Lemma 1.

If n ≥ 1 and $Q_n\left(x\right)$ is the PBAS, then $m_Q\le -1$ and $M_Q\ge 1$.

Proof. 

We split the two-dimensional space ${ℝ}^2$ into subspaces using the curves $m_Q=\pm 1$ and $M_Q=\pm 1$ (see Figure 1).

Figure 1. The set of possible values $m_Q$ and $M_Q$.

In the following, we consider each subspace separately.

Subspace 1. Let us assume that PBAS $Q_n\left(x\right)$ satisfies the condition: $m_Q\le M_Q\le -1$ (see Figure 1, Subspace 1), then $\forall x\in \left[-1,1\right]:Q_n\left(x\right)\le -1$, $1+Q_n\left(x\right)\le 0, 1-Q_n\left(x\right)\ge 0$; therefore:

$$\begin{gathered} \Vert Q_n\left(x\right)\Vert ={{\displaystyle \int }}_{-1}^0\left|1+Q_n\left(x\right)\right|dx+{{\displaystyle \int }}_0^1\left|1-Q_n\left(x\right)\right|dx \\ ={{\displaystyle \int }}_{-1}^0-1-Q_n\left(x\right)dx+{{\displaystyle \int }}_0^{1}1-Q_n\left(x\right)dx=-{{\displaystyle \int }}_{-1}^1{Q}_n\left(x\right)dx\ge -{{\displaystyle \int }}_{-1}^1-1dx=2 \end{gathered}$$

From Corollary 3, it follows that for $n\ge 1$ the PBAS has the property $\Vert Q_n\left(x\right)\Vert \le 1$. Therefore, we came to a contradiction and our assumption is not correct.

Subspace 2. Let us assume that the PBAS $Q_n\left(x\right)$ satisfies the condition: $m_Q<-1$ and $-1<M_Q<1$ (see Figure 1, Subspace 2), then $\forall x\in \left[-1,1\right]: 1-Q_n\left(x\right)\ge 0$ and $1-Q_n\left(x\right)\ge 0$:

$$\Vert Q_n\left(x\right)\Vert ={{\displaystyle \int }}_{-1}^0\left|1+Q_n\left(x\right)\right|dx+{{\displaystyle \int }}_0^{1}1-Q_n\left(x\right)dx$$

We calculate $\Vert Q_n\left(x\right)+1-M_Q\Vert$ and find

$$\Vert Q_n\left(x\right)+1-M_Q\Vert ={{\displaystyle \int }}_{-1}^0\left|2+Q_n\left(x\right)-M_Q\right|dx+{{\displaystyle \int }}_0^1{M}_Q-Q_n\left(x\right)dx$$

We subtract from $\Vert Q_n\left(x\right)\Vert$ the value $\Vert Q_n\left(x\right)+1-M_Q\Vert$ and find:

$$\begin{gathered} \Vert Q_n\left(x\right)\Vert -\Vert Q_n\left(x\right)+1-M_Q\Vert ={{\displaystyle \int }}_{-1}^0\left|1+Q_n\left(x\right)\right|-\left|2+Q_n\left(x\right)-M_Q\right|dx+1-M_Q \\ ={{\displaystyle \int }}_{-1}^0\left|1+Q_n\left(x\right)\right|-\left|2+Q_n\left(x\right)-M_Q\right|+1-M_{Q}dx \end{gathered}$$

Considering that

$$\forall x\in \left[-1,0\right]:\left|2+Q_n\left(x\right)-M_Q\right|\le \left|1+Q_n\left(x\right)\right|+\left|1-M_Q\right|=\left|1+Q_n\left(x\right)\right|+1-M_Q,$$

then

$$\left|1+Q_n\left(x\right)\right|-\left|2+Q_n\left(x\right)-M_Q\right|+1-M_Q\ge 0$$

Therefore, $\Vert Q_n\left(x\right)\Vert -\Vert Q_n\left(x\right)+1-M_Q\Vert \ge 0$. If $\Vert Q_n\left(x\right)\Vert -\Vert Q_n\left(x\right)+1-M_Q\Vert >0$, then $Q_n\left(x\right)$ is not a PBAS, so $\Vert Q_n\left(x\right)\Vert -\Vert Q_n\left(x\right)+1-M_Q\Vert =0$; then, $\forall x\in \left[-1,0\right]:1+Q_n\left(x\right)\ge 0$ and

$$\Vert Q_n\left(x\right)\Vert ={{\displaystyle \int }}_{-1}^0\left|1+Q_n\left(x\right)\right|dx+{{\displaystyle \int }}_0^{1}1-Q_n\left(x\right)dx=2+{{\displaystyle \int }}_{-1}^0{Q}_n\left(x\right)dx-{{\displaystyle \int }}_0^1{Q}_n\left(x\right)dx$$

Let $\lambda =\frac{2}{1+M_Q}>1$, then

$$\begin{gathered} \forall x\in \left[-1,0\right]: \lambda Q_n\left(x\right)+\frac{1-M_Q}{1+M_Q}+1=\lambda Q_n\left(x\right)+\lambda =\lambda \left(Q_n\left(x\right)+1\right)\ge 0 \\ \forall x\in \left[-1,0\right]:1-\lambda Q_n\left(x\right)-\frac{1-M_Q}{1+M_Q}=\lambda M_Q-\lambda Q_n\left(x\right)=\lambda \left(M_Q-Q_n\left(x\right)\right)\ge 0 \end{gathered}$$

Therefore,

$$\begin{gathered} \Vert \lambda Q_n\left(x\right)+\frac{1-M_Q}{1+M_Q}\Vert =\lambda {{\displaystyle \int }}_{-1}^{0}1+Q_n\left(x\right)dx+\lambda {{\displaystyle \int }}_0^1{M}_Q-Q_n\left(x\right)dx \\ =\lambda \cdot \left(1+M_Q\right)+\lambda \left({{\displaystyle \int }}_{-1}^0{Q}_n\left(x\right)dx-{{\displaystyle \int }}_0^1{Q}_n\left(x\right)dx\right)=2+\lambda \left({{\displaystyle \int }}_{-1}^0{Q}_n\left(x\right)dx-{{\displaystyle \int }}_0^1{Q}_n\left(x\right)dx\right) \end{gathered}$$

since $\lambda >1$ и ${{\displaystyle \int }}_{-1}^0{Q}_n\left(x\right)dx-{{\displaystyle \int }}_0^1{Q}_n\left(x\right)dx\le -1$, then

$$\lambda \left({{\displaystyle \int }}_{-1}^0{Q}_n\left(x\right)dx-{{\displaystyle \int }}_0^1{Q}_n\left(x\right)dx\right)<{{\displaystyle \int }}_{-1}^0{Q}_n\left(x\right)dx-{{\displaystyle \int }}_0^1{Q}_n\left(x\right)dx$$

Therefore,

$$\Vert \lambda Q_n\left(x\right)+\frac{1-M_Q}{1+M_Q}\Vert <\Vert Q_n\left(x\right)\Vert$$

it means that $Q_n\left(x\right)$ is not a PBAS. We came to a contradiction.

Subspace 3. Let us assume that the PBAS $Q_n\left(x\right)$ satisfies the condition: $-1<m_Q<M_Q<1$ (see Figure 1, Subspace 3), then $\forall x\in \left[-1,1\right]:-1<Q_n\left(x\right)<1$, $1+Q_n\left(x\right)>0, 1-Q_n\left(x\right)>0$. Let $M=\max \left(\left|m_Q\right|,\left|M_Q\right|\right)<1$. If $M=0$, then $Q_n\left(x\right)=0$ and $\Vert Q_n\left(x\right)\Vert =2$; from the other side, $\forall n\ge 1:\Vert Q_n\left(x\right)\Vert \le 1$. Therefore, we came to a contradiction and $M\ne 0$. Let $\lambda =\frac{1}{M}>1$ and $\forall x\in \left[-1,1\right]:-1\le \lambda Q_n\left(x\right)\le 1$, $1+\lambda Q_n\left(x\right)>0, 1-\lambda Q_n\left(x\right)>0$. We calculate the value $\Vert Q_n\left(x\right)\Vert$ and find:

$$\Vert Q_n\left(x\right)\Vert ={{\displaystyle \int }}_{-1}^{0}1+Q_n\left(x\right)dx+{{\displaystyle \int }}_0^{1}1-Q_n\left(x\right)dx=2+\left({{\displaystyle \int }}_{-1}^0{Q}_n\left(x\right)dx-{{\displaystyle \int }}_0^1{Q}_n\left(x\right)dx\right)$$

Since, according to the conditions of Theorem 1 and Corollary 3, $n\ge 1$ and $\Vert Q_n\left(x\right)\Vert \le 1$. Hence,

$${{\displaystyle \int }}_{-1}^0{Q}_n\left(x\right)dx-{{\displaystyle \int }}_0^1{Q}_n\left(x\right)dx\le -1.$$

We calculate $\Vert \lambda \cdot Q_n\left(x\right)\Vert$ and find

$$\begin{gathered} \Vert \lambda \cdot Q_n\left(x\right)\Vert ={{\displaystyle \int }}_{-1}^{0}1+\lambda \cdot Q_n\left(x\right)dx+{{\displaystyle \int }}_0^{1}1-\lambda \cdot Q_n\left(x\right)dx \\ =2+\lambda \left({{\displaystyle \int }}_{-1}^0{Q}_n\left(x\right)dx-{{\displaystyle \int }}_0^1{Q}_n\left(x\right)dx\right) \end{gathered}$$

Since $\lambda >1$ и ${{\displaystyle \int }}_{-1}^0{Q}_n\left(x\right)dx-{{\displaystyle \int }}_0^1{Q}_n\left(x\right)dx\le -1$,

$$\lambda \left({{\displaystyle \int }}_{-1}^0{Q}_n\left(x\right)dx-{{\displaystyle \int }}_0^1{Q}_n\left(x\right)dx\right)<{{\displaystyle \int }}_{-1}^0{Q}_n\left(x\right)dx-{{\displaystyle \int }}_0^1{Q}_n\left(x\right)dx$$

Therefore,

$$2+\lambda \left({{\displaystyle \int }}_{-1}^0{Q}_n\left(x\right)dx-{{\displaystyle \int }}_0^1{Q}_n\left(x\right)dx\right)<2+\left({{\displaystyle \int }}_{-1}^0{Q}_n\left(x\right)dx-{{\displaystyle \int }}_0^1{Q}_n\left(x\right)dx\right)$$

and

$$\Vert \lambda \cdot Q_n\left(x\right)\Vert <\Vert Q_n\left(x\right)\Vert$$

Therefore, we came to a contradiction and our assumption is not correct.

Subspace 4. Let us assume that the PBAS $Q_n\left(x\right)$ satisfies the condition: $M_Q>1$ and $-1<m_Q<1$ (see Figure 1, Subspace 4).

$$\Vert Q_n\left(x\right)\Vert ={{\displaystyle \int }}_{-1}^{0}1+Q_n\left(x\right)dx+{{\displaystyle \int }}_0^1\left|1-Q_n\left(x\right)\right|dx$$

we calculate $\Vert Q_n\left(x\right)-1-m_Q\Vert$ and get

$$\Vert Q_n\left(x\right)-1-m_Q\Vert ={{\displaystyle \int }}_{-1}^0{Q}_n\left(x\right)-m_{Q}dx+{{\displaystyle \int }}_0^1\left|2-Q_n\left(x\right)+m_Q\right|dx$$

we subtract from $\Vert Q_n\left(x\right)\Vert$ the value $\Vert Q_n\left(x\right)-1-m_Q\Vert$ and get:

$$\begin{gathered} \Vert Q_n\left(x\right)\Vert -\Vert Q_n\left(x\right)-1-m_Q\Vert =1+m_Q+{{\displaystyle \int }}_0^1\left|1-Q_n\left(x\right)\right|-\left|2-Q_n\left(x\right)+m_Q\right|dx \\ ={{\displaystyle \int }}_0^1\left|1-Q_n\left(x\right)\right|-\left|2-Q_n\left(x\right)+m_Q\right|+1+m_{Q}dx \end{gathered}$$

Considering that $\forall x\in \left[0,1\right]:\left|2-Q_n\left(x\right)+m_Q\right|\le \left|1-Q_n\left(x\right)\right|+\left|1+m_Q\right|=\left|1-Q_n\left(x\right)\right|+1+m_Q,$ then $\forall x\in \left[0,1\right]:\left|1-Q_n\left(x\right)\right|-\left|2-Q_n\left(x\right)+m_Q\right|+1+m_Q\ge 0$; therefore, $\Vert Q_n\left(x\right)\Vert -\Vert Q_n\left(x\right)-1-m_Q\Vert \ge 0$. If $\Vert Q_n\left(x\right)\Vert -\Vert Q_n\left(x\right)-1-m_Q\Vert >0$, then $Q_n\left(x\right)$ is not a PBAS, so $\Vert Q_n\left(x\right)\Vert -\Vert Q_n\left(x\right)-1-m_Q\Vert =0$ and $\forall x\in \left[0,1\right]:1-Q_n\left(x\right)\ge 0$ and

$$\Vert Q_n\left(x\right)\Vert =2+{{\displaystyle \int }}_{-1}^0{Q}_n\left(x\right)dx-{{\displaystyle \int }}_0^1{Q}_n\left(x\right)dx$$

let $\lambda =\frac{2}{1-m_Q}>1$, then

$$\begin{gathered} \forall x\in \left[-1,0\right]: \lambda Q_n\left(x\right)-\frac{1+m_Q}{1-m_Q}+1=\lambda Q_n\left(x\right)-\lambda m_Q=\lambda \left(Q_n\left(x\right)-m_Q\right)\ge 0 \\ \forall x\in \left[0,1\right]: 1-\lambda Q_n\left(x\right)+\frac{1+m_Q}{1-m_Q}=\lambda -\lambda Q_n\left(x\right)=\mathsf{\lambda }\left(1-Q_n\left(x\right)\right)\ge 0 \end{gathered}$$

Therefore,

$$\begin{gathered} \Vert \lambda Q_n\left(x\right)-\frac{1+m_Q}{1-m_Q}\Vert =\lambda {{\displaystyle \int }}_{-1}^0{Q}_n\left(x\right)-m_{Q}dx+\lambda {{\displaystyle \int }}_0^{1}1-Q_n\left(x\right)dx \\ =2+\lambda \left({{\displaystyle \int }}_{-1}^0{Q}_n\left(x\right)dx-{{\displaystyle \int }}_0^1{Q}_n\left(x\right)dx\right) \end{gathered}$$

since $\lambda >1$ and ${{\displaystyle \int }}_{-1}^0{Q}_n\left(x\right)dx-{{\displaystyle \int }}_0^1{Q}_n\left(x\right)dx\le -1$, then

$$\left({{\displaystyle \int }}_{-1}^0{Q}_n\left(x\right)dx-{{\displaystyle \int }}_0^1{Q}_n\left(x\right)dx\right)<{{\displaystyle \int }}_{-1}^0{Q}_n\left(x\right)dx-{{\displaystyle \int }}_0^1{Q}_n\left(x\right)dx$$

Therefore,

$$\Vert \lambda Q_n\left(x\right)-\frac{1+m_Q}{1-m_Q}\Vert <Q_n\left(x\right)$$

it means that $Q_n\left(x\right)$ is not a PBAS. We came to a contradiction.

Subspace 5. Let us assume that the PBAS $Q_n\left(x\right)$ satisfies the condition: $M_Q\ge m_Q\ge 1$ (see Figure 1, Subspace 5); therefore, $\forall x\in \left[-1,1\right]:Q_n\left(x\right)\ge 1$, $1+Q_n\left(x\right)\ge 0, 1-Q_n\left(x\right)\le 0$ means

$$\begin{gathered} \Vert Q_n\left(x\right)\Vert ={{\displaystyle \int }}_{-1}^0\left|1+Q_n\left(x\right)\right|dx+{{\displaystyle \int }}_0^1\left|1-Q_n\left(x\right)\right|dx \\ ={{\displaystyle \int }}_{-1}^{0}1+Q_n\left(x\right)dx+{{\displaystyle \int }}_0^1{Q}_n\left(x\right)-1dx={{\displaystyle \int }}_{-1}^1{Q}_n\left(x\right)dx\ge {{\displaystyle \int }}_{-1}^{1}1dx=2 \end{gathered}$$

From Corollary 3, it follows that for $n\ge 1$, the PBAS has the property $\Vert Q_n\left(x\right)\Vert \le 1$. This means that we have come to a contradiction and our assumption is not correct.

Subspace 6. Let us assume that the PBAS $Q_n\left(x\right)$ satisfies the condition: $m_Q=-1$ and $-1<M_Q<1$ (see Figure 1, Subspace 6), then

$$\begin{gathered} \Vert Q_n\left(x\right)\Vert ={{\displaystyle \int }}_{-1}^{0}1+Q_n\left(x\right)dx+{{\displaystyle \int }}_0^{1}1-Q_n\left(x\right)dx \\ =2+{{\displaystyle \int }}_{-1}^0{Q}_n\left(x\right)dx-{{\displaystyle \int }}_0^1{Q}_n\left(x\right)dx \end{gathered}$$

Let $\lambda =\frac{2}{1+M_Q}>1$, then

$$\begin{gathered} \forall x\in \left[-1,0\right]:\lambda Q_n\left(x\right)+\frac{1-M_Q}{1+M_Q}+1=\lambda +\lambda Q_n\left(x\right)=\lambda \left(1+Q_n\left(x\right)\right)\ge 0 \\ \forall x\in \left[0,1\right]: 1-\lambda Q_n\left(x\right)-\frac{1-M_Q}{1+M_Q}=\lambda M_Q-\lambda Q_n\left(x\right)=\lambda \left(M_Q-Q_n\left(x\right)\right)\ge 0 \end{gathered}$$

Therefore,

$$\begin{gathered} \Vert \lambda Q_n\left(x\right)+\frac{1-M_Q}{1+M_Q}\Vert ={{\displaystyle \int }}_{-1}^0\lambda +\lambda Q_n\left(x\right)dx+{{\displaystyle \int }}_0^1\lambda M_Q-\lambda Q_n\left(x\right)dx \\ =2+\lambda \left({{\displaystyle \int }}_{-1}^0{Q}_n\left(x\right)dx-{{\displaystyle \int }}_0^1{Q}_n\left(x\right)dx\right) \end{gathered}$$

Since $\lambda >1$ и ${{\displaystyle \int }}_{-1}^0{Q}_n\left(x\right)dx-{{\displaystyle \int }}_0^1{Q}_n\left(x\right)dx\le -1$,

$$\lambda \left({{\displaystyle \int }}_{-1}^0{Q}_n\left(x\right)dx-{{\displaystyle \int }}_0^1{Q}_n\left(x\right)dx\right)<{{\displaystyle \int }}_{-1}^0{Q}_n\left(x\right)dx-{{\displaystyle \int }}_0^1{Q}_n\left(x\right)dx$$

Therefore,

$$\Vert \lambda Q_n\left(x\right)+\frac{1-M_Q}{1+M_Q}\Vert <Q_n\left(x\right)$$

This means that $Q_n\left(x\right)$ is not a PBAS.

Subspace 7. Let us assume that $Q_n\left(x\right)$ satisfies the condition: $M_Q=1$ and $-1<m_Q<1$ (see Figure 1, Subspace 7). Then,

$$\begin{gathered} \Vert Q_n\left(x\right)\Vert ={{\displaystyle \int }}_{-1}^{0}1+Q_n\left(x\right)dx+{{\displaystyle \int }}_0^{1}1-Q_n\left(x\right)dx \\ =2+{{\displaystyle \int }}_{-1}^0{Q}_n\left(x\right)dx-{{\displaystyle \int }}_0^1{Q}_n\left(x\right)dx \end{gathered}$$

Let $\lambda =\frac{2}{1-m_Q}>1$, then

$$\begin{gathered} \forall x\in \left[-1,0\right]: \lambda Q_n\left(x\right)-\frac{1+m_Q}{1-m_Q}+1=\lambda Q_n\left(x\right)-\lambda m_Q=\lambda \left(Q_n\left(x\right)-m_Q\right)\ge 0 \\ \forall x\in \left[0,1\right]:1-\lambda Q_n\left(x\right)+\frac{1+m_Q}{1-m_Q}=\lambda -\lambda Q_n\left(x\right)=\lambda \left(1-Q_n\left(x\right)\right) \ge 0 \end{gathered}$$

Therefore,

$$\begin{gathered} \Vert \lambda Q_n\left(x\right)-\frac{1+m_Q}{1-m_Q}\Vert =\lambda {{\displaystyle \int }}_{-1}^0{Q}_n\left(x\right)-m_{Q}dx+\lambda {{\displaystyle \int }}_0^{1}1-Q_n\left(x\right)dx \\ =2+\lambda \left({{\displaystyle \int }}_{-1}^0{Q}_n\left(x\right)dx-{{\displaystyle \int }}_0^1{Q}_n\left(x\right)dx\right) \end{gathered}$$

Since $\lambda >1$ and ${{\displaystyle \int }}_{-1}^0{Q}_n\left(x\right)dx-{{\displaystyle \int }}_0^1{Q}_n\left(x\right)dx\le -1$,

$$\lambda \left({{\displaystyle \int }}_{-1}^0{Q}_n\left(x\right)dx-{{\displaystyle \int }}_0^1{Q}_n\left(x\right)dx\right)<{{\displaystyle \int }}_{-1}^0{Q}_n\left(x\right)dx-{{\displaystyle \int }}_0^1{Q}_n\left(x\right)dx$$

Therefore,

$$\Vert \lambda Q_n\left(x\right)-\frac{1+m_Q}{1-m_Q}\Vert <Q_n\left(x\right)$$

This means that $Q_n\left(x\right)$ is not a PBAS.

Subspace 8. Since in all seven cases we have come to a contradiction, if $Q_n\left(x\right)$ is a PBAS, it satisfies the boundary conditions defining Subspace 8 (See, Figure 1).

Lemma 1 is proven. □

Lemma 2.

For$n\ge 1$, there exists the PBAS odd function$Q_n^1\left(x\right)$.

Proof. 

The existence of the PBAS $Q_n\left(x\right)$ follows from Theorem [11] p. 160. Since for $n\ge 1$, the PBAS $Q_n\left(x\right)$ is not an even function, so $Q_n\left(x\right)$ is either a general function or an odd function.

Let us assume that $Q_n\left(x\right)$ is a general function; it can be represented in the form $Q_n\left(x\right)=Q_n^0\left(x\right)+Q_n^1\left(x\right)$, where $Q_n^0\left(x\right)$ is an even function and $Q_n^1\left(x\right)$ is an odd function. It follows from Property 3 that $\Vert Q_n\left(x\right)\Vert \ge \Vert Q_n^1\left(x\right)\Vert$. Considering that $Q_n\left(x\right)$ is the PBAS, $\Vert Q_n\left(x\right)\Vert =\Vert Q_n^1\left(x\right)\Vert$, so the odd function $Q_n^1\left(x\right)$ is the PBAS. Therefore, for any $n\ge 1$, there is the PBAS $Q_n\left(x\right)$, which is an odd function.

Lemma 2 is proven. □

Corollary 4.

Let$n\ge 1$,$Q_n^1\left(x\right)$be a PBAS odd function, $M_Q>1$, and $m_Q<-1$.

Proof. 

We assume that PBAS is the odd function $Q_n^1\left(x\right)$ and $M_Q=-m_Q=1$.

Let us consider the function $R\left(x\right)=\lambda Q_n^1\left(x\right)$, where $\lambda \in ℝ$. Since $Q_n^1\left(x\right)$ is an odd function, $R\left(x\right)$ is also an odd function. We calculate $\Vert Q_n^1\left(x\right)\Vert$ and $\Vert R\left(x\right)\Vert$ using Property 2 and find:

$$\begin{gathered} \Vert Q_n^1\left(x\right)\Vert =2{{\displaystyle \int }}_0^{1}1-Q_n^1\left(x\right)dx \\ \Vert R\left(x\right)\Vert =2{{\displaystyle \int }}_0^1\left|1-\lambda Q_n^1\left(x\right)\right|dx \end{gathered}$$

Let us show that there exists $\lambda >1$, for which the inequality $\Vert Q_n^1\left(x\right)\Vert >\Vert R\left(x\right)\Vert$ is satisfied.

$$\begin{gathered} {{\displaystyle \int }}_0^{1}1-Q_n^1\left(x\right)dx>{{\displaystyle \int }}_0^1\left|1-\lambda Q_n^1\left(x\right)\right|dx \\ {{\displaystyle \int }}_0^{1}1-Q_n^1\left(x\right)-\left|1-\lambda Q_n^1\left(x\right)\right|dx>0 \end{gathered}$$

We denote as $G_{+}$ a set of all $x\in \left[0,1\right]$ for which the inequality $1-\lambda Q_n^1\left(x\right)\ge 0$ holds and $G_{-}$ for which the inequality $1-\lambda Q_n^1\left(x\right)\le 0$ holds. We then find:

$$\begin{gathered} {{\displaystyle \int }}_0^{1}1-Q_n^1\left(x\right)-\left|1-\lambda Q_n^1\left(x\right)\right|dx=\underset{G_{+}}{{\displaystyle \int }}\lambda Q_n^1\left(x\right)-Q_n^1\left(x\right)dx+\underset{G_{-}}{{\displaystyle \int }}2-Q_n^1\left(x\right)-\lambda Q_n^1\left(x\right)dx \\ =\left(\lambda -1\right)\underset{G_{+}}{{\displaystyle \int }}{Q}_n^1\left(x\right)dx+\underset{G_{-}}{{\displaystyle \int }}2-Q_n^1\left(x\right)-\lambda Q_n^1\left(x\right)dx \\ =\left(\lambda -1\right)\underset{G_{+}}{{\displaystyle \int }}{Q}_n^1\left(x\right)dx+\underset{G_{-}}{{\displaystyle \int }}2dx-\underset{G_{-}}{{\displaystyle \int }}{Q}_n^1\left(x\right)+\lambda Q_n^1\left(x\right)dx \\ =\left(\lambda -1\right)\underset{G_{+}}{{\displaystyle \int }}{Q}_n^1\left(x\right)dx+2\left|G_{-}\right|-\left(1+\lambda \right)\underset{G_{-}}{{\displaystyle \int }}{Q}_n^1\left(x\right)dx \\ =\lambda \left(\underset{G_{+}}{{\displaystyle \int }}{Q}_n^1\left(x\right)dx-\underset{G_{-}}{{\displaystyle \int }}{Q}_n^1\left(x\right)dx\right)+2\left|G_{-}\right|-{{\displaystyle \int }}_0^1{Q}_n^1\left(x\right)dx \\ =\lambda \left({{\displaystyle \int }}_0^1{Q}_n^1\left(x\right)dx-2\underset{G_{-}}{{\displaystyle \int }}{Q}_n^1\left(x\right)dx\right)+2\left|G_{-}\right|-{{\displaystyle \int }}_0^1{Q}_n^1\left(x\right)dx \\ \ge \lambda {{\displaystyle \int }}_0^1{Q}_n^1\left(x\right)dx-2\lambda \left|G_{-}\right|+2\left|G_{-}\right|-{{\displaystyle \int }}_0^1{Q}_n^1\left(x\right)dx=\left(\lambda -1\right)\left({{\displaystyle \int }}_0^1{Q}_n^1\left(x\right)dx-2\left|G_{-}\right|\right) \end{gathered}$$

where $\left|G_{-}\right|$ is the length of the set $G_{-}$.

We denote $g\left(\lambda \right)=\left\{\left|G_{-}\right|\right|G_{-}=\left\{x\right|1-\lambda Q_n^1\left(x\right)\le 0\& 0\le x\le 1\left\}\right\}$.

Since $n\ge 1$ and $\forall x\in \left[0,1\right]: Q_n^1\left(x\right)\le 1$, then $g\left(1\right)=0$ and $\forall \lambda >1: g\left(\lambda \right)<1$.

Let us consider two cases.

Case 1: If $\forall x\in \left[0,1\right]: Q_n^1\left(x\right)<1$, then there is such a number $x_a\in \left[0,1\right]$ for which $\forall x\in \left[0,1\right]: Q_n^1\left(x\right)\le Q_n^1\left(x_a\right)=M_Q^a$ holds. If $M_Q^a\le 0$, then ${{\displaystyle \int }}_0^{1}1-Q_n^1\left(x\right)dx\ge 1$; therefore, $\Vert Q_n^1\left(x\right)\Vert \ge 2>1$ so $Q_n^1\left(x\right)$ is not the PBAS. If $M_Q^a>0$, we choose as $\lambda$ the value $\lambda =\frac{1}{M_Q^a}>1$, for which the inequality $\Vert Q_n^1\left(x\right)\Vert >\Vert R\left(x\right)\Vert$ holds, and $Q_n^1\left(x\right)$ is not a PBAS. Therefore, we came to a contradiction.

Case 2: If $M_Q^a=1$, then $g\left(\lambda \right)$ is an increasing function; that is, $\xi >1$, for which the inequality ${{\displaystyle \int }}_0^1{Q}_n^1\left(x\right)dx-2\left|G_{-}\right|=0$ holds. Therefore, for any $\lambda \in \left(1,\xi \right)$, the following inequality holds:

$${{\displaystyle \int }}_0^{1}1-Q_n^1\left(x\right)-\left|1-\lambda Q_n^1\left(x\right)\right|dx>0$$

Therefore, we came to a contradiction. If $M_Q=1$ and $m_Q=-1$, then $\forall n\ge 1:Q_n^1\left(x\right)$, which is not the PBAS.

The corollary is proven. □

5. The Number of PBAS Odd Functions

In Lemma 2, it is proved that for $n\ge 1$, the PBAS is an odd function, but the question of their number remains open. The following theorem will answer this question.

Theorem 1.

If$n\ge 1$, then there is only one odd function$Q_n^1\left(x\right)$that is the PBAS. Depending on the$n$, the function$Q_n^1\left(x\right)$is determined as follows:

If $n$ is odd, then

$$Q_n^1\left(x\right)=x{\displaystyle \sum }_{i=1}^{\frac{n+1}{2}}\frac{1}{\sin \frac{i\cdot \pi }{n+3}}{\displaystyle \prod }_{j=1, j\ne i}^{\frac{n+1}{2}}\frac{x^2-{\sin }^2\frac{j\cdot \pi }{n+3}}{{\sin }^2\frac{i\cdot \pi }{n+3}-{\sin }^2\frac{j\cdot \pi }{n+3}}$$

and

$$\Vert Q_n^1\left(x\right)\Vert =2\tan \frac{\pi }{2n+6};$$

If $n$ is even, then

$$Q_n^1\left(x\right)=x{\displaystyle \sum }_{i=1}^{\frac{n}{2}}\frac{1}{\sin \frac{i\cdot \pi }{n+2}}{\displaystyle \prod }_{j=1, j\ne i}^{\frac{n}{2}}\frac{x^2-{\sin }^2\frac{j\cdot \pi }{n+2}}{{\sin }^2\frac{i\cdot \pi }{n+2}-{\sin }^2\frac{j\cdot \pi }{n+2}}$$

and

$$\Vert Q_n^1\left(x\right)\Vert =2\tan \frac{\pi }{2n+4}.$$

Proof. 

Let us consider two cases.

Case 1. $n$ is an odd number.

We consider the points $0<x_1<x_2<\dots <x_u\le 1$ such that $\forall i=\overline{1,u}:Q_n^1\left(x_i\right)=1$. According to Corollary, 4 the value $M_Q^a$ satisfies the condition $M_Q^a>1$. Considering that the function $Q_n^1\left(x\right)$ is an odd continuous function, then at least one point $x_1\in \left[0,1\right]$ is such that $Q_n^1\left(x\right)=1$ exists.

Let us consider the question of the number of zeroes of the function $F\left(x\right)=\frac{d{Q}_n^1\left(x_i\right)}{dx}$. Since the function $Q_n^1\left(x\right)$ is an odd continuous function, then $F\left(x\right)$ is an even function. The number of zeroes of $F\left(x\right)$ is less or equal to $n-1$, of which non-negative numbers are less than or equal to $\frac{n-1}{2}$. Therefore, the number of solutions to the equation $Q_n^1\left(x\right)=1$ satisfying the question $x\in \left(0,1\right]$ is less than or equal to $\frac{n-1}{2}+1=\frac{n+1}{2}$. That is, $u\le \frac{n+1}{2}$.

Let us consider the points $0=y_0<y_1<y_2<\dots <y_v<y_{v+1}=1$. In each of the points $y_1,y_2,\dots ,y_v$ the value of the function $f\left(x\right)=1-Q_{2v-1}^1\left(x\right)=1-{\displaystyle \sum }_{i=0}^{v-1}{a}_{2i+1}{x}^{2i+1}$ changes its sign.

$$\begin{gathered} I_v=\frac{\Vert Q_{2v-1}^1\left(x\right)\Vert }{2}={{\displaystyle \int }}_0^1\left|1-Q_n^1\left(x\right)\right|dx={\displaystyle \sum }_{i=0}^v{\left(-1\right)}^i{{\displaystyle \int }}_{y_i}^{y_{i+1}}f\left(x\right)dx \\ =2{\displaystyle \sum }_{i=1}^v{\left(-1\right)}^{i+1}F\left(y_i\right)+{\left(-1\right)}^{v}F\left(y_{v+1}\right) \end{gathered}$$

where $F\left(x\right)=x-{{\displaystyle \sum }}_{i=0}^{v-1}\frac{a_{2i+1}}{2i+2}{x}^{2i+2}$.

We calculate the values of the partial derivatives $\forall i=\overline{1,v}$:

$$\frac{\partial F\left(y_i\right)}{\partial y_i}=1-{\displaystyle \sum }_{i=0}^{v-1}{a}_{2i+1}{y}_i^{2i+1}-{\displaystyle \sum }_{i=0}^{v-1}\frac{\partial a_{2i+1}}{\partial y_i}\cdot \frac{y_i^{2i+2}}{2i+2}$$

Since $1-{{\displaystyle \sum }}_{i=0}^{v-1}{a}_{2i+1}{y}_i^{2i+1}=0$ by the definition, then:

$$\frac{\partial F\left(y_i\right)}{\partial y_i}=-{\displaystyle \sum }_{i=0}^{v-1}\frac{\partial a_{2i+1}}{\partial y_i}\cdot \frac{y_i^{2i+2}}{2i+2}$$

We calculate the values of the partial derivatives $\forall i\ne j$:

$$\frac{\partial F\left(y_i\right)}{\partial y_j}=-{\displaystyle \sum }_{i=0}^{v-1}\frac{\partial a_{2i+1}}{\partial y_j}\cdot \frac{y_i^{2i+2}}{2i+2}$$

The necessary condition for the value $\Vert Q_{2v+1}^1\left(x\right)\Vert$ to be minimal is: $\forall i=\overline{1,v}: \frac{\partial I_v}{\partial y_i}=0$; therefore,

$$\begin{gathered} \frac{\partial I_v}{\partial y_i}=-2{\displaystyle \sum }_{j=1}^v{\left(-1\right)}^{j+1}{\displaystyle \sum }_{k=0}^{v-1}\frac{\partial a_{2k+1}}{\partial y_i}\cdot \frac{y_j^{2k+2}}{2k+2}-{\left(-1\right)}^v{\displaystyle \sum }_{k=0}^{v-1}\frac{\partial a_{2k+1}}{\partial y_i}\cdot \frac{1}{2k+2} \\ =-{\displaystyle \sum }_{k=0}^{v-1}\frac{\partial a_{2k+1}}{\partial y_i}\cdot \frac{1}{2k+2}\left(2{\displaystyle \sum }_{j=1}^v{\left(-1\right)}^{j+1}{y}_j^{2k+2}+{\left(-1\right)}^v\right) \end{gathered}$$

Solving the system $\frac{\partial I_v}{\partial y_i}=0$ [12], we find that $\forall k=\overline{0,v-1}:$

$$2{\displaystyle \sum }_{j=1}^v{\left(-1\right)}^{j+1}{y}_j^{2k+2}+{\left(-1\right)}^v=0$$

Considering that $\forall i=\overline{1,v}: y_i>0$; therefore, $\forall i=\overline{1,v}: y_i=\sin \frac{i\cdot \pi }{2v+2}$ [12].

Using the Lagrange interpolation formula, we calculate the value $Q_{2v-1}^1\left(x\right)$, and we find $Q_{2v-1}^1\left(x\right)={{\displaystyle \sum }}_{i=1}^v{l}_i\left(x\right)-{{\displaystyle \sum }}_{i=1}^v{\overline{l}}_i\left(x\right)$, where

$$\begin{gathered} l_i\left(x\right)={\displaystyle \prod }_{j=1}^v\frac{x+y_j}{y_i+y_j}\cdot {\displaystyle \prod }_{j=1, j\ne i}^v\frac{x-y_j}{y_i-y_j} \\ {\overline{l}}_i\left(x\right)=-{\displaystyle \prod }_{j=1, j\ne i}^v\frac{x+y_j}{y_i-y_j}\cdot {\displaystyle \prod }_{j=1}^v\frac{x-y_j}{y_i+y_j} \end{gathered}$$

Then,

$$\begin{gathered} Q_{2v-1}^1\left(x\right)={\displaystyle \sum }_{i=1}^v\left({\displaystyle \prod }_{j=1}^v\frac{x+y_j}{y_i+y_j}\cdot {\displaystyle \prod }_{j=1, j\ne i}^v\frac{x-y_j}{y_i-y_j}+{\displaystyle \prod }_{j=1, j\ne i}^v\frac{x+y_j}{y_i-y_j}\cdot {\displaystyle \prod }_{j=1}^v\frac{x-y_j}{y_i+y_j} \right) \\ ={\displaystyle \sum }_{i=1}^v{\displaystyle \prod }_{j=1, j\ne i}^v\frac{x-y_j}{y_i-y_j}{\displaystyle \prod }_{j=1, j\ne i}^v\frac{x+y_j}{y_i+y_j}\cdot \left(\frac{x+y_i}{2y_i}+\frac{x-y_j}{2y_i}\right) \\ =x{\displaystyle \sum }_{i=1}^v\frac{1}{y_i}{\displaystyle \prod }_{j=1, j\ne i}^v\frac{x-y_j}{y_i-y_j}{\displaystyle \prod }_{j=1, j\ne i}^v\frac{x+y_j}{y_i+y_j} \\ =x{\displaystyle \sum }_{i=1}^v\frac{1}{y_i}{\displaystyle \prod }_{j=1, j\ne i}^v\frac{x^2-\underset{j}{\overset{2}{y}}}{y_i^2-y_j^2} \end{gathered}$$

Let $F\left(x\right)={{\displaystyle \sum }}_{i=1}^v\frac{a_i}{2i}{x}^{2i}$ and $\frac{dF\left(x\right)}{dx}=Q_{2v-1}^1\left(x\right)$, so $I_v$ is equal to

$$\begin{gathered} I_v={{\displaystyle \int }}_0^1\left|1-Q_{2v-1}^1\left(x\right)\right|dx={\displaystyle \sum }_{i=0}^v{\left(-1\right)}^i{{\displaystyle \int }}_{\sin \frac{i\cdot \pi }{2v+2}}^{\sin \frac{\left(i+1\right)\cdot \pi }{2v+2}}1-Q_{2v-1}^1\left(x\right)dx \\ =2{\displaystyle \sum }_{i=1}^v{\left(-1\right)}^{i+1}\sin \frac{i\cdot \pi }{2v+2}+{\left(-1\right)}^v+2{\displaystyle \sum }_{j=1}^v{\left(-1\right)}^{j}F\left(\sin \frac{j\cdot \pi }{2v+2}\right)+{\left(-1\right)}^{v+1}F\left(1\right) \end{gathered}$$

We calculate the value $2{{\displaystyle \sum }}_{j=1}^v{\left(-1\right)}^{j}F\left(\sin \frac{j\cdot \pi }{2v+2}\right)+{\left(-1\right)}^{v+1}F\left(1\right)$, and we obtain:

$$\begin{gathered} 2{\displaystyle \sum }_{j=1}^v{\left(-1\right)}^{j}F\left(\sin \frac{j\cdot \pi }{2v+2}\right)+{\left(-1\right)}^{v+1}F\left(1\right)=2{\displaystyle \sum }_{j=1}^v{\left(-1\right)}^j{\displaystyle \sum }_{i=1}^v\frac{a_i}{2i}{\sin }^{2i}\frac{j\cdot \pi }{2v+2}+{\left(-1\right)}^{v+1}{\displaystyle \sum }_{i=1}^v\frac{a_i}{2i} \\ ={\displaystyle \sum }_{i=1}^v\frac{a_i}{2i}\left(2{\displaystyle \sum }_{j=1}^v{\left(-1\right)}^j{\sin }^{2i}\frac{j\cdot \pi }{2v+2}+{\left(-1\right)}^{v+1}\right) \end{gathered}$$

Considering that (2) holds, $\forall i=\overline{1,v}: 2{{\displaystyle \sum }}_{j=1}^v{\left(-1\right)}^j{\sin }^{2i}\frac{j\cdot \pi }{2v+2}+{\left(-1\right)}^{v+1}=-\left(2{{\displaystyle \sum }}_{j=1}^v{\left(-1\right)}^{j+1}{\sin }^{2i}\frac{j\cdot \pi }{2v+2}+{\left(-1\right)}^v\right)=0$, then

$$2{\displaystyle \sum }_{j=1}^v{\left(-1\right)}^{j}F\left(\sin \frac{j\cdot \pi }{2v+2}\right)+{\left(-1\right)}^{v+1}F\left(x\right)=0$$

and

$$I_v={{\displaystyle \int }}_0^1\left|1-Q_{2v-1}^1\left(x\right)\right|dx=2{\displaystyle \sum }_{i=1}^v{\left(-1\right)}^{i+1}\sin \frac{i\cdot \pi }{2v+2}+{\left(-1\right)}^v$$

If $v$ is even, then

$$I_v=2{\displaystyle \sum }_{i=1}^{v/2}\sin \frac{\left(2i-1\right)\cdot \pi }{2v+2}-2{\displaystyle \sum }_{i=1}^{v/2}\sin \frac{i\cdot \pi }{v+1}+1$$

Using the formula $\sin \left(\alpha -\beta \right)=\sin \alpha \cos \beta -\sin \beta \cos \alpha$, where $\alpha =\frac{2i\pi }{2v+2}=\frac{i\pi }{v+1}$ and $\beta =\frac{\pi }{2v+2}$, we have

$$\begin{gathered} {\displaystyle \sum }_{i=1}^{v/2}\sin \frac{\left(2i-1\right)\cdot \pi }{2v+2}={\displaystyle \sum }_{i=1}^{v/2}\left(\sin \frac{i\pi }{v+1}\cos \frac{\pi }{2v+2}-\sin \frac{\pi }{2v+2}\cos \frac{i\pi }{v+1}\right) \\ =\cos \frac{\pi }{2v+2}{\displaystyle \sum }_{i=1}^{v/2}\sin \frac{i\pi }{v+1}-\sin \frac{\pi }{2v+2}{\displaystyle \sum }_{i=1}^{v/2}\cos \frac{i\pi }{v+1} \end{gathered}$$

Since $\frac{1}{2}+{{\displaystyle \sum }}_{i=1}^n\cos ix=\frac{\sin \left(n+\frac{1}{2}\right)x}{2\sin \frac{1}{2}x}$ and ${{\displaystyle \sum }}_{i=1}^n\sin ix=\frac{\cos \frac{x}{2}-\cos \left(n+\frac{1}{2}\right)x}{2\sin \frac{1}{2}x}$ ([13] p. 2), where $n=\frac{v}{2}$ and $x=\frac{\pi }{v+1}$, we have:

$$\begin{gathered} {\displaystyle \sum }_{i=1}^{v/2}\cos \frac{i\pi }{v+1}=\frac{\sin \left(\frac{v}{2}+\frac{1}{2}\right)\frac{\pi }{v+1}}{2\sin \frac{\pi }{2v+2}}-\frac{1}{2}=\frac{1}{2\sin \frac{\pi }{2v+2}}-\frac{1}{2} \\ {\displaystyle \sum }_{i=1}^{v/2}\sin \frac{i\cdot \pi }{v+1}=\frac{\cos \frac{\pi }{2v+2}-\cos \left(\frac{v}{2}+\frac{1}{2}\right)\frac{\pi }{v+1}}{2\sin \frac{\pi }{2v+2}}=\frac{\cos \frac{\pi }{2v+2}}{2\sin \frac{\pi }{2v+2}} \end{gathered}$$

Therefore,

$$\begin{gathered} I_v=2\left(\cos \frac{\pi }{2v+2}\cdot \frac{\cos \frac{\pi }{2v+2}}{2\sin \frac{\pi }{2v+2}}-\sin \frac{\pi }{2v+2}\left(\frac{1}{2\sin \frac{\pi }{2v+2}}-\frac{1}{2}\right)\right)-\frac{\cos \frac{\pi }{2v+2}}{\sin \frac{\pi }{2v+2}}+1 \\ =\frac{{\cos }^2\frac{\pi }{2v+2}+{\sin }^2\frac{\pi }{2v+2}}{\sin \frac{\pi }{2v+2}}-\frac{\cos \frac{\pi }{2v+2}}{\sin \frac{\pi }{2v+2}} \end{gathered}$$

Using the basic trigonometric identities ${\cos }^{2}2\alpha +{\sin }^{2}2\alpha =1$ and $1-\cos 2\alpha =2{\sin }^2\alpha$, $\sin 2\alpha =2\sin \alpha \cos \alpha$, where $\alpha =\frac{\pi }{4v+4}$ we obtain:

$$I_v=\frac{1-\cos \frac{\pi }{2v+2}}{\sin \frac{\pi }{2v+2}}=\frac{2{\sin }^2\frac{\pi }{4v+4}}{2\sin \frac{\pi }{4v+4}\cos \frac{\pi }{4v+4}}=\tan \frac{\pi }{4v+4}$$

If $v$ is odd, then

$$I_v=2{\displaystyle \sum }_{i=1}^{\frac{v+1}{2}}\sin \frac{\left(2i-1\right)\cdot \pi }{2v+2}-2{\displaystyle \sum }_{i=1}^{\frac{v-1}{2}}\sin \frac{i\cdot \pi }{v+1}-1$$

Using the formula $\sin \left(\alpha -\beta \right)=\sin \alpha \cos \beta -\sin \beta \cos \alpha$, where $\alpha =\frac{2i\pi }{2v+2}=\frac{i\pi }{v+1}$ and $\beta =\frac{\pi }{2v+2}$, we have

$$\begin{gathered} {\displaystyle \sum }_{i=1}^{\frac{v+1}{2}}\sin \frac{\left(2i-1\right)\cdot \pi }{2v+2}={\displaystyle \sum }_{i=1}^{\frac{v+1}{2}}\left(\sin \frac{i\pi }{v+1}\cos \frac{\pi }{2v+2}-\sin \frac{\pi }{2v+2}\cos \frac{i\pi }{v+1}\right) \\ =\cos \frac{\pi }{2v+2}{\displaystyle \sum }_{i=1}^{\frac{v+1}{2}}\sin \frac{i\pi }{v+1}-\sin \frac{\pi }{2v+2}{\displaystyle \sum }_{i=1}^{\frac{v+1}{2}}\cos \frac{i\pi }{v+1} \end{gathered}$$

Since ${{\displaystyle \sum }}_{i=1}^n\sin ix=\frac{\cos \frac{x}{2}-\cos \left(n+\frac{1}{2}\right)x}{2\sin \frac{1}{2}x}$ [13] p. 2, where $n=\frac{v+1}{2}$ and $x=\frac{\pi }{v+1}$ we find:

$$\begin{gathered} {\displaystyle \sum }_{i=1}^{\frac{v+1}{2}}\sin \frac{i\pi }{v+1}=\frac{\cos \frac{\pi }{2v+2}-\cos \left(\frac{v+1}{2}+\frac{1}{2}\right)\frac{\pi }{v+1}}{2\sin \frac{\pi }{2v+2}} \\ =\frac{\cos \frac{\pi }{2v+2}-\cos \left(\frac{\pi }{2}+\frac{\pi }{2v+2}\right)}{2\sin \frac{\pi }{2v+2}} \end{gathered}$$

According to the reduction formula $\cos \left(\frac{\pi }{2}+\frac{\pi }{2v+2}\right)=-\sin \frac{\pi }{2v+2}$, we have:

$${\displaystyle \sum }_{i=1}^{\frac{v+1}{2}}\sin \frac{i\pi }{v+1}=\frac{\cos \frac{\pi }{2v+2}+\sin \frac{\pi }{2v+2}}{2\sin \frac{\pi }{2v+2}}$$

Using the formula $\frac{1}{2}+{{\displaystyle \sum }}_{i=1}^n\cos ix=\frac{\sin \left(n+\frac{1}{2}\right)x}{2\sin \frac{1}{2}x}$ [13] p. 2, where $n=\frac{v+1}{2}$ and $x=\frac{\pi }{v+1}$ we find:

$${\displaystyle \sum }_{i=1}^{\frac{v+1}{2}}\cos \frac{i\pi }{v+1}=\frac{\sin \left(\frac{v+1}{2}+\frac{1}{2}\right)\frac{\pi }{v+1}}{2\sin \frac{\pi }{2v+2}}-\frac{1}{2}=\frac{\sin \left(\frac{\pi }{2}+\frac{\pi }{2v+2}\right)}{2\sin \frac{\pi }{2v+2}}-\frac{1}{2}$$

According to the reduction formula $\sin \left(\frac{\pi }{2}+\frac{\pi }{2v+2}\right)=\cos \frac{\pi }{2v+2}$, we obtain:

$${\displaystyle \sum }_{i=1}^{\frac{v+1}{2}}\cos \frac{i\pi }{v+1}=\frac{\cos \frac{\pi }{2v+2}}{2\sin \frac{\pi }{2v+2}}-\frac{1}{2}$$

Since ${{\displaystyle \sum }}_{i=1}^n\sin ix=\frac{\cos \frac{x}{2}-\cos \left(n+\frac{1}{2}\right)x}{2\sin \frac{1}{2}x}$ [13] p. 2, where $n=\frac{v-1}{2}$ and $x=\frac{\pi }{v+1}$ we find:

$$\begin{gathered} {\displaystyle \sum }_{i=1}^{\frac{v-1}{2}}\sin \frac{i\cdot \pi }{v+1}=\frac{\cos \frac{\pi }{2v+2}-\cos \left(\frac{v-1}{2}+\frac{1}{2}\right)\frac{\pi }{v+1}}{2\sin \frac{\pi }{2v+2}} \\ =\frac{\cos \frac{\pi }{2v+2}-\cos \left(\frac{\pi }{2}-\frac{\pi }{2v+2}\right)}{2\sin \frac{\pi }{2v+2}} \end{gathered}$$

According to the reduction formula $\cos \left(\frac{\pi }{2}-\frac{\pi }{2v+2}\right)=\sin \frac{\pi }{2v+2}$, we find:

$${\displaystyle \sum }_{i=1}^{\frac{v-1}{2}}\sin \frac{i\cdot \pi }{v+1}=\frac{\cos \frac{\pi }{2v+2}-\sin \frac{\pi }{2v+2}}{2\sin \frac{\pi }{2v+2}}$$

Therefore,

$$\begin{gathered} I_v=2\left(\cos \frac{\pi }{2v+2}\cdot \frac{\cos \frac{\pi }{2v+2}+\sin \frac{\pi }{2v+2}}{2\sin \frac{\pi }{2v+2}}-\sin \frac{\pi }{2v+2}\left(\frac{\cos \frac{\pi }{2v+2}}{2\sin \frac{\pi }{2v+2}}-\frac{1}{2}\right)\right) \\ -2\frac{\cos \frac{\pi }{2v+2}-\sin \frac{\pi }{2v+2}}{2\sin \frac{\pi }{2v+2}}-1=\frac{1-\cos \frac{\pi }{2v+2}}{\sin \frac{\pi }{2v+2}}=\tan \frac{\pi }{4v+4} \end{gathered}$$

Therefore, $\forall v\in N:\Vert Q_{2v-1}^1\left(x\right)\Vert =2I_v=2\tan \frac{\pi }{4v+4}$.

Since $\forall v\in N:I_{v-1}>I_v$, then the smallest value $\Vert Q_{2v-1}^1\left(x\right)\Vert$ at the maximum $v$, considering that $v\le u\le \frac{n+1}{2}$, then $v=\frac{n+1}{2}$ and $2v+2=n+3$.

Case 2. If $n$ is an even number, then the result is obtained similarly to case 1, except $v=\frac{n}{2}$ and $2v+2=n+2$.

The theorem is proved. □

From Theorem 1, it follows that for $n\ge 1,$ there is a unique odd function that is the PBAS, which is constructed using the Lagrange interpolation formula, and the interpolation nodes are an alternative to Chebyshev for Chebyshev polynomials of the second kind.

Example 2.

Construct the PBAS for$n=3$and$n=4$, which are odd functions.

Solution

If$n=3$, then, according to Theorem 1, the PBAS is given by the following formula:

$$\begin{gathered} Q_3^1\left(x\right)=x{\displaystyle \sum }_{i=1}^2\frac{1}{\sin \frac{i\cdot \pi }{6}}{\displaystyle \prod }_{j=1, j\ne i}^2\frac{x^2-{\sin }^2\frac{j\cdot \pi }{6}}{{\sin }^2\frac{i\cdot \pi }{6}-{\sin }^2\frac{j\cdot \pi }{6}} \\ =x\left(\frac{1}{\sin \frac{\pi }{6}}\cdot \frac{x^2-{\sin }^2\frac{\pi }{3}}{{\sin }^2\frac{\pi }{6}-{\sin }^2\frac{\pi }{3}}+\frac{1}{\sin \frac{\pi }{3}}\cdot \frac{x^2-{\sin }^2\frac{\pi }{6}}{{\sin }^2\frac{\pi }{3}-{\sin }^2\frac{\pi }{6}}\right)=2x\left(-2x^2+\frac{3}{2}+\frac{2\sqrt{3}}{3}{x}^2-\frac{\sqrt{3}}{6}\right) \\ =\frac{4\sqrt{3}-12}{3}{x}^3+\frac{9-\sqrt{3}}{3}x \end{gathered}$$

If$n=4$, then, according to Theorem 1, the PBAS is given by the following formula:

$$Q_4^1\left(x\right)=x{\displaystyle \sum }_{i=1}^2\frac{1}{\sin \frac{i\cdot \pi }{6}}{\displaystyle \prod }_{j=1, j\ne i}^2\frac{x^2-{\sin }^2\frac{j\cdot \pi }{6}}{{\sin }^2\frac{i\cdot \pi }{6}-{\sin }^2\frac{j\cdot \pi }{6}}=\frac{4\sqrt{3}-12}{3}{x}^3+\frac{9-\sqrt{3}}{3}x$$

Let us pay attention to the fact that$Q_3^1\left(x\right)=Q_4^1\left(x\right)$. This fact can be generalized: if$n$is even and$n\ge 2$, then$Q_n^1\left(x\right)=Q_{n-1}^1\left(x\right)$.

6. The Number of PBAS of the Neither Function

Let us investigate the problem of the existence of PBAS $Q_n\left(x\right)$.

Theorem 2.

If n ≥ 1, then the following statements are true:

1. 

If$n$is an odd number, then there is no PBAS$Q_n\left(x\right)$.

2. 

If$n$is an even number, then there is an infinite number of PBAS$Q_n\left(x\right)$.

Proof. 

From Theorem 1, it follows that there is a unique odd function $Q_n^1\left(x\right)$ that is a PBAS. Let us show that there exists an even function $Q_n^0\left(x\right)\ne 0$, such that: $\Vert Q_n\left(x\right)=Q_n^1\left(x\right)\Vert$. For this, we calculate $\Vert Q_n\left(x\right)\Vert -\Vert Q_n^1\left(x\right)\Vert$ and find:

$$\Vert Q_n\left(x\right)\Vert -\Vert Q_n^1\left(x\right)\Vert ={{\displaystyle \int }}_0^1\left|1-Q_n^0\left(x\right)-Q_n^1\left(x\right)\right|+\left|1+Q_n^0\left(x\right)-Q_n^1\left(x\right)\right|-2\left|1-Q_n^1\left(x\right)\right|dx$$

where $Q_n\left(x\right)=Q_n^0\left(x\right)+Q_n^1\left(x\right)$, $Q_n^0\left(x\right)$ is an even function, and $Q_n^1\left(x\right)$ is an odd function.

$\Vert Q_n\left(x\right)\Vert -\Vert Q_n^1\left(x\right)\Vert$ is equal to zero only if the condition $\forall x\in \left[0,1\right]:$ $\left|1-Q_n^0\left(x\right)-Q_n^1\left(x\right)\right|+\left|1+Q_n^0\left(x\right)-Q_n^1\left(x\right)\right|-2\left|1-Q_n^1\left(x\right)\right|=0$ holds, equivalent to:

$$\forall x\in \left[0,1\right] и Q_n^1\left(x\right)\le 1: \{\begin{array}{c}1-Q_n^0\left(x\right)-Q_n^1\left(x\right)\ge 0,\\ 1+Q_n^0\left(x\right)-Q_n^1\left(x\right)\ge 0;\end{array}\iff Q_n^1\left(x\right)-1\le Q_n^0\left(x\right)\le 1-Q_n^1\left(x\right)$$

and

$$\forall x\in \left[0,1\right] и Q_n^1\left(x\right)\ge 1: \{\begin{array}{c}1-Q_n^0\left(x\right)-Q_n^1\left(x\right)\le 0,\\ 1+Q_n^0\left(x\right)-Q_n^1\left(x\right)\le 0;\end{array}\iff 1-Q_n^1\left(x\right)\le Q_n^0\left(x\right)\le Q_n^1\left(x\right)-1$$

Therefore: $\forall x\in \left[0,1\right]:-\left|1-Q_n^1\left(x\right)\right|\le Q_n^0\left(x\right)\le \left|1-Q_n^1\left(x\right)\right|$.

Since $Q_n^1\left(x_i\right)$ is an odd-function PBAS, it follows from Theorem 1 that there are points $x_1,x_2,\dots ,x_u\in \left(0,1\right]$ such that $\forall i=\overline{1,u}:Q_n^1\left(x_i\right)=1$. Since $Q_n^1\left(x_i\right)$ is an odd-function PBAS, it follows from the proof of Theorem 1 that if $n$ is an odd number, then $u=\frac{n+1}{2}$. Otherwise, $u=\frac{n}{2}$.

Substituting $x_1,x_2,\dots ,x_u$ into the inequalities $-\left|1-Q_n^1\left(x\right)\right|\le Q_n^0\left(x\right)\le \left|1-Q_n^1\left(x\right)\right|$ we find $\forall i=\overline{1,u}:0\le Q_n^0\left(x_i\right)\le 0$; therefore, the necessary condition is $\forall i=\overline{1,u}:Q_n^0\left(x_i\right)=0$. Since the function $Q_n^0\left(x\right)$ is an even function, $\forall i=\overline{1,u}:Q_n^0\left(-x_i\right)=0$; therefore, $Q_n^0\left(x\right)$ is divisible by the polynomial ${{\displaystyle \prod }}_{i=1}^u\left(x^2-x_i^2\right)$ and $\mathrm{deg}{Q}_n^0\left(x\right)\ge 2u$. Let us consider two cases.

Case 1. If $n$ is an odd number, then $\mathrm{deg}{Q}_n^0\left(x\right)\ge 2u=n+1.$ Therefore, there is no even polynomial satisfying the condition $\mathrm{deg}{Q}_n^0\left(x\right)\le n$. Hence, if $n$ is an odd number, there is no PBAS that is a function of general form.

Case 2. If $n$ is an even number, then $\mathrm{deg}{Q}_n^0\left(x\right)\ge 2u=n$. From the other side, $\mathrm{deg}{Q}_n^0\left(x\right)\le n$; therefore, $\mathrm{deg}{Q}_n^0\left(x\right)=n$. To construct the polynomial $Q_n^0\left(x\right)$ we consider the polynomial of the form:

$$Z_n\left(x\right)=\frac{Q_n^1\left(x\right)-1}{{{\displaystyle \prod }}_{i=1}^{n/2}\left(x-x_i\right)}$$

where $\forall i=\overline{1,\frac{n}{2}}:x_i=\sin \frac{i\pi }{n+2}$.

We consider the equation $Q_n^1\left(x\right)-1=0$, $\forall i=\overline{1,\frac{n}{2}}:Q_n^1\left(x_i\right)-1=0$; therefore, according to Rolle’s theorem, in each of the intervals $\left(x_i,x_{i+1}\right)$, at least one point ${\xi }_i\in \left(x_i,x_{i+1}\right)$ exists for which $F\left({\xi }_i\right)=0$, where $F\left(x\right)=\frac{d\left(Q_n^1\left(x\right)-1\right)}{dx}=\frac{d{Q}_n^1\left(x\right)}{dx}$ and $i\in \overline{1,\frac{n}{2}-1}$. Since $Q_n^1\left(x\right)$ is an odd function, $F\left(x\right)$ is an even function; therefore, $\forall i\in \overline{1,\frac{n}{2}-1}:F\left(-{\xi }_i\right)=0$. Considering that $\mathrm{deg}F\left(x\right)=n-2$, then, according to the main theorem of algebra, the equation $F\left(x\right)=0$ over the field of real numbers can have at most $n-2$ roots—considering their multiplicity—so $\pm {\xi }_i$ are roots of multiplicity one. Since $\pm {\xi }_i$ are roots of multiplicity one, the function $F\left(x\right)$ passing through $\pm {\xi }_i$ changes its sign; therefore, $\left(-\infty ,-{\xi }_{\frac{n}{2}-1}\right)$, $\left(-{\xi }_{\frac{n}{2}-1},-{\xi }_{\frac{n}{2}-2} \right)$,…, $\left(-{\xi }_2,-{\xi }_1 \right)$,$\left(-{\xi }_1,{\xi }_1 \right)$, $\left({\xi }_1,{\xi }_2 \right)$,…,$\left({\xi }_{\frac{n}{2}-2},{\xi }_{\frac{n}{2}-1} \right)$, $\left({\xi }_{\frac{n}{2}-1},+\infty \right)$ are the intervals of the increase or decrease in the function $Q_n^1\left(x\right)$. Therefore, the equation $Q_n^1\left(x\right)-1=0$ has at most one solution for each of the intervals. Taking into account that the intervals $\left(-{\xi }_1,{\xi }_1 \right)$, $\left({\xi }_1,{\xi }_2 \right)$,…,$\left({\xi }_{\frac{n}{2}-2},{\xi }_{\frac{n}{2}-1} \right)$, $\left({\xi }_{\frac{n}{2}-1},+\infty \right)$, solutions of the equation $Q_n^1\left(x\right)-1=0$ are respectively $x_1,x_2,\dots ,x_{\frac{n}{2}}$; therefore, $\psi \ge 0$ does not exist, and $\forall i=\overline{1,\frac{n}{2}}:\psi \ne x_i$ and $Q_n^1\left(\psi \right)-1=0$.

Let us show that $x_i$ is a root of multiplicity one of the equation $Q_n^1\left(x\right)-1=0$. We suppose that there exists $k$, for which $x_k$ is a root of multiplicity greater than one of $Q_n^1\left(x\right)-1=0$; therefore, $x_k$ is also a root of the equation $\forall i=\overline{1,\frac{n}{2}-1}:\pm {\xi }_i$ and $x_k$.

Provided that $\mathrm{deg}F\left(x\right)=n-2$, we have come to a contradiction. Therefore $x_i$ is a root of multiplicity one of the equation $Q_n^1\left(x\right)-1=0$, so if there exists $\gamma \in R$ for which the condition $Z_n\left(\gamma \right)=0$ is satisfied, then $\gamma <0$ and one of the two conditions $\forall x\ge 0:Z_n\left(x\right)>0$ or $\forall x\ge 0:Z_n\left(x\right)<0$ hold.

Since $Z_n\left(0\right)=\frac{Q_n^1\left(0\right)-1}{{{\displaystyle \prod }}_{i=1}^{\frac{n}{2}}\left(-x_i\right)}=\frac{{\left(-1\right)}^{\frac{n}{2}+1}}{{{\displaystyle \prod }}_{i=1}^{\frac{n}{2}}{x}_i}$, then if $\frac{n}{2}$ is an even number, then $\forall x\ge 0:Z_n\left(x\right)<0$, otherwise $\forall x\ge 0:Z_n\left(x\right)>0$.

Let us consider the function $R_n\left(x\right)$, given by the following formula:

$$R_n\left(x\right)=\frac{Z_n\left(x\right)}{{\displaystyle \prod }_{j=1}^{\frac{n}{2}}\left(x+x_j\right)}$$

The function $R_n\left(x\right)$ is continuous on the interval $\left[0,1\right]$. According to the Weierstrass theorem, it is bounded; that is, there exist $x_m^R,x_M^R\in \left[0,1\right]$ such that $\forall x\in \left[0,1\right]:R_n\left(x_m^R\right)\le R\left(x\right)\le R_n\left(x_M^R\right)$. Considering that $\forall x\in \left[0,1\right]:{{\displaystyle \prod }}_{j=1}^{\frac{n}{2}}\left(x+x_j\right)>0$, we find that if $\frac{n}{2}$ is even number, then $R_n\left(x_m^R\right)<R_n\left(x_M^R\right)<0$. Otherwise, $0<R_n\left(x_m^R\right)<R_n\left(x_M^R\right)$. If $\frac{n}{2}$ is even number, $\tau =-R_n\left(x_M^R\right)$; otherwise, $\tau =R_n\left(x_m^R\right)$ and we find the function $Q_n^0\left(x\right)=\tau {{\displaystyle \prod }}_{i=1}^{n/2}\left(x^2-x_i^2\right)$ satisfying $\forall x\in \left[0,1\right]:-\left|1-Q_n^1\left(x\right)\right|\le Q_n^0\left(x\right)\le \left|1-Q_n^1\left(x\right)\right|$. Since $Q_n\left(x\right)=Q_n^0\left(x\right)+Q_n^1\left(x\right)$, it follows from Corollary 2 that $\forall \varphi \in \left[0,\frac{\pi }{2}\right]:{\sin }^2\varphi \cdot Q_n\left(x\right)+{\cos }^2\varphi \cdot Q_n^1\left(x\right)=Q_n^1\left(x\right)$, so $Q_{\varphi ,n}\left(x\right)={\sin }^2\varphi \cdot Q_n\left(x\right)+{\cos }^2\varphi \cdot Q_n^1\left(x\right)$ is the PBAS and $Q_{\varphi ,n}\left(x\right)={\sin }^2\varphi \cdot Q_n\left(x\right)+{\cos }^2\varphi \cdot Q_n^1\left(x\right)={\sin }^2\varphi \cdot Q_n^0\left(x\right)+Q_n^1\left(x\right)$. It is also worth noting that ${\overline{Q}}_n\left(x\right)=-Q_n^0\left(x\right)+Q_n^1\left(x\right)$ is a PBAS, so ${\overline{Q}}_{\varphi ,n}\left(x\right)={\sin }^2\varphi \cdot {\overline{Q}}_n\left(x\right)+{\cos }^2\varphi \cdot Q_n^1\left(x\right)=-{\sin }^2\varphi \cdot Q_n^0\left(x\right)+Q_n^1\left(x\right)$ is the PBAS.

The theorem is proven. □

Example 3.

Construct the general form PBAS for$n=4$.

Solution follows from Example 2 that$Q_4^1\left(x\right)=\frac{4\sqrt{3}-12}{3}{x}^3+\frac{9-\sqrt{3}}{3}x$. Calculating$Z_4\left(x\right)$, we have

$$Z_4\left(x\right)=\frac{Q_4^1\left(x\right)-1}{\left(x-\frac{1}{2}\right)\left(x-\frac{\sqrt{3}}{2}\right)}=\frac{4\sqrt{3}-12}{3}x-\frac{4\sqrt{3}}{3}$$

We calculate$R_4\left(x\right)$and find:

$$\begin{gathered} R_4\left(x\right)=\frac{Z_4\left(x\right)}{\left(x+\frac{1}{2}\right)\left(x+\frac{\sqrt{3}}{2}\right)}=\frac{\frac{4\sqrt{3}-12}{3}x-\frac{4\sqrt{3}}{3}}{\left(x+\frac{1}{2}\right)\left(x+\frac{\sqrt{3}}{2}\right)}=\frac{\frac{4\sqrt{3}}{3}\left(x+\frac{1}{2}\right)-4\left(x+\frac{\sqrt{3}}{2}\right)}{\left(x+\frac{1}{2}\right)\left(x+\frac{\sqrt{3}}{2}\right)} \\ =\frac{\frac{4\sqrt{3}}{3}}{x+\frac{\sqrt{3}}{2}}-\frac{4}{x+\frac{1}{2}} \end{gathered}$$

We calculate the derivative of the function$R_4\left(x\right)$and find:

$$\frac{d{R}_4\left(x\right)}{dx}=-\frac{\frac{4\sqrt{3}}{3}}{{\left(x+\frac{\sqrt{3}}{2}\right)}^2}+\frac{4}{{\left(x+\frac{1}{2}\right)}^2}$$

Since there are no critical points on the segment$\left[0,1\right]$, the function$R_4\left(x\right)$takes the maximum and minimum values at the ends of the segment. If we calculate$R_4\left(0\right)$and$R_4\left(1\right)$, respectively, we have:$R_4\left(0\right)=-\frac{16}{3}$and

$$R_4\left(1\right)=\frac{\frac{4\sqrt{3}-12}{3}-\frac{4\sqrt{3}}{3}}{\left(1+\frac{1}{2}\right)\left(1+\frac{\sqrt{3}}{2}\right)}=-\frac{16}{6+3\sqrt{3}}$$

Therefore,$\tau =\frac{16}{6+3\sqrt{3}}$and

$$Q_{4,\mu }^0=\mu \left(x^2-\frac{1}{4}\right)\left(x^2-\frac{3}{4}\right)=\mu \left(x^4-x^2+\frac{3}{16}\right)=\mu \cdot \frac{U_5\left(x\right)}{32\cdot x}$$

where$\mu$is any number satisfying the condition$\mu \in \left[-\tau ,\tau \right]$, and$U_5\left(x\right)$is a Chebyshev polynomial of the second kind. Thus, the PBAShas the form$Q_{4,\mu }\left(x\right)=\mu x^4+\frac{4\sqrt{3}-12}{3}{x}^3-\mu x^2+\frac{9-\sqrt{3}}{3}x+\frac{3}{16}\mu$.

Lemma 3.

If$n$is an even number, then

$$\forall i=\overline{1,\frac{n}{2}}:{\alpha }_i={\displaystyle \prod }_{j=1, j\ne i}^{\frac{n}{2}}\left({\sin }^2\frac{i\cdot \pi }{n+2}-{\sin }^2\frac{j\cdot \pi }{n+2}\right)=\frac{{\left(-1\right)}^{\frac{n}{2}-i}}{\frac{n+2}{2^n}\cdot {\sin }^2\frac{2i\cdot \pi }{n+2}}$$

Proof. 

As $\forall x,y\in R:{\sin }^{2}x-{\sin }^{2}y=\sin \left(x-y\right)\cdot \sin \left(x+y\right)$, then

$${\alpha }_i={\displaystyle \prod }_{j=1,i\ne j}^{n/2}\sin \frac{\left(i+j\right)\pi }{n+2}\sin \frac{\left(i-j\right)\pi }{n+2}$$

Consider two cases.

Case 1: If $i=\frac{n}{2}$ then

$${\alpha }_{\frac{n}{2}}={\displaystyle \prod }_{j=1}^{\frac{n}{2}-1 }\sin \frac{\left(\frac{n}{2}+j\right)\pi }{n+2}\sin \frac{\left(\frac{n}{2}-j\right)\pi }{n+2}=\frac{{\displaystyle \prod }_{j=1}^{n-1}\sin \frac{j\cdot \pi }{n+2}}{\sin \frac{n\cdot \pi }{2n+4}}$$

Because ${{\displaystyle \prod }}_{j=1}^{n+1}\sin \frac{j\cdot \pi }{n+2}=\frac{n+2}{2^{n+1}}$, we have

$${\alpha }_{\frac{n}{2}}=\frac{n+2}{2^n{\sin }^2\frac{2\pi }{n+2}}$$

Case 2. If $i\ne \frac{n}{2}$ then

$${\alpha }_i=\frac{1}{\sin \frac{2i\pi }{n+2}\sin \frac{i\pi }{n+2}}{\displaystyle \prod }_{j=i-\frac{n}{2}}^{-1}\sin \frac{j\pi }{n+2}{\displaystyle \prod }_{j=1}^{i+\frac{n}{2}}\sin \frac{j\pi }{n+2}$$

Because $\sin \frac{j\pi }{n+2}=-\sin \frac{\left(n+2+j\right)\pi }{n+2}$, we obtain

$$\begin{gathered} {\alpha }_i=\frac{{\left(-1\right)}^{\frac{n}{2}-i}}{\sin \frac{2i\cdot \pi }{n+2}\sin \frac{i\cdot \pi }{n+2}}{\displaystyle \prod }_{j=i-\frac{n}{2}}^{-1}\sin \frac{\left(n+2+j\right)\pi }{n+2}{\displaystyle \prod }_{j=1}^{i+\frac{n}{2}}\sin \frac{j\cdot \pi }{n+2} \\ =\frac{{\left(-1\right)}^{\frac{n}{2}-i}}{\sin \frac{2i\cdot \pi }{n+2}\sin \frac{i\cdot \pi }{n+2}}{\displaystyle \prod }_{j=\frac{n}{2}+i+2}^{n+1}\sin \frac{j\cdot \pi }{n+2}{\displaystyle \prod }_{j=1}^{i+\frac{n}{2}}\sin \frac{j\cdot \pi }{n+2} \\ =\frac{{\left(-1\right)}^{\frac{n}{2}-i}}{\sin \frac{2i\cdot \pi }{n+2}\sin \frac{i\cdot \pi }{n+2}\sin \frac{\left(\frac{n}{2}+i+1\right)\pi }{n+2}}{\displaystyle \prod }_{j=1}^{n+1}\sin \frac{j\cdot \pi }{n+2} \end{gathered}$$

As ${{\displaystyle \prod }}_{j=1}^{n+1}\sin \frac{j\cdot \pi }{n+2}=\frac{n+2}{2^{n+1}}$, $\sin \frac{\left(\frac{n}{2}+i+1\right)\pi }{n+2}=\cos \frac{i\cdot \pi }{n+2}$, and $2\cdot \cos \frac{i\cdot \pi }{n+2}\cdot \sin \frac{i\cdot \pi }{n+2}=\sin \frac{2i\cdot \pi }{n+2}$,

$${\alpha }_i=\frac{{\left(-1\right)}^{\frac{n}{2}-i}}{{\sin }^2\frac{2i\cdot \pi }{n+2}}\cdot \frac{2^n}{n+2}$$

Lemma 3 is proven. □

Theorem 3.

If$n$is an even number, then PBAS is defined as

$$Q_{\mu ,n}\left(x\right)=\mu {\displaystyle \prod }_{i=1}^{n/2}\left(x^2-x_i^2\right)+Q_n^1\left(x\right),$$

where$\mu \in \left[-\tau ,\tau \right]$,$x_i=\sin \frac{i\cdot \pi }{n+2}$, and$\tau =\frac{2^{n+1}}{n+2}\tan \frac{\pi }{2n+4}$.

Proof. 

Using the theorem on the expansion of rational functions in the case of different roots [14], we represent $R_n\left(x\right)$ as partial fraction decomposition:

$$R_n\left(x\right)=\frac{Z_n\left(x\right)}{{\displaystyle \prod }_{j=1}^{n/2}\left(x+x_j\right)}={\displaystyle \sum }_{j=1}^{n/2}\frac{b_j}{x+x_j},$$

where $\forall j=\overline{1,\frac{n}{2}}:b_j\in R$. Therefore, we have

$$Z_n\left(x\right)={\displaystyle \sum }_{j=1}^{n/2}{b}_j{{\displaystyle \prod }}_{i=1,i\ne j }^{n/2}\left(x+x_i\right)$$

Calculating the values of $Z_n\left(x\right)$ at the point $x=-x_j$, we obtain:

$$Z_n\left(-x_j\right)=b_j{{\displaystyle \prod }}_{i=1,i\ne j }^{n/2}\left(x_i-x_j\right)$$

On the other hand, $Z_n\left(x\right)=\frac{Q_n^1\left(x\right)-1}{{{\displaystyle \prod }}_{i=1}^{n/2}\left(x-x_i\right)}$, hence

$$Z_n\left(-x_j\right)=\frac{-2}{{{\displaystyle \prod }}_{i=1}^{n/2}\left(-x_j-x_i\right)}={\left(-1\right)}^{\frac{n}{2}+1}\cdot \frac{2}{{{\displaystyle \prod }}_{i=1}^{n/2}\left(x_j+x_i\right)}$$

Since $Z_n\left(-x_j\right)=b_j{{\displaystyle \prod }}_{i=1,i\ne j }^{n/2}\left(x_i-x_j\right)={\left(-1\right)}^{\frac{n}{2}+1}\cdot \frac{2}{{{\displaystyle \prod }}_{i=1}^{n/2}\left(x_j+x_i\right)}$, it follows that

$$b_j={\left(-1\right)}^{\frac{n}{2}+1}\cdot \frac{1}{x_j{{\displaystyle \prod }}_{i=1,i\ne j }^{\frac{n}{2}}\left(x_i^2-x_j^2\right)}=\frac{1}{x_j{{\displaystyle \prod }}_{i=1,i\ne j }^{\frac{n}{2}}\left(x_j^2-x_i^2\right)}.$$

Using Lemma 3, we find

$$b_j={\left(-1\right)}^{\frac{n}{2}+j}\cdot \dot{\frac{2^n}{n+2}}\cdot \frac{x_{2j}^2}{x_j}.$$

Therefore,

$$\begin{gathered} R_n\left(x\right)={\left(-1\right)}^{\frac{n}{2}}\cdot \frac{2^n}{n+2}\cdot {\displaystyle \sum }_{j=1}^{\frac{n}{2}}{\left(-1\right)}^j\cdot \frac{x_{2j}^2}{x_j}\cdot \frac{1}{x+x_j} \\ ={\left(-1\right)}^{\frac{n}{2}}\cdot \frac{2^{n+2}}{n+2}\cdot {\displaystyle \sum }_{j=1}^{\frac{n}{2}}{\left(-1\right)}^j\cdot \frac{x_j-x_j^3}{x+x_j}. \end{gathered}$$

Calculating $\frac{d{R}_n\left(x\right)}{dx}$, we have

$$\frac{d{R}_n\left(x\right)}{dx}=-{\displaystyle \sum }_{j=1}^{\frac{n}{2}}\frac{b_j}{{\left(x+x_j\right)}^2}.$$

Let us show that $\forall x\in \left[0,1\right]: \frac{d{R}_n\left(x\right)}{dx}\ne 0$. Using the corollary of the Cauchy–Schwarz inequality ${\left({{\displaystyle \sum }}_{i=1}^n{u}_i{v}_i\right)}^2\le \left({{\displaystyle \sum }}_{i=1}^n{v}_i\right)\left({{\displaystyle \sum }}_{i=1}^n{u}_i^2{v}_i\right),$ we have

$$\begin{gathered} {\left({\displaystyle \sum }_{b_j>0}\frac{b_j}{x+x_j} \right)}^2\le \left({\displaystyle \sum }_{b_j>0}{b}_j\right)\left({\displaystyle \sum }_{b_j>0 }\frac{b_j}{{\left(x+x_j\right)}^2}\right) \\ {\left({\displaystyle \sum }_{b_j<0}\frac{b_j}{x+x_j} \right)}^2\le -\left({\displaystyle \sum }_{b_j<0}{b}_j\right)\left({\displaystyle \sum }_{b_j<0 }\frac{b_j}{{\left(x+x_j\right)}^2}\right) \end{gathered}$$

Therefore,

$$\begin{gathered} \frac{{\left({{\displaystyle \sum }}_{b_j>0}\frac{b_j}{x+x_j} \right)}^2}{{{\displaystyle \sum }}_{b_j>0}{b}_j}\le {\displaystyle \sum }_{b_j>0 }\frac{b_j}{{\left(x+x_j\right)}^2} \\ \frac{{\left({{\displaystyle \sum }}_{b_j<0}\frac{b_j}{x+x_j} \right)}^2}{-{{\displaystyle \sum }}_{b_j<0}{b}_j}\le {\displaystyle \sum }_{b_j<0 }\frac{b_j}{{\left(x+x_j\right)}^2} \end{gathered}$$

Let us add two inequalities:

$$\frac{{\left({{\displaystyle \sum }}_{b_j>0}\frac{b_j}{x+x_j} \right)}^2}{{{\displaystyle \sum }}_{b_j>0}{b}_j}+\frac{{\left({{\displaystyle \sum }}_{b_j<0}\frac{b_j}{x+x_j} \right)}^2}{-{{\displaystyle \sum }}_{b_j<0}{b}_j}\le {\displaystyle \sum }_{j=1}^{n/2}\frac{b_j}{{\left(x+x_j\right)}^2}$$

As $\forall x\in \left[0,1\right]: \frac{{\left({{\displaystyle \sum }}_{b_j>0}\frac{b_j}{x+x_j} \right)}^2}{{{\displaystyle \sum }}_{b_j>0}{b}_j}>0$ and $\frac{{\left({{\displaystyle \sum }}_{b_j<0}\frac{b_j}{x+x_j} \right)}^2}{-{{\displaystyle \sum }}_{b_j<0}{b}_j}>0$ then ${{\displaystyle \sum }}_{j=1}^{n/2}\frac{b_j}{{\left(x+x_j\right)}^2}>0$. Therefore, $\frac{d{R}_n\left(x\right)}{dx}$ does not change sign on the interval [0, 1]. The minimum and maximum of the function $R_n\left(x\right)$ will be reached at the ends of the interval. Let us calculate the value of the function $R_n\left(x\right)$ at the points $x=0$ and $x=1$:

$$\begin{gathered} R_n\left(0\right)={\left(-1\right)}^{\frac{n}{2}}\cdot \frac{2^{n+2}}{n+2}{\displaystyle \sum }_{j=1}^{n/2}{\left(-1\right)}^j\left(1-x_j^2\right) \\ {R}_n\left(1\right)={\left(-1\right)}^{\frac{n}{2}}\cdot \frac{2^{n+2}}{n+2}{\displaystyle \sum }_{j=1}^{n/2}{\left(-1\right)}^j\left(x_j-x_j^2\right) \end{gathered}$$

Considering that

$$\begin{gathered} {\displaystyle \sum }_{j=1}^{n/2}{\left(-1\right)}^j=\frac{-1+{\left(-1\right)}^{n/2}}{2}, \\ {\displaystyle \sum }_{j=1}^{n/2}{\left(-1\right)}^j{x}_j=\frac{{\left(-1\right)}^{n/2}}{2}-\frac{1}{2}\tan \frac{\pi }{2n+4}, \\ {\displaystyle \sum }_{j=1}^{n/2}{\left(-1\right)}^j{x}_j^2=\frac{{\left(-1\right)}^{n/2}}{2}, \end{gathered}$$

we have

$$\begin{gathered} R_n\left(0\right)={\left(-1\right)}^{\frac{n}{2}+1}\cdot \frac{2^{n+1}}{n+2} \\ {R}_n\left(1\right)={\left(-1\right)}^{\frac{n}{2}+1}\cdot \frac{2^{n+1}}{n+2}\tan \frac{\pi }{2n+4} \end{gathered}$$

As $\forall n\ge 2$ and ${\left|n\right|}_2=0:\left|R_n\left(0\right)\right|>\left|R_n\left(1\right)\right|$, considering Theorem 2, we obtain

$$\tau =\left|R_n\left(1\right)\right|=\frac{2^{n+1}}{n+2}\tan \frac{\pi }{2n+4}.$$

The theorem is proven. □

7. Conclusions

Homomorphic encryption enables the computing of encrypted data without access to the secret key. It has become a promising mechanism for the secure computation, storage, and communication of confidential data in cloud services [15]. Practical scenarios include robot control systems, machine learning models, image processing, and many others [6,7,8,9,10,16,17,18]. A challenge of processing encrypted information is finding a cryptographically compatible sign function approximation.

State-of-the-art works have mainly focused on constructing the polynomial of best approximation of the sign function (PBAS) on the union of the intervals $\left[-1,-ϵ\left]{{\displaystyle \cup }}^{}\right[ϵ,1\right]$. In this paper, we provide a construction of the PBAS on the complete interval $\left[-1,1\right]$ and prove that:

If $n=0,$ then PBAS has the form $Q_n\left(x\right)=a_0$, where $\left|a_0\right|\le 1$.

If $n\ge 1,$ then there is a unique PBAS odd function, which can be calculated using the zeros of the Chebyshev polynomial of the second kind.

If $n\ge 1$ and $n$ is an odd number, then there are no PBAS of the general form.

If $n\ge 1$ and $n$ is an even number, then there is an uncountable set of PBAS of the general form.

Future studies include assessing the accuracy and efficiency of PBAS on real systems, e.g., over privacy-preserving neural networks with homomorphic encryption, where the non-linear activation function is replaced with a PBAS to operate with encrypted data.