Abstract
The paper describes essential reaction–diffusion models with delay arising in population theory, medicine, epidemiology, biology, chemistry, control theory, and the mathematical theory of artificial neural networks. A review of publications on the exact solutions and methods for their construction is carried out. Basic numerical methods for integrating nonlinear reaction–diffusion equations with delay are considered. The focus is on the method of lines. This method is based on the approximation of spatial derivatives by the corresponding finite differences, as a result of which the original delay PDE is replaced by an approximate system of delay ODEs. The resulting system is then solved by the implicit Runge–Kutta and BDF methods, built into Mathematica. Numerical solutions are compared with the exact solutions of the test problems.
Keywords:
delay models; nonlinear delay reaction–diffusion equations; exact solutions; numerical methods; method of lines; Mathematica MSC:
35K57; 35R10; 35C05; 65M20
1. Introduction
In natural science, there are numerous nonlinear systems that are hereditary when the quantities under consideration depend both on the present state and on the history of the process. In particular, the state of the system may be determined only by a certain moment in the past. These systems are referred to as systems with delay. To model such systems, one should use the differential equations containing not only the unknown function but also the function , where t is the time and is the delay [1,2]. Typically, the delay time is assumed to be constant. The simplest ordinary differential equation (ODE) with delay has the form
where F is a function. Delay ODEs arise in population theory [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23], medicine [24,25,26,27,28,29,30,31,32,33,34,35], epidemiology [36,37,38,39,40,41,42,43,44], economy [45,46,47,48], climatology [49], mechanics [50], control theory [51], the mathematical theory of artificial neural networks [52,53,54,55,56,57], etc.
However, the processes occurring in such systems are often spatially inhomogeneous, which leads to the use of more complex reaction–diffusion equations (RDEs) with a constant delay (see, e.g, [58,59]):
where , is the diffusion coefficient, and F is the kinetic function. In the special case, when in (2), we have a simple physical interpretation: the substance transfer in a local non-equilibrium medium possesses inertial properties, i.e., the reaction of the system is not instantaneous but delayed for .
In most cases, models described by nonlinear delay RDEs (2) are obtained by formally adding the diffusion term to the right side of the delay ODE (1). With this approach, random walks are modeled, in which the movement of each considered object (subject) is due to Fickian diffusion, when the flow is proportional to the concentration gradient and the proportionality constant is negative. For example, in population dynamics models, a phenomenon similar to diffusion arises from the tendency of any species to migrate to regions with a lower population density [60]. For simplicity, it is generally assumed that food is supplied continuously and uniformly in time and space. Thus, food will become scarce in regions with a higher population density, and species will tend to migrate to regions with a lower density in order to have a higher chance of survival. Papers [61,62,63] discuss the diffusion process from an ecological point of view.
Remark 1.
The formal introduction of the diffusion term into the right side of a delay ODE can lead to some difficulties. The fact is that, although diffusion and delay are related to space and time, respectively, they are not independent of each other, because the individuals, cells, neurons, molecules, etc., are not at the same location at previous times. Possible ways to overcome this problem by introducing a distributed (non-local) delay are discussed in [64].
Nonlinear delay RDEs of form (2) and related, more complex equations and systems arise in various applications, such as population theory [65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80], medicine [81,82,83,84,85,86,87,88,89], epidemiology [90,91,92,93,94,95,96,97,98,99,100], biology [101,102,103,104,105,106], chemistry [58,107,108,109,110], control theory [59,111,112,113], the theory of artificial neural networks [114,115,116,117,118,119], and many others (see [59,120]). Some models described by nonlinear delay RDEs are considered below.
Delay greatly complicates the study of nonlinear equations of form (2). Such equations have solutions of a traveling-wave type , where (see, for example, [59,121,122,123]), but do not have self-similar solutions , which non-delay RDEs often admit. More complex exact solutions of nonlinear delay RDEs were obtained in [124,125,126,127,128,129,130,131,132,133,134]. Some exact solutions are given below.
The known methods of the numerical integration of non-delay RDEs, after certain modification, can also be used in solving initial-boundary value problems for delay RDEs. The method of lines and finite-difference methods are most widely used (see [120], Section 5.2). The method of lines allows one to reduce a partial differential equation (PDE) with delay to a system of delay ODEs. The resulting system can be solved using Mathematica [135], Maple [136], or MATLAB [137], which are not designed for solving delay PDEs directly (for other data on using Maple and Mathematica for scientific research, see [138]). Below, these numerical methods will be considered in more detail.
It is important to note that delay differential equations have a number of specific features [59,120,139,140] that are not inherent in non-delay equations and significantly complicate obtaining adequate numerical solutions. The fact is that even in the absence of delay, theoretical estimates of the accuracy of numerical solutions of nonlinear RDEs contain constants that depend on the smoothness of the solution and cannot be calculated a priori (this applies to non-smooth solutions, which are typical for delay equations). The practical convergence of numerical methods, based on the refinement of the grid, also cannot fully guarantee the reliability of the schemes used and the accuracy of calculations (especially near the values of the problem parameters corresponding to unstable solutions, or near those values of variables that correspond to singularities of the equation or large gradients of solutions).
In many cases, the most efficient and most illustrative way to assess the range of the applicability and accuracy of numerical methods is a direct comparison of numerical and exact solutions of test problems constructed using delay RDEs, allowing solutions in elementary functions. In the final part of the paper, some test problems containing free parameters are presented, and the numerical and exact solutions of these test problems are compared. The numerical solutions are obtained by the method of lines in combination with the implicit Runge–Kutta and BDF methods built into Mathematica.
2. Models Using Delay RDEs
2.1. Models of Population Theory
At present, much attention is paid to reaction–diffusion models with delay in population theory. The delay characterizes the average reproductive age, i.e., the average time from the moment of birth (sometimes from the moment the egg is laid) to the moment of becoming sexually mature. The diffusion logistic equation with delay has the form [66,141,142]:
where is the population density, is the population growth rate, k is the carrying capacity of the environment, is the average reproductive age, is the diffusion coefficient. The corresponding delay ODE (with ) is called the Hutchinson equation and is widely studied [16,17,19,20]. A more complex reaction–diffusion model, taking into account the limited food supply, is considered in [65,66].
The diffusive Nicholson’s blowflies equation with delay, describing the dynamics of the blowfly population, has the form
where is the maximum possible per capita egg production rate (corrected for egg to adult survival), is the population size at which the population achieves maximum reproductive success, is the per capita adult death rate, is the time it takes for an egg to develop into a sexually mature adult. Stability of solutions of the diffusive Hutchinson’s equation with delay (4) is studied in [72,73,74,75,76].
The reaction–diffusion Lotka–Volterra model with several delays is described by the system of equations:
where and are the unknown functions; , (; ); and are the delays. System (5) describes the interaction of two species (in the case , we have two independent diffusion logistic equations (3)). The unknown functions and and the coefficients , , () are non-negative and have a physical meaning similar to functions and coefficients of Equation (3). The delays and , as in the diffusion logistic equation, characterize the average reproductive age of individuals, and the delays and are responsible for the time required for changes in the size of one population to lead to changes in another. All delays are non-negative and can be equal to zero in certain models. Terms with nonzero coefficients and distinguish the considered model from the diffusion logistic equation. These coefficients are responsible for the interaction between two populations. In the case of cooperative interaction, when one species persists in the absence of the other, and when the species mutually increase each other’s growth rate, both coefficients and are positive. In the case of competitive interaction, an increase in one population leads to a decrease in another (for example, an increase in the number of predators leads to a decrease in the population of prey), and the coefficients and are negative. Delay Lotka–Volterra cooperative models are discussed in [67,68], competitive models in [69,70,78], three-species model in [71].
In [68], a simpler than (5) system was studied in the form
where , , with boundary and initial conditions
- For all , the trivial solution of system (6) is stable for and unstable for .
- Under the conditions from item , there exists a value such that the stationary solution of system (6) is asymptotically stable for and unstable for .
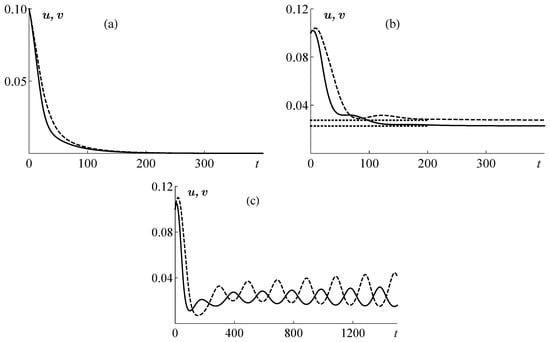
Figure 1 shows graphs of the numerical solutions of problems (6)–(8) at the point obtained in Mathematica by a combination of the method of lines (for ) and the BDF method for , , and various b and (see [120], Section 6.2.4). Figure 1a corresponds to the case of a stable trivial equilibrium, Figure 1b to a stable positive stationary solution, Figure 1c to an unstable positive stationary solution. The dotted lines in Figure 1b correspond to the stationary solution, which, for , has the values , .
Remark 2.
Paper [68] provides graphs of solutions obtained for other parameter values by other methods: using MATLAB by combining the method of steps and an implicit numerical method of integrating PDEs.
2.2. Models Describing the Spread of Epidemics and the Development of Diseases
Models of the spread of epidemics and the development of diseases are related to models of population theory. Models of the spread of epidemics describe the dynamics of interactions between susceptible, infectious, and immune individuals (sometimes other groups of individuals are also considered). The best known cause of the delay in epidemiological models is the latent period of the disease in the infected organism: it takes some time before the infection in the infected host develops to a level sufficient for further transmission. Sometimes the latent period coincides with the incubation period, that is, the time from the moment of infection to the first signs of the manifestation of the disease. However, in general, these two periods do not coincide. Due to the high mobility of people within one country or even around the world, spatially homogeneous models do not adequately describe the spread of the disease. To make the model more realistic, it is necessary to take into account the heterogeneity of space. If the environment is spatially continuous, random diffusion is often used to describe population mobility, leading to models based on RDEs [61].
The main difference between models of disease development from models of the spread of epidemics is to explicitly take into account an intermediate agent (virus) in the process of transmission of infection from an infected cell to an uninfected one. Infection occurs not from a contact between an infected and susceptible individual, as is the case in epidemic models, but from a contact between a susceptible cell and a virus. Such models take into account the intracellular delay between the moment of cell infection and the start of cell production of new viruses.
The delay diffusion SIR model of the spread of epidemics of Kermack–Mckendrick type is described by the system of equations:
Here, , , are the population densities of susceptible, infected, and removed from the population (due to the acquisition of immunity or death) individuals; is a function with delay; is the transmission coefficient (the average number of contacts of an infectious individual per unit of time); is the recovery rate of infected individuals; , , are the diffusion coefficients. In system (9), the nonlinear term is responsible for mass incidence, and the removal from the population occurs in proportion to the share of infected individuals ; Model (9) is called the SIR model because individuals move from Susceptible to Infectious and then Removed.
Other epidemic models are discussed, for example, in [90,91,92,93,94,95,96,97,98,99]. Systems of six equations, including two nonlinear delay RDEs, describing the dynamics of the spread of the COVID-19 epidemic, are considered in [100]. Related to models of the spread of epidemics, models of the development of diseases inside the organism, for example, hepatitis B, are proposed in [81,82,83,84,85,86]. Models of interaction between immune and tumor cells are explored in [87,88,89].
2.3. Other Delay Reaction–Diffusion Models
To describe the dynamics of a homogeneous population of mature circulating blood cells of density , the following delay RDE can be used [101,102]:
where , , n, and are some parameters, the description of which can be found in [143]. Similar equations and systems were also studied in [103,104,105,106].
The Belousov–Zhabotinsky reaction is a class of chemical reactions occurring in an oscillatory mode in which some reaction parameters (color, concentration of components, temperature, etc.) change periodically, forming a complex spatiotemporal structure of the reaction medium (see [144,145,146]). To study circular spatiotemporal waves that arise in a solution prepared in a certain way, a model with delay is used [58,107,108,109,110]:
where and are the dimensionless concentrations of bromous acid and bromide ions, respectively, and (), , and are dimensionless parameters (see [146]).
Delay RDEs are used to describe the heat treatment of metal sheets [59,111,112,113]. The delay is responsible for the time between the moment the temperature values are taken, and the signal arrives at the controllers.
Delay RDEs and systems of such equations are widely used in the mathematical theory of artificial neural networks, the results of which are used for signal and image processing, in pattern recognition problems, in associative machine memory, in determining the speed of moving objects. The delay occurs in artificial neural networks due to the finite switching speed of amplifiers and the finite speed of signal propagation between neurons [114,115,116,117,118,119].
Remark 3.
The models considered above and some other models based on ODEs, RDEs, and systems with delays are discussed in detail in [120], Section 6.
3. Exact Solutions of Nonlinear Delay RDEs
3.1. The Concept of ‘Exact Solution’
The general solution of nonlinear delay RDEs cannot be found even in the simplest cases. This means that we can only search for and study particular solutions, which are often referred to as exact solutions. In our study, we will use the concept of ‘exact solution’ for nonlinear delay RDEs in the same way as it was used in [126,128,147,148].
3.2. Exact Solutions of Traveling-Wave Type
RDEs of form (2) admit exact solutions of traveling-wave type:
where k and are nonzero constants. Substituting (12) into (2), we obtain the nonlinear ODE with constant delay:
where , .
Representable in elementary functions, exact solutions of traveling-wave type to reduced nonlinear delay ODEs (13) and the corresponding original delay RDEs (2), whose kinetic function contains arbitrary functions, were obtained in [123].
Numerous studies have been devoted to the existence and stability of traveling-wave solutions of delay RDEs (see, for example, [58,67,76,79,80,149] and references therein).
3.3. More Complex Exact Solutions
Numerous papers contain more complex exact solutions expressed in elementary functions with a generalized or functional separation of variables for various classes of nonlinear delay PDEs. Solutions are constructed by the method of functional constraints [126] or its modifications [127,131,150]. The method of functional constraints is to seek for solutions with a generalized
or functional
separation of variables, which must satisfy one of two functional constraints:
Thus, an admissible form of the exact solution is found, which is then substituted into the original equation to determine the final form.
Papers [125,126,127,128,131] present exact solutions with generalized and functional separation of variables for nonlinear RDEs of form (2) in which the kinetic function F depends on one or more arbitrary functions of one/two arguments, or on free parameters, and for more complex delay equations of a higher order:
Paper [133] contains exact solutions with generalized separation of variables (generalized traveling wave) of the form for nonlinear delay RDEs with variable coefficients
it also describes a method for constructing such solutions based on grouping the coefficients of the equation in order to reduce it to a delay ODE of a second order. Exact solutions of such and similar equations are also considered in [150,151,152].
Exact solutions of nonlinear RDEs with several delays are considered in [127]; with proportional delay (for , where is some constant), in [147]; and with a time-varying delay in [126,127]. Papers [127,131] give exact solutions to equations with a nonlinear transport coefficient:
In [153], there are exact solutions of nonlinear delay Klein–Gordon equations:
and, in [139,154], of nonlinear delay equation of telegraph type:
Papers [130,132] contain a large number of exact solutions for nonlinear systems of delay RDEs. The ‘generating equations’ method for constructing such solutions is proposed in [132]. In [155], exact solutions for systems of Lotka–Volterra type with several delays are constructed.
Papers [156,157] describe a method for constructing exact solutions of nonlinear delay PDEs based on exact solutions of simpler PDEs without delay; nonlinear equations of higher orders, nonlinear equations with varying delay of a general form, and systems of nonlinear delay equations are considered.
A number of studies are devoted to the search for exact solutions of delay PDEs by methods of group analysis. In [124], nonlinear RDEs of form (2) were investigated; four equations that admit invariant solutions were obtained (for two of them, only degenerate solutions linear in x were found). In [158], eight nonlinear and two linear Klein–Gordon equations (14) admitting invariant solutions were established. One linear and seven nonlinear Klein–Gordon equations with varying delay were found in [159].
Remark 4.
A large number of exact solutions of nonlinear delay PDEs and methods for their construction are considered in [120], Sections 3 and 4.
3.4. Some Exact Solutions with Separation of Variables
Equation 1. Consider the nonlinear RDE with a constant delay:
. Equation (15) has a solution with multiplicative separation of variables, periodic in space coordinate x, of the form:
where , , are arbitrary constants, and the function satisfies the first-order ODE with a constant delay:
. Equation (15) has another solution with multiplicative separation of variables of the form:
where , , are arbitrary constants, and the function satisfies the first-order ODE with a constant delay:
. Equation (15) has a degenerate solution with multiplicative separation of variables of the form:
where and are arbitrary constants, and the function satisfies the delay ODE (16) with .
. Equation (15) also has the solution with multiplicative separation of variables of mixed type:
where , , , are arbitrary constants, and the function satisfies the second order ODE with a constant delay:
Solution (19) can be treated as a nonlinear superposition of two traveling-wave solutions.
Remark 5.
. Equation (15) admits a solution of the form:
where c is an arbitrary constant, and is a -periodic function to be determined.
For convenience, we denote the general solution of problem (21) by . It has the form:
where , , , are arbitrary constants, for which series (22) and (23) and its derivatives , converge (convergence, for example, can certainly be ensured if we set for , where N is an arbitrary natural number).
We single out the following particular cases:
- (i)
- (ii)
- (iii)
Summing up, we have the exact solution of Equation (15):
where c is an arbitrary constant, and the -periodic function is determined by formulas (22) and (23).
. Equation (15) also admits a solution of the form:
where c is an arbitrary constant, is -antiperiodic function.
The general solution of problem (26), which for convenience we denote by , has the form:
where , , , are arbitrary constants, for which series (27) and (28) and its derivatives and converge. Decaying as , -antiperiodic in time solutions of problem (26) are given by Formulas (27) and (28) with ,
Summing up, we have the exact solution of Equation (15):
where c is an arbitrary constant, and the -antiperiodic function is determined by Formulas (27) and (28).
Remark 6.
Equation 2. The nonlinear RDE with a constant delay
admits a solution with multiplicative separation of variables of the form
Here, the functions and are described, respectively, by the ODE and the ODE with constant delay:
where is an arbitrary constant.
Remark 7.
The second-order ODE (30) does not explicitly depend on x and its general solution can be expressed implicitly. This equation has the particular one-parameter solution:
where is an arbitrary constant.
Equation 3. Consider the nonlinear RDE with a constant delay:
. Equation (31) has an exact solution with additive separation of variables, quadratic in x, of the form:
where and are arbitrary constants, and the function is described by the first-order ODE with a constant delay:
. Equation (31) also has a more general than (32) solution of the form:
where , , , , are arbitrary constants, and the function is described by the second-order ODE with a constant delay:
The values in (34) correspond to a traveling-wave solution.
Remark 8.
The delay ODE (33) has a particular solution, linear in t, of the form , where is an arbitrary constant, and λ is the root of the algebraic (transcendental) equation .
. Equation (35) for has a solution with additive separation of variables, periodic in space coordinate x, of the form:
where and are arbitrary constants, and the function satisfies the delay ODE:
. Equation (35) for has another solution with additive separation of variables of the form:
where and are arbitrary constants, and the function satisfies the delay ODE: (37).
. Equation (35) with has a degenerate solution with additive separation of variables of the form:
where the function satisfies the delay ODE (37) for .
. Equation (35) for also has a more general than (36) solution of the form:
where , , , are arbitrary constants, and the function is described by the delay ODE:
Unlike (36), solution (39) is not periodic in x; it describes the nonlinear interaction of a periodic standing wave and a traveling wave.
. Equation (35) for also has a more general than (38) solution of the form:
where , , , are arbitrary constants, and the function satisfies the delay ODE (40).
More complex exact solutions of Equation (35) (containing any number of arbitrary parameters) can be obtained using the above solutions and the following theorem.
Theorem 1
(on nonlinear superposition of solutions). Let be some solution of the nonlinear delay Equation (35) and the function be any τ-periodic solution of the linear diffusion equation with a source (21). Then, the sum
is also a solution of Equation (35). The general form of the function is defined by Formulas (22) and (23).
This theorem is proved by direct substitution of Formula (41) into the original delay Equation (35) using the equation for the function v (21).
Remark 9.
Equation 5. Consider the equation
. Equation (42) admits a solution with generalized separation of variables of the form
where the functions and are determined from the ODEs:
The linear ODE (44) is easy to integrate; the nonlinear ODE (45) is autonomous, and its general solution can be represented in an implicit form.
. More complex exact solutions of Equation (42) (containing any number of arbitrary parameters) can be obtained using the above solutions (43)–(45) and the following theorem.
Theorem 2
(generalizes Theorem 1). Let be some solution of the nonlinear delay Equation (42), and the function be any τ-periodic solution of the linear diffusion equation with a source (21). Then, the sum
where , is also a solution of Equation (42). The general form of the function is defined by Formulas (22) and (23).
This theorem is proved by direct substitution of Formula (46) into the original delay Equation (42) using the equation for the function v (21).
Formula (46) makes it possible to obtain a wide class of exact solutions of the nonlinear delay Equation (42). As the simplest particular solution of Equation (42), in (46), one can use the constant , which satisfies the algebraic (or transcendental) equation . As a function in (46), one can also take simple particular solutions of the form and and also a more complex traveling-wave solution , where and are arbitrary constants, and the function satisfies the delay ODE:
Alternatively, the exact solution (43) can be used.
Equation 6. Consider now the equation
which differs from Equation (42) by the sign of the parameter k in the kinetic term. The following theorem is true.
Theorem 3.
Theorem 3 is proved by direct verification and allows one to obtain a wide class of exact solutions to the nonlinear delay Equation (47). As a particular solution in (48), one can use, for example, a spatially homogeneous solution , a stationary solution , or a traveling-wave solution .
Equation 7. The more complex nonlinear delay equation
where , , are arbitrary functions (in this case, one of the two functions f or g can be set equal to zero without loss of generality) admits an exact solution of the form:
where N is any positive integer; the functions , , , are determined from the ODEs:
Note that the third nonlinear equation admits the trivial solution ; in this case, the remaining equations become linear ODEs with constant coefficients.
Equation 8. The nonlinear delay equation
where , , are arbitrary functions, has an exact solution of the form:
where N is any positive integer; the functions , , , are determined from the ODEs:
Equation 9. The nonlinear delay equation
where , , are arbitrary functions, admits an exact solution of the form:
where N is any positive integer; the functions , , are determined from the ODEs:
Note that the last equation is isolated (i.e., does not depend on the functions of other equations).
Equation 10. The nonlinear delay equation
where and are arbitrary functions, has an exact solution of the form:
where the functions and are determined from the nonlinear system of ODEs:
4. Methods for Numerical Integration of Delay RDEs
4.1. Preliminary Remarks. Time-Domain Decomposition Method
Problem for the delay RDE. Consider the initial-boundary value problem for the quasilinear RDE with a constant delay:
where , , , with the initial conditions:
and the homogeneous boundary conditions of the first kind:
Remark 10.
The problem that is described by the delay RDE (50) with the initial data (51) and the inhomogeneous boundary conditions of the first kind
where and are predefined functions, by substituting is reduced to an initial-boundary value problem with delay with homogeneous boundary conditions for the function . In this case, the transformed equation will explicitly depend on the variables x and t, which is an insignificant complication of the problem.
Time-domain decomposition method. In the case of a constant delay, one can decompose the considered time interval by dividing into several segments of equal length: (see, for example, [160]). Then, problem (50)–(52) on the segment takes the form:
Here, we take into account that for . Let the function be obtained as a solution to problem (53), which is a problem without delay. Then, we can proceed to solving the subproblem on the next segment , which is written as follows:
Here, for . Arguing further in a similar way, we can eventually construct a solution to the original problem (50)–(52). Each subproblem is a problem without delay, which can be solved by any known analytical or numerical method for PDEs without delay (for example, finite-difference or finite-element methods).
Remark 11.
The time domain decomposition method is a natural generalization of the method of steps, which is used to solve the Cauchy problems for delay ODEs (see [2]). If in Equation (50), then the subproblems on all the intervals will be linear.
4.2. Method of Lines. Numerical Integration Using Mathematica
Preliminary remarks. Formulation of the problem. At the moment, the theory for solving delay ODEs is quite well developed in comparison with the theory of solving delay RDEs. This applies to both analytical (see, for example, [1,2,19,161,162,163,164,165,166]) and numerical methods (see, for example, [167,168,169]). In addition, widespread software such as Maple, Mathematica, and MATLAB allow solving first-order delay ODEs [135,136,137]. Therefore, it is useful to reduce the delay PDE to a system of delay ODEs and then solve it, not the original equation. This approach is often implemented using the method of lines [170]. A large number of programs that analyze models for delay PDEs using the method of lines are contained in the book [35].
Let us introduce the spatial grid: , , where is the stepsize, N is the number of spatial intervals, and reduce problem (50)–(52) to the system of ODEs by approximating the spatial derivative with the finite difference and writing the equation at the point :
where . System (55) contains unknown functions and the same number of equations, as well as two known functions and .
Remark 12.
Higher accuracy can be achieved if we discretize using Chebyshev–Gauss–Lobatto points [171,172,173,174].
The main problem with this approach is that the resulting system of delay ODEs often turns out to be stiff. A system is called stiff if it describes processes occurring on very different time scales [175,176]. When solving such problems numerically, restrictions on the stepsize are imposed, not to improve accuracy but to ensure the stability of the algorithm [175], and usually only excessively small steps are suitable. Solving such a system requires the development and application of special methods with increased stability [167,177]. Usually, these are algorithms from the class of implicit Runge–Kutta [168,178,179] and BDF methods [175,176,180]. The schemes of Rosenbrock type [181,182,183,184] are also suitable.
In Mathematica, stiff ODE systems with a constant delay (including those with several delays) are solved numerically using the command NDSolve [135,185,186]. Without additional options, NDSolve uses an adaptive procedure, in which, during the calculation, methods are changed, and values of parameters are selected automatically. Using the option Method of the command NDSolve, one can manually specify one of the built-in methods for solving stiff ODE systems, namely the implicit Runge–Kutta [187,188] method or the implicit multi-step method based on the backward differentiation formula (BDF method) [189]. To describe these methods, we will use the Cauchy problem in vector form:
where , , are column vectors. Problem (55) is a special case of problem (56).
Implicit Runge–Kutta method. Implicit Runge–Kutta schemes for stiff ODE systems (56) are defined by the formulas [168,187,188]:
where is a column vector of auxiliary functions , each of which corresponds to the unknown function , time layer , and stage m, , , ; is the stepsize, are the weights of the quadrature formula (), are the coefficients defining the nodes of the quadrature formula, are the weights of intermediate quadrature formulas. If the value lies outside the grid points, the delay function values are calculated using interpolation on the interval , where is such an integer that . If , the delay function values coincide with the values , which were calculated earlier on the layer . Different Runge–Kutta methods are generated by different quadrature formulas, which are defined by sets of coefficients , , and .
The method based on Formulas (57) and (58) is an implicit M-stage method. For , we have an explicit method for ODE systems. In the case of , the values are determined successively from separate nonlinear equations. In the case of , the values must be calculated simultaneously for all stages from the system of equations, which, by default, is solved in Mathematica by Newton’s method (see the description of this method in [176]).
To successfully solve stiff problems, it is important to choose the appropriate coefficients of quadrature formulas. In Mathematica, by default, coefficient values are determined automatically. However, one can choose the type of these coefficients manually using the setting Coefficients of the option Method of the command NDSolve [188]. For example, these may be the coefficients based on the Lobatto quadrature formulas [190,191]. The first and last nodes of the Lobatto quadrature formula coincide with the beginning and end of the integration interval; therefore, , . The remaining coefficients are the zeros of the derivatives of the Legendre polynomials:
As a result, quadrature formulas of order are obtained. The weights and the coefficients of the Lobatto quadrature formulas are determined from the conditions:
In Mathematica, the stepsize of schemes (57) and (58) is determined automatically based on the estimate of the local error of solution [187]. For this, the solutions obtained by the original method with the order of approximation p and weights are compared with the solutions of the auxiliary method with order and weights (by default ). In this case, the coefficients and of both methods coincide, and hence the values also coincide, which eliminates the need to solve the nonlinear system a second time (58).
Remark 13.
In problems with solutions reaching high-order absolute values (see, for example, test problem 2 below), the commandNDSolvewith the Runge–Kutta method chosen can take minutes and tens of minutes to calculate a solution. The method running time can be significantly reduced to several seconds by increasing the allowable absolute and relative errors using the options AccuracyGoal → q and PrecisionGoal → p. Given the values of q and p, the program will try to ensure that the error of the numerical solution does not exceed the value.
BDF method. The BDF method is built into Mathematica as part of the IDA package from SUNDIALS (SUite of Nonlinear and DIfferential/ALgebraic equation Solvers), developed at the Center for Applied Scientific Computing of Lawrence Livermore National Laboratory [189]. The program code of the IDA methods (see user manual [180]) is based on DASPK [192,193] that are Fortran codes for solving large-scale differential–algebraic systems.
The M-step BDF method for system (56) is based on the formula [175,176,180]:
If the value lies outside the grid, the values are calculated by interpolation on the interval , where is an integer such that . If , the values coincide with the values , which were calculated earlier on the layer . The system of nonlinear algebraic Equations (61) can be solved by one or another iterative method, for example, Newton’s method.
In order for the BDF method to have the p-th order of approximation, one should set ([176] p. 255):
The highest achievable order of approximation of the M-step BDF method is M.
Assuming in (61) and (62), we obtain the formula for the first-order implicit Euler method:
For , , and , we have the relations ([176] p. 256):
determining BDF methods of the second, third, and fourth order of approximation, respectively.
In Mathematica, the BDF method on every time layer computes an estimate of the local truncation error, the stepsize and order M are automatically chosen so that , where the n-th component of the vector is given by
The values of the constants p and q are found using the options PrecisionGoal and AccuracyGoal of the command NDSolve. By default, the norm is automatically chosen by the command NDSolve depending on the method of integration (but can be set manually). For the BDF method, this is the norm of the form [194].
The steps are chosen automatically by the command NDSolve. The maximum number of steps the algorithm uses to construct a solution is estimated by the value of the initial step [195]. This can lead to problems if, for example, the solution grows exponentially without limit (see, for example, test problem 2). One can remove the restriction on the maximum number of steps using the option MaxSteps inside the command NDSolve.
Algorithm of the numerical integration of the delay reaction–diffusion problems by the method of lines using Mathematica. The flowchart of the numerical integration of the initial-boundary value problem (55) using Mathematica is shown in Figure 2. The algorithm can be described as the following sequence:
- .
- Formulate the problem consisting of the equation, initial, and boundary conditions.
- .
- Choose the number of spatial steps N.
- .
- Apply the method of lines and obtain the system of delay ODEs and initial conditions (and two algebraic relations on the edge of the region).
- .
- Choose the time interval of integration.
- .
- Solve the system from using methods of the command NDSolve.
- .
- In case of errors during calculation, try to reduce the time interval from and obtain the solution on a shorter time interval.
- .
- As a result, the values of the unknown function on all time layers, the values of absolute and relative errors (if the exact solution is known), plots and animations of the numerical solution (together with the exact solution) are obtained.
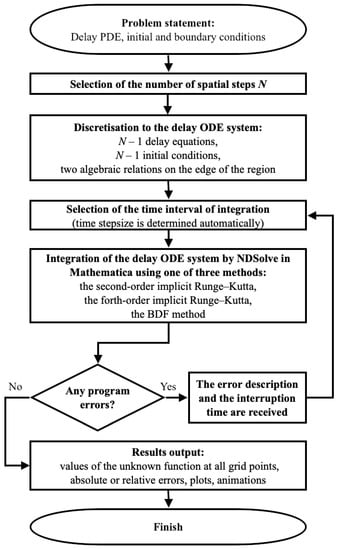
Figure 2.
The flowchart of the numerical integration of delay reaction–diffusion problems by the method of lines.
Remark 14.
In addition to a uniform grid in x, one can also use non-uniform grids. For non-uniform grids with the variable step , the second derivative is approximated as:
where (for ).
Remark 15.
The method of lines can also be used for the numerical integration of the more complex delay hyperbolic problems of a fairly general form [120]:
where ; functions p, q, and f can also depend on t explicitly. This equation includes, as special cases, delay reaction–diffusion equations (, ), delay equations of Klein–Gordon type (, ), nonlinear delay telegraph equations (, ).
In the cases of 2D and 3D delay RDEs, the terms and are replaced, respectively, by and . In particular, in the two-dimensional case on uniform grids, the Laplace operator () is approximated as follows:
where , , (; ), and , are stepsizes over spatial coordinates x and y.
4.3. Finite-Difference Methods
Explicit finite-difference scheme. Optimization of data storage in RAM. Consider the uniform spatial grid , where is the spatial stepsize. Let s be the time stepsize such that , where M is an integer. We approximate the time derivative by a finite difference of the form:
and the spatial derivative, by the second order finite difference:
As seen from (64), to calculate the values on layer , one needs the data not only from the previous layer k but also from layer . Therefore, it is necessary to keep in RAM the values from all the time layers within the delay range, as these values are used to obtain the solution. The process is complicated by the need to control the condition
so that the explicit scheme (64) is stable.
When solving problems with delay, it is required to store a sufficiently large amount of data with the possibility of constant access to it. Most often, the amount of data exceeds the amount of fast cache memory of the CPU, which means that it is necessary to interact with the RAM. This means that the speed of calculations depends on the speed of interaction with the RAM. Note that low read/write speeds of external drives make them even more useless for our purposes.
In [196], the algorithm that can significantly reduce the need for RAM is discussed. It is proposed to store data, not from all time layers but only from some so called base layers, and to restore intermediate values using interpolation. During the calculation, the number of base time layers within the delay range can be changed to maintain a balance between the accuracy of the algorithm and the amount of data stored and depends on the smoothness of the function. The type of interpolation is selected based on the parameters and properties of a particular model.
The smoothness of the function is determined by the formula [196]:
Let us introduce a parameter p such that each p-th layer within the delay range is a base layer. To minimize interpolation errors, but maintain a sufficiently high computational speed, it is recommended to choose the values of p from a range from 1 to 20. If the values of the function u change too quickly, then to maintain the required accuracy of the algorithm, all layers should be saved, i.e., . If the function changes slowly (), one should take . In this case, the proposed algorithm demonstrates the best efficiency. In [196], the empirical rule for calculating the optimal number of base layers for reaction–diffusion problems is proposed:
The total number of stored layers q in the delay range depends on the parameter p and the time stepsize s. In the simplest case, when p and s are fixed, one can use the formula .
Let be the time of the j-th base layer (), be the value of the function u on the j-th base layer. To restore the values of the intermediate layers from the q base layers, i.e., to find the values of for , one can use the Newton interpolation polynomial [196]:
where the divided differences are determined by the formulas:
It is important that the described algorithm does not depend on the numerical scheme, but only establishes the rules of data storage. Therefore, it can be easily generalized for use with other difference schemes.
Implicit finite-difference scheme. Using the time decomposition, problem (50)–(52) is solved step by step on the intervals , , ⋯ The uniform grid is constructed according to the rules: (), (), where is the spatial stepsize, is the time stepsize, M is an integer. The time derivative is approximated by the finite difference:
and the spatial derivative by the second-order finite difference:
Given that for , the implicit finite-difference scheme for problem (50)–(52) on this interval has the form:
On the next interval , the values of will also be known and equal to the corresponding values of calculated on the previous interval . Performing the calculations on successive intervals, we obtain a solution for the en–time interval. In [160], the conditions for the uniqueness of the solution of scheme (65) were established. In [197], the convergence of this scheme with order was proved and its stability was studied.
Remark 16.
Scheme (65) is a nonlinear system of difference equations, which can be solved by iterative methods, for example, the Picard–Schwarz method [160] or the method of upper and lower solutions [198,199,200,201].
Finite-difference scheme with weights. Consider problem (50)–(52) in the region . Construct a uniform grid according to the rules: (), (), where is the spatial stepsize, and is the time stepsize, M is an integer.
Denoting , we write the scheme with weights (see, for example, [202]):
where . The weight value corresponds to the explicit scheme. For , we have a tridiagonal system of linear algebraic equations, which is solved by the tridiagonal matrix algorithm. For , the scheme is unconditionally stable (more on stability, including for , see [202]).
Remark 17.
A related scheme with weights for a hyperbolic delay equation is considered, for example, in [203], and for a parabolic equation with a delay in the diffusion term in [204].
Higher-order finite-difference schemes. For sufficiently smooth solutions of Equation (50), one can use the following stable multi-step finite-difference scheme of order [205]:
where the difference operator is defined as
Remark 18.
For related, more complex delay RDEs, similar multi-step higher-order finite-difference schemes are given in [206,207].
Two special finite-difference schemes for a linear problem. In [208], two special finite-difference schemes for problem (50)–(52) with the linear kinetic function are considered. The proposed schemes have the same stability region, as the original problem. This is provided by the choice of spatial and time stepsizes, as well as a special method of approximation.
Both schemes use the same grid. The spatial stepsize is calculated by the formula , where h is the standard stepsize of a rectangular grid; time stepsize is , where M is an integer, . Note that the intervals , , … contain, in the general case, a non-integer number of time steps in contrast to the schemes considered above.
To build the first scheme, the trapezoid rule is applied, when the spatial derivative and the delay term are calculated as average values from two adjacent time layers:
where . The grid function approximates the function in the point using the linear interpolation:
Then, Equation (50) is approximated as follows:
The second finite-difference scheme is based on the use of the second-order backward differentiation formula for approximating the time derivative and has the form:
Using linear interpolation (67) for and rearranging the terms, we have
Here, it is necessary to have the values (), which can be obtained using the first difference scheme.
5. Construction, Choice, and Use of Test Problems for Delay RDEs
5.1. Basic Principles for Choosing Test Problems
For nonlinear delay RDEs, when choosing test problems designed to check the adequacy and evaluate the accuracy of the corresponding numerical and approximate analytical methods, it is useful to be guided by the following principles.
- .
- The most reliable test problems are obtained by using exact solutions of delay RDEs.
- .
- It is preferable to choose simple test problems, the solutions of which are expressed in terms of elementary functions.
- .
- It is preferable to choose test problems containing free parameters (that can be arbitrarily varied over a wide range) or arbitrary functions.
- .
- One can choose test problems from a wider class of similar equations (there is no need to use exact solutions of the equation under consideration, which are not always possible to obtain).
- .
- To check the adequacy and evaluate the accuracy of numerical methods, it is better to use several different test problems.
- .
- Testing of numerical methods should begin with simple test problems that have monotonic solutions with small gradients of the unknowns.
- .
- Numerical methods should be tested on test problems with large gradients of the unknowns in the initial or boundary conditions (for example, for rapidly oscillating initial conditions).
- .
- It is useful to test numerical methods on rapidly growing solutions at sufficiently large times.
- .
- If possible, the accuracy of numerical methods should be checked on test problems near the critical values of the parameters and independent variables that determine the singular points of the equation, unstable solutions, or solutions with large gradients.
It is important to emphasize that well-chosen test problems make it possible to compare and improve ‘workable’ numerical methods and filter out unsuitable ones.
Remark 19.
For nonlinear RDEs with delay, one cannot limit oneself to test problems obtained using exact solutions of the simpler nonlinear RDEs without delay.
5.2. Construction of Test Problems
Examples of exact solutions of delay RDEs that can be used to formulate test problems. To construct test problems, one should use the known exact solutions of nonlinear delay RDEs. A large number of such solutions can be found in ([120], Sections 3 and 4).
Consider the nonlinear delay RDE
which depends on five parameters , b, k, s, and is a special case of Equation (49) for , . Let us choose its parameters so that it has the stationary solutions and . The trivial stationary solution already exists for any values of the parameters. For the second stationary solution to exist, we substitute into (68) and, after elementary transformations, we have . As a result, we arrive at the equation
which can be written in the alternative form:
where .
For , Equation (69) becomes Fisher–KPP equation, and for , it becomes the diffusion logistic equation with delay. Below are two groups of the simplest exact solutions to Equation (69).
- (i)
- Solutions for :where ; A, B are arbitrary constants.
- (ii)
- Solutions for :where ; , are arbitrary constants;
To test numerical methods of nonlinear delay RDEs, one can choose the above exact solutions of Equation (69). Let us note the qualitative features of some solutions that are useful for comparison with the results of numerical calculations.
The first and fourth solutions from group (i) are periodic in spatial variable x. These solutions are useful as test solutions for initial-boundary value problems with boundary conditions of the first and second kind on the interval (). By appropriately choosing the values of the free constants A and B, one can make the unknown function on the boundary equal to zero or one (for boundary conditions of the first kind) or obtain the zero derivative with respect to x on the boundary (for boundary conditions of the second kind). In the case of problems with mixed boundary conditions, it is convenient to consider these solutions on the intervals (). The initial conditions at (or ) are determined from the solutions used as test problems. It is useful to compare the numerical and exact solutions of test problems for k close to unity (when the solutions change little in time) and for sufficiently large k (when the solutions change quickly).
Solutions from group (ii) for are periodic in time and for rapidly oscillate in time and space. Such solutions are useful for estimating the accuracy of numerical methods for problems with large gradients.
The test problems are formulated as follows: the chosen equation and its exact solution are supplemented with initial conditions at and boundary conditions at and , which are obtained from the used exact solution. Some test problems formulated in this way are given below.
Test problems for delay RDEs. Using the known exact solutions, we formulate several model test problems for delay RDEs, which can be used to check the adequacy and evaluate the accuracy of numerical methods. All test problems contain free parameters.
Test problem 1. Let us assume the following in the first formula of (70):
and obtain the exact solution of Equation (69):
Substituting into it, and then and , we find the initial conditions:
and the boundary conditions:
As a result, we have a test problem, which is described by Equation (69) with the parameter b from (72), the initial conditions (74), and the boundary conditions (75). The exact solution of this test problem is given by Formula (73), where , .
Remark 20.
Test problem 2. It can be shown by direct verification that Equation (68) for
admits the exact solution
Thus, we have a test problem, which is described by Equation (68) with the parameters (76), the initial conditions (78), and boundary conditions(79). The exact solution of this test problem is given by Formula (77), where , .
Now, consider the nonlinear five-parameter delay RDE:
which is a special case of Equation (42) for and becomes Fisher–KPP equations in the degenerate cases or .
Test problem 3. Let us assume that
Then, the test problem, described by Equations (80) and (81), initial conditions
and boundary conditions
has the exact solution in the region , .
The solution was obtained using Formula (43), where , and is the corresponding solution of the linear ODE (44).
Test problem 4. Let us assume that
5.3. Comparison of Numerical and Exact Solutions of Nonlinear Delay RDEs
Preliminary remarks. Numerical solutions of all test problems were obtained in Mathematica by the method of lines in combination with the second-order implicit Runge–Kutta method (with the coefficients of the Lobatto type) and the BDF method. The calculations were carried out on the interval for three delays , , and (sometimes additional values and were taken). Some test problems could not be solved on such a large interval. The integration procedure was interrupted with an error with an indication of the interruption time. Nevertheless, in most cases, an adequate numerical solution of the problem was obtained after shortening the time interval in a suitable way.
The absolute and relative errors of the numerical solution of a test problem for a delay RDE are, respectively, determined by the formulas:
where is the value of the exact solution of the test problem on the time layer at the point .
Comparison of exact and numerical solutions of test problems. In the previous section, four test problems for nonlinear delay RDEs (delay equations of the Fisher–KPP type) were formulated. In this section, we discuss the results of the numerical integration of the test problems and compare the obtained numerical solutions with the exact solutions of these problems. The numbering and wording of the test problems considered below are the same as the numbering and wording of the test problems given in the previous section.
Test problem 1. The exact solution of test problem 1 for , , and is monotonically decaying in time. The relative error of the numerical solution becomes noticeable only at sufficiently large times, when the solution is practically equal to zero. For the numerical methods used, with an increase in the delay (from 0.05 to 5), the time interval on which the methods operate with a small relative error increases. At , the numerical solution obtained by the second-order implicit Runge–Kutta method begins to differ from the exact solution when the solution reaches absolute values of the order of for and for ; the numerical solution by the BDF method begins to differ, reaching absolute values of the order of for and for .
The numerical solutions of the ODE system with of test problem 1, which were obtained by the second-order implicit Runge–Kutta method, and the corresponding exact solutions are shown in Figure 3 for , , and and the delays and (using a logarithmic scale along the u-axis). The results obtained by the BDF method look similar and are therefore omitted.
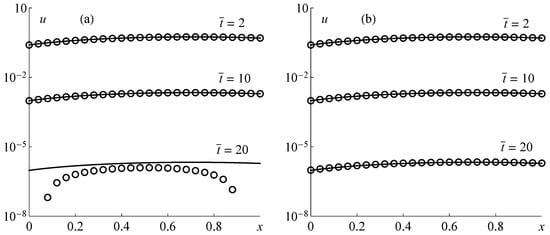
Figure 3.
The exact solutions (solid lines) and numerical solutions obtained by the combination of the method of lines and the second-order implicit Runge–Kutta method (circles) of test problem 1 for , , , and at different times for two delays: (a) and (b) .
The absolute errors of the numerical solutions obtained by the second-order implicit Runge–Kutta and BDF methods for five different delay times are presented in Table 1.

Table 1.
The absolute errors of the numerical solutions of test problem 1 for , , and five different delays on the interval .
Test problem 2. The exact solution of test problem 2 for grows exponentially in time. The program execution is interrupted with an error when the solution reaches high order values. For the second-order Runge–Kutta method, these are values of the order of . For , the numerical solution can be obtained on the en–interval up to ; for , up to ; and for , up to . The BDF method works better: until the solution reaches values of the order of . For and , the numerical solution can be obtained on the en–interval up to and for , up to . We also note that the BDF method allows one to obtain a solution in just a few seconds, while the second-order implicit Runge–Kutta method takes minutes and tens of minutes (see Remark 13 about a possible reduction in the calculation time).
The numerical solutions of the ODE system with of test problem 2, which were obtained by the BDF method, and the corresponding exact solutions are shown in Figure 4 for and the delays and (using a logarithmic scale along the u-axis). The results obtained by the Runge–Kutta method look similar and are therefore omitted.
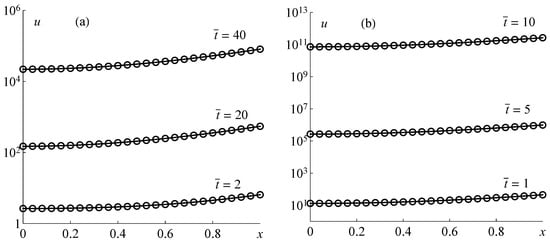
Figure 4.
The exact solutions (solid lines) and the numerical solutions obtained by the combination of the method of lines and the BDF method (circles) of test problem 2 for and at different times for two delays: (a) and (b) .
The relative errors of the numerical solutions obtained by the second-order implicit Runge–Kutta and BDF methods are presented in Table 2.

Table 2.
The relative errors of the numerical solutions of test problem 2 for and three different delays .
Test problem 3. The numerical solutions of the ODE system with of test problem 3, which were obtained by the second-order implicit Runge–Kutta method, and the corresponding exact solutions are shown in Figure 5 for , and the moderate delay . The results obtained by the BDF method look similar and are therefore omitted. Both methods demonstrate a good approximation of the exact solution over the en–interval .
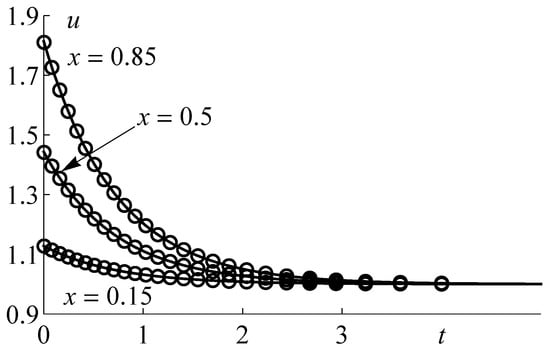
Figure 5.
The exact solutions (solid lines) and numerical solutions obtained by the combination of the method of lines and the second-order implicit Runge–Kutta method (circles) of test problem 3 for , , and at different times .
Table 3 presents the relative errors of the numerical solutions of test problem 3 obtained by the BDF and the second-order implicit Runge–Kutta methods at moderate and large delays on the interval .

Table 3.
The relative errors of the numerical solutions of test problem 3 for , , and three different delays on the interval .
For , , and sufficiently small delay times and , the numerical solution of test problem 3 begins to deviate strongly from the exact solution in the region where the stationary state is reached. After that, the program execution is interrupted with an error. This happens due to the fact that the parameter b, which is included in the equation of the test problem and defined in (81), grows indefinitely as as 0. As a result, the stationary solution , to which the solution of the problem under consideration tends as , becomes unstable for small (in the linear approximation, the proof of this fact is given below).
To illustrate the described situation, consider the dependences on time of the numerical and exact solutions for a fixed (see Figure 6), for , , and the small delays and . The choice of the midpoint is due to the fact that it was at this point that the maximum deviation of the numerical solution from the exact one was observed. For , both the numerical methods used adequately work only on a very short initial segment (slightly before reaching the asymptote); then, the second-order implicit Runge–Kutta method gives a downward nonmonotone oscillating curve that has nothing to do with the exact solution, and the BDF method leads to a curve that strongly deviates from the exact solution, rising sharply upwards. For , both the Runge–Kutta method and the BDF method provide a fairly accurate approximation of the exact solution over a fairly significant time interval (reaching the asymptote), and the BDF method has a slightly larger time range of applicability. The time dependence of the error of the numerical solution obtained by the BDF method is monotonic, in contrast to the nonmonotonic dependence for the Runge–Kutta method. In both cases, the errors increase sharply sometime after the steady state is established. Let us show that the values and lie inside the region of instability of the stationary solution of the considered delay equation.
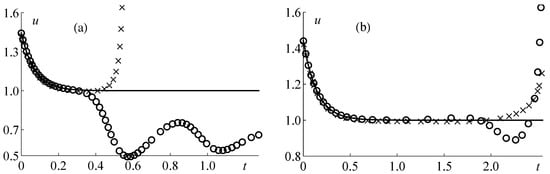
Figure 6.
The exact solutions (solid lines) and the numerical solutions (the second-order implicit Runge–Kutta method—circles, the BDF method—crosses) of test problem 3 at the point for , , and two delays: (a) and (b) .
Equation (80) of test problem 3 has the form
and admits the stationary solution (the solution of the test problem under consideration asymptotically tends to this solution as ). To analyze the linear stability/instability of the solution , consider perturbed solutions of the form [134]:
where is a small parameter, is the spectral parameter to be determined. On the boundaries and of the considered region, the perturbed solution (88) is equal to 1 for any t. Substituting (88) into Equation (87). Discarding terms of order and higher, after reduction by , we obtain the characteristic equation for the :
For , , and , the characteristic Equation (89) has the negative root . It follows that the second term in Formula (88) grows exponentially as and the considered stationary solution of the delay RDE (80) is unstable in the linear approximation for . As the delay increases to (the values of other parameters do not change), there are also one or two real negative roots of the transcendental Equation (89), while for , this equation has no real negative roots.
For , , , the characteristic Equation (89) has the complex root with the negative real part . Therefore, the considered stationary solution of the delay RDE (80) is also unstable in the linear approximation for .
Remark 21.
The value lies outside the region of instability of the stationary solution of test problem 3. In this case, the characteristic Equation (89) has the root with , and, as noted earlier, numerical methods work well.
Test problem 4. The numerical solutions of the ODE system with of test problem 4, which were obtained by the second-order implicit Runge–Kutta method, and the corresponding exact solutions are shown in Figure 7 for , , and the delay . The results obtained by the BDF method look similar and are therefore omitted.
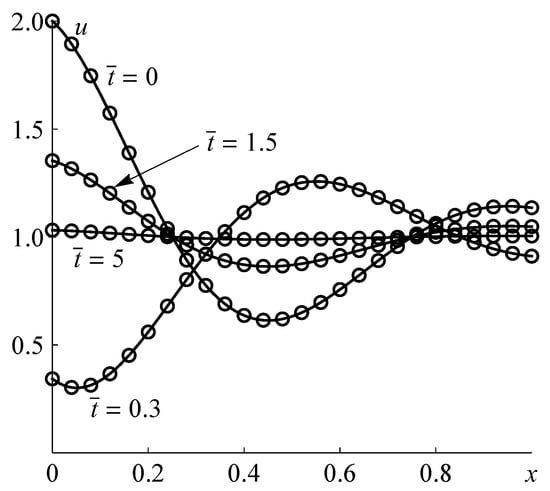
Figure 7.
The exact solutions (solid lines) and the numerical solutions obtained by the combination of the method of lines and the second-order implicit Runge–Kutta method (circles) of test problem 4 for , , and at different times .
The relative errors of the numerical solutions of test problem 4 at moderate and large delays on the interval are identical to two significant digits for the BDF and the second-order implicit Runge–Kutta methods. Values of the errors are presented in Table 4.

Table 4.
The relative errors of the numerical solutions of test problem 4 for , and three different delays on the interval .
Note that for delays of the order of unity (for example, ), the oscillations of the solution are not high-frequency and do not lead to problems in the numerical integration of the considered test problem, in contrast to the case of small delays, which is discussed below.
For small delays and and for and , the numerical solution of the ODE system of test problem 4 with could not be obtained either by the Runge–Kutta or the BDF method. This is primarily due to the fact that the parameter b, which is included in the equation of the test problem and defined in (84), grows indefinitely as as (in this case, the coefficient b grows much faster than in test problem 3). An additional complicating factor for small delays is the rapid oscillations of the solution in a small neighborhood of the left boundary , whereas in the rest of the considered region . Obtaining adequate numerical results in such cases is possible only at small spatial stepsizes in the region of the boundary layer type, where the solution changes rapidly. Using a variable spatial stepsize, that is, a different number of ODEs for regions with and without fast oscillations, in the method of lines is difficult, because it is difficult to determine in advance in which region high-frequency oscillations occur. The use of a small stepsize in the en–area of calculations is associated with an excessive increase in the running time of the method.
Remark 22.
The combination of the method of lines and the BDF method built into Mathematica is used in Section 2.1 to solve the initial-boundary value problem for the diffusion system of the Lotka–Volterra type.
6. Brief Conclusions
The phenomena associated with delay occur in biology, biomedicine, ecology, physics, chemistry, chemical technology, control theory, etc. Usually, models describing such phenomena are based on delay ODEs. However, as shown in the paper, in many cases, delay PDEs, namely delay RDEs, are more useful. Based on the analysis of the extensive literature data, it has been established that for the majority of interesting cases considered, the diffusion term can be given a clear and well-defined physical meaning. It is important that such equations have a number of physical features associated with the possible non-smoothness and instability of their solutions.
The paper has discussed the concept of the ‘exact solution’ of nonlinear delay RDEs. Nonlinear delay RDEs containing one or more arbitrary functions and methods allowing one to construct exact solutions for such equations have been considered. Exact solutions represented in elementary functions and containing free parameters have been obtained. Such exact solutions have been used to formulate test problems for checking the accuracy of the numerical methods.
It has been shown that the use of the method of lines for integrating delay RDEs, i.e., approximating the spatial derivatives by the corresponding finite differences, leads to the replacement of the original delay RDE with an approximate system of delay ODEs, which makes it possible to use the standard numerical methods of the modern software, such as Mathematica. The Mathematica command ‘NDSolve’ allows one to solve systems of delay ODEs by different methods, such as the implicit Runge–Kutta and BDF methods. However, with this approach, questions related to the accuracy and stability of the numerical integration of the original equation remain unexplored.
To interpret the results of the numerical integration, determine their adequacy to the considered processes, and evaluate the limits of applicability depending on the values of the parameters of the problem, the paper has proposed an approach based on a comparison of exact and numerical solutions of specially formulated test problems. Test initial-boundary value problems are formulated on the basis of nonlinear delay RDEs of a general form in which the arbitrary functions are specified. The initial and boundary conditions are chosen so that the known exact solutions of these equations satisfy these conditions (the uniqueness of the solutions is not investigated). On the basis of a linear analysis of the stability of the simplest stationary solutions of the formulated problem, the parametric regions of its stability/instability are determined. In these regions, numerical solutions of the corresponding initial-boundary value problems can be obtained and compared with the exact solution. The absolute or relative calculation error and the values of the parameters for which the numerical method can be applied can also be established. To sum up, this approach allows one to test the adequacy and estimate the accuracy of the numerical methods by the comparison of the exact and numerical solutions of test problems.
Author Contributions
Conceptualization and methodology, V.G.S. and A.V.V.; formal analysis and investigation, V.G.S.; software and visualization, V.G.S.; writing—original draft preparation, V.G.S.; writing—review and editing, V.G.S. and A.V.V.; supervision, V.G.S.; project administration, V.G.S. and A.V.V.; funding acquisition, A.V.V. All authors have read and agreed to the published version of the manuscript.
Funding
The study was supported by the Ministry of Education and Science of the Russian Federation, Russia, within the framework of the State Assignment (Reg. No. AAAA-A20-120011690135-5 and No. AAAA-A20-120092190052-9).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors thank A.D. Polyanin for his attention to the work and for very helpful comments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bellman, R.; Cooke, K.L. Differential-Difference Equations; Academic Press: New York, NY, USA, 1963. [Google Scholar]
- Elsgolt’s, L.E.; Norkin, S.B. Introduction to the Theory and Application of Differential Equations with Deviating Arguments; Academic Press: New York, NY, USA, 1973. [Google Scholar]
- Györi, I.; Trofimchuk, S. On the existence of rapidly oscillatory solutions in the Nicholson blowflies equation. Nonlinear Anal. 2002, 48, 1033–1042. [Google Scholar] [CrossRef]
- Kulenovic, M.R.S.; Ladas, G. Linearized oscillations in population dynamics. Bull. Math. Biol. 1987, 49, 615–627. [Google Scholar] [CrossRef]
- Liz, E.; Tkachenko, V.; Trofimchuk, S. A global stability criterion for scalar functional differential equation. SIAM J. Math. Anal. 2003, 35, 596–622. [Google Scholar] [CrossRef]
- Wei, J.; Li, M. Hopf bifurcation analysis in a delayed Nicholson blowflies equation. Nonlinear Anal. 2005, 60, 1351–1367. [Google Scholar] [CrossRef]
- Giang, D.; Lenbur, Y.; Seidman, T. Delay effect in models of population growth. J. Math. Anal. Appl. 2005, 305, 631–643. [Google Scholar] [CrossRef][Green Version]
- Karakostas, G.; Philos, C.; Sficas, Y. Stable steady state of some population model. J. Dyn. Differ. Equ. 1992, 4, 161–190. [Google Scholar] [CrossRef]
- So, J.W.-H.; Yu, J.S. Global attractivity and uniform persistence in Nicholson’s blowflies. Differ. Equ. Dyn. Syst. 1994, 2, 11–18. [Google Scholar]
- Berezansky, L.; Braverman, E. On oscillation of a food-limited population model with time delay. Abstr. Appl. Anal. 2003, 1, 55–66. [Google Scholar] [CrossRef]
- Wan, A.; Wei, J. Hopf bifurcation analysis of a food-limited population model with delay. Nonlinear Anal. Real World Appl. 2010, 11, 1087–1095. [Google Scholar] [CrossRef]
- Gourley, S.A.; Chaplain, M.A.J. Travelling fronts in a food-limited population model with time delay. Proc. R. Soc. Edin. A 2002, 132, 75–89. [Google Scholar] [CrossRef]
- So, J.W.-H.; Yu, J.S. On the uniform stability for a ’food-limited’ population model with time delay. Proc. R. Soc. Edin. A 1995, 125, 991–1002. [Google Scholar] [CrossRef]
- Gopalsamy, K.; Kulenovic, M.R.S.; Ladas, G. Environmental periodicity and time delays in a ‘food-limited’ population model. J. Math. Anal. Appl. 1990, 147, 545–555. [Google Scholar] [CrossRef]
- Gopalsamy, K.; Kulenovic, M.R.S.; Ladas, G. Time lags in a ‘food-limited’ population model. Appl. Anal. 1988, 31, 225–237. [Google Scholar] [CrossRef]
- Kolesov, A.Y.; Rosov, N.K. The theory of relaxation oscillations for Hutchinson’s equation. Sb. Math. 2011, 202, 829. [Google Scholar] [CrossRef]
- Jones, G.S. Asymptotic behavior and periodic solutions of a nonlinear differential-difference equation. Proc. Natl. Acad. Sci. USA 1961, 47, 879–882. [Google Scholar] [CrossRef]
- Hutchinson, G.E. Circular causal systems in ecology. Ann. N. Y. Acad. Sci. 1948, 50, 221–246. [Google Scholar] [CrossRef]
- Kuang, Y. Delay Differential Equations with Applications in Population Dynamics; Academic Press: San Diego, CA, USA, 2012. [Google Scholar]
- Wright, E.M. A non-linear difference-differential equation. J. Reine Angew. Math. 1955, 194, 66–87. [Google Scholar] [CrossRef]
- Gurney, W.S.C.; Blythe, S.P.; Nisbet, R.M. Nicholson’s blowflies revisited. Nature 1980, 287, 17–21. [Google Scholar] [CrossRef]
- Berezansky, L.; Braverman, E.; Idels, L. Nicholson’s blowflies differential equations revisited: Main results and open problems. Appl. Math. Model. 2010, 34, 1405–1417. [Google Scholar] [CrossRef]
- Pokusaev, B.G.; Vyazmin, A.V.; Zakharov, N.S.; Khramtsov, D.P.; Nekrasov, D.A. Unsteady mass transfer of nutrients in gels with channels of different spatial structures. Theor. Found. Chem. Eng. 2020, 54, 277–288. [Google Scholar] [CrossRef]
- Gourley, S.A.; Kuang, Y.; Nagy, J.D. Dynamics of a delay differential equation model of hepatitis B virus infection. J. Biol. Dyn. 2008, 2, 140–153. [Google Scholar] [CrossRef] [PubMed]
- Nelson, P.W.; James, D.M.; Perelson, A.S. A model of HIV-1 pathogenesis that includes an intracellular delay. Math. Biosci. 2000, 163, 201–215. [Google Scholar] [CrossRef]
- Nelson, P.W.; Perelson, A.S. Mathematical analysis of delay differential equation models of HIV-1 infection. Math. Biosci. 2002, 179, 73–94. [Google Scholar] [CrossRef]
- Culshaw, R.V.; Ruan, A. A delay-differential equation model of HIV infection of CD4+ T-cells. Math. Biosci. 2000, 165, 27–39. [Google Scholar] [CrossRef]
- Mittler, J.E.; Sulzer, B.; Neumann, A.U.; Perelson, A.S. Influence of delayed viral production on viral dynamics in HIV-1 infected patients. Math. Biosci. 1998, 152, 143–163. [Google Scholar] [CrossRef]
- Herz, A.V.; Bonhoeffer, S.; Anderson, R.M.; May, R.M.; Nowak, M.A. Viral dynamics in vivo: Limitations on estimates of intracellular delay and virus decay. Proc. Natl. Acad. Sci. USA 1996, 93, 7247–7251. [Google Scholar] [CrossRef]
- Liu, B. New results on the positive almost periodic solutions for a model of hematopoiesis. Nonlinear Anal. Real World Appl. 2014, 17, 252–264. [Google Scholar] [CrossRef]
- Berezansky, L.; Braverman, E. Mackey—Glass equation with variable coefficients. Comput. Math. Appl. 2006, 51, 1–16. [Google Scholar] [CrossRef]
- Saker, S.H. Oscillation and global attractivity of hematopoiesis model with delay time. Appl. Math. Comput. 2003, 136, 27–36. [Google Scholar] [CrossRef]
- Mackey, M.C.; Glass, L. Oscillation and chaos in physiological control system. Science 1977, 197, 287–289. [Google Scholar] [CrossRef]
- González-Parra, G.; Sultana, S.; Arenas, A.J. Mathematical modeling of toxoplasmosis considering a time delay in the infectivity of oocysts. Mathematics 2022, 10, 354. [Google Scholar] [CrossRef]
- Schiesser, W.E. Time Delay ODE/PDE Models: Applications in Biomedical Science and Engineering; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- McCluskey, C.C. Complete global stability for an SIR epidemic model with delay—Distributed or discrete. Nonlinear Anal. Real World Appl. 2010, 11, 55–59. [Google Scholar] [CrossRef]
- Ma, W.; Song, M.; Takeuchi, Y. Global stability of an SIR epidemic model with time delay. Appl. Math. Lett. 2004, 17, 1141–1145. [Google Scholar] [CrossRef]
- Takeuchi, Y.; Ma, W.; Beretta, E. Global asymptotic properties of a delay SIR epidemic model with finite incubation times. Nonlinear Anal. 2000, 42, 931–947. [Google Scholar] [CrossRef]
- Beretta, E.; Takeuchi, Y. Global stability of an SIR epidemic model with time delays. J. Math. Biol. 1995, 33, 250–260. [Google Scholar] [CrossRef]
- Beretta, E.; Takeuchi, Y. Convergence results in SIR epidemic model with varying population sizes. Nonlinear Anal. 1997, 28, 1909–1921. [Google Scholar] [CrossRef]
- Anderson, R.M.; May, R.M. Population biology of infectious diseases: Part I. Nature 1979, 280, 361–367. [Google Scholar] [CrossRef]
- Cooke, K.L. Stability analysis for a vector disease model. Rocky Mt. J. Math. 1979, 9, 31–42. [Google Scholar] [CrossRef]
- Yang, W. Modeling COVID-19 pandemic with hierarchical quarantine and time delay. Dyn. Games Appl. 2021, 11, 892–914. [Google Scholar] [CrossRef]
- Kashkynbayev, A.; Rihan, F.A. Dynamics of fractional-order epidemic models with general nonlinear incidence rate and time-delay. Mathematics 2021, 9, 1829. [Google Scholar] [CrossRef]
- Kalecki, M. A macrodynamic theory of business cycles. Econometrica 1935, 3, 327–344. [Google Scholar] [CrossRef]
- Zhang, X.; Zhu, H. Hopf bifurcation and chaos of a delayed finance system. Complexity 2019, 2019, 6715036. [Google Scholar] [CrossRef]
- Chen, X.; Liu, H.; Xu, C. The new result on delayed finance system. Nonlinear Dyn. 2014, 78, 1989–1998. [Google Scholar] [CrossRef]
- Cesare, L.D.; Sportelli, M. A dynamic IS-LM model with delayed taxation revenues. Chaos Solitons Fractals 2005, 25, 233–244. [Google Scholar] [CrossRef]
- Suarez, M.J.; Schopf, P.S. A delayed action oscillator for ENSO. J. Atmos. Sci. 1988, 45, 3283–3287. [Google Scholar] [CrossRef]
- Kalmár-Nagy, T.; Stépxaxn, G.; Moon, F.C. Subcritical HOPF bifurcation in the delay equation model for machine tool vibrations. Nonlinear Dyn. 2001, 26, 121–142. [Google Scholar] [CrossRef]
- Sleptsov, V.V.; Afonin, V.L.; Ablaeva, A.E.; Dinh, B.P. Development of an information measuring and control system for a quadrocopter. Russ. Technol. J. 2021, 9, 26–36. (In Russian) [Google Scholar] [CrossRef]
- Wu, J.; Campbell, S.A.; Bélair, J. Time-delayed neural networks: Stability and oscillations. In Encyclopedia of Computational Neuroscience; Springer: New York, NY, USA, 2015; pp. 2966–2972. [Google Scholar]
- Zhao, H. Exponential stability and periodic oscillatory of bidirectional associative memory neural network involving delays. Neurocomputing 2006, 69, 424–448. [Google Scholar] [CrossRef]
- Lu, H.T.; Chung, F.L.; He, Z.Y. Some sufficient conditions for global exponential stability of delayed Hopfield neural networks. Neural Netw. 2004, 17, 537–544. [Google Scholar] [CrossRef]
- Cao, J. New results concerning exponential stability and periodic solutions of delayed cellular neural networks. Phys. Lett. A 2003, 307, 136–147. [Google Scholar] [CrossRef]
- Cao, J.; Liang, J.; Lam, J. Exponential stability of high-order bidirectional associative memory neural networks with time delays. Physica D 2004, 199, 425–436. [Google Scholar] [CrossRef]
- Arik, S. Global asymptotic stability of a larger class of neural networks with constant time delay. Phys. Lett. A 2003, 311, 504–511. [Google Scholar] [CrossRef]
- Wu, J.; Zou, X. Traveling wave fronts of reaction-diffusion systems with delay. J. Dyn. Differ. Equ. 2001, 13, 651–687. [Google Scholar] [CrossRef]
- Wu, J. Theory and Applications of Partial Functional Differential Equations; Springer: New York, NY, USA, 1996. [Google Scholar]
- Cohen, D.S.; Rosenblat, S. Multi-species interactions with hereditary effects and spatial diffusion. J. Math. Biol. 1979, 7, 231–241. [Google Scholar] [CrossRef]
- Murray, J.D. Mathematical Biology, 3rd ed.; Springer: New York, NY, USA, 2002. [Google Scholar]
- Britton, N.F. Reaction-Diffusion Equations and Their Applications to Biology; Springer: New York, NY, USA, 1986. [Google Scholar]
- Cantrell, R.S.; Cosner, C. Spatial Ecology via Reaction—Diffusion Equations; John Wiley & Sons: Chichester, UK, 2003. [Google Scholar]
- Gourley, S.A.; So, J.W.-H.; Wu, J.H. Nonlocality of reaction-diffusion equations induced by delay: Biological modeling and nonlinear dynamics. J. Math. Sci. 2004, 124, 5119–5153. [Google Scholar] [CrossRef]
- Davidson, F.A.; Gourley, S.A. The effects of temporal delays in a model for a food-limited, diffusing population. J. Math. Anal. Appl. 2001, 261, 633–648. [Google Scholar] [CrossRef]
- Su, Y.; Wei, J.; Shi, J. Hopf bifurcation in a reaction-diffusion population model with delay effect. J. Differ. Equ. 2009, 247, 1156–1184. [Google Scholar] [CrossRef]
- Huang, J.; Zou, X. Traveling wavefronts in diffusive and cooperative Lotka—Volterra system with delays. J. Math. Anal. Appl. 2002, 271, 455–466. [Google Scholar] [CrossRef]
- Li, W.-T.; Yan, X.-P.; Zhang, C.-H. Stability and Hopf bifurcation for a delayed cooperation diffusion system with Dirichlet boundary conditions. Chaos Solitons Fractals 2008, 38, 227–237. [Google Scholar] [CrossRef]
- Faria, T. Stability and bifurcation for a delayed predator–prey model and the effect of diffusion. J. Math. Anal. Appl. 2001, 254, 433–463. [Google Scholar] [CrossRef]
- Lv, G.; Wang, M. Traveling wave front in diffusive and competitive Lotka—Volterra system with delays. Nonlinear Anal. Real World Appl. 2010, 11, 1323–1329. [Google Scholar] [CrossRef]
- Al Noufaey, K.S. Stability analysis of a diffusive three-species ecological system with time delays. Symmetry 2021, 13, 2217. [Google Scholar] [CrossRef]
- Yang, Y.; So, J.W.-H. Dynamics for the diffusive Nicholson blowflies equation. In Dynamical Systems and Differential Equations; Chen, W., Hu, S., Eds.; Southwest Missouri State University: Springfield, MO, USA, 1998; Volume 2, pp. 333–352. [Google Scholar]
- So, J.W.-H.; Yang, Y. Dirichlet problem for the diffusive Nicholson’s blowflies equation. J. Differ. Equ. 1998, 150, 317–348. [Google Scholar] [CrossRef]
- Saker, S.H. Oscillation of continuous and discrete diffusive delay Nicholson’s blowflies models. Appl. Math. Comput. 2005, 167, 179–197. [Google Scholar] [CrossRef]
- Yi, T.; Zou, X. Global attractivity of the diffusive Nicholson blowflies equation with Neumann boundary condition: A non-monotone case. J. Differ. Equ. 2008, 245, 3376–3388. [Google Scholar] [CrossRef]
- Mei, M.; So, J.; Li, M.; Shen, S. Asymptotic stability of travelling waves for Nicholson’s blowflies equation with diffusion. Proc. R. Soc. EdinburghSect. A 2004, 134, 579–594. [Google Scholar] [CrossRef]
- Gourley, S.A.; Kuang, Y. Wavefronts and global stability in time-delayed population model with stage structure. Proc. R. Soc. Lond. A 2003, 459, 1563–1579. [Google Scholar]
- Pao, C. Global asymptotic stability of Lotka—Volterra competition systems with diffusion and time delays. Nonlinear Anal. Real World Appl. 2004, 5, 91–104. [Google Scholar] [CrossRef]
- Faria, T.; Trofimchuk, S. Nonmonotone travelling waves in a single species reaction–diffusion equation with delay. J. Differ. Equ. 2006, 228, 357–376. [Google Scholar] [CrossRef][Green Version]
- Trofimchuk, E.; Tkachenko, V.; Trofimchuk, S. Slowly oscillating wave solutions of a single species reaction–diffusion equation with delay. J. Differ. Equ. 2008, 245, 2307–2332. [Google Scholar] [CrossRef][Green Version]
- Hattaf, K.; Yousfi, N. A generalized HBV model with diffusion and two delays. Comput. Math. Appl. 2015, 69, 31–40. [Google Scholar] [CrossRef]
- Hattaf, K.; Yousfi, N. Global dynamics of a delay reaction–diffusion model for viral infection with specific functional response. Comput. Appl. Math. 2015, 34, 807–818. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, Z. Dynamics of a diffusive HBV model with delayed Beddington—DeAngelis response. Nonlinear Anal. Real World Appl. 2014, 15, 118–139. [Google Scholar] [CrossRef]
- Chí, N.C.; Vales, E.Á.; Almeida, G.G. Analysis of a HBV model with diffusion and time delay. J. Appl. Math. 2012, 2012, 578561. [Google Scholar] [CrossRef]
- Xu, R.; Ma, Z.E. An HBV model with diffusion and time delay. J. Theor. Biol. 2009, 257, 499–509. [Google Scholar] [CrossRef]
- Wang, K.; Wang, W. Propagation of HBV with spatial dependence. Math. Biosci. 2007, 210, 78–95. [Google Scholar] [CrossRef]
- Banerjee, S.; Sarkar, R.R. Delay-induced model for tumor–immune interaction and control of malignant tumor growth. Biosystems 2008, 91, 268–288. [Google Scholar] [CrossRef]
- Piotrowska, M.J.; Foryś, U. A simple model of carcinogenic mutations with time delay and diffusion. Math. Biosci. Eng. 2013, 10, 861–872. [Google Scholar]
- Jia, Y. Bifurcation and pattern formation of a tumor–immune model with time-delay and diffusion. Math. Comput. Simul. 2020, 178, 92–108. [Google Scholar] [CrossRef]
- Yang, J.; Liang, S.; Zhang, Y. Travelling waves of a delayed SIR epidemic model with nonlinear incidence rate and spatial diffusion. PLoS ONE 2011, 6, e21128. [Google Scholar] [CrossRef]
- Gan, Q.; Xu, R.; Yang, P. Travelling waves of a delayed SIRS epidemic model with spatial diffusion. Nonlinear Anal. Real World Appl. 2011, 12, 52–68. [Google Scholar] [CrossRef]
- Xu, Z. Traveling waves in a Kermack—Mckendrick epidemic model with diffusion and latent period. Nonlinear Anal. 2014, 111, 66–81. [Google Scholar] [CrossRef]
- Bai, Z.; Wu, S.-L. Traveling waves in a delayed SIR epidemic model with nonlinear incidence. Appl. Meth. Comput. 2015, 263, 221–232. [Google Scholar] [CrossRef]
- Cheng, Y.; Lu, D.; Zhou, J.; Wei, J. Existence of traveling wave solutions with critical speed in a delayed diffusive epidemic model. Adv. Differ. Equ. 2019, 2019, 494. [Google Scholar] [CrossRef]
- Berezovsky, F.; Karev, G.; Song, B.; Castillo-Chavez, C. A simple epidemic model with surprising dynamics. Math. Biosci. Eng. 2005, 2, 133–152. [Google Scholar] [CrossRef]
- Li, J.; Sun, G.-Q.; Jin, Z. Pattern formation of an epidemic model with time delay. Phys. Stat. Mech. Its Appl. 2014, 403, 100–109. [Google Scholar] [CrossRef]
- Liu, P.-P. Periodic solutions in an epidemic model with diffusion and delay. Appl. Math. Comput. 2015, 265, 275–291. [Google Scholar] [CrossRef]
- Cai, Y.; Yan, S.; Wang, H.; Lian, X.; Wang, W. Spatiotemporal dynamics in a reaction-diffusion epidemic model with a time-delay in transmission. Int. J. Bifurc. Chaos Appl. Sci. Eng. 2015, 25, 1550099. [Google Scholar] [CrossRef]
- Hwang, T.-W.; Kuang, Y. Deterministic extinction effect of parasites on host populations. J. Math. Biol. 2003, 46, 17–30. [Google Scholar] [CrossRef]
- Zhu, C.-C.; Zhu, J. Dynamic analysis of a delayed COVID-19 epidemic with home quarantine in temporal-spatial heterogeneous via global exponential attractor method. Chaos Solitons Fractals 2021, 143, 110546. [Google Scholar] [CrossRef]
- Wang, X.; Li, Z. Dynamics for a type of general reaction-diffusion model. Nonlinear Anal. 2007, 67, 2699–2711. [Google Scholar] [CrossRef]
- Ramirez-Carrasco, C.; Molina-Garay, J. Existence and approximation of traveling wavefronts for the diffusive Mackey—Glass equation. Aust. J. Math. Anal. Appl. 2021, 18, 1–12. [Google Scholar]
- Ling, Z.; Lin, Z. Traveling wavefront in a Hematopoiesis model with time delay. Appl. Math. Lett. 2010, 23, 426–431. [Google Scholar] [CrossRef][Green Version]
- Wang, X.; Zhang, H.; Li, Z.X. Oscillation for a class of diffusive hematopoiesis model with several arguments. Acta Math. Sin. Eng. Ser. 2012, 28, 2345–2354. [Google Scholar] [CrossRef]
- Ling, Z.; Zhu, L. Traveling wavefronts of a diffusive hematopoiesis model with time delay. Appl. Math. 2014, 5, 2172–2718. [Google Scholar] [CrossRef][Green Version]
- Pan, X.; Shu, H.; Wang, L.; Wang, X.-S. Dirichlet problem for a delayed diffusive hematopoiesis model. Nonlinear Anal. Real World Appl. 2019, 48, 493–516. [Google Scholar] [CrossRef]
- Ma, S. Traveling wavefronts for delayed reaction-diffusion systems via a fixed point theorem. J. Differ. Equ. 2001, 171, 294–314. [Google Scholar] [CrossRef]
- Lin, G.; Li, W.-T. Travelling wavefronts of Belousov—Zhabotinskii system with diffusion and delay. Appl. Math. Lett. 2009, 22, 341–346. [Google Scholar] [CrossRef]
- Trofimchuk, E.; Pinto, M.; Trofimchuk, S. Traveling waves for a model of the Belousov—Zhabotinsky reaction. J. Differ. Equ. 2013, 254, 3690–3714. [Google Scholar] [CrossRef]
- Zhang, G.-B. Asymptotics and uniqueness of traveling wavefronts for a delayed model of the Belousov—Zhabotinsky reaction. Appl. Anal. 2020, 99, 1639–1660. [Google Scholar] [CrossRef]
- Wang, P.K.C. Asymptotic stability of a time-delayed diffusion system. J. Appl. Mech. 1963, 30, 500–504. [Google Scholar] [CrossRef]
- Vandewalle, S.; Gander, M.J. Optimized overlapping Schwarz methods for parabolic PDEs with time-delay. In Domain Decomposition Methods in Science and Engineering; Springer: Berlin/Heidelberg, Germany, 2005; pp. 291–298. [Google Scholar]
- Zubik-Kowal, B. Delay partial differential equations. Scholarpedia 2008, 3, 2851. [Google Scholar] [CrossRef]
- Liang, J.; Cao, J. Global exponential stability of reaction-diffusion recurrent neural networks with time-varying delays. Phys. Lett. A. 2003, 314, 434–442. [Google Scholar] [CrossRef]
- Lou, X.-Y.; Cui, B.-T. Asymptotic synchronization of a class of neural networks with reaction-diffusion terms and time-varying delays. Comput. Math. Appl. 2006, 52, 897–904. [Google Scholar] [CrossRef]
- Wang, K.; Teng, Z.; Jiang, H. Global exponential synchronization in delayed reaction-diffusion cellular neural networks with the Dirichlet boundary conditions. Math. Comput. Model. 2010, 52, 12–24. [Google Scholar] [CrossRef]
- Yang, Z.; Xu, D. Global dynamics for non-autonomous reaction-diffusion neural networks with time-varying delays. Theor. Comput. Sci. 2008, 403, 3–10. [Google Scholar] [CrossRef]
- Wang, L.; Gao, Y. Global exponential robust stability of reaction–diffusion interval neural networks with time-varying delays. Phys. Lett. A 2006, 350, 342–348. [Google Scholar] [CrossRef]
- Lu, J.G. Global exponential stability and periodicity of reaction–diffusion delayed recurrent neural networks with Dirichlet boundary conditions. Chaos Solitons Fractals 2008, 35, 116–125. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Sorokin, V.G.; Zhurov, A.I. Differential Equations with Delay: Properties, Methods, Solutions and Models; IPMech RAS: Moscow, Russia, 2022; 464p. (In Russian) [Google Scholar]
- Mei, M.; Lin, C.K.; Lin, C.T.; So, J.W.H. Traveling wavefronts for time-delayed reaction-diffusion equation: (I) Local nonlinearity. J. Differ. Equ. 2009, 247, 495–510. [Google Scholar] [CrossRef]
- Lv, G.; Wang, Z. Stability of traveling wave solutions to delayed evolution equation. J. Dyn. Control Syst. 2015, 21, 173–187. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Sorokin, V.G. Nonlinear delay reaction-diffusion equations: Traveling-wave solutions in elementary functions. Appl. Math. Lett. 2015, 46, 38–43. [Google Scholar] [CrossRef]
- Meleshko, S.V.; Moyo, S. On the complete group classification of the reaction-diffusion equation with a delay. J. Math. Anal. Appl. 2008, 338, 448–466. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Zhurov, A.I. Exact solutions of linear and nonlinear differential-difference heat and diffusion equations with finite relaxation time. Int. J. Non-Linear Mech. 2013, 54, 115–126. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Zhurov, A.I. Functional constraints method for constructing exact solutions to delay reaction-diffusion equations and more complex nonlinear equations. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 417–430. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Zhurov, A.I. Exact separable solutions of delay reaction-diffusion equations and other nonlinear partial functional-differential equations. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 409–416. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Zhurov, A.I. New generalized and functional separable solutions to nonlinear delay reaction-diffusion equations. Int. J. Non-Linear Mech. 2014, 59, 16–22. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Zhurov, A.I. Nonlinear delay reaction-diffusion equations with varying transfer coefficients: Exact methods and new solutions. Appl. Math. Lett. 2014, 37, 43–48. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Zhurov, A.I. Non-linear instability and exact solutions to some delay reaction-diffusion systems. Int. J. Non-Linear Mech. 2014, 62, 33–40. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Zhurov, A.I. The functional constraints method: Application to non-linear delay reaction-diffusion equations with varying transfer coefficients. Int. J. Non-Linear Mech. 2014, 67, 267–277. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Zhurov, A.I. The generating equations method: Constructing exact solutions to delay reaction-diffusion systems and other non-linear coupled delay PDEs. Int. J. Non-Linear Mech. 2015, 71, 104–115. [Google Scholar] [CrossRef]
- Polyanin, A.D. Generalized traveling-wave solutions of nonlinear reaction-diffusion equations with delay and variable coefficients. Appl. Math. Lett. 2019, 90, 49–53. [Google Scholar] [CrossRef]
- Sorokin, V.G.; Polyanin, A.D. Nonlinear partial differential equations with delay: Linear stability/instability of solutions, numerical integration. J. Phys. Conf. Ser. 2019, 1205, 012053. [Google Scholar] [CrossRef]
- Wolfram Language Documentation. Delay Differential Equations. Available online: http://reference.wolfram.com/mathematica/tutorial/NDSolveDelayDifferentialEquations.html (accessed on 29 April 2022).
- Maple Programming Help. Numeric Delay Differential Equation Examples. Available online: http://www.maplesoft.com/support/help/Maple/view.aspx?path=examples/NumericDDEs (accessed on 29 April 2022).
- MATLAB Documentation. Delay Differential Equations. Available online: http://www.mathworks.com/help/matlab/delay-differential-equations.html (accessed on 29 April 2022).
- Shingareva, I.K.; Lizárraga-Celaya, C. Maple and Mathematica. A Problem Solving Approach for Mathematics, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Polyanin, A.D.; Sorokin, V.G.; Vyazmin, A.V. Exact solutions and qualitative features of nonlinear hyperbolic reaction-diffusion equations with delay. Theor. Found. Chem. Eng. 2015, 49, 622–635. [Google Scholar] [CrossRef]
- Jordan, P.M.; Dai, W.; Mickens, R.E. A note on the delayed heat equation: Instability with respect to initial data. Mech. Res. Commun. 2008, 35, 414–420. [Google Scholar] [CrossRef]
- Luckhaus, S. Global boundedness for a delay differential equation. Trans. Am. Math. Soc. 1986, 294, 767–774. [Google Scholar]
- Friesecke, G. Exponentially growing solutions for a delay-diffusion equation with negative feedback. J. Differ. Equ. 1992, 98, 1–18. [Google Scholar] [CrossRef]
- Mackey, M.C. Unified hypothesis for the origin of aplastic anemia and periodic hematopoiesis. Blood 1978, 51, 941–956. [Google Scholar] [CrossRef]
- Belousov, B.P. Periodical process of oxidation of malonic acid solution. In Sbornik Referatov po Radiatsionnoy Meditsine; Medgiz: Moscow, Russia, 1959. (In Russian) [Google Scholar]
- Zaikin, A.N.; Zhabotinsky, A.M. Concentration wave propagation in two-dimensional liquid-phase self-oscillating system. Nature 1970, 225, 535–537. [Google Scholar] [CrossRef]
- Murray, J.D. On traveling wave solutions in a model for Belousov—Zhabotinskii reaction. J. Theor. Biol. 1976, 56, 329–353. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Sorokin, V.G. Nonlinear pantograph-type diffusion PDEs: Exact solutions and the principle of analogy. Mathematics 2021, 9, 511. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Zhurov, A.I. Multi-parameter reaction-diffusion systems with quadratic nonlinearity and delays: New exact solutions in elementary functions. Mathematics 2022, 10, 1529. [Google Scholar] [CrossRef]
- Smith, H.L.; Zhao, X.Q. Global asymptotic stability of travelling waves in delayed reaction-diffusion equations. SIAM J. Math. Anal. 2000, 31, 514–534. [Google Scholar] [CrossRef]
- Aibinu, M.O.; Thakur, S.C.; Moyo, S. Exact solutions of nonlinear delay reaction-diffusion equations with variable coefficients. Partial Differ. Equ. Appl. Math. 2021, 4, 100170. [Google Scholar] [CrossRef]
- Polyanin, A.D. Functional separable solutions of nonlinear reaction-diffusion equations with variable coefficients. Appl. Math. Comput. 2019, 347, 282–292. [Google Scholar] [CrossRef]
- Polyanin, A.D. Functional separable solutions of nonlinear convection-diffusion equations with variable coefficients. Commun. Nonlinear Sci. Numer. Simul. 2019, 73, 379–390. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Zhurov, A.I. Generalized and functional separable solutions to nonlinear delay Klein—Gordon equations. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 2676–2689. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Sorokin, V.G. New exact solutions of nonlinear wave type PDEs with delay. Appl. Math. Lett. 2014, 108, 106512. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Sorokin, V.G. Reductions and exact solutions of Lotka—Volterra and more complex reaction-diffusion systems with delays. Appl. Math. Lett. 2022, 125, 107731. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Sorokin, V.G. A method for constructing exact solutions of nonlinear delay PDEs. J. Math. Anal. Appl. 2021, 494, 124619. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Sorokin, V.G. Construction of exact solutions to nonlinear PDEs with delay using solutions of simpler PDEs without delay. Commun. Nonlinear Sci. Numer. Simul. 2021, 95, 105634. [Google Scholar] [CrossRef]
- Long, F.-S.; Meleshko, S.V. On the complete group classification of the one-dimensional nonlinear Klein—Gordon equation with a delay. Math. Methods Appl. Sci. 2016, 39, 3255–3270. [Google Scholar] [CrossRef]
- Long, F.-S.; Meleshko, S.V. Symmetry analysis of the nonlinear two-dimensional Klein—Gordon equation with a time-varying delay. Math. Methods Appl. Sci. 2017, 40, 4658–4673. [Google Scholar] [CrossRef]
- He, Q.; Kang, L.; Evans, D.J. Convergence and stability of the finite difference scheme for nonlinear parabolic systems with time delay. Numer. Algorithms 1997, 16, 129–153. [Google Scholar] [CrossRef]
- Hale, J.K.; Lunel, S.M.V. Introduction to Functional Differential Equations; Springer: New York, NY, USA, 1993. [Google Scholar]
- Driver, R.D. Ordinary and Delay Differential Equations; Springer: New York, NY, USA, 1977. [Google Scholar]
- Kolmanovskii, V.; Myshkis, A. Applied Theory of Functional Differential Equations; Kluwer: Dordrecht, The Netherlands, 1992. [Google Scholar]
- Smith, H.L. An Introduction to Delay Differential Equations with Applications to the Life Sciences; Springer: New York, NY, USA, 2010. [Google Scholar]
- Kolmanovskii, V.; Myshkis, A. Introduction to the Theory and Applications of Functional Differential Equations; Springer: New York, NY, USA, 1999. [Google Scholar]
- Erneux, T. Applied Delay Differential Equations; Springer: New York, NY, USA, 2009. [Google Scholar]
- Shampine, L.F.; Thompson, S. Numerical Solution of Delay Differential Equations. In Delay Differential Equations; Springer: Boston, MA, USA, 2009. [Google Scholar]
- Bellen, A.; Zennaro, M. Numerical Methods for Delay Differential Equations; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Kuang, J.; Cong, Y. Stability of Numerical Methods for Delay Differential Equations; Science Press: Beijing, China, 2005. [Google Scholar]
- Van Der Houwen, P.J.; Sommeijer, B.P. On the stability of predictor-corrector methods for parabolic equations with delay. IMA J. Numer. Anal. 1986, 6, 1–23. [Google Scholar] [CrossRef]
- Jackiewicz, Z.; Zubik-Kowal, B. Spectral collocation and waveform relaxation methods for nonlinear delay partial differential equations. Appl. Numer. Math. 2006, 56, 433–443. [Google Scholar] [CrossRef]
- Peiraviminaei, A.; Ghoreishi, F. Numerical solutions based on Chebyshev collocation method for singularly perturbed delay parabolic PDEs. Math. Meth. Appl. Sci. 2014, 37, 2112–2119. [Google Scholar] [CrossRef]
- Mead, J.; Zubik-Kowal, B. An iterated pseudospectral method for delay partial differential equations. Appl. Numer. Math. 2005, 55, 227–250. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Abdelkawy, M.A.; Mallawi, F. An accurate Chebyshev pseudospectral scheme for multi-dimensional parabolic problems with time delays. Bound. Value Probl. 2015, 2015, 103. [Google Scholar] [CrossRef]
- Bocharov, G.A.; Marchuk, G.I.; Romanyukha, A.A. Numerical solution by LMMs of stiff delay differential systems modelling an immune response. Numer. Math. 1996, 73, 131–148. [Google Scholar] [CrossRef]
- Samarskii, A.A.; Gulin, A.V. Numerical Methods; Nauka: Moscow, Russia, 1989. (In Russian) [Google Scholar]
- Baker, C.T.H.; Paul, C.A.H.; Willé, D.R. Issues in the numerical solution of evolutionary delay differential equations. Adv. Comput. Math. 1995, 3, 171–196. [Google Scholar] [CrossRef]
- In’t Hout, K.J. A new interpolation procedure for adapting Runge—Kutta methods to delay differential equations. BIT 1992, 32, 634–649. [Google Scholar] [CrossRef]
- Oberle, H.J.; Pesch, H.J. Numerical treatment of delay differential equations by Hermite interpolation. Num. Math. 1981, 37, 235–255. [Google Scholar] [CrossRef]
- Hindmarsh, A.; Taylor, A. User Documentation for IDA: A Differential-Algebraic Equation Solver for Sequential and Parallel Computers; Lawrence Livermore National Laboratory Report UCRL-MA-136910; Lawrence Livermore National Laboratory: Livermore, CA, USA, 1999.
- Rosenbrock, H.H. Some general implicit processes for the numerical solution of differential equations. Comput. J. 1963, 5, 329–330. [Google Scholar] [CrossRef]
- Cong, Y.; Cai, J.; Kuang, J. The GPL-stability of Rosenbrock methods for delay differential equation. Appl. Math. Comput. 2004, 150, 533–542. [Google Scholar] [CrossRef]
- Lukyanenko, D.; Yeleskina, T.; Prigorniy, I.; Isaev, T.; Borzunov, A.; Shishlenin, M. Inverse problem of recovering the initial condition for a nonlinear equation of the reaction-d-iffusion-advection type by data given on the position of a reaction front with a time delay. Mathematics 2021, 9, 342. [Google Scholar] [CrossRef]
- Argun, R.L.; Volkov, V.T.; Lukyanenko, D.V. Numerical simulation of front dynamics in a nonlinear singularly perturbed reaction-diffusion problem. J. Comput. Appl. Math. 2022, 412, 114294. [Google Scholar] [CrossRef]
- Wolfram Language Documentation. The Numerical Method of Lines. Available online: http://reference.wolfram.com/language/tutorial/NDSolveMethodOfLines.html (accessed on 29 April 2022).
- Wolfram Language Documentation. NDSolve. Available online: http://reference.wolfram.com/language/ref/NDSolve.html (accessed on 29 April 2022).
- Wolfram Language Documentation. “ExplicitRungeKutta” Method for NDSolve. Available online: http://reference.wolfram.com/language/tutorialNDSolveExplicitRungeKutta.html (accessed on 29 April 2022).
- Wolfram Language Documentation. “ImplicitRungeKutta” Method for NDSolve. Available online: http://reference.wolfram.com/language/tutorial/NDSolveImplicitRungeKutta.html (accessed on 29 April 2022).
- Wolfram Language Documentation.IDA Method for NDSolve. Available online: http://reference.wolfram.com/language/tutorial/NDSolveIDAMethod.html (accessed on 29 April 2022).
- Liu, H.; Sun, G. Implicit Runge—Kutta methods based on Lobatto quadrature formula. Int. J. Comput. Math. 2005, 82, 77–88. [Google Scholar] [CrossRef]
- Hairer, E.; Wanner, G. Solving Ordinary Differential Equations II: Stiff and Differential-Algebraic Problems, 2nd ed.; Springer: Berlin, Germany, 1996. [Google Scholar]
- Brown, P.N.; Hindmarsh, A.C.; Petzold, L.R. Using Krylov Methods in the Solution of Large-Scale Differential-Algebraic Systems. SIAM J. Sci. Comput. 1994, 15, 1467–1488. [Google Scholar] [CrossRef]
- Brown, P.N.; Hindmarsh, A.C.; Petzold, L.R. Consistent Initial Condition Calculation for Differential-Algebraic Systems. SIAM J. Sci. Comput. 1998, 19, 1495–1512. [Google Scholar] [CrossRef]
- Wolfram Language Documentation. Norms in NDSolve. Available online: http://reference.wolfram.com/language/tutorial/NDSolveVectorNorm.html (accessed on 29 April 2022).
- Wolfram Language Documentation. Numerical Solution of Differential Equations. Available online: http://reference.wolfram.com/language/tutorial/NumericalSolutionOfDifferentialEquations.html (accessed on 29 April 2022).
- Bratsun, D.; Zakharov, A. Adaptive numerical simulations of reaction-diffusion systems with history and time-delayed feedback. In ISCS 2013: Interdisciplinary Symposium on Complex Systems: Emergence, Complexity and Computation; Springer: Berlin, Germany, 2014; Volume 8, pp. 70–81. [Google Scholar]
- Ferreira, J.A.; Da Silva, P.M. Energy estimates for delay diffusion-reaction equations. J. Comput. Math. 2008, 26, 536–553. [Google Scholar]
- Lu, X. Monotone method and convergence acceleration for finite-difference solutions of parabolic problems with time delays. Numer. Methods Partial. Differ. Equ. 1995, 11, 591–602. [Google Scholar] [CrossRef]
- Lu, X. Combined iterative methods for numerical solutions of parabolic problems with time delays. Appl. Math. Comput. 1998, 89, 213–224. [Google Scholar] [CrossRef]
- Pao, C.V. Numerical methods for systems of nonlinear parabolic equations with time delays. J. Math. Anal. Appl. 1999, 240, 249–279. [Google Scholar] [CrossRef][Green Version]
- Pao, C.V. Finite difference reaction-diffusion systems with coupled boundary conditions and time delays. J. Math. Anal. Appl. 2002, 272, 407–434. [Google Scholar] [CrossRef][Green Version]
- Lekomtsev, A.; Pimenov, V. Convergence of the scheme with weights for the numerical solution of a heat conduction equation with delay for the case of variable coefficient of heat conductivity. Appl. Math. Comput. 2015, 256, 83–93. [Google Scholar] [CrossRef]
- Pimenov, V.G.; Tashirova, E.E. Numerical methods for solving a hereditary equation of hyperbolic type. Proc. Steklov Inst. Math. 2013, 281, s126–s136. [Google Scholar] [CrossRef]
- Wu, F.; Wang, Q.; Cheng, X.; Chen, X. Linear θ-method and compact θ-method for generalised reaction-diffusion equation with delay. Int. J. Differ. Equ. 2018, 2018, 6402576. [Google Scholar] [CrossRef]
- Sun, Z.; Zhang, Z. A linearized compact difference scheme for a class of nonlinear delay partial differential equations. Appl. Math. Model. 2013, 37, 742–752. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, C. A new linearized compact multisplitting scheme for the nonlinear convection-reaction-diffusion equations with delay. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 3278–3288. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, D.; Zhang, C.; Xu, D. Multistep finite difference schemes for the variable coefficient delay parabolic equations. J. Differ. Equ. Appl. 2016, 22, 745–765. [Google Scholar] [CrossRef]
- Huang, C.; Vandewalle, S. Unconditionally stable difference methods for delay partial differential equations. Numer. Math. 2012, 122, 579–601. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).