Robust Multi-Label Classification with Enhanced Global and Local Label Correlation

Abstract

Data representation is of significant importance in minimizing multi-label ambiguity. While most researchers intensively investigate label correlation, the research on enhancing model robustness is preliminary. Low-quality data is one of the main reasons that model robustness degrades. Aiming at the cases with noisy features and missing labels, we develop a novel method called robust global and local label correlation (RGLC). In this model, subspace learning reconstructs intrinsic latent features immune from feature noise. The manifold learning ensures that outputs obtained by matrix factorization are similar in the low-rank latent label if the latent features are similar. We examine the co-occurrence of global and local label correlation with the constructed latent features and the latent labels. Extensive experiments demonstrate that the classification performance with integrated information is statistically superior over a collection of state-of-the-art approaches across numerous domains. Additionally, the proposed model shows promising performance on multi-label when noisy features and missing labels occur, demonstrating the robustness of multi-label classification.

1. Introduction

Multi-label learning [1,2,3] aims at learning a mapping from features to labels and determines a group of associated labels for unseen instances. The traditional “is-a” relation between instances and labels has thus been upgraded with the “has-a” relation. With the advancement of automation and networking, the expenditure continuously collecting data decreases significantly, resulting in a collection of advanced algorithms to cope with concept cognition [4,5,6,7,8,9,10]. However, it is a non-trivial task to collect massive high-quality data, as unexpected device failure or data falsification happens from time to time. Therefore, how to effectively cope with flawed multi-label data is frequently discussed in [11,12,13,14].

Label correlations are frequently exploited as auxiliary information for classifier construction as they approximately recover the joint probability density among labels. The appearance possibility of the label “bee” will be higher if the labels “flower” and “butterfly” are present in a picture. The global label correlation means the label relation holds universally, and the local label correlation otherwise. The label correlation of “flower, butterfly, and bee” is global if the picture is in the natural scene case. It degenerates as local if the picture describes the flowers in the house without butterflies and bees. As a result, the premise of global label correlation and local label correlation concurring is more reasonable. However, both label correlations are vulnerable to the feature noise and missing label, as they are inherent in the observed data itself. Recent papers focus on label correlation. Guo et al. [15] utilized Laplacian manifold regularization to recover the missing labels. Sun et al. [16] imposed sparse constraint and linear self-recovery to deal with the weakly supervised labels and noisy features. Zhang et al. [17] addressed the noise in latent features and latent labels via bi-sparsity regularization. Lou et al. [18] introduced a fuzzy weighting strategy on both observed features and instances to resist the impact of noisy features. Fan et al. [19] adopted manifold learning to exploit both global and local label correlations with selected features. Nevertheless, most of them examine the model robustness explicitly with either feature space or label space. The classification performance on the concurrence of both noisy features and missing labels will be more reliable if we strengthen the robustness of both global and local label correlations in latent data representation.

For multi-label classifiers, the evaluation metrics emphasize the accuracy and ranking of relevant labels [20]. Either from an instance perspective or a label perspective, the minority distributions of related labels amplify sensitivity to model parameter selections. In other words, inaccurate information, including feature noise [21,22] and label missing [23,24,25], may skew the estimation of model parameters. Subspace learning is an effective method to uncover the underlying structural representations. The label correlation estimation in subspace gains better credibility due to the removal of distractive information. Chen et al. [26] learned a shared latent projection via linear low-dimensional transformation, which is solved by a generalized eigenvalue problem. Chen et al. [27] adopted a neural factorization machine on both the feature side and label side to exploit feature and label correlations. Wang et al. [28] restrained the subspace dimension by relaxing the performance difference to a pre-trained model and preserving the largest parameters in the corresponding round. Huang et al. [29] sought a latent label space by minimizing the distance difference of pairwise label correlation constraint on explicit and implicit labels. However, these approaches neither examine the potentially flawed data nor take full advantage of the concurrence of global and local label correlation.

Based on subspace learning and manifold learning, we present a novel method called Robust Global and Local label Correlation (RGLC) to leverage both global and local label correlation extracted from the latent representation, as illustrated in Figure 1. Inspired by [30,31], subspace learning is employed to reconstruct a clean feature representation. As the evaluation metrics work in the observed label matrix, we generate latent label representation via matrix factorization and train a model from noise-free feature representation to latent label representation. During this training, we coupled with global and local label learning. Compared with existing multi-label algorithms, the contributions of RGLC are enumerated as follows:

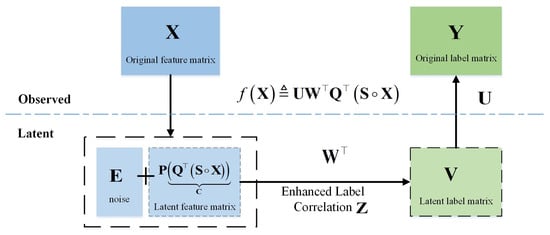
Figure 1. Framework of RGLC. Instead of directly learning global and local label correlations Z from the observed feature matrix X to observed label matrix Y, we attempt to train the RGLC (i.e., $f\left(\mathbf{X}\right)$) model from latent feature matrix (i.e., $\mathbf{C}\triangleq {\mathbf{Q}}^{\top }\left(\mathbf{S}\circ \mathbf{X}\right)$) to latent label matrix (i.e., $\mathbf{V}$). It exploits global and local label correlations Z on latent features and labels with linear mapping ${\mathbf{W}}^{\top }$.

• For the first time, we exploit both global label correlations and local label correlations to regularize the learning from latent features to latent labels. The integrated intrinsic label correlation in RGLC robustly handles multi-label classification problems in different fields.
• The subspace learning and matrix decomposition are jointly incorporated to deduce latent features and latent labels from flawed multi-label data. The two modules strengthen the robustness of RGLC when completing multi-label classification tasks with noisy features and missing labels.
• We intensively examine RGLC from different aspects of modularity, complexity, convergence, and sensitivity. The satisfactory performance demonstrates the superiority of enhanced global and local label correlations.

We structure the remaining into five sections. We review related works of robust subspace learning, manifold regularization and global and local label correlation in Section 2. Section 3 details the components of the presented multi-label model (RGLC). Section 3.2 explains the optimization solving of RGLC. Extensive comparisons are completed and analyzed in Section 4. We discuss the characteristics of RGLC in Section 5. Finally, we summarize the findings and values of the proposed algorithm and suggest future research directions in Section 6.

2. Related Work

2.1. Robust Subspace Learning

Subspace learning is an effective strategy to strengthen model robustness. As far as the goal of subspace learning, there are roughly three solutions in single-view based multi-label learning [32]: (i) only reduce the feature matrix $\mathbf{X}$ to ${\mathbf{X}}_0$; (ii) only reduce the label matrix $\mathbf{Y}$ to ${\mathbf{Y}}_0$; and (iii) reduce the label matrix $\mathbf{Y}$ and feature matrix $\mathbf{X}$ to ${\mathbf{X}}_0$ and ${\mathbf{Y}}_0$, respectively. The commonness of these methods is that the generated subspace is compact with the low-rank property. Recently, many approaches prefer the embedded strategy, which means subspace learning and classifier construction are optimized alternatively. For the first category, wrapping multi-label classification with label-specific features generation model (WRAP) [33] learnt the linear model from ${\mathbf{X}}_0$ to $\mathbf{Y}$ and the embedded label-specific features simultaneously. For the second category, latent relative label importances for the multi-label learning model (RLIM) [34] learns the relative label importance while training the classifier from $\mathbf{X}$ to ${\mathbf{Y}}_0$. For the third category, the independent feature and label components model (IFLC) [35] learns the classifier from the latent feature subspace (i.e., ${\mathbf{X}}_0$) to the latent label subspace (i.e., ${\mathbf{Y}}_0$) by maximizing the independence individually and maximizing correlations jointly. In this paper, we employ different strategies for latent representation learning on the feature and label sides. Concretely, the latent feature subspace learning takes an embedded strategy by constructing a linear regression from ${\mathbf{X}}_0$ to $\mathbf{Y}$ without the consideration of label correlation. The latent label subspace learning takes an embedded method by constructing a linear regression from ${\mathbf{X}}_0$ to ${\mathbf{Y}}_0$.

2.2. Manifold Regularization

Manifold regularization [36] constrains the distribution of output similarity based on instance similarity. Cai proposed feature manifold learning and sparse regularization for the multi-label feature selection model (MSSL) [37], and it preserved feature geometric structure by feature manifold learning. Other scholars proposed a manifold regularized discriminative feature selection (MDFS) model [38]. It designed a feature embedding method that retains local label correlation via manifold regularization. There is also a Bayesian model with label manifold regularization and label confidence constraint (BM-LRC) [39]. It applied label manifold regularization on topic and document levels to estimate label similarity for multi-label text classification. Feng considered a regularized matrix factorization for the multi-label learning (RMFL) model [40]. It preserved topological information in local features through label manifold regularization. In this paper, we employ manifold regularization on latent label subspace learning to optimize the coefficients in the linear regression model.

2.3. Global and Local Label Correlation

Effective utilization of global and local label correlation is beneficial to improving multi-label classification if label information is assumed to be plausible. We explore accurate label correlations from the label subspace constrained by manifold regularization. Recent works [41,42,43] focus on local label correlations. Multi-label learning with global and local label correlation (GLOCAL) [31] is proposed for the first time, which attempts to deal with multi-label missing labels by exploiting both global and local label correlation in latent label subspace. The global and local label manifold regularizers use the pairwise label correlation. Global and local multi-view multi-label learning (GLMVML) [44] extended GLOCAL to a multi-view situation. Global–local label correlation (GLC) [45] solved the partial multi-label learning problem by simultaneously taking label coefficient matrix and consistency among the coefficient matrix as global and local label correlation regularizers, respectively. In this paper, we learn both global label correlations and local label correlations in latent label subspace, which constitutes a component of objective functions for the multi-label classifier.

3. Materials and Methods

We recall some essential notations here. Given multi-label instance $\left(\mathbf{X},\mathbf{Y}\right)$, where $\mathbf{X}=\left[{\mathbf{x}}_1,{\mathbf{x}}_2,\dots ,{\mathbf{x}}_n\right]\in {\mathcal{R}}^{d\times n}$ is the original feature matrix, d is the feature count, and n is the instance count. $\mathbf{Y}=\left[{\mathbf{y}}_1,{\mathbf{y}}_2,\dots ,{\mathbf{y}}_n\right]\in {\{-1,1\}}^{l\times n}$ constitutes the ground-truth label matrix, where ${\mathbf{y}}_i=\left[y_{i1},\dots ,y_{ij},\dots ,y_{il}\right]$ denotes the label association information of ${\mathbf{x}}_i$ across label space, with $y_{ij}=1$ if ${\mathbf{x}}_i$ is associated with the j-th label, and $y_{ij}=-1$ otherwise. l is the label count.

Let $\mathbf{Q}\in {\mathcal{R}}^{d\times m}$ and $\mathbf{U}\in {\mathcal{R}}^{l\times k}$ denote two transformation matrices imposed on ${\mathbf{X}\in \mathcal{R}}^{d\times n}$ and $\mathbf{Y}\in {\mathcal{R}}^{l\times n}$, respectively. We explain the model components by learning a latent feature matrix ${\mathbf{C}\in \mathcal{R}}^{m\times n}$($m\ll d$) first (Section 3.1.1) and then learning a latent label matrix ${\mathbf{V}\in \mathcal{R}}^{k\times n}$($k\ll l$) (Section 3.1.2), which is regularized by global and local manifold (Section 3.1.3) and learning latent label correlations Z (Section 3.1.4). The model output for unseen instances is presented finally (Section 3.1.5). The pipeline also applies to the case with noisy features and missing labels. We explain the problem solving in Section 3.2.

3.1. Proposed Model

3.1.1. Learning Latent Features

Inspired by [30], we seek a latent feature matrix $\mathbf{C}$ which is the low-rank representation of $\mathbf{X}$ with both informative and discriminative information by imposing reconstruction constraints. To obtain informativeness through imposing the reconstruction constraint:

$$\mathbf{X}={\mathbf{PQ}}^{\top }\mathbf{X}+\mathbf{E}$$

(1)

where $\mathbf{Q}\in {\mathcal{R}}^{d\times m}$ transforms the original feature matrix $\mathbf{X}$ to the latent feature matrix $\mathbf{C}$ and $\mathbf{P}\in {\mathcal{R}}^{d\times m}$ reconstructs the original feature matrix $\mathbf{X}$ from latent feature matrix $\mathbf{C}$. To ensure a non-trivial solution, we add orthogonal constraint on $\mathbf{P}$, denoted as ${\mathbf{P}}^{\top }\mathbf{P}=\mathbf{I}$. $\mathbf{E}\in {\mathcal{R}}^{d\times n}$ separates the noise from feature matrix $\mathbf{X}$. The desired latent feature matrix should minimize the classification error, and we assume that the classifier from the latent feature matrix $\mathbf{C}$ to label matrix $\mathbf{Y}$ is a linear regression model. The smaller the regression loss is, the better the reconstructed feature becomes. We require the simplicity of $\mathbf{R}$ and $\mathbf{E}$, as they do not participate in the procedure of latent label learning. We use indicator matrix $\mathbf{S}$ and $\mathbf{J}$ to simulate the feature ($\widehat{\mathbf{X}}$) and missing label, respectively. Hence, we have the objective function as:

$$\begin{array}{cc}\hfill \underset{\mathbf{R},\mathbf{Q},\mathbf{E},\mathbf{P}}{min}& \frac{1}{2}{∥\mathbf{J}\circ \left(\mathbf{Y}-{\mathbf{RQ}}^{\top }\widehat{\mathbf{X}}\right)∥}_F^2+\frac{1}{2}{\lambda }_1{∥\mathbf{Q}∥}_F^2+{\lambda }_2\left({∥\mathbf{E}∥}_1+\frac{1}{2}{∥\mathbf{R}∥}_F^2\right)\hfill \\ \hfill & s.t.\widehat{\mathbf{X}}={\mathbf{PQ}}^{\top }\widehat{\mathbf{X}}+\mathbf{E},{\mathbf{P}}^{\top }\mathbf{P}=\mathbf{I},\widehat{\mathbf{X}}=\mathbf{S}\circ \mathbf{X}\hfill \end{array}$$

(2)

where ${∥·∥}_F^2$ denotes the Frobenius norm, $\mathbf{R}$ is the weight of the classifier and ${\lambda }_1$, ${\lambda }_2⩾0$ are all tradeoff parameters balancing the complexity between $\mathbf{Q}$ and $\mathbf{R}$, $\mathbf{E}$. The elements $S_{ij}=1$ and $J_{ij}=1$ in $\mathbf{S}$ and $\mathbf{J}$ hold if they are not noisy features and missing labels, $S_{ij}=0$ and $J_{ij}=0$ otherwise. We do not consider label correlation here, as the original label matrix may contain the missing labels. We learn the latent features (${\mathbf{Q}}^{\top }\left(\mathbf{S}\circ \mathbf{X}\right)$) in a label-by-label fashion. For simplicity, we denote:

$$\mathbf{C}\triangleq {\mathbf{Q}}^{\top }\left(\mathbf{S}\circ \mathbf{X}\right)$$

(3)

3.1.2. Learning Latent Labels

The ground-truth label matrix $\mathbf{Y}\in {\mathcal{R}}^{l\times n}$ is transformed to the latent label matrix $\mathbf{V}\in {\mathcal{R}}^{k\times n}$ by the transformation matrix $\mathbf{U}\in {\mathcal{R}}^{l\times k}$ satisfying $\mathbf{Y}\approx \mathbf{UV}$, where $k<l$. The classifier

$$g\left(\mathbf{x}\right)={\mathbf{W}}^{\top }\mathbf{C}$$

(4)

is learnt from the latent feature matrix $\mathbf{C}$ to the latent label matrix $\mathbf{V}$. We assume the mapping is also linear. Therefore, we obtain the latent label matrix $\mathbf{V}$ by minimizing the reconstruction error of latent labels and square loss of the classifier prediction performance described as:

$$\underset{\mathbf{U},\mathbf{V},\mathbf{W}}{min}{∥\mathbf{J}\circ (\mathbf{Y}-\mathbf{UV})∥}_F^2+{\lambda }_1{∥\mathbf{V}-{\mathbf{W}}^{\top }\mathbf{C}∥}_F^2+{\lambda }_3\left({∥\mathbf{U}∥}_F^2+{∥\mathbf{V}∥}_F^2+{∥\mathbf{W}∥}_F^2\right)$$

(5)

where $J_{ij}=1$ if $y_{ij}$ is observable, and $J_{ij}=0$ otherwise. $\mathbf{W}\in {\mathcal{R}}^{m\times k}$ is a linear transformation from $\mathbf{C}$ to $\mathbf{V}$, and $\mathbf{U}\in {\mathcal{R}}^{l\times k}$ is a transformation matrix from $\mathbf{V}$ to $\mathbf{Y}$. ${∥\mathbf{U}∥}_F^2+{∥\mathbf{V}∥}_F^2+{∥\mathbf{W}∥}_F^2$ is the regularization item.

3.1.3. Global and Local Manifold Regularizer

Applying global and local manifold regularizers on label representation is conducive to distinguishing the similarity of different instances of latent features in both the global and local sense. The two regularization terms can guide the model to exploit global and local label correlation. We compute global and local manifold regularizers in a pairwise way. This idea is inspired by [31]. $\mathbf{G}=\{{\mathbf{G}}_0,{\mathbf{G}}_1,\dots ,{\mathbf{G}}_i,\dots ,{\mathbf{G}}_j,\dots ,{\mathbf{G}}_h\}$ is the output set of the classifier based on different groups of instances and the classifier is trained from the latent feature $\mathbf{C}$ to the latent label $\mathbf{Y}$. $\mathbf{C}=\{{\mathbf{C}}_0,{\mathbf{C}}_1,\dots ,{\mathbf{C}}_i,\dots ,{\mathbf{C}}_j\dots ,{\mathbf{C}}_h\}$ denotes a group of instance sets with latent features, where ${\mathbf{C}}_i\in {\mathcal{R}}^{m\times n_i}$ and ${\mathbf{C}}_j\in {\mathcal{R}}^{m\times n_j}$ are the $\mathit{i}$th and $\mathit{j}$th latent features containing $n_i$ and $n_j$ instances. ${\mathbf{Y}}_i$ and ${\mathbf{Y}}_j$ are corresponding latent label representations of ${\mathbf{C}}_i$ and ${\mathbf{C}}_j$, respectively. We definite the global manifold regularizer as:

$$tr\left({\mathbf{G}}_0^{\top }{\mathbf{L}}_0{\mathbf{G}}_0\right)$$

(6)

which should be minimized. ${\mathbf{G}}_0={\mathbf{UW}}^{\top }{\mathbf{C}}_0$ is the label outputs on all instances, where ${\mathbf{C}}_0=\mathbf{C}$. ${\mathbf{L}}_0=diag\left({\mathbf{S}}_0\mathbf{1}\right)-{\mathbf{S}}_0$ is the Laplacian matrix of ${\mathbf{S}}_0\in {\mathcal{R}}^{l\times l}$, where $diag(·)$ denotes the diagonal of matrix and $\mathbf{1}$ denotes a vector of ones. ${\mathbf{S}}_0$ is a global label correlation matrix measured by the cosine similarity among all latent labels (denoted as ${\mathbf{Y}}_0$), where ${\mathbf{Y}}_0=\mathbf{Y}$. $tr(·)$ is the matrix trace. Similarly, for the ith local manifold regularizer, we have:

$$tr\left({\mathbf{G}}_i^{\top }{\mathbf{L}}_i{\mathbf{G}}_i\right)$$

(7)

which should also be minimized. ${\mathbf{G}}_i={\mathbf{UW}}^{\top }{\mathbf{C}}_i$$\left(1⩽i,j⩽h\right)$ is the label output of ith groups of instances. For simplicity, we assume that each local similarity corresponds to only one set of instances, which means the corresponding intersection of instances between two arbitrary ${\mathbf{C}}_i$ and ${\mathbf{C}}_j$ is empty. ${\mathbf{L}}_i=diag\left({\mathbf{S}}_i\mathbf{1}\right)-{\mathbf{S}}_i$ is the Laplacian matrix of ${\mathbf{S}}_i\in {\mathcal{R}}^{l\times l}$, where $diag(·)$ denotes the diagonal of the matrix and $\mathbf{1}$ denotes a vector of ones. ${\mathbf{S}}_i$ is a local label correlation matrix measured by the cosine similarity of ith local label subset (denoted as ${\mathbf{Y}}_i$), where ${\mathbf{Y}}_i\subset \mathbf{Y}$. $tr(·)$ is the matrix trace. Thus, (5) can be rewritten as:

$$\begin{array}{cc}\hfill \underset{\mathbf{U},\mathbf{V},\mathbf{W}}{min}& {∥\mathbf{J}\circ (\mathbf{Y}-\mathbf{UV})∥}_F^2+{\lambda }_1{∥\mathbf{V}-{\mathbf{W}}^{\top }\mathbf{C}∥}_F^2+{\lambda }_3\left({∥\mathbf{U}∥}_F^2+{∥\mathbf{V}∥}_F^2+{∥\mathbf{W}∥}_F^2\right)\hfill \\ & +{\lambda }_4\left(tr\left({\mathbf{G}}_0^{\top }{\mathbf{LG}}_0\right)+\sum _{i=1}^{h}tr\left({\mathbf{G}}_i^{\top }{\mathbf{L}}_i{\mathbf{G}}_i\right)\right)\hfill \end{array}$$

(8)

where $\mathbf{J}$ is an indicator matrix with $J_{ij}=1$ if $y_{ij}$ is observable and $J_{ij}=0$ otherwise.

3.1.4. Learning Label Correlations

The cosine similarity measured on the original label matrix $\mathbf{Y}$ may be dubious when a missing label occurs. One alternative solution is to learn the Laplacian matrix on $\mathbf{Y}$, which stores the fluctuations on pairwise label correlations when an arbitrary label $l_i$ changes. Considering the symmetric positive definite property of the Laplacian matrix, we decompose ${\mathbf{L}}_i$ as ${\mathbf{Z}}_i{\mathbf{Z}}_i^{\top }$, with ${\mathbf{Z}}_i\in {\mathcal{R}}^{l\times k}$. To avoid a trivial solution, we add the diagonal constraint $diag\left({\mathbf{Z}}_i{\mathbf{Z}}_i^{\top }\right)=\mathbf{1}$ for all ${\mathbf{Z}}_i,i=1,\dots ,h$. To unify the optimization processing on label correlation, we assume the global label correlation matrix is a linear combination of local label correlation matrices. Thus, the global label Laplacian matrix is the linear combination of the local label Laplacian matrix. Then, (8) is rewritten as:

$$\begin{array}{cc}\hfill \underset{\mathbf{U},\mathbf{V},\mathbf{W},\mathbf{Z}}{min}& {∥\mathbf{J}\circ \left(\mathbf{Y}-\mathbf{UV}\right)∥}_F^2+{\lambda }_1{∥\mathbf{V}-{\mathbf{W}}^{\top }\mathbf{C}∥}_F^2+{\lambda }_3\left({∥\mathbf{U}∥}_F^2+{∥\mathbf{V}∥}_F^2+{∥\mathbf{W}∥}_F^2\right)\hfill \\ \hfill & +\sum _{i=1}^h\left(\frac{{\lambda }_4{n}_i}{n}tr\left({\mathbf{G}}_0^{\top }{\mathbf{Z}}_i{\mathbf{Z}}_i^{\top }{\mathbf{G}}_0\right)\right)+\sum _{i=1}^h\left({\lambda }_{4}tr\left({\mathbf{G}}_i^{\top }{\mathbf{Z}}_i{\mathbf{Z}}_i^{\top }{\mathbf{G}}_i\right)\right)\hfill \\ \hfill & s.t.diag\left({\mathbf{Z}}_i{\mathbf{Z}}_i^{\top }\right)=\mathbf{1},i=1,2,\dots ,h\hfill \end{array}$$

(9)

where symbol ∘ denotes Hadamard (element-wise) product. ${\lambda }_1$, ${\lambda }_3$ and ${\lambda }_4⩾0$ are tradeoff parameters.

3.1.5. Predicting Labels for Unseen Instances

With the latent feature matrix $\mathbf{C}$, the latent label matrix $\mathbf{V}$ and the classifier $g\left({\mathbf{x}}_i\right)$ obtained from Section 3.1.1, Section 3.1.2, Section 3.1.3 and Section 3.1.4, we present the model output here. For an unseen instance ${\mathbf{x}}_i$, the label prediction in the original label space is denoted as:

$$f\left({\mathbf{x}}_i\right)=\mathbf{U}g\left({\mathbf{x}}_i\right)$$

(10)

By substituting (3) and (4) into (10), the final prediction of an unseen instance is as follows:

$$f\left({\mathbf{x}}_i\right)={\mathbf{UW}}^{\top }{\mathbf{Q}}^{\top }\left({\mathbf{S}}_i\circ {\mathbf{x}}_i\right)$$

(11)

3.2. Optimization

3.2.1. Solving (2)

We use the Alternating Direction Method of Multipliers (ADMM) to solve the objective function in (2). By introducing constraint $\mathbf{A}={\mathbf{RQ}}^{\top }$, the objective function is renewed as:

$$\begin{array}{cc}\hfill \underset{\mathbf{Q},\mathbf{R},\mathbf{E},\mathbf{A},\mathbf{P}}{min}& \frac{1}{2}{∥\mathbf{J}\circ \left(\mathbf{Y}-\mathbf{A}\widehat{\mathbf{X}}\right)∥}_F^2+\frac{1}{2}{\lambda }_1{∥\mathbf{Q}∥}_F^2+{\lambda }_2\left({∥\mathbf{E}∥}_1+\frac{1}{2}{∥\mathbf{R}∥}_F^2\right)\hfill \\ \hfill & s.t.\widehat{\mathbf{X}}={\mathbf{PQ}}^{\top }\widehat{\mathbf{X}}+\mathbf{E},{\mathbf{P}}^{\top }\mathbf{P}=\mathbf{I},\mathbf{A}={\mathbf{RQ}}^{\top }\hfill \end{array}$$

(12)

The augmented Lagrangian function $\mathcal{J}$ is:

$$\begin{array}{cc}\hfill \mathcal{J}=arg\underset{\mathbf{A},\mathbf{R},\mathbf{Q},\mathbf{E},\mathbf{P},{\mathbf{Y}}_1,{\mathbf{Y}}_2}{min}& \frac{1}{2}{∥\mathbf{J}\circ \left(\mathbf{Y}-\mathbf{A}\widehat{\mathbf{X}}\right)∥}_F^2+\frac{1}{2}{\lambda }_1{∥\mathbf{Q}∥}_F^2+{\lambda }_2{∥\mathbf{E}∥}_1+\frac{1}{2}{\lambda }_2{∥\mathbf{R}∥}_F^2\hfill \\ \hfill & +⟨{\mathbf{Y}}_1,\widehat{\mathbf{X}}-{\mathbf{PQ}}^{\top }\widehat{\mathbf{X}}-\mathbf{E}⟩+⟨{\mathbf{Y}}_2,\mathbf{A}-{\mathbf{RQ}}^{\top }⟩\hfill \\ \hfill & +\frac{\mu }{2}\left({∥\widehat{\mathbf{X}}-{\mathbf{PQ}}^{\top }\widehat{\mathbf{X}}-\mathbf{E}∥}_F^2+{∥\mathbf{A}-{\mathbf{RQ}}^{\top }∥}_F^2\right)\hfill \\ \hfill & s.t.{\mathbf{P}}^{\top }\mathbf{P}=\mathbf{I}\hfill \end{array}$$

(13)

where ${\mathbf{Y}}_1$,${\mathbf{Y}}_2$ are Lagrange multipliers, $⟨·,·⟩$ denotes the Frobenius inner product and $\mu >0$ is a penalty parameter.

Update A (Line 3 in Algorithm 1):

$$\begin{array}{cc}\hfill \mathcal{J}=arg\underset{\mathbf{A}}{min}& \frac{1}{2}{∥\mathbf{J}\circ \left(\mathbf{Y}-\mathbf{A}\widehat{\mathbf{X}}\right)∥}_F^2+\frac{\mu }{2}{∥\mathbf{A}-{\mathbf{RQ}}^{\top }+\frac{{\mathbf{Y}}_2}{\mu }∥}_F^2\hfill \end{array}$$

(14)

Let $\frac{\partial \mathcal{J}}{\partial \mathbf{A}}=0$, we have:

$$\begin{array}{c}\hfill \mathbf{A}=\left(\mathbf{J}\circ {\mathbf{Y}\widehat{\mathbf{X}}}^{\top }+\mu \left({\mathbf{RQ}}^{\top }+\frac{{\mathbf{Y}}_2}{\mu }\right)\right){\left({\widehat{\mathbf{X}}\widehat{\mathbf{X}}}^{\top }+\mu \mathbf{I}\right)}^{-1}\end{array}$$

(15)

Update P (Line 4 in Algorithm 1):

$$\begin{array}{cc}\hfill \mathcal{J}=arg\underset{\mathbf{P}}{min}& {∥\widehat{\mathbf{X}}-{\mathbf{PQ}}^{\top }\widehat{\mathbf{X}}-\mathbf{E}+\frac{{\mathbf{Y}}_1}{\mu }∥}_F^2\hfill \\ \hfill & s.t.{\mathbf{P}}^{\top }\mathbf{P}=\mathbf{I}\hfill \end{array}$$

(16)

Problem (16) is a classic orthogonal procrustes problem [46], given $\mathbf{M}=\widehat{\mathbf{X}}-\mathbf{E}+\frac{{\mathbf{Y}}_1}{\mu }$.

Update Q (Line 5 in Algorithm 1):

$$\mathcal{J}=arg\underset{\mathbf{Q}}{min}\frac{1}{2}{\lambda }_1{∥\mathbf{Q}∥}_F^2+\frac{\mu }{2}{∥\widehat{\mathbf{X}}-{\mathbf{PQ}}^{\top }\widehat{\mathbf{X}}-\mathbf{E}+\frac{{\mathbf{Y}}_1}{\mu }∥}_F^2+\frac{\mu }{2}{∥\mathbf{A}-{\mathbf{RQ}}^{\top }+\frac{{\mathbf{Y}}_2}{\mu }∥}_F^2$$

(17)

Let $\frac{\partial \mathcal{J}}{\partial \mathbf{Q}}=0$, we have:

$$\mathbf{Q}\left({\lambda }_1\mathbf{I}+\mu {\mathbf{R}}^{\top }\mathbf{R}\right)+\mu \widehat{\mathbf{X}}{\widehat{\mathbf{X}}}^{\top }\mathbf{Q}=\mu \widehat{\mathbf{X}}{\mathbf{M}}^{\top }\mathbf{P}+\mu {\mathbf{B}}^{\top }\mathbf{R}$$

(18)

where $\mathbf{B}=\mathbf{A}-\frac{{\mathbf{Y}}_2}{\mu }$. Q is renewed by a Sylvester equation [47].

Update R (Line 6 in Algorithm 1):

$$\mathcal{J}=arg\underset{\mathbf{R}}{min}\frac{1}{2}{\lambda }_2{∥\mathbf{R}∥}_F^2+\frac{\mu }{2}{∥\mathbf{A}-{\mathbf{RQ}}^{\top }+\frac{{\mathbf{Y}}_2}{\mu }∥}_F^2$$

(19)

Let $\frac{\partial \mathcal{J}}{\partial \mathbf{R}}=0$, we have:

$$\mathbf{R}=\mu \mathbf{HQ}{\left({\lambda }_3\mathbf{I}+\mu {\mathbf{Q}}^{\top }\mathbf{Q}\right)}^{-1}$$

(20)

where $\mathbf{H}=\mathbf{A}-\left(\frac{{\mathbf{Y}}_2}{\mu }\right)$.

Update E (Line 7 in Algorithm 1):

$$\mathcal{J}=arg\underset{\mathbf{E}}{min}{\lambda }_2{∥\mathbf{E}∥}_1+\frac{\mu }{2}{∥\widehat{\mathbf{X}}-{\mathbf{PQ}}^{\top }\widehat{\mathbf{X}}-\mathbf{E}+\frac{{\mathbf{Y}}_1}{\mu }∥}_F^2$$

(21)

which has the closed-form solution [48] shown below:

$$\mathbf{E}=S_{\frac{{\lambda }_2}{\mu }}\left[\widehat{\mathbf{X}}-{\mathbf{PQ}}^{\top }\widehat{\mathbf{X}}+\frac{{\mathbf{Y}}_1}{\mu }\right]$$

(22)

where $S_{\frac{{\lambda }_2}{\mu }}\left[t\right]=sgn\left(t\right)max\left(\left|t\right|-\frac{{\lambda }_2}{\mu },0\right)$, $sgn(·)$ is a sign function with 1 if the input is greater than 0, 0 if the input is 0 and −1 otherwise.

Update ${\mathbf{Y}}_1$, ${\mathbf{Y}}_2$, and $\mu$ (Line 8 in Algorithm 1):

$$\left\{\begin{array}{cc}{\mathbf{Y}}_1={\mathbf{Y}}_1+\mu (\widehat{\mathbf{X}}-{\mathbf{PQ}}^{\top }\widehat{\mathbf{X}}-\mathbf{E});\hfill & \\ {\mathbf{Y}}_2={\mathbf{Y}}_2+\mu (\mathbf{A}-{\mathbf{RQ}}^{\top });\hfill & \\ \mu =min({\mu }_{max},\rho \mu ).\hfill \end{array}\right.$$

(23)

where $\rho \to 1^{+}$.

3.2.2. Solving (9)

We employ the alternating minimization to solve the objective function in (9). We implement the solving for U, V, and W via manopt toolbox [49].

Update ${\mathbf{Z}}_i$ (Line 13 in Algorithm 1):

$$\begin{array}{cc}\hfill \underset{{\mathbf{Z}}_i}{min}& \frac{{\lambda }_4{n}_i}{n}tr\left({\mathbf{G}}_0^{\top }{\mathbf{Z}}_i{\mathbf{Z}}_i^{\top }{\mathbf{G}}_0\right)+{\lambda }_{4}tr\left({\mathbf{G}}_i^{\top }{\mathbf{Z}}_i{\mathbf{Z}}_i^{\top }{\mathbf{G}}_i\right)\hfill \\ \hfill & s.t.diag\left({\mathbf{Z}}_i{\mathbf{Z}}_i^{\top }\right)=\mathbf{1}\hfill \end{array}$$

(24)

for each $i\in \{1,\dots ,h\}$. We solve it with projected gradient descent. ${\mathbf{Z}}_i$ is calculated by solving the gradient of ${\mathbf{Z}}_i$:

$${▽}_{{\mathbf{Z}}_i}=\frac{{\lambda }_4{n}_i}{n}{\mathbf{UW}}^{\top }{\mathbf{CC}}^{\top }{\mathbf{WU}}^{\top }{\mathbf{Z}}_i+{\lambda }_4{\mathbf{UW}}^{\top }{\mathbf{C}}_i{\mathbf{C}}_i^{\top }{\mathbf{WU}}^{\top }{\mathbf{Z}}_i$$

(25)

To satisfy the constraint $diag\left({\mathbf{Z}}_i{\mathbf{Z}}_i^{\top }\right)=\mathbf{1}$, we update the jth row of ${\mathbf{Z}}_i$ (i.e., ${\mathbf{z}}_{i,j,:})$ by ${\mathbf{z}}_{i,j,:}/∥{\mathbf{z}}_{i,j,:}∥$.

Update V (Line 15 in Algorithm 1):

$$\underset{\mathbf{V}}{min}{∥\mathbf{J}\circ \left(\mathbf{Y}-\mathbf{UV}\right)∥}_F^2+{\lambda }_1{∥\mathbf{V}-{\mathbf{W}}^{\top }\mathbf{C}∥}_F^2+{\lambda }_3{∥\mathbf{V}∥}_F^2$$

(26)

$\mathbf{V}$ is calculated by solving the gradient of $\mathbf{V}$:

$${▽}_{\mathbf{V}}={\mathbf{U}}^{\top }\left(\mathbf{J}\circ (\mathbf{UV}-\mathbf{Y})\right)+{\lambda }_1(\mathbf{V}-{\mathbf{W}}^{\top }\mathbf{C})+{\lambda }_3\mathbf{V}$$

(27)

Update U (Line 16 in Algorithm 1):

$$\underset{\mathbf{U}}{min}{∥\mathbf{J}\circ \left(\mathbf{Y}-\mathbf{UV}\right)∥}_F^2+{\lambda }_3{∥\mathbf{U}∥}_F^2+\sum _{i=1}^h\frac{{\lambda }_4{n}_i}{n}tr\left({\mathbf{G}}_0^{\top }{\mathbf{Z}}_i{\mathbf{Z}}_i^{\top }{\mathbf{G}}_0\right)+\sum _{i=1}^h{\lambda }_{4}tr\left({\mathbf{G}}_i^{\top }{\mathbf{Z}}_i{\mathbf{Z}}_i^{\top }{\mathbf{G}}_i\right)$$

(28)

$\mathbf{U}$ is calculated by solving the gradient of $\mathbf{U}$:

$$\begin{array}{cc}\hfill {▽}_{\mathbf{U}}=& \mathbf{J}\circ (\mathbf{UV}-\mathbf{Y}){\mathbf{V}}^{\top }+{\lambda }_3\mathbf{U}\hfill \\ & +\sum _{i=1}^h\frac{{\lambda }_4{n}_i}{n}{\mathbf{Z}}_i{\mathbf{Z}}_i^{\top }\mathbf{U}{\mathbf{W}}^{\top }\mathbf{C}{\mathbf{C}}^{\top }\mathbf{W}+\sum _{i=1}^h{\lambda }_4{\mathbf{Z}}_i{\mathbf{Z}}_i^{\top }\mathbf{U}{\mathbf{W}}^{\top }{\mathbf{C}}_i{\mathbf{C}}_i^{\top }\mathbf{W}\hfill \end{array}$$

(29)

Update W (Line 17 in Algorithm 1):

$$\begin{array}{cc}\hfill \underset{\mathbf{W}}{min}& {\lambda }_1{∥\mathbf{V}-{\mathbf{W}}^{\top }\mathbf{C}∥}_F^2+{\lambda }_3{∥\mathbf{W}∥}_F^2\hfill \\ & +\sum _{i=1}^h\frac{{\lambda }_4{n}_i}{n}tr\left({\mathbf{G}}_0^{\top }{\mathbf{Z}}_i{\mathbf{Z}}_i^{\top }{\mathbf{G}}_0\right)+\sum _{i=1}^h{\lambda }_{4}tr\left({\mathbf{G}}_i^{\top }{\mathbf{Z}}_i{\mathbf{Z}}_i^{\top }{\mathbf{G}}_i\right)\hfill \end{array}$$

(30)

$\mathbf{W}$ is calculated by solving the gradient of $\mathbf{W}$:

$$\begin{array}{cc}\hfill {▽}_{\mathbf{W}}=& {\lambda }_1\mathbf{C}({\mathbf{C}}^{\top }\mathbf{W}-{\mathbf{V}}^{\top })+{\lambda }_3\mathbf{W}\hfill \\ & +\sum _{i=1}^h\frac{{\lambda }_4{n}_i}{n}{\mathbf{CC}}^{\top }{\mathbf{WU}}^{\top }{\mathbf{Z}}_i{\mathbf{Z}}_i^{\top }\mathbf{U}+\sum _{i=1}^h{\lambda }_4{\mathbf{C}}_i{\mathbf{C}}_i^{\top }{\mathbf{WU}}^{\top }{\mathbf{Z}}_i{\mathbf{Z}}_i^{\top }\mathbf{U}\hfill \end{array}$$

(31)

3.3. Computational Complexity Analysis

This section analyzes the computational complexity of proposed RGLC (see Algorithm 1).

Algorithm 1: RGLC

3.3.1. Complexity Analysis of Solving (2)

The most time-consuming steps are the calculation of matrix A and matrix Q. Firstly, the complexity of calculating A (step 3) is $O(lnd+ldm+d^{2}l+d^3)$. Secondly, the complexity of calculating P (step 4) is $O(max(d^{2}n,d^{2}m))$. Thirdly, the complexity of calculating Q (step 5) is $O(d^3+max(d^{2}n,d^{2}m)+d^{2}n+m^{2}l)$. Finally, the complexity of computing R (step 6) is $O(m^3+m^{2}d+max(dlm,m^{2}l))$. Since the dimensionality of d is usually larger than instance count n, and the instance count n is much larger than l, we have the complexity of solving (2) as $O\left({\tau }_1(d^{2}l+2d^3+3d^{2}n)\right)$, where ${\tau }_1$ is the iteration count.

3.3.2. Complexity Analysis of Solving (9)

The most time-consuming steps are the calculation of matrix Z. Firstly, the complexity of calculating Z (step 13) is $O(h{l}^2{k}^2{m}^{2}n+{\tau }_{2}hmn)$, where $O\left({\tau }_{2}hmn\right)$ denotes the complexity for the generation of local instance groups with K-means algorithms, and ${\tau }_2$ is the iteration counts. Secondly, the complexity of calculating V (step 15) is $O(max(k^{2}ln,kmn))$. Thirdly, the complexity of calculating U (step 16) is $O\left(h{l}^2{k}^2{m}^2{n}^2\right)$. Finally, the complexity of computing W (step 17) is $O\left(h{m}^{2}n{k}^3{l}^2\right)$. As we adopt gradient descent for Z, V, U, and W, the gradient decreases to zero at the rate of $\frac{1}{\sqrt{{\tau }_3}}$. Therefore, the complexity of solving (9) is $O\left({\tau }_{3}h{l}^2{k}^2{m}^{2}n\right)$, where ${\tau }_3$ is the iteration count.

In a nutshell, the complexity is $max(O\left({\tau }_1(d^{2}l+2d^3+3d^{2}n)\right),O\left({\tau }_{3}h{l}^2{k}^2{m}^{2}n\right))$.

4. Results

4.1. Experimental Settings

We conduct extensive experiments to examine the robustness of RGLC on twelve benchmarks, where bibtex, corel5k, enron, genbase, mediamill, medical, scene are from Mulan http://mulan.sourceforge.net/datasets.html (accessed on 21 January 2022) [50], languagelog and slashdot are from Meka http://waikato.github.io/meka/datasets/ (accessed on 21 January 2022) [51] and art, business, and health are from MDDM www.lamda.nju.edu.cn/code_MDDM.ashx (accessed on 21 January 2022) [52]. Table 1 summarizes the data characteristics from domains including images, text, video, and biology. For each dataset, we introduce the example count (#n), the feature dimensionality (#f), the label count (#q), the average number of associated labels per instance (#c) and the domain.

Table 1. Characteristics of datasets.

Datasets	#n	#f	#q	#c	Domain
art	5000	462	26	1.64	text
bibtex	7395	1836	159	2.402	text
business	5000	438	30	1.59	text
corel5k	5000	499	374	3.522	image
enron	1702	1001	53	3.378	text
genbase	662	1185	27	1.252	biology
health	5000	612	32	1.66	text
languagelog	1460	1004	75	1.18	text
mediamill	43907	120	101	4.376	video
medical	978	1449	45	1.245	text
scene	2407	294	6	1.074	image
slashdot	3782	1079	22	1.18	text

We adopt six evaluation metrics (Hamming Loss, Ranking Loss, One Error, Coverage, Average Precision, and Micro F1) [53] to evaluate the classification performance. The last two achieve better performance if the values are large, and the remaining metrics obtain better performance if the values are small. Let $Y_i$ and $\overline{Y_i}$ denote the relevant and irrelevant label set in ground truth and n be the unseen instances count; then, the formulas of metrics are enumerated as:

(1)

Hamming Loss (abbreviated as Hl) evaluates the average difference between predictions and ground truth (see Formula (32)). The smaller the value of Hamming loss is, the better the performance of an algorithm becomes.

$$Hl=\frac{1}{n}\sum _{i=1}^n\frac{1}{l}\left|f\left({\mathbf{x}}_i\right)\Delta {\mathbf{Y}}_i\right|$$

(32)

where $\Delta$ is the set symmetric difference and $|·|$ is the set cardinality.

(2)

Ranking Loss (abbreviated as Rkl) evaluates the fraction that an irrelevant label ranks before the relevant label in label predictions (see Formula (33)). The smaller the value of Ranking Loss is, the better the performance of an algorithm becomes.

$$Rkl=\frac{1}{n}\sum _{i=1}^n\frac{1}{\left|{\mathbf{Y}}_i\right|\left|\overline{{\mathbf{Y}}_i}\right|}\times \left|\left\{\left(l_a,l_b\right)\left|r_i\left(l_a\right)>r_i\left(l_b\right)\wedge \left(l_a,l_b\right)\in {\mathbf{Y}}_i\times \overline{{\mathbf{Y}}_i}\right.\right\}\right|$$

(33)

where $r_i\left(l_j\right)$ denotes the ranking position in ascending order for the j-th label on the i-th instance. $|·|$ is the set cardinality.

(3)

One Error (abbreviated as Oe) evaluates whether the average fraction that the label ranks first in prediction is the irrelevant label (see Formula (34)). The smaller the value of One Error is, the better the performance of an algorithm becomes.

$$Oe=\frac{1}{n}\sum _{i=1}^n\left[\left[\left(\underset{l_j}{argmin{r}_i\left(l_j\right)}\right)\notin {\mathbf{Y}}_i\right]\right]$$

(34)

where $\left[\left[·\right]\right]$ is equal to 1 if the condition holds, and it equals 0 otherwise. The operator $r_i\left(l_j\right)$ denotes the ranking position in ascending order for the j-th label on the i-th instance.

(4)

Coverage (abbreviated as Cvg) evaluates the average fraction for inclusion of all ground-truth labels in the ranking of label predictions (see Formula 35). The smaller the value of Coverage is, the better the performance of an algorithm becomes.

$$Cvg=\frac{1}{n}\sum _{i=1}^n\underset{l_j\in {\mathbf{Y}}_i}{max}{r}_i\left(l_j\right)-1$$

(35)

where $r_i\left(l_j\right)$ denotes the ranking position in ascending order for the j-th label on the i-th instance.

(5)

Average Precision (abbreviated as Ap) evaluates the average precision of actually relevant labels ranking before a relevant label examined by label predictions (see Formula 36). The larger the value of Average Precision is, the better the performance of an algorithm becomes.

$$Ap=\frac{1}{n}\sum _{i=1}^n\frac{1}{\left|{\mathbf{Y}}_i\right|}\sum _{l_j\in {\mathbf{Y}}_i}\frac{\left|l_s\in {\mathbf{Y}}_i\left|r_i\left(l_s\right)⩽r_i\left(l_j\right)\right.\right|}{r_i\left(l_j\right)}$$

(36)

where $|·|$ is the set cardinality.

The configurations used for comparing algorithms are enumerated as follows:

• Multi-label learning with label-specific features (LIFT) http://palm.seu.edu.cn/zhangml/files/LIFT.rar (accessed on 21 January 2022) [54]: Generating cluster-based label-specific features for multi-label.
• Learning label-specific features (LLSF) https://jiunhwang.github.io/ (accessed on 21 January 2022) [55]: Learning label-specific features to promote multi-label classification performance.
• Multi-label twin support vector machine (MLTSVM) http://www.optimal-group.org/Resource/MLTSVM.html (accessed on 21 January 2022) [56]: Providing multi-label learning algorithm with twin support vector machine.
• Global and local label correlations (Glocal) http://www.lamda.nju.edu.cn/code_Glocal.ashx (accessed on 21 January 2022) [31]: Learning global and local correlation for multi-label.
• Hybrid noise-oriented multilabel learning (HNOML) [17]: A feature and label noise-resistance multi-label model.
• Manifold regularized discriminative feature selection for multi-label learning (MDFS) https://github.com/JiaZhang19/MDFS (accessed on 21 January 2022) [38]: Learning discriminative features via manifold regularization.
• Multilabel classification with group-based mapping (MCGM) https://github.com/JianghongMA/MC-GM (accessed on 21 January 2022) [43]: Group-based local correlation with local feature selection.
• Fast random k labelsets (fRAkEL) http://github.com/KKimura360/fast_RAkEL_matlab (accessed on 21 January 2022) [57]: A fast version of Random k-labelsets.
• RGLC: Proposed model. ${\lambda }_1$,${\lambda }_2$,${\lambda }_3$, and ${\lambda }_4$ are searched in $\{{10}^{-5},{10}^{-4},\dots ,1\}$. Cluster number $h=5$ and $\rho =1.01$, as they have limited impacts on considered metrics.

Firstly, we explore the robustness of the baseline performance compared with the eight state-of-the-art multi-label classification algorithms across different domains. Secondly, we examine the contribution of included components by an ablation study. For the first two experiments, both S and J are all ones for baseline comparisons. Thirdly, we examine the robustness of RGLC with noisy features and missing labels. Lastly, we analyze convergence and sensitivity with noisy features and missing labels. For fairness, we present the results from the average of six times five-fold cross-validation. We conduct the entire experiments on a computer with an Intel(R) Core i7-10700 2.90GHz CPU and 32GB RAM running on a Windows 10 operating system.

To simulate noisy features and missing labels, we randomly replace 1 with 0 in each column of the indicator matrix S and J using the strategy in article [17]. The replacements are increased from 0% to 80% with 20% being the step size. The experimental comparison is on the datasets of business and health.

4.2. Learning with Benchmarks

Table 2 elaborates the experimental results of selected algorithms across all considered datasets. We first calculate the nine-algorithm performance rank on the same dataset and then calculate the average of one-algorithm performance rank among the twelve datasets. We obtain the value of the “Avg rank” of one algorithm and then rank it to get the value in ().

Table 2. Comparison of each algorithm (mean ± std). Best results and second best are in bold and underlined, respectively. (↓ the smaller the better, ↑ the larger the better).

Dataset	Hamming Loss (↓)
	LIFT	LLSF	MLTSVM	Glocal	HNOML	MDFS	MCGM	fRAkEL	RGLC
art	0.053 ± 0.001	0.057 ± 0.002	0.066 ± 0.001	0.062 ± 0.004	0.062 ± 0.001	0.061 ± 0.001	0.086 ± 0.006	0.136 ± 0.004	0.060 ± 0.002
bibtex	0.013 ± 0.001	0.015 ± 0.001	0.017 ± 0.001	0.014 ± 0.001	0.015 ± 0.001	0.013 ± 0.001	0.047 ± 0.006	0.046 ± 0.002	0.012 ± 0.001
business	0.028 ± 0.001	0.034 ± 0.002	0.025 ± 0.001	0.029 ± 0.001	0.030 ± 0.001	0.027 ± 0.002	0.033 ± 0.003	0.046 ± 0.002	0.025 ± 0.002
corel5k	0.010 ± 0.001	0.024 ± 0.002	0.015 ± 0.001	0.010 ± 0.001	0.009 ± 0.001	0.010 ± 0.001	0.201 ± 0.017	0.026 ± 0.001	0.009 ± 0.001
enron	0.109 ± 0.001	0.067 ± 0.001	0.062 ± 0.002	0.076 ± 0.006	0.056 ± 0.002	0.051 ± 0.002	0.062 ± 0.004	0.204 ± 0.008	0.057 ± 0.004
genbase	0.003 ± 0.001	0.001 ± 0.001	0.002 ± 0.001	0.003 ± 0.003	0.003 ± 0.003	0.005 ± 0.001	0.003 ± 0.001	0.002 ± 0.001	0.002 ± 0.004
health	0.035 ± 0.002	0.037 ± 0.001	0.037 ± 0.001	0.039 ± 0.002	0.047 ± 0.001	0.044 ± 0.001	0.048 ± 0.003	0.074 ± 0.004	0.033 ± 0.002
languagelog	0.016 ± 0.001	0.025 ± 0.001	0.029 ± 0.001	0.018 ± 0.001	0.016 ± 0.001	0.016 ± 0.001	0.028 ± 0.001	0.184 ± 0.007	0.015 ± 0.001
mediamill	0.030 ± 0.001	0.034 ± 0.001	0.033 ± 0.001	0.033 ± 0.001	0.033 ± 0.001	0.032 ± 0.001	0.035 ± 0.001	0.051 ± 0.005	0.032 ± 0.001
medical	0.013 ± 0.001	0.014 ± 0.001	0.014 ± 0.002	0.015 ± 0.001	0.014 ± 0.042	0.016 ± 0.016	0.016 ± 0.001	0.051 ± 0.005	0.011 ± 0.001
scene	0.094 ± 0.005	0.114 ± 0.002	0.143 ± 0.003	0.111 ± 0.006	0.147 ± 0.005	0.085 ± 0.008	0.119 ± 0.005	0.291 ± 0.020	0.089 ± 0.012
slashdot	0.017 ± 0.001	0.026 ± 0.001	0.212 ± 0.008	0.020 ± 0.001	0.020 ± 0.001	0.019 ± 0.001	0.029 ± 0.004	0.044 ± 0.002	0.016 ± 0.002
Avg rank	3.2500(2)	5.0833(5)	5.4583(7)	5.1250(6)	4.8750(4)	3.8750(3)	7.2917(8)	8.2500(9)	1.7917(1)
Dataset	Ranking Loss (↓)
	LIFT	LLSF	MLTSVM	Glocal	HNOML	MDFS	MCGM	fRAkEL	RGLC
art	0.113 ± 0.005	0.171 ± 0.006	0.625 ± 0.006	0.154 ± 0.016	0.122 ± 0.003	0.146 ± 0.002	0.345 ± 0.017	0.454 ± 0.015	0.143 ± 0.005
bibtex	0.078 ± 0.004	0.090 ± 0.002	0.659 ± 0.008	0.159 ± 0.005	0.136 ± 0.005	0.170 ± 0.006	0.252 ± 0.012	0.495 ± 0.005	0.074 ± 0.003
business	0.031 ± 0.002	0.055 ± 0.001	0.250 ± 0.004	0.049 ± 0.007	0.046 ± 0.004	0.038 ± 0.004	0.353 ± 0.021	0.185 ± 0.008	0.045 ± 0.003
corel5k	0.128 ± 0.003	0.190 ± 0.007	0.891 ± 0.002	0.148 ± 0.004	0.137 ± 0.002	0.132 ± 0.002	0.224 ± 0.012	0.812 ± 0.007	0.172 ± 0.003
enron	0.329 ± 0.006	0.189 ± 0.007	0.499 ± 0.012	0.132 ± 0.008	0.143 ± 0.007	0.088 ± 0.003	0.404 ± 0.014	0.424 ± 0.019	0.089 ± 0.011
genbase	0.003 ± 0.001	0.002 ± 0.002	0.006 ± 0.008	0.002 ± 0.001	0.002 ± 0.002	0.006 ± 0.002	0.031 ± 0.037	0.006 ± 0.006	0.003 ± 0.003
health	0.040 ± 0.003	0.094 ± 0.006	0.383 ± 0.012	0.081 ± 0.006	0.055 ± 0.005	0.058 ± 0.001	0.285 ± 0.012	0.259 ± 0.009	0.061 ± 0.002
languagelog	0.163 ± 0.007	0.232 ± 0.010	0.731 ± 0.014	0.193 ± 0.006	0.287 ± 0.016	0.159 ± 0.007	0.311 ± 0.021	0.546 ± 0.020	0.131 ± 0.010
mediamill	0.050 ± 0.001	0.047 ± 0.001	0.602 ± 0.005	0.056 ± 0.003	0.047 ± 0.001	0.060 ± 0.001	0.451 ± 0.008	0.132 ± 0.023	0.054 ± 0.001
medical	0.029 ± 0.006	0.035 ± 0.004	0.168 ± 0.018	0.201 ± 0.033	0.021 ± 0.059	0.043 ± 0.004	0.227 ± 0.023	0.131 ± 0.023	0.023 ± 0.005
scene	0.080 ± 0.007	0.113 ± 0.008	0.278 ± 0.009	0.096 ± 0.005	0.110 ± 0.010	0.076 ± 0.005	0.095 ± 0.010	0.243 ± 0.022	0.093 ± 0.008
slashdot	0.042 ± 0.003	0.035 ± 0.005	0.484 ± 0.022	0.069 ± 0.007	0.061 ± 0.008	0.050 ± 0.005	0.416 ± 0.035	0.144 ± 0.012	0.057 ± 0.004
Avg rank	2.4583(1)	4.3750(5)	8.5833(9)	4.7500(6)	3.3750(3)	3.5000(4)	7.5000(8)	7.4167(7)	3.0417(2)
Dataset	One Error (↓)
	LIFT	LLSF	MLTSVM	Glocal	HNOML	MDFS	MCGM	fRAkEL	RGLC
art	0.458 ± 0.026	0.471 ± 0.015	0.523 ± 0.007	0.468 ± 0.020	0.475 ± 0.011	0.610 ± 0.011	0.569 ± 0.069	0.303 ± 0.017	0.448 ± 0.006
bibtex	0.386 ± 0.009	0.358 ± 0.022	0.422 ± 0.010	0.528 ± 0.137	0.617 ± 0.007	0.532 ± 0.011	0.752 ± 0.025	0.194 ± 0.007	0.374 ± 0.011
business	0.106 ± 0.007	0.133 ± 0.008	0.092 ± 0.006	0.119 ± 0.009	0.126 ± 0.005	0.117 ± 0.010	0.660 ± 0.047	0.068 ± 0.007	0.116 ± 0.012
corel5k	0.690 ± 0.012	0.658 ± 0.010	0.745 ± 0.007	0.675 ± 0.021	0.727 ± 0.014	0.727 ± 0.017	0.722 ± 0.029	0.393 ± 0.012	0.644 ± 0.021
enron	0.637 ± 0.021	0.381 ± 0.027	0.139 ± 0.007	0.293 ± 0.037	0.300 ± 0.017	0.264 ± 0.010	0.760 ± 0.033	0.089 ± 0.018	0.230 ± 0.026
genbase	0.003 ± 0.000	0.003 ± 0.004	0.001 ± 0.001	0.002 ± 0.003	0.006 ± 0.003	0.017 ± 0.006	0.144 ± 0.060	0.002 ± 0.003	0.001 ± 0.003
health	0.238 ± 0.032	0.274 ± 0.010	0.236 ± 0.014	0.272 ± 0.015	0.293 ± 0.015	0.374 ± 0.017	0.476 ± 0.029	0.124 ± 0.006	0.254 ± 0.013
languagelog	0.690 ± 0.015	0.803 ± 0.025	0.679 ± 0.013	0.707 ± 0.026	0.773 ± 0.011	0.783 ± 0.025	0.852 ± 0.036	0.594 ± 0.033	0.676 ± 0.018
mediamill	0.137 ± 0.003	0.159 ± 0.004	0.134 ± 0.004	0.154 ± 0.003	0.191 ± 0.007	0.161 ± 0.003	0.960 ± 0.014	0.071 ± 0.012	0.151 ± 0.004
medical	0.163 ± 0.014	0.189 ± 0.017	0.113 ± 0.020	0.143 ± 0.032	0.154 ± 0.177	0.237 ± 0.025	0.510 ± 0.059	0.071 ± 0.012	0.142 ± 0.024
scene	0.240 ± 0.021	0.286 ± 0.015	0.177 ± 0.013	0.264 ± 0.011	0.292 ± 0.014	0.224 ± 0.019	0.208 ± 0.160	0.153 ± 0.024	0.258 ± 0.018
slashdot	0.091 ± 0.021	0.337 ± 0.023	0.086 ± 0.008	0.118 ± 0.013	0.332 ± 0.021	0.093 ± 0.019	0.790 ± 0.049	0.295 ± 0.010	0.092 ± 0.014
Avg rank	4.2083(4)	5.9583(6)	3.7917(3)	4.9583(5)	6.9583(8)	6.4583(7)	8.0000(9)	1.6250(1)	3.0417(2)
Dataset	Coverage (↓)
	LIFT	LLSF	MLTSVM	Glocal	HNOML	MDFS	MCGM	fRAkEL	RGLC
art	4.478 ± 0.181	0.245 ± 0.009	11.68 ± 0.129	5.903 ± 0.404	0.180 ± 0.005	5.299 ± 0.090	1131 ± 45.46	0.329 ± 0.013	0.211 ± 0.009
bibtex	22.10 ± 1.176	0.163 ± 0.005	0.501 ± 0.004	37.54 ± 1.114	0.214 ± 0.007	0.281 ± 0.012	1459 ± 32.58	0.416 ± 0.008	0.149 ± 0.004
business	1.949 ± 0.122	0.098 ± 0.003	9.307 ± 0.296	2.808 ± 0.289	0.087 ± 0.009	2.201 ± 0.199	951.9 ± 32.76	0.112 ± 0.005	0.086 ± 0.004
corel5k	113.6 ± 2.824	0.397 ± 0.014	340.2 ± 1.197	112.7 ± 1.269	0.320 ± 0.009	214.7 ± 8.136	73.21 ± 5.391	0.439 ± 0.007	0.384 ± 0.005
enron	33.91 ± 0.721	0.433 ± 0.027	30.89 ± 0.774	18.04 ± 0.872	0.356 ± 0.019	12.86 ± 0.408	328.3 ± 9.465	0.423 ± 0.030	0.240 ± 0.026
genbase	0.403 ± 0.054	0.010 ± 0.001	0.292 ± 0.167	0.352 ± 0.081	0.012 ± 0.003	0.565 ± 0.119	11.37 ± 5.464	0.016 ± 0.005	0.014 ± 0.004
health	2.549 ± 0.099	0.160 ± 0.006	11.91 ± 0.346	4.595 ± 0.350	0.106 ± 0.008	3.186 ± 0.076	829.8 ± 28.33	0.162 ± 0.008	0.124 ± 0.003
languagelog	13.14 ± 1.557	0.275 ± 0.001	30.79 ± 1.403	17.86 ± 0.308	0.293 ± 0.016	12.63 ± 0.770	163.4 ± 4.265	0.309 ± 0.014	0.143 ± 0.006
mediamill	17.63 ± 0.121	0.165 ± 0.001	57.99 ± 0.506	19.36 ± 0.229	0.163 ± 0.003	19.69 ± 0.314	0.861 ± 0.009	0.089 ± 0.019	0.151 ± 0.004
medical	1.811 ± 0.342	0.049 ± 0.004	4.648 ± 0.700	5.737 ± 0.828	0.033 ± 0.065	2.783 ± 0.347	78.17 ± 10.64	0.089 ± 0.019	0.037 ± 0.008
scene	0.482 ± 0.041	0.105 ± 0.007	0.887 ± 0.052	0.568 ± 0.033	0.108 ± 0.009	0.465 ± 0.025	444.7 ± 34.90	0.149 ± 0.014	0.089 ± 0.041
slashdot	0.857 ± 0.116	0.044 ± 0.005	9.644 ± 0.323	2.288 ± 0.208	0.056 ± 0.006	0.046 ± 0.004	742.9 ± 47.83	0.089 ± 0.009	0.055 ± 0.004
Avg rank	6.0833(6)	2.5833(3)	7.5833(8)	6.9167(7)	2.1667(2)	5.7500(5)	8.3333(9)	3.8333(4)	1.7500(1)
Dataset	Average Precision (↑)
	LIFT	LLSF	MLTSVM	Glocal	HNOML	MDFS	MCGM	fRAkEL	RGLC
art	0.622 ± 0.016	0.600 ± 0.009	0.461 ± 0.007	0.606 ± 0.021	0.619 ± 0.008	0.526 ± 0.006	0.220 ± 0.014	0.538 ± 0.015	0.626 ± 0.003
bibtex	0.563 ± 0.009	0.587 ± 0.014	0.324 ± 0.009	0.357 ± 0.010	0.360 ± 0.006	0.409 ± 0.007	0.164 ± 0.009	0.418 ± 0.008	0.589 ± 0.006
business	0.894 ± 0.004	0.859 ± 0.005	0.756 ± 0.003	0.875 ± 0.011	0.880 ± 0.005	0.882 ± 0.009	0.176 ± 0.022	0.708 ± 0.024	0.882 ± 0.007
corel5k	0.286 ± 0.007	0.251 ± 0.007	0.089 ± 0.003	0.273 ± 0.007	0.254 ± 0.004	0.254 ± 0.004	0.302 ± 0.043	0.160 ± 0.005	0.298 ± 0.008
enron	0.346 ± 0.014	0.556 ± 0.012	0.450 ± 0.011	0.642 ± 0.013	0.617 ± 0.008	0.654 ± 0.012	0.175 ± 0.004	0.427 ± 0.015	0.695 ± 0.018
genbase	0.995 ± 0.002	0.994 ± 0.004	0.989 ± 0.006	0.995 ± 0.003	0.993 ± 0.003	0.985 ± 0.005	0.892 ± 0.045	0.992 ± 0.007	0.996 ± 0.005
health	0.802 ± 0.019	0.755 ± 0.007	0.631 ± 0.008	0.762 ± 0.010	0.769 ± 0.011	0.703 ± 0.009	0.312 ± 0.019	0.651 ± 0.006	0.787 ± 0.005
languagelog	0.397 ± 0.027	0.266 ± 0.019	0.267 ± 0.011	0.387 ± 0.019	0.296 ± 0.033	0.319 ± 0.020	0.104 ± 0.006	0.183 ± 0.017	0.408 ± 0.013
mediamill	0.719 ± 0.002	0.695 ± 0.003	0.465 ± 0.004	0.692 ± 0.002	NA	0.686 ± 0.003	0.066 ± 0.001	0.764 ± 0.005	0.698 ± 0.001
medical	0.875 ± 0.012	0.864 ± 0.016	0.799 ± 0.024	0.766 ± 0.028	0.887 ± 0.151	0.805 ± 0.016	0.411 ± 0.048	0.764 ± 0.005	0.893 ± 0.015
scene	0.857 ± 0.013	0.821 ± 0.009	0.756 ± 0.005	0.840 ± 0.006	0.820 ± 0.010	0.867 ± 0.011	0.715 ± 0.027	0.797 ± 0.016	0.845 ± 0.011
slashdot	0.893 ± 0.025	0.664 ± 0.006	0.658 ± 0.014	0.875 ± 0.010	0.887 ± 0.010	0.882 ± 0.013	0.100 ± 0.014	0.592 ± 0.005	0.885 ± 0.012
Avg rank	2.5417(2)	4.9583(6)	7.2500(8)	4.4583(3)	4.5417(5)	4.6667(4)	8.2500(9)	6.5000(7)	1.8333(1)
Dataset	Micro F1(↑)
	LIFT	LLSF	MLTSVM	Glocal	HNOML	MDFS	MCGM	fRAkEL	RGLC
art	0.359 ± 0.010	0.416 ± 0.015	0.373 ± 0.004	0.346 ± 0.021	0.225 ± 0.007	0.152 ± 0.002	0.420 ± 0.014	0.246 ± 0.007	0.394 ± 0.015
bibtex	0.370 ± 0.013	0.487 ± 0.006	0.356 ± 0.003	0.239 ± 0.010	0.328 ± 0.002	0.273 ± 0.007	0.224 ± 0.021	0.181 ± 0.007	0.293 ± 0.006
business	0.731 ± 0.008	0.687 ± 0.013	0.733 ± 0.002	0.698 ± 0.005	0.675 ± 0.007	0.703 ± 0.014	0.702 ± 0.018	0.615 ± 0.014	0.710 ± 0.018
corel5k	0.073 ± 0.002	0.205 ± 0.041	0.119 ± 0.003	0.037 ± 0.009	0.006 ± 0.002	0.024 ± 0.001	0.194 ± 0.017	0.061 ± 0.004	0.123 ± 0.008
enron	0.241 ± 0.010	0.479 ± 0.016	0.501 ± 0.010	0.445 ± 0.021	0.483 ± 0.011	0.504 ± 0.026	0.552 ± 0.022	0.200 ± 0.012	0.521 ± 0.015
genbase	0.970 ± 0.014	0.991 ± 0.005	0.987 ± 0.007	0.980 ± 0.018	0.956 ± 0.036	0.938 ± 0.012	0.972 ± 0.009	0.975 ± 0.013	0.992 ± 0.031
health	0.643 ± 0.018	0.627 ± 0.004	0.609 ± 0.009	0.582 ± 0.015	0.201 ± 0.004	0.381 ± 0.023	0.509 ± 0.164	0.446 ± 0.018	0.594 ± 0.014
languagelog	0.172 ± 0.039	0.205 ± 0.023	0.221 ± 0.009	0.058 ± 0.010	0.074 ± 0.019	0.070 ± 0.023	0.263 ± 0.008	0.028 ± 0.005	0.133 ± 0.014
mediamill	0.556 ± 0.003	0.505 ± 0.003	0.474 ± 0.004	0.508 ± 0.003	0.465 ± 0.004	0.520 ± 0.004	0.514 ± 0.003	0.458 ± 0.034	0.533 ± 0.001
medical	0.753 ± 0.030	0.755 ± 0.029	0.759 ± 0.026	0.714 ± 0.024	0.708 ± 0.077	0.668 ± 0.019	0.698 ± 0.013	0.458 ± 0.034	0.798 ± 0.016
scene	0.760 ± 0.008	0.591 ± 0.026	0.674 ± 0.008	0.588 ± 0.009	0.602 ± 0.015	0.746 ± 0.024	0.617 ± 0.019	0.427 ± 0.037	0.653 ± 0.015
slashdot	0.772 ± 0.013	0.737 ± 0.012	0.643 ± 0.011	0.774 ± 0.017	0.745 ± 0.005	0.745 ± 0.020	0.682 ± 0.029	0.581 ± 0.012	0.778 ± 0.015
Avg rank	3.5833(2)	3.8333(4)	3.7500(3)	5.8333(7)	6.5417(8)	6.0417(6)	4.5000(5)	8.1667(9)	2.7500(1)

We employ the Friedman test [58] to quantify the differences between all considered algorithms. We introduce four symbols to detail the processing of Friedman statistics $F_F$ (see Formula (37)), including comparing algorithms number (k), datasets number (N), the performance rank of the j-th algorithm on the i-th dataset ($r_i^j$) and the average rank of the j-th algorithm over all the datasets ($R_j=\frac{1}{N}{\sum }_{i=1}^N{r}_i^j$). With the null hypothesis (i.e., $H_0$) of all algorithms obtaining identical performance, we have the F-distribution with $k-1$ degrees of freedom as the numerator and $(k-1)(N-1)$ degrees of freedom as the denominator:

$$F_F=\frac{\left(N-1\right){\chi }_F^2}{N\left(k-1\right)-{\chi }_F^2}$$

(37)

where

$${\chi }_F^2=\frac{12N}{k\left(k+1\right)}\left[\sum _j{R}_j^2-\frac{k{\left(k+1\right)}^2}{4}\right]$$

(38)

Table 3 presents the value of Friedman statistics $F_F$ for all considered metrics and the referenced critical difference (CD). As shown in Table 3, at the significance level $\alpha =0.05$, we reject the null hypothesis (i.e., $H_0$) of statistically indistinguishable performance among the considered algorithms for all considered evaluation metrics. The result implies that it is feasible to examine whether RGLC gains statistical superiority over other algorithms by conducting the post hoc test such as the Holm test [58].

Table 3. Summary of the Friedman statistics $F_F$ ($k=9$, $N=12$) and the critical value at significance level $\alpha =0.05$ in terms of each evaluation measure (k:# comparing algorithms; N:# datasets).

Metric	${\mathit{F}}_{\mathit{F}}$	Critical Value
Hamming Loss	49.0944	2.0454
Ranking Loss	64.9111
One Error	53.1111
Coverage	78.3778
Average Precision	55.3000
Micro F1	39.0833

Table 4 presents the statistical result of RGLC compared with remaining algorithms by the Holm test (see Formula (39)) at significance level ($\alpha =0.05$). We use RGLC as the control algorithm and nominate it as $A_1$. We stipulate the remaining comparing algorithms as $A_j$ in the order of average rank across all datasets in each evaluation metric, where $2⩽j⩽k$.

$$z_j=\left(R_1-R_j\right)/\phantom{\left(R_1-R_j\right)\sqrt{\frac{k\left(k+1\right)}{6N}}}\sqrt{\frac{k\left(k+1\right)}{6N}}\left(2⩽j⩽k\right)$$

(39)

Table 4. Comparison of RGLC (control algorithm) against the remaining approaches. The test statistics $z_i$ and p-value are determined by the Holm test at significance level $\alpha$ = 0.05. Algorithms that are statistically inferior than RGLC are in bold size.

Hamming Loss					Ranking Loss
j	algorithm	$z_j$	p	$\alpha /(k-j+1)$	j	algorithm	$z_j$	p	$\alpha /(k-j+1)$
2	fRA$\mathbf{k}$EL	−5.7765	0.000000	0.006	2	MLTSVM	−4.9566	0.000000	0.006
3	MCGM	−4.9194	0.000001	0.007	3	MCGM	−3.9876	0.000067	0.007
4	MLTSVM	−3.2796	0.001040	0.008	4	fRA$\mathbf{k}$EL	−3.9131	0.000091	0.008
5	Glocal	−2.9814	0.002869	0.010	5	Glocal	−1.5279	0.126537	0.010
6	LLSF	−2.9442	0.003238	0.013	6	LLSF	−1.1925	0.233065	0.013
7	HNOML	−2.7578	0.005819	0.017	7	MDFS	−0.4099	0.681879	0.017
8	MDFS	−1.8634	0.062407	0.025	8	HNOML	−0.2981	0.765627	0.025
9	LIFT	−1.3044	0.192106	0.050	9	LIFT	0.5218	1.000000	0.050
One Error					Coverage
j	algorithm	$z_j$	p	$\alpha /(k-j+1)$	j	algorithm	$z_j$	p	$\alpha /(k-j+1)$
2	MCGM	−4.4348	0.000009	0.006	2	MCGM	−5.8883	0.000000	0.006
3	HNOML	−3.5031	0.000460	0.007	3	MLTSVM	−5.2175	0.000000	0.007
4	MDFS	−3.0559	0.002244	0.008	4	Glocal	−4.6212	0.000004	0.018
5	LLSF	−2.6087	0.009089	0.010	5	LIFT	−3.8759	0.000106	0.010
6	Glocal	−1.7143	0.086474	0.013	6	MDFS	−3.5778	0.000347	0.013
7	LIFT	−1.0434	0.296763	0.017	7	fRAkEL	−1.8634	0.062407	0.017
8	MLTSVM	−0.6708	0.502348	0.025	8	LLSF	−0.7454	0.456057	0.025
9	fRAkEL	1.2671	1.000000	0.050	9	HNOML	−0.3727	0.709388	0.050
Average Precision					Micro F1
j	algorithm	$z_j$	p	$\alpha /(k-j+1)$	j	algorithm	$z_j$	p	$\alpha /(k-j+1)$
2	MCGM	−5.7392	0.000000	0.006	2	fRA$\mathbf{k}$EL	−4.8448	0.000001	0.006
3	MLTSVM	−4.8448	0.000001	0.007	3	HNOML	−3.3914	0.000695	0.007
4	fRA$\mathbf{k}$EL	−4.1740	0.000030	0.008	4	MDFS	−2.9442	0.003238	0.008
5	LLSF	−2.7951	0.005189	0.010	5	Glocal	−2.7578	0.005819	0.010
6	MDFS	−2.5342	0.011270	0.013	6	MCGM	−1.5652	0.117525	0.013
7	HNOML	−2.4224	0.015418	0.017	7	LIFT	−0.9690	0.332564	0.017
8	Glocal	−2.3479	0.018881	0.025	8	MLTSVM	−0.8944	0.371093	0.025
9	LIFT	−0.6336	0.526373	0.050	9	LLSF	−0.7454	0.456057	0.050

The p-value of $z_j$ (denoted as $p_j$) is calculated by standard normal distribution. For significance level $\alpha =0.05$, we examine whether $p_j$ is smaller than $\alpha /\left(k-j+1\right)$ for $j=2,3,\dots ,9$. Specially, the Holm test continues until there exists a $j^{*}$th step, where $j^{*}$ denotes the first j with $p_j⩾\alpha /\left(k-j+1\right)$. $j^{*}$ is configured as $k+1$ if $p_j<\alpha /\left(k-j+1\right)$ hold for all j.

Accordingly, we have the following findings based on reported experimental comparisons:

• From Table 2, we observe that for all six evaluation metrics, RGLC achieves the best performance or second-best performance in 66.67% (4/6) and 33.33% (2/6) cases according to the rank of “Avg rank” in terms of Hamming Loss, Ranking Loss, One Error, Coverage, Average Precision, and Micro F1. It is only inferior to LIFT and fRAkEL according to the rank of the value of “Avg rank” in Table 2 based on the evaluation metric Ranking Loss and One Error, respectively. Specifically, RGLC achieves 24 (33.33%) best (the number of values indicated in bold) and 18 (25%) second-best performances (the number of values indicated in underlined) on 72 observations (12 datasets × 6 metrics). In contrast, the second-best method is LIFT, which achieves 12 (16.67%) best and 18 (25%) second-best performances on 72 observations (12 datasets × 6 metrics).
• The Holm test in Table 4 shows that RGLC is statistically superior to other algorithms to varying degrees in all metrics, with the best performance in Average Precision (better than seven algorithms) and the worst performance in Ranking Loss (better than three algorithms). Concretely, RGLC significantly outperforms MCGM in terms of all metrics except Micro F1, significantly outperforms MLTSVM in terms of Hamming Loss, Ranking Loss, Coverage, and Average Precision, significantly outperforms Glocal in terms of Hamming Loss, Coverage, Average Precision, and Micro F1, significantly outperforms HNOML in terms of Hamming Loss, One Error, Average Precision, and Micro F1, significantly outperforms MDFS in terms of One Error, Coverage, Average Precision, and Micro F1, significantly outperforms fRAkEL in terms of Hamming Loss, Ranking Loss, Average Precision, and Micro F1, significantly outperforms LLSF in terms of Hamming Loss, One Error, and Average Precision and significantly outperforms LIFT in terms of Coverage.

4.3. Ablation Study

Table 5 shows the functionality of latent features, latent labels, global label correlation, and the local label correlation.

Table 5. Comparison of each component in RGLC. Best results are in bold size. ↓: the smaller the better; ↑: the larger the better.

Dataset	Hamming Loss (↓)					Dataset	Ranking Loss (↓)
	RGLC	RGLC-LF	RGLC-LL	RGLC-GC	RGLC-LC		RGLC	RGLC-LF	RGLC-LL	RGLC-GC	RGLC-LC
art	0.060(2)	0.062(5)	0.061(4)	0.060(2)	0.060(2)	art	0.143(1)	0.156(5)	0.153(4)	0.146(3)	0.144(2)
bibtex	0.012(1)	0.014(5)	0.013(3)	0.013(3)	0.013(3)	bibtex	0.074(1)	0.131(5)	0.085(2.5)	0.085(2.5)	0.089(4)
business	0.025(1)	0.028(4)	0.028(4)	0.027(2)	0.028(4)	business	0.045(1)	0.051(5)	0.050(4)	0.046(2)	0.047(3)
corel5k	0.009(2)	0.009(2)	0.010(4.5)	0.009(2)	0.010(4.5)	corel5k	0.172(2)	0.161(1)	0.199(5)	0.177(3)	0.195(4)
enron	0.057(1)	0.073(5)	0.072(4)	0.071(3)	0.068(2)	enron	0.089(1)	0.128(5)	0.125(3.5)	0.122(2)	0.125(3.5)
genbase	0.002(3)	0.001(1)	0.003(5)	0.002(3)	0.002(3)	genbase	0.003(4)	0.002(1.5)	0.003(4)	0.002(1.5)	0.003(4)
health	0.033(1)	0.039(5)	0.037(3.5)	0.036(2)	0.037(3.5)	health	0.061(1)	0.081(5)	0.075(4)	0.069(2)	0.070(3)
languagelog	0.015(1)	0.018(5)	0.017(4)	0.016(2.5)	0.016(2.5)	languagelog	0.131(1)	0.226(5)	0.178(3)	0.187(4)	0.179(2)
mediamill	0.032(1)	0.033(3.5)	0.033(3.5)	0.033(3.5)	0.033(3.5)	mediamill	0.054(1)	0.056(2.5)	0.056(2.5)	0.057(4)	0.058(5)
medical	0.011(2)	0.018(5)	0.011(2)	0.011(2)	0.012(4)	medical	0.023(3.5)	0.039(5)	0.019(1)	0.022(2)	0.023(3.5)
scene	0.089(1)	0.121(5)	0.116(4)	0.110(2.5)	0.110(2.5)	scene	0.093(1)	0.102(5)	0.095(3.5)	0.094(2)	0.095(3.5)
slashdot	0.016(1)	0.022(5)	0.017(3)	0.017(3)	0.017(3)	slashdot	0.057(1)	0.070(5)	0.069(4)	0.068(3)	0.067(2)
Avg. Rank	1.417(1)	4.208(5)	3.708(4)	2.542(2)	3.125(3)	Avg Rank	1.542(1)	4.167(5)	3.417(4)	2.583(2)	3.292(3)
Dataset	One Error (↓)					Dataset	Coverage (↓)
	RGLC	RGLC-LF	RGLC-LL	RGLC-GC	RGLC-LC		RGLC	RGLC-LF	RGLC-LL	RGLC-GC	RGLC-LC
art	0.448(1)	0.468(5)	0.458(2)	0.460(3)	0.459(4)	art	0.211(1)	5.96(5)	0.225(4)	0.215(3)	0.214(2)
bibtex	0.374(2)	0.491(5)	0.364(1)	0.380(3)	0.383(4)	bibtex	0.149(1)	33.15(5)	0.163(3)	0.161(2)	0.169(4)
business	0.116(1)	0.122(4.5)	0.122(4.5)	0.118(2.5)	0.118(2.5)	business	0.086(1)	2.864(5)	0.094(4)	0.087(2)	0.088(3)
corel5k	0.644(1)	0.647(2)	0.652(5)	0.650(3)	0.651(4)	corel5k	0.384(1)	129.5(5)	0.445(4)	0.405(2)	0.439(3)
enron	0.230(1)	0.283(5)	0.264(2)	0.279(4)	0.266(3)	enron	0.240(1)	17.44(5)	0.314(3)	0.310(2)	0.319(4)
genbase	0.001(1)	0.006(3)	0.003(3.5)	0.002(2)	0.003(3.5)	genbase	0.015(4)	0.348(5)	0.014(2.5)	0.012(1)	0.014(2.5)
health	0.254(1)	0.272(5)	0.262(4)	0.255(2)	0.256(3)	health	0.143(4)	4.595(5)	0.135(3)	0.127(1)	0.129(2)
languagelog	0.676(2)	0.743(5)	0.665(1)	0.689(4)	0.678(3)	languagelog	0.143(1)	20.58(5)	0.188(2)	0.198(4)	0.193(3)
mediamill	0.151(1)	0.153(2)	0.169(5)	0.167(3.5)	0.167(3.5)	mediamill	0.151(1)	19.28(5)	0.180(2)	0.185(3)	0.187(4)
medical	0.142(1)	0.162(5)	0.155(4)	0.147(2)	0.149(3)	medical	0.037(3)	2.496(5)	0.031(1)	0.038(4)	0.036(2)
scene	0.258(1)	0.281(5)	0.269(3)	0.276(4)	0.268(2)	scene	0.089(1)	0.599(5)	0.091(2)	0.092(3)	0.093(4)
slashdot	0.092(1)	0.116(5)	0.108(4)	0.104(2)	0.105(3)	slashdot	0.055(1)	2.317(5)	0.065(4)	0.064(3)	0.062(2)
Avg. Rank	1.167(1)	4.292(5)	3.250(4)	2.917(2)	3.208(3)	Avg Rank	1.667(1)	5.000(5)	2.875(3)	2.500(2)	2.958(4)
Dataset	Average Precision (↑)					Dataset	Micro F1 (↑)
	RGLC	RGLC-LF	RGLC-LL	RGLC-GC	RGLC-LC		RGLC	RGLC-LF	RGLC-LL	RGLC-GC	RGLC-LC
art	0.626(1)	0.606(5)	0.614(3.5)	0.614(3.5)	0.618(2)	art	0.394(1)	0.349(5)	0.353(2)	0.338(3.5)	0.338(3.5)
bibtex	0.589(1)	0.433(5)	0.580(2)	0.573(3)	0.570(4)	bibtex	0.293(4)	0.254(5)	0.348(1)	0.305(3)	0.334(2)
business	0.882(1)	0.873(4.5)	0.873(4.5)	0.878(2)	0.876(3)	business	0.710(2)	0.707(4.5)	0.708(3)	0.714(1)	0.707(4.5)
corel5k	0.298(1)	0.283(5)	0.289(4)	0.292(2)	0.291(3)	corel5k	0.123(2)	0.056(4)	0.188(1)	0.037(5)	0.090(3)
enron	0.695(1)	0.648(5)	0.662(2)	0.658(4)	0.661(3)	enron	0.521(1)	0.457(5)	0.464(4)	0.467(3)	0.480(2)
genbase	0.996(1.5)	0.994(4)	0.995(3)	0.996(1.5)	0.993(5)	genbase	0.991(1)	0.985(2)	0.972(5)	0.976(3.5)	0.976(3.5)
health	0.787(1)	0.762(5)	0.772(4)	0.779(2)	0.778(3)	health	0.594(2)	0.582(5)	0.596(1)	0.593(3)	0.590(4)
languagelog	0.408(2)	0.346(5)	0.416(1)	0.401(4)	0.405(3)	languagelog	0.133(2)	0.134(1)	0.127(3)	0.089(4)	0.071(5)
mediamill	0.698(1)	0.693(2)	0.680(5)	0.683(3)	0.681(4)	mediamill	0.533(1)	0.509(2)	0.490(5)	0.493(3)	0.492(4)
medical	0.893(1)	0.862(5)	0.886(4)	0.887(2.5)	0.887(2.5)	medical	0.798(1)	0.703(5)	0.794(2.5)	0.794(2.5)	0.779(4)
scence	0.845(1)	0.829(5)	0.839(2.5)	0.836(4)	0.839(2.5)	scene	0.653(1)	0.543(5)	0.581(4)	0.628(2)	0.622(3)
slashdot	0.885(1)	0.867(5)	0.875(2.5)	0.875(2.5)	0.878(4)	slashdot	0.778(1)	0.773(2)	0.767(5)	0.769(4)	0.772(3)
Avg. Rank	1.208(1)	4.625(5)	3.167(3)	2.833(2)	3.250(4)	Avg Rank	1.583(1)	3.792(5)	3.042(2)	3.125(3)	3.458(4)

We devise four degenerate versions of RGLC: (i) RGLC-LF, which learns both global and local label correlation without latent features; (ii) RGLC-LL, which learns both global and local label correlation without latent labels; (iii) RGLC-GC, which learns local label correlation only on both latent features and latent labels; and (iv) RGLC-LC, which learns global label correlation only on both latent features and latent labels. The lower the rank is, the better the performance becomes. For the degenerate versions, the larger difference in the ranking of the algorithms to RGLC is, the more significant the component in boosting classification performance and vice versa.

As shown in Table 5, RGLC achieves the best performance across all metrics on average. Latent feature learning contributes most among all components, and latent label learning contributes almost the same as local label correlation. The global label correlation has the least contribution to boosting performance.

4.4. Learning with Noisy Features and Missing Labels

In this section, we evaluate the fluctuations of RGLC with the concurrence of noisy features and missing labels.

Figure 2 illustrates the classification performance on dataset art.

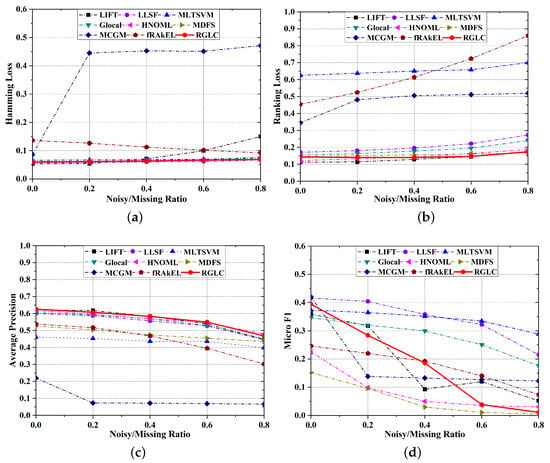
Figure 2. Robustness experiments with noisy features and missing labels on dataset art on metric (a) Hamming Loss, (b) Ranking Loss, (c) Average Precision, and (d) Micro F1.

As can be observed, the performance of all metrics degenerates as the ratio of noisy features and missing labels increases. For most cases, RGLC fluctuates least as the noisy features and missing labels increase.

Figure 3 illustrates the classification performance of the dataset business.

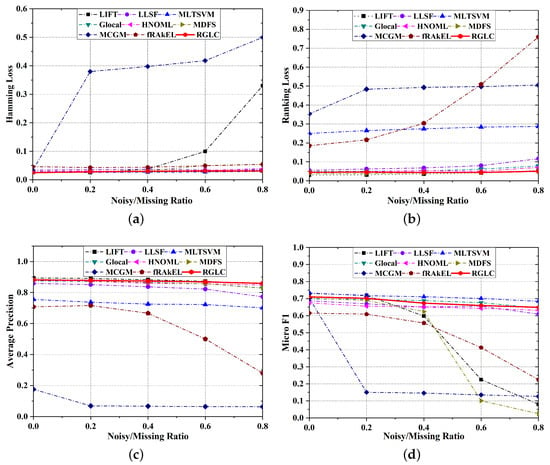
Figure 3. Robustness experiments with noisy features and missing labels on dataset business on metric (a) Hamming Loss, (b) Ranking Loss, (c) Average Precision, and (d) Micro F1.

As can be observed, the performance of all metrics degenerates as the ratio of noisy features and missing labels increases. For most cases, RGLC fluctuates the least as the noisy features and missing labels increase.

Figure 4 illustrates the classification performance of dataset health.

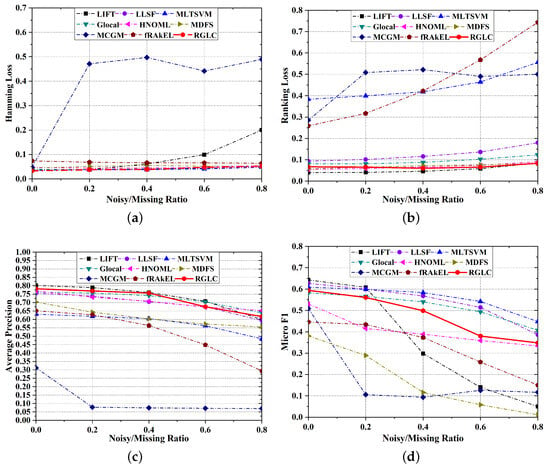
Figure 4. Robustness experiments with noisy features and missing labels on dataset health on metric (a) Hamming Loss, (b) Ranking Loss, (c) Average Precision, and (d) Micro F1.

As can be observed, the performance of all metrics degenerates as the ratio of noisy features and missing labels increases. For most cases, RGLC fluctuates least as the noisy features and missing labels increase.

4.5. Convergence

Furthermore, we study the convergence of RGLC. Without losing generality, we report the variations of two objective functions on datasets bibtex and corel5k in Figure 5, given 60% noisy features and missing labels presence.

Figure 5. Convergence of RGLC on the bibtex and corel5k datasets with 60% noisy features and missing labels. (a,c) are the convergence of (2), whereas (b,d) are the convergence of (9).

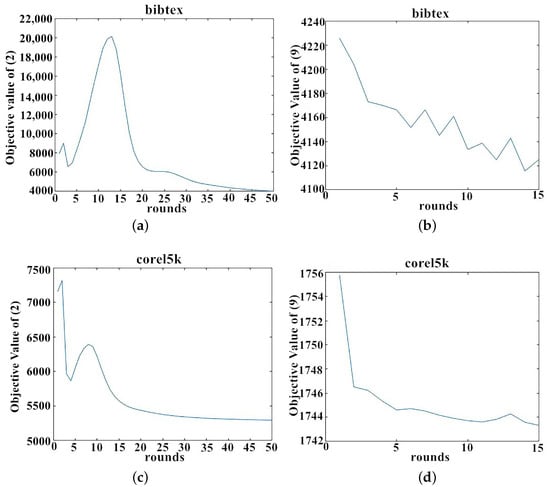
As can be observed, values of both objective functions converge quickly in a few iterations. Similar phenomena also apply to other datasets. The runtime comparisons of all algorithms in Table 6 show that the computational complexity of RGLC is acceptable on large-scale datasets.

Table 6. Runtime (in seconds) for learning with 60% noisy features and missing labels. Best results are in bold size.

Dataset	Algorithms
	LIFT	LLSF	MLTSVM	Glocal	HNOML	MDFS	MCGM	fRAkEL	RGLC
art	162.4(9)	0.337(2)	87.41(8)	26.34(3)	50.16(5)	56.06(6)	65.80(7)	0.317(1)	27.97(4)
bibtex	1033(9)	5.432(2)	630.5(8)	349.3(5)	370.6(6)	253.8(4)	246.4(3)	1.658(1)	482.9(7)
business	201.1(9)	0.420(2)	99.48(8)	24.24(3)	45.95(5)	46.66(6)	77.64(7)	0.168(1)	30.04(4)
corel5k	466.2(9)	5.469(2)	425.9(8)	106.3(5)	83.31(4)	133.7(6)	160.7(7)	4.298(1)	72.57(3)
enron	22.02(7)	0.559(1)	5.107(4)	35.04(8)	8.611(5)	5.007(3)	10.77(6)	0.608(2)	81.94(9)
genbase	2.463(6)	0.546(2)	1.089(4)	15.73(8)	2.783(7)	0.620(3)	2.007(5)	0.293(1)	46.28(9)
health	538.0(9)	0.647(2)	94.44(8)	21.69(3)	64.63(6)	50.77(4)	72.75(7)	0.284(1)	51.47(5)
mediamill	1555(9)	9.209(1)	454.1(8)	154.9(3)	438.9(7)	435.5(6)	224.3(5)	12.60(2)	198.8(4)
medical	8.858(7)	1.313(2)	2.958(4)	30.12(9)	5.576(5)	1.552(3)	7.183(6)	0.347(1)	29.87(8)
scene	11.94(9)	0.143(1)	2.131(3)	4.158(5)	7.412(8)	5.917(7)	5.451(6)	0.906(2)	4.143(4)
slashdot	36.72(7)	0.459(1)	15.55(3)	15.10(2)	40.08(8)	21.69(5)	17.29(4)	24.45(6)	59.77(9)
Total&Rank	7.50(9)	1.50(1)	5.50(7)	4.50(4)	5.50(7)	4.42(3)	5.25(5)	1.58(2)	5.50(7)

4.6. Sensitivity

We also study the sensitivity of involved parameters (${\lambda }_1$, ${\lambda }_2$, ${\lambda }_3$, and ${\lambda }_4$) and report the fluctuations in the health dataset in Figure 6.

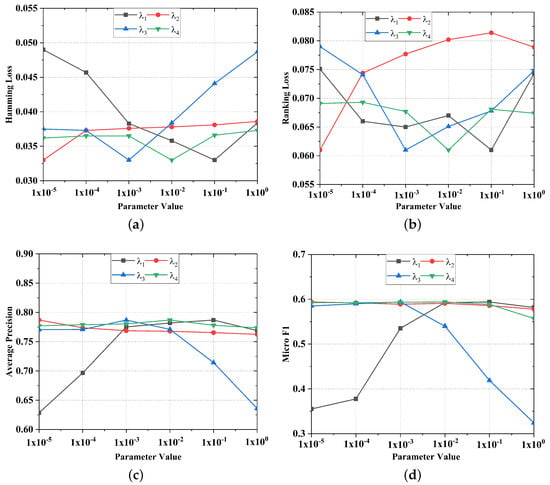
Figure 6. Performance fluctuations of ${\lambda }_1$, ${\lambda }_2$, ${\lambda }_3$, and ${\lambda }_4$ on the health dataset with 20% noisy features and missing labels on metric (a) Hamming Loss, (b) Ranking Loss, (c) Average Precision, and (d) Micro F1.

The larger ${\lambda }_1$ is, the higher the significance of potential representation is, and the smaller ${\lambda }_2$ and ${\lambda }_3$ are, the lower the complexity of the model on the feature side and label side. The larger ${\lambda }_1$ is, the smaller ${\lambda }_2$ and ${\lambda }_3$ are, and the more satisfactory the Average Precision, Hamming Loss, Micro F1, and Ranking Loss are. However, the results can deteriorate if ${\lambda }_3$ is too small, which means the latent labels are less important than latent features. A larger ${\lambda }_4$ means higher importance of the label manifold. The contribution of the label manifold is smaller than the latent feature and latent label, yet it is larger than the model parameters. Similar phenomena also apply to other datasets. Consequently, we recommend the settings of parameters ${\lambda }_1$, ${\lambda }_2$, ${\lambda }_3$, and ${\lambda }_4$ in the order of ${\lambda }_1⩾{\lambda }_4⩾{\lambda }_3⩾{\lambda }_2$.

5. Discussion

This section discusses the robustness of RGLC. The experimental results on benchmarks indicate that RGLC gains the best performance on average across different domains. This means RGLC is competent for multi-label classification. The ablation study examines the functionality of included modules (i.e., latent features, latent labels, global label correlations and local label correlation). It reveals that all modules contribute to the performance improvement, and local label correlation is more conducive than global label correlation. Such a conclusion coincides with perception, as global label correlation is more challenging than local label correlation when data are automatically collected. In real applications, the data collection is inevitably affected by noise and missing. The degenerations of RGLC on three large-scale datasets are negligible for metrics Hamming Loss, Ranking Loss, Coverage, and Average Precision. It implies the availability for uncontrolled cases demonstrating model robustness. The convergence analysis implies that the objective values of RGLC converge in limited rounds. Nevertheless, the computational complexity is not very satisfying, which means the computation in each iteration is considerable. Partial reasons stem from the optimization on a large number of intermediate matrix (A, P, Q, R, E, W, U, V, Z). Future work should focus on the acceleration of RGLC.

6. Conclusions

This paper formulated a robust multi-label classification method RGLC by exploiting enhanced global and local label correlations. Unlike the existing multi-label approaches, which realize robustness by either exploiting label correlations or reconstructing data representation, we tackle it simultaneously by learning global label correlations and local label correlations from the low-rank latent space. We strengthen the reliability of global label correlations and local label correlations by combining subspace learning and manifold regularization. Extensive studies on multiple domains demonstrate the robust performance of RGLC over a collection of state-of-the-art multi-label algorithms. We further demonstrate the robustness of RGLC in the presence of noisy features and missing labels, which is more realistic in multi-label data collection. In the future, we intend to validate whether RGLC shows robustness for more categories of noisy features and missing labels.