A Multi-View Ensemble Width-Depth Neural Network for Short-Term Wind Power Forecasting
Abstract
:1. Introduction
- For the SWPF task, the existing machine learning methods rarely consider the compromise between prediction accuracy and computation cost. Although BLS [24] has attracted considerable attention for its fast training speed and incremental learning algorithm, the prediction performance of BLS is also limited. Because BLS has problems such as the randomness of its parameter settings [26] and its sensitivity to the number of enhanced nodes, vulnerability to noise, and lack of uncertainty expression ability. Furthermore, although various deep learning models can achieve promising performance, computation costs are high.
- Most hybrid machine learning methods rarely consider how to establish a multi-view learning mechanism, which may degenerate the predictive accuracy. Although researchers [15,30,31] have introduced decomposition in single models, the models cannot comprehensively learn original data characteristics, so that the robustness of the models is limited.
- The attention mechanism is integrated into CNN [32] and GRU [33] for obtaining stable performance and providing feature selection, respectively. However, this technology is rarely considered for adjusting network structures while applying to different regression tasks, which may limit the improvement of model performance on other data sets.
- Most existing models seldom consider how to effectively and stably connect two distinctly different models. For instance, a fully connected neural network is used to connect two different models in [35], which may cause gradient disappearing or exploding while connecting two much different models.
- A novel width-depth integration model with a global view and a local view is introduced for short-term wind power forecasting. Different from other multi-view models, our model focuses on improving model performance and reducing the computational cost of the global view learning subnetwork (deBLS) as much as possible.
- The deBLS model is developed by rationally replacing the feature nodes with the multiple encoder nodes, which can improve the learning ability of BLS. Furthermore, the deBLS introduced an attention mechanism of adjusting the enhancement nodes to achieve higher prediction accuracy.
- An effective feature fusion model FDDM is proposed for rationally combining the deBLS and CEEMDAN-DBN, which can promise optimal predictive performance.
2. The Proposed MVEW-DNN
2.1. Local View Subnetwork
2.1.1. Empirical Mode Decomposition with Adaptive Noise (CEEMDAN)
- Step 1
- Add Gaussian white noise to to get a new signal , . Perform EMD on the new signal to get the :
- Step 2
- Average to get , as show in Formula (2). Then, calculate the residual after removing :
- Step 3
- Add Gaussian white noise to to get a new signal and perform EMD on the new signal to get the . Then, and residual can be obtained:
- Step 4
- The above steps are repeated until the obtained residual signal is a monotonic function and the decomposition signal cannot be continued. At this time, the number of intrinsic mode function is . Finally, the original signal is decomposed into
2.1.2. Deep Belief Network (DBN)
2.2. Global View
- Step 1
- By feature mapping, the original data is mapped into nodes , as shown in Formula (7). Here, is a linear transform. Then, by increasing the depth, a three-layer sparse encoder is used to perform feature extraction on nodes to obtain .
- Step 2
- By enhancing and transforming with , the enhancement nodes can be obtained as
| Algorithm 1: Attention Mechanism Algorithm. |
| // Our attention mechanism Algorithm is located on lines 11 to 13 Original data is divided into training set and testing set. The training set consists of train-x and train-y, the testing set consists of test-x and test-y. Input: train-x, train-y, test-x Output: Process: while 1
|
- Step 3
- Calculate the weight matrix . The predictive result can be expressed as . Furthermore, during the training phase, the actual value is known, and therefore, the weight matrix can be calculated as shown in Formula (9), where is the pseudo-inverse of :
2.3. FDDM
| Algorithm 2: FDDM Algorithm. |
| : Cross-validation fold : The length of the test set (the number of output nodes) : Fusion weight of deBLS : Prediction validation data (Real validation data) of deBLS : Prediction test data of deBLS : Fusion weight of DBN : Prediction validation data (Real validation data) of DBN : Prediction test data of DBN : Correlation test threshold (11) (12) Process:
|
2.4. Evaluation Criteria
3. Results and Discussion
3.1. Data Description and Experiment Settings
3.1.1. Data Description
3.1.2. Experiment Settings
3.2. Models
- Autoregressive Integrated Moving Average (ARIMA) [49] is a seasonal model expressed as . Here, refers to the number of periods in each season, and , D, and Q refer to autoregressive, differencing, and moving average terms for the seasonal part of the ARIMA model, respectively.
- Random Vector Functional Link (RVFL) Network [50] is a multilayer perceptron (MLP). Its input and output are directly linked; only the output weights are selected as adaptive parameters. However, the remaining parameters are set to random values that are independently preselected. RVFL can also obtain promising prediction performance on SWPF tasks.
- MOGWO-ELM [51] can provide promising SWPF by integrating the variational mode decomposition (VMD), the extreme learning machine model, the error factor, and a nonlinear ensemble method.
- IVMD-SE-MCC-LSTM [52] is composed of the improved variational mode decomposition (IVMD), sample entropy (SE), the maximum correntropy criterion (MCC), and long short-term memory (LSTM) neural network. Here, the parameter K of the IVMD is determined by the MCC; the decomposed subseries is reconstructed by SE to improve the prediction efficiency. Then, the MCC is also utilized to replace the mean square error in the classic LSTM network.
- Multi-view Neural Network Ensemble [41] is an ensemble of Radial Basis Function Neural Networks (RBFNN). In this ensemble neural network, a long short-term memory network (LSTM) and a multi-resolution wavelet transform are first used to extract the features for training. Then, the extracted feature data is input into multiple RBFNN networks for prediction. The output layer of the Multi-view Neural Network Ensemble is a local generalization error model, which assigns the corresponding weights to the output of multiple RBFNN networks. Finally, these output results of RBFNN are weighted and summed to provide the final predictive results.
3.3. Results
3.4. Ablation Investigations of MVEW-DNN
3.4.1. Effect of the Local View Learning Subnetwork
3.4.2. Effect of the Global Network
3.4.3. Effect of FDDM
3.5. Parameter Selection Experiments
3.6. Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| SWPF | Short-term wind power forecasting |
| CEEMDAN | Complete ensemble empirical mode decomposition with adaptive noise |
| BLS-AEN | BLS network with Addition Enhancement Nodes |
| BLS-A | The BLS network with Attention Mechanism |
| deBLS | Deep encoder board learning system |
| MVEW-DNN | Multi-view ensemble-based width-depth neural network |
| Variables | |
| The original wind power data | |
| The th decomposition in CEEMDAN | |
| The randomly generated weight matrix | |
| The randomly generated bias matrix | |
| The feature nodes | |
| The feature nodes group | |
| The enhancement nodes | |
| The enhancement nodes group | |
| The output of our proposed model | |
| The fusion weight of deBLS | |
| The fusion weight of DBN | |
| Indices | |
| k | The IMF index |
| n | The index of the feature nodes |
| m | The index of the enhancement nodes |
| The signal-to-noise ratio | |
| The adjusting weights in attention mechanism algorithm | |
| The regularization parameter for sparse regularization | |
| The shrinkage parameter in deBLS | |
| The correlation test threshold | |
References
- Hong, T.; Pinson, P.; Wang, Y.; Weron, R.; Yang, D.; Zareipour, H. Energy forecasting: A review and outlook. IEEE Open Access J. Power Energy 2020, 7, 376–388. [Google Scholar] [CrossRef]
- Singh, U.; Rizwan, M. A Systematic Review on Selected Applications and Approaches of Wind Energy Forecasting and Integration. J. Inst. Eng. Ser. B 2021, 102, 1061–1078. [Google Scholar] [CrossRef]
- Kerem, A.; Saygin, A.; Rahmani, R. A green energy research: Forecasting of wind power for a cleaner environment using robust hybrid metaheuristic model. Environ. Sci. Pollut. Res. 2021. [Google Scholar] [CrossRef]
- Liu, H.; Li, Y.; Duan, Z.; Chen, C. A review on multi-objective optimization framework in wind energy forecasting techniques and applications. Energy Convers. Manag. 2020, 224, 113324. [Google Scholar] [CrossRef]
- Maciejowska, K.; Nitka, W.; Weron, T. Enhancing load, wind and solar generation for day-ahead forecasting of electricity prices. Energy Econ. 2021, 99, 105273. [Google Scholar] [CrossRef]
- Rodriguez, H.; Flores, J.J.; Morales, L.A.; Lara, C.; Guerra, A.; Manjarrez, G. Forecasting from incomplete and chaotic wind speed data. Soft Comput. 2019, 23, 10119–10127. [Google Scholar] [CrossRef]
- Yang, B.; Zhong, L.; Wang, J.; Shu, H.; Zhang, X.; Yu, T.; Sun, L. State-of-the-art one-stop handbook on wind forecasting technologies: An overview of classifications, methodologies, and analysis. J. Clean. Prod. 2021, 283, 124628. [Google Scholar] [CrossRef]
- Foley, A.M.; Leahy, P.G.; Marvuglia, A.; McKeogh, E.J. Current methods and advances in forecasting of wind power generation. Renew. Energy 2012, 37, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Zjavka, L.; Mišák, S. Direct wind power forecasting using a polynomial decomposition of the general differential equation. IEEE Trans. Sustain. Energy 2018, 9, 1529–1539. [Google Scholar] [CrossRef]
- Jacondino, W.D.; da Silva Nascimento, A.L.; Calvetti, L.; Fisch, G.; Beneti, C.A.; da Paz, S.R. Hourly day-ahead wind power forecasting at two wind farms in northeast brazil using WRF model. Energy 2021, 230, 120841. [Google Scholar] [CrossRef]
- Zhang, F.; Li, P.C.; Gao, L.; Liu, Y.Q.; Ren, X.Y. Application of autoregressive dynamic adaptive (ARDA) model in real-time wind power forecasting. Renew. Energy 2021, 169, 129–143. [Google Scholar] [CrossRef]
- Xie, W.; Zhang, P.; Chen, R.; Zhou, Z. A nonparametric Bayesian framework for short-term wind power probabilistic forecast. IEEE Trans. Power Syst. 2018, 34, 371–379. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, C. Application of ARMA model in ultra-short term prediction of wind power. In Proceedings of the 2013 International Conference on Computer Sciences and Applications IEEE, Washington, DC, USA, 14–15 December 2013; pp. 361–364. [Google Scholar]
- Jia, M.; Shen, C.; Wang, Z. A distributed incremental update scheme for probability distribution of wind power forecast error. Int. J. Electr. Power Energy Syst. 2020, 121, 106151. [Google Scholar] [CrossRef]
- Zhang, C.; Peng, T.; Nazir, M.S. A novel hybrid approach based on variational heteroscedastic Gaussian process regression for multi-step ahead wind speed forecasting. Int. J. Electr. Power Energy Syst. 2022, 136, 107717. [Google Scholar] [CrossRef]
- He, Y.; Zhang, W. Probability density forecasting of wind power based on multi-core parallel quantile regression neural network. Knowl.-Based Syst. 2020, 209, 106431. [Google Scholar] [CrossRef]
- Pearre, N.S.; Swan, L.G. Statistical approach for improved wind speed forecasting for wind power production. Sustain. Energy Technol. Assess. 2018, 27, 180–191. [Google Scholar]
- Hu, T.; Wu, W.; Guo, Q.; Sun, H.; Shi, L.; Shen, X. Very short-term spatial and temporal wind power forecasting: A deep learning approach. CSEE J. Power Energy Syst. 2019, 6, 434–443. [Google Scholar]
- Zendehboudi, A.; Baseer, M.A.; Saidur, R. Application of support vector machine models for forecasting solar and wind energy resources: A review. J. Clean. Prod. 2018, 199, 272–285. [Google Scholar] [CrossRef]
- Li, R.; Ke, Y.Q.; Zhang, X.Q. Wind power forecasting based on time series and SVM. Electr. Power 2012, 45, 64–68. [Google Scholar]
- Sun, W.; Wang, Y. Short-term wind speed forecasting based on fast ensemble empirical mode decomposition, phase space reconstruction, sample entropy and improved back-propagation neural network. Energy Convers. Manag. 2018, 157, 1–12. [Google Scholar] [CrossRef]
- Hu, H.; Wang, L.; Lv, S.X. Forecasting energy consumption and wind power generation using deep echo state network. Renew. Energy 2020, 154, 598–613. [Google Scholar] [CrossRef]
- Shetty, R.P.; Sathyabhama, A.; Pai, P.S. An efficient online sequential extreme learning machine model based on feature selection and parameter optimization using cuckoo search algorithm for multi-step wind speed forecasting. Soft Comput. 2021, 25, 1277–1295. [Google Scholar] [CrossRef]
- Chen, C.P.; Liu, Z. Broad learning system: An effective and efficient incremental learning system without the need for deep architecture. IEEE Trans. Neural Netw. Learn. Syst. 2017, 29, 10–24. [Google Scholar] [CrossRef] [PubMed]
- Hu, Q.; Zhang, R.; Zhou, Y. Transfer learning for short-term wind speed prediction with deep neural networks. Renew Energy 2016, 85, 83–95. [Google Scholar] [CrossRef]
- Xu, L.; Chen, C.P.; Han, R. Sparse Bayesian broad learning system for probabilistic estimation of prediction. IEEE Access 2020, 8, 56267–56280. [Google Scholar] [CrossRef]
- Yan, J.; Liu, Y.; Han, S.; Wang, Y.; Feng, S. Reviews on uncertainty analysis of wind power forecasting. Renew. Sustain. Energy Rev. 2015, 52, 1322–1330. [Google Scholar] [CrossRef]
- Jiajun, H.; Chuanjin, Y.; Yongle, L.; Huoyue, X. Ultra-short term wind prediction with wavelet transform, deep belief network and ensemble learning. Energy Convers. Manag. 2020, 205, 112418. [Google Scholar] [CrossRef]
- Chen, C.R.; Ouedraogo, F.B.; Chang, Y.M.; Larasati, D.A.; Tan, S.W. Hour-Ahead Photovoltaic Output Forecasting Using Wavelet-ANFIS. Mathematics 2021, 9, 2438. [Google Scholar] [CrossRef]
- Wang, G.; Wang, X.; Wang, Z.; Ma, C.; Song, Z. A VMD–CISSA–LSSVM Based Electricity Load Forecasting Model. Mathematics 2022, 10, 28. [Google Scholar]
- Devi, A.S.; Maragatham, G.; Boopathi, K.; Rangaraj, A.G. Hourly day-ahead wind power forecasting with the EEMD-CSO-LSTM-EFG deep learning technique. Soft Comput. 2020, 24, 12391–12411. [Google Scholar] [CrossRef]
- Zhao, X.; Bai, M.; Yang, X.; Liu, J.; Yu, D.; Chang, J. Short-term probabilistic predictions of wind multi-parameter based on one-dimensional convolutional neural network with attention mechanism and multivariate copula distribution estimation. Energy 2021, 234, 121306. [Google Scholar] [CrossRef]
- Niu, Z.; Yu, Z.; Tang, W.; Wu, Q.; Reformat, M. Wind power forecasting using attention-based gated recurrent unit network. Energy 2020, 196, 117081. [Google Scholar] [CrossRef]
- Shahid, F.; Zameer, A.; Muneeb, M. A novel genetic LSTM model for wind power forecast. Energy 2021, 223, 120069. [Google Scholar] [CrossRef]
- Khan, N.; Ullah, F.U.M.; Haq, I.U.; Khan, S.U.; Lee, M.Y.; Baik, S.W. AB-Net: A Novel Deep Learning Assisted Framework for Renewable Energy Generation Forecasting. Mathematics 2021, 9, 2456. [Google Scholar] [CrossRef]
- Duan, J.; Wang, P.; Ma, W.; Fang, S.; Hou, Z. A novel hybrid model based on nonlinear weighted combination for short-term wind power forecasting. Int. J. Electr. Power Energy Syst. 2022, 134, 107452. [Google Scholar] [CrossRef]
- Wu, Y.K.; Su, P.E.; Hong, J.S. Stratification-based wind power forecasting in a high-penetration wind power system using a hybrid model. IEEE Trans. Ind. Appl. 2016, 52, 2016–2030. [Google Scholar] [CrossRef]
- Ogliari, E.; Guilizzoni, M.; Giglio, A.; Pretto, S. Wind power 24-h ahead forecast by an artificial neural network and an hybrid model: Comparison of the predictive performance. Renew. Energy 2021, 178, 1466–1474. [Google Scholar] [CrossRef]
- Hong, Y.Y.; Rioflorido, C.L.P.P. A hybrid deep learning-based neural network for 24-h ahead wind power forecasting. Appl. Energy 2019, 250, 530–539. [Google Scholar] [CrossRef]
- Ribeiro, M.H.D.M.; da Silva, R.G.; Moreno, S.R.; Mariani, V.C.; dos Santos Coelho, L. Efficient bootstrap stacking ensemble learning model applied to wind power generation forecasting. Int. J. Electr. Power Energy Syst. 2022, 136, 107712. [Google Scholar] [CrossRef]
- Lai, C.S.; Yang, Y.; Pan, K.; Zhang, J.; Yuan, H.; Ng, W.W.; Gao, Y.; Zhao, Z.; Wang, T.; Shahidehpour, M.; et al. Multi-view neural network ensemble for short and mid-term load forecasting. IEEE Trans. Power Syst. 2020, 36, 2992–3003. [Google Scholar] [CrossRef]
- Nguyen, L.H.; Pan, Z.; Openiyi, O.; Abu-gellban, H.; Moghadasi, M.; Jin, F. Self-boosted time-series forecasting with multi-task and multi-view learning. arXiv 2019, arXiv:1909.08181. [Google Scholar]
- Zhong, C.; Lai, C.S.; Ng, W.W.; Tao, Y.; Wang, T.; Lai, L.L. Multi-view deep forecasting for hourly solar irradiance with error correction. Sol. Energy 2021, 228, 308–316. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A Complete Ensemble Empirical Mode Decomposition with Adaptive Noise. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 4144–4147. [Google Scholar]
- Flores, J.H.F.; Engel, P.M.; Pinto, R.C. Autocorrelation and Partial Autocorrelation Functions to Improve Neural Networks Models on Univariate Time Series Forecasting. In Proceedings of the The 2012 International Joint Conference on Neural Networks (IJCNN) IEEE, San Diego, CA, USA, 10–15 June 2012; pp. 1–8. [Google Scholar]
- Global Energy Forecasting Competition 2012—Wind Forecasting. Available online: https://www.kaggle.com/c/GEF2012-wind-forecasting/data (accessed on 14 October 2021).
- Kisvari, A.; Lin, Z.; Liu, X. Wind power forecasting—A data-driven method along with gated recurrent neural network. Renew. Energy 2021, 163, 1895–1909. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhu, C.; Song, C.; Li, Y.; Chen, X.; Yong, B. Improvement of reliability and wind power generation based on wind turbine real-time condition assessment. Int. J. Electr. Power Energy Syst. 2019, 113, 344–354. [Google Scholar] [CrossRef]
- Putz, D.; Gumhalter, M.; Auer, H. A novel approach to multi-horizon wind power forecasting based on deep neural architecture. Renew. Energy 2021, 178, 494–505. [Google Scholar] [CrossRef]
- Ren, Y.; Suganthan, P.N.; Srikanth, N.; Amaratunga, G. Random vector functional link network for short-term electricity load demand forecasting. Inf. Sci. 2016, 367, 1078–1093. [Google Scholar] [CrossRef]
- Hao, Y.; Tian, C. A novel two-stage forecasting model based on error factor and ensemble method for multi-step wind power forecasting. Appl. Energy 2019, 238, 368–383. [Google Scholar] [CrossRef]
- Duan, J.; Wang, P.; Ma, W. Short-term wind power forecasting using the hybrid model of improved variational mode decomposition and Correntropy Long Short-term memory neural network. Energy 2021, 214, 118980. [Google Scholar] [CrossRef]

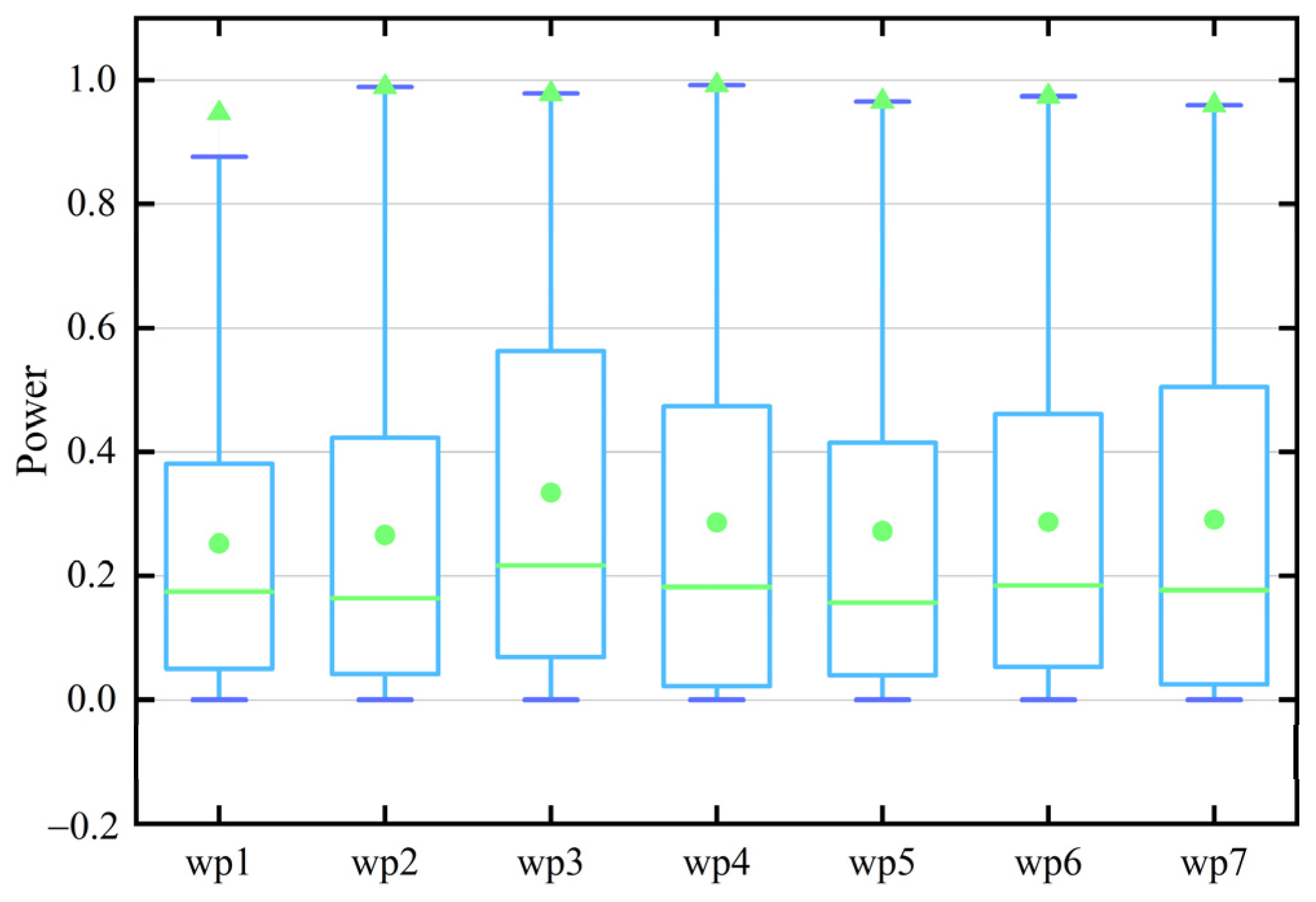
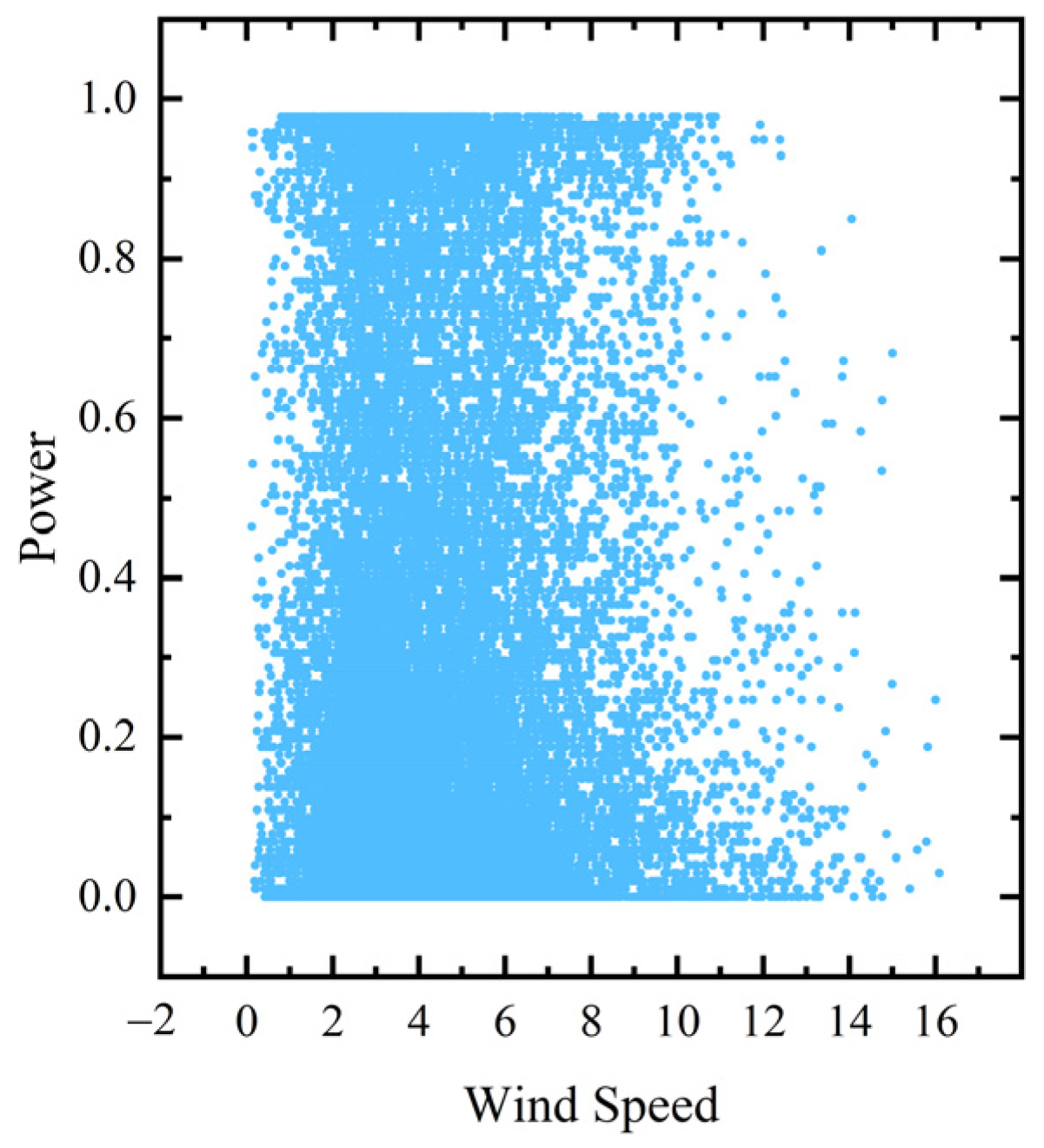
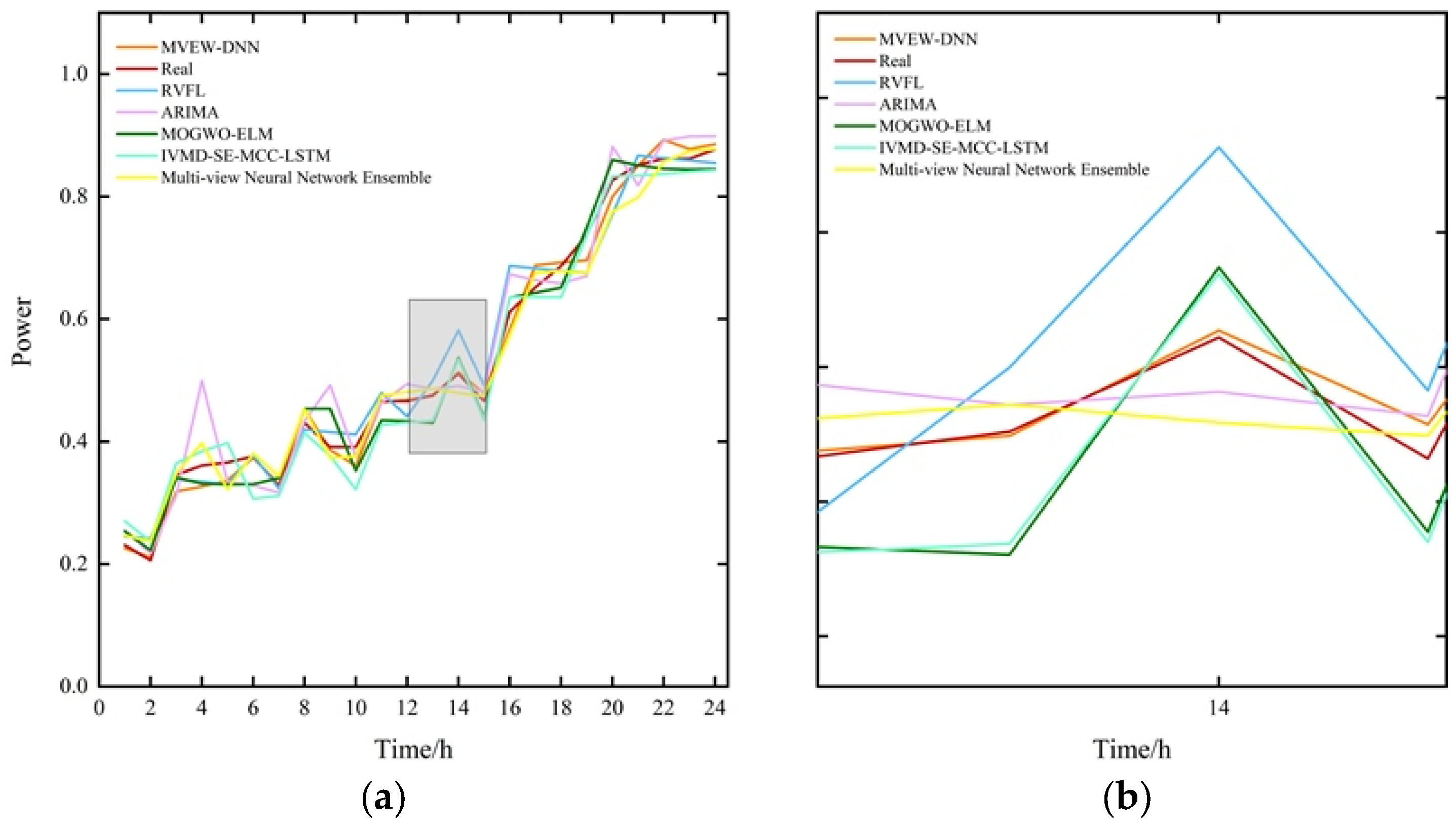

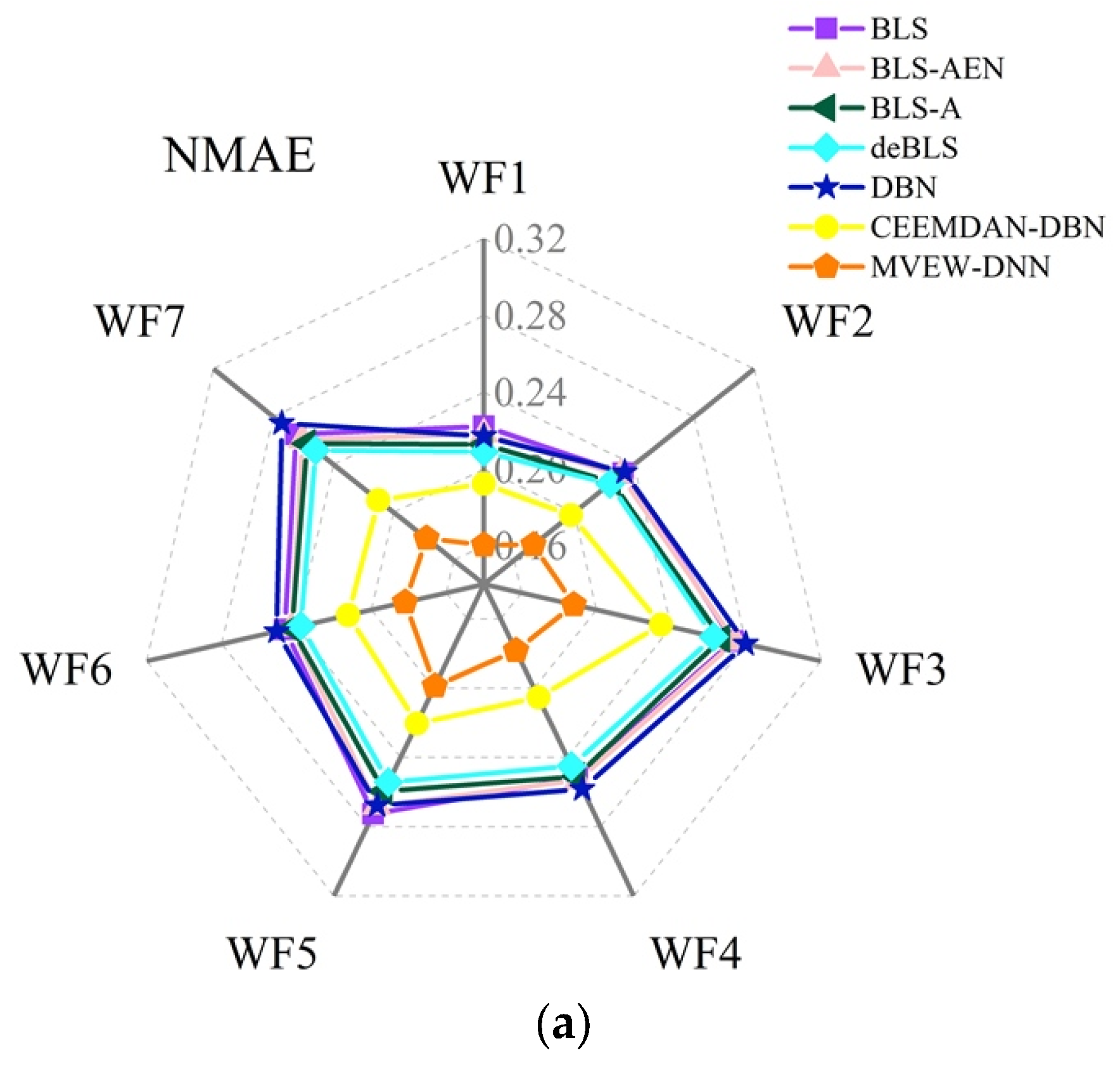

| Data Set | Metrics | ARIMA | RVFL | MOGWO-ELM | IVMD-SE-MCC-LSTM | Multi-View Neural Network Ensemble | MVEW-DNN |
|---|---|---|---|---|---|---|---|
| WF1 | NRMSE | 0.4477 | 0.3417 | 0.2534 | 0.2547 | 0.2758 | 0.2103 |
| NMAE | 0.3285 | 0.2505 | 0.2042 | 0.2058 | 0.1916 | 0.1603 | |
| TIC | 0.5878 | 0.651 | 0.4118 | 0.4131 | 0.6618 | 0.3381 | |
| WF2 | NRMSE | 0.4744 | 0.3494 | 0.2761 | 0.2766 | 0.2944 | 0.2236 |
| NMAE | 0.3458 | 0.2575 | 0.2306 | 0.2275 | 0.241 | 0.173 | |
| TIC | 0.571 | 0.6543 | 0.4219 | 0.4253 | 0.4145 | 0.3281 | |
| WF3 | NRMSE | 0.5442 | 0.4566 | 0.3188 | 0.3119 | 0.2839 | 0.2378 |
| NMAE | 0.4178 | 0.3373 | 0.2744 | 0.268 | 0.2386 | 0.1879 | |
| TIC | 0.5503 | 0.7596 | 0.398 | 0.3865 | 0.3714 | 0.2784 | |
| WF4 | NRMSE | 0.5008 | 0.4023 | 0.2992 | 0.2925 | 0.2664 | 0.2264 |
| NMAE | 0.3686 | 0.2935 | 0.2505 | 0.2465 | 0.1859 | 0.1784 | |
| TIC | 0.5586 | 0.7166 | 0.4217 | 0.4035 | 0.6372 | 0.2954 | |
| WF5 | NRMSE | 0.4978 | 0.425 | 0.3208 | 0.3221 | 0.3863 | 0.2502 |
| NMAE | 0.36 | 0.308 | 0.2591 | 0.2603 | 0.2738 | 0.1988 | |
| TIC | 0.5838 | 0.7119 | 0.453 | 0.4535 | 0.7101 | 0.3113 | |
| WF6 | NRMSE | 0.4804 | 0.4057 | 0.2915 | 0.2882 | 0.302 | 0.2328 |
| NMAE | 0.356 | 0.2936 | 0.2414 | 0.2349 | 0.208 | 0.1821 | |
| TIC | 0.5504 | 0.7219 | 0.4078 | 0.4092 | 0.6483 | 0.2977 | |
| WF7 | NRMSE | 0.5041 | 0.4058 | 0.3025 | 0.2973 | 0.3872 | 0.5041 |
| NMAE | 0.368 | 0.2953 | 0.2599 | 0.2541 | 0.2367 | 0.368 | |
| TIC | 0.5492 | 0.7502 | 0.4218 | 0.4108 | 0.6439 | 0.5492 |
| Data Set | Metrics | CEEMDAN-DBN | DBN |
|---|---|---|---|
| WF1 | NRMSE | 0.2519 | 0.2702 |
| NMAE | 0.1925 | 0.2172 | |
| TIC | 0.3388 | 0.4146 | |
| WF2 | NRMSE | 0.2454 | 0.2778 |
| NMAE | 0.1979 | 0.2338 | |
| TIC | 0.3595 | 0.4141 | |
| WF3 | NRMSE | 0.2845 | 0.3278 |
| NMAE | 0.2346 | 0.2798 | |
| TIC | 0.3275 | 0.4021 | |
| WF4 | NRMSE | 0.2555 | 0.3024 |
| NMAE | 0.2054 | 0.2583 | |
| TIC | 0.3364 | 0.4077 | |
| WF5 | NRMSE | 0.2736 | 0.3327 |
| NMAE | 0.2204 | 0.2678 | |
| TIC | 0.3592 | 0.4561 | |
| WF6 | NRMSE | 0.2533 | 0.3002 |
| NMAE | 0.2124 | 0.2506 | |
| TIC | 0.3155 | 0.4049 | |
| WF7 | NRMSE | 0.2512 | 0.3178 |
| NMAE | 0.2102 | 0.2745 | |
| TIC | 0.3296 | 0.4195 |
| Data Set | Metrics | BLS | BLS-AEN | BLS-A | deBLS |
|---|---|---|---|---|---|
| WF1 | NRMSE | 0.2776 | 0.2713 | 0.2628 | 0.2548 |
| NMAE | 0.2223 | 0.2184 | 0.213 | 0.209 | |
| TIC | 0.4082 | 0.4128 | 0.3998 | 0.3783 | |
| WF2 | NRMSE | 0.2817 | 0.2783 | 0.2759 | 0.2757 |
| NMAE | 0.2329 | 0.2313 | 0.2255 | 0.2241 | |
| TIC | 0.418 | 0.4219 | 0.4257 | 0.4362 | |
| WF3 | NRMSE | 0.3238 | 0.3199 | 0.3127 | 0.3126 |
| NMAE | 0.2731 | 0.2742 | 0.2669 | 0.2628 | |
| TIC | 0.3863 | 0.3975 | 0.3791 | 0.3879 | |
| WF4 | NRMSE | 0.3074 | 0.3028 | 0.2999 | 0.2956 |
| NMAE | 0.2521 | 0.2531 | 0.251 | 0.245 | |
| TIC | 0.4174 | 0.4215 | 0.4206 | 0.4053 | |
| WF5 | NRMSE | 0.339 | 0.3321 | 0.3205 | 0.3179 |
| NMAE | 0.2727 | 0.2683 | 0.2597 | 0.2543 | |
| TIC | 0.4451 | 0.4526 | 0.4508 | 0.4443 | |
| WF6 | NRMSE | 0.3052 | 0.2944 | 0.2925 | 0.2892 |
| NMAE | 0.2462 | 0.2428 | 0.2424 | 0.2376 | |
| TIC | 0.408 | 0.4117 | 0.4071 | 0.3917 | |
| WF7 | NRMSE | 0.3203 | 0.3054 | 0.3023 | 0.2997 |
| NMAE | 0.2652 | 0.2608 | 0.2576 | 0.2521 | |
| TIC | 0.4181 | 0.4247 | 0.4016 | 0.4085 |
| Data Set | Metrics | CEEMDAN-DBN | deBLS | MVEW-DNN |
|---|---|---|---|---|
| WF1 | NRMSE | 0.2519 | 0.2548 | 0.2103 |
| NMAE | 0.1925 | 0.209 | 0.1603 | |
| TIC | 0.3388 | 0.3783 | 0.3381 | |
| WF2 | NRMSE | 0.2454 | 0.2757 | 0.2236 |
| NMAE | 0.1979 | 0.2241 | 0.173 | |
| TIC | 0.3595 | 0.4362 | 0.3281 | |
| WF3 | NRMSE | 0.2845 | 0.3126 | 0.2378 |
| NMAE | 0.2346 | 0.2628 | 0.1879 | |
| TIC | 0.3275 | 0.3879 | 0.2784 | |
| WF4 | NRMSE | 0.2555 | 0.2956 | 0.2264 |
| NMAE | 0.2054 | 0.245 | 0.1784 | |
| TIC | 0.3364 | 0.4053 | 0.2954 | |
| WF5 | NRMSE | 0.2736 | 0.3179 | 0.2502 |
| NMAE | 0.2204 | 0.2543 | 0.1988 | |
| TIC | 0.3592 | 0.4443 | 0.3113 | |
| WF6 | NRMSE | 0.2533 | 0.2892 | 0.2328 |
| NMAE | 0.2124 | 0.2376 | 0.1821 | |
| TIC | 0.3155 | 0.3917 | 0.2977 | |
| WF7 | NRMSE | 0.2512 | 0.2997 | 0.2271 |
| NMAE | 0.2102 | 0.2521 | 0.1782 | |
| TIC | 0.3296 | 0.4085 | 0.2926 |
| ω | NRMSE | NMAE | TIC |
|---|---|---|---|
| 0.5 | 0.3275 | 0.2794 | 0.3881 |
| 0.6 | 0.3268 | 0.2692 | 0.3857 |
| 0.7 | 0.3263 | 0.2792 | 0.3835 |
| 0.8 | 0.3257 | 0.2891 | 0.3814 |
| Wind Farm | deBLS (s) | CEEMDAN-DBN (s) | FDDM (s) | MVEW-DNN (s) |
|---|---|---|---|---|
| WF1 | 0.654 | 142.582 | 0.984 | 144.22 |
| WF2 | 0.833 | 135.888 | 0.994 | 137.715 |
| WF3 | 0.438 | 149.442 | 0.643 | 150.523 |
| WF4 | 0.394 | 160.626 | 0.717 | 161.737 |
| WF5 | 0.423 | 188.86 | 0.815 | 190.098 |
| WF6 | 0.417 | 163.324 | 0.893 | 164.634 |
| WF7 | 0.433 | 172.055 | 0.927 | 173.415 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wan, J.; Huang, J.; Liao, Z.; Li, C.; Liu, P.X. A Multi-View Ensemble Width-Depth Neural Network for Short-Term Wind Power Forecasting. Mathematics 2022, 10, 1824. https://doi.org/10.3390/math10111824
Wan J, Huang J, Liao Z, Li C, Liu PX. A Multi-View Ensemble Width-Depth Neural Network for Short-Term Wind Power Forecasting. Mathematics. 2022; 10(11):1824. https://doi.org/10.3390/math10111824
Chicago/Turabian StyleWan, Jing, Jiehui Huang, Zhiyuan Liao, Chunquan Li, and Peter X. Liu. 2022. "A Multi-View Ensemble Width-Depth Neural Network for Short-Term Wind Power Forecasting" Mathematics 10, no. 11: 1824. https://doi.org/10.3390/math10111824
APA StyleWan, J., Huang, J., Liao, Z., Li, C., & Liu, P. X. (2022). A Multi-View Ensemble Width-Depth Neural Network for Short-Term Wind Power Forecasting. Mathematics, 10(11), 1824. https://doi.org/10.3390/math10111824






