Capacity Investment and Process Efficiency at Flexible Firms
Abstract
:1. Introduction
2. Literature Review
3. The Model
4. The Analysis
4.1. Best-Response Output under Capacity Constraint
- D1.
- is the output by firm j, the best response to which is for firm i not to produce.
- D2.
- , is the output by firm i when firm j does not produce.
- D3.
- satisfies , so that is the output by firm j, the best response to which is for firm i to produce x units.
- (1)
- ;
- (2)
- :
- a.
- b.
- where , , and are as defined in D1–D3, respectively.
- (1)
- ;
- (2)
- :
- (1)
- , ;
- (2)
- :where , , , and , where , for , and , and, moreover:
- (a)
- , if ;
- (b)
- , if .
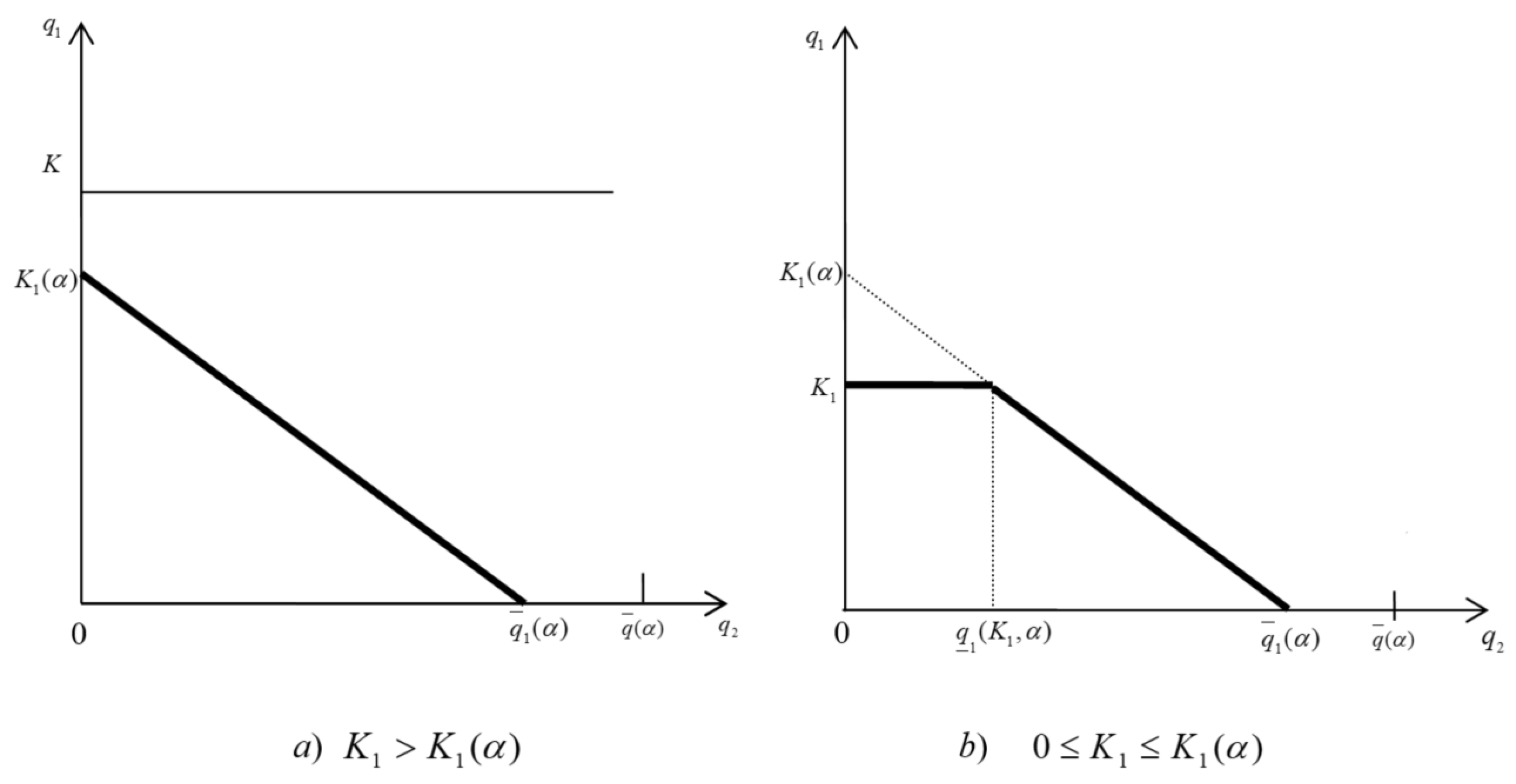
4.2. Capacity Investment
- (1)
- When , ;
- (2)
- When ≤, .
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Proof of Lemma 1
Appendix B. Proof of Lemma 2
- Case 1:
- for , so that decreases and attains optimum at . This is Part (a).
- Case 2:
- : the value of is influenced by .If , then so that decreases and , regardless of .If , then , and we check if the capacity is binding.decreases in and . ; and it strictly decreases in . by definition D2, so that if and otherwise. We consider these two situations separately.
- Case 2.1:
- , .Since decreases in , and capacity is unbinding.By concavity, .
- Case 2.2:
- , .
Appendix C. Proof of Theorem 1
- Case 1:
- Case 2:
Appendix D. Proof of Proposition 2
References
- Siagian, H.; Tarigan, Z.; Jie, F. Supply chain integration enables resilience, flexibility, and innovation to improve business performance in COVID-19 era. Sustainability 2021, 13, 4669. [Google Scholar] [CrossRef]
- Gerwin, D. Manufacturing flexibility: A strategic perspective. Manag. Sci. 1993, 39, 395–410. [Google Scholar] [CrossRef]
- Fine, C.H.; Freund, R.M. Optimal investment in product-flexible manufacturing capacity. Manag. Sci. 1990, 36, 449–466. [Google Scholar] [CrossRef] [Green Version]
- Van Mieghem, J.A.; Dada, M. Price versus Production Postponement: Capacity and Competition. Manag. Sci. 1999, 45, 1631–1649. [Google Scholar] [CrossRef] [Green Version]
- Netessine, S.; Dobson, G.; Shumsky, R.A. Flexible service capacity: Optimal investment and the impact of demand correlation. Oper. Res. 2002, 50, 375–388. [Google Scholar] [CrossRef] [Green Version]
- Tomlin, B.; Wang, Y. On the value of mix flexibility and dual sourcing in unreliable newsvendor networks. Manuf. Serv. Oper. Manag. 2005, 7, 37–57. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.; Ng, C.T.; Ni, Y. Flexible capacity strategy in an asymmetric oligopoly market with competition and demand uncertainty. Nav. Res. Logist. 2017, 64, 117–138. [Google Scholar] [CrossRef]
- Jordan, W.C.; Graves, S. Principles on the benefits of manufacturing process flexibility. Manag. Sci. 1995, 41, 577–594. [Google Scholar] [CrossRef] [Green Version]
- Graves, S.; Tomlin, B. Process flexibility in supply chains. Manag. Sci. 2003, 49, 907–919. [Google Scholar] [CrossRef] [Green Version]
- Roller, L.; Tombak, M. Strategic Choice of Flexible Production Technologies and Welfare Implications. J. Ind. Econ. 1990, 38, 417–431. [Google Scholar] [CrossRef] [Green Version]
- Roller, L.; Tombak, M. Competition and investment in flexible technologies. Manag. Sci. 1993, 39, 107–114. [Google Scholar] [CrossRef]
- Chod, J.; Rudi, N. Resource Flexibility with Responsive Pricing. Oper. Res. 2005, 53, 532–548. [Google Scholar] [CrossRef] [Green Version]
- Goyal, M.; Netessine, S. Strategic Technology Choice and Capacity Investment under Demand Uncertainty. Manag. Sci. 2007, 55, 192–207. [Google Scholar] [CrossRef] [Green Version]
- Persentili, E.; Alptekin, S.E. Product flexibility in selecting manufacturing planning and control strategy. Int. J. Prod. Res. 2000, 38, 2011–2021. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Webster, S. Product Flexibility Strategy Under Supply and Demand Risk. Manuf. Serv. Oper. Manag. 2021, in press. [Google Scholar]
- Cao, G.; Wang, Z. Product flexibility of competitive manufactures: The effect of debt financing. Ann. Oper. Res. 2021, 307, 53–74. [Google Scholar] [CrossRef]
- Vives, X. Commitment, Flexibility and Market Outcomes. Int. J. Ind. Organ. 1986, 4, 217–229. [Google Scholar] [CrossRef]
- Boyer, M.; Moreaux, M. Capacity Commitment versus Flexibility. J. Econ. Strategy 1997, 6, 347–376. [Google Scholar] [CrossRef]
- Hagspiel, V.; Huisman, K.J.; Kort, P.M. Volume flexibility and capacity investment under demand uncertainty. Int. J. Prod. Econ. 2016, 178, 95–108. [Google Scholar] [CrossRef]
- Ritchken, P.; Wu, Q. Capacity investment, production flexibility, and capital structure. Prod. Oper. Manag. 2021, 30, 4593–4613. [Google Scholar] [CrossRef]
- De Giovanni, D.; Massabò, I. Capacity investment under uncertainty: The effect of volume flexibility. Int. J. Prod. Econ. 2018, 198, 165–176. [Google Scholar] [CrossRef]
- Anupindi, R.; Jiang, L. Capacity Investment under Postponement Strategies, Market Competition, and Demand Uncertainty. Manag. Sci. 2008, 54, 1876–1890. [Google Scholar] [CrossRef]
- Stigler, G. Production and Distribution in the Short Run. J. Political Econ. 1939, 47, 304–327. [Google Scholar] [CrossRef]
- Marschak, T.; Nelson, R. Flexibility, Uncertainty and Economic Theory. Metroeconomica 1962, 14, 42–60. [Google Scholar] [CrossRef]
- Mills, D. Demand Fluctuations and Endogenous Firm Flexibility. J. Ind. Econ. 1984, 33, 55–71. [Google Scholar] [CrossRef]
- Mills, D. Flexibility and Firm Diversity with Demand Fluctuations. Int. J. Ind. Organ. 1986, 4, 302–315. [Google Scholar] [CrossRef]
- Lariviere, M.A. A Note on Probability Distributions with Increasing Generalized Failure Rates. Oper. Res. 2006, 54, 602–604. [Google Scholar] [CrossRef] [Green Version]
- Hossain, M.; Bhatti, M.; Ali, M. An Econometric Analysis of Major Manufacturing Industries. Manag. Audit. J. 2004, 19, 790–795. [Google Scholar] [CrossRef]



| Flexibility | Production Efficiency | |
|---|---|---|
| Monopoly | product flexible: Fine and Freund [3] volume flexible: Van Mieghem and Dada [4] (downside) De Giovanni and Massabo [21] (both upside and downside) | - |
| Duopoly/ Oligopoly | product flexible: Roller and Tombak [10,11] volume flexible: Vives [17] (upside) Anupindi and Jiang [22] (downside) | Stigler [23], Marschak and Nelson [24], Mills [25,26] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Y.; Fan, R.-N. Capacity Investment and Process Efficiency at Flexible Firms. Mathematics 2022, 10, 1692. https://doi.org/10.3390/math10101692
Jiang Y, Fan R-N. Capacity Investment and Process Efficiency at Flexible Firms. Mathematics. 2022; 10(10):1692. https://doi.org/10.3390/math10101692
Chicago/Turabian StyleJiang, Yanmin, and Rui-Na Fan. 2022. "Capacity Investment and Process Efficiency at Flexible Firms" Mathematics 10, no. 10: 1692. https://doi.org/10.3390/math10101692
APA StyleJiang, Y., & Fan, R.-N. (2022). Capacity Investment and Process Efficiency at Flexible Firms. Mathematics, 10(10), 1692. https://doi.org/10.3390/math10101692





