1. Introduction
Linear regression (LR) model utilized in numerous areas of application [
1]: for example, engineering, economics, ecological, social sciences, and medicines, among many others. Hence, linear regression is a potent and flexible technique in order to address regression issues. Thus, the trend of LR model is an extensive topic with important interest for researchers according [
2,
3,
4].
Moreover, according to [
5,
6,
7], the topic related to inventories play a key role because represent around 60% about operational cost for the organizations. Generally, the inventories are classified as following: (1) raw material, (2) work in process, (3) spare parts, and (4) finish good, etc. In addition, the interest related to inventory is due to cost management strategies by organizations [
8,
9,
10,
11]. Based on operation research, the inventories can be used in order to addressed considerable reduction cost. Therefore, the forecast method is imperative in order to determine the quantities with accuracy avoiding minimal error [
12]. In this mode, the literature review explains the use of several methods focused to forecast of the inventories: for example, Linear regression and time series [
13,
14], Neural Networks [
11,
15], Machine Learning [
16], and Bayesian principal component regression model [
17], among others [
10,
18].
Additionally, dimensional analysis (DA) presents extensive interest in engineering [
19,
20]. DA has the potential to model, simplification the scale and dimension of the variable [
21]. Thus, applications of neural networks [
22], Matrix manipulations [
23], physical sciences applications [
24], revolutionary dimensional analysis methods [
25,
26], and statistical theories for dimensional analysis [
27].
Therefore, dimensional analysis (DA) is a proficient tool that involves the interrelationship of the data or arguments under analysis. Much different research on DA is related to the statistical situation [
28,
29,
30,
31]. In this mode, Dovi [
32], reported the improving the statistical accuracy of dimensional analysis correlations. However, this work does not consider the attitude of the decisors.
The literature reveal a substantial interest in dealing with the next crucial gaps:
The vital element is the instability of the prediction method [
33,
34];
Minimize the median squared difference between observed and fitted response [
35];
Verify the efficacy of the algorithm, the greatest robustness, and accuracy in forecast results [
12,
36,
37,
38,
39,
40,
41].
Based on the aforementioned considerations, the concrete contributions of this paper are the following:
We formulate a method to attack the drawbacks related to efficiency, instability, and minimal error.
This study explores the significant application of linear regression model under Dimensional Analysis.
The novelty of the current study also lies in considering the grade of importance of the decision makers or experts involved implied to solve the problem.
Finally, the proposed includes an application of DA to linear regression to deal with an inventory forecast problem.
The remainder of this paper is structured as follows:
Section 2 presents basic concepts. The research methodology is described in
Section 3. A numerical case study is presented in
Section 4.
Section 5 provides the discussions of findings. Finally, the conclusion is given in
Section 6.
2. Basic Concepts
This section introduces the basic concepts used in this document.
2.1. Linear Regression
The linear regression (LR) method used to approximate a pendent variable reported to the values or changes of other variables studied in a linear shape.
Definition 1. Let and be two variables within a random and continued distribution. In this mode, assuming a numerical data set mapped by for , where and . A reasonable form of relation between the response variable called Y and the regressor X is the linear relationship. In this manner, a model can be represented as follows, where of dimension n is a mapping in space , captured by a vector of analysis related to metrics involved, and , which is built by χ and Γ; In this mode, the simple linear regression depicted by means of Equation (1):where χ is the value stand for the value of when , also called the intersection, and Γ is the change in called the slope of the line. 2.2. Dimensional Analysis
The mathematical expresion of DA is depicted by Equation (
2) as follows:
where:
is the numerical argument for ;
is the best numerical datum taken from the data set under analysis;
is the grade of altitude or weight of the decision (expert) within a vector.
In this sense, the parameter for and
Definition 2. In this mode can be introduced the mean for based on the Equation (3). Considering , a numerical data set of that maintains random conditions and continue distribution is created: The solution in terms of the original argument is obtained by substituting :then: Example 1. Assuming a set called , it will receive a vector weight and has been determined to be . Then, applying Equation (5), we will obtain the result for this example: 3. Main Results
In this section, we present the generalized linear regression method under the Dimensional Analysis environment.
3.1. Generalized Linear Regression Method under Dimensional Analysis Environment
This section presents a generalized linear regression method under the Dimensional Analysis environment called (GLR-DA):
Let
A be the mean of
x, and let
depict the ideal value of
x under dimensional analysis. Then:
B represents
y, and
depicts the ideal value of
y under dimensional analysis. Then:
where
is a vector of responses;
is a normally scattered vector of random data obtaining the expected value
, also called the intersection;
is the weight vector corresponding to
x; and
x is the full rank matrix of not random variables.
3.2. Compute the Mean and Variance Estimators
The estimated values of the parameters
and
given in the regression line (9) are found by using the method of the least-squares and get
In addition to the assumptions that the error
D in the model is a random variable with mean
and variance
constant, also suppose that
are independent from one run of the experiment to another. In this sense, under random conditions, the mean
presented in Equation (
12) and the variance
in Equation (
14) can be obtained as follows: In
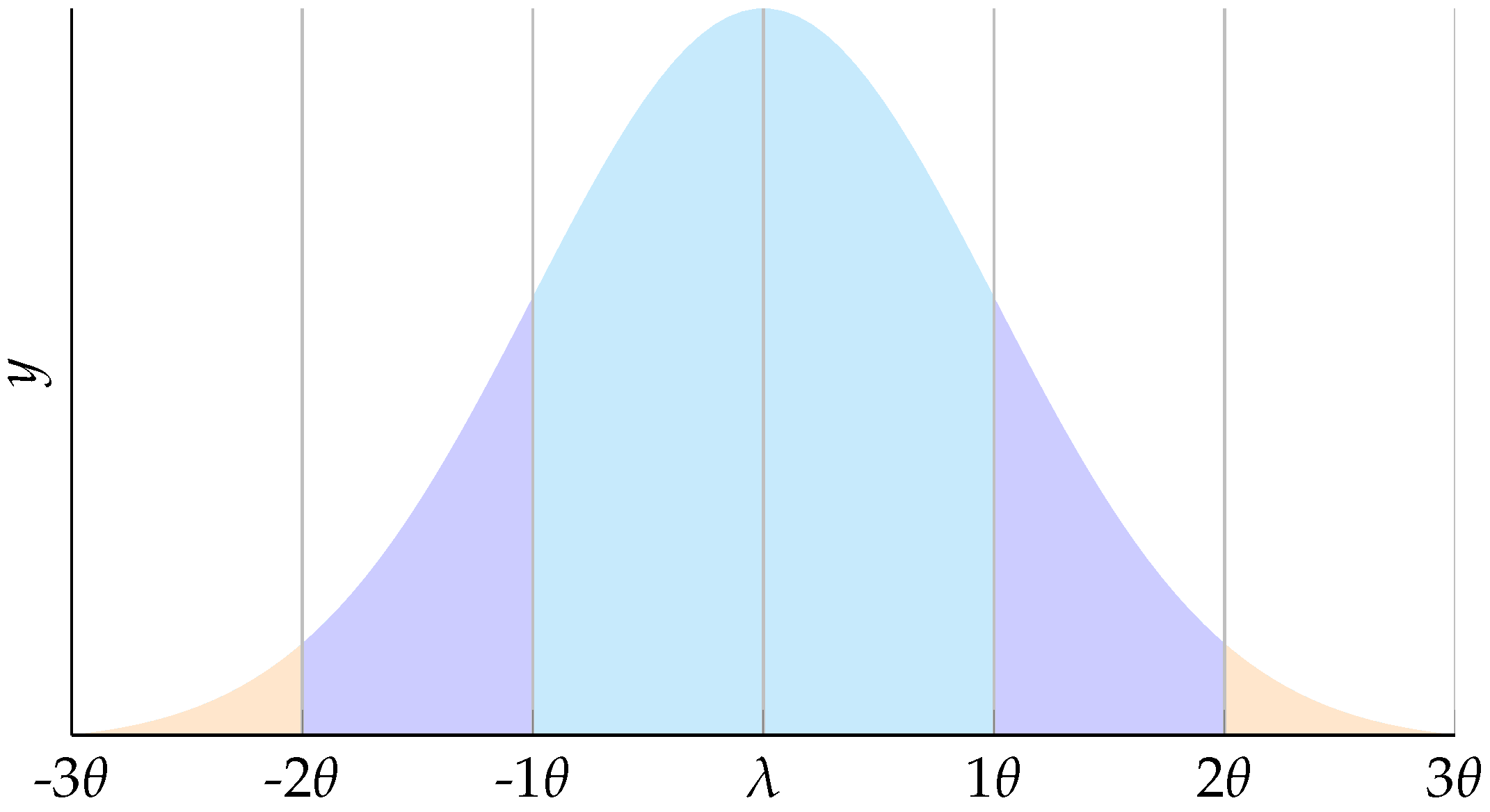
Figure 1 depict the random conditions for error
D.
Thus, the mathematical expectation is:
The covariance
is depicted as follows:
where:
To determine related bias information, it is imperative obtain the variance. In this sense, it is possible to carry out a modelization of error called
:
Thus, the difference between observations
and estimated value of
is given as:
Moreover, the difference between observations
and estimated value of
is given as:
and the aggregation error of
and
, respectively, converge in the Equation (
17):
In addition, the sum of the squares of the error can be presented as follows:
Then, assuming that
, the solution for Equation (
18) and using Equations (
14)–(
16) can be obtained as follows:
Then, the sum of the squares of the error (SSE) is depicted as follows:
Additionally, an unbiased estimator of the mean square error (MSE) is:
4. Numerical Example
In this section, two numerical cases are presented to demonstrate our proposal.
4.1. Numerical Example from a Real Case Study
A real case is considered in a manufacturing company’s need to establish a forecast related to inventory handling. This company is facing problems related to the forecast accuracy of raw material. In this mode, the data set used in this study will be under an inventory prediction problem. Our proposed GLR-DA will addressing a inventory problem to estimate the inventory conditions. The data considered are depicted in
Table 1.
The approach requires a pairwise comparison of the variables
x and
y based on the following model according Equation (
5). In
Table 2, the results obtained for each parameter
A and
B are depicted.
The following results applying our method proposed are depicted in
Table 3.
Hence, the SME is obtained using Equation (
20):
The Pearson correlation [
42] is presented in
Table 4, where a strong correlation between the information for each variable is observed.
Finally, it is important to consider that the correlation coefficient is around to 98.27%. It is a strong value to confirm that the forecast obtained with our proposal is proficient and robust.
4.2. Numerical Example 2
The data for this experiment were taken from [
43] focused on a sales estimation study. In this mode, the data are presented in
Table 5, and for convenience,
x represents the weeks and
y describes the sales.
According to the results represents in
Table 6, it can be see that our proposal has the potential to handle sales estimation problems.
In addition, the SME is obtained using Equation (
20):
5. Validations
In this section, statistical tests such as the normal probability test, correlation, means, standard deviation, confidence interval, and Tukey’s test were used. We conducted the statistical tests in order to evaluate the methodology proposal as followings.
In this manner, the normal probability test is realized to appraisal the data distribution. It can be observed in
Figure 2 that the normal test results are consistent.
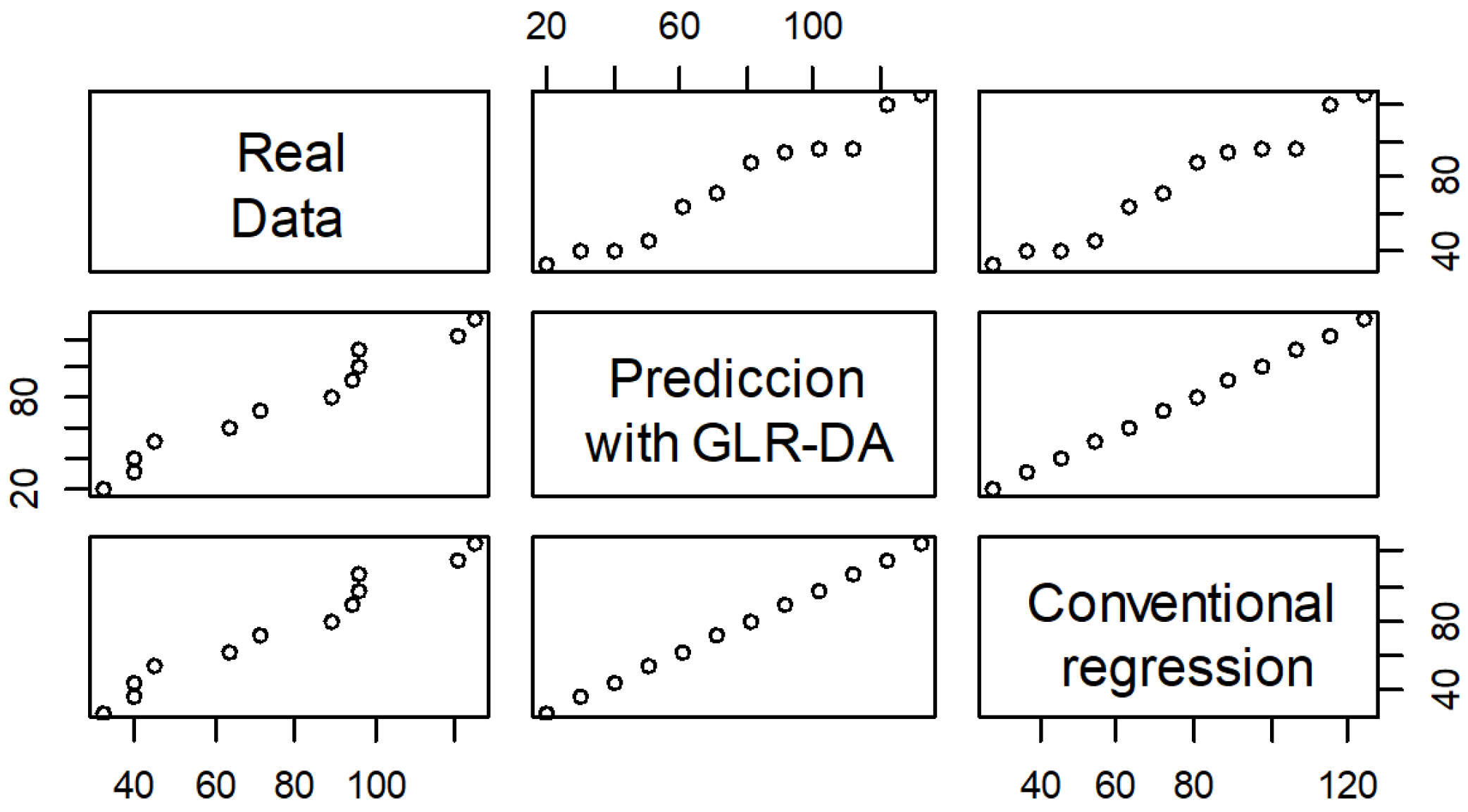
Thus, a cross-validation of the correlation of the information is presented in
Figure 3. In fact, the chart presented is very interesting, showing the correlation of the data analyzed with proposed GLR-DA and the conventional linear regression method.
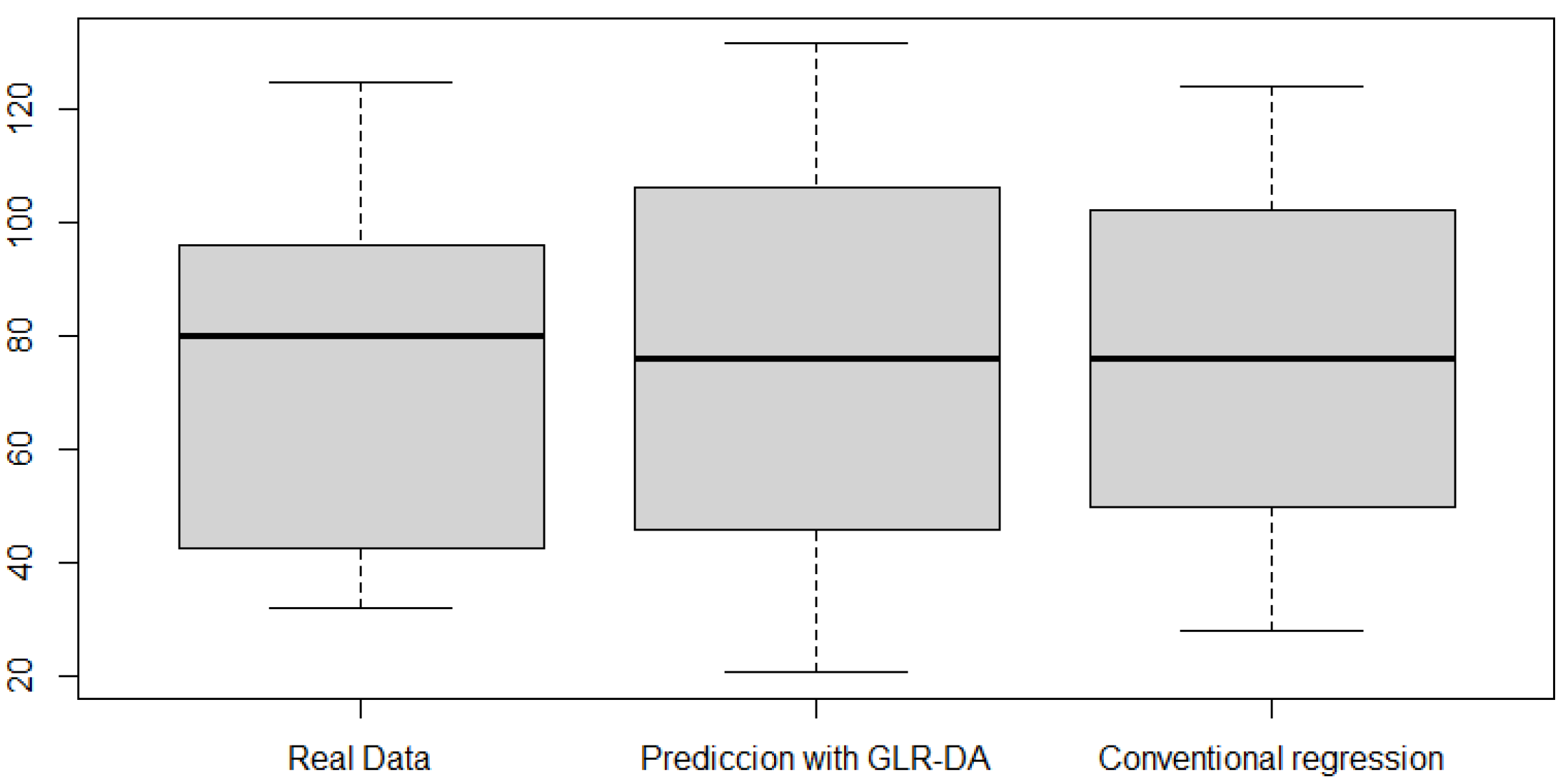
In addition, the box plot is presented in
Figure 4. The data analyzed show small variations with respect to their means.
A statistical summary report is depicted in
Table 7. It can be considered that the means and standard deviations are similar.
Then, a confidence interval was carried out to validate the information, and the results are depicted in
Table 8. It can be observed that difference does not exist between the means analyzed.
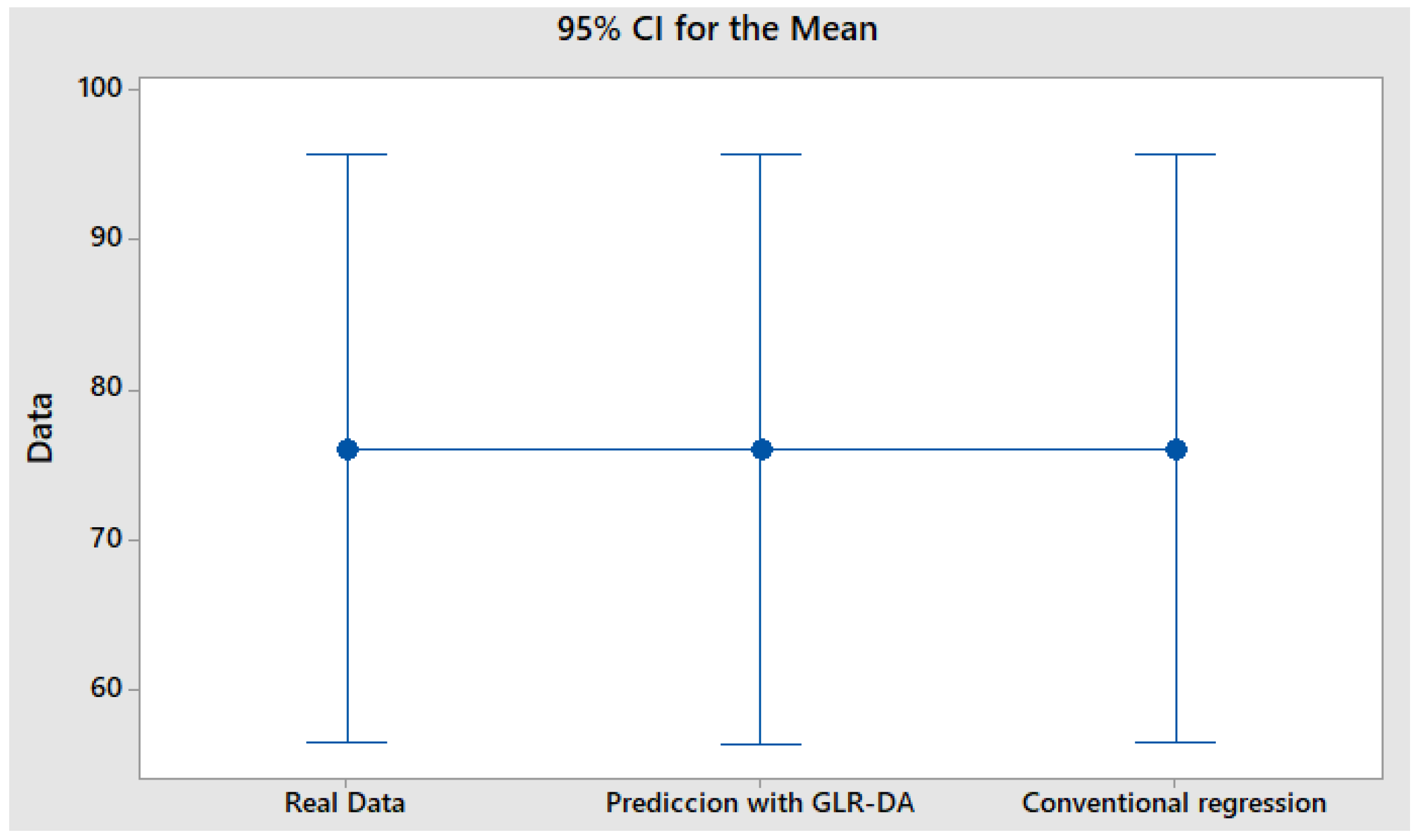
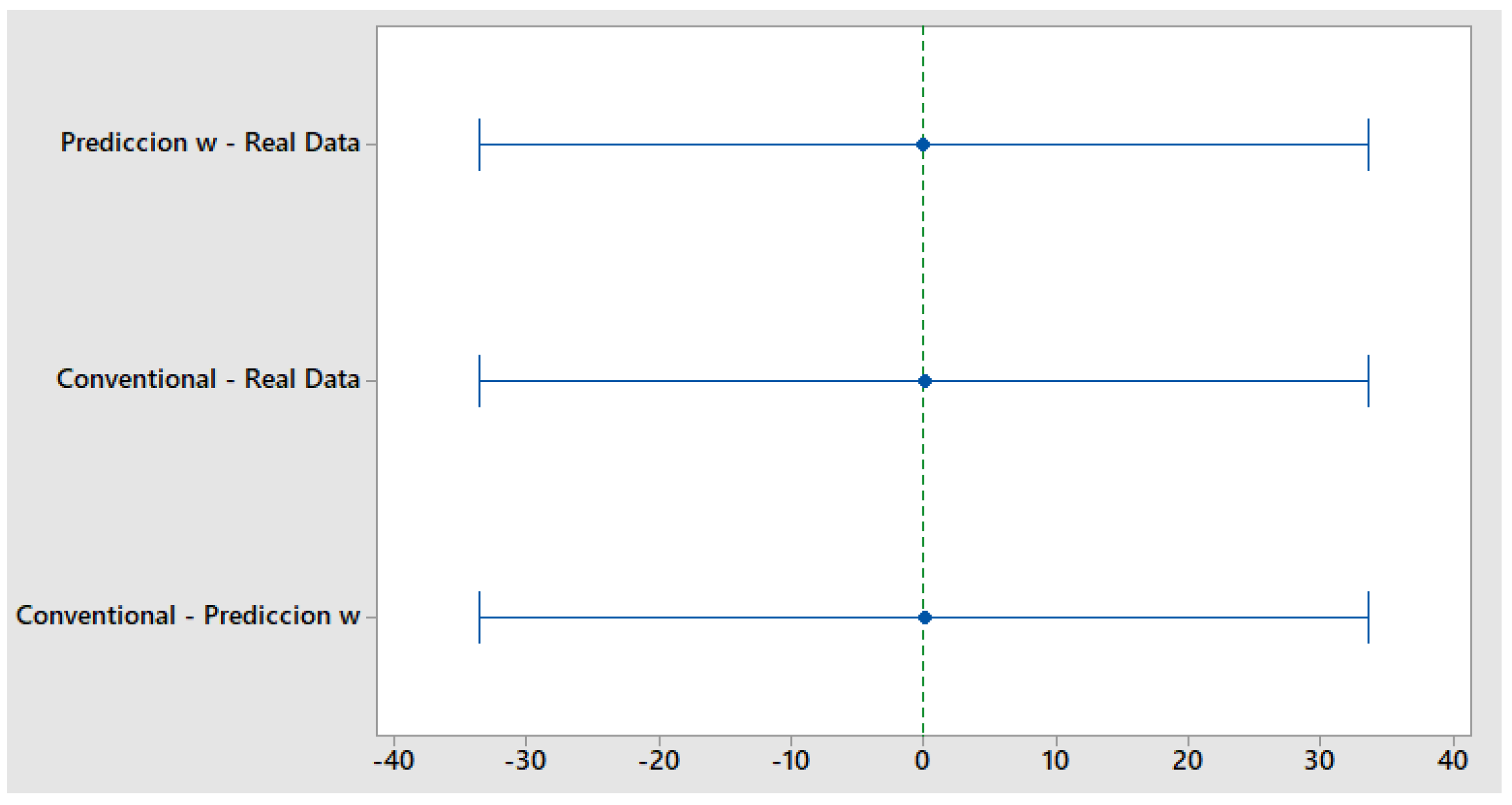
In addition, it can be seen in
Figure 5 the confidence interval with tendency within limit.
Hence, information was grouped using the Tukey’s Method [
44]. The test was conducted using a 95% confidence, and the results are presented in
Table 9. It can be see that the means are not significantly different.
Tukey simultaneous tests for differences of means. In this mode, using a individual confidence level = 98.04%. According to comparison of treatment means by Tukey’s Multiple the findings confirm the consistency about our proposal as shown in
Table 10.
Using the information presented in
Figure 6. It can be observed that the means have similar performances. In this manner, we can determine that they contain the same results.
6. Discussion and Conclusions
The linear regression using dimensional analysis is an alternative manner to obtain forecasts. In addition, the methodology’s findings proposed can potentially manipulate regression situation. Likewise, we carried out the different validations to confirm the consistency and stability of the results. Hence, the means comparisons using Tukey test explain the significant contribution to confirm the proficient results with our proposal. According to the different statistical tests realized, we can confirm the effectiveness of our proposal. In addition, the findings about the results from our proposal are reproducible. Therefore, based on those results, we confirm that our proposal is capable of dealing with efficiency, instability, and minimal error focused on the inventory forecast condition.
The literature revised indicates that linear regression continues to be an important topic to be investigated for academics. Nowadays, advances in technology and complexity are demanding accuracy forecast. At the same time, the companies face challenges in addressing the information in a sophisticated manner. Future research can be addressed to implement fuzzy applications and implement a software environment. In addition, it can be interesting to perform comparisons in other fields, for example, health, economics, agriculture, etc.
Author Contributions
Conceptualization, L.P.-D. and D.L.-C.; methodology, L.P.-D. and H.G.; validation, L.P.-D., D.L.-C. and J.L.G.A.; formal analysis, L.P.-D., D.L.-C. and H.G.; investigation, L.P.-D., D.L.-C. and H.G.; resources, L.P.-D., D.L.-C. and J.L.G.A.; data curation, L.P.-D., D.L.-C. and J.L.G.A.; writing—original draft preparation, L.P.-D., D.L.-C. and H.G.; writing—review and editing, L.P.-D., D.L.-C. and J.L.G.A.; visualization, L.P.-D., D.L.-C. and J.L.G.A.; supervision, L.P.-D., D.L.-C. and J.L.G.A.; funding acquisition, L.P.-D., D.L.-C. and H.G. All authors have read and agreed to the published version of the manuscript.
Funding
The APC was funded by National Council of Science and Technology (CONACYT).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
The authors would like to thank the constructive comments of the reviewers which improved the quality of the paper. The authors are very grateful to the Universidad Autónoma de Ciudad Juárez. The author (Harish Garg) is grateful to DST-FIST grant SR/FST/MS-1/2017/13 for providing technical support.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DA | Dimensional Analysis |
| LR | Linear regression |
| SSE | Sum of the squares of the error |
| GLR-DA | Generalized linear regression method under Dimensional Analysis environment called |
| MSE | The mean square error named |
References
- Hothorn, T.; Bretz, F.; Westfall, P. Simultaneous inference in general parametric models. Biom J. J. Math. Methods Biosci. 2008, 50, 346–363. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, M.; Hu, S.; Ge, Y.; Heuvelink, G.B.; Ren, Z.; Huang, X. Using multiple linear regression and random forests to identify spatial poverty determinants in rural China. Spat. Stat. 2020, 42, 100461. [Google Scholar] [CrossRef]
- Cook, J.R.; Stefanski, L.A. Simulation-extrapolation estimation in parametric measurement error models. J. Am. Stat. Assoc. 1994, 89, 1314–1328. [Google Scholar] [CrossRef]
- Park, J.Y.; Phillips, P.C. Statistical inference in regressions with integrated processes: Part 2. Econom. Theory 1989, 5, 95–131. [Google Scholar] [CrossRef] [Green Version]
- Johnston, F.; Boylan, J.E.; Shale, E.A. An examination of the size of orders from customers, their characterisation and the implications for inventory control of slow moving items. J. Oper. Res. Soc. 2003, 54, 833–837. [Google Scholar] [CrossRef]
- Babai, M.; Chen, H.; Syntetos, A.; Lengu, D. A compound-Poisson Bayesian approach for spare parts inventory forecasting. Int. J. Prod. Econ. 2021, 232, 107954. [Google Scholar] [CrossRef]
- Mansur, A.; Kuncoro, T. Product inventory predictions at small medium enterprise using market basket analysis approach-neural networks. Procedia Econ. Financ. 2012, 4, 312–320. [Google Scholar] [CrossRef] [Green Version]
- Dekker, R.; Bloemhof, J.; Mallidis, I. Operations Research for green logistics–An overview of aspects, issues, contributions and challenges. Eur. J. Oper. Res. 2012, 219, 671–679. [Google Scholar] [CrossRef] [Green Version]
- Bakker, M.; Riezebos, J.; Teunter, R.H. Review of inventory systems with deterioration since 2001. Eur. J. Oper. Res. 2012, 221, 275–284. [Google Scholar] [CrossRef]
- Saha, E.; Ray, P.K. Modelling and analysis of inventory management systems in healthcare: A review and reflections. Comput. Ind. Eng. 2019, 137, 106051. [Google Scholar] [CrossRef]
- van Steenbergen, R.; Mes, M. Forecasting demand profiles of new products. Decis. Support Syst. 2020, 139, 113401. [Google Scholar] [CrossRef]
- Kourentzes, N.; Trapero, J.R.; Barrow, D.K. Optimising forecasting models for inventory planning. Int. J. Prod. Econ. 2020, 225, 107597. [Google Scholar] [CrossRef] [Green Version]
- Wilson, B.T.; Knight, J.F.; McRoberts, R.E. Harmonic regression of Landsat time series for modeling attributes from national forest inventory data. ISPRS J. Photogramm. Remote Sens. 2018, 137, 29–46. [Google Scholar] [CrossRef]
- Seifbarghy, M.; Amiri, M.; Heydari, M. Linear and nonlinear estimation of the cost function of a two-echelon inventory system. Sci. Iran. 2013, 20, 801–810. [Google Scholar]
- Ryu, S.; Noh, J.; Kim, H. Deep neural network based demand side short term load forecasting. Energies 2017, 10, 3. [Google Scholar] [CrossRef]
- Dalla Corte, A.P.; Souza, D.V.; Rex, F.E.; Sanquetta, C.R.; Mohan, M.; Silva, C.A.; Zambrano, A.M.A.; Prata, G.; de Almeida, D.R.A.; Trautenmüller, J.W.; et al. Forest inventory with high-density UAV-Lidar: Machine learning approaches for predicting individual tree attributes. Comput. Electron. Agric. 2020, 179, 105815. [Google Scholar] [CrossRef]
- Junttila, V.; Laine, M. Bayesian principal component regression model with spatial effects for forest inventory variables under small field sample size. Remote Sens. Environ. 2017, 192, 45–57. [Google Scholar] [CrossRef]
- Ulrich, M.; Jahnke, H.; Langrock, R.; Pesch, R.; Senge, R. Distributional regression for demand forecasting in e-grocery. Eur. J. Oper. Res. 2021, 294, 831–842. [Google Scholar] [CrossRef] [Green Version]
- Georgi, H. Generalized dimensional analysis. Phys. Lett. 1993, 298, 187–189. [Google Scholar] [CrossRef] [Green Version]
- Butterfield, R. Dimensional analysis for geotechnical engineers. Geotechnique 1999, 49, 357–366. [Google Scholar] [CrossRef]
- Cheng, Y.T.; Cheng, C.M. Scaling, dimensional analysis, and indentation measurements. Mater. Sci. Eng. R Rep. 2004, 44, 91–149. [Google Scholar] [CrossRef]
- Bellamine, F.; Elkamel, A. Model order reduction using neural network principal component analysis and generalized dimensional analysis. Eng. Comput. 2008, 25, 443–463. [Google Scholar] [CrossRef]
- Moran, M.; Marshek, K. Some matrix aspects of generalized dimensional analysis. J. Eng. Math. 1972, 6, 291–303. [Google Scholar] [CrossRef]
- Longo, S. Principles and Applications of Dimensional Analysis and Similarity; Springer Nature Switzerland AG: Cham, Switzerland, 2022. [Google Scholar]
- Szava, I.R.; Sova, D.; Peter, D.; Elesztos, P.; Szava, I.; Vlase, S. Experimental Validation of Model Heat Transfer in Rectangular Hole Beams Using Modern Dimensional Analysis. Mathematics 2022, 10, 409. [Google Scholar] [CrossRef]
- Szirtes, T. Applied Dimensional Analysis and Modeling; Butterworth-Heinemann: Oxford, UK, 2007. [Google Scholar]
- Shen, W.; Lin, D.K. Statistical theories for dimensional analysis. Stat. Sin. 2019, 29, 527–550. [Google Scholar] [CrossRef]
- Shen, W.; Davis, T.; Lin, D.K.; Nachtsheim, C.J. Dimensional analysis and its applications in statistics. J. Qual. Technol. 2014, 46, 185–198. [Google Scholar] [CrossRef]
- Albrecht, M.C.; Nachtsheim, C.J.; Albrecht, T.A.; Cook, R.D. Experimental design for engineering dimensional analysis. Technometrics 2013, 55, 257–270. [Google Scholar] [CrossRef]
- Bridgman, P.W. Dimensional Analysis; Yale University Press: New Haven, CT, USA, 1922. [Google Scholar]
- Gibbings, J.C. Dimensional Analysis; Springer Nature & Business Media: New York, NY, USA, 2011. [Google Scholar]
- Dovi, V.; Reverberi, A.; Maga, L.; De Marchi, G. Improving the statistical accuracy of dimensional analysis correlations for precise coefficient estimation and optimal design of experiments. Int. Commun. Heat Mass Transf. 1991, 18, 581–590. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef] [Green Version]
- Kohli, S.; Godwin, G.T.; Urolagin, S. Sales Prediction Using Linear and KNN Regression. In Advances in Machine Learning and Computational Intelligence; Springer: Singapore, 2021; pp. 321–329. [Google Scholar]
- Gentleman, J.F. New developments in statistical computing. Am. Stat. 1986, 40, 228–237. [Google Scholar] [CrossRef]
- Liang, K.Y.; Zeger, S.L. Longitudinal data analysis using generalized linear models. Biometrika 1986, 73, 13–22. [Google Scholar] [CrossRef]
- Prion, S.K.; Haerling, K.A. Making Sense of Methods and Measurements: Simple Linear Regression. Clin. Simul. Nurs. 2020, 48, 94–95. [Google Scholar] [CrossRef]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: New York, NY, USA, 2013; Volume 26. [Google Scholar]
- Wright, J.; Yang, A.Y.; Ganesh, A.; Sastry, S.S.; Ma, Y. Robust face recognition via sparse representation. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 31, 210–227. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cheng, J.; Ai, M. Optimal designs for panel data linear regressions. Stat. Probab. Lett. 2020, 163, 108769. [Google Scholar] [CrossRef]
- Huseyin Tunc, B.G. A column generation based heuristic algorithm for piecewise linear regression. Expert Syst. Appl. 2021, 171, 114539. [Google Scholar] [CrossRef]
- Fieller, E.C.; Hartley, H.O.; Pearson, E.S. Tests for rank correlation coefficients. I. Biometrika 1957, 44, 470–481. [Google Scholar] [CrossRef]
- Conrad, S. Sales data and the estimation of demand. J. Oper. Res. Soc. 1976, 27, 123–127. [Google Scholar] [CrossRef]
- Tukey, J.W. Comparing individual means in the analysis of variance. Biometrics 1949, 5, 99–114. [Google Scholar] [CrossRef]
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).