School Timetabling Optimisation Using Artificial Bee Colony Algorithm Based on a Virtual Searching Space Method
Abstract
1. Introduction
2. Problem Formulation
2.1. Terminology
2.2. School Timetabling Concept Model
2.3. Symbols and Notations
| L | Total number of educators |
| O | Total number of units |
| K | Total number of classes in a school week |
| P | Maximum preference value |
| E | Maximum expertise value |
| V | Number of classes that an educator is allowed to deliver in a school week |
| H | Number of hours in a school day (e.g., from 8:00 a.m. to 6:00 p.m., there are 10 h) |
| D | Number of days in a school week |
| M | Maximum number of hours a class lasts |
| d | |
| t | |
| r | |
| c | |
| p | * |
| e | * |
| A | |
| u | Number of units that cannot be allocated with educators |
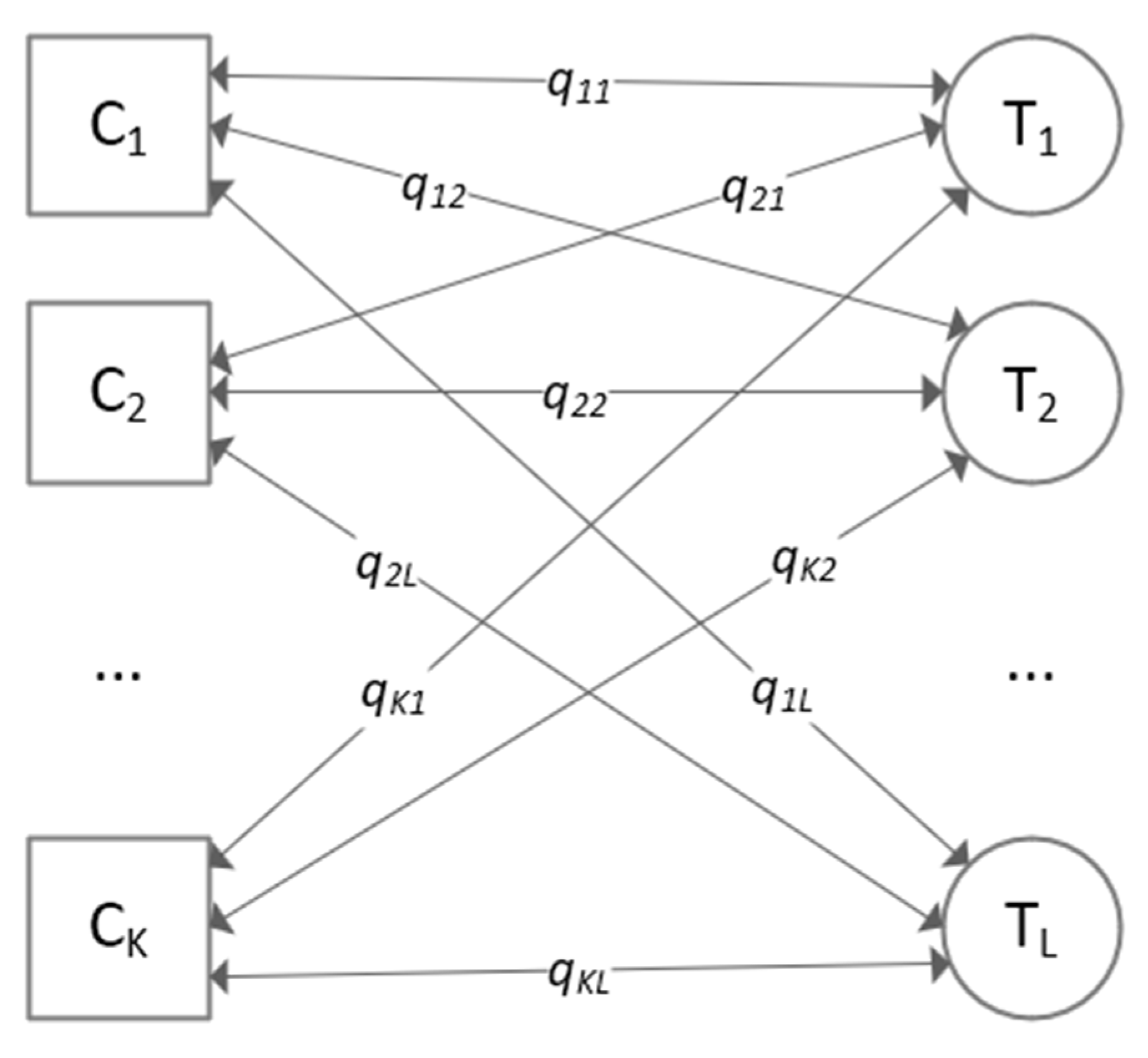
| * When p = 0, it indicates that an educator does not prefer a unit. When e = 0, it means that the educator is not capable to deliver the unit. By default, all the p and e are 0. They need to be set by educators and the head of school. | |
| Set of timeslots that educator is available in the school week. If educator is available during a whole school week, then . | |
| Set of timeslots that class is scheduled to in the school week. If class is scheduled in the first three hours of the school week, then . |
2.4. Hard Constraints
2.5. Soft Constraints
- Educators will be assigned to the most preferred units.
- Units will be allocated to the educators who are more capable to teach.
- All units must be allocated to educators.
2.6. Objective Function
3. Related Bio-Inspired Optimisation Methods
4. The Proposed Approach
4.1. The Basic Concept of Educator Allocation
4.2. ABC Algorithm
4.3. A Modified ABC Algorithm for Proposed STP
| Algorithm 1. Pseudocode of the modified ABC algorithm. |
| /*Initialisation stage*/ 01: Retrieve the scheduled course timetable and educators’ profiles 02: Define the neighbour search range, number of Traits and read parameters 03: Initialise the food source and construct school timetable, satisfying all hard constraints as in Equations (1)–(4) 04: Evaluate school timetable’s objective values with Equation (6) 05: Send the employed bees to the current food sources 06: Iteration = N 07: FOR (each iteration) /∗Employed Bee Phase∗/ 08: FOR (each employed bee) 09: Seek new food source from neighbourhood in VSS, satisfying Equations (1)–(4) 10: Construct school timetables and evaluate their objective value with Equation (6); apply greedy selection 11: END FOR 12: Calculate the probability p for each food source with Equation (9) /∗Onlooker Bee Phase∗/ 13: FOR (each onlooker bee) 14: Send onlooker bees to food sources based on p 15: Find a new food source in its neighbourhood in VSS, satisfying Equations (1)–(4) 16: Construct school timetables and evaluate their objective value with Equation (6); apply greedy selection and set Trait + 1 if applicable 17: END FOR /∗Scout Bee Phase∗/ 18: IF (any onlooker bee becomes scout bee) 19: Send scout bee to a randomly produced food source, satisfying Equations (1)–(4) 20: END IF 21: Memorise the best solution achieved so far 22: END FOR 23: Output the best solution achieved |
- Integrate VSS construction approach in neighbour population process (Steps 9 and 15 in Algorithm 1) instead of forming a whole searching space beforehand.
- Integrate school timetable constructor approach to generate solutions in every objective value evaluation process (Steps 3, 10 and 16 in Algorithm 1) instead of picking up solutions directly when populate.
4.4. Virtual Searching Space Construction
4.4.1. How VSS Works
4.4.2. The Implementation of VSS in Modified ABC Algorithm
| Algorithm 2. Pseudocode of VSS. |
| 01: Randomly select first educator (index is ) from the given educator list. 02: Randomly generate neighbour search range . 03: Randomly generate number . 04: Set the second educator’s index 05: If , repeat Step 2 ( is the number of educators). 06: Swap and . |
4.5. School Timetable Construction
| Algorithm 3. Pseudocode of school timetable solution construction. |
| 1: Receive an educator list and the number of units an educator can take 2: FOR (V) 3: FOR (K) 4: FOR (each unallocated educator in the educator list) 5: IF (the educator is available and prefer to teach the class) 6: Allocate the educator to the class 7: Modify the educator’s availability 8: IF (all classes are allocated with an educator) 9: Return constructed school timetable 10: FOR (each unallocated class in the course timetable) 10: FOR (L) 12: IF (the educator can and is available to teach the class) 13: Allocate the educator to the class 14: Modify the educator’s availability 15: Return constructed school timetable |
5. Experimental Section
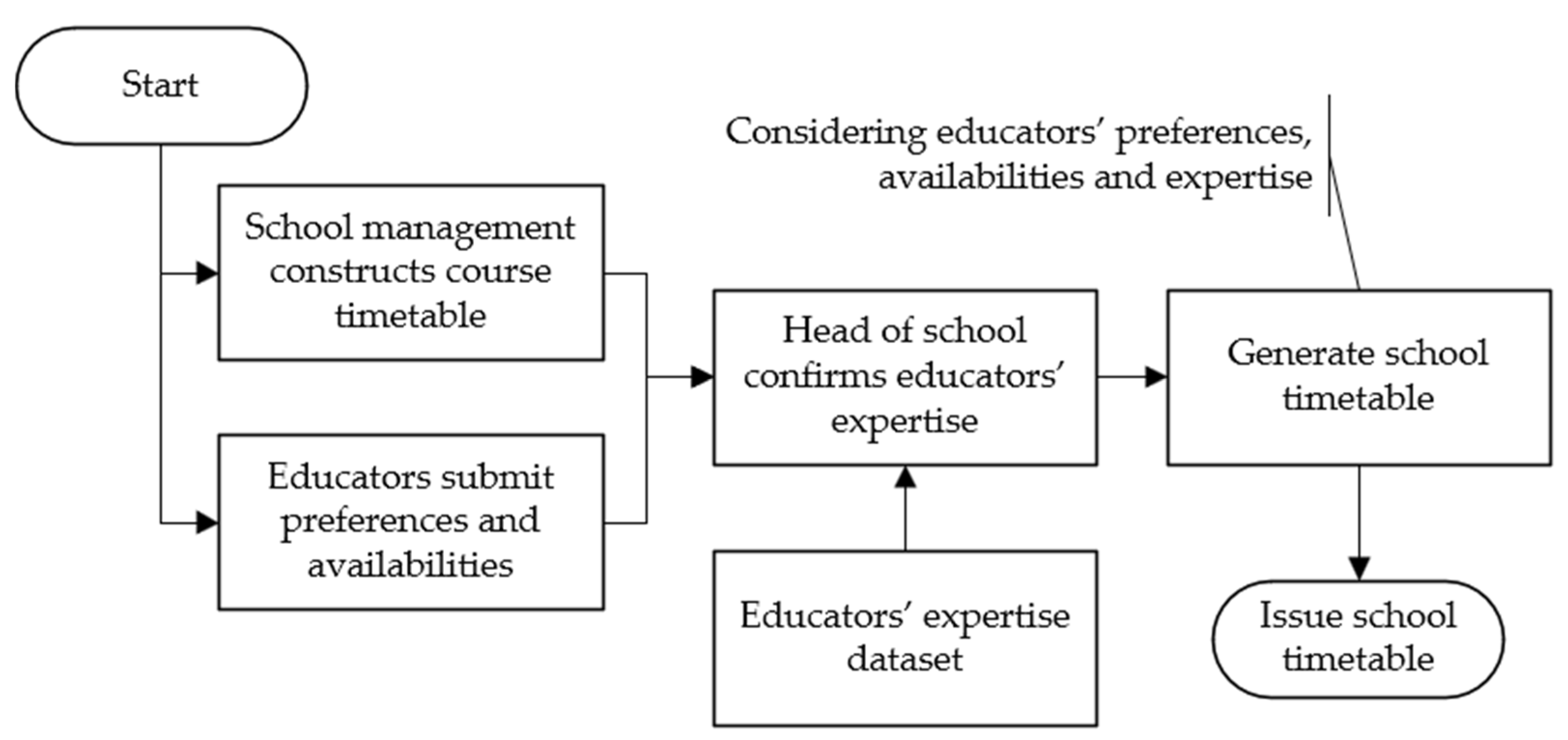
- The course timetable is prescheduled and fixed based on the course enrolment information. The class activities have been scheduled in the weekly timeslots.
- Before planning a school timetable, educators will submit their expression of interest to the administration, including the units they want to teach and the preferences towards each unit.
- Educators need to provide their unavailability form in the school week. The number of unavailable hours cannot be more than 3 h.
- The head of school will confirm and adjust each educator’s expertise against a unit.
- The goal of the school timetabling is to satisfy educators’ preferences and classes’ qualities and attempt to ensure every unit is allocated to an educator.
5.1. Experimental Settings
- K = 300 (Total number of classes in a school week)
- L = 150 (Total number of educators)
- V = 5 (Number of classes that an educator is allowed to deliver in a school week)
- H = 8 (Number of hours in a school day)
- D = 5 (Number of days in a school week)
- P = 3 (Maximum preference value)
- E = 3 (Maximum expertise value)
- d = 1 or 2 (Duration of each class)
- Maximum unavailable timeslots an educator can have in a week: 3
- Operating System: Windows 10 Pro Edition.
- Integrated development environment: IntelliJ IDEA 2020.3.2.
- Programming language: Java.
- Computer hardware system: Intel® Core™ i7-1065G7 1.30GHz Processor with 16.0 GB of memory.
5.2. Experimental Results
- The proposed approach can obtain a feasible solution in a gigantic searching space in a short time. In Sample A, the time spent for the best solution is 4.742 s.
- Deploying more bees can help improve objective value. Sample B has a better result than Sample A in objective value (43.4970 to 42.4299 on average), as Sample B populates twenty bees and Sample A deploys five bees.
- Increasing the number of program iterations can obtain a better result. Sample D has a better objective function value over Sample A (43.6596 over 42.4299 on average), as Sample D has 10,000 iterations and Sample A has 1000 iterations.
- Increasing both the number of bees and the number of iterations can improve the result. Comparing Sample A and Sample F, the objective value improves from 42.4299 to 44.7148 on average, but the time spent also increased significantly (from 4.983 s to 197.513 s on average).
- Expanding the neighbourhood can slightly improve the result. Sample C expands the neighbourhood three times compared to Sample A, but the result only improves 0.85% (from 42.4299 to 42.7910 on average).
- Increasing the exploitation will not benefit the solution and instead provides worse results. Compared to Sample A, although Sample E triples the number of traits, the objective value decreases and the number of unallocated units increases. This is because exploitation reduces the opportunity of exploration, which is also proven by comparing the results between Sample D and Sample H as well as between Sample F and Sample G.
- Sample J enlarges the variables. Although the improvement of the result is obvious, the time spent is significant. Compared to Sample A, the objective value is increased by 10.3% (from 42.4299 to 46.8359), but the time Sample J spends is 165 times than that of Sample A.
- All the CVs are lower than 8%, indicating that the proposed ABC can provide solutions stably.
6. Comparison Study
| Items | Proposed ABC | CP | ||
|---|---|---|---|---|
| Best | Average | Best | Average | |
| Time spent (seconds) | 4.742 | 4.983 | 3.5 | 3.6108 |
| Unallocated classes 1 | 0 | 0.5 | 12 | 12 |
| Objective function values | 44.0740 | 42.4299 | 30.5128 | 30.1158 |
- CP is slightly faster than the modified ABC algorithm in solution-seeking (3.6108 s over 4.983 s on average).
- The modified ABC algorithm can allocate all the non-conflict classes. However, CP has 12 allocatable classes left.
- The modified ABC algorithm can seek a solution that is 40.88% better than CP in terms of objective function values gaining (42.4299 against 30.1158 on average).
7. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wren, A. Scheduling, Timetabling and Rostering—A Special Relationship? In International Conference on the Practice and Theory of Automated Timetabling; Springer: Berlin/Heidelberg, Germany, 1995; pp. 46–75. [Google Scholar]
- Schaerf, A. A Survey of Automated Timetabling. Artif. Intell. Rev. 1999, 13, 87–127. [Google Scholar] [CrossRef]
- Valouxis, C.; Gogos, C.; Alefragis, P.; Housos, E. Decomposing the High School Timetable Problem. In Proceedings of the Practice and Theory of Automated Timetabling (PATAT 2012), Son, Norway, 29–31 August 2012. [Google Scholar]
- Bashab, A.; Ibrahim, A.O.; AbedElgabar, E.E.; Ismail, M.A.; Elsafi, A.; Ahmed, A.; Abraham, A. A Systematic Mapping Study on Solving University Timetabling Problems Using Meta-Heuristic Algorithms. Neural Comput. Appl. 2020, 32, 17397–17432. [Google Scholar] [CrossRef]
- Garey, M.R.; Johnson, D.S.; Stockmeyer, L. Some Simplified NP-Complete Problems. In Proceedings of the Sixth Annual ACM Symposium on Theory of Computing, Seattle, WA, USA, 30 April–2 May 1974; pp. 47–63. [Google Scholar]
- Odeniyi, O.; Omidiora, E.; Olabiyisi, S.; Oyeleye, C. A Mathematical Programming Model and Enhanced Simulated Annealing Algorithm for the School Timetabling Problem. Asian J. Res. Comput. Sci. 2020, 5, 21–38. [Google Scholar] [CrossRef]
- Pillay, N. A Survey of School Timetabling Research. Ann. Oper. Res. 2014, 218, 261–293. [Google Scholar] [CrossRef]
- Beligiannis, G.N.; Moschopoulos, C.N.; Kaperonis, G.P.; Likothanassis, S.D. Applying Evolutionary Computation to the School Timetabling Problem: The Greek Case. Comput. Oper. Res. 2008, 35, 1265–1280. [Google Scholar] [CrossRef]
- Post, G.; Ahmadi, S.; Daskalaki, S.; Kingston, J.H.; Kyngas, J.; Nurmi, C.; Ranson, D.; Ruizenaar, H. An XML Format for Benchmarks in High School Timetabling. Ann. Oper. Res. 2012, 194, 385–397. [Google Scholar] [CrossRef]
- Wilke, P.; Ostler, J. Solving the School Time Tabling Problem Using Tabu Search, Simulated Annealing, Genetic and Branch & Bound Algorithms. In Proceedings of the 7th International Conference on the Practice and Theory of Automated Timetabling (PATAT 2008), Montreal, Canada, 19–22 August 2008. [Google Scholar]
- Babaei, H.; Karimpour, J.; Hadidi, A. A Survey of Approaches for University Course Timetabling Problem. Comput. Ind. Eng. 2015, 86, 43–59. [Google Scholar] [CrossRef]
- Feizi-Derakhshi, M.-R.; Babaei, H.; Heidarzadeh, J. A Survey of Approaches for University Course Timetabling Problem. In Proceedings of the 8th International Symposium on Intelligent and Manufacturing Systems, Adrasan, Turkey, 27–28 September 2012; Sakarya University Department of Industrial Engineering: Adrasan, Turkey, 2012; pp. 307–321. [Google Scholar]
- Salhi, S. Heuristic Search: The Emerging Science of Problem Solving; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Fonseca, G.H.; Santos, H.G.; Carrano, E.G.; Stidsen, T.J. Integer Programming Techniques for Educational Timetabling. Eur. J. Oper. Res. 2017, 262, 28–39. [Google Scholar] [CrossRef]
- Pillay, N.; Qu, R. Hyper-Heuristics: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Fong, C.W.; Asmuni, H.; McCollum, B. A Hybrid Swarm-Based Approach to University Timetabling. IEEE Trans. Evolut. Comput. 2015, 19, 870–884. [Google Scholar] [CrossRef]
- Ishak, S.; Lee, L.S.; Ibragimov, G. Hybrid Genetic Algorithm for University Examination Timetabling Problem. Malays. J. Math. Sci. 2016, 10, 145–178. [Google Scholar]
- Kouhbanani Nejad, S.F.; Farid, D.; Sadeghi, H. Selection of Optimal Portfolio Using Expert System in Mamdani Fuzzy Environment. Ind. Manag. Stud. 2018, 16, 131–151. [Google Scholar]
- Bělohlávek, R.; Dauben, J.W.; Klir, G.J. Fuzzy Logic and Mathematics: A Historical Perspective; Oxford University Press: Oxford, UK, 2017. [Google Scholar]
- Junn, K.Y.; Obit, J.H.; Alfred, R.; Bolongkikit, J. A Formal Model of Multi-agent System for University Course Timetabling Problems; Springer: Singapore, 2019; pp. 215–225. [Google Scholar]
- Odeniyi, O.; Omidiora, E.; Olabiyisi, S.; Aluko, J. Development of a Modified Simulated Annealing to School Timetabling Problem. Int. J. Appl. Inf. Syst. 2015, 8, 16–24. [Google Scholar] [CrossRef]
- Sutar, S.R.; Bichkar, R.S. Genetic Algorithms Based Timetabling Using Knowledge Augmented Operators. Int. J. Comput. Sci. Inf. Secur. 2016, 14, 570. [Google Scholar]
- Ahmed, L.N.; Özcan, E.; Kheiri, A. Solving High School Timetabling Problems Worldwide Using Selection Hyper-Heuristics. Expert Syst. Appl. 2015, 42, 5463–5471. [Google Scholar] [CrossRef]
- Domrös, J.; Homberger, J. An Evolutionary Algorithm for High School Timetabling. In Proceedings of the Ninth International Conference on the Practice and Theory of Automated Timetabling (PATAT 2012), Son, Norway, 29–31 August 2012. [Google Scholar]
- Sørensen, M.; Stidsen, T.R. High School Timetabling: Modeling and Solving a Large Number of Cases in Denmark. In Proceedings of the Ninth International Conference on the Practice and Theory of Automated Timetabling (PATAT 2012), Son, Norway, 29–31 August 2012; pp. 359–364. [Google Scholar]
- Fonseca, G.H.; Santos, H.G.; Carrano, E.G. Late Acceptance Hill-Climbing for High School Timetabling. J. Sched. 2016, 19, 453–465. [Google Scholar] [CrossRef]
- Skoullis, V.I.; Tassopoulos, I.X.; Beligiannis, G.N. Solving the High School Timetabling Problem Using a Hybrid Cat Swarm Optimization Based Algorithm. Appl. Soft Comput. 2017, 52, 277–289. [Google Scholar] [CrossRef]
- Katsaragakis, I.V.; Tassopoulos, I.X.; Beligiannis, G.N. A Comparative Study of Modern Heuristics on the School Timetabling Problem. Algorithms 2015, 8, 723–742. [Google Scholar] [CrossRef]
- Babaei, H.; Karimpour, J.; Oroji, H. Using Fuzzy C-Means Clustering Algorithm for Common Lecturers Timetabling among Departments. In Proceedings of the 2016 6th International Conference on Computer and Knowledge Engineering (ICCKE), Mashhad, Iran , 20–20 October 2016; IEEE: Manhattan, NY, USA, 2016; pp. 243–250. [Google Scholar]
- Oprea, M. MAS_UP-UCT: A Multi-Agent System for University Course Timetable Scheduling. Int. J. Comput. Commun. Control 2007, 2, 94–102. [Google Scholar] [CrossRef]
- Tkaczyk, R.; Ganzha, M.; Paprzycki, M. AgentPlanner-Agent-Based Timetabling System. Informatica 2016, 40, 3–17. [Google Scholar]
- Tan, J.S.; Goh, S.L.; Kendall, G.; Sabar, N.R. A Survey of the State-of-the-Art of Optimisation Methodologies in School Timetabling Problems. Expert Syst. Appl. 2021, 165, 113943. [Google Scholar] [CrossRef]
- Karaboga, D.; Gorkemli, B.; Ozturk, C.; Karaboga, N. A Comprehensive Survey: Artificial Bee Colony (ABC) Algorithm and Applications. Artif. Intell. Rev. 2014, 42, 21–57. [Google Scholar] [CrossRef]
- Bolaji, A.L.A.; Khader, A.T.; Al-Betar, M.A.; Awadallah, M.A. University Course Timetabling Using Hybridized Artificial Bee Colony with Hill Climbing Optimizer. J. Comput. Sci. 2014, 5, 809–818. [Google Scholar] [CrossRef]
- Bolaji, A.L.A.; Khader, A.T.; Al-Betar, M.A.; Awadallah, M.A. A Hybrid Nature-Inspired Artificial Bee Colony Algorithm for Uncapacitated Examination Timetabling Problems. J. Intell. Syst. 2015, 24, 37–54. [Google Scholar] [CrossRef]
- Alzaqebah, M.; Abdullah, S. Hybrid Bee Colony Optimization for Examination Timetabling Problems. Comput. Oper. Res. 2015, 54, 142–154. [Google Scholar] [CrossRef]
- Zhu, K.; Li, L.D.; Li, M. A Survey of Computational Intelligence in Educational Timetabling. IJMLC 2021, 11, 40–47. [Google Scholar] [CrossRef]
- Kristiansen, S.; Stidsen, T.R. A Comprehensive Study of Educational Timetabling—A Survey; DTU Management Engineering Report; Department of Management Engineering, Technical University of Denmark: Lyngby, Denmark, 2013. [Google Scholar]
- Chen, M.C.; Goh, S.L.; Sabar, N.R.; Kendall, G. A Survey of University Course Timetabling Problem. Perspect. Trends Oppor. IEEE Access. 2021, 9, 106515–106529. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Adrianto, D. Comparison Using Particle Swarm Optimization and Genetic Algorithm for Timetable Scheduling. J. Comput. Sci. 2014, 10, 341. [Google Scholar] [CrossRef][Green Version]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE: Manhattan, NY, USA, 1995; pp. 1942–1948. [Google Scholar]
- Patrick, K.; Godswill, Z. Greedy Ants Colony Optimization Strategy for Solving the Curriculum Based University Course Timetabling Problem. J. Adv. Math. Comput. Sci. 2016, 14, 1–10. [Google Scholar] [CrossRef]
- Neshat, M.; Sepidnam, G.; Sargolzaei, M.; Toosi, A.N. Artificial Fish Swarm Algorithm: A Survey of the State-of-the-Art, Hybridization, Combinatorial and Indicative Applications. Artif. Intell. Rev. 2014, 42, 965–997. [Google Scholar] [CrossRef]
- Yang, X.-S. Firefly Algorithms for Multimodal Optimization. International Symposium on Stochastic Algorithms; Springer: Berlin/Heidelberg, Germany, 2009; pp. 169–178. [Google Scholar]
- Eusuff, M.M.; Lansey, K.E. Optimization of Water Distribution Network Design Using the Shuffled Frog Leaping Algorithm. J. Water Resour. Plan. Manag. 2003, 129, 210–225. [Google Scholar] [CrossRef]
- Clerc, M.; Kennedy, J. The Particle Swarm-Explosion, Stability, and Convergence in a Multidimensional Complex Space. IEEE Trans. Evolut. Comput. 2002, 6, 58–73. [Google Scholar] [CrossRef]
- Dorigo, M.; Birattari, M. Swarm Intelligence. Scholarpedia 2007, 2, 1462. [Google Scholar] [CrossRef]
- Ilyas, R.; Iqbal, Z. Study of Hybrid Approaches Used for University Course Timetable Problem (UCTP). In Proceedings of the 2015 IEEE 10th Conference on Industrial Electronics and Applications (ICIEA), Auckland, New Zealand, 15–17 June 2015; IEEE: Manhattan, NY, USA, 2015; pp. 696–701. [Google Scholar]
- Oner, A.; Ozcan, S.; Dengi, D. Optimization of University Course Scheduling Problem with a Hybrid Artificial Bee Colony Algorithm. In Proceedings of the 2011 IEEE Congress of Evolutionary Computation (CEC), New Orleans, LA, USA, 5–8 June 2011; IEEE: Manhattan, NY, USA, 2011; pp. 339–346. [Google Scholar]
- Alzaqebah, M.; Abdullah, S. An Adaptive Artificial Bee Colony and Late-Acceptance Hill-Climbing Algorithm for Examination Timetabling. J. Sched. 2014, 17, 249–262. [Google Scholar] [CrossRef]
- Karaboga, D. An Idea Based on Honey Bee Swarm for Numerical Optimization; Technical Report-TR06; Erciyes University: Kayseri, Turkey, 2005. [Google Scholar]
- Veček, N.; Mernik, M.; Filipič, B.; Črepinšek, M. Parameter Tuning with Chess Rating System (CRS-Tuning) for Meta-Heuristic Algorithms. Inf. Sci. 2016, 372, 446–469. [Google Scholar] [CrossRef]
- Ma, M.; Liang, J.; Guo, M.; Fan, Y.; Yin, Y. SAR Image Segmentation Based on Artificial Bee Colony Algorithm. Appl. Soft Comput. 2011, 11, 5205–5214. [Google Scholar] [CrossRef]
- Zhang, C.; Ouyang, D.; Ning, J. An Artificial Bee Colony Approach for Clustering. Expert Syst. Appl. 2010, 37, 4761–4767. [Google Scholar] [CrossRef]
- Xu, C.; Duan, H.; Liu, F. Chaotic Artificial Bee Colony Approach to Uninhabited Combat Air Vehicle (UCAV) Path Planning. Aerosp. Sci.Technol. 2010, 14, 535–541. [Google Scholar] [CrossRef]
- Samanta, S.; Chakraborty, S. Parametric Optimization of Some Non-Traditional Machining Processes Using Artificial Bee Colony Algorithm. Eng. Appl. Artif. Intell. 2011, 24, 946–957. [Google Scholar] [CrossRef]
- Bukchin, Y.; Raviv, T. Constraint Programming for Solving Various Assembly Line Balancing Problems. Omega 2018, 78, 57–68. [Google Scholar] [CrossRef]


| Class ID | Preference | Expertise |
|---|---|---|
| 2 | 3 | |
| 1 | 1 | |
| … | … | … |
| 3 | 2 | |
| … | … | … |
| 0 | 0 |
| Mon | Tue | Wed | Thu | Fri | |
|---|---|---|---|---|---|
| 8:00 a.m. | Y | N | Y | N | N |
| 9:00 a.m. | Y | N | N | N | N |
| 10:00 a.m. | Y | Y | N | N | N |
| 11:00 a.m. | Y | Y | Y | N | N |
| 12:00 p.m. | N | Y | Y | N | N |
| 1:00 p.m. | N | N | Y | N | Y |
| 2:00 p.m. | N | N | Y | N | Y |
| 3:00 p.m. | N | Y | Y | N | Y |
| 4:00 p.m. | N | N | Y | N | Y |
| 5:00 p.m. | Y | N | Y | N | Y |
| 6:00 p.m. | Y | N | Y | N | Y |
| A region | B region | ||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| A | A | A | A | A | A | B | B | B | B | B | B |
| B | B | C | C | D | D | A | A | C | C | D | D |
| C | D | B | D | B | C | C | D | A | D | A | C |
| D | C | D | B | C | B | D | C | D | A | C | A |
| C region | D region | ||||||||||
| 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| C | C | C | C | C | C | D | D | D | D | D | D |
| A | A | B | B | D | D | A | A | B | B | C | C |
| B | D | A | D | A | B | B | C | A | C | A | B |
| D | B | D | A | B | A | C | B | C | A | B | A |
| Sample | Num of Bees | Neighbour Range | Num of Iterations | Num of Traits |
|---|---|---|---|---|
| A | 5 | 5 | 1000 | 10 |
| B | 20 | 5 | 1000 | 10 |
| C | 5 | 30 | 1000 | 10 |
| D | 5 | 5 | 10,000 | 10 |
| E | 5 | 5 | 1000 | 30 |
| F | 20 | 30 | 10,000 | 10 |
| G | 20 | 30 | 10,000 | 30 |
| H | 5 | 5 | 10,000 | 30 |
| I | 20 | 30 | 10,000 | 30 |
| J | 40 | 60 | 20,000 | 60 |
| Sample | Objective Values | Time Spent (Seconds) | Unallocated Classes | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Avg. | Best | Std. Dev. | CV | Avg. | Best | Std. Dev. | CV | Avg 1 | Best | |
| A | 42.4299 | 44.0740 | 0.9697 | 2.285% | 4.983 | 4.742 | 0.2712 | 5.443% | 0.5 | 0 |
| B | 43.4970 | 44.7037 | 0.6937 | 1.594% | 18.8521 | 18.453 | 0.4208 | 2.232% | 0.1 | 0 |
| C | 42.7910 | 43.7407 | 0.6779 | 1.584% | 5.0719 | 4.834 | 0.1950 | 3.846% | 0.5 | 0 |
| D | 43.6596 | 44.8518 | 0.6690 | 1.532% | 48.843 | 47.238 | 2.4431 | 5.002% | 0 | 0 |
| E | 41.9709 | 43.9256 | 1.0925 | 2.603% | 4.9919 | 4.818 | 0.1732 | 3.470% | 1 | 0 |
| F | 44.7148 | 45.3703 | 0.4201 | 0.939% | 197.513 | 193.957 | 2.2012 | 1.114% | 0 | 0 |
| G | 44.5255 | 45.1481 | 0.2849 | 0.639% | 201.0127 | 194.826 | 6.5969 | 3.281% | 0 | 0 |
| H | 42.5502 | 43.2222 | 0.4757 | 1.118% | 50.3867 | 46.775 | 3.9439 | 7.827% | 0.3 | 0 |
| I | 44.4592 | 45.8148 | 0.5484 | 1.228% | 206.4878 | 197.141 | 7.1228 | 3.449% | 0 | 0 |
| J | 46.8359 | 47.1481 | 0.2448 | 0.522% | 831.6302 | 813.494 | 441.1553 | 4.467% | 0 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, K.; Li, L.D.; Li, M. School Timetabling Optimisation Using Artificial Bee Colony Algorithm Based on a Virtual Searching Space Method. Mathematics 2022, 10, 73. https://doi.org/10.3390/math10010073
Zhu K, Li LD, Li M. School Timetabling Optimisation Using Artificial Bee Colony Algorithm Based on a Virtual Searching Space Method. Mathematics. 2022; 10(1):73. https://doi.org/10.3390/math10010073
Chicago/Turabian StyleZhu, Kaixiang, Lily D. Li, and Michael Li. 2022. "School Timetabling Optimisation Using Artificial Bee Colony Algorithm Based on a Virtual Searching Space Method" Mathematics 10, no. 1: 73. https://doi.org/10.3390/math10010073
APA StyleZhu, K., Li, L. D., & Li, M. (2022). School Timetabling Optimisation Using Artificial Bee Colony Algorithm Based on a Virtual Searching Space Method. Mathematics, 10(1), 73. https://doi.org/10.3390/math10010073








