Abstract
The problem of finite-time boundedness for a class of linear switched positive time-varying delay systems with interval uncertainties and exogenous disturbance is addressed. This characteristic research is that the studied systems include the finite-time bounded subsystems and finite-time unbounded subsystems. Both a slow mode-dependent average dwell time and a fast mode-dependent average dwell time switching techniques are utilized reasonably. And by applying a copositive Lyapunov-Krasovskii functional, novel delay-dependent sufficient criteria are derived to guarantee such systems to be finite-time bounded concerning the given parameters and designed switching signal. Furthermore, new finite-time boundedness criteria of the systems without interval uncertainties are also obtained. Finally, the efficiency of the theoretical results is presented in two illustrative examples.
1. Introduction
Several phenomena can be modeled such as switched systems that compose a family of subsystems and a logical law called a switching signal that determines the switching manner among the multiple subsystems [1,2,3,4]. When all subsystems of switched systems are positive under the specific switching rules, the systems are well known as switched positive systems (SPSs). Their applications can encounter in various areas, such as compartmental model [5], water-quality model [6], formation flying [7], congestion control [8], wireless power control [9], and network communication using transmission control protocol [10]. Furthermore, the system’s behavior that relies not only on the present state but also on the past state is discovered in many situations, for example, fluid and mechanical transmissions, metallurgical processes, and networked communications. An essential class of dynamical systems with the behavior are referred to as time-delay systems [11,12,13]. Nevertheless, the existence of the time delay in the systems may cause chaos and instability. Therefore, several beneficial results on SPSs, including time delay as well as time-varying delay, have been published, see [14,15,16,17,18,19].
Stability analysis of differential equations and dynamical systems has been extensively studied in the literature [20,21,22,23]. Remarkably, the concept of classical Lyapunov stability has been utilized to analyze the behavior of the systems over an infinite time interval. Nonetheless, there are some cases where the mentioned stability can not describe the mechanism of studied systems, such as some constraints of operation time and requirements about the transient performance of the systems [24,25,26,27]. Hence, a concept of finite-time stability (FTS), which can keep state trajectories of the considered systems within a prescribed bound over a fixed time interval under some given constraints of the initial condition [28,29,30], has been adopted to deal with those cases. In addition, FTS can be extended to the finite-time boundedness (FTB) if exogenous disturbances or the influence of perturbing forces are taken into account together [31]. However, it is well known that the Lyapunov stability and FTS (FTB) are completely independent concepts. Namely, any dynamical system may be the Lyapunov stability but not FTS (FTB), and vice versa [32,33].
Most of the existing researches for studying the Lyapunov stability, FTS, and FTB of switched systems are based on the types of time-dependent switching signals. Examples of time-dependent switching signals are dwell time (DT), average dwell time (ADT), and mode-dependent average dwell time (MDADT), comprising slow mode-dependent average dwell time (SMDADT) and fast mode-dependent average dwell time (FMDADT). The topic of FTS, FTB, and stability over the infinite time interval of SPSs with time delay has been investigated and reviewed in the following. In [34], Liu and Dang analyzed the stability of SPSs with delays. Later, Jian and Weiqun [35] studied the FTS and FTB for the continuous-time and discrete-time SPSs with time-varying delay. Depending on the ADT approach, the issue of FTB and -gain for SPSs with multiple time delays was discussed in [36]; however, the problem of stability for SPSs with time delay was examined in [37]. As mentioned in [38], Liu et al. used the MDADT method to derive some stability conditions of SPSs with time delay. Reference [39] dealt with the static output-feedback finite-time control problems for SPSs with time-varying delay by employing the MDADT strategy. The researches mentioned above mainly concentrate on the only stable (bounded) subsystems. Nevertheless, the switched systems composing both stable (bounded) subsystems and unstable (unbounded) subsystems can be implemented widely in practical applications [40,41,42,43,44]. Among them, in [40], Pashaei and Hashemzadeh derived new FTS and FTB conditions for linear switched delayed systems with finite-time unstable and unbounded subsystems by using the ADT tactic. Meanwhile, in [41], Tan et al. investigated FTS and FTB problems of switched systems consisting of both finite-time stable and unstable subsystems by employing the MDADT method. Based on Lyapunov-like functions, FTS and FTB issues of nonlinear switched systems with subsystems that are not finite-time stable or finite-time bounded were discussed by utilizing the ADT strategy in [42]. Still, the time delay phenomena and the positivity of the systems were not considered in the references [41,42]. For SPSs, in [43], Zhang et al. studied the stability problem of linear SPSs with stable and unstable subsystems by adopting a multiple copositive Lyapunov function combined with the ADT approach. Furthermore, the stability of nonlinear switched delayed systems, including stable and unstable subsystems, was analyzed in [44].
For real-world applications, several systems can represent in the form of uncertainties, which indicate the differences or errors between reality and simulation. Nonetheless, the dynamical systems, including the slight uncertainties, may lead to the instability of those systems. Consequently, many researchers have devoted themselves to studying the FTS, FTB, and stability of the systems with uncertainties during the last decades [45,46,47,48,49,50,51,52]. However, to the best of our knowledge, there is no result on the FTB for a class of SPSs, including time-varying delay, interval uncertainties, exogenous disturbance, and finite-time unbounded subsystems in the literature. This practical idea is the motivation of the present paper. The main contributions of this study are highlighted in the following. (i) The FTB problem of the underlying systems with finite-time bounded subsystems and finite-time unbounded subsystems is investigated by applying the SMDADT and FMDADT techniques. (ii) New delay-dependent sufficient criteria (DDSC) for FTB of the systems are derived. (iii) The corresponding result for SPSs, including time-varying delay and exogenous disturbance without interval uncertainties, is also provided. (iv) Unlike the existing results in [36,37,40,42,43,44], both the SMDADT and FMDADT methods that are less conservative and more applicable in practice than the ADT switching law are employed for studying the FTB of the systems.
The organization of this paper is arranged as follows. The next section, the system descriptions and preliminaries are proposed. Then, in Section 3, the main results are presented. Next, in Section 4, two numerical examples are shown to support and validate our theoretical results. Lastly, the conclusions are reported in Section 5.
Notations: The following notations are exploited throughout this article. The sets of non-negative integers and positive integers are denoted by and , respectively. and refer to the vectors of n-tuples of real and positive real numbers, respectively. The set of all real matrices is represented by . and are the dimensional identity matrix and the transpose of matrix A, respectively. For given vector , is the ith component of . The notation stands for non-negative (positive) vector, namely, all components of are non-negative (positive) for vector . Let be the 1-norm of . The matrix A is called non-negative matrix if all entries are non-negative and defined by . In addition, is the 1-norm of a matrix .
2. System Descriptions and Preliminaries
A class of linear switched time-varying delay system with interval uncertainties and exogenous disturbance can be stated as
where . is the switching signal, which is a piecewise constant function of time t. N is the number of subsystems or modes of the switched system. Without loss of generality, we suppose that is continuous from the right everywhere: . Let be a sequence of the switching instants, where is the initial time and is the mth switching instant, . We impose that and the ith subsystem is activated when . Based on the logical rule of the switching signal at the switching instant , system (1) switches from the jth subsystem to the ith subsystem, where . The time-varying delay satisfies and , where and d are known constants. For the interval uncertain of system (1), , and satisfy
and
where are the given constant system matrices with appropriate dimensions for all . As shown in [39], the exogenous disturbance is continuous satisfying the condition:
where and are a time constant and a known constant, respectively. is a vector-valued initial state on with the norm . Furthermore, let be the set of switching signal which has only finite number of switching for any finite-time interval.
Next, we will introduce some definitions, lemma, and assumption for studying system (1).
Definition 1
([39]). System (1) is said to be positive if for any initial function , for any exogenous disturbance and for any switching signal , the corresponding trajectory holds for all .
Definition 2
([39]). A matrix is said to be a Metzler matrix if all off-diagonal elements are non-negative.
Lemma 1
([39]). System (1) is positive if and only if are Metzler matrices, , and for all .
In general, several real systems can be modeled by systems in the form of interval uncertainties. Thus, the assumption of the interval uncertainties for studying the FTB of system (1) with exogenous disturbance is stated as follows.
Assumption 1
([10,48]). For each , and in system (1), there are the known Metzler matrices and the matrices such that , , and , where are the given constant system matrices with appropriate dimensions for all .
Definition 3
([36] (Finite-Time Boundedness)). Given two constants , a time constant , two vectors , and a switching signal . System (1) is said to be finite-time bounded with respect to if the solution of the system satisfies the condition:
,
where satisfies inequality (2).
The finite set is split into and ; namely, where denotes the set of finite-time bounded subsystems with respect to the required parameters and represents the set of finite-time unbounded subsystems with respect to the same required parameters , respectively.
The definitions of both the SMDADT and FMDADT switching laws are stated as follows.
Definition 4
([41]). For any and a switching signal , let be the numbers of the pth subsystem being activated and be the total running time of the pth subsystem, . We say that σ has the SMDADT if there exist two constants and such that
Definition 5
([41]). For any and a switching signal , let be the numbers of the qth subsystem being activated and be the total running time of the qth subsystem, . We say that σ has the FMDADT if there exist two constants and such that
3. Main Results
In this section, we investigate the problem of the FTB for system (1) with exogenous disturbance and interval uncertainties. The subsystems of the studied system are both finite-time bounded and finite-time unbounded. First, a class of quasi-alternative switching signals (QASSs) for system (1) is designed by utilizing a similar approach studied in [33,41].
(a) If , then ;
(b) If , then .
This implies that the considered system can switch from a finite-time bounded subsystem to any other subsystems, but cannot switch from a finite-time unbounded subsystem to another finite-time unbounded subsystem.
For convenience, we first define important symbols used in our main theorem as follows:
where represents the kth row and lth column entry of system matrices . And
where denotes the kth row and lth column entry of system matrices . Thus, we are ready to derive new DDSC for the FTB of system (1) with finite-time bounded and finite-time unbounded subsystems by designing QASSs above and using the MDADT method in the following theorem. Without loss of generality, we can select the constants in (3) and (4) satisfying and , .
Theorem 1.
Consider system (1) with exogenous disturbance satisfying Assumption 1. Let be given constants. For given two constants , the time constant , and two vectors . Suppose that there exist positive vectors and constants such that
hold for every . Then system (1) is positive and finite-time bounded with respect to under the switching signals with SMDADT satisfying
and FMDADT satisfying
where
, is the kth element of the vector , for , and is defined as in (5).
Proof.
We divide the proof process into the following two steps.
Step 1. We will prove that system (1) is positive.
By Assumption 1, it is immediate that are Metzler matrices and the matrices for all . However, the system matrices for system (1) are supposed to be interval uncertain, namely, , , and , for all . Thus, it is obvious that are also Metzler matrices, , and for all . According to Lemma 1, we can conclude that system (1) is positive.
Step 2. We will prove the FTB for system (1) under the switching signals with SMDADT satisfying condition (14) and FMDADT satisfying condition (15).
For any , let be the switching time instants over where and . For we construct the following copositive Lyapunov-Krasovskii functional (CLKF) candidate for system (1):
where Along the trajectory of system (1), we have
for We observe that
for Together with , and for all , one has
for According to the conditions (7) and (8), we obtain
for Substituting the conditions (9) and (10) into the inequality (17), it yields
for , and . Setting and integrating both sides of the inequality (18) during the period for , , it leads to
Considering the change of the value of the CLKF (16) at the switching time instants and the positivity of in system (1). According to the condition (11), we get
for all , and . Similarly, using the condition (12), we have
for all . Based on the relationship among the inequalities (19)–(21) for , we can derive
where , and is the kth element of the vector . It yields that
By the property of the exogenous disturbance in (2), it is immediate that
Using the CLKF (16), the conditions (9) and (10), and Definition 3 for the following estimations:
and
where . From the inequality (22), we have
Let . Hence,
for all . It follows from the condition (13) and the inequality (14) that
for all . Utilizing the inequalities (24) and (25), we arrive at
for all . It can be concluded by Definition 3 that system (1) is finite-time bounded with respect to for the switching signal with SMDADT (14) and FMDADT (15). □
Remark 1.
As in [33,41], in our switching scheme, we design slow and fast switching for bounded subsystems and unbounded subsystems, respectively. It gives the lower bounds that bounded subsystems should dwell on and provides the upper bounds for unbounded subsystems. In addition, one can note that if the bounded subsystem is activated, any subsystem can be activated at the next switching time instance. Nevertheless, if an unbounded subsystem is activated, the next activated system must be a bounded subsystem.
Another FTB result of system (1) without its interval uncertainty will be presented as follows:
Corollary 1.
Consider system (1) with exogenous disturbance. Let , be given constants. For given two constants , the time constant , and two vectors . Suppose that there exist positive vectors and constants such that
hold for every . Then system (1) is positive and finite-time bounded with respect to under the switching signals with SMDADT satisfying
and FMDADT satisfying
where
, is the kth element of the vector , for , and D is defined as in (6).
Proof.
With the same symbols in Theorem 1, this corollary can be proved by utilizing the following CLKF candidate for system (1):
where The remainder of the proof is similar to that of Theorem 1. Hence, the detail is omitted. □
4. Numerical Simulations
In this section, we provide two numerical examples together with the simulation results to demonstrate the correctness and effectiveness of our theoretical analysis presented in the previous section.
Example 1.
The FTB problem for system (1) comprising of two subsystems is studied in this example. The system data are given as follows:
Under the given time-varying delay above, we select and . According to Definition 2, one can see that and are Metzler matrices. Furthermore, it is obvious that , and . By Lemma 1 and Assumption 1, the studied system is positive. For the numerical simulations, we set the initial condition as , and let the system matrices be
and
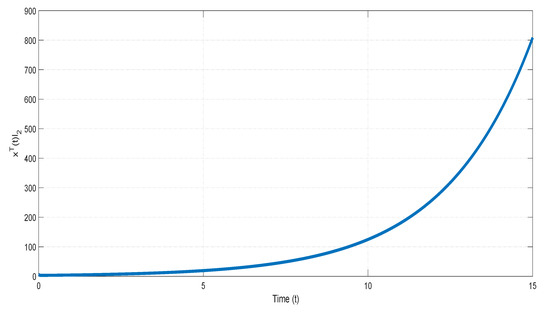
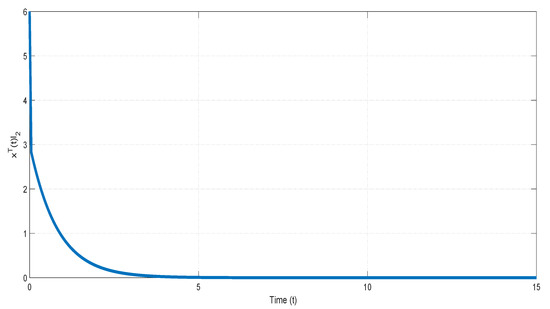
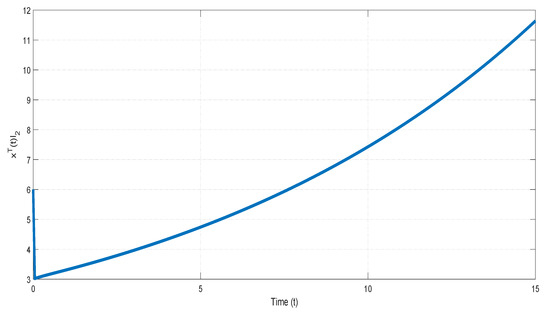
Given two positive vectors and . Then, we assign the positive constants and the time constant , which satisfies . From the condition of the exogenous disturbance defined as in (2), it is obvious that . The value of for the first subsystem and the second subsystem are shown respectively in Figure 1 and Figure 2. From two subsystems of the simulations, it is verified that the first subsystem is not finite-time bounded and the second one is finite-time bounded.

Figure 1.
The value of of the first subsystem in Example 1.

Figure 2.
The value of of the second subsystem in Example 1.
As defined in (5), it is obviously that
For given sclars and , we can get a set of feasible solution for Theorem 1:
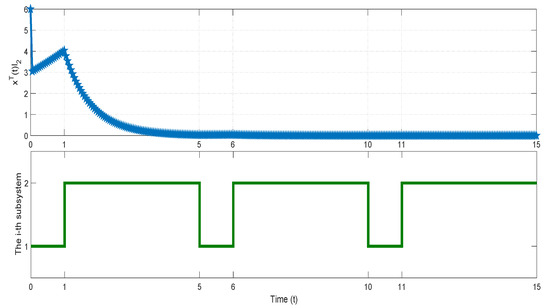
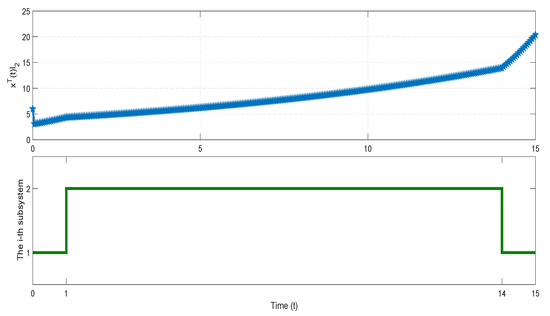
Thus, system (1) is finite-time bounded with respect to under the switching signal with SMDADT and FMDADT , which satisfy the conditions specified by (14) and (15), respectively. Let and for the first subsystem and the second subsystem, respectively. The value of of system (1) under the corresponding switching signal is depicted in Figure 3. The plot indicates that the value of at does not exceed . Consequently, we can conclude that system (1) is finite-time bounded with respect to .

Figure 3.
The value of of the system in Example 1 under the corresponding switching signal.
Example 2.
The same two constants and d can be selected as in Example 1. The positivity of the system in this example is also summarized as in Example 1. For the numerical simulations, we set the initial condition as , and let the system matrices be
and
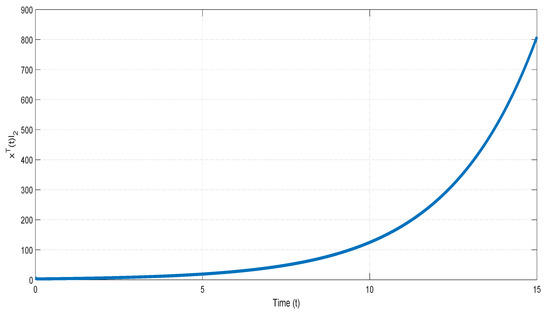
Let and . Next, we choose the same positive constants , , and which are given in Example 1. The value of for the first subsystem and the second subsystem are depicted respectively in Figure 4 and Figure 5. From two subsystems of the simulations, it is verified that the first subsystem is not finite-time bounded and the second one is finite-time bounded.

Figure 4.
The value of of the first subsystem in Example 2.

Figure 5.
The value of of the second subsystem in Example 2.
By (5), we can get the same proposed in Example 1. For given sclars , , and , we can get a set of feasible solution for Theorem 1:
Hence, system (1) is finite-time bounded with respect to under the switching signal with SMDADT and FMDADT . Let and for the first subsystem and the second subsystem, respectively. The value of of the system under the corresponding switching signal is presented in Figure 6. It can be seen that the value of increases significantly, but does not exceed the specified value of . Therefore, the studied system in this example is finite-time bounded with respect to .

Figure 6.
The value of of the system in Example 2 under the corresponding switching signal.
5. Conclusions
In this paper, the FTB problem for a class of SPSs, including time-varying delay, interval uncertainties, exogenous disturbance, and finite-time unbounded subsystems, has been studied. The design of QASSs for the systems whose subsystems are bounded and unbounded has been addressed. By taking advantage of the positivity of the considered systems combined with the SMDADT and the FMDADT methods, the suitable CLKF has been constructed, and some computable sufficient conditions for FTB have been formulated in the main theorem. Furthermore, novel DDSC of systems without the interval uncertainties have also been acquired in the corollary. Lastly, two numerical examples have been presented to illustrate the validity of the theoretical analysis.
Author Contributions
Conceptualization, formal analysis, investigation, methodology, software, validation, visualization, writing—original draft preparation, and writing—review and editing, T.M. and S.Y.; resources, S.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by Chiang Mai University. Suriyon Yimnet was supported by Post-Doctoral Fellowship of Chiang Mai University, Thailand.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
This research was supported by Chiang Mai University. This work contains a number of improvements based on comments and suggestions provided by Thaned Rojsiraphisal, Kanyuta Poochinapan, Ben Wongsaijai, Nuttawoot Nupo, and Attapol Praleah. Finally, we would like to thank the reviewers for their valuable comments to improve the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liberzon, D. Switching in Systems and Control; Springer: Boston, MA, USA, 2003. [Google Scholar]
- Mahmoud, M.S. Switched Time-Delay Systems: Stability and Control; Springer: New York, NY, USA, 2010. [Google Scholar]
- Wang, D.; Shi, P.; Wang, W. Robust Filtering and Fault Detection of Switched Delay Systems; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Rajchakit, G. Switching design for the robust stability of nonlinear uncertain stochastic switched discrete-time systems with interval time-varying delay. J. Comput. Anal. Appl. 2014, 16, 10–19. [Google Scholar]
- Haddad, W.M.; Chellaboina, V.; Hui, Q. Nonnegative and Compartmental Dynamical Systems; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Mahmoud, M.S. Switched delay-dependent control policy for water-quality systems. IET Control Theory Appl. 2009, 3, 1599–1610. [Google Scholar] [CrossRef]
- Zhang, J.; Sun, Y. Practical exponential stability of discrete-time switched linear positive systems with impulse and all modes unstable. Appl. Math. Comput. 2021, 409, 126408. [Google Scholar] [CrossRef]
- Bolajraf, M.; Tadeo, F.; Alvarez, T.; Rami, M.A. State-feedback with memory for controlled positivity with application to congestion control. IET Control Theory Appl. 2010, 4, 2041–2048. [Google Scholar] [CrossRef]
- Mason, O.; Shorten, R. On linear copositive Lyapunov functions and the stability of switched positive linear systems. IEEE Trans. Autom. Control 2007, 52, 1346–1349. [Google Scholar] [CrossRef] [Green Version]
- Feng, S.; Wang, J.; Zhao, J. Stability and robust stability of switched positive linear systems with all modes unstable. IEEE/CAA J. Autom. Sinica 2019, 6, 167–176. [Google Scholar] [CrossRef]
- Fridman, E. Introduction to Time-Delay Systems: Analysis and Control; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Kharitonov, V. Time-Delay Systems: Lyapunov Functionals and Matrices; Springer: New York, NY, USA, 2012. [Google Scholar]
- Wu, M.; He, Y.; She, J.-H. Stability Analysis and Robust Control of Time-Delay Systems; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Xiang, M.; Xiang, Z. Exponential stability of discrete-time switched linear positive systems with time-delay. Appl. Math. Comput. 2014, 230, 193–199. [Google Scholar] [CrossRef]
- Xiang, M.; Xiang, Z.; Lu, X.; Liu, Q. Stability, L1-gain and control synthesis for positive switched systems with time-varying delay. Nonlinear Anal. Hybrid Syst. 2013, 9, 9–17. [Google Scholar] [CrossRef]
- Xiang, M.; Xiang, Z. Finite-time L1 control for positive switched linear systems with time-varying delay. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 3158–3166. [Google Scholar] [CrossRef]
- Yu, T.; Zhong, Y.; Chen, T.; Chen, C. Finite-time stabilization of uncertain switched positive linear systems with time-varying delays. Discret. Dyn. Nat. Soc. 2015, 2015, 954782. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, X.; Lu, X.; Liu, Q. Stabilization of positive switched delay systems with all modes unstable. Nonlinear Anal. Hybrid Syst. 2018, 29, 110–120. [Google Scholar] [CrossRef]
- Yang, G.; Hao, F.; Zhang, L.; Li, B. Exponential stability for continue-time switched positive delay systems with all unstable subsystems. IEEE Access 2019, 7, 165428–165436. [Google Scholar] [CrossRef]
- Chousurin, R.; Mouktonglang, T.; Wongsaijai, B.; Poochinapan, K. Performance of compact and non-compact structure preserving algorithms to traveling wave solutions modeled by the Kawahara equation. Numer. Algorithms 2020, 85, 523–541. [Google Scholar] [CrossRef]
- Tamang, N.; Wongsaijai, B.; Mouktonglang, T.; Poochinapan, K. Novel algorithm based on modification of Galerkin finite element method to general Rosenau-RLW equation in (2+1)-dimensions. Appl. Numer. Math. 2020, 148, 109–130. [Google Scholar] [CrossRef]
- Disyadej, T.; Promjan, J.; Poochinapan, K.; Mouktonglang, T.; Grzybowski, S.; Muneesawang, P. High voltage power line maintenance & inspection by using smart robotics. In Proceedings of the 2019 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 18–21 February 2019; pp. 1–4. [Google Scholar]
- Wongsaijai, B.; Charoensawan, P.; Chaobankoh, T.; Poochinapan, K. Advance in compact structure-preserving manner to the Rosenau-Kawahara model of shallow-water wave. Math. Methods Appl. Sci. 2021, 44, 7048–7064. [Google Scholar] [CrossRef]
- Lin, X.; Zhang, W.; Yang, Z.; Zou, Y. Finite-time boundedness of switched systems with time-varying delays via sampled-data control. Int. J. Robust Nonlinear Control 2020, 30, 2953–2976. [Google Scholar] [CrossRef]
- Puangmalai, J.; Tongkum, J.; Rojsiraphisal, T. Finite-time stability criteria of linear system with non-differentiable time-varying delay via new integral inequality. Math. Comput. Simul. 2020, 171, 170–186. [Google Scholar] [CrossRef]
- Saravanan, S.; Ali, M.S.; Rajchakit, G.; Hammachukiattikul, B.; Priya, B.; Thakur, G.K. Finite-time stability analysis of switched genetic regulatory networks with time-varying delays via Wirtinger’s integral inequality. Complexity 2021, 2021, 9540548. [Google Scholar] [CrossRef]
- Rojsiraphisal, T.; Mobayen, S.; Asad, J.H.; Vu, M.T.; Chang, A.; Puangmalai, J. Fast terminal sliding control of underactuated robotic systems based on disturbance observer with experimental validation. Mathematics 2021, 9, 1935. [Google Scholar] [CrossRef]
- Amato, F.; Ambrosino, R.; Ariola, M.; Tommasi, G.D.; Pironti, A. On the finite-time boundedness of linear systems. Automatica 2019, 107, 454–466. [Google Scholar] [CrossRef]
- Amato, F.; Ariola, M.; Dorato, P. Finite-time control of linear systems subject to parametric uncertainties and disturbances. Automatica 2001, 37, 1459–1463. [Google Scholar] [CrossRef]
- Amato, F.; Ariola, M.; Cosentino, C. Finite-time stability of linear time-varying systems: Analysis and controller design. IEEE Trans. Autom. Control 2010, 55, 1003–1008. [Google Scholar] [CrossRef]
- Weiss, L.; Infante, E.F. Finite time stability under perturbing forces and on product spaces. IEEE Trans. Autom. Control 1967, 12, 54–59. [Google Scholar] [CrossRef]
- Hien, L.V. An explicit criterion for finite-time stability of linear nonautonomous systems with delays. Appl. Math. Lett. 2014, 30, 12–18. [Google Scholar] [CrossRef]
- Yimnet, S.; Niamsup, P. Finite-time stability and boundedness for linear switched singular positive time-delay systems with finite-time unstable subsystems. Syst. Sci. Control. Eng. 2020, 8, 541–568. [Google Scholar] [CrossRef]
- Liu, X.; Dang, C. Stability analysis of positive switched linear systems with delays. IEEE Trans. Autom. Control 2011, 56, 1684–1690. [Google Scholar] [CrossRef]
- Jian, S.; Weiqun, W. Finite-time stability and boundedness for positive switched systems with time-varying delay under state-dependent switching. Trans. Inst. Meas. Control. 2017, 39, 43–51. [Google Scholar] [CrossRef]
- Liu, Y.; Tao, W.; Lee, L.; Lu, J. Finite-time boundedness and L2-gain analysis for switched positive linear systems with multiple time delays. Int. J. Robust Nonlinear Control 2017, 27, 3508–3523. [Google Scholar]
- Zhao, X.; Zhang, L.; Shi, P. Stability of a class of switched positive linear time-delay systems. Int. J. Robust Nonlinear Control 2013, 23, 578–589. [Google Scholar] [CrossRef]
- Liu, L.-J.; Zhao, X.; Wu, D. Stability of switched positive linear time-delay systems. IET Control Theory Appl. 2019, 13, 912–919. [Google Scholar] [CrossRef]
- Liu, J.; Lian, J.; Zhuang, Y. Output feedback L1 finite-time control of switched positive delayed systems with MDADT. Nonlinear Anal. Hybrid Syst. 2015, 15, 11–22. [Google Scholar] [CrossRef]
- Pashaei, S.; Hashemzadeh, F. New finite-time stability and boundedness conditions for time-delay switched linear systems with finite-time unstable and unbounded subsystems. In Proceedings of the 27th Iranian Conference on Electrical Engineering (ICEE2019), Yazd, Iran, 30 April–2 May 2019. [Google Scholar]
- Tan, J.; Wang, W.; Yao, J. Finite-time stability and boundedness of switched systems with finite-time unstable subsystems. Circuits Syst. Signal Process. 2019, 38, 2931–2950. [Google Scholar] [CrossRef]
- Li, X.; Lin, X.; Li, S.; Zuo, Y. Finite-time stability of switched nonlinear systems with finite-time unstable subsystems. J. Frankl. Inst. 2015, 352, 1192–1214. [Google Scholar] [CrossRef]
- Zhang, J.-S.; Wang, Y.-W.; Xiao, J.-W.; Shen, Y.-J. Stability analysis of switched positive linear systems with stable and unstable subsystems. Int. J. Syst. Sci. 2014, 45, 2458–2465. [Google Scholar] [CrossRef]
- Tian, Y.; Cai, Y.; Sun, Y. Stability of switched nonlinear time-delay systems with stable and unstable subsystems. Nonlinear Anal. Hybrid Syst. 2017, 24, 58–68. [Google Scholar] [CrossRef]
- Rajchakit, G.; Rojsiraphisal, T.; Rajchakit, M. Robust stability and stabilization of uncertain switched discrete-time systems. Adv. Differ. Equ. 2012, 134, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Ma, R.; Wang, X.; Liu, Y. Robust stability of switched positive linear systems with interval uncertainties via multiple time-varying linear copositive Lyapunov functions. Nonlinear Anal. Hybrid Syst. 2018, 30, 285–292. [Google Scholar] [CrossRef]
- Zhang, J.; Han, Z. Robust stabilization of switched positive linear systems with uncertainties. Int. J. Control Autom. Syst. 2013, 11, 41–47. [Google Scholar] [CrossRef]
- Rojsiraphisal, T.; Niamsup, P.; Yimnet, S. Global uniform asymptotic stability criteria for linear uncertain switched positive time-varying delay systems with all unstable subsystems. Mathematics 2020, 8, 2118. [Google Scholar] [CrossRef]
- Moradi, E.; Jahed-Motlagh, M.R.; Yazdi, M.B. Delay-dependent finite-time stabilization of uncertain switched time-delay systems with norm-bounded disturbance. IETE J. Res. 2018, 64, 195–208. [Google Scholar] [CrossRef]
- Puangmalai, W.; Puangmalai, J.; Rojsiraphisal, T. Robust finite-time control of linear system with non-differentiable time-varying delay. Symmetry 2020, 12, 680. [Google Scholar] [CrossRef]
- Rajchakit, G. Robust stability and stabilization of nonlinear uncertain stochastic switched discrete-time systems with interval time-varying delays. Appl. Math. Inf. Sci. 2012, 6, 555–565. [Google Scholar]
- Rajchakit, G. Switching design for the asymptotic stability and stabilization of nonlinear uncertain stochastic discrete-time systems. Int. J. Nonlinear Sci. Numer. Simul. 2013, 14, 33–44. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).