Effective Optimisation of the Patient Circuits of an Oncology Day Hospital: Mathematical Programming Models and Case Study
Abstract
:1. Introduction
2. Motivation: The Problem of the ODH in Santiago de Compostela (Spain)
3. Literature Review
4. Contribution of the Paper
- The first contribution was to measure the times involved in the circuit for all patients visiting the centre during a normal working week. Despite the difficulty of this task, the collaboration of each and every one of the CHUS professionals involved has been very valuable and has not only served to feed the models developed in the work, but has also shed light on the true reality of the times of the different stages of the circuit. This is of great use to the aforementioned professionals and in making different decisions aimed at improving the service.
- Then, the model proposed in [17] was selected as it represents a problem very close to that of ODH and solves it very efficiently, and its objective and restrictions were adapted to fully represent our problem. The data collected have been used for the definition of the model parameters. A data-driven procedure is used to determine the ready times at which each patient can receive cancer treatment. While providing promising initial results, this model is deterministic and is not able to capture the underlying stochasticity in the mix of patients.
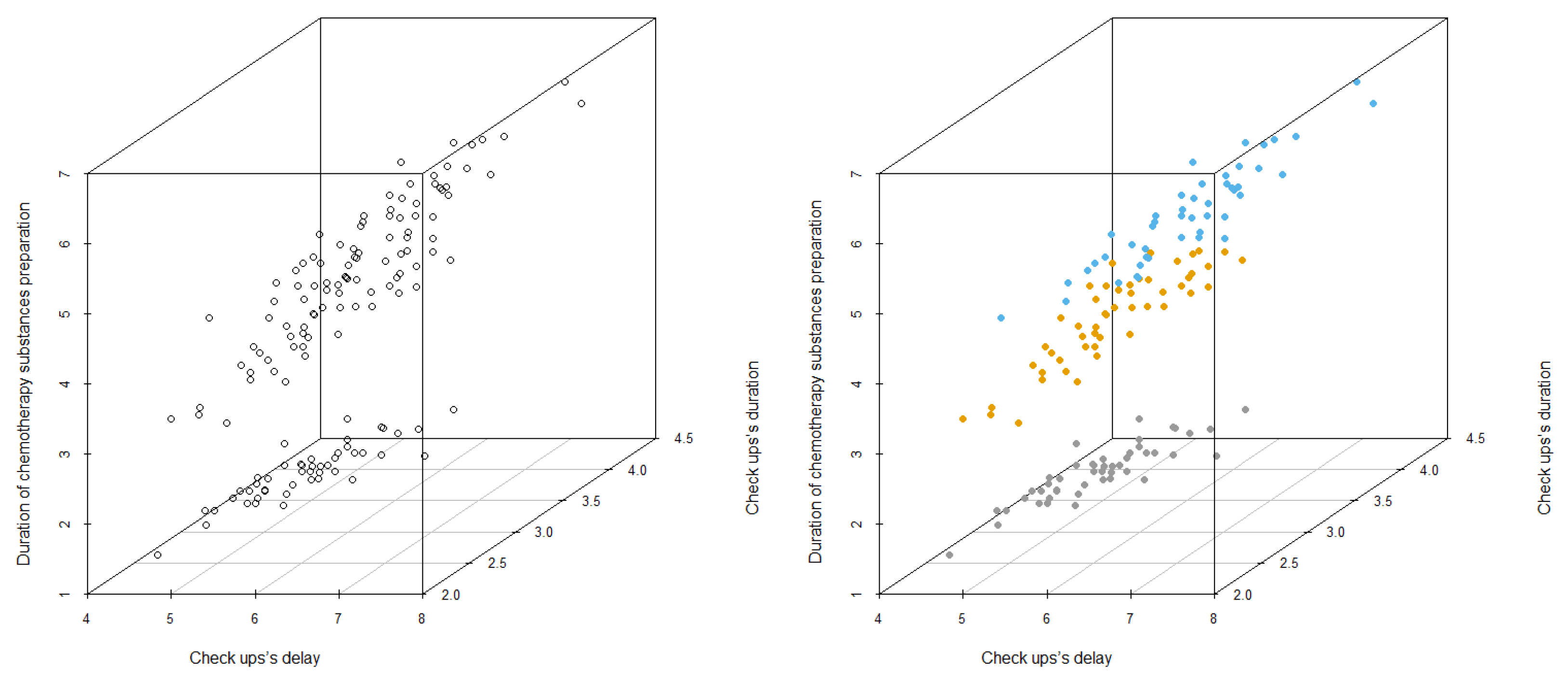
- Thus, a second model is proposed, which generalises the previous one and, following the [22] approach, it is based on the data driven construction of different scenarios obtained from cluster analysis methods, that take into account the stochasticity of the times of the different stages of the process and the consequent variety in the patient mix. This second model achieves the objective of not only scheduling treatment appointments but also rescheduling appointments with oncologists from the original ones. In addition, an improvement in patient waiting times is achieved by comparing the results provided by the model with the available data. All models are programmed with the AMPL [33] language and solved with the Gurobi ( https://www.gurobi.com/, last accessed 20 Decemer 2021) solver in a fast way (seconds). The PC used for this work was a Lenovo Intel(R) Core(TM) i7-1065G7, 8 GB RAM, Windows 10 64-bit operating system.
- Finally, the results obtained in both models feed a third and last model created to assign the nurses in charge of providing the treatment to the patients.
5. Materials and Methods
5.1. Deterministic Model for Treatment Appointments
5.1.1. Parameters
- P: it establishes the number of patients with a chemotherapic appointment.
- K: it establishes the number of chemotherapic chairs available.
- T: it establishes the number of time slots used to split the 14 daily working hours.
- with p∈: chemotherapic treatments’ duration of each patient.
- with p∈: it establishes, for each patient, the first time slot where his chemotherapic treatment could be scheduled.
- with t∈: number of available nurses inside the chemotherapic room for each time slot.
5.1.2. Variables
- with p and t : binary variable that is equal to 1 if the p patient begins his treatment in the time slot t.
- : integer variable that establishes which time slot will be the first one with no treatment associated.
- and : positive real variables. We will use them in order to ponder both parts of the bi-objective function.
5.1.3. Mathematical Model
- Important Differences between the Models of the ODH and Those Presented in Previous Related Investigations:
5.2. Stochastic Model of Oncologist and Treatment Appointments
5.2.1. Parameters
5.2.2. Variables
- with p and t : binary variable, for scenario 1, that is equal to 1 if the p patient begins his treatment in the time slot t.
- with p and t : binary variable, for scenario 2, that is equal to 1 if the p patient begins his treatment in the time slot t.
- with p and t : binary variable, for scenario 3, that is equal to 1 if the p patient begins his treatment in the time slot t.
- with p and t : binary variable, for scenario 4, that is equal to 1 if the p patient begins his treatment in the time slot t.
- with p and t : (first stage) binary variable that is equal to 1 if the p patient is scheduled for the oncologist in the time slot t.
5.2.3. Objective Function of the Mathematical Model
- represents the period in which he starts his treatment,
- represents the period in which he is scheduled for the oncologist.
- is the waiting time of patient p from the theoretical exit of the appointment with the oncologist to the start of treatment, and
- is the total waiting time from the theoretical exits of the appointment with the oncologist to the start of treatments, in scenario 1.
5.3. Model of Nurse-to-Patient Allocation
5.3.1. Parameters
- P: it establishes the number of patients with a chemotherapic appointment.
- T: it establishes the number of time slots used to split the 14 working hours.
- wth t∈: number of available nurses inside the chemotherapic room for each time slot.
- with p∈ and t∈: binary parameter that is equal to 1 if patient p has his appointment scheduled for time slot t.
5.3.2. Variables
- with p ∈, t and i : binary variable that is equal to 1 if patient p begins his appointment during time slot t assisted by nurse i.
5.3.3. Mathematical Model
6. Results of the Case Study
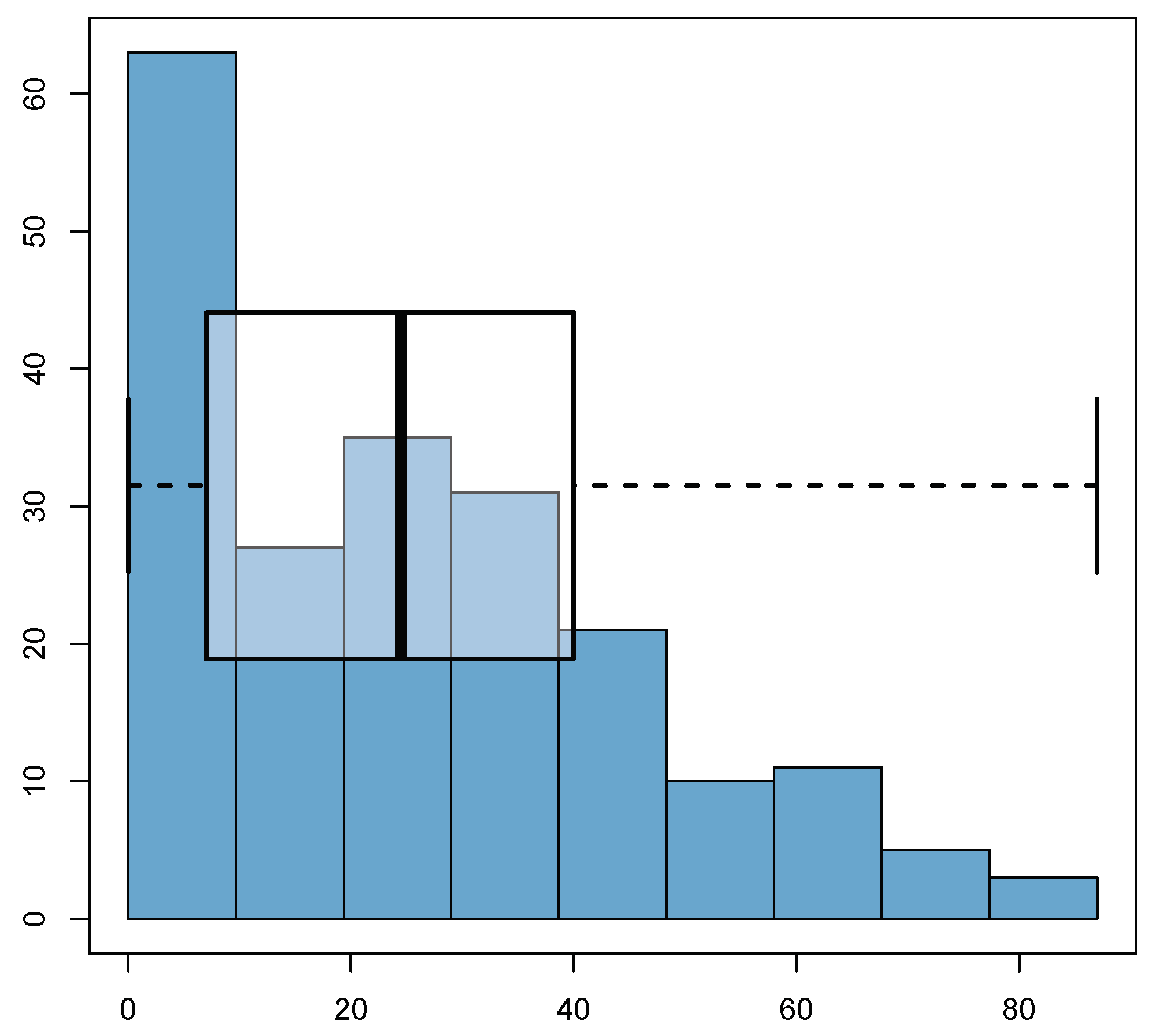
6.1. Summary of the Collected Data
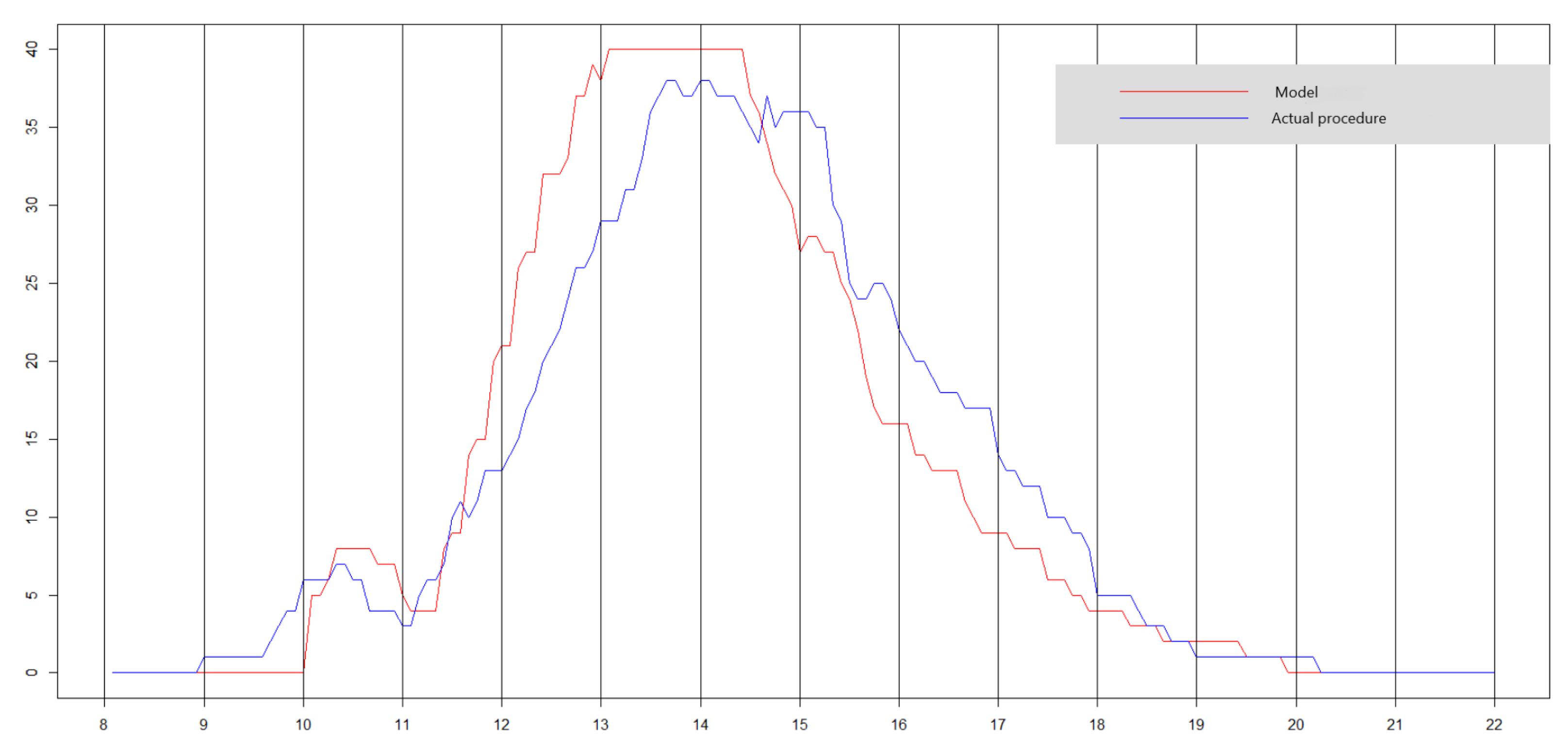
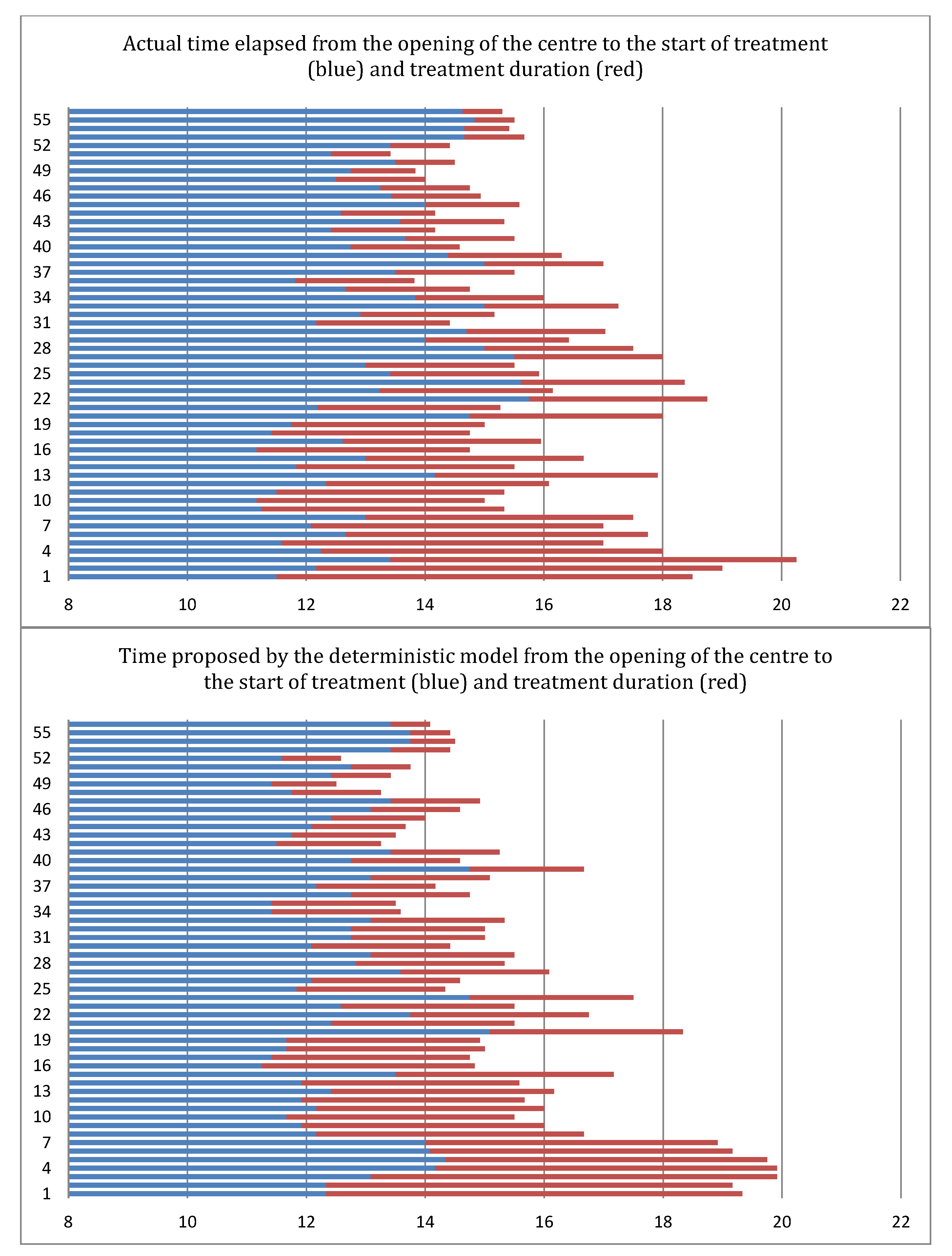
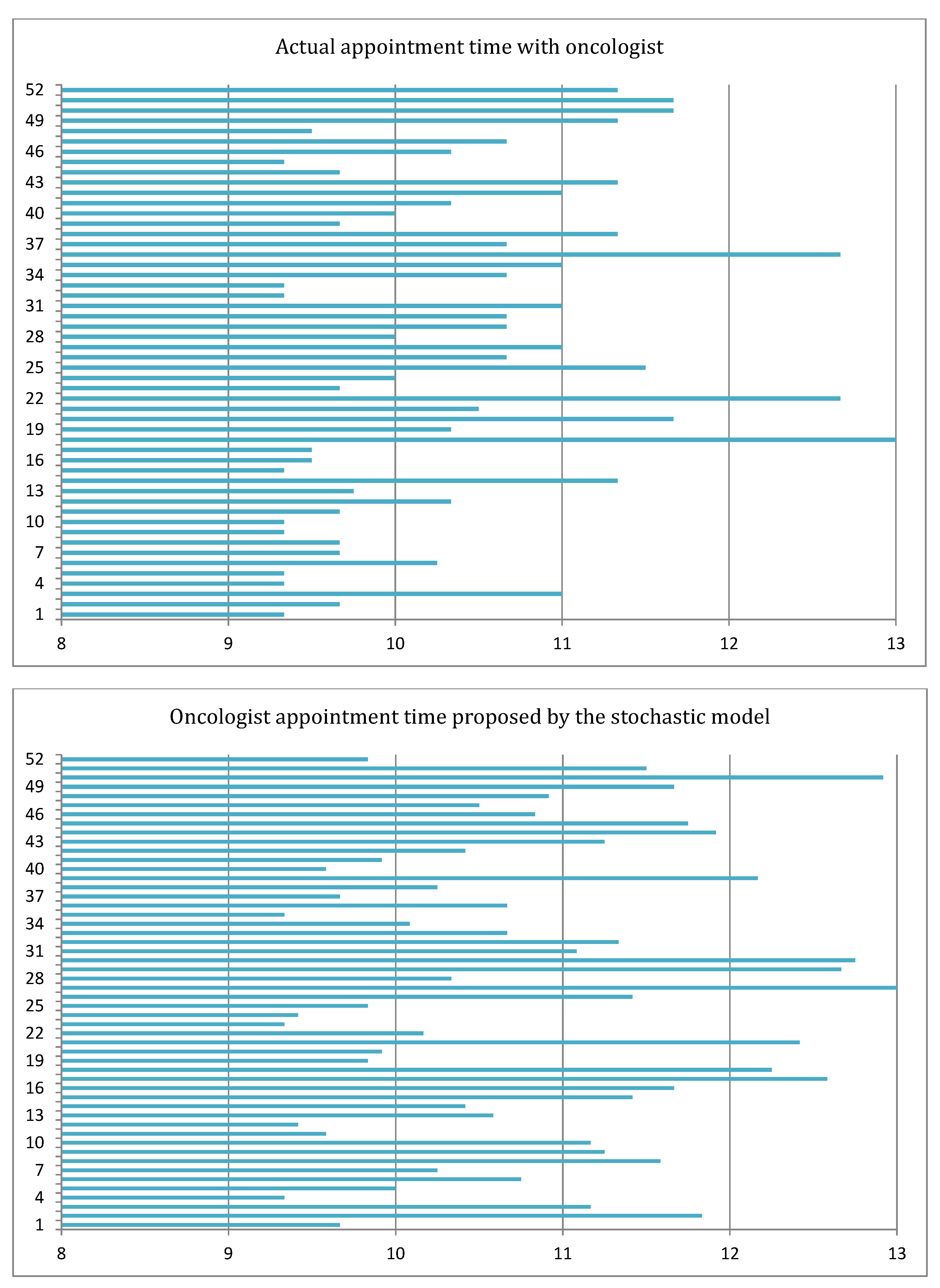
6.2. Results of the Deterministic Model
6.3. Results of the Stochastic Model
7. Discussion, Conclusions and Framework for a Further Research Agenda
Framework for a Further Research Agenda
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AMPL | A Mathematical Programming Language |
| CHUS | Hospital Clínico Universitario of Santiago de Compostela |
| ODH | Onco-haematological Day Hospital |
| IDIS | Healt Research Institute of Santiago de Compostela |
| LGOM | Learning-based outpatient management |
| ONCOMET | Translational Medical Oncology Group |
| OpenSolver | Excel add-in for solving optimization models |
| SCHA | Santiago de Compostela Health Area |
| SERGAS | Galician Health Service |
Appendix A. The Two-Stage Stochastic Model in Extensive Form
- param #Number of patients assigned to the working day
- param ; #Duration of patients’ chemotherapy treatments
- param ; #Number of time intervals that constitute the working day
- param ; #Number of available nurses during each time interval
- param integer; #Minutes consumed by delay of appointments, their duration and preparation of
- chemotherapy substances (scenario 1)
- param integer; #Idem scenario 2
- param integer; #Idem scenario 3
- param integer; #Idem scenario 4
- param ; #Number of available chemotherapy chairs
- param ; #Number of nurses working during the day
- param M; #Number of treatments that a nurse can simultaneously supervise
- set E1; #Cancer type I patients
- set E2; #Cancer type II patients
- set E3; #Cancer type III patients
- var c binary; #Medical check-ups schedule
- var y binary; #Chemotherapy treatments schedule at scenario 1
- var f binary; #Idem at scenario 2
- var x binary; #Idem at scenario 3
- var z binary; #Idem at scenario 4
- 0.287*sum ((sum(t*y[p,t]))-(sum(t*c[p,t]))- 2.6)
- +0.272*sum ((sum(t*f[p,t]))-(sum(t*c[p,t]))-4.2)
- +0.364*sum ((sum(t*x[p,t]))-(sum(t*c[p,t]))-2.2)
- +0.078*sum ((sum(t*z[p,t]))-(sum(t*c[p,t]))-1.8);
- subject to restriction0 :
- sum c[p,t]=0; #Impossible to program medical check-ups before 09:20
- subject to restriction0b :
- sum c[p,t]=0; #Impossible to program medical check-ups after 13:00
- subject to restriction0c :
- sum c[p,t]=1; #Each patient has his medical check-up programmed
- subject to restriction1 :
- sum y[p,t]=1; #At scenario 1, each patient begins his treatment
- subject to restriction1b :
- sum f[p,t]=1; #At scenario 2, idem
- subject to restriction1c :
- sum x[p,t]=1; #At scenario 3, idem
- subject to restriction1d :
- sum z[p,t]=1; #At scenario 4, idem
- subject to restriction2 {p in 1..P}:
- (sum{t in 1..T}(t*y[p,t]))-(sum{t in 1..T}(t*c[p,t]))-q-1≥0;
- #Each chemotherapy treatment begins after substances are ready and after the medical check-up is finished (scenario 1)
- subject to restriction2b {p in 1..P}:
- (sum{t in 1..T}(t*f[p,t]))-(sum{t in 1..T}(t*c[p,t]))-u-1≥0; #At scenario 2, idem
- subject to restriction2c {p in 1..P}:
- (sum{t in 1..T}(t*x[p,t]))-(sum{t in 1..T}(t*c[p,t]))-v-1≥0; #At scenario 3, idem
- subject to restriction2d {p in 1..P}:
- (sum{t in 1..T}(t*z[p,t]))-(sum{t in 1..T}(t*c[p,t]))-s-1≥0; #At scenario 4, idem
- subject to restriction3 {t in 1..T}:
- sum{p in 1..P, a in max(1,t-l[p]+1)..t} y[p,a]≤K; #At scenario 1, there aren’t more ongoing treatments than chairs
- subject to restriction3b {t in 1..T}:
- sum{p in 1..P, a in max(1,t-l[p]+1)..t} f[p,a]≤K; #At scenario 2, idem
- subject to restriction3c {t in 1..T}:
- sum{p in 1..P, a in max(1,t-l[p]+1)..t} x[p,a]≤K; #At scenario 3, idem
- subject to restriction3d {t in 1..T}:
- sum{p in 1..P, a in max(1,t-l[p]+1)..t} z[p,a]≤K; #At scenario 4, idem
- subject to restriction4 {t in 1..T}:
- sum{p in 1..P}((1-1/M)*y[p,t])≤Ndisp[t]; #At scenario 1, nurses can begin one treatment for time interval
- subject to restriction4b {t in 1..T}:
- sum{p in 1..P}((1-1/M)*f[p,t])≤Ndisp[t]; #At scenario 2, idem
- subject to restriction4c {t in 1..T}:
- sum{p in 1..P}((1-1/M)*x[p,t])≤Ndisp[t]; #At scenario 3, idem
- subject to restriction4d {t in 1..T}:
- sum{p in 1..P}((1-1/M)*z[p,t])≤Ndisp[t]; #At scenario 4, idem
- subject to restriction5 {t in 1..T}:
- sum{p in 1..P}((1/M)*(sum{a in max(1,t-l[p]+1)..t}y[p,a]))≤Ndisp[t];#At each time interval, it is not possible to have more than 16 ongoing treatments for each available nurse (scenario 1)
- subject to restriction5b {t in 1..T}:
- sum{p in 1..P}((1/M)*(sum{a in max(1,t-l[p]+1)..t}f[p,a]))≤Ndisp[t]; #At scenario 2, idem
- subject to restriction5c {t in 1..T}:
- sum{p in 1..P}((1/M)*(sum{a in max(1,t-l[p]+1)..t}x[p,a]))≤Ndisp[t]; #At scenario 3, idem
- subject to restriction5d {t in 1..T}:
- sum{p in 1..P}((1/M)*(sum{a in max(1,t-l[p]+1)..t}z[p,a]))≤Ndisp[t]; #At scenario 4, idem
- subject to restriction6 {t in 16..60}:
- sum{p in E1, a in t..t+2} c[p,t]≤3; #Cancer type I medical specialists can only handle 1 patient per 15 min
- subject to restriction6b {t in 16..60}:
- sum{p in E2, a in t..t+2} c[p,t]≤3; #Cancer type II idem
- subject to restriction6c {t in 16..60}:
- sum{p in E3, a in t..t+2} c[p,t]≤3; #Cancer type III idem
- #Following constraints ensure that every 15 min the number of starting treatments do not exceed nurses working capacity:
- subject to restriction7 {t in 1..24}:
- sum{p in 1..P, a in t..t+2} y[p,a]≤5;
- subject to restriction7b {t in 1..24}:
- sum{p in 1..P, a in t..t+2} f[p,a]≤5;
- subject to restriction7c {t in 1..24}:
- sum{p in 1..P, a in t..t+2} x[p,a]≤5;
- subject to restriction7d {t in 1..24}:
- sum{p in 1..P, a in t..t+2} z[p,a]≤5;
- subject to restriction8 {t in 25..84}:
- sum{p in 1..P, a in t..t+2} y[p,a]≤6;
- subject to restriction8b {t in 25..84}:
- sum{p in 1..P, a in t..t+2} f[p,a]≤6;
- subject to restriction8c {t in 25..84}:
- sum{p in 1..P, a in t..t+2} x[p,a]≤6;
- subject to restriction8d {t in 25..84}:
- sum{p in 1..P, a in t..t+2} z[p,a]≤6;
- subject to restriction9 {t in 85..108}:
- sum{p in 1..P, a in t..t+2} y[p,a]≤3;
- subject to restriction9b {t in 85..108}:
- sum{p in 1..P, a in t..t+2} f[p,a]≤3;
- subject to restriction9c {t in 85..108}:
- sum{p in 1..P, a in t..t+2} x[p,a]≤3;
- subject to restriction9d {t in 85..108}:
- sum{p in 1..P, a in t..t+2} z[p,a]≤3;
- subject to restriction10 {t in 109..165}:
- sum{p in 1..P, a in t..t+2} y[p,a]≤2;
- subject to restriction10b {t in 109..165}:
- sum{p in 1..P, a in t..t+2} f[p,a]≤2;
- subject to restriction10c {t in 109..165}:
- sum{p in 1..P, a in t..t+2} x[p,a]≤2;
- subject to restriction10d {t in 109..165}:
- sum{p in 1..P, a in t..t+2} z[p,a]≤2;
References
- Alvarado, M.M.; Cotton, T.G.; Ntaimo, L.; Pérez, E.; Carpentier, W.R. Modeling and simulation of oncology clinic operations in discrete event system specification. Simulation 2018, 94, 105–121. [Google Scholar] [CrossRef]
- Brozos-Vázquez, E. Patients´ satisfaction when visiting day Hospital in Santiago de Compostela. Presented at the 1st Oncology Quality Care Symposium “Towards Excellence in Oncology Care”, Madrid, Spain, 15–16 November 2019. [Google Scholar]
- López-Rodríguez, R. Patient waiting time from the appointment with the oncologist to the administration of intravenous treatment in the University Clinical Hospital of Santiago de Compostela. Presented at the 1st Oncology Quality Care Symposium “Towards Excellence in Oncology Care”, Madrid, Spain, 15–16 November 2019. [Google Scholar]
- Ahmadi-Javid, A.; Jalali, Z.; Klassen, K.J. Outpatient appointment systems in healthcare: A review of optimization studies. Eur. J. Oper. Res. 2017, 258, 3–34. [Google Scholar] [CrossRef]
- Elleuch, M.A.; Hassena, A.B.; Abdelhedi, M.; Pinto, F.S. Real-time prediction of COVID-19 patients health situations using Artificial Neural Networks and Fuzzy Interval Mathematical modeling. Appl. Soft Comput. 2021, 110, 107643. [Google Scholar] [CrossRef] [PubMed]
- Gür, S.; Eren, T.; Alakaş, H.M. Surgical operation scheduling with goal programming and constraint programming: A case study. Mathematics 2019, 7, 251. [Google Scholar] [CrossRef] [Green Version]
- Horvat, A.M.; Dudic, B.; Radovanov, B.; Melovic, B.; Sedlak, O.; Davidekova, M. Binary programming model for rostering ambulance crew-relevance for the management and business. Mathematics 2021, 9, 64. [Google Scholar] [CrossRef]
- Hanna, T.P.; King, W.D.; Thibodeau, S.; Jalink, M.; Paulin, G.A.; Harvey-Jones, E.; O’Sullivan, D.E.; Booth, C.M.; Sullivan, R.; Aggarwal, A. Mortality due to cancer treatment delay: Systematic review and meta-analysis. BMJ 2020, 371, m4087. [Google Scholar] [CrossRef] [PubMed]
- Naiker, U.; FitzGerald, G.; Dulhunty, J.M.; Rosemann, M. Time to wait: A systematic review of strategies that affect out-patient waiting times. Aust. Health Rev. 2018, 42, 286–293. [Google Scholar] [CrossRef]
- Williams, M.V.; Drinkwater, K.J.; Jones, A.; O’Sullivan, B.; Tait, D. Waiting times for systemic cancer therapy in the United Kingdom in 2006. Br. J. Cancer 2008, 99, 695–703. [Google Scholar] [CrossRef]
- Chan, K.; Li, W.; Medlam, G.; Higgins, J.; Bolderston, A.; Yi, Q.; Wenz, J. Investigating patient wait times for daily outpatient radiotherapy appointments (a single-centre study). J. Med. Imaging Radiat. Sci. 2010, 41, 145–151. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, B.A.; Khairatul, K.; Farnaza, A. An assessment of patient waiting and consultation time in a primary healthcare clinic. Malays. Fam. Physician J. 2017, 12, 14–21. [Google Scholar]
- Yu, W.; Shen, Z.; Mi, Y. Reducing outpatients’ waiting time in oncology clinic by improving management software. Acad. J. Educ. Res. 2017, 5, 392–398. [Google Scholar]
- Turkcan, A.; Zeng, B.; Lawley, M. Chemotherapy operations planning and scheduling. IIE Trans. Healthc. Syst. Eng. 2012, 2, 31–49. [Google Scholar] [CrossRef]
- Liang, B.; Turkcan, A.; Ceyhan, M.E.; Stuart, K. Improvement of chemotherapy patient flow and scheduling in an outpatient oncology clinic. Int. J. Prod. Res. 2015, 53, 7177–7190. [Google Scholar] [CrossRef]
- Heshmat, M.; Eltawil, A. Solving operational problems in outpatient chemotherapy clinics using mathematical programming and simulation. Ann. Oper. Res. 2019, 298, 289–306. [Google Scholar] [CrossRef]
- Hesaraki, A.F.; Dellaert, N.P.; de Kok, T. Generating outpatient chemotherapy appointment templates with balanced flowtime and makespan. Eur. J. Oper. Res. 2019, 275, 304–318. [Google Scholar] [CrossRef]
- Benzaid, M.; Lahrichi, N.; Rousseau, L.M. Chemotherapy appointment scheduling and daily outpatient–nurse assignment. Health Care Manag. Sci. 2020, 23, 34–50. [Google Scholar] [CrossRef] [PubMed]
- Issabakhsh, M.; Lee, S.; Kang, H. Scheduling patient appointment in an infusion center: A mixed integer robust optimization approach. Health Care Manag. Sci. 2021, 24, 117–139. [Google Scholar] [CrossRef]
- Harnpornchai, N.; Autchariyapanitkul, K.; Sirisrisakulchai, J.; Sriboonchitta, S. Optimal outpatient appointment system with uncertain parameters using adaptive-penalty genetic algorithm. J. Adv. Comput. Intell. Intell. Inform. 2015, 19, 585–592. [Google Scholar] [CrossRef]
- Castaing, J.; Cohn, A.; Denton, B.; Weizer, A. A stochastic programming approach to reduce patient wait times and overtime in an outpatient infusion center. IIE Trans. Healthc. Syst. Eng. 2016, 6, 111–125. [Google Scholar] [CrossRef]
- Leeftink, A.G.; Vliegen, I.M.H.; Hans, E.W. Stochastic integer programming for multi-disciplinary outpatient clinic planning. Health Care Manag. Sci. 2019, 22, 53–67. [Google Scholar] [CrossRef] [Green Version]
- Demir, N.B.; Gul, S.; Çelik, M. A stochastic programming approach for chemotherapy appointment scheduling. Nav. Res. Logist. 2021, 68, 112–133. [Google Scholar] [CrossRef]
- Liang, B. Chemotherapy Scheduling and Nurse Assignment. Ph.D. Thesis, Northeastern University, Boston, MA, USA, 2015. [Google Scholar]
- Yokouchi, M.; Aoki, S.; Sang, H.; Zhao, R.; Takakuwa, S. Operations analysis and appointment scheduling for an outpatient chemotherapy department. In Proceedings of the 2012 Winter Simulation Conference (WSC), Berlin, Germany, 9–12 December 2012; pp. 1–12. [Google Scholar]
- Huggins, A.; Claudio, D.; Pérez, E. Improving resource utilization in a cancer clinic: An optimization model. In Proceedings of the 2014 Industrial and Systems Engineering Research Conference, Toronto, ON, Canada, 31 May–3 June 2014. [Google Scholar]
- Santibáñez, P.; Chow, V.S.; French, J.; Puterman, M.L.; Tyldesley, S. Reducing patient wait times and improving resource utilization at British Columbia Cancer Agency’s ambulatory care unit through simulation. Health Care Manag. Sci. 2009, 12, 392–407. [Google Scholar] [CrossRef] [PubMed]
- Suss, S.; Bhuiyan, N.; Demirli, K.; Batist, G. Toward implementing patient flow in a cancer treatment center to reduce patient waiting time and improve efficiency. J. Oncol. Pract. 2017, 13, 530–537. [Google Scholar] [CrossRef] [PubMed]
- Issabakhsh, M. A Simulation-based Optimization Approach for Integrated Outpatient Flow and Medication Management. Ph.D. Thesis, University of Miami, Coral Gables, FL, USA, 2021. [Google Scholar]
- Creps, J.; Lotfi, V. A dynamic approach for outpatient scheduling. J. Med. Econ. 2017, 20, 786–787. [Google Scholar] [CrossRef]
- Laurainne, P. Optimisation du Parcours Patient en Hôpital de Jour en Oncohématologie par Simulation Intégrée à une Démarche Kaizen. Master’s Thesis, University of Montreal, Montreal, QC, Canada, 2016. [Google Scholar]
- Laurainne, P.; Jobin, M.H.; Cordeau, J.F.; Becker, G.; Shanti, A.; Kurtz, J.E.; Gourieux, B. Optimisation du parcours patient en hôpital de jour en oncohématologie par simulation intégrée à une démarche kaizen. Logist. Manag. 2017, 25, 34–42. [Google Scholar] [CrossRef]
- Fourer, R.; Gay, D.; Kernighan, B.W. AMPL. A Modeling Language for Mathematical Programming; Thomson: Stamford, CT, USA, 2003. [Google Scholar]
- Birge, J.R.; Louveaux, F. Introduction to Stochastic Programming, 2nd ed.; Springer Series in Operations Research and Financial Engineering: New York, NY, USA, 2011. [Google Scholar]
- Shapiro, A.; Dentcheva, D.; Ruszczynski, A. Lectures on Stochastic Programming: Modeling and Theory; SIAM: Philadelphia, PA, USA, 2009. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedmand, J. The Elements of Statistical Learning, 2nd ed.; Springer Series in Statistics: New York, NY, USA, 2008; Volume 1. [Google Scholar]
- Verderame, P.M.; Elia, J.A.; Li, J.; Floudas, C.A. Planning and scheduling under uncertainty: A review across multiple sectors. Ind. Eng. Chem. Res. 2010, 49, 3993–4017. [Google Scholar] [CrossRef]
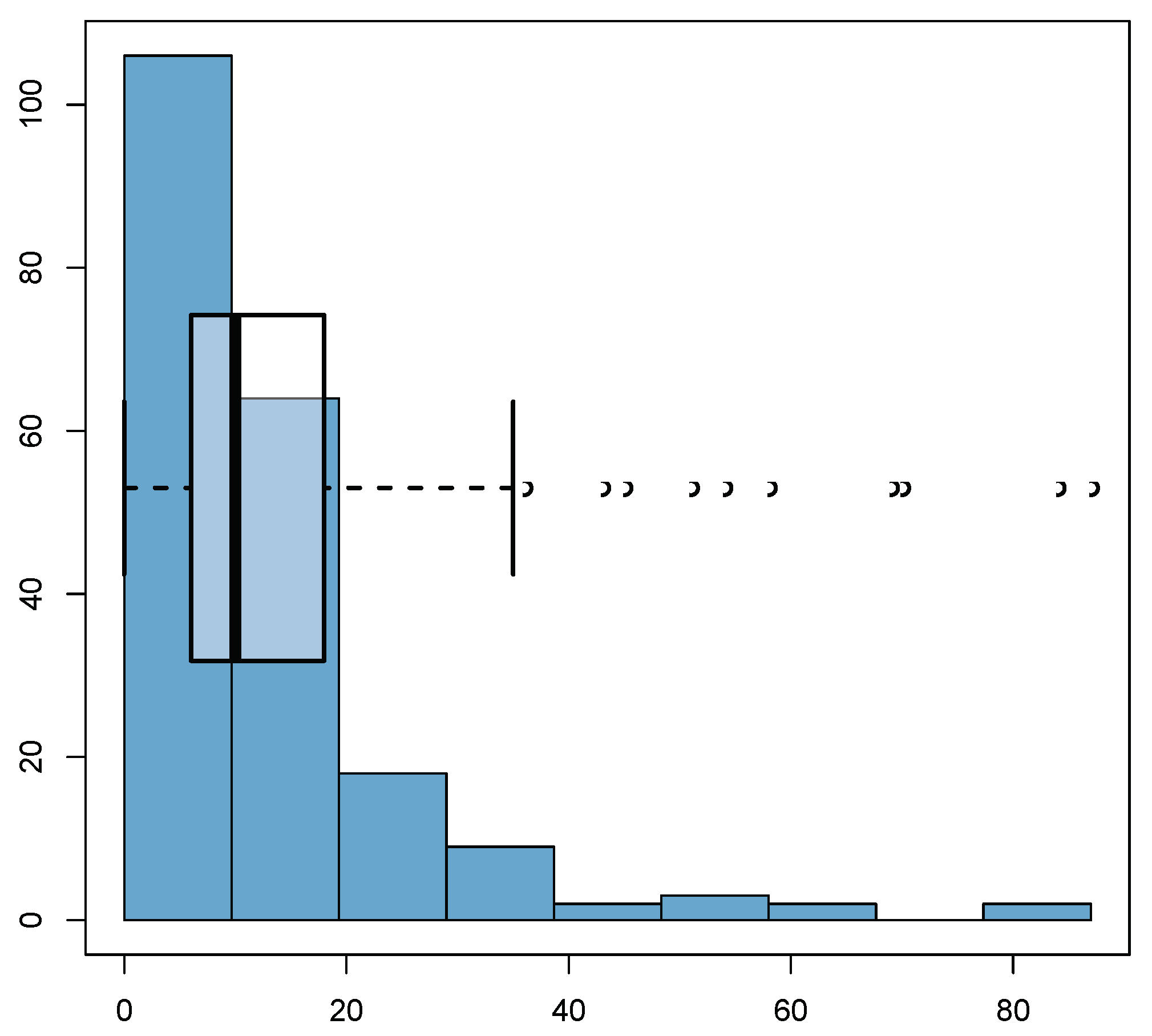
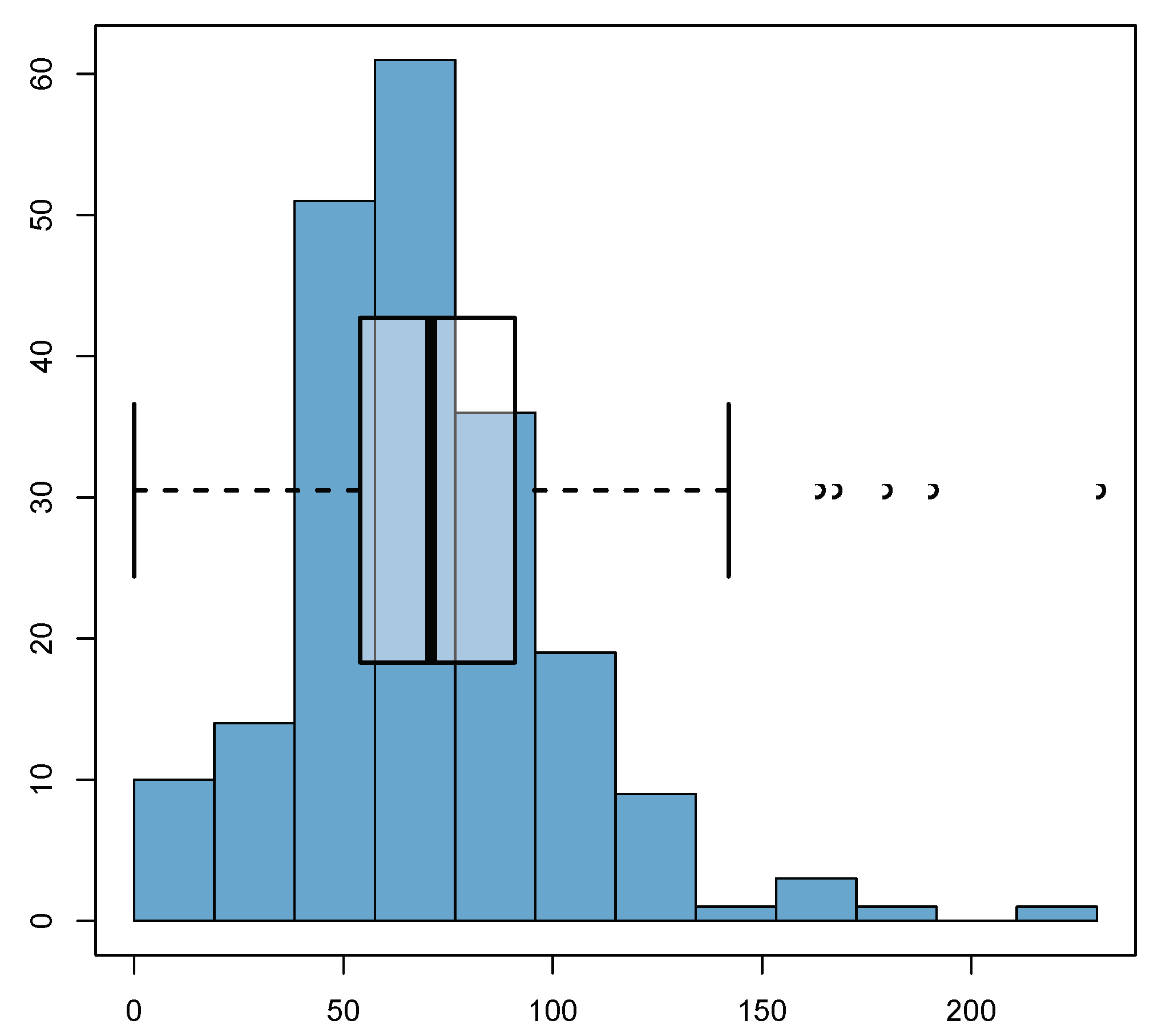
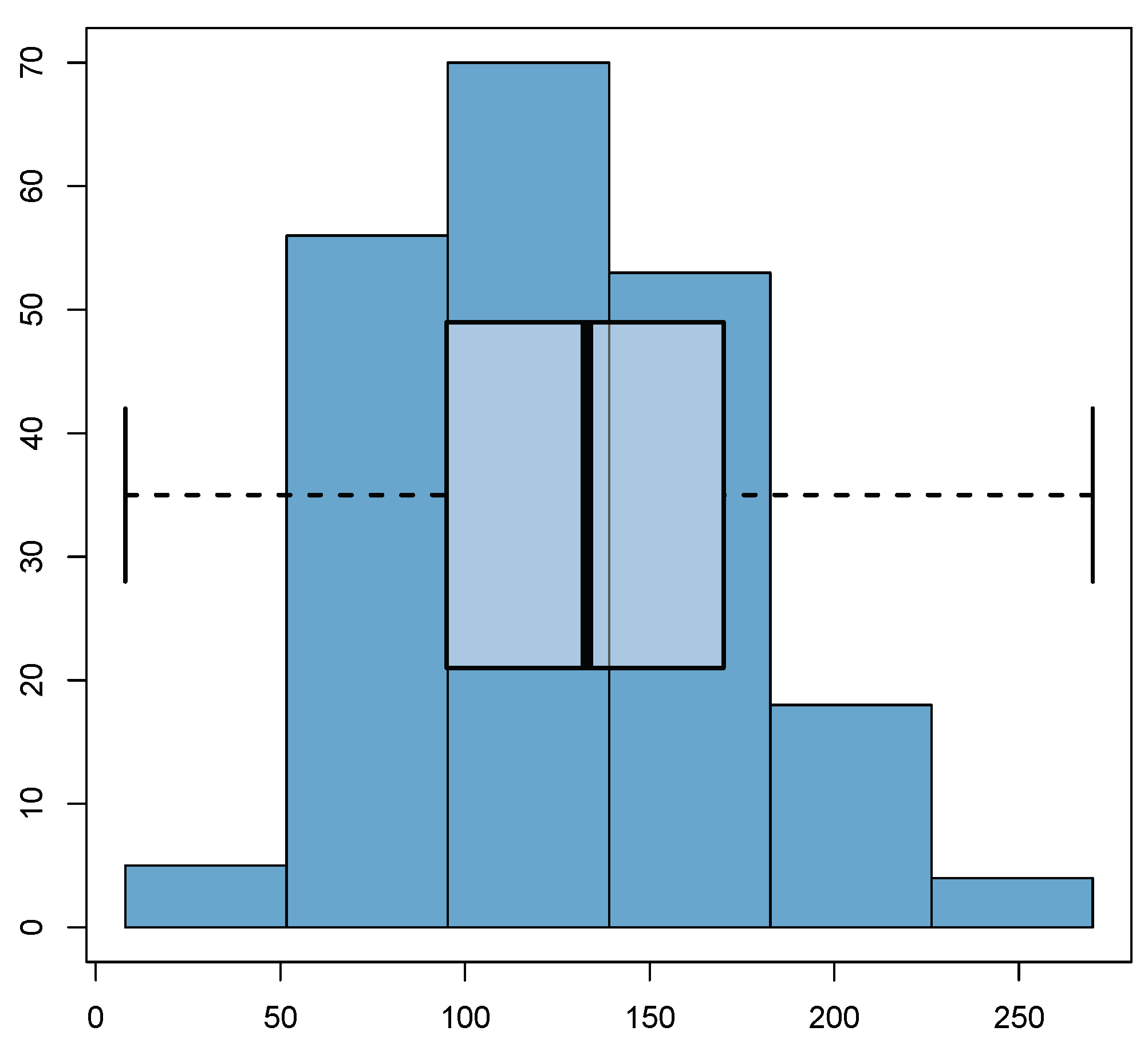
| 1 | 2 | 3 | 4 | |
| Average length of oncology appointments | 2.6 | 4.2 | 2.2 | 1.8 |
| % of patients in each scenario | 28.7 | 27.2 | 36.4 | 7.7 |
| Monday | 7339 | 9255 | 7900 | 6250 | 4600 | 56 |
| Tuesday | 10,382 | 13,375 | 11,675 | 9275 | 7115 | 72 |
| Wednesday | 7351 | 9790 | 8190 | 6360 | 4480 | 61 |
| Thursday | 5906 | 7790 | 6360 | 4860 | 3360 | 50 |
| Friday | 5810 | 8075 | 6615 | 5085 | 3555 | 51 |
| Total | 36,788 | 48,285 | 40,740 | 31,830 | 23,110 | 290 |
| Duration of the Time Intervals: | 5 min | 10 min | 15 min |
|---|---|---|---|
| Monday | 9255 | 9770 | 10,815 |
| Tuesday | 13,375 | 14,120 | 15,420 |
| Wednesday | 9790 | 10,320 | 10,890 |
| Thursday | 7790 | 8180 | 8250 |
| Friday | 8075 | 8470 | 9285 |
| Total | 48,285 | 50,860 | 54,660 |
| 1 | 29 | 72 | 61 | 29 | 54 | 60 | 50 |
| 2 | 30 | 65 | 46 | 30 | 44 | 46 | 47 |
| 3 | 19 | 55 | 49 | 31 | 82 | 65 | 61 |
| 4 | 23 | 77 | 81 | 32 | 27 | 59 | 57 |
| 5 | 25 | 56 | 41 | 33 | 18 | 54 | 45 |
| 6 | 27 | 50 | 57 | 34 | 24 | 66 | 50 |
| 7 | 37 | 50 | 53 | 35 | 21 | 67 | 45 |
| 8 | 24 | 46 | 57 | 36 | 45 | 74 | 53 |
| 9 | 22 | 57 | 57 | 37 | 27 | 84 | 61 |
| 10 | 30 | 60 | 49 | 38 | 13 | 57 | 41 |
| 11 | 65 | 43 | 76 | 39 | 39 | 45 | 44 |
| 12 | 59 | 49 | 72 | 40 | 46 | 42 | 50 |
| 13 | 82 | 50 | 52 | 41 | 28 | 80 | 49 |
| 14 | 69 | 51 | 74 | 42 | 33 | 91 | 81 |
| 15 | 12 | 66 | 53 | 43 | 12 | 80 | 65 |
| 16 | 9 | 80 | 69 | 44 | 40 | 41 | 44 |
| 17 | 12 | 53 | 57 | 45 | 49 | 39 | 47 |
| 18 | 12 | 65 | 43 | 46 | 44 | 60 | 66 |
| 19 | 40 | 55 | 41 | 47 | 30 | 90 | 67 |
| 20 | 8 | 82 | 69 | 48 | 84 | 42 | 52 |
| 21 | 21 | 53 | 42 | 49 | 39 | 81 | 85 |
| 22 | 35 | 63 | 55 | 50 | 36 | 93 | 69 |
| 23 | 18 | 65 | 61 | 51 | 30 | 84 | 58 |
| 24 | 18 | 63 | 65 | 52 | 22 | 68 | 65 |
| 25 | 46 | 38 | 44 | 53 | 19 | 72 | 53 |
| 26 | 43 | 38 | 39 | 54 | 26 | 70 | 41 |
| 27 | 45 | 52 | 47 | 55 | 24 | 84 | 61 |
| 28 | 8 | 80 | 65 | 56 | 61 | 56 | 73 |
| Check-ups’ delays | 49 | 14 | 15 | 41 |
| Oncological check-ups | 13 | 21 | 11 | 9 |
| Substance preparation | 63 | 42 | 90 | 147 |
| Treatments | 125 | 77 | 116 | 197 |
| Patients | 59 | 56 | 75 | 16 |
| % Patients | 28.6% | 27.2% | 36.4% | 7.8% |
| Monday | 7339 | 6029 | 17.74 | 56 |
| Tuesday | 10,382 | 7544 | 27.3 | 72 |
| Wednesday | 7351 | 6392 | 13.0 | 61 |
| Thursday | 5906 | 5239 | 11.3 | 50 |
| Friday | 5810 | 5344 | 8.0 | 51 |
| Total | 36,788 | 30,548 | 17.0 | 290 |
1 | 2 | 3 | 4 | ||||
|---|---|---|---|---|---|---|---|
| 7339 | 6550 | 3585 | 6385 | 10,975 | 6029 | 215 | |
| Probabilities | 28.6 | 27.2 | 36.4 | 7.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
González-Maestro, A.; Brozos-Vázquez, E.; Casas-Méndez, B.; López-López, R.; López-Rodríguez, R.; Reyes-Santias, F. Effective Optimisation of the Patient Circuits of an Oncology Day Hospital: Mathematical Programming Models and Case Study. Mathematics 2022, 10, 62. https://doi.org/10.3390/math10010062
González-Maestro A, Brozos-Vázquez E, Casas-Méndez B, López-López R, López-Rodríguez R, Reyes-Santias F. Effective Optimisation of the Patient Circuits of an Oncology Day Hospital: Mathematical Programming Models and Case Study. Mathematics. 2022; 10(1):62. https://doi.org/10.3390/math10010062
Chicago/Turabian StyleGonzález-Maestro, Adrián, Elena Brozos-Vázquez, Balbina Casas-Méndez, Rafael López-López, Rosa López-Rodríguez, and Francisco Reyes-Santias. 2022. "Effective Optimisation of the Patient Circuits of an Oncology Day Hospital: Mathematical Programming Models and Case Study" Mathematics 10, no. 1: 62. https://doi.org/10.3390/math10010062
APA StyleGonzález-Maestro, A., Brozos-Vázquez, E., Casas-Méndez, B., López-López, R., López-Rodríguez, R., & Reyes-Santias, F. (2022). Effective Optimisation of the Patient Circuits of an Oncology Day Hospital: Mathematical Programming Models and Case Study. Mathematics, 10(1), 62. https://doi.org/10.3390/math10010062







