Inference for the Process Performance Index of Products on the Basis of Power-Normal Distribution
Abstract
:1. Introduction
2. Motivation and Organization
3. The Inference Methods
3.1. Maximum Likelihood Estimation Method
- (a)
- (b)
- The approximate confidence interval of can be presented bywhere is the PPI of the power-normal distribution and defined byThe approximate confidence interval of can be obtained by
- (a)
- The MLEs of , and can be the simultaneous solutions of the Equations (17)–(19). Denote them by , and , respectively, and let . Let , , , , , , We obtain the following results:andHence, the exact Fisher information matrix can be presented byBecause contains unknown parameters, the plug-in version of , denoted by , can be used to find the asymptotic distribution of . We can be shown thatThe delta method indicates that the asymptotic mean and variance of are and , respectively. Moreover, using Central limit theorem, we can show that the asymptotic distribution of is normal. Hence, we can show thatWe prove Theorem 1a.
- (b)
- Using invariant property, the MLE of can be obtained byThe gradient of is . Moreover, we can show that the asymptotical variance of isand the asymptotic distribution of can be obtained byThen, the approximate confidence interval of can be obtained byWe prove Theorem 1b. □
3.2. Bootstrap Methods
- The PBP method
- Step 1:
- Obtain the MLE of based on a large sample of size n and denote the MLE by .
- Step 2:
- Generate a bootstrap sample of size n from the power-normal distribution with parameter .
- Step 3:
- Implement Step 2 B times, where B is a large number and denote all obtained MLE of by , . Let , be the MLE of based on B bootstrap samples.
- Step 4:
- Construct the empirical distribution of based on the bootstrap samples and denote the empirical distribution of by . The bootstrap confidence interval of can be obtained by , where is the th quantile function of such that for .
- The BCP method
- Step 1:
- Implement Step 1 to Step 3 of the PBP method to obtain the bootstrap sample of .
- Step 2:
- The approximate confidence interval of can be obtained by
3.3. Discussions
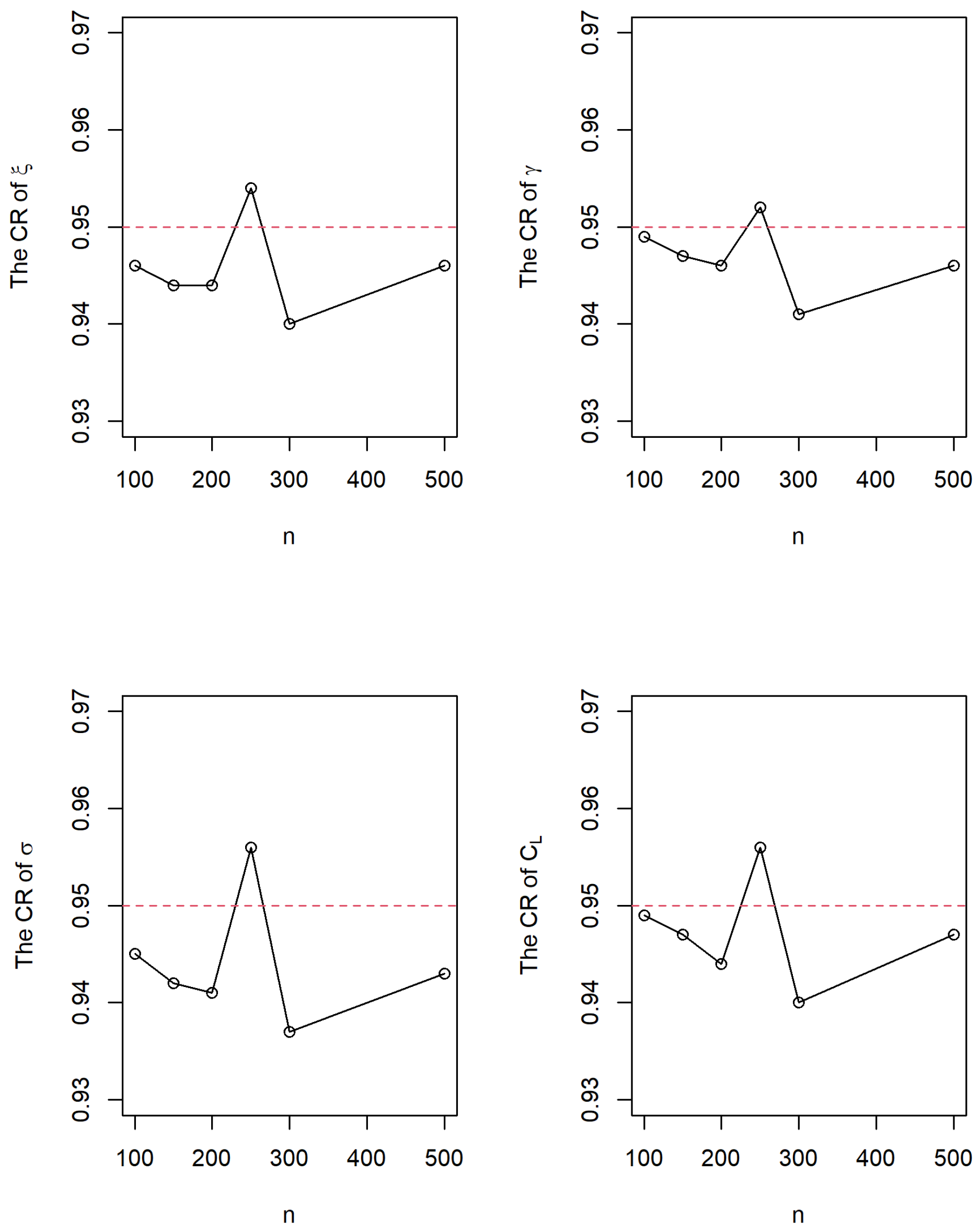
4. Monte Carlo Simulations
- When the value of is small () or large (), the rBias and rsqMSE are larger than that in the cells of and 2 even the sample size increases to 500. These findings indicate that we may consider a bias-correction method to obtain a more reliable MLE of , and then we can obtain the more reliable MLEs of and . The bias-correction maximum likelihood estimation method is another issue and can be a future study.
- Based on the values of in Table 1, we find that the performance of the maximum likelihood estimation method get worse as the value of the shape parameter is increased when the sample size is small. The findings imply that the maximum likelihood estimation method could not be a satisfactory method to obtain the reliable estimates of the model parameters if the power-normal distribution has a big shape parameter when the sample size is small. A big sample of 500 or more is requested to obtain the reliable MLEs of the model parameters if the power-normal distribution has a big shape parameter. For the power-normal distribution with a small to moderate shape parameter, a sample of 250 or 300 is enough to obtain the reliable MLEs of model parameters.
- The MLE of underestimates its true value. The bias of and is larger than the bias of . Because is a function of and , the bias of could be inflated due to the underestimated . We also find that the bias of cannot be significantly reduced when the sample size increases. How to reduce the bias of the MLE of can be a future study.
- The can be a good estimate of in terms of the rBise and rsqMSE in Table 1.
- Some cells of rBias and rsqMSE for , and could not decrease as the sample size increases. Carefully check these cells, we can find these values are close. The slightly differences are caused by random error in simulation. We can treat them at a close level of rBias and rsqMSE.
- The MLE is a plug-in function of the MLEs of and . Hence, the estimation performance of depends on the quality of and . can be a good estimate of for the power-normal distribution if its shape parameter is small to moderate.
- Because the power-normal distribution with a small to moderate shape parameter can characterize a wide range of real skewed data. The maximum likelihood method can be a potential estimation method to obtain reliable estimates of model parameters.
5. Example
- Stage 1:
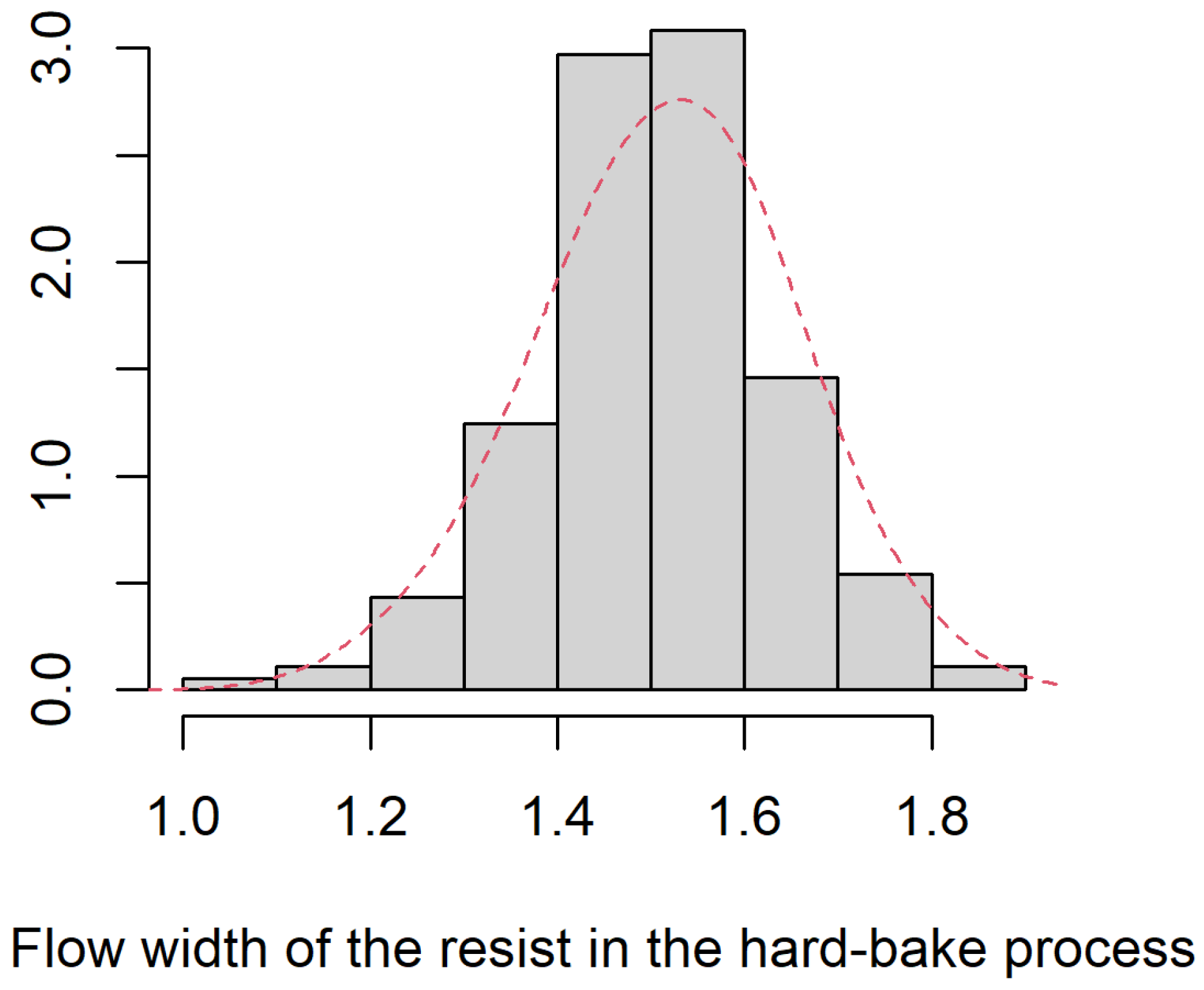
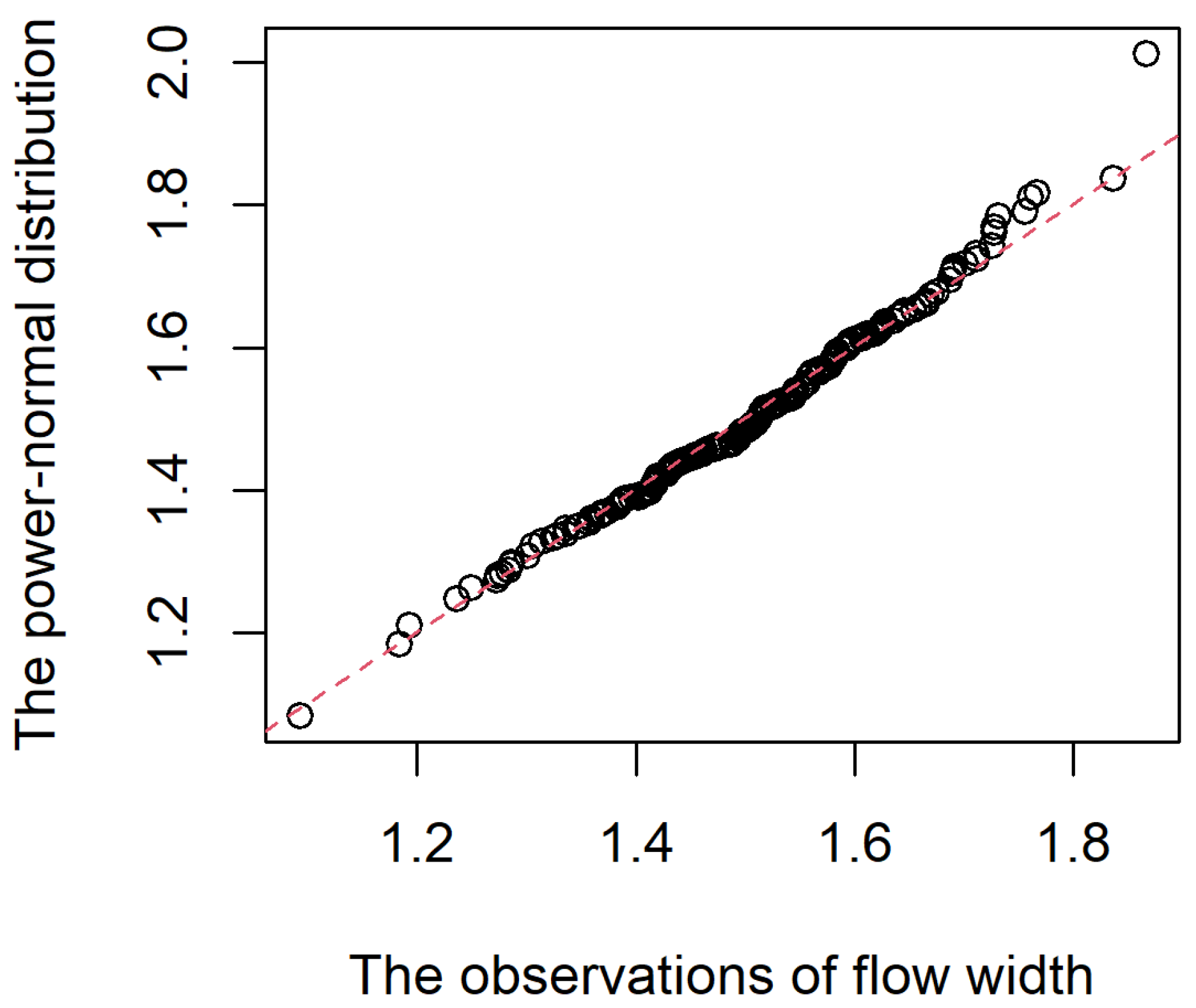
- Modeling: Using the proposed maximum likelihood estimation in Section 3.1 with the initial values of , and , where and are the sample mean and standard deviation of the data set, respectively. Based on the simulation results in Table 1, a random sample of should be okay to obtain reliable MLEs of the model parameters when is close to 1. We obtain the MLEs , and for the power-normal distribution. The dashed line in Figure 2 is the density curve of the power-normal distribution based on the obtained MLEs. We can see that the power-normal distribution has a good fitting to this data set.The quantile-to-quantile plot based on the flow width data and the power-normal distribution is presented in Figure 3. All the dots are plotted around the straight line. Hence, the quantile-to-quantile plot indicates that the power-normal distribution can be the right model to characterize the flow width data. The test statistic of the Kolmogorov-Smirnov test based on the flow width data and power-normal distribution is with the p-value of . Based on the Kolmogorov-Smirnov test, we conclude that the power-normal distribution can be a good model to characterize the flow width data. Because the MLE of the shape parameter, , is closed to 1, this estimate indicates that the distribution of the flow width data has a slightly skewed shape.Refer to the lower specification limit of suggested by [2], we let . The MLE of the can be . The high value of the indicates a good process capability for the flow width of the resist in the hard-bark process. Based on the original sample with 185 observations of flow width, the PBP and BCP confidence intervals of the model parameters and are obtained and reported in Table 2. We can find that the obtained PBP and BCP intervals for each parameter are close. Two bootstrap intervals of recommend a good quality for the flow width of the resist in the hard-bake manufacturing process due to two lower limits of are significantly larger than 1.
- Stage 2:
- The impact of the sample size on the quality of the confidence interval of: In this stage, 315 observations are generated from the model obtained in Stage 1 to investigate the impact of the sample size on the quality of the PBP and BCP intervals of . We merge the original 185 observations with the generated observations. The merged sample has a size of 500. We are interested in studying how much the length of confidence interval can be reduced when the sample size increases. The PBP and BCP confidence intervals of are evaluated based on the first 300 and all 500 observations in the merged sample. All computation results are reported in Table 3.From Table 3 we can find that the lengths of PBP and BCP confidence intervals are reduced when the sample size increases. Both the PBP and BCP methods are competitive for estimating , and . The PBP method outperforms the BCP method to estimate with a shorter length of confidence interval. Table 3 also indicates the quality of the PBP, and BCP methods can be significantly improved when the sample size increases. The BCP method significantly outperforms the PBP method for evaluating the in terms of the length of confidence interval.
6. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pan, J.; Wu, S. Process capability analysis for non-normal relay test data. Microelectron. Reliab. 1997, 37, 421–428. [Google Scholar] [CrossRef]
- Montgomery, D.C. Statistical Quality Control: A Modern Introduction, 7th ed.; John Wiley & Sons: New York, NY, USA, 2012. [Google Scholar]
- Hong, C.-W.; Wu, J.-W.; Cheng, C.-H. A look at the Burr and related distribution. Appl. Math. Comput. 2007, 184, 336–350. [Google Scholar]
- Lee, H.-M.; Wu, J.-W.; Lei, C.-L.; Hung, W.L. Implementing lifetime performance index of products with two-parameter exponential distribution. Int. J. Syst. Sci. 2011, 42, 1305–1321. [Google Scholar] [CrossRef]
- Wu, S.-F.; Chiu, C.-J. Computational testing algorithmic procedure of assessment for lifetime performance index of products with two-parameter exponential distribution based on the multiply type II censored sample. J. Stat. Comput. Simul. 2014, 84, 2016–2122. [Google Scholar] [CrossRef]
- Wu, S.-F.; Lin, Y.-P. Computational testing algorithmic procedure of assessment for lifetime performance index of products with one-parameter exponential distribution under progressive type I interval censoring. Math. Comput. Simul. 2016, 120, 79–90. [Google Scholar] [CrossRef]
- Lee, W.-C.; Wu, J.-W.; Hong, C.-W. Assessing the lifetime performance index of products from progressively type II right censored data using Burr XII model. Math. Comput. Simul. 2009, 79, 2167–2179. [Google Scholar] [CrossRef]
- Ahmadi, M.V.; Doostparast, M.; Ahmadi, J. Statistical inference for the lifetime performance index based on generalised order statistics from exponential distribution. Int. J. Syst. Sci. 2009, 46, 1094–1107. [Google Scholar] [CrossRef]
- Lee, W.-C.; Wu, J.-W.; Hong, M.-L. Assessing the lifetime performance index of Rayleigh products based on the Bayesian estimation under progressive type II right censored samples. J. Comput. Appl. Math. 2011, 235, 1676–1688. [Google Scholar] [CrossRef]
- Ahmadi, M.V.; Doostparast, M.; Ahmadi, J. Estimating the lifetime performance index with Weibull distribution based on progressive first-failure censoring scheme. J. Comput. Appl. Math. 2013, 239, 93–102. [Google Scholar] [CrossRef]
- Goto, M.; Inoue, T. Some properties of power-normal distribution. Jpn. J. Biom. 1980, 1, 28–54. [Google Scholar] [CrossRef]
- Goto, M.; Inoue, T.; Tsuchiya, Y. On estimation of parameters in power-normal distribution. Bull. Inform. Cybern. 1984, 21, 41–53. [Google Scholar] [CrossRef]
- Goto, M.; Matsubara, Y.; Tsuchiya, Y. Power-normal distribution and its applications. Rep. Stat. Appl. Res. 1983, 30, 8–28. [Google Scholar]
- Freeman, J.; Modarres, R. Inverse Box-Cox: The power-normal distribution. Stat. Probab. Lett. 2006, 76, 764–772. [Google Scholar] [CrossRef]
- Castillo, N.O.; Gallardo, D.I.; Bolfarine, H.; Gómez, H. Truncated power-normal distribution with application to non-negative measurements. Entropy 2018, 433, 433. [Google Scholar] [CrossRef] [Green Version]
- Maruo, K.; Goto, M. Percentile estimation based on the power-normal distribution. Comput. Stat. 2013, 28, 241–356. [Google Scholar] [CrossRef]
- Gupta, R.D.; Gupta, R.C. Analyzing skewed data by power normal model. Test 2008, 17, 197–210. [Google Scholar] [CrossRef]
- Maruo, K.; Shirahata, S.; Goto, M. Underlying assumptions of the power-normal distribution. Behaviormetrika 2011, 38, 85–95. [Google Scholar] [CrossRef]
- Azzalini, A. A class of distributions which includes the normal ones. Scand. J. Stat. 1985, 12, 171–178. [Google Scholar]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; Chapman & Hall: New York, NY, USA, 1993. [Google Scholar]
- Lio, Y.L.; Tsai, T.-R.; Chiang, J.-Y. Estimation of the lower confidence limit of the breaking strength percentiles under progressive type-II censoring. J. Chin. Inst. Ind. Eng. 2012, 29, 16–29. [Google Scholar] [CrossRef]
- Dey, S.; Saha, M.; Maiti, S.S.; Jun, C.-H. Bootstrap confidence intervals of generalized process capability index Cpyk for for Lindley and power Lindley distributions. Commun. Stat.-Simul. Comput. 2018, 47, 249–262. [Google Scholar] [CrossRef]
- Besseris, G.J. Evaluation of robust scale estimators for modified Weibull process capability indices and their bootstrap confidence intervals. Comput. Ind. Eng. 2019, 128, 135–149. [Google Scholar] [CrossRef]
- Park, C.; Dey, S.; Ouyang, L.; Byun, J.-H.; Leeds, M. Improved bootstrap confidence intervals for the process capability index Cpk. Commun. Stat.-Simul. Comput. 2020, 49, 2583–2603. [Google Scholar] [CrossRef]
| rBias | rsqMSE | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.5 | 100 | 0.2096 | −0.5994 | −1.2269 | 1.1320 | 0.7258 | 33.0214 | 2.0278 | 2.2301 | 240 |
| 150 | 0.2390 | −2.6064 | −1.2264 | 0.8151 | 0.6571 | 13.5733 | 2.0054 | 1.4548 | 70 | |
| 200 | 0.2434 | −2.9725 | −1.2176 | 0.6825 | 0.6370 | 4.8467 | 1.9865 | 1.1086 | 25 | |
| 250 | 0.2475 | −3.1008 | −1.2152 | 0.6299 | 0.6251 | 4.5750 | 1.9792 | 0.9567 | 11 | |
| 300 | 0.2462 | −3.1453 | −1.2109 | 0.5905 | 0.6134 | 4.5548 | 1.9772 | 0.8447 | 8 | |
| 500 | 0.2544 | −3.2785 | −1.2104 | 0.5447 | 0.5987 | 4.5559 | 1.9692 | 0.7335 | 0 | |
| 1 | 100 | 0.2712 | 3.0260 | −0.9345 | 0.8341 | 0.6417 | 26.4524 | 1.4044 | 2.2745 | 511 |
| 150 | 0.3016 | 0.4983 | −0.9383 | 0.5427 | 0.5659 | 14.5790 | 1.3798 | 1.3561 | 212 | |
| 200 | 0.3241 | −0.2356 | −0.9473 | 0.4684 | 0.5425 | 4.6232 | 1.3725 | 0.9842 | 94 | |
| 250 | 0.3276 | −0.4745 | −0.9443 | 0.4186 | 0.5235 | 3.5571 | 1.3619 | 0.8349 | 33 | |
| 300 | 0.3337 | −0.6071 | −0.9467 | 0.3985 | 0.5155 | 1.8356 | 1.3588 | 0.7632 | 26 | |
| 500 | 0.3420 | −0.7792 | −0.9463 | 0.3538 | 0.4969 | 1.4421 | 1.3504 | 0.6235 | 2 | |
| 2 | 100 | 0.2551 | 7.9755 | −0.8761 | 0.2849 | 0.6422 | 45.1581 | 1.2072 | 2.4265 | 1126 |
| 150 | 0.2928 | 2.6819 | −0.8825 | 0.0267 | 0.5485 | 16.8547 | 1.1900 | 1.4013 | 652 | |
| 200 | 0.3273 | 1.2177 | −0.9007 | −0.0075 | 0.5182 | 7.0036 | 1.1902 | 1.0722 | 402 | |
| 250 | 0.3281 | 0.8255 | −0.8962 | −0.0736 | 0.4936 | 4.0130 | 1.1793 | 0.8994 | 261 | |
| 300 | 0.3342 | 0.5714 | −0.8965 | −0.0970 | 0.4778 | 2.4949 | 1.1746 | 0.8284 | 159 | |
| 500 | 0.3510 | 0.2852 | −0.9045 | −0.1194 | 0.4655 | 1.1307 | 1.1691 | 0.6901 | 39 | |
| 5 | 100 | 0.0847 | 10.9240 | −1.3410 | −2.9791 | 0.8151 | 46.2667 | 2.2549 | 6.9958 | 2210 |
| 150 | 0.1213 | 5.6620 | −1.3496 | −3.3633 | 0.7422 | 26.0057 | 2.2591 | 5.8119 | 1808 | |
| 200 | 0.1431 | 3.1266 | −1.3552 | −3.4987 | 0.7058 | 12.2067 | 2.2567 | 5.4787 | 1470 | |
| 250 | 0.1549 | 2.4277 | −1.3586 | −3.5532 | 0.6930 | 10.3026 | 2.2525 | 5.4107 | 1265 | |
| 300 | 0.1595 | 1.8131 | −1.3582 | −3.6083 | 0.6773 | 6.7543 | 2.2513 | 5.3588 | 1164 | |
| 500 | 0.1811 | 1.0443 | −1.3662 | −3.6470 | 0.6558 | 2.8148 | 2.2494 | 5.2462 | 721 | |
| PBP | BCP | |||
|---|---|---|---|---|
| Parameter | Lower Limit | Upper Limit | Lower Limit | Upper Limit |
| 1.2716 | 1.6886 | 1.2575 | 1.6842 | |
| 0.0839 | 5.5656 | 0.0944 | 5.9333 | |
| 0.0511 | 0.1932 | 0.0535 | 0.1965 | |
| 1.4040 | 13.4726 | 1.2975 | 12.7272 | |
| PBP | BCP | ||||
|---|---|---|---|---|---|
| Parameter | Lower Limit | Upper Limit | Lower Limit | Upper Limit | |
| 300 | 1.4302 | 1.6886 | 1.1832 | 1.5994 | |
| 0.1089 | 1.8209 | 0.3820 | 5.4131 | ||
| 0.0588 | 0.1512 | 0.0925 | 0.2001 | ||
| 2.8738 | 11.7485 | 0.9781 | 6.3928 | ||
| 500 | 1.4595 | 1.6634 | 1.2955 | 1.5825 | |
| 0.1902 | 1.5053 | 0.4523 | 4.1516 | ||
| 0.0734 | 0.1453 | 0.0975 | 0.1784 | ||
| 3.1750 | 9.0023 | 1.6642 | 5.8747 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, J.; Xin, H.; Zheng, C.; Tsai, T.-R. Inference for the Process Performance Index of Products on the Basis of Power-Normal Distribution. Mathematics 2022, 10, 35. https://doi.org/10.3390/math10010035
Zhu J, Xin H, Zheng C, Tsai T-R. Inference for the Process Performance Index of Products on the Basis of Power-Normal Distribution. Mathematics. 2022; 10(1):35. https://doi.org/10.3390/math10010035
Chicago/Turabian StyleZhu, Jianping, Hua Xin, Chenlu Zheng, and Tzong-Ru Tsai. 2022. "Inference for the Process Performance Index of Products on the Basis of Power-Normal Distribution" Mathematics 10, no. 1: 35. https://doi.org/10.3390/math10010035
APA StyleZhu, J., Xin, H., Zheng, C., & Tsai, T.-R. (2022). Inference for the Process Performance Index of Products on the Basis of Power-Normal Distribution. Mathematics, 10(1), 35. https://doi.org/10.3390/math10010035







