Symmetry Methods and Conservation Laws for the Nonlinear Generalized 2D Equal-Width Partial Differential Equation of Engineering

Abstract

In this work, we study the generalized 2D equal-width equation which arises in various fields of science. With the aid of numerous methods which includes Lie symmetry analysis, power series expansion and Weierstrass method, we produce closed-form solutions of this model. The exact solutions obtained are the snoidal wave, cnoidal wave, Weierstrass elliptic function, Jacobi elliptic cosine function, solitary wave and exponential function solutions. Moreover, we give a graphical representation of the obtained solutions using certain parametric values. Furthermore, the conserved vectors of the underlying equation are constructed by utilizing two approaches: the multiplier method and Noether’s theorem. The multiplier method provided us with four local conservation laws, whereas Noether’s theorem yielded five nonlocal conservation laws. The conservation laws that are constructed contain the conservation of energy and momentum.

1. Introduction

It is well established that numerous physical phenomena of the real world are modeled by the nonlinear partial differential equations (NPDE). Therefore, finding the exact solutions of the NPDEs plays a vital role in the understanding of these physical phenomena. NPDEs appear in various fields of sciences, which include the fields of biology, quantum mechanics, economics, optical fibers, fluid dynamics, chaos theory and plasma physics, just to mention a few. For instance, the Ginzburg–Landau equation [1] was used to describe superconductivity and was postulated as a phenomenological model which could describe type-I superconductors without examining their microscopic properties; the Fokas–Lenells equation [2] is an important model that is used in solitary wave theory and optical fibers phenomena; the Black–Scholes equation [3] is mostly used in finance—for example, it may be used as the governing model for the price evolution of a European call; the nonlinear elastic circular rod equation [4] was used to analyze the solitary strain waves in the nonlinear elastic rod that produce some results on the effect of the geometrical and physical parameters of the rod on the waves—just to name a few. Scholars and researchers have dedicated most of their time to investigating some of these models, and for this reason, there are a number of solution methods suggested in the literature. These solution methods include, amongst others, Bäcklund transformations [5,6,7], the extended simplest equation method [8], the extended Jacobi elliptic function technique [9], power series technique [10], tanh method [11], Lie symmetry technique [12,13,14,15,16,17,18], bifurcation method [19] and $(G^{\prime }/G)-$expansion method [20].

Conservation laws have vast applications in the study of differential equations (DEs) and are known as the fundamental laws of nature as they play a huge role in physics, applied mathematics and other fields of science such as chemistry, biology, geology and engineering. There are techniques brought forward in the literature which aid in deriving conserved vectors which include the classical Noether’s theorem, the multiplier method, the Ibragimov’s new theorem and the partial Lagrangian method [21,22,23,24,25,26,27,28,29,30,31]. It should be noted that Noether’s theorem can only be applied to DEs which have a Lagrangian formulation. However, many DEs exist that do not have a Lagrangian and as a result Nother’s theorem cannot be used to derive their conservation laws. In such a situation the general method of multipliers can be invoked to construct conservation laws. Thus, the general multiplier method provides us with the conservation laws of a DE irrespective of whether or not the DE comes from a variational principle.

The nonlinear third-order PDE given by

$$\begin{array}{l}{u}_t+2\alpha u{u}_x+u_{txx}=0\hfill \end{array}$$

(1)

is known as the equal-width (EW) equation and was first introduced by Morrison et al. [32] as the mathematical model that describes nonlinear dispersive waves, for example, the waves created in shallow water channel. Several works has been conducted on this equation. For instance, in [33], the authors presented some closed-form solutions and conservation laws for this equation. The authors of [34] invoked the Petrov–Galerkin method utilizing quadratic B-spline spatial finite elements to derive solutions for this equation. In [35], the extended simple equation method along with the exponential expansion method were employed to derive its exact solutions.

The modified equal-width (MEW) equation reads

$$\begin{array}{l}{u}_t+2\alpha u^2{u}_x+u_{txx}=0\hfill \end{array}$$

(2)

and models the simulation of one-dimensional wave propagation in nonlinear media with dispersion processes. More work that has been performed on MEW equation can be found in [35,36,37,38] and the references therein.

In [39], the authors studied the general form of the equal width (GEW) equation with power law nonlinearity that reads

$$\begin{array}{l}{u}_t+a{u}^p{u}_x-\mu u_{txx}=0\hfill \end{array}$$

(3)

and presented exact solitary wave solutions. In addition, analytical expressions of three invariants of motion for these solitary wave solutions were derived. Recently, the traveling wave solution of the GEW Equation (3) was found in [40] by using the Lie symmetry method along with the sine-cosine method.

The generalized equal width-Burgers equation

$$\begin{array}{l}{u}_t+a{u}^p{u}_x-\delta u_{xx}-\mu u_{txx}=0\hfill \end{array}$$

(4)

describes the propagation of nonlinear and dispersive waves with certain dissipative effects. The exact solitary wave solutions of (4) were derived in [39].

Recently, Equation (2) was generalized to the two-dimensional modified equal-width equation, which reads [41]

$$\begin{array}{l}{u}_t+u^2{u}_x-\mu (u_{txx}+u_{tyy})=0,\hfill \end{array}$$

(5)

where $\mu$ is a real constant. Firstly, Lie symmetries were computed, and thereafter, one-dimensional and two-dimensional subalgebras were obtained. These were then utilized to perform the symmetry reductions of (5) to ordinary differential equations.

In this work, we further generalize (5) to the two-dimensional equal-width (2D-EW) equation with power law nonlinearity, viz.,

$$\begin{array}{l}{u}_t+u^n{u}_x+\alpha u_{txx}+\beta u_{tyy}=0\hfill \end{array}$$

(6)

with $\alpha$, $\beta$ and n being nonzero constants. In this work, we provide the exact solutions of the 2D-EW Equation (6). The classical symmetry method was employed to obtain point symmetries of this model, and thereafter, symmetries were used to reduce (6) to some nonlinear ordinary differential equations (NODEs). Various solution methods were then utilized to construct solutions of these NODEs, which consequently provides us with the exact solutions of the 2D-EW Equation (6). Moreover, the obtained solutions were described graphically for certain parametric values. Finally, we derive both local and nonlocal conservation laws for this model by invoking two distinct approaches.

2. Symmetries, Reductions and Solutions

In this section, we firstly compute Lie symmetries of the 2D-EW Equation (6) and thereafter perform symmetry reductions to obtain various NODEs. By employing different techniques on these NODE, we then construct closed-form solutions of the Equation (6).

2.1. Lie Symmetries

We consider the one-parameter group of transformations

$$\begin{array}{ll}\hfill & \overline{t}\to t+a\tau (t,x,y,u),\overline{x}\to x+a\xi (t,x,y,u),\hfill \\ \hfill & \overline{y}\to y+a\varphi (t,x,y,u),\overline{u}\to u+a\eta (t,x,y,u)\hfill \end{array}$$

(7)

with a small parameter a, for which the corresponding vector field is

$$\begin{array}{l}\mathcal{Z}=\tau \frac{\partial }{\partial t}+\xi \frac{\partial }{\partial x}+\varphi \frac{\partial }{\partial y}+\eta \frac{\partial }{\partial u}.\hfill \end{array}$$

(8)

The vector field $\mathcal{Z}$ is a Lie symmetry of Equation (6) whenever

$$\begin{array}{l}{\mathcal{Z}}^{\left[3\right]}(u_t+u^n{u}_x+\alpha u_{txx}+\beta u_{tyy}){|}_{\left(6\right)}=0.\hfill \end{array}$$

(9)

Here ${\mathcal{Z}}^{\left[3\right]}$ is the third prolongation of (8); see for example [14]. Expanding Equation (9) and separating the various derivatives of u lead to the determining equations:

$$\begin{array}{ll}\hfill & {\tau }_u=0,{\tau }_x=0,{\tau }_y=0,{\tau }_{tt}=0,{\xi }_t=0,{\xi }_u=0,{\xi }_x=0,\hfill \\ \hfill & {\xi }_y=0,{\varphi }_t=0,{\varphi }_u=0,{\varphi }_x=0,{\varphi }_y=0,n\eta +u{\tau }_t=0.\hfill \end{array}$$

(10)

Solving the above equations, we end up with

$$\begin{array}{l}\mathcal{Z}=\left(C_{1}t+C_2\right)\frac{\partial }{\partial t}+C_3\frac{\partial }{\partial x}+C_4\frac{\partial }{\partial y}-\frac{C_1}{n}u\frac{\partial }{\partial u},\hfill \end{array}$$

(11)

where $C_1,\cdots ,C_4$ are arbitrary constants. Thus, we see that the Lie symmetries of the 2D-EW Equation (6) are

$$\begin{array}{l}{\mathcal{Z}}_1=\frac{\partial }{\partial t},{\mathcal{Z}}_2=\frac{\partial }{\partial x},{\mathcal{Z}}_3=\frac{\partial }{\partial y},{\mathcal{Z}}_4=nt\frac{\partial }{\partial t}-u\frac{\partial }{\partial u}.\hfill \end{array}$$

(12)

Here, the symmetries ${\mathcal{Z}}_1,{\mathcal{Z}}_2,{\mathcal{Z}}_3$ represent the translation symmetries, whereas ${\mathcal{Z}}_4$ is the scaling symmetry.

2.2. Symmetry Reductions Using ${\mathcal{Z}}_1,{\mathcal{Z}}_2,{\mathcal{Z}}_3$

We use the symmetry $\mathcal{Z}={\mathcal{Z}}_1+a{\mathcal{Z}}_2+b{\mathcal{Z}}_3$, ($a,b$ constants) to reduce the 2D-EW Equation (6) to a NODE. The characteristic equations of symmetry $\mathcal{Z}$ give the invariants

$$\begin{array}{ll}\hfill & f=x-at,g=y-bt,u(t,x,y)=\Gamma (f,g),\hfill \end{array}$$

which reduce (6) to the NPDE

$$a{\Gamma }_f+b{\Gamma }_g-{\Gamma }^n{\Gamma }_f+\alpha a{\Gamma }_{fff}+\alpha b{\Gamma }_{ffg}+\beta a{\Gamma }_{fgg}+b\beta {\Gamma }_{ggg}=0.$$

(13)

Equation (13) has two translation symmetries ${\zeta }_1=\partial /\partial f,{\zeta }_2=\partial /\partial g.$ Symmetry $\zeta ={\zeta }_1+\nu {\zeta }_2$ produces the invariants

$$\begin{array}{l}z=g-\nu f,\Gamma (f,g)=\Psi \left(z\right)\hfill \end{array}$$

and these invariants transform the NPDE (13) to the NODE

$$\begin{array}{l}\left(a\nu -b\right){\Psi }^{\prime }\left(z\right)-\nu {\Psi }^n{\Psi }^{\prime }\left(z\right)+(a\alpha {\nu }^3-\alpha b{\nu }^2+\beta \nu a-\beta b){\Psi }^{‴}\left(z\right)=0,\hfill \end{array}$$

(14)

which we rewrite as

$$\begin{array}{l}A{\Psi }^{\prime }\left(z\right)-\nu {\Psi }^n\left(z\right){\Psi }^{\prime }\left(z\right)+B{\Psi }^{‴}\left(z\right)=0,\hfill \end{array}$$

(15)

where $A=a\nu -b,B=a\alpha {\nu }^3-\alpha b{\nu }^2+\beta \nu a-\beta b$ and $z=(a\nu -b)t-\nu x+y$.

2.3. Solution of (6) Using Kudryashov’s Method

We engage Kudryashov’s method [42] to construct the closed-form solution for the 2D-EW Equation (6). To do this, we start by removing the power n in the NODE (15) using the transformation

$$\Psi \left(z\right)=F^{1/n}\left(z\right).$$

(16)

Thus, the NODE (15) becomes

$$\begin{array}{ll}\hfill & (1-3n+2n^2)B{F}^{\prime }{\left(z\right)}^3+3n(a-n)BF\left(z\right)F^{\prime }\left(z\right)F^{″}\left(z\right)+n^{2}BF{\left(z\right)}^2{F}^{‴}\left(z\right)\hfill \\ \hfill & -n^2\nu F{\left(z\right)}^3{F}^{\prime }\left(z\right)+A{n}^{2}F{\left(z\right)}^2{F}^{\prime }\left(z\right)=0.\hfill \end{array}$$

(17)

Next, we assume that the NODE (17) has the solution of the form

$$\begin{array}{l}F\left(z\right)=\sum _{k=0}^J{C}_k{V}^k\left(z\right),\hfill \end{array}$$

(18)

where $C_k$ is the unknown constants to be determined and the function $V\left(z\right)$ satisfies the Riccati equation

$$\begin{array}{l}{V}^{\prime }\left(z\right)=V^2\left(z\right)-V\left(z\right),\hfill \end{array}$$

(19)

whose solution is

$$\begin{array}{l}V\left(z\right)=\frac{1}{1+exp\left(z\right)}.\hfill \end{array}$$

(20)

By using the balancing procedure [35] on Equation (17), we obtain $J=2$. Hence, (18) becomes

$$\begin{array}{l}F\left(z\right)=C_0+C_{1}V\left(z\right)+C_2{V}^2\left(z\right).\hfill \end{array}$$

(21)

Inserting the value of $F\left(z\right)$ from (21) into (17) and using (19), we obtain an equation which splits into nine algebraic equations:

$$\begin{array}{ll}\hfill & n^2\nu C_0^3{C}_1-A{n}^2{C}_0^2{C}_1-B{n}^2{C}_0^2{C}_1=0,\hfill \\ \hfill & 4B{C_2}^3-n^2\nu {C_2}^4+2B{n}^2{C_2}^3+6Bn{C_2}^3=0,\hfill \\ \hfill & 2n^2\nu C_2^4-7n^2\nu C_1{C}_2^3+12B{n}^2{C}_1{C}_2^2-6B{n}^2{C}_2^3+30Bn{C}_1{C}_2^2-24Bn{C}_2^3-24B{C}_2^3\hfill \\ \hfill & +12B{C}_1{C}_2^2=0,\hfill \\ \hfill & 2n^2\nu C_0^3{C}_2-n^2\nu C_0^3{C}_1+3n^2\nu C_0^2{C}_1^2+A{n}^2{C}_0^2{C}_1-2A{n}^2{C}_0^2{C}_2-2A{n}^2{C}_0{C}_1^2\hfill \\ \hfill & +7B{n}^2{C_0}^2{C}_1-8B{n}^2{C_0}^2{C}_2+B{n}^2{C}_0{C}_1^2-3Bn{C}_0{C}_1^2=0,\hfill \\ \hfill & 3n^2\nu C_0{C}_1^3-2n^2\nu C_0^3{C}_2-3n^2\nu C_0^2{C}_1^2+9n^2\nu C_0^2{C}_1{C}_2+2A{n}^2{C}_0^2{C}_2\hfill \\ \hfill & +2A{n}^2{C}_0{C}_1^2-6A{n}^2{C}_0{C}_1{C}_2-A{n}^2{C}_1^3-12B{n}^2{C_0}^2{C}_1+38B{n}^2{C}_0^2{C}_2\hfill \\ \hfill & +2B{n}^2{C}_0{C}_1^2+12Bn{C}_0{C}_1^2-18Bn{C}_0{C}_1{C}_2-B{C}_1^3=0,\hfill \\ \hfill & 7n^2\nu C_1{C}_2^3-6n^2\nu C_0{C_2}^3-9n^2\nu C_1^2{C}_2^2+2A{n}^2{C}_2^3+12B{n}^2{C}_0{C}_2^2\hfill \\ \hfill & +12B{n}^2{C}_1^2{C}_2-18B{n}^2{C}_1{C}_2^2+2B{n}^2{C}_2^3+36Bn{C}_0{C}_2^2+18Bn{C}_1^2{C}_2\hfill \\ \hfill & 12Bn{C}_2^3-66Bn{C}_1{C}_2^2+6B{C}_1^2{C}_2-36B{C}_1{C}_2^2+24B{C_2}^3=0,\hfill \\ \hfill & 6n^2\nu C_0{C}_2^3-15n^2\nu C_0{C}_1{C}_2^2-5n^2\nu C_1^3{C}_2+9n^2\nu C_1^2{C}_2^2+5A{n}^2{C}_1{C}_2^2-2A{n}^2{C}_2^3\hfill \\ \hfill & +30B{n}^2{C}_0{C}_1{C}_2-12B{n}^2{C}_0{C}_2^2+2B{n}^2{C}_1^3-21B{n}^2{C}_1^2{C}_2+5B{n}^2{C}_1{C}_2^2\hfill \\ \hfill & +30Bn{C}_0{C}_1{C}_2-96Bn{C}_0{C}_2^2+3Bn{C}_1^3-39Bn{C}_1^2{C}_2+42Bn{C}_1{C}_2^2+B{C}_1^3\hfill \\ \hfill & +36B{C}_1{C}_2^2-18B{C}_1^2{C}_2-8B{C}_2^3=0,\hfill \\ \hfill & 6n^2\nu C_0^2{C}_2^2-9n^2\nu C_0^2{C}_1{C}_2-3n^2\nu C_0{C}_1^3+12n^2\nu C_0{C}_1^2{C}_2+n^2\nu C_1^4+6A{n}^2{C}_0{C}_1{C}_2\hfill \\ \hfill & +A{n}^2{C}_1^3-4A{n}^2{C}_0{C_2}^2-4A{n}^2{C}_1^2{C}_2+6B{n}^2{C}_0^2{C}_1-54B{n}^2{C}_0^2{C}_2-9B{n}^2{C}_0{C}_1^2\hfill \\ \hfill & +24B{n}^2{C}_0{C}_1{C}_2+8B{n}^2{C}_0{C}_2^2+B{n}^2{C}_1^3-B{n}^2{C}_1^2{C}_2-15Bn{C}_0{C}_1^2+66Bn{C}_0{C}_1{C}_2\hfill \\ \hfill & +3B{C}_1^3-24Bn{C}_0{C_2}^2+3Bn{C}_1^3-3Bn{C}_1^2{C}_2-6B{C}_1^2{C}_2=0,\hfill \\ \hfill & 15n^2\nu C_0{C}_1{C}_2^2-6n^2\nu C_0^2{C}_2^2-12n^2\nu C_0{C}_1^2{C}_2-n^2\nu C_1^4+5n^2\nu C_1^3{C}_2\hfill \\ \hfill & +4A{n}^2{C}_0{C}_2^2+4A{n}^2{C}_1^2{C}_2-5A{n}^2{C}_1{C}_2^2+24B{n}^2{C}_0^2{C}_2+6B{n}^2{C}_0{C}_1^2-12B{C}_1{C}_2^2\hfill \\ \hfill & +10B{n}^2{C}_1^2{C}_2-54B{n}^2{C}_0{C}_1{C}_2-8B{n}^2{C}_0{C}_2^2-3B{n}^2{C}_1^3+B{n}^2{C}_1{C}_2^2+6Bn{C}_0{C}_1^2\hfill \\ \hfill & +84Bn{C}_0{C}_2^2-78Bn{C}_0{C}_1{C}_2-6Bn{C}_1^3+24Bn{C}_1^2{C}_2-6Bn{C}_1{C}_2^2-3B{C}_1^3\hfill \\ \hfill & +18B{C}_1^2{C}_2=0.\hfill \end{array}$$

(22)

Using Maple, we attain the solution of the above algebraic equations in the form

$$C_0=0,C_1=\frac{2A}{\nu }(n^2+3n+2),C_2=-\frac{2A}{\nu }(n^2+3n+2),B=-n^{2}A.$$

(23)

Thus, corresponding to the above values, we obtain the solution for the 2D-EW Equation (6) in the form

$$\begin{array}{l}u(t,x,y)={\left\{\frac{2}{\nu }A(n^2+3n+2)\left(\frac{exp\left(z\right)}{{\left\{1+exp\left(z\right)\right\}}^2}\right)\right\}}^{\frac{1}{n}},\hfill \end{array}$$

(24)

where $z=(a\nu -b)t-\nu x+y$. Figure 1 demonstrates the wave profile of solution (24) for the values $a=2,b=6,\nu =8,n=1,A=1$ and $t=0$.

Figure 1. The 3D and 2D wave profile of solution (24).

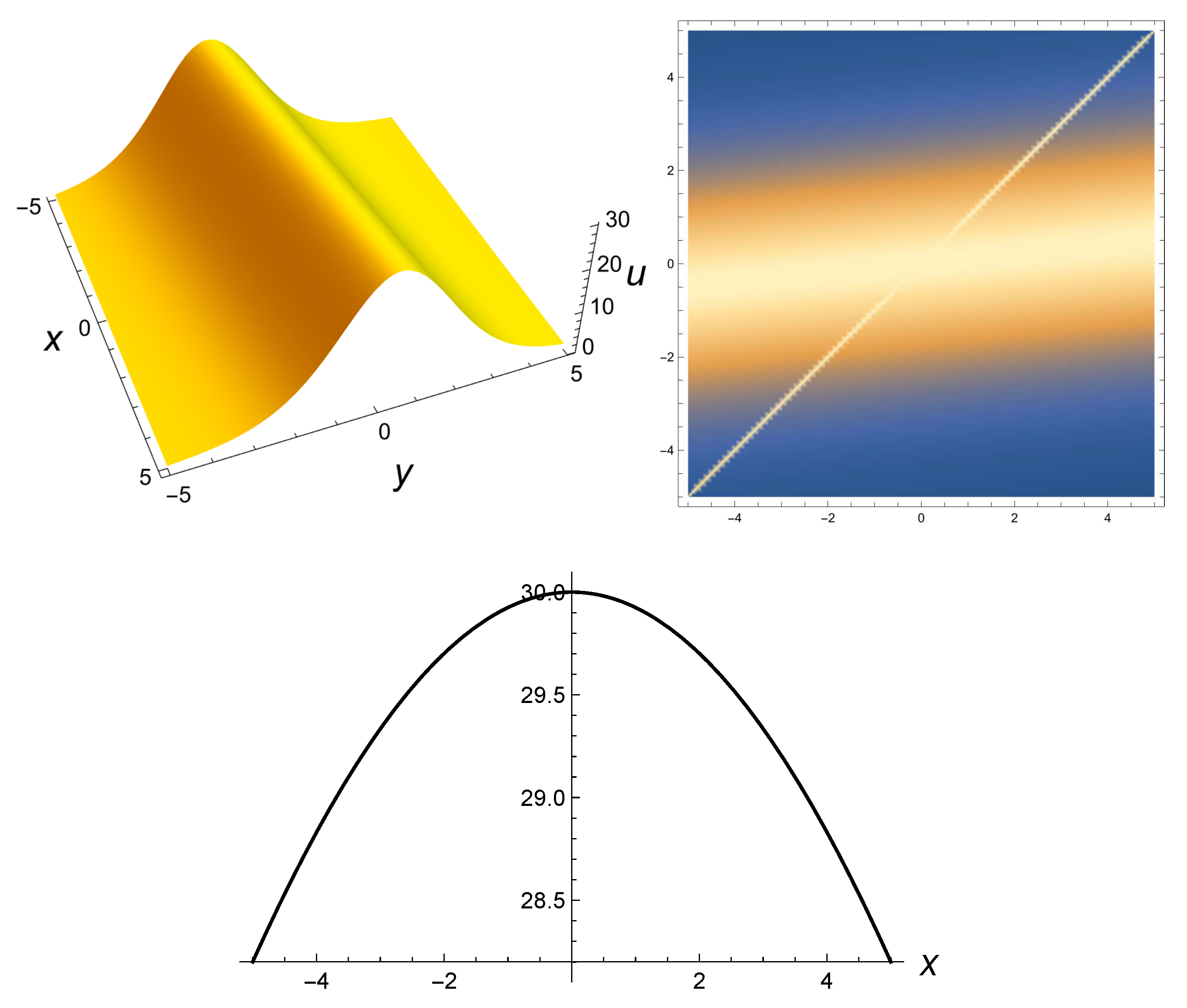
2.4. Solitary Wave Solution of (6)

We now seek the solitary wave solution for 2D-EW Equation (6). To achieve this task, we focus on the NODE (15). Integrating this NODE twice and taking the constants of integration to be zero, we obtain

$${\Psi }^{\prime 2}-\frac{2\nu }{B(n+1)(n+2)}{\Psi }^{n+2}+\frac{A}{B}{\Psi }^2=0.$$

(25)

Using the transformation $\Psi \left(z\right)=V^{1/n}\left(z\right)$, the NODE (25) becomes

$$V^{\prime 2}-\frac{2n^2\nu }{B(n+1)(n+2)}{V}^3+\frac{n^{2}A}{B}{V}^2=0,$$

(26)

whose solution is

$$V\left(z\right)=\frac{A(n+1)(n+2)}{2\nu }{\sec \mathrm{h}}^2\left(\sqrt{-\frac{A{n}^2}{4B}}\left(z\pm K\right)\right),$$

where $K=\left(\sqrt{A(n+1)(n+2)}{C}_1\right)/2$ and $C_1$ is an integration constant. Thus, the solution 2D-EW Equation (6) is

$$u(t,x,y)={\left\{\frac{A(n+1)(n+2)}{2\nu }{\sec \mathrm{h}}^2\left(\sqrt{-\frac{A{n}^2}{4B}}\left(z\pm K\right)\right)\right\}}^{1/n},$$

(27)

where $C_1$ is the integration constant and $z=(a\nu -b)t-\nu x+y$. In Figure 2, we give the illustration of the solution (27) for the values $\nu =0.9,A=0.18,a=0.2,b=0.2,n=1,$ $K=0$ and time $t=0.1$.

Figure 2. The 3D and 2D solution profiles of (27).

2.5. Solutions of (6) for $n=1$

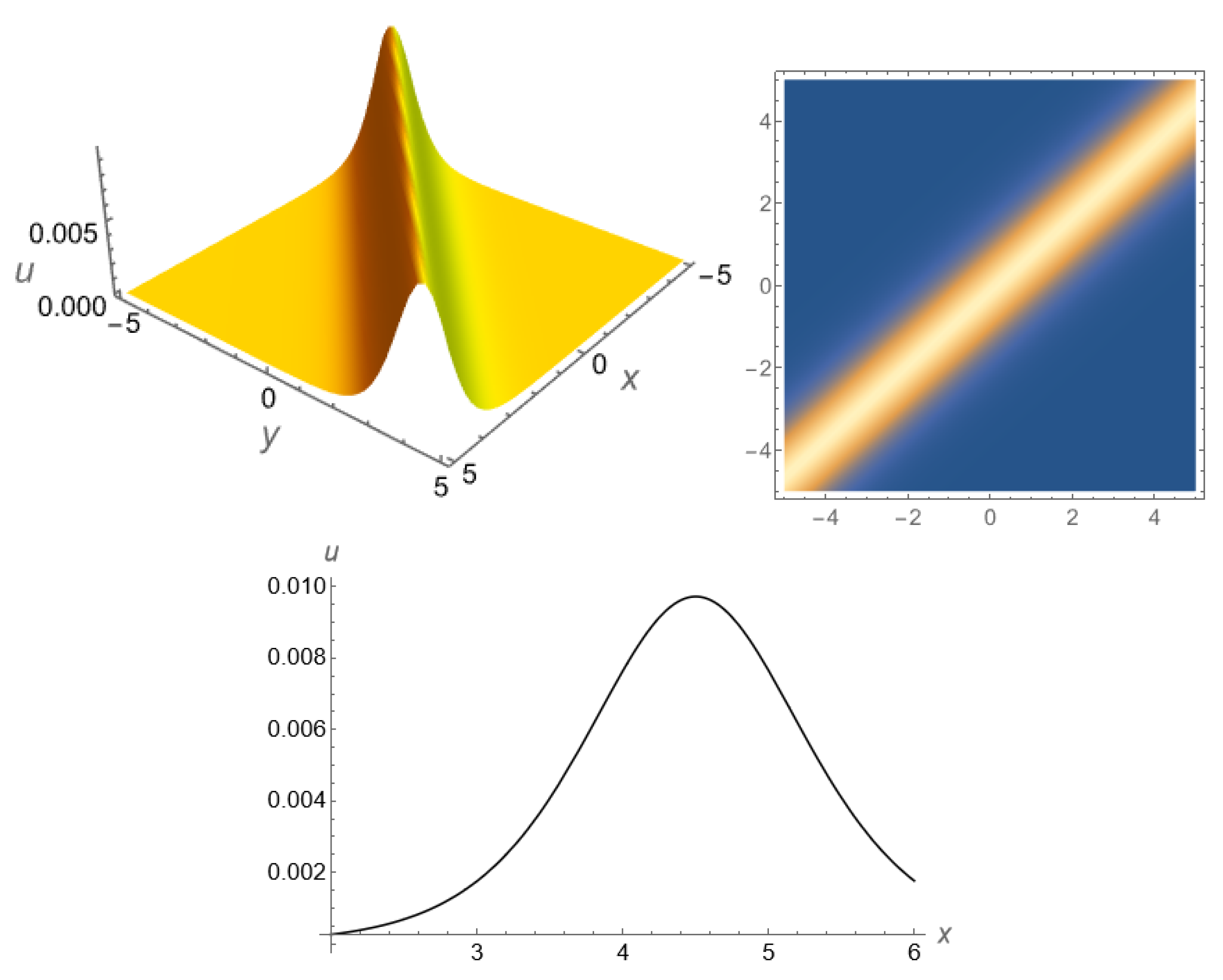
2.5.1. Solution via Direct Integration

We now seek the solution for 2D-EW Equation (6) for $n=1$ via the direct integration. Substituting $n=1$ into (15) and integrating the resultant equation twice gives

$$\begin{array}{l}{\Psi }^{\prime 2}=\frac{\nu }{3B}{\Psi }^3-\frac{A}{B}{\Psi }^2-\frac{2c_1}{B}\Psi -\frac{2c_2}{B},\hfill \end{array}$$

(28)

where $c_1,c_2$ are arbitrary constants. To gain the solution for the NODE (28), we assume that ${\kappa }_1,{\kappa }_2,{\kappa }_3$ are the real roots of the cubic polynomial

$${\Psi }^3-\frac{3A}{\nu }{\Psi }^2-\frac{6c_1}{\nu }\Psi -\frac{6c_2}{\nu }$$

with ${\kappa }_1>{\kappa }_2>{\kappa }_3$. Then, Equation (28) can be written as

$$\begin{array}{l}{\Psi }^{\prime 2}=\frac{\nu }{3B}(\Psi -{\kappa }_1)(\Psi -{\kappa }_2)(\Psi -{\kappa }_3),\hfill \end{array}$$

whose solution [43,44] is

$$\begin{array}{l}\Psi \left(z\right)={\kappa }_2+({\kappa }_1-{\kappa }_2){\mathrm{cn}}^2\left\{\sqrt{\frac{\nu ({\kappa }_1-{\kappa }_3)}{12B}}(z-z_0),{\mathcal{R}}^2\right\},{\mathcal{R}}^2=\frac{{\kappa }_1-{\kappa }_2}{{\kappa }_1-{\kappa }_3},\hfill \end{array}$$

where $z_0$ is a constant and (cn) is the Jacobi cosine function. Consequently, the solution for the 2D-EW Equation (6) is

$$\begin{array}{l}u(t,x,y)={\kappa }_2+({\kappa }_1-{\kappa }_2){\mathrm{cn}}^2\left\{\sqrt{\frac{\nu ({\kappa }_1-{\kappa }_3)}{12B}}(z-z_0),{\mathcal{R}}^2\right\},\hfill \end{array}$$

(29)

where $z=(a\nu -b)t-\nu x+y$. Figure 3 depicts the solution (29) graphically for the parametric values ${\kappa }_1=1,{\kappa }_2=-54,{\kappa }_3=-64,B=15,\nu =1.2,b=0.2,\nu =0.6,a=-4,$ $z_0=0$ and $t=-15$.

Figure 3. The 3D and 2D solution profiles of (29).

2.5.2. Solution via Weierstrass Elliptic Function Method

We begin by writing Equation (28) in the form

$$\begin{array}{l}{\Psi }^{\prime 2}\left(z\right)-k_1{\Psi }^3\left(z\right)-k_2{\Psi }^2\left(z\right)-k_3\Psi \left(z\right)-k_4=0,\hfill \end{array}$$

(30)

where the coefficients $k_1,k_2,k_3,k_4$ are expressed as $k_1=\nu /\left(3B\right),k_2=-A/B,k_3=-2c_1/B,k_4=-2c_2/B$. Now, using the transformation

$$\begin{array}{l}\Psi =\mathcal{V}-\frac{k_2}{3k_1},\hfill \end{array}$$

(31)

Equation (30) reduces to

$$\begin{array}{l}{\mathcal{V}}^{\prime }\left(\xi \right)=4{\mathcal{V}}^3\left(\xi \right)-g_2^2\mathcal{V}\left(\xi \right)-g_3^2,\xi =\sqrt{\frac{k_1}{4}}z,\hfill \end{array}$$

(32)

whose general solution [45] is given by

$$\begin{array}{l}\mathcal{V}\left(\xi \right)=\wp \left(\xi ;g_2^2;g_2^3\right)-\frac{k_2}{3k_1},\xi =\sqrt{\frac{k_1}{4}}z,\hfill \end{array}$$

(33)

where ℘ is the Weierstrass elliptic function and $g_2^2,g_3^2$ are the invariants that are given by

$$\begin{array}{l}{g}_2^2=\frac{4k_3}{k_1}-\frac{k_2^2}{3k_1^2},g_3^2=\frac{4k_4}{k_1}-\frac{4k_2{k}_3}{3k_1^2}+\frac{8k_2^3}{27k_1^3}.\hfill \end{array}$$

Thus, going back to our original variables, we obtain the solution of the 2D-EW equation as

$$\begin{array}{l}u(t,x,y)=\wp \left(\sqrt{\frac{k_1}{4}}z;g_2^2;g_2^3\right)-\frac{k_2}{3k_1}\hfill \end{array}$$

(34)

where $z=(a\nu -b)t-\nu x+y$. Figure 4 illustrates the solution (34) with the parameters assigned to be $k_1=4,k_2=0,k_3=1,k_4=2,a=3,\nu =0.1,b=9$ and $t=0$.

Figure 4. The 3D and 2D solution profiles of (34).

2.5.3. Solution via the Extended Jacobi Elliptic Function Method

We now construct exact explicit solutions of the 2D-EW Equation (6) in terms of the Jacobi elliptic functions [9]. We apply this method to NODE (15) for the case when $n=1$. For this case, the NODE (15) becomes

$$A{\Psi }^{\prime }\left(z\right)-\nu \Psi \left(z\right){\Psi }^{\prime }\left(z\right)+B{\Psi }^{‴}\left(z\right)=0.$$

(35)

The equations that are used are the first-order ODEs

$$H^{\prime }{\left(z\right)}^2=(1-H{\left(z\right)}^2)(1-\omega +\omega H{\left(z\right)}^2)$$

(36)

and

$$H^{\prime }{\left(z\right)}^2=(1-H{\left(z\right)}^2)(1-\omega H{\left(z\right)}^2)$$

(37)

whose solutions are the Jacobi elliptic cosine and the Jacobi elliptic sine functions, respectively, given by

$$\begin{array}{ll}\hfill & H\left(z\right)=\mathrm{cn}\left(z\right|\omega )\hfill \end{array}$$

(38)

and

$$\begin{array}{ll}\hfill & H\left(z\right)=\mathrm{sn}\left(z\right|\omega ),\hfill \end{array}$$

(39)

where $0\le \omega \le 1$.

Cnoidal wave solutions

We now consider the solution of the NODE (35) in the form

$$\Psi \left(z\right)=\sum _{j=-M}^M{A}_{j}H{\left(z\right)}^j,$$

(40)

where $A_j$ is the undetermined constants and M is the integer greater than zero, obtained by the balancing procedure. Using the balancing procedure on NODE (35), we obtain $M=2$. Thus, (40) becomes

$$\begin{array}{l}\Psi \left(z\right)=A_{-2}H{\left(z\right)}^{-2}+A_{-1}H{\left(z\right)}^{-1}+A_0+A_{1}H\left(z\right)+A_{2}H{\left(z\right)}^2.\hfill \end{array}$$

(41)

Using the above value of $\Psi$ in (35) and invoking (36), we obtain the following algebraic equations:

$$\begin{array}{ll}\hfill & 12\alpha a{\nu }^3{A}_{-2}-12\alpha a{\nu }^3\omega A_{-2}-12a\nu \beta \omega A_{-2}+12a\nu \beta A_{-2}+12\alpha b{\nu }^2\omega A_{-2}-12\alpha b{\nu }^2{A}_{-2}\hfill \\ \hfill & +12b\beta \omega A_{-2}-12b\beta A_{-2}-\nu A_{-2}^2=0,\hfill \\ \hfill & 2\alpha a{\nu }^3{A}_{-1}-2\alpha a{\nu }^3\omega A_{-1}-2a\nu \beta \omega A_{-1}+2a\nu \beta A_{-1}+2\alpha b{\nu }^2\omega A_{-1}-2\alpha b{\nu }^2{A}_{-1}\hfill \\ \hfill & +2b\beta \omega A_{-1}-2b\beta A_{-1}-\nu A_{-2}{A}_{-1}=0,\hfill \\ \hfill & 16\alpha a{\nu }^3\omega A_{-2}-8\alpha a{\nu }^3{A}_{-2}+16a\nu \beta \omega A_{-2}-8a\nu \beta A_{-2}+2a\nu A_{-2}-16\alpha b{\nu }^2\omega A_{-2}\hfill \\ \hfill & +8\alpha b{\nu }^2{A}_{-2}-16b\beta \omega A_{-2}+8b\beta A_{-2}-2b{A}_{-2}-\nu A_{-1}^2-2A_{-2}{A}_0\nu =0,\hfill \\ \hfill & 2\alpha a{\nu }^3\omega A_{-1}-\alpha a{\nu }^3{A}_{-1}+2a\nu \beta \omega A_{-1}-a\nu \beta A_{-1}+a\nu A_{-1}-2\alpha b{\nu }^2\omega A_{-1}-A_{-1}b\hfill \\ \hfill & +\alpha A_{-1}b{\nu }^2-2A_{-1}b\beta \omega +A_{-1}b\beta -A_{-1}{A}_0\nu -A_{-2}{A}_1\nu =0,\hfill \\ \hfill & \alpha a{\nu }^3{A}_1-2\alpha a{\nu }^3\omega A_1-2a\nu \beta \omega A_1+a\nu \beta A_1-a\nu A_1+2\alpha b{\nu }^2\omega A_1-\alpha b{\nu }^2{A}_1\hfill \\ \hfill & +2b\beta \omega A_1-b\beta A_1+b{A}_1+\nu A_0{A}_1+\nu A_{-1}{A}_2=0,\hfill \\ \hfill & 8\alpha a{\nu }^3{A}_2-16\alpha a{\nu }^3\omega A_2-16a\nu \beta \omega A_2+8a\nu \beta A_2-2a\nu A_2+16\alpha b{\nu }^2\omega A_2-8\alpha b{\nu }^2{A}_2\hfill \\ \hfill & +16b\beta \omega A_2-8b\beta A_2+2b{A}_2+\nu A_1^2+2\nu A_0{A}_2=0,\hfill \\ \hfill & 2\alpha a{\nu }^3\omega A_1+2a\nu \beta \omega A_1-2\alpha b{\nu }^2\omega A_1-2b\beta \omega A_1+\nu A_1{A}_2=0,\hfill \\ \hfill & 12\alpha a{\nu }^3\omega A_2+12a\nu \beta \omega A_2-12\alpha b{\nu }^2\omega A_2-12b\beta \omega A_2+\nu A_2^2=0.\hfill \end{array}$$

Solving the above system, using Mathematica, we obtain

$$\begin{array}{l}{A}_{-2}=\frac{12(1-\omega )(a\nu -b)\left(\alpha {\nu }^2+\beta \right)}{\nu },A_0=4(a\nu -b)\left\{\frac{\left((2\omega -1)\left(\alpha {\nu }^2+\beta \right)+1\right)}{\nu }\right\},\hfill \\ A_{-1}=0,A_1=0,A_2=\frac{12\omega (b-a\nu )\left(\alpha {\nu }^2+\beta \right)}{\nu }.\hfill \end{array}$$

(42)

Therefore, the solution to the 2D-EW Equation (6) is

$$\begin{array}{ll}u(t,x,y)=\hfill & \left\{\frac{12(a\nu -b)(\alpha {\nu }^2+\beta )}{\nu }\right\}\{\frac{1-\omega }{{\mathrm{cn}}^2\left(z\right|\omega )}-\omega {\mathrm{cn}}^2\left(z\right|\omega )\}\hfill \\ \hfill & +4(a\nu -b)\left\{\frac{((2\omega -1)(\alpha {\nu }^2+\beta )+1)}{\nu }\right\},\hfill \end{array}$$

(43)

where $0\le \omega \le 1$ and $z=(a\nu -b)t-\nu x+y$.

Snoidal wave solutions

Substituting (41) into (35) and making use of (37), we obtain an algebraic equation, which splits and yields the algebraic equations:

$$\begin{array}{ll}\hfill & 12\alpha b{\nu }^2{A}_{-2}-12\alpha a{\nu }^3{A}_{-2}-12a\nu \beta A_{-2}+12b\beta A_{-2}+\nu A_{-2}^2=0,\hfill \\ \hfill & \nu A_{-2}{A}_{-1}-2\alpha a{\nu }^3{A}_{-1}-2a\nu \beta A_{-1}+2\alpha b{\nu }^2{A}_{-1}+2b\beta A_{-1}=0,\hfill \\ \hfill & 8\alpha a{\nu }^3\omega A_{-2}+8\alpha a{\nu }^3{A}_{-2}+8a\nu \beta \omega A_{-2}+8a\nu \beta A_{-2}-2a\nu A_{-2}-8\alpha b{\nu }^2\omega A_{-2}\hfill \\ \hfill & +2\nu A_{-2}{A}_0-8\alpha b{\nu }^2{A}_{-2}-8b\beta \omega A_{-2}-8b\beta A_{-2}+2b{A}_{-2}+\nu A_{-1}^2=0,\hfill \\ \hfill & \alpha a{\nu }^3\omega A_{-1}+\alpha a{\nu }^3{A}_{-1}+a\nu \beta \omega A_{-1}+a\nu \beta A_{-1}-a\nu A_{-1}-\alpha b{\nu }^2\omega A_{-1}-\alpha b{\nu }^2{A}_{-1}\hfill \\ \hfill & +\nu A_{-1}{A}_0-b\beta \omega A_{-1}-b\beta A_{-1}+b{A}_{-1}+\nu A_{-2}{A}_1=0,\hfill \\ \hfill & a\nu A_1-\alpha a{\nu }^3\omega A_1-\alpha a{\nu }^3{A}_1-a\nu \beta \omega A_1-a\nu \beta A_1+\alpha b{\nu }^2\omega A_1+\alpha b{\nu }^2{A}_1+b\beta \omega A_1\hfill \\ \hfill & +b\beta A_1-b{A}_1-\nu A_0{A}_1-\nu A_{-1}{A}_2=0,\hfill \\ \hfill & 8\alpha b{\nu }^2\omega A_2-8\alpha a\nu {\nu }^2\omega A_2-8\alpha a\nu {\nu }^2{A}_2-8a\nu \beta \omega A_2-8a\nu \beta A_2+2a\nu A_2+8\alpha b{\nu }^2{A}_2\hfill \\ \hfill & +8b\beta \omega A_2+8b\beta A_2-2b{A}_2-\nu A_1^2-2A_0\nu A_2=0,\hfill \\ \hfill & 2\alpha a\nu {\nu }^2\omega A_1+2a\nu \beta \omega A_1-2\alpha b{\nu }^2\omega A_1-2b\beta \omega A_1-\nu A_1{A}_2=0,\hfill \\ \hfill & 12\alpha a\nu {\nu }^2\omega A_2+12a\nu \beta \omega A_2-12\alpha b{\nu }^2\omega A_2-12b\beta \omega A_2-\nu A_2^2=0.\hfill \end{array}$$

The solution of the above system, using Mathematica, is

$$\begin{array}{lll}\hfill & \hfill & A_{-2}=\frac{12(a\nu -b)\left(\alpha {\nu }^2+\beta \right)}{\nu },A_0=(b-a\nu )\left\{\frac{\left(4(\omega +1)\left(\alpha {\nu }^2+\beta \right)-1\right)}{\nu }\right\}\hfill \\ \hfill & \hfill & A_{-1}=0,A_1=0,A_2=\frac{12\omega (a\nu -b)\left(\alpha {\nu }^2+\beta \right)}{\nu }.\hfill \end{array}$$

(44)

Therefore, the solution for 2D-EW Equation (6) is

$$\begin{array}{ll}u(t,x,y)=\hfill & \left\{\frac{12(a\nu -b)\left(\alpha {\nu }^2+\beta \right)}{\nu }\right\}\left\{\frac{1}{{\mathrm{sn}}^2\left(z\right|\omega )}+\omega {\mathrm{sn}}^2\left(z\right|\omega )\right\}\hfill \\ \hfill & +(b-a\nu )\left\{\frac{\left(4(\omega +1)\left(\alpha {\nu }^2+\beta \right)-1\right)}{\nu }\right\},\hfill \end{array}$$

(45)

where $0\le \omega \le 1$ and $z=(a\nu -b)t-\nu x+y$.

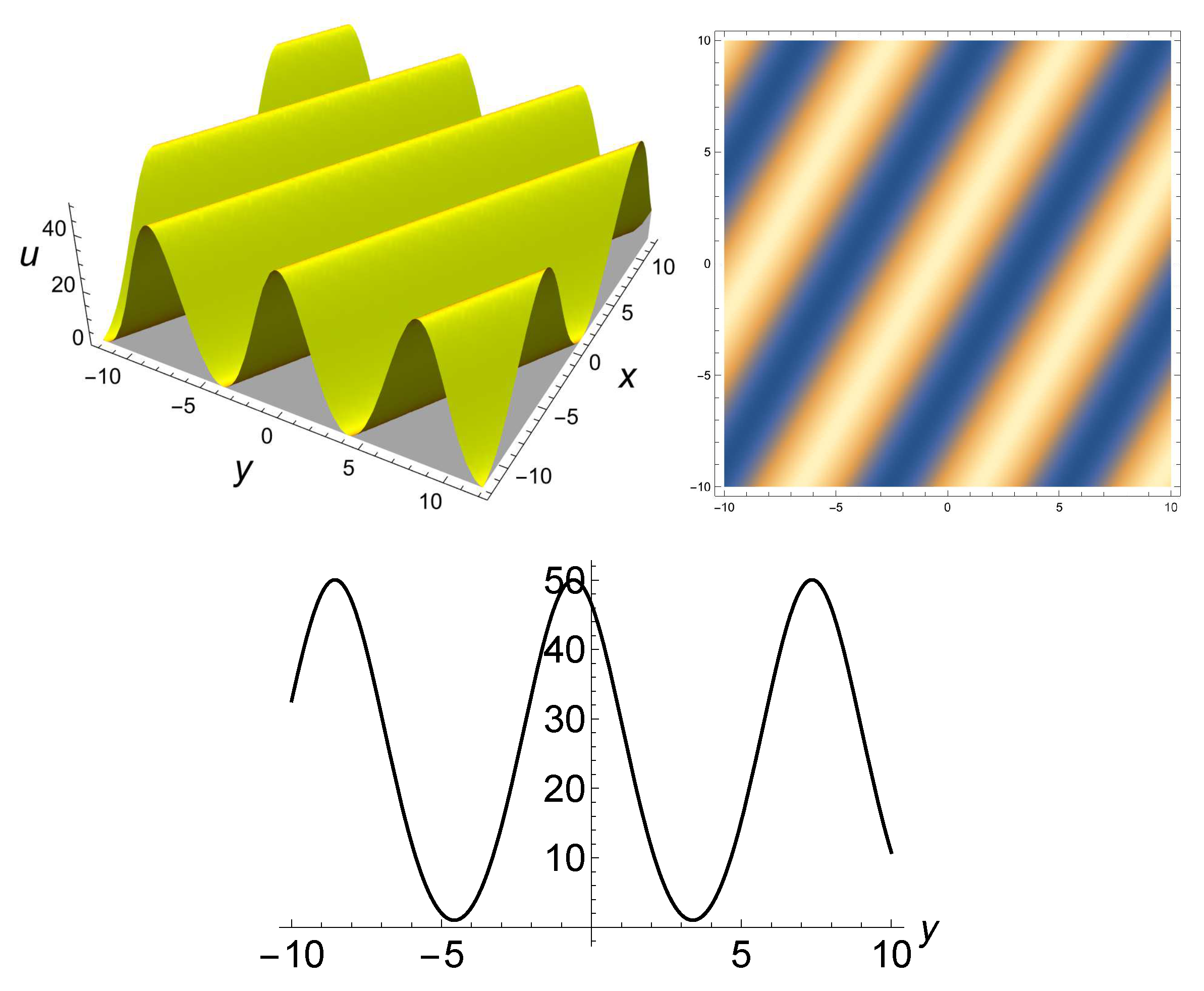
2.6. Solution of (6) for $n=2$ Using ${\mathcal{Z}}_4$

We use the symmetry ${\mathcal{Z}}_4$ to reduce then 2D-EW Equation (6) for $n=2$. This symmetry has the invariants

$$\begin{array}{ll}\hfill & r=x,s=y,u(t,x,y)=\frac{1}{t^{1/2}}\mathcal{P}(r,s)\hfill \end{array}$$

(46)

and they reduce Equation (6) to the NLPDE

$$\begin{array}{l}\alpha {\mathcal{P}}_{rr}+\beta {\mathcal{P}}_{ss}-2{\mathcal{P}}^2{\mathcal{P}}_r+\mathcal{P}=0.\hfill \end{array}$$

(47)

Equation (47) has two translation symmetries

$$\begin{array}{ll}\hfill & W_1=\frac{\partial }{\partial r},W_2=\frac{\partial }{\partial s}.\hfill \end{array}$$

Consider the symmetry $W=W_1+c{W}_2$. This gives the invariants

$$\begin{array}{l}\mathcal{P}(r,s)=\mathcal{Q}\left(z\right),z=s-cr,\hfill \end{array}$$

which reduces Equation (47) to the NODE

$$\begin{array}{l}\beta {\mathcal{Q}}^{″}+\alpha c^2{\mathcal{Q}}^{″}+2c{\mathcal{Q}}^2{\mathcal{Q}}^{\prime }+\mathcal{Q}=0.\hfill \end{array}$$

(48)

Power series solution

We find the solution of NODE (48) using the power series expansion method [10]. To obtain the power series solutions, we use the hypothesis

$$\begin{array}{l}\mathcal{Q}\left(z\right)={\displaystyle \sum _{j=0}^{\infty }}{A}_j{z}^j,\hfill \end{array}$$

(49)

where $A_j,j=0,1,\cdots$ are constants to be determined. From (49), we have

$$\begin{array}{l}{\mathcal{Q}}^{\prime }\left(z\right)={\displaystyle \sum _{j=0}^{\infty }}(j+1)A_{j+1}{z}^j,{\mathcal{Q}}^{″}\left(z\right)={\displaystyle \sum _{j=0}^{\infty }}(j+1)(j+2)A_{j+2}{z}^j.\hfill \end{array}$$

(50)

Substituting the values of $\mathcal{Q},{\mathcal{Q}}^{\prime },{\mathcal{Q}}^{″}$ from (49) and (50) into the NODE (48), we obtain

$$\begin{array}{ll}\hfill & \left(\beta +\alpha c^2\right)\sum _{j=0}^{\infty }(j+1)(j+2)A_{j+2}{z}^j+2c{\left(\sum _{j=0}^{\infty }{A}_j{z}^j\right)}^2\left(\sum _{j=0}^{\infty }(j+1)A_{j+1}{z}^j\right)\hfill \\ \hfill & +\sum _{j=0}^{\infty }{A}_j{z}^j=0\hfill \end{array}$$

(51)

and this simplifies to

$$\begin{array}{ll}\hfill & \left(\beta +c^2\alpha \right)\sum _{j=0}^{\infty }(j+1)(j+2)A_{j+2}{z}^j+2c\sum _{j=0}^{\infty }\sum _{i=0}^j\sum _{k=0}^i(j-i+1)A_k{A}_{i-k}{A}_{j-i+1}{z}^j\hfill \\ \hfill & +\sum _{j=0}^{\infty }{A}_j{z}^j=0.\hfill \end{array}$$

(52)

Hence, by inspecting the coefficients for $j=0$ and $j\ge 1$, we have

$$A_{j+2}=-\frac{1}{(\beta +\alpha c^2)(j+2)(j+1)}\left\{2c\sum _{i=0}^j\sum _{k=0}^i(j-i+1)A_k{A}_{i-k}{A}_{j-i+1}+A_j\right\},$$

(53)

for $j\ge 0$ and $A_0,A_1$ are arbitrary constants. Thus, reverting to the original variables, the solution of the 2D-EW Equation (6) is

$$u(t,x,y)=A_0+A_1\left(y-cx\right)+A_{j+2}{\left(y-cx\right)}^{j+2},$$

(54)

where the coefficients $A_2,A_3,A_4,\cdots$ are obtained from the recursive formula (53).

3. Conservation Laws

We now derive conservation laws for the 2D-EW Equation (6) by invoking two approaches. Firstly, we employ the multiplier method, and secondly, we use the Noether’s theorem.

3.1. Conservation Laws Using the Multiplier Method

We consider the zeroth-order multipliers for Equation (6), that is the multipliers $\mathcal{M}$ that depend on the variables $t,x,y$ and u only. We obtain the multipliers by using the determining equation

$$E_u\left\{\mathcal{M}\left(u_t+u^n{u}_x+\alpha u_{txx}+\beta u_{tyy}\right)\right\}=0,$$

(55)

where $E_u$ is the Euler–Lagrange operator defined by

$$E_u={\partial }_u-D_t{\partial }_{u_t}-D_x{\partial }_{u_x}-D_y{\partial }_{u_y}-D_t{D}_x^2{\partial }_{u_{txx}}-D_t{D}_y^2{\partial }_{u_{tyy}}+\cdots .$$

(56)

Here, $D_t,D_x,D_y$ are the total derivatives and are given by

$$\begin{array}{ll}{D}_t=\hfill & {\partial }_t+u_t{\partial }_u+u_{tt}{\partial }_{u_t}+u_{tx}{\partial }_{u_x}+u_{ty}{\partial }_{u_y}+\cdots ,\hfill \\ D_x=\hfill & {\partial }_x+u_x{\partial }_u+u_{tx}{\partial }_{u_t}+u_{xx}{\partial }_{u_x}+u_{xy}{\partial }_{u_y}+\cdots ,\hfill \\ D_y=\hfill & {\partial }_y+u_y{\partial }_u+u_{ty}{\partial }_{u_t}+u_{xy}{\partial }_{u_x}+u_{yy}{\partial }_{u_y}+\cdots .\hfill \end{array}$$

Expanding (55) and separating on various derivatives of u, we obtain

$$\begin{array}{l}\beta {\mathcal{M}}_{tyy}+{\mathcal{M}}_t=0,{\mathcal{M}}_{tu}=0,{\mathcal{M}}_{uu}=0,{\mathcal{M}}_x=0,\hfill \end{array}$$

(57)

which, upon solving, yields

$$\mathcal{M}={\mathbf{C}}_{\mathbf{1}}u+F\left(y\right)+G\left(t\right)sin(y/\sqrt{\beta })+H\left(t\right)cos(y/\sqrt{\beta }),$$

(58)

where ${\mathbf{C}}_{\mathbf{1}}$ is a constant and $F,G,H$ are arbitrary functions of their arguments. Now, the conserved quantities of 2D-EW Equation (6) are derived using the divergence identity

$$\begin{array}{l}{D}_t{C}^t+D_x{C}^x+D_y{C}^y=\mathcal{M}\left(u_t+u^n{u}_x+\alpha u_{txx}+\beta u_{tyy}\right)\hfill \end{array}$$

with $C^t$ representing conserved density and $C^x$, $C^y$ being spatial fluxes.

Case 1. The multiplier ${\mathcal{M}}_1=u$ gives the conserved vector $(C_1^t,C_1^x,C_1^y)$, where

$$\begin{array}{ll}{C}_1^t=\hfill & \frac{1}{2}{u}^2-\frac{1}{6}\left(\alpha u_x^2+\beta u_y^2\right)+\frac{1}{3}\left(\alpha u{u}_{xx}+\beta u{u}_{yy}\right),\hfill \\ C_1^x=\hfill & \frac{1}{n+2}{u}^{n+2}-\frac{1}{3}\alpha u_t{u}_x+\frac{2}{3}\alpha u{u}_{tx},\hfill \\ C_1^y=\hfill & \frac{2}{3}\beta u{u}_{ty}-\frac{1}{3}\beta u_t{u}_y;\hfill \end{array}$$

(59)

Case 2. For the multiplier ${\mathcal{M}}_2=F\left(y\right)$, we obtain the conserved vector whose components are

$$\begin{array}{ll}{C}_2^t=\hfill & \left(\frac{1}{3}\beta u_{yy}+\frac{1}{3}\alpha u_{xx}+u\right)F\left(y\right)-\frac{1}{3}\beta u_y{F}^{\prime }\left(y\right)+\frac{1}{3}\beta u{F}^{″}\left(y\right),\hfill \\ C_2^x=\hfill & \left(\frac{2}{3}\alpha u_{tx}+\frac{1}{n+1}{u}^{n+1}\right)F\left(y\right),\hfill \\ C_2^y=\hfill & \frac{2}{3}\beta u_{ty}F\left(y\right)-\frac{1}{3}\beta u_t{F}^{\prime }\left(y\right);\hfill \end{array}$$

(60)

Case 3. Using the multiplier ${\mathcal{M}}_3=G\left(t\right)sin\left(y/\sqrt{\beta }\right)$, we attain the conservation law whose components are

$$\begin{array}{ll}{C}_3^t=\hfill & -\frac{1}{3}\left\{\sqrt{\beta }{u}_{y}cos\left(\frac{y}{\sqrt{\beta }}\right)-\left(\alpha u_{xx}+\beta u_{yy}+2u\right)sin\left(\frac{y}{\sqrt{\beta }}\right)\right\}G\left(t\right),\hfill \\ C_3^x=\hfill & \left\{\left(\frac{1}{n+1}{u}^{n+1}+\frac{2}{3}\alpha u_{tx}\right)G\left(t\right)+\frac{1}{3}\alpha u_x{G}^{\prime }\left(t\right)\right\}sin\left(\frac{y}{\sqrt{\beta }}\right),\hfill \\ C_3^y=\hfill & \left\{\frac{2}{3}\beta u_{ty}G\left(t\right)-\frac{1}{3}\beta u_y{G}^{\prime }\left(t\right)\right\}sin\left(\frac{y}{\sqrt{\beta }}\right)+\left\{\frac{2}{3}\sqrt{\beta }u{G}^{\prime }\left(t\right)-\frac{1}{3}\sqrt{\beta }{u}_{t}G\left(t\right)\right\}cos\left(\frac{y}{\sqrt{\beta }}\right);\hfill \end{array}$$

Case 4. Finally, the multiplier ${\mathcal{M}}_4=H\left(t\right)cos\left(y/\sqrt{\beta }\right)$ gives the conserved vector $(C_4^t,C_4^x,C_4^y)$, where

$$\begin{array}{ll}{C}_4^t=\hfill & \frac{1}{3}\left\{\sqrt{\beta }{u}_{y}sin\left(\frac{y}{\sqrt{\beta }}\right)+\left(\alpha u_{xx}+\beta u_{yy}+2u\right)cos\left(\frac{y}{\sqrt{\beta }}\right)\right\}H\left(t\right),\hfill \\ C_4^x=\hfill & \left\{\left(\frac{1}{n+1}{u}^{n+1}+\frac{2}{3}\alpha u_{tx}\right)H\left(t\right)-\frac{1}{3}\alpha u_x{H}^{\prime }\left(t\right)\right\}cos\left(\frac{y}{\sqrt{\beta }}\right),\hfill \\ C_4^y=\hfill & \left\{\frac{2}{3}\beta u_{ty}H\left(t\right)-\frac{1}{3}\beta u_y{H}^{\prime }\left(t\right)\right\}cos\left(\frac{y}{\sqrt{\beta }}\right)+\left\{\frac{1}{3}\sqrt{\beta }{u}_{t}H\left(t\right)-\frac{2}{3}\sqrt{\beta }u{H}^{\prime }\left(t\right)\right\}sin\left(\frac{y}{\sqrt{\beta }}\right).\hfill \end{array}$$

3.2. Conservation Laws Using Noether’s Theorem

The 2D-EW Equation (6) is a third-order NPDE and, as a result, does not have a Lagrangian. We however overcome this limitation by using the transformation $u={\mathcal{V}}_x$, and this transforms the 2D-EW Equation (6) to the variational equation

$${\mathcal{V}}_{tx}+{\mathcal{V}}_x^n{\mathcal{V}}_{xx}+\alpha {\mathcal{V}}_{txxx}+\beta {\mathcal{V}}_{txyy}=0,$$

(61)

which has a second-order Lagrangian $\mathcal{L}$ given by

$$\mathcal{L}=-\frac{1}{2}{\mathcal{V}}_t{\mathcal{V}}_x-\frac{1}{(n+1)(n+2)}{\mathcal{V}}_x^{n+2}+\frac{1}{2}\alpha {\mathcal{V}}_{tx}{\mathcal{V}}_{xx}+\frac{1}{2}\beta {\mathcal{V}}_{ty}{\mathcal{V}}_{xy},n\ne -1,-2,$$

(62)

because $E_u\mathcal{L}=0$ on the Equation (61). Here, the Euler operator $E_u$ is given by

$$\begin{array}{l}{E}_u=\frac{\partial }{\partial \mathcal{V}}-D_t\frac{\partial }{\partial {\mathcal{V}}_t}-D_x\frac{\partial }{\partial {\mathcal{V}}_x}+D_t{D}_x\frac{\partial }{\partial {\mathcal{V}}_{tx}}+D_x^2\frac{\partial }{\partial {\mathcal{V}}_{xx}}+D_x{D}_y\frac{\partial }{\partial {\mathcal{V}}_{xy}}.\hfill \end{array}$$

The determining equation for Noether symmetries is

$$\begin{array}{l}{\mathcal{Z}}^{\left[2\right]}\mathcal{L}+\left\{D_t\left(\tau \right)+D_x\left(\xi \right)+D_y\left(\varphi \right)\right\}\mathcal{L}-D_t\left(B^t\right)-D_x\left(B^x\right)-D^y\left(B^y\right)=0,\hfill \end{array}$$

(63)

where ${\mathcal{Z}}^{\left[2\right]}$ is the second prolongation of

$$\begin{array}{l}\mathcal{Z}=\tau (t,x,y,\mathcal{V})\frac{\partial }{\partial t}+\xi (t,x,y,\mathcal{V})\frac{\partial }{\partial x}+\varphi (t,x,y,\mathcal{V})\frac{\partial }{\partial y}+\eta (t,x,y,\mathcal{V})\frac{\partial }{\partial \mathcal{V}}\hfill \end{array}$$

and $(B^t,B^x,B^y)$ are gauge functions that depend on $(t,x,y,\mathcal{V})$. Expanding (63), we obtain an equation which is then separated by various derivatives of $\mathcal{V}$ to give the following PDEs:

$$\begin{array}{ll}\hfill & {\tau }_x=0,{\tau }_y=0,{\tau }_{\mathcal{V}}=0,{\xi }_t=0,{\xi }_y=0,{\xi }_{xx}=0,{\xi }_{\mathcal{V}}=0,{\varphi }_t=0,{\varphi }_{\mathcal{V}}=0,{\varphi }_x=0,\hfill \\ \hfill & {\eta }_{tx}=0,{\eta }_{tx}=0,{\eta }_x=0,B_{\mathcal{V}}^t=0,{\eta }_{\mathcal{V}\mathcal{V}}=0,{\eta }_{x\mathcal{V}}=0,{\eta }_{t\mathcal{V}}=0,{\eta }_{x\mathcal{V}}=0,{\eta }_{yy}=0,\hfill \\ \hfill & {\eta }_{y\mathcal{V}}=0,{\eta }_{t\mathcal{V}}=0,2{\eta }_{\mathcal{V}}-{\varphi }_y=0,B_{\mathcal{V}}^x+\frac{1}{2}{\eta }_t=0,{\eta }_{\mathcal{V}}+\frac{1}{2}{\varphi }_y=0,B_{\mathcal{V}}^t+\frac{1}{2}{\eta }_x=0,\hfill \\ \hfill & {\varphi }_y+2{\eta }_{\mathcal{V}}-2{\xi }_x=0,B_t^t+B_x^x+B_y^y=0,{\tau }_t+{\xi }_x+n{\xi }_x-{\varphi }_y-(n+2){\eta }_{\mathcal{V}}=0.\hfill \end{array}$$

Solving the above overdetermined system of equations, we obtain

$$\begin{array}{ll}\hfill & \tau =c_1,\xi =c_2,\varphi =c_3,\eta =yg\left(t\right)+f\left(t\right),\hfill \\ \hfill & B^t=F_4(t,x,y),B^x=-\frac{1}{2}y\mathcal{V}{g}^{\prime }\left(t\right)-\frac{1}{2}\mathcal{V}{f}^{\prime }\left(t\right)+F_5(t,x,y),B^y=F_6(t,x,y),\hfill \end{array}$$

where $c_1,c_2,c_2$ are constants, whereas $f,g,F_4,F_5,F_6$ are arbitrary functions of their arguments. We take $F_4=F_5=F_6=0$, since they contribute to the trivial part of the conservation laws. Thus, the Noether symmetries and their gauge functions are

$$\begin{array}{ll}\hfill & {\mathcal{Z}}_1=\frac{\partial }{\partial t},B_1^t=0,B_1^x=0,B_1^y=0,\hfill \\ \hfill & {\mathcal{Z}}_2=\frac{\partial }{\partial x},B_2^t=0,B_2^x=0,B_2^y=0,\hfill \\ \hfill & {\mathcal{Z}}_3=\frac{\partial }{\partial y},B_3^t=0,B_3^x=0,B_3^y=0,\hfill \\ \hfill & {\mathcal{Z}}_4=f\left(t\right)\frac{\partial }{\partial \mathcal{V}},B_4^t=0,B_4^x=-\frac{1}{2}\mathcal{V}{f}^{\prime }\left(t\right),B_4^y=0,\hfill \\ \hfill & {\mathcal{Z}}_5=yg\left(t\right)\frac{\partial }{\partial \mathcal{V}},B_5^t=0,B_5^x=-\frac{1}{2}y\mathcal{V}{g}^{\prime }\left(t\right),B_5^y=0.\hfill \end{array}$$

Corresponding to each of the above Noether symmetries, we obtain the following nonlocal conserved vectors for the 2D-EW Equation (6) by invoking formulas given in [24]:

Case 1.${\mathcal{Z}}_1=\partial /\partial t$

$$\begin{array}{ll}{T}_1^t=\hfill & \frac{1}{4}\alpha u_x{u}_t-\frac{1}{(n+1)(n+2)}{u}^{n+2}+\left(\frac{1}{4}\alpha u_{xx}+\frac{1}{4}\beta u_{yy}\right)\int u_{t}dx\hfill \\ \hfill & +\frac{1}{4}\beta u_t\int u_{yy}dx,\hfill \\ T_1^x=\hfill & -\frac{1}{2}\alpha u_t^2+\left(\frac{3}{4}\alpha u_{tx}+\frac{1}{n+1}{u}^{n+1}+\frac{1}{2}\int u_{t}dx+\frac{1}{4}\beta \int u_{tyy}dx\right)\int u_{t}dx\hfill \\ \hfill & -\left(\frac{1}{4}\beta \int u_{yy}dx+\frac{1}{4}\alpha u_x\right)\int u_{tt}dx,\hfill \\ T_1^y=\hfill & \frac{1}{2}\beta u_{ty}\int u_{t}dx-\frac{1}{2}\beta u_t\int u_{ty}dx;\hfill \end{array}$$

Case 2.${\mathcal{Z}}_2=\partial /\partial x$

$$\begin{array}{ll}{T}_2^t=\hfill & \frac{1}{4}\alpha u{u}_{xx}-\frac{1}{4}\alpha u_x^2+\frac{1}{4}\beta u{u}_{yy}-\frac{1}{4}\beta u_x\int u_{yy}dx+\frac{1}{2}{u}^2,\hfill \\ T_2^x=\hfill & \frac{1}{n+2}{u}^{n+2}+\frac{3}{4}\alpha u{u}_{tx}-\frac{1}{4}\alpha u_x{u}_t+\frac{1}{4}\beta u\int u_{tyy}dx+\frac{1}{4}\beta u_t\int u_{yy}dx,\hfill \\ T_2^y=\hfill & \frac{1}{2}\beta u{u}_{ty}-\frac{1}{2}\beta u_t{u}_y;\hfill \end{array}$$

Case 3.${\mathcal{Z}}_3=\partial /\partial y$

$$\begin{array}{ll}{T}_3^t=\hfill & -\frac{1}{4}\alpha u_x{u}_y-\frac{1}{4}\beta u_y\int u_{yy}dx+\left(\frac{1}{4}\alpha u_{xx}+\frac{1}{4}\beta u_{yy}+\frac{1}{2}u\right)\int u_{y}dx,\hfill \\ T_3^x=\hfill & \left(\frac{1}{n+1}{u}^{n+1}+\frac{3}{4}\alpha u_{tx}+\frac{1}{4}\beta \int u_{tyy}dx+\frac{1}{2}\int u_{t}dx\right)\int u_{y}dx\hfill \\ \hfill & -\left(\frac{1}{4}\alpha u_x+\frac{1}{4}\beta \int u_{yy}dx\right)\int u_{ty}dx-\frac{1}{2}\alpha u_t{u}_y,\hfill \\ T_3^y=\hfill & -\frac{1}{(n+1)(n+2)}{u}^{n+2}+\frac{1}{2}\alpha u_x{u}_t+\frac{1}{2}\beta u_{ty}\int u_{y}dx-\frac{1}{2}u\int u_{t}dx;\hfill \end{array}$$

Case 4.${\mathcal{Z}}_4=f\left(t\right)\partial /\partial \mathcal{V}$

$$\begin{array}{ll}{T}_4^t=\hfill & \left(-\frac{1}{4}\beta u_{yy}-\frac{1}{4}\alpha u_{xx}-\frac{1}{2}u\right)f\left(t\right),\hfill \\ T_4^x=\hfill & \left(-\frac{1}{n+1}{u}^{n+1}-\frac{3}{4}\alpha u_{tx}-\frac{1}{4}\beta \int u_{tyy}dx-\frac{1}{2}\int u_{t}dx\right)f\left(t\right)+\left(\frac{1}{4}\alpha u_x\right.\hfill \\ \hfill & \left.+\frac{1}{4}\beta u_{yy}+\frac{1}{2}\int udx\right)f^{\prime }\left(t\right),\hfill \\ T_4^y=\hfill & -\frac{1}{2}\beta f\left(t\right)u_{ty};\hfill \end{array}$$

Case 5.${\mathcal{Z}}_5=yg\left(t\right)\partial /\partial \mathcal{V}$

$$\begin{array}{ll}{T}_5^t=\hfill & \left(-\frac{1}{4}\alpha y{u}_{xx}-\frac{1}{4}\beta y{u}_{yy}-\frac{1}{2}yu\right)g\left(t\right),\hfill \\ T_5^x=\hfill & \left(-\frac{1}{n+1}y{u}^{n+1}-\frac{3}{4}\alpha y{u}_{tx}-\frac{1}{4}\beta y\int u_{tyy}dx-\frac{1}{2}y\int u_{t}dx\right)g\left(t\right)\hfill \\ \hfill & +\left(\frac{1}{4}\alpha y{u}_x+\frac{1}{4}\beta y\int u_{yy}dx+\frac{1}{2}y\int udx\right)g^{\prime }\left(t\right),\hfill \\ T_5^y=\hfill & \left(\frac{1}{2}\beta u_t-\frac{1}{2}\beta y{u}_{ty}\right)g\left(t\right).\hfill \end{array}$$

We note that due to the presence of arbitrary functions f and g, we obtain infinitely many conservation laws.

4. Conclusions

In this work, we investigated the 2D-EW Equation (6), which is used to model nonlinear dispersive waves. We computed Lie point symmetries of (6), and as a result, we obtained four symmetries that include the three translation and one scaling symmetries. Moreover, we performed symmetry reductions and obtained several NODEs, which were solved with the aid of various techniques. The methods included the Kudryashov’s method, power series expansion method, extended Jacobi elliptic method and the Weierstrass elliptic function method. The exact solutions obtained are the snoidal wave, cnoidal wave, Weierstrass elliptic function, Jacobi elliptic cosine function, solitary wave and exponential function solutions. Furthermore, the graphical representation for certain solutions was also presented for certain parametric values in 2D and 3D, so as to give the reader a better understanding of these solutions. Finally, using two techniques, the conservation laws for the underlying equation were constructed. The techniques utilized were the multiplier method which gave four local conservation laws and the classical Noether’s theorem, which gave five nonlocal conservation laws. The conservation laws that were constructed contained the conservation of energy and momentum.