Weak Approximations of the Wright–Fisher Process
Abstract
:1. Introduction
2. Preliminaries
- 1.
- the scheme is a potential weak νth-order discretization scheme for the operator A.
- 2.
- is a function such that defined on solves for .
3. First-Order Weak Approximation of Wright–Fisher Equation
3.1. Approximation of the Stochastic Part
3.2. Algorithm
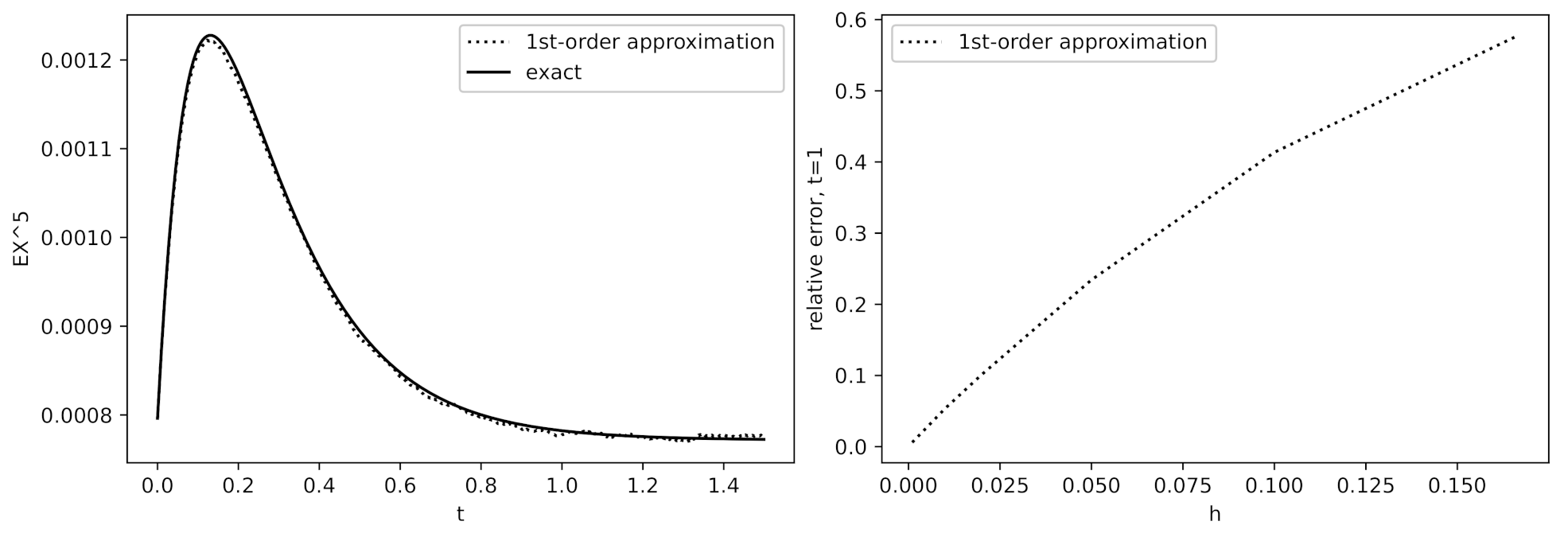
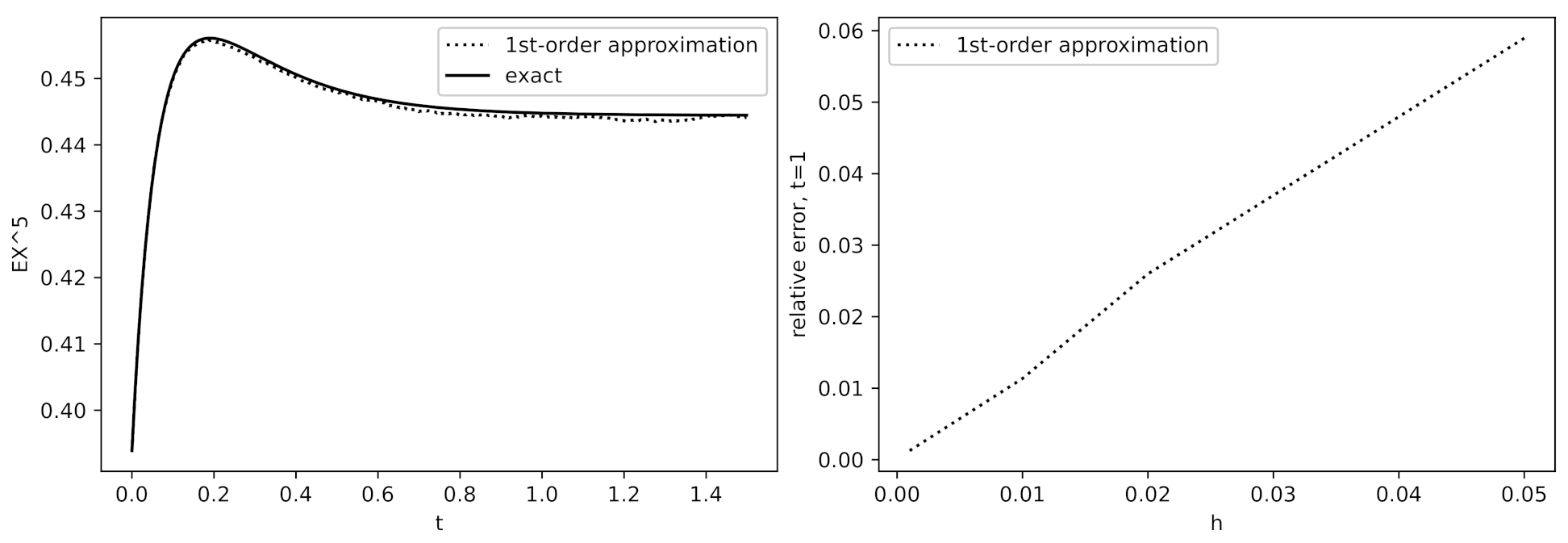
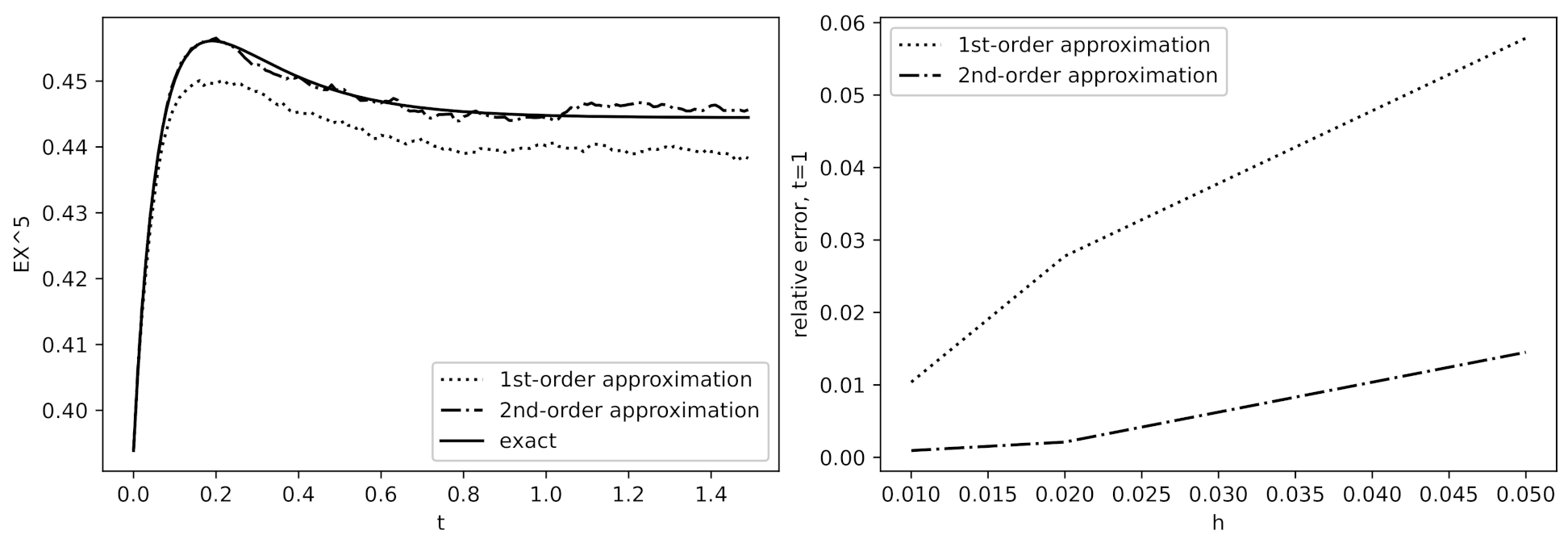
3.3. Simulation Examples
4. Second-Order Weak Approximation of Wright–Fisher Equation
4.1. Approximation of the Stochastic Part
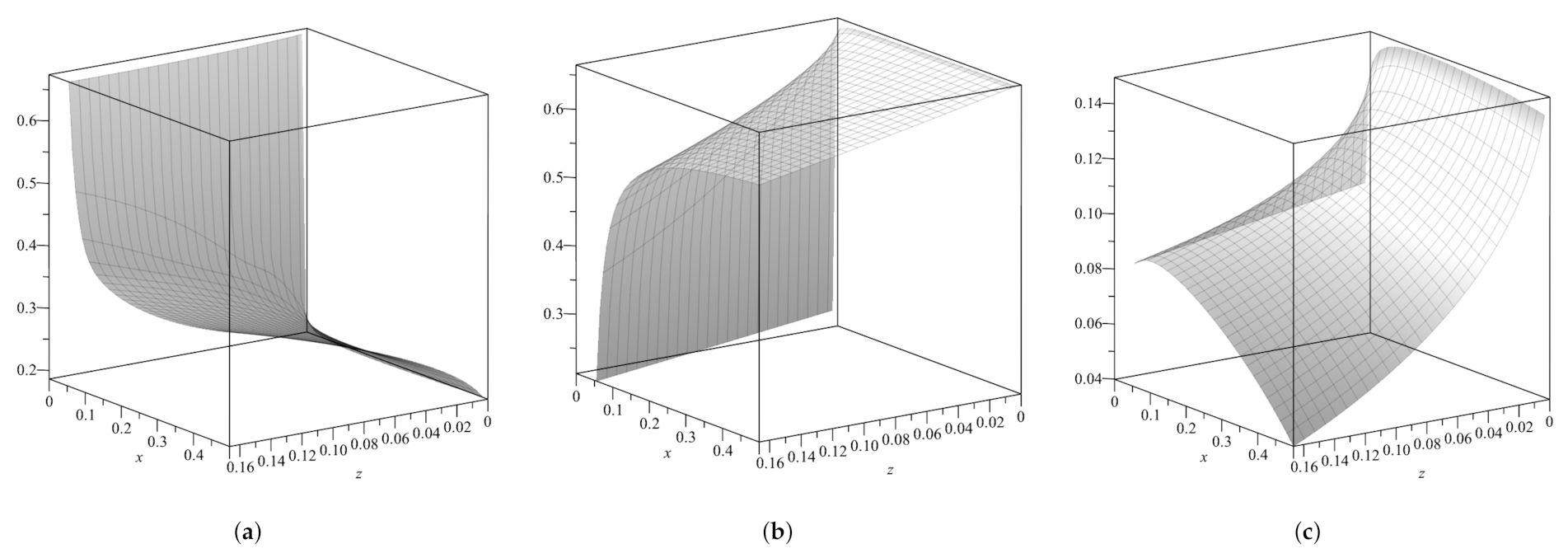
4.2. Calculation of the Parameters
4.3. Positivity of the Solution
4.4. The Second Main Result
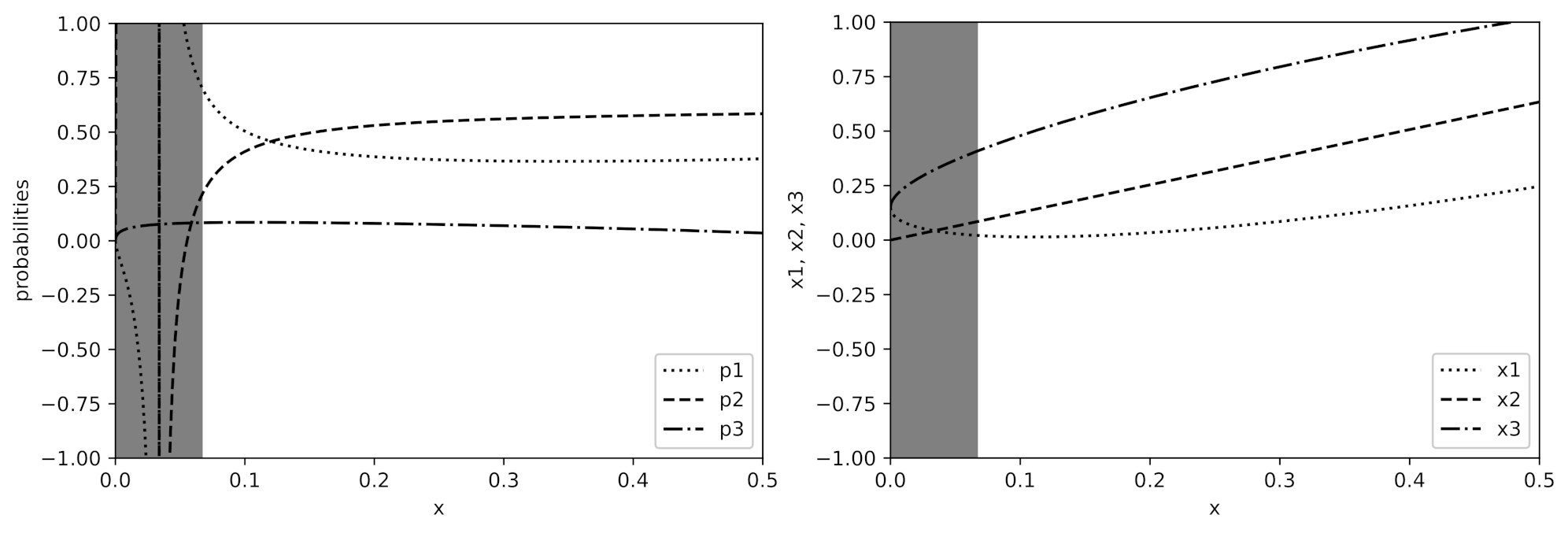
4.5. Algorithm for Second-Order Approximation
- 1.
- Draw a uniform random variable U from the interval [0, 1].
- 2.
- (where D is given by (5))
- 3.
- If , then
- 3.1.
- if , thencalculate , according to (50)–(52),calculate , according to (34),if then else if thenelse if then elseelsecalculate according to (53),,if then elseelse
- 3.2.
- do step 3.1 with , ,.
- 4.
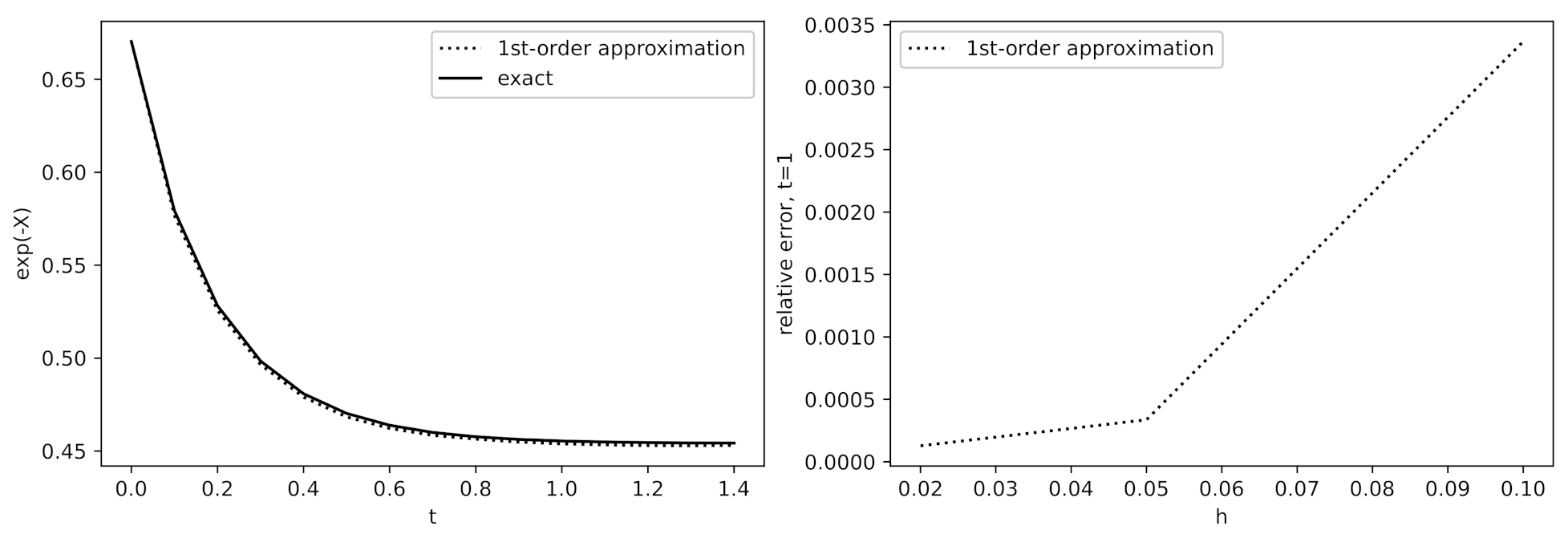
4.6. Simulation Examples
5. Probabilistic Proof of Regularity of Solutions of the Kolmogorov Backward Equation
- (1)
- the moments are infinitely continuously differentiable and
- (2)
- all formal partial derivatives of the series in (57),converge uniformly for (for any fixed ).
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| WF | Wright–Fisher model |
| CIR | Cox–Ingersoll–Ross model |
| PDE | Partial differential equation |
| B | Brownian motion |
| The set of positive integers | |
| The set of nonnegative integers, | |
| The set of real numbers | |
| The set of positive real numbers | |
| A subclass of , see Definition 3. | |
| if, for some and | |
| A discretization scheme of the WF process | |
| The solution of the deterministic part of the WF equation | |
| The solution of the stochastic part of the WF equation | |
| A discretization scheme of | |
| The mean of a random variable X | |
| The th-order remainder of a discretization scheme | |
| A | The generator of the WF process |
| The generator of the stochastic part of the WF process |
References
- Milstein, G.N.; Tretyakov, M.V. Stochastic Numerics for Mathematical Physics; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Alfonsi, A. Affine Diffusions and Related Processes: Simulation, Theory and Applications; Bocconi & Springer Series; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Cox, J.C.; Ingersoll, J.E.; Ross, S.A. A theory of the term structure of interest rates. Econometrica 1985, 53, 385–407. [Google Scholar] [CrossRef]
- Alfonsi, A. High order discretization schemes for the CIR process: Application to affine term structure and Heston models. Math. Comput. 2010, 79, 209–237. [Google Scholar] [CrossRef]
- Lileika, G.; Mackevičius, V. Weak approximation of CKLS and CEV processes by discrete random variables. Lith. Math. J. 2020, 60, 208–224. [Google Scholar] [CrossRef]
- Lileika, G.; Mackevičius, V. Second-order weak approximations of CKLS and CEV processes by discrete random variables. Mathematics 2021, 9, 1337. [Google Scholar] [CrossRef]
- Epstein, C.L.; Mazzeo, R. Wright–Fisher diffusion in one dimension. SIAM J. Math. Anal. 2010, 42, 568–608. [Google Scholar] [CrossRef]
- Krantz, S.G.; Parks, H.R. A Primer of Real Analytic Functions, 2nd ed.; Birkhäuser: Boston, MA, USA, 2002. [Google Scholar]
- Ksendal, B. Stochastic Differential Equations: An Introduction with Applications, 5th ed.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2000. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mackevičius, V.; Mongirdaitė, G. Weak Approximations of the Wright–Fisher Process. Mathematics 2022, 10, 125. https://doi.org/10.3390/math10010125
Mackevičius V, Mongirdaitė G. Weak Approximations of the Wright–Fisher Process. Mathematics. 2022; 10(1):125. https://doi.org/10.3390/math10010125
Chicago/Turabian StyleMackevičius, Vigirdas, and Gabrielė Mongirdaitė. 2022. "Weak Approximations of the Wright–Fisher Process" Mathematics 10, no. 1: 125. https://doi.org/10.3390/math10010125
APA StyleMackevičius, V., & Mongirdaitė, G. (2022). Weak Approximations of the Wright–Fisher Process. Mathematics, 10(1), 125. https://doi.org/10.3390/math10010125




