Next Article in Journal
Teacher Recruitment: Factors That Predict High School Students’ Willingness to Become Teachers
Previous Article in Journal
Supportive Peer Feedback in Tertiary Education: Analysis of Pre-Service Teachers’ Perceptions
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Education Sciences
Volume 9
Issue 4
10.3390/educsci9040281
education-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Knowledge Acquisition of Biology and Physics University Students—the Role of Prior Knowledge

by
Torsten Binder
1,*,
Philipp Schmiemann
1 and
Heike Theyssen
2,*
1
Biology Education, University of Duisburg-Essen, 45117 Essen, Germany
2
Physics Education, University of Duisburg-Essen, 45117 Essen, Germany
*
Authors to whom correspondence should be addressed.
Educ. Sci. 2019, 9(4), 281; https://doi.org/10.3390/educsci9040281
Submission received: 20 September 2019 / Revised: 20 November 2019 / Accepted: 24 November 2019 / Published: 27 November 2019
Browse Figures
Versions Notes

Abstract

:
This study investigates the knowledge acquisition of biology and physics freshmen students with special regard to differences between high school (HS) high performing and low performing students. Our study is based on a prior knowledge model, which describes explicit knowledge as a composite of four knowledge types: knowledge of facts, knowledge of meaning, integration of knowledge, and application of knowledge. As a first outcome-oriented approach, we operationalize knowledge acquisition via the changes in these knowledge types between the beginning and the end of the first year. To investigate the knowledge acquisition, a test set was constructed that covers these knowledge types. It was administered to 162 biology and 101 physics students at university. We used an Item Response Theory approach to scale the data. Repeated measures ANOVAs were used to analyze the acquisition of the knowledge types. We separated HS low, medium, and high achievers by high school grade point average (HS GPA). The knowledge acquisition of the HS low achievers did not differ from other groups. However, the HS low achievers did not only start with less prior knowledge but also were not able to reach the prior knowledge of the HS high achievers within the first year. Our findings concerning knowledge acquisition may be used to support and improve students’ knowledge acquisition in a targeted way by focusing on selected knowledge types.

1. Introduction

Science students in the introductory phase of university courses often struggle with mastering new subject-specific challenges [1]. If a student can withstand these subject-specific challenges or not, was part of numerous prediction studies on academic achievement (e.g., [2,3,4,5,6]). Here, high school grade point average (HS GPA) turns out to be the best single predictor for university achievement internationally [5,7]. Potential reasons for high predictive power of the HS GPA may be differences in the students’ subject specific prior knowledge as well as in their knowledge acquisition during the first year. However, up to now, much remains unknown about the (differences in) subject specific prior knowledge of HS low and high achievers and their knowledge acquisition during the first year at university. Therefore, to improve students’ performance and to contribute to the development of more effective science courses, it seems necessary to understand how students’ knowledge changes during the first year.

1.1. Theories of Knowledge

There are several theoretical models of knowledge [8,9,10] that are only sporadically adapted for student assessment so far. Knowledge and its key dimensions have been studied in research on cognition and learning for years. Bloom [8] provides a widely accepted definition of prior knowledge (The prefix “prior” stresses the role of knowledge as a prerequisite for learning. It does not imply that prior knowledge is a different type or subtype of knowledge.):
“[Prior knowledge comprises a student’s] cognitive entry behaviors [as] those prerequisite types of knowledge, skills, and competencies which are essential to the learning of a particular new task or set of tasks”.
[8] (p. 32)
Most studies seem to agree that knowledge is a complex, multidimensional construct [3,9,10,11,12]. For example, Dochy and Alexander [10] define prior knowledge as dynamic in nature, structured, explicit or tacit, and partitioned in multiple knowledge types and skills. The most common accepted distinction is made between knowing-that (declarative/conceptual knowledge) and knowing-how (procedural, strategic knowledge) [9,10,13,14,15]. Declarative knowledge is defined as knowledge of specific facts, meanings, concepts, symbols, and principles in a particular field of study [14,15], while procedural knowledge is defined as the conversion of declarative knowledge into functional units [14]. The main difference between these two knowledge types is that procedural knowledge refers to actions directly and helps handling tasks and problems, whereas declarative knowledge does not [13,16]. Procedural knowledge is goal-orientated and mediates problem-solving processes [17]. As such, declarative and procedural knowledge are domain specific [9].
In recent science education research, Hailikari et al. [3] and Hailikari and Nevgi [2] proposed a model of explicit knowledge that distinguishes four knowledge types, two rather declarative and two rather procedural. The definitions of these knowledge types are based on the theoretical work of Mayer [18], Bloom [8], Dochy and Alexander [10], and Krathwohl [19]. In the model by Hailikari and colleagues [3], declarative knowledge is categorized as knowledge of facts, a reproduction of isolated domain-specific facts, and knowledge of meaning, the reproduction of domain-specific concepts or principles. While knowledge of facts is a simple recognition or reproduction of single facts on a low level of abstraction, knowledge of meaning requires the students to describe common concepts [3]. In addition to those declarative knowledge types, Hailikari et al. [3] describe the integration of knowledge as “the lower level of procedural knowledge” (p. 325). The integration of knowledge considers the structural aspect of prior knowledge [20] and is defined as “the ability to see interrelations between [domain-specific] concepts and how different phenomena are linked to each other” [3] (p. 325). This comprises the ability to compare those concepts and their interrelations [3]. The integration of knowledge must not be confused with knowledge integration framework (see below), as it does not address the complexity of a normative idea, but rather the ability to see and express interrelations between subject-specific concepts [3]. As a fourth knowledge type that can clearly be classified as procedural knowledge, the application of knowledge is defined as the knowledge to solve novel domain-specific tasks and problems [3]. The application of knowledge helps students to build a subject-specific representation of a problem and develop an appropriate solution on this basis.
The model of Hailikari and colleagues [3] suggests that knowledge is represented on a continuum on which types of knowledge with different underlying cognitive processes can be separated. The described knowledge model has already been used in a variety of empirical studies in science education (e.g., [2,3,21,22]). These studies used the model for the assessment of general chemistry, organic chemistry, and mathematics knowledge of university students. However, in some of those studies only a single or a few items were used for knowledge assessment. Therefore, analyses of the underlying knowledge construct were not possible and only vague empirical evidence exists that these knowledge types can be assessed separately. Hence, we wanted to develop an adequate assessment instrument that allows for a proper assessment of different knowledge types.

1.2. Assessment of Knowledge Types

Dochy [20] formulated a guideline for the design of test items for assessing specific knowledge types. In the guidelines, he proposes using items that require the appreciation, recognition, and reproduction of information to measure declarative knowledge, and items that require production and application to measure procedural knowledge. A study by Kyllonen and Stephens [23] applies similar guidelines. They designed two tests, one for each knowledge type, and modeled two latent knowledge types. In this study and many others, knowledge and its types were assessed in a multiple-choice test format (e.g., [24]). However, there is reason to doubt the appropriateness of using multiple-choice items to measure the characteristics of all types of declarative and procedural knowledge. Therefore, more elaborate assessments of knowledge types in chemistry and mathematics have been used [2,3,25]. In these, specific types of items were used to assess the four knowledge types that require different cognitive processes when dealing with the subject-specific content. Their assessment included multiple-choice and short answer items. Nonetheless, it was not possible to distinguish knowledge types using statistical methods because only a few items were used. Hence, a broader assessment is needed to provide evidence for the theoretically assumed four-dimensional structure of knowledge.

1.3. Learning and Knowledge Acquisition in Science at University Level

The overall goal of higher education is to develop students’ knowledge in certain domains. Numerous studies focused on learning at the university level in general (e.g., biology [26,27], mathematics [28], and physics [29]) by using theoretical models of knowledge to address and promote learning (e.g., [27]). Recent studies about learning often apply knowledge integration theory (for details, see [30]) as a design rationale for the assessment of learning and instruction (e.g., [31,32]). Research about knowledge integration addresses the increasingly complex cognition of students, whereas abilities of lower complexity (i.e., not eliciting relevant ideas) are viewed as a prerequisite of more complex cognitive abilities (i.e., normative ideas or multiple scientifically valid links between normative ideas) [31]. Liu, Lee, and Linn [32] were able to build valid and reliable assessments to measure the knowledge integration of high school students for four years in different science cohorts. Their assessment took advantage of different item formats. They were able to construct effective assessment to address the quality of students’ answers. However, the studies on knowledge integration do not address science students at university and do not differentiate between the knowledge acquisition of different groups of students.
Examples for studies that assess different types of knowledge and differentiate between different groups of students, are the studies by Hailikari and colleagues [2,3]. The knowledge model by Hailikari et al. [3] defines four knowledge types by the complexity of a task and the cognitive processes that are needed to solve it. Their research dealing with knowledge types at the university level aims at predicting academic achievement (e.g., [2,3,25]). Their studies and other studies on academic achievement employ subject-specific tests to assess students’ prior knowledge and grades at the end of the semester as an indicator of their learning outcomes. For example, Hailikari and Nevgi [2] provide cognitive predictors for academic achievement in chemistry. Based on their detailed definitions of prior knowledge types, they predicted students’ achievement in chemistry, concluding that students with sophisticated prior knowledge (application of knowledge, integration of knowledge) are more successful at passing the final chemistry exams. The results of the study indicate that sophisticated prior knowledge and higher order thinking approaches (e.g., problem solving) are important prerequisites for academic learning at university. Binder et al. [21] adapted the prior knowledge model by Hailikari et al. [3] to predict biology and physics students’ achievement in the introductory phase at university. For biology students, declarative knowledge (knowledge of meaning) was shown to be a good predictor for passing all subject-specific exams in the first two semesters. For physics students, knowledge of meaning as well as application of knowledge predicted the students’ success in all subject-specific exams. However, these studies were aimed at assessing students’ suitability for university and because of the different measures at the beginning and end of the semester, they only enable a very indirect evaluation of changes in knowledge over time. To track and evaluate such changes, the utilized knowledge tests must be the same or at least linked over different time points.
Insights into the (different) outcomes of students’ learning that are measured with identical or linked knowledge tests at the beginning and the end of the first year could help to identify groups of students that might benefit from additional training, addressing certain knowledge types. This, in turn, might guide the planning of meaningful course adjustments. In this context, Dochy and Alexander [10] claimed that an assessment of knowledge types could lead to an enhanced learning process, better course design, better modular education design, and development of knowledge-based instructional systems.

2. Purpose

The above-mentioned studies either address the knowledge integration of the students or they aim at predicting students’ academic achievement by analyzing cognitive traits as predictors. Knowledge integration studies mainly focus on the development of students’ understanding of science concepts and the nature of science itself [31]. Therefore, they focus on ongoing conceptual understanding, but not on different knowledge types or the knowledge acquisition of different groups of students. On the other hand, prediction studies focus on different predictors of academic achievement and groups of students but do not address the knowledge acquisition of university students directly. Therefore, a detailed assessment of HS high achievers’ and HS low achievers’ knowledge types and knowledge acquisition seems fruitful to us. A differentiated evaluation of the acquisition of knowledge types for groups of students, which performed differently in educational settings before, could reveal differences not only in their prior knowledge but also in their knowledge acquisition at university. Findings could lead to effective interventions fostering specific knowledge types.
To address the knowledge acquisition of university students, we wanted to examine the acquisition of the four knowledge types described by Hailikari et al. [3] over the first year for groups of students with contrasting preconditions for academic achievement. Because of its high predictivity for academic achievement [5,7], and analogous to Hailikari et al. [3], we chose the HS GPA to define these groups and distinguished between HS high, medium, and low achieving students. This grouping enables us to evaluate if the overall HS achievement is connected to subject-specific knowledge acquisition at university.
For our study, we chose the subjects biology and physics. This choice was based on the assumption that they pose different challenges to student learning. In Germany, first year biology courses focus on learning new taxonomy and terminology, and understanding interrelations in biological systems (e.g., in botany), in physics courses the students shall learn to solve subject-specific problems (e.g., in mechanics). Therefore, declarative types of knowledge could be of special interest for biology students, whereas in physics applicable knowledge could be helpful in the courses. The finding that different knowledge types are predictive for academic success in both subjects [21] supports this assumption.
This could lead to differential knowledge acquisition in the different subjects and to findings that inform a subject specific adjustment of university lectures.
Beforehand, we need a measurement instrument suitable for a reliable and valid assessment of the four knowledge types in each subject. To do so, we developed subject and knowledge type specific tests (see below) and examined whether the knowledge types proposed by Hailikari et al. [3] can be distinguished empirically.

3. Materials and Methods

3.1. Test Development and Design

To assess the four knowledge types in biology and physics, we developed four tests for each subject (for examples see Supplementary Materials). The subject-specific knowledge in biology and physics was differentiated according to the four knowledge types knowledge of facts, knowledge of meaning, integration of knowledge, and application of knowledge [3]. We did so in order to account for the complex nature of knowledge and to avoid underrepresentation of the addressed construct [16,33] by focusing on selected knowledge types. To further increase the validity of the measures, we followed Dochy and Alexander [10], assessing each knowledge type using an assessment method that considered the specific characteristics of each.
We assessed knowledge of facts using multiple-choice tasks, which only require marking one correct answer from four choices (single select). To measure knowledge of meaning, we employed a set of 15 constructed response tasks, which asked for definitions of subject-specific concepts or principles. The students were asked to write down a correct definition in a few words or a sentence.
To assess integration of knowledge, a construct-a-map concept-mapping task [34] was used. Concept mapping tasks can reveal the organization of and relationships between subject-specific concepts [35,36]. We administered a pre-structured map to the students, which contained 12 concepts to allow for a time-saving handling. We asked them to link the concepts and construct propositions by writing down a linking phrase. A constructed proposition indicates both declarative knowledge about the two concepts and students’ understanding of these concepts [34,37,38]. The concept mapping test can test for procedural knowledge shown by the students in picking up different concepts, think about relationships, and conceptualize propositions [34,38]. Concept mapping tests can be scored through various scoring methods, depending on which different aspects of learning outcomes shall be assessed (see below). To assess the integration of knowledge, the degree to which the maps communicate understanding of interrelationships of concepts should be scored [38].
Application of knowledge was assessed through a card-sorting task (e.g., [39,40]). We used 12 subject-specific problems in each subject, wherein every problem represented one item. The students were not asked to solve these problems, but to sort them based on the underlying problem scheme [39] they would use to actually solve the problems. The problems were designed so that one of four different problem schemes are favorable to solve them, for example, the conservation of energy in physics or expansion of the surface area in biology (for example see Supplementary Materials). Thus, three problems can be treated according to the same scheme.
Our test topics were based on the curriculum of the bachelor study programs in biology or physics. In the curricula of both subjects, certain subject-specific domains are important prerequisites for upcoming domains in the following semesters. In biology, cellular biology, botany, and zoology there are basic classes in the first year, which provide students with basic knowledge that is required for advanced classes such as genetics or evolutionary biology in the following semesters. In physics, the mechanics classes are the basic classes, which prepare students for the more advanced courses. To increase the curricular validity of the tests, we used recurring facts and concepts from high school and university curricula for the tasks.

3.2. Procedure

The study was conducted during students’ first years at university. Subject-specific knowledge was assessed at the beginning of the first semester, and after the second semester. We employed a parallel design for both cohorts (biology and physics), only changing the subjects of the knowledge tests according to students’ majors. We administered all tasks as paper and pencil tests. We introduced the students to the task techniques required, for example, how to construct a concept map. For this purpose, we explained each type of task via a short presentation in advance. In addition, the students received written instructions in the test booklets.

3.3. Sample

The study was conducted at two universities in Germany. In total, 268 freshmen participated in the study. Of these, 162 students were majoring in biology and 106 in physics. 64% of the biology students were female (N = 105), and only 22 % of the physics students (N = 22). The average age of the physics students was Md = 20. The average age of the biology students was Md = 21. For the analysis of knowledge acquisition, the sample was reduced to 161 students (N = 104 in biology, N = 57 in physics) due to dropout during the first year. All students volunteered to participate in the study and received an incentive. The test results had no influence on the evaluation of the students’ course achievements and lecturers have received aggregated test results, if any. In addition, all measures followed ethical and privacy guidelines.

3.4. Scoring and Data Analysis

In this section, the scoring of the tests for the knowledge types is elaborated. Each assessment format required a specific scoring method. We describe how each test was scored and how the raw data were scaled using item response theory (IRT) models.

3.4.1. Knowledge of Facts

The items for knowledge of facts were scored dichotomously as right or wrong. One point was awarded for selecting the right answer, and zero points for choosing a wrong answer.

3.4.2. Knowledge of Meaning

For the knowledge of meaning test, students’ answers were rated using a rubric. For a full description of a principle or concept, a student had to correctly describe one or more aspects of the concept. These aspects and the correct descriptions were specified in the coding frame. For every aspect of a concept described correctly according to the coding frame, one point was assigned. For the different concepts up to four aspects were rated. Therefore, the scoring method implied polytomous scoring of the knowledge of meaning items (for examples, see the Supplementary Materials). To assure for a fair scoring and scaling of the knowledge of meaning tests, we added up the correctly mentioned aspects per student without weighting and used Item Response Theory (IRT) for scaling (see Section 3.5, “Scaling”).

3.4.3. Integration of Knowledge

Various possibilities to score concept maps exist, including scoring map components such as nodes, counting the number of propositions, or scoring the complexity of the structure (e.g., [41]). However, Yin et al. [34] noted that these measures are highly uncertain and differ between people and maps. Therefore, we employed a scoring method based on scoring of the links used and knowledge administered in the linking phrases (e.g., [38,42]). Each linking phrase was scored dichotomously. No link or a link with a wrong linking phrase was awarded zero points. A link with a correct linking phrase was awarded one point. This type of scoring considers both the structure of the map (from sparsely linked to highly linked) and quality of the phrases. Higher scores show highly interlinked concepts with correct connections and are interpreted as a measure for the degree of conceptual understanding.

3.4.4. Application of Knowledge

For each item in the application of knowledge test, one point was awarded if the student sorted a task by a suitable problem scheme to address the problem. Since the exact descriptions of the problem schemes differ between students, suitable schemes were defined for each problem in a coding frame. For example, if “conservation of energy” was the intended scheme, answers explicitly equating the relevant forms of energy in words or in a formula were awarded one point, too. This results in dichotomous measures for each problem.

3.5. Scaling

Empirical studies using knowledge tests often employ IRT models in the data analysis [43,44]. The Rasch model is most often used, which is a 1-PL model for dichotomous data [45]. The partial credit model (PCM) adjusts the Rasch model for polytomous data [46]. Both models can be applied to scale items with different formats [47], to analyze the dimensionality of a construct, and in a longitudinal analysis.
Thus, we used IRT models to scale our data. We scaled for the biology and physics sample separately and linked the two points of measurement using items with constant difficulty (see below). The PCM was the most appropriate model for the polytomous scoring of the knowledge of meaning test and different item formats to assess knowledge types (multiple-choice and constructed response items). The PCM estimates the difficulty of each item step of an item and a person’s ability based on this stepwise modelling. Therefore, we applied a PCM to our data.
As a precondition for the longitudinal analysis, we wanted to ensure the factorial validity of the four knowledge types. Therefore, we performed model comparisons between several uni- and multidimensional PCMs for the biology and physics sample. Based on the theoretical framework, three empirical models were employed for the data structure: The unidimensional PCM-model representing subject-specific prior knowledge, a two-dimensional PCM-model representing declarative and procedural knowledge, and a four-dimensional PCM-model representing the four knowledge types. The model with the best fit could be examined through comparing information criteria (AIC, BIC) and likelihood ratio tests. The Bayesian Information Criterion (BIC) is an information criterion for model selection in which the deviance is divided by the model parameters considering sample size. The Akaike Information Criterion (AIC) is also an information criterion that adds a penalty term for the number of parameters in the model. The model with the lowest information criterion is preferred [48].
For the model representing the best fit for our data, we calculated and examined reliabilities and item fit values. A measure for the appropriateness of an item for the probabilistic model is the item fit measure infit MNSQ, which should be between 0.7 and 1.3 [49].
For longitudinal data scaling, the two points of measurement (beginning of the first and end of the second semester) were linked by certain items per test [50]. To do so, we performed a differential item functioning (DIF) analysis for all items between the measurement points. In a first step, we scaled the data of every point of measurement separately (using the four-dimensional PCM, see section “4.1 Results”). Then, we mean–mean equated the item difficulties of both points of measurement to position them on the same scale. Items with a change in item difficulty larger than 0.638 logits were flagged for DIF following [51]. For the linking, we used items with a constant item parameter (difficulty) over the measurement points. We inserted the item parameters of these items in the models for both points of measurement. The linking of items per test positions the person’s ability parameters (Warm’s Mean Weighted Likelihood Estimates (WLE); [52]) for the measurement points on a continuum. The item difficulty of non-linking items was computed based on the responses of the measurement point. For all items without DIF, we used the item difficulties of the second measurement point as initial difficulties in the PCM. Finally, the WLE was calculated for each knowledge type and measurement point respectively.

3.6. Data Analysis

To determine person parameters for the knowledge in all knowledge types, we conducted IRT scaling and all fit and DIF analyses using the software R [53] with the package TAM (Test Analysis Modules, [54]). In addition, IBM SPSS statistics 23 was used for the analysis of knowledge type acquisition. To answer our research question, we performed a repeated measure multivariate analysis of variance (MANOVA) for those students who participated at both measurement points. The factor ‘group’, based on the students HS GPA, was included as a between-subject factor in the analysis. We used time (point of measurement) and the knowledge types as within-subject factors in the repeated measures MANOVA. To address between-subjects effects in more detail, we used Oneway MANOVAs, with the four knowledge types as dependent variables and the (HS achiever) group as the independent variable. Effect sizes (partial η2) from the analyses are interpreted according to Cohen [55] (small effect: partial η2 > 0.01, medium effect: partial η2 > 0.06, large effect: partial η2 > 0.14).

4. Results

4.1. Precondition: Validity

To validate our interpretations of the test scores, we examined different validity-supporting evidences (e.g., [56]). Each test’s content was based on the topics of the curriculum of the first year. In addition, the lecturers were involved in the test development. Therefore, it is reasonable that test contents fit the subject specific requirements of the first year. We applied well-established methods to assess different types of knowledge. Each method is proven to challenge students’ knowledge differently and therefore to assess different aspects of knowledge (see above). The two tests assessing application of knowledge are based on card-sorting tasks, which is a well-established assessment method [57,58]. However, due to our adaption of the method (see above) we put special effort into its validation and applied an argument-based approach to validity according to Kane (e.g., [56]). The results of several validation studies underpin that the test scores can validly be interpreted as measures for initial problem solving procedures on subject-specific problems and are therefore suitable to assess application of knowledge (for further information, see [59]).
An important aspect of validity is the question if the proposed four knowledge types can be empirically distinguished. Therefore, we tested the model fit of the three IRT models through information criteria and likelihood ratio tests. Information criteria and likelihood ratio tests were estimated for both data sets: biology and physics. All models were based on the data from the first measurement point. The four-dimensional model (types of knowledge) and two-dimensional model (declarative/procedural knowledge) were nested within the one-dimensional model (knowledge), and all items used in the one-dimensional model were employed in the more restrictive models. The information criteria are presented in Table 1.
Lower values in deviance, AIC or BIC indicate a better fit of the IRT model to the data, as they are so-called penalty scores. In both subjects, the four-dimensional model demonstrates the lowest information criteria, indicating that a four-dimensional latent construct fits the data best.
Likelihood ratio tests were used to test the differences in models’ deviance for significance. The results are presented in Table 2. The differences in deviance are significant for all pairwise comparisons of the three models.
The ranges of the latent correlations between the knowledge types are shown for both measurement points in Table 3. The multidimensional scaling estimated the true score of each type of knowledge. Correlations were computed between these true scores at each point of measurement. Both findings, the latent correlations and the likelihood ratio tests suggest that the knowledge types can be assessed and interpreted separately from each other. This supports construct validity of the test scores drawn from our assessment.

4.2. Precondition: Reliability and Item Fit Analysis

The four-dimensional IRT model was used to estimate the person and item parameters. The person parameters for this scaling are on the same scale for both measurement points and can be compared in further analyzes. For the biology items, the infit MNSQ ranges from 0.82 to 1.23. For the physics items of all tests, the infit MNSQ ranges from 0.73 to 1.26. The test reliability of this scaling of the prior knowledge tests is provided in Table 4. The fit measures of all items used in both subjects are acceptable [49,51]. We used the person ability parameters generated by this four-dimensional model in all further analyses.

4.3. Distinguishing HS High and Low Achieving Students

To answer our research question, namely, how the different knowledge types develop over the first year for HS high achievers and HS low achievers in biology and physics courses, we examined the acquisition of the four knowledge types over the first year. To distinguish between HS high achieving and HS low achieving students we split each sample (biology and physics) in three performance groups (tertiles). The HS GPA in Germany is usually ranked on a scale from 1.0 to 4.0, with 1.0 as the highest grade. Descriptive statistics for the three groups are provided in Table 5.

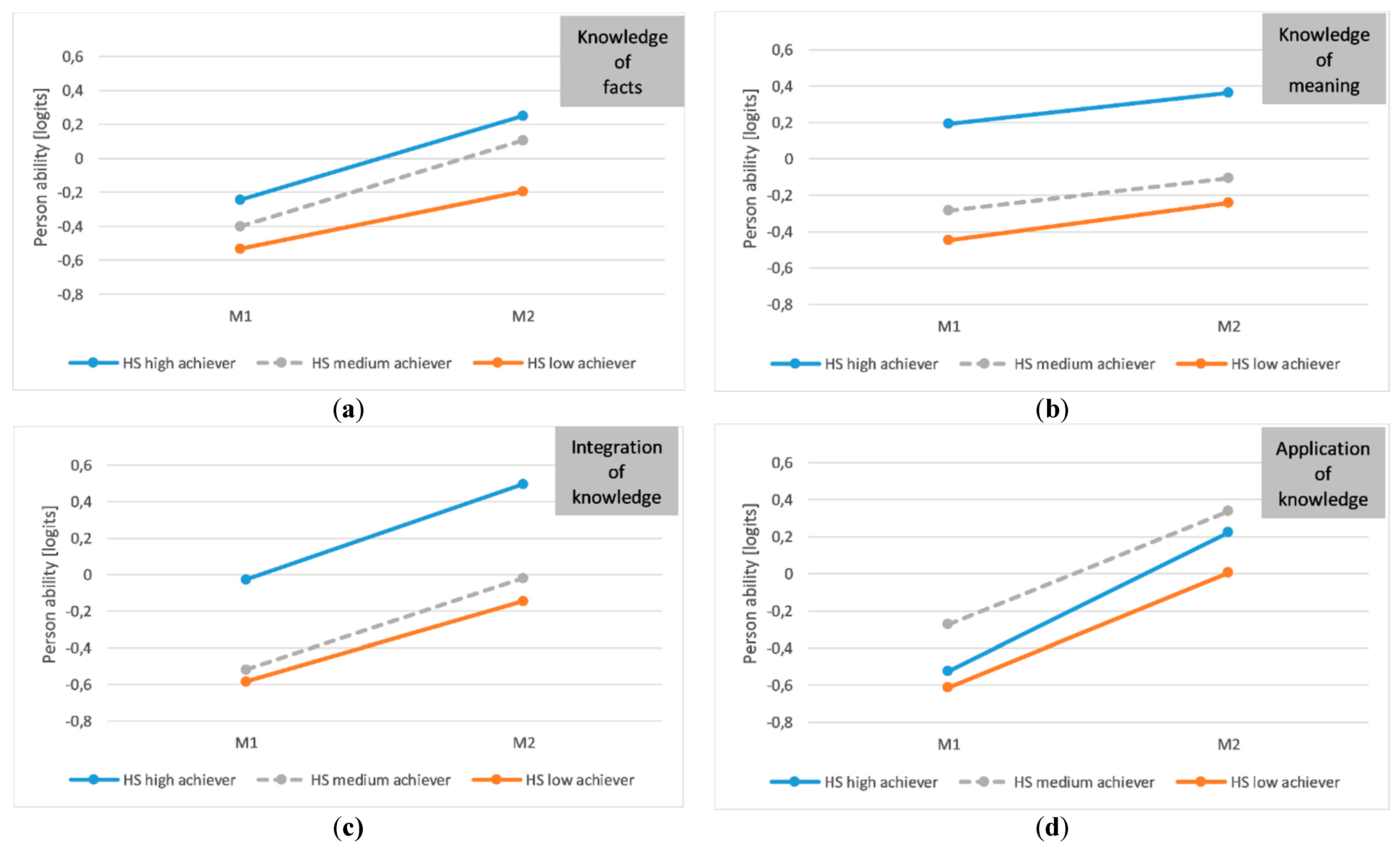
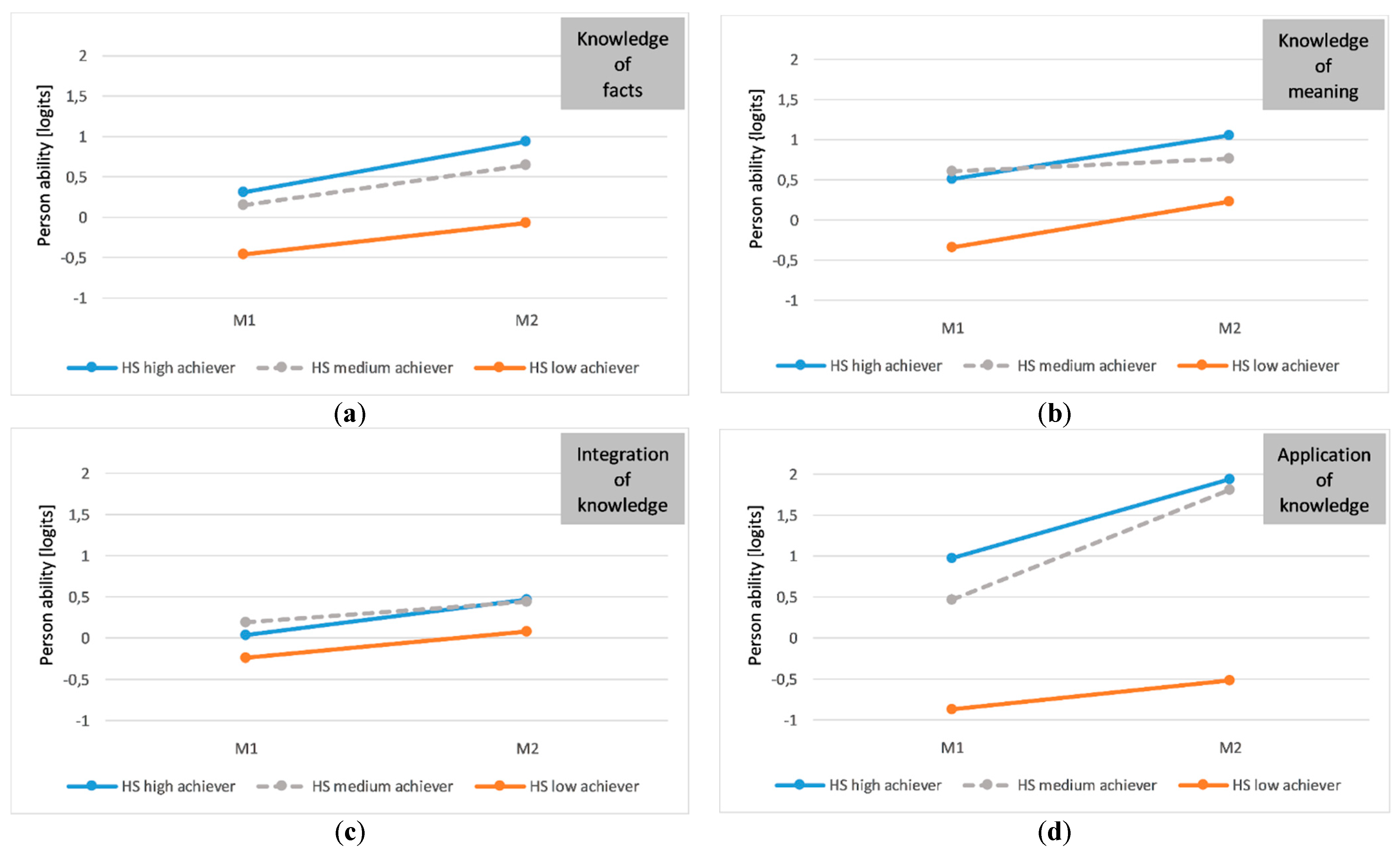
4.4. Knowledge Type Acquisition: Biology and Physics Sample

Table 6 shows the results of the MANOVA with time and knowledge type as within-subjects factors and (HS GPA) group as between-subjects factor for the biology and physics sample. In both samples, we found significant effects of time and of group. This indicates that the whole samples of biology and physics students acquire knowledge with a large effect size during the first year and that over both measurement points the HS achiever groups differ in their knowledge with a medium effect size. The interactions of time and group are not significant and so are the interactions of time, group and knowledge type, indicating that in both samples the HS GPA groups do not differ in their acquisition of knowledge types at university (biology sample: Figure 1, physics sample: Figure 2).
To address the differences between the HS GPA groups further, especially with regard to the students’ knowledge when they are entering university, we performed a MANOVA using the knowledge types at the first measurement point as dependent variables and the HS achievement groups as independent variables.
In the biology sample, there are significant medium effects for group in knowledge of meaning (F(2, 101) = 4.76, p = 0.011, partial η2 = 0.09) and integration of knowledge (F(2,101) = 17.50, p = 0.006, partial η2 = 0.10). Post hoc comparison with Bonferroni correction reveals significant differences between HS high achievers and HS low achievers in knowledge of meaning. For the integration of knowledge, the HS high achiever group differs significantly from the HS medium achievers’ group (p = 0.029) and from the HS low achievers’ group (Table 7 and Figure 1).
In the physics sample, there are significant large effects for knowledge of facts (F(2, 54) = 5.57; p = 0.006, partial η2 = 0.17), knowledge of meaning (F(2, 54) = 10.76; p < 0.001, partial η2 = 0.28) and application of knowledge (F(2, 54) = 7.66; p < 0.001, partial η2 = 0.22). Post hoc comparisons indicate that both the HS high and medium achiever groups significantly outperform the HS low achiever group in these three knowledge types (Table 8 and Figure 2).

5. Discussion

The aim of our study was to analyze the acquisition of subject specific knowledge over the first year in biology and physics studies for groups of students that performed differently in high school. To do so, we modelled the subject specific knowledge through four knowledge types according to Hailikari et al [3] and created assessment tools to measure these four knowledge types in biology and physics. The assessments were to distinguish between the four knowledge types and to produce reliable measures for each. In this section, we discuss test dimensionality, reliability, and knowledge type acquisition for different HS achievement groups in biology and physics.

5.1. Preconditions: Dimensionality and Reliability

As prerequisites for the analysis of the acquisition of the four knowledge types, we evaluated the dimensionality and reliability of the constructed assessments. Hailikari et al. [3] contended the advantage of using different methods to assess different knowledge types. To increase the validity of the measurement of each knowledge type, we applied a specific method to assess each. Each method was selected based on the theoretical description of the cognitive processes associated with the specific knowledge type.
Regarding reliability, the items used in both subjects show acceptable fit measures [51], hence, a reliable test set for the assessment of prior knowledge types was created.
To examine dimensionality, we analyzed the fit of an a priori predicted IRT model with our gathered data based on theoretical assumptions. For both subject-specific test sets, the information criteria and likelihood ratio tests confirmed that the four-dimensional model fits the given data best. Therefore, the results support the assumption that each test scale is an indicator for one knowledge type. The theoretical distinction made by Hailikari et al. [3] can be reproduced with scales for each knowledge type. Our finding backs those of Hailikari et al. [25], who found small intercorrelations between different knowledge types in pharmaceutical chemistry as a first indicator for separate knowledge types. Furthermore, the finding supports the construct validity of our assessments.

5.2. Knowledge Type Acquisition: Biology and Physics Sample

Students’ knowledge in both samples increases over the first year at university. This increase shows a large effect size and applies for the three HS GPA groups (HS high, medium, and low achievers) in the same way (non-significant interaction of time and group, see Table 6 and Table 7, Figure 1 and Figure 2). Therefore, freshmen courses in biology and physics seem to support students’ knowledge acquisition equivalently, regardless of their previous performance at school.
However, in both subjects, the HS GPA low achievers start with significantly lower prior knowledge in subject-specific knowledge types (biology: knowledge of meaning and integration of knowledge; physics: knowledge of facts, knowledge of meaning, and application of knowledge). Due to the similar knowledge acquisition among the HS achievement groups, HS low achievers are not able to compensate for this difference during the first year at university. Furthermore, the mean knowledge of the HS low achievers’ group does not reach the mean prior knowledge of the HS high achievers group in the respective knowledge types (Figure 1 and Figure 2). Our findings may suggest that the initial knowledge gap rather than differences in students’ knowledge acquisition during the first year contributes to the lower academic achievement of the HS low achiever group that is predicted by the HS GPA.
In the physics sample, the largest differences between the HS achievement groups are evident in application of knowledge. It is known that elaborate applicable knowledge as well as declarative knowledge are attributes of expertise in physics [39,57,58] and has shown to be a good predictor for grades in physics [21,57].
For the biology sample, we discovered the largest differences between the HS GPA achievement groups in knowledge of meaning and integration of knowledge. These knowledge types require the students to understand subject-specific concepts and the interrelations between those concepts. Since the biology courses in Germany require to learn the terminology and taxonomy of different domains, these knowledge types might be helpful, to link this specific knowledge to existing concepts and principles. In this regard, knowledge of meaning has also been proven to be a good predictor for academic achievement in the introductory biology courses [21]. Consequently, our results show that the HS GPA is able to indicate differences in those specific knowledge types that are correlated with academic achievement at university level, although the HS GPA itself is not a subject-specific measure.

6. Conclusions and Outlook

In biology and physics courses knowledge in all knowledge types is acquired during the first year at university and this holds for students with different preconditions from high school in a very similar way. However, HS low achieving students enter the physics and biology courses with far less prior knowledge in subject-specific knowledge types compared to the HS high achieving students and are not able to bridge the knowledge gap over the first year at university without further support. This finding leads to two conclusions. First, the HS GPA of a student seems to indicate the prior knowledge of the students rather than their ability to acquire subject-specific knowledge. Second, to reduce dropout, especially the differences in prior knowledge should be addressed to enable more students to have academic achievement. This underlines the need for preparatory courses that support especially HS low achievers to enhance their subject specific knowledge before or at the beginning of the first year at university. Our results give hints which knowledge types should be in the focus of respective subjects and courses. Furthermore, our assessments can be implemented to evaluate students’ prior knowledge types and to assign them to preparatory courses or to evaluate the outcomes of the courses with regard to knowledge type acquisition.
A limitation of our study is that gender distributions systematically differ between the biology and physics sample, because both samples show typical gender distributions. Thus, the factor gender could explain our subject-specific findings to some extent.
The knowledge model by Hailikari et al. [3] is a model of explicit knowledge. It is conceivable that other types of knowledge are acquired during the first year at university (e.g., strategic knowledge or conditional knowledge) beyond the four analyzed knowledge types. Our research could be extended to other knowledge types in future research to find relations between the different knowledge types and academic achievement. Furthermore, the operationalization of knowledge acquisition via changes in knowledge over time is only a first outcome-oriented approach to the description of a complex process that is influenced by many other factors like course design or students’ actual learning strategies.
On the other hand, our study is based on a sample from only two [country] universities by now. Thus, replicability and generalizability of our findings are subjects of further research, too. In addition, the analysis of correlations between the HS GPA and subject specific knowledge types could be extended to other STEM subjects.

Supplementary Materials

The following are available online at https://www.mdpi.com/2227-7102/9/4/281/s1.

Author Contributions

Conceptualization, P.S. and H.T.; Formal analysis, T.B.; Funding acquisition, P.S. and H.T.; Investigation, T.B.; Methodology, T.B., P.S. and H.T.; Project administration, P.S. and H.T.; Supervision, P.S. and H.T.; Validation, T.B.; Visualization, T.B.; Writing—original draft, T.B.; Writing—review & editing, T.B., P.S. and H.T.

Funding

This research was funded by Deutsche Forschungsgemeinschaft, grant number SCHM 2664/2-1; Deutsche Forschungsgemeinschaft, grant number TH 1288/5-1; Deutsche Forschungsgemeinschaft, grant number LE 645/14-1; Deutsche Forschungsgemeinschaft, grant number SU 187/16-1.

Acknowledgments

We would like to thank all students for participating and all members of ALSTER research group for their collaboration, especially Angela Sandmann and Bernd Sures.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Chen, X. STEM Attrition: College Students’ Paths Into and Out of STEM Fields (NCES 2014-001); National Center for Education Statistics; Institute of Education Sciences; U.S. Department of Education: Washington, DC, USA, 2013.
  2. Hailikari, T.; Nevgi, A. How to Diagnose At-risk Students in Chemistry: The case of prior knowledge assessment. Int. J. Sci. Educ. 2010, 32, 2079–2095. [Google Scholar] [CrossRef]
  3. Hailikari, T.; Nevgi, A.; Lindblom-Ylänne, S. Exploring alternative ways of assessing prior knowledge, its components and their relation to student achievement: A mathematics based case study. Stud. Educ. Eval. 2007, 33, 320–337. [Google Scholar] [CrossRef]
  4. Hailikari, T. Assessing University Students’ Prior Knowledge: Implications for Theory and Practice; University of Helsinki: Helsinki, Finland, 2009. [Google Scholar]
  5. Trapmann, S.; Hell, B.; Weigand, S.; Schuler, H. Die Validität von Schulnoten zur Vorhersage des Studienerfolgs-eine Metaanalyse. Z. Pädagogische Psychol. 2007, 21, 11–27. [Google Scholar] [CrossRef]
  6. Trapmann, S.; Hell, B.; Hirn, J.O.W.; Schuler, H. Meta-Analysis of the relationship between the Big Five and academic success at university. Z. Psychol./J. Psychol. 2007, 215, 132–151. [Google Scholar] [CrossRef]
  7. Robbins, S.B.; Lauver, K.; Le, H.; Davis, D.; Langley, R.; Carlstrom, A. Do psychosocial and study skill factors predict college outcomes? A meta-analysis. Psychol. Bull. 2004, 130, 261. [Google Scholar] [CrossRef]
  8. Bloom, B.S. Human Characteristics and School Learning; McGraw-Hill: New York, NY, USA, 1976. [Google Scholar]
  9. De Jong, T.; Ferguson-Hessler, M.G.M. Types and Qualities of Knowledge. Educ. Psychol. 1996, 31, 105–113. [Google Scholar] [CrossRef]
  10. Dochy, F.; Alexander, P.A. Mapping prior knowledge: A framework for discussion among researchers. Eur. J. Psychol. Educ. 1995, 10, 225–242. [Google Scholar] [CrossRef]
  11. Dochy, F.; De Rijdt, C.; Dyck, W. Cognitive prerequisites and learning: How far have we progressed since Bloom? Implications for educational practice and teaching. Act. Learn. High. Educ. 2002, 3, 265–284. [Google Scholar] [CrossRef]
  12. Bratianu, C.; Bejinaru, R. The Theory of Knowledge Fields: A Thermodynamics Approach. Systems 2019, 7, 20. [Google Scholar] [CrossRef]
  13. Richter-Beuschel, L.; Grass, I.; Bögeholz, S. How to Measure Procedural Knowledge for Solving Biodiversity and Climate Change Challenges. Educ. Sci. 2018, 8, 190. [Google Scholar] [CrossRef]
  14. Alexander, P.A.; Judy, J.E. The interaction of domain-specific and strategic knowledge in academic performance. Rev. Educ. Res. 1988, 58, 375–404. [Google Scholar] [CrossRef]
  15. Posner, M.I.; Boies, S.J. Components of attention. Psychol. Rev. 1971, 78, 391. [Google Scholar] [CrossRef]
  16. Messick, S. The Psychology of Educational Measurement. J. Educ. Meas. 1984, 21, 215–237. [Google Scholar] [CrossRef]
  17. Corbett, A.T.; Anderson, J.R. Knowledge Tracing: Modelling the Acquisition of Procedural Knowledge. User Model. User Adopt. Interact. 1995, 4, 253–278. [Google Scholar] [CrossRef]
  18. Mayer, R.E. Rote Versus Meaningful Learning. Theory Pract. 2002, 41, 226–232. [Google Scholar] [CrossRef]
  19. Krathwohl, D.R. A Revision of Bloom’s Taxonomy: An Overview. Theory Pract. 2002, 41, 212–218. [Google Scholar] [CrossRef]
  20. Dochy, F. Assessment of Prior Knowledge as a Determinant for Future Learning; Lemma, B.V., Ed.; Jessica Kingsley Publishers: Utrecht, The Netherlands; London, UK, 1992. [Google Scholar]
  21. Binder, T.; Sandmann, A.; Friege, G.; Sures, B.; Theyßen, H.; Schmiemann, P. Assessing prior knowledge types as predictors of academic achievement in the introductory phase of biology and physics study programmes using logistic regression. Int. J. Stem Educ. 2019, 6, 33. [Google Scholar] [CrossRef]
  22. Hailikari, T.; Katajavuori, N.; Lindblom-Ylanne, S. The relevance of prior knowledge in learning and instructional design. Am. J. Pharm. Educ. 2008, 72, 113. [Google Scholar] [CrossRef]
  23. Kyllonen, P.C.; Stephens, D.L. Cognitive abilities as determinants of success in acquiring logic skill. Learn. Individ. Differ. 1990, 2, 129–160. [Google Scholar] [CrossRef]
  24. Asikainen, M.A. Probing University Students’ Pre-Knowledge in Quantum Physics with QPCS Survey. Eurasia J. Math. Sci. Technol. Educ. 2017, 13, 1615–1632. [Google Scholar] [CrossRef]
  25. Hailikari, T.; Nevgi, A.; Komulainen, E. Academic self-beliefs and prior knowledge as predictors of student achievement in Mathematics: A structural model. Educ. Psychol. 2008, 28, 59–71. [Google Scholar] [CrossRef]
  26. Bissonnette, S.A.; Combs, E.D.; Nagami, P.H.; Byers, V.; Fernandez, J.; Le, D.; Realin, J.; Woodham, S.; Smith, J.I.; Tanner, K.D. Using the Biology Card Sorting Task to Measure Changes in Conceptual Expertise during Postsecondary Biology Education. CBE Life Sci. Educ. 2017, 16, ar14. [Google Scholar] [CrossRef] [PubMed]
  27. Crowe, A.; Dirks, C.; Wenderoth, M.P. Biology in bloom: Implementing Bloom’s Taxonomy to enhance student learning in biology. CBE Life Sci. Educ. 2008, 7, 368–381. [Google Scholar] [CrossRef] [PubMed]
  28. Reid, A.; Wood, L.N.; Smith, G.H.; Petocz, P. Intention, Approach and Outcome: University Mathematics Students’ Conceptions of Learning Mathematics. Int. J. Sci. Math. Educ. 2005, 3, 567–586. [Google Scholar] [CrossRef]
  29. Wang, W.; Coll, R.K. An Investigation of Tertiary-level Learning in Some Practical Physics Courses. Int. J. Sci. Math. Educ. 2005, 3, 639. [Google Scholar] [CrossRef]
  30. Geller, C.; Neumann, K.; Boone, W.J.; Fischer, H.E. What Makes the Finnish Different in Science? Assessing and Comparing Students’ Science Learning in Three Countries. Int. J. Sci. Educ. 2014, 36, 3042–3066. [Google Scholar] [CrossRef]
  31. Liu, L.; Lee, H.; Hofstetter, C.; Linn, M. Assessing Knowledge Integration in Science: Construct, Measures, and Evidence. Educ. Assess. 2008, 13, 33–55. [Google Scholar] [CrossRef]
  32. Liu, O.L.; Lee, H.S.; Linn, M.C. Measuring knowledge integration: Validation of four-year assessments. J. Res. Sci. Teach. 2011, 48, 1079–1107. [Google Scholar] [CrossRef]
  33. Messick, S. VALIDITY; ETS Research Report Series; Educational Testing Service: Princeton, NJ, USA, 1987; p. i-208. [Google Scholar]
  34. Yin, Y.; Vanides, J.; Ruiz-Primo, M.A.; Ayala, C.C.; Shavelson, R.J. Comparison of two concept-mapping techniques: Implications for scoring, interpretation, and use. J. Res. Sci. Teach. 2005, 42, 166–184. [Google Scholar] [CrossRef]
  35. Buntting, C.; Coll, R.K.; Campbell, A. Student Views of Concept Mapping Use in Introductory Tertiary Biology Classes. Int. J. Sci. Math. Educ. 2006, 4, 641–668. [Google Scholar] [CrossRef]
  36. Jonassen, D.H.; Grabowski, B.L. (Eds.) Handbook of Individual Differences, Learning and Instruction; Erlbaum: Hillsdale, MI, USA, 1993. [Google Scholar]
  37. McClure, J.R.; Sonak, B.; Suen, H.K. Concept Map Assessment of Classroom Learning: Reliability, Validity, and Logistical Practicality. J. Res. Sci. Teach. 1999, 36, 475–492. [Google Scholar] [CrossRef] [Green Version]
  38. Rice, D.C.; Ryan, J.M.; Samson, S.M. Using concept maps to assess student learning in the science classroom: Must different methods compete? J. Res. Sci. Teach. 1998, 35, 1103–1127. [Google Scholar] [CrossRef]
  39. Chi, M.T.H.; Feltovich, P.J.; Glaser, R. Categorization and Representation of Physics Problems by Experts and Novices; Learning Research and Development Center, University of Pittsburgh: Pittsburgh, PA, USA, 1981. [Google Scholar]
  40. Moseley, B.J.; Okamoto, Y.; Ishida, J. Comparing US and Japanese elementary school teachers’ facility for linking rational number representations. Int. J. Sci. Math. Educ. 2007, 5, 165–185. [Google Scholar] [CrossRef]
  41. Ruiz-Primo, M.A.; Schultz, S.E.; Li, M.; Shavelson, R.J. Comparison of the reliability and validity of scores from two concept-mapping techniques. J. Res. Sci. Teach. 2001, 38, 260–278. [Google Scholar] [CrossRef]
  42. Rye, J.A.; Rubba, P.A. Scoring concept maps: An expert map-based scheme weighted for relationships. Sch. Sci. Math. 2002, 102, 33–44. [Google Scholar] [CrossRef]
  43. Boone, W.J.; Scantlebury, K. The role of Rasch analysis when conducting science education research utilizing multiple-choice tests. Sci. Educ. 2006, 90, 253–269. [Google Scholar] [CrossRef]
  44. Neumann, I.; Neumann, K.; Nehm, R. Evaluating Instrument Quality in Science Education: Rasch-based analyses of a Nature of Science test. Int. J. Sci. Educ. 2011, 33, 1373–1405. [Google Scholar] [CrossRef] [Green Version]
  45. Rasch, G. Probabilistic Models for Some Intelligence and Attainment Tests; University of Chicago Press: Chicago, IL, USA, 1960. [Google Scholar]
  46. Masters, G.N. A Rasch model for partial credit scoring. Psychometrika 1982, 47, 149–174. [Google Scholar] [CrossRef]
  47. Sykes, R.C.; Yen, W.M. The Scaling of Mixed-Item-Format Tests with the One-Parameter and Two-Parameter Partial Credit Models. J. Educ. Meas. 2000, 37, 221–244. [Google Scholar] [CrossRef]
  48. Burnham, K.P.; Anderson, D.R. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach, 2nd ed.; Springer: New York, NY, USA, 2010. [Google Scholar]
  49. Bond, T.G.; Fox, C.M. Applying the Rasch Model: Fundamental Measurement in the Human Sciences, 2nd ed.; Lawrence Erlbaum Associates: Mahwah, NJ, USA, 2007. [Google Scholar]
  50. Hartig, J.; Kuhnbach, O. Estimating change using the plausible value technique within multidimensional Rasch-models. In Veränderungsmessung Längsschnittstudien in der empirischen Erziehungswissenschaft [Estimating Change and Longitudianl Studies in the Empirical Social Sciences]; Ittel, A., Merkens, H., Eds.; VS Verlag für Sozialwissenschaften: Wiesbaden, Germany, 2006; pp. 27–44. [Google Scholar]
  51. Wilson, M. Constructing Measures: An Item Response Modeling Approach; CD Enclosed; Psychology Press: New York, NY, USA, 2005. [Google Scholar]
  52. Warm, T.A. Weighted likelihood estimation of ability in item response theory. Psychometrika 1989, 54, 427–450. [Google Scholar] [CrossRef]
  53. R Development Core Team. R: A Language and Environment for Statistical Computing; R Development Core Team: Vienna, Austria, 2008; Available online: http://www.R-project.org/ (accessed on 17 June 2018).
  54. Kiefer, T.; Robitzsch, A.; Wu, M.L. TAM—Test Analysis Modules. 2018. Available online: http://cran.r-project.org/web/packages/TAM/index.html (accessed on 20 January 2019).
  55. Cohen, J. Statistical power analysis. Curr. Dir. Psychol. Sci. 1992, 1, 98–101. [Google Scholar] [CrossRef]
  56. Kane, M.T. Validating the interpretations and uses of test scores. J. Educ. Meas. 2013, 50, 1–73. [Google Scholar] [CrossRef]
  57. Friege, G.; Lind, G. Types and Qualities of Knowledge and their Relations to Problem Solving in Physics. Int. J. Sci. Math. Educ. 2006, 4, 437–465. [Google Scholar] [CrossRef]
  58. Chi, M.T.H.; Glaser, R.; Rees, E. Expertise in Problem Solving. In Advances in the Psychology of Human Intellegence; Sternberg, R.J., Ed.; Erlbaum: Hillsdale, MI, USA, 1982; pp. 7–75. [Google Scholar]
  59. Binder, T.; Theyßen, H.; Schmiemann, P. Erfassung von fachspezifischen Problemlöseprozessen mit Sortieraufgaben in Biologie und Physik [Assessing Subject-specific Problem Solving Processes Using Sorting Tasks in Biology and Physics]. Zeitschrift für Didaktik der Naturwissenschaften 2019. [Google Scholar] [CrossRef]
  60. Adams, R.J. Reliability as a measurement design effect. Stud. Educ. Eval. 2005, 31, 162–172. [Google Scholar] [CrossRef]
Education 09 00281 g001 550
Figure 1. Students’ abilities for the four different knowledge types in biology for HS high, medium and low achiever. M1 and M2: measurements at the beginning and the end of the first year, (a) knowledge of facts, (b) knowledge of meaning, (c) integrations of knowledge, (d) application of knowledge.
Figure 1. Students’ abilities for the four different knowledge types in biology for HS high, medium and low achiever. M1 and M2: measurements at the beginning and the end of the first year, (a) knowledge of facts, (b) knowledge of meaning, (c) integrations of knowledge, (d) application of knowledge.
Education 09 00281 g001
Education 09 00281 g002 550
Figure 2. Students’ abilities for the four different knowledge types in physics for HS high, medium, and low achiever. M1 and M2: measurements at the beginning and the end of the first year, (a) knowledge of facts, (b) knowledge of meaning, (c) integrations of knowledge, (d) application of knowledge.
Figure 2. Students’ abilities for the four different knowledge types in physics for HS high, medium, and low achiever. M1 and M2: measurements at the beginning and the end of the first year, (a) knowledge of facts, (b) knowledge of meaning, (c) integrations of knowledge, (d) application of knowledge.
Education 09 00281 g002
Table
Table 1. Information criteria for the different probabilistic models tested.
Table 1. Information criteria for the different probabilistic models tested.
SubjectDimensionsNPDevianceAICBIC
Biologyknowledge (1D)10717478.2417692.2418022.61
Biologydeclarative versus procedural knowledge (2D)10917418.8217636.8217973.37
Biologyknowledge types (4D)11617278.1017510.1017868.27
Physicsknowledge (1D)12511156.0211406.0211731.67
Physicsdeclarative versus procedural knowledge (2D)12711111.8711365.8711696.73
Physicsknowledge types (4D)13410986.4211254.4211603.52
NP = number of parameters; AIC = Akaike information criterion; BIC = Bayesian information criterion [49].
Table
Table 2. Likelihood ratio tests for the model comparisons.
Table 2. Likelihood ratio tests for the model comparisons.
SubjectComparisondfΧ2empΧ2critp
Biology1D versus 2D259.4218.42<0.001
Biology2D versus 4D7140.7229.84<0.001
Biology1D versus 4D9200.1433.70<0.001
Physics1D versus 2D244.1518.42<0.001
Physics2D versus 4D7125.4529.84<0.001
Physics1D versus 4D9169.6033.70<0.001
df = degrees of freedom; Χ2emp = empirical Chi-square value; Χ2crit = critical Chi-square value; p = p-value of the model comparison [52].
Table
Table 3. Ranges of latent correlations between the four knowledge types in the four-dimensional IRT models of the longitudinal scaling.
Table 3. Ranges of latent correlations between the four knowledge types in the four-dimensional IRT models of the longitudinal scaling.
Measurement PointLatent Correlations (Biology Model)Latent Correlations (Physics Model)
10.47 < rlat < 0.670.52 < rlat < 0.78
20.24 < rlat < 0.590.61 < rlat < 0.86
Table
Table 4. Infit MNSQ range and Warm’s Mean Weighted Likelihood Estimates (WLE) reliability coefficients (e.g., [60]) for the tests.
Table 4. Infit MNSQ range and Warm’s Mean Weighted Likelihood Estimates (WLE) reliability coefficients (e.g., [60]) for the tests.
SubjectTestsMeasureM1M2
Biologyknowledge of
facts		Infit MNSQ (Reliability)0.94–1.06
(0.60)		0.85–1.15
(0.74)
knowledge of meaningInfit MNSQ (Reliability)0.90–1.09
(0.71)		0.82–1.15
(0.72)
integration of knowledgeInfit MNSQ (Reliability)0.94–1.05
(0.58)		0.92–1.19
(0.60)
application of knowledgeInfit MNSQ (Reliability)0.91–1.23
(0.71)		0.89–1.10
(0.68)
Physicsknowledge of
facts		Infit MNSQ (Reliability)0.88–1.16
(0.77)		0.84–1.26
(0.62)
knowledge of meaningInfit MNSQ (Reliability)0.85–1.15
(0.68)		0.85–1.12
(0.61)
integration of knowledgeInfit MNSQ (Reliability)0.86–1.23
(0.75)		0.94–1.13
(0.52)
application of knowledgeInfit MNSQ (Reliability)0.73–1.22
(0.77)		0.75–1.22
(0.66)
Table
Table 5. Descriptive statistics of the high school grade point average (HS GPA) tertiles.
Table 5. Descriptive statistics of the high school grade point average (HS GPA) tertiles.
SubjectnMdSDGroup Name
Biology361.500.20Low HS GPA
(HS high achievers)
342.100.16Medium HS GPA
(HS medium achievers)
342.700.30High HS GPA
(HS low achievers)
Physics181.350.20Low HS GPA
(HS high achievers)
201.900.15Medium HS GPA
(HS medium achievers)
192.600.30High HS GPA
(HS low achievers)
n = sample size, Md = median; SD = standard deviation.
Table
Table 6. Results of the MANOVAs.
Table 6. Results of the MANOVAs.
SubjectFactor/sSum of SquaresdfFppartial η2Observed Power
BiologyTime40.99162.49<0.0010.3821.0
Group26.6923.940.0220.0720.69
Time*Group0.2520.1870.8300.0040.08
Time*Knowledge type*Group0.3533.89 10.1140.9760.0020.07
PhysicsTime32.81164.50<0.0010.5441.0
Group97.98214.62<0.0010.3510.99
Time*Group1.0221.000.3750.0360.21
Time*Knowledge type*Group5.253.44 11.590.1910.0560.43
1 Value with Greenhouse-Geisser correction, due to significant Mauchly Test of Sphericity.
Table
Table 7. Descriptive statistics and post hoc comparison of the HS achievement groups in biology.
Table 7. Descriptive statistics and post hoc comparison of the HS achievement groups in biology.
Knowledge TypeHS Achievement M (SD)Sig. 1
Knowledge of meaningHS low achiever−0.45 (0.89)−
HS medium achiever−0.29 (1.07)p = 1.000
HS high achiever−0.19 (0.74)p = 0.012
Integration of knowledgeHS low achiever−0.58 (0.71)−
HS medium achiever−0.52 (0.88)p = 1.000
HS high achiever−0.03 (0.75)p = 0.011
1 post hoc comparison with Bonferroni correction: p-value in comparison to the HS low achievers.
Table
Table 8. Descriptive statistics and post hoc comparison of the HS achievement groups in physics.
Table 8. Descriptive statistics and post hoc comparison of the HS achievement groups in physics.
Knowledge TypeHS AchievementM (SD)Sig. 1
Knowledge of factsHS low achiever−0.45 (0.70)−
HS medium achiever0.15 (0.61)p = 0.042
HS high achiever0.31 (0.90)p = 0.008
Knowledge of meaningHS low achiever−0.34 (0.65)−
HS medium achiever0.60 (0.74)p = 0.001
HS high achiever0.51 (0.69)p < 0.001
Application of knowledgeHS low achiever−0.87 (1.75)−
HS medium achiever0.47 (1.40)p = 0.021
HS high achiever0.97 (1.26)p < 0.001
1 post hoc comparison with Bonferroni correction: p-value in comparison to the HS low achievers.

Share and Cite

MDPI and ACS Style

Binder, T.; Schmiemann, P.; Theyssen, H. Knowledge Acquisition of Biology and Physics University Students—the Role of Prior Knowledge. Educ. Sci. 2019, 9, 281. https://doi.org/10.3390/educsci9040281

AMA Style

Binder T, Schmiemann P, Theyssen H. Knowledge Acquisition of Biology and Physics University Students—the Role of Prior Knowledge. Education Sciences. 2019; 9(4):281. https://doi.org/10.3390/educsci9040281

Chicago/Turabian Style

Binder, Torsten, Philipp Schmiemann, and Heike Theyssen. 2019. "Knowledge Acquisition of Biology and Physics University Students—the Role of Prior Knowledge" Education Sciences 9, no. 4: 281. https://doi.org/10.3390/educsci9040281

APA Style

Binder, T., Schmiemann, P., & Theyssen, H. (2019). Knowledge Acquisition of Biology and Physics University Students—the Role of Prior Knowledge. Education Sciences, 9(4), 281. https://doi.org/10.3390/educsci9040281

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop