Educing AI-Thinking in Science, Technology, Engineering, Arts, and Mathematics (STEAM) Education
Abstract
1. Introduction
1.1. The Theoretical Basis of AI-Thinking
1.2. The Role of AI in Education
2. Research Problem and Research Questions
2.1. Research Problem
- Science: the scientific concept of entropy will be explored by measuring it in the dataset.
- Technology: a user-friendly AI-based Bayesian network software, Bayesialab, will be used.
- Engineering: a civil engineering example will be used to explore the relationship between concrete compressive strength and the variables within the mixture.
- Arts: different concrete compressive strengths might be required by the artist for creating different kinds of art works, and the artist might also have to work with pre-existing conditions or in places where cement or water or other materials might not be abundant.
- Mathematics: the mathematical formula of the Bayesian Theorem will be explained and utilized to make predictive inferences from the data.
2.2. Research Questions
3. Methods
3.1. Rationale for Using the AI-Based Bayesian Network Approach
3.2. The Bayesian Theorem
3.3. The Research Model
- Descriptive Analytics of “What Has Already Happened?” in Section 4:
- Purpose: to use descriptive analytics to discover the motifs in the collected data.For descriptive analytics, BN modeling will utilize the parameter estimation algorithm to automatically detect the data distribution of each column in the dataset. Further descriptive statistical techniques will be employed to understand more about the current baseline conditions of the concrete mixture variables and the corresponding compressive strengths. These techniques include the use of curves analysis and the Pearson correlation analysis.
- Predictive Analytics Using “What-If?” Hypothetical Scenarios in Section 5:
- Purpose: to use predictive analytics to perform in-silico experiments with fully controllable parameters in the concrete mixture variables for the prediction of counterfactual outcomes in the concrete compressive strengths. A probabilistic Bayesian approach will be used to simulate various scenarios where constraints might exist (e.g., scarcity of water and/or cement) to better inform STEAM practitioners about how different combinations of the concrete mixture could produce different levels of concrete compressive strengths. For predictive analytics, counterfactual simulations will be employed to explore the motif of the data. The predictive performance of the BN model will be evaluated using tools that include the gains curve, the lift curve, the receiver operating characteristic (ROC) curve, as well as by statistical bootstrapping of the data inside each column of the dataset (which is also the data distribution in each node of the BN model) by 100,000 times, in order to generate a larger dataset to measure its precision, reliability, Gini index, lift index, calibration index, the binary log-loss, the correlation coefficient R, the coefficient of determination R2, root mean square error (RSME), and normalized root mean square error (NRSME).
4. Preparation of Data Prior to Machine Learning
4.1. Dataset of the Concrete Mixture Variables and Their Corresponding Concrete Compressive Strengths
4.2. Codebook of the Dataset
4.3. Software Used: Bayesialab
4.4. Pre-Processing: Checking for Missing Values or Errors in the Data
5. Overview of the BN Approach Used to Machine-Learn the Data
6. Supervised Machine Learning Using the Naïve Bayes Approach
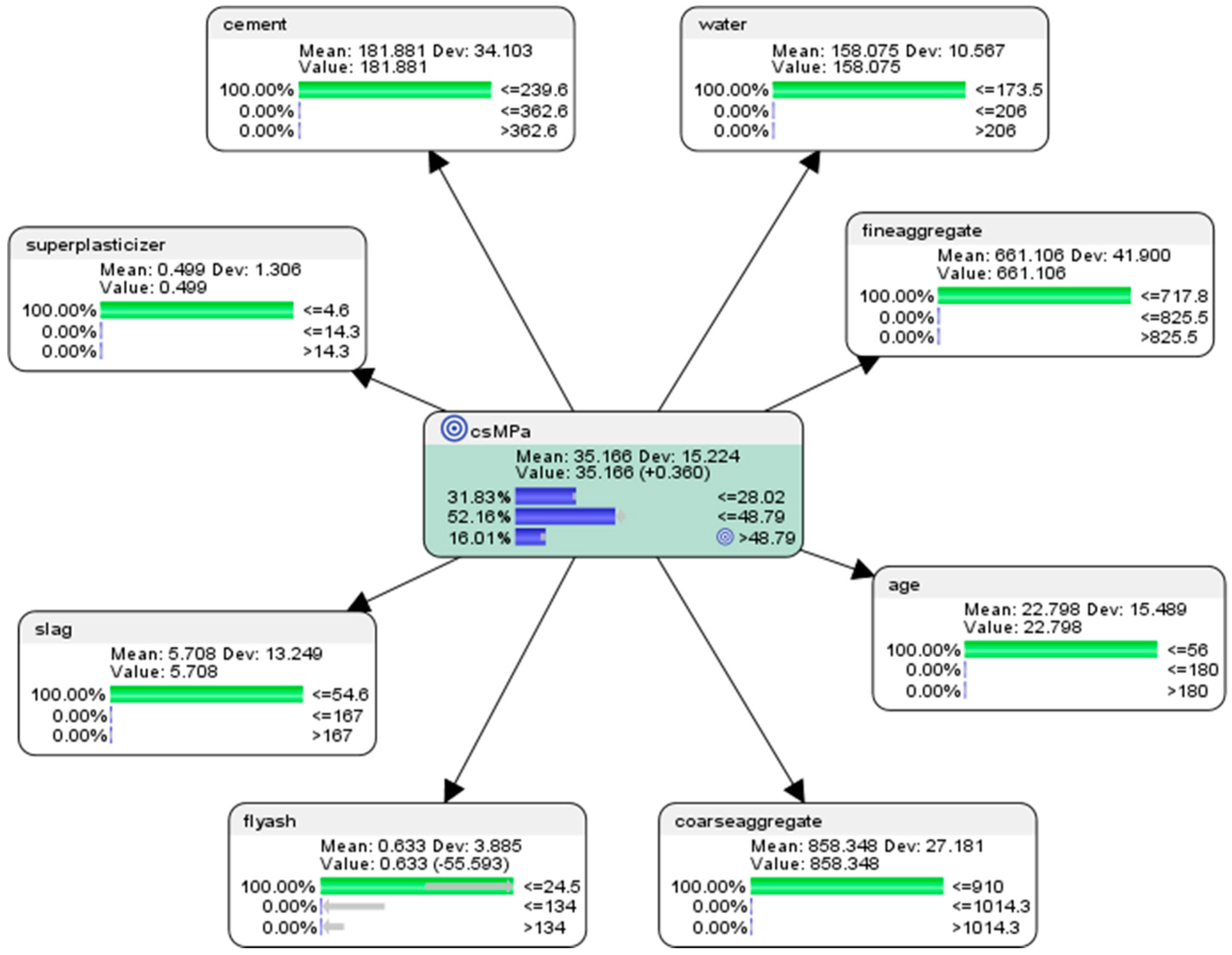
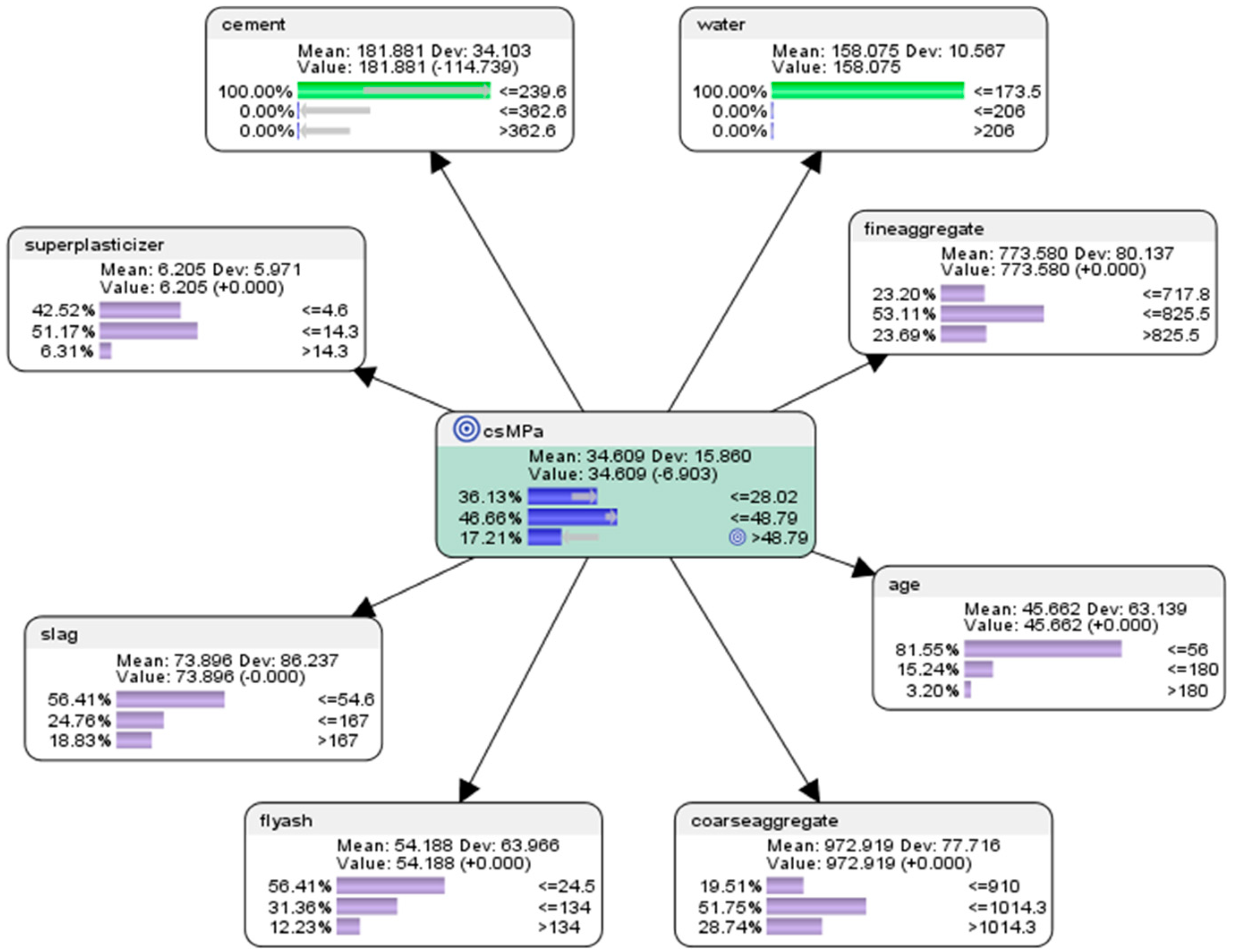
6.1. “What Had Happened?” Descriptive Analytics Using Supervised Machine Learning with Naive Bayes Approach
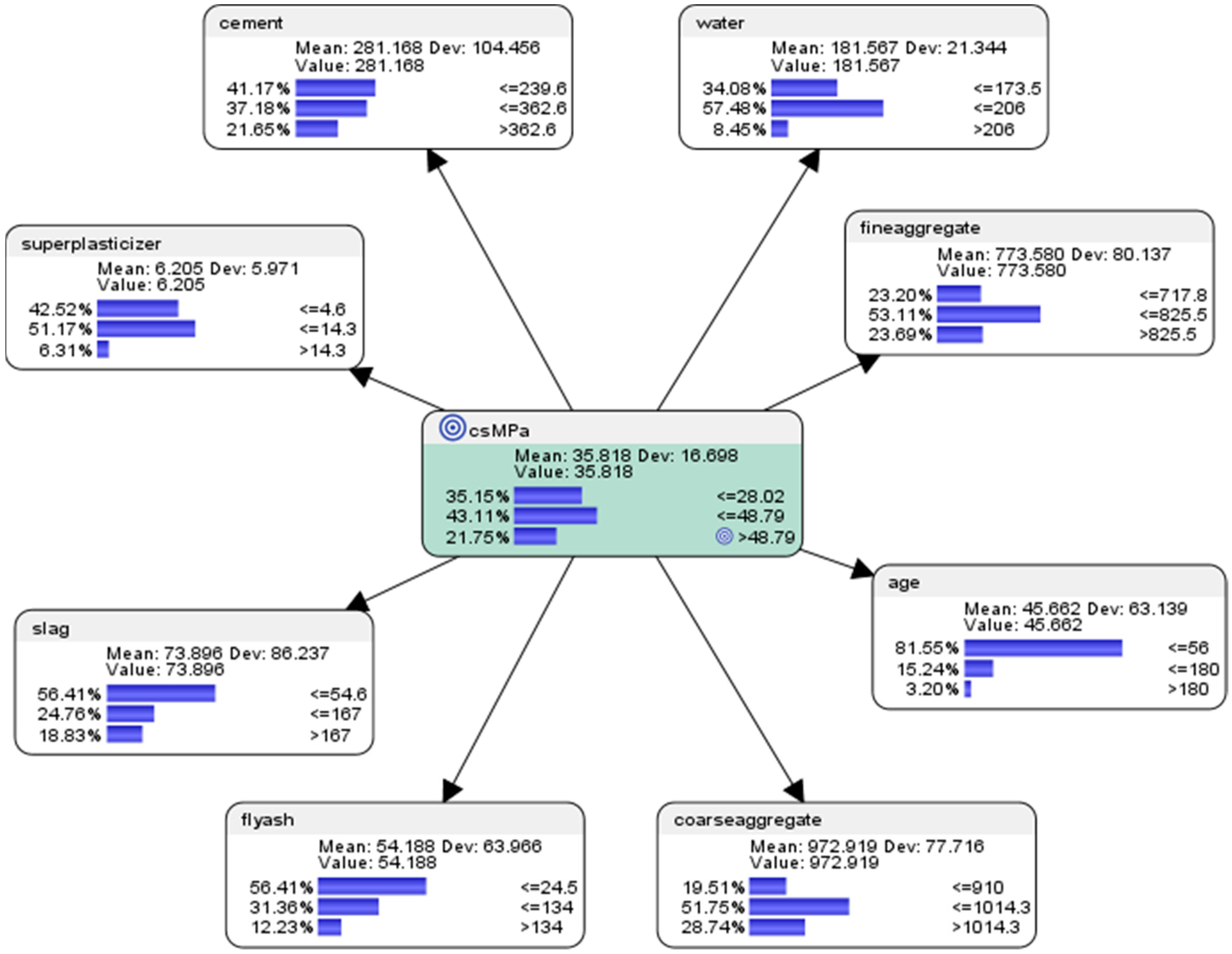
- For the node concrete compressive strength (csMPa), there was 35.15% probability of achieving low compressive strength of <=28.02 MPa (where MegaPasal is the SI unit for pressure); there was 43.11% probability of achieving mid compressive strength of >28.02 and <=48.79 MPa; and there was 21.75% of achieving high compressive strength of >48.79 MPa.
- For the attribute cement, 41.17% of the combinations in the collected data used low-level amounts of concrete in the mix (<=239.6 kg in a meter-cube mixture); 37.18% of the combinations in the collected data used mid-level amounts of concrete in the mix (>239.6 but <=362.6 kg in a meter-cube mixture); and 21.65% of the combinations in the collected data used high-level amounts of concrete in the mix (>362.6 kg in a meter-cube mixture).
- For the attribute superplasticizer, 42.52% of the combinations in the collected data used low-level amounts of superplasticizer in the mix (<=4.6 kg in a meter-cube mixture); 51.17% of the combinations in the collected data used mid-level amounts of superplasticizer in the mix (>4.6 but <=14.3 kg in a meter-cube mixture); and 6.31% of the combinations in the collected data used high-level amounts of superplasticizer in the mix (>14.3 kg in a meter-cube mixture).
- For the attribute slag, 56.41% of the combinations in the collected data used low-level amounts of slag in the mix (<=54.6 kg in a meter-cube mixture); 24.76% of the combinations in the collected data used mid-level amounts of slag in the mix (>54.6 but <=167 kg in a meter-cube mixture); and 18.83% of the combinations in the collected data used high-level amounts of slag in the mix (>167 kg in a meter-cube mixture).
- For the attribute flyash, 56.41% of the combinations in the collected data used low-level amounts of flyash in the mix (<=24.5 kg in a meter-cube mixture); 31.36% of the combinations in the collected data used mid-level amounts of flyash in the mix (>24.5 but <=134 kg in a meter-cube mixture); and 12.23% of the combinations in the collected data used high-level amounts of flyash in the mix (>134 kg in a meter-cube mixture).
- For the attribute coarseaggregate, 19.51% of the combinations in the collected data used low-level amounts of superplasticizer in the mix (<=910 kg in a meter-cube mixture); 51.75% of the combinations in the collected data used mid-level amounts of superplasticizer in the mix (>910 but <=1014.3 kg in a meter-cube mixture); and 28.74% of the combinations in the collected data used high-level amounts of superplasticizer in the mix (>1014.3 kg in a meter-cube mixture).
- For the attribute age, 81.55% of the combinations in the collected data had utilized low-level amounts of age in the mix (<=56 days); 15.24% of the combinations in the collected data had utilized mid-level amounts of age in the mix (>56 but <=180 days); and 3.20% of the combinations in the collected data used high-level amounts of age in the mix (>180 days).
- For the attribute fineaggregate, 23.20% of the combinations in the collected data used low-level amounts of fineaggregate in the mix (<=717.8 kg in a meter-cube mixture); 53.11% of the combinations in the collected data used mid-level amounts of fineaggregate in the mix (>717.8 but <=825.5 kg in a meter-cube mixture); and 23.79% of the combinations in the collected data used high-level amounts of fineaggregate in the mix (>825.5 kg in a meter-cube mixture).
- For the attribute water, 34.08% of the combinations in the collected data used low-level amounts of water in the mix (<=173.5 kg in a meter-cube mixture); 57.48% of the combinations in the collected data used mid-level amounts of water in the mix (>173.5 but <=206 kg in a meter-cube mixture); and 8.45% of the combinations in the collected data used high-level amounts of water in the mix (>206 kg in a meter-cube mixture).
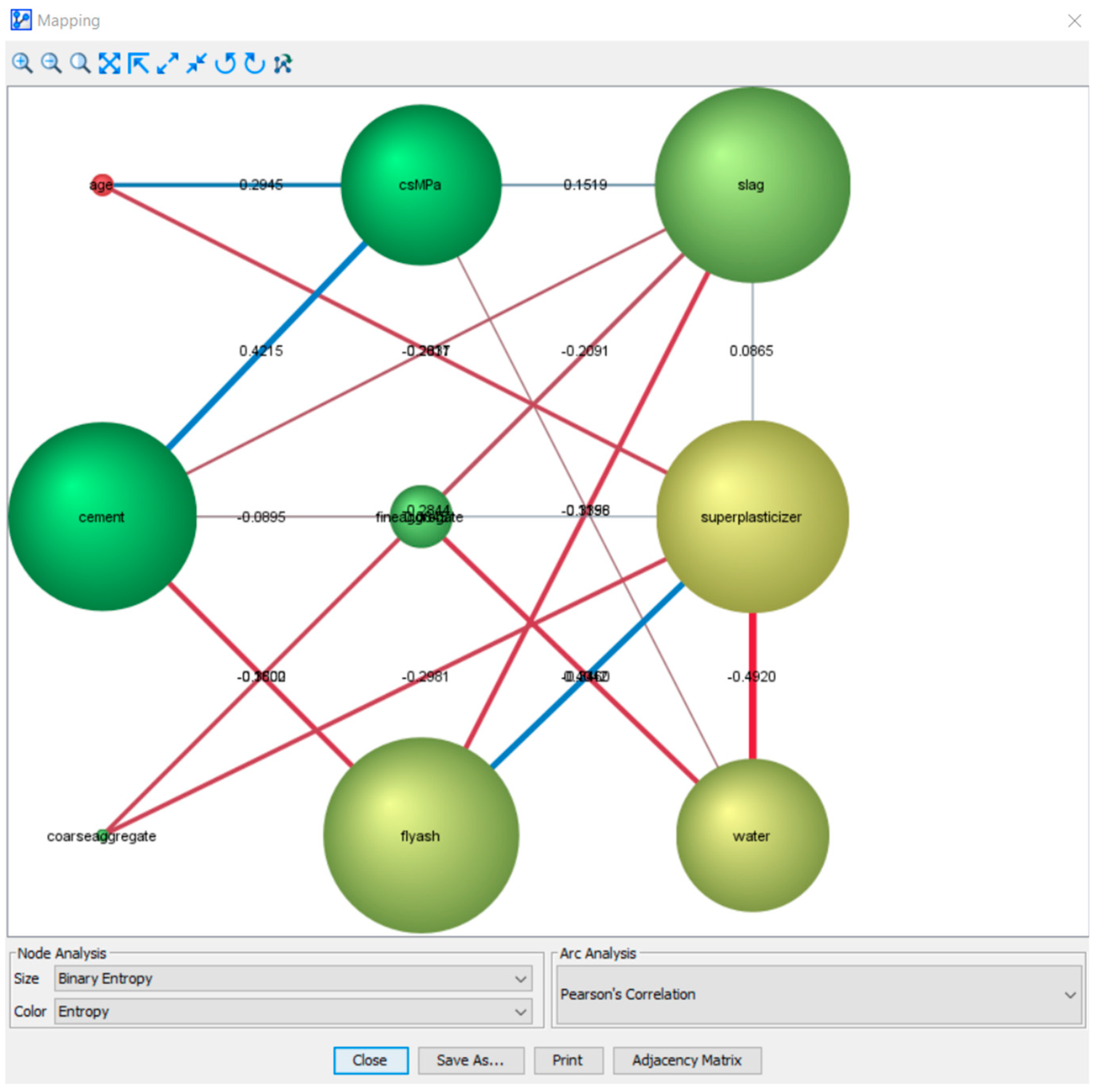
6.2. “What Has Happened?” Descriptive Analytics Using Pearson Correlation Analysis
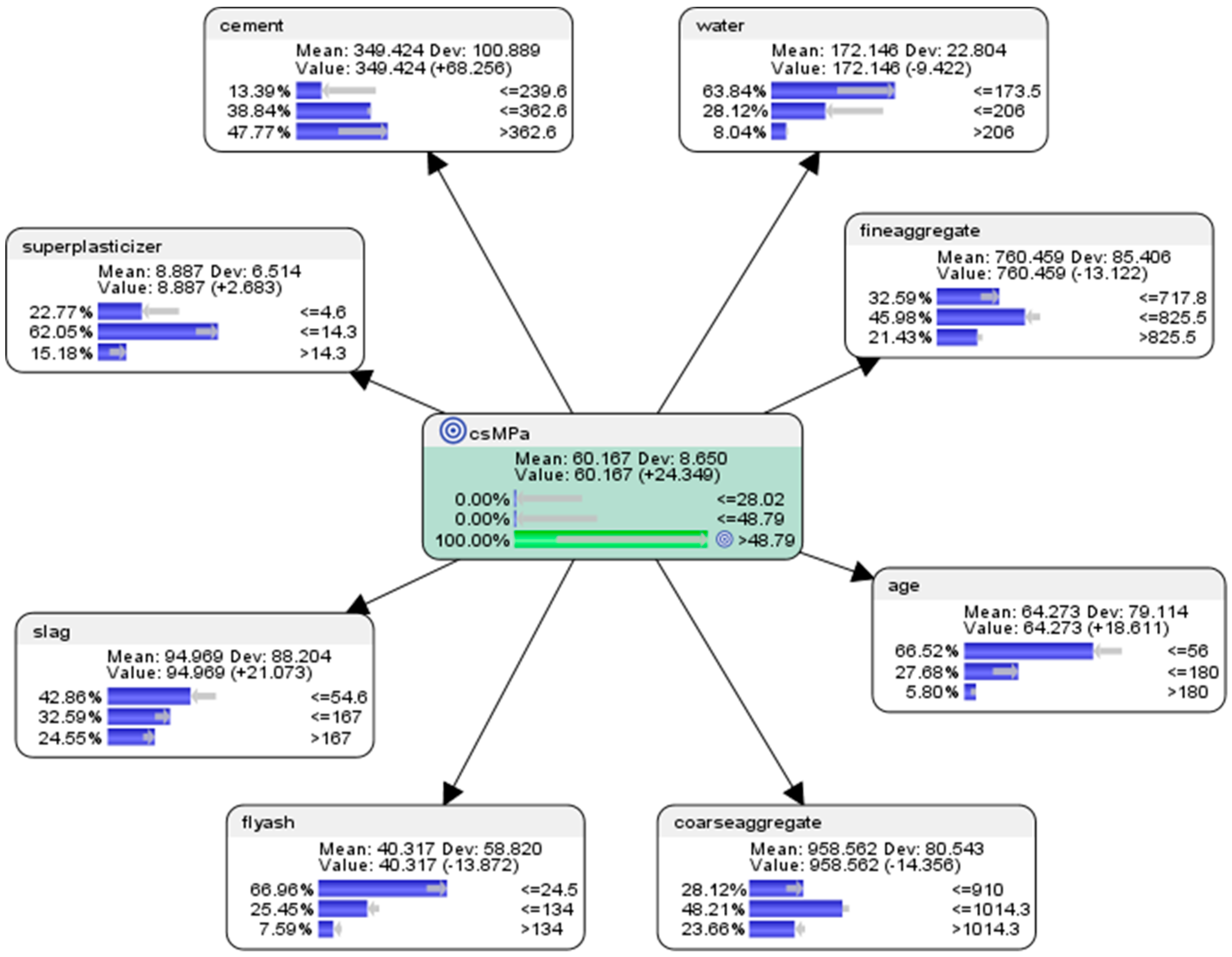
6.3. “What-If?” Predictive Analytics Using the Naïve Bayes Approach
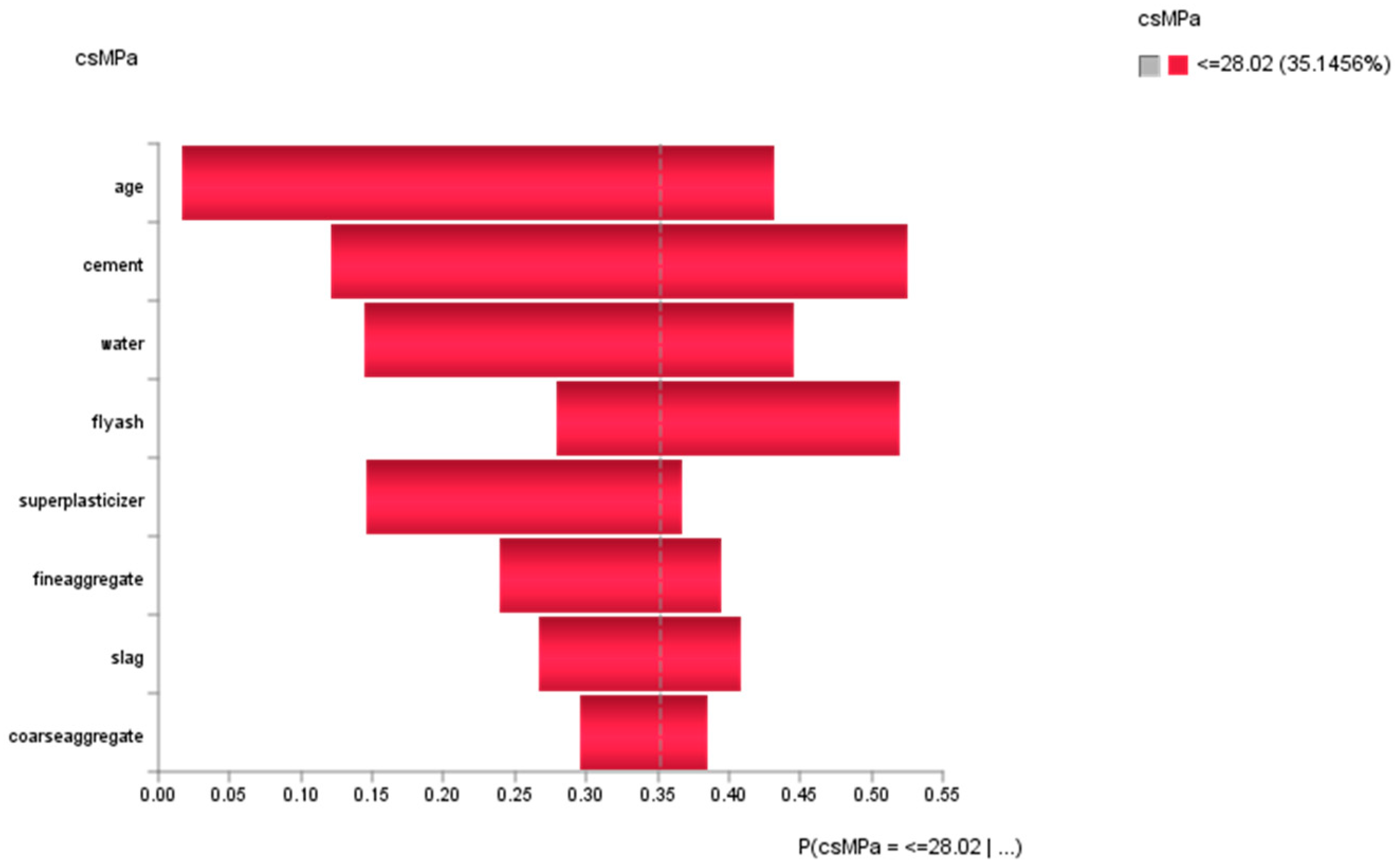
- For the attribute cement, the probability of achieving high concrete compressive strength would be 13.39% if the low-level amount of concrete was used in the mixture (<=239.6 kg in a meter-cube mixture); the probability of achieving high concrete compressive strength would be 38.84% if the mid-level amount of concrete was used in the mix (>239.6 but <=362.6 kg in a meter-cube mixture); and the probability of achieving high concrete compressive strength would be 47.77% if the high-level amount of concrete in the mix was used in the mix (>362.6 kg in a meter-cube mixture).
- For the attribute superplasticizer, the probability of achieving high concrete compressive strength would be 22.77% if the low-level amount of superplasticizer was used in the mixture (<=4.6 kg in a meter-cube mixture); the probability of achieving high concrete compressive strength would be 62.05% if the mid-level amount of superplasticizer was used in the mixture (>4.6 but <=14.3 kg in a meter-cube mixture); and the probability of achieving high concrete compressive strength would be 15.18% if the high-level amount of superplasticizer was used in the mixture (>14.3 kg in a meter-cube mixture).
- For the attribute slag, the probability of achieving high concrete compressive strength would be 42.86% if the low-level amount of slag was used in the mixture (<=54.6 kg in a meter-cube mixture); the probability of achieving high concrete compressive strength would be 32.59% if the mid-level amount of slag was used in the mixture (>54.6 but <=167 kg in a meter-cube mixture); and the probability of achieving high concrete compressive strength would be 24.55% if the high-level amount of slag was used in the mixture (>167 kg in a meter-cube mixture).
- For the attribute flyash, the probability of achieving high concrete compressive strength would be 66.96% if the low-level amount of flyash was used in the mixture (<=24.5 kg in a meter-cube mixture); the probability of achieving high concrete compressive strength would be 25.45% if the mid-level amount of flyash was used in the mixture (>24.5 but <=134 kg in a meter-cube mixture); and the probability of achieving high concrete compressive strength would be 7.59% if the high-level amount of flyash was used in the mixture (>134 kg in a meter-cube mixture).
- For the attribute coarseaggregate, the probability of achieving high concrete compressive strength would be 28.12% if the low-level amount of coarseaggregate was used in the mixture (<=910 kg in a meter-cube mixture); the probability of achieving high concrete compressive strength would be 48.21% if the mid-level amount of coarseaggregate was used in the mixture (>910 but <=1014.3 kg in a meter-cube mixture); and the probability of achieving high concrete compressive strength would be 23.66% if the high-level amount of coarseaggregate was used in the mixture (>1014.3 kg in a meter-cube mixture).
- For the attribute age, the probability of achieving high concrete compressive strength would be 66.52% if the low-level amount of age had been utilized in the mixture (<=56 days); the probability of achieving high concrete compressive strength would be 27.68% if the mid-level amount of age had been utilised in the mix (>56 but <=180 days); and the probability of achieving high concrete compressive strength would be 5.80% if the high-level amount of age had been utilised in the mix (>180 days).
- For the attribute fineaggregate, the probability of achieving high concrete compressive strength would be 32.59% if the low-level amount of fineaggregate was used in the mix (<=717.8 kg in a meter-cube mixture); the probability of achieving high concrete compressive strength would be 45.98% if the mid-level amount of fineaggregate was used in the mix (>717.8 but <=825.5 kg in a meter-cube mixture); and the probability of achieving high concrete compressive strength would be 21.43% if the high-level amount of fineaggregate was used in the mix (>825.6 kg in a meter-cube mixture).
- For the attribute water, the probability of achieving high concrete compressive strength would be 63.84% if the low-level amount of water was used in the mix (<=173.5 kg in a meter-cube mixture); the probability of achieving high concrete compressive strength would be 28.12% if the mid-level amount of water was used in the mix (>173.5 but <=206 kg in a meter-cube mixture); and the probability of achieving high concrete compressive strength would be 8.04% if the high-level amount of water was used in the mix (>206 kg in a meter-cube mixture).
7. Semi-Supervised Machine Learning Approach
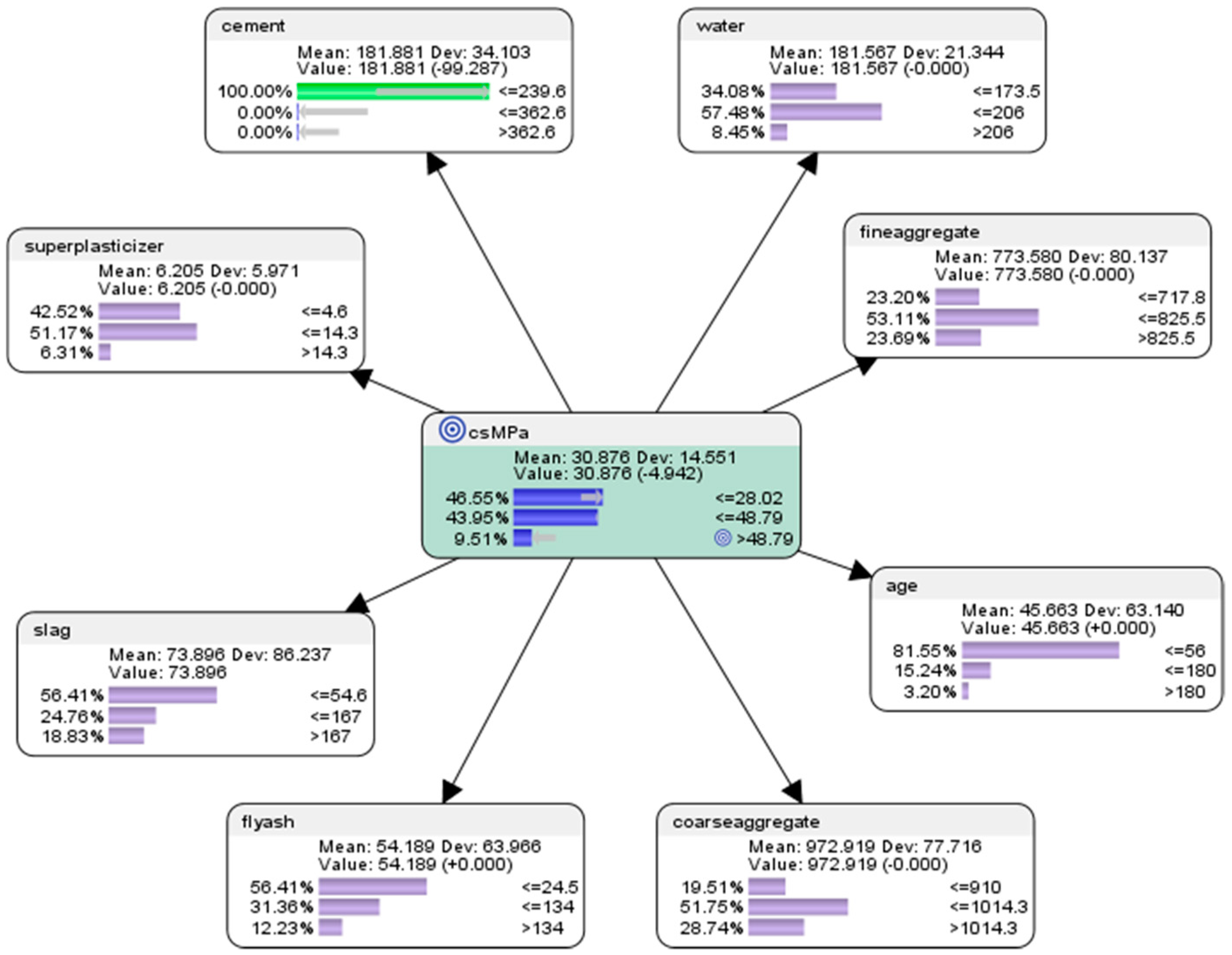
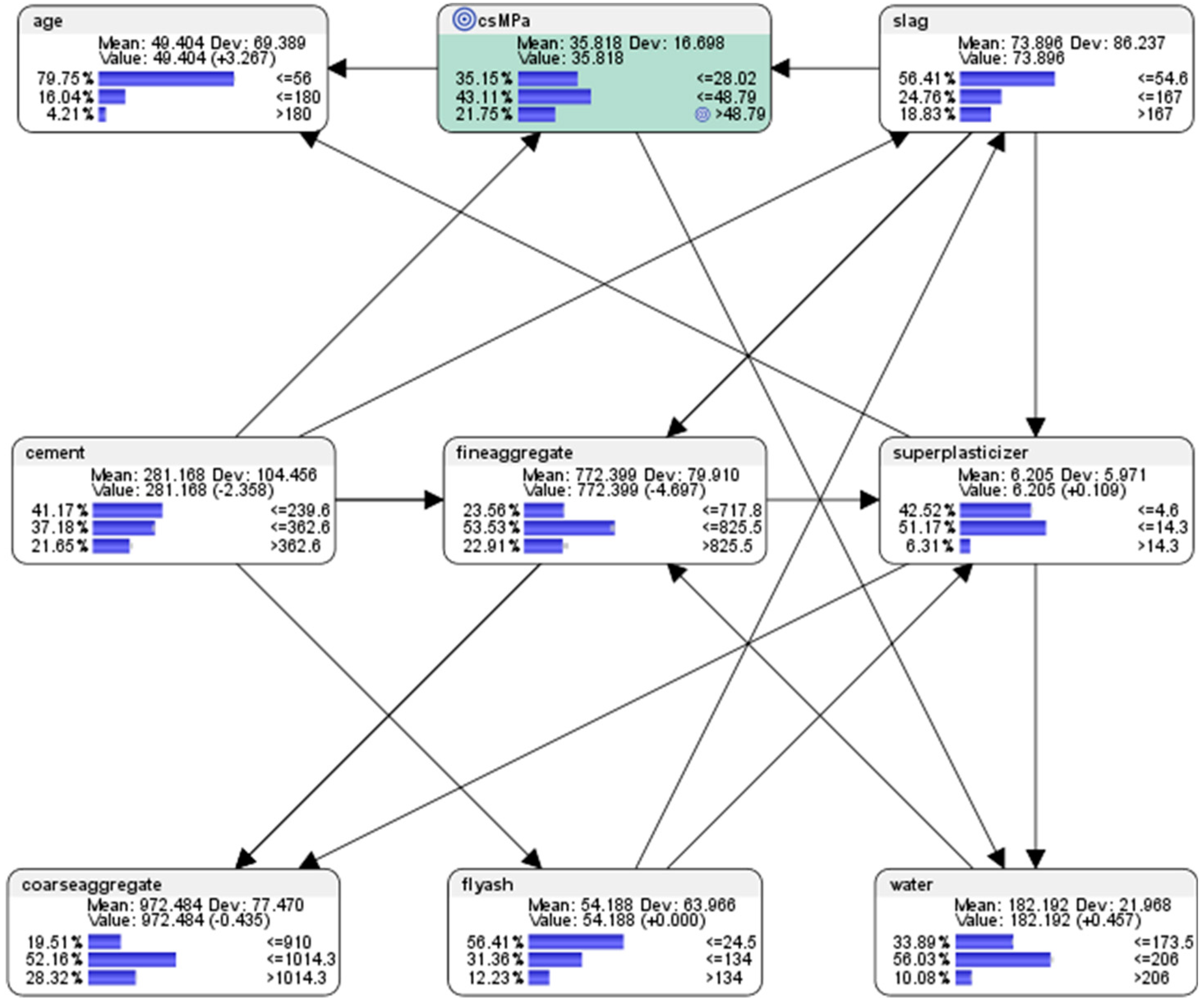
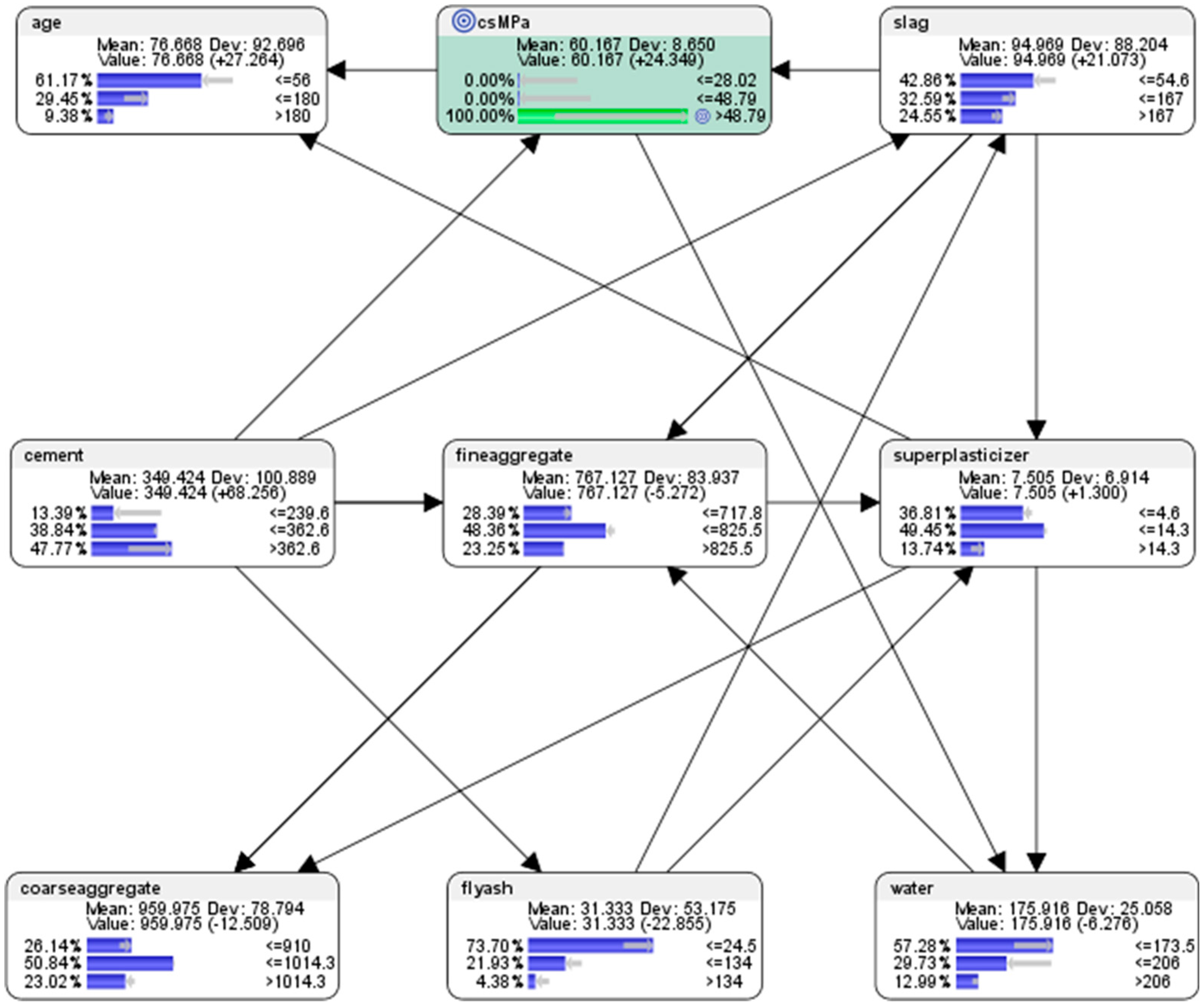
7.1. Descriptive Analytics Using the Semi-Supervised Bayesian Network Machine Learning Approach
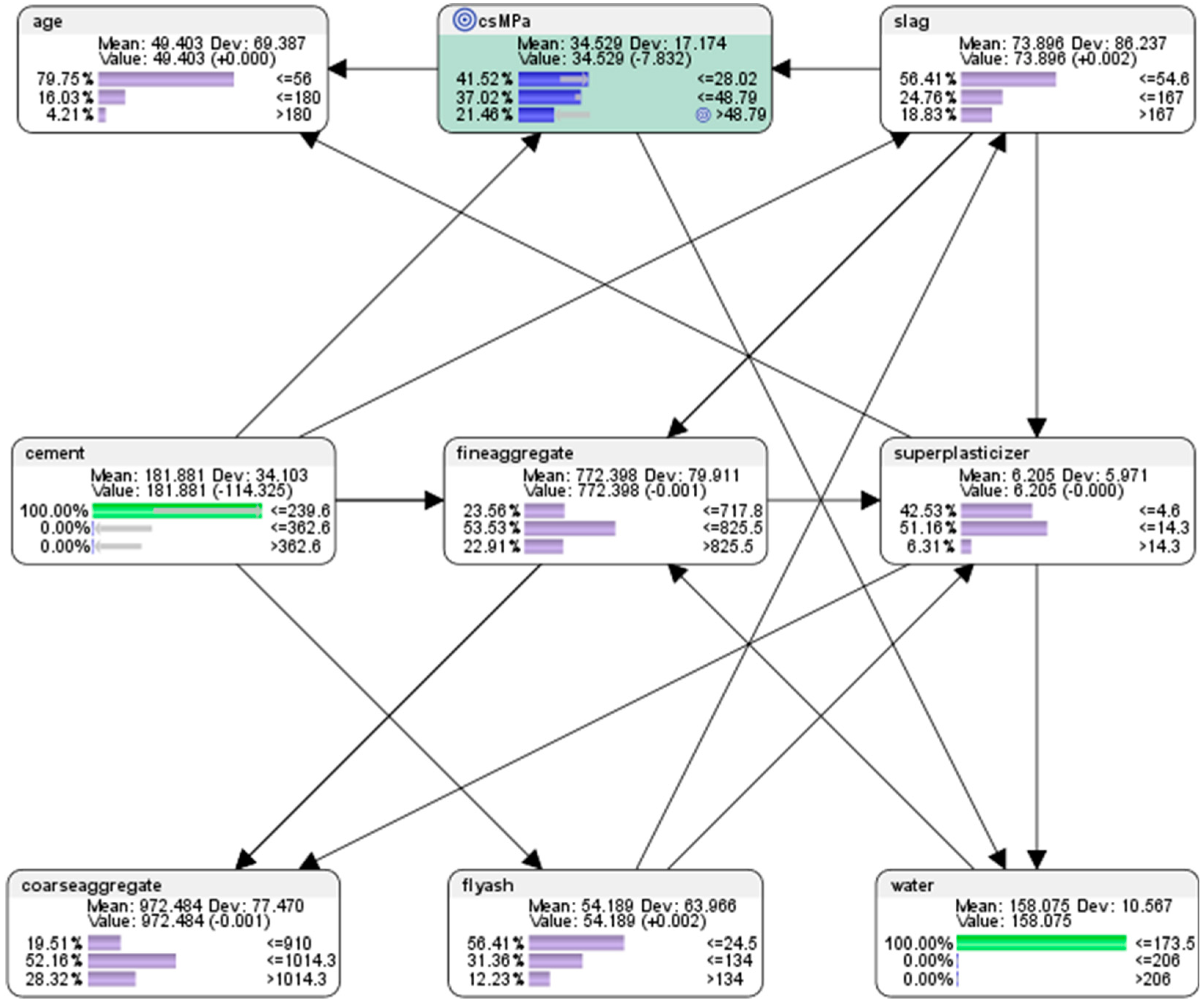
- For the node (csMPa) concrete compressive strength, there was 35.15% probability of achieving low compressive strength of <=28.02 MPa (where MegaPasal is the SI unit for pressure); there was 43.11% probability of achieving mid compressive strength of >28.02 and <=48.79 MPa; and there was 21.75% of achieving high compressive strength of >48.79 MPa.
- For the attribute cement, 41.17% of the combinations in the collected data used the low-level amounts of concrete in the mix (<=239.6 kg in a meter-cube mixture); 37.18% of the combinations in the collected data used the mid-level amounts of concrete in the mix (>239.6 but <=362.6 kg in a meter-cube mixture); and 21.65% of the combinations in the collected data used the high-level amounts of concrete in the mix (>362.6 kg in a meter-cube mixture).
- For the attribute superplasticizer, 42.52% of the combinations in the collected data used the low-level amounts of superplasticizer in the mix (<=4.6 kg in a meter-cube mixture); 51.17% of the combinations in the collected data used the mid-level amounts of superplasticizer in the mix (>4.6 but <=14.3 kg in a meter-cube mixture); and 6.31% of the combinations in the collected data used the high-level amounts of superplasticizer in the mix (>14.3 kg in a meter-cube mixture).
- For the attribute slag, 56.41% of the combinations in the collected data used the low-level amounts of slag in the mix (<=54.6 kg in a meter-cube mixture); 24.76% of the combinations in the collected data used the mid-level amounts of slag in the mix (>54.6 but <=167 kg in a meter-cube mixture); and 18.83% of the combinations in the collected data used the high-level amounts of slag in the mix (>167 kg in a meter-cube mixture).
- For the attribute flyash, 56.41% of the combinations in the collected data used the low-level amounts of flyash in the mix (<=24.5 kg in a meter-cube mixture); 31.36% of the combinations in the collected data used the mid-level amounts of flyash in the mix (>24.5 but <=134 kg in a meter-cube mixture); and 12.23% of the combinations in the collected data used the high-level amounts of flyash in the mix (>134 kg in a meter-cube mixture).
- For the attribute coarseaggregate, 19.51% of the combinations in the collected data used low-level amounts of superplasticizer in the mix (<=910 kg in a meter-cube mixture); 52.16% of the combinations in the collected data used the mid-level amounts of superplasticizer in the mix (>910 but <=1014.3 kg in a meter-cube mixture); and 28.32% of the combinations in the collected data used the high-level amounts of superplasticizer in the mix (>1014.3 kg in a meter-cube mixture).
- For the attribute age, 79.75% of the combinations in the collected data had utilised the low-level amounts of age in the mix (<=56 days); 16.04% of the combinations in the collected data had utilised the mid-level amounts of age in the mix (>56 but <=180 days); and 4.21% of the combinations in the collected data used the high-level amounts of age in the mix (>180 days).
- For the attribute fineaggregate, 23.56% of the combinations in the collected data had used the low-level amounts of fineaggregate in the mix (<=717.8 kg in a meter-cube mixture); 53.53% of the combinations in the collected data used the mid-level amounts of fineaggregate in the mix (>717.8 but <=825.5 kg in a meter-cube mixture); and 22.91% of the combinations in the collected data used the high-level amounts of fineaggregate in the mix (>825.5 kg in a meter-cube mixture).
- For the attribute water, 33.89% of the combinations in the collected data had used the low-level amounts of water in the mix (<=173.5 kg in a meter-cube mixture); 56.03% of the combinations in the collected data used the mid-level amounts of water in the mix (>173.5 but <=206 kg in a meter-cube mixture); and 10.08% of the combinations in the collected data used the high-level amounts of water in the mix (>206 kg in a meter-cube mixture).
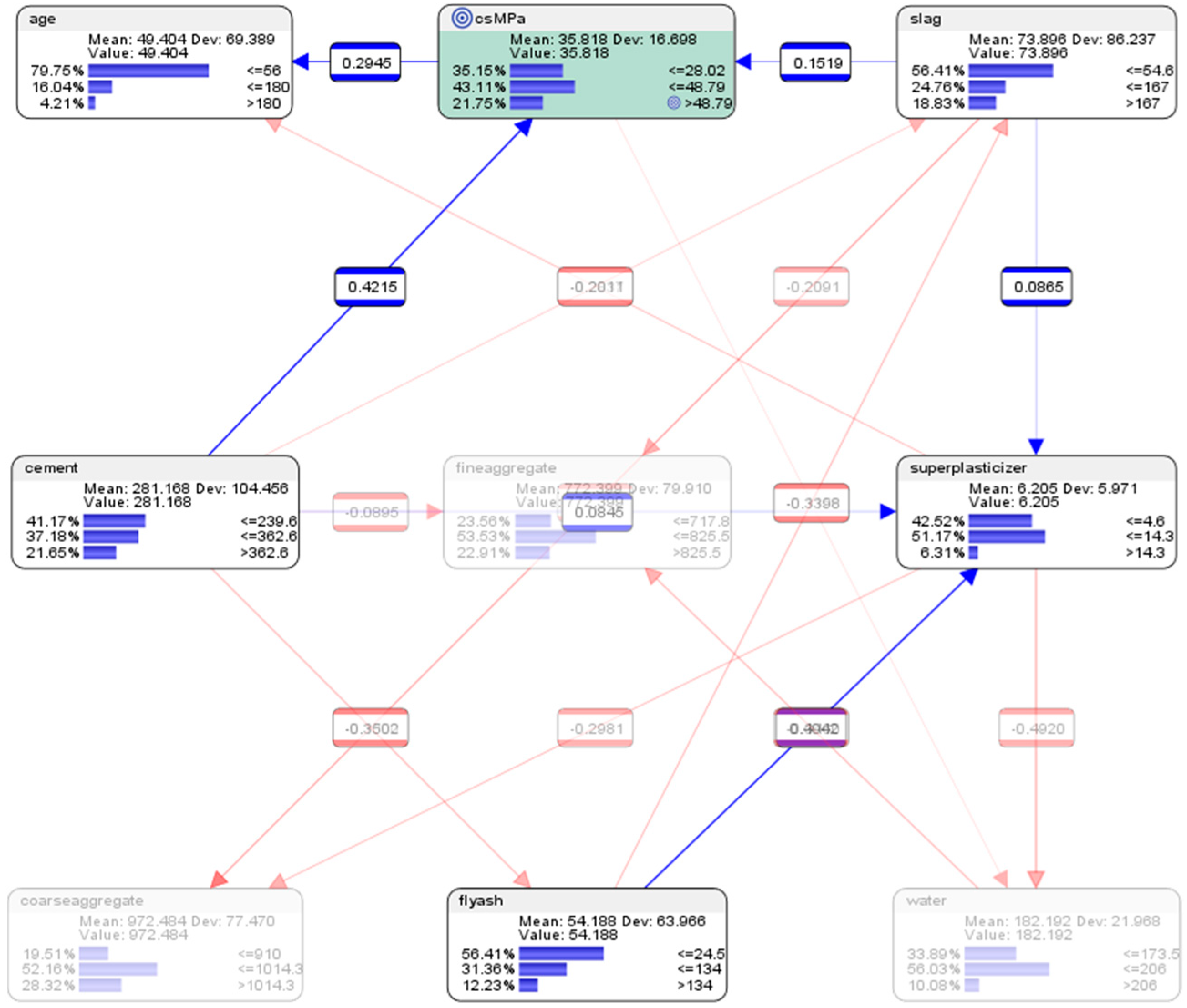
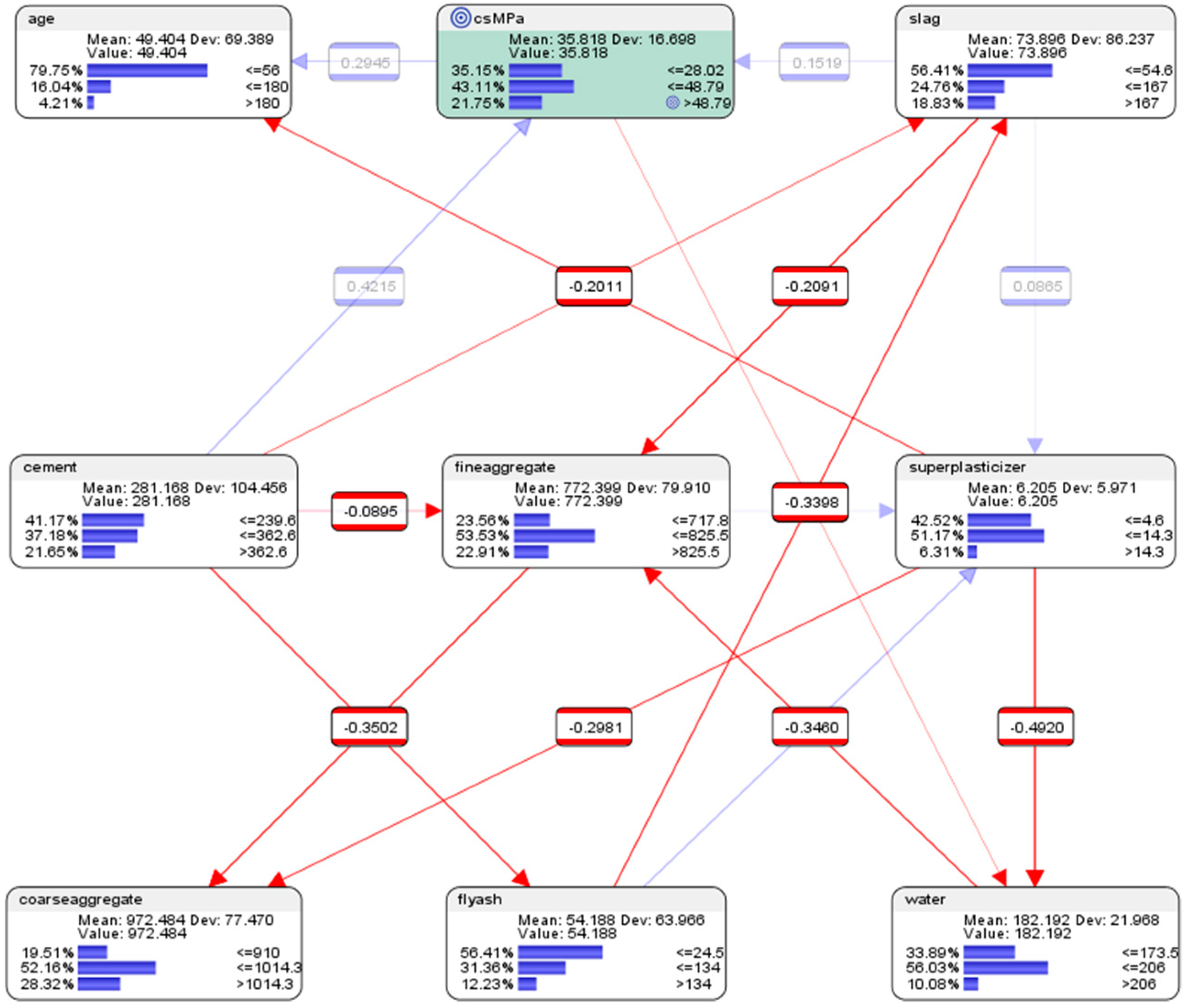
7.2. Descriptive Analytics of the Semi-Supervised BN Model Using Pearson Correlations
7.3. Descriptive Analytics: Mapping of Entropy in the Semi-Supervised BN Model
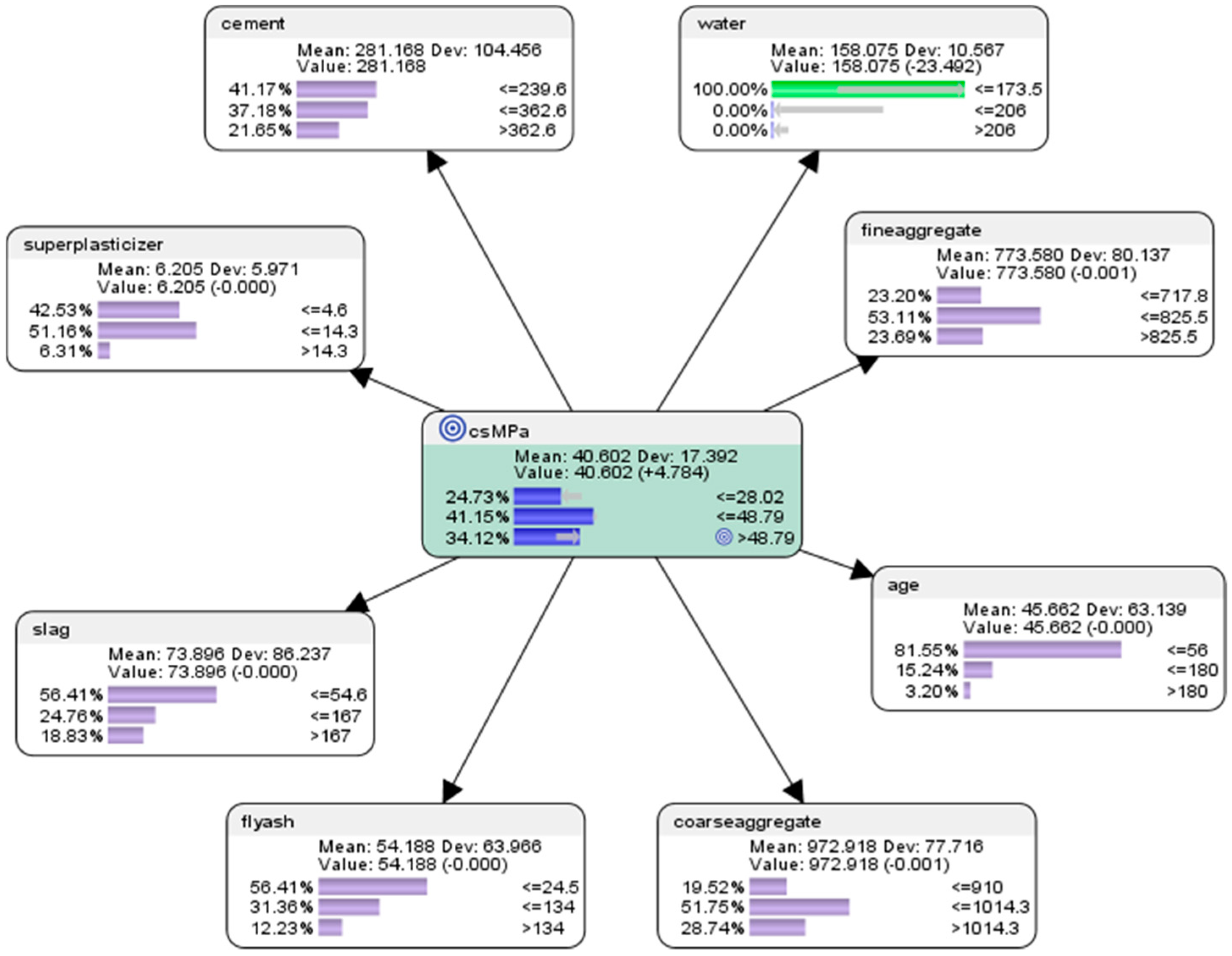
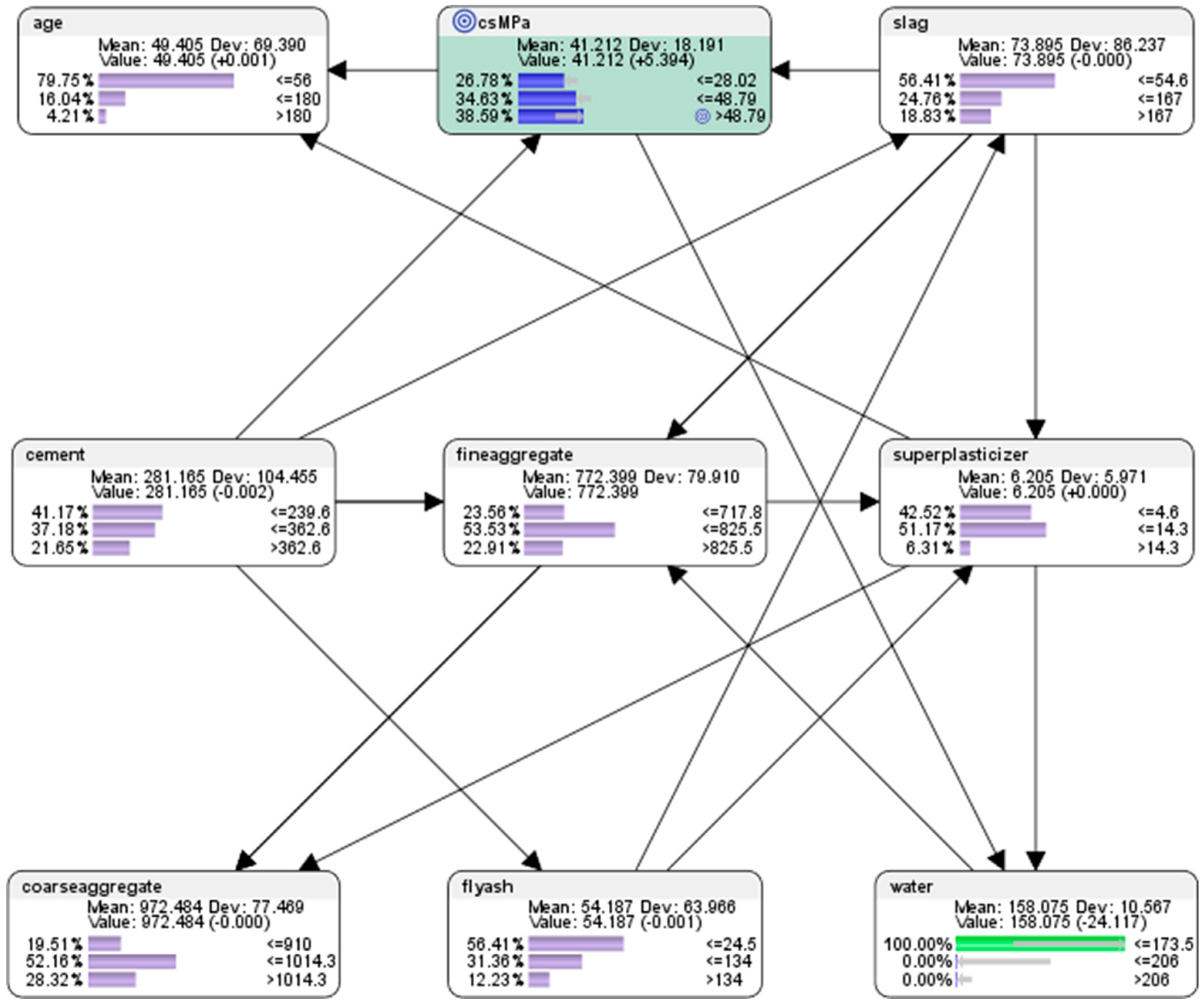
7.4. Predictive Analytics of the Semi-Supervised BN Model
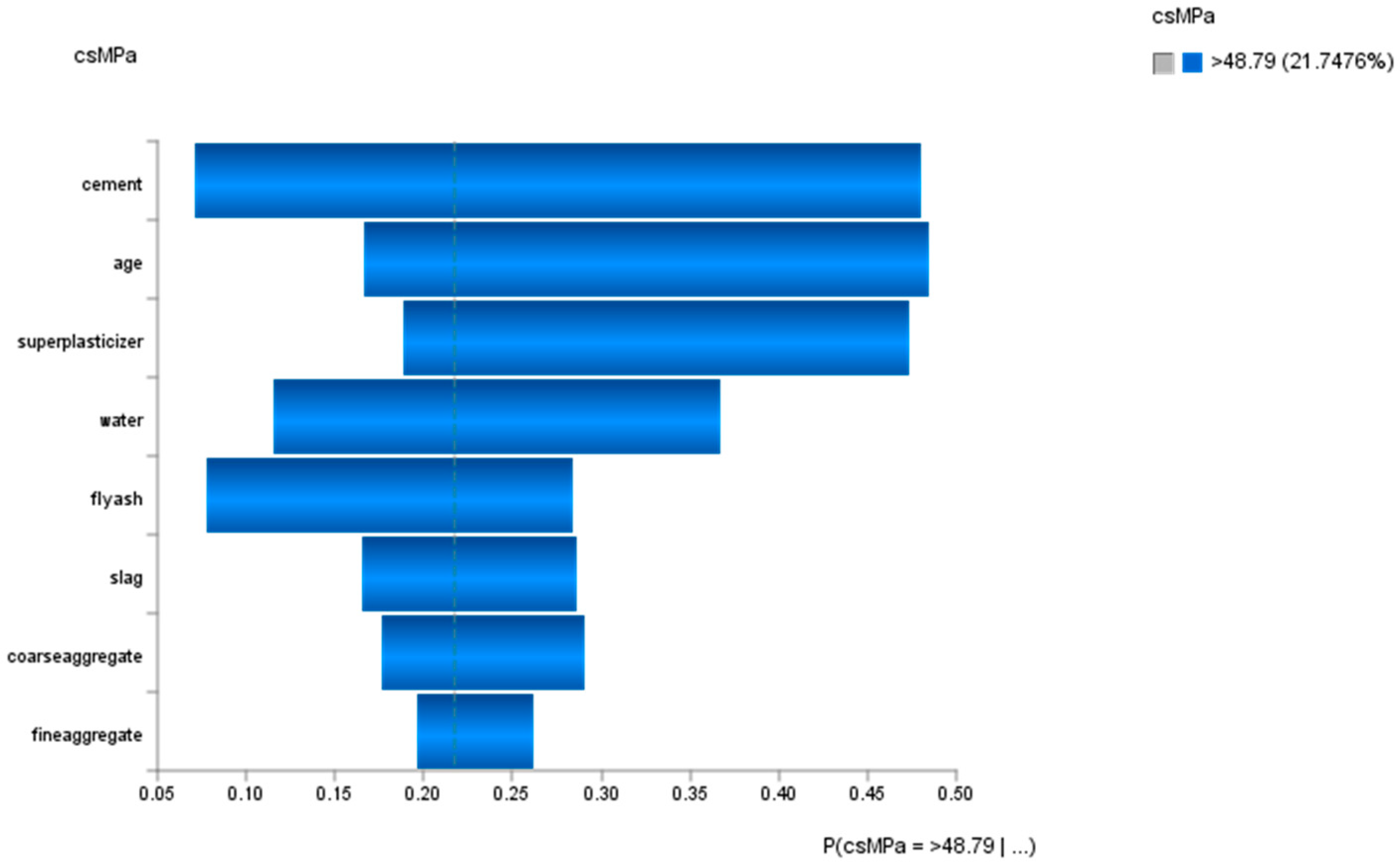
- For the attribute cement, the probability of achieving high concrete compressive strength would be 13.39% if the low-level amount of concrete was used in the mixture (<=239.6 kg in a meter-cube mixture); the probability of achieving high concrete compressive strength would be 38.84% if used the mid-level amount of concrete was used in the mix (>239.6 but <=362.6 kg in a meter-cube mixture); and the probability of achieving high concrete compressive strength would be 47.77% if the high-level amount of concrete in the mix was used in the mix (>362.6 kg in a meter-cube mixture). This was the same as the counterfactual results for concrete presented in hypothetical scenario 6.3.1 (see Figure 9).
- For the attribute superplasticizer, the probability of achieving high concrete compressive strength would be 36.81% if low-level amount of superplasticizer was used in the mixture (<=4.6 kg in a meter-cube mixture); the probability of achieving high concrete compressive strength would be 49.45% if the mid-level amount of superplasticizer was used in the mixture (>4.6 but <=14.3 kg in a meter-cube mixture); and the probability of achieving high concrete compressive strength would be 13.74% if the high-level amount of superplasticizer was used in the mixture (>14.3 kg in a meter-cube mixture). This was slightly different compared to the counterfactual results for superplasticizer presented in hypothetical scenario 6.3.1 (see Figure 9), as there were more possible relations between the mix components in this semi-supervised machine learning model.
- For the attribute slag, the probability of achieving high concrete compressive strength would be 42.86% if the low-level amount of slag was used in the mixture (<=54.6 kg in a meter-cube mixture); the probability of achieving high concrete compressive strength would be 32.59% if the mid-level amount of slag was used in the mixture (>54.6 but <=167 kg in a meter-cube mixture); and the probability of achieving high concrete compressive strength would be 24.55% if the high-level amount of slag was used in the mixture (>167 kg in a meter-cube mixture). This was the same as the counterfactual results for slag presented in hypothetical scenario 6.3.1 (see Figure 9).
- For the attribute flyash, the probability of achieving high concrete compressive strength would be 73.70% if the low-level amount of flyash was used in the mixture (<=24.5 kg in a meter-cube mixture); the probability of achieving high concrete compressive strength would be 21.93% if the mid-level amount of flyash was used in the mixture (>24.5 but <=134 kg in a meter-cube mixture); and the probability of achieving high concrete compressive strength would be 4.38% if the high-level amount of flyash was used in the mixture (>134 kg in a meter-cube mixture). This was slightly different compared to the counterfactual results for flyash presented in hypothetical scenario 6.3.1 (see Figure 9), as there were more possible relations between the mix components in this semi-supervised machine learning model.
- For the attribute coarseaggregate, the probability of achieving high concrete compressive strength would be 26.14% if the low-level amount of coarseaggregate was used in the mixture (<=910 kg in a meter-cube mixture); the probability of achieving high concrete compressive strength would be 50.84% if the mid-level amount of coarseaggregate was used in the mixture (>910 but <=1014.3 kg in a meter-cube mixture); and the probability of achieving high concrete compressive strength would be 23.02% if the high-level amount of coarseaggregate was used in the mixture (>1014.3 kg in a meter-cube mixture). This was slightly different compared to the counterfactual results for coarseaggregate presented in hypothetical scenario 6.3.1 (see Figure 9), as there were more possible relations between the mix components in this semi-supervised machine learning model.
- For the attribute age, the probability of achieving high concrete compressive strength would be 61.17% if the low-level amount of age had been utilized in the mixture (<=56 days); the probability of achieving high concrete compressive strength would be 29.45% if the mid-level amount of age had been utilised in the mix (>56 but <=180 days); and the probability of achieving high concrete compressive strength would be 9.38% if the high-level amount of age had been utilised in the mix (>180 days). This was slightly different compared to the counterfactual results for age presented in hypothetical scenario 6.3.1 (see Figure 9), as there were more possible relations between the mix components in this semi-supervised machine learning model.
- For the attribute fineaggregate, the probability of achieving high concrete compressive strength would be 28.39% if the low-level amount of fineaggregate was used in the mix (<=717.8 kg in a meter-cube mixture); the probability of achieving high concrete compressive strength would be 48.36% if the mid-level amount of fineaggregate was used in the mix (>717.8 but <=825.5 kg in a meter-cube mixture); and the probability of achieving high concrete compressive strength would be 23.25% if the high-level amount of fineaggregate was used in the mix (>825.6 kg in a meter-cube mixture). This was slightly different compared to the counterfactual results for fineaggregate presented in hypothetical scenario 6.3.1 (see Figure 9), as there were more possible relations between the mix components in this semi-supervised machine learning model.
- For the attribute water, the probability of achieving high concrete compressive strength would be 57.28% if the low-level amount of water was used in the mix (<=173.5 kg in a meter-cube mixture); the probability of achieving high concrete compressive strength would be 29.73% if the mid-level amount of water was used in the mix (>173.5 but <=206 kg in a meter-cube mixture); and the probability of achieving high concrete compressive strength would be 12.99% if the high-level amount of water was used in the mix (>206 kg in a meter-cube mixture). This was slightly different compared to the counterfactual results for water presented in hypothetical scenario 6.3.1 (see Figure 9), as there were more possible relations between the mix components in this semi-supervised machine learning model.
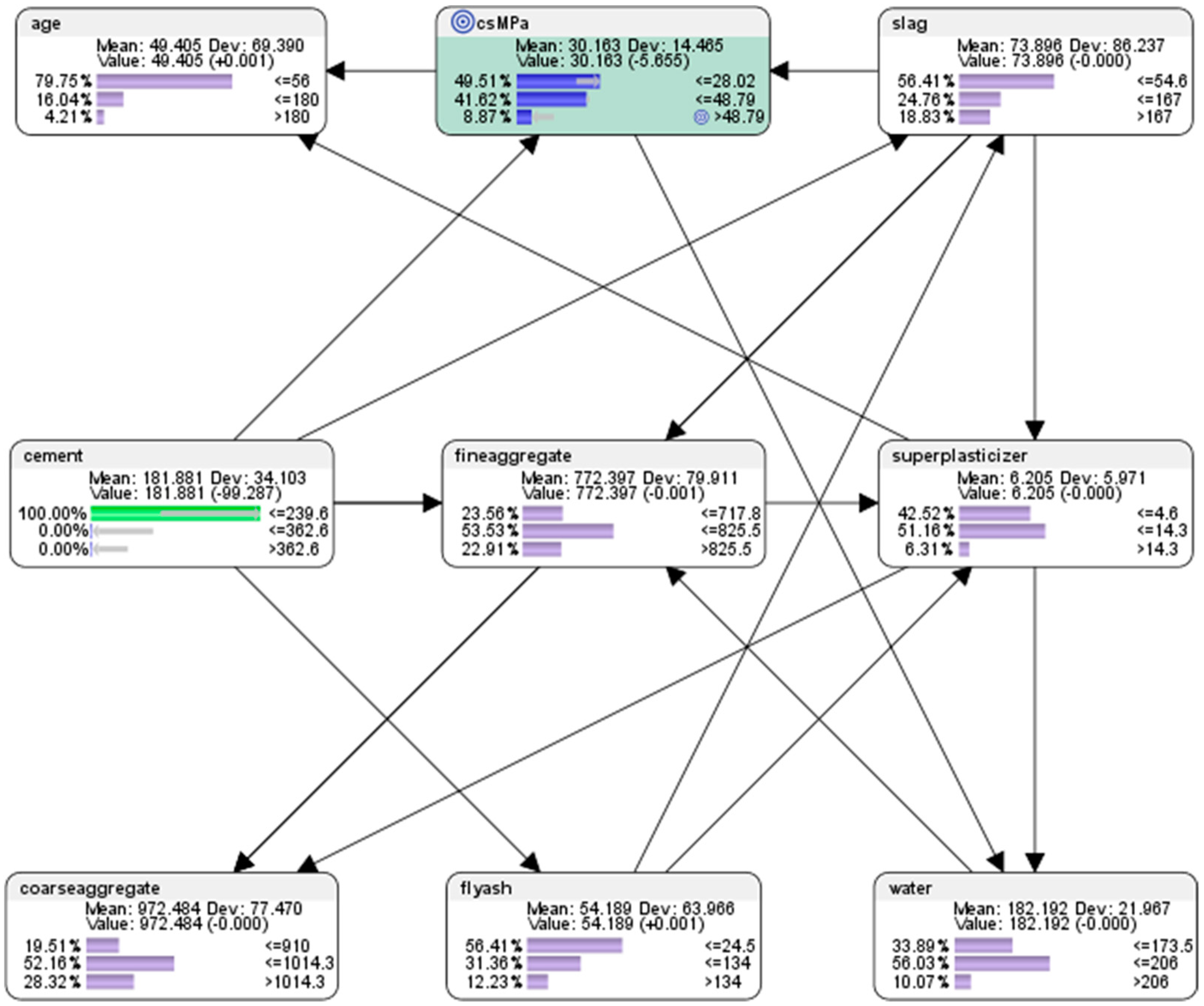
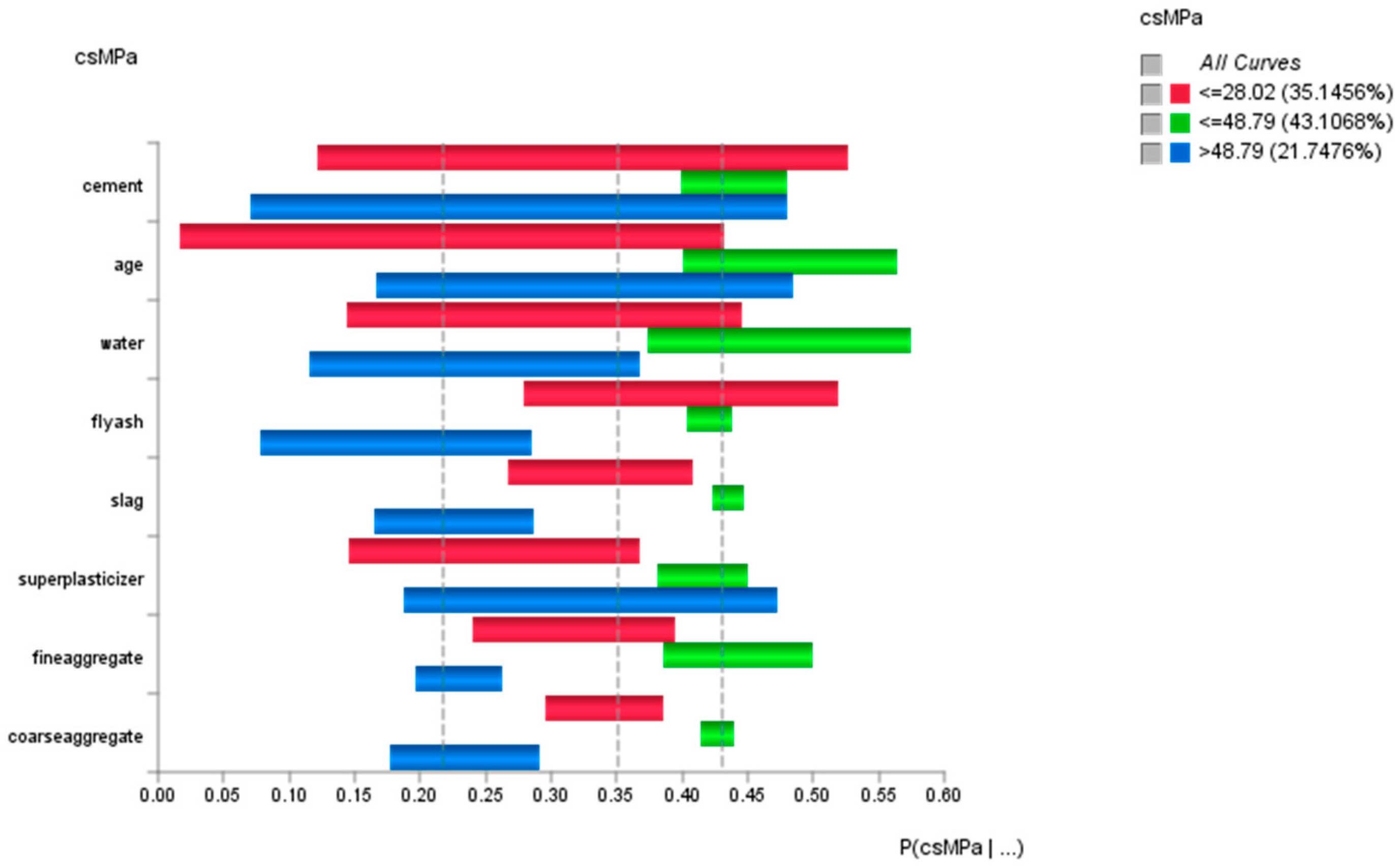
7.5. Analysis of How Concrete Compressive Strength Is Sensitive to Changes in the Variables of the Mixture
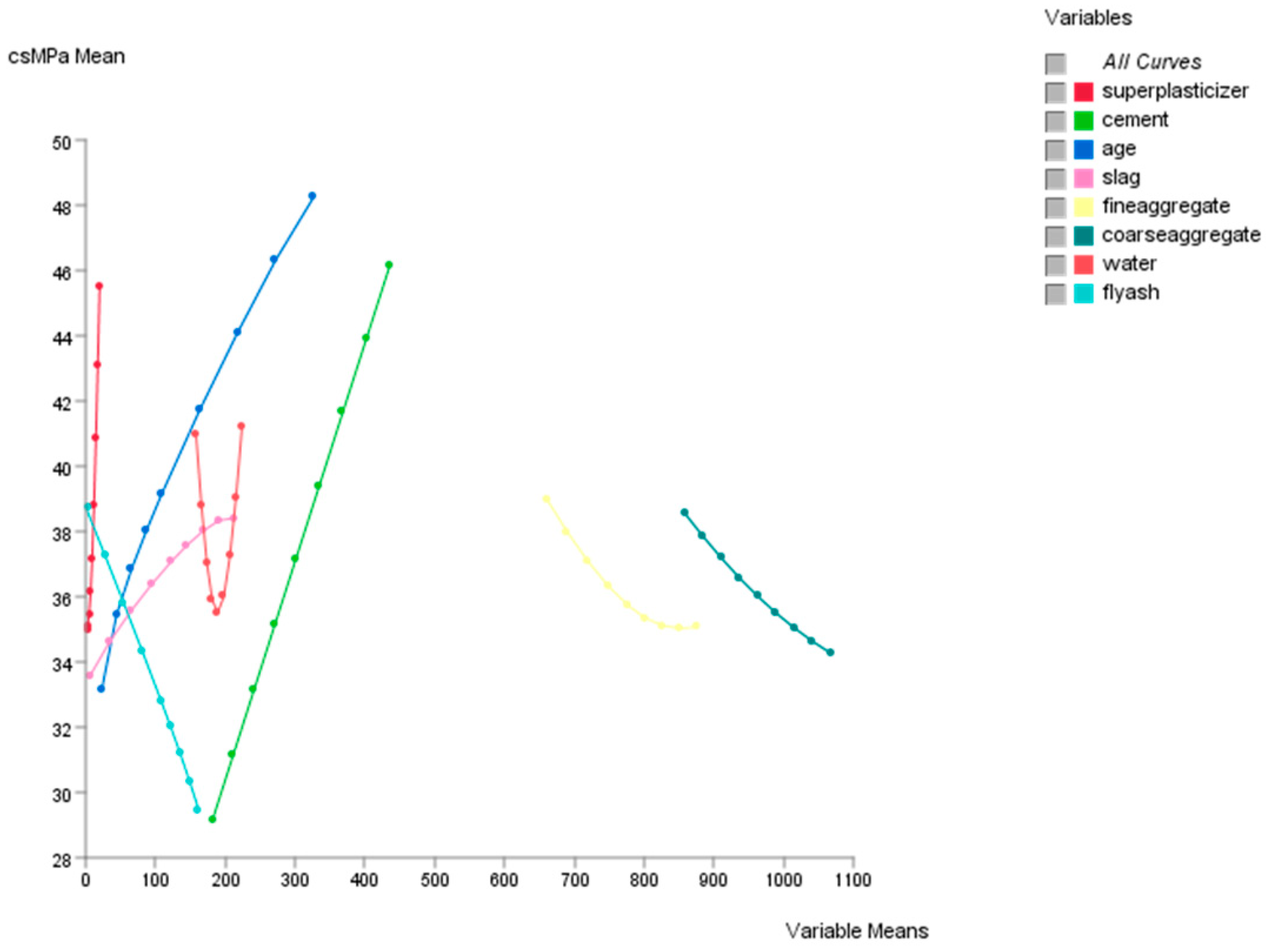
7.6. Descriptive Analytics: Curves Analysis
8. Evaluation of the Predictive Performance of the Bayesian Network model
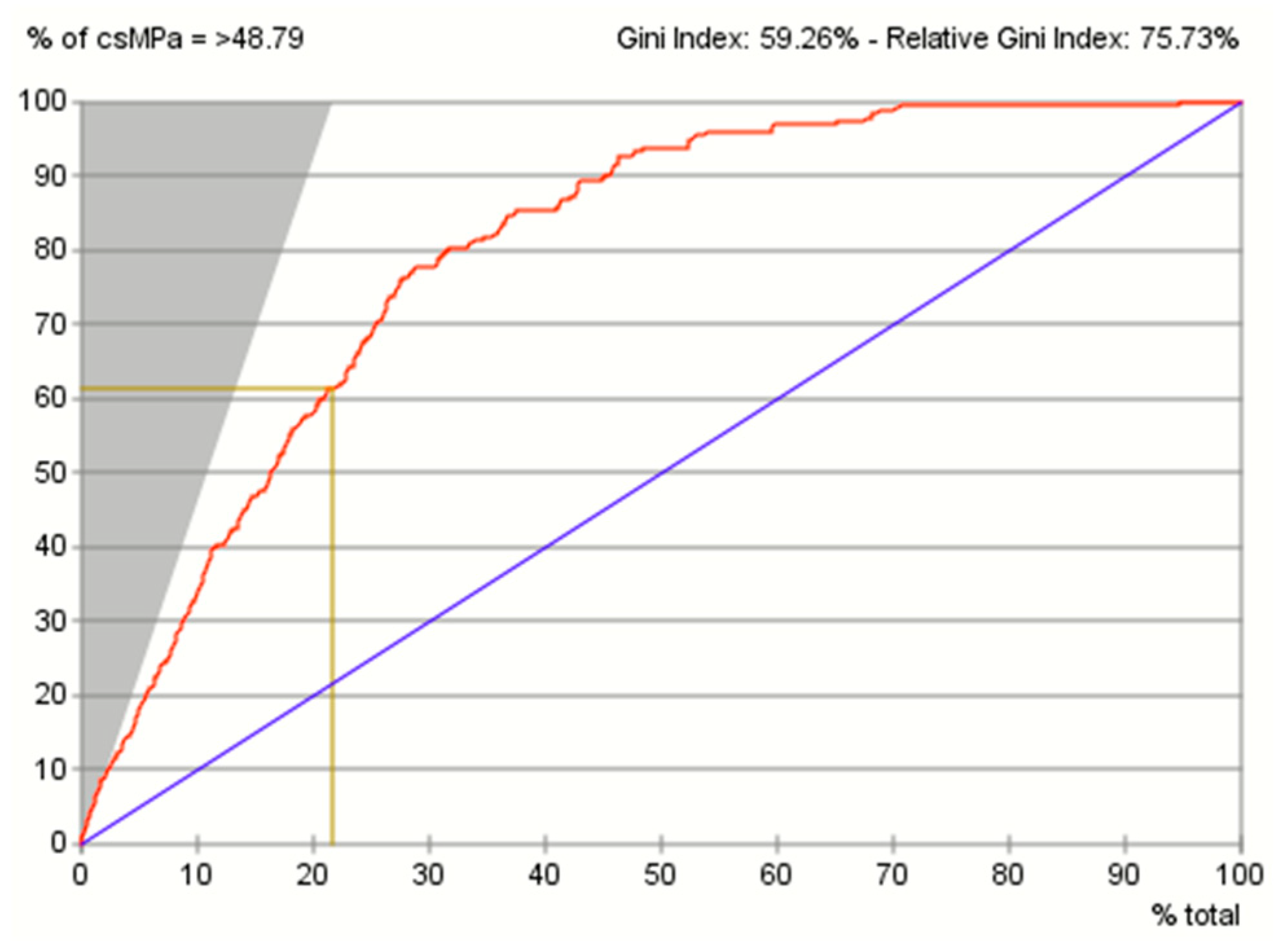
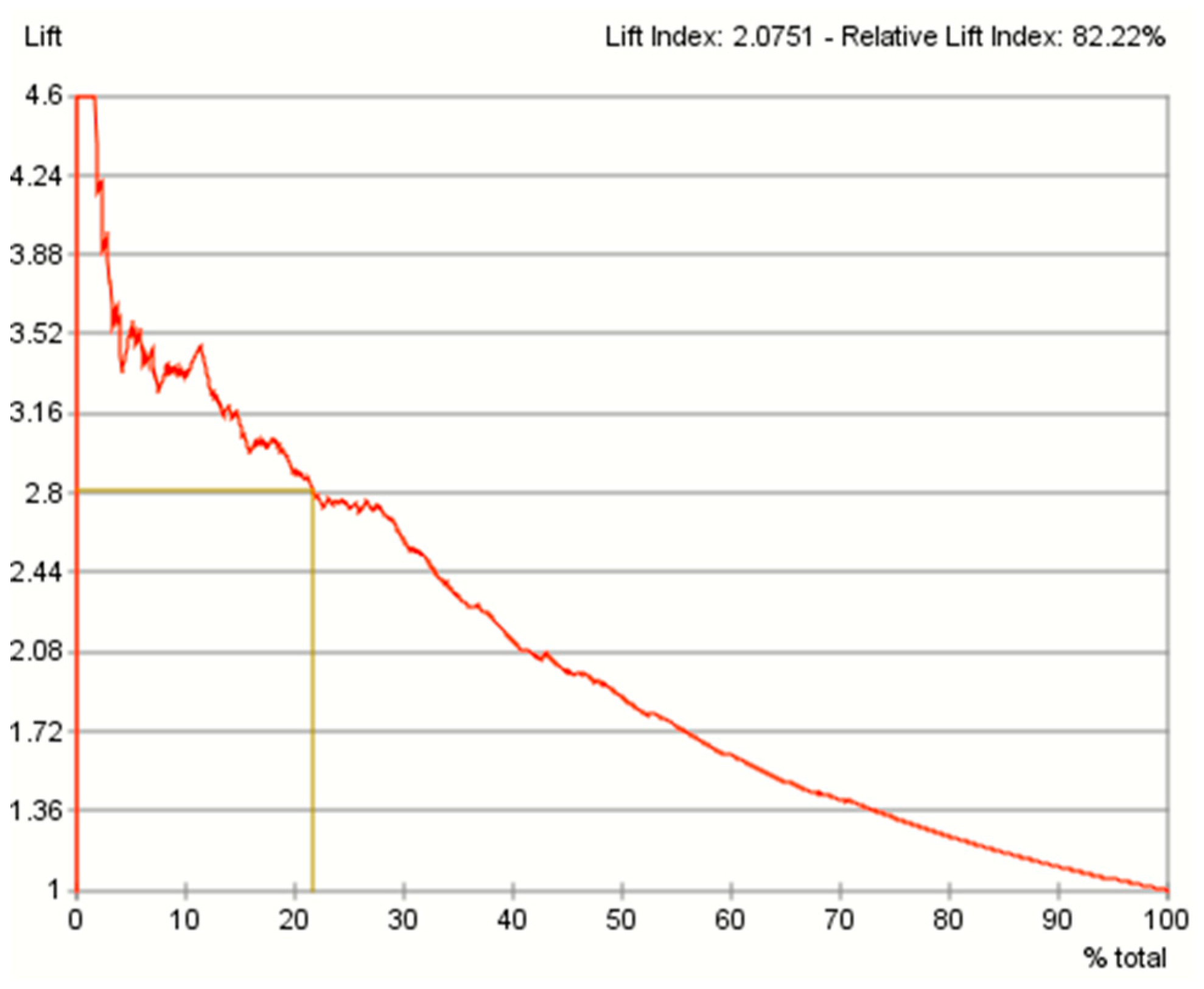
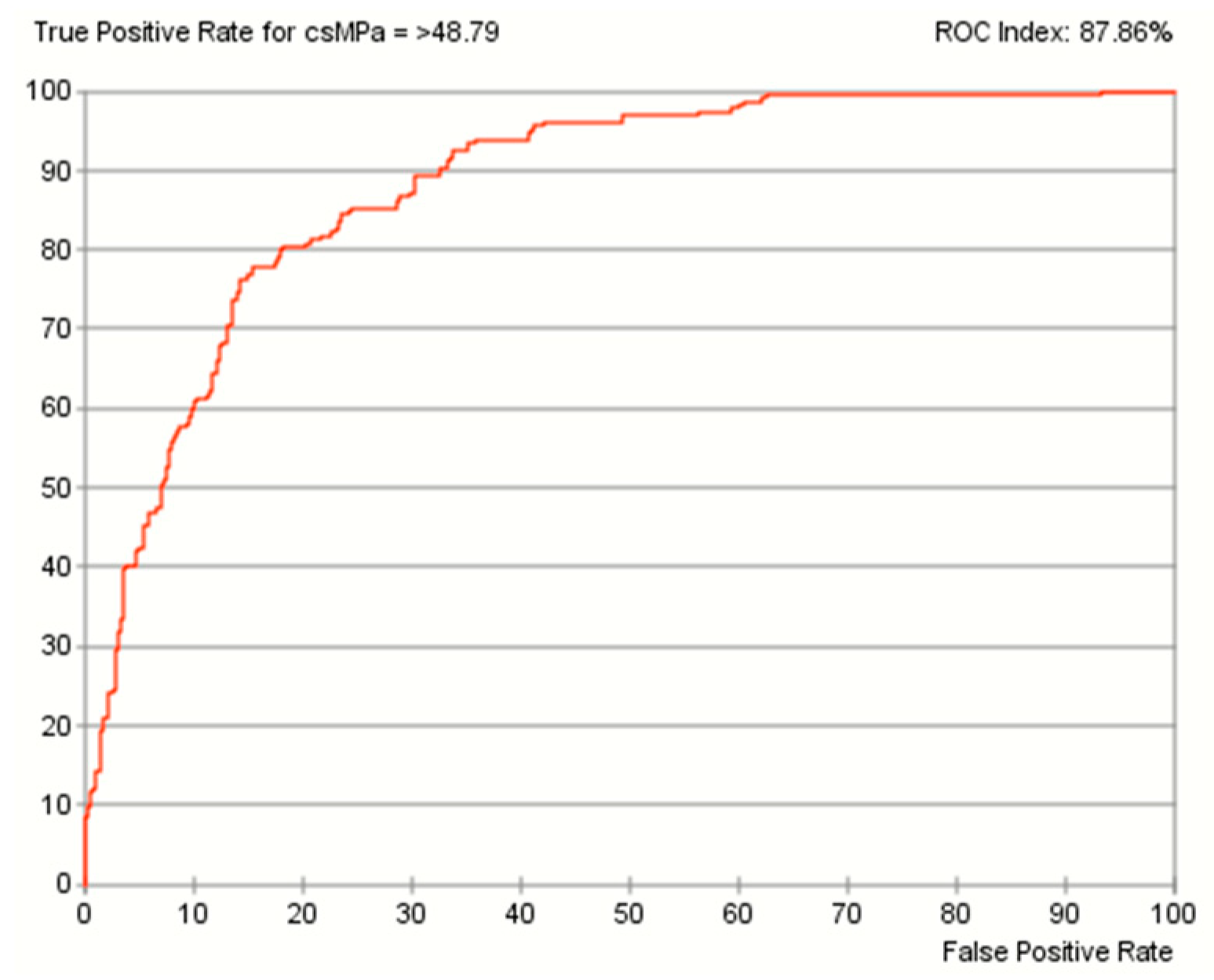
8.1. Evaluation of the Predictive Performance Using the Gains Curve, Lift Curve and ROC Curve
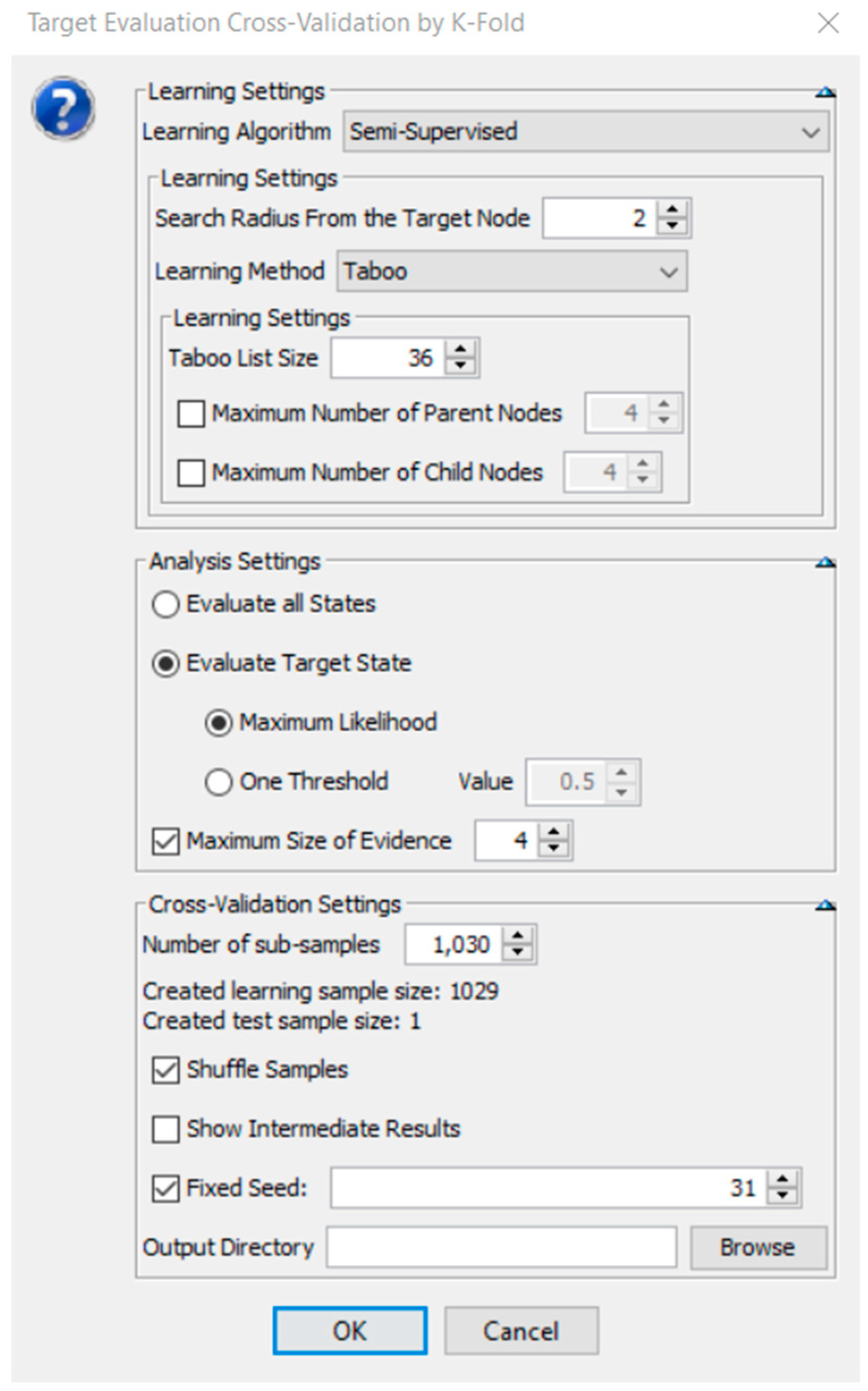
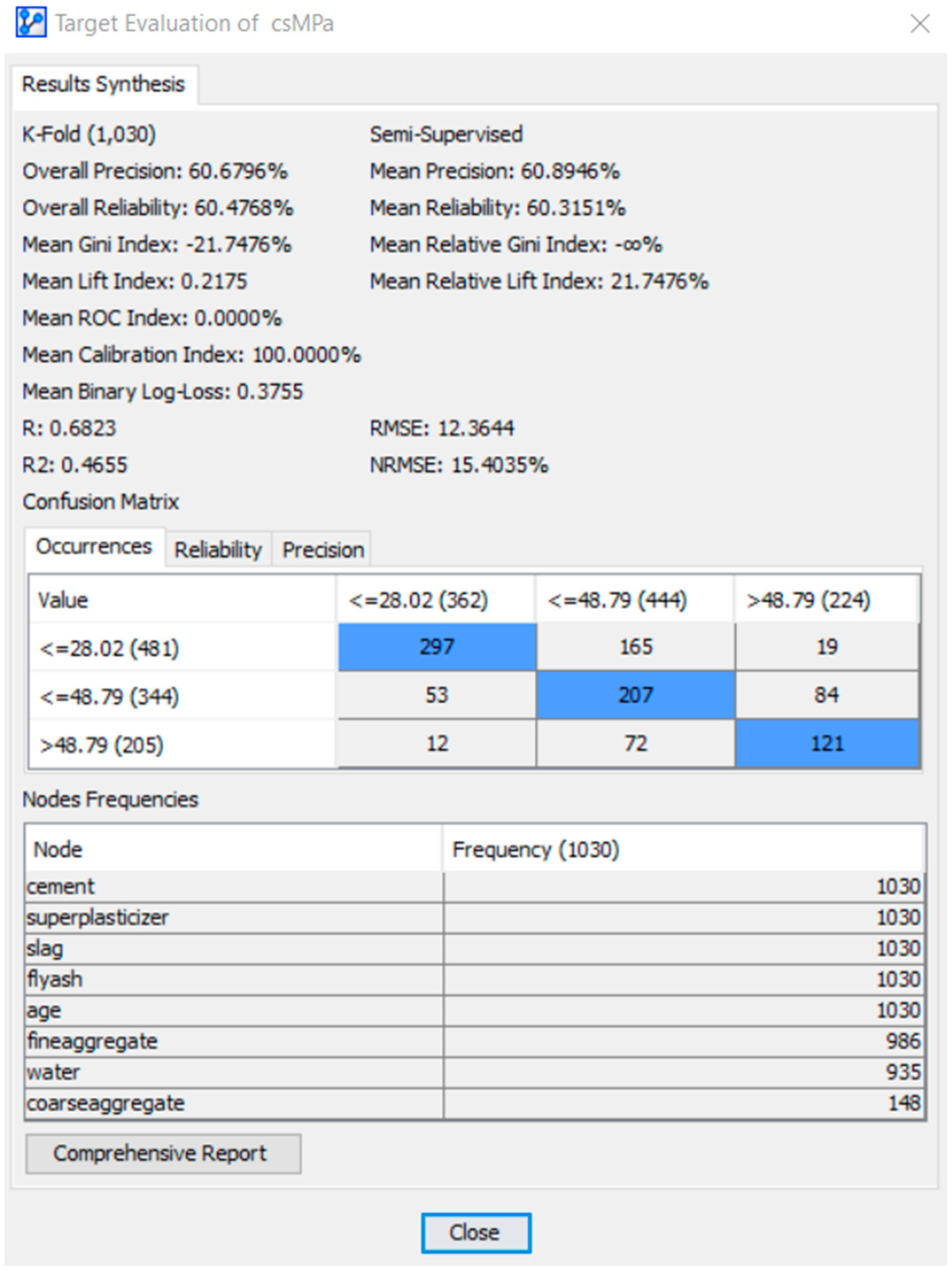
8.2. Target Evaluation Cross-Validation by K-Fold
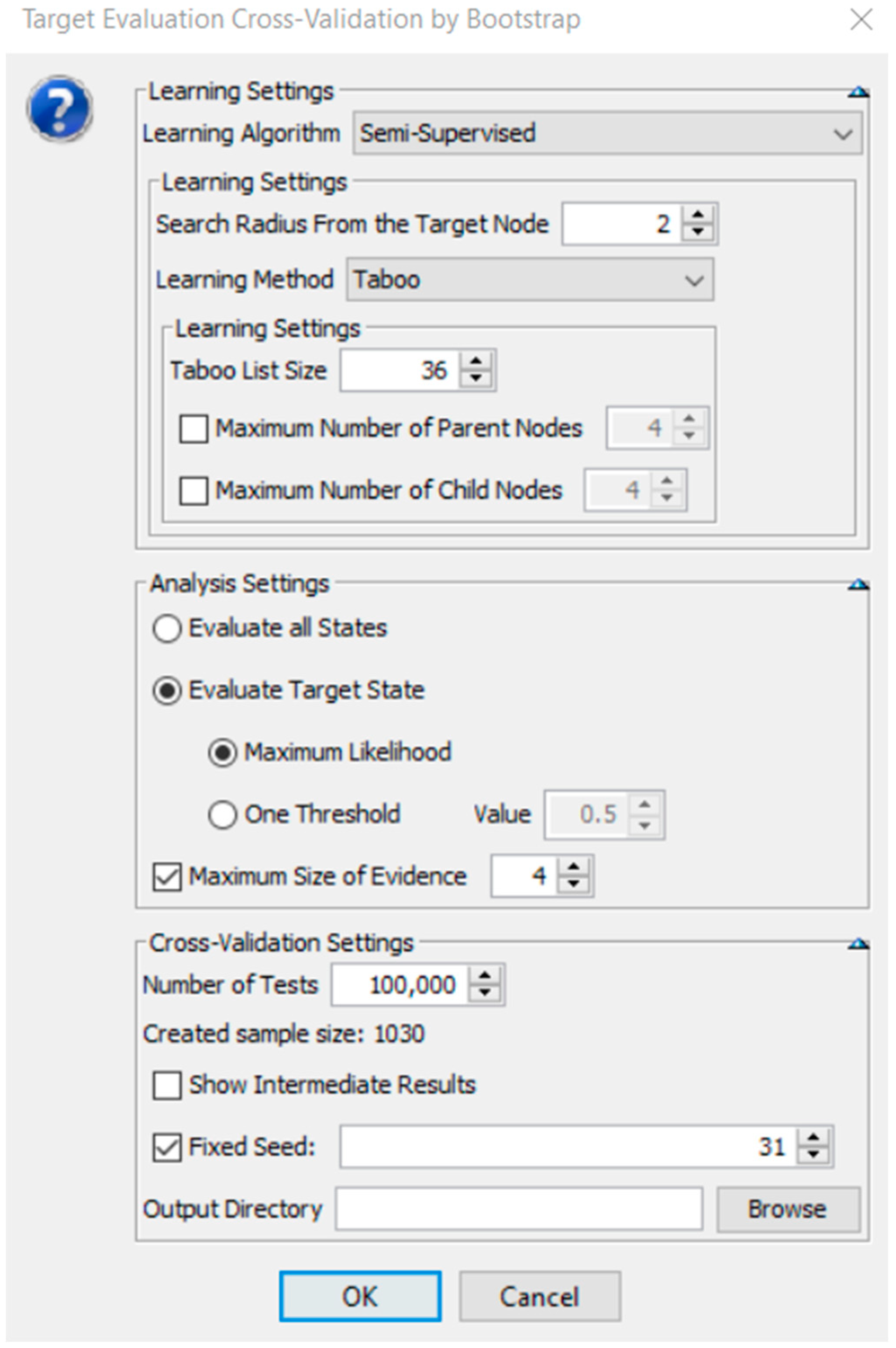
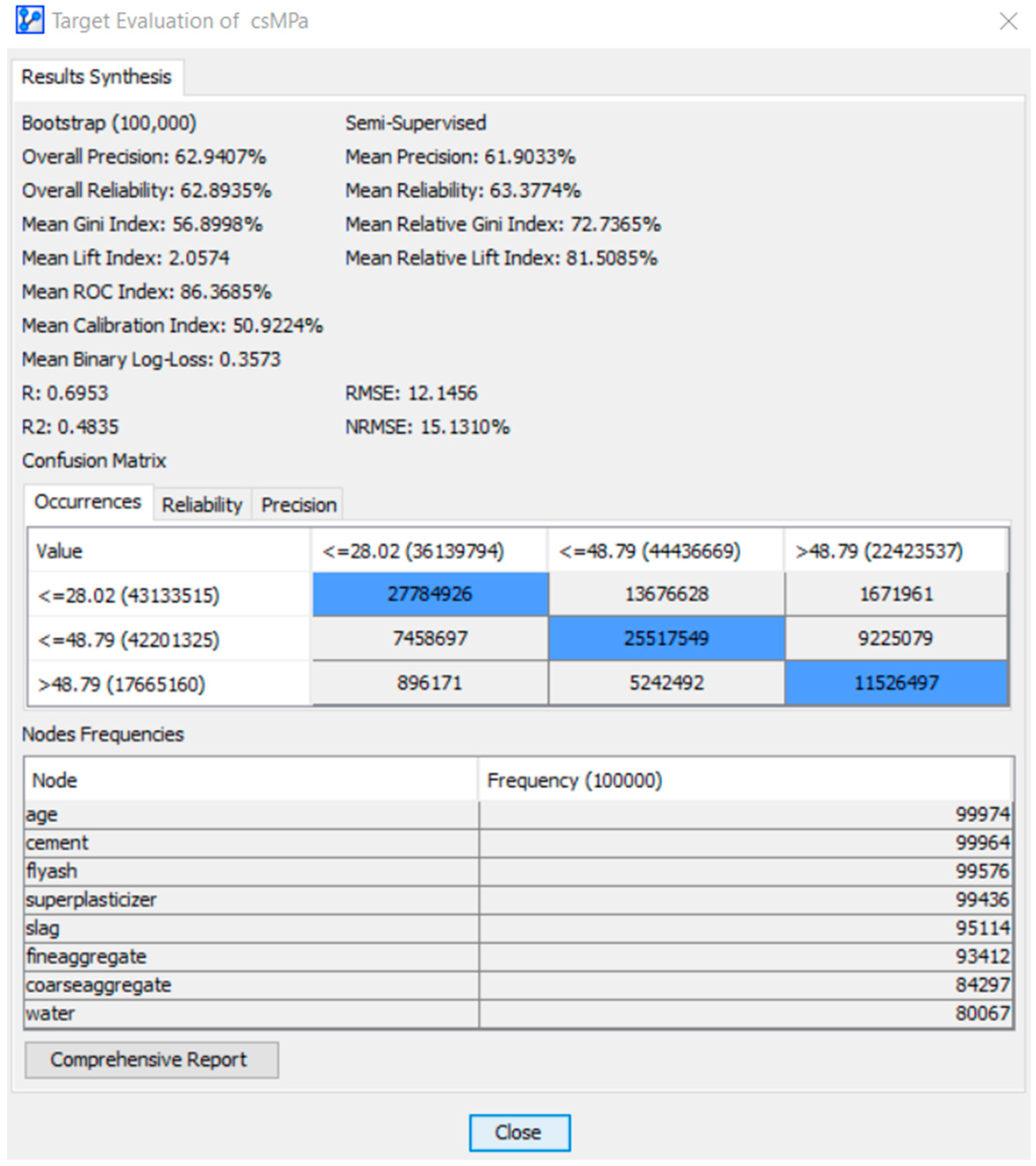
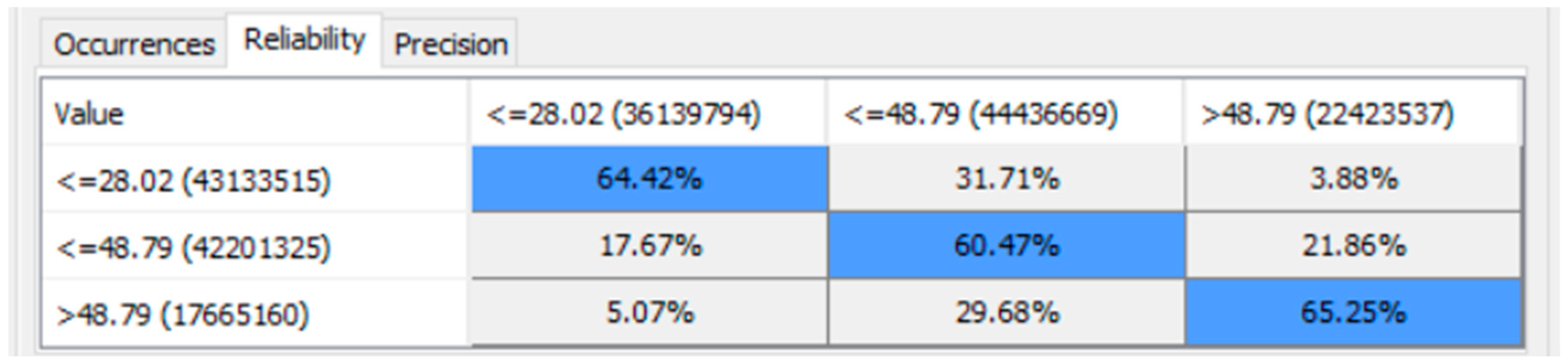
8.3. Statistical Bootstrapping to 100,000 Times for the Data in Each Node of the BN
8.4. Limitations of the Study
9. Discussion and Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zeng, D. From Computational Thinking to AI Thinking. IEEE Intell. Syst. 2013, 28, 2–4. [Google Scholar]
- Gadanidis, G. Artificial intelligence, computational thinking, and mathematics education. Int. J. Inf. Learn. Technol. 2017, 34, 133–139. [Google Scholar] [CrossRef]
- Rad, P.; Roopaei, M.; Beebe, N. AI Thinking for Cloud Education Platform with Personalized Learning. In Proceedings of the 51st Hawaii International Conference on System Sciences, Waikoloa Village, HI, USA, 2–6 January 2018; pp. 3–12. [Google Scholar]
- Beigman Klebanov, B.; Burstein, J.; Harackiewicz, J.M.; Priniski, S.J.; Mulholland, M. Reflective Writing About the Utility Value of Science as a Tool for Increasing STEM Motivation and Retention—Can AI Help Scale Up? Int. J. Artif. Intell. Educ. 2017, 27, 791–818. [Google Scholar] [CrossRef]
- Rosenberg, L. Artificial Swarm Intelligence, a Human-in-the-Loop Approach to A.I. In Proceedings of the the Thirtieth AAAI Conference on Artificial Intelligence (AAAI-16), Phoenix, AZ, USA, 12–19 February 2016; pp. 4381–4382. [Google Scholar]
- Davis, B.; Sumara, D. Complexity and Education: Inquiries into Learning, Teaching, and Research; Routledge: Mahwah, NJ, USA, 2006. [Google Scholar]
- Davis, B. Complexity and Education: Vital simultaneities. Educ. Philos. Theory 2008, 40, 50–65. [Google Scholar] [CrossRef]
- Luckin, R.; Holmes, W.; Griffiths, M.; Forcier, L.B. Intelligence Unleashed. An Argument for AI in Education; Pearson: London, UK, 2016. [Google Scholar]
- Neller, T.W. AI education: Open-access educational resources on AI. AI Matters 2017, 3, 12–13. [Google Scholar] [CrossRef]
- Roll, I.; Wylie, R. Evolution and Revolution in Artificial Intelligence in Education. Int. J. Artif. Intell. Educ. 2016, 26, 582–599. [Google Scholar] [CrossRef]
- Chi, M.T.; Wylie, R. The ICAP framework: Linking cognitive engagement to active learning outcomes. Educ. Psychol. 2014, 49, 219–243. [Google Scholar] [CrossRef]
- Hake, R.R. Interactive-engagement versus traditional methods: A six-thousand-student survey of mechanics test data for introductory physics courses. Am. J. Phys. 1998, 66, 64–74. [Google Scholar] [CrossRef]
- Lee, J.; Davari, H.; Singh, J.; Pandhare, V. Industrial Artificial Intelligence for industry 4.0-based manufacturing systems. Manuf. Lett. 2018, 18, 20–23. [Google Scholar] [CrossRef]
- Hill, P.; Barber, M. Preparing for a Renaissance in Assessment; Pearson: London, UK, 2014. [Google Scholar]
- Correa, M.; Bielza, C.; Pamies-Teixeira, J. Comparison of Bayesian networks and artificial neural networks for quality detection in a machining process. Expert Syst. Appl. 2009, 36, 7270–7279. [Google Scholar] [CrossRef]
- Georgiopoulos, M.; DeMara, R.F.; Gonzalez, A.J.; Annie, S.W.; Mansooreh, M.; Gelenbe, E.; Kysilka, M.; Secretan, J.; Sharma, C.A.; Alnsour, A.J. A Sustainable Model for Integrating Current Topics in Machine Learning Research into the Undergraduate Curriculum. IEEE Trans. Educ. 2009, 52, 503–512. [Google Scholar] [CrossRef]
- Martínez-Tenor, Á.; Cruz-Martín, A.; Fernández-Madrigal, J.-A. Teaching machine learning in robotics interactively: The case of reinforcement learning with Lego® Mindstorms. Interact. Learn. Environ. 2019, 27, 293–306. [Google Scholar] [CrossRef]
- Heys, J. Machine Learning as a Tool to Identify Critical Assignments. Chem. Eng. Educ. 2018, 52, 243–250. [Google Scholar]
- Pearl, J. Causality: Models, Reasoning, and Inference, 2nd ed.; Cambridge University Press: Cambridge, UK, 2010; ISBN 978-0-521-89560-6. [Google Scholar]
- Pearl, J. Causes of Effects and Effects of Causes. Sociol. Methods Res. 2015, 44, 149–164. [Google Scholar] [CrossRef]
- Pearl, J. Fusion, propagation, and structuring in belief networks. Artif. Intell. 1986, 29, 241–288. [Google Scholar] [CrossRef]
- Loveland, D.W. Automated Theorem Proving: A Logical Basis; Elsevier North-Holland, Inc.: New York, NY, USA, 1978; ISBN 0-7204-0499-1. [Google Scholar]
- Moore, R.C. Logic and Representation; Center for the Study of Language (CSLI): Stanford, CA, USA, 1995; Volume 39. [Google Scholar]
- Minsky, M. Steps toward artificial intelligence. Trans. Inst. Radio Eng. 1961, 49, 8–30. [Google Scholar] [CrossRef]
- Domingos, P.; Pazzani, M. On the optimality of the simple Bayesian classifier under zero–one loss. Mach. Learn. 1997, 29, 103–130. [Google Scholar] [CrossRef]
- Hand, D.; You, K. Idiot’s Bayes—Not so stupid after all? Int. Stat. Rev. 2001, 69, 385–398. [Google Scholar]
- Bayes, T. A Letter from the Late Reverend Mr. Thomas Bayes, F.R.S. to John Canton, M.A. and F. R. S. In The Royal Society, Philosophical Transactions (1683–1775); The Royal Society Publishing: London, UK, 1763; Volume 53, pp. 269–271. [Google Scholar]
- van de Schoot, R.; Kaplan, D.; Denissen, J.; Asendorpf, J.B.; Neyer, F.J.; van Aken, M.A.G. A Gentle Introduction to Bayesian Analysis: Applications to Developmental Research. Child Dev. 2014, 85, 842–860. [Google Scholar] [CrossRef]
- Hox, J.; van de Schoot, R.; Matthijsse, S. How few countries will do? Comparative survey analysis from a Bayesian perspective. Surv. Res. Methods 2012, 6, 87–93. [Google Scholar]
- Lee, S.-Y.; Song, X.-Y. Evaluation of the Bayesian and maximum likelihood approaches in analyzing structural equation models with small sample sizes. Multivar. Behav. Res. 2004, 39, 653–686. [Google Scholar] [CrossRef] [PubMed]
- Button, K.S.; Ioannidis, J.P.; Mokrysz, C.; Nosek, B.A.; Flint, J.; Robinson, E.S.; Munafao, M.R. Power failure: Why small sample size undermines the reliability of neuroscience. Nat. Rev. Neurosci. 2013, 14, 365–376. [Google Scholar] [CrossRef] [PubMed]
- Kaplan, D.; Depaoli, S. Bayesian structural equation modeling. In Handbook of Structural Equation Modeling; Hoyle, R., Ed.; Guilford Press: New York, NY, USA, 2012; pp. 650–673. [Google Scholar]
- Walker, L.J.; Gustafson, P.; Frimer, J.A. The application of Bayesian analysis to issues in developmental research. Int. J. Behav. Dev. 2007, 31, 366–373. [Google Scholar] [CrossRef]
- Zhang, Z.; Hamagami, F.; Wang, L.; Grimm, K.J.; Nesselroade, J.R. Bayesian analysis of longitudinal data using growth curve models. Int. J. Behav. Dev. 2007, 31, 374–383. [Google Scholar] [CrossRef]
- Kaplan, D. Causal inference with large-scale assessments in education from a Bayesian perspective: A review and synthesis. Large-Scale Assess. Educ. 2016, 4, 7. [Google Scholar] [CrossRef] [PubMed]
- Levy, R. Advances in Bayesian Modeling in Educational Research. Educ. Psychol. 2016, 51, 368–380. [Google Scholar] [CrossRef]
- Mathys, C. A Bayesian foundation for individual learning under uncertainty. Front. Hum. Neurosci. 2011, 5, 39. [Google Scholar] [CrossRef] [PubMed]
- Muthén, B.; Asparouhov, T. Bayesian structural equation modeling: A more flexible representation of substantive theory. Psychol. Methods 2012, 17, 313–335. [Google Scholar] [CrossRef]
- Bekele, R.; McPherson, M. A Bayesian performance prediction model for mathematics education: A prototypical approach for effective group composition. Br. J. Educ. Technol. 2011, 42, 395–416. [Google Scholar] [CrossRef]
- Millán, E.; Agosta, J.M.; Pérez de la Cruz, J.L. Bayesian student modeling and the problem of parameter specification. Br. J. Educ. Technol. 2002, 32, 171–181. [Google Scholar] [CrossRef]
- Shannon, C.E. The lattice theory of information. Trans. IRE Prof. Group Inf. Theory 1953, 1, 105–107. [Google Scholar] [CrossRef]
- Cowell, R.G.; Dawid, A.P.; Lauritzen, S.L.; Spieglehalter, D.J. Probabilistic Networks and Expert Systems: Exact Computational Methods for Bayesian Networks; Springer: New York, NY, USA, 1999; ISBN 978-0-387-98767-5. [Google Scholar]
- Jensen, F.V. An Introduction to Bayesian Networks; Springer: New York, NY, USA, 1999; ISBN 0-387-91502-8. [Google Scholar]
- Korb, K.B.; Nicholson, A.E. Bayesian Artificial Intelligence; Chapman & Hall/CRC: London, UK, 2010; ISBN 978-1-4398-1591-5. [Google Scholar]
- Tsamardinos, I.; Aliferis, C.F.; Statnikov, A. Time and sample efficient discovery of Markov blankets and direct causal relations. In Proceedings of the Ninth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 24–27 August 2003; p. 673. [Google Scholar]
- Guoyi, C.; Hu, S.; Yang, Y.; Chen, T. Response surface methodology with prediction uncertainty: A multi-objective optimisation approach. Chem. Eng. Res. Des. 2012, 90, 1235–1244. [Google Scholar]
- Fox, R.J.; Elgart, D.; Christopher Davis, S. Bayesian credible intervals for response surface optima. J. Stat. Plan. Inference 2009, 139, 2498–2501. [Google Scholar] [CrossRef]
- Miró-Quesada, G.; Del Castillo, E.; Peterson, J.J. A Bayesian approach for multiple response surface optimization in the presence of noise variables. J. Appl. Stat. 2004, 31, 251–270. [Google Scholar] [CrossRef]
- Myers, R.H.; Montgomery, D.C.; Anderson-Cook, C.M. Response Surface Methodology: Process and Product Optimization Using Designed Experiments, 3rd ed.; Wiley and Sons, Inc.: Somerset, NJ, USA, 2009; ISBN 978-0-470-17446-3. [Google Scholar]
- Yeh, I.-C. Analysis of Strength of Concrete Using Design of Experiments and Neural Networks. J. Mater. Civ. Eng. 2006, 18, 597–604. [Google Scholar] [CrossRef]
- Zheng, B.; Chang, Yu.; Wang, Xi.; Good, W.F. Comparison of artificial neural network and Bayesian belief network in a computer-assisted diagnosis scheme for mammography. In Proceedings of the IJCNN’99. International Joint Conference on Neural Networks, Washington, DC, USA, 10–16 July 1999; Volume 6, pp. 4181–4185. [Google Scholar]
- Yeh, I.-C. Design of High-Performance Concrete Mixture Using Neural Networks and Nonlinear Programming. J. Comput. Civ. Eng. 1999, 13, 36–42. [Google Scholar] [CrossRef]
- Yeh, I. Modeling Concrete Strength with Augment-Neuron Networks. J. Mater. Civ. Eng. 1998, 10, 263–268. [Google Scholar] [CrossRef]
- Yeh, I.-C. Modeling of strength of high-performance concrete using artificial neural networks. Cem. Concr. Res. 1998, 28, 1797–1808. [Google Scholar] [CrossRef]
- Yeh, I.-C. Prediction of strength of fly ash and slag concrete by the use of artificial neural networks. J. Chin. Inst. Civil Hydraul. Eng. 2003, 15, 659–663. [Google Scholar]
- How, M.-L.; Hung, W.L.D. Educational Stakeholders’ Independent Evaluation of an Artificial Intelligence-Enabled Adaptive Learning System Using Bayesian Network Predictive Simulations. Educ. Sci. 2019, 9, 110. [Google Scholar] [CrossRef]
- Conrady, S.; Jouffe, L. Bayesian Networks and BayesiaLab: A Practical Introduction for Researchers; Bayesia: Franklin, TN, USA, 2015; ISBN 0-9965333-0-3. [Google Scholar]
- Bayesia, S.A.S. BayesiaLab: Missing Values Processing. Available online: http://www.bayesia.com/bayesialab-missing-values-processing (accessed on 2 June 2019).
- Bayesia, S.A.S. R2-GenOpt* Algorithm. Available online: https://library.bayesia.com/pages/viewpage.action?pageId=35652439#6c939073de75493e8379c0fff83e1384 (accessed on 19 March 2019).
- Lauritzen, S.L.; Spiegelhalter, D.J. Local computations with probabilities on graphical structures and their application to expert systems. J. R. Stat. Soc. 1988, 50, 157–224. [Google Scholar] [CrossRef]
- Kschischang, F.; Frey, B.; Loeliger, H. Factor graphs and the sum product algorithm. IEEE Trans. Inf. Theory 2001, 47, 498–519. [Google Scholar] [CrossRef]
- Clausius, R. The Mechanical Theory of Heat, with Its Applications to the Steam-Engine and to the Physical Properties of Bodies; John van Voorst: London, UK, 1867. [Google Scholar]
- How, M.-L.; Hung, W.L.D. Harnessing Entropy via Predictive Analytics to Optimize Outcomes in the Pedagogical System: An Artificial Intelligence-Based Bayesian Networks Approach. Educ. Sci. 2019, 9, 158. [Google Scholar] [CrossRef]
- Common Core State Standards for English Language Arts & Literacy in History/Social Studies, Science, and Technical Subjects. Available online: http://www.corestandards.org/ (accessed on 8 July 2019).
- Toner, P. Workforce Skills and Innovation: An Overview of Major Themes in the Literature; OECD Publishing: Paris, France, 2011. [Google Scholar]
- Hmelo-Silver, C.E.; Golan Duncan, R.; Chinn, C.A. Scaffolding and achievement in problem based and inquiry learning: A response to kirschner, sweller, and clark (2006). Educ. Psychol. 2007, 42, 99–107. [Google Scholar] [CrossRef]
- Silapachote, P.; Srisuphab, A. Teaching and learning computational thinking through solving problems in Artificial Intelligence: On designing introductory engineering and computing courses. In Proceedings of the IEEE International Conference on teaching, Assessment, and Learning for Engineering (TALE), Bangkok, Thailand, 7–9 December 2016. [Google Scholar]
- Wing, J.M. Computational thinking. Commun. ACM 2006, 49, 33–35. [Google Scholar] [CrossRef]
- Bayesia, S.A.S. Bayesialab. Available online: https://www.bayesialab.com/ (accessed on 18 March 2019).
- Bayes Fusion LLC. GeNie. Available online: https://www.bayesfusion.com/genie/ (accessed on 18 March 2019).
- Norsys Software Corp. Netica. Available online: https://www.norsys.com/netica.html (accessed on 18 March 2019).
- Bayes Server LLC. Bayes Server. Available online: https://www.bayesserver.com/ (accessed on 18 March 2019).



| Name | Description |
|---|---|
| Cement | input variable: Kg in a m3 mixture |
| Blast Furnace Slag | input variable: Kg in a m3 mixture |
| Fly Ash | input variable: Kg in a m3 mixture |
| Water | input variable: Kg in a m3 mixture |
| Superplasticizer | input variable: Kg in a m3 mixture |
| Coarse Aggregate | input variable: Kg in a m3 mixture |
| Fine Aggregate | input variable: Kg in a m3 mixture |
| Age | input variable: Day (1~365) |
| Concrete compressive strength | Output variable: MPa |
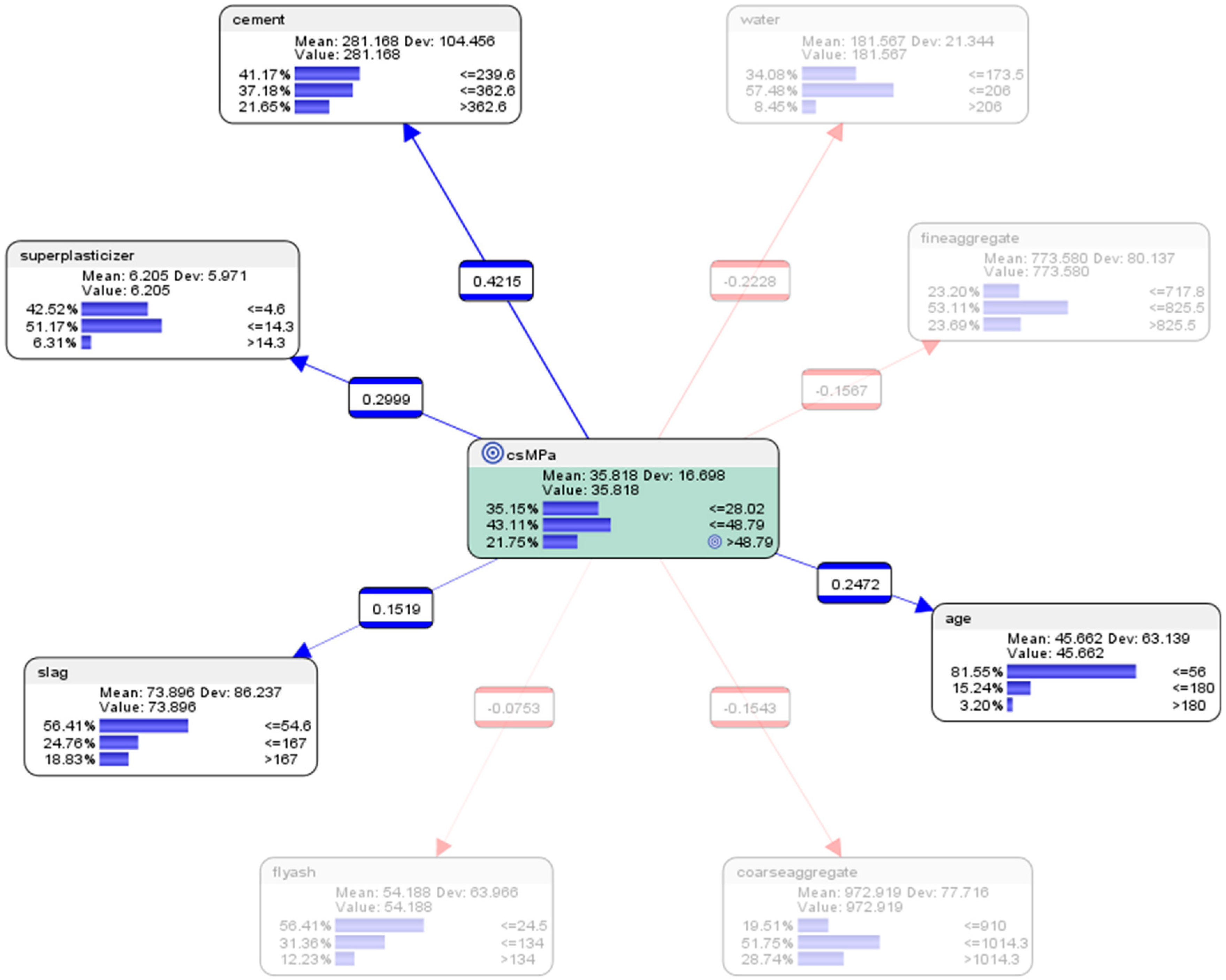
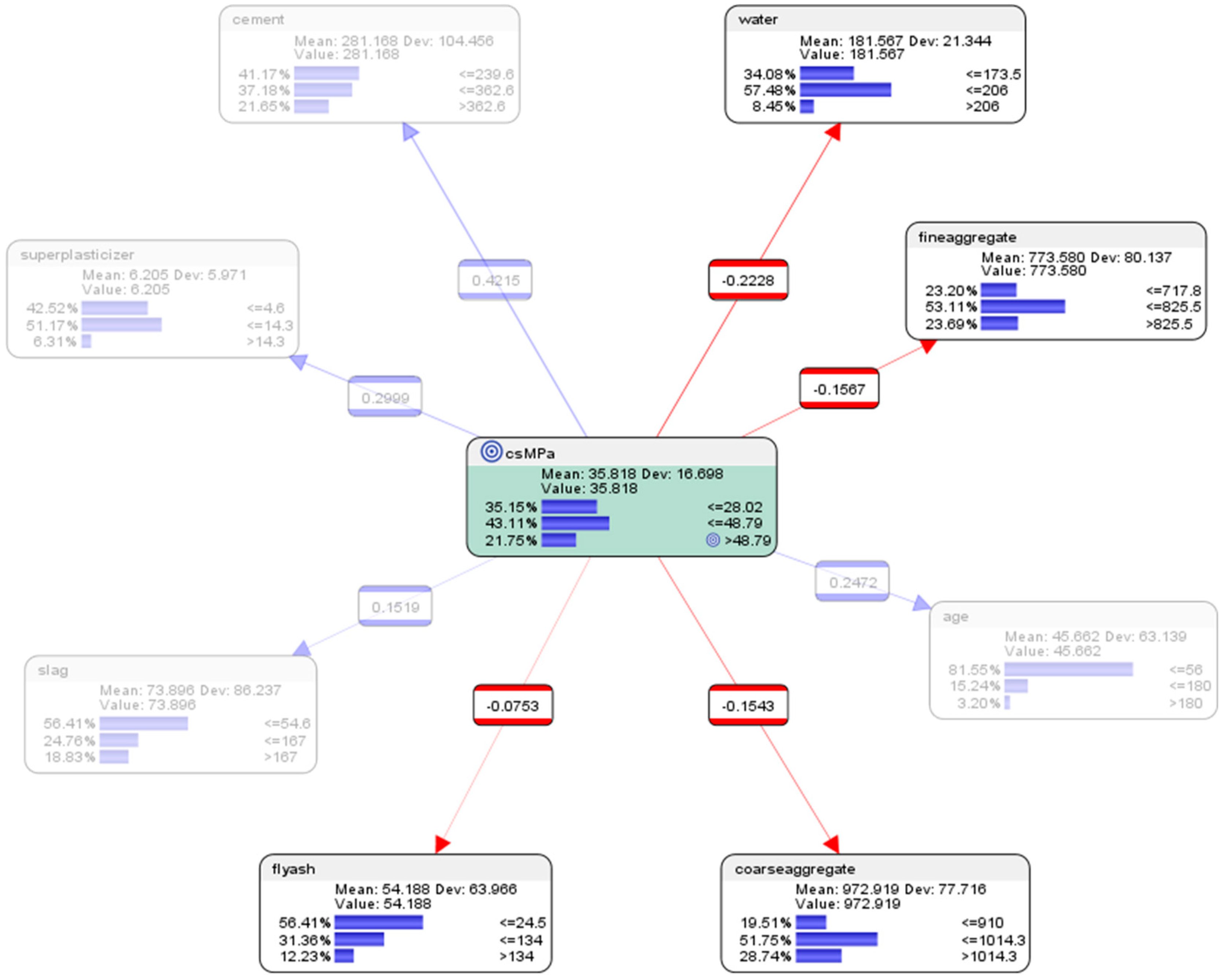
| Parent | Child | KL Divergence | Mutual Information | G-Test | df | p-Value | Pearson’s Correlation |
|---|---|---|---|---|---|---|---|
| csMPa | cement | 0.1359 | 0.1359 | 194.0049 | 4 | 0.0000% | 0.4215 |
| csMPa | water | 0.1125 | 0.1125 | 160.6493 | 4 | 0.0000% | −0.2228 |
| csMPa | age | 0.0891 | 0.0891 | 127.2237 | 4 | 0.0000% | 0.2472 |
| csMPa | superplasticizer | 0.0689 | 0.0689 | 98.3567 | 4 | 0.0000% | 0.2999 |
| csMPa | fineaggregate | 0.0260 | 0.0260 | 37.1368 | 4 | 0.0000% | −0.1567 |
| csMPa | coarseaggregate | 0.0208 | 0.0208 | 29.6499 | 4 | 0.0006% | −0.1543 |
| csMPa | slag | 0.0206 | 0.0206 | 29.3990 | 4 | 0.0006% | 0.1519 |
| csMPa | flyash | 0.0186 | 0.0186 | 26.5392 | 4 | 0.0025% | −0.0753 |
| Parent | Child | KL Divergence | Mutual Information | G-Test | df | p-Value | Pearson’s Correlation |
|---|---|---|---|---|---|---|---|
| flyash | superplasticizer | 0.4372 | 0.3004 | 428.9930 | 4 | 0.0000% | 0.4042 |
| fineaggregate | coarseaggregate | 0.3303 | 0.1275 | 193.7040 | 4 | 0.0000% | −0.1800 |
| cement | fineaggregate | 0.3037 | 0.0255 | 53.7375 | 4 | 0.0000% | −0.0895 |
| water | fineaggregate | 0.2930 | 0.1155 | 198.8320 | 4 | 0.0000% | −0.3460 |
| slag | fineaggregate | 0.2792 | 0.0450 | 72.3311 | 4 | 0.0000% | −0.2091 |
| superplasticizer | water | 0.2514 | 0.2254 | 356.7480 | 4 | 0.0000% | −0.4920 |
| slag | coarseaggregate | 0.2434 | 0.0825 | 129.5773 | 4 | 0.0000% | −0.2844 |
| flyash | slag | 0.2238 | 0.1289 | 183.9886 | 4 | 0.0000% | −0.3398 |
| cement | csMPa | 0.2226 | 0.1359 | 194.0049 | 4 | 0.0000% | 0.4215 |
| slag | superplasticizer | 0.2187 | 0.0338 | 48.3312 | 4 | 0.0000% | 0.0865 |
| superplasticizer | coarseaggregate | 0.2086 | 0.0891 | 106.7541 | 4 | 0.0000% | −0.2981 |
| cement | superplasticizer | 0.1989 | 0.0739 | 105.5544 | 4 | 0.0000% | 0.0845 |
| csMPa | age | 0.1464 | 0.1160 | 127.2237 | 4 | 0.0000% | 0.2945 |
| cement | slag | 0.1304 | 0.0355 | 50.6310 | 4 | 0.0000% | −0.2011 |
| superplasticizer | age | 0.1240 | 0.0936 | 81.2284 | 4 | 0.0000% | −0.2837 |
| cement | flyash | 0.1158 | 0.1158 | 165.4023 | 4 | 0.0000% | −0.3502 |
| slag | csMPa | 0.1073 | 0.0206 | 29.3990 | 4 | 0.0006% | 0.1519 |
| csMPa | water | 0.1041 | 0.0781 | 160.6493 | 4 | 0.0000% | −0.1156 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
How, M.-L.; Hung, W.L.D. Educing AI-Thinking in Science, Technology, Engineering, Arts, and Mathematics (STEAM) Education. Educ. Sci. 2019, 9, 184. https://doi.org/10.3390/educsci9030184
How M-L, Hung WLD. Educing AI-Thinking in Science, Technology, Engineering, Arts, and Mathematics (STEAM) Education. Education Sciences. 2019; 9(3):184. https://doi.org/10.3390/educsci9030184
Chicago/Turabian StyleHow, Meng-Leong, and Wei Loong David Hung. 2019. "Educing AI-Thinking in Science, Technology, Engineering, Arts, and Mathematics (STEAM) Education" Education Sciences 9, no. 3: 184. https://doi.org/10.3390/educsci9030184
APA StyleHow, M.-L., & Hung, W. L. D. (2019). Educing AI-Thinking in Science, Technology, Engineering, Arts, and Mathematics (STEAM) Education. Education Sciences, 9(3), 184. https://doi.org/10.3390/educsci9030184





