Pre-Service Teachers’ Knowledge of Relational Structure of Physics Concepts: Finding Key Concepts of Electricity and Magnetism
Abstract
1. Introduction
- Which concepts and conceptual elements have high connectivity, and of which type?
- How do the concepts with high connectivity of distinct types differ in their content?
- How does individual students’ knowledge relate to group-level knowledge?
2. Relational Knowledge and its Cartography: A Network View
2.1. Relational Knowledge
2.2. Relational Knowledge as Networked Lexicon
2.3. Cartography of Networked Lexicons
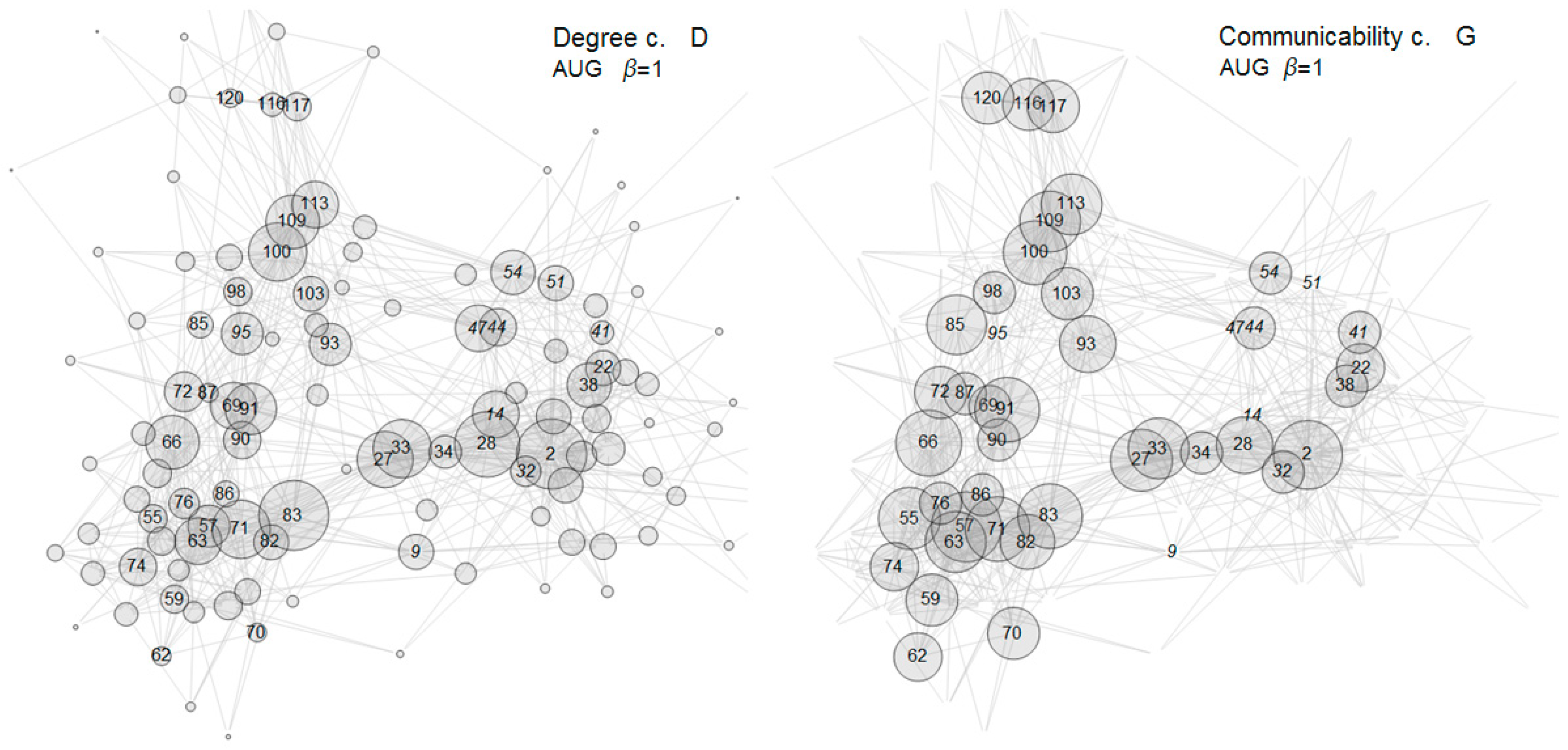
- Local connectivity. Local connectivity of a node is simply the strength of all its connections to neighbouring nodes, thus providing the local epistemic support for the node. If the node has many well-substantiated connections, the epistemic support of the node is strong. Local connectivity is operationalized as Degree centrality, D (see Appendix A).
- Local cohesion. Local cohesion of a node is related to the number of neighbours of the node that are also connected. Such triadically connected patterns are mutually supporting and give rise to cyclic structures. Of these, the triadic cycle is of special interest, since it connects the closest neighbours transitively and confers strong local coherence of the system. Local cohesion is operationalized as the Local Clustering coefficient, C (see Appendix A).
- Global contiguity. Global contiguity is related to global connectivity and the availability of long paths connecting two distantly separated knowledge elements in the network. Such long contiguous paths are pathways to transmit supporting information, needed in substantiating knowledge elements not only within the local neighbourhood but also in the network as whole. Global contiguity is operationalized here as Communicability Centrality, G (see Appendix A). Communicability Centrality is directly related to knowledge elements’ role in mediating between the other elements in the system. High global contiguity obviously also implies high global cohesion, in the sense that distant elements are nevertheless interconnected. Therefore, we do not need a separate measure for global cohesion.
3. Empirical Sample, Its Preparation, and Method of Analysis
3.1. Content Analysis
- Level of using ontologically correct properties for nodes;
- Level of factually correct statements.
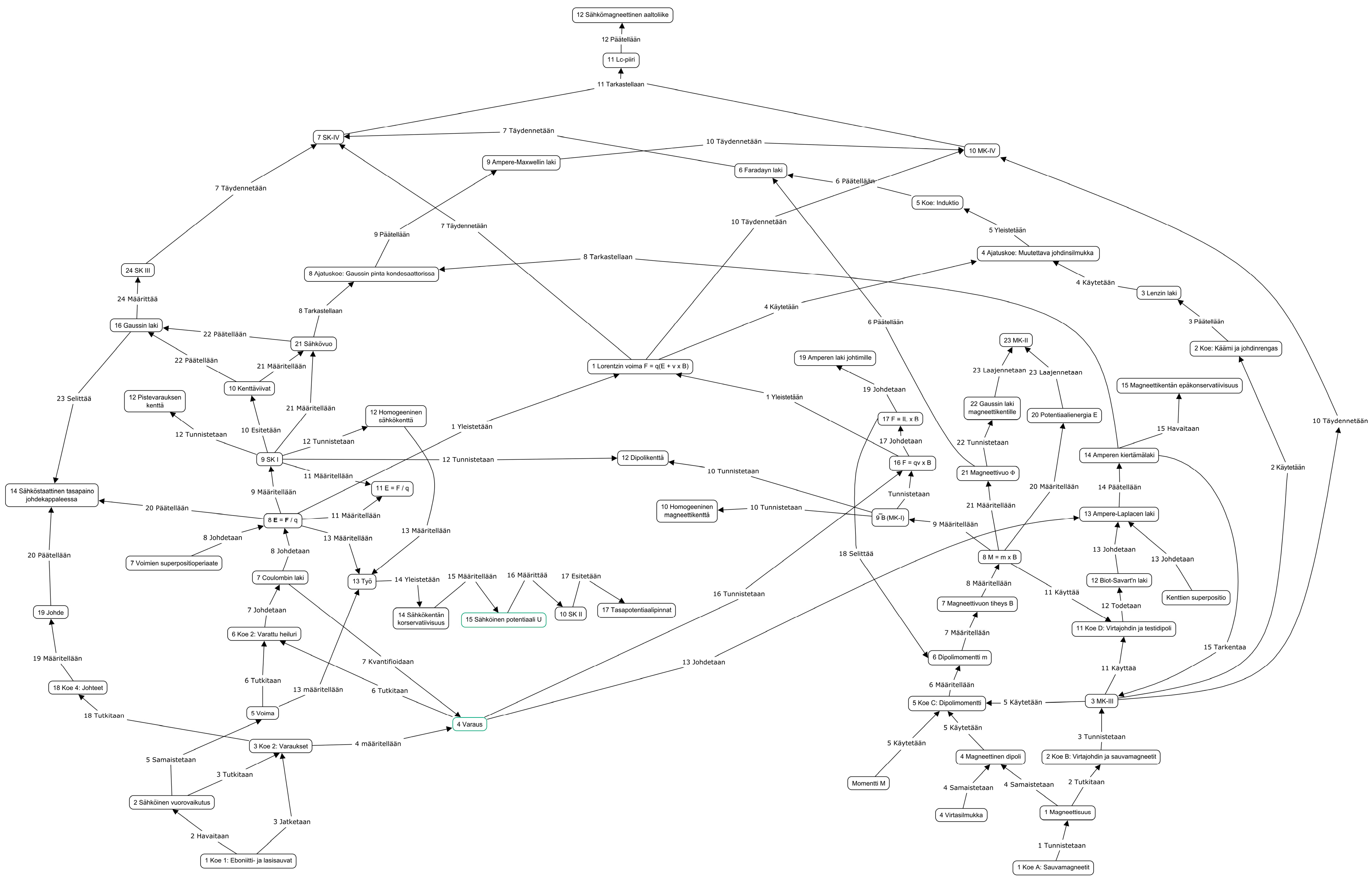
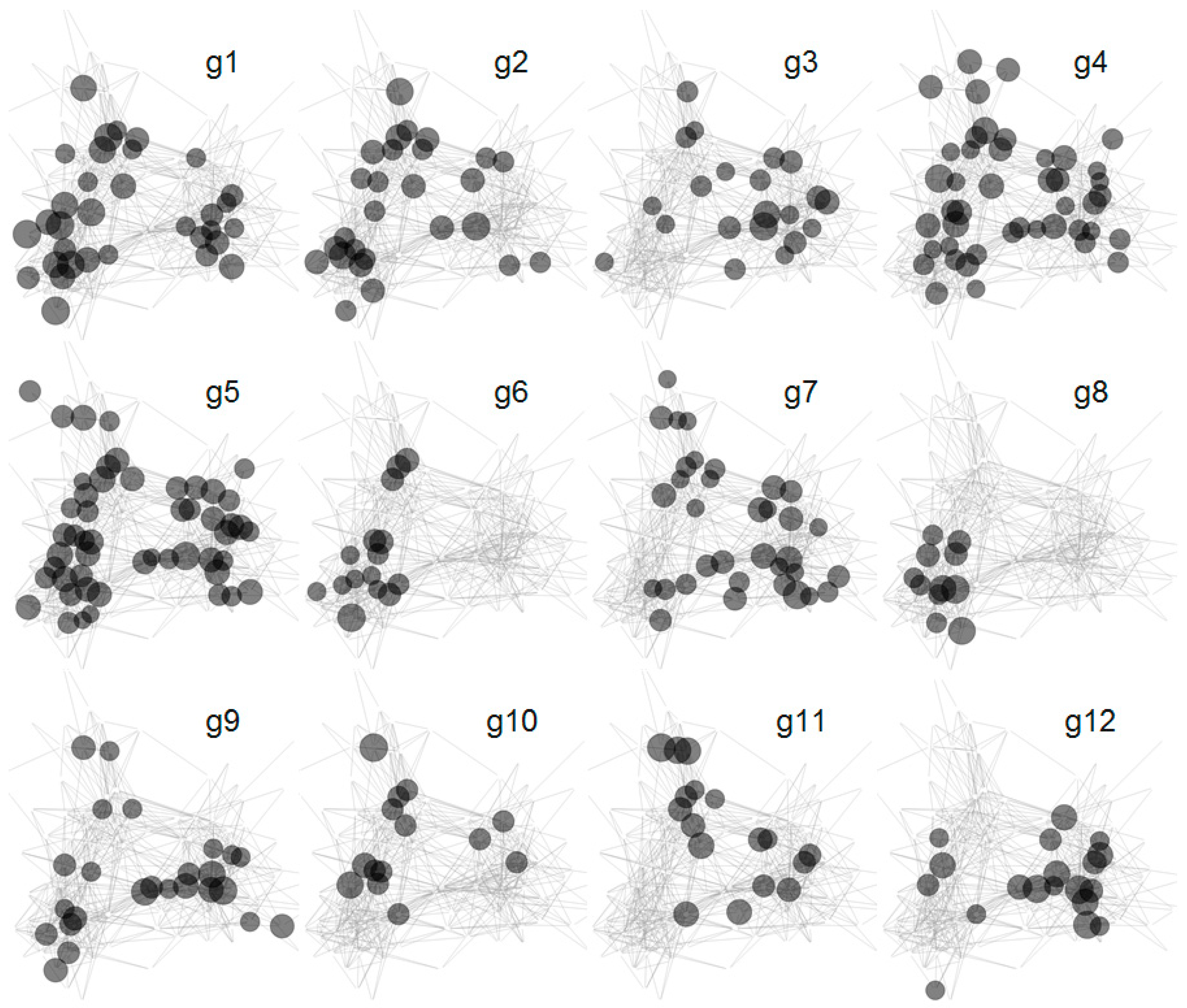
3.2. Construction of Collated Networks for Cartography
- Collated, authentic network (COL-A): contains all the substantiated nodes, found from students’ concept networks, as weighted connections. The weights are related to the epistemic analysis of the nodes and ignore partially substantiated connections. This network contains 692 different links.
- Collated, optimized network (COL-O): is otherwise similar to COL-A but all links are taken as fully substantiated.
- Augmented network (AUG): contains all connections found in the 12 individual networks and some additional connections, which three experts (one professor and two university lecturers) evaluated as possible connections and for which they could provide proper substantiations. The augmented network contains 787 links and can be taken to represent experts’ knowledge, because three experts refined it to the extent that they deemed to provide an adequate representation of the topic.
4. Results
4.1. Finding Key Concepts from Relational Structure
- Nodes which rank high in D are also often high-ranking in G, but clear differences emerge.
- Nodes which rank high in D and G are different from nodes which rank high in C.
4.2. Content of Key Concepts
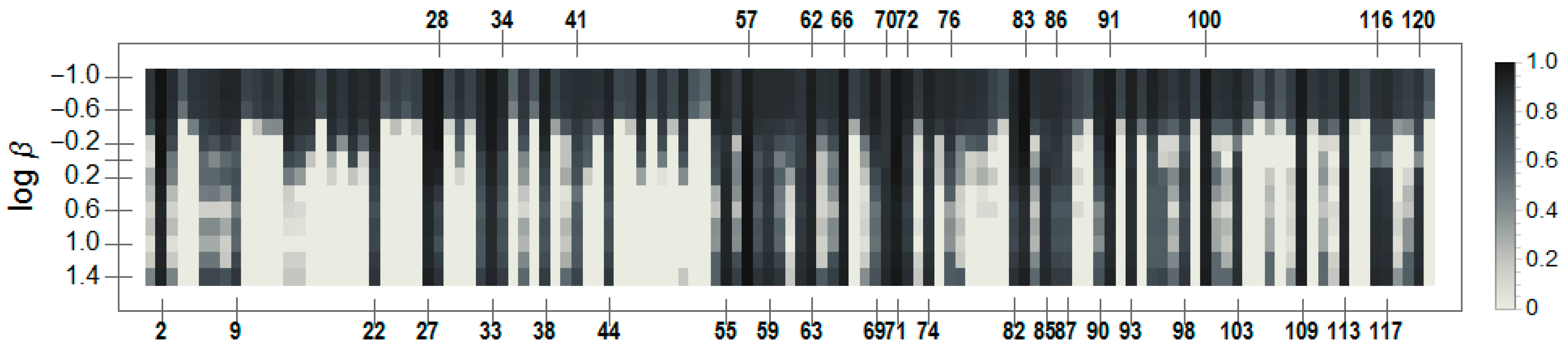
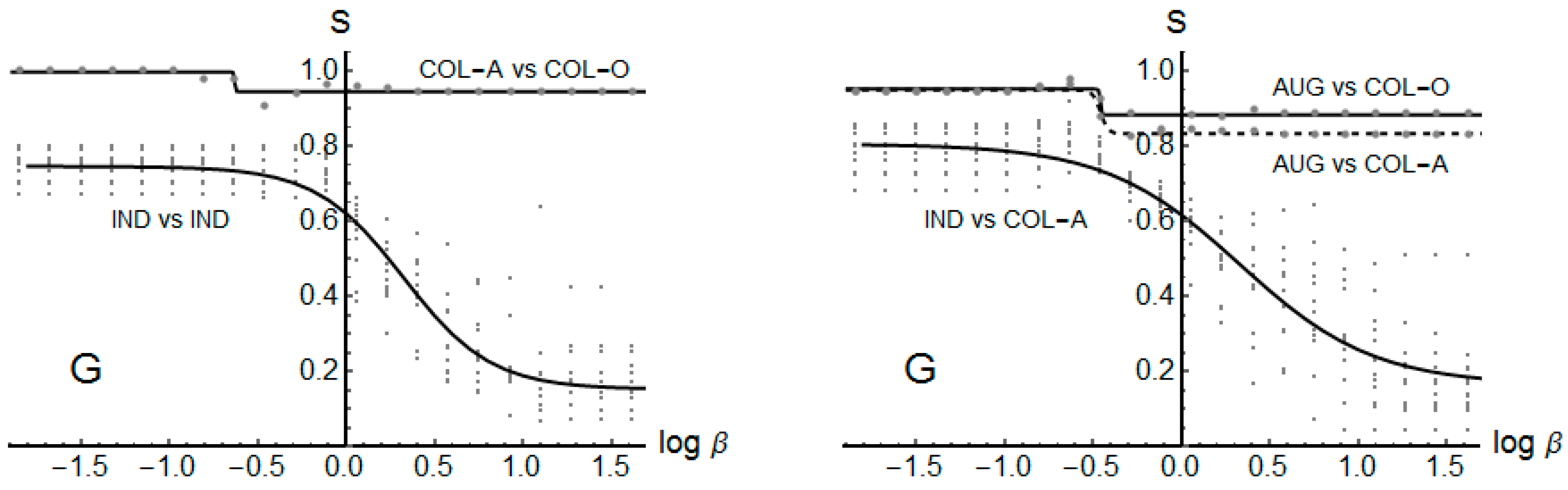
4.3. Similarity Comparisons
5. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A: Mathematical Models of Analysis
A1. The Centralities
| Observable | Operationalized Property | Mathematical Definition | |
|---|---|---|---|
| D | Degree centrality | Local connectivity in terms of number links attached to a node. | |
| C | Clustering coefficient | Local cohesion as relative number of triadic transitive connections of the node. | |
| G | Communicability centrality | Global contiguity as number of paths of a node to all other nodes to which it is contiguously connected. |
A2. Reliability Analysis
A3. Similarity Analysis
Appendix B: Design principles of concept networks
- Concepts: Named concepts, terms, or quantities.
- Laws: Relations between concepts, terms, or quantities.
- Models: Context-specific explanatory constructs.
- Experiments: Descriptions of experiments or demonstrations.
References
- Bransford, J.D.; Brown, A.L.; Crocking, R.R. How experts differ from novices. In How People Learn: Brain, Mind, Experience, and School, Chapter 2, Expanded ed.; National Academy Press: Washington, DC, USA, 2000. [Google Scholar]
- Schwendimann, B.A. Making Sense of Knowledge Integration Maps. In Digital Knowledge Maps in Education: Technology-Enhanced Support for Teachers and Learners; Ifenthaler, D., Hanewald, R., Eds.; Springer: New York, NY, USA, 2014; pp. 17–40. [Google Scholar]
- Schvaneveldt, R.W.; Durso, F.T.; Dearholt, D.W. Network structures in proximity data. In The Psychology of Learning and Otivation: Advances in Research and Theory; Bower, G., Ed.; Academic Press: New York, NY, USA, 1989. [Google Scholar]
- Schvaneveldt, R.W. Pathfinder Associative Networks: Studies in Knowledge Organization; Ablex Publishing: Westport, CT, USA, 1990. [Google Scholar]
- Guerrero-Bote, V.P.; Zapico-Alonso, F.; Espinosa-Calvo, M.E.; Gómez Crisóstomo, R.; Moya-Anegón, F. Binary Pathfinder: An improvement to the Pathfinder algorithm. Inf. Process. Manag. 2006, 42, 1484–1490. [Google Scholar] [CrossRef]
- Clariana, R.B. Deriving Individual and Group Knowledge Structure from Network Diagrams and from Essays. In Digital Knowledge Maps in Education: Technology-Enhanced Support for Teachers and Learners; Ifenthaler, D., Hanewald, R., Eds.; Springer: New York, NY, USA, 2014; pp. 117–130. [Google Scholar]
- Derman, A.; Eilks, I. Using a word association test for the assessment of high school students’ cognitive. structures on dissolution. Chem. Educ. Res. Pract. 2016, 17, 902–913. [Google Scholar] [CrossRef]
- Nicoll, G.; Fransisco, J.; Nakhleh, M. A three-tier system for assessing concept map links: A methodological study. Int. J. Sci. Educ. 2001, 23, 863–875. [Google Scholar] [CrossRef]
- İngeç, Ş.K. Analysing Concept Maps as an Assessment Tool in Teaching Physics and Comparison with the Achievement Tests. Int. J. Sci. Educ. 2009, 31, 1897–1915. [Google Scholar] [CrossRef]
- Yin, Y.; Vanides, J.; Ruiz-Primo, M.; Ayala, C.C.; Shavelson, R.J. Comparison of two concept-mapping techniques: Implications for scoring, interpretation, and use. J. Res. Sci. Teach. 2005, 42, 166–184. [Google Scholar] [CrossRef]
- Ruiz-Primo, M.; Shavelson, R.J. Problems and issues in the use of concept maps in science assessment. J. Res. Sci. Teach. 1996, 33, 569–600. [Google Scholar] [CrossRef]
- Savelsbergh, E.R.; Jong, T.; Ferguson-Hessler, M.G.M. Choosing the right solution approach: The crucial role of situational knowledge in electricity and magnetism. Phys. Rev. Spec. Top. Phys. Educ. Res. 2011, 7, 010103. [Google Scholar] [CrossRef]
- Blown, E.; Bryce, T.G.K. Conceptual Coherence Revealed in Multi-Modal Representations of Astronomy Knowledge. Int. J. Sci. Educ. 2010, 32, 31–67. [Google Scholar] [CrossRef]
- Gómez, E.J.; Benarroch, A.; Marín, N. Evaluation of the degree of coherence found in students’ conceptions concerning the particulate nature of matter. J. Res. Sci. Teach. 2006, 43, 577–598. [Google Scholar] [CrossRef]
- Savelsbergh, E.R.; Jong, T.; Ferguson-Hessler, M. Situational knowledge in physics: The case of electrodynamics. J. Res. Sci. Teach. 2002, 39, 928–951. [Google Scholar] [CrossRef]
- Nousiainen, M. Coherence of pre-service physics teachers’ views of the relatedness of physics concepts. Sci. Educ. 2013, 22, 505–525. [Google Scholar] [CrossRef]
- Koponen, I.T.; Nousiainen, M. Pre-service physics teachers’ understanding of the relational structure of physics concepts: Organising subject contents for purposes of teaching. Int. J. Sci. Math. Educ. 2013, 11, 325–357. [Google Scholar] [CrossRef]
- Koponen, I.T.; Nousiainen, M. Concept networks in learning: Finding key concepts in learners’ representations of the interlinked structure of scientific knowledge. J. Complex Netw. 2014, 2, 187–202. [Google Scholar] [CrossRef]
- Lachner, A.; Nückles, M. Bothered by abstractness or engaged by cohesion? Experts’ explanations enhance novices’ deep-learning. J. Exp. Psychol. Appl. 2015, 21, 101–115. [Google Scholar] [CrossRef] [PubMed]
- Lachner, A.; Gurlitt, J.; Nückles, M. A Graph-Oriented Approach to Measuring Expertise- Detecting Structural Differences between Experts and Intermediates. In Proceedings of the Annual Meeting of the Cognitive Science Society 2012, Sapporo, Japan, 1–4 August 2012; Miyake, N., Peebles, D., Cooper, R.P., Eds.; Curran Associates: New York, NY, USA, 2012; pp. 653–658. [Google Scholar]
- Lachner, A.; Nückles, M. Tell me why! Content knowledge predicts process-orientation of math researchers’ and math teachers’ explanations. Instr. Sci. 2016, 44, 221–242. [Google Scholar] [CrossRef]
- Lachner, A.; Jarodzka, H.; Nückles, M. What makes an expert teacher? Investigating teachers’ professional vision and discourse abilities. Instr. Sci. 2016, 44, 197–203. [Google Scholar] [CrossRef]
- Koponen, I.T.; Pehkonen, M. Coherent Knowledge Structures of Physics Represented as Concept Networks in Teacher Education. Sci. Educ. 2010, 19, 259–282. [Google Scholar] [CrossRef]
- Koponen, I.T.; Nousiainen, M. Modelling students’ knowledge organisation: Genealogical conceptual networks. Phys. A Stat. Mech. Appl. 2018, 495, 405–417. [Google Scholar] [CrossRef]
- Goldwater, M.B.; Schalk, L. Relational categories as a bridge between cognitive and educational research. Psychol. Bull. 2016, 142, 729–757. [Google Scholar] [CrossRef]
- Halford, G.S.; Wilson, W.H.; Phillips, S. Relational knowledge: The foundation of higher cognition. Trends Cogn. Sci. 2010, 14, 497–505. [Google Scholar] [CrossRef]
- Goldwater, M.B.; Markman, A.B.; Stilwell, C.H. The empirical case for role-governed categories. Cognition 2011, 118, 359–376. [Google Scholar] [CrossRef] [PubMed]
- Doumas, L.A.A.; Hummel, J.E.; Sandhofer, C.M. A theory of the discovery and predication of relational concepts. Psychol. Rev. 2008, 115, 1–43. [Google Scholar] [CrossRef] [PubMed]
- Hoyningen-Huene, P. Systematicity: The Nature of Science; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Rescher, N. Cognitive Systematization: A Systems-Theoretic Approach to a Coherentist Theory of Knowledge; Rowman & Littlefield: Totowa, NJ, USA, 1979. [Google Scholar]
- Rescher, N. Methodological Pragmatism: A Systems-Theoretic Approach to the Theory of Knowledge; Blackwell: Bristol, UK, 1977. [Google Scholar]
- Chi, M.T.H.; Ohlsson, S. Complex Declarative Learning. In Cambridge Handbook of Thinking and Reasoning; Holyoak, K.J., Morrison, R.G., Eds.; Cambridge University Press: New York, NY, USA, 2005. [Google Scholar]
- Kuhn, T.S. The Road since Structure; University of Chicago Press: Chicago, IL, USA, 2000. [Google Scholar]
- Vitevitch, M.S.; Castro, N. Using network science in the language sciences and clinic. Int. J. Speech-Lang. Pathol. 2015, 17, 13–25. [Google Scholar] [CrossRef] [PubMed]
- Stella, M.; Beckage, N.M.; Brede, M. Multiplex lexical networks reveal patterns in early word acquisition in children. Sci. Rep. 2017, 7, 46730. [Google Scholar] [CrossRef] [PubMed]
- Börner, K. Atlas of Knowledge: Anyone Can Map; MIT Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Börner, K.; Klavans, R.; Patek, M.; Zoss, A.M.; Biberstine, J.R.; Light, R.P.; Larivière, V.; Boyack, K.W. Design and Update of a Classification System: The UCSD Map of Science. PLoS ONE 2012, 7, e39464. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Chen, Y.; Horowitz, M.; Hou, H.; Liu, Z.; Pellegrino, D. Towards an explanatory and computational theory of scientific discovery. J. Informetr. 2009, 3, 191–209. [Google Scholar] [CrossRef]
- Costa, L.; Rodrigues, F.A.; Travieso, G.; Villas Boas, P.R. Characterization of complex networks: A survey of measurements. Adv. Phys. 2007, 56, 167–242. [Google Scholar] [CrossRef]
- Estrada, E. The Structure of Complex Networks: Theory and Applications; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Zweig, K.A. Network Analysis Literacy: A Practical Approach to the Analysis of Networks; Springer: Wien, Austria, 2016. [Google Scholar]
- Larson, J.R. In Search of Synergy in Small Group Performance; Psychology Press: New York, NY, USA, 2010. [Google Scholar]
- Majidi, S. A comparison between the organization of knowledge of university physics teachers and the textbooks they use: Biot-Savart law and Ampére’s law. J. Sci. Math. Educ. 2013, 12, 1281–1314. [Google Scholar] [CrossRef]
- Majidi, S.; Mäntylä, T. Knowledge Organization in Physics Textbooks: A Case Study of Magnetostatics. J. Balt. Sci. Educ. 2011, 10, 285–299. [Google Scholar]
- McClure, J.R.; Sonak, B.; Suen, H.K. Concept map assessment of classroom learning: Reliability, validity, and logistical practicality. J. Res. Sci. Teach. 1999, 36, 475–492. [Google Scholar] [CrossRef]
- Kinchin, I.M.; De-Leij, F.; Hay, D.B. The evolution of a collaborative concept mapping activity for undergraduate microbiology students. J. Furth. High. Educ. 2005, 29, 1–14. [Google Scholar] [CrossRef]
- Kinchin, I.M.; Hay, D.B.; Adams, A. How a qualitative approach to concept map analysis can be used to aid learning by illustrating patterns of conceptual development. Educ. Res. 2000, 42, 43–57. [Google Scholar] [CrossRef]
- Turnbull, L.; Hütt, M.; Ioannides, A.A.; Kininmonth, S.; Poeppl, R.; Tockner, K.; Bracken, L.J.; Keesstra, S.; Liu, L.; Masselink, R.; et al. Connectivity and complex systems: Learning from a multi-disciplinary perspective. Appl. Netw. Sci. 2018, 3, 11. [Google Scholar] [CrossRef]
- Krauss, S.; Brunner, M.; Kunter, M.; Baumert, J.; Blum, W.; Neubrand, M.; Jordan, A. Pedagogical content knowledge and content knowledge of secondary mathematics teachers. J. Educ. Psychol. 2008, 100, 716–725. [Google Scholar] [CrossRef]
- Hinds, P.J.; Patterson, M.; Pfeffer, J. Bothered by abstraction: The effect of expertise on knowledge transfer and subsequent novice performance. J. Appl. Psychol. 2001, 86, 1232–1243. [Google Scholar] [CrossRef] [PubMed]
- Kolaczyk, E.D. Statistical Analysis of Network Data; Springer: New York, NY, USA, 2009. [Google Scholar]
- Csardi, G.; Nepusz, T. The Igraph software package for complex network research. Interj. Complex Syst. 2006, 1695, 1–9. [Google Scholar]

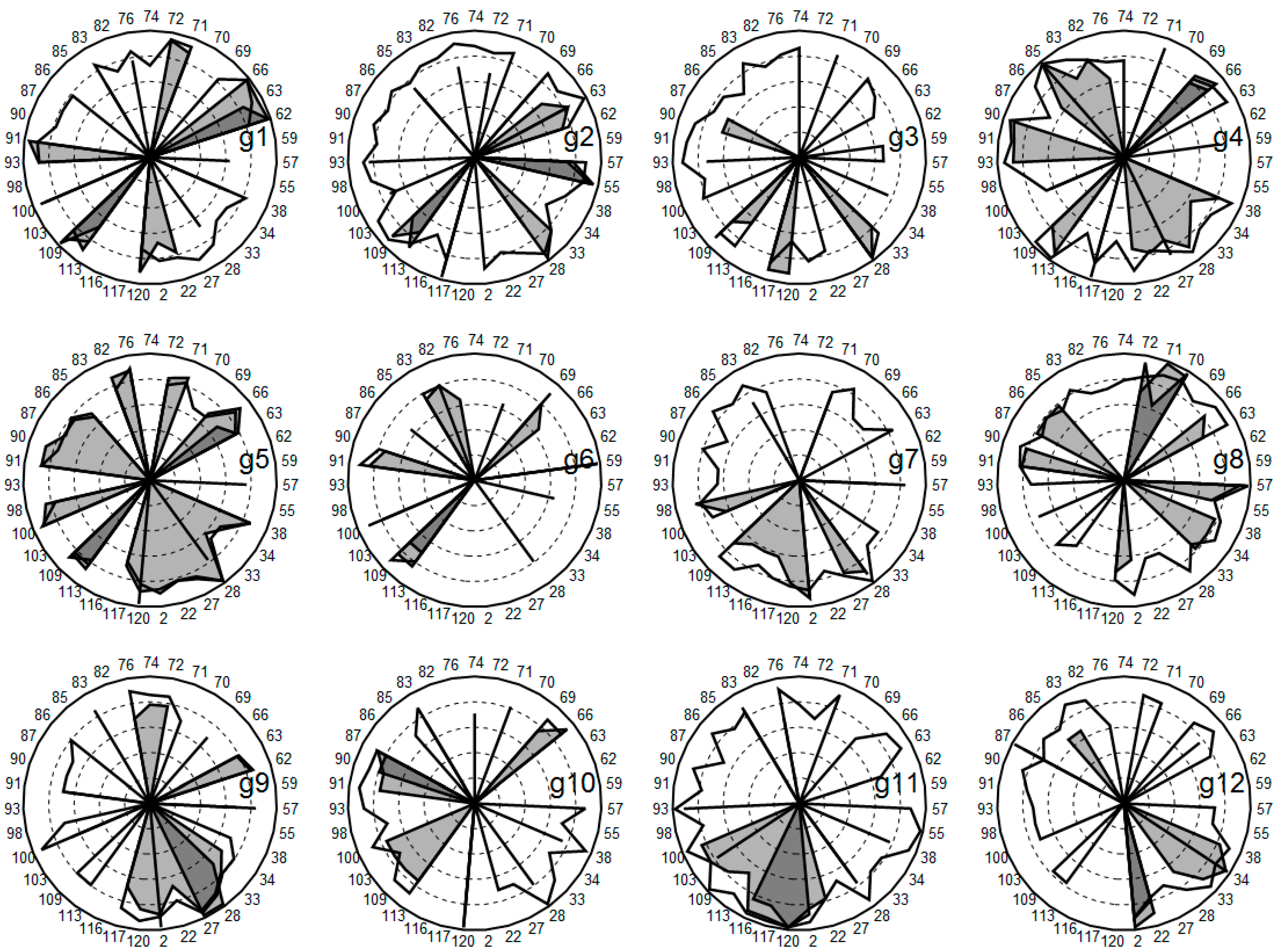
| Node | Description | Node | Description |
|---|---|---|---|
| 2 | Electric charge Q | 70 | Magnetic interaction M = m × B |
| 9 | Superposition of forces (p) | 71 | Magnetic flux density (e) |
| 14 | Electric flux density D (in vacuum) | 72 | Electric current I |
| 22 | Electric field E as conservative field | 74 | Örsted’s experiment |
| 27 | Superposition of fields (p) | 76 | Biot-Savart law (e) |
| 28 | Electric field E defined as E = F/q | 82 | Ampere-Laplace law (integral form) |
| 32 | Mechanical work in E-field | 83 | Magnetic force F = qv × B |
| 33 | Work and conservation of energy (p) | 85 | B as non-conservative field |
| 34 | Energy conservation (p) | 86 | Magnetic potential energy |
| 38 | Electric potential (as grad E) | 87 | Magnetic field (defined through 86) |
| 41 | Equipotential surfaces | 90 | Ampere’s circuital law |
| 44 | Electric field defined through potential | 91 | Magnetic field H (defined through 90) |
| 47 | Electric flux | 93 | Lorentz’s force F = q(E + v × B) |
| 51 | Gauss’ law defining D | 95 | Electromagnetic induction (experiment) |
| 54 | Electric field defined as source field | 98 | Lenz’s law |
| 55 | Ferromagnet (bar magnet) | 100 | Induction law (Faraday-Henry law) |
| 57 | Magnetic interaction (through force) | 103 | Electromotive force (emf) |
| 59 | Magnetic dipole (as theoretical model) | 109 | Rotational electric field (e) |
| 62 | Magnetic interaction as action-at-dist. | 113 | Ampere-Maxwell law |
| 63 | Magnetic moment m (e) | 116 | Resonance frequency (in RCL circuit) |
| 66 | Magnetic flux density B (t) | 117 | Resonance (RCL) circuit (experiment) |
| 69 | Magnetic flux Ф | 120 | Electromagnetic (propagating) waves |
| AUG | COL | IND opt | IND (β = 1) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Node | β = 1 | All | Z | DEG | Opt β = 1 | aut β = 1 | opt All | n10 | n20 | n30 | n10 | n20 | n30 |
| R | N | R | R | R | N | N | N | N | N | N | N | ||
| 57 | 1 | 10 | +6.8 | 20 | 1 | 1 | 10 | 4 | 4 | 7 | |||
| 2 | 2 | 10 | −5.0 | 2 | 10 | 12 | 5 | 4 | 7 | 11 | 5 | 7 | 9 |
| 66 | 3 | 10 | 9 | 8 | 2 | 10 | 4 | 6 | 8 | 4 | 7 | 7 | |
| 91 | 4 | 10 | 10 | 2 | 3 | 10 | 5 | 6 | 8 | 5 | 7 | 8 | |
| 83 | 5 | 10 | −2.1 | 1 | 3 | 5 | 10 | 5 | 8 | 10 | 3 | 9 | 11 |
| 71 | 6 | 10 | +2.6 | 5 | 5 | 4 | 10 | 4 | 8 | 10 | 3 | 9 | 9 |
| 100 | 7 | 10 | −2.5 | 4 | 6 | 8 | 10 | 6 | 8 | 9 | 6 | 7 | 7 |
| 55 | 8 | 8 | +3.3 | 9 | 9 | 1 | 3 | 3 | 1 | 2 | 3 | ||
| 27 | 9 | 10 | 7 | 2 | 3 | 4 | 3 | 4 | 4 | ||||
| 113 | 10 | 10 | 11 | 15 | 15 | 10 | 4 | 7 | 11 | 5 | 8 | 11 | |
| 109 | 11 | 10 | 8 | 11 | 7 | 10 | 7 | 9 | 11 | 8 | 10 | 11 | |
| 63 | 12 | 10 | +2.4 | 13 | 4 | 6 | 10 | 5 | 8 | 9 | 4 | 6 | 8 |
| 33 | 13 | 10 | 6 | 8 | 2 | 3 | 5 | 1 | 3 | 4 | |||
| 85 | 14 | 7 | +4.4 | 12 | 10 | 6 | 1 | 1 | 3 | 1 | 1 | 4 | |
| 93 | 15 | 10 | 19 | 1 | 5 | 6 | 4 | 6 | 6 | ||||
| 28 | 16 | 6 | −4.0 | 3 | 14 | 13 | 5 | 7 | 11 | 12 | 8 | 11 | 12 |
| 82 | 17 | 9 | +2.8 | 7 | 11 | 10 | 2 | 3 | 3 | 1 | 2 | 4 | |
| 120 | 18 | 6 | +2.9 | 22 | 6 | 4 | 6 | 3 | 6 | 7 | |||
| 117 | 19 | 6 | 23 | 14 | 6 | 1 | 6 | 6 | 3 | 5 | 7 | ||
| 116 | 17 | 6 | +2.1 | 6 | 2 | 2 | 1 | 1 | 3 | ||||
| 103 | 19 | 8 | 25 | 1 | 2 | 3 | 1 | 1 | 3 | ||||
| 72 | 20 | 9 | 21 | 18 | 17 | 10 | 2 | 4 | 4 | 2 | 4 | 4 | |
| 70 | 21 | 7 | +5.8 | 19 | 22 | 8 | 2 | 2 | 2 | 2 | 2 | ||
| 59 | 22 | 7 | 16 | 23 | 8 | 1 | 1 | 3 | 1 | 1 | 1 | ||
| 74 | 23 | 10 | 23 | 13 | 21 | 10 | 2 | 6 | 7 | 3 | 5 | ||
| 62 | 24 | 7 | +4.6 | 20 | 8 | 2 | 1 | 2 | |||||
| 22 | 25 | 7 | 22 | 25 | 8 | 1 | 2 | 1 | 2 | ||||
| Concept | C | Concept | C |
|---|---|---|---|
| 107. Definition of mutual inductance | 1.00 | 39. Experiment of electric potential | 0.90 |
| 89. Derivation of Ampere circ. law | 1.00 | 13. Model of interaction through E | 0.87 |
| 4. Experiment of Millikan’s oil drop | 1.00 | 29. Model of electric state | 0.83 |
| 52. Model of E-field, specific | 1.00 | 118. Model of RCL-circuit | 0.79 |
| 50. Derivation of Gauss’s law | 1.00 | 119. Experiment of RCL-circuit, receiver | 0.73 |
| 48. Definition of Electric flux density | 1.00 | 80. Experiment of force on wire F = ILb | 0.70 |
| 37. Derivation of Potential | 1.00 | 115. Definition of alternating current | 0.67 |
| 81. Model of current element | 1.00 | 114. Experiment of coil in magnetic field | 0.67 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koponen, I.T.; Nousiainen, M. Pre-Service Teachers’ Knowledge of Relational Structure of Physics Concepts: Finding Key Concepts of Electricity and Magnetism. Educ. Sci. 2019, 9, 18. https://doi.org/10.3390/educsci9010018
Koponen IT, Nousiainen M. Pre-Service Teachers’ Knowledge of Relational Structure of Physics Concepts: Finding Key Concepts of Electricity and Magnetism. Education Sciences. 2019; 9(1):18. https://doi.org/10.3390/educsci9010018
Chicago/Turabian StyleKoponen, Ismo T., and Maija Nousiainen. 2019. "Pre-Service Teachers’ Knowledge of Relational Structure of Physics Concepts: Finding Key Concepts of Electricity and Magnetism" Education Sciences 9, no. 1: 18. https://doi.org/10.3390/educsci9010018
APA StyleKoponen, I. T., & Nousiainen, M. (2019). Pre-Service Teachers’ Knowledge of Relational Structure of Physics Concepts: Finding Key Concepts of Electricity and Magnetism. Education Sciences, 9(1), 18. https://doi.org/10.3390/educsci9010018





