Abstract
Do your peers in the classroom have an effect on your vocabulary learning? The purpose of this study was to determine if group-level peer characteristics and group-level peer achievement account for individual-level differences in vocabulary achievement using a large sample of students in kindergarten through second grade (n = 389,917). We applied a mixed-modeling approach to control for students nested among peers, and used quantile regression to test if group-level peer effects functioned similarly across the range of conditional student ability in vocabulary knowledge. Group-level peer effects were more strongly related to vocabulary achievement for students at the low end of the conditional distribution of vocabulary. The difference in vocabulary achievement between children with and without an individualized education program increased as quantiles of the conditional vocabulary distribution increased. Children with lower relative fall scores had better spring scores when they were in homogenous classrooms (i.e., their peers had similar levels of achievement). The importance of classroom composition and implications for accounting for peer effects are discussed.
1. Introduction
The assumption that there are robust peer effects in the classroom is the driving force behind many policy and practical decisions. Discussions around school choice [1,2] and tracking (i.e., ability grouping) [3] are based on the notion that peers influence achievement, which is neither a new nor a novel idea. The first report to address peer or classroom composition effects was the 1966 Coleman Report [4]. The Coleman Report examined the educational opportunities of minority group peers and the relations between student achievement and school type and quality. The report suggested that minority students achieved less and were more affected by school quality than the average Caucasian student [4]. Indeed, classroom compositions matter: schools with a higher average social class or higher skill levels tend to have greater parental support, fewer behavioral and disciplinary problems, and are more likely to retain high quality teachers [5]. In response to the Coleman Report, school composition, and thus classroom composition, were subsequently influenced by reassignment efforts to adjust intellectual, racial, ethnic, and income compositions to more balanced levels [6,7]. Later, in a natural experiment in the early 2000s, whereby a large county in North Carolina reassigned students to schools on the basis of income levels, higher achieving peers were better for a student’s achievement after accounting for race, ethnicity, income, and parental education [8]. Even as school systems have reacted to the Coleman Report by attempting to differentially group students, researchers have looked to more rigorous methodologies to better understand if and how peers relate to individual student achievement [1,2,9]. This research, spanning a variety of ideologies, grades, and outcomes, points to a lack of consensus on the nature and size of peer effects on educational achievement.
1.1. What are Peer Effects?
Peer effects are the behavioral, demographic, and achievement level variables that students possess and which can affect their peers’ learning within the classroom [10,11]. Such peer effects might include social class or social status in the form of free or reduced lunch classification, family income, or unemployment rates. Additionally, group-level differences in achievement rates might affect peer outcomes, such that depending on if they are placed in classrooms with higher or lower group-level (peer group) achievement, students might experience differential achievement outcomes based on how well or how poorly their peers do academically. Finally, student specific characteristics, such as race, ethnicity, or gender, might have an effect on their peers’ achievement levels [8]. The focus of the present study was how the presence of higher achieving peers might have influenced the performance of other peers while controlling for certain demographic characteristics and ignoring the social structure (i.e., the peer relationships) within the classroom.
Establishing that our interest is in the effects of peer achievement, there are a few ways in which the effects of group-level demographic variables and achievement levels on individual-level achievement might manifest in the classroom. One such way could be through interactions with higher-achieving students in small group learning or cooperative activities. If a child does learn from their peers, it would follow that being paired with more highly-skilled peers in small group exercises would have a direct effect on their learning [9]. There might also be indirect effects: if a classroom’s achievement levels are particularly high, the teacher might choose to use a higher-quality method than if the classroom’s achievement levels are low [10].
Hoxby and Weingarth [8] suggested a few models of peer effects that are relevant to the current study. One such model is the Boutique model, whereby students will have higher achievement when surrounded by similarly-leveled peers. If teachers recognize their students are similarly leveled, they might create and tailor their core content to reflect their students’ shared ability levels. A related model is the Focus model, where a student performs better when the classroom is homogenous, even when the student is not part of that homogenous group. The Rainbow model suggests the opposite: heterogeneity in the classroom is best for students, as they must arrive at their own answers in their own ways, and benefit from others’ differing perspectives [8].
Two final models might also be relevant: The Bad Apple model and the Shining Light model. Both of these models posit that individual students can have large effects on their peers, by either “spoiling” the classroom through very low performance, or by improving classroom performance through being the “shining light” of high achievement. For students with individual education programs (IEPs) or with a disability status, their presence might influence their peers’ achievement, should that student’s performance reflect the Bad Apple or Shining Light model of influence. However, students with learning disabilities are more likely to be rejected than comparison children before even examining their achievement scores [12,13].
In the present study, we will explore if and how peer effects manifest through the lens of these models of peer behavior, and how the effects of having a peer with an IEP or disability affects their vocabulary outcomes. Further, we will examine if outcomes for students with an IEP or disability status are affected by their peers’ achievements.
1.2. Why Are Peer Achievement Effects Inconsistent?
Wilkinson, Parr, Fung, Hattie, & Townsend [10] posited several reasons that findings on peer effects have been largely inconsistent. First, they suggested that, descriptively, there are compositional and peer effects, but that these effects may be inconsequential to learning above and beyond a child’s initial status. Second, they reasoned that the peer effects may be limited to only certain clusters of students, and not manifest as significant findings at the population mean. Third, they proposed that findings are small because reciprocal relations between students, teachers, and schools organization/management is not sufficiently explored. And lastly, they recommended that methodological and analytic differences within previous studies have “fail[ed] to model peer effects in theoretically-appropriate ways” [10] (p. 527).
Measurement and modeling choices continue to affect how peer effects are determined. Using a linear-in-means model, Burke and Sass [14] found small or negligible peer effects on mathematics and reading achievement (improvements in peer achievement increased own achievement by around ¼ of a percentile). However, using a nonlinear approach by categorizing students in to low-, middle-, and high-type students based on baseline reading achievement, they found that middle- and high-type students significantly benefitted from average improvement in peer achievement in elementary school, but low-type students’ achievement was unaffected by peers [14].
1.3. Specific Peer Achievement Effects on Language Outcomes
Presently, we focus on the effects peers may have on vocabulary knowledge, an important component of oral language skills. Previous studies on peer achievement effects have focused on mathematical outcomes or general reading skills [1,8,14] and general language skills in Dutch [15,16]. We chose vocabulary knowledge as our outcome because it is specifically implicated in many educational outcomes. Vocabulary achievement is a particularly strong and direct predictor of reading comprehension skills from first grade through fourth grade [17,18,19]. Vocabulary knowledge is also a direct and/or indirect predictor of discourse-level listening comprehension [20,21]. The lexical quality hypothesis also supports vocabulary knowledge as a word learning mechanism that leads to faster and more accurate word decoding skills [22,23]. Moreover, vocabulary has been found to be a malleable factor among other peer effect studies with pre-school aged children [24,25,26]. Within the present study, because oral language is important for skilled reading, and since it may be a malleable factor from an early age, we focused on the effects peers may have on vocabulary learning in the early elementary years (specifically, kindergarten through second grade) to look at the effects of peers on vocabulary achievement both before and after formal reading instruction begins. Understanding how peers influence the vocabulary learning of their classmates can help us to understand if there are optimal ways to structure classrooms to promote vocabulary learning as a facilitator of future skilled reading.
1.4. The Present Study
In an effort to address methodological limitations of the peer effects literature, we presently employed the use of multilevel quantile regression. Hoxby and Weingarth [8] discussed that a linear-in-means model, whereby student outcomes are a linear function of the conditional mean of peers’ outcomes (i.e., the peer effect is homogenous), is an insufficient way to model peer effects:
“…we have seen that the data consistently rejects the Linear-in-Means model as a standalone explanation of peer effects. Thus, researchers’ common reliance on the Linear-in-Means model guarantees that any effects of peers that operate non-linearly or through moments other than the mean become omitted variables.”[8] (p. 29)
In quantile regression, the level of importance of a predictor may be different depending on the quantile of the conditional distribution for an outcome variable [27,28]: the model goes beyond simple linear mean effects models to investigate differential relations between predictors and outcomes. Quantile regression, which has been popular in economics for some time, has of late become increasingly popular in the developmental and psychological sciences [29]. Recent advances in quantile regression have introduced the ability to analyze conditional relations in the context of multilevel models, which are relevant to the present study [30,31,32,33].
Research Questions
The purpose of this study was to analyze individual effects, peer effects, and the interaction between individuals and peers at various quantiles of the conditional distribution of vocabulary achievement at the end of each of grades K-2. To that end, we answered the following research questions:
- What are the effects of group-level peer achievement on individual-level vocabulary achievement at each of grades K-2 after controlling for race/ethnicity and free-or-reduced lunch status?
- Controlling for individual levels of vocabulary achievement in the fall, are there moderating effects of peer characteristics, such as group-level IEP status or disability status, in the classroom on end-of-year individual-level vocabulary outcomes at each of grades K-2?
- Are there differences in the relations of and interactions between these predictor variables (i.e., fall achievement levels, peer group achievement, and group-level IEP or disability status) across quantiles of the conditional distribution of vocabulary outcomes at each of grades K-2?
- Are there grade-related differences in how peers’ achievement and group-level IEP or disability status affects individual-level performance on end-of-year vocabulary achievement?
2. Materials and Methods
2.1. Data
To address the research questions, the data used in this study were obtained from the Progress Monitoring and Reporting Network (PMRN) database of the archive data core maintained by the Florida Center for Reading Research (FCRR). The archive data core is a historic, centralized data repository that captured student performance in grades K-12 on screening, diagnostic, progress monitoring, and state achievement data pertaining to reading skills. Queried data from the data core for this study stemmed from the 2012/13 school year and reflected students’ performance on the Florida Assessments for Instruction in Reading (FAIR). All school districts in Florida (N = 72) voluntarily selected to administer the FAIR. In grades K-2, a classroom teacher delivered the FAIR, a battery of early reading and pre-reading skills used for screening and progress monitoring.
2.2. Participants
Participants were a total of 389,917 students in kindergarten (n = 154,220), first (n = 122,435), and second grade (n = 113,262). Students were in 23,233 classes, in 1,869 schools, in 72 school districts. Demographic composition by grade and for the full sample is displayed in Table 1 along with the demographic distributions of all K-12 students in Florida. In general, the sample is representative of the statewide population with the exception of percent of students eligible for free or reduced-price lunch and the percentage of migrant students. The sample used in this study included proportionally more students eligible for free or reduced-price lunch (65.8% versus 57.6%) and proportionally more migrant students (1.5% versus 0.5%).

Table 1.
Demographic distribution of participants by grade.
2.3. Measures
2.3.1. Vocabulary
The primary construct of interest was vocabulary achievement, which was measured using the FAIR Vocabulary test. The Vocabulary test is administered in the fall and spring of grades kindergarten through 2 as part of the Broad Diagnostic Inventory of the FAIR. According to the K-2 FAIR Technical Report [34], the Vocabulary test measures a student’s breadth and depth of vocabulary and indicates the need for vocabulary instruction. In the test, the student is asked to label objects, actions, or attributes, and is prompted in cases where an answer requires further precision. Words for the test were selected to tap into academic language at the K-2 grade levels. The FAIR Vocabulary test has a reported IRT precision estimate of 0.80, and concurrent correlations of 0.75 to 0.83 with the Expressive Vocabulary Test, 2nd edition [35], and the fall scores explain 24–29% of variance in spring comprehension scores on the SAT-10 [36].
2.3.2. Peer Effects and Relative Status
The peer effect was conceptualized as the relation between classroom peers’ initial abilities and end of year vocabulary. Peer effects were calculated in three ways: (1) the average fall vocabulary of the classroom peers (peer group mean), (2) the standard deviation of fall vocabulary of the classroom peers (peer group SD), and (3) the percent of students with IEPs in the classroom (peer group IEP). Additionally, rather than focus on absolute status in the fall, this study sought to determine whether or not peer effects were dependent on students’ relative status compared to their peers in the fall. To quantify relative status, within each peer group, each student’s fall vocabulary score was transformed to a z-score, that is, a relative status score of −1 would represent a student performing a standard deviation below their peers in the fall, and concordantly, a relative status score of 1 indicates a student performed a standard deviation above their peers in the fall.
2.4. Analysis
To address the research questions, peers were first identified using the approach explained below. Afterwards, two sets of related analyses were conducted: conditional means based multilevel models (i.e., conventional hierarchical linear modeling; HLM), and linear quantile mixed models (LQMM). Both analyses were run as two-level models with students (level 1) nested in classrooms (level 2). Because we were interested to determine whether the impact of peers varied within grade and between grades, each set of analyses was run separately for each grade, kindergarten (K), first grade (G1), and second grade (G2). This allowed for a more nuanced analysis of the impact of peers at each grade level, rather than simply including grade as a statistical control. For both the HLM and LQMM, all main effects were allowed to vary randomly. All variables—except for IEP status—were centered such that resulting coefficients could be interpreted as standardized effects.
2.4.1. Identifying Peers
The FAIR was administered three times per year, and data were entered at each assessment point (fall, winter, spring). In addition to the FAIR scores, a district, school, and teacher identifier were included. As not all students remained with the same teacher throughout the year, it was necessary to identify the most likely set of peers for each student in the dataset. For each student, a peer variable was created. The peer variable was the teacher most consistently associated with the student across the 3 assessment points. For example, for a student that had teacher “Ms. Scott” in the fall and teacher “Ms. Jones” in winter and spring, the peer variable would be teacher “Ms. Jones.” Similarly, for a student that had teacher “Ms. Scott” in the fall and spring, but teacher “Ms. Jones” in winter, the peer variable would be teacher “Ms. Scott.” If there was not a consistent teacher across two or more assessment periods (in 0.8% of cases), the peer variable was the teacher from the first assessment period with data. Approximately 72% of students were in the same peer group at all three assessment periods, 19% of students were with the same peer group at assessment periods 2 and 3, 7% of students were with the same peer group at assessment periods 1 and 2, 1% of students were with the same peer group at assessment periods 1 and 3. The remaining less than 1% of students were not with a consistent peer group for two or more assessment periods; 0.7% were assigned with their peer group from assessment period 1, 0.2% were in assessment period 2, none were in the third assessment period. For the purposes of this study, the peer variable (associated with a unique teacher within a school and district) became the peer group identifier. Thus, students are considered nested within peers (i.e., teachers within schools within districts).
2.4.2. Hierarchical Linear Modeling (HLM)
To identify the most parsimonious model, a standard multilevel building process was conducted at each grade. Four models were tested: (1) an unconditional baseline model, (2) an individual predictors model–relative status and IEP (a dummy variable identifying if a student had an IEP), (3) a peer predictors model–the individual predictors model with the addition of the peer group mean, peer group SD (peer standard deviation), and peer group IEPs (percentage of peers with IEP status), and (4) individual by peer interaction model–the peer effects model with the addition of interactions between relative status and all peer effects and interactions between IEP and all peer effects. Across all grades, the fourth model, the individual by peer interaction model, was the best-fitting model according to deviance index (whereby lower values are deemed better; see online Supplemental Materials for a table with fit indices for each model by grade).
2.4.3. Linear Quantile Mixed Modeling (LQMM)
The final model from the HLM analyses at each grade were then analyzed as a linear quantile mixed model (LQMM) in two phases. LQMMs extend the traditional HLM analyses to a quantile regression framework, allowing the estimation of the independent variables at differing quantiles of the outcome variable. Quantile regression conditions the outcome variable at various points of the distribution, which results in conditional estimates at the specified quantiles without a loss of power [27,28,29]. Because of the large sample sizes, we tested the LQMMs at 0.05 intervals between the 0.05 and 0.95 quantiles of FAIR Vocabulary in spring. This allowed us to test whether peer effects functioned similarly for a wide range of student vocabulary achievements.
In the first phase, at each grade, each individual predictor was tested separately to determine if, in the absence of other variables or interactions, the predictor functioned differently at each quantile. Additionally, each interaction (with corresponding main effects) was tested separately to determine if, in the absence of other variables or interactions, the interaction or main effects functioned differently at each quantile. In the second phase, at each grade, only the predictors and interactions (with corresponding main effects), that were substantive (i.e., coefficient > 0.1) and/or varied substantively (i.e., the absolute difference in the minimum and maximum coefficient size across quantiles was >0.1) across quantiles were entered into a final model. This final model is used for interpretation.
3. Results
3.1. Descriptive Statistics
Table 2 contains the descriptive statistics for the kindergarten, first grade, and second grade students. On average, children in kindergarten grew 3.35 points in vocabulary between fall and spring. Grade 1 students grew somewhat less, i.e., 2.7 points on average. Grade 2 students grew the most, 3.42 points on average. There was no indication of problematic skewness or kurtosis, though a number of children in all grades were at the floor (0) and ceiling (24) of the FAIR vocabulary measure.

Table 2.
Descriptive statistics for vocabulary achievement outcomes.
3.2. HLM Results
The ICCs of the unconditional models were 0.370, 0.345, and 0.366 for K, G1, and G2 respectively. This suggests that 37%, 35%, and 37% of the variance in spring scores was due to differences between peer groups (i.e., classrooms) at each of grades K-2, respectively, with 63%, 65%, and 63% of the remaining variance in vocabulary due to individual differences among students. The large ICCs indicated that there were meaningful differences among the classrooms in children’s spring vocabulary achievement. Therefore, we turned to the three conditional models to explore the individual and peer main effects and the individual by peer interaction effects.
Model fit was ascertained for each of the three conditional models (see online Supplemental Materials for the fit indices of all tested models). According to the deviance index (whereby lower values are deemed better), the final model with all individual by peer interactions had the best fit for all grades. These models explained 55% of variance at the peer level and 54% of variance at the individual level in kindergarten (Appendix A, Table A1), 68% of variance at the peer level and 63% of variance at the individual level in first grade (Appendix A, Table A2), and 54% of variance at the peer level and 44% of variance at the individual level in second grade (Appendix A, Table A3).
Conditional Model Effects
Among the student-level main effects, relative status was strongly associated with spring vocabulary across grades (0.484 ≤ β ≤ 0.558; ps < 0.001). Students with IEPs had significantly lower spring vocabulary scores across grades (−0.111 ≤ β ≤ −0.177; ps < 0.001).
Among the peer-level main effects, the peer group mean was positively associated with spring vocabulary across grades (0.484 ≤ β ≤ 0.558). The peer group SD (peer group standard deviation), though statistically significant in first and second grade, was not substantively significant in predicting spring vocabulary in any grade (0.004 ≤ β ≤ 0.021). Similarly, although the effect of peer group IEP status was statistically significant in first grade, it was not substantively related to spring vocabulary in any grade (−0.015 ≤ β ≤ −0.002).
Among the interaction effects, several were statistically significant; however, with the exception of relative status by peer group SD, there were no substantive interactions (−0.059 ≤ β ≤ 0.070). The relative status by peer group SD interaction (RSxPSD) was significant across grades (0.115 ≤ β ≤ 0.126), suggesting that the relation between peer group SD and spring vocabulary was stronger for individuals with higher relative status.
3.3. LQMM Results
At each grade, each of the individual and interaction effects included in the HLMs, regardless of significance or magnitude, were tested separately in LQMMs to identify substantive effects and/or effects with substantive ranges across the quantiles. Then, effects which were substantive (absolute value greater than 0.1) or varied substantively (absolute value of range greater than 0.1) were included in a single final model for each grade. Across all models, as quantiles increased the intercept steadily increased, which is expected given that the model conditions the regression equation at each quantile, and the scores are normally distributed across a wide range of student skills (the intercept is not discussed further as it is not of primary concern). The main effects and interaction effects from each grade are discussed next.
3.3.1. Kindergarten
The significant effects included in the kindergarten model were the intercept, main effects for relative status, IEP, peer group mean, peer group SD, and the interaction term for relative status by peer group SD (RSxPSD). A quantile process plot of all effects except for intercept is provided in Figure 1. At all quantiles, relative status was the strongest predictor of spring vocabulary (0.406 ≤ β ≤ 0.589), but this relation was stronger at lower quantiles than at higher quantiles. The next strongest predictor of spring vocabulary was peer group mean (0.272 ≤ β ≤ 0.469). As with relative status, peer group mean was more strongly associated with spring vocabulary at lower quantiles than higher quantiles. The third strongest predictor was IEP status (−0.251 ≤ β ≤ −0.108). This effect increased over the quantiles: the difference between individuals with and without an IEP was larger as quantiles increased. The peer group SD, which was included because of the interaction term with relative status (RSxPSD), was statistically but not substantively significant in some quantiles (−0.030≤ β ≤ 0.018).

Figure 1.
Kindergarten quantile plot with 95% confidence interval bands. PM = peer group mean; SD = peer group SD; RS = relative status; RSxSD = relative status by peer group SD interaction.
The RSxPSD interaction effect decreased from 0.151 to 0.096 as quantiles increased. This interaction is plotted in Figure 2 for classrooms at the low end of the conditional vocabulary distribution (0.25 quantile) and for classrooms high end of the conditional vocabulary distribution (0.75 quantile). For classrooms at the low end of the conditional distribution (top panel), if a child had low relative status (i.e., they were lower than their peers in the fall), that child did better in spring when the classroom was relatively homogenous (i.e., the peer SD was low (PSD)). However, if a child had high relative status (i.e., higher vocabulary than their peers in the fall), that child did worse in lower classrooms if the classroom was homogenous (i.e., low PSD), and did better if the classroom was relatively heterogeneous (i.e., high PSD). This pattern held for classrooms at the high end of the conditional distribution: children with low relative status did better in classrooms that were relatively homogenous (low PSD), and children with high relative status did better in classrooms that were relatively heterogeneous (high PSD).

Figure 2.
Kindergarten RSxSD interaction at the 0.25 quantile (top) and the 0.75 quantile (bottom). PSD = peer group standard deviation; RS = relative status.
3.3.2. First Grade
The first grade model included the same predictors as kindergarten with the addition of an IEPxSD interaction. Other than the addition of the IEPxSD interaction, results were similar to kindergarten. A quantile process plot of all effects except for the intercept is provided in Figure 3. Relative status was the strongest predictor of the conditional vocabulary distribution within the 0.05 to 0.95 quantile band (0.389 ≤ β ≤ 0.593). The effect of relative status decreased as quantiles increased. The second strongest predictor was PM (0.309 ≤ β ≤ 0.495). As with RS, the PM effect decreased as quantiles increased. The third strongest predictor was IEP (−0.217 ≤ β ≤ −0.075). As in K, the IEP effect increased as quantiles increased: the difference between individuals with and without IEPS was larger for students in upper quantiles than in lower quantiles. The last main effect tested was peer group SD which, unlike in kindergarten where it was not substantive, was substantive at the higher quantiles (−0.046 ≤ β ≤ 0.113), suggesting that peer group SD may be a stronger predictor for students in upper quantiles than lower quantiles.

Figure 3.
First grade quantile plot with 95% confidence interval bands.
The RSxPSD interaction effect generally decreased from the 0.05 to 0.95 quantile (0.036 ≤ β ≤ 0.135). Figure 4 contains the plots of this interaction effect. As with kindergarten, individuals with low relative status did better in classes with low peer SDs, and students with high relative status did better in classes with high peer SDs. However, for children with low relative status in classrooms at the high end of the conditional distribution (0.75 quantile, bottom panel), the classroom homogeneity did not matter (i.e., there was no difference in performance between low PSD and high PSD). For children with high relative status, when peer SD was high, children had better spring vocabulary achievement, regardless of class performance (low or high end of conditional distribution).
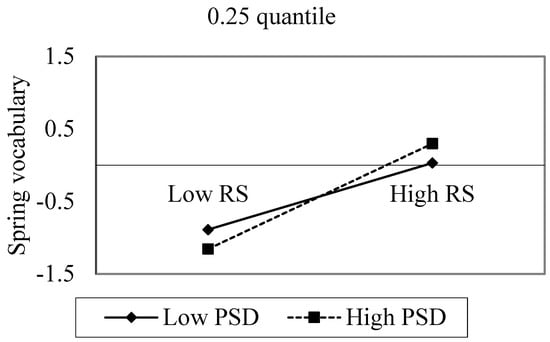

Figure 4.
First grade RSxSD interaction at the 0.25 quantile (top) and the 0.75 quantile (bottom) PSD = peer group standard deviation; RS = student’s relative status.
The IEPxSD interaction, while statistically significant in some quantiles, was not practically substantive (−0.028 ≤ β ≤ 0.001). This interaction is plotted in Figure 5. Regardless of general classroom performance (top or bottom panel), children had higher spring vocabulary scores when they did not themselves have an IEP compared to children who did have an IEP.

Figure 5.
First grade IEPxSD interaction at the 0.25 quantile (top) and the 0.75 quantile (bottom). PSD = peer group standard deviation.
3.3.3. Second Grade
The second grade model included the same predictors as that of the first grade with the addition of a main effect for peer IEP status and an IEP by relative status interaction. A quantile process plot of all effects except for intercept is provided in Figure 6. Across quantiles, relative status was the strongest predictor of achievement in second grade (0.296 ≤ β ≤ 0.532), with the effect decreasing as quantiles increased. The second strongest predictor was peer group mean (0.281 ≤ β ≤ 0.481). As with relative status, the peer group mean effect decreased as quantiles increased. However, from the 0.55 through 0.85 quantile, there was no discernable difference (when accounting for confidence intervals) between the magnitude of the relative status and peer group mean effects.

Figure 6.
Quantile effects plot for second grade. Note. IEPxRS = IEP by relative status interaction, IEPxSD = IEP by peer SD interaction, PM = peer mean, RS = student’s relative status, RSxSD = student’s relative status by peer SD interaction, PSD = peer group SD. Intercept is not included. Gray area represents the 95% confidence band.
The third strongest predictor was IEP (−0.235 ≤ β ≤ −0.090). However, unlike relative status and peer group mean, the absolute value of the IEP effect increased as quantiles increased, i.e., the impact of having an IEP was much higher for higher achieving students. While the main effect for peer group SD was not substantive (−0.045 ≤ β ≤ 0.057), it did have a substantive range (0.102). The main effect for peer IEP status was neither substantive in magnitude (−0.033 ≤ β ≤ 0.001) nor in range (0.034).
As in K and first grade, the RSxSD interaction effect for second grade generally decreased (0.144 ≤ β ≤ 0.041). Students with low relative status had better spring vocabulary scores in classrooms at the low end of the conditional vocabulary distribution when that class was more homogenous (low PSD; Figure 7, top panel), but for students with low relative status in classrooms at the high end of the conditional vocabulary distribution, classroom homogeneity did not matter in predicting their spring vocabulary scores (Figure 7, bottom panel).

Figure 7.
Second grade RSxSD interaction at the 0.25 quantile (top) and the 0.75 quantile (bottom). PSD = peer group standard deviation.
The IEP by peer group SD (IEPxPSD), while statistically significant in some quantiles, was not practically substantial. For students who did not have an IEP, they performed better than their counterparts who did have an IEP regardless of classroom homogeneity or conditional classroom performance (See Figure 8).

Figure 8.
Second grade IEPxPSD interaction at the 0.25 quantile (top) and the 0.75 quantile (bottom). PSD = peer group SD.
The IEP by relative status interaction (IEPxRS) plots are presented in Figure 9. The association between relative status and spring vocabulary was more pronounced for individuals with an IEP at the higher quantiles (Figure 9). For students at the lower end of the conditional vocabulary distribution, regardless of relative status, students performed slightly better in spring when they did not have an IEP (Figure 9, top panel). This effect was much more substantial in classrooms at the higher end of the conditional vocabulary distribution (Figure 9, bottom panel): a student with low relative status who did not have an IEP performed nearly a half standard deviation higher in spring vocabulary compared to a similar student with low relative status but who had an IEP. There was a small, but significant difference favoring students who had high relative status but no IEP compared to students with high relative status but who did have an IEP.

Figure 9.
Second grade IEPxRS interaction at the 0.25 quantile (top) and the 0.75 quantile (bottom). RS = student’s relative status.
3.4. Summary
In the present study, we investigated how individual-level vocabulary knowledge was affected by their peers’ achievement levels for students in grades K-2. Taken together, there were consistent findings across grades K-2 on the influence of relative status, peer group average achievement, homogeneity of peer achievement in fall vocabulary, and the influence of having students with IEPs in the classroom on spring vocabulary achievement. Across all grades, students’ fall vocabulary, relative to their classroom peers, was the strongest predictor of spring vocabulary. However, the predictive nature of relative status was stronger at lower quantiles. Similarly, the effect of the peer average vocabulary was stronger for students at the lower quantiles. An opposite trend was found among IEP status and heterogeneity of the classroom. That is, having an IEP had a stronger effect among students at the higher quantiles, and, students at the higher quantiles were more positively affected by a heterogeneous classroom than by a homogenous classroom. There was a trend where the peer group SD had a stronger effect for students in upper quantiles than lower quantiles. Among students with low relative status in classrooms at the high end of the conditional distribution, classroom homogeneity did not matter. For children with high relative status, when peer SD was high, children had better spring vocabulary achievement, regardless of class performance. Across grades, peer IEP status did not have a substantive effect on individuals’ performance.
4. Discussion
4.1. Peer-Level Achievement Effects on Individual-Level Vocabulary Achievement
Students’ fall vocabulary status—relative to their peers—had the strongest association with spring vocabulary achievement. This finding corroborates a finding in Dutch-speaking second grade students, whereby student background characteristics and their prior achievement explained about 70% of the variance in their language achievement [15]. Compared to other predictors, relative status had the strongest association to vocabulary achievement across grades, but the magnitude of the association declined across the quantiles of vocabulary achievement.
This study supports the importance of peer achievement. Across grades, it was second only to relative status in predicting spring vocabulary. Interestingly, by second grade, for students between the 0.55 and 0.85 quantile, there was no discernable difference in the relation between spring vocabulary and relative status and the relation between spring vocabulary and peer group mean. Convergent with other studies of peer effects, this study supported a prior hypothesis that the relation between peer group mean and individual-level vocabulary outcomes was stronger for students at lower quantiles than higher quantiles. Regardless, the average vocabulary levels of students’ peers in the fall is an important predictor of individual students’ spring vocabulary.
Our study examined at-risk children’s vocabulary knowledge from schools with high rates of free and reduced lunch status, which can be considered a proxy for low SES. Students from lower SES households tend to have different learning trajectories for their language skills [37], and vocabulary size tends to be the oral language component which is most sensitive to the effects of low SES [38]. In a study of Dutch language learners in grades 4 to 6, language gains for low-SES students improved as the percentage of low-SES peers increased in their classroom; i.e., more homogenous classrooms lead to larger gains [16]. We measured homogeneity as the standard deviation of peers’ initial vocabulary achievement. While peer group SD was not a strong predictor in Kindergarten, it increased in magnitude in first and second grade, and it increased across the quantiles. Perhaps the more interesting finding across grades regarding peer group SD was the interaction of peer group SD with relative status. Students’ relative status moderated the influence of peer group SD: students with lower relative status did better in classes that were more homogeneous, and students with higher relative status did better in classes that were more heterogeneous. This finding pits models of peer effects against each other: the Boutique model or the Focus model of peer effects supports classroom homogeneity as good for improving achievement levels [8], but our findings suggest that classroom homogeneity might positively impact vocabulary learning only for the children at the lowest end of the vocabulary achievement spectrum.
Disability Status
Although students with disabilities did not perform as well as their peers, the influence of the disability was limited to the individual with the disability. The percentage of students with disabilities in a classroom never had a substantive relation with spring vocabulary. This suggests that while having a disability has substantial implications for the individual, the presence of individuals with disabilities in a classroom is not related to individuals’ achievement after accounting for other factors such as relative status and peer achievement. This finding is the opposite of what would be found in a “Bad Apple model” of peer effects [8] (p. 6), whereby the presence of a student with poor outcomes negatively affects the outcomes of other students.
While having a disability did not moderate any effects in Kindergarten, having a disability did interact with the peer group SD effect in first and second grade, and IEP status also interacted with relative status effect in second grade. This interaction was more pronounced in the upper quantiles: in first and second grade, the relation between peer group SD and spring vocabulary was weaker for students with disabilities. In second grade, the relation between relative status and spring vocabulary was stronger for individuals with IEPs.
4.2. Limitations
The present study discovered significant peer effects in the classroom on vocabulary achievement, but the study is not without limitations. We discuss some important limitations of our study below.
4.2.1. School Reassignment and Peer Effects
Voluntary reassignment based on school choice initiatives can greatly affect the estimation of peer effects. Families may self-select into certain schools based on their own family characteristics (e.g., income, job locations, residence) or based on their child’s characteristics (e.g., higher performing students may be reassigned to magnet schools or gifted programs). Additionally, homogenous classrooms may be created by families self-selecting into schools with better characteristics (e.g., higher performing classrooms and teachers) or through school assignment of students with similar abilities to the same classrooms, creating homogenous levels of child ability that would not have occurred given natural placement [1]. Given that the majority of schools in this sample are Title I schools, which have a disproportionately high level of students with low achievement, self-selection into these schools is unlikely. However, there are some schools that do choose to be represented in the state archival database that may be higher-achieving or have magnet/gifted programs for high-ability or gifted students.
One noted limitation to this study is that we did not control for students who moved classrooms or did not have a consistent peer group. This decision was made because 72% of students remained with the same peer group across the full year, and less than 1% of students did not have a consistent peer group (i.e., they were with a different teacher at all three assessment points). Thus, while there was a considerable amount of movement between peer groups, the overwhelming majority (over 99%) of students had the same peer group for at least two-thirds of the academic year. Therefore, for these analyses, we did not consider removing or statistically controlling for the less than 1% of individuals that did not have a consistent peer group. Future research may consider investigating student mobility as another potential peer effect.
4.2.2. Theoretical and Empirical Difficulties in Measuring Peer Effects
Studying peer effects is difficult, particularly the nature of measuring and estimating the effects themselves. Selection bias is often an issue: an observer may assume that high achievement is an effect of being in a high-achieving group instead of being a cause for belonging to it [1]. One way this might manifest is if teachers select students who were high-achieving in the previous school year, thus creating a homogenous classroom of high-achieving students. Our findings suggest, however, that building a homogenous classroom of high achievers may negatively impact those students, particularly with respect to their vocabulary achievement.
Secondly, previous models of peer effects have attempted to disentangle the mean-level differences in achievement through something known as the baseline model. This baseline model assumes that there are linear relations between a student and their peers’ achievement levels; thus, a student’s score is linearly affected by the average classroom score [1]. This is problematic if one is interested in effects outside of the mean level–such as in our study. We addressed the limitations of the baseline model by employing a multi-level quantile regression approach with random effects. This allowed us to examine the effects at the tails for both low-achieving and high-achieving students without a loss of power through median splits or multi-group modeling. Future studies should consider incorporating quantile regression approaches to condition their regression models at certain quantiles of achievement.
4.2.3. Missing Variables that Might Further Affect Individual-Level Achievement
Within the present study, we were able to include only achievement-related variables and to account for those peer characteristics that were provided by the PMRN database, i.e., gender, race, free-or-reduced lunch status, IEP status, and disability status. As such, we are missing potentially important variables that could influence the effects of peers on individual-level student achievement. First, we have no knowledge of students’ parental support or engagement in their schools and classrooms. Previous studies have suggested that students with higher achievement may have more engaged parents [5], but this may be a bidirectional relation, such that more engaged parents may cause higher achievement, and higher achievement may cause parents to be more engaged. Further, we did not account for additional potentially important parent-level characteristics that may explain additional variance in the vocabulary learning of these children.
4.3. Implications and Future Directions
On average, regardless of level of achievement (i.e., where you condition the distribution of vocabulary achievement), the context of the classroom matters. Understanding and accounting for these effects has important implications for educational research, especially with regard to drawing correct conclusions on classroom effectiveness practices [13]. The present findings suggest that peers’ average achievement and the homogeneity of peer performance have differential impacts on students’ vocabulary knowledge outcomes. Classroom compositions can greatly impact the learning environment [6]; our findings suggest that a student with low relative levels of fall vocabulary knowledge would benefit from being in a class with similarly-leveled students. However, a student with high relative levels of fall vocabulary knowledge would benefit from being placed in a class with peers of ranging levels of vocabulary achievement.
Additionally, across grades and quantiles, there was a negative relation between having a disability and end-of-grade vocabulary achievement, and this relation consistently increased in magnitude. There was a greater difference between students with and without disabilities in the upper quantiles than in the lower quantiles. This suggests that lower-achieving students with and without disabilities are more similar than higher-achieving students with and without disabilities, which has implications for both planning of intervention and remedial services. Among students in lower quantiles, providing services should be dependent on students’ relative status to their peers, rather than disability status. However, because the discrepancy between students with and without disabilities increases in the upper quantiles, intervention should still be provided to students with disabilities. Taking the homogeneity of the classroom and the impact of having a disability together, practical implications can be found in structuring the classroom to meet the needs of all students. For example, while having a wide range of abilities may be beneficial for higher achieving students, planning small-group instruction with similarly achieving peers may be a way to meet the needs of lower achieving students.
The present findings leave us with important avenues for future research. First, we did not explore how classroom contexts matter, other than peers’ performance and characteristics. Other classroom characteristics, such as teacher years of experience [12], curricular decisions [25,26], and class size [12], could have large impacts on student outcomes independent of peer effects. Indeed, a large study of students found that teacher experience and classroom size predicted student outcomes independent of peer achievement [12], but the mechanism of why these effects occur is still not known. Experimental studies that randomize students to teachers with similar levels of experience and similar class sizes might yield more insight in to how peer effects manifest when classroom conditions are controlled. However, one must proceed with caution: adjusting peer compositions too wildly can have unintended negative effects, particularly for lower achieving students [39].
5. Conclusions
Classroom contexts matter for students’ vocabulary achievement, which is an important predictor of reading comprehension and education outcomes. The results of our study showed that young children’s vocabulary achievement is highly dependent on their relative status and the characteristics of their classroom (i.e., peer performance). For students with relatively low fall scores, their spring scores tend to be higher when they are in classrooms with homogenous peers. For students with relatively high fall scores, they often have higher scores in spring when their peers have varying levels of performance. The literature on peer effects would greatly benefit from studies aimed at understanding how and why these peer effects manifest in an effort to improve outcomes for students at the lowest ends of the distribution.
Supplementary Materials
The following are available online at http://www.mdpi.com/2227-7102/8/4/181/s1, Table S1: HLM Fit Indices for Kindergarten, Table S2: HLM Fit Indices for Grade 1, Table S3: HLM Fit Indices for Grade 2.
Author Contributions
Conceptualization, Y.P. & J.S.F.; Data Curation, Y.P.; Formal Analysis: J.S.F. & Y.P.; Methodology, J.S.F. & Y.P.; Visualization, Y.P.; Writing—Original Draft Preparation, J.M.Q. & J.S.F.; Writing—Review & Editing, J.M.Q. & Y.P.
Funding
This research was funded in part by the National Institute of Child Health and Human Development, [P50HD052120], and the Institute of Education Sciences [R305A130131, R305F100005].
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
Appendix A

Table A1.
HLM Model for Kindergarten.
Table A1.
HLM Model for Kindergarten.
| β | SE | df | t | |
|---|---|---|---|---|
| Fixed Effects | ||||
| Intercept | 0.020 | 0.005 | 7777 | 3.832 *** |
| RS | 0.551 | 0.002 | 8981 | 269.188 *** |
| IEP | −0.138 | 0.007 | 7527 | −18.587 *** |
| PM | 0.438 | 0.006 | 2782 | 77.042 *** |
| PSD | 0.004 | 0.005 | 3425 | 0.707 |
| PIEPS | −0.002 | 0.005 | 1996 | −0.320 |
| IEPxRS | 0.041 | 0.006 | 45,890 | 6.544 *** |
| IEPxPM | 0.006 | 0.006 | 4846 | 0.924 |
| IEPxPSD | −0.015 | 0.006 | 4702 | −2.476 * |
| IEPxPIEPS | −0.016 | 0.005 | 2441 | −2.846 |
| RSxPM | −0.027 | 0.002 | 7573 | −13.804 *** |
| RSxPSD | 0.126 | 0.002 | 7846 | 63.711 *** |
| RSxPIEPS | −0.001 | 0.002 | 10,630 | −0.296 |
| Random effects | ||||
| Var. | SD | Χ2 (df = 6) | ||
| Intercept | 0.168 | 0.410 | ||
| RS | 0.009 | 0.097 | 782.1 *** | |
| IEP | 0.014 | 0.117 | 47.0 *** | |
| pm | 0.021 | 0.146 | 355.4 *** | |
| sd | 0.006 | 0.079 | 34.6 *** | |
| IEPZ | 0.001 | 0.027 | 21.8 ** | |
| Residual | 0.291 | 0.539 | ||
*** <0.001; ** <0.01; * <0.05.

Table A2.
HLM Model for First Grade.
Table A2.
HLM Model for First Grade.
| β | SE | df | t | ||
|---|---|---|---|---|---|
| Fixed Effects | |||||
| Intercept | 0.006 | 0.005 | 6998 | 1.375 | |
| RS | 0.558 | 0.002 | 8751 | 257.864 *** | |
| IEP | −0.111 | 0.007 | 7512 | −15.248 *** | |
| PM | 0.468 | 0.005 | 3029 | 91.278 *** | |
| PSD | 0.021 | 0.005 | 3473 | 4.268 *** | |
| PIEPS | −0.015 | 0.005 | 1982 | −3.244 ** | |
| IEPxRS | 0.047 | 0.006 | 51,300 | 7.536 *** | |
| IEPxPM | 0.002 | 0.006 | 4833 | 0.379 | |
| IEPxPSD | −0.018 | 0.006 | 4636 | −3.021 ** | |
| IEPxPIEPS | 0.005 | 0.006 | 2716 | 0.803 | |
| RSxPM | −0.051 | 0.002 | 7165 | −24.841 *** | |
| RSxPSD | 0.119 | 0.002 | 7308 | 57.967 *** | |
| RSxPIEPS | 0.001 | 0.002 | 10,000 | 0.505 | |
| Random effects | |||||
| Var. | SD | Χ2 (df = 6) | |||
| Intercept | 0.112 | 0.335 | |||
| RS | 0.008 | 0.092 | 558.0 *** | ||
| IEP | 0.011 | 0.104 | 35.7 *** | ||
| pm | 0.017 | 0.131 | 282.4 *** | ||
| sd | 0.008 | 0.087 | 119.8 *** | ||
| IEPZ | 0.004 | 0.065 | 59.7 *** | ||
| Residual | 0.311 | 0.558 | |||
*** <0.001; ** <0.01; * <0.05.

Table A3.
HLM Model for Second Grade.
Table A3.
HLM Model for Second Grade.
| β | SE | df | t | ||
|---|---|---|---|---|---|
| Fixed Effects | |||||
| Intercept | 0.022 | 0.006 | 6718 | 3.943 *** | |
| RS | 0.484 | 0.002 | 8138 | 200.374 *** | |
| IEP | −0.177 | 0.008 | 7031 | −22.330 *** | |
| PM | 0.438 | 0.006 | 2504 | 73.096 *** | |
| PSD | 0.013 | 0.006 | 2677 | 2.302 * | |
| PIEPS | −0.008 | 0.006 | 1678 | −1.422 | |
| IEPxRS | 0.070 | 0.007 | 52,240 | 10.516 *** | |
| IEPxPM | 0.010 | 0.007 | 4825 | 1.503 | |
| IEPxPSD | −0.011 | 0.007 | 4620 | −1.692 | |
| IEPxPIEPS | −0.020 | 0.006 | 3057 | −3.191 ** | |
| RSxPM | −0.059 | 0.002 | 6522 | −26.032 *** | |
| RSxPSD | 0.115 | 0.002 | 6710 | 50.200 *** | |
| RSxPIEPS | 0.000 | 0.002 | 8587 | 0.131 | |
| Random effects | |||||
| Var. | SD | Χ2 (df = 6) | |||
| Intercept | 0.170 | 0.412 | |||
| RS | 0.009 | 0.097 | 641.3 *** | ||
| IEP | 0.020 | 0.143 | 103.1 *** | ||
| pm | 0.014 | 0.119 | 140.5 *** | ||
| sd | 0.004 | 0.066 | 40.6 *** | ||
| IEPZ | 0.002 | 0.044 | 10.2 | ||
| Residual | 0.357 | 0.597 | |||
*** <0.001; ** <0.01; * <0.05.
References
- Hoxby, C. Peer Effects in the Classroom: Learning from Gender and Race Variation; Working Paper 7867; National Bureau of Economic Research: Cambridge, MA, USA, 2000; Available online: http://www.nber.org/papers/w7867.pdf (accessed on 22 October 2018).
- Zimmer, R.W.; Toma, E.F. Peer Effects in Private and Public Schools across Countries. J. Policy Anal. Manag. 2000, 19, 75–92. [Google Scholar] [CrossRef]
- Hattie, J.A.C. Classroom Composition and Peer Effects. Int. J. Educ. Res. 2002, 37, 449–481. [Google Scholar] [CrossRef]
- Coleman, J.S.; Campbell, E.Q.; Hobson, C.J.; McPartland, J.; Mood, A.M.; Weinfeld, F.D.; York, R.L. Equality of Educational Opportunity; OE-38001; National Center for Education Statistics: Washington, DC, USA, 1966; p. 746.
- Willms, J.D. Monitoring School Performance: A Guide for Educators; Routledge: Abingdon, UK, 2003. [Google Scholar]
- Dar, Y.; Resh, N. Classroom Intellectual Composition and Academic Achievement. Am. Educ. Res. J. 1986, 23, 357–374. [Google Scholar] [CrossRef]
- Leiter, J. Classroom Composition and Achievement Gains. Sociol. Educ. 1983, 56, 126–132. [Google Scholar] [CrossRef]
- Hoxby, C.M.; Weingarth, G. Taking Race out of the Equation: School Reassignment and the Structure of Peer Effects; Working Paper 7867; Harvard University: Cambridge, MA, USA, 2003; p. 47. [Google Scholar]
- Thrupp, M.; Lauder, H.; Robinson, T. School Composition and Peer Effects. Int. J. Educ. Res. 2002, 37, 483–504. [Google Scholar] [CrossRef]
- Wilkinson, I.A.G.; Parr, J.M.; Fung, I.Y.Y.; Hattie, J.A.C.; Townsend, M.A.R. Discussion: Modeling and Maximizing Peer Effects in School. Int. J. Educ. Res. 2002, 37, 521–535. [Google Scholar] [CrossRef]
- Sacerdote, B. Peer Effects in Education: How Might They Work, How Big Are They and How Much Do We Know Thus Far? In Handbook of the Economics of Education; Hanushek, E.A., Machin, S., Woessmann, L., Eds.; Elsevier: Amsterdam, The Netherlands, 2011; Volume 3, pp. 249–277. [Google Scholar]
- Bryan, T.H. Peer Popularity of Learning Disabled Children: A Replication. J. Learn. Disabil. 1976, 9, 307–311. [Google Scholar] [CrossRef]
- Vaughn, S.; Elbaum, B.E.; Schumm, J.S. The Effects of Inclusion on the Social Functioning of Students with Learning Disabilities. J. Learn. Disabil. 1996, 29, 599–608. [Google Scholar] [CrossRef]
- Burke, M.A.; Sass, T.R. Classroom Peer Effects and Student Achievement. J. Labor. Econ. 2013, 31, 51–82. [Google Scholar] [CrossRef]
- De Fraine, B.D.; Damme, J.V.; Landeghem, G.V.; Opdenakker, M.-C.; Onghena, P. The Effect of Schools and Classes on Language Achievement. Br. Educ. Res. J. 2003, 29, 841–859. [Google Scholar] [CrossRef]
- Peetsma, T.; van der Veen, I.; Koopman, P.; van Schooten, E. Class Composition Influences on Pupils’ Cognitive Development. Sch. Eff. Sch. Improv. 2006, 17, 275–302. [Google Scholar] [CrossRef]
- Foorman, B.R.; Petscher, Y.; Herrera, S. Unique and Common Effects of Decoding and Language Factors in Predicting Reading Comprehension in Grades 1–10. Learn. Individ. Differ. 2018, 63, 12–23. [Google Scholar] [CrossRef]
- Guo, Y.; Tompkins, V.; Justice, L.; Petscher, Y. Classroom Age Composition and Vocabulary Development Among At-Risk Preschoolers. Early Educ. Dev. 2014, 25, 1016–1034. [Google Scholar] [CrossRef] [PubMed]
- Quinn, J.M.; Wagner, R.K.; Petscher, Y.; Lopez, D. Developmental Relations between Vocabulary Knowledge and Reading Comprehension: A Latent Change Score Modeling Study. Child Dev. 2015, 86, 159–175. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.-S. Language and Cognitive Predictors of Text Comprehension: Evidence from Multivariate Analysis. Child Dev. 2015, 86, 128–144. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.-S.G. Direct and Mediated Effects of Language and Cognitive Skills on Comprehension of Oral Narrative Texts (Listening Comprehension) for Children. J. Exp. Child Psychol. 2016, 141, 101–120. [Google Scholar] [CrossRef] [PubMed]
- Perfetti, C. Reading Ability: Lexical Quality to Comprehension. Sci. Stud. Read. 2007, 11, 357–383. [Google Scholar] [CrossRef]
- Perfetti, C.; Hart, L. The Lexical Quality Hypothesis. In Precursors of Functional Literacy; Verhoeven, L.T., Elbro, C., Reitsma, P., Eds.; John Benjamins Publishing: Amsterdam, The Netherlands, 2002; pp. 189–214. ISBN 978-90-272-1806-3. [Google Scholar]
- Henry, G.T.; Rickman, D.K. Do Peers Influence Children’s Skill Development in Preschool? Econ. Educ. Rev. 2007, 26, 100–112. [Google Scholar] [CrossRef]
- Justice, L.M.; Logan, J.A.R.; Lin, T.-J.; Kaderavek, J.N. Peer Effects in Early Childhood Education: Testing the Assumptions of Special-Education Inclusion. Psychol. Sci. 2014, 25, 1722–1729. [Google Scholar] [CrossRef] [PubMed]
- Justice, L.M.; Petscher, Y.; Schatschneider, C.; Mashburn, A. Peer Effects in Preschool Classrooms: Is Children’s Language Growth Associated with Their Classmates’ Skills? Child Dev. 2011, 82, 1768–1777. [Google Scholar] [CrossRef] [PubMed]
- Koenker, R.; Bassett, G. Regression Quantiles. Econometrica 1978, 46, 33–50. [Google Scholar] [CrossRef]
- Petscher, Y. Do Our Means of Inquiry Match Our Intentions? Front. Psychol. 2016, 7. [Google Scholar] [CrossRef] [PubMed]
- Petscher, Y.; Logan, J.A.R. Quantile Regression in the Study of Developmental Sciences. Child Dev. 2014, 85, 861–881. [Google Scholar] [CrossRef] [PubMed]
- Galarza, C.E.; Lachos, V.H. Package ‘qrNLMM’; R Package version 1.4. 2015. Available online: https://cran.r-project.org/package=qrNLMM (accessed on 22 October 2018).
- Galarza, C.E.; Lachos, V.H.; Bandyopadhyay, D. Quantile Regression in Linear Mixed Models: A Stochastic Approximation EM Approach. Stat. Interface 2017, 10, 471–482. [Google Scholar] [CrossRef] [PubMed]
- Geraci, M. Linear Quantile Mixed Models: The Lqmm Package for Laplace Quantile Regression. J. Stat. Softw. 2014, 57, 1–29. [Google Scholar] [CrossRef]
- Geraci, M.; Bottai, M. Linear Quantile Mixed Models. Stat. Comput. 2014, 24, 461–479. [Google Scholar] [CrossRef]
- Florida Department of Education. Florida Assessments for Instruction in Reading Kindergarten—Grade 2 Technical Manual; Florida Department of Education: Tallahassee, FL, USA, 2009. [Google Scholar]
- Williams, K. Expressive Vocabulary Test, 2nd ed.; Pearson: San Antonio, TX, USA, 2007. [Google Scholar]
- Harcourt Brace Educational Measurement. Stanford Achievement Test, 10th ed.; Harcourt Assessment: San Antonio, TX, USA, 2003. [Google Scholar]
- Hoff, E. Interpreting the Early Language Trajectories of Children from Low-SES and Language Minority Homes: Implications for Closing Achievement Gaps. Dev. Psychol. 2013, 49, 4–14. [Google Scholar] [CrossRef] [PubMed]
- Hart, B.; Risley, T.R. Meaningful Differences in the Everyday Experience of Young American Children; Meaningful Differences in the Everyday Experience of Young American Children; Paul H Brookes Publishing: Baltimore, MD, USA, 1995. [Google Scholar]
- Carrell, S.E.; Sacerdote, B.I.; West, J.E. From Natural Variation to Optimal Policy? The Lucas Critique Meets Peer Effects; Working Paper 16865; National Bureau of Economic Research: Cambridge, MA, USA, 2011; Available online: http://www.nber.org/papers/w16865 (accessed on 22 October 2018).
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).