Abstract
Past research has identified elements underlying modeling as a core science and engineering practice, as well as dimensions along which students’ learn how to use models and how they perceive the nature of modeling. To extend these findings by a perspective on how modeling practice can be used in classrooms, we used design-based research to investigate how the modeling practice elements, i.e., construct, use, evaluate, and revise, were integrated in a middle school unit about water quality that included using an online modeling tool. We focus on N = 3 groups as cases to track and analyze 7th grade students’ modeling practice and metamodeling knowledge across the unit. Students constructed, used, evaluated, and revised their models based on data they collected and concepts they learned. Results indicate most students succeeded in constructing complex models using the modeling tool by consecutively adding and specifying variables and relationships. This is a positive finding compared to prior research on students’ metamodeling knowledge. Similar to these studies, we observed several basic metamodeling conceptions and generally less progress in this field than in students’ models. We discuss implications for applying modeling practice in classrooms and explain how students make use of the different modeling practice elements by developing their models in the complexity and quality dimensions.
1. Introduction
Developing and using scientific models is an important practice for science and engineering [1]. Models are tools that are used to explain and predict phenomena; they represent interactions between system components and help to solve problems and communicate ideas [2]. Stachowiak identified three major features that define models: (i) Models are mappings (or representations) of originals; (ii) they are always a reduction of this original in that they represent a selection of the original’s attributes and (iii) this selection is a pragmatic one with regards to the model user, the specific time it is used in, and with regards to the specific function the model is designed for [3] (pp. 131–133). Developing and using models is a core science practice, and system models is one of the crosscutting concepts that links all scientific domains in A Framework for K-12 Science Education [1]. Even though students have been found to use models differently than scientists (e.g., by using models more as a simple representations of something rather than, like scientists, as a tool for explaining/predicting phenomena and answering questions, thus generating knowledge), recent publications (e.g., Ref. [4]) have highlighted the importance of engaging students in a modeling practice more similar to that used by scientists. Like scientists, students are expected to learn how to construct, use, evaluate, and revise models and to understand the purpose and nature of scientific models and the modeling practice [5,6]. Our work follows this conceptualization, where students conduct the different elements of the modeling practice to make sense of phenomena and answer a driving question.
Some research has been carried out on the development of students’ modeling practice. These studies show that students do not have enough opportunities to engage with models and to develop modeling practices in science classrooms [5]. In recent years, learning progressions for supporting students’ modeling practice have been suggested [2,7,8] and different technological tools for supporting students with developing their modeling practice have been produced and tested in classrooms [9,10]. However, more research is needed to better understand the process of how the modeling practice can be integrated into classrooms. This is particularly important with regards to using technological tools in modeling in order to understand better how these may affect students’ modeling practice and knowledge.
To address these gaps in understanding the development of students’ modeling practice, we set to investigate the enactment of modeling lessons using an online modeling tool, focusing on how the modeling practice elements were integrated in the lessons of a water quality unit. Our analysis of students’ learning focusses on two main data sources: The development of students’ models across the unit and connected explanations the students provided, as well as students answers to questions about the nature and purposes of models and modeling in a pre-/post-survey.
2. Theoretical Background
Students’ engagement in modeling has been analyzed to consist of two major components: First, the modeling practice itself: constructing, using, evaluating, and revising models. Second, developing knowledge about the purposes of modeling and the nature of models (also referred to as metamodeling knowledge, e.g., Ref. [2]). Both of these aspects are addressed in the article and we structure the following sections accordingly.
2.1. Elements of the Modeling Practice
Developing and using models is one of the science and engineering practices used in A Framework for K-12 Science Education [1]:
“Science often involves the construction and use of a wide variety of models and simulations to help develop explanations about natural phenomena. Models make it possible to go beyond observables and imagine a world not yet seen. Models enable predictions of the form ‘if … then … therefore’ to be made in order to test hypothetical explanations.”(p. 50)
According to the US-based National Research Council (NRC) [1], by Grade 12, students are expected to be able to construct and use models to explain and predict phenomena, use different types of models, develop their modeling knowledge, revise their models based on new knowledge and empirical data, use computational simulations as tools for investigating systems, and construct and use models to test and compare different design solutions. Students are expected to apply multiple cycles of using and revising their models [5], specifically by comparing predictions of the observed phenomenon with their real-world observations and then—should the two differ substantially—go back and adjust the model to have a more accurate model that is better at explaining and predicting the phenomenon. A consequence of this is that students not only work on a single model, but that they are also able to compare between different versions of a model in terms of their explanatory and predictive power. As written in the NRC: “Models can be evaluated and refined through an iterative cycle of comparing their predictions with the real world and then adjusting them, thereby potentially yielding insights into the phenomenon being modeled” [1] (p. 57).
Scientific models (from here on are referred to simply as ‘models’) are tools that represent components in a system and the relationships between them, used to explain and predict phenomena [1,2,11]. Using models encompasses making pragmatic (see above) reductions amongst the attributes of an original and mapping these onto the representation that serves as the model [3]. In extension of Stachowski’s elements of modeling, Gouvea and Passmore make clear that models are more than depictions of something (models of), but rather need to be seen with regard to aims and intents of the model and the modeler (models for) [4]. Clement [12] described the modeling practice as cycles of hypothesis development that include constructing, testing, and revising models. In this seminal study, Clement examined the formation process of a new explanatory model for testing and predicting phenomena by scientists. In this process, scientists start with an initial model which develops in a dialectic model construction process into a final model using both empirical and theoretical data. This iterative modeling cycle was called the explanatory model construction. Schwarz and colleagues [2] defined the modeling practice as a process that includes the elements of constructing, using, evaluating, and revising models:
- Constructing models: Models are built to represent students’ current understanding of phenomena. Students are expected to not just use provided models in the classroom, but to engage in the process of building their own models. This should promote their ownership and agency of knowledge building;
- Using models: Models can be used for different purposes, including communicating current understanding of ideas and to explain and predict phenomena. Students are expected to use models by testing them against data sources;
- Evaluating models: At the heart of the scientific process stands the constant evaluation of competing models. This is what drives the consensus knowledge building of the scientific community. Students should be able to share their models with peers and critique each other’s models by testing them against logical reasoning and empirical evidence;
- Revising models: Models are generative tools. They represent the current understanding of scientific ideas. It lies in the nature of models that they are revised when new (e.g., additional variables) or more accurate ideas or insights (e.g., advanced measurements) are available. When new knowledge and understanding accumulates or changes, students should revise their models to better represent their latest ideas. In this article, we use a broad definition of the term revise, including any changes that students conduct in their models, thus also encompassing the simple addition of model elements. If we refer to revise in the narrow sense, this is pointed out. In these cases, we mean changing elements of the model that had been added in an earlier model version.
Engaging students in the modeling practice has been shown to support students’ content knowledge acquisition [13], their epistemological understanding of the nature of science and modeling knowledge [6,14,15,16,17,18,19], their abilities to evaluate and critique scientific ideas [3,4], and their scientific reasoning [20]. Developing and using models has also been shown to contribute to the development of students’ agency and identity as constructors and evaluators of scientific knowledge [4,5,21].
2.2. Progression in Students’ Metamodeling Knowledge
The development of students’ metamodeling knowledge is comparatively well studied [6,15,16,18,19]. Schwarz & White [6] classified students’ metamodeling knowledge into four knowledge types: nature of scientific models, nature of the process of modeling, evaluation of models, and purpose of models. Schwarz and colleagues [2] defined metamodeling knowledge as understanding the nature of models, the purpose of modeling, as well as the criteria used to evaluate models. Students with advanced modeling knowledge should understand that models are sensemaking tools used to build knowledge about the world, that models are abstract representations and not exact copies of reality, and that the nature of models is to be evaluated and revised based on new evidence. Grosslight and colleagues [22] established a classification of students’ conceptual understanding of the nature of models. At level 1, students consider models as a copy of reality, but at a different scale. At level 2, students still consider models as a representation of reality, but understand that models are constructed and used for a specific purpose and that some components of the models may be different from reality. At the highest level, level 3, students consider models as tools to test and evaluate ideas about natural phenomena and they realize that the modeler plays an important role in how models are constructed and used [15,18].
Despite all that is known about the critical role of models and modeling in science education and the need to support students’ accordingly, not enough studies have provided an in-depth analysis of how the elements of the modeling practice were coherently used in science lessons, and how the teacher, the curricular materials, and the modeling tools can support students in developing their modeling practice and knowledge.
2.3. Rationale and Research Questions
Building upon the theoretical framework of Schwarz and colleagues [2] and the gaps in existing literature mentioned above, we set out to explore the results of the enactment of a middle school unit about water quality that integrated an online modeling tool and provided students with several opportunities to construct, use, evaluate, and revise their models. We examined the process that was carried out in the classroom, the development of students’ models, including prompts where students provided details about why they specified the relationships between variables the way they did, as well as the changes in their metamodeling knowledge. Specifically, we investigate the following research and development questions:
- How were the elements of the modeling practice used in the unit integrating the modeling tool?
- How did students’ modeling practice develop throughout the unit with regard to constructing, using, evaluating, and revising models?
- What was the change in students’ metamodeling knowledge about the nature of models and modeling across the unit?
3. Methodology
This qualitative study is part of a design-based research and development project [23] aimed at investigating if and how middle school students (7th grade, ages 12–13) develop modeling practice when using an online modeling tool. This study focuses on classrooms in which the modeling tool was integrated with the enactment of a water quality unit.
We examine the water quality unit classroom enactment, in which students used the modeling tool. Analysis focused on how the modeling tool and modeling practice elements were integrated in the lessons, as found in classroom observations, video recordings of lessons, and teacher’s reflection. Analysis also focused on the progress of three focus group students that were selected for in-depth analysis across the unit. We analyze two main data sources: (i) Student models in combination with their responses to prompts about why they specified the model and its relationships in the way they did, as well as (ii) students’ responses to questions about the nature of models and modeling collected in online surveys at the very beginning and the very end of the unit. In the following, we refer to these as pre- and post-surveys, respectively. The details of the learning context and our research methods are described in the following.
3.1. Context
The following section provides an overview of the employed software, SageModeler, and describes how students can work with it. The details of the teaching context are presented afterwards. As a principle, the participating students always learned about the specific contents (i.e., variables affecting water quality) first and then later applied and reflected on their knowledge through the modeling practice.
3.1.1. SageModeler Software
Students in our study used a free, web-based, open-source modeling software called SageModeler [24]. SageModeler is a tool for model building and testing interactions between variables and is aimed at secondary students. It is designed to scaffold students’ modeling practice, i.e., constructing, using, evaluating, and revising models. Modeling in SageModeler is done with a focus on system-level, thus requiring students to apply system thinking and causal reasoning.
The first step for students, after determining the question or phenomenon that their model addresses, is to identify which variables are important for explaining or predicting a phenomenon within the boundaries of the investigated system. These variables were brought up during a whole class discussion, facilitated by the teacher, where students were prompted to come up with ideas for factors that may impact the water quality. As a result, students’ models are always a representation of their conceptual understanding of the system. After having identified relevant variables, students start building their initial model by dragging boxes as representations of these variables to a blank drawing canvas. These boxes can be described and personalized by adding pictures and labels.
Second, students define the relationships between these variables using arrows, specifying the relationship both by graphs and by adding explanatory text that can help them understand the interactions. Being designed for a wide range of grade bands, SageModeler can be used at different levels of sophistication. Students in the water quality unit worked with a semi-quantitative approach. In this setting, students are asked to specify relationships through short phrases that consist of the two variable names and the interaction effect between them, which students selected from a drop-down menu (Figure 1). The rationale behind this approach is to avoid unnecessary cognitive load or a potential decrease in motivation that might occur when specifying relationships through formulas. Students’ specification of relationships is further supported by the software requesting them to enter an explanation for why they specified the relationship in the way they did.
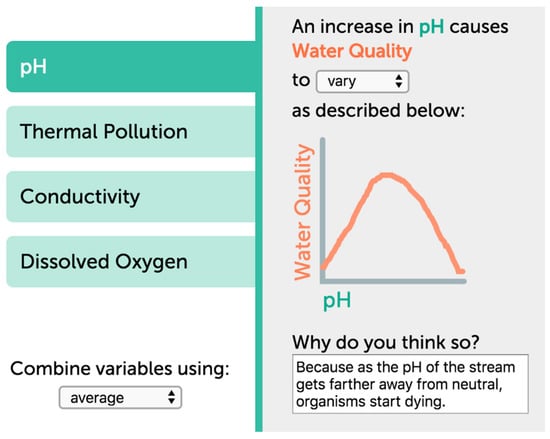
Figure 1.
Screenshot of the semi-quantitative specification of relationships between the variables pH and water quality in SageModeler.
In the third step of using SageModeler, students run simulations of their model. The data output of these simulations can be visualized in graphs. In the fourth step, students proceed to using the output data to evaluate their model. SageModeler is embedded in the Common Data Analysis Platform, CODAP [25] that enables students to analyze their model output and compare it against their own real-life observations or empirical data [26]. This comparison allows students to derive conclusions about the completeness and accuracy of their models. Students can also evaluate their peers’ models or compare competing models in terms of how well they explain and predict the target phenomenon.
SageModeler is a content free software, meaning that students can build complete models that will run, even if they are inconsistent with a scientific explanation of the modeled phenomenon. Therefore, it is the responsibility of the model builder to test their models to see if they work the way that they think they should work or if it compares with empirical data. Section 3.1.2 below describes how this was enacted in the unit.
SageModeler has been developed by the Concord Consortium in collaboration with researchers from out project group at Michigan State University and the University of Massachusetts, and is based on an earlier system-dynamics modeling tool—Model-It [27]. The main design principles of SageModeler include:
- Visualizing variables and relationships in diagrams in a way that students can customize;
- Using drag-and-drop functionality for constructing models and preparing diagrams;
- Defining relationships between variables without the dependence on equations;
- Performing exploratory data analysis through an environment designed for students and integrated into SageModeler.
SageModeler was iteratively developed in a multi-year process, during which the software was revised and the functionality and user interface features were developed. Several studies found that middle and high school students benefit from using the modeling tool and that it contributes to their learning and development of the modeling practice [28,29,30,31].
Several professional learning opportunities were provided for a cohort of middle and high school teachers, including the teacher taking part in this study, to introduce the modeling tool. In these professional learning meetings, teachers engaged with the modeling practice element of constructing, using, evaluating, and revising models, including also some reflection about the nature or models and modeling. The teachers were introduced to the following elements and integrated these in their curricular units: plan, build, test, revise, and share. These elements represent a slight differentiation of the modeling practice elements defined by Schwartz and colleagues [2]—see above. The purpose of using this adapted sequence of elements for classrooms was to connect to what teachers knew and worked with in earlier professional training. Both versions of these elements are aligned in that they refer to similar activities in the classroom, they are only structured differently (e.g., build and share are equivalent to construct; evaluate includes aspects of test and share).
3.1.2. Water Quality Unit for Middle School
In this section, we provide an overview of the teaching and learning setting, in which the students applied the SageModeler tool in learning about water quality. At the beginning of the results section, we add to this—with a developmental perspective in mind—by focusing on how the elements of the modeling practice were integrated into this software-based modeling unit.
Middle school students in the water quality unit investigated a complex phenomenon, a local stream and its mini-watershed, within a project-based learning unit [32,33] focused on three-dimensional learning [1]. The goal was for students to create models of the stream system by representing the various factors that influence water quality in order to answer the unit’s driving question, “How healthy is our stream for freshwater organisms and how do our actions on land potentially impact the stream and the organisms that live in it?” Students’ models were intended to allow them to make predictions of water quality based on changing variables in their models. Accordingly, the goal for the models specifically was to have the best possible explanatory and predictive power for answering the driving question. Students were to evaluate the quality of their model by getting feedback from their peers and by evaluating the data their models produced against the data the students collected or information the students analyzed in class.
This unit was developed and enacted in classroom by the third author of this article. The teacher taught this unit about water quality for several years. The software SageModeler was the major difference between this enactment of the unit and other years’ of teaching it. In our experience, data collection itself did not impact the teaching significantly due to the teacher’s familiarity with the research conducted in her classroom in previous studies. The students were relaxed and did not interact substantially with the researchers present in the classroom.
A component of the project included a 6-week period where student groups learned about various water quality tests and then collected and analyzed several pieces of stream data at a particular section of the stream. Students engaged in three separate data collection experiences after completing lessons related to the various water quality tests. The data collection points were roughly 2 weeks apart. Students collected pH and temperature data during the first data collection opportunity, conductivity data during the second, and dissolved oxygen data during the third. Data included quantitative water tests and qualitative observations of the water in the stream, the surrounding area near the stream, and the surrounding mini-watershed, all of which could impact the stream through water run-off. Students also recorded current and previous weather conditions. Observations related to potential consequences for organisms in the stream were also recorded. For example, one water quality test explored the amount of dissolved solids in the stream with a focus on road salt, nitrates, and phosphates. Students used conductivity probes to obtain the amount of dissolved solids. They made observations that included looking for conditions that could affect the variables in the model or be an explanation for the data the students recorded, for example snow (indicating the possibility of road salt runoff), nearby lush lawns (fertilizer that contains nitrates and phosphates), or algae in the water (excess nitrates and phosphates in the water causing algal blooms). There was not enough time for students to collect longitudinal data of the different water quality measures, so students’ insights for building their models did not only stem from field data, but also from what they had learned in previous lessons. For example, when exploring the variable pH, the students, before measuring pH in their stream, learned about the pH measure itself, its range, and under which conditions different freshwater organisms can sustain life. The students explored the pH of substances used on land, how these can get into the stream water, and how they would impact pH. After measuring pH in their stream later on, the students can estimate how healthy their stream may be in terms of pH.
To explain the health of the stream for supporting freshwater organisms, students analyzed both quantitative and qualitative evidence and constructed an evolving explanation over time [34] as more data was collected. This was done following each data collection experience. Students also collaborated to develop models, using a similar iterative approach [32], thus building models that continuously develop.
The practices of developing and using models, the crosscutting concepts of cause and effect, systems, patterns, and stability and change, and disciplinary core ideas from Earth and Human Activity, and Ecosystems: Interactions, Energy, and Dynamics related to the water quality of a stream for freshwater organisms were the focus of the unit.
Access to the water quality unit is freely available online [24]. The unit consisted of three main lessons. In the first 2-day lesson, the teacher introduced the modeling tool, demonstrated how to use it, and asked students to construct initial models in small groups that included the pH and temperature variables affecting the water quality variable. On the second day of the lesson, the teacher discussed several issues related to modeling and using the modeling tool and allowed students to continue working on their models. This included adding the secondary variables that would affect the water quality measurements variables (the causes of changes in pH and temperature). The second modeling lesson 2 weeks later was taught by a substitute, a retired teacher who had taught the water quality unit before but without using the modeling tool. In this lesson, students were instructed to further develop their models to include the conductivity variable. In the third and final modeling lesson, taking place another 2 weeks after lesson two, the teacher further discussed the development of the models and students further developed their models to include the dissolved oxygen variable.
3.2. Population
One experienced middle school teacher and main designer of the water quality unit (third author of this article) taught four seventh grade classes at an independent middle school in a small midwestern US city. The teacher had been teaching the water quality unit for several years and was therefore well experienced with the concepts and investigations carried out in the unit. During the professional learning workshops, the teacher learned about the modeling practice and tool and worked together with the research team to integrate the modeling practice elements and the modeling tool to the water quality unit.
Fifty percent of students self-identified as students of color. About 15% of students were on financial aid. This study observed roughly a 6-week long portion of the unit on water quality, which we described in the previous section. In total, 55 students in four different classes taught by the same teacher participated in the unit lessons in the fall of 2017. As part of the unit, students worked in groups of two or three on the construction and revision of their models.
3.3. Data Collection and Analyses
3.3.1. Classroom Observations, Video Recordings and Teacher Reflection Notes
In order to explore how the teacher directed students to construct, use, evaluate, and revise their models during the enactment of the water quality unit, all three lessons in which the modeling tool was used were observed. The classroom observations were performed by two researchers, with at least one of them in the classroom for each modeling lesson. To support the observations, video recordings were taken of these lessons. Whole-class discussions during the observed lessons were transcribed and analyzed to investigate the instructions and scaffolds provided by the teacher for using the modeling tool and supporting students’ modeling practice. It should be noted that, in this study, we did not perform an in-depth video analysis, as the available recordings were not systematic enough for a detailed analysis (e.g., some aspects of the teaching-learning process were hard or impossible to record due to technical limitations). Thus, the video recordings were used to provide illustrated examples of how the modeling elements were addressed and enacted in the lessons, as described by the teacher and observed in the classroom observations. The teacher also provided both written and orally discussed reflection notes following the enactment of the unit.
After this study was being reviewed by the ethics committee (IRB) of Michigan State University, all students in our study received opt-out forms for their parents to sign in case study participation or specific elements like video-recording were not approved. Sensitive data (e.g., classroom videos) were stored on a secured database. All student information in this article is anonymized. The study was conducted in accordance with the Declaration of Helsinki, §23.
3.3.2. Student Models and Connected Prompts about Reasons for Specifying Relationships
All student work related to the modeling practice was submitted in an online system, thus making student work accessible to the teacher and the research group. Students’ models, produced during the unit (in the following, we refer to these as initial model, first revision model, and second revision model), as well as student responses to prompts within the modeling tool where students explained relationships in their models, were analyzed. Because of technicalities of the learning platform, researchers had access only to 11 groups that produced a full set of three model iterations and were taken for analysis. The other eight groups performed all model revisions in the lessons, but their later models were not accessible. The specifics of the group selection criteria for the general analysis of students’ models are summarized in Figure 2 below.

Figure 2.
Process and criteria for selecting the groups for the student model analysis (N = 11, top part) and the focus case analysis (N = 3, bottom part).
The expectations for students’ models had both fixed and flexible aspects: Students were required to include a set of four first-order variables in their models, but students were free to add second-level (background) variables as they liked. The students also connected the variables as they found most suitable. The reason for this was that the teacher, after several years of experience with this unit, found it helpful to structure the unit by the first-order variables (or clusters of variables, if including the respective background factors). Since the students’ models were growing to oftentimes substantial complexity over the unit, structuring the unit by the first-order variables provided a scaffold for students to structure their models around. At the same time, it provided a valuable commonality between all groups that helped students to analyze and evaluate their peers’ models for providing each other feedback. Using SageModeler, in comparison to, for example, paper-and-pencil models, increased students’ freedom in modeling, as it allowed for a quick and easy way to revise those parts of their model that the students were free to set up as they found suitable. More specifically, it facilitated making changes to models after feedback from peers and after running simulations. The model analysis focused on the first-order variables only, i.e., those variables and relationships which students measured in the field and which directly affected the dependent variable of the model, water quality [32]. The first-order variables included:
- pH: Expected to vary in its effect on water quality, since neutral pH is most preferable for most living organisms. First, this relationships is increasing from acidic to neutral conditions, and then decreasing from neutral to basic conditions. This variable was added in the initial model;
- Temperature: Expected to have a decreasing effect on water quality: As the temperature increases, the water quality should decrease. This variable was added in the initial model;
- Conductivity: Expected to have a decreasing effect on water quality. This variable was added in the first model revision;
- Dissolved oxygen: Expected to have an increasing effect on water quality. This variable was added in the second model revision.
The variable turbidity was also included in some of the students’ models. However, due to time limitations, it was not expected to be part of the students’ final model, so we did not include this variable in our analysis. We did not include second-level variables (i.e., those affecting the variables directly connected to the water quality) into the analysis either, as these differed largely between groups and would have made comparability difficult. Basic relationships (increasing, decreasing or varying) were analyzed. Advanced types of relationships (about the same, a lot, etc.) were not analyzed, as the teacher focused on getting students to accurately identify patterns of relationships between variables, but less on students ability to define more mathematically appropriate relationships.
We categorized students’ models as follows:
- Models that included all the required variables and accurate relationships that were categorized as fully complete models;
- Models that did not include the above-mentioned variables or where relationships were categorized as incomplete and classified into several types of incompleteness.
Amongst these, the following types of incompleteness emerged from students’ models:
- Undefined relationships: Variables are connected, but relationship type not determined;
- Inaccurate relationships: Relationship types between variables are not accurately defined;
- Missing variables: Required variables do not appear in the model;
- Unconnected variables: Variables appear in the model, but are not connected to any other variables;
- Unrelated variables: Additional variables are directly connected to the dependent variable;
- Inaccurate labels: Labels of variables were not accurately named.
An inter-rating was conducted on all groups models (N = 11) by two independent raters, indicating a substantial agreement of 89% (weighted Cohen’s Kappa = 0.74). Differences in scoring were further discussed between raters until full agreement was achieved.
Qualitative analysis of focus student groups’ written responses for each of the relationships in their model was performed in order to investigate the groups’ model development throughout the lessons and examine possible changes in their metamodeling knowledge following the enactment of the unit. In the first iteration of the model, the teacher directed students to fill in the text box which asks, “Why do you think so?” after defining each of the relationships between variables in their models. However, neither the substitute teacher nor the teacher asked students to do so in the following two modeling cycles, and, as a result, only a few groups filled out these boxes in the second and third models. Hence, this element was analyzed in combination with students’ models and not separately. Analysis of responses focused on the level of reasoning used by the students—from simple repetition of the defined increase or decrease relationship (e.g., “Because when the pH changes the water quality changes.”, group C), to a response that included causal reasoning or detailed examples (e.g., “As the temperature increases, more organisms start to die and algae take resources.”, group D).
3.3.3. Selection of Focus Case Groups
Of the 11 student groups, we decided to conduct an in-depth case analysis on a sample of these groups, and applied the following criteria with the goal of selecting three cases. First, we selected groups that covered different competency ranges, including a complete and fully accurate model, an incomplete model that was later revised, as well as a model that appeared particularly interesting due to having additional variables. Regarding the groups with incomplete models, we chose to select a group that had inaccuracies in the initial or first revision model, rather than in their final model, because of the absence of later model revisions. A final criterion was to use groups that represented both genders. Figure 2 summarized the selection process for the focus case groups.
Each group was comprised of two students. Analysis of these focus students included the group models, as well as student responses to the prompt “Why do you think so?” for the relationships between variables connected to the water quality variable. Here, students provided insight into their choice of relationships between variables in the model. As an additional insight, we compared our observations to recordings from classroom observations, but these were not a systematically analyzed data source.
3.3.4. Pre- and Post-Modeling Surveys
Our second data source comprised students’ answers to four questions about the nature of models and modeling in an online survey that was administered by the teacher in the beginning and upon completion of the unit. Based on the works of Schwarz and colleagues [2], we refer to these as metamodeling questions. These questions were derived from previously used and validated questionnaires about students’ metamodeling knowledge [15,22]. The questions in the pre- and post-surveys were:
- Q1
- Your friend has never heard about scientific models. How would you describe to him what a scientific model is?
- Q2
- Describe how you or your classmates would use a scientific model;
- Q3
- Describe how a scientist uses a scientific model;
- Q4
- What do you need to think about when creating, using, and revising a scientific model?
Metamodeling understanding has been discussed to be different from, but related to—and ideally integrated with—students’ modeling practice [2,35]. While the teacher spoke about different aspects of the nature of models across the unit occasionally, improving metamodeling knowledge was not a specific learning goal of the unit, neither was it taught in depth. With regards to previous research, the purpose of including these questions in our research was therefore to see if students’ modeling practice in class also resulted in changes in students’ understanding about the nature of models and modeling.
Even though students worked in pairs on their models, their answers to the metamodeling questions usually differed from their partners’ answers distinctly, thus leading us to analyze the answers on a student-by-student basis and not at group level. Students’ responses were analyzed across the four metamodeling questions, not separating a student’s answer systematically by the four questions. This was done due to the oftentimes similar or related responses the students provided to the four metamodeling questions.
When analyzing students’ responses to the metamodeling questions, we did not construct specific categories for students’ understanding, as initial attempts in this direction had the tendency to blur the sometimes less obvious differences in students’ conceptions. Instead, an iterative process was used to draw conclusions about students’ answers. First, we noted observations about students’ conceptions from individual groups. Second, we checked whether these findings also appeared in other groups, and then refined or adapted our first conclusions. Lastly, we went back to verify if our conclusion still described the student utterances from the initially analyzed group adequately. The analysis focuses specifically on three types of comparisons: (i) pre- versus post-survey; (ii) how students conceptualized model use by students versus model use by scientists, and (iii), comparisons between the three cases. The analysis of students’ responses to the metamodeling questions was interpretational and could not, due to the few analyzed students, rely on ratings or categorization. Hence, a methodologically adequate inter-rating had to be replaced by cross-checking of conclusions between the first and second author.
3.3.5. Teacher and Unit Developer Reflections
The teacher of this unit played an important role in analyzing and reflecting on the data presented in this article. The teacher contributed to writing the article by sharing her reflections on the enactment of the unit, thereby providing us with important insights about the process that was carried out and experienced by the students. These reflections were integrated in the article by continuous discussions with the other authors and shared writing of the article in an iterative process.
4. Results
To investigate the three research questions of this paper, we first examine how specifically the teaching and learning process functioned with regards to integrating the modeling practice into the water quality unit using the modeling tool. Afterwards, we focus on students’ developing models, combined with their responses to prompts for why they specified the relationships between variables the way they did. Lastly, we present our analysis of students’ responses to pre- and post-unit survey questions about their metamodeling knowledge.
4.1. Modeling Practice Elements Integrated in the Water Quality Unit
The first research question (How can the elements of the modeling practice be integrated in a unit using the modeling tool?) was investigated by examining the observations notes and video recordings of the modeling lessons together with the reflection notes made by the class teacher, as the third author of this article. In the following section, we describe the learning and modeling process, as carried out in one of the classes. All other classes were taught in a similar way by the same teacher.
After student groups collected two pieces of water quality data, pH and temperature, the teacher probed students to assess their prior understandings of what scientific models were and their ideas on the purpose for constructing models. Building from student responses, a discussion followed that models are tools that assist scientists with explaining and predicting phenomena because they illustrate relationships between variables [7]. The teacher then informed student groups that they would collaborate to create a model of the stream system based on their current knowledge; they would represent the various variables that had been investigated so far and that the students had learned influence water quality. Students were informed that their models were working models, meaning that their models would develop over time. As they collected more water quality data they would add to and modify their models. On the classroom board, during the whole-class instruction, the modeling elements were written and discussed: plan, build, test, revise, and share. On one occasion, when referring to these elements, the teacher said:
“What we’ve been doing now, we’ve been planning [points at the word ‘plan’ on the board]. That’s the first part of thinking about a model, to plan what should be in the model. And we want to think about the various variables. What is it that we want to model? What is it that we want to use to be able to predict or to explain?”
After this, the teacher introduced students to the modeling program, SageModeler, by modeling a simple, non-science example where the various components of the program were illustrated. This allowed the students to see how the tool worked. Students were then asked what the various factors (variables) for their model would be if they were to build a model to address the unit’s driving question based on what they knew so far. Students accurately responded that the variables would be the water quality measures that they had conducted on the stream (pH, temperature, and water quality) and the factors that influenced the water quality measures. The teacher informed students that the modeling tool included no content—no science ideas—and that they would need to create a model that portrayed their own science ideas. Students would be responsible to plan, build, test, revise, and share their models that accurately modeled the stream phenomenon. In order to assist students in determining if their models worked the way that they thought they should work, students were provided with the following guidelines:
- Students were instructed to set each of their independent variables to the best possible conditions of a healthy stream and then run a simulation of their models by producing an output graph to determine if the water quality (the dependent variable) was set to the highest possible water quality;
- Students were instructed to test portions of their models (pH and water quality or temperature and water quality, for example) to systematically verify if those parts of the model ‘worked’. This meant students checked if the relationship between these variables was scientifically appropriate in that it matched the data the students had collected or the information they had learnt about in class beforehand;
- Students were instructed to select and set one independent variable on their models while keeping all other variables set at the best condition for water quality and then predict the impact on the overall water quality of the selected variable. They then had to test their model to see if their prediction and the results matched.
If any of the three model testing procedures worked differently than the student groups expected, students were asked to further evaluate their models by considering the following questions:
- Do I need to evaluate and revise the relationships in my model by evaluating the relationship type setting (more and more, less and less, etc.)? Are my relationships accurate?
- Do I need to rethink my science ideas?
Students were asked to evaluate if their model was complete and accurate or if their current thinking was problematic. As part of the process, students would both share their models and critique classmates’ models to get feedback from their peers and the teacher so that their models would provide a more complete and scientifically appropriate explanation. While working on their models, the teacher rotated between student groups to provide support and specific guidance. Some groups were asked to share their models with the entire class. In the following lesson, the teacher provided the students with an opportunity to reflect on the initial models they constructed in the previous lesson. In the beginning of this lesson, the teacher reminded the students about the elements of the modeling practice and asked them to test their current models to see if they work the way they would like them to work before adding the new variables:
“How many of you finished? [several students raise hands] … so what we want to do today, finish that first... Now today, if we get finished with this, and remember, so we plan, we build, we test...you remember we test it, how many of you tested it? [several students raise hands]. OK, you played around with the stuff, you got a data table. OK, so we make sure we test those today and revise it if it doesn’t quite work the way we want it towork, right?”
After a few minutes of discussion about testing and revising the model, the teacher instructed the students to add the new variables to their models once they felt confident about having the appropriate model:
“So we have to ask ourselves, Does this work? If you get to the way that it works, the way you think it works, then now we can expand our model ... you are going to plan, and build it, you are going to test it, you are going to see if it runs the way you think and then you will revise it.”
A second iteration of modeling occurred following data collection of a third water quality measure, conductivity, which represents the amount of dissolved solids. Students expanded their initial models to include all three water quality measures. A similar process was followed; students planned, built, tested, revised, and shared their models.
Several lessons later, after collecting dissolved oxygen and turbidity data from the stream, students had a third and final iteration that resulted in a model that reflected five water quality tests. Because it was the end of the semester, most groups did not have time to include turbidity in their models, simply due to time constraints. At the beginning of this model revision, the teacher reviewed what was done so far with the models and what students would be expected to add during this final revision. However, in this lesson, the teacher did not ask the students to test and revise their current models before adding the new variables:
“So we have been using this modeling program ... we’re trying to model relationships between various water quality measures, right? And the health of the stream and its organisms. And you have in there right now pH, temperature, and conductivity and what we are going to do today is add dissolved oxygen.”
After adding the dissolved oxygen variable, the teacher discussed with the students adding more connections between the variables in their models. Following this discussion, students were given time to add additional cross-variable relationships to their models:
“You have created a very complex model of a very complex system, right? The water quality is a really complex system. And for lots of you, you have your four water quality measures all connected to here [points at water quality variable in an example model projected on the screen], which is very important, it affects our relationships. But then there is also some of these kinds of relationships [cross referencing with her hands] that even make the model more complex. Right? So if we are really going to model the complexity of this phenomenon we also have to look for relationships in between.”
Summary: Students developed a model of a stream system, growing over time in quality and complexity, as new water quality data were collected. All the three observed iterations of modeling included the modeling practice elements: (i) building an initial model with the pH, temperature and water quality variables; (ii) adding the conductivity variable, and (iii) adding the dissolved oxygen variable. Following each new data collection, students were asked to revise their models by performing the following elements: Testing their existing models for accuracy and completeness, planning what variables to add to their model, adding those variables and defining their relationships with the other variables in the model, testing the model for expected outcome, and revising their model if necessary. Students were directed to receive feedback from their classroom peers during the modeling process and had several opportunities to share their models with other groups and with the entire class.
4.2. Development of Students’ Models and Metamodeling Knowledge
To address the second research question, ‘How did students’ modeling practice develop throughout the unit with regard to constructing, using, evaluating, and revising models?’, models developed by 11 groups were analyzed with a focus on how students included the appropriate variables and relationships at each modeling iteration cycle. Six of the 11 groups had complete and accurate models at the end of each of the modeling cycles. In the following, we present types of incompleteness found in the remaining five groups’ models as an umbrella term to signify that an element of a student’s model had not reached its required final form, as expected by the curriculum. Broadly, we distinguish two aspects under this umbrella term that occur throughout this article: We speak of inaccuracy when an element is present, but it may be specified in a less-than-ideal way with regards to using the model for making predictions or explanations of the observed phenomenon. We speak, more specifically, of incompleteness, if a model element is missing (i.e., a relationship or variable). We observed several different types of incompleteness in the models of five of our 11 groups (Table 1).

Table 1.
Types of incomplete models found in students’ models.
From the 11 groups of students that produced all three models during the lessons, three representative groups were taken for qualitative in-depth analysis. The first two cases represented a type of modeling: Group E produced fully complete models with all accurate variables and relationships in all models, representing the five groups that were able to accurately complete the task of building and revising their model in all modeling lessons. Group C had one inaccurate definition of relationship between variables that was revised in the next revision. This group is one of the two groups that were able to identify and revise prior inaccuracy in their models in a later modeling lesson and hence revise elements of their model in the narrow sense of its meaning (see theoretical background). In the third case, Group A’s model represented an exceptional case of a group that went beyond the expected system to be modeled.
We report findings for these three cases concerning the development in students’ models across the water quality unit (RQ 2) in the following section, as well as students’ answers to the metamodeling questions in the pre- and post-surveys about the nature and uses of models and modeling (RQ 3).
4.2.1. Case 1: A complete Model (Group E)
Student model. Five of the 11 analyzed groups had a complete and accurate model throughout the unit with regards to the variables expected at the three modeling cycles, amongst them Kara and Sandy (here and in all following cases, students’ real names have been replaced by pseudonyms) in group E (Figure 3). In the initial model, they included high level causal reasoning for both water quality measurements, as written in their prompt text boxes. For the relationship between pH and water quality, they wrote “Because as the pH of the stream gets farther away from neutral, organisms start dying.”, and for the relationship between thermal pollution and water quality they wrote, “Because as the temperature difference increases, the water quality gets worse. For example, algae grows more in warm water and causes more thermal pollution. Then fish start to die.” While the students did not provide exactly how they believed algae growth contributes to the warming of water, these responses can be counted as causal-mechanistic and also include an example to demonstrate the effect on specific species. Including an example was only found in this group’s reasoning. In their reasoning for the first model revision, the group wrote the following explanation for the relationship between conductivity and water quality: “Because as the conductivity increases, the quality of the water gets worse and worse.” This is a low-level response because it is only repeating the chosen relationship without providing causal reasoning. Similar low-level reasoning was also provided in the third modeling cycle, where they wrote the following explanation for the relationship between dissolved oxygen and water quality: “Because as the dissolved oxygen increases, the water quality will rapidly get better, but then it will increase by less”.
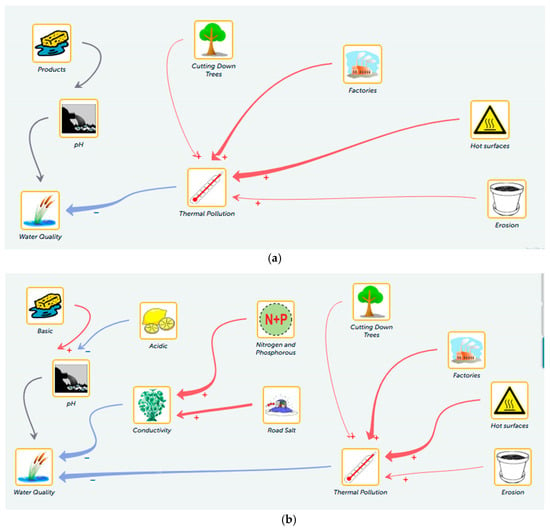
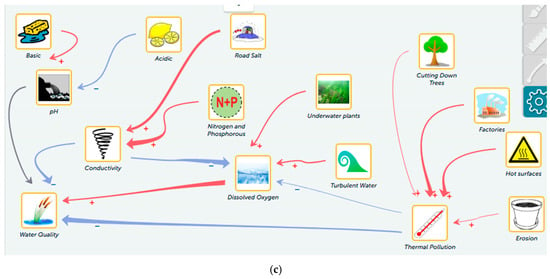
Figure 3.
Models submitted by case 1 (group E). (a) Initial model; (b) first model revision; (c) second model revision. Red arrows represent increasing and blue arrows decreasing relationships between variables. Black arrows denote varying influences, where students draw the assumed relationship on a graph.
Metamodeling knowledge. While students’ models from virtually all groups showed substantial progress across the water quality unit, students’ answers to the metamodeling questions about the modeling practice showed fewer and less pronounced changes.
We observed three dominant conceptions widely used amongst all participating students. All of these can be seen in the answers of group E. First, the most characteristic response was that students described models as a simple visualization, often seen as something used to show things that are otherwise hard to perceive due to their size (scaling) or with the goal to share information with others.
For example:
Quote 1: “Scientists use models to show/describe phenomena that their peers may need to see.” [Sandy, pre-survey, question 3]
Second, many students in both pre- and post-surveys reported that they needed to pay close attention to the model’s accuracy and to it being ‘up-to-date’. Students did not specify what they meant by up-to-date, but it is likely that they were referring to the variables they added into their models as they progressed through the unit. As the third prominent feature, students indicated that a good model has to be simple [3]. Notably, students in group E transgressed these rather basic conceptions and added that models need to be parsimonious (Quotes 2 and 3) in that they focus only on the essential concepts involved in the process. A positive surprise was here that Sandy even realized that models are, in fact, not accurate (Quote 4):
Quote 2: “A scientific model should be clear with no unneeded parts. It should also be up to date on all current information.” [Kara, pre-survey, question 4]Quote 3: “You need to think about all of the scientific ideas and concepts involved, our model should be accurate, and the best models are simple and don’t have unnecessary parts.” [Kara, post-survey, question 4]Quote 4: “I think about how […] not everything will be exact.” [Sandy, pre-survey, question 4]
Students in group E showed development from pre- to post-survey in terms of their perception of model uses: Kara, in the pre-survey, focused on showing, understanding or explaining information. In the post-survey, she indicated models can be used to explore how scientific ideas work (unlike what scientists use models for) or, to explain difficult issues or to test predictions (like scientists do). Seen in the context of all participating students in the unit, conceptions about using models for predictions were rare. Similar to Kara, Sandy started (pre-survey) with a focus on using models for representation and on specific aspects of designing the model (Quote 5). The student then shifted, in the post-survey, to a focus on using models to explore interactions (Quote 6).
Quote 5: “I think about how there may be a need for a key, the scale […]” [Sandy, pre-survey, question 4];Quote 6: “We could use scientific models to model how things affect our stream.” [Sandy, post-survey, question 2]
Students in group E did not show consistent distinctions between how they (as students) may use models versus how scientists use them. In the pre-survey, students used almost the same conceptions for both scientists and themselves; in the post-survey, the students from group E indicated that students can use advanced practices of modeling (i.e., test predictions, focus on interactions).
Summary. In Case 1 (Group E), the students’ model could account as a high level explanation of the stream’s water quality. It was characterized by accurately showing all relevant variables and the relationships between them throughout the three modeling cycles. They also demonstrated examples of high level causal reasoning for defining the relationships between variables in their initial model. Students’ conceptions about the nature of models and modeling included typical lower-level conceptions that we also observed across multiple other participating students (e.g., models as visualizations). However, group E extended these simple conceptions by sophisticated and rare conceptions regarding the inaccuracy of all models and the possibility to use models for making predictions.
4.2.2. Case 2: An incomplete model revised in later modeling iterations (Group C)
Students’ model. Five of the 11 groups in our sample showed a total of nine instances of incomplete (e.g., missing or unconnected variable, undefined relationship) or inaccurate (e.g., inaccurate labels or relationships) models (see Table 1). Of the five instances that we observed specifically in students’ initial model and in the first model revision, only two were revised in the following model submission, thus falling into the category of a model (element) revision in the narrow sense. For these two cases, we assume that students appropriately tested, evaluated, and revised their models and may have just ran out of time to complete their models. Rick and Ron of group C were one of these groups.
The students produced an incomplete initial model, in which the relationship between temperature and water quality was defined as ‘vary’ and was drawn as an increasing and then decreasing relationship (Figure 4b). Their explanation for this relationship provided a basic reasoning: “When temperature changes, the water quality changes.” The relationship between pH and water quality was also basic and not causal: “Because when the pH changes the water quality changes.”
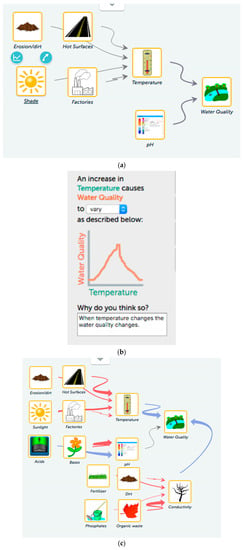
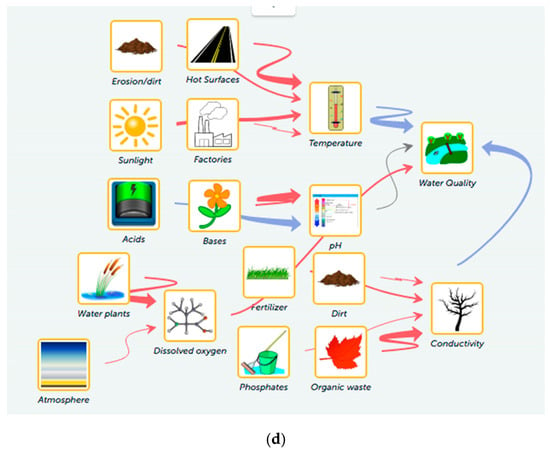
Figure 4.
Models submitted by Case 2 (Group C). (a) Initial model; (b) relationship between temperature and water quality as specified by students in their initial model; (c) first model revision; (d) second model revision. Red arrows represents increasing and blue arrows decreasing relationships between variables. Black arrows denote varying influences, where students draw the assumed relationship on a graph.
In the first model revision, the students changed the relationship between temperature and water quality to be a decreasing relationship, therefore improving their model to be more accurate. They also added the conductivity variable to their model.
In their third model, Rick and Ron added the dissolved oxygen variable and accurately defined the effect of it on water quality. They added an explanation to this relationship that did not include any causal reasoning: “D.O. [dissolved oxygen] is good so it will cause water quality to increase” (Figure 4d).
Metamodeling knowledge. In group C, Rick was one of only very few students in our unit to indicate that models are never perfect (Quote 7, see also Quote 4 above), that there are competing models (Quote 8) and that they constantly change (Quote 9):
Quote 7: “[…] All models should be simplistic. All models have right and wrong factors.” [Rick, pre-survey, question 1]Quote 8: “They [models] are simple, and there can be many correct models about one phenomenon.” [Rick, post-survey, question 1]Quote 9: “[…] They are constantly changing, so if you have to change it, you’re ok. […].” [Rick, pre-survey, question 4]
Students in this Group showed some development from pre- to post-survey with students’ understanding becoming more refined. For instance, Rick went from an understanding that scientists (Q3) use models to “represent and test things” to a more specific understanding that they use models to “test different theories on scientific phenomena.” The same student indicated before the unit only that change is a regular process in modeling (Quote 9 above), while specifying at post also when the model should be changed:
Quote 10: “You might have to change it, if your theory doesn’t work, that’s when you revise it […].” [Rick, post-survey, question 4]
Unlike in Case 1 (Group E), students in Case 2 (Group C) seemed to see differences between how they as students use models versus how scientists use models. Both students appeared to associate more advanced aspects of modeling with scientists compared to how students use models:
Quotes 11: [Rick, pre-survey, questions 2&3];Students: “[…] to scale something.”Scientists: “[…] represent and test things”;Quotes 12: [Ron, post-survey, questions 2&3];Students: “To see what happens in a smaller version.”Scientists: “[…] show other people what will happen in a smaller version.”
Summary. Students in Case 2 (Group C) stood out by being one of only two groups that revised an earlier incomplete model in the narrow sense of the meaning. Their reasons for defining the relationships between variables in their model did not prove to be of high level causal reasoning. While they appeared to distinguish between how models can be used by scientists versus students, they specified their understanding from pre- to post-survey and expressed rare and advanced conceptions referring to competing models and model revisions.
4.2.3. Case 3: A Complete Model with Additional Variables (Group A)
Student model. Of the 11 groups with all three model submissions, Group A was a particularly interesting case because the students provided a model that would not be considered to confirm to the expectations in the strictest sense (i.e., with regards to the expected variables at the different modeling iterations). However, the students’ model can neither be considered to have strictly incomplete or incorrect sections.
The students, Dave and Zack, constructed a complete and accurate initial model. They had the expected variables and relationships of temperature and pH affecting water quality. They provided a low-level response for explaining the effect of temperature on water quality that just repeated the defined relationship: “The higher the temperature the lower the water quality,” but did not write any response for the pH and water quality relationship.
In the first model revision, Dave and Zack accurately added the conductivity variable to their model, and added a low-level response to its effect on the water quality that describes the type of relationship but not the causal reasoning of it: “First conductivity is fine for a little bit, but then it starts lowering the water quality by a lot.” However, in this modeling cycle, they also added another variable that was not expected to be directly connected to the water quality: bacteria. In their explanation for this relationship they wrote: “The bacteria takes in a lot of the oxygen in the water making it unsuitable for organisms to live in it.” This response provides causal reasoning for this relationship. They decided to directly connect the bacteria variable to water quality and not to the mediating variable, oxygen level in the water, that was mentioned in the students’ response and was added to the model as ‘dissolved oxygen’. In the second model revision, Dave and Zack did not change the relationship between the bacteria and water quality variable. A reason for this may be linked to real-life experiences by students and the related preconceptions, where students learn that bacteria presence in water is ‘bad’ in a direct way (i.e., without mediating variables) for humans or other organisms. In addition, the teacher’s focus on the upcoming model revision lay on integrating dissolved oxygen as a variable, hence probably distracting students from going back and working on the bacteria variable.
The students also added dissolved oxygen as a variable before they were expected to (first model revision, Figure 5b). While they did not connect this variable in their first model revision before this variable was formally required in class, they did go back to it in their second and final model revision and connected the variable accurately, even though they did not provide an explanation for this relationship (Figure 5c). Even though they were triggered to do so, this may be considered an example for a model revision in the narrow sense, i.e., going back to revise a model element that was entered in an earlier model version.
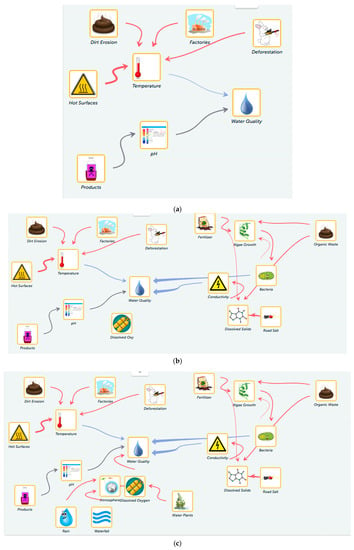
Figure 5.
Models submitted by case 3 (Group A). (a) Initial model; (b) first model revision; (c) second model revision. Red arrows represents increasing and blue arrows decreasing relationships between variables. Black arrows denote varying influences, where students draw the assumed relationship on a graph.
Metamodeling knowledge. Like many other students in our study, both students in Case 3 (Group A) indicated—both during the pre- and post-surveys—that models are used for scaling (Quote 13) and visualization (Quote 14):
Quote 13: “If we can’t see something from the naked eye, you can make a model to see what it looks like up close.” [Dave, pre-survey, question 2]
Quote 14: “[...] a model of something that is being studied. It can be visualized and created to model almost anything.” [Zack, post-survey, question 1]
Similarly and connected to this conception, the students in case 3 put their focus on basic aspects of modeling that might indicate the students’ modeling practice to be more model-of -oriented [4], instead of conceptualizing their modeling as a way to test or generate knowledge (model-for view [4]). For example, the students mentioned that models have to always be correct (Quote 15) and that they have to pay attention to the specifics of model construction and design (Quote 16):
Quote 15: “So that they are always correct.” [Dave, post-survey, question 4]Quote 16: “What is [going to] represent what.” [Zack, pre/post-surveys, question 4]
(Note: This likely refers to pictures students chose for variables in their models).
Unlike in Case 1, students in Case 3 did not attribute additional, more advanced aspects of model usage to students as model users. However, Group A associated more advanced levels of model uses to scientists. For Zack, the understanding of model uses became also more refined from pre- to post-survey:
Quote 17: “They [scientists] use models to explain a theory.” [Dave, pre-survey, question 3]Quote 18: “Scientists use scientific models to predict what things could turn out as.” [Zack, pre-survey, question 3]Quote 19: “To hypothesize on how somethings works.” [Zack, post-survey, question 3]
Summary. In Case 3 (Group A), students produced an interesting model that showed they tried to integrate their own ideas into their models. The students provided mixed results in terms of their ability to go back and revise earlier aspects of their model. While their reasons for defining the relationships were of low-level causal reasoning, the students’ conceptions about modeling were focused both on basic (e.g., models have to be always correct) and advanced uses of models, while the latter was associated more with scientists’ uses of models.
5. Discussions
We start the discussion focusing on relevant issues with regards to how the different elements of modeling can be integrated into classroom practice when using the modeling tool (RQ1). The discussion of findings related to students’ models (RQ2) and their metamodeling conceptions (RQ3) are then used as a basis to draw implications regarding the sequence and structure of students’ learning. We discuss the findings from the unit enactment, indicating that the modeling practice elements were used in mini-cycles after each time new knowledge was developed by the students, thereby having their models grow in quality and complexity. We conclude by reviewing limitations and research method.
5.1. Incorporating the Elements of the Modeling Practice
All of the modeling practice elements described by Schwarz and colleagues [2] were integrated in the water quality unit: Students constructed their initial models, used the models to test the relationships between the variables against collected empirical data, evaluated the accuracy of their models by receiving feedback from the teacher and classroom peers, and revised their models based on the feedback and newly acquired knowledge. The elements were used in several lessons designed to engage students with the modeling tool in what we refer to as ‘modeling cycles.’ These modeling cycles refer to the iterative modeling cycle suggested by Clement [12], in which students construct, use, evaluate, and revise their models to test a hypothesis.
As suggested by others, our study reinforces the notion that technology tools, especially computational modeling tools, can support students’ development of the modeling practice, provided there are appropriate scaffolds and teacher support [9,10]. In this study, we found that using the computational modeling tool provided the students with an opportunity to engage with all the elements of the modeling practice, most prominently with regards to constructing and revising models as they grew in complexity.
It was hard to find clear evidence of students going back to revise their model in the narrow sense, i.e., by changing elements of their model added in an earlier model version. As we also saw, some groups had a tendency to not revise earlier parts of their models when given the opportunity in the next modeling iteration. This might point to the need for specific instructional support to be placed on the elements of evaluating and revising existing models, specifically ensuring enough working time and scaffolds to test, evaluate, and revise their models, including earlier parts. We suggest including more peer-critique activities, such as gallery walk or showcases of models, with sufficient time for students to revise problematic, earlier elements of their models afterwards.
In Section 5.4 below, we summarize the implications for supporting student’ modeling practice that we derive both from our findings, as well as from reflections by the teacher of the water quality unit.
5.2. Development of Students’ Models and Related Explanations
Models are tools used to show the modeler’s explanation of complex phenomena [11]. In all cases examined in this study, students’ models developed in both their complexity and quality, integrating additional variables at each modeling cycle to improve their model’s explanatory and predictive power and to fully address the driving question of the unit. In comparison to prior studies on students’ metamodeling knowledge [17,35,36], these findings for students’ progress in the modeling practice is generally positive. Other research on students’ progress in the modeling practice has, however, found comparable results [2]. Even though this would have to be properly investigated by future research, these combined findings may point towards progress in the performance of students’ modeling practice (i.e., constructing, using, evaluating, and revising of models) being more likely observable in classrooms than the progress in students’ metamodeling knowledge (unless, of course, instruction specifically targets this aspect).
Novak and Treagust [34], investigating the water quality unit addressed in this paper, suggested that students face several challenges when required to integrate new knowledge into their existing explanation of phenomena, in what they refer to as the evolving explanation. The advantages and challenges with the notion of models growing in the quality and complexity dimension, presented in this paper, aligns with those presented by Novak and Treagust [34], with students’ evolving explanation. Students’ challenges may include ignoring new knowledge, cognitive difficulties in changing their existing explanations, or lack of experience in revising their explanation. These challenges were also reflected in some the results presented in this paper.
While we observed that students were able to add to their models and develop the models’ complexity profoundly, we found only two out of five groups that clearly went back to revise instances of incompleteness of an earlier model in a later revision. At the same time, it was hard to find clear cases where students should have made revisions for earlier models’ incompleteness, but ended up not doing so. The absence of clear examples from this field is partially caused by the difficulty to exclude time constraints as a source of model incompleteness and in the fact that, due to the guidance by the teacher and the class-internal model evaluation cycles, there were comparatively few possibilities for students to end up with missing or inaccurate elements in their model. Hence, we can conclude that it was much easier to observe processes of adding complexity to models than to observe processes of going back and revising earlier parts of the model. We can only tentatively conclude a tendency for students rather to add to the model then to revise parts that they entered in earlier model versions. From the in-class observations and the teachers’ reflections, we can, however, confirm that the students revised elements of their model that they had entered in the same lesson. We conclude that these students may have had difficulties realizing that earlier elements of their model may need to be evaluated and revised, as well. Another relevant conclusion to be drawn here is that the context we worked with (water quality) included many variables, leading to substantial complexity of students’ models. Especially for students at the lower end of the performance spectrum, it is important to provide practice opportunities for students, such as we provided (see above), in which they can conduct the different elements of the modeling practice in SageModeler in a simple, everyday context before they turn to more complex contexts.
5.3. Development of Students’ Metamodeling Knowledge
Students’ answers to the questions on metamodeling knowledge revealed that many students in our enactment employed basic conceptions about the nature of models and modeling. These have also been found in other studies: For example, students typically considered models to be simple visualizations, sometimes used for scaling [3,22,37], or students thought about models as a means of sharing information with others [38]. While students often indicated that models help to better understand something (e.g., Zack in Case 3), the more sophisticated view that models can help spark creative insight was mostly absent [35]. This is reflected in the distinction made by Passmore and colleagues [4], where using models of (i.e., model as a representation of something) refers to a more simple conceptualization of modeling than using model for a specific purpose (i.e., answering a questions, explaining/predicting a phenomenon). Those conceptions reported by prior studies as higher-level conceptions—such as that models are used to explain or predict (cf. Cases 1 and 3), that models are usually not exact (cf. Quote 4) or even that models are for testing different hypotheses (cf. Group 2)—did occur amongst our students, but were rare [37,38].
The difference between pre- and post- survey questions showed less pronounced differences than the changes in students’ models with only half of the students in our three cases showing clear changes. The observed developments concerned, for example, students moving from simple conceptions of models as visualizations to using models to understand interactions between variables (respective students as modeler) or included refinements in understanding of model uses (scientist as modeler). We noticed that students’ models developed more pronouncedly across the unit than students’ answers to the metamodeling question. This seems to be in line with findings by other studies that report few changes in students’ metamodeling understanding across teaching units [38], as well as across secondary school grade bands [35]. This finding also appears logical with regards to the focus of the water quality unit, which was put on the development of student models, while much less classroom time was devoted to the nature of models and modeling. Furthermore, as neither the students nor the teacher had any benefit from improving their metamodeling understanding besides the epistemological merit, we did not observe any indices for teaching-to-the-test. Teaching and learning with the modeling practice should ideally be a combination of both learning to do the different elements of the modeling cycle and developing metamodeling understanding [2]. With this perspective, our results highlight that students’ performance on these two dimensions of modeling do not automatically co-develop if the teaching lies prominently on one of them. However, the results do suggest that a prominent focus in instruction on the modeling practice can still trigger students to also further develop aspects of their metamodeling understanding.
Case 2 (Group C) stood out by being one of only two groups that clearly revised a part of an earlier, incomplete model. Interestingly, Case 2 (Group C) was also one of few groups that provided advanced conceptions about not only that, but also when models change (Quote 10). This finding raised the question to what extent students with more advanced modeling practices also possess a more refined understanding about the nature of models and modeling or to what extend metamodeling knowledge may be a predictor of students’ modeling practice (compare Ref. [18]).
Seen across groups, when students thought of themselves as model users, they seemed to think more about models as a visualization. In contrast, when our students thought about scientists’ uses of models, modeling was more associated with prediction and testing of theories. This reflects the pragmatic element of models as user-specific tools [3]. If the students believe that a model is mostly a visualization, then it might also be less relevant for them to go back and fix an earlier incomplete model, since they might not consider the model in its entirety being used for explaining and predicting, in which case an earlier incomplete model would have substantial influences on the result.
5.4. Implications: Integrating the Modeling Practice Elements to Develop Quality and Complexity of Models
Our observations during the unit, as well as our findings showed that most students were able to construct complex models and that they were able to add in additional variables and relationships later on, thus suggesting they were able to conceptualize the resulting complexity of their models. The data and observations provided us with too few instances to allow us to draw definitive conclusions about differences in student performance between the elements of the modeling cycle (i.e., construct, use, evaluate, revise, [2,12,39]). However, we were able to draw more general conclusions with regards to the balance of students’ modeling practice between increasing the complexity of their models (i.e., adding and connecting elements) and working on revisions of earlier parts or generally improving the quality of their model:
- Only two out of five groups with incomplete models in the initial model and the first model revision revised (parts of) earlier versions of their model they had submitted in previous lessons (revision in the narrow sense). We were only able to observe students making revisions to elements of their model they had added right before in the same lesson;
- Students’ answers to the meta-modeling questions:
- ◯
- often focused on the requirements to have complete or up-to-date models, thus suggesting a focus on having included all the required elements (for similar findings, see, e.g., Ref. [35]). A related finding by Sins and colleagues [18] points at the relationship between students’ epistemological knowledge and their modeling practice, indicating that students with low epistemic beliefs rather focused on model surface features, instead of the models’ predictive or explanatory features;
- ◯
- described models as tools for visualization or assistance in learning, communicating, and understanding. In contrast, they rarely described modeling with regards to using models for predictions or testing (for similar findings see, e.g., Ref. [6,36]);
- ◯
- devoted little attention to aspects of model revision in the narrow sense, i.e., going back and changing elements that had been specified earlier. For future research, it may be useful to determine if differences in performance can be found quantitatively between the elements of modeling practice, such as those in students’ conceptualization of aspects of metamodeling knowledge described by Krell and colleagues. [35].
Based on our findings, we suggest that students’ work in developing their models might be dominantly a reflection of growing complexity, while the quality of their model (i.e., its predictive and explanatory power) does develop, but less pronouncedly. In contrast, an idealized modeling practice would be described not only in terms of developing model complexity, but, more importantly, by a stronger development in model quality, compared to the model’s complexity.
In Figure 6, we illustrate how students in the examined study applied the modeling practice elements when learning the water quality unit. The figure shows a simplified process across the modelling lessons, by which students’ models develop from an initial to a final model via several cycles of modeling. Students’ models grow in complexity when they add variables or relationships between variables (vertical dimension), increasing the interactions between components in the modeled system. Students’ models also develop in terms of their quality (horizontal dimension). The quality dimension refers to both the accuracy of the model and the completeness in addressing the models’ ability to predict and explain the target phenomenon.
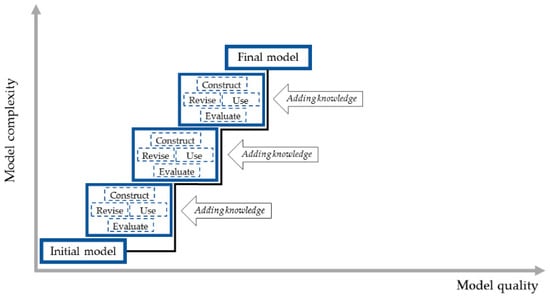
Figure 6.
Illustration of the process in which the modeling practice elements were integrated in the water quality unit, in relation to the growing dimensions of model quality and complexity.
In the illustration of the modeling process presented in Figure 6, solid blue lines indicate both the different (preliminary) versions of the students’ model and mini-modeling cycles that the students conducted. Within each of these, dashed lines indicate that our data does not allow us to draw definitive conclusions about how specifically students apply or differentiate between the different elements of the modeling practice or in how far the elements of the modeling cycle may have become automatized for the students.
Ideally, as students gain new knowledge in their investigation, their models are expected to evenly develop in both the complexity and quality level. Both teachers and curricular materials should provide sufficient support to balance the progression of students’ models within this` zone. However, students’ models may shift away from the balanced zone. As seen in this study, several student groups were able to remain within the balanced zone by constructing and revising models that are accurate and complete in all modeling iteration. Several student groups failed to produce fully complete models, probably due to students’ tendency to focus more on adding new parts, but less on revising older sections of the model, or because of not being provided with sufficient time to test, evaluate, and revise their existing models before adding the new variables.
The purpose of the suggested model is to provide a structure that can be used to develop student-centered curriculum materials for modeling practice. Importantly, the suggested model is not a critique or revision of prior models about modeling (e.g., Ref. [2,37]). Instead, this model has a more specific focus in that it describes how students experience the modeling practice elements in the classroom, where adding complexity (i.e., variables and relationships) is a defining element of their work progress. The distinction that our model addresses between the classic modeling cycle and the process our students seemed to employ can be aligned with the work of previous authors. For example, Schwarz and colleagues’ [2] second levels on the dimension of ‘understanding models as changeable entities’ (revise model due to authority request, to clarify something or to add to the model) is equivalent to the level our model suggests student predominantly operate at. In Upmeier zu Belzen and Krüger’s [37] model, our work refers to the dimension ‘changing model’ and puts students at competence level 2.
As seen in our study, several groups did not have a fully complete model at the end of the modeling process. Some of these groups did not revise incomplete elements of their existing models in the following modeling cycle. We suggest that attention should be placed on the mini-modeling cycles to make sure students are provided with sufficient time and scaffolds to test and revise their existing models before adding the new variables and relationships. Maintaining the balance between the model complexity and model quality dimensions is not easy, as was found in our study. It is the responsibility of the teacher and teaching materials to support students in balancing between these two dimensions during the modeling lessons, explicitly focusing on the different modeling practice elements in each cycle. By balancing between the dimensions, students’ modeling practice can develop to integrate high levels of modeling abilities and understanding of the nature of models and modeling [2].
The visualization of the modeling process in Figure 6 is derived from observations made among a small number of students. We have still had no chance to show empirically that this model is able to predict observable student data about their modeling practice with greater accuracy than other or simpler models. This is a task for future research.
5.5. Limitations of Methods
The small scale of our study did not allow us to draw any quantitative comparisons between students’ models or metamodeling knowledge, e.g., from pre- to post-surveys. We conducted an in-depth analysis of only three groups to avoid methodological difficulties. This allowed us some interesting insights by identifying more subtle changes in students’ conceptions that would have been blurred by a focus on a larger group. It appeared important for our research questions to exclude, as far as possible, that incompleteness or inaccuracy in students’ models were caused by too little work time. However, the resulting criteria for case selection, which required that groups had to have all three model stages submitted, meant also that we most likely report a positive selection of cases, i.e., students that performed above average in terms of their modeling practice and metamodeling conceptions.
A related limitation of this study lies in the generally above-average students in our sample. Our study was intended as a proof-of-concept for how the practice of modeling may be enacted in classrooms using the new modeling software. While the sample was justified to these ends and while the employed software has been successfully used also with lower-performing students in various classes and in various contexts [28,29,30,31], further studies need to verify with more representative samples the findings of this study.
A methodological difficulty was that, for many of the participating student groups beyond the cases presented here, we cannot clearly identify if students’ models could be clearly counted as having a type of incompleteness, or, whether this was due to a time constraint. Additionally, not all students reliably provided information in the explanatory fields for their models, thus limiting the power of analyzing students’ model explanations and leading us to analyze them in addition to students’ models, but not as a separate data source. The reason behind this did not lie in technical problems, but in a pedagogical choice by the teacher, who put less focus on the explanatory fields towards the end of the unit, thus inhibiting reliable interpretation of developmental trends across the unit based on this data.
Our analysis is partially limited with regard to how students applied and thought about the different elements of the modeling cycle (i.e., construct, use, evaluate, revise), due to limited insight during classroom observations on how students evaluated each other’s models. In connection to this, the metamodeling questions (specifically Q4) turned out to be problematic, as we asked about all practice elements in one question and may thereby prevent students from writing about individual practices separately. It should also be noted that the range of questions was limited and does not cover all possible aspects of metamodeling knowledge [6,35,37]. Additionally, as students had a tendency to provide shorter answers in the post- than in the pre-survey, our reports about changes in conceptions from pre- to post-survey are likely a conservative estimate.
Lastly, the larger frame of our project (multiple collaborating teachers with individual units in different schools and states) limited us to the online assessment of students’ models, the related prompts, and the online-survey modality of our meta-modeling questions. As a consequence, we were unable to systematically ask students follow-up questions about their models or modeling conceptions, as one may have done in in-depth interview analysis.
Summary. Altogether, we found that integrating the modeling tool in the water quality unit supported students’ ability to apply the different elements of the modeling practice, as well as it tended to expand students’ metamodeling knowledge. This study contributes to existing literature by providing an example of how the modeling practice can be integrated into classroom practice by using a state-of-the-art computational modeling tool and by providing insights into the learning gains and hurdles that students and teachers can face. Our results indicate that the modeling practice elements were experienced by the students in mini-cycles of constructing, using, evaluating, and revising their models as new knowledge was gained, which contributed to the development of their models in both quality and complexity. Results also suggest that students face several challenges when using modeling tools and developing their modeling practice, mostly when evaluating and revising existing models. Our results suggest that using an online modeling tool can support students’ modeling practice given the appropriate time and scaffolds.
Author Contributions
Conceptualization, T.B., S.T.O., A.M.N.; Methodology, T.B., S.T.O.; Software: Concord Consortium at Concord, MA, USA; Analysis, T.B., S.T.O.; Writing—Original Draft Preparation, T.B., S.T.O., A.M.N.; Writing—Review & Editing, T.B., S.T.O.; Visualization, T.B., S.T.O.; Supervision, T.B., S.T.O.; Project Administration, T.B.; Funding and Acquisition, T.B.
Funding
This work was supported by the National Science Foundation (NSF) under grants DRL-1417809 and DRL-1417900. Any opinions, findings, conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the NSF.
Acknowledgments
We thank the NSF for financial report. From a larger perspective than the study presented here, we would like to thank our colleagues from our research group, specifically Joseph Krajcik from Michigan State University and Dan Damelin from the Concord Consortium, as well the collaborating teachers who worked with us on the software development (SageModeler), the different curriculum units, and the conducted research. We are especially grateful to our project’s advisory board for their continued and valuable support.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- National Research Council [NRC]. A Framework for K-12 Science Education: Practices, Crosscutting Concepts, and Core Ideas; The National Academies Press: Washington, DC, USA, 2012; ISBN 978-0-309-21742-2. [Google Scholar]
- Schwarz, C.V.; Reiser, B.J.; Davis, E.A.; Kenyon, L.; Achér, A.; Fortus, D.; Krajcik, J. Developing a learning progression for scientific modeling: Making scientific modeling accessible and meaningful for learners. J. Res. Sci. Teach. 2009, 46, 632–654. [Google Scholar] [CrossRef]
- Stachowiak, H. Allgemeine Modelltheorie (General Model Theory); Springer: Vienna, Austria, 1973. [Google Scholar]
- Gouvea, J.; Passmore, C. ‘Models of’ versus ‘Models for’. Sci. Educ. 2017, 26, 49–63. [Google Scholar] [CrossRef]
- Lehrer, R.; Schauble, L. Cultivating model-based reasoning in science education. In The Cambridge Handbook of the Learning Sciences; Sawyer, R.K., Ed.; Cambridge University Press: New York, NY, USA, 2005; pp. 371–387. [Google Scholar]
- Schwarz, C.V.; White, B.Y. Metamodeling knowledge: Developing students’ understanding of scientific modeling. Cogn. Instr. 2005, 23, 165–205. [Google Scholar] [CrossRef]
- Schwarz, C.; Reiser, B.J.; Acher, A.; Kenyon, L.; Fortus, D. MoDeLS: Challenges for defining a learning progression for scientific modeling. In Learning Progressions in Science; Alonzo, A., Gotwals, A.W., Eds.; Sense Publishers: Rotterdam, The Netherlands, 2012; pp. 101–138. ISBN 978-9460918223. [Google Scholar]
- Pierson, A.E.; Clark, D.B.; Sherard, M.K. Learning progressions in context: Tensions and insights from a semester-long middle school modeling curriculum. Sci. Educ. 2017, 101, 1061–1088. [Google Scholar] [CrossRef]
- Fretz, E.B.; Wu, H.K.; Zhang, B.; Davis, E.A.; Krajcik, J.S.; Soloway, E. An investigation of software scaffolds supporting modeling practices. Res. Sci. Educ. 2002, 32, 567–589. [Google Scholar] [CrossRef]
- Quintana, C.; Reiser, B.J.; Davis, E.A.; Krajcik, J.; Fretz, E.; Duncan, R.G.; Kyza, E.; Edelson, D.; Soloway, E. A scaffolding design framework for software to support science inquiry. J. Learn. Sci. 2004, 13, 337–386. [Google Scholar] [CrossRef]
- Harrison, A.G.; Treagust, D.F. A typology of school science models. Int. J. Sci. Educ. 2000, 22, 1011–1026. [Google Scholar] [CrossRef]
- Clement, J. Learning via model construction and criticism. In Handbook of Creativity; Sternberg, R., Ed.; Springer: Boston, MA, USA, 1989; pp. 341–381. ISBN 978-0521576048. [Google Scholar]
- Bamberger, Y.M.; Davis, E.A. Middle-school science students’ scientific modelling performances across content areas and within a learning progression. Int. J. Sci. Educ. 2013, 35, 213–238. [Google Scholar] [CrossRef]
- Fortus, D.; Shwartz, Y.; Rosenfeld, S. High school students’ meta-modeling knowledge. Res. Sci. Educ. 2016, 46, 787–810. [Google Scholar] [CrossRef]
- Gilbert, J.K. Models and modelling: Routes to more authentic science education. Int. J. Sci. Math. Educ. 2004, 2, 115–130. [Google Scholar] [CrossRef]
- Gobert, J.D.; Pallant, A. Fostering students' epistemologies of models via authentic model-based tasks. J. Sci. Educ. Technol. 2004, 13, 7–22. [Google Scholar] [CrossRef]
- Krell, M.; Krüger, D. University students’ meta-modelling knowledge. Res. Sci. Tech. Educ. 2017, 35, 261–273. [Google Scholar] [CrossRef]
- Sins, P.H.; Savelsbergh, E.R.; van Joolingen, W.R.; van Hout-Wolters, B.H. The relation between students’ epistemological understanding of computer models and their cognitive processing on a modelling task. Int. J. Sci. Educ. 2009, 31, 1205–1229. [Google Scholar] [CrossRef]
- Pluta, W.J.; Chinn, C.A.; Duncan, R.G. Learners’ epistemic criteria for good scientific models. J. Res. Sci. Teach. 2011, 48, 486–511. [Google Scholar] [CrossRef]
- Zangori, L.; Peel, A.; Kinslow, A.; Friedrichsen, P.; Sadler, T.D. Student development of model-based reasoning about carbon cycling and climate change in a socio-scientific issues unit. J. Res. Sci. Teach. 2017, 54, 1249–1273. [Google Scholar] [CrossRef]
- Passmore, C.; Gouvea, J.S.; Giere, R. Models in science and in learning science: Focusing scientific practice on sense-making. In International Handbook of Research in History, Philosophy and Science Teaching; Matthews, M., Ed.; Springer: Dordrecht, The Netherlands, 2014; pp. 1171–1202. ISBN 978-94-007-7654-8. [Google Scholar]
- Grosslight, L.; Unger, C.; Jay, E.; Smith, C. Understanding models and their use in science: Conceptions of middle and high school students and experts. J. Res. Sci. Teach. 1991, 28, 799–822. [Google Scholar] [CrossRef]
- Edelson, D. Design research: What we learn when we engage in design. J. Learn. Sci. 2002, 11, 105–121. [Google Scholar] [CrossRef]
- Concord Consortium, Building Models Project. Available online: https://learn.concord.org/building-models (accessed on 14 September 2018).
- Concord Consortium, Common Online Data Analysis Platform Project (CODAP). Available online: https://codap.concord.org/ (accessed on 14 September 2018).
- Finzer, W.; Damelin, D. Design perspective on the Common Online Data Analysis Platform. In Proceedings of the 2016 Annual Meeting of the American Educational Research Association (AERA), Washington, DC, USA, 8–12 April 2016. [Google Scholar]
- Jackson, S.; Krajcik, J.; Soloway, E. Model-It: A design retrospective. In Innovations in Science and Mathematics Education: Advanced Designs for Technologies of Learning; Jacobsen, M., Kozma, R., Eds.; Lawrence Erlbaum: Mahwah, NJ, USA, 2000; pp. 77–115. ISBN 978-0805828467. [Google Scholar]
- Bielik, T.; Opitz, S. Supporting secondary students’ modeling practice using a web-based modeling tool. In Proceedings of the 2017 Annual Meeting of the National Association for Research in Science Teaching (NARST), San Antonio, TX, USA, 22–25 April 2017. [Google Scholar]
- Damelin, D. Technical and conceptual challenges for students designing systems models. In Proceedings of the Annual Meeting of the 2017 National Association for Research in Science Teaching (NARST), San Antonio, TX, USA, 22–25 April 2017. [Google Scholar]
- Damelin, D.; Krajcik, J.; McIntyre, C.; Bielik, T. Students making system models: An accessible approach. Sci. Scope 2017, 40, 78–82. [Google Scholar] [CrossRef]
- Stephens, L.; Ke, L. Explanations and relationships in students’ mental and external models. In Proceedings of the 2017 Annual Meeting of the National Association for Research in Science Teaching (NARST), San Antonio, TX, USA, 22–25 April 2017. [Google Scholar]
- Novak, A.M. Using technologies to support middle school students in building models of stream water quality. In Proceedings of the 2017 Annual Meeting of the National Association for Research in Science Teaching (NARST), San Antonio, TX, USA, 22–25 April 2017. [Google Scholar]
- Krajcik, J.; Shin, N. Project-based learning. In The Cambridge Handbook of the Learning Sciences, 2nd ed.; Sawyer, R., Ed.; Cambridge University Press: New York, NY, USA, 2015; pp. 275–297. [Google Scholar]
- Novak, A.M.; Treagust, D.F. Adjusting claims as new evidence emerges: Do students incorporate new evidence into their scientific explanations? J. Res. Sci. Teach. 2018, 55, 526–549. [Google Scholar] [CrossRef]
- Krell, M.; Upmeier zu Belzen, A.; Krüger, D. Students’ levels of understanding models and modelling in Biology: Global or aspect-dependent? Res. Sci. Educ. 2014, 44, 109–132. [Google Scholar] [CrossRef]
- Justi, R.; van Driel, J. A case study of the development of a beginning chemistry teacher's knowledge about models and modelling. Res. Sci. Educ. 2005, 35, 197–219. [Google Scholar] [CrossRef]
- Upmeier zu Belzen, A.; Krüger, D. Modellkompetenz im Biologieunterricht (Model competence in biology education). Zeitschr. Did. Naturw. 2010, 16, 41–57. [Google Scholar]
- Crawford, B.A.; Cullin, M.J. Supporting prospective teachers’ conceptions of modelling in science. Int. J. Sci. Educ. 2004, 26, 1379–1401. [Google Scholar] [CrossRef]
- Clement, J.; Rea-Ramirez, M. Model Based Learning and Instruction in Science; Springer: Dordrecht, The Netherlands, 2008; ISBN 9781402064937. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).