1. Introduction
This paper evaluates the effectiveness of implementing group work in mathematics, in terms of student performance and students’ perceptions of this didactic form of learning during tutorial sessions. Mathematics educators are always striving to improve learner performance and achievements in the field of mathematics. The issues of learning problems in mathematics and the lack of metacognitive awareness of mathematical thinking and problem-solving skills [
1] still seem to persist, and despite differences amongst educators on an effective learning methodology, it can be suggested that there is at least a concurrence with respect to the reduced level of accomplishment amongst learners in mathematics [
2].
In the mid-1980s there was a reform movement in mathematics education as a reaction to dissatisfaction with conventional teaching approaches [
3]. Specific reports recommending the restructuring of mathematical delivery [
4] marked the need for modifications in teaching methodology. The National Council of Teachers of Mathematics [
5] endorses the use of increasingly intensive and effective instructional interventions for students learning mathematics, suggesting that these can be used during tutorial sessions as well. Employing multiple models and ways of structuring topics can present rich adaptions of mathematics content to effectively support student’s needs [
5]. Educators must therefore be encouraged to present active learning activities so that students can construct knowledge, and one way to accomplish this is to familiarise students with group work [
4,
6].
The current delivery of lectures often finds university students learning mathematics through conservative behaviouristic methods [
1], leaving them to be passive and dependent on their lecturers [
7]. Modern, enhanced taught mathematics focuses on a constructivist approach, asking students to face new challenges with prior knowledge and to absorb and adopt new information, thus allowing them to form their own significant interpretation and meaningful understanding of the taught material [
8].
Without denying the importance of traditional mathematical lecturing, and acknowledging that, in a competitive academic environment, students are more often rewarded for individual effort, this study aims to reinforce and add to the current research literature on group work, though with a particular emphasis on the field of mathematics at a higher educational level. This would allow once-skeptical educators who have perceived group work as ineffective and problematic in this subject area to recognise and appreciate the value and benefits of also assigning group work to their students [
9]. More explicitly, the research question posed is the following: can group work be considered an effective method of learning for the subject of mathematics, and can it enhance the student learning experience at a higher educational level? This study investigates the effectiveness of group work in university-level mathematics, a higher-level application perhaps slightly lacking in research output, by examining any improved student performance upon adoption of group work interaction as well as examining student perceptions of working in groups. In addition, the study considers whether group work learning can deepen student understanding of the module content and aid them in developing higher critical and thinking skills.
This paper begins with a brief literature review documenting the adoption of group work in education, particularly those relating directly to mathematics. Collaborative and cooperative group work are highlighted, including a description of the main shortcomings and benefits experienced by the practitioner. The paper continues with the methodology used to carry out the evaluation of the effectiveness of group work in mathematics during tutorial sessions. The findings from the investigation are then discussed and analysed using both qualitative and quantitative techniques. Finally, some concluding remarks and possible future assessments are presented.
2. Literature Review
Group work is centered upon the constructivism model of learning [
10,
11,
12,
13]. According to the report from the National Council of Teachers of Mathematics [
4,
5], it is said that group work in mathematical education plays an essential role in students’ question acquisition and in criticising constructively [
14], all leading to productive and beneficial outcomes in student learning.
The number of research studies carried out over recent years has increased noticeably in the field of mathematics at the primary and secondary school levels [
15]. Substantial research within the mathematics education sector indicates that employing small groups for various activities and exercises does lead to constructive and beneficial outcomes for student learning.
From a review by Webb [
16,
17] concerning studies investigating peer interaction and achievement in small scale groups, various compatible outcomes were achieved. Conveying a clarification or simplification of an idea, solution or method to another group member was positively related to achievement, whereas experiencing non-responsive feedback from a group member, specifically no feedback or feedback that was irrelevant to what one has said or done, was characterised by a negative relation to achievement [
16,
17]. Webb’s review also interestingly revealed that group work was most useful when students were taught how to work in groups and how to present, provide and accept assistance. This received aid was most fruitful and functional when it was in the form of detailed explanations and then applied by the student to the existing task or to a different task. Slavin’s research showed positive effects from group work on cross-ethnic relations and enhancing student achievement [
18]. Yackel, Cobb and Wood found that small-scale group work problem-solving followed by whole class dialogue generated many learning opportunities that do not usually occur in a conservative tutorial or class, comprising opportunities for collaborative discussion and resolution of contrasting viewpoints [
19].
Over the past years, many studies have been conducted in order to investigate how effective competitive, individualistic, and cooperative group work methodologies are in endorsing and encouraging productivity and achievement [
20,
21]. Acknowledging these studies and using meta-analysis to study achievement in cooperative learning, the results showed that the average student learning through cooperative approaches performed at about two-thirds a standard deviation above the average student learning within a competitive (an effect size of 0.67) or individualistic (effect size equal to 0.64) structured lesson [
22], prompting higher achievement levels when considering cooperative group work learning compared to competitive or individualistic learning strategies.
Group work plays a fundamental role both in cooperative and in collaborative learning methods, and has attracted significant research interest [
21,
22,
23,
24,
25,
26,
27,
28,
29]. Studies demonstrate that these pedagogical customs of group work do produce higher achievement and more positive relationships amongst students, compared to competitive or individualistic experiences.
Research suggests that collaborative learning has quickly turned into a strong promoter of group work in educational institutions at all levels [
24]. In collaborative learning, participants brainstorm, share information and work, tackle the same problem together continuously within their groups and learn from each other so their combined collaborative achievement surpasses the simple sum of individual contributions [
29]. As Damon and Phelps clearly state, this is structurally different from cooperative learning, which refers to discrete practices and concepts such as specific role assignments in a group and goal related liability of both members and the group, so that each student is responsible for the entire concluding result [
23]. Curtis discusses that cooperative learning mostly deals with tasks that are divisible into more or less independent subtasks, where cooperating parties work in parallel to process individual subtasks in an autonomous, independent way [
28] as opposed to collaborative learning where a shared solution to a problem is built simultaneously, collectively and in liaison with all members of the group.
Group collaboration can take a variety of forms and has been investigated in a broad range of contexts, including classroom-based learning [
30], computer-based learning [
31], web-based and e-learning [
32]. What these collaborations, however, have in common is that two or more learners interact in a synchronous form to negotiate shared meaning and jointly and continuously solve problems [
26].
Since learning mathematics can often be viewed as a lonely, individualistic or competitive matter, with students developing mathematical anxiety or avoidance, collaborative and cooperative learning through group work can address these problems and enhance students’ progress and achievements [
33].
Group work interaction helps all members learn concepts and problem solving strategies, improve self-confidence and overcome the fear of mistakes [
6,
14,
34]. Mathematics does offer opportunities for creative thinking, exploring open ended questions, and posing intriguing problems, and group work can help to face these trials and difficult tasks that are well beyond the capacities of individual work at that developmental phase. Group work can also be a convenient and helpful tool to help develop a supportive attitude towards learning. In a study by Bernero, the students who struggled with mathematics continued to stress and strain about it and became discouraged with individual work, but improved both academically and socially when it came to group work, due to an increase in self-assurance [
34].
Group work, however, can also sometimes lead to unsuccessful operation, mainly due to a lack of understanding of the important elements that arbitrate its effectiveness. Group efforts can be unproductive in many aspects. For instance, less capable members of the group can sometimes leave it to others to accomplish and conclude the group’s exercises [
35], whereas more capable student members might put in less effort to avoid doing all the work [
35]. The amount of time spent explaining concepts can be positively correlated with the amount of time learning, so more capable members might learn a great deal by providing detailed explanations of the taught material to less able students struggling to comprehend as a captive audience [
35].
The educator plays a vital role in the effective running of group work. During group work, the educator should act ‘both as an academic expert and as a classroom manager’ [
20], be able to specify the academic objectives and aims of the lesson, make instructional decisions, and explain the task clearly defining the assignment goals [
25]. There are different grading models available for assessing group work. Some assess the end product only, while others assess both the process and the final outcome. The grading can be conducted entirely by the educators or by the students using a form of peer assessment. The benefits of peer assessment for student learning have been well documented [
36,
37]. Another option is for the educator to award an overall mark for the end product where each individual group member has a scaled grade according to their level of contribution as determined by their peers or lecturer, ensuring that all grading must align with the learning outcomes for the module [
38].
3. Methodology
This investigation was carried out during tutorial time to first year Civil Engineering students, undertaking a Mathematics module in their second semester. The group work sessions were conducted over four weeks to the whole class, whilst studying the specific topic of Integration. The remaining tutorial sessions of the second semester involved practical exercises in the outstanding chapters of the syllabus, with students attempting these in an individualistic manner. Previous experience has led to the opinion that students find Integration the most challenging and difficult to understand topic within the whole syllabus. As a result, selecting this chapter seemed to be suitable in order to demonstrate the potential effectiveness of group work in enhancing the students learning experience. The tutorial sessions had a steady attendance of 23 students, of which 4 were female. None of the students surveyed had been in a group work environment in Mathematics before, but have had this form of learning experience in their other modules. All the students who attended agreed to participate in this research.
3.1. Group Work Setup
Group work was conducted whilst studying the Integration chapter, over four weeks during one hour tutorial sessions which ran twice per week, and the following material relating to Integration was covered:
Week 1: Integration by Substitution;
Week 2: Integration by Parts;
Week 3: Integration using Partial Fraction decomposition;
Week 4: Applications of Integration in the Civil Engineering field.
For this investigation, the educator provided a vital role in the effective running of group work in mathematics. The lecturer was able to specify the academic objectives and aims of the session, make instructional decisions (such as size group, how long groups should stay together, student assignment roles) and clarify the task clearly defining the assignment goals.
Students were paired up in groups, making sure that each group consisted of a mixture of calibers of students, in other words, weaker and stronger students were arranged to work together, but never a group consisting solely of weak students. The problems that the students had to tackle in their group work were based on the theory taught in lecture, and were either provided by the lecturer or set by the actual group members. The latter was a more complex challenge for the students, as they had to think and produce, within their groups, suitable and workable problems that were then given to other fellow groups for them to tackle. The group work interaction was at times collaborative but also cooperative in nature, with students tackling and working together on the same problem or on specific role assignments.
For instance, students were asked in their respective groups to consider a curve of their choice, which had to consist of a product of functions, be able to plot it on a Cartesian plane either manually or employing graphical software tools, and then, by applying the integration techniques learnt during the lectures, the remaining task was to determine the area of the region bounded by the curve and the axis or by the curve and straight lines of their choice. In this problem, each group member was assigned a role to fulfill, working cooperatively, but simultaneously each student was responsible for the concluding solution.
During the intervention, the role of each group member was observed by the lecturer, making sure that there was sufficient collaboration and cooperation and that each student contributed equally to the final outcome. The educator provided guidance and support during group work activities, observed the group interaction and student engagement, gave hints or clarifications, provided encouragement, drew members into the discussion, behaved in a friendly and constructive manner, managed to balance too much or too little assistance and intervened when necessary in a facilitative way in order to enable successful completion of the task by the group.
Upon completion of the problems, the results were handed back to the team which had posed the task initially, or simply to another fellow group, in order to mark and provide appropriate feedback to their peers. In this way, not only were students deepening their understanding of the theory with the help of their classmates, but they were also learning to communicate, to deliberate, to assess and to improve their mistakes accordingly.
In order to investigate the effectiveness of group work in mathematics, a more detailed and substantial quantitative approach was employed using two sets of level 4 classes, where all students had engineering-based backgrounds. For clarification purposes, the cohort which was engaged in group work shall be referred to as the Experimental class and the other class which had no group work involvement during the semester shall be considered as the Control class. To benefit from accurate and feasible conclusions on the effectiveness of group work, an indirect approach was accomplished by comparing these two classes. More specifically, in the Experimental class, only the teaching and learning on Integration was delivered in the form of group work during tutorial time, whereas the remaining syllabus was covered under normal learning arrangements. The control class, which consisted of 16 students, had their teaching and learning experience delivered under normal traditional arrangements throughout the whole semester.
3.2. Data Collection
A questionnaire (see
Appendix A) was administered on the experience of group work during the sessions, as well as an investigation into the exam results from the end of semester examinations. Students were invited to participate in the study, which was voluntary due to ethical considerations and involved completion of questionnaires, observations of collaborative activity with hand written observations made by the educator. The survey was administered only to the Experimental class, with all 23 students completing the questionnaires. Some questions required opinionated handwritten replies and the rest of the responses were sought on 3-point Likert scales ranging from “Disagree” to “Agree”.
At the end of the semester, with the aid of the outputs of the final exams, the performance of the students in the Integration questions was compared with the analogous performance of the students in the rest of the assessed questions (Integration vs. Rest of examinable questions). This difference in performance between the questions in the Experimental class was additionally later then compared with the corresponding difference in performance of the students in the Control Class.
The Integration questions within the end of year examinations for each cohort, the Experimental and the Control Class, had a different percentage weighting, specifically 60% of the exam from the Experimental Class had Integration questions assigned to it, whereas the examination for the Control Class had 50% of Integration examinable material. When regarding the performance of students in Integration questions compared to their performance of the rest of the assessed questions, this weighting was taken into consideration. Thus, not only was the student’s performance on the integration topic assessed relative to the rest of the syllabus for the class with group work learning, but also a comparison was made with the analogous performance of students not experiencing group work from another cohort, the control class. Hence, any difference in the level of difficulty of the Integration questions with respect to the rest of the questions in the exam and any dissimilarities in the academic capabilities and strengths of the students of the two cohorts were taken into account in the analysis.
In this context the authors employed, as a tool to measure the effectiveness of group work, the ratio of student performance on integration questions relative to their performance in the remaining questions, and from here on after this ratio shall be considered as the performance ratio. This performance ratio shall be used as an indicator to evaluate the effectiveness of group working. The authors suggest that this ratio be calculated by examining the quotient of student’s performance in individual integration questions over the remaining exam questions respectively.
For example, in the Experimental Class, a randomly selected student managed to accumulate 44 out of the 60 marks that relate to the Integration topic, hence approximately 73.3% ((44/60) × 100) was the total percentage of allocated marks from the Integration questions. 16 out of the 40 marks were received for the remaining questions, hence 40% ((16/40) × 100) was the total percentage of successful marks from the rest of the questions in the exam. Applying the suggested performance indicator, the performance ratio for this specific student was 1.83 (73.3%/40%).
It must be noted for elucidation purposes that a performance ratio value greater than 1.0 indicates that a student performed better in the integration section of the exam compared to the rest of the questions in the exam paper, due to the value of the numerator of the performance ratio quotient being greater than the denominator value.
4. Results and Discussion
4.1. Qualitative Analysis: Discussion of the Findings from the Questionnaire Survey
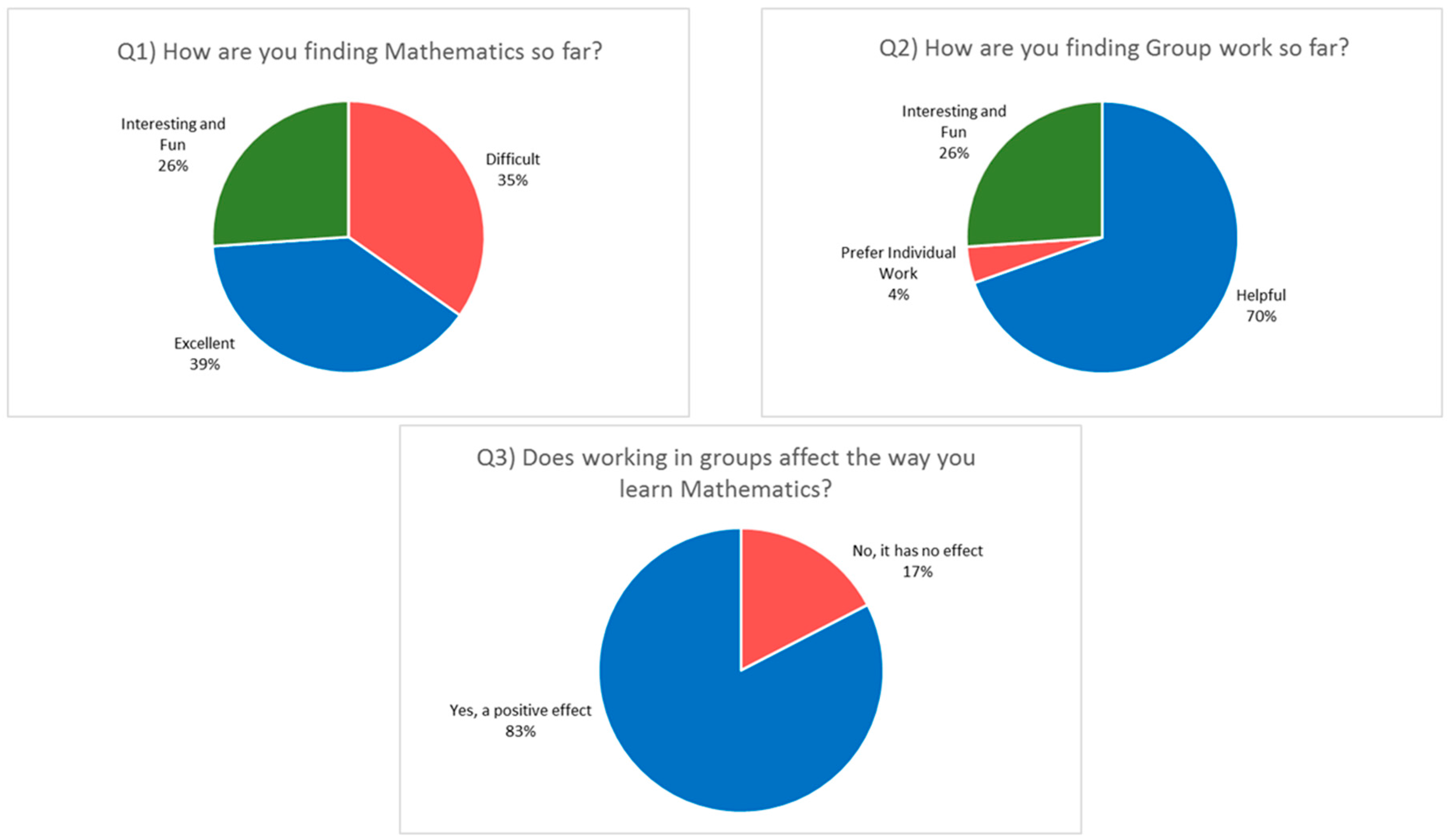
The evaluation survey filled in by all students of the Experimental class is the main source of feedback examined as the qualitative analysis section of this project. The results of the first three questions of the survey, which required individual comments of opinion, have been summarised and grouped in a thematic way by considering the response frequency, and depicted as
Figure 1.
From these responses, it is deduced that in general students perceive mathematics as a difficult, challenging and yet rewarding subject, with all students agreeing that their group work experience in this hard module has been helpful and enjoyable. More detailed individual comments are that group work was found to be constructive, deepening the student’s understanding of Integration. The majority of the participants believe that working in groups positively affected the way they learn mathematics and allowed them to develop their critical thinking and analytical skills. Acknowledging that group work allows for collaboration between classmates, it strengthened their confidence in the subject, and it served as another learning approach to reinforce their mathematical knowledge.
As part of the opinioned responses, a couple of students did mention a few possible foreseeable drawbacks of working in groups, namely that it can slow down the lesson and that this form of learning can be nonproductive if only one member of the group does all the work.
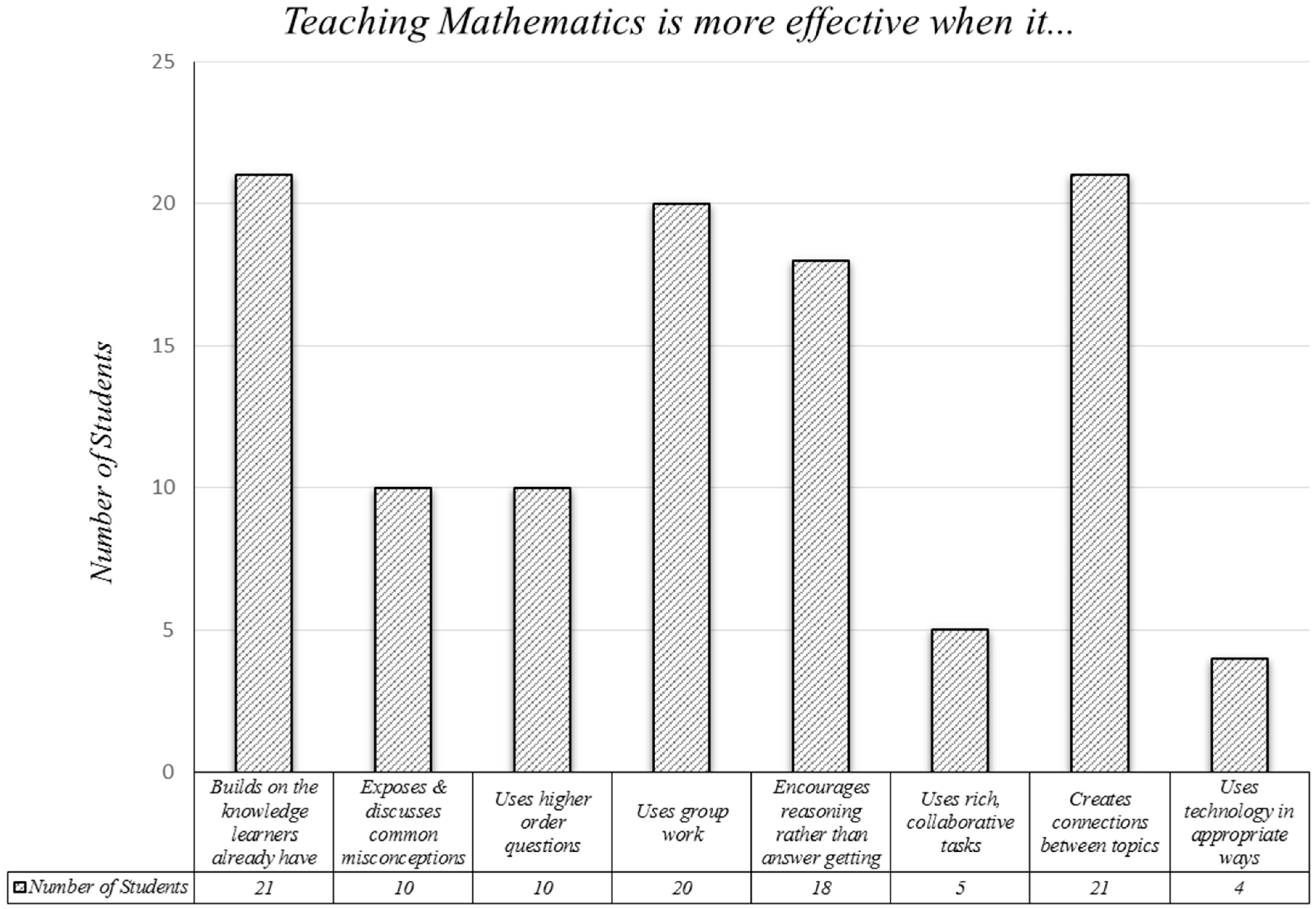
Figure 2 is a bar chart showing students responses about their perception of what contributes to the effectiveness of teaching mathematics. More than 86% of the students believed that teaching mathematics is more effective when it builds on previous knowledge, when it creates connections between topics and most importantly when it uses group work as a didactic approach. More than three quarters of the responses also referred to encouraging reasoning rather than simply getting an answer as another effective teaching strategy for mathematics.
An unexpected outcome of this specific question is that only a few students (4 out of the 23 students) consider teaching mathematics to be more effective when it uses technology. In this era, with the current advancements in technology, it can only be assumed that students would perhaps expect or demand the teaching delivery to be more updated and in compliance with the changing technological improvements. However, based upon these responses, it seems that students do not consider it necessary for mathematics to conform to a more technological method of delivering effective teaching.
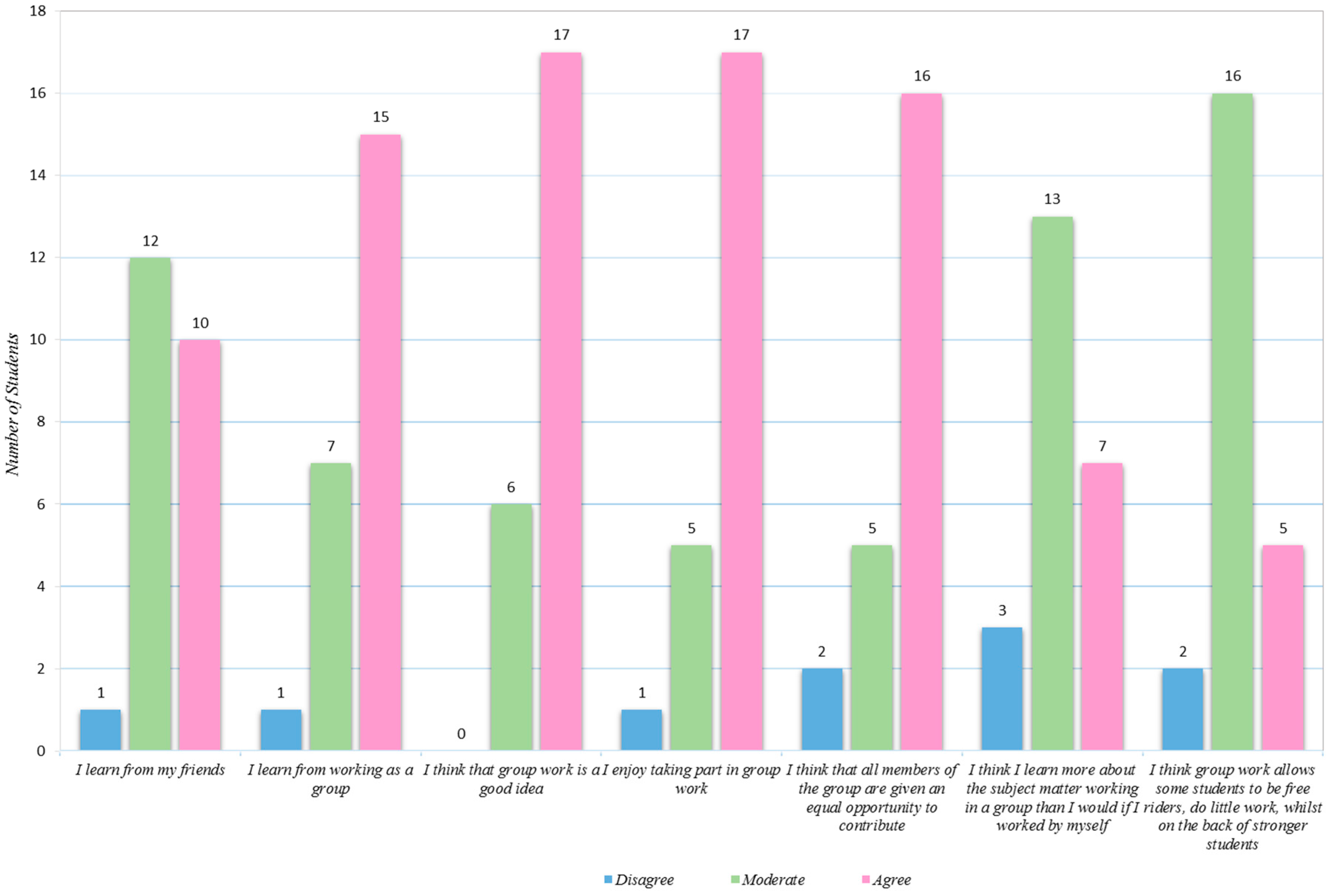
Figure 3 depicts using a bar chart, an analysis of the Likert scale data of the questionnaire. The significant conclusions here are that the majority of students agree that they learn from working as a group, believe that group work is a good idea, enjoyed taking part in group work and think that all group members were given an equal opportunity to contribute to the final outcome of the group activity.
Most students also seem to be indifferent to the issue that group work allows some students to be free riders, or that they learn more by being in a group as opposed to working individually. Additionally, taking into account the educators’ views of group work for this intervention, it can be assumed that group work becomes useful for social reasons as well as the positive effects on learning mathematics. It was noted that learning within groups helped to improve students’ attitude towards mathematics and allowed the struggling students to get over their anxiety about the subject. Moreover, this way of learning seemed to be more fun and enjoyable for learners assisting them to learn through discussion instead of memorisation during mathematics lessons.
4.2. Quantitative Analysis: Findings from the Data Retrieved from the End-of-Year Examinations
The end-of-year mathematics examination results for the respective semesters were retrieved and outputs were gathered in order to extrapolate interesting and valuable conclusions for this research study. To determine whether group work was effective in the learning of mathematics, the main objective of the investigation, it was necessary to be able to produce an empirical indicator to aid in this analysis. Examining each student’s performance ratio (refer to section 3.2 to recall how this ratio was individually calculated) in both the Experimental and the Control classes, the following average performance ratios were derived, approximated to three decimal places:
These average performance ratios show that students working in groups performed better in the integration-related questions compared to the class which did not have any group work arrangements. The data analysis indicates that when students worked in groups their performance in the integration related questions improved by around 109% () compared to the performance of the students that attended a normal class environment.
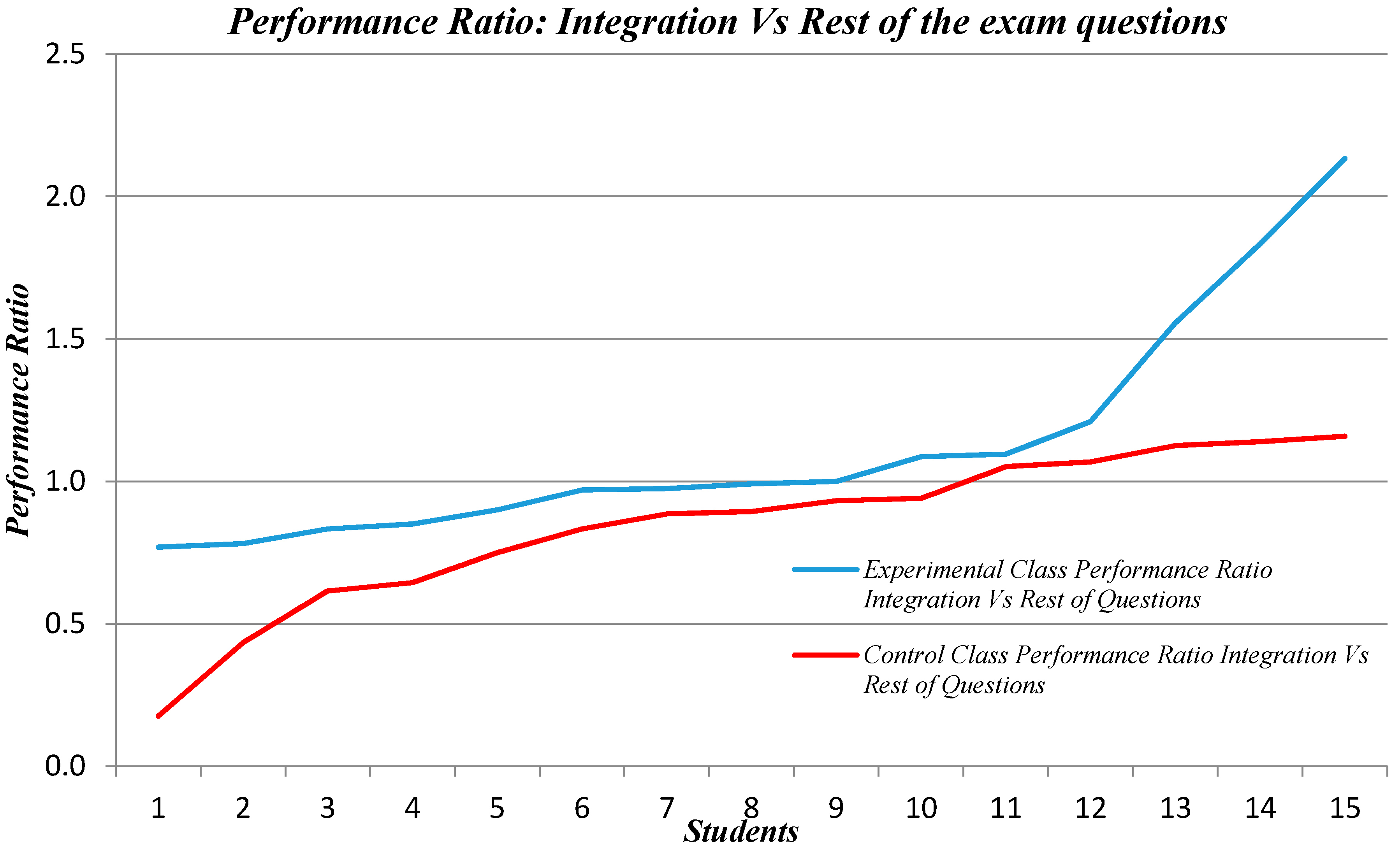
Figure 4 below illustrates the performance ratio of the students that attended the experimental class (blue) against this of the students that attended the control class (red). The ratios present the individual students’ performances and are displayed in increasing performance value. It must be noted that as the cohort numbers of these classes were different, specifically 23 students for the experimental class and 16 for the control class, the upper and lower end values of the performance ratios have been truncated in order to provide a more realizable, feasible and longitudinal comparison.
The analysis of these results indicate that, throughout the spectrum, the performance ratio values of students learning integration in the experimental class were always higher than those of the students of the control class, as can be seen by the blue line always having an upward trend above the red line. Hence, this figure clearly portrays and supports the benefits of group work on the topic of integration.
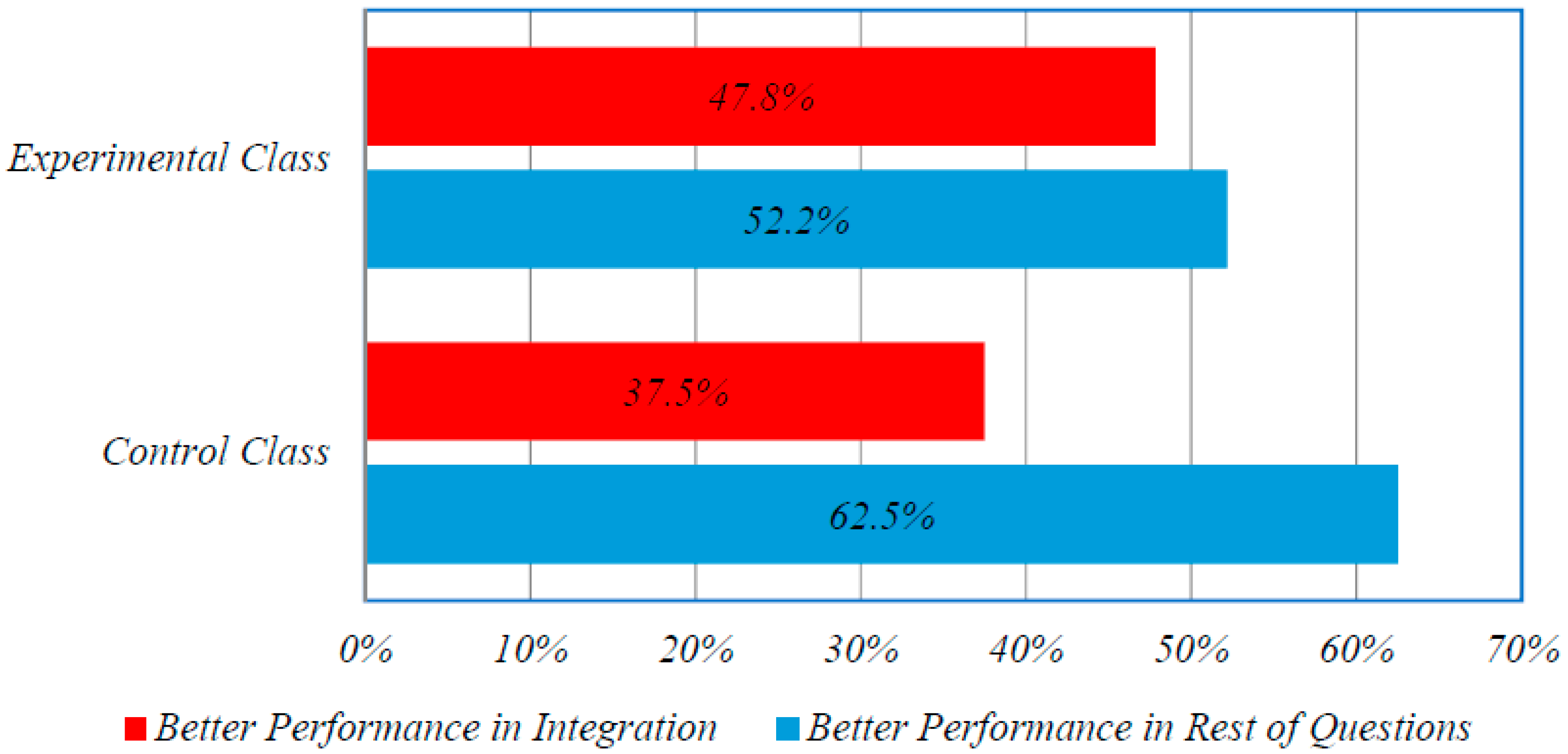
Figure 5 below presents the percentage of students that performed better in the Integration topic compared to the rest of the questions in the exam for each class. Recall that a performance ratio greater than 1.0 indicates a better performance in the integration section of the exam. The results show that when students worked in groups 47.8% of the class achieved better marks in Integration (11 out of the 23 performance ratios were greater than the value 1) whilst only 37.5% of the students performed better in integration when working in normal class arrangements (6 out of the 16 students). These percentages also highlight the efficiency of group work in teaching mathematics.
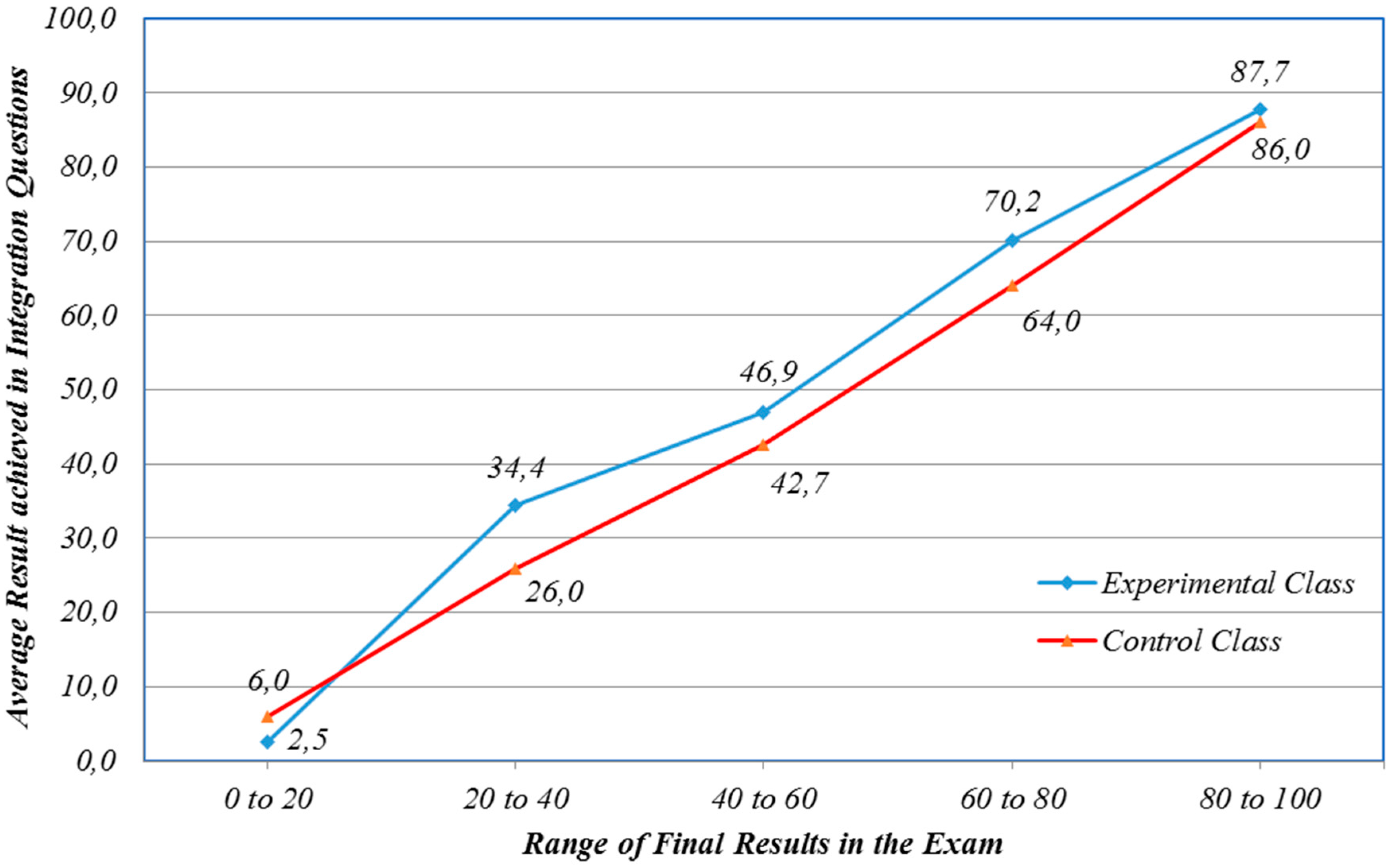
Figure 6 presents the average result achieved by students in integration questions with respect to the different range of overall performance in the exam. Students were clustered in performance categories over 20% intervals. Students were arranged in these categories in order to assess group work effectiveness for the different academic strength levels of the students.
The results illustrate the beneficial effect of group work for almost all student categories. For example, students achieving a final result between 60% and 80% in their exam presented an average mark of 70.2% in the integration section when working in groups. In the Control class this percentage corresponded to 64%. This trend was similar throughout the performance categories and emphasises the effectiveness of group work in mathematics for this study.
By now placing the emphasis on an important aspect of this project, the size of the effect on the performance of students using group work in mathematics, the so called “effect size” promotes a more scientific approach to accumulate this knowledge. Effect size is simply a way of quantifying the effectiveness of a particular intervention, relative to some comparison. It allows the researcher to move beyond the simplistic ‘does it work or not?’ to the far more sophisticated, ‘How well does it work?’ The effect size (
d-index) is therefore an important tool in reporting and interpreting effectiveness, and for this study, it is defined as the difference in the average performance ratio of the experimental class relative to the control class, divided by the average of the two class standard deviations, pooled standard deviation [
39].
Based on the data gathered from the examination of the Experimental and Control classes, an analysis of this goal based on the average performance ratio of each class on the topic of integration was accomplished and the results are listed in the table below
| Statistical Measure | Output |
| Experimental Class Average Performance Ratio Mean: | 1.807 |
| Control Class Average Performance Ratio Mean: | 0.863 |
| Experimental Class Standard Deviation: | 4.431 |
| Control Class Standard Deviation: | 0.281 |
| Experimental Class Size: | 23 |
| Control Class Size: | 16 |
| Pooled Standard Deviation: | 3.140 |
| d-index (Effect Size): | 0.301 |
| Variance of d-index: | 0.113 |
| Margin of Error: | 0.659 |
| Lower Confidence Limit: | −0.358 |
| Upper Confidence Limit: | 0.960 |
The analysis deduced an effect size of 0.3, meaning that the performance of the average student in the experimental class is 0.3 standard deviations above the average student in the control class and hence exceeds the scores of 62% of the control class (see Interpretations of effect size table in [
39]). In other words, based on the data gathered from the examination scripts for these two classes, with this effect size value, this analysis quantifiably shows and supports previously stated deductions that group work in mathematics does moderately improve students’ performance.
If an effect size is calculated from a very large sample, it is likely to be more accurate than one calculated from a small sample. This margin for error can be quantified using the idea of a confidence interval. Due to the small sample size of this study, this error analysis shall also be employed so as to provide more substantial results.
To calculate a 95% confidence interval for an effect size, a formula given by Hedges and Olkin is used [
40]. The results emanating from the detailed investigation of the performance ratios for the two types of classes show that the standard error of the effect size is
with the margin of error being
. Hence, the 95% confidence interval is
This can be interpreted as meaning that the true effect size of student’s performance due to group work on the topic of Integration is very likely (95% confident) to lie between −0.36 and 0.96.
5. Conclusions
This study set out to evaluate the effectiveness of implementing group work in a university-level mathematics module, in terms of student performance and students’ perceptions of this didactic form of learning. Observing the group interaction and the group’s solutions, it is possible to say that group work learning helped to deepen students’ understanding of the material, a conclusion that is also reflected in the final examination results prompting higher performance levels for the class which underwent group work learning on the specific topic of Integration.
The educator taking part in this intervention further observed that students did attempt to be critical and developed their analytical thinking skills whilst working in a group. Struggling students that once became discouraged with individual work experienced reduced strain and felt less stress when tackling a mathematical problem whilst collaborating with fellow group members. Perhaps this increase in self-esteem and greater social competence could in the long run, also contribute to a more positive attitude towards the university experience. Moreover, it was observed that students found themselves discussing the importance of different proposed solutions, searching for applicable problems, and surpassing their capacities for individual work at that developmental stage.
In addition, the findings discussed in the previous section do relate to similar experiences described in literature by educators who have adopted group work techniques in their own practice. Specifically, Tarmizi and Bayata [
1] found that collaborative problem-based learning in a group environment did have a significant influence on student performance, and Kocak et al. [
14] observed that students who study mathematics in a group are encouraged to discuss and learn to be more attentive in class, resulting in better understanding mathematics instead of memorizing the relevant information and proofs. Edwards and Jones [
27] describe the perspectives of secondary school students who have had considerable experience with collaborative small group work in mathematics and D’Souza and Wood [
33] describe tertiary students’ views and opinions of group work based on in-depth interviews, though both studies allow for only a descriptive qualitative approach to support their results. Thus, building and scientifically expanding upon previous studies and literature, both the qualitative and quantitative analysis in this paper provide encouraging and positive reflections on group work in mathematics at a tertiary context level, reinforcing the effectiveness of this didactic method. Adapting this method of learning at the university level but also in a subject that students always find challenging and a subtopic that students always struggle with (an extrapolation from educator’s teaching experience) has led to findings in this study that are significant and can complement the existing literature on this evergreen method of learning.
While the outcomes of this study are positive and endorse the benefits of group work, one possible limitation of this study was the relatively small sample size of both the experimental and control classes. In view of this, one possible improvement would be to consider larger control and experimental class sizes as well as extending the duration and period of group work interaction. The authors invite researchers to investigate this in greater detail and possibly enhance the findings of this study so that they can be generalized to a broader context.
From a wider perspective, businesses and employers are continuously looking for employees who are able to work collaboratively on projects and to tackle and solve tasks as a team. Consequently, it is vital to be able to give students the practice and training to develop these skills by working in groups on a variety of problems and helping them see this teaching and learning method as a fun and enjoyable one, adding further that when students are motivated and inspired, their learning capabilities are usually enhanced.
It is important, however, to mention that the group work model is not necessarily the answer to all encountered pedagogical failing practices. The role of the educator is still key with regard to determining what is effective for one particular class or student and it is the educator’s choice that is relevant to the approach which has the greatest influence based on personal experience with mathematical modules. The barriers for educators using group work in mathematics in tertiary education could be considered to be time management concerns, assessment issues and the impact of their experience and own knowledge.
Being reflective in one’s teaching philosophy and always being enthusiastic to adapt teaching styles in order to accommodate the diverse backgrounds of students, their abilities and motivation levels are traits that will conceivably have the most impact in teaching mathematics effectively.