Abstract
Inertial technology has been used in a wide range of applications such as guidance, navigation, and motion tracking. However, there are few undergraduate courses that focus on the inertial technology. Traditional inertial navigation systems (INS) and relevant testing facilities are expensive and complicated in operation, which makes it inconvenient and risky to perform teaching experiments with such systems. To solve this issue, this paper proposes the idea of using smartphones, which are ubiquitous and commonly contain off-the-shelf inertial sensors, as the experimental devices. A series of curriculum experiments are designed, including the Allan variance test, the calibration test, the initial leveling test and the drift feature test. These experiments are well-selected and can be implemented simply with the smartphones and without any other specialized tools. The curriculum syllabus was designed and tentatively carried out on 14 undergraduate students with a science and engineering background. Feedback from the students show that the curriculum can help them gain a comprehensive understanding of the inertial technology such as calibration and modeling of the sensor errors, determination of the device attitude and accumulation of the sensor errors in the navigation algorithm. The use of inertial sensors in smartphones provides the students the first-hand experiences and intuitive feelings about the function of inertial sensors. Moreover, it can motivate students to utilize ubiquitous low-cost sensors in their future research.
1. Introduction
Inertial technology has been used in a wide range of applications such as guidance, navigation, and motion tracking. However, there are few undergraduate courses that focus on inertial technology. This creates a potential mismatch between knowledge acquisition of inertial navigation technology and teaching curriculum. Also, this phenomenon leads to lack of the necessary knowledge when students start their research on navigation during their graduate programs. Some of the reasons for this fact are that traditional inertial systems are bulky, have a complicated data collection process, and require a special power supply, which makes the education process hard to implement. With the development of manufacturing and electrical technologies, the inertial measurement units (IMU) have become much cheaper. However, even a low-end IMU can cost almost one thousand dollars, which is still expensive when used for teaching. Furthermore, expensive inertial equipment may be broken because of incorrect use.
Smartphones are prevalent among college school students and much research has investigated the use of smartphones as teaching devices [1,2,3,4,5,6]. The smartphones are equipped with Micro-Electro-Mechanical System (MEMS) inertial sensors including gyroscopes (gyros) and accelerometers [2]. These embedded inertial sensors have brought about better user experience and boosted the development of smartphones [7]. From the perspective of teaching, smartphones with off-the-shelf inertial sensors are ideal candidates for teaching experiments because they are light-weight and easy to operate. It is also convenient to collect the inertial sensor data since many free data collection Apps are available in the App stores and no extra infrastructure needs to be installed. It is possible to use them for teaching experiments and the in-class budget for hardware cost can be significantly reduced. Therefore, this paper proposes the idea of using smartphones for teaching inertial navigation technology and designs a curriculum with well-selected experiments, which solves the issues mentioned previously.
The MEMS inertial sensors have been used in various fields that relate to motion, not only in the latest devices such as smart glasses, watches and gyro-stabilized cameras, but also in the motion tracking of objects such as athletes and electric wires in the wind. The MEMS inertial sensors in consumer electric products are low-cost and have low power consumption but suffer from significant sensor errors. As an example, the inertial sensor errors used in iPhone 4 are trial-axis gyroscopes and trial-axis accelerometers produced by STMicroelectronics. Their performance specifications are shown in Table 1 [8].
The gyro and accelerometer biases can reach thousands of deg/h and thousands of mGal. Such errors, if not compensated for, will accumulate and lead to attitude and position drifts due to the integration process in the inertial navigation algorithm. For 2-D navigation, the uncompensated gyro and accelerometer biases will result in position errors of approximate and , respectively, where and are the gyro and accelerometer biases at temperature T, t is the time that INS works alone, g is the value of the local gravity. Also, the uncompensated sensor scale factor errors may introduce position errors proportional to time squared. Therefore, proper calibration and modeling of sensor errors becomes a key point when using low-cost inertial sensors.

Table 1.
Specifications of inertial sensors in iPhone 4 smartphone.
| Sensor feather | STMicroelectronics | |
|---|---|---|
| Gyro (L3G4200D) | Accelerometer (LIS331DLH) | |
| Operating temperature range | −40 °C ~ 85 °C | −40 °C ~ 85 °C |
| Measurement range | ±2 g | |
| Scale factor | ||
| Scale factor error | N/A | ±10% |
| Bias error | ±20 mg | |
| Non-linearity | 0.2% FS | N/A |
| Noise density | ||
The courses are designed based on several key principles. First, the courses should be able to provide students an overall understanding of the inertial navigation technology. Second, the courses should combine fundamental theories and practices, and place more emphasis on the latter. The fundamental theories should be interspersed with practice instead of being instilled to the students directly. In addition, what the students get from the courses should benefit their further learning of inertial navigation technology. Moreover, the experiments contained in the courses should be easy to implement. Based on the above principles, a curriculum containing four experiments is designed to help students acquire knowledge of inertial navigation technology. The experiments include the Allan variance test, the calibration test, the initial leveling test and the drift feature test. The Allan variance test can help the students learn components of the stochastic errors in inertial sensor outputs and thus enhance their understanding of the sensor error modeling in applications such as the GNSS/INS integrated navigation. The calibration test is designed to help the students learn the most commonly used method of determining deterministic sensor errors (i.e., the six-position calibration method). The initial leveling test can lead the students to a basic understanding of attitude determination. Finally, the drift feature test can help the students understand the drift features of the navigation solutions (including position, velocity, and attitude) from inertial navigation systems.
All of the four experiments are designed on the principle that no specialized equipment is required, which can greatly reduce teaching expenses. Moreover, they are flexible and convenient to carry out and are suitable for class teaching purposes. Example tests are also provided as a reference. The smartphone used in example tests was an iPhone 4. The data collection App used in the test was the Sensor Data which can record the 3-D gyro and accelerometer data with configurable sample rates from 1–100 Hz. In each example test, the data sampling frequency was set as 100 Hz.
2. Curriculum Design Principles
The courses are designed for higher grade undergraduate students with a science and engineering background, especially for those who want to further study the inertial navigation technology. In other words, the courses are prepared for the students who intend to study inertial navigation technology in depth, instead of all students. Hence, the courses are defined as elective. When designing the course, the following principles are followed:
- ●
- The courses should be able to help students have an overall understanding of the inertial navigation technology. Also, the courses should help students realize the importance of the algorithms (e.g., the Allan variance analysis algorithm, the calibration algorithm, and the initial leveling algorithm) in the inertial navigation technology.
- ●
- The courses should combine the fundamental theories and practices, and place more emphasis on the latter.
- ●
- The courses should be fundamental but enlightening. The knowledge gained from the courses should help students get prepared for a deeper learning of inertial technology.
According to these principles, the courses containing fundamental theories and well-designed tests are developed. In each course, the fundamental theories are used to guide the experiment implementation and help the students understand the outcomes of the tests. The experiments can in turn help the students master the theories.
3. Curriculum Design
In this section, the details of the curriculum experiments are presented. Example tests and results are also provided as a reference. Subsection 3.1 introduces the Allan variance analysis method and presents the detailed analysis steps, Subsection 3.2 presents the inertial sensor error models and shows a calibration procedure without the need for any specialized tools, Subsection 3.3 presents the initial leveling test, and Subsection 3.4 introduces the drift test and the results.
3.1. Allan Variance Test
The sensor outputs are influenced by deterministic errors and stochastic errors [9]. The requirements for accurate estimation of navigation information necessitate proper modeling of the stochastic errors. To identify the component and determine the coefficient of the stochastic errors contained in the sensor outputs is very important for optimizing the performance of these sensors. Allan variance analysis is an effective tool to identify stochastic errors, such as quantization noise, white noise, correlated noise, sinusoidal noise, random walk, and flicker noise [10,11]. The computation of Allan variance can be described as follows.
First, divide the entire collection of data into K = N/T clusters, where N is the length of the data and T is the cluster length or cluster time, and calculate the average for each cluster:
Then, change the cluster time T from small to large to get a series of variances related to T. For each T, the Allan variance can be calculated as follows:
where is the value of Allan variance value when the data collection is divided into T clusters.
Finally, draw the log-log plot of the Allan variance (i.e., the square root of the Allan variance versus the cluster length T) and analyze the error characteristics.
The accuracy of the Allan variance increases with the number of independent clusters. The accuracy of the computation for K cluster averages can be written as [12]:
The detailed definition and analysis procedure of the Allan variance method can also be found in [13]. A typical Allan variance plot with different noise types is shown in Figure 1 [13].
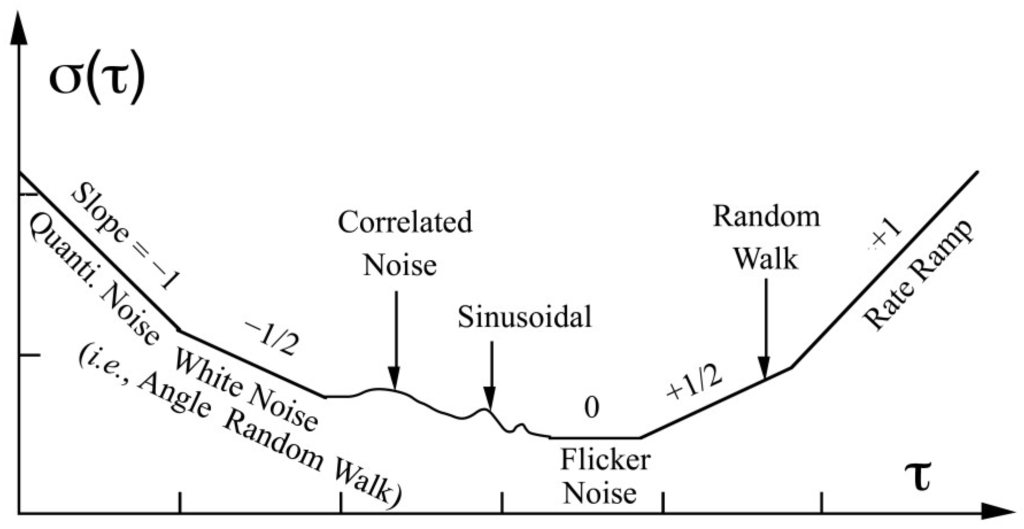
Figure 1.
Sample plot of Allan variance analysis results.
The noise parameters of different stochastic errors can be determined by the Allan variance analysis method. These parameters can also be used to calculate the power spectral density (PSD) values of the corresponding noises [14]. The Allan variance and PSD values of some typical stochastic errors contained in the inertial sensor outputs are listed in Table 2.
The sensor errors components can be determined by inspecting the log-log Allan variance plot because different components show different behaviors. For instance, the valley bottom in the Allan-variance plot corresponds to the bias instability error; white noise is represented by a slope of −1/2 in a log-log Allan variance plot, and the magnitude of this noise can be read off the slope line at .

Table 2.
Features of typical stochastic error sources in inertial sensors.
| Noise Types | Allan Variance | Noise Coefficient | Curve Slope | |
|---|---|---|---|---|
| Quantization Noise | Q | −1 | ||
| White Noise | N | −1/2 | 1 | |
| Flicker Noise (Bias Instability) | B | 0 | -- | |
| Angular Rate/Acceleration Random Walk | K | +1/2 | 3 | |
| Ramp Noise | R | +1 |
3.1.1. Test Description
To get reliable analysis results, the tested smartphone should be placed on a stable platform to isolate external disturbances. In this paper, the example test was carried out in a laboratory at Wuhan University. Eight hours of static data was collected at room temperature (25 °C).
3.1.2. Test Results
Figure 2 shows the Allan variance curves of the sensors in the tested iPhone 4. For both the accelerometer and gyro curves, a straight line with a slope of −1/2 fit to the beginning of the curves. This outcome indicated that white noise was the dominant noise for the short cluster times. The coefficients of the stochastic errors contained in the sensor outputs were calculated and are listed in Table 3.
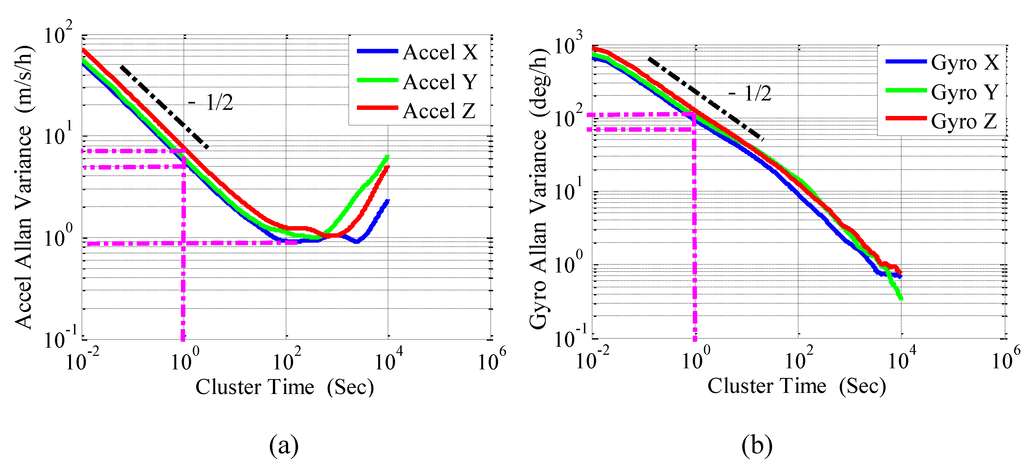
Figure 2.
Allan variance curves of the accelerometers and gyros in iPhone 4.
Result shows that the white noise coefficients of the x-, y- and z-axis accelerometers were 5.7, 6.1, and 7.7 , respectively. These results fit the reference values in the product specification. Also, the calculated gyro white noise coefficients fit the reference values in the product specification. The valley bottom points indicate that the accelerometer bias instability is about 30 mGal. The gyro Allan variance curve shows no valley bottom, which means the identification of the long-term gyro stochastic errors such as bias instability requires longer static time.

Table 3.
Coefficients of noises contained in the sensor outputs.
| Sensor | Noise Coefficient | |
|---|---|---|
| White Noise | Flicker Noise (Bias Instability) | |
| Accel_X | 5.7 | 25 mGal |
| Accel_Y | 6.1 | 30 mGal |
| Accel_Z | 7.7 | 35 mGal |
| Gyro_X | 94.2 | -- |
| Gyro_Y | 106.3 | -- |
| Gyro_Z | 123.1 | -- |
Since the Allan variance algorithm is difficult for beginners, an Allan variance analysis function should be provided by the lecturer. After the collection of static data, the students can draw the Allan variance plots with the analysis function. With the Allan variance plots, the students can be guided to think about the following questions: (a) what are the dominate noises in the sensors outputs? and (b) how to estimate the parameters of the noises based on the Allan variance plots? After the students have calculated the parameters, the lecturer can guide the students to investigate if the analysis results match the product specification or not. Through this experiment the students can learn different types of stochastic errors contained in inertial sensors. Additionally, they can master the method of determining the coefficients of typical stochastic errors with the Allan variance analysis method, thus enhancing their understanding of the sensor error modeling in applications such as the GNSS/INS integrated navigation.
3.2. Calibration Test
MEMS sensors are small-sized, light-weighted, and with low power consumption. However, they suffer from significant sensor errors due to manufacturing imperfections. The major deterministic error sources in inertial sensor outputs are biases, scale factor errors and non-orthogonalities [15]. In this section, we will first introduce the sensor error models and the six-position calibration method, and then present the calibration test and the results.
3.2.1. Sensor Error Models
The output of accelerometers and gyros can be written as:
Where and are the error vectors of the accelerometer-derived specific forces and the gyro-derived angular velocities, and are the true specific forces and the true angular velocities, is the identity matrix, and are the diagonal matrices containing the scale factor errors, and are the accelerometer and the gyro biases, and are the skew-symmetric matrix containing the non-orthogonalities, and and represent the accelerometer and gyro noises.
3.2.2. Six-Position Calibration Method
Calibration is known as a fundamental way to remove the majority part of the deterministic sensor errors [16]. Among many of the calibration methods, the six-position static and rate tests method is most commonly used due to its reliability and simplicity of implementation. The six-position static and rate tests can be used together to get a full set of sensor errors (i.e., biases, scale factor errors and non-orthogonalities).
The six-position static and rate tests require each of the accelerometer sensor axes to be pointed alternately upwards and downwards (see Figure 3) and each of the gyro sensor axes to be rotated both clockwise and anti-clockwise with known angles (see Figure 4). All the accelerometer errors and the gyro bias can be estimated using the two-position static tests in the zenith direction, while the gyro scale factor errors and the gyro non-orthogonalities can be estimated using the rotation test data [17]. Since the accelerometer scale factor errors are calibrated by comparing the vertical accelerometer output with the local gravity, a quasi-horizontal platform is required to keep the axis vertical.
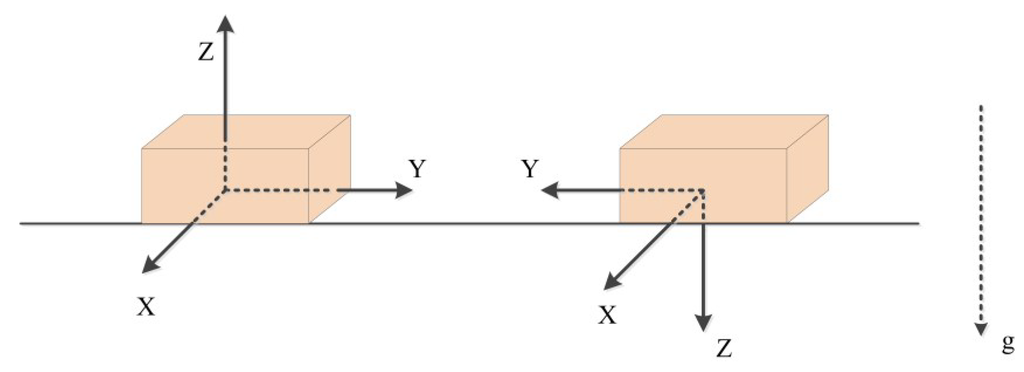
Figure 3.
Two static positions for the calibration of accelerometer errors.
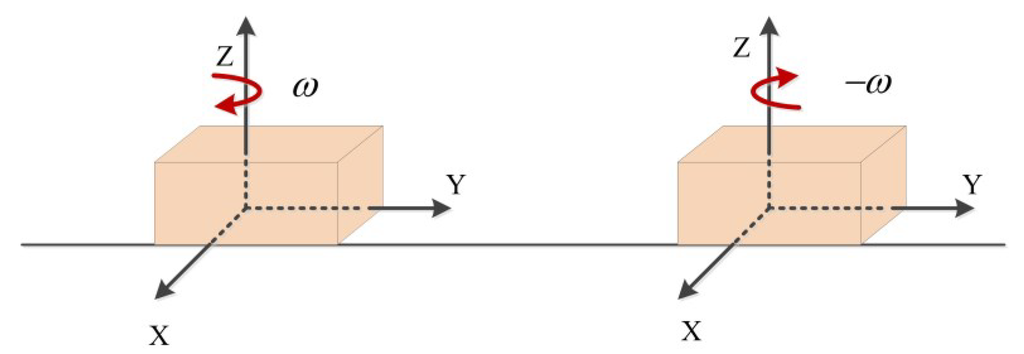
Figure 4.
Rotations for the calibration of gyro scale factor errors and non-orthogonalities.
In principle, the Earth’s rotation whose magnitude is 15 deg/h can be used as the reference signal for the calibration of gyro scale factor errors and non-orthogonalities. However, MEMS gyros have significant noise, which will mask the Earth’s rotation rate. Hence, the reference signal for the calibration of gyro scale factor errors should be provided artificially. Syed et al. introduced a turntable to provide strong rotation signals for the gyro calibration [18]. However, it is inconvenient and costly to calibrate low-end inertial sensors in smartphones with such specialized tools for the class teaching purpose. To reduce the calibration cost and improve the simplicity of the implementation, the required rotations can be performed by hand with an alignment tool such as a leveled platform with a flange or any flat with a right corner. The platform is used to provide a leveled plane for the accelerometer calibration while the flange can be used to provide an orientation reference for the gyro calibration. With this tool, a rotation with known angles can be performed as follows: first, align one edge of the smartphone closely to the flange; then, rotate the smartphone anti-clockwise around its vertical axis on the surface of the platform until the smartphone is back to its initial orientation with the help of the flange; finally, perform a clockwise rotation using the same method. The process is shown in Figure 5. The scale factor errors and non-orthogonalities can be estimated by comparing the gyro-derived angles with the reference angle (i.e., ).
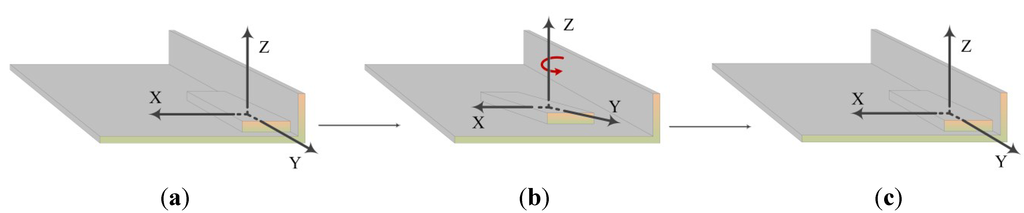
Figure 5.
Reference rotation performed by hand with simple alignment tools (a) Original position; (b) Rotate the smartphone around its z-axis; (c) Back to its original orientation.
After the static and dynamic data collection, the full set of deterministic sensor errors (i.e., accelerometer and gyro biases, scale factor errors, and non-orthogonalities) can be calculated. The detailed calculation procedure can be found in Appendix A.
3.2.3. Error Compensation
Neglecting sensor noises, Equations (1) and (2) can be transformed into the following form:
Then, the compensated sensor outputs can be represented as:
Each sampling data of gyro and accelerometer can be compensated with Equations (8) and (9) to provide more reliable navigation solutions.
3.2.4. Test Description
Each sensor axis of the inertial sensors was kept pointing upwards and downwards for a period of 7 min, respectively. The smartphone was also rotated both clockwise and counter-clockwise around its x-, y-, and z- axis for an angle of . The gyro and accelerometer outputs are shown in Figure 6.
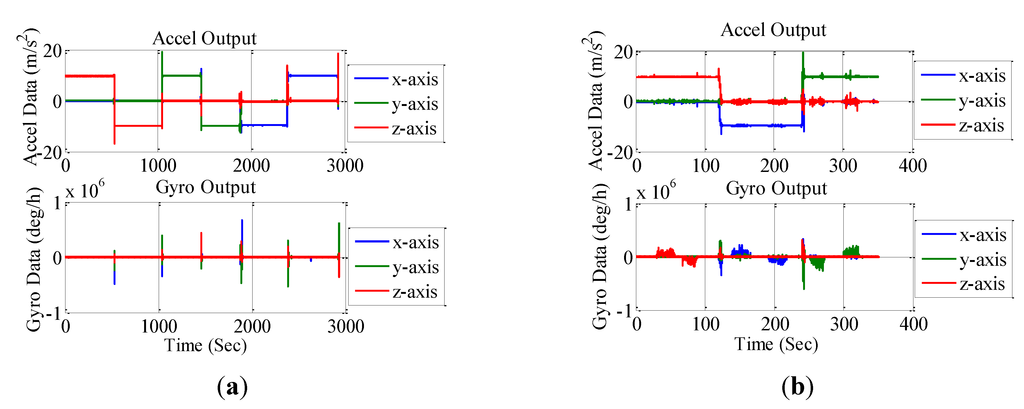
Figure 6.
Sensor outputs in six-position static and rate tests.
3.2.5. Test Results
The calibration results of the accelerometer and gyro errors are shown in Table 4 and Table 5, respectively. It can be seen from the tables that the accelerometer biases reached 8000 . This error will cause a position drift of 150 meters in 60 s. The scale factor errors and non-orthogonalities of both gyros and accelerometers reached more than ten thousand ppm. This outcome shows the necessity of the calibration of the scale factor errors and non-orthogonalities. The uncompensated gyro errors will introduce systematic errors in the estimation of attitude and further affect the estimation of velocity and position. The gyro biases obtained from the calibration were not as significant as those demonstrated in specification, which were beyond our expectation. This might be because of the on-site calibration from the smartphone company. Generally speaking, these calibrated sensor errors meet the performance of the low-end MEMS inertial sensors.

Table 4.
Accelerometer errors in the tested iPhone 4.
| Bias | Scale Factor | Non-Orthogonality | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | ||||||||||||
| Value | 2061 | 416 | 8066 | 14,030 | −605 | −800 | 5100 | 16,914 | −2010 | −2960 | −16,686 | 8186 |

Table 5.
Gyro errors in the tested iPhone 4.
| Bias | Scale Factor | Non-Orthogonality | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | ||||||||||||
| Value | 13 | 3 | −25 | 17,826 | 18,511 | 23,512 | 10,411 | 12,419 | −8317 | 5625 | −16,546 | 2812 |
Before the implementation of the test, the lecturer should introduce the definition of deterministic errors (i.e., biases, scale factor errors, and the non-orthogonalities) and guide students to think about questions such as (a) the effects of deterministic errors on the navigation solution and (b) the benefits of using “two positions” (e.g., making an accelerometer pointing upwards and downwards when calibrating it) in the calibration scheme. Through this course, students should be able to master both the calibration scheme and the calculation of deterministic errors. Also, they can learn the magnitude of the deterministic errors in different grades of IMUs.
These calibrated sensor errors were then used to compensate the sensor outputs in the drift tests. Results show that the navigation drifts were effectively reduced after compensation using these errors.
3.3. Initial Leveling Using Accelerometers
Low-end MEMS accelerometers are widely used for tilt sensing in consumer electronics and industrial applications, such as entertainment, screen rotation, and automobile security alert systems. The orientation of a smartphone can be defined by its roll, pitch, and heading rotations from an initial position, as show in Figure 7 [19]. The tilt of a device can be expressed by the roll and pitch angles [20]. Initial leveling using accelerometer is the process to determine roll and pitch angles.
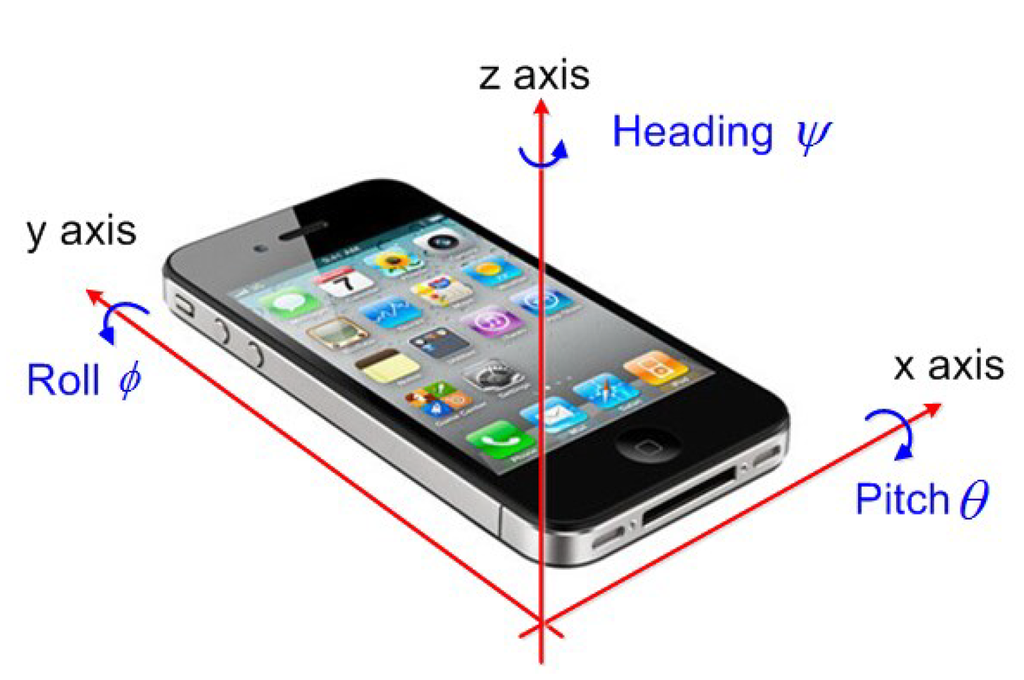
Figure 7.
Definition of rotation angles.
3.3.1. Pitch and Roll Estimation
Accelerometer measures the composition of linear acceleration and the local gravity. When there is no acceleration, the accelerometer output is a measurement of projections of the local gravity and can be used to determine the accelerometer pitch and roll orientation angles.
The roll, pitch, and heading can be described in mathematical method using rotation matrices. The rotation matrices describing the pitch, roll and heading rotations are:
Different ordering of these three rotation matrices will result in different composite rotation matrix R. Here, we use the sequence of heading, roll and finally pitch rotation. The according composite rotation matrix can be expressed as:
The composite rotation matrix describes the orientation relationship between the local geographic coordinate system and the smartphone body frame. The projection of the local gravity to the three-axis accelerometers can be expressed by:
Then, the roll and pitch angles can be calculated as follows:
where is the local gravity value and , , and are the average output of the x-, y-, and z-axis accelerometer, respectively.
3.3.2. Test and Results
In the example experiment, the smartphone was used to measure the tilt of an inclined plane. A turntable was used to provide known orientation reference to investigate the accuracy of leveling using the smartphone. However, the turntable is not necessary and can be replaced by any inclined platform in real class teaching experiments. The smartphone was fixed on the turntable platform, and the horizontal axis was changed to the place of 10 degrees, 20 degrees and finally 30 degrees for four minutes. The accelerometer outputs during the tests are shown in Figure 8.
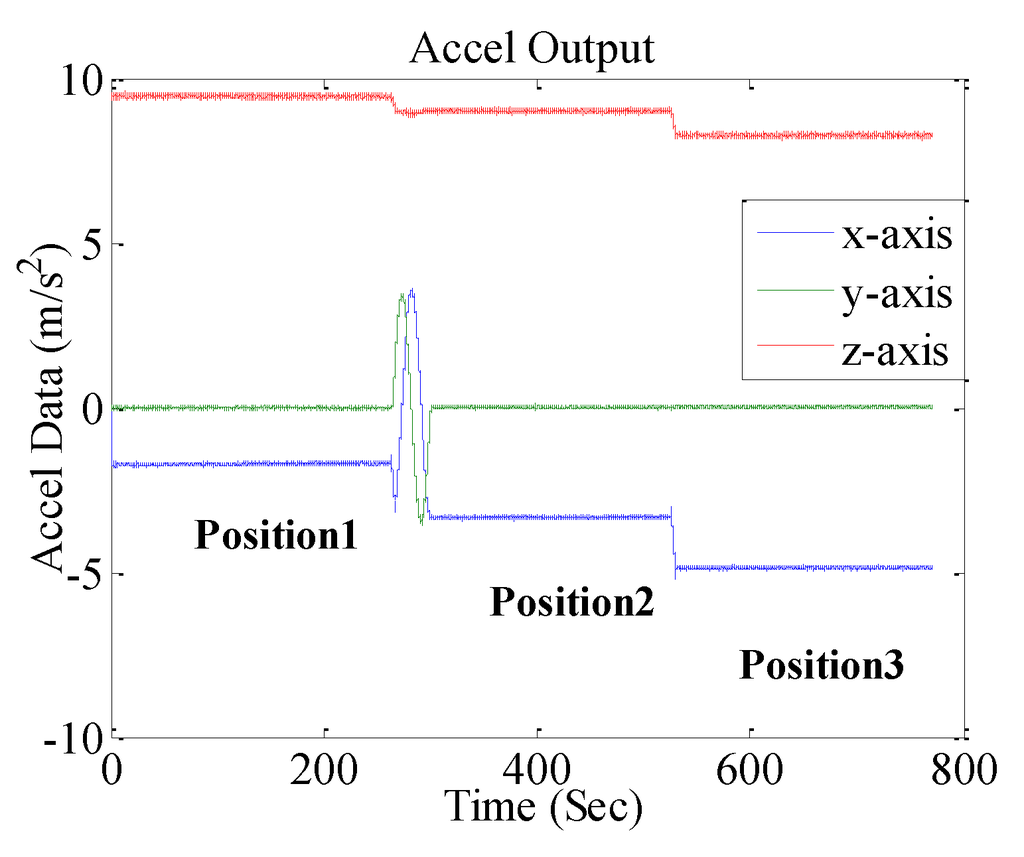
Figure 8.
Outputs of accelerometers in the tilt measuring test at three positions.
The orientation angles calculated using Equations (15) and (16) are shown in Table 6.

Table 6.
Results of initial leveling.
| Position | Roll (deg) | Pitch (deg) | ||||
|---|---|---|---|---|---|---|
| Measured | Reference | Error | Measured | Reference | Error | |
| Position 1 | 10.7061 | 10.0254 | 0.6807 | −0.4680 | −0.3826 | −0.0754 |
| Position 2 | 20.3614 | 20.0254 | 0.3360 | −0.4892 | −0.3826 | −0.0066 |
| Position 3 | 30.0755 | 30.0254 | 0.0501 | −0.4930 | −0.3826 | −0.0104 |
The max errors of the roll and pitch angles are 0.6807 deg and −0.0574 deg, respectively. This accuracy is acceptable in applications such as electronic device orientation sensing.
In the course, the students can be guided to learn the definition of the roll, pitch, and heading angles and the determination of these angles using the accelerometer outputs. Students can learn the basic attitude determination algorithm through this experiment.
3.4. Drift Features of INS
An INS utilizes gyros and accelerometers to maintain an estimate of the position, velocity, and attitude of vehicles such as aircrafts, surface ships, and submarines [21]. The INS is independent from external references once initialized, which makes it immune to most external interference such as jamming or decoy signaling. However, the accuracy of INS may degrade rapidly with time and distance due to accumulation of sensor errors [22]. Therefore, the drift experiment is designed to lead the students to learn the drift features of the inertial navigation.
3.4.1. Test Description and Results
The smartphone was placed on a stable platform and kept static for about 2 min. To investigate the effectiveness of calibration, the sensor outputs were also compensated with the deterministic errors (i.e., biases, scale factor errors, and non-orthogonalities) obtained in Section 3.2.5. The uncompensated and compensated sensor outputs are shown in Figure 9 and Figure 10, respectively.
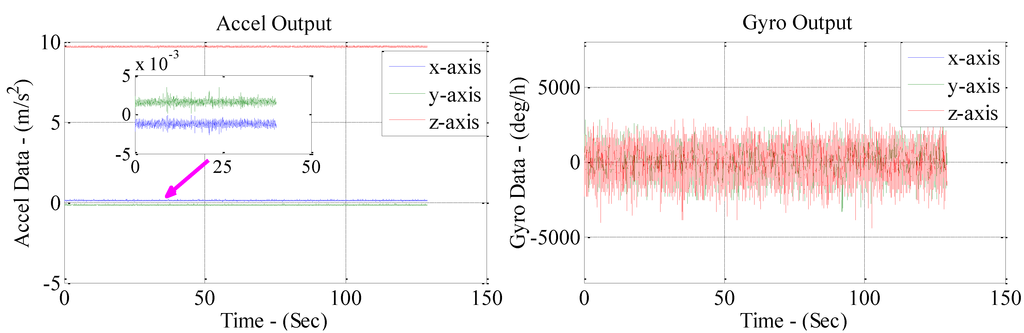
Figure 9.
Uncompensated accelerometer and gyro outputs in the drift tests.
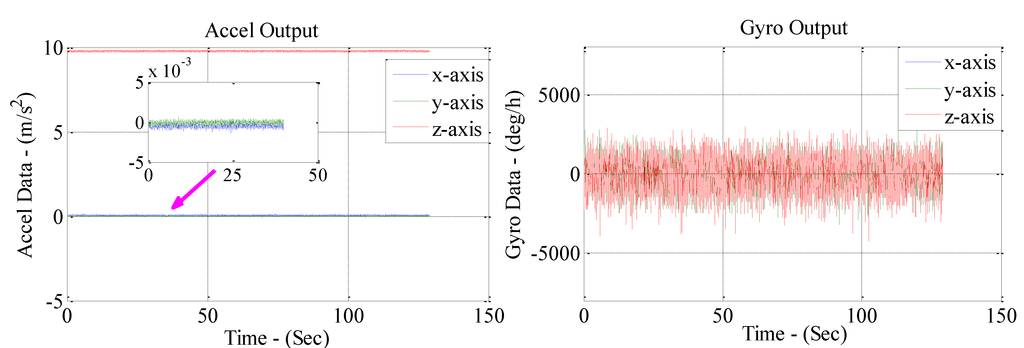
Figure 10.
Compensated accelerometer and gyro outputs in the drift tests.
Since the smartphone was placed on a quasi-level platform with the z-axis pointing upwards, the input for the z-axis should be the local gravity and the input for the x- and y-axis accelerometer should be zero. However, it can be seen from Figure 9 that the uncompensated x-axis and y-axis accelerometer outputs had an offset of zero, which was probably caused by biases and non-orthogonalities. Figure 10 shows that the offset was eliminated after compensation, which illustrated the validity of calibration.
3.4.2. Result of INS Algorithm
The sensor outputs were used to derive the navigation solution. Since the smartphone was kept static on a platform, the reference for position and attitude were the initial position and orientation, and the reference for velocity was zero. Two sets of navigation solutions were obtained with the compensated and uncompensated sensor outputs, respectively. The derived navigation solutions are shown in Figure 11a–c. In each figure, the reference navigation information is illustrated as the red lines. The derived navigation solution with the compensated and uncompensated sensor outputs are represented by the green and blue lines, respectively.

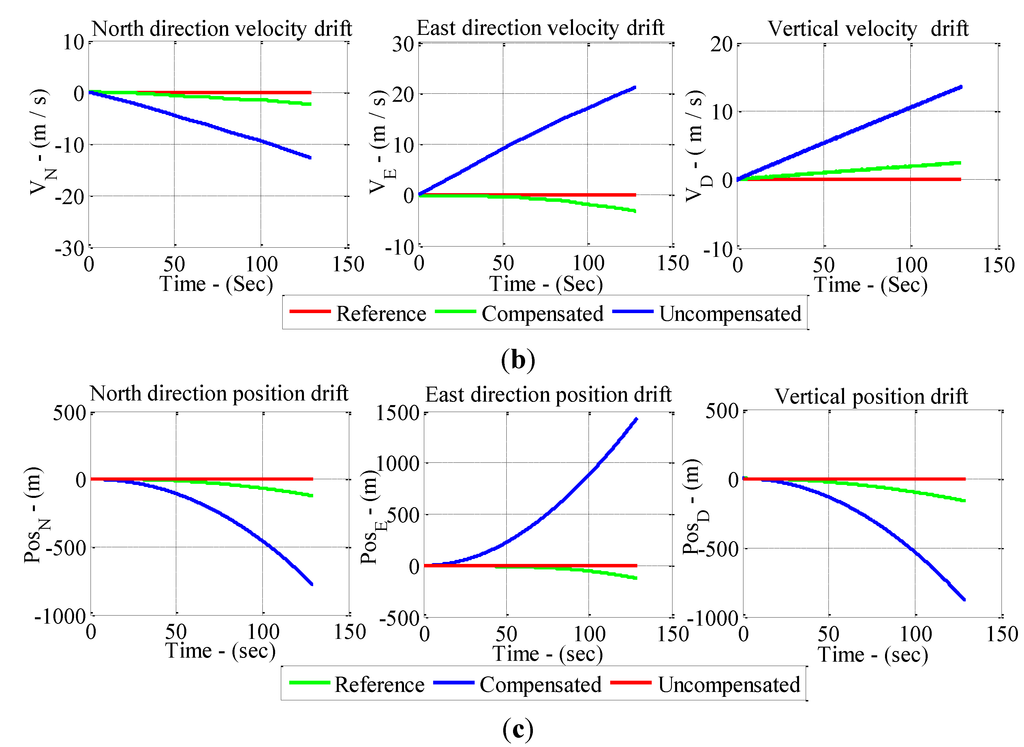
Figure 11.
Navigation solutions and drifts.
The navigation solutions with sensor error compensation had much smaller drifts than those without compensation. The velocity drifts without compensation reached more than 10 m/s. After compensation, the velocity drifts reduced to less than 5 m/s. The position drifts were also reduced from the 1 km level to 100~200 m. The attitude compensation effect was less remarkable, which should be due to the fact that the original gyro biases were relatively small. The results further verified the effectiveness of calibration. Figure 11 also shows that the attitude estimation derived by inertial sensors had relatively small drifts and can maintain an accuracy of half a degree after 2 min of reckoning. However, the velocity and position still show relatively large drifts even after compensation. This may be caused by the instabilities of the MEMS sensor errors due to factors such as the temperature variation [23]. The stochastic errors, which are impossible to eliminate, might also contribute to the drifts. Another reason is that the velocity and position errors are affected by not only the accelerometer errors but also the attitude errors. Due to the existence of the attitude errors, both the acceleration and the local gravity will be projected in the wrong direction. The drift errors of the MEMS inertial navigation solutions in this test meet the level of the low-end MEMS inertial sensors in the smartphone in general.
In this course, the students are led to calibrate the deterministic errors in the sensor outputs and make a comparison between the sensor outputs before and after compensation to examine the effect of compensation. An INS algorithm functions package should be provided by the lecturer. Before the data collection, the orientation of the smartphone should be determined to provide initial attitude for the INS algorithm. After the students get the navigation solution, they are guided to explore the error sources in the navigation solution and to think about why velocity and position drift faster than attitude. Through this experiment, the students can understand the drift features of INS and learn the importance of compensating for deterministic errors. They can also be guided to obtain an awareness to optimize the performance of inertial sensors.
4. Course Arrangement
The practice in the curriculum consists of the Allan variance test, the calibration test, the initial leveling test, and the drift feature test. A navigation software package containing the Allan variance analysis function and the INS mechanization function should be included in the curriculum. The static data for the Allan variance analysis can be collected during the night before the class to save class hours. Considering the contents of the courses, each of the courses is taught during one day (six class hours). The detailed arrangement for the courses is listed in Table 7 as a reference. The courses can be tailored based on the requirements of the lecturer and the students.

Table 7.
Course arrangement.
| Course | Course Length | Course Objectives & Arrangement |
|---|---|---|
| Allan variance test | 1 day (6 class hours) | Objective: |
| Understand the principle of the Allan variance method Master the method of identifying different stochastic errors and determining their parameters with the Allan variance analysis method | ||
| Arrangement: | ||
| Get familiar with the Allan variance package and draw the Allan variance plots (3 class hours) | ||
| Pick out the main error components of errors and determine the parameters of the errors (3 class hours) | ||
| Calibration test | 1 day (6 class hours) | Objective: |
| Understand the sensor error models and the compensation models | ||
| Master the calibration of deterministic errors with the six-position calibration method | ||
| Arrangement: | ||
| Data collection (3 class hours) | ||
| Calculate the sensor errors (3 class hours) | ||
| Initial leveling | 1 day (6 class hours) | Objective: |
| Learn about the initial leveling algorithm and obtaining an basic concept of the attitude angles | ||
| Arrangement: | ||
| Data collection (3 class hours) | ||
| Calculate the pitch and roll angles (3 class hours) | ||
| Drift feature test | 1 day (6 class hours) | Objective: |
| Investigate the contribution of the IMU compensation | ||
| Master the INS navigation solution method | ||
| Get experience about the drift features of the INS solutions | ||
| Arrangement: | ||
| Collect IMU data and compensate for the sensor errors (3 class hours) | ||
| Process the IMU data to get the navigation solution (i.e., attitude, velocity, and position) with both the compensated and uncompensated data (3 class hours) |
5. Course Implementation
The curriculum was tentatively carried out on 14 students with a science and engineering background. Each course follows the following steps when implemented:
- Introduce course contents and arrangement, explain the course objectives, and introduce fundamental theories, concepts, terms and the relationship between the algorithms.
- Present the students some real-world scenarios for the used algorithms. These scenarios can help the students understand the role of the algorithms in inertial navigation and get interested in the algorithms. For example, when introducing the Allan variance analysis method, the students should also be guide to learn how the noise parameters affect the performance of the integrated navigation system in practice.
- Introduce the experiment procedures to the students. Once the students had mastered the procedures, they will be able to design and conduct the experiments. The lecturer will guide the students in designing the experiment.
- Guide the students to predict the test results. Before data processing, the students are guided to predict the outcome of the test results in advance. Then, they can see whether the test outcomes meet their expectations. After that, the students are able to understand the theories in depth.
After the courses, the students were invited to take a survey on the difficulty and effect of the courses. The students thought the course difficulty was moderate. Some students thought the curriculum was innovative because the smartphones instead of the bulky professional equipment were used. Most students thought the curriculum was very helpful as they can gain first-hand inertial navigation knowledge such as modeling of the stochastic sensor errors, calibration of the deterministic errors, the effect of sensor errors on the navigation solution, and the drift feature of INS. More importantly, some students also mentioned that they were inspired to use inertial technology in their research field.
6. Conclusions and Summary
In this paper, smartphones are introduced for inertial technology teaching experiments. A series of experiments are designed, including the Allan variance test, the six-position calibration test, the initial leveling test, and the drift test. These experiments can guide students in gaining a comprehensive understanding of inertial navigation, including the characteristics of sensor errors, drift features of the inertial navigation systems, detection and modeling of stochastic errors, and calibration of deterministic errors. Results of real teaching experiences show that the use of the MEMS inertial sensors inside smartphones can reduce teaching expenses. More importantly, this paper explores an interesting way to convey professional knowledge through use of personal devices. After taking the course, the students realized that inertial technology is not only a high-end technology, but also a technology that is related to human lives. The outcome of this paper also provides guidance for improving the teaching experience in other subjects by taking advantage of new and current technologies.
Acknowledgment
This work is supported by the Undergraduate Curriculum Develop Program of China (surveying engineering) (275534), the National Natural Science Foundation of China (41174028, 41231174), and the National High Technology Research and Develop Program of China (2012AA12A206).
Author Contributions
Xiaoji Niu: the original idea of the work was proposed by him, the structure of this paper was also designed by him, and the research is supported by his research funds. Qingjiang Wang: the tests and the writing of the paper were mainly carried out by him. You Li: guided the implementation of the tests, provided many reference documents, and improved the paper structure and language style. Qingli Li: participated in the implementation of the tests, and part of the test data was processed by her. Jingnan Liu: gave much valuable advice on the implementation of the tests, and gave much advice which greatly improved the quality of the paper.
Appendix A. Sensor Error Calculation of the Six-Position and Rate Tests Method
Estimation of Accelerometer Errors
To estimate a full set of accelerometer errors, the output of a triad of accelerometers is represented in matrix form.
The diagonal elements are the scale factors, the off diagonal elements represent the non-orthogonalities and the components are the biases. In the calibration scheme, the axis of each accelerometer is kept pointing upwards and downwards for a period of time and the ideal acceleration can be represented as follows:
Then, the design matrix can be denoted by and the measured acceleration of the accelerometer is denoted by .
In this case, the column vector of the matrix should be:
and are similar with and . Then, the matrix can be estimated by the least-square method.
Estimation of Gyro Errors
Different from the calculation of the accelerometer errors, it is better to estimate the gyro errors through a two-step method, instead of using the least-square method directly. The first step is to calculate the biases using static data. The other step is to calculate the scale factor errors and non-orthogonalities with dynamic data.
Estimation of Gyro Biases
The bias of the i-axis gyro can be calculated by:
where and are the gyro outputs when the axis points upwards and downwards, respectively.
Estimation of Gyro Scale Factors
The scale factors of the i-axis (i = x, y, z) gyro can be estimated using the same idea as the six-position method.
where is gyro scale factor of the i-axis gyro, and represent the angle derived by the integration of the i-axis gyro output when the IMU is rotated around this axis by clockwise and counter-clockwise, respectively. For the designed eight-step calibration scheme, the value of is 90.
Estimation of Gyro Non-Orthogonalities
The non-orthogonalities cause each axis to be affected by the signal of the other two axes. When the turntable is rotated around i-axis, the output of j-axis will be affected by this rotation due to the non-orthogonalities between i-axis and j-axis. Thus, the non-orthogonalities between i-axis and j-axis can be estimated by the output of the j-axis when the IMU is rotated around i-axis in both clockwise and counter-clockwise direction.
where is the non-orthogonalities of i-axis to j-axis, and are the output of j-axis when the IMU is rotated around i-axis by in clockwise and counter-clockwise direction.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Herrington, A. Using a smartphone to create digital teaching episodes as resources in adult education. Fac. Educ. Papers 2009, 78, 138. [Google Scholar]
- Chandgadkar, A.; Knottenbelt, W. An Indoor Navigation System for Smartphones; Imperial College London: London, UK, 2013. [Google Scholar]
- Yu, F. Mobile/smartphone use in higher education. In Proceedings of the 2012 Southwest Decision Sciences Institute, University of Central Arkansas, Conway, AR, USA, 22 February 2012; pp. 831–839.
- Herrington, J.; Herrington, A.; Mantei, J.; Olney, I.; Ferry, B. Using Mobile Technologies to Develop New Ways of Teaching and Learning; University of Wollongong: New South Wales, Australia, 2009. [Google Scholar]
- Handal, B.; MacNish, J.; Petocz, P. Adopting mobile learning in tertiary environments: Instructional, curricular and organizational matters. Educ. Sci. 2013, 3, 359–374. [Google Scholar] [CrossRef]
- Hendeby, G.; Gustafsson, F.; Wahlström, N. Teaching Sensor Fusion and Kalmanfiltering Using a Smartphone. In Proceedings of the 19th World Congress of the International Federation of Automatic Control (IFAC), Cape Town, South Africa, 24–29 August 2014.
- Shala, U.; Rodriguez, A. Indoor Positioning Using Sensor-Fusion in Android Devices; HKR: Hong Kong, China, 2011. [Google Scholar]
- ST. Mems Motion Sensor: Ultra-Stable Three-Axis Digital Output Gyroscope. Available online: http://www.st.com/web/en/resource/technical/document/datasheet/CD00265057.pdf (accessed on 15 February 2015).
- Hou, H.; el-Sheimy, N. Inertial Sensors Errors Modeling Using Allan Variance. In Proceedings of the 16th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS/GNSS 2003), Portland, OR, USA, 9–12 September 2003; pp. 2860–2867.
- El-Sheimy, N.; Hou, H.; Niu, X. Analysis and modeling of inertial sensors using allan variance. IEEE Trans. Instrum. Meas. 2008, 57, 140–149. [Google Scholar] [CrossRef]
- Niu, X.; Chen, Q.; Zhang, Q.; Zhang, H.; Niu, J.; Chen, K.; Shi, C.; Liu, J. Using allan variance to analyze the error characteristics of gnss positioning. GPS Solut. 2014, 18, 231–242. [Google Scholar] [CrossRef]
- IEEE standard specification format guide and test procedure for linear, single-axis, non-gyroscopic accelerometers. In IEEE Std 1293–1998; IEEE: New York, NY, USA, 1999; pp. 1–121.
- IEEE standard specification format guide and test procedure for single-axis interferometric fiber optic gyros. In IEEE Std 952–1997; IEEE: New York, NY, USA, 1998; pp. 1–95.
- IEEE standard specification format guide and test procedure for single-axis laser gyros. In IEEE Std 647–2006 (Revision of IEEE Std 647–1995); IEEE: New York, NY, USA, 2006; pp. 1–76.
- Aggarwal, P.; Syed, Z.; Niu, X.; el-Sheimy, N. A standard testing and calibration procedure for low cost mems inertial sensors and units. J. Navig. 2008, 61, 323–336. [Google Scholar] [CrossRef]
- Chatfield, A.B.C. Fundamentals of High Accuracy Inertial Navigation; AIAA: Reston, VA, USA, 1997; Volume 174. [Google Scholar]
- El-Diasty, M.; Pagiatakis, S. Calibration and stochastic modelling of inertial navigation sensor errors. J. Glob. Position. Syst. 2008, 7, 170–182. [Google Scholar] [CrossRef]
- Syed, Z.; Aggarwal, P.; Goodall, C.; Niu, X.; el-Sheimy, N. A new multi-position calibration method for mems inertial navigation systems. Meas. Sci. Technol. 2007, 18, 1897. [Google Scholar] [CrossRef]
- Pedley, M. Tilt sensing using a three-axis accelerometer. In Freescale Semiconductor Application Note; Freescale Semiconductor: Austin, TX, USA, 2013. [Google Scholar]
- Luczak, S.; Oleksiuk, W.; Bodnicki, M. Sensing tilt with mems accelerometers. IEEE Sens. J. 2006, 6, 1669–1675. [Google Scholar] [CrossRef]
- Titterton, D.; Weston, J.L. Strapdown Inertial Navigation Technology; IET: London, UK, 2004; Volume 17. [Google Scholar]
- Woodman, O.J. An introduction to inertial navigation. In University of Cambridge, Computer Laboratory, Technology Report UCAMCL-TR-696; University of Cambridge: Cambridge, UK, 2007; Volume 14, p. 15. [Google Scholar]
- Berman, Z. Inertial Sensors: Further Developments in Low-Cost Calibration and Testing. In Proceedings of the Position Location and Navigation Symposium (PLANS), IEEE/ION, Myrtle Beach, SC, USA, 23–26 April 2012; pp. 837–848.
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/4.0/).