Abstract
Background: Recent research emphasizes the need to synthesize empirical studies on “K–12” math teachers’ professional development (PD) programs and their impact on student learning. Objective: This meta-analysis examines how teachers’ participation in PD programs affects students’ math achievement, analyzing the influence of program characteristics, such as duration, PD teaching approach, modality, grade level, type of math content, PD category, and study design. Design: Using online databases, 30 randomized or quasi-experimental studies from the U.S. and Canada (2003–2021) were selected, yielding 164 independent effect sizes, as some studies reported multiple interventions. Results: Only 1% of publications met the inclusion criteria. Most were excluded due to duplication, geographic location, lack of K–12 focus, missing data, or non-empirical content. PD was most effective when programs were under a year, focused on geometry, combined content and pedagogy, targeted grades 6–8, used online video, were reform-initiated, and employed randomized designs. Modality did not significantly impact outcomes. Conclusions: While extensive research exists on PD best practices, few studies empirically link program features to student achievement. This study offers evidence that well-designed math PD can significantly improve student outcomes, providing actionable insights for educators and policymakers.
1. Introduction
1.1. Rationale
There has been significant scrutiny on mathematics teaching and learning, spurred by the underperformance of U.S. students compared to their international counterparts in assessments such as the Trends in International Mathematics and Science Study (TIMMS) and Programme for International Student Assessment (PISA) (Bicer et al., 2014, 2015; Bicer & Capraro, 2016; Buckhalter, 2019; PISA, 2022; Polly et al., 2018; Provasnik et al., 2016; TIMSS, 2019). Researchers agree that teachers are the primary catalysts for change in student learning and achievement, prompting a focus on improving math teacher quality and effectiveness. For over three decades, literature has emphasized the critical role of teachers’ content knowledge, pedagogical knowledge, and instructional practices in improving math proficiency (Ball et al., 2008; Hill & Luft, 2015; Shulman, 1986). Comparing these domains involves examining how each uniquely and interactively contributes to effective teaching. Content knowledge refers to a teacher’s mastery of subject matter, pedagogical knowledge to instructional strategies and learning processes, and classroom practices to the application of both in instructional settings. Together, they form an integrated framework for evaluating and improving teaching effectiveness.
Given the paramount importance of elevating teaching standards, learning outcomes, and student performance in mathematics to bridge the U.S. achievement gap, the implementation of standards-based accountability measures, exemplified by initiatives like the No Child Left Behind Act of 2001, has been pursued (Capraro et al., 2016).
Within this context, professional development (PD) participation has emerged as a key avenue for enhancing pedagogical skills and classroom practices, thereby positively influencing student achievement (Buckhalter, 2019; Capraro et al., 2016; Scher & O’Reilly, 2009). In this study, PD is defined as the formal acquisition of skills and knowledge through workshops, professional meetings, coaching, and mentoring within schools or districts, aimed at strengthening teachers’ content and pedagogical knowledge. Student achievement refers to gains in math performance as measured by grades, test scores, and state assessments.
Amid ongoing debates regarding which PD aspects most significantly affect student outcomes, this study will evaluate duration, PD teaching approach, modality, grade level, type of math content, PD category, and study design. A meta-analysis methodology will be used to systematically combine and statistically analyze the results of multiple independent studies on the same topic, thereby assessing their overall impact on student achievement. Despite substantial investment in PD initiatives, few empirical studies demonstrate their effect on student outcomes or clarify which specific components are most effective in improving student learning. Nevertheless, continued concerns about low U.S. math achievement underscore the need to determine which PD components best enhance students’ learning.
This study seeks to address that gap by examining the relationship between PD and student achievement. Specifically, it will synthesize quantitative results from studies conducted between 2003 and 2021 that employed scientific methods and reported numerical findings to provide empirical evidence on the role of PD and its components in improving achievement.
1.2. Objectives
To achieve this goal, a meta-analysis methodology was employed to evaluate the effect size of professional development (PD) on students’ achievement. Additionally, a meta-regression analysis was conducted to explore how effect sizes vary across seven theoretical moderators: duration, PD teaching approach, modality, grade level, type of math content, PD category, and study design. The inclusion of study design as a moderator allows for a more nuanced understanding of how methodological rigor influences reported outcomes. It also allows the analysis to account for potential variability in outcomes attributable to the rigor of the research design rather than the intervention itself. These moderators are defined below:
- Duration (short-term indicates one-time or less than one year; one academic year, or multiple years), representing the length of time the professional development intervention was implemented.
- PD Teaching Approach refers to the three categories of content knowledge only (CK), pedagogy only (PK), or a combination of pedagogy and content knowledge (PCK). These terms come from Shulman’s (1986) framework and describe the types of PD intervention in studies included in this meta-analysis to enhance educators’ knowledge, instructional skills, and classroom practices.
- Modality (workshop only, workshop plus coaching, or workshop plus other support strategies), indicating the format or delivery method through which professional learning experiences were provided to educators.
- Grade Level (K–2nd, 3rd–5th, 6th–8th, or 9th–12th), denoting the student grade levels taught by the teachers who received the PD intervention.
- Type of Math Content (geometry, algebra, or other math domains), referring to the specific mathematical knowledge, concepts, and procedures addressed in the PD program.
- PD Category refers to professional learning communities (PLCs), formative assessment, curriculum, online/video-based, reform-initiated math, PD approach, cooperative learning, or technology describing the thematic area or framework around which the PD was organized. PD approach refers to studies with PD programs that did not fit into predefined categories and did not specify the type of PD delivered but were activities aimed at improving instruction or enhancing teacher skills and knowledge (Desimone, 2009).
- Study Design (randomized or quasi-experimental). A randomized study design involves randomly assigning participants to either a treatment (intervention) group or a control (comparison) group, which helps control for selection bias and enhances internal validity. In contrast, a quasi-experimental design lacks random assignment but still includes an intervention and comparison group, allowing for evaluation of the PD’s effects under more naturalistic or constrained conditions.
These moderators were examined to explore how variations in PD characteristics and study methodology may influence student achievement outcomes.
1.3. Literature Review
1.3.1. Importance of Professional Development for Math Teachers
Over the past 20 years, education reforms have emphasized teachers as key agents for improving student achievement (Buckhalter, 2019; Scher & O’Reilly, 2009). With the current focus on math instruction and the ongoing demand for professional development (PD), it is necessary to synthesize past studies to identify which PD components most benefit students. Although many studies have explored PD for math teachers, variations in methodology (e.g., self-reporting vs. observation), content focus (e.g., teacher perceptions), and sample size have led to inconsistent results. Furthermore, many have focused only on teacher outcomes, with much of the literature being theoretical rather than empirical.
Professional development is consistently recognized as essential for improving teacher knowledge and skills. Research repeatedly shows that educational improvement rarely occurs without PD (Guskey & Sparks, 2004). As global education reforms set high expectations for student learning (Borko, 2004), the need for effective PD is urgent. There is broad agreement in the literature that PD enhances the quality of U.S. schools (Desimone, 2011).
Research supports the role of PD in strengthening teachers’ content and pedagogical knowledge, which improves teaching, learning, and student achievement. For instance, a review of 57 studies by Wilson et al. (2002) found a positive link between teachers’ subject matter knowledge and student achievement. That study concluded that education coursework, especially research-based math practices and teaching strategies, directly impacts teacher performance. In contrast, simply taking more math courses had limited effects on student outcomes.
Math education scholars have emphasized that the depth of math knowledge needed for teaching goes beyond accumulating coursework (Ball et al., 2008). While content knowledge is important, the challenge lies in teachers’ ability to transfer that knowledge effectively through instruction.
1.3.2. Topics Covered in Professional Development
Given the diverse learning needs of 21st-century students, it is crucial for teachers to possess a solid foundation in content knowledge, content-specific instructional strategies, and pedagogical content knowledge (understanding how students learn), enabling them to tailor instruction to meet all students’ needs (Killion, 2002). Educational reforms have consistently targeted teachers’ education as a means to enhance instruction with the aim of improving students’ learning outcomes (Desimone, 2011).
Two key types of teacher knowledge are content knowledge and pedagogical content knowledge (PCK). Both are essential for promoting higher math achievement (Hill et al., 2005). Teachers cannot help students grasp math concepts if they themselves lack understanding. Subject matter knowledge forms the foundation of teaching (Loucks-Horsley & Matsumoto, 1999; Kleickmann et al., 2013). Teachers must not only know the correct answers but also understand why those answers are correct (Shulman, 1986).
Pedagogical content knowledge emphasizes understanding student learning processes (Shulman, 1986). Cohen (1990) illustrated this with a teacher who used manipulatives during a lesson, assuming this alone would aid student understanding. However, the teacher lacked knowledge of how to use manipulatives effectively. This example highlights the need for both pedagogical and content knowledge in PD to promote high-quality instruction and student learning (Desimone, 2011). Research has shown a relationship between these knowledge types and effective teaching (Grossman, 1990; Leinhardt & Smith, 1985). Garet et al. (2001), in the first major quantitative study on this topic, concluded that PD should focus on subject matter content and how students learn it (Desimone, 2011).
1.3.3. Outcome of Professional Development
Over the past two decades, research has consistently emphasized that PD is essential for improving teacher quality and student achievement. According to Sowder, professional development should focus on how students learn math and on strengthening teachers’ content knowledge (Krawec & Montague, 2014; Sowder, 2007). Effective PD enhances teachers’ learning and practice, ultimately supporting student outcomes (Kang et al., 2013). Teachers’ knowledge and its classroom application directly influence student learning and the ability to apply concepts (Early et al., 2016; Killion, 2002).
Research confirms that professional learning opportunities can enhance teachers’ content knowledge (Hill, 2011). Evidence shows a positive relationship between students’ math achievement and their teachers’ math knowledge/training (Yoon et al., 2007). Hill et al. (2005) found that the combination of teachers’ math knowledge and pedagogical content knowledge had a greater effect on student achievement than content knowledge alone. Although both knowledge types are important, their connection and how professional development should address them remain unclear (Even, 1993).
A 2007 meta-analysis by the Council of Chief State School Officers examined professional development’s effects on student achievement (Blank & de las Alas, 2009). It highlighted that PD programs with multiple, sustained activities were most effective (Blank, 2013). Programs had greater impact when they included six key components: content focus, longer duration, multiple activities, hands-on learning, specific goals, and collective teacher participation (Blank, 2013).
For over 20 years, rigorous studies have shown that mathematics professional development programs for teachers are most effective when they have three characteristics: sustained activities over time, focus on subject matter and how students learn it, and opportunities for teacher collaboration on curriculum and instruction (Desimone et al., 2002; Desimone et al., 2007; Garet et al., 2001; McLaughlin & Talbert, 2001; Tournaki et al., 2011). When looking at the sustained duration of PD, Desimone (2009), Darling-Hammond et al. (2017), and more recent studies (Goldberg et al., 2023; Wischgoll & Prediger, 2024) confirm that PD is most effective when it is sustained over time, not one-day workshops but programs extending across weeks or months, often 30 plus hours.
In support of effective PD focusing on mathematics content and student understanding, it has been found that when PD is designed to target mathematical knowledge for teaching (MKT) and pedagogical content knowledge (PCK), addressing teachers’ ability to explain math and understand how students think about it increases teachers’ effectiveness in the classroom (Tzur et al., 2022; Hill et al., 2005) by offering a deep engagement with the math concepts, including analysis of student work and misconceptions, also including instructional strategies for conceptual understanding and problem solving.
The last of the three characteristics is active teacher engagement and collaboration, such as video analysis of teaching, collaborative lesson planning, lesson study, and discussion of student thinking, which promotes peer learning, reflections and progressional dialogue, which lead to lasting instructional change (Larison et al., 2022; Skott, 2022; Desimone, 2009). These are aligned with prior findings linking such professional development with student achievement (Cohen & Hill, 2001).
In addition, empirical analyses have identified five effective PD components: content focus, active learning, coherence, duration, and collective participation. While these influence teacher knowledge and practice, their impact on student achievement has been more modest (Desimone, 2011; Capraro et al., 2016).
While extensive research outlines best practices in professional development (PD), relatively few studies empirically link specific program features to measurable gains in student achievement. Within the mathematics education research community, the existing body of work is heavily weighted toward theoretical discussions, with limited empirical evidence identifying which PD components most effectively enhance student learning. This study addresses that gap by presenting empirical findings on the relationship between well-designed mathematics PD and student achievement. In doing so, it offers evidence that targeted, high-quality PD can yield significant improvements in student outcomes, thereby providing actionable insights for educators and policymakers.
2. Method
2.1. Protocol, Information Sources, Search, and Selection of Sources of Evidence
Our study was developed in accordance with the Preferred Reporting Items for Systematic Reviews and Meta-Analyses extension for Scoping Reviews (PRISMA-ScR) (Tricco et al., 2018). These guidelines are designed to enhance the transparency, clarity, and completeness of scoping reviews by providing a structured framework for reporting key elements of the review process. The objective of this research is to provide a comprehensive assessment of the impact of K–12 mathematics teachers’ professional development (PD) programs on student achievement by summarizing, comparing, and integrating findings from the empirical literature. This study seeks to address a gap in existing research by offering empirical evidence on the relationship between mathematics teacher PD and student achievement outcomes. Specifically, this study aims to answer the following research questions:
- What is the impact of recent evaluated professional development programs on students’ mathematics achievement?
- Do the effects vary across different PD components, such as duration, PD teaching approach, modality, grade level, type of math content, PD category, and study design, that have been theoretically and practically linked to improved student outcomes?
A meta-analysis methodology was employed to assess effect sizes, examining the impact of various professional development (PD) components (duration, PD teaching approach, modality, type of math content, grade level, professional development category, and study design) on students’ achievement. This study aimed to investigate potential variations in effect size based on the duration of the program, the type of professional development teaching approaches, the modality of the PD program, the grade level of the PD program, the type of math content taught in the PD program, the professional development category of the program, and the study design of the program.
Out of 3018 reviewed independent research studies, 30 samples of K–12th grade professional development program studies were collected, with each study’s features systematically coded. Some studies reported multiple interventions, leading to their inclusion as multiple studies, thereby increasing the number of effect sizes to 164.
2.2. Eligibility Criteria
This review applied rigorous inclusion criteria to provide researchers and educators with reliable information on the effectiveness of each K–12th grade mathematics professional development program. The studies had to meet the following criteria: (a) conducted between 2003 and 2021; (b) focused on Kindergarten–12th grade mathematics teachers’ professional development intervention programs in the United States or Canada; (c) published or unpublished studies (e.g., dissertations, unpublished reports, conference presentations, reports to funding agencies); (d) included quantitative outcomes of students’ mathematics achievement; (e) designed rigorously (experimental or quasi-experimental), involving pre–posttests and/or treatment and control groups, with each primary study featuring a control or comparison group; (f) included sufficient quantitative data (sample size [N], mean [M], and standard deviation [SD]) to calculate effect size(s).
This meta-analysis focused on publications from the United States and Canada due to their contextual relevance, reflecting local curricula, educational policies, and cultural practices. These sources are also more readily accessible, primarily published in English, and directly support analyses of region-specific initiatives and cross-national comparisons within North America (Desimone, 2009).
Furthermore, to evaluate the effectiveness of professional development for mathematics teachers, this study prioritizes studies employing experimental and quasi-experimental research designs. These methodologies offer the strongest empirical basis for establishing causal inferences, thereby enhancing internal validity and enabling more robust conclusions about the impact of professional development interventions.
2.3. Data Charting Process and Data Items
Studies from the period of 2003–2021 were collected through a comprehensive literature search focusing on professional development programs for K–12th grade mathematics teachers. The search encompassed dissertations, conference papers, and journals of educational organizations. Various methods were employed, including computer searches, journal scans, dissertation searches, and conference paper databases. Electronic searches were conducted using educational databases, such as EBSCOhost, ERIC WorldCat, Teacher Reference Center, and ERIC ProQuest. Key descriptors used in the search included combinations, such as professional development and math teachers; professional development and math teachers and student achievement; professional development and math achievement; professional development and math content knowledge; professional development and pedagogical knowledge and teacher quality; professional development and math teacher and pedagogical knowledge; professional development and math teacher and pedagogical and content knowledge and student achievement; and professional development for math teachers and education and student achievement. To mitigate publication bias, efforts were made to include both the published and unpublished literature (Card, 2015; Cheung & Slavin, 2016).
After removing duplicates and excluding studies conducted outside the United States and Canada, the second screening involved reviewing the title and abstract of each study. Studies meeting the criteria of being an intervention professional development program for K–12th grade mathematics teachers proceeded to further evaluation. These evaluations focused on student outcomes, empirical data, and study design. Finally, the empirical data of each study were reviewed, and studies lacking sufficient data to calculate mean effect size(s) were excluded.
Figure 1 illustrates the process employed to document the number of studies reviewed and ultimately included in the meta-analysis of the effects of professional development programs on students’ achievement. Initially, there were 3018 potential studies considered for inclusion in this study. Following the critical synthesis of the professional development literature, 30 out of 76 (39.5%) studies were identified as implementing an experimental or quasi-experimental design and having sufficient data to examine the effects of interventions on student achievement. Although a total of 30 studies included intervention math scores, 24 studies reported on more than one intervention, thus considered as having multiple studies, resulting in an increased number of effect sizes to 164 (see Table 1). Table 1 provides an overview of the studies meeting the inclusion criteria for this meta-analysis study.
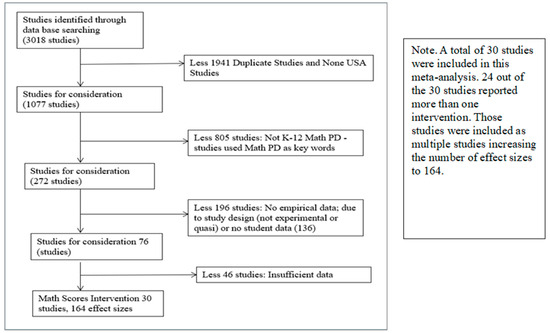
Figure 1.
Kindergarten–12th grade mathematics teachers’ professional development studies search and review process.

Table 1.
Impact of professional development for K–12 mathematics teachers on student achievement.
2.4. Critical Appraisal of Individual Sources of Evidence
Each article meeting the inclusion criteria underwent coding by one of the review authors, with the codes then verified by the other author. Any coding discrepancies were resolved through discussion until consensus was reached. The coded data included author(s) name, study name, publication year and status, program components, grade level, study design, study duration, sample size, sample characteristics, professional development teaching approach, PD modality, math content type, professional development category, outcome measures, and effect sizes.
Initially, the focus variables of the research were identified as the duration of PD programs, PD teaching approaches, and PD intervention modalities. However, the research scope was expanded to include additional variables such as math content types, students’ grade levels, and professional development categories. These variables could potentially moderate the effects in the review, distinguishing between substantive factors related to population and intervention characteristics and methodological factors (study design) unrelated to these characteristics (Pellegrini et al., 2021).
Effect size quantifies the magnitude of difference or relationship strength (Cook et al., 2018; Cooper, 2015). A larger effect size between groups indicates a stronger relationship between them, influencing the likelihood of finding statistically significant results (Cook et al., 2018; Card, 2015). However, since outcome measures used in studies may vary, standardized effect sizes are employed to facilitate comparisons across studies that may not use the same measurement scales (Institute for Educational Science (IES), 2022).
In alignment with What Works Clearinghouse (WWC) guidelines, this study uses Hedges’ g to quantify the effect sizes of professional development programs, as it provides a standardized and unbiased measure of impact, particularly suitable for education research with varying sample sizes (Institute for Educational Science (IES), 2022). At the outset of our analysis, the overall random effect model was employed for the 164 effect sizes to assess the impact of K–12th grade mathematics teachers’ PD programs on students’ math achievement in this study (refer to Table 2). Subsequently, a meta-regression model was utilized to evaluate the effect sizes of moderators in this study. Seven moderators were considered: duration of the program; professional development teaching approach; modality of the PD program; students’ grade level; type of math content taught in the PD program; professional development category and study design.

Table 2.
Mean effect size and the test for heterogeneity: professional development and student achievement.
Since our data included multiple effect sizes for 24 of the included studies, this allowed the opportunity to employ a multivariate meta-regression model with robust variance estimation (RVE), which accounted for the dependence of the covariance structure. Another advantage of using this approach is that the statistical significance of each moderator is calculated, leading to an explanation of the variation in the effect sizes (Hedges et al., 2010; Pellegrini et al., 2021).
3. Results
3.1. Results from Overall Model
The meta-analysis study utilized Comprehensive Meta Analysis software (Version 4) (Borenstein et al., 2022). A total of 30 studies met the inclusion criteria. Among them, 24 studies reported on more than one intervention math score, resulting in 164 effect sizes (refer to Table 2). Hence, the analysis is based on 164 studies. Hedge’s (g) was employed as the effect size index to compute the standardized mean difference. The random effect model indicated a mean effect size of 0.228 (95% CI: 0.173 to 0.283) across the 164 studies.
The model revealed a Q-value of 5661.753, with 163 degrees of freedom, yielding a p-value < 0.001. Consequently, the null hypothesis was rejected, providing evidence against the equality of true effect sizes across all included studies. I2, representing the proportion of variance in observed effects attributable to true effects rather than sampling error, was calculated at 97.121%. T2, the variance of true effect sizes, was estimated at 0.112 in g units, with T, the standard deviation of true effect sizes, at 0.334 in g units.
Under the assumption of normally distributed true effects in g units, the prediction interval was determined to be −0.435 to 0.891. In other words, this interval encompasses the true effect size in 95% of comparable populations (Borenstein, 2019; Borenstein et al., 2021; IntHout et al., 2016; Lasserson et al., 2019).
The results revealed a statistically significant small effect (g = 0.228, p < 0.000) of rigorously evaluated professional development (PD) programs on math students’ achievement. The collective effect sizes of the 164 intervention math scores in this meta-analysis imply a positive overall impact of professional development mathematics interventions on students’ achievement. Specifically, K–12th grade mathematics teachers who participated in these programs facilitated better student outcomes compared to those whose teachers did not engage in similar professional development interventions.
3.2. Critical Appraisal Within Sources of Evidence
Every effort was made in this meta-analysis to include both published and unpublished studies on the impact of professional development programs for K–12th grade mathematics teachers and students’ achievement, aiming to mitigate potential publication bias. This is crucial because studies reporting null or negative effects are often less likely to be published compared to those reporting positive significant effects (Card, 2015). If the selection of studies in this review is biased, it could undermine the validity of the results (Card, 2015; Lin & Chu, 2018; Rothstein et al., 2005). Hence, several steps were taken to assess the potential for publication bias.
First, a funnel plot was generated, plotting the standardized difference in means (x-axis) against the standard error (y-axis) (refer to Figure 2). The funnel plot indicated no apparent publication bias, with studies evenly distributed on both sides of the average random effect size. In the presence of bias, the distribution would be asymmetrical, with a concentration of studies on one side of the average, indicating potential missing studies.
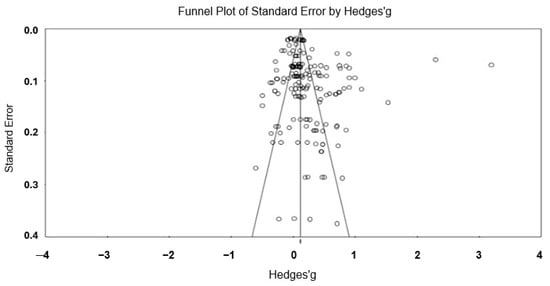
Figure 2.
Funnel plot: professional development and student achievement for publication bias.
Second, a classic fail-safe analysis was conducted to test the robustness of the meta-analytic findings. The Z-value for the observed studies was highly statistically significant (Z = 31.59994, p < 0.000), suggesting a substantial effect size. To render the combined two-tailed p-value non-significant (p > 0.050), 2467 null studies, each with an average effect size of zero, would need to exist but were excluded from this meta-analysis. This indicates an absence of publication bias.
Furthermore, to ensure the robustness of the meta-analysis, the file drawer problem was addressed. This problem refers to the hypothetical non-significant studies presumed to be unpublished and stored away (“in the file drawer”), which, if included, could nullify the observed effect (Borenstein, 2019). For a robust effect, the fail-safe N tolerance level to the file drawer problem should exceed 5K + 10 (where k is the number of studies) (Rosenthal, 1979; Takacs & Kassai, 2019). With 164 studies included in this meta-analysis, the fail-safe N should be larger than 830 [5(164) + 10 = 830] to consider the results robust. Given that including 2467 missing studies is improbable, the results of this study can be considered stable and robust.
3.3. Results from Models with Moderators
Following the implementation of the overall random effect model to assess the impact of professional development (PD) programs for K–12th grade mathematics teachers on students’ math achievement (as displayed in Table 2) and the absence of publication bias, a meta-regression model was employed to examine the effect sizes of seven identified moderators within this meta-analysis.
Table 3 presents the outcomes of the meta-regression analysis for these moderators: duration of the program (less than 1 year, 1 year versus multiple years); professional development teaching approach (content only, pedagogy only, content and pedagogy); modality of the PD program (workshop only, workshop plus coaching, workshop plus other support); students’ grade level (K—2nd, 3rd–5th, 6th–8th, and 9th–12th); type of math content taught in the PD program (geometry, algebra, and all other types of mathematics); professional development category [professional learning community, formative assessment, curriculum, online PD, reformed initiated math, combined types of PD, cooperative learning, and technology (calculator, computer software) PD]; and study design (randomized and non-randomized).

Table 3.
Professional development and student achievement: meta-regression analyses with individual moderators.
3.4. Duration
Upon evaluating the moderator of duration, the coefficient for short-term professional development (PD) duration (one-time or less than 1 year) was found to be 0.2167 (refer to Table 3). This indicates that the mean effect size for studies incorporating short-term PD in students’ math achievement scores was 0.2167 points higher than for studies involving PD lasting one academic year. The average effect size for short-term PD (one-time or less than 1 year) is calculated as 0.1344 + 0.2167, resulting in 0.3511. The 95% confidence interval for the difference in means ranges from 0.0843 to 0.3490. The Z-value for the difference is 3.21, with a corresponding p-value of 0.0013, indicating a significant difference in effect size between short-term PD and PD lasting one academic year. Among the various PD durations analyzed, only the short-term PD group showed significance. This suggests that the effect size is likely higher in studies involving short-term PD in students’ math achievement scores compared to studies involving PD lasting one academic year.
The Q-value for the model is 10.30 with 2 degrees of freedom, yielding a p-value of 0.0058. T2, the variance of true effects about the subgroup means, is 0.1159, and T, the standard deviation of true effects about the subgroup means, is 0.3405. I2, representing the proportion of variance in observed effects reflecting variation in true effects rather than sampling error, is calculated at 97.09%. Additionally, the Q-value for the residual variance is 5541.86 with 161 degrees of freedom, and a p-value of 0.000, indicating statistical significance. This suggests that there is evidence of true effects varying within subgroups.
The R2 analog is 0.00, indicating that 0% of the variance in true effects can be explained by the difference between subgroups. The absolute effect size for PD lasting one academic year is 0.1344, while for short-term PD (one-time or less than 1 year), it is 0.1344 + 0.2167, totaling 0.3511 (refer to Table 3 and Figure 3).
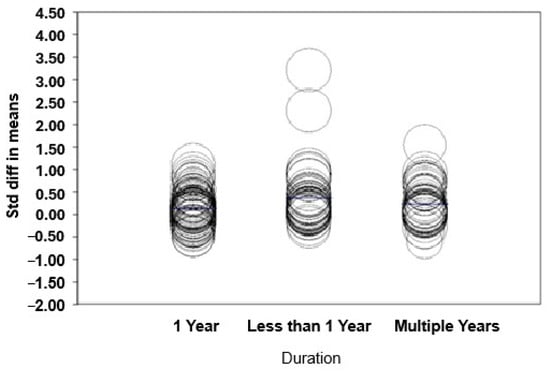
Figure 3.
Effect size comparison of duration.
In summary, regarding the duration of K–12th grade mathematics intervention PD programs, students whose teachers participated in short-term PD (one-time or less than 1 year) outperformed those whose teachers attended PD lasting one academic year in mathematics assessments. Moreover, evidence indicates that students’ math achievement in classes where teachers underwent multiple years of PD did not significantly differ from those whose teachers participated in PD for one academic year. These findings suggest that longer PD periods do not necessarily enhance student achievement, possibly due to teacher attrition from longer programs. The data also suggest that students whose teachers engaged in shorter PD durations exhibited better math achievement scores. These positive outcomes associated with shorter PD durations may be attributed to better alignment with teachers’ schedules.
3.5. Professional Development Teaching Approaches
The coefficient for content and pedagogy professional development (PD) (Y) is 0.1441 (refer to Table 3). This indicates that the mean effect size for studies incorporating content and pedagogy PD in students’ math achievement scores was 0.1441 points higher than for studies involving pedagogy-only professional development. The average effect size for content and pedagogy PD is calculated as 0.1444 + 0.1441, resulting in 0.2885. The 95% confidence interval for the difference in means ranges from 0.0151 to 0.2730. The Z-value for the difference is 2.19, with a corresponding p-value of 0.0285, indicating a significant difference in effect size between content and pedagogy PD and pedagogy-only PD.
Among the various professional development teaching approaches analyzed, only the content and pedagogy category showed significance. This suggests that the effect size is likely higher in studies involving content and pedagogy PD in students’ math achievement scores compared to studies involving pedagogy-only PD.
For the model, the Q-value is 4.80 (df = 2, p = 0.0908), T2 is 0.1139, T is 0.3374, and I2 is 97.07%. The Q-value for the residual variance is 5500.93 (df = 161, p = 0.000), and the R2 analog is 0.00.
The absolute effect size for pedagogy-only PD is 0.1444, whereas for content and pedagogy PD, it is 0.1444 + 0.1441, totaling 0.2885 (refer to Table 3 and Figure 4).

Figure 4.
Effect size comparison of PD teaching approaches.
3.6. Modality
The results for the three groups (workshop only, workshop plus coaching, and workshop plus other support) were used to analyze the professional development modality approaches, and their impact on student achievement indicated no significant impact on student achievement (refer to Table 3).
3.7. Grade
The coefficient for grade levels 6th grade–8th grade (Y) is 0.4362 (refer to Table 3). This indicates that the mean effect size for studies including grade levels 6th–8th grade students’ math achievement scores was 0.4362 points higher than for studies involving grade levels K–2nd grade students’ math achievement scores. The average effect size for grade levels 6th–8th grade is calculated as 0.1467 + 0.4362, resulting in 0.5829. The 95% confidence interval for the difference in means ranges from 0.2812 to 0.5912. The Z-value for the difference is 5.52, with a corresponding p-value of 0.0000, indicating a significant difference in effect size between 6th and 8th grade studies and K–2nd grade studies.
Among the different grade levels analyzed, only the 6th–8th grade category showed significance. This suggests that the effect size is likely higher in studies involving 6th–8th grade students’ math achievement scores compared to studies involving K–2nd grade students’ math achievement scores.
For the model, the Q-value is 531.13 (df = 3, p = 0.0000), T2 is 0.0908, T is 0.3013, and I2 is 96.28%. The Q-value for the residual variance is 4306.35 (df = 160, p = 0.0000), and the R2 analog is 0.19, indicating that 19% of the variance in true effects can be explained by the difference between subgroups.
The absolute effect size for K–2nd grade is 0.1467, whereas for 6th–8th grade, it is 0.1467 + 0.4362, totaling 0.5829 (refer to Table 3 and Figure 5). These results suggest that professional development tailored for 6th–8th grade students yields better outcomes for middle school students compared to younger children.
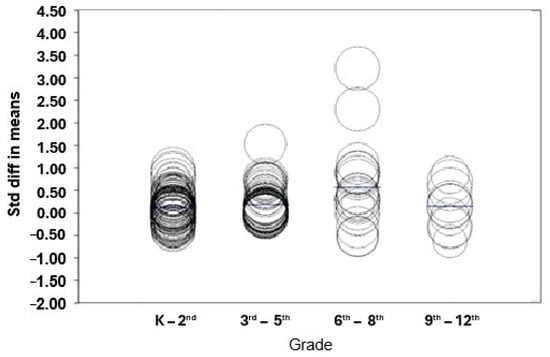
Figure 5.
Effect size comparison of grade.
3.8. Math Type
The coefficient for geometry (Y) is 0.3146 (refer to Table 3). This indicates that the mean effect size for studies including geometry students’ math achievement scores was 0.3146 points higher than for studies involving algebra students’ math achievement scores. The average effect size for geometry is calculated as 0.3113 + 0.3146, resulting in 0.6259. The 95% confidence interval for the difference in means ranges from 0.0222 to 0.6069. The Z-value for the difference is 2.11, with a corresponding p-value of 0.0349, indicating a significant difference in effect size between professional development studies that include geometry content and those that include algebra content.
Among the different types of math content analyzed, only geometry showed significance. This suggests that the effect size is likely higher in studies involving students’ geometry math achievement scores compared to studies involving students’ algebra math achievement scores.
For the model, the Q-value is 17.06 (df = 8, p = 0.0295), T2 is 0.1056, T is 0.3249, and I2 is 96.88%. The Q-value for the residual variance is 5156.82 (df = 161, p = 0.0000), and the R2 analog is 0.06, indicating that 6% of the variance in true effects can be explained by the difference between subgroups.
The absolute effect size for algebra is 0.3113, whereas for geometry, it is 0.3113 + 0.3146, totaling 0.6259 (refer to Table 3 and Figure 6). In summary, geometry is the most effective, followed by algebra, and all other math types are less effective than algebra (0.3113 − 0.1241 = 0.1872). While all other types of math content are significantly less effective than algebra at a 0.05 significance level, their significance level was 0.0784, which is less than 0.10.
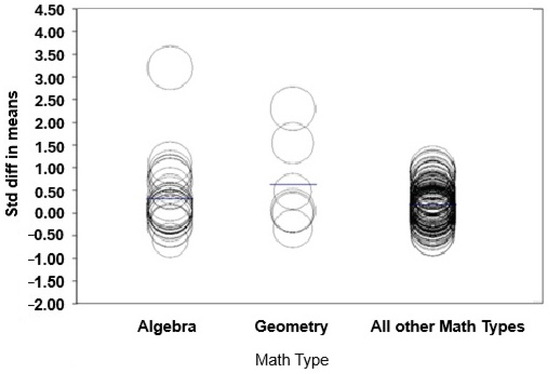
Figure 6.
Effect size comparison of math type.
3.9. Professional Development Category
The coefficient for online video professional development (Y) is 0.7663 (refer to Table 3). This indicates that the mean effect size for studies including online video PD students’ math achievement scores was 0.7663 points higher than for studies involving cooperative learning PD students’ math achievement scores. The average effect size for online video PD is calculated as −0.2902 + 0.7663, resulting in 0.4761. The 95% confidence interval for the difference in means ranges from 0.1168 to 1.4158. The Z-value for the difference is 2.31, with a corresponding p-value of 0.0207, indicating a significant difference in effect size between online video professional development studies and cooperative learning professional development studies.
Similarly, the coefficient for reformed initiated math professional development (Y) is 0.7296, indicating that the mean effect size for studies including reformed initiated math PD students’ math achievement scores was 0.7296 points higher than for studies involving cooperative learning PD students’ math achievement scores. The average effect size for reformed initiated math PD is calculated as −0.2902 + 0.7296, resulting in 0.4394. The 95% confidence interval for the difference in means ranges from 0.0702 to 1.3890. The Z-value for the difference is 2.17, with a corresponding p-value of 0.0301, indicating a significant difference in effect size between reformed initiated math professional development studies and cooperative learning professional development studies. When analyzing the different professional development categories, two categories were found to be significant. It was concluded that the effect size is likely higher in studies including online video professional development studies and reformed initiated math professional development studies students’ math achievement scores compared to studies including cooperative learning professional development students’ math achievement scores.
For the model, the Q-value is 42.45 (df = 7, p = 0.0000), T2 is 0.0920, T is 0.3034, and I2 is 96.42%. The Q-value for the residual variance is 4359.25 (df = 156, p = 0.0000), and the R2 analog is 0.18, indicating that 18% of the variance in true effects can be explained by the difference between subgroups.
The absolute effect size for cooperative learning PD is −0.2902, whereas for online video PD, it is −0.2902 + 0.7663, resulting in 0.4761, and for reformed initiated math PD, it is −0.2902 + 0.7296, resulting in 0.4394 (refer to Table 3 and Figure 7).
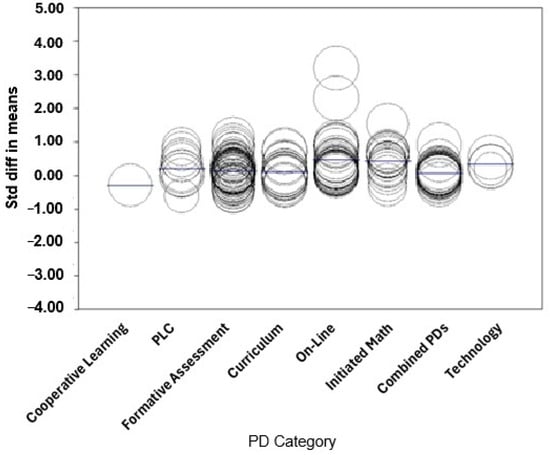
Figure 7.
Effect size comparison of PD category.
3.10. Study Design
The coefficient for randomized study design (Y) is 0.1571 (refer to Table 3). This indicates that the mean effect size for studies including randomized study design students’ math achievement scores was 0.1571 points higher than for studies involving quasi-experimental design studies students’ math achievement scores. The average effect size for randomized study design is calculated as 0.1275 + 0.1571, resulting in 0.2846. The 95% confidence interval for the difference in means ranges from 0.0419 to 0.2723. The Z-value for the difference is 2.67, with a corresponding p-value of 0.0075, indicating a significant difference in effect size between randomized study design professional development studies and professional development studies that used a quasi-experimental design.
When analyzing the different professional development study designs, it was concluded that the effect size is likely higher in studies including randomized study designs for students’ math achievement scores compared to studies using quasi-experimental designs for students’ math achievement scores.
For the model, the Q-value is 7.15 (df = 1, p = 0.0075), T2 is 0.1141, T is 0.3378, and I2 is 97.13%. The Q-value for the residual variance is 5652 (df = 162, p = 0.0000), and the R2 analog is 0.00, indicating that 0% of the variance in true effects can be explained by the difference between subgroups.
The absolute effect size for quasi-experimental design is 0.1275, whereas for randomized study design, it is 0.1275 + 0.1571, resulting in 0.2846 (refer to Table 3 and Figure 8). In summary, randomized design is significantly better (0.1571) than professional development studies that used quasi-experimental design.
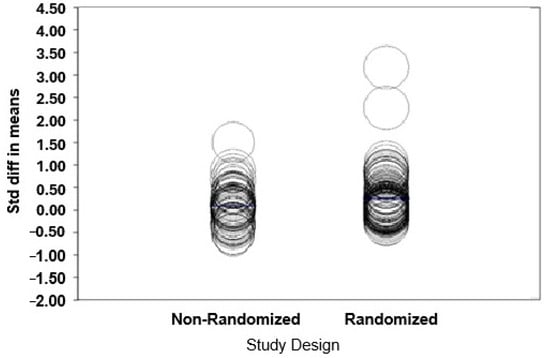
Figure 8.
Effect size comparison of study designs.
4. Discussion and Summary of Evidence
With teacher effectiveness being at the forefront of students’ learning and achievement, there is a need for continued study on the effects of professional development (PD) on students’ achievement. Many research articles evaluate the effects of PD on teachers, using teacher reports on changes in their knowledge and teaching practices. However, there are few studies that link PD to students’ achievement. Over the past two decades, numerous studies have examined professional development for teachers. However, empirical evidence on the effects that professional development programs, their components, and delivery modalities have on students’ achievement has been one of the main missing dimensions of many previous studies. This meta-analysis attempted to fill the gap in the literature by offering empirical evidence regarding the impact of K–12th grade professional development programs for mathematics teachers on students’ achievement by answering the following questions:
- (1)
- What is the impact of evaluated recent professional development programs on students’ math achievement?
- (2)
- Do effects vary among the evaluated PD components (duration, teaching approaches, modality, grade level, math content, type of PD program, and study design) that have been asserted through theory and practice to be beneficial to improving students’ achievement?
4.1. Overall Effect of Professional Development
In accordance with the first research question, this analysis revealed that the pooled effect estimate is a modest but statistically significant effect of 0.228 (p ≤ 0.001) of evaluated math-focused professional development programs on students’ achievement. This effect size indicates that the average math score of students whose teachers participated in the professional development programs achieved an estimated 0.228 standard deviation higher score on the math assessment than students whose teachers did not participate in these programs. For example, if a student in the comparison group scored in the 50th percentile, an equivalent student whose teacher participated in these professional development programs would score in the 59th percentile. The results of this meta-analysis demonstrate that the average impact of evaluated recent professional development programs on math students’ achievement is 0.228 (p ≤ 0.001), providing evidence that K–12th grade mathematics PD programs in this study had a modest positive effect on students’ achievement. Scholars and policymakers view PD as a means to increase teachers’ quality (Darling-Hammond et al., 2017; Foster et al., 2013) and effectiveness, leading to student gains. In support of the overall findings in this study, teachers who participated in the math intervention programs outperformed students whose teachers did not participate in the intervention. Research has shown that teacher quality is a significant factor in students’ academic gains (Boyd et al., 2006; Clotfelter et al., 2007; Rivkin et al., 2005). In response to the impact of evaluated recent professional development programs on students’ math achievement in this meta-analysis, the results showed that teachers were able to utilize what they learned in the classroom, which had a positive impact on their students’ learning.
Many reported studies show that professional development programs that focus on content or pedagogy or both; activities that are sustained over time; offering workshops and sustained follow-up support after the initial professional workshop; duration of program; coherence within the PD; active learning where teachers engage with materials and each other are positively related to student achievement (Blank, 2013; Darling-Hammond et al., 2009; Desimone, 2009; Early et al., 2016; Garet et al., 2001; Hill, 2007; Taylor et al., 2017; Tournaki et al., 2011; Yoon et al., 2007). Even though the PD research community has come up with some guidelines for developing effective PD (Borko et al., 2010; Desimone et al., 2002; Ingvarson et al., 2005; Penuel et al., 2007), there are still mixed outcomes of PD studies and limited empirical research-based evidence on the effectiveness of PD (Kisa, 2014). Some studies have positive results (Franke et al., 2001; Taylor et al., 2017), while others are not as successful (Jacob et al., 2017; Jacobs et al., 2020; Santagata et al., 2010).
For the purpose of deeper understanding, the current study further focused on those program components that have been found to be effective in the PD literature. There were seven moderators in this study, such as duration, PD teaching approach, modality, math type, grade, PD category, and study design. A meta-regression was used to combine and contrast components of PD programs by calculating the statistical significance of each moderator and its categories and explaining the variation in the effect sizes (Hedges et al., 2010; Pellegrini et al., 2021).
In response to whether the PD components that have been asserted through theory and practice are being beneficial to improving students’ achievement, this study used meta-regression to examine the similarities and differences among the moderators and their categories (see Table 3). These components of the PD programs are discussed below.
4.2. Duration
In this meta-analysis, when making comparisons of the impact that the math-focused professional development program studies may have on students’ achievement based on duration (short-term indicates; one-time or less than 1 year; one academic year, and multiple years) of the programs, it was found that only one group (short-term) had a significant effect on students’ achievement. The effect size for short-term PD was 0.2167 points higher than the average effect size for studies that included a duration of one academic year of professional development. The absolute effect size for PD that lasted one academic year is 0.1344. The average effect size for short-term PD is 0.3511.
It was concluded that the effect size is probably higher in studies that included the short-term PD (one-time or less than 1 year) students’ math achievement scores as compared with studies that included PD that lasted one academic year of professional development. Out of the 30 studies in this analysis, there are five short-term duration (less than 1 year) math intervention programs (Agodini & Harris, 2016; Bicer & Capraro, 2016; Clements et al., 2016; Heller et al., 2007; O’Dwyer et al., 2010) where the results showed that all or some of their independent effects had a positive statistically significant impact on students’ mathematics achievement (refer to Table 1).
In summary of the duration of K–12 teachers mathematics intervention professional development programs, it was found that students whose teachers participated in a one-time or less-than-1-year mathematics intervention PD program outperformed students whose teachers attended a 1-academic-year math intervention PD on their mathematics assessment. The evidence also showed that students’ mathematics achievement of teachers who attended multiple years of math intervention PD was not significantly different than students whose teachers attended one academic year of math intervention PD.
In conclusion, the evidence showed that longer periods of PD do not make a difference in students’ achievement; thus, this could be due to teachers dropping out of the PD program because of the program duration. Based on the data, it also showed that students whose teachers took PD for shorter time periods had better mathematics achievement scores. While it is commonly assumed that longer PD programs are more effective, our analysis supports studies indicating that shorter, focused PD interventions can lead to more immediate and measurable improvements in student outcomes (Garet et al., 2001; Yoon et al., 2007). In addition, shorter PD programs are often more intensive and strategically designed, enabling teachers to quickly absorb and apply new strategies in their classrooms. These sessions may also be better aligned with teachers’ time constraints, increasing both engagement and implementation fidelity. Moreover, research on shorter-duration PD frequently measures outcomes shortly after the intervention, making it easier to detect direct impacts on instruction and student achievement. These positive outcomes associated with shorter PD durations may be attributed to better alignment with teachers’ schedules, allowing them to engage more effectively. The results from the analysis in this study are contrary to the prior research that stated that the length of a professional development program is one of the key elements for improving teaching or learning. The longer the duration of the program, the more time teachers have to increase their content knowledge, pedagogical knowledge, or both in a professional setting. In contrast, longer-term PD programs may be subject to diminished effects over time if teachers are not given sustained opportunities to reinforce or apply what they learned. As noted by Yoon et al. (2007), the timing of outcome measurement is also critical. Extended PD studies often assess achievement months or even years after the intervention, during which key content may be forgotten or inconsistently applied. Even though short workshops have been found to have little to no effect on teaching and learning (Hill, 2007), previous research has found that for teachers who received an average of 49 h of professional development, their students’ achievement increased by 21 percentile points. It was also found that studies that offered more than 14 h of professional development had a statistically significant positive impact on students’ achievement (Yoon et al., 2007). More recent research has also confirmed that sustained PD spanning weeks, months or 30 or more hours is most effective (Darling-Hammond et al., 2017; Desimone, 2009; Goldberg et al., 2023; Wischgoll & Prediger, 2024). Conversely, Guskey and Yoon (2009) found no significant gains in student achievement when teachers received only 5–14 h of PD. The five studies’ (O’Dwyer et al., 2010 (100 h); Heller et al., 2007 (10 h); Agodini & Harris, 2016 (less than 1 year); Bicer & Capraro, 2016 (48 h) and Clements et al., 2016 (24 h)) duration time in this meta-analysis spans from 10 h to 100 h. These findings contribute to the ongoing debate about the relationship between PD duration and student achievement.
Due to the mixed reviews from previous studies about the amount of time needed for teachers to participate in professional development to have a positive impact on students’ achievement and the results of this meta-analysis, it is concluded that the current findings do not totally align with theory and practice in regard to the amount of participation hours in math intervention PD for it to be beneficial in improving students’ achievement. These findings highlight the potential of well-structured, time-efficient PD models and suggest that duration alone is not a reliable predictor of effectiveness; instead, the intensity, focus, and timing of implementation may play a more critical role.
4.3. Professional Development Teaching Approach
In this meta-analysis, when analyzing the different professional development teaching approaches (content only, pedagogy only, and content and pedagogy), content and pedagogy were the only categories that were found to be significant. The mean effect size for studies that included content and pedagogy was 0.1441 points higher than the mean effect size for studies that included pedagogy only. The average effect size for studies that included content and pedagogy is 0.2885. The analysis showed that there is a significant difference in the effect size of content and pedagogy professional development studies than pedagogy-only professional development studies. In this body of research, there are 13 studies (Buckhalter, 2019; Jiang et al., 2011; Polly et al., 2017; O’Dwyer et al., 2010; Heller et al., 2007; Dash et al., 2012; Van Haneghan et al., 2004; Krupa, 2011; Kuchey et al., 2009; Agodini & Harris, 2016; Bicer & Capraro, 2016; Krawec & Montague, 2014; Schoen et al., 2018) that included content and pedagogy-focused professional development math intervention programs that showed some positive statistically significant independent effects on student achievement (refer to Table 1).
Teachers having strong content knowledge are essential for students’ achievement in mathematics (Desimone et al., 2006). Content knowledge is the subject matter knowledge that teachers need to teach to their students (Hill et al., 2005). Earlier research has shown that there is a positive relationship between teachers’ content knowledge and higher student achievement (Desimone et al., 2006; Wilson et al., 2002). Pedagogical knowledge entails teachers knowing how to teach their students and how they learn (Killion, 2002). Therefore, teachers having a deep understanding of mathematical concepts (content knowledge) along with the needed knowledge to teach the mathematics (pedagogical knowledge) is more important than either of these alone for increasing students’ achievement (Hill et al., 2005). It has been found that students’ math achievement is greater when teachers have strong content knowledge and pedagogical knowledge (Patel et al., 2012).
The results of this study support the previous literature that content and pedagogy-focused professional development is an effective way to increase teachers’ mathematical knowledge. Overall, these results suggest that content and pedagogy-focused PD is likely to have a positive impact on student achievement by increasing teachers’ capacity to teach the math curriculum.
4.4. Modality
The professional development literature has also supported a variety of modalities for delivering PD. In general, professional development is delivered via workshops, coaching, courses, online, and in other ways. In this meta-analysis, professional development modalities are workshop only, workshop plus coaching, and workshop plus some other support strategies. The results for the three modalities used to analyze the professional development modality approaches and their impact on student achievement were found to have no significant impact on student achievement.
4.5. Grade Level
When analyzing the different grade levels in this study, there was only one grade level that was found to be significant. It showed that the effect size is probably higher in studies that included 6th–8th grade students’ math achievement scores as compared with studies that included K–2nd grade students’ math achievement scores. The mean effect size for the studies that included grade levels 6th–8th grade students’ math achievement scores was 0.4362 points higher than the mean effect size for the studies that included grade levels K–2nd grade students’ math achievement (0.1467) scores. It was concluded that the effect size is probably higher in studies that included 6th–8th grade students’ math achievement scores as compared with studies that included K–2nd grade students’ math achievement. Based on this study’s findings, it is concluded that professional development works better for middle school students compared to younger children and high school students. Research has also shown that there have been many professional development programs for elementary (K–5th grade) teachers that were superficial in nature, offering fragmented explanations and disconnected activities covering important topics (Hill, 2007). Previous research has also found that elementary teachers participate in instructional strategies PD more often than PD that is focused on the in-depth study of mathematics (Yoon et al., 2007). This could be attributed to why the effect size is probably higher in studies that included 6th–8th grade students’ math achievement scores as compared with studies that included K–2nd grade students’ math achievement.
4.6. Math Type
In this analysis, there are three categories included in the moderator of math type (geometry, algebra, and all other math types). Geometry was the only group that was found to be significant. The mean effect for studies that included geometry students’ math achievement scores was 0.3146 points higher than the mean effect size for studies that included algebra (0.3113) students’ math achievement scores. The average effect size for geometry is 0.6259. It was concluded that the effect size is probably higher in studies that included students’ geometry math achievement scores as compared with studies that include students’ algebra math achievement scores. All other math types were less effective than algebra (0.1872), with a significance level of 0.0784.
Geometry is considered the core of mathematics and perceived as the means for solving real-life issues along with making the subject matter of mathematics interesting (Sunzuma & Maharaj, 2019). Teachers can benefit from geometry PD by obtaining a deeper understanding of the mathematics and developing skills of critical thinking, problem solving, conjectures, deductive reasoning, logical argument, and proof (Jones, 2003; Sunzuma & Maharaj, 2019). Geometric representations can enhance teacher/student understanding of other mathematical concepts, such as fractions, multiplication in arithmetic, the relationships between graphs and functions, and graphical representation of data in statistics (Jones, 2003; Sunzuma & Maharaj, 2019). There are three geometry PD studies (Jiang et al., 2011; Seago et al., 2014; Kuchey et al., 2009) that are included in this meta-analysis. All grade levels were represented in the geometry sample of this study, except Kindergarten and 4th grade; 1st–3rd grade Kuchey et al. (2009); 5th–10th grade Seago et al. (2014); and 9th–12th grade (Jiang et al., 2011). According to the research literature, geometry is a difficult topic for teachers (Healy & Hoyles, 2000; Mashingaidze, 2012; Sunzuma & Maharaj, 2019). It is also mentioned that many curricula are avoided including geometry in the syllabus (Jones, 2003; Mashingaidze, 2012).
With the results of this investigation showing that geometry PD had a positive impact on students’ mathematics achievement, it is with hope that more sustained geometry PD opportunities will be offered to teachers of all grade levels to increase their content knowledge, pedagogical knowledge, and confidence in teaching the subject matter along with promoting students’ academic gains.
4.7. PD Category
There are seven types of professional development [PLC, formative assessment, curriculum, online (video), reform-initiated math, PD approach, cooperative learning, and technology] categories in this meta-analysis. Two of the professional development categories were found to be significant, the online (video) PD and reform-initiated math PD.
The online (video) PD students’ math achievement scores were 0.7663 points higher than the mean effective size for the studies that included cooperative learning PD (−0.2902) students’ math achievement scores. The average effect size for online (video) PD is 0.4761. It was also found that the mean effect size for the studies that included reform-initiated math PD students’ math achievement scores was 0.7296 points higher than the mean effective size for the studies that included cooperative learning PD (−0.2902) students’ math achievement scores. The average effect size for reform-initiated math PD is 0.4394.
It was concluded that the effect size is probably higher in studies in this analysis that included online (video) PD students’ math achievement scores and reform-initiated math professional development students’ math achievement scores as compared with studies that included cooperative learning professional development students’ math achievement scores.
Online PD programs are becoming more common. Online PD programs are used frequently due to the ease of delivery plus easy access by teachers. Teachers can review the online material many times at their own convenience. The online professional development learning opportunities for teachers in this study were implemented as online math courses that focused on teachers’ knowledge and instructional practices. Three online math-focused professional development programs in this study were O’Dwyer et al. (2010), Dash et al. (2012), and Clements et al. (2016).
There were two reform-initiative-based professional development programs in this study. One of the programs was titled the Maysville Mathematics Initiative (MMI) program for a Maryland school district (high-poverty district) (Kuchey et al., 2009). The other program was the Initiative for Catholic Schools (ICS) program (Van Haneghan et al., 2004). Both programs were designed to improve teaching strategies and content knowledge for elementary teachers, leading to student gains.
On the other hand, Jozsa’s (2017) study included the cooperative learning PD for teachers that was implemented in five Chicago suburban advanced algebra and trigonometry high school mathematics classrooms. In this PD program, teachers received training on strategies and techniques that assisted student participants when learning in a cooperative learning environment. Cooperative learning was defined in this meta-analysis as “instruction where students work together in order to achieve a common objective or goal” (Jozsa, 2017, p. 18).
4.8. Study Design
In this analysis, when making comparisons of the impact that the math-focused professional development program studies may have on students’ achievement based on study design (randomized and quasi-experimental), it was found that the randomized study design had a significant effect on students’ achievement. The mean effect size for the studies that included randomized study design students’ math achievement scores was 0.1571 points higher than the mean effective size for the quasi-experimental design students’ math achievement scores. The average effect size for randomized study design is 0.2846, whereas the average quasi-experimental design studies’ average effect size is 0.1275.
It was concluded that the effect size is probably higher in studies that included randomized study design students’ math achievement scores as compared with studies that used quasi-experimental design students’ math achievement scores. Randomized design is significantly better (0.1571) than professional development studies that used a quasi-experimental design.
4.9. Limitations
The experimental research community has agreed that randomized designed research studies are always a better study design than quasi-experimental design (Steiner et al., 2009). One limitation of this meta-analysis study design is that the extent of conclusions of this study is based on the randomized and quasi-experimental designs. In addition, a limitation of the experimental design is that whatever threats to the internal validity exist within the studies will be the same threats in a meta-analysis. Lastly, a limitation of this meta-analysis is the lack of available randomized studies; therefore, quasi-experimental design studies were included in this analysis (Card, 2015).
The results of this study support the previous literature that states that randomized studies are the “gold standard” of research design for establishing causal relationships between an intervention and an outcome (Shadish et al., 2002; Steiner et al., 2009).
5. Conclusions
In conclusion, it was found that professional development is most effective when programs are implemented for a short period of time (less than a year); focused on geometry, content and pedagogy; 6th–8th grade students; online video PD; reform-initiated math PD; and randomized study design. There was no significant difference in the modality approaches on students’ achievement. This study provides important empirical evidence that supports the notion that recent math-focused professional development programs had a significant positive effect on students’ achievement. While much more research needs to be conducted in this area, this study adds to the body of literature by offering evidence regarding the positive effects of professional development programs on students’ achievement.
Author Contributions
Conceptualization, A.V.F. and M.C.; methodology, A.V.F. and M.C.; software, A.V.F. and M.C.; validation, A.V.F. and M.C.; formal analysis, A.V.F. and M.C.; investigation, A.V.F. and M.C.; resources, A.V.F.; data curation, A.V.F. and M.C.; writing—original draft preparation, A.V.F.; writing—review and editing, A.V.F. and M.C.; visualization, M.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data analyzed in this study are available in the published articles included in the meta-analysis, which are fully cited in the reference list. No new data were created.
Acknowledgments
During the preparation of this manuscript, the authors used Comprehensive Meta-Analysis (CMA), version [4.0] (Biostat, Englewood, NJ, USA) for the purpose of conducting statistical analyses and synthesizing effect sizes across studies. The authors have reviewed and edited the output and take full responsibility for the content of this publication.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Agodini, R., & Harris, B. (2016). How teacher and classroom characteristics moderate the effects of four elementary math curricula. The Elementary School Journal, 117(2), 216–236. [Google Scholar] [CrossRef]
- Allen, T. Y. (2013). The Impact of professional learning communities on third-grade math scores [ProQuest dissertations and theses, Union University]. [Google Scholar]
- Ball, L. D., Thames, H. M., & Phelps, G. (2008). Content knowledge for teaching: What makes it special? Journal of Teacher Education, 59(5), 389–407. [Google Scholar] [CrossRef]
- Bicer, A., & Capraro, R. M. (2016). Longitudinal effects of technology integration and teacher professional development on students’ mathematics achievement. Eurasia Journal of Mathematics, Science and Technology Education, 13(3), 815–833. [Google Scholar] [CrossRef]
- Bicer, A., Navruz, B., Capraro, R. M., & Capraro, M. M. (2014). STEM schools vs. non-STEM schools: Comparing students’ mathematics state-based test performance. International Journal of Global Education, 3(3), 8–18. [Google Scholar]
- Bicer, A., Navruz, B., Capraro, R. M., Capraro, M. M., Oner, T. A., & Boedeker, P. (2015). STEM schools vs. non-STEM schools: Comparing students’ mathematics growth rate on high-stakes test performance. International Journal of New Trends in Education and Their Implications, 6(1), 138–150. [Google Scholar]
- Blank, R. K. (2013). What research tells us: Common characteristics of professional learning that leads to student achievement. Journal of Staff Development, 34(1), 50–53. [Google Scholar]
- Blank, R. K., & de las Alas, N. (2009). Effects of teacher professional development on gains in student achievement: How meta-analysis provides scientific evidence useful to education leaders. Council of Chief State School Officers. [Google Scholar]
- Borenstein, M. (2019). Common mistakes in meta-analysis and how to avoid them. Biostat, Inc. [Google Scholar]
- Borenstein, M., Hedges, L. E., Higgins, J. P. T., & Rothstein, H. R. (2022). Comprehensive meta-analysis (Version 4). Biostat, Inc. Available online: www.Meta-Analysis.com (accessed on 2 February 2024).
- Borenstein, M., Hedges, L. V., Higgins, J. P., & Rothstein, H. R. (2021). Introduction to meta-analysis. John Wiley & Sons. [Google Scholar]
- Borko, H. (2004). Professional development and teacher learning: Mapping the terrain. Educational Researcher, 33(8), 3–15. [Google Scholar] [CrossRef]
- Borko, H., Jacobs, J., & Koellner, K. (2010). Contemporary approaches to teacher professional development. International Encyclopedia of Education, 7(2), 548–556. [Google Scholar]
- Boyd, D., Grossman, P., Lankford, H., Loeb, S., & Wyckoff, J. (2006). How changes in entry requirements alter the teacher workforce and affect student achievement. Education Finance and Policy, 1(2), 176–216. [Google Scholar] [CrossRef]
- Buckhalter, B. (2019). An examination of the relationship among the intentions, features, affordances, and outcomes of Saturday academy for math professional development for mathematics teachers [Electronic theses and dissertations, University of Mississippi]; 1558p. Available online: https://egrove.olemiss.edu/etd/1558 (accessed on 5 December 2014).
- Capraro, R. M., Capraro, M. M., Scheurich, J. J., Jones, M., Morgan, J., Huggins, K. S., Corlu, M. S., Younes, R., & Han, S. (2016). Impact of sustained professional development in STEM on outcome measures in a diverse urban district. The Journal of Educational Research, 109(2), 181–196. [Google Scholar] [CrossRef]
- Card, N. A. (2015). Applied meta-analysis for social science research. Guilford Publications. [Google Scholar]
- Cavalluzzo, L., Geraghty, T. M., Steele, J. L., Holian, L., Jenkins, F., Alexander, J. M., & Yamasaki, K. Y. (2014). “Using Data” to inform decisions: How teachers use data to inform practice and improve student performance in mathematics. Results from a randomized experiment of program efficacy. CNA Corporation. [Google Scholar]
- Cheung, A., & Slavin, R. (2016). How methodological features affect effect sizes in education. Educational Researcher, 45(5), 283–292. [Google Scholar] [CrossRef]
- Clements, D. H., Sarama, J., Layzer, C., Unlu, F., Wolfe, C. B., Spitler, M. E., & Weiss, D. (2016). Effects of TRIAD on mathematics achievement: Long-term impacts. Society for Research on Educational Effectiveness. Available online: https://eric.ed.gov/?id=ED567218 (accessed on 21 August 2025).
- Clotfelter, C. T., Ladd, H. F., & Vigdor, J. L. (2007). Teacher credentials and student achievement: Longitudinal analysis with student fixed effects. Economics of Education Review, 26(6), 673–682. [Google Scholar] [CrossRef]
- Cohen, D. K. (1990). A revolution in one classroom: The case of Mrs. Oublier. Educational Evaluation and Policy Analysis, 12(3), 311–329. [Google Scholar] [CrossRef]
- Cohen, D. K., & Hill, H. C. (2001). Learning policy: When state education reform works. Yale University Press. [Google Scholar]
- Cook, B. G., Cook, L., & Therrien, W. J. (2018). Group–difference effect sizes: Gauging the practical importance of findings from group–experimental research. Learning Disabilities Research & Practice, 33(2), 56–63. [Google Scholar]
- Cooper, H. (2015). Research synthesis and meta-analysis: A step-by-step approach (Vol. 2). Sage publications. [Google Scholar]
- Darling-Hammond, L., Hyler, M. E., & Gardner, M. (2017). Effective teacher professional development. Learning Policy Institute. Available online: https://learningpolicyinstitute.org/product/effective-teacher-professional-development-report (accessed on 19 September 2019).
- Darling-Hammond, L., Wei, R. C., Andree, A., Richardson, N., & Orphanos, S. (2009). Professional learning in the learning profession (Vol. 12). National Staff Development Council. [Google Scholar]
- Dash, S., de Kramer, R. M., Masters, J., & Russell, M. (2012). Impact of online professional development on teacher quality and student achievement in fifth grade mathematics. Journal of Research on Technology in Education, 45(1), 1–26. [Google Scholar] [CrossRef]
- Desimone, L. (2011). Outcomes: Content-focused learning improves teacher practice and student results. Journal of Staff Development, 32(4), 65–68. [Google Scholar]
- Desimone, L. M. (2009). Improving impact studies of teachers’ professional development: Toward better conceptualizations and measures. Educational Researcher, 38(3), 181–199. [Google Scholar] [CrossRef]
- Desimone, L. M., Porter, A. C., Garet, M., Suk Yoon, K., & Birman, B. (2002). Does professional development change teachers’ instruction? Results from a three-year study. Educational Evaluation and Policy Analysis, 24, 81–112. [Google Scholar] [CrossRef]
- Desimone, L. M., Smith, T. M., & Phillips, K. J. R. (2007). Does policy influence mathematics and science teachers’ participation in professional development? Teachers College Record, 109(5), 1086–1122. [Google Scholar] [CrossRef]
- Desimone, L. M., Smith, T. M., & Ueno, K. (2006). Are teachers who need sustained, content-focused professional development getting it? An administrator’s dilemma. Educational Administration Quarterly, 42(2), 179–215. [Google Scholar] [CrossRef]
- Early, D. M., Berg, J. K., Alicea, S., Si, Y., Aber, J. L., Ryan, R. M., & Deci, E. L. (2016). The impact of every classroom, every day on high school student achievement: Results from a school-randomized trial. Journal of Research on Educational Effectiveness, 9(1), 3–29. [Google Scholar] [CrossRef]
- Even, E. (1993). Subject-matter knowledge and pedagogical content knowledge prospective secondary teachers and the function concept. Journal for Research in Mathematics Education, 24(2), 94–116. [Google Scholar] [CrossRef]
- Foster, J. M., Toma, E. F., & Troske, S. P. (2013). Does teacher professional development improve math and science outcomes and is it cost effective? Journal of Education Finance, 38(3), 255–275. [Google Scholar] [CrossRef]
- Franke, M. L., Carpenter, T. P., Levi, L., & Fennema, E. (2001). Capturing teachers’ generative change: A follow-up study of professional development in mathematics. American Educational Research Journal, 38(3), 653–689. [Google Scholar] [CrossRef]
- Garet, M. S., Heppen, J. B., Walters, K., Parkinson, J., Smith, T. M., Song, M., Garrett, R., Yang, R., & Borman, G. D. (2016). Focusing on mathematical knowledge: The impact of content-intensive teacher professional development. NCEE 2016–4010. National Center for Education Evaluation and Regional Assistance. [Google Scholar]
- Garet, M. S., Porter, A. C., Desimore, L., Birman, B. F., & Yoon, K. S. (2001). What makes professional development effective? Results from a national sample of teachers. American Educational Research Journal, 38(4), 915–945. [Google Scholar] [CrossRef]
- Goldberg, C., Riconscente, M. M., & Nye, B. D. (2023). A promising approach to scaling up professional development: Intelligent, interactive, virtual professional development with just-in-time feedback. Journal of Mathematics Teacher Education. Advance online publication. [Google Scholar] [CrossRef]
- Grossman, P. L. (1990). The making of a teacher: Teacher knowledge and teacher education. Teachers College Press. [Google Scholar]
- Guskey, T., & Sparks, D. (2004). Linking professional development to improvements in student learning. In E. M. Guyton, & J. R. Dangel (Eds.), Researching linking teacher preparation and student performance: Teacher education yearbook Xll (pp. 233–247). Roman & Littlefield Publishing Company. [Google Scholar]
- Guskey, T. R., & Yoon, K. S. (2009). What works in professional development? Phi Delta Kappan, 90(7), 495–500. [Google Scholar] [CrossRef]
- Healy, L., & Hoyles, C. (2000). A study of proof conceptions in algebra. Journal for Research in Mathematics Education, 31(4), 396–428. [Google Scholar] [CrossRef]
- Hedges, L. V., Tipton, E., & Johnson, M. C. (2010). Robust variance estimation in meta-regression with dependent effect size estimates. Research Synthesis Methods, 1(1), 39–65. [Google Scholar] [CrossRef]
- Heller, J. I., Curtis, D. A., Rabe-Hesketh, S., & Verboncoeur, C. J. (2007). The effects of math pathways and pitfalls on students’ mathematics achievement (pp. 1–43). National Science Foundation Report. [Google Scholar]
- Hill, H. C. (2007). Learning in the teaching workforce. The Future of Children, 17(1), 111–127. [Google Scholar] [CrossRef]
- Hill, H. C. (2011). The nature and effects of middle school mathematics teacher learning experiences. Teachers College Record, 113(1), 205–234. [Google Scholar] [CrossRef]
- Hill, H. C., Rowan, B., & Ball, D. L. (2005). Effects of teachers’ mathematical knowledge for teaching on student achievement. American Educational Research Journal, 42(2), 371–406. [Google Scholar] [CrossRef]
- Hill, K., & Luft, J. (2015). Exploring beginning teachers’ content knowledge. In Newly hired teachers of science: A better beginning (pp. 57–74). Sense Publishers. [Google Scholar] [CrossRef]
- Ingvarson, L., Meiers, M., & Beavis, A. (2005). Factors affecting the impact of professional development programs on teachers’ knowledge, practice, student outcomes & efficacy. Education Policy Analysis Archives, 13(10), 1–28. [Google Scholar] [CrossRef]
- Institute for Educational Science (IES). (2022). What works clearinghouse-procedures and standards handbook (Version 5.0). Institute for Educational Science. Available online: https://ies.ed.gov/ncee/wwc/Docs/referenceresources/Final_WWC-HandbookVer5_0-0-508.pdf (accessed on 2 February 2024).
- IntHout, J., Ioannidis, J. P., Rovers, M. M., & Goeman, J. J. (2016). Plea for routinely presenting prediction intervals in meta-analysis. BMJ Open, 6(7), e010247. [Google Scholar] [CrossRef]
- Jacob, R., Hill, H., & Corey, D. (2017). The impact of a professional development program on teachers’ mathematical knowledge for teaching, instruction, and student achievement. Journal of Research on Educational Effectiveness, 10(2), 379–407. [Google Scholar] [CrossRef]
- Jacobs, J. K., Koellner, K., Seago, N., Garnier, H., & Wang, C. (2020). Professional development to support the learning and teaching of geometry. In The language of mathematics: How the teacher’s knowledge of mathematics affects instruction (pp. 143–173). Rowman & Little Publishers. [Google Scholar]
- Jayanthi, M., Gersten, R., Taylor, M. J., Smolkowski, K., & Dimino, J. (2017). Impact of the developing mathematical ideas professional development program on grade 4 students’ and teachers’ understanding of fractions (REL 2017-256). Regional Educational Laboratory Southeast. [Google Scholar]
- Jiang, Z., White, A., & Rosenwasser, A. (2011). Randomized control trials on the dynamic geometry approach. Journal of Mathematics Education at Teachers College, 2(2), 8–17. [Google Scholar]
- Jones, K. (2003). Issues in the teaching and learning of geometry. In Aspects of teaching secondary mathematics (pp. 137–155). Routledge. [Google Scholar]
- Jozsa, A. (2017). Cooperative learning in the advanced algebra and trigonometry mathematics high school classroom [Doctoral dissertation, University of St. Francis]. [Google Scholar]
- Kang, H. S., Cha, J., & Ha, B. W. (2013). What should we consider in teachers’ professional development impact studies? Based on the conceptual framework of Desimone. Creative Education, 4(4A), 11–18. [Google Scholar] [CrossRef]
- Killion, J. (2002). What works in the high school results-based staff development (pp. 1–120). National Staff Development Council. National Education Association. [Google Scholar]
- Kisa, Z. (2014). A quasi-experimental study of the effect of mathematics professional development on student achievement [Doctoral dissertation, University of Pittsburg]. Available online: https://d-scholarship.pitt.edu/22789/ (accessed on 21 August 2025).
- Kleickmann, T., Richter, D., Kunter, M., Elsner, J., Besser, M., Krauss, S., & Baumert, J. (2013). Teachers’ content knowledge and pedagogical content knowledge: The role of structural differences in teacher education. Journal of Teacher Education, 64(1), 90–106. [Google Scholar] [CrossRef]
- Krawec, J., & Montague, M. (2014). The role of teacher training in cognitive strategy instruction to improve math problem solving. Learning Disabilities Research & Practice, 29(3), 126–134. [Google Scholar] [CrossRef]
- Krupa, E. E. (2011). Evaluating the impact of professional development and curricular implementation on student mathematics achievement: A mixed methods study [ProQuest dissertations and theses, North Carolina State University]. [Google Scholar]
- Kuchey, D., Morrison, J. Q., & Geer, C. H. (2009). A professional development model for math and science educators in catholic elementary schools: Challenges and successes. Catholic Education: A Journal of Inquiry and Practice, 12(4), 475–497. [Google Scholar][Green Version]
- Larison, R., Richards, J., & Sherin, M. G. (2022). Tools for supporting teacher noticing about classroom video in online professional development. Journal of Mathematics Teacher Education, 27(2), 139–161. [Google Scholar] [CrossRef]
- Lasserson, T. J., Thomas, J., & Higgins, J. P. (2019). Starting a review. In Cochrane handbook for systematic reviews of interventions (pp. 1–12). Wiley-Blackwell. [Google Scholar] [CrossRef]
- Leinhardt, G., & Smith, D. A. (1985). Expertise in mathematics instruction: Subject matter knowledge. Journal of Educational Psychology, 77, 247–271. [Google Scholar] [CrossRef]
- Lin, L., & Chu, H. (2018). Quantifying publication bias in meta-analysis. Biometrics, 74(3), 785–794. [Google Scholar] [CrossRef] [PubMed]
- Loucks-Horsley, S., & Matsumoto, C. (1999). Research on professional development for teachers of mathematics and science: The state of the scene. School Science and Mathematics, 99(5), 258–271. [Google Scholar] [CrossRef]
- Mashingaidze, S. (2012). The teaching of geometric (isometric) Transformations at secondary school level: What approach to use and why? Asian Social Science, 8(15), 197. [Google Scholar] [CrossRef]
- McGatha, M. B., Bush, W. S., & Rakes, C. (2009). The effects of professional development in formative assessment on mathematics teaching performance and student achievement. Journal of MultiDisciplinary Evaluation, 6(12), 32–43. [Google Scholar] [CrossRef]
- McLaughlin, M. W., & Talbert, J. E. (2001). Professional communities and the work of high school teachers. University of Chicago Press. [Google Scholar]
- O’Dwyer, L. M., Masters, J., Dash, S., De Kramer, R. M., Humez, A., & Russelle, M. (2010). E-learning for educators effects of on-line professional development on teachers and their students: Executive summary of four randomized trials. InTASC Report. Available online: https://search.issuelab.org/resource/e-learning-for-educators-effects-of-on-line-professional-development-on-teachers-and-their-students-findings-from-four-randomized-trials (accessed on 5 December 2014).
- Patel, N., Franco, S., Miura, Y., & Boyd, B. (2012). Including curriculum focus in mathematics professional development for middle-school mathematics teachers. School Science and Mathematics, 112(5), 300–309. [Google Scholar] [CrossRef]
- Pellegrini, M., Lake, C., Neitzel, A., & Slavin, R. E. (2021). Effective programs in elementary mathematics: A meta-analysis. AERA Open, 7, 2332858420986211. [Google Scholar] [CrossRef]
- Penuel, W. R., Fishman, B. J., Yamaguchi, R., & Gallagher, L. P. (2007). What makes professional development effective? Strategies that foster curriculum implementation. American Educational Research Journal, 44(4), 921–958. [Google Scholar] [CrossRef]
- Phelan, J., Choi, K., Vendlinski, T., Baker, E., & Herman, J. (2011). Differential improvement in student understanding of mathematical principles following formative assessment intervention. The Journal of Educational Research, 104, 330–339. [Google Scholar] [CrossRef]
- Phelan, J. C., Choi, K., Niemi, D., Vendlinski, T. P., Baker, E. L., & Herman, J. (2012). The effects of POWERSOURCE© assessments on middle-school students’ math performance. Assessment in Education: Principles, Policy & Practice, 19(2), 211–230. [Google Scholar]
- PISA. (2022). Highlights of U.S. PISA 2022 results web report (NCES 2023-115). U.S. Department of Education. Institute of Education Sciences, National Center for Education Statistics. Available online: https://nces.ed.gov/surveys/pisa/pisa2022/ (accessed on 2 February 2025).
- Polly, D., Wang, C., Martin, C., Lambert, R., Pugalee, D., & Middleton, C. (2018). The influence of mathematics professional development, school-level, and teacher-level variables on primary students’ mathematics achievement. Early Childhood Education Journal, 46, 31–45. [Google Scholar] [CrossRef]
- Polly, D., Wang, C., Martin, C., Lambert, R. G., Pugalee, D. K., & Middleton, C. W. (2017). The influence of an internet-based formative assessment tool on primary grades students’ number sense achievement. School Science and Mathematics, 117(3–4), 127–136. [Google Scholar] [CrossRef]
- Provasnik, S., Malley, L., Stephens, M., Landeros, K., Perkins, R., & Tang, J. H. (2016). Highlights from TIMSS and TIMSS advanced 2015: Mathematics and science achievement of U.S. students in grades 4 and 8 and in advanced courses at the end of high school in an international context. U.S. Department of Education, National Center for Education Statistics. Available online: https://nces.ed.gov/pubsearch/pubsinfo.asp?pubid=2017002 (accessed on 2 February 2025).
- Rivkin, S. G., Hanushek, E. A., & Kain, J. F. (2005). Teachers, schools, and academic achievement. Econometrica, 73(2), 417–458. [Google Scholar] [CrossRef]
- Rosenthal, R. (1979). The file drawer problem and tolerance for null results. Psychological Bulletin, 86(3), 638. [Google Scholar] [CrossRef]
- Ross, J. A., Bruce, C., & Hogaboam-Gray, A. (2006). The impact of a professional development program on student achievement in grade 6 mathematics. Journal of Mathematics Teacher Education, 9, 551–577. [Google Scholar] [CrossRef]
- Rothstein, H. R., Sutton, A. J., & Borenstein, M. (2005). Publication Bias in Meta-Analysis. In H. R. Rothstein, A. J. Sutton, & M. Borenstein (Eds.), Bias in meta-analysis: Prevention, assessment and adjustments (pp. 1–7). John Wiley & Sons, Ltd. [Google Scholar]
- Santagata, R., Kersting, N., Givvin, K. B., & Stigler, J. W. (2010). Problem implementation as a lever for change: An experimental study of the effects of a professional development program on students’ mathematics learning. Journal of Research on Educational Effectiveness, 4(1), 1–24. [Google Scholar] [CrossRef]
- Scher, L., & O’Reilly, F. (2009). professional development for K–12 math and science teachers: What do we really know? Journal of Research on Educational Effectiveness, 2, 209–249. [Google Scholar] [CrossRef]
- Schoen, R. C., LaVenia, M., & Tazaz, A. M. (2018). Effects of the first year of a three-year CGI teacher professional-development program on grades 3–5 student achievement: A multisite cluster-randomized trial (Research Report No. 2018-25). Learning Systems Institute, Florida State University. [Google Scholar]
- Schoen, R. C., LaVenia, M., Tazaz, A. M., Farina, K., Dixon, J. K., & Secada, W. G. (2020). Replicating the CGI experiment in diverse environments: Effects on grade 1 and 2 student mathematics achievement in the first program year (Research Report No. 2020-02). Florida State University. [Google Scholar] [CrossRef]
- Seago, N. M., Jacobs, J. K., Heck, D. J., Nelson, C. L., & Malzahn, K. A. (2014). Impacting teachers’ understanding of geometric similarity: Results from field testing of the learning and teaching geometry professional development materials. Professional Development in Education, 40(4), 627–653. [Google Scholar] [CrossRef]
- Shadish, W., Cook, T. D., & Campbell, D. T. (2002). Experimental and quasi-experimental designs for generalized causal inference (Vol. 1195). Houghton Mifflin. [Google Scholar]
- Shulman, L. S. (1986). Those who understand: Knowledge growth in teaching. Educational Researcher, 15(2), 4–14. [Google Scholar] [CrossRef]
- Skott, J. (2022). Lesson study beyond its initial adaptation: A case without external support. Journal of Mathematics Teacher Education, 27(2), 163–183. [Google Scholar] [CrossRef]
- Sowder, J. T. (2007). The mathematical education and development of teachers. In F. Lester (Ed.), Second handbook of research on mathematics teaching and learning (pp. 157–223). Information Age Publishing. [Google Scholar]
- Steiner, P. M., Wroblewski, A., & Cook, T. D. (2009). Randomized experiments and quasi-experimental designs in educational research. In The sage handbook of educational evaluation (pp. 75–95). Sage Publications, Inc. [Google Scholar][Green Version]
- Sunzuma, G., & Maharaj, A. (2019). In-service teachers’ geometry content knowledge: Implications for how geometry is taught in teacher training institutions. International Electronic Journal of Mathematics Education, 14(3), 633–646. [Google Scholar] [CrossRef]
- Takacs, Z. K., & Kassai, R. (2019). The efficacy of different interventions to foster children’s executive function skills: A series of meta-analyses. Psychological Bulletin, 145(7), 653. [Google Scholar] [CrossRef] [PubMed]
- Taylor, J. A., Roth, K., Wilson, C. D., Stuhlsatz, M. A., & Tipton, E. (2017). The effect of an analysis-of-practice, videocase-based, teacher professional development program on elementary students’ science achievement. Journal of Research on Educational Effectiveness, 10(2), 241–271. [Google Scholar] [CrossRef]
- TIMSS. (2019). TIMSS 2019 U.S. highlights web report (NCES 2021-021). U.S. Department of Education. Institute of Education Sciences, National Center for Education Statistics. Available online: https://nces.ed.gov/timss/results19/index.asp (accessed on 5 December 2014).
- Tournaki, E., Lyublinskaya, I., & Carolan, B. (2011). An ongoing professional development program and its impact on teacher effectiveness. The Teacher Educator, 46(4), 299–315. [Google Scholar] [CrossRef]
- Tricco, A. C., Lillie, E., Zarin, W., O’BRien, K. K., Colquhoun, H., Levac, D., Moher, D., Peters, M. D., Horsley, T., Weeks, L., Hempel, S., Akl, E. A., Chang, C., McGowan, J., Stewart, L., Hartling, L., Aldcroft, A., Wilson, M. G., Garritty, C., … Straus, S. E. (2018). PRISMA Extension for Scoping Reviews (PRISMA-ScR): Checklist and Explanation. Annals of Internal Medicine, 169(7), 467–473. [Google Scholar] [CrossRef] [PubMed]
- Tzur, R., Stephens, A. C., Harkness, S. S., Johnson, H. L., Xin, Y. P., & Ely, R. (2022). Collaborative learning in practice-based mathematics methods courses: A developmental study. Mathematics Education Research Journal, 34(2), 259–281. [Google Scholar] [CrossRef]
- Van Haneghan, J. P., Pruet, S. A., & Bamberger, H. J. (2004). Mathematics reform in a minority community: Student outcomes. Journal of Education for Students Placed at Risk, 9(2), 189–211. [Google Scholar] [CrossRef]
- Wilson, S. M., Floden, R. E., & Ferrini-Mundy, J. (2002). Teacher preparation research: An insider’s view from the outside. Journal of Teacher Education, 53, 190–204. [Google Scholar] [CrossRef]
- Wischgoll, A., & Prediger, S. (2024). Studying efficacy of particular design elements in online teacher professional development courses: An experimental study on systematizing videos for enhancing teachers’ PCK. Zeitschrift für Erziehungswissenschaft. Advance online publication. [Google Scholar] [CrossRef]
- Wood, T., Mazzocco, M. M., Calhoon, M. B., Crowe, E. C., & Connor, C. M. (2020). The effect of peer-assisted mathematics learning opportunities in first grade classrooms: What works for whom? Journal of Research on Educational Effectiveness, 13(4), 601–624. [Google Scholar] [CrossRef]
- Yoon, K. S., Duncan, T., Lee, S. W. Y., Scarloss, B., & Shapley, K. (2007). Reviewing the evidence on how teacher professional development affects student achievement (Issues & 142 Answers Report, REL 2007-No.33). U.S. Department of Education Evaluation, Institute of Education Sciences, National Center for Education and Regional Assistance, Regional Educational Laboratory Southwest. Available online: https://files.eric.ed.gov/fulltext/ED498548.pdf (accessed on 10 December 2014).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).