Abstract
This study is focused on the analysis of the level of geometric thinking of 15-year-old Slovak pupils in relation to the difficulty of geometric problems, their gender, and their assessment in mathematics. The main aim of this study was to determine the level of geometric thinking of 15-year-old Slovak pupils, to examine the relationship between their mathematics assessment and the level of geometric thinking, and to find out gender differences in relation to the different levels of geometric thinking. The van Hiele test was adapted and applied to a representative sample of 15-year-old Slovak pupils to determine the level of geometric thinking. We used reliability/item analysis. The reliability of the knowledge test (after adaptation) was assessed using Cronbach’s alpha (0.64). The validity of the test was demonstrated by the correlation of the Usiskin test results with pupils’ mathematics grades (Goodman–Kruskal’s gamma, p < 0.05). Statistical analysis showed that 15-year-old Slovak pupils achieve different levels of geometric thinking depending on the difficulty of the tasks. Pupil achievement declined significantly as task difficulty increased. Pupils had the greatest difficulty with tasks classified as the fifth (rigorous) and partly the fourth (deductive) van Hiele level, which require a deep understanding of geometric systems and the ability to prove logically. The lower-level tasks (visualization, analysis, and abstraction) were able to differentiate students according to different levels of geometric thinking. The results showed a significant positive relationship (Goodman–Kruskal’s gamma, p < 0.05) between the pupils’ overall mathematics scores (expressed as a grade) and their level of geometric thinking as detected by the van Hiele test. The analysis of gender differences (Duncan’s test, p < 0.05) showed that in the less challenging tasks, corresponding to the first three van Hiele levels (visualization, analysis, abstraction), girls performed statistically significantly better than boys. In the more challenging tasks, classified as the fourth (deductive) and fifth (rigorous) levels of geometric thinking, there were no statistically significant differences between boys and girls. In the more challenging tasks, the performances of both genders were comparable. The presented study identifies significant deficits in the development of higher levels of geometric thinking among 15-year-old Slovak pupils. These findings strongly imply the necessity for the transformation of the curriculum, textbooks, and didactic approaches with the aim of systematically developing deductive and rigorous reasoning, while it is essential to account for the demonstrated gender differences in performance.
1. Introduction
Geometry and the development of pupils’ geometric thinking are among the key mathematical competences and among the competences for the life of individuals. Geometric competences are applicable in various professions (e.g., architecture and construction, engineering, design, cartography, astronomy, surveying, computer graphics and animation, physics, etc.). It is therefore important to develop pupils’ geometric thinking as an integral part of their wider mathematical education. The results of international assessments of Slovak pupils in both mathematics and geometry have been discouraging in recent years, which may contribute to their lack of interest in STEM subjects. A comparative analysis of primary mathematics education in Slovakia and abroad (Scholtzová, 2014) shows that the results of Slovak pupils in geometry, already in the first years, are at a significantly lower level compared to foreign countries (Australia, Finland, France, Croatia, Ireland, Japan, Germany, and Italy).
In addition to international assessments, regular assessments of the level of mathematical knowledge of 15-year-old pupils (pupils in the 9th grade of primary school, or pupils of the same age in 8-year grammar schools) called “Testovanie 9” are carried out in Slovakia. The average pass rate for all pupils in 2024 was 58.2% in mathematics. Boys achieved better results (boys 60.1%, girls 56.2%), but the difference was not substantively significant. The test results showed that pupils were least successful in the topic of Geometry and Measurement, with a success rate of 53.9%, and performed better in the topics of Numbers, Variables, Numerical Operations with Numbers, Relations, Functions, Tables, and Diagrams, with a success rate of 65.6% (NIVAM, 2024). The results on gender differences in solving geometry problems by topic have not been published.
In light of the ongoing educational reform and curriculum re-evaluation in Slovakia (Ministry of Education, Research, Development and Youth of the Slovak Republic, 2023), there is an urgent need for empirical insights into the current state of geometric thinking among pupils to effectively inform these pivotal changes. While the development of geometric reasoning is universally recognized as crucial, a research gap exists regarding a comprehensive, up-to-date analysis of Slovak pupils’ specific strengths and weaknesses across van Hiele levels, providing direct, evidence-based recommendations for the design of new curricula and textbooks.
Geometric thinking is a key area of mathematics education that develops students’ spatial abilities, logical thinking, and analytical skills. Consequently, identifying and understanding the level of geometric thinking in context is essential for optimizing the teaching process and promoting mathematical literacy.
This study focuses on the analysis of students’ geometric thinking with respect to gender differences and mathematics assessment. Exploring these factors contributes to a deeper understanding of the complex relationship between students’ individual characteristics and their performance in mathematics.
The aim of this study is to analyze the correlation between gender, mathematics assessment, and pupils’ level of geometric thinking. The results of this study can provide valuable information for educational research and practice.
2. Theoretical Framework
The theoretical framework of this study is based on models of geometric thinking, in particular van Hiele’s model, which describes the development of pupils’ levels of geometric thinking. Furthermore, we focus on the analysis of gender differences in mathematical learning, considering the possible causes of these differences (biological, sociocultural, pedagogical). At the same time, we observe trends in mathematics assessment and the correspondence of this assessment with the performance of pupils in geometry.
2.1. Geometric Thinking and Its Testing
Geometric thinking is a cognitive skill that enables us to understand and interact with the spatial structures and forms in our environment. It involves the ability to visualize, analyze, and manipulate geometric objects and concepts (Clements & Battista, 1992; Battista, 2007; Newcombe & Shipley, 2015; Jablonski & Ludwig, 2023). Therefore, key aspects of geometric thinking include the following:
- visual perception (the ability to perceive and interpret visual information of geometric figures, their size, position, and relationships between them),
- spatial imagination (the ability to mentally manipulate and rotate objects in space),
- analytical thinking (the ability to decompose and compose more complex geometric figures into simpler components and to identify their properties and relationships),
- logical reasoning (the ability to use logical procedures to solve geometric situations, problems, and the ability to produce geometric proofs),
- abstract thinking (the ability to understand and work with abstract geometric concepts that are not just related to concrete models).
Research on the levels of geometric thinking of pupils in different age groups has been carried out by Dina van Hiele-Geldof and Pierre van Hiele (Fuys et al., 1984; Van Hiele, 1986; Van Hiele, 1999). They divided the development of geometric thinking into several levels, as follows:
- (1)
- Level 0: visualization (recognition)—children make decisions based on perception, not cognition, and the base term is visual prototype as an ideal example;
- (2)
- Level 1: analysis (description)—children identify individual components that are significant parts of geometric shapes;
- (3)
- Level 2: abstraction (informal deduction, ordering, relational, simple deduction)—pupils perceive relationships between properties and between classes of geometric shapes;
- (4)
- Level 3: deduction (formal deduction)—students understand the role of axioms and definitions;
- (5)
- Level 4: rigor (axiomatization)—students are able to understand formal aspects of deduction, such as creating new systems and comparing existing mathematical systems.
The levels are hierarchical and sequential, meaning that students cannot reach one level without understanding the previous level.
In addition to categorizing levels, van Hiele’s theory also provided educational implications in the form of phases of learning. A systematic review of studies on geometric reasoning or van Hiele’s phases of learning was provided by Trimurtini et al. (2022). They showed that the use of interventions (e.g., aids, technology) in individual studies had an effect in the phases of learning. On the other hand, they recommended more thorough research on how to reach the highest level of geometric reasoning. Several other studies have built on van Hiele’s work and validated individual levels in different age groups (Musser et al., 2001; Mason, 2002; Feza & Webb, 2005; Knight, 2006; Levenson et al., 2011; Marchis, 2012; Haviger & Vojkůvková, 2015), often using Usiskin’s van Hiele test.
Usiskin’s van Hiele test is one of the most well-known tools for diagnosing the level of geometric thinking of pupils (Usiskin, 1982). The test is designed to reveal how pupils perceive, understand, and use geometric concepts. The tasks in the test become progressively more difficult, are aligned with the five van Hiele levels and require pupils to have increasingly higher levels of abstract thinking. The test contains 25 problems evenly categorized into five groups. Each group tests one of the van Hiele levels of geometric reasoning (recognizing and naming, analyzing properties, classifying and relating, understanding and forming definitions, proving and axiomatizing) (Van Hiele, 1986). The test has been used in different countries. In the context of Slovakia, the results from its neighboring countries are particularly interesting. Haviger and Vojkůvková (2015) tested 215 students aged 15–17.
They noted that the test results reveal a trend in students’ geometric thinking similar to that observed in the United States, reflecting the emphasis placed on geometry instruction in Czech education at the first two levels and, to some extent, at the third level. Czech pupils had difficulties with problems at the fourth level. They also stated that the translation into Czech is not completely clean and clear, due to fundamental differences in terminology (note a similar problem as in Slovakia). Longitudinal research (2015–2016) was conducted in Hungary by Győry and Kónya (2018), who investigated the quantitative transformation of geometric reasoning of students aged 14–16 (8th–10th grade) specializing in mathematics using the Usiskin test. The Usiskin test helped them to identify the levels of geometric thinking, thus contributing to the understanding of the geometric thinking process of gifted students and the finding that structured instruction in accordance with the van Hiele model leads to a significant improvement in the understanding of geometric concepts.
Overall, the results of many research studies suggest that the Usiskin test is an effective tool for diagnosing geometric thinking in 15-year-old students (Chen et al., 2019; Cardinali & Piergallini, 2022). Given that the van Hiele test (Usiskin, 1982) is generally recognized as a good test that reflects van Hiele levels of geometric thinking, we sought the authors’ permission, adapted and used it to test Slovak 15-year-olds (9th grade elementary school pupils, or the corresponding grade of 8-year-old gymnasium pupils). We were interested in three factors—pupils’ level of geometric thinking, gender differences, and the relationship between pupils’ level of geometric thinking and their mathematics scores.
2.2. Gender Aspects of Geometric Thinking and Assessment in Mathematics
The general and often frequent public opinion is that there are differences between the mathematical performance of males/boys and females/girls, and these are due to biological factors. This view is challenged by Kersey et al. (2019), who argue that gender differences in mathematical thinking are not rooted in biological factors, based on a comparison of the neural processes underlying how boys and girls engage with mathematics. Even a meta-analysis of research on gender and mathematics performance (Lindberg et al., 2010) did not show a difference in mathematics performance between the sexes. The study (Petersen & Shibley Hyde, 2014) also reports that despite the stereotype that boys are more successful in mathematics than girls, gender differences in mathematics performance are trivial.
Overall, these findings support the notion that men and women function similarly in mathematics. Nevertheless, there are gender differences in STEM occupations, which are thus neither due to biological factors (Kersey et al., 2019) nor due to different mathematical abilities or different mathematical performance (Petersen & Shibley Hyde, 2014). The results of the study (Ghasemi & Burley, 2019) showed that we still do not know why women are still underrepresented in STEM fields, even though the differences in mathematical performance are negligible. However, they found that the extent of gender differences varied between nations, suggesting that it is important to examine gender differences across countries and regions. The findings are supported by a study (García Perales & Palomares Ruiz, 2021), whose conclusions state that gender differences in mathematics performance may be explained by factors such as intelligence or certain personality traits, and contextual factors, such as stereotypes and the family itself. Thus, it is more likely that other aspects influence mathematics performance, such as socioeconomic status, cultural influences, and so on (Else-Quest et al., 2010). Therefore, it is relevant to examine gender aspects in a regional context to identify potential causes of gender differences in mathematics or geometry.
Although gender differences in the mathematics performance of 15-year-olds have not been clearly demonstrated, girls earn better grades in mathematics courses than boys through the end of high school (Lindberg et al., 2010).
The relationship between students’ performance in geometry and in overall mathematics was investigated by Erdogan et al. (2011), using the end-of-year student grades obtained from official records as the measure of performance. They found that there were significant gender differences. Girls scored significantly better than boys. At the same time, this study showed a significant relationship between achievement in overall mathematics and in geometry. Thus, there is a suggestion that mathematics scores may well reflect geometry scores.
In this study, we refer to student assessment in mathematics as a numerical representation of student performance in mathematics. This expression is determined by comparison with a criterion, and in our case, it is the achievement of national content and performance standards. The evaluation of pupils’ performance is typically conducted by the teacher at the end of the term, encompassing both cognitive and affective dimensions—including test scores, oral examination outcomes, and the analysis of students’ work. The grade reflects not merely the result of a single test, but a comprehensive evaluation conducted by the teacher over the entire period. In line with Erdogan et al. (2011), we acknowledge that various factors may influence pupils’ grades, potentially contributing to gender differences or discrepancies between geometric reasoning levels and overall mathematics achievement.
In summary, extensive research has examined gender differences in mathematics, particularly in relation to pupil performance as measured by tests or grades. Findings suggest that significant gender disparities typically begin to emerge in high school (Hyde et al., 1990). This study offers an analysis of the geometric thinking of 15-year-old Slovak pupils, focusing on mathematics achievement in the context of gender differences. It answers the following questions:
Question 1.
What level of geometric thinking do 15-year-old Slovak pupils have?
Question 2.
What is the relationship between mathematics grades and the level of geometric thinking of pupils?
Question 3.
What are the gender differences in pupils’ levels of geometric thinking?
3. Methodology of the Research
3.1. Research Sample
The research was carried out on a representative sample of 15-year-old pupils (specifically 9th grade pupils in elementary schools or the corresponding grade in 8-year grammar school) with the Slovak language of instruction in Slovakia, which was generated by the National Institute of Certified Measurements. Given the representativeness of the statistical population with a size of n = 738 pupils, the answers of the participating pupils can be considered relevant in terms of the focus of the sample survey. As the research sample of 15-year-old primary school students (selected based on geographical location, school size, and rural or urban classification, as shown in Figure 1) is representative, the results of the knowledge test allow for generalizable conclusions about the geometric reasoning level of 15-year-old pupils across Slovakia in the specified calendar year.
Figure 1.
Location of the research sample.
3.2. Research Tool—The Process of Translation and Cultural Adaptation of the Test
At the heart of any measurement process is the acquisition of data, which must be objective, reliable, and valid. For our investigation of the level of geometric reasoning of 15-year-old pupils in Slovakia, Professor Usiskin’s knowledge test was used. Based on the analysis of the test, we identified potential terminological differences. A key obstacle in the standardization of the test was the inconsistency between local mathematical terminology and its counterparts in international contexts for certain concepts. The most serious differences were related to the Slovak exclusive definitions of geometric figures, which are often formulated inclusively abroad. This concerns, for example, quadrilaterals, which are understood and defined inclusively abroad (e.g., a square is a subset of rhombi) in contrast to the Slovak exclusive categorization system (squares are a separate category, and rhombi are also defined separately as quadrilaterals with congruent sides whose internal angles are not right angles). These terminological differences may cause Slovak pupils problems in understanding the relationships between the shapes. Another problem is the often-misused translation or designation of a rectangle that is not a square. In Slovakia, we have a special term (rectangle) which is used in English-speaking countries as oblong. We were concerned that by translating, we might change the nature of some of the tasks. For this reason, we have incorporated five of our own (original) tasks into the test with the intention of reflecting the differences in mathematical terminology in Slovakia and abroad. This set of five tasks aimed to verify and compare the pupils’ answers to the original tasks with those from our set (an example of one pair of tasks is given in Table 1). The original tasks involved terms that we identified as potentially suspicious due to differences in national terminology. The test, after translation and modification, was reviewed by three mathematician colleagues, who acknowledged the relevance of the changes. Subsequently, the test was back-translated into English to ensure the fidelity of the original translation. At the same time, we piloted the test on a small group of students to determine the comprehensibility of the items and instructions given in the test. In the pilot testing, we did not verify the statistical indicators of the test.

Table 1.
A sample of the original task and a sample of the author’s task, which aimed to verify the translated concept.
The final version of the test consisted of the test itself and an answer sheet. The introduction to the test provided information about the aims and reasons for testing and instructions before the test was administered. On the answer sheet, pupils indicated their assigned identification codes to ensure anonymous test processing, along with their gender and their mathematics grade from the previous semester’s report card. Pupils were given 45 min to complete the test, corresponding to the duration of a standard class period. The test was administered in person by members of the research team, all of whom received prior training to ensure standardized implementation.
Before the actual statistical evaluation of the obtained research data, we considered it necessary to verify it in terms of its reliability. The verification of the knowledge test was aimed at assessing its reliability and identifying suspect items, reducing its overall reliability, as well as identifying the items that have the greatest impact on the mean value and variability of the overall test score.
4. Level of Geometric Thinking of Pupils (Verification of the Research Tool)
4.1. Reliability Analysis and Internal Consistency of the Test
Before the statistical evaluation of the obtained research data, we considered it necessary to verify its basic characteristics. The verification of the knowledge test was aimed at assessing its reliability and identifying suspect items, reducing its overall reliability, as well as identifying the items that have the greatest impact on the mean value and variability of the overall test score. To verify the validity of the test, we used pupils’ mathematics grades, which represent a valid criterion. Given that this is an ordinal variable, we used non-parametric correlation, specifically Goodman–Kruskal’s gamma, to evaluate validity. To verify reliability, we used reliability analysis, primarily average inter-item correlation, Cronbach’s alpha, and standardized alpha. Item analysis was used to identify suspicious tasks, primarily item-total correlation and alpha if deleted.
As part of the statistical testing, we applied a multivariate exploratory technique, namely, reliability/item analysis of the administered research instrument. The reliability of the knowledge test was assessed using Cronbach’s alpha, standardized reliability coefficient, and correlation coefficient. The results derived from the aforementioned analysis are presented in Table 2. By examining the reliability and individual items of the test, we can either strengthen its overall validity or avoid relying on a poorly constructed assessment that would produce meaningless results, no matter how sophisticated the subsequent analyses may be.

Table 2.
Overall statistics of the administered knowledge test.
For the verification process of the research instrument, a total of 30 knowledge tasks were included in the statistical measurement, of which the first 25 tasks were the original tasks of the Usiskin test, and the last five were the original tasks, the significance of which we have described above. The initial 25 tasks were grouped into five levels of difficulty (hereafter referred to as difficulty levels T0 to T4), with the last comparative quintet of tasks labelled T5. Each of the van Hiele levels in the Usiskin test contained five tasks, which for the purposes of analysis we have labelled with indices from 1 to 5, i.e., T01–T05, T11–T15, … T41–T45 (T level task). Similarly, we also labelled the five author tasks.
The reliability coefficient value of 0.64 (64%) reflects the proportion of the sum of the variability of the scale items to the total variability of the test. Both reliability estimates (Cronbach’s alpha and standardized alpha) are similar, i.e., the item variability is approximately the same. This fact indicates the internal consistency of the items within the administered knowledge test (Table 2). The results show that the test (measurement procedure) can be considered stable.
The knowledge test can be regarded as reliable based on the group of items T01–T55; however, the low average inter-item correlation rate (0.05) suggests that its reliability could be improved through the removal or modification of certain items.
Table 3 presents the approximated statistics of the knowledge test following the removal of each respective item. Reported are the mean test score values, variance values, standard deviation values, Cronbach’s coefficient alpha values, and correlation values between the item in question and the overall test score.

Table 3.
Statistics of the administered test after deleting the relevant items.
An analysis of the statistical indicators related to the responses of the observed group of pupils on individual items of the knowledge test reveals several noteworthy findings (see Table 3). The statistical analysis shows items that increased the most or decreased the least in mean test score after removing them (12.9377). Looking at the mean values obtained for the total score of the research instrument after removing the respective item, we note that items T01 (12.0136), T02 (12.0366), T03 (12.0149) and T04 (12.1829) were rated most positively by the respondents, as the mean value of the test score decreased the most after their removal. It was somewhat expected that respondents performed best on items T01, T02, T03, and T04, as these correspond to the lowest van Hiele level of geometric reasoning.
Measurement using the scale showed (Table 3) that most of the items of the administered research instrument correlate with the total score of the scale, and the reliability coefficient—Cronbach’s alpha (0.64) decreased when these items were removed. For eight items, i.e., T33 (0.6435), T34 (0.6535), T35 (0.6411), T41 (0.6502), T43 (0.6407), T44 (0.6487), T45 (0.6413), and T53 (0.6480) we observe the opposite condition, in these cases the reliability coefficient (Alpha if deleted) increased. In the context of the findings obtained in these eight items, it is possible to speak of items reducing the overall reliability of the research instrument, so we will subject them to a deeper qualitative analysis.
An intriguing finding is that the test items most detrimental to the overall reliability of the knowledge assessment were concentrated at the fifth difficulty level (T4). These are specifically the knowledge test items labelled T41, T43, T44, and T45. The next group of test items that were identified as suspect was at the fourth (T3) level of difficulty. In this case, these were knowledge test items (=items) under the labels T33, T34, and T35. These are items that are aimed at testing students’ deductive reasoning ability. At this level, pupils can construct their own proofs and understand the meaning of definitions, theorems, and proofs.
We can consider as positive the finding that within the last sixth quintuplet (T5) of test items, labelled T51–T55, only one test item was identified as suspect (T53), potentially reducing the overall reliability of the knowledge test. It should be noted that in the case of the sixth and final quintet of T51–T55 items, these were items that are not a standard part of the knowledge test of Prof. Usiskin’s knowledge test, but they were additionally included by us in the content design of the administered test for the purposes of our sample survey. On the other hand, results of the verification of the research instrument confirmed that the first (T0), second (T1), and third (T2) levels of the test item difficulty do not show any suspicious items that would reduce the overall reliability of the developed research instrument.
Table 3 illustrates the correlations between individual item totals and the total test score (Item-total correlation). As shown in the table, a positive correlation—a directly proportional linear relationship between the respective item and the total test score—was identified for most of the items tested. The exceptions are items T33 (0.0571), T34 (−0.1745), T35 (0.0973), T41 (−0.0466), T43 (0.0946), T44 (−0.0153), T45 (0.0828) and T53 (0.0198), which do not correlate with any other items on the test, from which we can conclude that the values vary independently. In these cases, a trivial positive correlation between the respective item and the total test score (correlation coefficient r < 0.1) or a negative correlation (correlation coefficient r < 0) has been identified, i.e., the values change together but in the opposite direction (while the values of one variable decreases the other variable I creases). Based on these results, the items just mentioned were identified as suspect.
Table 3 shows that the overall resulting standard deviation of the students’ responses did not differ significantly after removing the respective items T01 to T55. Individual items/tasks contribute to the stability of the entire test; none of the items/tasks examined significantly affects the overall variability of the test. In terms of this statistical indicator, the most homogeneous pupil responses were recorded for items T34, T41, and T44. For these three items, we observe the phenomenon where the value of the standard deviation (3.9048) decreased the least after removing them—standard deviation after removing item T34: 3.94; standard deviation after removing item T41: 3.90; standard deviation after removing item T44: 3.89. This is a task that looked at pupils’ responses when judging individual true/false statements in commonly used geometry (item T34), a task that looked at pupils’ responses when judging individual true/false statements in F-geometry (item T41), and a task that looked at pupils’ responses when judging true/false statements for rectangles (item T44). For all other tested items, we observe a slightly more significant decrease in the value of the standard deviation (3.9048) after removing them than for items T34, T41, and T44. Regarding this statistical measure, the highest standard deviation values were observed for items T34, T41, and T44, occurring concurrently with the highest mean scores on the overall test. This means that when the above trio of items were excluded, the most significant deviations from the mean value of the test score occurred, and thus the greater variance (after excluding T34: 15.5258; after excluding T41: 15.2251; after excluding T44: 15.1201).
Based on the above, in the next part of the paper, we focus on a more detailed statistical analysis of the partial results of the reliability assessment of the items within the fourth (T3) and fifth (T4) domains of inquiry, i.e., those domains within which some items of the research instrument used were identified as suspect. The results of the pilot testing for the specified areas of the research instrument are presented in Table 4, based on an analysis of the responses received.

Table 4.
Results of the significance test of the coefficient of association of items T01 to T55 on the factor grade in mathematics.
4.2. Interpretation of the Results of the Finding—Level of Geometric Thinking of Pupils
The statistical analysis showed that the overall accuracy and reliability of the test for 15-year-old Slovak students can be increased by removing four items, T41, T43, T44, and T45 of the fifth level, and three items, T33, T34, and T35 of the fourth van Hiele level of geometric reasoning.
The fifth, rigorous level of geometric thinking is characterized by the ability to analyze different geometric systems and compare them. The concept of the Slovak mathematics curriculum, and therefore also mathematics textbooks for primary school pupils, is focused on working with Euclidean geometry. They do not include problems and tasks that would develop thinking about other geometric systems. The school geometry problems are linked to constructions and proofs of Euclidean geometry as a basis for other mathematical areas and applications of mathematics. In the didactics of mathematics (also based on insights from developmental psychology), it is assumed that the fifth level of thinking is achieved by students with more mathematical experience. These are more characteristic of grammar school and university studies of geometry in Slovak education.
Therefore, it is understandable that the items of this level reduced the reliability of the test; the fifth level was too abstract for 15-year-old Slovak pupils. The exception was item T42—the angle trisection problem. This problem is cited by some mathematics teachers as a historical and geometric curiosity for pupils, that some problems cannot be solved by standard geometry tools. It is usually a problem that is classified for exceptionally gifted pupils or pupils with extended mathematics lessons, or for pupils who are more deeply interested in mathematics. This may be one interpretive reason why item T42 was the only Level 5 item that did not exhibit reliability concerns.
The tasks included in the fourth level (T3) of geometric reasoning are aimed at testing the level of pupils’ deductive reasoning. At this level, pupils can produce their own proofs, understanding of definitions, theorems, and proofs. To determine the truth of statements in this part of the test, it is essential to have a basic understanding of propositional logic, including logical connectives, operations with statements, quantifiers, and so on. Since three of the five items (T33, T34, and T35) of this level reduce the test’s reliability, we can conclude the following:
- Items were vaguely worded, i.e., they contained unfamiliar concepts for the pupils.
- The items were too difficult for our pupils.
- The items had a low discriminative ability and thus did not distinguish between better and worse pupils.
- The pupils chose the answer randomly, i.e., guessed the answer, without mastering the material.
At this point, it is unclear whether the issue with these items lies in the incomprehensibility of certain geometric concepts used in this part of the test or in the failure to grasp the elements of logic and evaluate the truth or falsity of compound statements. Considering that items T31 and T32 are of a similar nature and did not raise concerns regarding reliability, we can conclude that the entire set of items in Level 4, T31–T35, may be relevant for the 15-year-old students. Therefore, we suggest only using the first 20 items of the test to assess the van Hiele level of geometric reasoning in 15-year-old Slovak pupils. The remaining five higher-level items will not provide relevant data. Accordingly, we recommend that items corresponding to the first four van Hiele levels of geometric thinking should also be administered in the national measurements of 9-graders (14 and 15-year-olds).
4.3. Pupils’ Level of Geometric Thinking and Mathematics Grade
The responses of the group of students in items T01–T55 of the knowledge test were considered in terms of their potential dependence on the segmentation factor grade in mathematics.
In examining the statistical dependence between pupils’ responses to items T01–T55 on the knowledge test and their segmentation factor grade in mathematics, the following null hypothesis was formulated:
Hypothesis 1.
Respondents’ answers to items T01 to T55 do not depend on the factor grade in mathematics.
As part of the statistical analysis, we verified the validity of the above null hypothesis, the latter representing de facto 30 partial null statistical hypotheses.
Table 4 shows that the differences in the scores for the knowledge tasks designed to assess the level of geometric reasoning of 15-year-old pupils in Slovakia, through items T01–T55, were statistically significant in most cases (p < 0.05), depending on the pupils’ grades in mathematics at the end of grade 8 in primary school. Based on this result, we reject the null statistical hypothesis and conclude that students’ responses to items T01 to T32, T34, T35, T42, T51, T52, T54, and T55 (under the given conditions) depend on the factor of grade in mathematics attained at the end of Grade 8 of primary school.
Based on the results of the Z test statistic, we can conclude (Table 4) that in the case of a statistically significant negative association, students with better grades achieved higher response scores on the knowledge test items. Conversely, in cases of a statistically significant positive association, students with lower grades achieved higher scores on the test items. The more negative the Gamma value, the more likely it is that students with better grades performed better on the test items. On the other hand, the larger and more positive the Gamma value, the more likely it is that students with lower grades scored better. The analysis showed that the test scores correlated with their mathematics scores, which is good for the validity of the test.
Table 4 provides a more detailed statistical picture of the dependence analyzed. As evident from the tabulated results, the level of association is statistically significant (p < 0.05) given the value of the Gamma correlation coefficient for the T15 items (G10 = −0.2972), T21 (G11 = −0.2471), T22 (G12 = −0.1072), T24 (G14 = −0.1299), T31 (G16 = −0.1108), T35 (G20 = −0.1410), T42 (G22 = −0.2755) and T54 (G29 = −0.1950) are small (G ∈ (0.10–0.29)).
Given the value of the Gamma correlation coefficient, a moderate degree (G ∈ (0.30–0.49)) of positive/negative (+/−) statistically significant association (p < 0.05) was demonstrated between the variable grade in mathematics (1/2/3/4/5) and item T01 (G1 = −0.4327), T03 (G3 = −0.4832), T04 (G4 = −0.3279), T05 (G5 = −0.4773), T12 (G7 = −0.4728), T13 (G8 = −0.4785), T25 (G15 = −0.3666), T32 (G17 = −0.4007), T34 (G19 = 0.3850), T51 (G26 = −0.3389), T52 (G27 = −0.3062) and T55 (G30 = −0.4108).
Table 4 also shows a high level (G ∈ (0.50–0.69)) of negative (−) statistically significant association (p < 0.05) between the mathematics grade variable (1/2/3/4/5) and items T02 (G2 = −0.6223), T11 (G6 = −0.5281), T14 (G9 = −0.5718), and T23 (G13 = −0.6208), respectively. Additionally, item T02 showed the highest value of the Gamma correlation coefficient (G = −0.6223; p < 0.001) compared to the remaining correlation coefficients (T11 × grade in mathematics; T14 × grade in mathematics; T23 × grade in mathematics). This suggests that pupils’ responses to item T02 show the greatest statistical dependence on the factor grade in mathematics obtained from the sample of pupils in our sample survey.
Based on the p-values obtained for items T33, T41, T43, T44, T45, and T53 of the administered knowledge test, we can conclude that students’ responses are independent of their mathematics grade at the end of Grade 8 in primary school, and the Gamma coefficients are statistically insignificant (p > 0.05). Based on this result, we do not reject the null statistical hypothesis, which means that pupils’ responses to items T33, T41, T43, T44, T45, and T53 (under the given conditions) do not depend on the factor of the grade achieved in mathematics at the end of Grade 8 of primary school.
The statistical analysis of the results of the geometric reasoning test of the students as a function of the factor of grade in mathematics showed that the test is valid. It is important to note that the van Hiele test specifically measures geometric thinking, while the pupils’ grades reflect their overall summative assessment in mathematics for the given year. Nevertheless, it has been shown that the pupils’ scores, as expressed by the mathematics grade, also correctly reflect the pupils’ performance in their geometry part.
5. An Analysis of the Dependence of the Level of Geometric Reasoning in Relation to Gender Differences
5.1. Data Survey
Based on the results obtained from the administration of the van Hiele test, we were interested in the divergence of the achievement scores of tasks T01–T45 of the knowledge test as a function of the combination of the within-group factor task difficulty level T (T0–T4) and the between-group factor respondent’s gender (0/1).
The statistical measures included tasks T01–T05; T11–T15; T21–T25; T31–T35; T41–T45 grouped into the first five levels of difficulty of the knowledge test (referred to in the text as) T0 to T4 (for clarification: T level task). The last set of five authors’ tasks (grouped under difficulty level T5), denoted by the indices T51–T55, were not included in the statistical analysis. As mentioned in the previous section, these were five tasks that were not constructed at a higher level of difficulty in terms of the requirements specified by the syllabus than the previous tasks T01–T05, T11–T15, … T41–T45). These were five tasks (T51–T55) of varying levels of difficulty, deliberately included in the administered knowledge test to cross-check responses to items that might pose challenges for pupils due to differences between Slovak and foreign mathematical terminology.
The research data were evaluated based on descriptive characteristics, and the statistical significance of differences (correct/incorrect) in students’ responses to items T01–T45 of the knowledge test was tested through an analysis of variance for repeated measures.
Table 5 shows the descriptive statistics of the final scores of the five items assessed, grouped within the reported five levels of difficulty T0–T4, i.e., T01–T05; T11–T15; T21–T25; T31–T35; T41–T45. Descriptive statistics are presented separately for each subgroup of the research sample segmented by the factor of respondent gender (0/1), while the table also includes data for the entire research population without respondent differentiation. Other factors such as the geographical location of the school, the school founder, regional disparity, or pupils’ study orientation were not considered. The values of the mean, standard deviation, standard error of the mean estimate, and 95% confidence interval of the mean of the scale value are reported.

Table 5.
Descriptive statistics of task scores across difficulty levels (T0–T4) segmented by the factor respondent gender.
The resulting standard deviations (Std. Dev.) of the respondents’ answers to the knowledge test items grouped within each difficulty level T0–T4 are not very different. The values of the final scores of the five items assessed ranged from 0.87 (T4 × male (0)) to a value of 4.21 (T0 × male (0)) with respect to the interval estimate of the mean score.
If we look at the results obtained in terms of this statistical indicator in more detail, the most heterogeneous answers were recorded for the tasks in the second (T1) level of difficulty within the group of girls (variability indicator 1.47), as well as within the group of boys (variability indicator 1.45). The values of the mean scores reported for these five T11–T15 tasks range from 2.36 to 2.65 (T11–T15 tasks assessed by girl students) and 2.52 to 2.83 (T11–T15 tasks assessed by boy students), based on the interval estimation of the mean score. On the contrary, the lowest standard deviation values (0.87 and 0.91, respectively), i.e., the lowest variability of the respondents’ answers, were recorded overall for the five tasks T41–T45 concentrated in the fifth (T4) level of difficulty, both in the boys’ group (0.87–1.05) and in the girls’ group (0.90–1.08). For the five T41–T45 tasks, the lowest overall mean response score was simultaneously recorded in the group of male respondents as well as in the group of female respondents (T4 × male (0) − 0.96; T4 × male (1) − 0.99).
The results of the mean scores of pupils’ responses to items T01–T45 of the knowledge test achieved within the reported five levels of difficulty T0–T4 when differentiating the respondents according to the intergroup factor gender (0/1) are graphically visualized in Figure 2, which shows the point and interval estimates of the mean scores separately for the group of boy respondents and separately for the group of girl respondents.
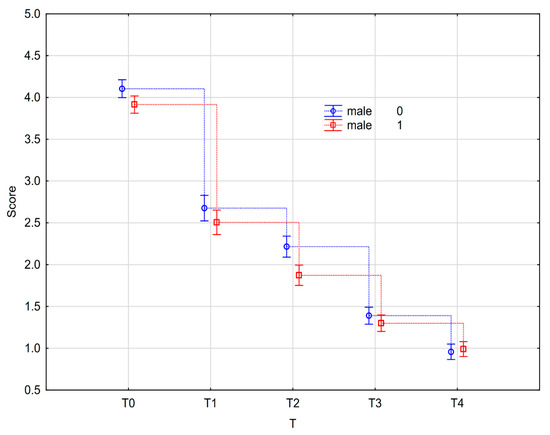
Figure 2.
Graph of the mean and confidence interval of the answers obtained in each difficulty level of the tasks T0–T4 depending on the factor respondent’s gender.
The question is whether the differences between respondents’ answers recorded in the different tasks T01–T45 of the knowledge test are random or statistically significant. To answer this question, we conducted a repeated measures analysis of variance. This statistical analysis was used to detect the dependence of respondents’ answers on a combination of the within-group factor task difficulty level T (T0–T4) and the between-group factor respondent gender (0/1).
Based on the exploration of the data, specifically the point and interval estimate of the mean scores (Table 5, Figure 2), we established the following global null hypothesis:
Hypothesis 2.
Task scores do not depend on the combination of the within-group factor T (T0–T4) and the between-group factor male (0/1).
The null statistical hypothesis was tested at the 5% significance level (α = 0.05). The hypothesized dependence or independence on the combination of the factors task difficulty level T (T0–T4) and respondent gender (0/1) was tested through parametric procedures.
5.2. Validation of the Used Statistical Methods
We applied analysis of variance for repeated measures to the data obtained using the sample survey. The assumption of analysis of variance with repeated measurements is equality of variances and covariances in the covariance matrix for repeated measurements. This assumption is called the sphericity condition of the covariance matrix. We did not need to verify the normality assumption because the research samples were sufficiently large.
We used Mauchley’s test of sphericity to test for equality of variances and covariances in the covariance matrix (Table 6).

Table 6.
Mauchley’s Sphericity Test.
In the case of testing the variables T01–T45 against the within-group factor task difficulty level T (T0–T4), the test is statistically significant (p-value < 0.001), which means that the assumption of homogeneity of variances is rejected. We note that for variables T01–T45, the sphericity condition of the covariance matrix for repeated measures is violated (Table 6). Therefore, we use modified significance tests for repeated measures to test the global null hypothesis (Table 7).

Table 7.
Tests of Homogeneity of Variances.
The assumption of equality of variances was tested under the respondent gender factor (0/1) using the parametric Hartley F-max test, Cochran’s C test, and Bartlett’s Chi-square test (Table 7).
Based on the results of Hartley’s F-max test, Cochran’s C test, and Bartlett’s Chi-square test, no violation of the assumption of equality of variances (p-values > 0.05) was identified for the respondent gender factor (0/1) for any of the examined difficulty levels (T0–T4) of the knowledge test items. Based on this, we can conclude that the variability of the scores achieved on tasks T01–T45 within each of the five levels of difficulty (T0–T4) is approximately the same for both boys and girls. The performance of both boys and girls can be considered stable. Therefore, there was no instance where girls scored similarly while boys showed significant variation, or vice versa—the variability in test scores was comparable for both boys and girls.
Unless the sphericity condition of the covariance matrix is satisfied, the magnitude of the Type I error increases. Therefore, in such cases, the degrees of freedom for the F-test used are adjusted by means of corrections to reach the declared significance level. To test for violations of the assumption of validity of the analysis of variance, we used the Greenhouse–Geisser correction for repeated measures analysis of variance (Table 8).

Table 8.
Greenhouse–Geisser correction for repeated measures of variance analysis.
Repeated measures adjusted tests of the significance of differences between the mean scores of knowledge tasks T1 (T01)–T25 (T45) as a function of a combination of the within-group factor task difficulty level T (T0–T4) and the between-group factor respondent gender (0/1) confirmed the significance of the differences tested (Table 8), since the variable p shows a value below the chosen significance level (5% = 0.05) in the Greenhouse–Geisser correction (lower bound) (p = 0.01).
Based on the results of the analysis of variance for repeated measures summarized in Table 8, we reject the stated global null hypothesis with 95% confidence and conclude that students’ responses to knowledge items T01–T45 of the administered test are statistically dependent on the combination of the within-group factor T (T0–T4) and the between-group factor male (0/1).
5.3. Multiple Comparison
After rejecting the global null hypothesis, we were interested to see among which specific pairs of groups, defined based on the combination of the factors T (T0–T4) x gender (0/1), the differences between the achievement scores of the knowledge tasks T01–T45 are statistically significant.
We used Duncan’s test to test the statistical significance of the contrasting effects of the factor task difficulty level and the simultaneous factor respondent gender (0/1).
Identification of homogeneous groups was performed through multiple comparisons. The results of the identification of homogeneous groups in the achievement scores of tasks T01–T45 of the knowledge test, depending on the combination of the within-group factor task difficulty level T (T0–T4) and the between-group factor respondent’s gender (0/1), are summarized in Table 9. As can be seen from Table 9, for the fourth (T3) and fifth (T4) task difficulty levels, we observe one homogeneous group each time (T3 x gender (0/1); T4 x gender (0/1)).

Table 9.
Duncan test for two-factor analysis of variance.
Based on the results obtained from the multiple comparisons, we can conclude that statistically significant differences (Table 9) were demonstrated between the different task difficulty levels T (T0–T4) (p < 0.05), as well as between boys and girls (in favor of girls) for the less difficult tasks (T0–T2) (p < 0.05).
In contrast, for the more difficult tasks (T3–T4) of the administered knowledge test, there were no statistically significant differences between boys and girls (p > 0.05) (Table 9). The table shows that the performance of boys and girls overlaps at the third (T3) and fourth (T4) levels of task difficulty.
The results of Duncan’s test (Table 9) aimed at revealing the relationships between each pair of groups defined according to the combination of the within-group factor task difficulty level T (T0–T4) and the between-group factor respondent’s gender (0/1) are shown in Figure 2. The graph clearly shows the interval estimates of the mean scores obtained in the individual task difficulty levels (T0–T4), whose pairs do not overlap, confirming the observed statistical dependence.
5.4. Interpretation of Results—Gender Differences by Difficulty Level
An interesting finding emerged from the analysis: statistically significant differences were observed between boys and girls (respondent gender factor (0/1)) in the lower-difficulty T0–T2 tasks, with girls outperforming boys. In the higher difficulty task levels T3 and T4, there were no significant differences between the two groups, or the differences disappeared.
Interpretation of this result is challenging and will require further analysis. In contrast to our results, many studies report that gender differences in mathematics are negligible, e.g., (Lindberg et al., 2010; Petersen & Shibley Hyde, 2014; Ghasemi & Burley, 2019). Gender differences in mathematics do not originate from biological differences between boys’ and girls’ brain processes in mathematical reasoning (Lindberg et al., 2010). In other words, research suggests that the way boys’ and girls’ brains process mathematical tasks is not fundamentally different. This supports the view that if there are differences in mathematics performance between the sexes, they are likely to be due to sociocultural factors, upbringing, stereotypes, or different opportunities to learn and develop mathematical skills, rather than innate biological predispositions (García Perales & Palomares Ruiz, 2021). Significant gender differences have been demonstrated by studies in relation to mathematics assessment (grade) in favor of girls (Erdogan et al., 2011). In our study, we demonstrated a significant and relevant relationship between mathematics assessment and geometry test scores. However, we do not know why girls scored better on geometric thinking in the first three levels of the van Hiele test.
We can consider that there is a ceiling effect. This means that girls were able to reach the ceiling (limits) of their geometric abilities in easier tasks, while boys still had room for improvement. In the more difficult tasks, these limits were pushed higher for both groups, and the differences narrowed. We observed a larger drop in task success between T2 and T3 levels for girls than for boys. Therefore, another possible interpretation is that girls may have a broader geometric background, but boys may have a greater potential for more challenging, and thus more abstract, tasks. Nevertheless, this interpretation must be approached with caution, as it touches upon prevailing social expectations and gender stereotypes related to mathematics.
On the other hand, with regards to the age of 14–15-year-olds, we also need to consider that significant developmental changes are taking place at this age, which may affect cognitive function, motivation, and self-esteem. These aspects may have an impact on the better performance of girls. Verification would require further specific research, but research suggests that differences in problem-solving in favor of boys emerge at secondary school age, later in life (Hyde et al., 1990).
Let us look at the results obtained in terms of the nature of the tasks themselves at each level of difficulty and in terms of the use of different strategies in solving the tasks, depending on gender. Gender differences in mathematical ability are generally small or non-existent in the wider population. If they occur, they may depend on the type of task (Halpern, 2004; Lindberg et al., 2010). Girls may prefer more visual and intuitive problem-solving strategies, whereas boys may prefer more analytical and logical approaches (Halpern, 2004). In simpler tasks, visualization and intuition may be sufficient, but in more challenging tasks, a deeper mathematical apparatus is needed (Žilková et al., 2018). In this context, we can explain the girls’ better performance on tasks from the visualization level T0 and the analysis level T1, which focus on the identification of shapes by appearance and on the knowledge of the properties of geometric shapes without a deeper understanding of the relationships between properties. On the other hand, the results of the T2 level, which focuses on the properties of shapes and other more abstract relationships between shapes, also favored girls, not boys, and the differences between the two were the largest.
Tasks in difficulty levels T3 and T4 were described above as requiring significantly higher mathematical skills (deduction and axiomatization), and the results showed that there was no significant difference between girls and boys. These findings are consistent with studies that have declared negligible gender differences in mathematics (Lindberg et al., 2010; Petersen & Shibley Hyde, 2014; Ghasemi & Burley, 2019).
6. Conclusions
To determine the level of geometric thinking of 15-year-old Slovak pupils, we adapted and administered the van Hiele test. We sought answers to three questions, as follows:
Question 1.
What level of geometric thinking do 15-year-old Slovak pupils have?
Question 2.
What is the relationship between mathematics grades and the level of geometric thinking of pupils?
Question 3.
What are the gender differences in pupils’ levels of geometric thinking?
We found statistically significant differences in the answers of Slovak pupils in the tasks of the van Hiele test in terms of the difficulty of individual levels. The level of difficulty of each of the five items had a significant effect on pupils’ performance.
This result points to the following three key findings:
- ▪
- Student performance deteriorated as the difficulty of the tasks increased
- ▪
- Tasks were able to discriminate between pupils with different levels of geometric thinking
- ▪
- Validation of the test in the Slovak population provided supporting arguments in favor of the validity of the test.
Based on the test results, it turned out that the items of the fifth, rigorous level of geometric thinking were too abstract for 15-year-old Slovak pupils and reduced the reliability of the test. Similarly, some items of the fourth, deductive level, were problematic, probably due to the difficulty of logical operations. There were also no significant gender differences at these levels. Thus, the results showed that 15-year-old Slovak pupils had difficulties in solving items that require a deep understanding of geometric systems and logical proofs. To determine the level of geometric thinking, tasks corresponding to level 4 of geometric thinking, i.e., tasks focused on deductive reasoning, were crucial.
Although the mathematics grade represents an overall assessment of pupils’ mathematical performance, statistical analysis showed that this grade also reflects well their level of geometric thinking as detected by the van Hiele test. This means that pupils with better grades in mathematics generally also achieve a higher level of geometric thinking.
The analysis showed that there is a statistically significant difference in pupils’ responses to the geometry tasks depending on the combination of task difficulty and gender. Specifically, although the overall variability in responses was similar for boys and girls, the mean scores achieved differed between genders within each level of task difficulty. Interestingly, for the less challenging tasks (at the visualization, analysis, and abstraction levels), girls scored statistically significantly better than boys. However, for the more challenging tasks at the inference and rigor levels, these differences between boys and girls disappeared, and their scores were not statistically different. The observed gender differences, where girls demonstrated higher success in lower-level geometric thinking tasks while both genders faced challenges in more demanding tasks, underscore the necessity for developing differentiated pedagogical approaches aimed at the effective development of geometric reasoning in all students.
This study, while providing valuable insights, has inherent limitations that need to be considered. Primarily, it focuses on 15-year-old Slovak pupils, which limits the direct generalizability of the findings to other age groups or cultural contexts. This study is also cross-sectional, meaning it does not provide insights into the dynamics of geometric thinking development over time, nor potential causal relationships between identified factors and performance. Finally, although factors such as task difficulty, gender, and overall mathematics grades were considered, this study did not delve into broader social, economic, or pedagogical influences that could also affect pupils’ level of geometric thinking.
Author Contributions
Conceptualization, K.Ž., J.Z. and M.M.; methodology, M.M. and J.Z.; software, M.M.; validation, M.M. and J.Z.; formal analysis, J.Z.; investigation, M.M.; resources, K.Ž. and J.Z.; data curation, M.M.; writing—original draft preparation, J.Z. and K.Ž.; writing—reviewing and editing, J.Z. and K.Ž.; visualization, M.M.; supervision, K.Ž.; project administration, K.Ž.; funding acquisition, K.Ž. All authors have read and agreed to the published version of the manuscript.
Funding
The preparation of this article was supported by the Cultural and Educational Grant Agency of the Ministry of Education, Science, Research and Sport of the Slovak Republic under the project No KEGA 077UK-4/2025 Edu-Steam laboratory in primary education teaching.
Institutional Review Board Statement
The research of this study was conducted according to the Internal Regulation No. 32/2022 “The internal quality assurance system for higher education of the Comenius University Bratislava”, part Eight “The Code of research ethics and rules of creative activity at Comenius University Bratislava”. The report protocols and focused interviews were anonymous, and we did not collect any personal data from students. For this reason, according to Internal Regulation No. 32/2022, ethics approval is not required for this type of study.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data are unavailable due to privacy and ethical restrictions according to Internal Regulation No. 32/2022.
Acknowledgments
The authors of the paper thank the valuable contributions and support partners from the Faculty of Education, Comenius University in Bratislava, and the Faculty of Natural Sciences and Informatics, University of Constantine the Philosopher in Nitra.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Battista, M. T. (2007). The development of geometric and spatial thinking. In D. S. Mewborn, P. Sztajn, D. Y. White, H. G. Wiebe, & R. L. Cramer (Eds.), Proceedings of the 29th annual meeting of the North American chapter of the international group for the psychology of mathematics education (Vol. 1, pp. 31–40). University of Nevada. [Google Scholar]
- Cardinali, A., & Piergallini, R. (2022). Learning non-euclidean geometries: Impact evaluation on Italian high-school students regarding the geometric thinking according to the van hiele theory. In Advances in education and educational trends series (pp. 87–98). inSciencePress. [Google Scholar] [CrossRef]
- Chen, Y.-H., Senk, S. L., Thompson, D. R., & Voogt, K. (2019). Examining psychometric properties and level classification of the van Hiele geometry test using CTT and CDM frameworks. Journal of Educational Measurement, 56(4), 425–453. [Google Scholar] [CrossRef]
- Clements, D. H., & Battista, M. T. (1992). Geometry and spatial reasoning. In D. A. Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 420–464). Macmillan. [Google Scholar]
- Else-Quest, N. M., Hyde, J. S., & Linn, M. C. (2010). Cross-cultural patterns of gender differences in mathematics: A meta-analysis. Psychological Bulletin, 136(1), 103–127. [Google Scholar] [CrossRef] [PubMed]
- Erdogan, A., Baloglu, M., & Kesici, S. (2011). Gender differences in geometry and mathematics achievement and self-efficacy beliefs in geometry. Egitim Arastirmalari-Eurasian Journal of Educational Research, 43, 91–106. [Google Scholar]
- Feza, N., & Webb, P. (2005). Assessment standards, Van Hiele levels, and grade seven learners’ understandings of geometry. Pythagoras, 62(62), 36–47. [Google Scholar] [CrossRef]
- Fuys, D., Geddes, D., & Tischler, R. (1984). English translation of selected writitngs of Dina van Hiele-Geldof and Pierre M. van Hiele. City University of New York. Available online: https://files.eric.ed.gov/fulltext/ED287697.pdf (accessed on 18 October 2024).
- García Perales, R., & Palomares Ruiz, A. (2021). Comparison between performance levels for mathematical competence: Results for the sex variable. Frontiers in Psychology, 12, 663202. [Google Scholar] [CrossRef] [PubMed]
- Ghasemi, E., & Burley, H. (2019). Gender, affect, and math: A cross-national meta-analysis of trends in international mathematics and science study 2015 outcomes. Large-Scale Assess Education, 7, 10. [Google Scholar] [CrossRef]
- Győry, Á., & Kónya, E. (2018). Development of high school students’ geometric thinking with particular emphasis on mathematically talented students. Teaching Mathematics and Computer Science, 16(1), 93–110. [Google Scholar] [CrossRef]
- Halpern, D. F. (2004). A cognitive-process taxonomy for sex differences in cognitive abilities. Current Directions in Psychological Science, 13(4), 135–139. [Google Scholar] [CrossRef]
- Haviger, J., & Vojkůvková, I. (2015). The van Hiele levels at Czech secondary schools (Vol. 171, pp. 912–918). Procedia-Social and Behavioral Sciences. [Google Scholar] [CrossRef][Green Version]
- Hyde, J. S., Fennema, E., & Lamon, S. J. (1990). Gender differences in mathematics performance: A meta-analysis. Psychological Bulletin, 107(2), 139–155. [Google Scholar] [CrossRef] [PubMed]
- Jablonski, S., & Ludwig, M. (2023). Teaching and learning of geometry—A literature review on current developments in theory and practice. Education Sciences, 13(7), 682. [Google Scholar] [CrossRef]
- Kersey, A. J., Csumitta, K. D., & Cantlon, J. F. (2019). Gender similarities in the brain during mathematics development. npj Science of Learning, 4, 19. [Google Scholar] [CrossRef] [PubMed]
- Knight, K. C. (2006). An investigation into the change in the Van Hiele levels of understanding geometry of pre-service elementary and secondary mathematics teachers. In Electronic theses and dissertations (p. 1361). The University of Maine. Available online: https://digitalcommons.library.umaine.edu/etd/1361 (accessed on 15 November 2024).
- Levenson, E., Tirosh, D., & Tsamir, P. (2011). Preschool geometry: Theory, research, and practical perspectives. Sense Publishers. [Google Scholar]
- Lindberg, S. M., Hyde, J. S., Petersen, J. L., & Linn, M. C. (2010). New trends in gender and mathematics performance: A meta-analysis. Psychological Bulletin, 136(6), 1123–1135. [Google Scholar] [CrossRef] [PubMed]
- Marchis, I. (2012). Preservice primary school teachers’ elementary geometry knowledge. Acta Didactica Napocensia, 5(2), 33–40. [Google Scholar]
- Mason, M. (2002). The van Hiele levels of geometric understanding. In Professional handbook for teachers, geometry: Explorations and applications (pp. 4–8). MacDougal Litteil Inc. [Google Scholar]
- Ministry of Education, Research, Development and Youth of the Slovak Republic. (2023). Curriculum reform [Kurikulárna reforma]. Available online: https://www.minedu.sk/41529-sk/kurikularna-reforma/ (accessed on 15 September 2024).
- Musser, G. L., Burger, W. F., & Peterson, B. E. (2001). Mathematics for elementary teachers (5th ed.). John Wiley & Sons. [Google Scholar]
- National Institute of Education and Youth (NIVAM). (2024). How did this year’s ninth graders perform in the national testing? We know the results of Testing 9 [Ako uspeli tohtoroční deviataci v celoštátnom testovaní? Poznáme výsledky Testovania 9 2024]. Available online: https://nivam.sk/ako-uspeli-tohtorocni-deviataci-v-celostatnom-testovani-pozname-vysledky-testovania-9-2024/ (accessed on 4 January 2025).
- Newcombe, N. S., & Shipley, T. F. (Eds.). (2015). Thinking spatially: Interdisciplinary perspectives. Psychology Press. [Google Scholar]
- Petersen, J., & Shibley Hyde, J. (2014). Chapter two—Gender-related academic and occupational interests and goals. In L. S. Liben, & R. S. Bigler (Eds.), Advances in child development and behavior (Vol. 47, pp. 43–76). JAI. [Google Scholar] [CrossRef]
- Scholtzová, I. (2014). Komparatívna analýza primárneho matematického vzdelávania na Slovensku a v zahraničí [Comparative Analysis of the Primary Mathematical Education in Slovakia and Abroad] (386p). University of Prešov, Faculty of Education. ISBN 978-80-555-1204-4. [Google Scholar]
- Trimurtini, S., Budi Waluya, S., Sukestiyarno, S., & Kharisudin, I. (2022). A systematic review on geometric thinking: A review research between 2017–2021. European Journal of Educational Research, 11(3), 1535. [Google Scholar] [CrossRef]
- Usiskin, Z. (1982). Van Hiele levels and achievement in secondary school geometry (CDASSG Project). The University of Chicago. [Google Scholar]
- Van Hiele, P. M. (1986). Structure and insight: A theory of mathematics education. Academic Press. [Google Scholar]
- Van Hiele, P. M. (1999). Developing geometric thinking through activities that begin with play. Teaching Children Mathematics, 5(6), 310–317. [Google Scholar] [CrossRef]
- Žilková, K., Partová, E., Kopáčová, J., Tkačik, Š., Mokriš, M., Budínová, I., & Gunčaga, J. (2018). Young children’s concepts of geometric shapes. Pearson. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).