A Proposal of Integration of Universal Design for Learning and Didactic Suitability Criteria

Abstract

Given the growing relevance of issues of educational inclusion at an international level, educational curricula have pointed out the need to address the diversity of students in the classroom. In this article, a theoretical reflection is proposed around the Universal Design for Learning (UDL) guideline—as inclusive principles for generic teaching and learning processes—and Didactic Suitability Criteria (DSC) guideline—as specific principles for mathematical teaching and learning processes—to establish relationships and seek complementarities between both references. To this end, firstly, a document analysis of literature about UDL was conducted; secondly, UDL and DSC guidelines were contrasted, relating UDL principles and verification points to DSC components and indicators to design a first proposal of an integrated guideline between both references; and, thirdly, an expert validation was conducted with researchers familiar with DSC to adjust the guideline originally proposed. As a main result, a proposal of integration of the UDL and DSC guidelines was designed, which intends to organise the reflection of (prospective and practising) mathematics teachers on their teaching practice. This integrated proposal not only seeks to address current curricular needs, but also to delve deeper into theoretical development that contributes to refining existing tools to encourage reflection on teaching practice.

1. Introduction

In the last two decades, issues of educational inclusion have been gaining relevance at an international level, which has been manifested in different theoretical, practical, and curricular developments (Cerna et al., 2021). The current Education Law in Spain (Head of State, 2020) points out the need to apply the principles of Universal Design for Learning to address the diversity of students, which is explicitly stated in the regulatory text of Law 3/2020 (known by its acronym LOMLOE in Spanish) as follows:

The principles and purposes of education include the effective fulfilment of children’s rights […], educational inclusion, and the application of the principles of Universal design for learning, that is, the need to provide students with multiple means of representation, action, and expression and ways of involvement in the information presented to them.

(Head of State, 2020, pp. 122872–122873, authors’ translation)

In the case of the basic education curriculum in Catalonia (Department of Education of Catalonia, 2022), this aspect is taken into consideration by making Universal Design for Learning one of the curricular vectors, that is, one of the transversal elements that should guide educational decisions in the deployment of the curriculum, which is explicitly stated in the regulatory text of Decree 175/2022 as follows:

Educational inclusion, personalised attention, student participation […], and positive coexistence, as well as early detection of learning difficulties, must be guaranteed […]. The organisational, methodological, and curricular measures adopted to guarantee the personalisation of learning, and the success of all people must be governed by the principles of universal design for learning.

(Department of Education of Catalonia, 2022, p. 7, authors’ translation)

In addition to these curricular demands, there is also the question of—both initial and continuing—teacher education programmes to develop inclusive teaching as part of the teachers’ professional competences (UNESCO, 2005, 2015), where the incorporation of the principles of Universal Design for Learning, so that teachers can apply them in the classroom, is one of the strategies for the development of this competence (Alba-Pastor, 2018) (see further details in Section 2.1).

One strategy that could help teachers incorporate these principles in the classroom is through reflection on their teaching practice, as it is considered a key strategy for its improvement (Schön, 1983, 1987). Furthermore, once this reflection becomes a habit in teachers, it can become the main mechanism for improving their teaching practice (Schoenfeld & Kilpatrick, 2008). This has led to various researchers in Mathematics Education proposing compilations of principles or criteria that seek to guide teaching practice so that it is of quality (for example, Bognar et al., 2025; Praetorius & Charalambous, 2018; Prediger et al., 2022; among others), one of which is the Didactic Suitability Criteria construct proposed by the Onto-Semiotic Approach (Godino et al., 2019). In general terms, this construct can be used as a tool to structure the teacher’s reflection and guide him or her in decision making when designing, implementing, and/or redesigning a mathematical teaching and learning process (see further details in Section 2.2). This construct has been implemented in different teacher education contexts for some time, especially in the Ibero-American context (Breda et al., 2018). For example, in the context of this study, the professionalising master’s programme specialising in mathematics, which is taught by the public universities of Catalonia (Spain), teaches prospective teachers to use the Didactic Suitability Criteria in their master’s degree final projects to assess the mathematical teaching and learning process—known as learning situation—that they implemented during their educational internships period. In this way, in addition to structuring teaching reflection on their practice, this construct allows prospective teachers to identify the aspects that need to be improved in a proposal to redesign their learning situation.

This study is part of a research project on the incorporation of Universal Design for Learning in the teaching reflection of prospective secondary and baccalaureate education mathematics teachers on their practice, who use the Didactic Suitability Criteria for such purposes. In this context, a proposal for integration between both references was designed (see further details in Section 3.1), which began to be implemented in the interuniversity master’s programme mentioned above with the prospective teachers of the 2023–2024 academic year. This integrated proposal not only seeks to address current curricular needs, but also to delve deeper into theoretical development that contributes to refining existing tools to encourage reflection on teaching practice.

Having said that, the study reported in this article is based on the Universal Design for Learning guideline—which is not specific to Mathematics Education—and the Didactic Suitability Criteria guideline—a tool specifically designed in Mathematics Education—with the aim of developing a theoretical reflection on the relationships and complementarities between both references. In this way, this article aims to answer the following question: What relationships and complementarities can be established between the Universal Design for Learning and the Didactic Suitability Criteria guideline? To answer this question, a theoretical reflection was conducted around the Universal Design for Learning and the Didactic Suitability Criteria guidelines to establish relationships and seek complementarities between both references that allow for the design of an integrated proposal that structures the teaching reflection of (prospective or practising) mathematics teachers on their practice.

The relevance of this study lies in the fact that, on the one hand, in the research agenda of Didactic Suitability Criteria as a methodological tool to guide teaching reflection on practice (Malet et al., 2021), the articulation of this construct with other topics in Mathematics Education has also been contemplated (for example, Hidalgo-Moncada et al., 2023, with self-regulated learning; Hummes, 2022, with Lesson Study; Sánchez et al., 2022, with creativity; among others) as well as with specific mathematical processes and objects (for example, Ledezma et al., 2024, with mathematical modelling; Posadas & Godino, 2017, with proportionality; Sol et al., 2024, with practical argumentation; among others). In this sense, the literature has not yet proposed a theoretical reflection that integrates inclusive principles for generic teaching and learning processes—such as Universal Design for Learning—with specific principles for mathematical teaching and learning processes—such as Didactic Suitability Criteria—in order to generate an integrated proposal between both references that enriches the teaching reflection on practice. On the other hand, there are studies (for example, Onoiu & Belletich, 2024; Sánchez et al., 2025; Sánchez-Serrano, 2022; among others) that report both the difficulties in implementing inclusive education in the classroom, as well as the lack of training of teachers to carry out this task. This is how, through teaching reflection on practice, the tool proposed in this article aims to meet this demand, taking into consideration that its usefulness is intended for both prospective and practising mathematics teachers.

2. Theoretical References

In this section, the two references considered for this research are explained, namely, Universal Design for Learning and Didactic Suitability Criteria.

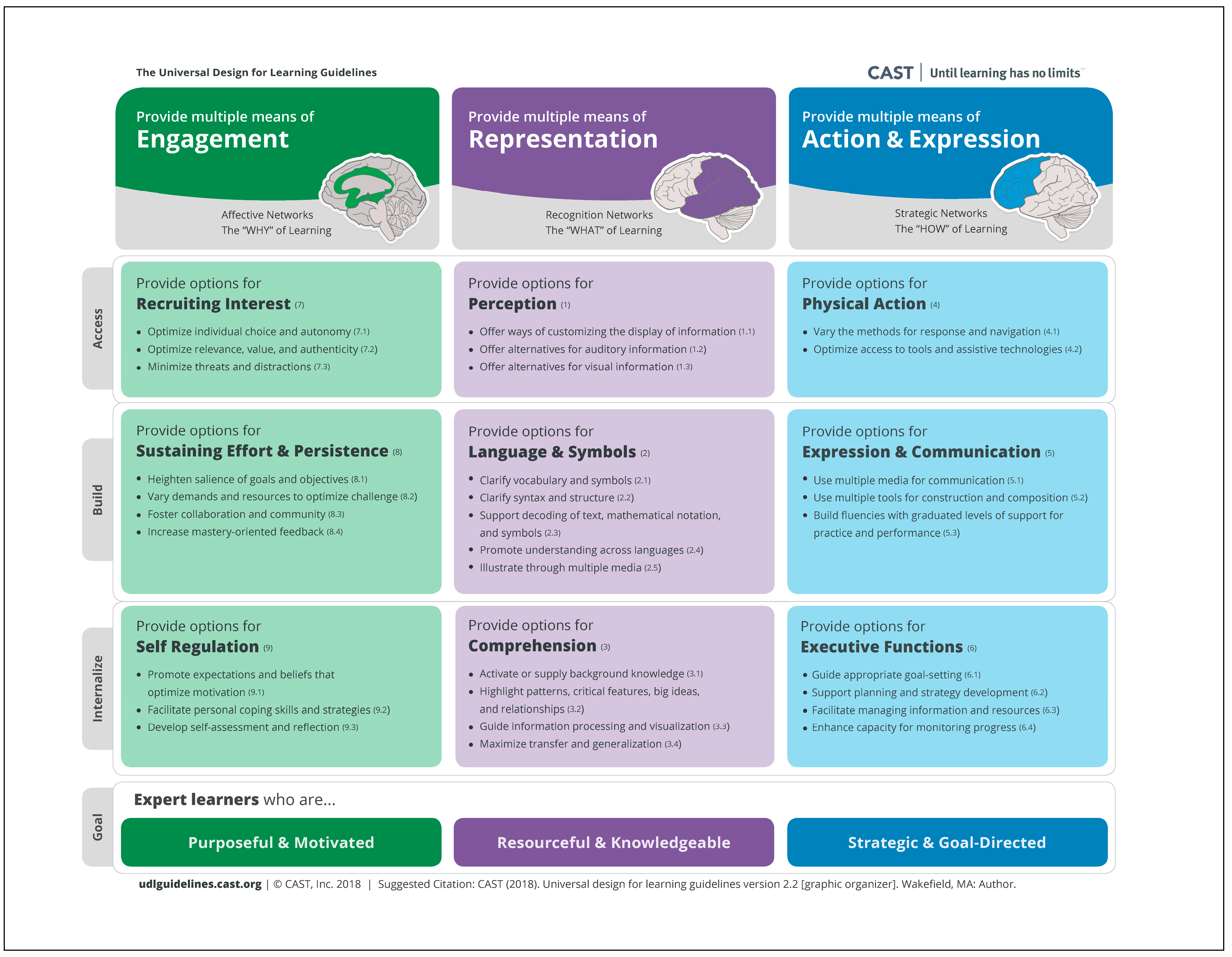
2.1. Universal Design for Learning

Universal Design for Learning (UDL) is understood as a practical framework based on educational research that allows teachers to respond to the individuals’ learning differences through the design of inclusive goals, methodologies, didactic resources, assessments, and environments (Gordon, 2024). Thus, in order to offer inclusive education, UDL is based on the following three principles (CAST, 2018a):

• Provide multiple means of engagement.
• Provide multiple means of representation.
• Provide multiple means of action and expression.

The first principle addresses affective aspects, such as motivation, self-perception, personal interests, or expectations, which have an important weight in the learning process and differ for each student. For this reason, UDL considers the following two dimensions of engagement (Alba-Pastor, 2018): an external dimension, which takes into consideration interest, effort, threats or distractions, levels of challenge and incorporation of supports, and feedback; and an internal dimension, associated with the development of metacognitive capacities and personal strategies that allow the student to self-evaluate.

The second principle addresses the diversity of ways in which people perceive and understand information. Experience and prior knowledge, the capacity to recognise main ideas, to construct new knowledge, or to apply it to new situations are unique to each student. In order for everyone to have adequate access to knowledge, UDL proposes offering multiple means of representation.

The third principle recognises the variability of learning styles of students, who interact with information in different ways to interpret it and construct new knowledge. It is also essential that they have a variety of options to communicate what they have learned. This last principle also includes the development of executive functions that allow for establishing long-term goals, developing strategies to achieve these goals, and monitoring progress.

From CAST (an acronym derived from Center for Applied Special Technology) in the United States, the UDL principles have been specified in a series of guidelines with their corresponding verification points that show examples of how to put these principles into practice. In turn, these guidelines are updated periodically through consultation processes and taking into consideration the findings of educational research (CAST, 2018a). Figure 1 presents version 2.2 of the UDL guideline, which was current in the context in which this study was conducted.

The original document by CAST (2018a) has been translated into several languages from English, and its different versions can be found at https://udlguidelines.cast.org/more/downloads (accessed on 10 January 2025).

2.2. Didactic Suitability Criteria

According to Godino et al. (2019), Mathematics Education, as a scientific and technological discipline, must address the following different types of problems:

• Epistemological problem.
• Ontological problem.
• Semiotic–cognitive problem.
• Educational–instructional problem.
• Ecological problem.
• Problem of teacher education.
• Problem of instruction optimisation.

To address this last problem, the Onto-Semiotic Approach proposes the notion of didactic suitability (Godino, 2013), derived from a consensual perspective on the principles of Mathematics Education that are broadly accepted by the educational community to guide mathematical teaching and learning processes. In this theoretical framework, the notion of didactic suitability is defined as follows:

the degree to which the process (or a part of the same) has certain characteristics considered as optimal or adequate for succeeding in the adaptation between the students’ personal meanings (learning) and the institutional meanings (teaching), taking into account the circumstances and available resources (environment).

(Godino et al., 2019)

The notion of didactic suitability is made concrete in a multidimensional construct Didactic Suitability Criteria (DSC), which considers six aspects (facets) intervening in a mathematical teaching and learning process.

Table 1. Didactic suitability criteria and their components.

Criteria	Description	Components
Epistemic	To assess whether the mathematics taught is ‘good mathematics’.	– Errors. – Ambiguities. – Richness of processes. – Representativeness of the complexity of the mathematical object.
Cognitive	To assess, before starting the teaching and learning process, whether what is intended to be taught is at a reasonable distance of what students know and, after the process, whether the achieved learning is close to what was intended to be taught.	– Prior knowledge. – Curricular adaptation to individual differences. – Learning. – High cognitive demand.
Interactional	To assess whether interaction has solved students’ doubts and difficulties.	– Teacher–student interaction. – Student interaction. – Autonomy. – Formative evaluation.
Mediational	To assess the adequacy of material and temporal resources used in the teaching and learning process.	– Material resources. – Number of students, schedule and classroom conditions. – Time.
Affective	To assess the students’ implication (interest, motivation) in the teaching and learning process.	– Interests and needs. – Attitudes. – Emotions.
Ecological	To assess the adequacy of the teaching and learning process to the educational project of the centre, curricular guidelines, conditions of the social and professional environment, etc.	– Adaptation to curriculum. – Intra- and interdisciplinary connections. – Social and labour usefulness. – Didactic innovation.

Source: Adapted from Breda et al. (2017) and Font et al. (2010, p. 102).

presents the DSC components based on the guideline proposed by Breda et al. (2017) and that allow this construct to be operational.

In turn, each of the DSC components has a set of observable indicators to assess the degree of didactic suitability of a mathematical teaching and learning process. As an example,

Table 2. Components and indicators of the epistemic criterion.

Components	Indicators
Errors	– Mathematically incorrect practices are not observed.
Ambiguities	– Ambiguities that could confuse students are not observed. – Definitions and procedures are clear and correctly expressed and adapted to the target educational level. – Explanations, evidence, and proofs are suitable for the target educational level. – The use of metaphors is controlled.
Richness of processes	– Relevant processes of mathematical activity (modelling, argumentation, problem solving, connections, etc.) are considered in the sequence of tasks.
Representativeness of the complexity of the mathematical object	– The partial meanings (definitions, properties, procedures, etc.) are a representative sample of the complexity of the mathematical notion chosen to be taught (as part of curriculum). – For one or more partial meanings, a representative sample of problems is provided. – Different modes of expression (verbal, graphical, symbolic, etc.) are used and treatments and conversions among them are made.

Source: Adapted from Breda et al. (2017, p. 1903).

presents the components and indicators of the epistemic criterion.

The discourse underlying the construction of DSC is located between two extreme positions. On one side, an objectivist/positivist position, which considers that research in Mathematics Education is capable of offering teachers “practices that work”, since there are objective data (evidence) that support them. According to researchers associated with this position, there are practices that are empirically validated—objectively—by quantitative methods that guarantee the control and verification of results. On the other side, a consensual position which, while believing that considering the results of research in Mathematics Education is important, also believes that improvements in mathematical teaching and learning processes must emanate from the argumentative discourse of the educational community as a whole (researchers, teachers, administrators, parents, etc.) when seeking to reach a consensus on “what can be considered better”. According to individuals associated with this position, principles must be agreed upon that can serve, firstly, to guide mathematical teaching and learning processes and, secondly, to assess their implementations.

Having said that, DSC are structured in a guideline—with criteria, components, and indicators—which allows (prospective and practising) mathematics teachers to organise reflection on their practice and, in this way, to guide a redesign for improvement. In general terms, DSC are a construct based on the principles and standards of the National Council of Teachers of Mathematics (National Council of Teachers of Mathematics, 2000), and which have been adopting the trends and results of research in Mathematics Education (Godino et al., 2023). However, DSC are not teaching guides to shape mathematical teaching and learning processes or to guide their actions and decisions like curricular materials do (Remillard, 2018). On the contrary, DSC are considered norms that act as principles and not as rules, since they do not operate in an exhaustive manner (they are applied or not applied, followed or not followed), since suitability can be understood as quality relativised and conditioned by the teacher’s context and judgement (Breda et al., 2018). Therefore, in the context of this research, DSC play a role in being guiding principles of Mathematics Education.

DSC are widely used as a theoretical–methodological tool for different purposes. Firstly, to analyse mathematical teaching and learning processes designed, implemented, and redesigned by teachers with the aim of achieving an improvement in the teaching of mathematics (for example, see Breda, 2020; Morales-López & Araya-Román, 2020; Morales-Maure et al., 2025; among others). Secondly, to systematically structure the teachers’ reflection in initial or continuing education programmes on the complexity of the mathematical objects they teach, and the factors involved in their study (for example, see Esqué & Breda, 2021; García-Marimón et al., 2021; Giacomone et al., 2018; among others). Finally, to analyse and assess the lessons included in textbooks (for example, see Burgos et al., 2020). The above has led to DSC being a construct that enjoys consensual acceptance in the research community in Mathematics Education (Breda et al., 2018), as well as other constructs that seek to guide teaching practice so that it is of quality. However, these compilations are only lists of criteria that are situated in a certain historical and cultural context, outside of which they may not generate consensus.

3. Methodology

As mentioned in the Introduction, the research reported in this article aims to develop a theoretical reflection on the relationships and complementarities between the UDL and DSC guidelines. In this section, the methodological aspects of this research are described.

3.1. Document Analysis and Theoretical Reflection

With the objective of developing a theoretical reflection on the relationships and complementarities between the UDL and DSC guidelines, firstly, a document analysis (Bowen, 2009) of literature about UDL was conducted, establishing as the main reference the document of guidelines proposed by CAST (2018a). The choice of this document is justified by the fact that it was the current reference version on UDL at the time of developing this theoretical reflection. This led to considering, as a starting point, UDL as guiding principles for generic teaching and learning processes, and DSC as guiding principles for mathematical teaching and learning processes.

Secondly, the UDL guideline was contrasted with that of DSC, according to the proposal by Breda et al. (2017). To this end, a triangulation was conducted by the authors as follows: firstly, each author related the UDL guideline (at the level of principles and verification points) with the DSC guideline (at the level of components and indicators) looking for complementarities between both; secondly, the relationships established by each author were compared, achieving an agreement percentage of 95% among the three; finally, the differences were discussed and a consensus was achieved, due to the authors’ experience in this type of analysis. In this way, a first proposal of the DSC guideline was designed, integrating the UDL guideline.

Finally, an expert validation was conducted in the seminars developed by the research group in charge of this project, where this guideline was shared with other researchers in Mathematics Education (affiliated with the Department of Language, Science, and Mathematics Education from the Faculty of Education of the University of Barcelona, Spain), who are familiar with DSC and have worked with this construct previously. This final validation implied some minor adjustments to the first proposal of guideline designed by the authors, specifically, regarding the refinement of some indicators of the original DSC guideline that were expanded and/or modified by the incorporation of UDL principles. Below, some examples of indicators that underwent minor modifications (highlighted in italics) during the expert validation are presented:

• Original indicator: “For one or more partial meanings, a representative sample of problems is provided. The use of different modes of expression (verbal, graphic, symbolic…), treatments and conversions amongst students are part of one or more of the constituents of partial sense” (Breda et al., 2017, p. 1903).
• Modified indicator: For one or more partial meanings, a representative sample of problems is provided; different modes of expression (verbal, graphical, symbolic, etc.) are used and treatments and conversions among them are made.
• Indicator proposed in the first version of the DSC-UDL guideline: To promote collaboration and communication through heterogeneous groups.
• Modified indicator: Collaboration and communication are promoted through heterogeneous groups.
• Indicator proposed in the first version of the DSC-UDL guideline: Different types of learning assessment are taken into account (initial, self-assessment, formative, and summative).
• Modified indicator: Different types of learning assessment are considered (initial, self-assessment, formative, and summative).

The results of this integrated proposal are presented in Section 4.

3.2. Research Context

In general terms, this research is framed within a project about the incorporation of UDL in the reflection of prospective secondary and baccalaureate education mathematics teachers on their teaching practice, who only use the DSC guideline to this end. The study field was the Interuniversity Master’s Programme in Teacher Training for Compulsory Secondary and Baccalaureate Education, Vocational Training, and Language Teaching (specialising in mathematics), which is taught by the public universities of Catalonia (Spain), during the 2023–2024 academic year. The entry profile for this master’s programme is made up of professionals from different fields of knowledge related to mathematics (mathematicians, engineers, architects, economists, etc.), who are interested in teaching at the school level.

The aim of this master’s programme is to provide initial professional training that gives prospective teachers the tools and knowledge to teach mathematics and to act as educators in the exercise of the tutoring function. The study plan of this programme is organised into the following modules:

• Complements of disciplinary training in mathematics.
• Teaching and learning of mathematics.
• Educational–psychological and social training.
• Innovation and introduction to research in mathematics education.
• Educational internships.
• Master’s degree final project.

In the “Innovation and introduction to research in mathematics education” module, the focus is on reflection on teaching and learning processes as a key element for introducing innovations that improve teaching practice. At the same time, the prospective teachers are provided with tools for planning, managing, and improving these teaching and learning processes. This module is made up of the following three blocks:

• Material resources and technologies for learning and knowledge in mathematics education.
• Evaluation.
• Introduction to research.

In this last block, the prospective teachers are introduced to the notion of didactic suitability, and they are taught to use the complete DSC guideline (with criteria, components, and indicators) based on the proposal by Breda et al. (2017). A particularity of this block during the 2023–2024 academic year is that, as part of the training cycle for teaching DSC (see further details in the following subsection), the UDL principles and the integrated guideline between both references were also presented. In this way, the prospective teachers had this new tool to be able to reflect on their practice by incorporating the UDL principles.

3.3. Structure of a Training Cycle for Teaching the Integrated DSC-UDL Guideline

In this subsection, the structure of a training cycle to teach the prospective teachers in the master’s programme how to use the DSC guideline integrating that of UDL is briefly explained. This training cycle is developed during the “Introduction to research” block and is guided by the professor in charge of the block (in this case, the third author of this article). This cycle has a total duration of five class sessions of two hours each and was attended by 88 prospective teachers enrolled in this master’s programme during the 2022–2023 academic year. This training cycle consists of eight steps described in the following paragraphs.

In a first step, the professor in charge of the block presents different classroom episodes to the prospective teachers and asks them—organised in working groups—to analyse these episodes based on their prior knowledge, beliefs, and values, but without being given any guideline. From their evaluative comments on these episodes, which each working group presents to the rest of the class group, the criteria that, in their opinion, should guide the teacher’s practice can be inferred. Having said that, the aim of this step is not to assess the prospective teachers’ prior knowledge, beliefs, and values, but rather to use their evaluative comments as a basis for inferring their criteria and developing the discussion in the next step. For example, if the prospective teachers comment that, in a certain classroom episode, the students were not motivated, it can be inferred that they consider it important to motivate their students and that, in addition, they value this action positively.

In a second step, the professor in charge of the block guides a discussion about whether these criteria are based on individual values (of the prospective teachers) or moral values (transmitted by the community interested in Mathematics Education). In this type of discussion, the following phenomenon has been made evident (Breda et al., 2018): first, (prospective or practising) mathematics teachers use certain criteria on how lessons should be taught so that they are of quality, increasingly better, etc., that is, criteria that guide teaching practice; second, these criteria are similar even when the characteristics of the teachers are different (in cultural, social, religious, educational terms, etc.), that is, criteria that enjoy a certain consensus in a significant part of the Mathematics Education community; finally, these criteria are related to current trends in the teaching of mathematics, and therefore, they are related to the results of research in and the theoretical constructs of Mathematics Education. In this second step, time is also devoted to explaining these current trends, such as the contextualised presentation of mathematical content, the incorporation of technologies in the classroom, among others.

In a third step, after having observed the phenomenon described in the second step, there is another discussion about how to determine the quality of a mathematical teaching and learning process through the following questions raised by the professor in charge of the block: What criteria should be used to design and redesign learning situations so that they become increasingly better? What role does Mathematics Education play in generating these criteria? To address these questions, reference is made to the two extreme positions between which the discourse underlying the construction of DSC is located, that is, the objectivist/positivist position and the consensual position (see Section 2.2).

In a fourth step, in line with the consensual position, the professor in charge of the block asks the prospective teachers to firstly establish a consensus in their working groups on the criteria that must be considered for a mathematical teaching and learning process to be qualified as ‘good’, ‘of quality’, ‘suitable’, etc., and, after that, to reach a consensus with the rest of the class group.

In a fifth step, there is a comment about, in Mathematics Education, various researchers have proposed compilations of principles or criteria that seek to guide teaching practice so that it is of quality (for example, National Council of Teachers of Mathematics, 2000; Praetorius & Charalambous, 2018; Prediger et al., 2022; among others), one of which is the DSC construct.

In a sixth step, the professor in charge of the block presents the notion of didactic suitability to the prospective teachers and explains DSC to them, which leads to a reflection on the relationship between the consensus established by the prospective teachers during the fourth step of this training cycle and their reinterpretation in terms of DSC. In this type of reflection, the phenomenon made evident in the second step of this training cycle can be refined with the following consideration (Breda et al., 2018): the criteria used by (prospective or practising) mathematics teachers to guide teaching practice can be reinterpreted in terms of DSC, even before knowing this construct.

In a seventh step, DSC are made operational through their components and indicators, using the guideline proposed by Breda et al. (2017), which, in turn, is an adaptation of the guideline designed by Godino (2013) to be used in training processes of secondary education mathematics teachers. Through different tasks, the working groups of prospective teachers agree on different components and indicators of the criteria, which fit easily with the guideline proposed by Breda et al. (2017). In this way, the aim is to generate a rubric—with criteria, components, and indicators—that helps the prospective teachers assess their teaching practice and guide the redesign of their learning situations. Since the teaching and learning process of the complete DSC guideline is the most important part of this training cycle, as well as being the one that takes the most time, a more detailed description of this step can be found in Llinares et al. (2022).

Finally, in an eighth step, the professor in charge of the block explains to the prospective teachers that UDL is a model that provides a frame of reference for the creation of learning contexts in which multiple means of engagement, representation, and action and expression are provided. He also comments that the universal aspect of UDL does not mean a solution for all students, but rather raises the need to design, from the beginning, activities, tasks, and flexible and personalised content according to the context of each classroom. UDL starts from assuming that people are different in the way they manage, contextualise, and express themselves, which is why a model is needed that allows for a multiplicity of options so that everyone can find their own learning path. Basically, this is a masterful explanation based on what is described in Section 2.1. of this article. This step ends with the presentation of the integrated DSC-UDL guideline as a tool for the prospective teachers to reflect on their teaching practice. Since the teaching and learning process of the complete DSC guideline is made in the seventh step of this training cycle, in the eighth step only the differences between the original guideline and the integrated DSC-UDL guideline are highlighted.

Although the training cycle for the teaching of the integrated DSC-UDL guideline described in this subsection ends in the eighth step, this cycle is linked to another developed in the “Master’s degree final project” module, where the prospective teachers apply this guideline to structure the reflection on the teaching practice carried out during the educational internship period. In this module, the tutor professors of the master’s programme are involved, who are around 30 (depending on the number of master’s students in each academic year) and, in addition to supervising the prospective teachers’ internship experiences in educational centres, are responsible for guiding the preparation of their master’s degree final projects (see a more detailed description of these documents in Ledezma et al., 2024).

4. Results

In this section, the proposal of integration of the UDL and DSC guidelines is presented, explaining the modifications or considerations made when analysing the components and indicators of each criterion. The complete DSC-UDL guideline is presented in Appendix A.

4.1. Epistemic Criterion

As stated above, the UDL guideline is presented as a transversal tool and not specific to Mathematics Education, and, in terms of this study, it is considered as guiding principles for generic teaching and learning processes. Regarding the description of the epistemic criterion, Table 1 states that this criterion is used to assess whether the mathematics being taught is ‘of quality’, so that the integration of the UDL guideline would not affect the statement of the epistemic criterion in the sense of adding new components or refining any of its indicators.

Having said that, verification points 2.1 (Clarify vocabulary and symbols) and 2.2 (Clarify syntax and structure) in Figure 1 can be related to the indicators of the Ambiguities component (see Table 2), since these verification points refer, for example, to situations in which the teacher explains the mathematical notation used or makes explicit the algebraic properties used to obtain a certain expression, which helps to avoid ambiguities in the presentation of contents. In the same way, verification point 2.3 (Support decoding of text, mathematical notation, and symbols) in Figure 1 can be related to one of the indicators of the Representativeness of the complexity of the mathematical object component (see Table 2), where the use of different languages to represent mathematical objects is stressed.

Therefore, the integration of the UDL guideline into the components and indicators of the epistemic criterion would not entail any change.

4.2. Cognitive Criterion

UDL assumes as a principle that students are diverse and, therefore, the planning of activities must contemplate different options for understanding (Indication 3: Provide options for comprehension). Within the cognitive criterion is the Curricular adaptation to individual differences component (see Table 1), whose indicator states that extension and support activities are included, so that the integration of the UDL guideline would entail, among others, the modification of this component, understanding that an adaptation is not made for certain students, but, from the beginning, alternatives are offered with activities that are sufficiently open to all. More specifically, this component is more closely related to the Differentiated Instruction approach (Tomlinson, 2000) than to UDL (see further discussion on this matter in Griful-Freixenet et al., 2020).

Having said that, in order to ensure that all students become expert learners, the UDL guideline suggests the use of tools that allow them to be aware of their learning, set personal goals, and continuously monitor their achievements.

Table 3. Components and indicators of the cognitive criterion integrating UDL.

Components	Indicators
Prior knowledge	– Students have the necessary prior knowledge to study the topic (they have been previously studied, or the teacher plans their study) and this prior knowledge is activated when necessary. – The intended meanings can be taught (reasonable difficulty) through their diverse components.
Consideration of individual differences 1	– Supports for students who need them and greater freedom for students who can do the task independently are provided (for example, setting challenges that allow for different levels of success; providing extension and support activities, and more or less guided activities; using concept maps; providing templates for notetaking). 2 – Collaboration and communication are promoted through heterogeneous groups.
Learning	– The diverse methods of assessment demonstrate the appropriation of intended or implemented knowledge/competences (evidence of learning). – Different types of learning assessment are considered (initial, self-assessment, formative, and summative). – Students are provided with instruments for self-assessment. – Different modes of expression are provided to demonstrate their learning.
High cognitive demand to promote meaningful understanding	– Relevant cognitive processes are activated (generalisation, intra-mathematical connections, changes in representation, conjectures, etc.). – Metacognitive processes that facilitate self-regulation are promoted.

^1. Curricular adaptation to individual differences (original component). ² Extension and support activities are included (original indicator). Source: Adapted from Breda et al. (2017, p. 1904) with modifications by the authors.

presents the components and indicators of the cognitive criterion with the proposed modifications highlighted in bold.

4.3. Interactional Criterion

In the UDL guideline, there are various verification points that refer to interactional aspects, both between students—verification point 8.3: Foster collaboration and community, in Figure 1—and between the teacher and students. Regarding the description of the interactional criterion, Table 1 states that this criterion is used to assess whether interaction in a mathematical teaching and learning process can resolve students’ doubts and difficulties, so the integration of the UDL guideline, in addition to having a close relationship with the DSC guideline, would have effects on the addition and refinement of some of its indicators.

Having said that, from the moment the teacher plans a teaching and learning process, he or she is considering students’ reactions, who may need a certain type of support or another, and how he or she will evaluate each student’s progress—verification points 5.3: Build fluencies with graduated levels of support for practice and performance; 6.4: Enhance capacity for monitoring progress; and 8.4: Increase mastery-oriented feedback, in Figure 1. In order to enable students to increase their autonomy during a teaching and learning process, it is necessary to guide the establishment of goals and the development of personal strategies—verification points 6.1: Guide appropriate goal setting; 6.2: Support planning and strategy development; and 8.1: Heighten salience of goals and objectives in Figure 1.

Table 4. Components and indicators of the interactional criterion integrating UDL.

Components	Indicators
Teacher–student interaction	– The teacher appropriately presents the topic (clear and well-organised presentation, not speaking too fast, emphasis on the key concepts of the topic, etc.). – Students’ conflicts of meaning are recognised and resolved (students’ silence, facial expressions, questions are correctly interpreted, an appropriate questions-and-answers game is conducted, etc.). – The aim is to reach a consensus based on the best argument. – Different rhetorical and rational resources are used to involve the students and catch their attention. – The inclusion of students into the classroom dynamics is facilitated—exclusion is not.
Student interaction	– Dialogue and communication among students are encouraged (for example, peer tutoring). – Inclusion in the group is favoured, and exclusion is discouraged. – In group work, objectives, roles, responsibilities, and rules are clearly established.
Autonomy	– Moments in which students take on the responsibility for their study (exploration, formulation, and validation) are considered. – Gradual support is offered to enable each student to advance in developing their skills, defining objectives, and developing strategies to achieve them.
Formative evaluation	– Systematic observation of the students’ cognitive progress. – Progress feedback that is informative, accessible, and explicit to students is regularly provided, highlighting effort and perseverance.

Source: Adapted from Breda et al. (2017, p. 1904) with modifications by the authors.

presents the components and indicators of the interactional criterion with the proposed modifications highlighted in bold.

4.4. Mediational Criterion

In the UDL guideline, there are also various verification points that refer to mediational aspects, due to the principles of providing multiple means of representation—especially, Indications 1: Provide options for perception and 2: Provide options for language and symbols—and providing multiple means of action and expression—especially, Indications 4: Provide options for physical action and 5: Provide options for expression and communication. Regarding the description of the mediational criterion, Table 1 states that this criterion is used to assess whether the material and temporal resources used in a mathematical teaching and learning process are adequate, so the integration of the UDL guideline, in addition to having a close relationship with the DSC guideline, would also have effects on the addition and refinement of some of its indicators.

Having said that, the use of resources (for example, certain digital tools) can be key to putting these UDL principles into practice. Time management should also be reconsidered, making the deadlines for carrying out an activity more flexible.

Table 5. Components and indicators of the mediational criterion integrating UDL.

Components	Indicators
Material resources (manipulative resources, calculators, computers, texts, and worksheets)	– Use of manipulative and technological resources that allow the introduction of good situations, languages, procedures, and arguments adapted to the intended meaning. – Definitions and properties are contextualised and motivated by using concrete situations, models, and visualisations. – The materials are accessible (use of recommended colours and fonts, assistants for creating tables of contents that allow practical navigation and description of images, automatic translators, etc.). – Different information channels are used.
Number of students, schedule and classroom conditions	– The number and distribution of students enable the intended teaching to be carried out. – The schedule of the course is appropriate (for example, not all the lessons are held at the last period). – The classroom and the distribution of students are appropriate for the development of the intended teaching and learning process.
Time (for group teaching/tutoring, time for learning)	– Adequacy of the intended/implemented meanings to the available time (contact or non-contact hours). – Time dedication to the most important or central contents of the topic. – Time dedication to the most difficult contents and deadlines for completing tasks are made more flexible when necessary.

Source: Adapted from Breda et al. (2017, p. 1905) with modifications by the authors.

presents the components and indicators of the mediational criterion with the proposed modifications highlighted in bold.

4.5. Affective Criterion

In the UDL guideline, a close relationship was found between the principle of providing multiple means of engagement and the description of the affective criterion, since Table 1 states that this criterion is used to assess the student’s implication in the teaching and learning process. The UDL guideline suggests increasing students’ motivation in the teaching and learning process by making them perceive that what they learn enables them to achieve their goals and interests—verification points 7.2: Optimise relevance, value, and authenticity; 9.1: Promote expectations and beliefs that optimise motivation; and 9.2: Facilitate personal coping skills and strategies, in Figure 1. These aspects are also covered by the Interests and needs and Emotions components of the affective criterion.

Having said that, what may be motivating for some may be a distraction or cause insecurity for others. In this situation, verification point 7.3 refers to minimising the feeling of insecurity and distractions by varying the levels of sensory stimulation, among other measures, which would have effects on the addition and refinement of the indicators of the Attitudes component.

Table 6. Components and indicators of the affective criterion integrating UDL.

Components	Indicators
Interests and needs	– Selection of interesting tasks for the students. – Proposition of situations that enable students to assess the utility of mathematics in everyday and professional life.
Attitudes	– Promotion of the implication in activities, perseverance, responsibility, etc., explicitly recognising effort. – Distractions are reduced. – Argumentation in situations of equity is favoured; argument is valued in its own right and not by the person who says it.
Emotions	– Promotion of self-esteem, avoiding rejection, phobia, or fear of mathematics. – Aesthetic qualities and precision of mathematics are emphasised.

Source: Adapted from Breda et al. (2017, p. 1905) with modifications by the authors.

presents the components and indicators of the affective criterion with the proposed modifications highlighted in bold.

4.6. Ecological Criterion

The transversal nature of the UDL guideline presents a close relationship between its three principles and the description of the ecological criterion, since Table 1 states that this criterion is used to assess the adequacy of the teaching and learning processes to the environment that transcends the educational field. More specifically, the Adaptation to curriculum and Didactic innovation components would motivate the application of UDL in teaching practice. On the other hand, the Intra- and interdisciplinary connections and Social and labour usefulness components could be related to students’ motivation, as indicated by the example of verification point 7.2, which has already been considered as part of the affective criterion (see Table 6).

Table 7. Components and indicators of the ecological criterion.

Components	Indicators
Adaptation to curriculum	– Contents, their implementation and assessment, correspond to the curricular guidelines.
Intra- and interdisciplinary connections	– Contents are related to other mathematical contents (connection of advanced mathematics with curricular mathematics and connection among different mathematical contents covered in the curriculum), or to contents of other disciplines (extra-mathematical context or to contents of other subjects from the educational stage).
Social and labour usefulness	– Contents are useful for social and labour insertion.
Didactic innovation	– Innovation based on research and reflective practice (introduction of new contents, technological resources, methods of assessment, classroom organisation, etc.).

Source: Adapted from Breda et al. (2017, p. 1905).

presents the components and indicators of the ecological criterion, where the integration of the UDL guideline would not entail any change.

5. Discussion and Conclusions

In this section, the results of the DSC-UDL integration are discussed, and the conclusions of this research are presented. The integrated proposal presented in this article not only intends to address the current curricular demands mentioned at the beginning of this article, providing a tool that includes the UDL principles from an operational point of view, but it also intends to facilitate reflection on teaching practice of both prospective and practising mathematics teachers in their lessons of this subject, considering the aspects that intervene in a teaching and learning process from a broader perspective that addresses the student diversity. Therefore, the scope of this tool is not limited to personal reflection, but also to the training processes that use DSC for Lesson Study and argumentative reflection (see an example in Sol et al., 2024).

Although the proposal presented in this article is innovative within the framework of research with the DSC construct, other types of proposals have also been reported in the literature that seek to incorporate UDL in mathematics classroom (for example, Novak & Marlow, 2024). The main difference with other proposals is that, in this work, an integration is made between a construct to improve the quality of mathematics lessons (DSC) and the UDL principles, while other proposals seek to concretise UDL in mathematics lessons (see Gartland et al., 2025). In other words, the main principle guiding UDL is that all students learn, from which the three principles presented in Figure 1 emerge; however, in terms of the Theory of Didactic Suitability (Godino et al., 2023), this situation can be reinterpreted as the definition of the cognitive criterion. Having said that, in the integrated DSC-UDL guideline, while the cognitive criterion is important, it is not the only one that teachers should consider, since it is not only about achieving universal learning, but also ensuring that this learning includes a mathematics of quality.

Now, as Alba-Pastor (2018) points out, the application of UDL principles has a more global approach that involves not only the school, but the entire educational system. Likewise, to respond to this need—both initial and continuing—teacher education programmes must develop inclusive teaching as part of the teachers’ professional competences (UNESCO, 2005, 2015), in order to reduce (or eliminate) barriers and limitations to carrying out this task (González-Ramírez et al., 2025; Peinado, 2025), which is where this proposal aims to contribute.

Resuming the research question posed in this article on what relationships and complementarities can be established between the UDL and DSC guidelines, three aspects can be mainly concluded.

Firstly, both references act as guiding principles for the teaching and learning processes, that is, they offer a consensual view of the elements to be considered in the different stages of the didactic design (preliminary study, planning, implementation, and assessment). However, while UDL act as a set of guiding principles for generic teaching and learning processes (of a transversal nature), DSC do so for mathematical teaching and learning processes (of a specific nature).

Secondly, given the transversal nature of UDL and the specific nature of DSC, there were two criteria of the latter reference that did not undergo modifications. On one hand, the epistemic criterion, whose purpose is to assess the quality of the mathematical content that is taught (or intended to be taught) in the classroom, and which already considers some indications based on UDL, such as: a) the clear use of vocabulary, symbols, syntaxis, and writing in its Ambiguities component; and b) the use of different languages to represent mathematical objects in its Representativeness of the complexity of the mathematical object component. On the other hand, the ecological criterion, whose purpose is to assess the adequacy of the teaching and learning processes to the environment that transcends the educational field, and which already considers some indications based on UDL in its four components.

Finally, the cognitive, interactional, mediational, and affective criteria were those that underwent modifications, which resulted not only in the adaptation of some of their components, but also in the expansion of some of the indicators of these components. These modifications were especially related to the assessment of student learning, their self-regulation, and the variability and accessibility of resources.

It should be noted that the integrated proposal presented in this article is a first version developed by the authors within the framework of a project about the incorporation of UDL in the reflection of prospective secondary and baccalaureate education mathematics teachers on their teaching practice, who only use DSC to this end. Therefore, this integrated DSC-UDL guideline is open to possible modifications as this research project progresses, with the contribution of both researchers in Mathematics Education and secondary and baccalaureate education teachers or other education professionals. Likewise, the update of the document of guidelines proposed by CAST (2024) is taken into consideration. However, the results of this research are considered relevant to provide a first integrated proposal between the UDL and DSC guidelines. The complete DSC-UDL guideline resulting of this research is presented in Appendix A.