Abstract
This paper presents research on the origin, scope, evolution, and rationale of knowledge about polynomials in high school mathematics. Within the framework of the Anthropological Theory of the Didactic, Croatian high school curricula and textbooks were analyzed, and four models of knowledge to be taught were identified in the period following the formal abandonment of New Math principles. None of the identified models provides a unified discourse that integrates knowledge about polynomials transposed from scholarly domains of algebra and mathematical analysis. In relation to other curricular content the knowledge about polynomials has two-fold importance: (1) contributing to the development of various techniques related to high school algebra and calculus; (2) serving as a fundamental example in the formation of the notion of a function. Thus, the observed reduction in polynomial content over the analyzed period affects both practical and theoretical knowledge. The findings suggest that curricular changes have primarily focused on the selection of knowledge, with scarce adaptations of knowledge to be taught compared to the knowledge before each curricular change. This has led to a persistent gap between algebraic and analytical approaches to polynomials, potentially influencing the learned knowledge even among the highest-achieving students. Despite polynomials’ epistemological and didactical potential to bridge high school algebra and calculus, their restriction to specific forms of algebraic expressions and linear and quadratic functions contributes more to the fragmentation of high school mathematics.
1. Introduction
Research on the transition from high school to undergraduate mathematics studies concerning the notion of a polynomial (Pleština & Milin Šipuš, 2022), highlights the relevance of epistemological inquiry into polynomial-related knowledge in high school mathematics. The fundamental role of polynomials in the discipline of mathematics (Barbeau, 2003; Stillwell, 2010) may induce significance of polynomial-related knowledge in the high school curriculum, as well as their interconnections with other curricular content. However, there is a gap in research directly addressing educational treatment of polynomials (Pleština, 2023). In existing studies, the approach to the polynomials is often not directly addressed, and there is a tendency to focus either on the algebraic or analytical aspects of polynomials, leaving a significant gap in understanding their comprehensive treatment within high school education.
To address this issue, this study undertakes a case analysis of the Croatian high school curriculum and textbooks, focusing on the period following the formal abandonment of New Math principles in Croatia. It examines the hypothesis that the variability in definitions of polynomials in high school education, which Bolondi et al. (2020) observed in primarily algebraic high school textbooks, reflects different approaches to polynomials across different mathematical domains of scholarly knowledge, particularly algebra and mathematical analysis.
The chosen theoretical framework, the Anthropological Theory of the Didactic (ATD), allows for an epistemological analysis of polynomial-related knowledge within the institution of Croatian high school education. The ATD enables addressing the relationship between scholarly knowledge and knowledge to be taught, as well as an examination of what should be taught about polynomials and for what purpose. The knowledge to be taught within the institution of Croatian high school education is delineated by the curriculum, which outlines the content and its organization, and by textbooks, which realize the curriculum. Therefore, both serve as resources for examining how scholarly knowledge is selected and adapted for high school teaching.
Although this study focuses on knowledge to be taught, insights from a questionnaire conducted among students who achieved excellent grades in mathematics and participated in mathematics competitions, who are therefore expected to demonstrate the highest level of learned knowledge, illustrate how epistemological gaps in the knowledge to be taught can constrain learned knowledge. While the sample is small and specific, the fact that constraints are evident even among the most successful students suggests that similar or even greater limitations may affect the learned knowledge by other students in the system.
1.1. Reference Studies
While research specifically focused on polynomials in high school education is relatively scarce, studies indicate that knowledge about polynomials is integrated into high school curricula in various countries.
In the 1980s, Dreyfus and Eisenberg (1990) observed that polynomial-related topics were marginalized in school curricula, a trend likely linked to the abandonment of the New Math in the United States, which subsequently influenced the educational systems of other countries. They argued for the importance of including polynomials and their associated theory in school education, beyond mere equation solving or root finding.
According to Weiss (2020), “polynomials occupy a central role in the secondary curriculum” (p. 76) in the United States as part of algebra, precalculus, and calculus. This curricular position could suggest their potential to serve as a unifying notion, connecting different curricular components.
However, Sultan and Artzt (2018), in a book for high school mathematics teachers, noted that the word “polynomial” is “probably the most misunderstood word in secondary school mathematics” (p. 81). Their observation could suggest that students encounter polynomials through various approaches, yet the relationships between these approaches remain hidden to students.
Adu-Gyamfi et al. (2017) and Llanos et al. (2015) examine polynomials within the precalculus part of the curriculum, while Bolondi et al. (2020) focus on polynomials in high school algebra
Adu-Gyamfi et al. (2017) investigated the understanding of graphical and algebraic representations of polynomials among high school students aged 15–17 in the United States. In their study, the notion of a polynomial encompasses terms like “polynomial relation”, “polynomial function”, “linear function”, “quadratic function”, and “polynomial”, without explicitly addressing their relationships. Llanos et al. (2015) investigated the same topic among students aged 14–17 in Argentina, employing the instructional format of study and research paths, a tool from the ATD. In their study polynomials are approached as functions, and they used terms “polynomial” and “polynomial function”. Both studies primarily focus on polynomials of the first and second degrees (i.e., linear and quadratic functions), yet the reason for this emphasis is not explicitly stated.
Bolondi et al. (2020), in their study on definition schemes, analyzed high school algebra textbooks from Italy, Spain, and North America for students in grades 9–11. They identified various definitions of polynomials based on notions such as “variable, algebraic expression, literal equation, algebraic sum, and monomials” (p. 5).
That the notion of an algebraic expression lacks a functional role in the modelling process is observed by Strømskag and Chevallard (2022) in their analysis of the notion of a formula in Norwegian- and English-language textbooks. They also observe that “we commonly speak of algebraic expressions without specifying what these expressions do express” (p. 392).
These studies highlight multiple aspects of polynomials in high school education, collectively calling for further epistemological investigation into polynomial-related knowledge. In particular, they raise questions about the interconnections and organization of this knowledge, its relationship with other notions in high school mathematics, as well as the notion of a polynomial in scholarly mathematics.
The process of didactic transposition, as a methodological tool within the ATD, enables the identification and analysis of what elements of disciplinary mathematical knowledge are selected and how they are adapted for teaching within a given institution. Strømskag and Chevallard (2022) examined the didactic transposition of algebraic knowledge into curricula and textbooks. Barbé et al. (2005), in their analysis of the transposition of the notion of limits into Spanish high school education, showed that the knowledge to be taught imposes constraints on teachers’ practice and, ultimately, on the learned knowledge.
As the literature review has shown, knowledge about polynomials is embedded within high school algebra, precalculus, and calculus. Therefore, analyzing the didactic transposition of polynomial-related knowledge enables an understanding of high school mathematics both as a whole and in terms of the relationships between its constituent parts. Since the didactic transposition of polynomials in high school education has not yet been addressed, this study aims to fill that gap by examining the case of the didactic transposition of knowledge about polynomials in Croatian high school education.
1.2. What Is a Polynomial in the Discipline of Mathematics?
Polynomials occupy a fundamental position within the discipline of mathematics (Barbeau, 2003; Stillwell, 2010). In algebra, when endowed with standard operations, polynomials have the structure of a ring and a vector space. The ring of polynomials over a field shares key properties with the ring of integers: division with remainder, the Euclidean algorithm, and the existence of greatest common divisors expressible as linear combinations. The notion of an irreducible polynomial generalizes the notion of a prime number, and the Fundamental Theorem of Algebra may be seen as an analogue of the Fundamental Theorem of Arithmetic. Consequently, certain algebraic techniques for solving algebraic equations arise from these properties. Polynomials also exhibit strong connections to number theory through modular arithmetic, Diophantine equations, Fermat’s little theorem, and more advanced topics such as Galois theory. In real and complex analysis, polynomials are continuous, differentiable, smooth, integrable, and analytic functions. They are foundational in approximation theory, where key results include Taylor’s theorem and the Stone–Weierstrass theorem. Polynomials are also of central importance in numerical mathematics, particularly through Horner’s algorithm, polynomial interpolation, and root-finding methods. Due to their geometric interpretability, computational simplicity, and numerical stability of those of degree at most three, polynomials are important for mathematical modeling.
The notion of a polynomial in the discipline of mathematics encompasses two approaches to polynomials, originating from two fundamental domains of mathematics: algebra and mathematical analysis (Markushevich, 1991). In this paper, one perspective on a polynomial is referred to as the formal-algebraic approach and is denoted as , while the second perspective is referred to as the functional approach and denoted by .
In scholarly algebra, a polynomial (over a commutative ring R with unit 1) is a formal expression, i.e., a finite formal sum of powers
where every is an element of the commutative ring , and is a formal variable (indeterminate). The meaning of the formal expression (1) is explained by the following definition (Lang, 2005). Let be the set of sequences , where such that all but finitely many are zero , i.e., sequences of the form are considered. The elements of the set are referred to as polynomials over , and are called the coefficients of the polynomial . Polynomials are added componentwise, and multiplication is performed according to the convolution rule. If the polynomial is denoted with , the polynomials , , can be inductively defined. It can be shown that , that is, the polynomial has the coefficient , and all other coefficients are . Furthermore, the mapping that associates each with the polynomial is an injective ring homomorphism. Since can be identified with , the definition of polynomial multiplication implies that . Finally, the polynomial can be expressed in the standard form (1). Hence, this perspective on a polynomial exemplifies the formal-algebraic approach .
In mathematical analysis, polynomials are real (or complex) functions of one or more real (or complex) variables. To illustrate, for the function defined by
for every , is a real polynomial of one real variable.
The functional approach is also present in the domain of algebra but always in relation to . Assuming that is a subring of a commutative ring , for each polynomial , an induced function is defined by for every (Lang, 2005).
The identification of a polynomial and an induced function is generally not possible. For the finite field (), let us consider polynomials , in the variable over , and their induced functions: defined by , for all , and defined by , for all . In the approach, the notation represents , and represents ; thus, these polynomials are not equal. However, the functions and are equal since and . Although an isomorphism can be established between the ring of polynomials with coefficients from an infinite field and the ring of corresponding induced functions, these are distinct mathematical objects with different meanings for their corresponding notions (variable, equality, operations).
In the cited works on mathematical education, the notion of a polynomial is restricted to polynomials with real (or possibly complex) coefficients, which enables the implicit use of the identification between the and approaches. However, the implicit identification of these approaches, resulting in different mathematical objects, can be particularly delicate for the development of the general notion of the function.
1.3. Theoretical Framework
The ATD is a theoretical framework for research in mathematics education, which highlights the institutional dependency of mathematical and didactic activities (Bosch et al., 2020; Chevallard & Bosch, 2020a). An institution in the ATD is a key term; it refers to any social structure wherein the didactic process unfolds or is facilitated (Chevallard & Bosch, 2020a). For example, research findings by Bolondi et al. (2020) and Sultan and Artzt (2018) indicate the dependence of knowledge about polynomials on the institution of high school textbooks.
The institutional dependency of knowledge is elucidated through the process of didactic transposition (Bosch & Gascón, 2006; Chevallard & Bosch, 2020b), which delineates institutional construction of knowledge into four stages: 1. scholarly knowledge generated within the academic community or by experts; 2. knowledge to be taught determined by the curriculum and textbooks; 3. taught knowledge by teachers within an observed institution; 4. learned knowledge by students. External didactic transposition entails the process of selecting and adapting scholarly knowledge into knowledge to be taught (Bosch & Winsløw, 2020; Bosch et al., 2021), while internal didactic transposition encompasses the remaining steps of didactic transposition that lead to learned knowledge (Chevallard, 1991).
For the analysis and description of knowledge in the process of didactic transposition, the notion of a praxeology is used as the basic unit for analyzing mathematical activities (Barbé et al., 2005). Praxeology is represented by an ordered quadruple , where: is the type of tasks, τ is the technique used to solve a task of type , is the technology that is the discourse of and explains , and is the theory that is a formal argument and thus justifies (Chevallard & Bosch, 2020a). The ordered pair is called a praxis block of praxeology and answers the question of knowing how to solve a task of type . The ordered pair is called the logos block of and answers the question of knowing why the technique can solve a task of type .
For example, the task belongs to the type of task “to solve quadratic equations” and can be solved using the technique of applying the formula for the solutions of a quadratic equation in radicals. The general form of this formula constitutes the technology, while its proof constitutes the theory of the praxeology.
Although all praxeologies include a technological and a theoretical component, scholarly praxeologies are typically characterized by a developed logos. In contrast, didactic transposition often involves the reduction or omission of certain elements of the scholarly logos, particularly the theory. For instance, while proof serves as a central form of justification in scholarly mathematics, it is frequently absent in the knowledge to be taught at the school level. Therefore, analyzing the structure of logos in praxeologies contributes to understanding the epistemic transformations that occur in the adaptation of disciplinary knowledge into school mathematics.
Praxeologies can be unified into new praxeologies (mathematical organizations) with a common technology or theory (Barbé et al., 2005). Praxeology is considered a punctual praxeology if it contains only one type of tasks. Punctual praxeologies that share a common logos block constitute a local praxeology. Local praxeologies that share a common theory constitute a regional praxeology.
The praxeology in which the type of tasks is “to solve quadratic equations” is an example of a punctual praxeology. This praxeology can be unified with another punctual praxeology whose type of task is “to discuss the solutions of a quadratic equation depending on a parameter”, which can be solved using a technique based on the relationship between the discriminant and the roots of the quadratic equation. These punctual praxeologies, which share a common logos block, constitute a local praxeology. If a theory is established regarding the relationship between the roots of a quadratic equation and the zeros of a quadratic function, these praxeologies can be further unified into a regional praxeology on quadratic functions, which may also include types of tasks such as “to draw the graph of a quadratic function”, “to determine the extremum and intervals of monotonicity of a quadratic function”, “to solve quadratic inequalities”, among others.
In the examination of the limit of a function in high school, Barbé et al. (2005) illustrated how the classification of praxeology can reveal the incompleteness and lack of coherence in the knowledge to be taught, imposing significant demands on teachers’ practice. Therefore, external didactic transposition provides insights into the conditions and constraints that shape the learning and teaching processes within the observed institution (Barbé et al., 2005).
During the analysis of the didactic transposition process for a particular object of knowledge, which includes praxeological analysis, the researcher creates, tests, and supplements the epistemological model of that knowledge with respect to reference institutions (Barbé et al., 2005; Chevallard & Bosch, 2020b). This enables an understanding and questioning of the dominant epistemology within the institution (Lucas et al., 2019). While “the epistemological model describes what is to be studied”, “educational ends point out why” (Gascón & Nicolás, 2022, p. 1155). The scholarly knowledge, briefly outlined in Section 1.2, along with the results of research in mathematics education, formed the basis for the development of a reference epistemological model through which the curriculum and textbooks were analyzed in this study.
2. Materials and Methods
2.1. Research Objectives
This paper examines the external didactic transposition of knowledge about polynomials in high school education. It addresses the selection, organization, and evolution of polynomial-related knowledge within high school mathematics, including its coherence and its relation to scholarly knowledge. To investigate these questions in a concrete context, the study takes the case of Croatian high school education between 1994 and 2024 as the object of analysis. The knowledge to be taught about polynomials, as defined by the Croatian curricula and textbooks, has been examined to address the following questions:
- What scholarly knowledge about polynomials has been transposed into high school education and why?
- How do polynomial-related praxeologies develop through high school education? How do they interact with other praxeologies?
- Have there been changes in the knowledge to be taught about polynomials over time, and if so, what are the possible implications of these changes?
2.2. Educational Context, Curricula and Textbook Analysis
After completing eight years of primary education (ages 7–14), Croatian students advance to high school, which includes vocational schools and grammar schools. Grammar school programs, lasting four years and targeting students aged 15–18, prepare students for university education. Due to the importance of polynomials in university education (Pleština & Milin Šipuš, 2022; Pleština, 2023), this study focuses on grammar schools as the reference institution. Grammar school programs can be divided into two groups: those with 3–5 h of mathematics lessons per week and those with 5–7 h per week, with the number of hours potentially varying from one grade to another within the same program. Textbooks are written according to this division. Additionally, Croatian regulations require that textbooks align with curriculum documents.
The analysis of curricula and textbooks has also provided insights into the process of external didactic transposition in Croatia. The curriculum specifies which notions are taught and in what order, but it usually does not detail how each notion is introduced. While the curriculum defines knowledge selection, textbooks provide insight into how the selected knowledge is adapted to be taught (Figure 1).
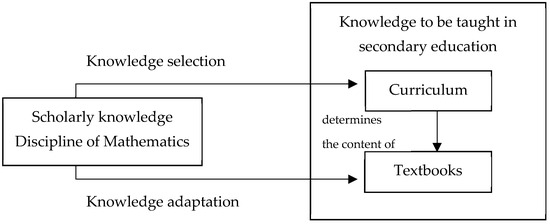
Figure 1.
The process of external didactic transposition in Croatia.
The period under study began in 1994 with the implementation of the curriculum (Ministarstvo Kulture i Prosvjete, 1994) that nominally renounces all the characteristics of the New Math movement (OECD, 1961). This curriculum, with some non-binding recommendations in 2003 (Ministarstvo Znanosti, Obrazovanja i Športa, 2003) and 2011 (Ministarstvo Znanosti, Obrazovanja i Športa, 2011), defined the knowledge to be taught until the reform in 2019 (Ministarstvo Znanosti i Obrazovanja, 2019). In 1994, there was a significant re-conceptualization of textbooks, where the knowledge to be taught was distanced from the more formal approach that had dominated in the previous decades. The non-binding curricular document from 2003 did not significantly influence textbooks regarding knowledge about polynomials, although it may have affected the taught knowledge, as it, along with the 2011 document, indicated a shift towards reducing polynomial content that was fully implemented in the 2019 curriculum.
The analysis of curriculum documents aimed to identify polynomial-related mathematical organizations. However, curriculum documents varied in how informative they were in determining the praxis and logos blocks of the praxeologies that constitute these organizations. The 1994 document included content descriptions, often using scholarly terminology, which determine how praxeologies would be structured in textbooks aligned with this document. In terms of defining praxis blocks, the 1994 document was less informative, as it rarely specified types of tasks and techniques. The subsequent curriculum documents provided more explicit guidance on the types of tasks and techniques. Since the identified mathematical organizations were not fully defined by the curriculum documents, a praxeological analysis of textbooks was necessary.
For each program and for each period (1994–2003, 2003–2011, 2011–2019, 2019–present) defined by the curricular documents, a set of the most frequently used high school textbooks, as identified by the Ministry, was subjected to praxeological analysis. Moreover, the analyzed textbooks constituted the reference literature for the state graduation exam, indicating the aim of ensuring that both taught knowledge and learned knowledge align with the knowledge presented in the textbooks.
Each lesson in the textbook was examined sequentially, following the prescribed curriculum order. Textbooks begin each lesson with theoretical notions, followed by solved examples that clarify these notions. Subsequently, the lesson includes exercises, where only final answers are provided at the end of the textbook. The analysis of each lesson comprised two phases. In the first phase, solved examples and theoretical notions underwent praxeological analysis. Types of tasks and associated techniques (praxis blocks) were identified from the analyzed examples, whereas explanations in the examples and theoretical notions informed technology and theory (the corresponding logos block). In the second phase, the authors of this paper solved tasks using techniques identified in the first phase while seeking to justify these techniques with theoretical knowledge from the textbooks. This process complemented the types of tasks by assessing whether the techniques could be elucidated by theoretical knowledge, essentially examining whether praxis and logos are consistent. By comparing praxeologies, their evolution was examined in relation to the scholarly knowledge presented in the scholarly mathematical literature (Markushevich, 1991; Barbeau, 2003; Stillwell, 2010; Lang, 2005). Figure 2 presents a definition, a solved example, and several tasks related to the division of polynomials, illustrating how the source of data1 was utilized in formulating the praxeologies.

Figure 2.
The scheme of textbook analysis.
The analysis of curricula and textbooks has led to the identification of models of knowledge to be taught about polynomials, differing in the scope of the notion, based on the following criteria: (1) the transposition of the definition of a polynomial, (2) praxeologies about polynomials that constitute these models, and (3) the interaction of praxeologies about polynomials with those concerning other content. The models are presented in Section 3.
2.3. Questionnaire Design and Implementation
Examples of how the knowledge to be taught can impose conditions on the learned knowledge were gathered through a questionnaire conducted with 14 final-year high school students (aged 18) during their preparation for the county-level mathematics competition. Afterwards, they completed their high school education under the curriculum introduced in 2019. Six students were in the 5–7 h per week mathematics program, and eight were in the 3–5 h per week program. Although the sample size was small, the fact that these students achieved excellent grades in mathematics and participated in mathematics competitions suggests that their knowledge should be closest to the targeted institutional knowledge, and perhaps even exceeds it.
Based on a thorough analysis of the curriculum and textbooks, the following questionnaire was designed:
- 1.
- Simplify the expressionExplain the steps you took.
- 2.
- Solve the equationExplain the steps you took.
- 3.
- Sketch the graph of the real function defined byExplain the steps you took.
The aim of the tasks was to examine the activation of knowledge about polynomials, as well as the justifications, within three mathematical organizations: (1) on algebraic expressions, (2) on equations, (3) on functions.
In all three tasks, the polynomials and appear. The roots of these polynomials are not easy to determine, making it difficult to factor each of them into linear and quadratic polynomials without using a Computer Algebra System (CAS). Although both polynomials have odd degrees and therefore each has at least one real root, it is not immediately clear whether they share any common root. The polynomial divides the , meaning that . This implies that all roots of are also roots of , with having two additional complex roots, which are the roots of the polynomial .
In the first task, students are expected to determine , and we may observe whether they use long division of polynomials or some other technique.
In the second task, we may observe whether students reason that if and only if , which is incorrect in this case since and have some roots in common, and these numbers are not the solutions of the equation .
In the third task, students should consider the polynomials as real functions of a real variable, i.e., defined as for all , and for all . They should conclude that the function is not defined at the zero of the function , i.e., the real root of the polynomial .
We consider that the prompt to graph the function will direct students’ focus toward the denominator in the function’s definition. As a result, it is likely that students will consider the roots of in the third task, even if they overlook them in the second task. Moreover, by including or excluding the real root of the in the domain of the function and the corresponding point in the graph of , students will demonstrate how they interpret the difference between the algebraic expression and the quotient of the functions and .
In the questionnaire, students were allowed to use any mathematical software they preferred, such as CAS and graphing calculators. However, they were still required to write out and explain their techniques. Their responses were subjected to praxeological analysis, with a focus on the techniques and justifications that they provided. Students’ responses were compared and interpreted in relation to the models of knowledge to be taught, as determined by the analysis of the curriculum and textbooks. This provides an illustration of how taught knowledge translates into learned knowledge, and how students navigate different mathematical organizations based on varying approaches to polynomials.
3. Results
By analyzing the external didactic transposition in Croatian high school education, four models of knowledge to be taught about polynomials have been identified. Models and , which have existed since 1994, correspond to programs with 3–5 h of mathematics lessons per week. Under the 2019 curriculum, was completely abolished, leaving as the sole model for this program. For the program with 5–7 h, model has been present since 1994 and has been completely replaced by model in 2019. The period between 2011 and 2019 was a transitional phase in which models and were gradually phased out. According to data from the Ministry regarding the distribution of students across high school programs, it can be inferred that before 2011, was the prevailing model, whereas after 2019, definitively became the prevailing model of knowledge to be taught.
The models are composed of mathematical organizations, that is, praxeologies, which are classified according to the extent to which they are grounded in knowledge about polynomials. Praxeologies whose praxis and logos blocks are explicitly based on knowledge about polynomials, and whose logos blocks include some form of definition of a polynomial, are referred to as praxeologies where a polynomial is the object of knowledge. Conversely, praxeologies whose logos block does not explicitly contain a definition of a polynomial, but where the polynomial appears merely as an instance of a more general notion (e.g., a function), are referred to as praxeologies where a polynomial is a component of knowledge. The latter are typically developed on the basis of the former.
Based on this classification, the results are presented as follows. Section 3.1 addresses the didactic transposition of definitions of polynomials, which form the foundation of the logos blocks of praxeologies where the polynomial is the object of knowledge, discussed in Section 3.2. Section 3.3 presents praxeologies where the polynomial is a component of knowledge, which activate some of the praxeologies introduced in Section 3.2.
3.1. Transposition of the Definitions of a Polynomial
In Croatian high school education, we encounter the definitions of linear and quadratic functions, as well as the following three types of definitions of a polynomial.
Definition 1.
A polynomial is an expression composed of variables and constants, obtained only by addition (subtraction) and multiplication. A monomial is the simplest expression obtained by the multiplication of constants and variables. The sum of two monomials is a binomial. The sum of three monomials is a trinomial.
Definition 2.
where .
A polynomial is an expression of the form
Definition 3.
Let
. A polynomial is a function
defined by
for every .
Models of knowledge to be taught differ with respect to the definitions of a polynomial. The representations of the definitions in the models are given in Table 1.

Table 1.
Representations of the definitions in the models.
Definition 3, included in models and , as well as the definitions of linear and quadratic functions that are part of all models, are special cases of the functional approach to polynomials. Definition 1, which is present in all the models, and Definition 2, which is present in and , indicate that is not the only approach to polynomials in Croatian high school education. Definition 2 can be justified by the formal-algebraic approach to polynomials. Although not explicitly stated in the analyzed textbooks, Definition 1 encompasses polynomials in multiple variables, whereas Definition 2 addresses polynomials in one variable. Definitions 1 and 2 do not define a variable. However, explanations in the textbooks imply that a variable is a general real number that is not predetermined, whereas a constant is a specific real number. Hence, it cannot be said that these definitions fully belong to the scholarly algebra. They may be regarded as a form of generalized arithmetic (Usiskin, 1988), designed to support students in building knowledge based on the properties of real numbers.
In all the models, the notion of an algebraic expression, defined as any expression consisting of variables and constants, obtained via the four basic algebraic operations and the use of parentheses, appears. The notion of an algebraic fraction, defined as the quotient of polynomials, is also present. From the definition of an algebraic expression and Definition 1, it follows that a polynomial is a special type of algebraic expression. In scholarly mathematics, the terms algebraic expression and algebraic fraction are used informally. From the perspective of mathematical logic (Weiss, 2020), the definition of an algebraic expression specifies only the alphabet. It does not specify what constitutes a well-defined sequence of symbols from the given alphabet, i.e., a well-defined string referred to as an algebraic expression. Not every finite sequence of symbols from the observed alphabet should be categorized as an algebraic expression (e.g., ), a point that Bolondi et al. (2020) have also noted. The distinction between an arbitrary string and an algebraic expression is only implicit in the models and it is built upon the generalization of operations with real numbers. Thus, the interpretation of strings is implicitly based on the school definition of a variable as a general real number.
3.2. Praxeologies Where a Polynomial Is the Object of Knowledge
Models of knowledge to be taught about polynomials are composed of some of the following praxeologies, presented in the order prescribed by the curricula: on polynomials, algebraic expressions, and algebraic fractions; on formal operations on polynomials in one variable; on linear functions; on quadratic equations; on quadratic functions; and on polynomials and algebraic equations. The representations of these praxeologies in the models are given in Table 2.

Table 2.
Representations of the praxeologies in the models.
3.2.1. Computing with Polynomials
Local praxeology unites praxeologies on polynomials in one or more variables and on algebraic fractions, through discourse on algebraic expressions, implicitly grounded in real numbers.
Praxeology (Table 3) consists of two punctual praxeologies (one generated with the type of tasks , and the other with ), united by the discourse on polynomials defined with Definition 1. The definition of a variable as a general real number, and the introduction of operations with polynomials, which are based on the generalization of some properties of addition and multiplication with real numbers, can be justified with the aim of generalizing the knowledge of arithmetic (Usiskin, 1988) acquired through the previous level of education. Except for the application of institutionalized formulas (), the logos of does not address when and why factorisation is possible or not. The fact that is not limited to polynomials in one variable raises the question of how to factor polynomials in multiple variables. In scholarly knowledge, to factor polynomials in multiple variables, they are often treated as polynomials in one variable with polynomials as coefficients. This approach is challenging to transpose into high school, considering that Definition 1 encompasses polynomials in both single and multiple variables. Consequently, the techniques of for factorising polynomials rely on techniques such as grouping polynomials (justified by the associativity of addition of real numbers), extracting common factors (justified by the distributivity of multiplication over addition of real numbers), and recognising institutionalised formulas about binomials and trinomials.

Table 3.
Praxeology on polynomials in one or more variables.
Praxeology (Table 4) consists of three punctual praxeologies (each generated by one type of tasks , , ) unified by the notion of an algebraic fraction. Since addition, multiplication, and simplification of algebraic fractions are introduced as generalized techniques for operations with rational numbers, the discourse of also exhibits features of generalized arithmetic.

Table 4.
Praxeology on algebraic fractions.
The knowledge of on factorisation forms the basis for the technique of simplifying algebraic fractions, which is essentially a method for dividing polynomials. Factoring polynomials yields a form from which the greatest common factor (GCF) of the polynomials in the numerator and denominator of the algebraic fraction, as well as the least common multiple (LCM) of polynomials in the denominator of algebraic fractions that need to be added or subtracted, can be identified. The terms GCF and LCM of polynomials inherently imply an order on the set of polynomials. However, since the degree of a polynomial is not discussed in , this order remains implicit. Therefore, recognition of the GCF and LCM of polynomials is based on an intuitive understanding of the complexity of expressions (syntax) and some analogies with the GCF and LCM of integers, which again points to the aspect of generalized arithmetic.
Although there are examples indicating for which values the variable of an algebraic fraction is undefined, when simplifying algebraic fractions (), the roots of the polynomial in the denominator of the algebraic fraction are generally disregarded. Instead, the variable is treated solely as a symbol, that is, indeterminate. For example, the claim , without specifying the set to which the variable belongs, exemplifies the approach .
The technique for determining the value of an algebraic expression for a given real number is partly justified by the discourse on the variable as a general real number. However, this discourse does not apply to tasks where an algebraic expression is substituted for a variable, for example, in a task where the value of the expression for needs to be calculated. Therefore, according to the functionality, the variable in the praxis block is treated as a placeholder and indeterminate.
Praxeology (Table 5) introduces division with a remainder for polynomials in one variable based on the analogy with integer division, which is a consequence of the transposition of the analogy between the ring of polynomials and the ring of integers.

Table 5.
Praxeology on formal operations on polynomials in one variable.
Long division serves as a technique for type of tasks related to the simplification of algebraic fractions in one variable; thus, can complete the praxis block of . For instance, the fraction can be simplified by dividing polynomials. However, in terms of the logos blocks of and , there is no discourse connecting the technique of division based on factorisation with the technique of long division. A common discourse would facilitate the comparison of the reliability and efficiency of these techniques depending on the specific task.
Although we indicated that Definition 2 closely aligns with the formal-algebraic approach , the discourse sometimes acknowledges that the notation
implies that the polynomial’s values depend on the choice of variable , which originates from the functional approach . Given that there are no types of tasks in the praxis block of that would necessitate this discourse, this can be a way to connect with types of tasks about calculating the value of an algebraic fraction in . On the other hand, the logos of is not grounded in the generalization of the properties of real numbers, as is the case for the logos of , nor is the variable treated as a general real number. Instead, both the praxis and logos of , are characterised by treating the variable solely as a symbol, which is a characteristic of the formal-algebraic approach .
3.2.2. Linear and Quadratic Equations, Inequalities, and Functions
Praxeology (Table 6) comprises knowledge about solving linear equations and inequalities, accompanied by a discourse on linear functions and their graphs.

Table 6.
Praxeology on linear functions.
The discourse results from the transposition of some knowledge about the functional approach to real first-degree polynomials and marks the beginning of developing analytical notions such as the monotonicity of functions, the zero of a function, and the graph of a function.
While this discourse, through the notion of a graph of function, provides techniques and justifications for solving equations and inequalities via the graphical method, solving linear equations via the substitution method and the method of opposite coefficients is not supported by the discourse, indicating the incompleteness of . Additionally, although and are activated in the praxis of when simplifying equations and inequalities, i.e., bringing equations and inequalities into the appropriate form to which the techniques of can be applied, there is no elucidation of the interrelation between the notions of a polynomial introduced in and and the notion of a linear function introduced in . Thus, given this absence of discourse unifying knowledge across these praxeologies, they do not converge into a broader mathematical organization, such as a new local or regional praxeology.
Knowledge about quadratic equations, inequalities, and functions is organized into two praxeologies: on quadratic equations and on quadratic functions. Praxeology (Table 7) is characterized by the approach to the second-degree polynomial—the quadratic trinomial. It complements the discourse of on factorisation by transposing the Fundamental Theorem of Algebra (FTA) for quadratic trinomials and provides an efficient technique for factorizing such polynomials via the quadratic formula.

Table 7.
Praxeology on quadratic equations.
Unlike , praxeology (Table 8) is characterized by the approaching the second-degree polynomial. Consequently, and diverge in their approaches to polynomials. Only discourse that identifies the zero point of the polynomial introduced as a function and solutions of the quadratic equation serves as a potential point of unification. However, since the quadratic function is defined exclusively as a real function, this identification introduces inconsistencies when the zero point of the polynomial is a complex number, as it is not an element of the domain of the function. Like in the case of linear functions and inequalities, the graph of a quadratic function also provides techniques and discourse for solving types of tasks involving quadratic inequalities. Through , the analytical knowledge of continues to evolve, introducing new notions such as the extremum of a quadratic function.

Table 8.
Praxeology on quadratic functions.
3.2.3. Polynomials and Algebraic Equations of Arbitrary Degree
Praxeology (Table 9) focuses on polynomials of arbitrary degree with the functional approach.

Table 9.
Praxeology on polynomials and algebraic equations of arbitrary degree.
Compared with other praxeologies, the logos of is notably more developed, as evidenced by the numerous slightly adapted results, including proofs, from scholarly knowledge, which not only explain the technique but also construct it. The discourse of and is incomplete regarding basic notions like polynomial equality, whereas the logos of defines it as the equality of functions and characterizes it by the degree and coefficients in the canonical representation of the polynomial. Polynomial algebra is also introduced based on the general notion of a function, that is, pointwise. However, the functional approach to polynomial algebra is not utilized in the praxis block , due to the selection of tasks of type , which can be solved using algebraic techniques from praxeology , without the need for a functional approach.
Praxeology establishes a connection between polynomials and algebraic equations, but it faces the same issue with complex zeros as . The developed logos of enables the determination of real solutions for any algebraic equation, either exactly ( and ) or approximately (and ), and allows the sketching of graphs of polynomials () without the need for limits and differential calculus. Without techniques and equations like cannot be solved without CAS tools. The approximate solving of algebraic equations and sketching graphs of polynomials without differential calculus is just one of the differences between model , which fully incorporates , and model , which includes it without the techniques , and (the components of praxeology that does not include are marked with * in Table 9).
3.3. Praxeologies Where a Polynomial Is a Component of Knowledge
In this section, the possibilities and limitations of the models are presented in relation to the content that activates knowledge about polynomials presented in Section 3.2. Knowledge about polynomials discussed in this section is typically mobilized as a part of technique associated with a broader type of tasks that is not specific to polynomials. More precisely, a praxeology from Section 3.2 contributes to the construction of techniques of a praxeology if solving the type of tasks with technique requires solving the type of tasks with technique .
Praxeologies where a polynomial is component of knowledge are grouped into organizations concerning: (1) equations and inequalities; (2) differential and integral calculus; and (3) other mathematical domains, such as analytical geometry, combinatorics, and statistics.
3.3.1. Equations and Inequalities
The absence of in model hinders the development of the technique of praxeology about algebraic equations based on the technique of polynomial division. Even in , where exists, insufficient discourse on the interrelation of polynomials and algebraic equations obstructs the activation of division in the praxis block of . For example, solving an equation like is challenging in using only factorization techniques of . Addressing this equation in remains difficult because lacks knowledge about the Rational Root Theorem (RRT). In and , the equation can be solved since the RRT is part of the logos of . It provides a technique for determining the root and then employs division to derive the polynomial , for which solutions can be determined via the techniques of . Thus, the lack of in and strongly impacts the development of techniques of and the selection of tasks (Table 10).

Table 10.
Examples of tasks in the praxis block of and techniques of utilized during their solving.
The discourse explaining techniques of hardly activates the discourse of both , where the approach is dominant, and , where the approach is dominant. Instead, the discourse of is based on the property of real numbers that if such that , then it follows that or , which is a transposition of the scholarly knowledge that a field has no zero divisors. This justification again points to the ambiguity of the variable in the discourses of and . Although in the scholarly knowledge, techniques of are justified by the knowledge that the polynomial ring has no zero divisors, this is difficult to transpose given the level and incoherence of the discourses of and .
Solving exponential, logarithmic, and trigonometric equations reduces to solving algebraic equations through appropriate substitution (Table 11); thus, the limitations of techniques and task selection of in and also lead to a reduction in the choice of tasks of these types.

Table 11.
Examples of equations that can be reduced to algebraic equations.
Unlike , which does not utilise the discourse of on linear functions, praxeology on algebraic inequalities employs it as justification for solving inequalities via graphical methods. Since and only include knowledge about sketching graphs of linear () and quadratic () functions without using differential calculus (which is taught later), it is necessary to first represent polynomials in algebraic inequalities as products of first- and second-degree polynomials. Justifying this technique requires transposing knowledge about the FTA.
Praxeology is activated through the praxis of praxeology on analytical geometry by solving systems of algebraic equations. However, polynomials in two variables are part of the logos of They are addressed through the classification of second-order curves, which emphasizes the polynomial form over the functional approach.
3.3.2. Differential and Integral Calculus
A polynomial as a real function of one real variable is part of the praxis blocks of praxeologies on the general notion of a function, on differential calculus, and on integral calculus.
In , the notion of a polynomial is narrowed down to specific forms of algebraic expressions, linear and quadratic functions. Consequently, the definition of a rational function is not explicitly covered in , and examples are limited to rational functions where both the numerator and denominator are polynomials of degree less than or equal to two, along with specific forms of degree three polynomials that can be factorised via techniques from . For example, the limit can be solved in model because polynomials can be factorized via the sum and difference of cubes formulas. On the other hand, is challenging to solve in models and , which do not include a discourse on the rational roots of polynomials. In and , this discourse with division allows the previous limit to be simplified to . The absence of the division technique in and the lack of discourse in affect the reduction in techniques for determining asymptotes (Katalenić et al., 2023) and sketching the graphs of rational functions.
The absence of discourse on polynomial equality in and prevents the existence of the technique of decomposing a rational function into partial fractions via the method of undetermined coefficients. This technique, along with division, is essential for solving integration problems involving rational functions. For example, even though the polynomial can be factorized via techniques present in models and , the integral cannot be solved via the techniques from these models due to their lack of the partial fraction decomposition technique.
3.3.3. Other Mathematical Domains
Praxeologies based on certain, due to a lack of discourse, isolated knowledge about polynomials are diverse and relate to number theory, combinatorics (e.g., the Binomial Theorem), statistics (e.g., linear regression), etc. For example, the technique for converting from one numerical system to another, derived from the application of Horner’s algorithm, exists in all models. However, in models , , and , it is not connected to polynomials due to the absence of the transposition of Horner’s algorithm and thus remains isolated praxis.
3.4. Examples of How Knowledge to Be Taught Can Condition Learned Knowledge
This section provides examples of how the knowledge to be taught can shape students’ learned knowledge. Table 12 presents the task completion rates from the questionnaire conducted among 14 students, as described in Section 2.3.

Table 12.
Completion rates for the tasks from the questionnaire.
Task to simplify the expression is of type of praxeology and of praxeology . Using techniques from that do not include polynomial root analysis but only manipulation of algebraic expressions, nine students factored the polynomial in the numerator, obtaining
from which they further concluded that
Only two out of these nine students provided an explanation of their techniques, and in their explanations, they did not use terms such as polynomial, roots of polynomials, polynomial division, GCF, etc. (Table 13, third row and second column). The remaining seven students who successfully solved the task by factoring only wrote out the calculation steps. Such responses can be explained by a lack of logos in , as the textbooks do not sufficiently emphasize the why behind the procedures (Table 3 and Table 4).

Table 13.
Analysis of the responses to the first question in the questionnaire.
Two students used the long division technique, which is part of the praxeologies and . For this task, long division is a more straightforward and efficient technique than factorization, as it eliminates the need for trial and error or reliance on CAS tools.
Three students attempted to solve through factorisation using techniques of praxeology but failed, despite the option to use CAS tools, which could have provided them with an idea of how to approach the problem. They explained that at school, they were not permitted to use any tools like CAS for such tasks. These three students also failed to solve the remaining two tasks in the questionnaire, which confirms that solving equations and sketching the graph of a rational function rely on the techniques from praxeologies and .
All students who solved also solved by using the result obtained in . They reduced solving the equation to solving the equation which has no solutions in the set of real numbers. All students solved the resulting quadratic equation via the technique of praxeology . However, only three of those eleven students explained their procedure. One student wrote that “ must not be zero” but did not determine the roots of the polynomial. The two students who used the long division technique in demonstrated knowledge that the polynomials and share the same real root, which they determined using CAS tools rather than using approximate techniques (, ) of praxeology . Therefore, it can be concluded that these students demonstrated knowledge aligned with model .
Only those two students who used the long division technique showed in their response to that the function defined by is not defined for the real root of the polynomial (Figure 3A). The remaining nine students sketched the graph of the quadratic function defined by via techniques of praxeology and wrote that , not distinguishing this function from the given function (Figure 3B). This issue also appears in the graph generated by mathematical software (Figure 4), which ignores the fact that the function is not defined at the real root of the polynomial .
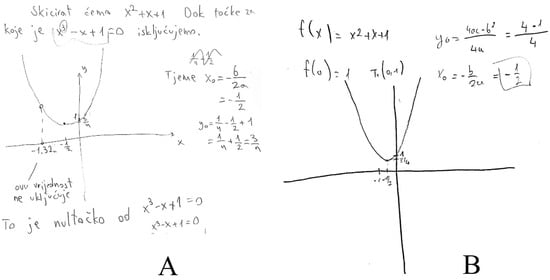
Figure 3.
Two types of responses to question about sketching the graph of a function that is not defined at the real root of the polynomial : response type (A) was provided by two students, while response type (B) was given by nine students.
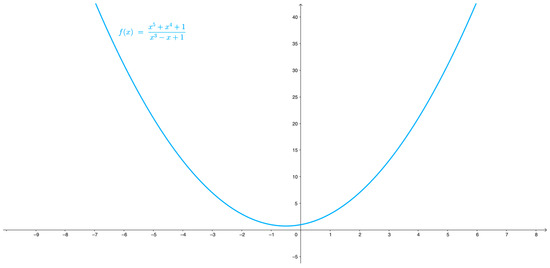
Figure 4.
Graph of the function defined by , generated by mathematical software.
4. Discussion and Conclusions
4.1. The Development of Knowledge to Be Taught and Its Connection to Scholarly Knowledge
4.1.1. Summary of Models of Knowledge to Be Taught
The four models of knowledge to be taught, namely , , , and , reflect varying levels of development in the treatment of polynomials within Croatian high school education, which, due to the interconnectedness of polynomial-related knowledge with other mathematical content, has implications for the overall high school mathematics.
Model represents the least developed model of knowledge to be taught. In this model, the polynomial is treated as a special algebraic expression, without an explicit general form (Definition 1), alongside knowledge about linear and quadratic functions. Model includes all the elements of but additionally introduces a definition of the polynomial that provides its general form as a polynomial of degree (Definition 2). In , computational techniques involving polynomials are presented solely as generalized arithmetic, and polynomial division with remainder is not defined. In contrast, supplements this with a formal approach to polynomial operations, including polynomial division. Neither nor has a sufficiently developed logos to support solving algebraic equations using methods other than polynomial factorization and applying the formula for solving quadratic equations in radicals. This limitation has consequences for solving equations and inequalities in general, as well as for analytic geometry. The fact that both and address only linear and quadratic functions within a functional approach constrains the development of the notion of rational functions, which poses a significant limitation for the development of calculus.
Model contains all the knowledge present in , and contains all the knowledge present in . In addition, both and include knowledge about polynomials of arbitrary degree as real functions of a real variable (Definition 3), which enables the development of calculus. has a sufficiently developed logos to support the exact or approximate determination of the roots of any algebraic equation, whereas does not support approximate root determination. also enables techniques for sketching the graph of a polynomial of arbitrary degree without using differential or integral calculus, while does not support this.
4.1.2. Transposition of Functional and Algebraic Approaches to Polynomials
The identified models of knowledge to be taught, comprise two types of praxeologies: , where the polynomial is the object of knowledge (Section 3.2) and those where the polynomial is a component of knowledge (Section 3.3).
The discourse of praxeologies (on linear functions), (on quadratic functions), and (on polynomials and algebraic equations of arbitrary degree) follows from the transposition of the functional approach to polynomials. In contrast, the discourse of praxeology (on quadratic equations) is a consequence of the formal-algebraic approach to polynomials. Praxeologies and , where the first encounters with polynomials occur, result from a more complex process of transposition, combining elements of both the and approaches.
The praxeology results from the transposition of scholarly knowledge about real numbers, identification of formal polynomials and induced functions, and the analogy between the ring of polynomials and the ring of integers. This transposition leads to the school notion of an algebraic expression and school definition of a polynomial focusing on syntax, while semantics is determined by defining the variable as a general real number. Although the properties of operations with algebraic expressions and polynomials are attempted to be justified through the generalization of operations with numbers (except for tasks where it is necessary to determine the value of an algebraic expression for a given real number), the environment of real numbers is not evident in the praxis block of , and the variable is treated solely as a symbol without meaning, which leans towards the approach. The inconsistency between the praxis and the logos blocks of has direct consequences for the types of tasks and the validity of techniques, indicating the fragility of knowledge in the transposition process (Kang & Kilpatrick, 1992). If it is defined that a fraction can be simplified when the numerator and the denominator are not coprime, and if this knowledge is extended to algebraic fractions through analogies between integers and polynomials, then the validity of techniques depends on how the variable is treated, that is, on the adopted approach to the polynomial. This can be illustrated by the following example. Consider the algebraic fraction . It may be concluded that the expression can be simplified if polynomials are treated formally, with and treated as indeterminate. In that case, , since is a common factor in both the numerator and the denominator. However, if the question is whether this fraction can be simplified for all real numbers for which it is defined, it must be observed that the expression is defined for and , but in this case, the value of the algebraic fraction is , and the numbers and are coprime.
In high school mathematics, in both the praxis and logos blocks, the objects of knowledge are exclusively polynomials with integer, rational, real, or complex coefficients, allowing implicit identification of polynomials as algebraic expressions (originating from the approach) and polynomials introduced as functions (originating from the approach). However, none of the models contain a discourse that would explain this identification and thereby unify praxeologies in the mathematical organization with a common and coherent discourse, which can represent a significant constraint on teachers’ didactic practice, as shown by Barbé et al. (2005) in the case of limits of functions. The lack of discourse creates tension not only between the definitions but also in the most basic techniques:
- Polynomial equalities and operations with polynomials as algebraic expressions (equalizing or adding coefficients with the same powers), versus operations with polynomials as functions (defined pointwise);
- Roots of a polynomial as an algebraic expression with real coefficients (which appear also as complex numbers), versus zeros of a polynomial as a real function (only real numbers).
Considering praxeologies where the polynomial is a component of knowledge, the formal-algebraic approach appears to be unnecessary in any of the models. Therefore, the definition of an algebraic expression, as well as the definition of a polynomial as an expression of a certain form, can be interpreted as a transitional phase towards the functional approach, culminating in differential and integral calculus, with the notion of a function at its core. Until then, content on some individual elementary functions and analytical notions has been adopted, starting with linear functions and continuing with quadratic functions. The dominant focus on linear and quadratic functions in and could be justified by the FTA and its implications, but this connection is not evident given the selected knowledge in the models.
Generally, the knowledge about equations, which is not accompanied by the discourse on functions, precedes the knowledge about inequalities, which is accompanied by the discourse on functions and their graphs. The organization of content in which topics transposed from the domain of algebra precede topics transposed from the domain of analysis point out one of the raisons d’être of polynomials in high school—the development of algebraic techniques on which the techniques of praxeologies based on functions will further develop. Specifically, and , for which the phenomenon of emptiness of interpretation is characteristic due to the status of the variable in the praxis blocks, and the inconsistency of praxis and logos blocks, demonstrate their reason for existence in the construction of techniques of praxeologies that accompany them, ranging from equation solving to differential and integral calculus. Generally, the dominant role of praxeologies where the polynomial is the object of knowledge is in the construction of techniques rather than the discourse for praxeologies where a polynomial is the component of knowledge.
4.1.3. Illustration of the Connection Between Knowledge to Be Taught and Learned Knowledge
Although the sample of students surveyed in the questionnaire is small, it includes top mathematics students whose knowledge represents the maximum that can be expected in the institution. Their responses are closest to institutional knowledge, and in some cases may even go beyond it. This makes the findings useful for illustrating possible limitations of the knowledge to be taught, even though they cannot be generalized, as other students are likely to demonstrate less knowledge and possibly different kinds of errors.
The knowledge demonstrated by nearly all surveyed students aligns with model , with only two students exhibiting knowledge consistent with model . Since students were free to choose the techniques for solving the tasks in the questionnaire, it cannot be concluded that those whose knowledge aligns with do not also possess some knowledge exclusive to model . However, while encompasses a subset of knowledge compared to , students can compensate for certain techniques, such as long division, by using other techniques related to algebraic expressions and CAS tools. What is missing in students’ work are the interpretations of techniques in different contexts and their justifications, leading to incorrect techniques that are built on algebra and thus ultimately hindering the development of the notion of a function. In particular, the technique of simplifying algebraic expressions, which lacks a clear interpretation in its isolated form, takes on interpretations when applied to equations and functions. However, these interpretations elude students. Students perform operations with algebraic expressions and polynomials, but without addressing notions consistently. They tend to approach functions algebraically rather than pointwise, and accordingly the initial understanding of polynomials as algebraic expressions conditions the knowledge about polynomials as functions. If this separation of mathematical organizations with different approaches to polynomials induces gaps in knowledge among the high achieving students, it is reasonable to expect that such difficulties would be visible, and maybe even more pronounced, among other students.
This insufficiently developed discourse on polynomials as both algebraic expressions and functions, along with the absence of a unifying discourse integrating these approaches, which are characteristics of all models, hinders the interpretation of techniques in different contexts, with the functional context being both the most delicate and essential for further learning in mathematics.
4.2. Changes in Knowledge to Be Taught During the Analyzed Period and Their Implications
Following previous discussion based on the analysis of curricula and textbooks, the following rationales for knowledge about polynomials in high school education over the observed period have been identified:
- i.
- Interconnectedness of knowledge. As with scholarly knowledge, knowledge about polynomials is closely intertwined with knowledge about equations, inequalities, analytical geometry, statistics, and differential and integral calculus. High school education begins with generalizing operations with real numbers through operations with polynomials, and based on these algebraic techniques, techniques in the aforementioned domains are developed;
- ii.
- Evolution of a function and analytical approach. Polynomials participate in the gradual evolution of the notion of a function, which occurs almost inductively, starting with linear functions and then progressing to quadratic functions. The inclusion of polynomials of higher degrees allows for the development of analytical notions through their graphs before introducing new techniques based on limits and differential calculus;
- iii.
- Analogies with integers. Analogies between integers and polynomials (properties of operations, division with remainder, Euclidean algorithm, Fundamental Theorem of Arithmetic and Fundamental Theorem of Algebra, prime numbers and irreducible polynomials, GCF and LCM) demonstrate how different objects can share similar properties.
Although the rationales i–iii are present throughout the entire thirty-year period, the reduction in polynomial content over the years diminishes the significance of reason iii and affects reason i due to the reduction in techniques. This reflects subtle shifts in high school education priorities. The unifying potential of algebra, highlighted by the New Math movement, has diminished. The lack of techniques increases the need for CAS tools, while the availability of such tools may in turn encourage the omission of certain techniques and contribute to the reshaping of the knowledge to be taught.
The dominant characteristic of polynomial teaching knowledge in high school remains consistent throughout the observed period: the lack of discourse that would unify, or at least reduce, the tension between the algebraic approach to polynomials as formal expressions and the analytical approach to polynomials as real or complex functions. The fact that teaching knowledge throughout the whole analyzed period exhibits phenomena of incompleteness and incoherence, along with the rationale for polynomials, with only variations in the emphasis of these reasons, suggests that despite the modifications, curriculum changes have not significantly altered the dominant epistemology (Lucas et al., 2019) or the educational ends and paradigms of high school education (Gascón & Nicolás, 2022). Since a complete analysis of the paradigm would require examining the taught knowledge, teaching practices, and the ecology of knowledge, the collected data suggest that, despite changes, the curricula continue to uphold the paradigm of visiting the works (Chevallard, 2015).
Instead, external didactic transposition—that is, the very selection and adaptation of knowledge for teaching (Bosch et al., 2021)—has unfolded as an iterative process, with knowledge being selected and adapted from already transposed knowledge. The phenomenon of iteration in the process of didactic transposition of high school knowledge about polynomials could also be related to other notions and is in line with the refined model of external didactic transposition presented by Bosch and Winsløw (2020) for undergraduate education—new university textbooks “draw more on previous textbooks than on scholarly sources” (Bosch & Winsløw, 2020, p. 379).
The phenomenon of iteration in the process of external didactic transposition calls for further investigation, particularly in understanding how to prevent greater curricular fragmentation, as well as how to establish connections when existing links are weakened or lost due to the marginalization or exclusion of certain knowledge, as seen in the case of polynomials.
The reduction in polynomial content over the years has led to even greater fragmentation: the notion of the polynomial has diminished, splitting into linear and quadratic functions on the one hand, and being subsumed into the school notion of an algebraic expression on the other, which is a syntactic notion lacking semantic interpretation. Interpretations of algebraic expressions occur only with the acquisition of new content, such as equations, inequalities, functions, limits, and differential and integral calculus. However, the absence of a discourse on the interference of learned operations on algebraic expressions without interpretations, and the new content whose techniques are built on these operations, may lead not only to a misunderstanding of techniques in specific contexts but also to the incorrect development of new techniques. CAS tools may both contribute to content reduction and assist in bridging the gaps caused by such reduction. However, when students’ knowledge is based primarily on techniques without underlying notions, they may struggle to critically evaluate the results produced by CAS and to recognize the limitations of these results.
Although this study focuses on the Croatian case, it raises a more general question about the role and status of polynomials in current high school mathematics. The lack of cohesion between content transposed from algebra and analysis, observed here, may not be specific to the Croatian context. The topics of other research on polynomials worldwide, suggests that similar forms of fragmentation may be present in other educational systems as well. The Croatian case thus serves as a concrete example through which a broader epistemological phenomenon may be hypothesized, which could be further explored through comparative research across different countries.
Addressing the gaps left by the curriculum and textbooks and fostering a more cohesive and interconnected approach to polynomials in high school mathematics could present a considerable challenge for teachers. Given that knowledge about polynomials is deeply interwoven with various mathematical domains, these disruptions extend beyond polynomials themselves, potentially affecting students’ knowledge of related notions. Future research could explore how teachers perceive the fragmentation of curricula content, the extent to which they can bridge these discontinuities, and the didactic strategies they employ or could employ to mitigate these challenges.
Author Contributions
Conceptualization, J.P., Ž.M.Š. and M.B.; methodology, J.P.; software, J.P.; validation, J.P., Ž.M.Š. and M.B.; formal analysis, J.P.; investigation, J.P.; resources, J.P.; data curation, J.P.; writing—original draft preparation, J.P.; writing—review and editing, J.P., Ž.M.Š. and M.B.; visualization, J.P. and M.B.; supervision, Ž.M.Š.; project administration, Ž.M.Š.; funding acquisition, not applicable. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki and approved by the Ethics Committee of the Faculty of Science, University of Split (protocol code: 053-01/21-01/0005; 2181-204-02-07-21-0002) (date of approval: 23 February 2021).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Data will be made available upon request.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ATD | Anthropological Theory of the Didactic |
| formal-algebraic approach to polynomials | |
| functional approach to polynomials | |
| CAS | Computer Algebra System |
Note
| 1 | Dakić, B. & Elezović, N. (2009). Matematika 1, 1. dio, 3rd. ed. Element, pp. 80–81. |
References
- Adu-Gyamfi, K., Bosse, M., & Chandler, K. (2017). Student connections between algebraic and graphical polynomial representations in the context of a polynomial relation. International Journal of Science and Mathematics Education, 15(5), 915–938. [Google Scholar] [CrossRef]
- Barbeau, E. J. (2003). Polynomials. Springer. [Google Scholar]
- Barbé, J., Bosch, M., Espinoza, L., & Gascón, J. (2005). Didactic restrictions on the teacher’s practice: The case of limits of functions in Spanish high schools. Educational Studies in Mathematics, 59, 235–268. [Google Scholar] [CrossRef]
- Bolondi, G., Ferretti, F., & Maffia, A. (2020). Monomials and polynomials: The long march towards a definition. Teaching Mathematics and its Applications, 39(1), 1–12. [Google Scholar] [CrossRef]
- Bosch, M., Chevallard, Y., García, F. J., & Monaghan, J. (Eds.). (2020). Working with the anthropological theory of the didactic in mathematics education. Routledge. [Google Scholar]
- Bosch, M., & Gascón, J. (2006). Twenty-five years of the didactic transposition. ICMI Bulletin, 58, 51–64. [Google Scholar]
- Bosch, M., Hausberger, T., Hochmuth, R., Kondratieva, M., & Winsløw, C. (2021). External didactic transposition in undergraduate mathematics. International Journal of Research in Undergraduate Mathematics Education, 7, 140–162. [Google Scholar] [CrossRef]
- Bosch, M., & Winsløw, C. (2020). The external didactic transposition of mathematics at the university level: Dilemmas and challenges. Educação Matemática Pesquisa: Revista do Programa de Estudos Pós-Graduados em Educação Matemática, 22(4), 373–386. [Google Scholar] [CrossRef]
- Chevallard, Y. (1991). La transposition didactique: Du savoir savant au savoir enseigné. La Pensée Sauvage. [Google Scholar]
- Chevallard, Y. (2015). Teaching mathematics in tomorrow’s society: A case for an oncoming counter paradigm. In S. J. Cho (Ed.), The proceedings of the 12th international congress on mathematical education (pp. 173–187). Springer. [Google Scholar]
- Chevallard, Y., & Bosch, M. (2020a). Anthropological theory of the didactic (ATD). In S. Lerman (Ed.), Encyclopedia of mathematics education (pp. 53–61). Springer. [Google Scholar] [CrossRef]
- Chevallard, Y., & Bosch, M. (2020b). Didactic transposition in mathematics education. In S. Lerman (Ed.), Encyclopedia of mathematics education (pp. 170–174). Springer. [Google Scholar] [CrossRef]
- Dreyfus, T., & Eisenberg, T. (1990). Polynomials: A theme which should not be forgotten. International Journal of Mathematical Education in Science and Technology, 21(3), 489–497. [Google Scholar] [CrossRef]
- Gascón, J., & Nicolás, P. (2022). Paradigm crisis in the step from tertiary to secondary mathematics education. International Journal of Mathematical Education in Science and Technology, 53(5), 1153–1169. [Google Scholar] [CrossRef]
- Kang, W., & Kilpatrick, J. (1992). Didactic transposition in mathematics textbooks. For the Learning of Mathematics, 12(1), 2–7. [Google Scholar]
- Katalenić, A., Čižmešija, A., & Milin Šipuš, Ž. (2023). Prospective mathematics teachers’ knowledge of asymptotes and asymptotic behaviour in calculus. International Journal of Science and Mathematics Education, 21, 131–158. [Google Scholar] [CrossRef]
- Lang, S. (2005). Undergraduate algebra (3rd ed.). Springer. [Google Scholar]
- Llanos, V., Otero, M., & Rojas, E. C. (2015). Polynomial functions resulting from the multiplication of curves in the framework of the research and study paths. Journal of Research in Mathematics Education, 4(1), 80–98. [Google Scholar] [CrossRef]
- Lucas, C., Fonseca, C., Gascón, J., & Schneider, M. (2019). The phenomenotechnical potential of reference epistemological models. In M. Bosch, Y. Chevallard, F. García, & J. Monaghan (Eds.), Working with the anthropological theory of the didactic in mathematics education: A comprehensive casebook (pp. 77–98). Routledge. [Google Scholar] [CrossRef]
- Markushevich, A. I. (1991). Polynomials. In M. Hazewinkel (Ed.), Encyclopaedia of mathematics (pp. 213–229). Springer. [Google Scholar]
- Ministarstvo Kulture i Prosvjete. (1994). Nastavni plan i program za stjecanje školske spreme u programima jezične, klasične i prirodoslovno-matematičke gimnazije koji se odnosi na predmet Matematika [Curriculum for acquiring school qualifications in the programs of linguistic, classical, and science-mathematics grammer school, pertaining to the subject of mathematics]. Glasnik Ministarstva Kulture i Prosvjete Republike Hrvatske. [Google Scholar]
- Ministarstvo Znanosti i Obrazovanja. (2019). Odluka o donošenju kurikuluma za nastavni predmet matematike za osnovne škole i gimnazije u Republici Hrvatskoj [Decision on the adoption of the curriculum for mathematics for primary schools and grammar schools in the Republic of Croatia]. Available online: https://narodne-novine.nn.hr/clanci/sluzbeni/2019_01_7_146.html (accessed on 25 September 2020).
- Ministarstvo Znanosti, Obrazovanja i Športa. (2003). Kurikularni pristupi promjenama u gimnaziji, Razrada okvirnog nastavnog plana i programa u funkciji rasterećenja učenika, Prirodno-matematičko-informatičko područje [Curricular approaches to changes in grammer schools, development of a curriculum in the function of student workload reduction, natural science-mathematics-computer field]. Zavod za Unapređivanje Školstva. [Google Scholar]
- Ministarstvo Znanosti, Obrazovanja i Športa. (2011). Nacionalni okvirni kurikulum za predškolski odgoj i obrazovanje te opće obvezno i srednjoškolsko obrazovanje [The national curriculum framework for preschool education and general compulsory and secondary education]. Available online: https://sredisnjikatalogrh.gov.hr/srce-arhiva/36/33329/Nacionalni_okvirni_kurikulum.pdf (accessed on 8 September 2020).
- OECD (Organisation for European Economic Co-Operation. Office for Scientific and Technical Personnel). (1961). New thinking in school mathematics. OECD. [Google Scholar]
- Pleština, J. (2023). Epistemological and didactic analysis of the notion of a polynomial [Doctoral dissertation, University of Zagreb]. [Google Scholar]
- Pleština, J., & Milin Šipuš, Ž. (2022). The notion of a polynomial in the secondary–tertiary transition. In M. Trigueros, B. Barquero, R. Hochmuth, & J. Peters (Eds.), Proceedings of the fourth conference of the international network for didactic research in university mathematics (pp. 100–109). Leibniz Universität Hannover. [Google Scholar]
- Stillwell, J. (2010). Mathematics and its history. Springer. [Google Scholar] [CrossRef]
- Strømskag, H., & Chevallard, Y. (2022). Elementary algebra as a modelling tool: A plea for a new curriculum. Recherches en Didactique des Mathématiques, 42(3), 371–409. [Google Scholar]
- Sultan, A., & Artzt, A. (2018). The mathematics that every secondary math teacher needs to know. Routledge. [Google Scholar]
- Usiskin, Z. (1988). Conceptions of school algebra and uses of variables. In A. F. Coxford, & A. P. Schulte (Eds.), The ideas of algebra, K-12 (pp. 8–19). National Council of Teachers of Mathematics. [Google Scholar]
- Weiss, M. (2020). Secondary mathematics for mathematicians and educators: A view from above. Routledge. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).