Understanding Fourth-Grade Student Achievement Using Process Data from Student’s Web-Based/Online Math Homework Exercises
Abstract
:1. Introduction
2. Literature Review
2.1. Attendance and Instructional Engagement
2.2. Timing of Homework Initiation
2.3. Problem Attempts and Persistence
2.4. Revisits to Homework or Problems
2.5. Time Spent on Homework
2.6. Uploading Written Work as Evidence of Reasoning
2.7. Summary
3. Context
4. Method
4.1. Sample
4.2. Data
4.3. Data Cleaning and Outliers
4.4. Statistical Models
5. Results
| All Three Years: Grade 4, Accelerated Level | ||||||
|---|---|---|---|---|---|---|
| Outcome | Principal Test (PT) score | |||||
| Predictor | All predictors | |||||
| Year | 2020–2021 | 2021–2022 | 2022–2023 | |||
| R-squared | 0.397 | 0.267 | 0.205 | |||
| F (p) | 12.5 (<0.01)9 | 8.71 (<0.01) | 7.35 (<0.01) | |||
| Adjusted R-squared | 0.365 | 0.250 | 0.186 | |||
| Root Mean Square Error | 0.696 | 0.772 | 0.709 | |||
| Sample size (n) | 141 | 303 | 293 | |||
| b | p | b | p | b | p | |
| Intercept | −0.166 | 0.030 | −0.450 | 0.000 | −0.403 | 0.000 |
| attendance | 0.069 | 0.385 | 0.294 | 0.000 | −0.033 | 0.518 |
| hw_revisits | 0.019 | 0.842 | −0.078 | 0.219 | −0.064 | 0.367 |
| problem_attempts | −0.069 | 0.445 | −0.310 | 0.000 | −0.103 | 0.113 |
| picture_upload | 0.238 | 0.008 | 0.134 | 0.025 | 0.239 | 0.000 |
| unsolved_problem_revisits | −0.223 | 0.026 | −0.137 | 0.057 | −0.224 | 0.000 |
| time_spent_on_hw | −0.538 | 0.000 | 0.026 | 0.683 | −0.029 | 0.663 |
| days_first_attempt | −0.131 | 0.134 | −0.007 | 0.909 | −0.134 | 0.032 |
| All Three Years: Grade 4, Advanced Level | ||||||
|---|---|---|---|---|---|---|
| Outcome | Principal Test (PT) score | |||||
| Predictor | All predictors | |||||
| Year | 2020–2021 | 2021–2022 | 2022–2023 | |||
| R-squared | 0.249 | 0.283 | 0.250 | |||
| F (p) | 4.97 (<0.01)10 | 8.96(<0.01) | 9.37 (<0.01) | |||
| Adjusted R-squared | 0.199 | 0.263 | 0.235 | |||
| Root Mean Square Error | 0.607 | 0.583 | 0.684 | |||
| Sample size (n) | 113 | 261 | 357 | |||
| b | p | b | p | b | p | |
| Intercept | 0.035 | 0.654 | 0.247 | 0.000 | 0.133 | 0.003 |
| attendance | 0.086 | 0.307 | 0.116 | 0.027 | 0.289 | 0.000 |
| hw_revisits | 0.056 | 0.597 | 0.131 | 0.052 | 0.073 | 0.238 |
| problem_attempts | −0.028 | 0.823 | −0.189 | 0.006 | −0.143 | 0.009 |
| picture_upload | 0.067 | 0.402 | 0.003 | 0.945 | 0.047 | 0.309 |
| unsolved_problem_revisits | −0.435 | 0.000 | −0.292 | 0.000 | −0.267 | 0.000 |
| time_spent_on_hw | −0.020 | 0.841 | −0.297 | 0.000 | −0.199 | 0.000 |
| days_first_attempt | −0.2152 | 0.019 | −0.0300 | 0.593 | −0.0632 | 0.256 |
| All Three Years: Grade 4, Honors Level | ||||||
|---|---|---|---|---|---|---|
| Outcome | Principal Test (PT) score | |||||
| Predictor | All predictors | |||||
| Year | 2020–2021 | 2021–2022 | 2022–2023 | |||
| R-squared | 0.278 | 0.273 | 0.195 | |||
| F (p) | 2.31(<0.05)11 | 5.11 (<0.05) | 2.88 (<0.05) | |||
| Adjusted R-squared | 0.158 | 0.243 | 0.155 | |||
| Root Mean Square Error | 0.498 | 0.561 | 0.579 | |||
| Sample size (n) | 50 | 176 | 147 | |||
| b | p | b | p | b | p | |
| Intercept | 0.354 | 0.019 | 0.336 | 0.000 | 0.487 | 0.000 |
| attendance | 0.162 | 0.164 | −0.031 | 0.615 | −0.013 | 0.853 |
| hw_revisits | 0.044 | 0.831 | −0.131 | 0.119 | 0.127 | 0.190 |
| problem_attempts | −0.120 | 0.521 | −0.170 | 0.055 | −0.024 | 0.810 |
| picture_upload | 0.0140 | 0.901 | 0.142 | 0.015 | 0.192 | 0.008 |
| unsolved_problem_revisits | −0.201 | 0.240 | −0.164 | 0.028 | −0.191 | 0.017 |
| time_spent_on_hw | −0.279 | 0.069 | −0.107 | 0.173 | −0.342 | 0.001 |
| days_first_attempt | −0.359 | 0.020 | −0.092 | 0.153 | −0.051 | 0.520 |
| Outcome | Principal Test (PT) Score | |||||||
|---|---|---|---|---|---|---|---|---|
| Predictor | All predictors | |||||||
| Curriculum | 4_1 Accelerated | 4_2 Advanced | 4_3 Honors | All levels, all years | ||||
| R-squared | 0.229 | 0.217 | 0.224 | 0.188 | ||||
| F (p) | 29.03 (<0.05)12 | 28.63 (<0.05)13 | 14.89 (<0.05)14 | 59.69 (2 × 10−77) | ||||
| Adjusted R-squared | 0.219 | 0.207 | 0.205 | 0.184 | ||||
| Root Mean Square Error | 0.757 | 0.700 | 0.580 | 0.812 | ||||
| Sample size (n) | 737 | 731 | 373 | 1841 | ||||
| b | p | b | p | b | p | b | p | |
| Intercept | −0.371 | 0.000 | 0.153 | 0.000 | 0.436 | 0.000 | −6.1 × 10−17 | 1.000 |
| attendance | 0.120 | 0.001 | 0.148 | 0.000 | −0.019 | 0.637 | 0.097 | 0.000 |
| hw_revisits | −0.061 | 0.153 | 0.072 | 0.098 | −0.013 | 0.825 | 5.5 × 10−5 | 0.998 |
| problem_attempts | −0.173 | 0.000 | −0.149 | 0.000 | −0.071 | 0.241 | −0.196 | 0.000 |
| picture_upload | 0.182 | 0.000 | 0.076 | 0.017 | 0.163 | 0.000 | 0.145 | 0.000 |
| unsolved_problem_revisits | −0.199 | 0.000 | −0.280 | 0.000 | −0.191 | 0.000 | −0.170 | 0.000 |
| time_spent_on_hw | −0.100 | 0.015 | −0.217 | 0.000 | −0.226 | 0.000 | −0.173 | 0.000 |
| days_first_attempt | −0.109 | 0.005 | −0.088 | 0.020 | −0.097 | 0.038 | −0.106 | 0.000 |
6. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| RSM | Russian School of Mathematics |
| 1 | The red regression line represents the model for all curricula combined. |
| 2 | The highest p-value for any Accelerated level Homework model was 6 × 10−18. |
| 3 | See note 2. |
| 4 | The highest p-value for any Advanced level Homework model was 5 × 10−10. |
| 5 | The highest p-value for any Honors level Homework model was 0.006. |
| 6 | See note 2. |
| 7 | See note 4. |
| 8 | See note 5. |
| 9 | The highest p-value for any Accelerated level Homework model was 2 × 10−12. |
| 10 | The highest p-value for any Advanced level Homework model was 6 × 10−5. |
| 11 | The highest p-value for any Honors level Homework model was 0.04. |
| 12 | See note 9. |
| 13 | See note 10. |
| 14 | See note 11. |
References
- Algozzine, B., Wang, C., & Violette, A. S. (2010). Reexamining the relationship between academic achievement and social behavior. Journal of Positive Behavior Interventions, 13(1), 3–16. [Google Scholar] [CrossRef]
- Alhassan, A., Zafar, B., & Mueen, A. (2020). Predict students’ academic performance based on their assessment grades and online activity data. International Journal of Advanced Computer Science and Applications (IJACSA), 11(4), 2020. [Google Scholar] [CrossRef]
- Balfanz, R., Herzog, L., & Mac Iver, D. J. (2007). Preventing student disengagement and keeping students on the graduation path in urban middle-grades schools: Early identification and effective interventions. Educational Psychologist, 42(4), 223–235. [Google Scholar] [CrossRef]
- Belsley, D. A., Kuh, E., & Welsch, R. E. (1980). Regression diagnostics. John Wiley and Sons. [Google Scholar]
- Bempechat, J. (2004). The motivational benefits of homework: A social-cognitive perspective. Theory Into Practice, 43(3), 189–196. [Google Scholar] [CrossRef]
- Bezirhan, U., von Davier, M., & Grabovsky, I. (2020). Modeling item revisit behavior: The hierarchical speed–accuracy–revisits model. Educational and Psychological Measurement, 81(2), 363–387. [Google Scholar] [CrossRef] [PubMed]
- Cohen, J., Cohen, P., West, S. G., & Aiken, L. S. (2013). Applied multiple regression/correlation analysis for the behavioral sciences. Routledge. [Google Scholar]
- Cohen, J. C. (1977). Statistical power analysis for the behavioral sciences (Rev. ed.). Academic Press. [Google Scholar]
- Cooper, H., Robinson, J. C., & Patall, E. A. (2006). Does homework improve academic achievement? A synthesis of research, 1987–2003. Review of Educational Research, 76(1), 1–62. [Google Scholar] [CrossRef]
- Epstein, J. L. (1983). Homework practices, achievements, and behaviors of elementary school students. Center for Research on Elementary and Middle Schools. (ERIC Document Reproduction Service No. ED301322). Available online: https://eric.ed.gov/?id=ED250351 (accessed on 1 June 2025).
- Fan, H., Xu, J., Cai, Z., He, J., & Fan, X. (2017). Homework and student’s achievement in math and science: A 30-year meta-analysis, 1986–2015. Educational Research Review, 20, 35–54. [Google Scholar] [CrossRef]
- Fateen, M., & Mine, T. (2021). Predicting student performance using teacher observation reports. Available online: https://eric.ed.gov/?id=ED615587 (accessed on 1 June 2025).
- Feng, M., & Roschelle, J. (2016, April 25–26). Predicting students’ standardized test scores using online homework. Third (2016) ACM Conference on Learning@Scale, Edinburgh, UK. [Google Scholar] [CrossRef]
- He, Q., & von Davier, M. (2016). Analyzing process data from problem-solving items with N-grams: Insights from a computer-based large-scale assessment. In Y. Rosen, S. Ferrara, & M. Mosharraf (Eds.), Handbook of research on technology tools for real-world skill development (pp. 750–777). IGI Global. [Google Scholar] [CrossRef]
- Ilina, O., Antonyan, S., Mirny, A., Brodskaia, J., Kosogorova, M., Lepsky, O., Belakurski, P., Iyer, S., Ni, B., Shah, R., Sharma, M., & Ludlow, L. (2024, April 24). Predicting fourth-grade student achievement using process data from student’s web-based/online math homework exercises. Roundtable Presentation at the New England Educational Research Association (NEERO) Annual Meeting, Portsmouth, NH, USA. [Google Scholar]
- Ilina, O., Antonyan, S., Mirny, A., Lepsky, O., Brodskaia, J., Balsara, M., Keyhan, K., Mylnikov, A., Quackenbush, A., Tarlie, J., Tyutyunik, A., Venkatesh, R., & Ludlow, L. H. (2023). Fourth grade student mathematics performance in an after-school program before and after COVID-19: Project-based learning for teachers and students as co-researchers. Journal of Teacher Action Research, 10(2). Available online: https://jtar-ojs-shsu.tdl.org/JTAR/article/view/94 (accessed on 1 June 2025).
- Kabakchieva, D. (2013). Predicting student performance by using data mining methods for classification. Cybernetics and Information Technologies, 1, 61–72. [Google Scholar] [CrossRef]
- Meylani, R., Bitter, G., & Castaneda, R. (2014). Predicting student performance in statewide high stakes tests for middle school mathematics using the results from third party testing instruments. Journal of Education and Learning, 3(3), 135–145. [Google Scholar] [CrossRef]
- Mogessie, M., Riccardi, G., & Rochetti, M. (2015, October 21–24). Predicting student’s final exam scores from their course activities. 2015 IEEE Frontiers in Education Conference (FIE) (pp. 1–9), El Paso, TX, USA. [Google Scholar] [CrossRef]
- Namoun, A., & Alshanqiti, A. (2020). Predicting student performance using data mining and learning analytics techniques: A systematic literature review. Applied Sciences, 11(1), 237. [Google Scholar] [CrossRef]
- Neter, J., & Wasserman, W. (1974). Applied linear statistical models. Irwin. [Google Scholar]
- Ramdass, D., & Zimmerman, B. J. (2011). Developing self-regulation skills: The important role of homework. Journal of Advanced Academics, 22(2), 194–218. [Google Scholar] [CrossRef]
- Richards-Babb, M., Drelick, J., Henry, Z., & Robertson-Honecker, J. (2011). Online homework, help or hindrance? What students think and how they perform. Journal of College Science Teaching, 40(4), 81–93. [Google Scholar]
- Rosário, P., Núñez, J. C., Vallejo, G., Cunha, J., Nunes, T., Suárez, N., Fuentes, S., & Moreira, T. (2015). The effects of teachers’ homework follow-up practices on students’ EFL performance: A randomized-group design. Frontiers in Psychology, 6, 1528. [Google Scholar] [CrossRef]
- Roschelle, J., Feng, M., Murphy, R., & Mason, C. (2016). Online mathematics homework increases student achievement. AERA Open, 2(4). [Google Scholar] [CrossRef]
- Russian School of Mathematics. (2020). About RSM: The Russian school of mathematics. Available online: https://www.russianschool.com/about (accessed on 1 June 2025).
- Shechtman, N., Roschelle, J., Feng, M., & Singleton, C. (2019). An efficacy study of a digital core curriculum for grade 5 mathematics. AERA Open, 5(2). [Google Scholar] [CrossRef]
- Valle, A., Regueiro, B., Núñez, J. C., Rodríguez, S., Piñeiro, I., & Rosário, P. (2016). Academic goals, student homework engagement, and academic achievement in elementary school. Frontiers in Psychology, 7, 463. [Google Scholar] [CrossRef]
- Vygotsky, L. (1997). Educational psychology. St. Lucie Press. (Original work published 1926). [Google Scholar]
- Wu, D., Li, H., Zhu, S., Yang, H. H., Bai, J., Zhao, J., & Yang, K. (2023). Primary students’ online homework completion and learning achievement. Interactive Learning Environments, 32, 4469–4483. [Google Scholar] [CrossRef]
- Yeary, E. E. (1978). What about homework? Today’s Education, September–October, 80–82. [Google Scholar]
- Yin, P., & Fan, X. (2001). Estimating R2 shrinkage in multiple regression: A comparison of different analytical methods. The Journal of Experimental Education, 69(2), 203–224. [Google Scholar] [CrossRef]
- Zimmerman, B. J., & Kitsantas, A. (2005). Homework practices and academic achievement: The mediating role of self-efficacy and perceived responsibility beliefs. Contemporary Educational Psychology, 30, 397–417. [Google Scholar] [CrossRef]
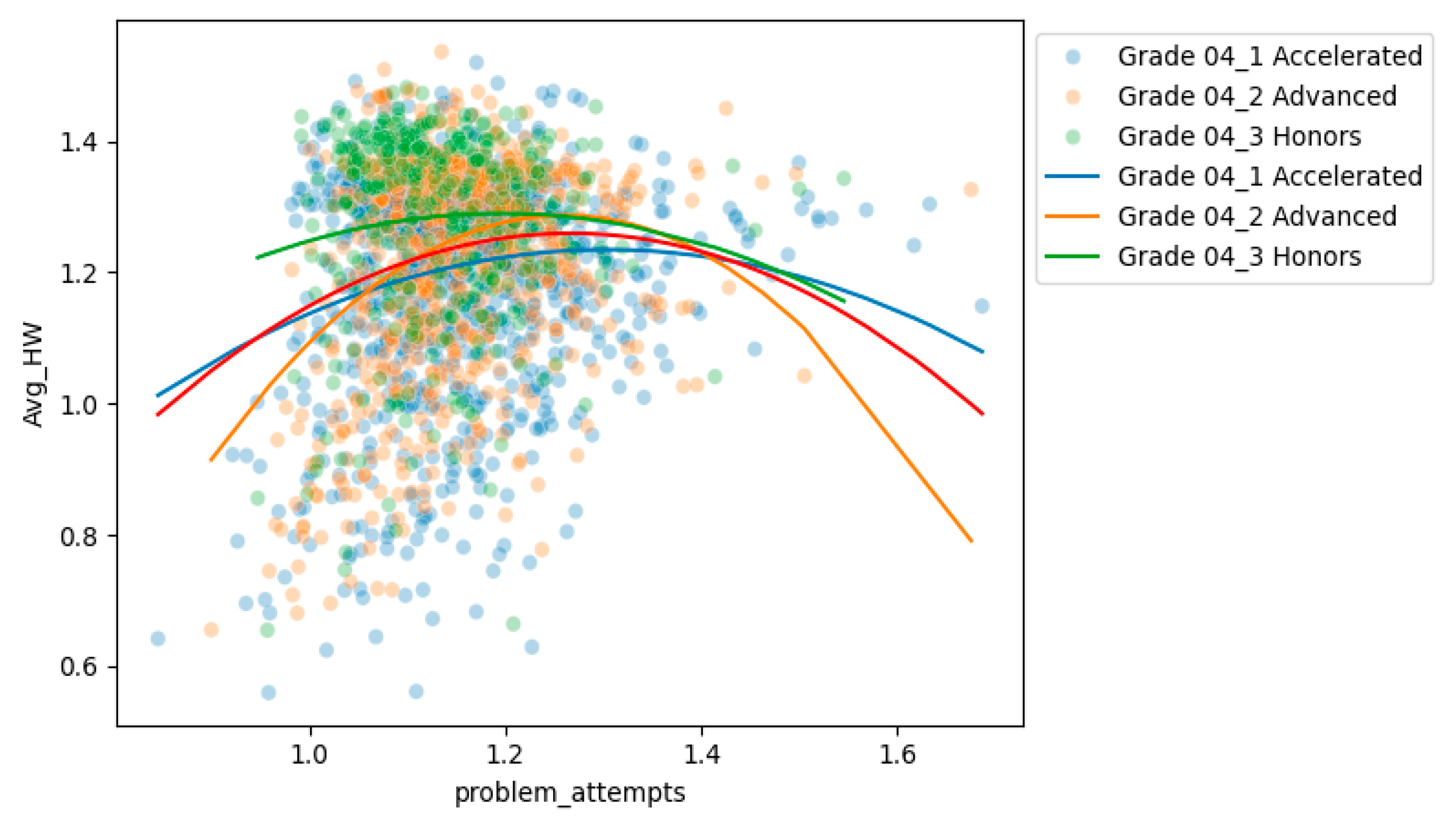
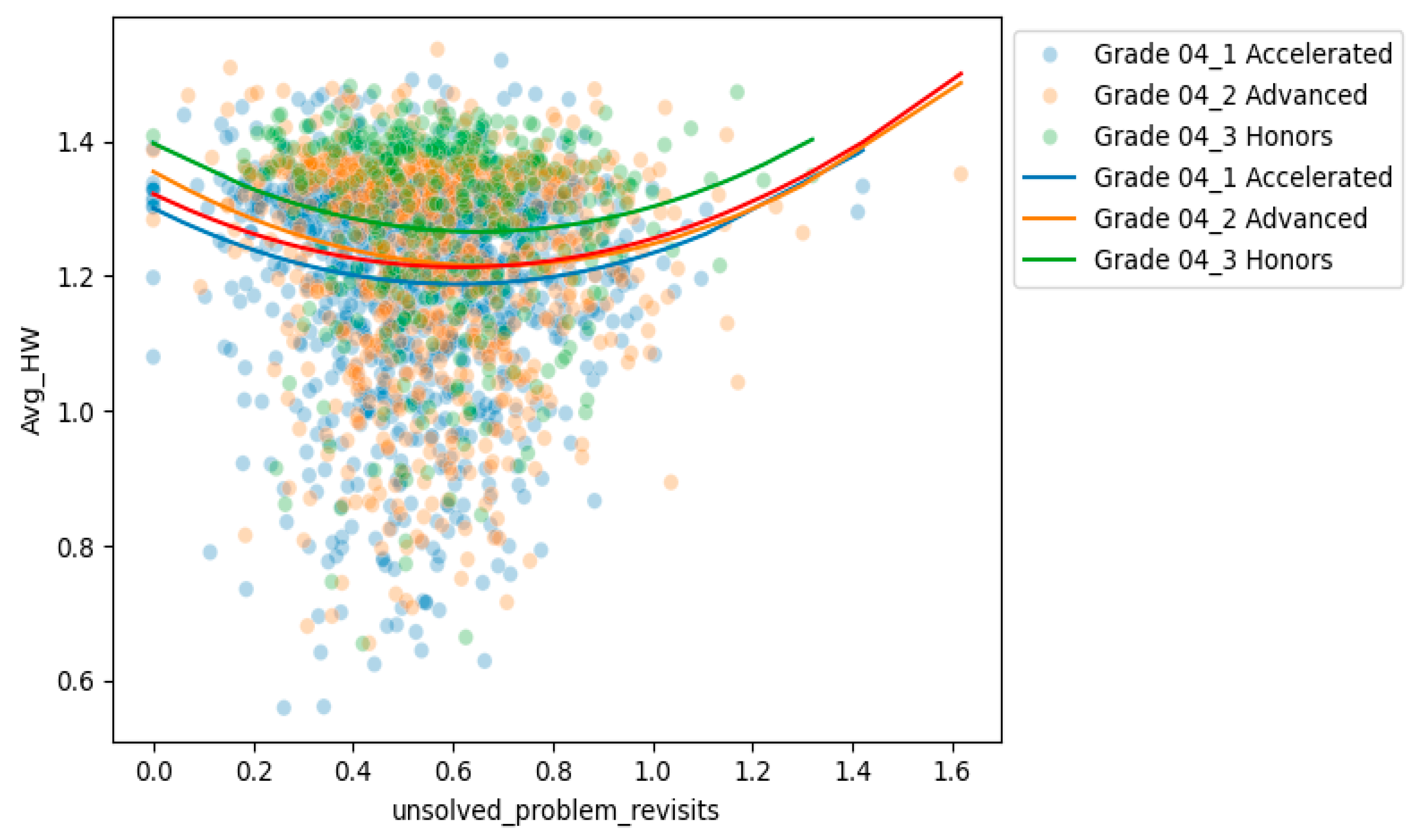
| Curriculum | 4_1 Accelerated | 4_2 Advanced | 4_3 Honors | Combined |
|---|---|---|---|---|
| Number of students, target—PT | 737 | 731 | 373 | 1841 |
| Boys | 361 | 367 | 222 | 950 |
| Girls | 376 | 364 | 151 | 891 |
| Number of students, target—% of problems solved in HW | 1084 | 799 | 406 | 2289 |
| Boys: | 548 | 405 | 245 | 1198 |
| Girls: | 536 | 394 | 161 | 1091 |
| Predictors | Description | Data Transformations |
|---|---|---|
| problem_attempts | Total number of times an answer was submitted to any student’s HW problem divided by the total number of problems in all HW assignments. Indicator of persistence | Square root |
| days_first_attempt | Average number of days between lesson end time and the first time student submits an answer to any problem in the HW assignment. Indicator of good homework habits | Square root |
| picture_upload | The number of times a student took a picture of their homework solution and uploaded it to RSM’s website divided by the total number of attempted homework assignment. Indicator of good homework habits | No transformation applied |
| time_spent_on_hw | The average time spent on solving homework assignments. When time is calculated, periods of inactivity (no answer submitted) of 15+ minutes are excluded. Indicator of persistence | Square root |
| unsolved_problem_revisits | If a problem was not solved during the first attempt—which can be several answer submissions in a row—this is how many times a student would return to it on average. A revisit is when a student worked (submitted an answer) on another problem before returning to that one. Indicator of consistency | Square root |
| hw_revisits | How many times a student comes back to their homework assignment on average. A revisit is coming back after a 12+ hours break. Indicator of consistency | Square root |
| attendance | The percentage of lessons attended excluding the first lesson. Some students join later or request a different weekday at the beginning of the year due to schedule conflicts, so we excluded the first lesson. Indicator of regular attendance | Arcsine |
| Predictors | Description | Data Transformations |
|---|---|---|
| PT | The score received for the Principal Test. The Principal Test is a 30 min test given in the second half of the school year to all RSM students. All students of the same curriculum receive identical questions. | Arcsine |
| Avg_HW | Average percentage of problems solved per homework assignment | Arcsine |
| All Three Years: Grade 4, Accelerated Level | ||||||
|---|---|---|---|---|---|---|
| Outcome | Homework (HW) score | |||||
| Predictor | All predictors | |||||
| Year | 2020–2021 | 2021–2022 | 2022–2023 | |||
| R-squared | 0.382 | 0.438 | 0.389 | |||
| F (p) | 10.86 (<0.013) | 22.53 (<0.01) | 21.74 (<0.01) | |||
| Adjusted R-squared | 0.352 | 0.422 | 0.374 | |||
| Root Mean Square Error | 0.660 | 0.546 | 0.598 | |||
| Sample size (n) | 241 | 386 | 457 | |||
| b | p | b | p | b | p | |
| Intercept | −0.178 | 0.030 | −0.139 | 0.027 | −0.069 | 0.233 |
| attendance | 0.141 | 0.023 | 0.142 | 0.001 | 0.101 | 0.005 |
| attendance_squared | −0.120 | 0.002 | −0.065 | 0.031 | −0.005 | 0.818 |
| hw_revisits | −0.045 | 0.507 | −0.228 | 0.000 | −0.265 | 0.000 |
| problem_attempts | 0.276 | 0.000 | 0.250 | 0.000 | 0.245 | 0.000 |
| problem_attempts_squared | −0.040 | 0.174 | −0.078 | 0.000 | −0.052 | 0.002 |
| picture_upload | 0.440 | 0.000 | 0.513 | 0.000 | 0.450 | 0.000 |
| unsolved_problem_revisits | −0.171 | 0.014 | −0.023 | 0.664 | −0.110 | 0.017 |
| unsolved_problem_revisits_squared | 0.057 | 0.049 | 0.033 | 0.340 | 0.057 | 0.029 |
| time_spent_on_hw | −0.078 | 0.212 | 0.113 | 0.023 | −0.000 | 0.978 |
| time_spent_on_hw_squared | 0.057 | 0.106 | 0.014 | 0.653 | −0.081 | 0.005 |
| days_first_attempt | −0.068 | 0.284 | −0.105 | 0.018 | −0.225 | 0.000 |
| All Three Years: Grade 4, Advanced Level | ||||||
|---|---|---|---|---|---|---|
| Outcome | Homework (HW) score | |||||
| Predictor | All predictors | |||||
| Year | 2020–2021 | 2021–2022 | 2022–2023 | |||
| R-squared | 0.477 | 0.388 | 0.523 | |||
| F (p) | 7.41 (<0.01)4 | 13.83 (<0.01) | 31.87 (<0.01) | |||
| Adjusted R-squared | 0.420 | 0.364 | 0.509 | |||
| Root Mean Square Error | 0.482 | 0.606 | 0.486 | |||
| Sample size (n) | 113 | 298 | 389 | |||
| b | p | b | p | b | p | |
| Intercept | 0.361 | 0.009 | 0.086 | 0.247 | 0.123 | 0.036 |
| attendance | 0.034 | 0.685 | 0.215 | 0.000 | 0.199 | 0.000 |
| attendance_squared | 0.052 | 0.546 | 0.050 | 0.189 | −0.025 | 0.354 |
| hw_revisits | −0.196 | 0.045 | −0.244 | 0.000 | −0.115 | 0.021 |
| problem_attempts | 0.430 | 0.002 | 0.410 | 0.000 | 0.452 | 0.000 |
| problem_attempts_squared | −0.182 | 0.022 | −0.133 | 0.000 | −0.115 | 0.000 |
| picture_upload | 0.400 | 0.000 | 0.357 | 0.000 | 0.434 | 0.000 |
| unsolved_problem_revisits | −0.338 | 0.003 | −0.173 | 0.003 | −0.159 | 0.000 |
| unsolved_problem_revisits_squared | 0.073 | 0.306 | 0.049 | 0.037 | 0.037 | 0.179 |
| time_spent_on_hw | 0.092 | 0.312 | −0.037 | 0.557 | −0.102 | 0.025 |
| time_spent_on_hw_squared | −0.106 | 0.174 | 0.029 | 0.469 | 0.036 | 0.182 |
| days_first_attempt | −0.277 | 0.001 | −0.169 | 0.002 | −0.164 | 0.000 |
| All Three Years: Grade 4, Honors Level | ||||||
|---|---|---|---|---|---|---|
| Outcome | Homework (HW) score | |||||
| Predictor | All predictors | |||||
| Year | 2020–2021 | 2021–2022 | 2022–2023 | |||
| R-squared | 0.467 | 0.355 | 0.327 | |||
| F (p) | 2.81 (<0.01)5 | 8.19 (<0.01) | 5.36 (<0.01) | |||
| Adjusted R-squared | 0.324 | 0.317 | 0.274 | |||
| Root Mean Square Error | 0.243 | 0.618 | 0.536 | |||
| Sample size (n) | 53 | 199 | 154 | |||
| b | p | b | p | b | p | |
| Intercept | 0.416 | 0.032 | 0.241 | 0.006 | 0.339 | 0.001 |
| attendance | 0.233 | 0.018 | 0.155 | 0.017 | 0.162 | 0.026 |
| attendance_squared | −0.048 | 0.539 | 0.045 | 0.123 | −0.008 | 0.875 |
| hw_revisits | 0.104 | 0.502 | −0.215 | 0.010 | −0.269 | 0.006 |
| problem_attempts | 0.286 | 0.144 | 0.119 | 0.214 | 0.106 | 0.318 |
| problem_attempts_squared | 0.002 | 0.989 | −0.092 | 0.021 | −0.040 | 0.308 |
| picture_upload | 0.250 | 0.009 | 0.387 | 0.000 | 0.378 | 0.000 |
| unsolved_problem_revisits | −0.437 | 0.005 | −0.015 | 0.846 | −0.070 | 0.437 |
| unsolved_problem_revisits_squared | 0.157 | 0.098 | 0.072 | 0.094 | 0.049 | 0.256 |
| time_spent_on_hw | −0.239 | 0.082 | 0.054 | 0.492 | 0.172 | 0.064 |
| time_spent_on_hw_squared | 0.030 | 0.666 | 0.005 | 0.913 | −0.004 | 0.936 |
| days_first_attempt | −0.178 | 0.110 | −0.117 | 0.077 | −0.142 | 0.071 |
| Outcome | Homework (HW) Score | |||||||
|---|---|---|---|---|---|---|---|---|
| Predictor | All predictors | |||||||
| Curriculum | 4_1 Accelerated | 4_2 Advanced | 4_3 Honors | All levels, all years | ||||
| R-squared | 0.380 | 0.450 | 0.330 | 0.360 | ||||
| F (p) | 59.73 (<0.01)6 | 58.57 (<0.01)7 | 17.63 (<0.01)8 | 116.41 (2 × 10−211) | ||||
| Adjusted R-squared | 0.374 | 0.442 | 0.311 | 0.357 | ||||
| Root Mean Square Error | 0.611 | 0.554 | 0.565 | 0.640 | ||||
| Sample size (n) | 1084 | 799 | 406 | 2289 | ||||
| b | p | b | p | b | p | b | p | |
| Intercept | −10.180 | 0.001 | 0.140 | 0.001 | 0.303 | 0.000 | 0.040 | 0.124 |
| attendance | 0.140 | 0.000 | 0.216 | 0.000 | 0.187 | 0.000 | 0.169 | 0.000 |
| attendance_squared | −0.042 | 0.011 | 0.003 | 0.879 | 0.038 | 0.066 | −0.004 | 0.733 |
| hw_revisits | −0.201 | 0.000 | −0.170 | 0.000 | −0.2289 | 0.000 | −0.197 | 0.000 |
| problem_attempts | 0.267 | 0.000 | 0.449 | 0.000 | 0.123 | 0.057 | 0.279 | 0.000 |
| problem_attempts_squared | −0.060 | 0.000 | −0.136 | 0.000 | −0.070 | 0.009 | −0.085 | 0.000 |
| picture_upload | 0.466 | 0.000 | 0.390 | 0.000 | 0.355 | 0.000 | 0.409 | 0.000 |
| unsolved_problem_revisits | −0.094 | 0.002 | −0.183 | 0.000 | −0.062 | 0.237 | −0.092 | 0.000 |
| unsolved_problem_revisits_squared | 0.051 | 0.002 | 0.048 | 0.003 | 0.068 | 0.014 | 0.050 | 0.000 |
| time_spent_on_hw | 0.018 | 0.563 | −0.063 | 0.065 | 0.090 | 0.093 | −0.002 | 0.923 |
| time_spent_on_hw_squared | −0.023 | 0.216 | 0.021 | 0.318 | −0.002 | 0.957 | −0.002 | 0.906 |
| days_first_attempt | −0.149 | 0.000 | −0.181 | 0.000 | −0.140 | 0.002 | −0.176 | 0.000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ilina, O.; Antonyan, S.; Kosogorova, M.; Mirny, A.; Brodskaia, J.; Singhal, M.; Belakurski, P.; Iyer, S.; Ni, B.; Shah, R.; et al. Understanding Fourth-Grade Student Achievement Using Process Data from Student’s Web-Based/Online Math Homework Exercises. Educ. Sci. 2025, 15, 753. https://doi.org/10.3390/educsci15060753
Ilina O, Antonyan S, Kosogorova M, Mirny A, Brodskaia J, Singhal M, Belakurski P, Iyer S, Ni B, Shah R, et al. Understanding Fourth-Grade Student Achievement Using Process Data from Student’s Web-Based/Online Math Homework Exercises. Education Sciences. 2025; 15(6):753. https://doi.org/10.3390/educsci15060753
Chicago/Turabian StyleIlina, Oksana, Sona Antonyan, Maria Kosogorova, Anna Mirny, Jenya Brodskaia, Manasi Singhal, Pavel Belakurski, Shreya Iyer, Brandon Ni, Ranai Shah, and et al. 2025. "Understanding Fourth-Grade Student Achievement Using Process Data from Student’s Web-Based/Online Math Homework Exercises" Education Sciences 15, no. 6: 753. https://doi.org/10.3390/educsci15060753
APA StyleIlina, O., Antonyan, S., Kosogorova, M., Mirny, A., Brodskaia, J., Singhal, M., Belakurski, P., Iyer, S., Ni, B., Shah, R., Sharma, M., & Ludlow, L. (2025). Understanding Fourth-Grade Student Achievement Using Process Data from Student’s Web-Based/Online Math Homework Exercises. Education Sciences, 15(6), 753. https://doi.org/10.3390/educsci15060753






