The Benefits of Modesty: Considering Incremental Professional Development for Mathematics Teachers

Abstract

Professional development (PD) for mathematics teachers often emphasizes transformative instructional change. However, a more modest, incremental approach may offer a higher likelihood of success in ways that complement transformational efforts. This Editorial discusses the potential advantages of incremental PD where teachers make small but meaningful improvements to their practice over time. We explore the differences between transformational PD and incremental PD as evidenced by the articles in this Special Issue. We also distinguish between varieties of incremental PD projects, from those that focus on a small piece of a larger instructional vision (piece-and-support incremental PD), those that set out to achieve a modest goal without appeal to a broader instructional transformation (modest-goal-with-support incremental PD), to a more radically modest approach that involves offering small, optional instructional suggestions without investments of time or training (nudge-based incremental PD). Ultimately, this Editorial, and this Special Issue as a whole, advocates for new conversations and investigations into how PD is structured and how the promoted instructional changes might spread among mathematics teachers.

1. Introduction

We, individually and now collaboratively, have been active in mathematics teacher professional development (PD) for more than 10 years (e.g., Candela, 2019; de Araujo et al., 2018; Herbel-Eisenmann et al., 2017; Otten, 2012), but recently we have stepped back to take a wider look at the field. Particularly in regard to the PD efforts aimed at influencing mathematics instruction, we share the view of Arbaugh (2025) and most of the other authors in this Special Issue that decades of dedicated efforts and high-quality work by brilliant and tireless scholars have failed to garner widespread change in mathematics instruction. Taking the United States as one example, there remains a large discrepancy between the type of mathematics instruction promoted by professional developers or scholars and the instruction commonly observed in classrooms across the country, the latter remaining largely procedural in focus and teacher-directed in style. Of course, the situation in other countries is different (e.g., Hansson, 2010; Kaur & Leong, 2021; Szendrei, 2007), but our own analysis of hundreds of secondary mathematics lessons across many states in the US (Otten et al., 2023, 2024a) and our experience with and inspection of research in elementary classrooms (Schweig et al., 2020) lead us to fully face the discrepancy. As Arbaugh (2025) puts it, “we have certainly developed pockets of teaching for mathematical understanding across the U.S. But we have yet to have widespread influence on the teaching of mathematics” (p. 4).

Based on these observations, we began wondering if it might be worthwhile for at least some of us in the mathematics education scholarly realm to consider an approach complementary to transformational PD, a term we use to refer to PD seeking large, transformational changes in instruction for the participating teachers (Otten et al., 2024c). This wondering led us to pursue incremental PD (Otten et al., 2022), which is our attempt to operationalize the notion that Star (2016) put forward about focusing on small improvements in mathematics teaching. By incremental PD, we mean PD that seeks only modest or small-scale changes in the participating teachers’ instructional practice, not a difficult or profound shift in their teaching. Note that incremental PD is defined by the scope of the PD and also the characteristics of the teachers involved (i.e., what is a modest change for one teacher may not be for another, and what may seem profound and out of reach for one teacher may be quite doable for another). Moreover, incremental PD refers to the approach taken within the PD; it does not specify the content of the PD (there are many small things one could focus on) nor the ultimate aim (i.e., what the PD is incrementing toward). But for us, these realizations spurred us to assemble a team of collaborators for our Practice-Driven PD project (www.PracticeDrivenPD.com), described below. We were also motivated to learn from other scholars who have been similarly discouraged by the lack of widespread success of transformational PD and who have made their own attempts to innovate their approach to PD or have attempted something akin to incremental PD.

Thus, in this Special Issue, we collect a variety of articles about innovative, and especially incremental, PD with mathematics teachers. With the remainder of this Editorial, we prepare readers for this Special Issue by (A) making some further comments about PD that has sought transformational changes to instruction, (B) pointing out some key differences between transformational PD and incremental PD while also identifying some varieties of incremental PD, and (C) describing our Practice-Driven PD project, which we argue is substantially different even from the other incremental PD efforts in this Special Issue.

2. A Broad Description of Transformational PD (With Concerns)

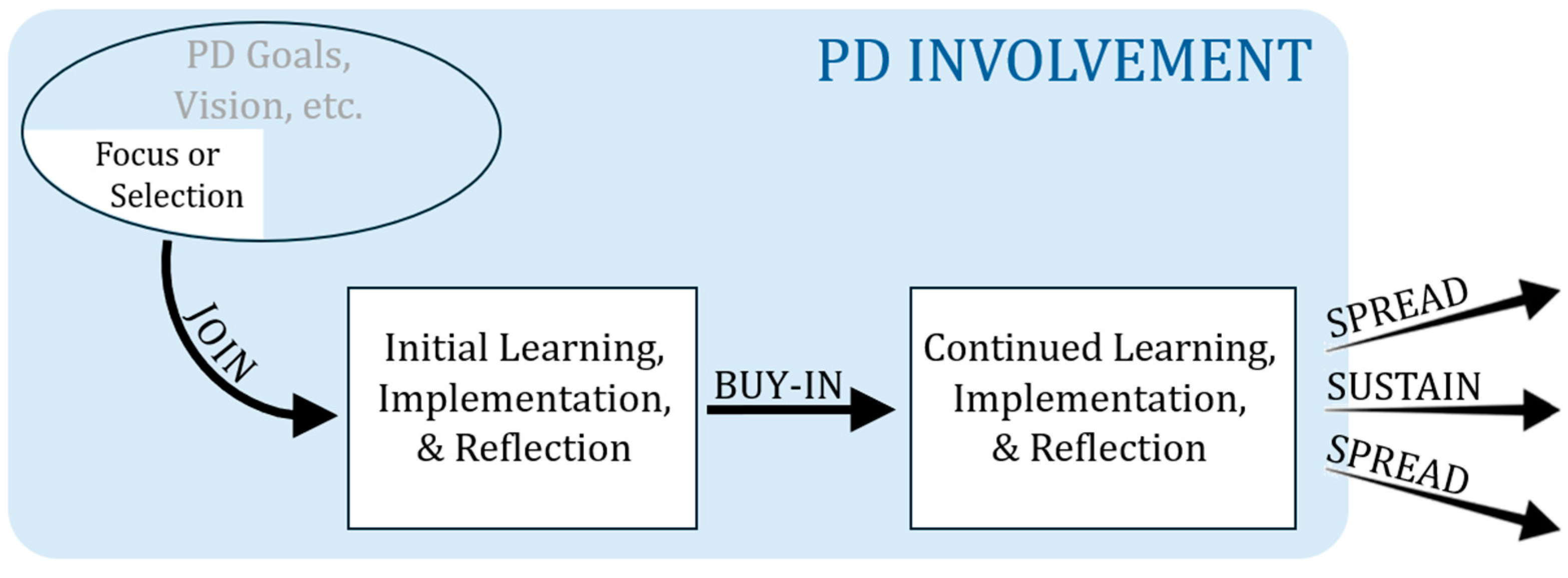
This section contains a broad overview of PD (Figure 1), admittedly missing many important elements and nuances, but we have attempted to represent the key elements that are contrasted in the subsequent sections. With that disclaimer in mind, we can say that our review of PD literature in mathematics education and our general involvement in the field has revealed that many PD efforts begin with the developers identifying a specific goal or focus for the PD. This often occurs before the PD even has teachers identified or signed on to the PD. Because we are especially interested in PD focused on mathematics instruction, examples of orienting PD goals or aims would be promoting a certain form of mathematical discourse (Herbel-Eisenmann et al., 2017; Smith & Stein, 2011), the implementation of certain types of mathematical tasks (Santagata et al., 2010), or reasoning routines (Kelemanik et al., 2016). In the case of Leshin et al. (2024) in this Special Issue, the PD goal is the enactment of Mindset Mathematics, which includes student-centered mathematical activity around challenging mathematical tasks and also a growth mindset stance in the classroom. We feel that these aims would be transformational in nature for the vast majority of teachers, at least in the US, and we believe most of the cited authors would agree with that characterization because they openly acknowledge the profundity of what they are pursuing.

We are not opposed to transformational goals or visions for instruction per se, but we are somewhat pessimistic about the likelihood of success at scale when they are made the starting point and the focus of PD efforts. One fundamental concern is that the goals of transformational PD are, by definition, quite distant from current, conventional mathematics teaching practice. This distance not only means that the PD-promoted changes will be difficult to enact but also that, if enacted, the changes may trigger backlash that falls upon the teacher because the instruction is noticeably different from the expectations of students, other teachers, administrators, parents, community members, etc. (Otten et al., 2024c). This distance might also lead to a feeling of separation between the “reality-based” teachers and the “idealistic” developers or scholars (hence the depiction in Figure 1 of the PD goals of transformational PD as spatially above the realm of implementation). Arbaugh (2025) expressed similar concerns about transformational PD goals, especially with regard to feasibility for many teachers. For example, she is supportive of the Five Practices (Smith & Stein, 2011) as an excellent approach to orchestrating mathematical discussions, but she has come to view it as too ambitious for many preservice teachers or even some in-service teachers to enact, and so she proposed narrowing in on just one aspect of the Five Practices, such as spending a semester on a certain pedagogical skill incorporated into the Five Practices and then proceeding incrementally from there.

But of course, the goals of transformational PD are shared by and inspiring to some teachers who want to develop those sorts of visions or forms of instruction. They would hopefully have opportunities to join a transformational PD project, most of which do typically involve teachers joining or becoming actively involved in the PD in some manner. This joining can take many forms (e.g., enrolling in a course, attending a workshop or summer institute, joining a book study, participating in a year-long or multi-year university-sponsored project, etc.) and it is often voluntary, but also sometimes compulsory. Even with this variety in formats and opportunities to join, we have a substantial concern that many mathematics teachers will be left out. It may be a capacity limitation because transformational PD is often intensive and expensive, so perhaps there is not room to include enough teachers to reach critical mass for widespread change, and there are also limitations on the teacher side because they may not have the time, energy, interest, or support necessary to join the transformational effort. In short, even if transformational PD was 100% successful in achieving instructional change with the teachers who join the project, it would still fail to reach the many teachers who cannot or do not participate.

Unfortunately, transformational PD is not 100% successful in bringing about the intended instructional change with its participants because, even after teachers join, there remains important and challenging work to do. There is usually some form of initial learning such as a PD kick-off or an introduction to the key ideas and rationales for the work and, although there is wide variation in PD models and activities, there might be some sort of initial implementation or attempt in practice which then spurs reflection, with the reflection often guided by the PD itself. These connections to practice and implementations are represented by the square boxes lying horizontally in the visual model (Figure 1). The hope is that teachers fully buy-in to the aims and practices promoted by the PD, but because the PD is transformational and thus pursuing things distal from conventional practice, this buy-in is not assured. As mentioned above, some teachers might have been on board from the start when they joined the PD, knowing full well its goals and intentions. Other teachers may be only curious (or externally compelled) to join the PD and so it may be later through the initial learning opportunities and the initial implementations that they become convinced of the merits of the PD. But as many scholars and developers state (e.g., Kelemanik et al., 2016; Lampert et al., 2013), transformational changes are often difficult to make, and many of the ambitious practices promoted may not go well at the beginning. For these and other reasons (e.g., a sincerely different vision of mathematics instruction or a different opinion about the problems and remedies in mathematics education held by the teacher than by the developer), we feel that buy-in levels for transformational PD are not uniformly high.

Nevertheless, there are many “pockets” of success, as Arbaugh (2025) refers to them, and to achieve that success, transformational PD often involves extended interactions for teachers within the PD and multiple opportunities for implementation and reflection. Indeed, duration and ongoing professional collaboration are often criteria for effective PD (Blank & de las Alas, 2009; Desimone, 2011), or effective transformational PD, as we would amend it. Through all of this, the PD is directly involved with teachers in various ways, as represented by the green coloration that surrounds the PD goals, the initial learning and implementations, and the continued learning and implementations of the promoted instruction. PD involvement can take many different forms, such as the presentation of content or examples of ambitious instruction, the analysis of artifacts from practice through the lens of the PD goals, facilitation of discussions around the PD aims and rationales, creation of opportunities for teachers to view one another’s teaching or to view and reflect upon one’s own teaching, a sequence of specific trainings for certain pedagogical skills that are assembled into the broader instructional transformation, or many other PD offerings and forms of involvement. Some of our concerns in this area are that substantial and lengthy PD involvement is costly on the PD side both in terms of resources as well as time and effort. It is also challenging on the teacher side because they are often already busy or overburdened with other responsibilities. In short, transformational PD often includes many components to try to promote the difficult (though important) changes in instruction it is pursuing. And when the changes do not occur, we have noticed that many PD leaders tend to view the solution as needing more resources, more involvement between the PD and the teachers, more buy-in from school leaders, students, and parents (in addition to buy-in from the teachers), or more alignment with regard to curriculum materials or assessments. But seeking or requiring more of these things would, in our view, possibly increase the local likelihood of success but would simultaneously reduce the likelihood of the transformational PD actually leading to widespread change.

Widespread change is the final element of our model (Figure 1). The hope of transformational PD is that it will sustain with the teachers involved, despite challenging contextual realities such as teacher turnover, administrator changes, curriculum adoption cycles, shifts in district priorities, and more. But this hope is not always realized (Karsenty & Brodie, 2023; Tirosh et al., 2015). There is also a hope, perhaps even more fleeting, that the profound instructional changes so hard-won through the transformational PD will also spread to other teachers and other schools. People have written about how this spread can occur (e.g., Bartell & Aguirre, 2019; Clarke & Hollingsworth, 2002; Coburn, 2003; Timperley et al., 2014), but it does not seem to have occurred yet, even after decades of our field’s best efforts. There are some important insights to be had, however, through the existing literature and through the work of Leshin et al. (2024) in this Special Issue, who explicitly studied the aspects of a transformational PD experience that teachers took up and sustained versus those aspects of the PD that were not sustained. Their PD was rooted in an intensive summer camp wherein teachers tried an ambitious model of instruction centered on Mindset Mathematics, and the authors then followed the teachers back to their regular school classrooms the next academic year to gather data. They found that teachers did, after the intensive work of the PD, take up and sustain certain instructional practices such as posing the open tasks supplied by the PD, giving collaboration time to students, and asking questions to push student reasoning. But other promoted practices were not sustained, such as explicitly including mindset messages in their teaching or making mathematical mistakes a focus of instruction. This kind of research, examining what is taken up from PD and why, is extremely valuable as we collectively reflect on the efficacy of transformational PD efforts and might help to alleviate our concern that those arrows on the right side of Figure 1, representing transformational changes to instructions that will sustain and spread, are merely hopeful rather than probable.

In summary, although we do not claim that the basic model presented here captures all instances of transformational PD, we do believe that many instances of transformational PD involve a goal or vision for instruction that is substantially different from conventional mathematics instruction and that the PD seeks teachers who will join the effort to try to enact those instructional changes. Subsequently, the teacher becomes involved with the PD for an extended period, requiring investments of time and energy to engage in various undertakings such as learning activities, the implementation of PD-promoted instruction, reflection, and more. This work is difficult, but the hope is that the changes become deep-seated and will therefore sustain for the teacher, possibly within a professional community that has formed via the PD, and then somehow the PD (or its goals and vision) will also spread to other teachers. But, as stated above and in many of the articles in this Special Issue, it is challenging to (A) reach a majority of teachers, (B) achieve the transformational changes with participating teachers, and (C) for such changes to spread beyond those directly involved in the PD. Thus, many scholars are investigating incremental approaches to PD that may avoid some of these concerns.

3. An Overview of Incremental PD Efforts Contained in This Special Issue (With Two Subtypes Identified)

Incremental PD, by definition, is more modest than transformational PD in the instructional shifts it expects from teachers. But as some of the articles in this Special Issue demonstrate, there can be a great deal of overlap between the incremental PD model and the transformational PD model, and there can be differences in the ways scholars have attempted to make their PD more incremental. Starting as in the previous section with the PD goals, we have identified two subtypes of incremental PD. The first subtype involves building PD around one piece of a larger goal or vision for mathematics instruction. In a sense, this form of PD takes a transformational goal and breaks it down into something more manageable and thus makes the PD incremental for teachers. The forms of initial learning and continued learning are similar to those discussed for transformational PD, but now the focus is more modest. We refer to this subtype as piece-and-support incremental PD because it centers on a piece of a larger (transformational or ambitious) instructional goal and provides support through robust PD involvement (see Figure 2).

Arbaugh’s (2025) example already mentioned, of spending a semester on just one aspect or precursor of Five Practices discussion orchestration, would fit in this piece-and-support incremental PD subtype. Several other detailed examples can also be found in this Special Issue. Bondurant (2024) and Litke et al. (2025) both identify equitable mathematics instruction as the ambitious, complex teaching phenomenon that is the ultimate goal of their PD efforts, but they allow the teachers in their PD to make a selection so that just one (or a small number) of simpler phenomena can be the focus of the PD. Bondurant had teachers read a book containing complex and challenging (and worthwhile!) ideas about mathematics pedagogy, but then to make their implementation and reflection more manageable, they identified just one aspect or idea from the book to focus on. Similarly, Litke et al. provided teachers with many different rubrics that elucidated various aspects of equitable instruction, and although all the rubrics are worthwhile, the PD consisted of coaches working with teachers to choose just one rubric to focus on for their own practice. In both cases, this element of teacher choice was hypothesized to increase teachers’ buy-in to the PD, which may be a tangible advantage that this form of incremental PD has over transformational PD while still sharing the same end goals as transformational PD.

The two examples just cited involved equitable instruction at the secondary school level. Marzocchi et al. (2024) worked instead at the university level, but they focused on a similar overarching goal, which they called equity-minded active instruction. The PD providers offered many different specific strategies and resources related to equity-minded active instruction, but the university mathematics instructors were free to select whichever they wanted to implement. This freedom for the instructors also included the option of choosing none of the strategies or resources; PD involvement was not obligatory. Similarly, Lee et al. (2024) offered free choice to teachers about what they wanted to access from online PD resources. In this case, the broad goal of the PD was the teaching and learning of statistics and data science, with a wide range of content-based material for teachers’ own knowledge enhancement as well as instructional material and insights into student tasks and thinking. Even though all teachers completed at least 20 h of module materials, there was variability in the order in which they completed modules, with fewer teachers completing a module on “Discourse” than on “What is statistics and data science?”, and even then tending to complete the “Discourse” module near the end of their learning experience. As with Leshin et al.’s (2024) study, we find it interesting to look closely at what teachers take up from PD and what they shy away from, though with Lee et al.’s (2024) PD, they were allowing teachers to take just one piece of a larger offering.

Within piece-and-support incremental PD, it is not always the teachers who make the selection. For Quebec Fuentes (2025), the broad goal of the PD is to facilitate mathematically rich small-group discourse, but recognizing that this is a challenging undertaking for most teachers, Quebec Fuentes, as the designer of the S³D approach to PD, made the choice to focus the teacher’s attention and efforts onto just one small group. In this way, after building awareness of the nuances of group dynamics and also finding success with the mathematical interactions in that single group, the teacher could increment this in the future to incorporate more groups. Elliott and Roberts (2024), with the stated endpoint of robust instructional routines for student interaction and mathematical thinking, also describe their careful process of breaking down the routines into component parts and trying to design the PD in such a way that the teachers would incrementally approach the full implementation of the routines.

This work is all meritorious and we feel that those interested in transformational PD and incremental PD alike will be interested in the results of these efforts to parse transformational goals for the purpose of promoting instructional change. We also expect that some scholars will have criticisms because they will argue that some of the complex and ambitious goals can only truly be approached by embracing their entirety and their complexity, that something is lost when the goals are sliced or partitioned. These points are well worth considering, but they should also be placed into dialog with the need for higher uptake and wider spread of the instruction being promoted. And there is another discussion to be had as well, wherein a large, transformational instructional goal does not enter the model at all.

This leads us to the second subtype of incremental PD. In this version, there is no lofty goal at all; instead, the instructional foci or the suggestions for practice from the PD are modest and close to teachers’ existing practice (see the oval in Figure 3, which is smaller and placed lower than the goal ovals in Figure 1 and Figure 2). One might refer to this as modest-goal-with-support incremental PD, and it is similar to what we have advocated for in the past (Otten et al., 2022), drawing inspiration not only from Star’s (2016) work but also Cortina and Višňovská’s (2023) research about teaching suggestions that will actually spread, as well as from curriculum research, where shifts in curriculum need to be not-too-far from teachers’ comfort zones (Choppin et al., 2018).

Within this Special Issue, Lesseig and Hoppe (2024) made their PD modest and manageable by encouraging teachers to focus on just one facet of instruction stemming from a specific question or aspect of practice they were interested in examining (e.g., using an open task, pursuing differentiation through student choice). Although these instructional changes might be built upon in future PD sessions, such expansion was not the stated goal of the PD. In that way, each PD session could stand on its own, with teachers free to investigate different aspects of practice and individualize their learning. Similarly, teachers who experienced PD from Jansen et al. (2024) were exposed in some manner to ideas of Rough Draft Math (Jansen, 2020), and they could try just one small suggestion in their own teaching. A teacher taking up even a single instructional move of allowing students to revise their mathematical thinking would be regarded as a PD success; the instructional change was not required or expected to be part of a broader vision of mathematics instruction. Admittedly, Jansen et al.’s (2024) article in this Special Issue encompasses several different studies and thus several different versions of PD from a single post shared on social media to a single conference session or a more extensive book study. The full notions of Rough Draft Math as articulated in the book (Jansen, 2020) might be fairly transformative for many teachers, and thus some of the incremental PD may be interpreted as the piece-and-support subtype, but in other instances where a specific, small-scale rough draft strategy is being shared and there is no reference to or expectation of teachers engaging with the broader instructional notions, we view it as an example of modest-goal-with-support incremental PD. (If a teacher simply grabs a suggestion off of social media and does not have any further interactions with the developers or scholars behind the suggestion, then the lack of follow-up support may actually make it an instance of the nudge-based incremental PD described in the next section.)

Thus far, we have discussed the foci of incremental PD, which can sometimes be a purposeful portion of a larger, transformational instructional goal (piece-with-support incremental PD), or it can be a modest, small-scale instructional suggestion made on its own merits without appeal to a more transformational goal (modest-goal-with-support incremental PD). A theme that emerged is the potential role of teacher choice in establishing the foci of incremental PD. In the next section, we describe our own Practice-Driven PD model which relies on teacher choice to an even greater extent, but first we must comment on the extent and types of PD involvement in the incremental PD projects reported in this Special Issue (represented by the blue coloration in Figure 2 and Figure 3). Readers may notice that transformational PD and the two subtypes of incremental PD already discussed (both “with-support”) have similar levels of PD involvement.

Other than portions of Jansen et al.’s (2024) work, all of the PD projects reported in this Special Issue involve teachers who join the PD in some manner. A few allow for minimal participation (i.e., Marzocchi et al., 2024; Lee et al., 2024), but the teachers nevertheless receive access to the PD materials and are visibly included in some group of teachers or instructors to whom the PD is offered. The other PD models all have some substantial form of expected participation. What is that involvement and what does the PD provide to the participating teachers? For Marzocchi et al. (2024) and Lee et al. (2024), the involvement is, as just alluded to, the opportunity to explore and consume PD resources and engage in interactions facilitated within the PD platform. For Elliott and Roberts (2024) and Lesseig and Hoppe (2024), the teachers are expected to actively participate in multiple cycles of the Mathematics Studio PD format, which is a structured approach to professional collaboration and reflection that draws inspiration from Japanese Lesson Study. In other cases, the PD offering was a graduate-level course that functioned as a professional learning community led by the university scholar (Bondurant, 2024), a coaching relationship established between the teachers and the scholars to engage together in video- and rubric-based reflection cycles (Litke et al., 2025), or a collaborative series of phases of setting instructional goals, planning instruction, and reflecting on implementation (Quebec Fuentes, 2025).

Just as the form of the PD involvement varies, so too does the duration. Within several of the incremental PD efforts, the duration was entirely up to the teachers and could be very short if they wished (Jansen et al., 2024; Marzocchi et al., 2024; Lee et al., 2024), but it could also be months or longer. Commitments of one semester or multiple academic quarters were entailed in the PD of Bondurant (2024) and Quebec Fuentes (2025), and other projects lasted for a year (Litke et al., 2025) or even multiple years (Lesseig & Hoppe, 2024; Elliott & Roberts, 2024). So, it is not the forms of support nor the duration of involvement that distinguishes incremental PD from transformational PD; both approaches can have substantial levels of involvement, and therefore the concerns about the resources necessary to enact the PD or the burdens placed on already-busy teachers are not alleviated by these types of incremental PD. But it is possible that, by having more modest aims, it might make the promoted instructional changes more likely to occur within incremental PD than in transformational PD. For similar reasons, the modest aims might make it easier for teachers to sustain and subsequently spread the instructional changes to others.

This leads us to the question of what happens after the PD involvement ends. As discussed above and attested by many of the authors in this Special Issue, there is substantial evidence pointing to the lack of sustainment and lack of spread for transformational PD. But would incremental PD fare any better? Given that most of the studies in this Special Issue were reporting detailed investigations of the PD that took place, it was beyond their scope to also study the sustainment and spread. But Leshin et al. (2024) did collect some of these data following their transformational PD effort, and it is worthwhile to consider why certain practices were taken up and sustained more readily than others. We hypothesize that the promoted practices more proximate to conventional instruction (or those that offer direct replacements of things in conventional instruction) had higher uptake. For example, the open tasks provided by the PD project could be directly inserted in place of lower-level tasks already in the standard curriculum, and this might be part of the reason it had relatively strong uptake. Similarly, the question types that push student reasoning can be directly inserted in place of other questions that teachers typically ask students as they work. But mindset messages are meta-textual in a manner that might not be usual for many teachers, and dedicating classroom attention to mathematical errors might be a substantial deviation from conventional instruction that focuses exclusively on correct procedures and concepts. Lee et al. (2024) also provided some data around notions of uptake by the teachers, even if they could not study the spread to other teachers. They found that modules recommended to users were accessed by more teachers and that a few modules were accessed by noticeably fewer teachers. This finding may be a simple matter of teacher interest, time constraints, and navigational layout in the PD platform. We noticed, however, that one of the least-accessed modules of “Discourse” happens to be related to what we described above as a transformational instructional aim. Moreover, “Comparing Distributions” addresses important statistical content that many math teachers need to be prepared to teach, but science and social studies teachers in the study may have found it less important to them, so it may be a matter of providing options that resonate with the specific teachers involved.

We have more thoughts on this matter, but we invite readers to consider this phenomenon independently, free from our persuasion. Overall, we are genuinely curious about whether the sustainment and spread of incremental PD might be different than transformational PD. We have collected this and other empirical questions to be explored about incremental PD in Appendix A. Next, we share a brief description of our own approach to incremental PD, which, like modest-goal-with-support incremental PD, has modest goals as its foundation but differs in several important regards.

4. A Summary of Practice-Driven PD (With an Explanation of Its Differences from Other Incremental PD)

Building off of initial attempts to support teachers with brief videos as part of the Two-Minute Teacher’s Guide (de Araujo & Otten, 2017), we have been working for several years with a team of mathematics educators to develop and study Practice-Driven Professional Development (www.PracticeDrivenPD.com). Our formal data collection involves distributing PD materials and studying classroom practice specifically with algebra teachers in the U.S., but our approach to the PD in general can be used for any grade level or mathematical content area (Otten et al., 2022). 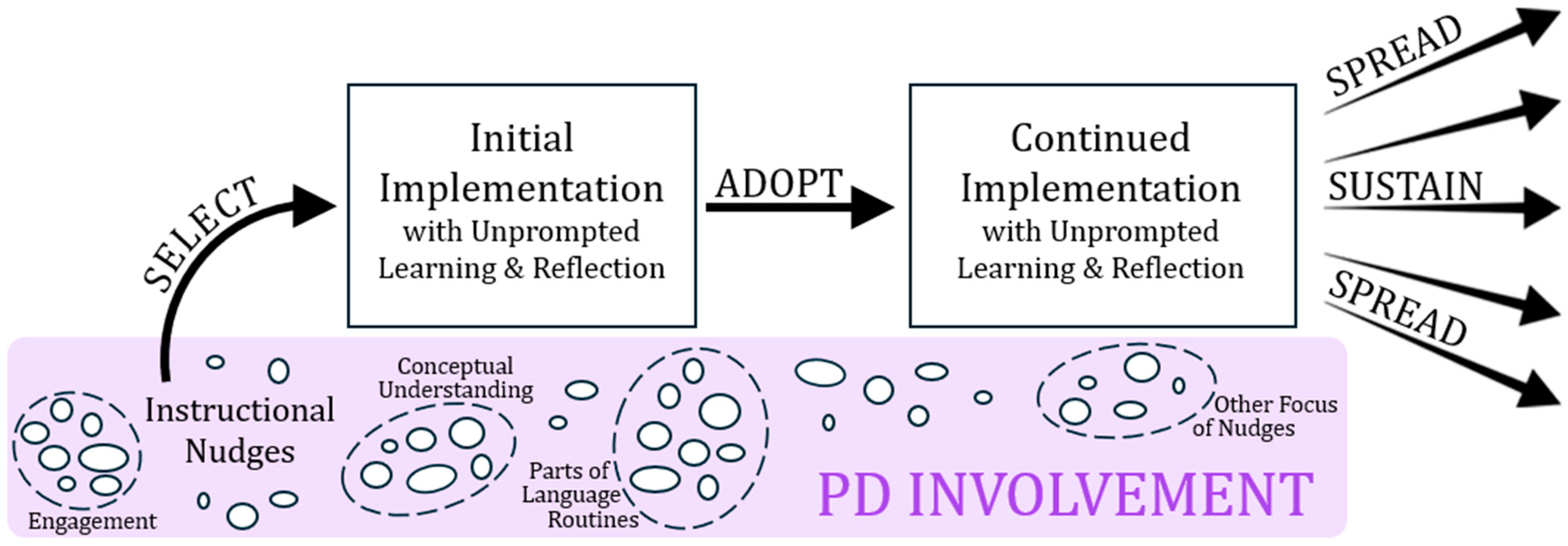Figure 4 displays a simple representation of Practice-Driven PD for the purpose of contrasting it with the transformational PD and also the other styles of incremental PD discussed above.

With regard to the starting point of the PD, we have no instructional vision or larger goal at play (at least not explicitly named or visible to teachers). Instead, PDPD consists of offering a wide variety of standalone instructional nudges. By instructional nudge, we mean a modest suggestion for teachers that is designed for easy implementation in their current practice (see www.PracticeDrivenPD.com for many examples, all of which can be represented on a single-page document or a short video). The nudges are designed to be (A) immediately comprehensible to teachers so that minimal time investment is needed to attempt the nudge (Cortina & Višňovská, 2023; Otten et al., 2022), (B) modest and in close proximity to conventional instructional practices so that teachers can easily identify where to implement it in their lessons and it works in a wide variety of contexts, and (C) to have a relatively high likelihood of success upon first attempt because this is influential in them continuing to employ the nudge and in potentially trying additional nudges. Although the instructional nudges can each stand alone, we have designed a few of them around (implicit) goals such as increased student engagement, opportunities for the development of conceptual understanding, and the implementation of incremental aspects of mathematical language routines (Zwiers et al., 2017). These (implicit) goals are represented by the dashed ovals in Figure 4 demarking subsets of instructional nudges, but overall, the PDPD approach involves simply making a wide variety of nudges available to teachers. We do not promote certain nudges over others and do not predetermine the “best” or “worst” nudges but instead trust the teachers to choose whichever nudges will work best for them, and we are actively studying the uptake of nudges, as revealed by those teacher choices. Thus, in PDPD, it is teacher selection that occurs as the link between the PD offering and the teachers’ actual practice, not a teacher joining the PD effort as in transformational PD and also most of the incremental PD examples in this Special Issue.

In this way, the PD involvement within the PDPD approach is minimal and, as professional developers, we never actually enter into the realm of practice (thus, in Figure 4, the purple coloration is only around the instructional nudges that were designed by the PD team, whereas Figure 1, Figure 2 and Figure 3 show PD involvement with the teachers in relation to learning, reflection, and practice). This is part of what we mean with our project title of Practice-Driven PD. The teachers are the sole drivers of their implementations of the instructional nudges, the learning or reflection that they have in relation to those nudges, and in the decision to continue implementing said nudges in practice. We do not need to pursue buy-in during extended project involvement because the only threshold to overcome is their act of selecting a nudge that interests them. We do not train them on how to implement the nudge “correctly” beyond what is on the one-page nudge document or in the brief nudge video; just as we trust the teachers with selection, we also trust the teachers with implementation and allow them freedom and agency in this regard. The absence of PD involvement, however, does not mean the role of the PD is minimal; it is still substantial and important, but it takes a completely different form than the extended supportive role, as seen in the PD models above. With PDPD, there are years of work carefully designing the instructional nudges to be clear, concise, worthwhile, and appealing to teachers (and especially appealing to teachers who are unlikely to be reached by more intensive forms of PD; see our web article (Otten et al., 2024b) for more on this important point). We also work to be responsive to teachers, so if we find that some instructional nudges are not working or are not being selected at all, we have to be willing to modify them or abandon them and create new nudges that will have higher uptake.

So, there is a great deal of effort and expertise that goes into the creation and distribution of instructional nudges, but once high-uptake nudges are created and available to teachers, the fact that PDPD involves no further investments of resources, time, or energy leads us to hypothesize that the sustainment and spread might be qualitatively and quantitatively different than the sustainment and spread of more intensive instructional changes. Because the nudges are close to conventional practice (and hence close to the current practice of many mathematics teachers) and they are compact and modest, this makes them not only easy for a teacher to implement but also easy for that teacher to share with others in their building, in their social network, or beyond. To be clear, we do not think that all of the available nudges will be taken up and spread, but we think it is plausible that some of them will. This instructional “survival of the fittest” (or Practical Selection, to extend the evolutionary analogy for incremental changes) together with inevitable tweaks and adaptations along the way can gradually lead to nudges that spread and improve mathematics instruction in modest but meaningful ways. Our hope would be that decades of this type of work would lead to more change than has occurred over the past few decades of PD efforts. And we acknowledge that teachers are already spreading small teaching ideas in this organic manner (see the popularity of Teachers Pay Teachers, or now TPT, for example), but in our view, the scholarly community of university-based mathematics educators and professional developers has not yet made concerted efforts in this way.

5. Conclusions

In this Editorial, we have drawn a broad contrast between transformational PD that pursues substantial changes in mathematics instruction and incremental PD that has more modest aims. We have also attempted to articulate some differences among the varieties of incremental PD, from piece-and-support incremental PD that focuses on a small, manageable part of what might eventually be a transformational change to modest-goal-and-support incremental PD that focuses on smaller instructional phenomena without explicit reference to a broader transformational change. We also briefly described our own Practice-Driven PD project, which has modest goals but does not entail extended PD support and so may be described as a particular attempt at nudge-based incremental PD. Because our project lacks the kind of PD support that is entailed in all the other forms of PD, it is possible some people may feel that Practice-Driven PD is not really PD at all, but we nevertheless have hypothesized that it is precisely the lower threshold for entry and the reduced investment of time and resources that might give nudge-based approaches the potential for sustainment and spread in ways that have not occurred from intensive transformational efforts.

Of course, in these pages, we have only given a brief overview of some of the dynamics at play with incremental and innovative attempts at PD for mathematics teachers. The remaining articles in this Special Issue feature a variety of starting points for PD and a variety of forms of PD support and involvement. The authors also share data and interpretations that show substantial promise for incremental approaches as something that can be successful with teachers while being mindful of all the constraints and burdens that teachers face. As you read the articles in this Special Issue, you can attend to the empirical questions the authors answer as well as additional questions that should be considered by the field. We have collected a variety of such questions in Appendix A, but we are sure there are many more that are worthwhile as we reflect on the state of PD in our field and discern a way forward. We also acknowledge a broad question: when we increment mathematics instruction, what are we incrementing toward? Transformational PD has a strength in its clarity of purpose, and at least the piece-and-support type of incremental PD may share this strength. But those engaging in modest-goal and nudge-based PD would be wise to consider their longer-term trajectory, even if specific PD efforts are purposefully small-scale. As Arbaugh (2025) cautions, there should still be orienting theories at work even for the most modest PD endeavors.

We close by thanking all of the scholars for their contributions to this Special Issue. We are truly honored to have helped bring this work to fruition and hope it spurs further reflection on PD for mathematics teachers and on the continued efforts to promote instructional improvements in mathematics classrooms. Even modest insights and small steps in the direction of improved understanding of the possibilities (and pitfalls) of incremental PD will have been worthwhile.