Observing Mathematical Learning Experiences in the Primary Years to Examine How Attitudes Towards Mathematics Are Enacted in the Classroom
Abstract
1. Introduction
1.1. Attitudes Towards Mathematics
1.2. Theoretical Framework
2. Materials and Methods
2.1. Participants
2.2. Methods
Analytical Approach to Developing an Observational Framework
- (a)
- Flanders’ Interaction Analysis Categories (FIAC)
- (b)
- Social Discourse Analysis
- (c)
- Pragmatics (Social Communication)
- (d)
- Non-verbal Communication
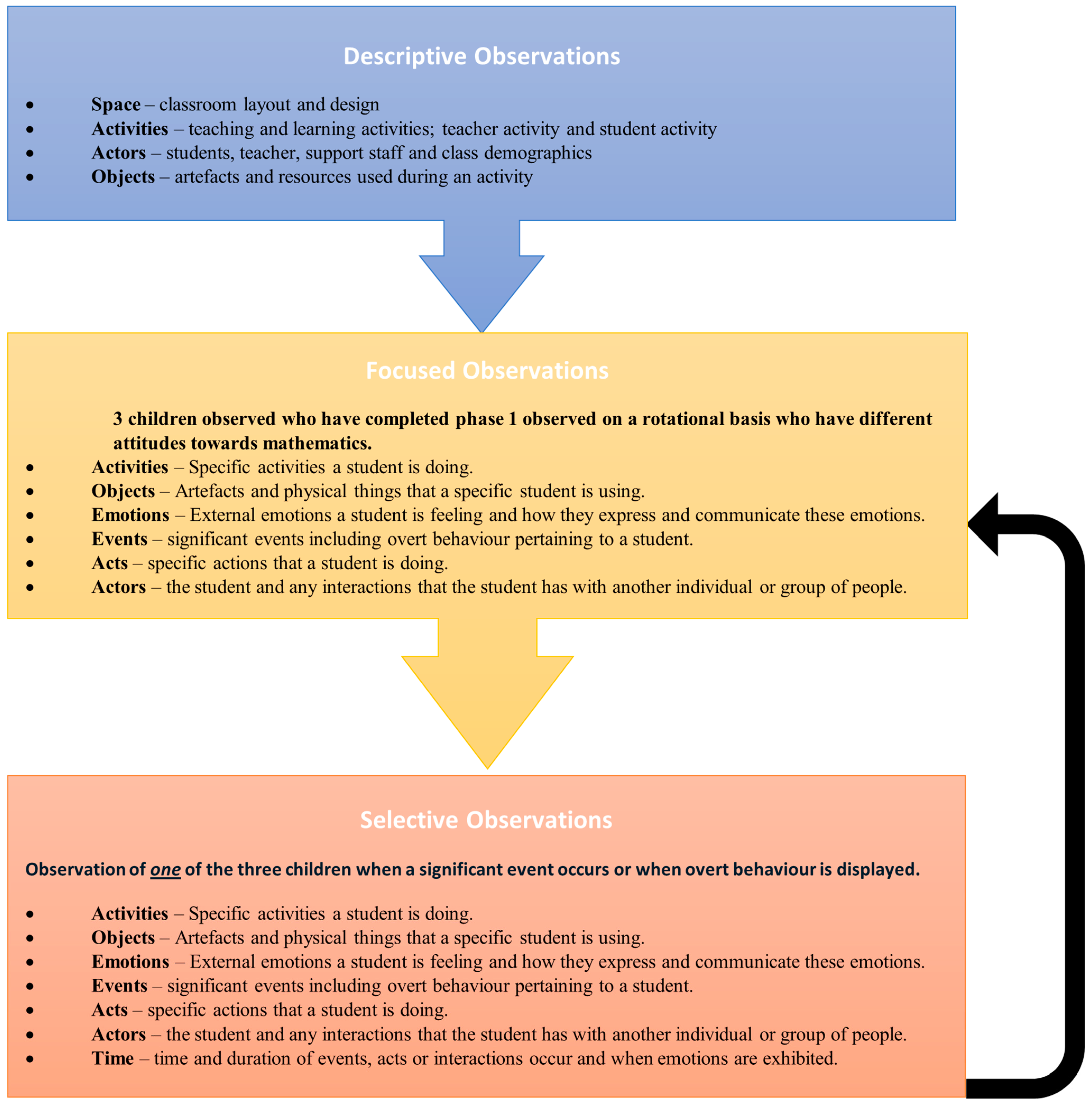
2.3. Observational Procedure
- Children’s drawings, written descriptions and interview responses were analysed to determine the nature of each child’s attitude towards mathematics;
- Three children were selected from each class who had completed research phases 1 and 2 and were classified as having three different attitudes towards mathematics;
- Descriptive observations of the classrooms were conducted;
- Focused systematic observations were conducted;
- Five-minute intervals were used to observe the three children;
- Observations of the children were conducted on a rotational basis;
- Selective observations were conducted when a significant event occurred or overt behaviour was exhibited by one of the three children;
- Focused observations were resumed when the child returned to the act before exhibiting overt behaviour or when the significant event ended.
2.4. Data Collection and Analysis
3. Results
3.1. Descriptive Observations
3.2. Focused Observations
3.3. Selective Observations
B56: I’ve just realised that I’ve eaten all of my lunch.
Peer: I’ll give you a chicken nugget.
B56: I’ve never had a chicken nugget before.
4. Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FIAC | Flanders’ Interaction Analysis Categories |
| TMA | Three-dimensional Model of Attitude |
| MTMA | Modified Three-dimensional Model of Attitude |
References
- Alibali, M. W., & Nathan, M. J. (2012). Embodiment in mathematics teaching and learning: Evidence from learners’ and teachers’ gestures. Journal of the Learning Sciences, 21(2), 247–286. [Google Scholar] [CrossRef]
- Andersen, P. A. (2008). Nonverbal communication: Forms and functions (2nd ed.). Waveland Press Inc. [Google Scholar]
- Attard, C., Ingram, N., Forgasz, H., Leder, G., & Grootenboer, P. (2016). Mathematics education and the affective domain. In K. Makar, S. Dole, J. Visnovska, M. Goos, A. Bennison, & K. Fry (Eds.), Research in mathematics education in Australasia 2012–2015 (pp. 73–96). Springer. [Google Scholar] [CrossRef]
- Bachman, R., & Neal, C. (2018, February 22–24). Draw yourself doing mathematics: Validating an instrument and a rubric. 45th Annual Meeting of the Research Council on Mathematics Learning: Let the Good Times Roll in Mathematics Learning, Baton Rouge, LA, USA. [Google Scholar]
- Cohen, D. (2007). Body language: What you need to know. Sheldon. [Google Scholar]
- Cohen, L., Manion, L., & Morrison, K. (2011). Research methods in education (7th ed.). Taylor & Francis Group. [Google Scholar]
- Creswell, J. (2012). Educational research planning, conducting, and evaluating quantitative and qualitative research (4th ed.). Pearson. [Google Scholar]
- Delamont, S. (1976). Beyond Flanders’ fields: The relationship of subject matter and individuality to classroom style. In M. Stubbs, & S. Delamont (Eds.), Explorations in classroom observations (pp. 101–131). John Wiley & Sons, Ltd. [Google Scholar]
- Delamont, S., & Hamilton, D. (1976). Classroom research: A critique and a new approach. In S. Delamont, & M. Stubbs (Eds.), Explorations in classroom observations (pp. 3–20). John Wiley & Sons, Ltd. [Google Scholar]
- de Vaus, D. (2014). Surveys in social research (6th ed.). Routledge/Taylor & Francis Group. [Google Scholar]
- Di Martino, P. (2004, July 14–18). From single beliefs to belief systems: A new observational tool. PublisherProceedings of the 28th Conference of the International Group for the Psychology of Mathematics Education, Bergen, Norway. [Google Scholar]
- Di Martino, P. (2019). Pupils’ view of problems: The evolution from kindergarten to the end of primary school. An International Journal, 100(3), 291–307. [Google Scholar] [CrossRef]
- Di Martino, P., & Zan, R. (2010). ‘Me and maths’: Towards a definition of attitude grounded on students’ narratives. Journal of Mathematics Teacher Education, 13(1), 27–48. [Google Scholar] [CrossRef]
- Di Martino, P., & Zan, R. (2011). Attitude towards mathematics: A bridge between beliefs and emotions. ZDM, 43(4), 471–482. [Google Scholar] [CrossRef]
- Flanders, N. A. (1965). Teacher influence, pupil attitudes, and achievement (Vol. 25040). US Department of Health, Education, and Welfare, Office of Education. [Google Scholar]
- Fraser, B. (1983). The domain of pragmatics. In Language and communication (pp. 29–59). Routledge. [Google Scholar]
- Geertz, C. (1993). The interpretation of cultures: Selected essays. Fontana Press. [Google Scholar]
- Goodykoontz, E. N. (2008). Factors that affect college students’ attitude toward mathematics. West Virginia University. [Google Scholar]
- Grootenboer, P., Lomas, G., & Ingram, N. (2008). The affective domain and mathematics education. In H. Forgasz, A. Barkatas, A. Bishop, B. Clarke, S. Keast, W.-T. Seah, P. Sullivan, & S. Willis (Eds.), Research in mathematics education in Australasia 2004–2007 (pp. 1–14). Sense Publishers. [Google Scholar]
- Grootenboer, P., & Marshman, M. (2016). Mathematics, affect and learning OECD: Middle school students’ beliefs and attitudes about mathematics education. Springer. [Google Scholar] [CrossRef]
- Grootenboer, P., Romiley, J., Stewart, B., & Thorpe, P. (2002). Kids talking about their learning in mathematics. Australian Primary Mathematics Classroom, 7(4), 16–21. [Google Scholar]
- Grossard, C., Chaby, L., Hun, S., Pellerin, H., Bourgeois, J., Dapogny, A., Ding, H., Serret, S., Foulon, P., & Chetouani, M. (2018). Children facial expression production: Influence of age, gender, emotion subtype, elicitation condition and culture. Frontiers in Psychology, 9, 446. [Google Scholar] [CrossRef] [PubMed]
- Hemmings, B., Grootenboer, P., & Kay, R. (2011). Predicting Mathematics achievement: The influence of prior achievement and attitudes. International Journal of Science and Mathematics Education, 9(3), 691–705. [Google Scholar] [CrossRef]
- Ingram, N., Hatisaru, V., Grootenboer, P., & Beswick, K. (2020). Researching the affective domain in mathematics education. In J. Way, C. Attard, J. Anderson, J. Bobis, H. McMaster, & K. Cartwright (Eds.), Research in mathematics education in Australasia 2016–2019 (pp. 147–175). Springer. [Google Scholar] [CrossRef]
- Kibrislioglu, N. (2015). An investigation about 6th grade students’ attitudes towards mathematics. Procedia—Social and Behavioral Sciences, 186, 64–69. [Google Scholar] [CrossRef]
- Kim, H., & Ahn, S. (2017). An analysis of verbal interaction in elementary school class using the Flanders Interaction Analysis Categories. Information, 20(4A), 2383–2389. [Google Scholar]
- Köğce, D., Yıldız, C., Aydın, M., & Altındağ, R. (2009). Examining elementary school students’ attitudes towards mathematics in terms of some variables. Procedia—Social and Behavioral Sciences, 1, 291–295. [Google Scholar] [CrossRef]
- Krause, C. M. (2016). The mathematics in our hands: How gestures contribute to constructing mathematical knowledge. Springer Spektrum. [Google Scholar]
- McDonough, A. (2002). PPELEM pupil perceptions of effective learning environments in mathematics: A simple way to learn about your children and inform your teaching of mathematics. Australian Primary Mathematics Classroom, 7(3), 14–19. [Google Scholar]
- McDonough, A., & Ferguson, S. (2014, June 29–July 3). PPELEM: A “Creative” interviewing procedure for gaining insights into teacher and student mathematics-related beliefs. 37th Annual Conference of the Mathematics Education Research Group of Australasia, Sydney, Australia. [Google Scholar]
- McDonough, A., & Sullivan, P. (2014). Seeking insights into young children’s beliefs about mathematics and learning. An International Journal, 87(3), 279–296. [Google Scholar] [CrossRef]
- McLeod, D. (1987). A constructivist approach to research on attitude toward mathematics. In International Conference on the Psychology of Mathematics Education (PME). PME. [Google Scholar]
- Mercer, N. (2004). Sociocultural discourse analysis: Analysing classroom talk as a social mode of thinking. Journal of Applied Linguistics, 1(2), 137–168. [Google Scholar] [CrossRef]
- Niss, M. (2007). Chapter 31—Reflections on the state of research and trends in research on mathematics teaching and learning: From here to utopia. In K. L. Frank (Ed.), Second handbook of research on mathematics teaching and learning: A project of the national council of teachers of mathematics (pp. 1293–1312). Information Age Publishing. [Google Scholar]
- OECD. (2012). Equity and quality in education. OECD Publishing. [Google Scholar] [CrossRef]
- Parsons, S. A., Nuland, L. R., & Parsons, A. W. (2014). The ABCs of student engagement. Phi Delta Kappan, 95(8), 23–27. [Google Scholar] [CrossRef]
- Pease, A., & Pease, B. (2006). The definitive book of body language (1st ed.). Bantam Books. [Google Scholar]
- Pepin, B. (2011). Pupils’ attitudes towards mathematics: A comparative study of Norwegian and English secondary students. ZDM, 43(4), 535–546. [Google Scholar] [CrossRef]
- Picker, S. H., & Berry, J. S. (2001). Your students’ image of mathematicians and mathematics. Mathematics Teaching in the Middle School, 7(4), 202–208. Available online: http://www.jstor.org/stable/41181109. [CrossRef]
- Quane, K. (2021). Curriculum implications of understanding the influence of peers on the nature of young children’s attitudes towards mathematics. Curriculum Perspectives, 41, 245–255. [Google Scholar] [CrossRef]
- Quane, K. (2024). The confluence of attitudes towards mathematics and pedagogical practice: Evaluating the use of mathematical manipulatives. Mathematics Education Research Journal. [Google Scholar] [CrossRef]
- Quane, K., Chinnappan, M., & Trenholm, S. (2019, June 30–July 4). The nature of young children’s attitudes towards mathematics (Mathematics Education Research: Impacting Practice). 42nd Annual Conference of the Mathematics Education Research Group of Australasia, Perth, Australia. [Google Scholar]
- Quane, K., Chinnappan, M., & Trenholm, S. (2023). Draw yourself doing mathematics: Developing an analytical tool to investigate the nature of young children’s attitudes towards mathematics. Mathematics Education Research Journal, 35(3), 445–473. [Google Scholar] [CrossRef]
- Spradley, J. (2016). Participant observation. Waveland Press, Inc. [Google Scholar]
- Stiles, D., McElrath, A., Lucas, J., Rajan, J., & Gupta, G. (2015). Adolescents’ drawings about school and school subjects: Perspectives of youth from India compared with youth from seven other countries. Journal of the Indian Academy of Applied Psychology, 41, 16–24. [Google Scholar]
- Stites, M. L., & Brown, E. T. (2021). Observing mathematical learning experiences in preschool. Early Child Development and Care, 191(1), 68–82. [Google Scholar] [CrossRef]
- TIMSS. (2016). TIMSS 2015 international results in mathematics. TIMSS and PIRLS International Study Center. Available online: http://timssandpirls.bc.edu/timss2015/international-results/ (accessed on 11 September 2016).
- Tucker, K. (2014). Mathematics through play in the early years (3rd ed.). SAGE Publications. [Google Scholar]
- Yasar, M. (2016). High school students’ attitudes towards mathematics. Eurasia Journal of Mathematics, Science and Technology Education, 12(4), 931. [Google Scholar] [CrossRef]
- Yelland, N., Diezmann, C., & Butler, D. A. (2014). Early mathematical explorations. Cambridge University Press. [Google Scholar]
- Yoon, C., Thomas, M. O. J., & Dreyfus, T. (2011). Gestures and insight in advanced mathematical thinking. International Journal of Mathematical Education in Science and Technology, 42(7), 891–901. [Google Scholar] [CrossRef]
- Zan, R., & Di Martino, P. (2007). Attitude toward mathematics: Overcoming the positive/negative dichotomy. The Montana Mathematics Enthusiast, 3(1), 157–168. [Google Scholar]


| Dimension | Sub-Dimension | Description | Attitude Classifications |
|---|---|---|---|
| Emotional Dimension | Emotional Tendency (ET) | Students’ feelings and emotional responses experienced during mathematical activities and tasks | Cannot be Classified |
| Extremely Negative | |||
| Negative | |||
| Neutral | |||
| Positive | |||
| Extremely Positive | |||
| Overall Sentiment (OS) | Students’ general reactions and emotional beliefs regarding mathematics, including non-verbal cues (posture, gestures and body language) and verbal cues over a series of mathematical learning experiences | Cannot be Classified | |
| Extremely Negative | |||
| Negative | |||
| Neutral | |||
| Positive | |||
| Extremely Positive | |||
| Vision of Mathematics | Tasks, Topics and Processes (TTP) | Types of mathematical learning experiences and processes students engage with during mathematical learning experiences; the mathematical topics and how students communicate their mathematical understanding and learning | Cannot be Classified |
| Minimal Vision of Mathematics | |||
| Low Vision of Mathematics | |||
| Developing Vision of Mathematics | |||
| High Vision of Mathematics | |||
| Exemplary Vision of Mathematics | |||
| Value and Appreciation (VA) | How and what students view as important and acknowledge as worthwhile about mathematics during mathematical learning experiences. That is, what students engage or disengage (actively or passively) with during mathematical learning experiences | Cannot be Classified | |
| No Value of Mathematics | |||
| Low Value of Mathematics | |||
| Some Value of Mathematics | |||
| High Value of Mathematics | |||
| Very High Value of Mathematics | |||
| Perceived Competence | Mathematical Mindset (MM) | Students’ perceptions of themselves related to their ability to do mathematics during mathematical learning experiences | Cannot be Classified |
| Fixed Mindset | |||
| Low Growth Mindset | |||
| Mixed Mindset | |||
| Growth Mindset | |||
| High Growth Mindset | |||
| Self-Concept (SC) | Students’ beliefs in their mathematical ability and their expectancy for success during mathematical learning experiences | Cannot be Classified | |
| Extremely Low Perceived Competence | |||
| Low Perceived Competence | |||
| Neutral Perceived Competence | |||
| High Perceived Competence | |||
| Very High Perceived Competence |
| Framework | Child’s Communication | Description |
|---|---|---|
| Interaction Analysis (FIAC) Flanders (1965) | Response | Talk by a student in response to the teacher. The teacher initiates the contact or solicits a students’ statement or structures the situation. Freedom to express personal ideas is limited. |
| Initiation | Talk by students that they initiate; expressing their own ideas; initiating a new topic; freedom to develop opinions and a line of thought, like asking thoughtful questions; going beyond the existing structure. | |
| Silence | Pauses, short periods of silence, no talking | |
| Confusion | Periods of confusion in which the observer cannot understand the communication. | |
| Pragmatics (social communication) Fraser (1983) | Beliefs | A student expresses beliefs that propositions are true. |
| Desires | A student expresses a desire concerning the action specified in the proposition. | |
| Commitment | A student expresses an intention to undertake a commitment associated with the action specified in the proposition. | |
| Evaluation | A student expresses a personal evaluation towards some past action. | |
| Sociocultural discourse analysis Mercer (2004) | Disputational talk | Disagreement and individual decision making, short exchanges consisting of assertions and challenges or counter assertions. There are few attempts made by the student to pool resources, to offer constructive criticism or make suggestions. |
| Cumulative talk | A student speaks positively but uncritically on what others have said. Characterised by repetitions, confirmations, and elaborations. | |
| Exploratory talk | Students engage critically but constructively with each other’s ideas. Statements and suggestions are offered for joint consideration that may be challenged or counter-challenged, but the challenges are justified, and an alternate hypothesis is offered. Students all actively participate, and opinions are sought and considered before decisions are jointly made. Compared to disputational and cumulative talk, exploratory talk is where knowledge is made more publicly accountable, and reasoning is visible. | |
| Non-Verbal Communication Andersen (2008) Pease and Pease (2006) | Facial Expressions | The face is the primary site of emotional communication. During social interactions, we examined faces to determine an individual’s emotional state. “Facial expressions are usually spontaneously communicated to others without conscious thought or linguistic representation” (Andersen, 2008, p. 145). |
| Posture and Body Language | “Emotions can be reliably identified from postures” (Andersen, 2008, p. 147) while “body language is an outward reflection of a person’s emotional condition” (Pease & Pease, 2006, p. 11). | |
| Gestures | Students’ hand gestures are used to support learning, or to communicate emotion. Gestures are read in clusters and context while looking for congruence; that is, words match gestures. Gestures can provide valuable insights into what a child may be feeling at a given time (Pease & Pease, 2006, p. 11). |
| Focused Observations | |||
|---|---|---|---|
| Class | Time Interval | Child | Nature of Attitude |
| Class 1 | 0–5 min | 1 | Neutral attitude |
| 5–10 min | 2 | Positive attitude | |
| 10–15 min | 3 | Neutral attitude | |
| 15–20 min | 1 | Neutral attitude | |
| 20–25 min | 2 | Positive attitude | |
| 25–30 min | 3 | Neutral attitude | |
| Year | R/1 | R/1/2 | 1/2 | 2 | 2/3 | 3 | 3/4/5/6 | Total |
|---|---|---|---|---|---|---|---|---|
| Number of classes | 1 | 2 | 3 | 2 | 3 | 1 | 1 | 13 |
| Number of observations | 3 | 24 | 9 | 6 | 9 | 3 | 16 | 70 |
| Number of participants for selective observations | 3 | 12 | 9 | 6 | 9 | 3 | 8 | 50 |
| Variable | B54 | B53 | B56 |
|---|---|---|---|
| Event | B54 is happily working with a male partner to discuss fractions. The boys are playing a matching game using fraction cards with circle images and numerical fractions. Both boys are taking turns, pointing to different shaded sectors and matching the pictorial representation to the numerical representation. | B53 is sitting cross-legged with three other students close by, not talking to others. All four students are working through a set of questions on Mathletics. At 11:08, B53 starts a conversation about a question. Another student points to part of the screen on the iPad, B53 finishes the set of questions and states, “I’m up to 300”. Another student replies, “340! I’m way ahead of you”. Once B53 has completed the set of questions, she turns around and begins to talk to other students. Then, she engages in a conversation with another student about going away on holiday. At 11:12, she returns to the iPad and begins to answer questions about numbers. | At 11:15, teacher calls “hands on top” and the class responds with “that means stop”. Second rotations begin. Students move to return or get the equipment required for the next task. At 11:17, B56 is given the task “Erika is buying 3 poppies. They cost $4.25 each. How much did it cost? How much change did she get from $20”. B56 is sitting with another female student, both girls on their iPads, whispering, playing with slime and involving other students nearby. B56 is eating and conversing with other students at the table. At 11:20, B56 has not started the problem. Another girl has opened her book and stuck the task in her book, stating, “I’m going to start my work”. B56 opens her book to a blank page and talks to another student, continuing to play with the slim. She stands and walks to the other side of the room * |
| Overt Behaviour | N/A | N/A | Yes. |
| Artefacts | Fraction cards: pictorial and numerical representations. Fractions are 4/8, 5/12, 2/3 and 3/5 | iPads–Mathletics | Task card, workbook, iPad. |
| Emotions | B54 appears content and happy to be working with a partner and playing the game. Happy to respond to teacher’s questions. Smiling. Appears confident. | Appears happy. Smiling, celebrating achievements. Head against windowsill | Distracted, actively disengaged, content in not completing the work. Appears to be unhappy. |
| Acts | Teacher checks work and gives feedback to the pair. B54 replies “I’m done!” Teacher asks further questions “What would this one be here be?” Pointing to a card. B54 is quick to respond, providing a clear justification. Teacher asks the boys to represent the fraction and then glue the task sheet in the book. | Observation occurs in the first set of mathematical rotations. Girls sitting by the window in a row each with their own iPad. | Observation begins at the end of the first round of rotations where students were completing a task on the iPads. Task given and not completed. |
| Activities | Small group work, game-based learning situated in mathematical rotations. The game has a focus on explanations and justifications. | Mathematical rotations: iPad–Mathletics. | Small group work with a word-based question. No manipulatives. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quane, K. Observing Mathematical Learning Experiences in the Primary Years to Examine How Attitudes Towards Mathematics Are Enacted in the Classroom. Educ. Sci. 2025, 15, 417. https://doi.org/10.3390/educsci15040417
Quane K. Observing Mathematical Learning Experiences in the Primary Years to Examine How Attitudes Towards Mathematics Are Enacted in the Classroom. Education Sciences. 2025; 15(4):417. https://doi.org/10.3390/educsci15040417
Chicago/Turabian StyleQuane, Kate. 2025. "Observing Mathematical Learning Experiences in the Primary Years to Examine How Attitudes Towards Mathematics Are Enacted in the Classroom" Education Sciences 15, no. 4: 417. https://doi.org/10.3390/educsci15040417
APA StyleQuane, K. (2025). Observing Mathematical Learning Experiences in the Primary Years to Examine How Attitudes Towards Mathematics Are Enacted in the Classroom. Education Sciences, 15(4), 417. https://doi.org/10.3390/educsci15040417