Assessment of the Sustainability of University Academic Programs for the Accreditation: A Complex Challenge

Abstract

The accreditation of university academic programs is a critical process in ensuring the quality and standards of higher education. A significant component of this process is the assignment of reference lecturers who make these academic programs sustainable. The problem of determining the appropriate faculty members to accredit university academic programs is a multifaceted challenge. The selection of reference lecturers for accreditation is influenced by various factors, including their academic positions, the subject area of their sectors according to the bachelor’s or master’s degree in which they are delivered, and the number of students enrolled compared to the degree classes. Moreover, the evolving nature of higher education, given its increased emphasis on interdisciplinary topics, further complicates this assessment due also to the presence of professors or researchers coming from other departments. The development of an optimization algorithm capable of simultaneously considering all the constraints of the problem is therefore needed to address these challenges and achieve to a balanced approach for a sustainable didactic offer. The optimization algorithm works by maximizing the number of lecturers available as reference lecturers for other departments and minimizing those needed from other departments and from external teaching contracts. The problem of reference lecturers does not refer to the department alone but to the entire atheneum.

1. Introduction

Universities are increasingly driven by competition to optimize the quality of their services, to redefine their programs, and to measure students’ and administrative staff’s satisfaction (Krift et al., 2024; Wu et al., 2023). Accreditation systems are becoming a method of quality assessing educational institutions worldwide by the competent agencies (Alenezi et al., 2023; Bonett-Balza et al., 2024; Jurvelin et al., 2018; Murmura et al., 2016). In Italy, the recommendations of the National Agency for the Evaluation of Universities and Research Institutes (ANVUR), according to ENQA “European Association for Quality Assurance in Higher Education” and EQAR “European Quality Assurance Register” (European Association for Quality Assurance in Higher Education (ENQA), 2015), are used in compliance with the (Ministerial Decree 289/2021, 2021) and general guidelines for three-year programs in the university system from the three-year period of 2021–2023, with DM 1154/2021 (Ministerial Decree 1154/2021, 2021). Self-assessment, assessment, initial and periodic accreditation of universities and study programs were used to define a Model of Periodic Accreditation of University and study programs called AVA. While European and international universities had adopted evaluation models following the formulation of European standards and guidelines for quality assurance in 2005, all Italian universities were required by law to adopt the AVA method from 2013 onwards (Mulvey et al., 2011). The AVA method provides a quality assurance system for the initial and periodic accreditation of universities and their academic programs and periodic assessment of quality requirements. The AVA method, which has been progressively updated to the final version AVA3, is designed to improve efficiency and effectiveness of teaching and research of universities, trying to stimulate competitiveness and quality through a set of reliable, pre-defined, and published criteria that are applied consistently and through reports that are regularly published by ANVUR, together with the results of its external assessment activities and the evaluation of university quality requirements. Furthermore, the AVA method strengthens the internal quality assurance in universities through a self-assessment approach, supporting the continuous improvement of teaching and academic research activities. In particular, the self-assessment approach consists of the verification of the efficiency and sustainability of the activities and the results achieved are evaluated on the basis of a set of indicators listed in the Annex A of DM 1154/2021, consistent with the standards and the Guidelines for Quality Assurance. The number of tenured professors and researchers appointed as reference professors in the active academic programs is one of those critical indicators, due to the high number of constraints in the DM. Reference professors make academic courses sustainable as they ensure that there are enough lecturers dedicated to that specific course. The presence of structured lecturers is a guarantor of course quality and sustainability in terms of teaching continuity as well. The term sustainability is used in the director’s decree for calculating the reference faculty. It indicates that for each activated course, there should be a sufficient number of faculty members to ensure that the time available for students is adequate. An academic course based mainly on contract lecturers would in fact be synonymous with lower teaching quality since continuity is not certain and the preparation, especially in terms of teaching ability, is not comparable to that of a structured lecturer (employed professor). The objective of the paper is to propose an optimization algorithm to simplify the self-assessment approach used by Italian universities in assigning reference lecturers to academic programs, ensuring compliance with regulatory requirements. This process, traditionally performed manually and in a complex manner, is addressed in the paper with the aim of reducing the time and difficulties involved, especially in departments with many faculty members and academic programs. Without using a mathematical algorithm, the coordinators of each academic program decide the reference lecturers autonomously, as they have no knowledge of the requirements of the other programs. This implies that overlapping situations may occur. The algorithm aims to improve the efficiency and sustainability of the educational offer, ensuring that ministerial constraints are met without overlaps between programs and optimizing resource allocation. Moreover, due to ministerial deadlines, this process must be completed within a rather narrow time window and cannot be activated before teaching duties are allocated. To the best of the authors’ knowledge, the problem of assigning lecturers to academic programs to guarantee a sustainable didactic offer and meet the accreditation constraints has not yet been studied in the literature before. However, the exploitation of operations research and, more specifically, of combinatorial optimization techniques to improve the quality of services offered by universities, is a well-established research stream. In particular, the University Timetabling problem has been broadly addressed. This problem consists of assigning didactic activities (courses or exams) to timeslots and to teaching rooms to make the best use of resources and to improve the students’ experience. A survey on the topic can be found in (Chen et al., 2021). The solution of the problem requires finding a feasible schedule which respects mandatory requirements (hard constraints), such as that no more than one course can be scheduled in a room on each timeslot, and that courses belonging to the same program cannot take place simultaneously, minimizing the violation of soft constraints which should be respected as well, such as a balance of workload along the week for all the study programs. Different solution techniques have been proposed to effectively handle this problem, such as single-solution-based metaheuristics (Assi et al., 2018; Ceschia et al., 2012; Goh et al., 2017; Lewis, 2010; Nagata, 2018) and population based metaheuristics (Avella et al., 2019; Chen & Shih, 2013; Sabar et al., 2012). Many real-case applications have been reported (Mallari et al., 2023). Prabodaine (Prabodanie, 2017) solves a real case arising at the Faculty of Applied Sciences, Wayamba, University of Sri Lanka, whereas (Avella et al., 2019) addressed a real case from the University of Sannio in Italy. Aladag et al. (Aladag et al., 2009) used data provided by the Department of Statistics at Hacettepe University in Turkey, while (Borchani et al., 2017) used data from the Faculty of Economics and Management Sciences of Sfax in Tunisia. The latter aims at minimizing the number of holes in the schedule and of isolated lectures in order to generate a more compact schedule. Almeida et al. (Almeida et al., 2015) also consider minimizing the number of holes between lectures while avoiding scheduling all the lectures of a course on the same day, using data provided by the Federal University of Rio Grande do Norte in Brasil. To stand out from competitors and secure their long-term sustainability, higher education institutions need to provide high-quality services. Various tools, methods, and models have been implemented to improve the quality of services and processes within higher education. A key aim of integrating IT into quality assurance management at universities is to boost applicant satisfaction with the educational experience, achieved through the use of software systems (Javed & Alenezi, 2023). The rest of this paper is organized as follows: Section 2 describes the problem and presents the mathematical formulation of the proposed optimization model; the behavior of the model is illustrated by means a real-case example in Section 3; while Section 4 explores the results obtained for different scenarios, showing the impact of restrictions on the optimal assessment; the scientific and practical implications of the research are presented in the conclusions reported in Section 5.

2. Materials and Methods

2.1. Problem Description

The reference lecturer assignment (RLA) problem deals with determining the best set of teachers for all the university academic programs (e.g., mechanical engineering, computer engineering, etc.), both in bachelor’s and master’s degrees. The system considered is a university academic department involving students and lecturers, each associated with one academic program. Each student is enrolled in a specific academic program, while each lecturer can teach in a set of them. Data on enrolments and teacher assignments are available to the decision-maker prior to the reference lecturer’s location process. The decision-makers considered in the problem are the department didactic delegate and the didactic manager. Their purpose is to effectively prove the sustainability of all the programs within the department for one academic year such that constraints imposed by law are all satisfied. To verify possession of the teaching requirement for the initial and periodic accreditation of the academic programs, the minimum numbers of reference lecturers are calculated considering the courses that will be actually held in bachelor’s degree, master’s degree, and single-cycle master’s degree programs in the current academic year, as reported in

Table 1. The minimum numbers of reference lecturers for traditional academic programs.

Study Courses Degree	n. Lecturers	Associate or Full Professors Required
Bachelor’s	9	5
Master’s	6	4

.

For the professional orientation academic programs (LP academic programs) the requirements are those reported in

Table 2. The minimum numbers of reference lecturers for professional academic programs.

Study Courses Degree	n. Lecturers	Associate or Full Professors Required	Professionals
Bachelor’s	4	2	5
Master’s	3	1	3

.

The term “professionals” refers to tenured or contract teaching entrusted to figures with specific professionalism and competence and employed mainly in characterizing training activities traineeships and workshops.

For academic programs with predominantly or remote delivery modes (Ministerial Decree no. 289/2021) the number of lecturers becomes as shown in

Table 3. The minimum numbers of reference lecturers for distance learning academic programs.

Study Courses Degree	n. Lecturers	Associate or Full Professors Required	Tutor
Bachelor’s	7	5	3
Master’s	3	2	2

.

The numbers of lecturers, additional specialist staff, and tutors for distance learning academic programs are defined with reference to the maximum number of students in the graduating class. The calculation of the reference number of students can be different and, in particular, it equals:

-

For academic programs with a national or local number of students, to the value of the quota of students enrolling in the first year;

-

For already accredited academic programs that have completed at least one cycle of studies, delivered by traditional or mixed mode, to the minimum value in the number of students enrolled in the first year referred to the two different academic years (e.g., for the purposes of defining the Academic Year (AY) 2022/2023, the required number of reference lecturers is calculated with respect to the lowest between the number of students enrolled in the first year of the AY 2019/2020 and the number of students enrolled in the first year in the AY 2020/2021);

-

For already accredited academic programs delivered remotely to the number of those enrolled for the first time in the program, measured in the same way as in the previous point;

-

For new academic programs proposed for accreditation, and for programs that have not yet completed a study cycle, to the maximum numbers given in Annex D of DM 1154/2021.

If the number of students exceeds the maximum numbers set out in Annex D, the number of reference lecturers (L_r) and that of additional specialist figures, is increased proportionally to the exceeding of these thresholds, according to the following Equation (1):

$$\begin{gathered} L_{new}=Lr·\left(1+W\right) \\ W=0 if n.students\le maximum number \\ W=\left({\displaystyle \frac{n.students}{maximum number}}-1\right) if n.students>maximum number \end{gathered}$$

(1)

where L_r is the reference lecturers, while L_new is the reference lectures required.

Each reference lecturer must have a teaching assignment of at least one course in the university academic programs. Each lecturer can only be counted once or, at most, be listed as a reference lecturer for 2 academic programs of study with a weight of 0.5 for each one.

Reference lecturers can be:

• Permanent professors;
• Permanent researchers, researchers pursuant to Article 24, paragraph 3, letters (a) and (b) of Law no. 240/10 (Law, 2010);
• Lecturers in agreement pursuant to Art. 6, paragraph 11 of Law n. 240/10, also from international universities and public research institutes (art. 3, paragraph 1 of Ministerial Decree no. 24786 of 27 November 2012)
• Fixed-term professors pursuant to Article 1, paragraph 12 of Law 230/05, with three-year appointments/assignments.

Lecturers on contract (Article 23 of Law 240/2010) may be counted within the limit maximum of half of the share of the reference teaching staff that is not reserved for permanent/tenured professors.

The lecturers referred to in points (c), (d), as well as any contract lecturers may contribute to the teaching requirements within the limit of one third of the total number of reference lecturers. For the academic programs for which the award of a double or joint degree is envisaged for all enrolled students, lecturers belonging to foreign universities (as per letter b) may contribute to the teaching requirements up to a limit of half of the total number of lecturers (Art. 23, c. 3 of Law no. 240/2010).

To comply with the teaching requirements, at least 50% of the reference lecturers must belong to macro-sectors corresponding to the basic or characterizing scientific disciplinary sectors of the academic program.

2.2. Mathematical Formulation

Before presenting the mathematical formulation of the problem, we introduce the following constants and sets involved in the model:

• I: set of lecturers (professors, researchers, or contract lecturers)
• J: set of study programs
• Dj: minimum number of reference lecturers needed for study program j
• Pj: minimum number of professors needed for study program j
• Ej: maximum number of contract lecturers allowed in study program j
• Aj: maximum number of reference lecturers, not giving basic or characterizing courses, allowed in study program j
• cij: constant indicating if teacher i gives at least one basic or characterizing course in study program j (1), gives another type of course (2) or does not teach in that program (0)
• Ri: role of teacher i (1 professor, 0 assistant professor, −1 contract lecturers)
• ei: binary constant stating if teacher i is affiliated with the department or is external
• fi: binary constant stating if i teaches also in other departments or not

The decision variables involved in the model are binary variables xij taking value equal to 1 if teacher i is selected as referent for study program j and 0 otherwise.

The model can be described as follows:

$$\min \sum _{i in I}\sum _{j in J}{e}_i{x}_{ij}$$

(2)

$$\sum _{i in I}{x}_{ij}=D_j\forall j in J$$

(3)

$$\sum _{i in I |r_i=1}{x}_{ij}\ge P_j\forall j in J$$

(4)

$$\sum _{i in I |r_i=-1}{x}_{ij}\le E_j\forall j in J$$

(5)

$$\sum _{i in I |c_{ij}=2}{x}_{ij}\le A_j\forall j in J$$

(6)

$$\sum _{j in J }{x}_{ij}\le 1\forall i in I$$

(7)

$$x_{ij}\le c_{ij }\forall i in I \forall j in J$$

(8)

The objective function consists of minimizing the number of external lecturers used as reference lecturers. Constraints (3) ensure that the required number of reference lecturers is assigned to each study program. Constraints (4) impose that the number of professors selected as reference lecturers is greater or equal to the minimum required, for each study program. Constraints (5) and constraints (6) limit the number of external lecturers and of lecturers not giving basic or characterizing courses selected as reference for the study program. Each teacher can be selected as referent for at most one study program, as imposed by constraints (7), among those in which it teaches, while cannot be assigned to programs in which he does not give any course.

The multi-objective aspect of the optimization model is implemented by considering four performance indicators in the problem of RLA: lecturers from other departments, internal lecturers of the analyzed department distinguishing between those who have or have not teaching duties in other departments, and external teaching contracts. The solutions obtained in the different scenarios are therefore evaluated considering the following:

(1)

Minimize the number of lecturers from other departments;

(2)

Maximize the number of internal lecturers not used that the Department to which RLA optimization model applies could lend to the other departments (e.g., they have courses in other departments);

(3)

Minimize the number of not used internal lecturers who have courses only in the department under consideration;

(4)

Minimize the number of external lecturers belonging to the set of contracts that the department makes.

3. Case Study

To validate the proposed optimization model, we considered a theoretical case study based on real-life observed conditions. The case study refers to the Engineering Department of an Italian university with fifteen bachelor’s degree courses, twelve master’s degree courses, two online master’s degree courses, and one professional bachelor’s degree course. Each academic program had enrolled fewer students than the maximum class level, except for three bachelor’s degree courses with planned numbers of 200, 200, and 220 students, respectively. In the first two cases, the number of reference lecturers grew to 10, while in the third, to 11. One of the master’s degree courses has 170 students enrolled, so the number of reference lecturers rose from 6 to 11, as reported in Equation 1. The total number of lecturers teaching in the department is 251, of whom 86 are researchers (R) and 165 are full or associate professors (P). Forty-eight of them teach also in other departments. The number of lecturers from other departments is 63, while the number of external lecturers under contracts is 47. All information relating to the individual subjects provided in the academic year under consideration (2022–2023) was provided by the didactic manager from the teaching duties assignment file. Four scenarios were considered to further evaluate the performance of the proposed model, namely: (1) “Double constraints”, (2) “Constraint on external lecturers only”, (3) “Constraint on internal lecturers only”, and (4) “No constraints”. Moreover, a scenario showing the result obtained manually was also included to prove the improvement achievable with the proposed model. The scenario is called (5) “Double constraints manually” because it takes both constraints into account.

3.1. Double Constraints

It was assumed that the external lecturers can be used only if they are part of a specific list agreed between the departments involved. In the case study, this list consisted of 21 lecturers, each of whom teaches at least one course in the engineering department. Twelve of them are full or associate professors. Moreover, we consider a second constraint in which a list of internal lecturers cannot be used because they are given as reference lecturers to other departments. In our case, the list consists of 12 lecturers, half of whom are researchers. Both constraints derive from the practices followed so far and could be overcome if the university were to manage the reference lecturer’s problem with the proposed algorithm.

3.2. Constraint on External Lecturers Only

This scenario assumes that the constraint is only considered on external lecturers from other departments.

3.3. Constraint on Internal Lecturers Only

Similarly to the previous scenario, only the constraint on internal lecturers being exposed as reference lecturers in other departments is considered.

3.4. No Constraints

This scenario considers the absence of constraints on lecturers from other departments or assigned to other departments. This scenario is only applicable if the university manages the reference lecturer for all the departments.

4. Results and Discussions

In order to emphasize the effectiveness of the proposed algorithm, the optimal solutions derived from the algorithm for each scenario in the sample case are compared to those obtained manually. Both sets of solutions are evaluated using the same performance indicators to provide a fair and consistent comparison. This comparison serves to highlight the improvements in efficiency and accuracy that the proposed algorithm offers over the traditional manual method, demonstrating its potential for real-world applications. Entering all the aforementioned parameters, the model was run using the solver Xpress 13.9 on a machine equipped with 11th Gen Intel(R) Core (TM) i7-1185G7 running at 3 Ghz and 32 GB of RAM. The algorithm generated an optimal solution with an execution time of less than 5 s.

The resulting optimal solution for each scenario is displayed in

Table 4. Different scenario solutions (R—researcher; P—Associate and Full Professors).

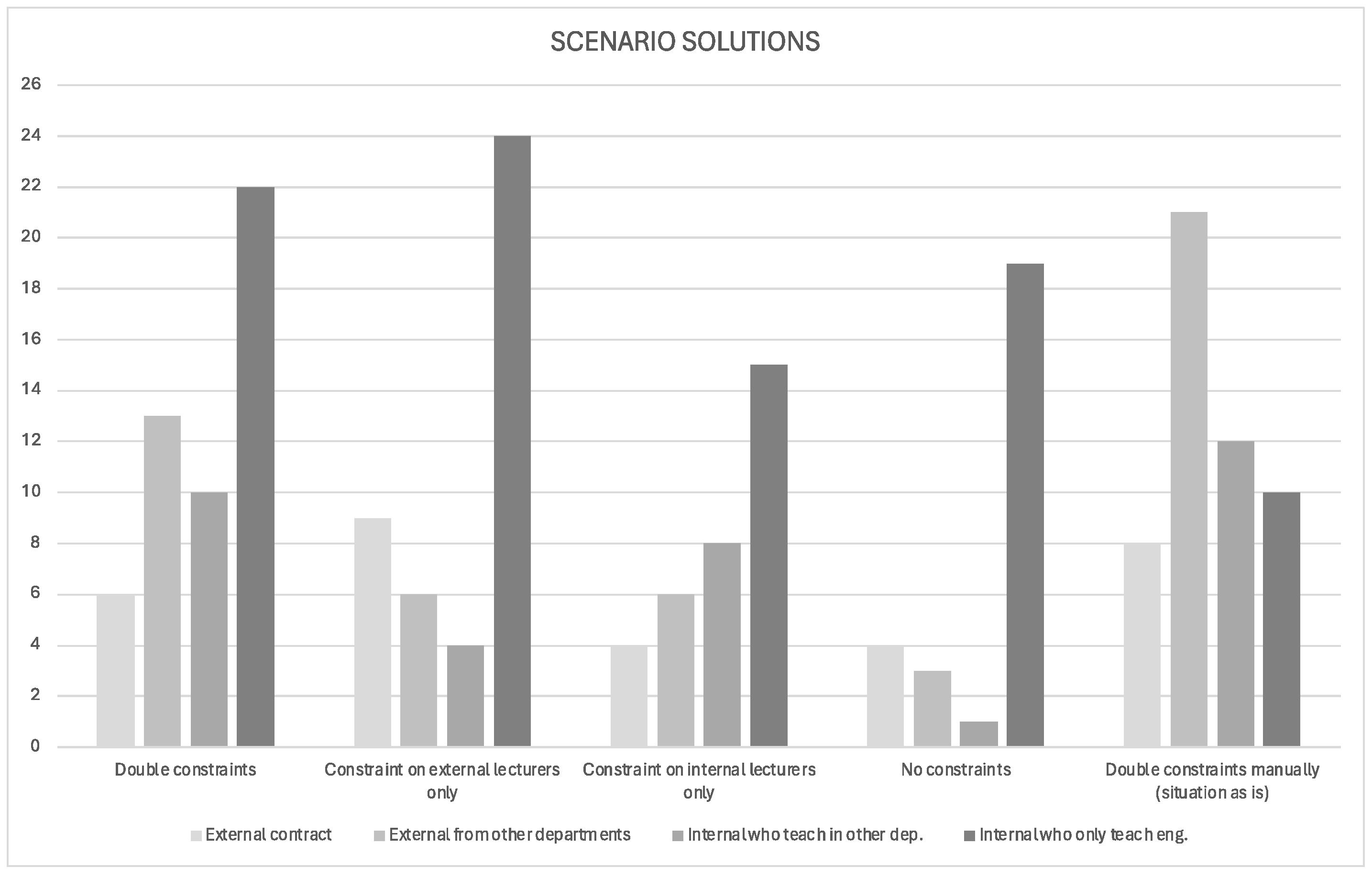
	Number of External Lecturers Used			Number of Internal Lecturers Not Used
Double constraints	19			32
	Contract lecturers	Other departments		who teach in other departments			who only teach engineering
	6	13		10			22
		R	P	R	P	R	P
		2	11	2	8	16	6
Constraint on external lecturers only	15			28
	Contract lecturers	Other departments		who teach in other departments			who only teach engineering
	9	6		4			24
		R	P	R	P	R	P
		3	3	1	3	17	7
Constraint on internal lecturers only	10			23
	Contract lecturers	Other departments		who teach in other departments			who only teach engineering
	4	6		8			15
		R	P	R	P	R	P
		2	4	1	7	14	1
No constraints	7			20
	Contract lecturers	Other departments		who teach in other departments			who only teach engineering
	4	3		1			19
		R	P	R	P	R	P
		1	2	0	1	15	4
Double constraints manually (situation as is)	29			22
	Contract lecturers	Other departments		who teach in other departments			who only teach engineering
	8	21		12			10
		R	P	R	P	R	P
		6	15	6	6	7	3

.

As reported in Figure 1, the best solution in terms of objective function is the scenario without constraints in which all the external lecturers are minimized. This solution obviously reduces unused internal lecturers as it aims at the sustainability of the individual department without taking into account the needs of others. However, this solution, if implemented at the university level, could find an optimal solution by minimizing exchanges between departments.

Upon consultation with the course coordinators, it was assessed by the department didactic delegate that the number of professors relative to researchers has a greater importance for each solution proposed. In particular, regarding the utilization of lecturers from other departments, the fewer professors relative to researchers, the more efficient the system is. Figure 2 shows that the best solution is one without constraints. It should also be noted that all solutions obtained by the algorithm are better than the ones found manually, even when both constraints are considered.

Figure 3 shows that the unconstrained solution has minimal reference lecturers’ availability for other departments. If the demands of other departments are considered, the double-constraint solution performs better than the manual solution both in terms of total number of lecturers and available professors.

Finally, Figure 4 shows the availability of internal lecturers, divided by role, who only teach in the analyzed department and therefore cannot be used elsewhere. This performance indicator is clearly minimized and the best solution is achieved manually. However, since the constraint of the reference lecturer is only on the minimum number, these lecturers can be deployed in the courses in which they teach.

5. Conclusions

This paper proposes an optimization algorithm that addresses the university’s reference lecturer assignment (RLA) problem, which concerns the allocation of a set of lecturers teaching in different courses of the analyzed department and in courses of other departments, over an academic year, such that the efficiency of the obtained solution is optimized. To the best of the author’s knowledge, it is the first time that research deals with the problem of reference lecturer assignment in light of the previous scientific literature. This paper has therefore both academic and practical significance: it creates the first step in the literature on RLA and it concretely helps universities in the self-quality assessment process, by improving its efficiency. The mathematical problem was modeled using different constraints, which define the boundaries of the problem. In proposing a quantitative approach to solve the reference lecturer assignment issue, the paper uses mathematical optimization techniques to achieve the best possible allocation. To validate the model, a case study was performed. The results indicate that all regulatory constraints are met, showing that the model can generate solutions that comply with the regulatory parameters without excluding any planned academic programs. Additionally, the results demonstrate a 76% improvement in reducing the use of external lecturers (from 29 to 7) when compared to 30 manually created RLA solutions, emphasizing the advantages of the proposed automatic algorithm. The results show that all the regulatory constraints are respected, indicating that the model could generate a solution that complies with the regulatory parameters without having to forego any of the academic programs planned to be included in the academic year. From an educational perspective, it is essential to address the issue of maintaining the standards required by regulations. The quality assurance system is specifically aimed at ensuring these standards. The proposed algorithm not only quickly selects the faculty members but also optimizes the outcome by minimizing the selection of contract lecturers. A course that features only tenured faculty is undoubtedly of higher quality compared to one that relies on contract lecturers. Also, the results show an average 76% improvement in terms of reduction in external lecturers used (from 29 to 7) when compared to 30 manually constructed RLA, highlighting the benefit of using the automatic algorithm proposed. The scenario analysis conducted analyzed the model’s behavior by implementing the following restrictions: (1) the imposition of giving internal lecturers as a reference in other departments and using external reference lecturers reported in a list, (2) only the imposition of giving internal lecturers as a reference in other department, (3) using external reference lecturers reported in a list, and (4) deleting both the constraints. The analysis shows that assuming these restrictions leads to sub-optimal solution in terms of objective function. The choice of which scenario has to be considered is then dependent on the use of the algorithm, i.e., if that it is run at department level or at university level. In terms of computational efficiency, the experimental case study proved the ability of the algorithm to solve real-world RLA problems, being able to yield an optimal assignment in a short time. Although this work effectively introduces a valuable decision-making tool, there are several areas for improvement that could enhance future research. These include testing the algorithm’s validity with a wider range of real-world scenarios in other universities, particularly those with more complex undergraduate and graduate programs, as well as exploring the efficiency of the proposed methodology in addressing the RLA problem. Heuristic algorithms can be developed to extend the application of the model from department-wide to university-wide cases, which have a much larger scale and entail higher computational complexity.