Analysis of Curricular Treatment of the Relationship Between Area and Perimeter in Two U.S. Curricula

Abstract

This study examines how two widely used elementary mathematics curricula, Bridges in Mathematics and Eureka Math, support grade 3 students’ conceptual understanding of the relationship between area and perimeter. Drawing on the mathematical treatment and emphasis component of the analytic framework, we identified distinct instructional strategies and learning opportunities. Findings indicate distinct instructional strategies and learning opportunities: Bridges in Mathematics emphasizes hands-on exploration, pattern recognition, and student-led reasoning using real-world contexts. In contrast, Eureka Math employs a more structured and symbolic approach, using multiplication, factor pairs, and line plots to support generalization and data-driven reasoning. Both curricula share strengths such as the use of visual supports, real-world contexts, and attention to student reasoning, yet they differ in how they scaffold conceptual development. Rather than recommending one curriculum over the other, the study highlights how each curriculum sequences ideas and supports mathematical reasoning, offering insights into curricular design and the learning experiences they foster.

1. Introduction

Mathematics textbooks, curriculum materials, and instructional resources have long been a cornerstone of classrooms globally (Valverde et al., 2002). They mediate curriculum policy (Valverde et al., 2002), support teachers’ instructional decisions (Stein et al., 2007) and promote curricular coherence across diverse educational settings (Schmidt et al., 2005). In recent decades, growing public scrutiny of school mathematics has intensified the prominence of curriculum materials in educational policy and practice, fueling a multi-billion-dollar international industry.

Following the release of the Common Core State Standards for Mathematics curriculum in the United States (National Governors Association Center for Best Practices & Council of Chief State School Officers, 2010), K–12 mathematics curricula in the U.S. have gone through major revisions in terms of content sequence, grade placements, and pedagogical approach to align with the national standards. Understanding the extent of alignment between mathematics textbooks and the Common Core State Standards for Mathematics (CCSSM) is significant for both scholarly inquiry and practical decisions related to curriculum adoption and teacher professional development (Porter et al., 2011; Zhou et al., 2022, 2023).

Prior studies on the alignment of mathematics textbooks with the CCSSM reveal a complex landscape, often challenging publishers’ claims of full adherence. A major theme emerging from these studies is that textbooks frequently exhibit significant areas of misalignment, particularly in their emphasis on procedural knowledge over the conceptual understanding and mathematical practices central to the CCSSM. For instance, Polikoff (2015) found that many textbooks systematically overemphasize procedures and memorization, failing to adequately address the higher levels of cognitive demands the standards promote. Hong et al. (2019) similarly found gaps in the coverage and sequencing of area measurement topics, which raise concerns about whether current curricula adequately support the development of key mathematical ideas.

Despite the decades of research, misconceptions about the relationship between area and perimeter persist among learners and educators. Studies consistently show that both pre-service and in-service teachers often hold the mistaken belief that a larger perimeter necessarily corresponds to a larger area (Ma, 2010; Livy et al., 2012; Tan Sisman & Aksu, 2016; Widjaja & Vale, 2021). Such misconceptions hinder flexible problem solving and suggest that instructional interventions may not be fully addressing the conceptual complexity of this topic.

CCSSM standard calls for instruction that supports students in recognizing the relationships between area and perimeter:

Solve real world and mathematical problems involving perimeters of polygons, including finding the perimeter given the side lengths, finding an unknown side length, and exhibiting rectangles with the same perimeter and different areas or with the same area and different perimeters (CCSS.MATH.CONTENT.3.MD.D.8).

This makes the concept particularly important for developing mathematical reasoning and spatial understanding in elementary grades.

While previous curriculum analyses focus on broad topics such as geometry and measurement (Polikoff, 2015; Hong et al., 2019), few have investigated the learning opportunities for students and teachers afforded by curricula at the concept level. The relationship between area and perimeter offers a compelling case study because it requires coordination of multiple representations, reasoning about counterexamples, and careful distinction between related but distinct measures.

The present study aims to address this gap by conducting a detailed comparison of two widely used curricula, Bridges in Mathematics and Eureka Math. These curricula were selected because they have high adoption rates nationally (EdReports, n.d.-a, n.d.-b; Kaufman et al., 2017), and both explicitly target the Grade 3 standards (i.e., CCSS.MATH.CONTENT.3.MD.D.8) for area and perimeter relationships. Understanding how these curricular materials structure learning opportunities for this concept can inform teachers’ instructional decisions, curriculum developers’ design choices, and researchers’ understanding of curriculum affordances. It is important to note that this analysis is limited to the design and content of the curriculum materials themselves and does not evaluate classroom implementation or student learning outcomes.

2. Literature and Theoretical Perspectives

2.1. Misconceptions and Challenges in Understanding Area–Perimeter Relationships

Research has shown both pre-service and in-service teachers often misunderstand the relationship. Livy et al. (2012) found that 72% of a group of pre-service primary teachers from Australia thought that an increase in perimeter would always result in an increase in area. Ma (2010) presented the question shown in Figure 1 to a group of 23 U.S. and 72 Chinese elementary school teachers. Notably, 96% of the U.S. teachers and 31% of the Chinese teachers believed the student’s claim was correct—either immediately or after some reflection.

An assumption about the existence of a “direct proportional relationship” between area and perimeter was reported among students of different ages as well as both pre-service and in-service teachers (e.g., Livy et al., 2012; Lo et al., 2019; Machaba, 2016; Tan Sisman & Aksu, 2016; Widjaja & Vale, 2021). For example, in Tan Sisman and Aksu’s (2016) study, only 5% of the 445 Turkish sixth-grade students participating in the study were able to correctly answer the following question, shown in Figure 2, that examines the relationship between the area and perimeter. Most of the students (62%) believed that since both shapes are made up of the same pieces, their perimeters are equal, indicating a lack of understanding that perimeter is a measure of boundary length and can change when parts of a shape’s boundary become internal after partitioning or rearrangement. Likewise, Lo et al. (2019) found that approximately 76.5% of U.S. seventh graders inaccurately responded ‘it gets shorter’ when questioned about the perimeter of a piece of paper after a single piece is removed. The actual change in perimeter (shorter, longer, or unchanged) is contingent upon the location and shape of the cut.

These findings illustrate persistent difficulty in understanding that the perimeter, as a property of the boundary, is independent of its internal area. Additionally, errors could stem from pervasive intuitive rules, such as “more A, then more B,” often seen across various significant STEM concepts (Tirosh & Stavy, 1999). The difficulty is compounded by shared variables, i.e., width and length. J. P. Smith and Barrett (2017) concluded in their review that “Overall, research has not yet produced a compelling explanation for this challenge or an effective instructional response” (p. 365). Furthermore, the enduring belief in a linear relationship between area and perimeter might also be attributed to a weak appreciation for the power of counterexamples in mathematical proof. Indeed, Widjaja and Vale (2021) found that a majority of 82 Australian students in grades 4–6 lacked the understanding of how one counterexample can disprove a mathematical statement.

Although instructional materials often ask students to compare rectangles with same areas and different perimeters (or vice versa) as suggested by the CCSSM, this approach appears to have limited long-term effectiveness, as seen by the difficulties faced by pre-service and in-service teachers discussed earlier. The insufficient impact of using rectangles may be due to its strong emphasis on numerical and logical data, whereas a true conceptual understanding of area, perimeter, and their interrelationship is fundamentally tied to intuition, spatial reasoning, and everyday experiences (Machaba, 2016). This study aims to contribute to this conversation by examining how two U.S. mathematics curricula support grade 3 students in developing a robust understanding of the relationship between area and perimeter.

2.2. Mathematics Curricula Analytical Lens

Curriculum materials shape how mathematical ideas are introduced, sequenced, and emphasized in classrooms, thereby influencing the opportunities students have to learn (Valverde et al., 2002; Stein et al., 2007). Effective curriculum goes beyond simply listing topics covered and delves into the nature and quality of engagement students have with mathematical content (Dietiker & Richman, 2021; Lo et al., 2024; Zhou et al., 2023).

In mathematics curriculum research, “learning opportunities” are recognized as a multifaceted for understanding and evaluating the quality of engagement students have with mathematical content (Remillard & Kim, 2000). Examining curricula at learning opportunities can illuminate the design decisions and pedagogical affordances that either support or constrain deep conceptual understanding.

Remillard and Kim (2000) conceptualize Mathematical Treatment and Emphasis of curricular materials as “aspects of mathematics emphasized and how mathematics is organized and presented for student learning” (p. 11). This construct highlights how mathematical content is presented, sequenced, and framed; the precision of definitions; the choice and variety of examples and non-examples; and the integration of visual, symbolic, and contextual representations.

Building on this conceptualization, Kim and Remillard (2000), in their comparative analysis of five curricula across grades 3–5 with a focus on number and operations, operationalized Mathematical Treatment and Emphasis into four analytic dimensions: scope and sequence, cognitive demand of student tasks, ongoing practice, and representation.

Our theoretical perspective was informed by this prior work, but we adapted it to align with the aims and scope of our study. Specifically, because our analysis focuses on a specific mathematical topic—the relationship between area and perimeter—in grade 3, rather than on broader curricular domains, we modified the analytic framework to attend more closely to topic-specific features. We therefore examine Mathematical Treatment and Emphasis through the following four adapted dimensions: overall lesson structures, introductory lesson, mathematical emphasis across the lesson sequence, and mathematical representation.

Overall lesson structures indicate captures how lessons are organized and displayed in relation to learning pathways (Remillard & Kim, 2000). Examining lesson structures provides insight into the extent of instructional coherence and how the overall sequencing supports student learning. Introductory lessons play a pivotal role in shaping the tone and trajectory of student learning (Lo et al., 2024). We attend to how the first encounters establish key connections, situate the mathematics in context, and expect approaches students may use. Mathematical emphasis across the lesson sequence considers how emphases are sustained, shifted, or deepened as lessons progress (Kim & Remillard, 2000). Mathematical representation provides a critical analytic lens for analyzing the ways in which the mathematical content is conveyed within the curricula (Kim & Remillard, 2000).

We chose not to include cognitive demand of student tasks as a separate analytic dimension. Although we recognize the importance of task demand in shaping student learning, our analysis is limited to classwork that directly mediates instruction, discourse, and in-class learning opportunities. In reviewing the tasks using M. S. Smith and Stein’s (1998) framework, we found that even tasks classified at lower levels (e.g., memorization) often served as essential foundations for subsequent reasoning and instruction. Categorizing tasks strictly by cognitive demand would therefore obscure their pedagogical role within the lesson sequence and add limited analytic value for this study.

The four dimensions of Mathematical Treatment and Emphasis informs our analysis of how the Bridges in Mathematics and Eureka Math curricula structure content, guide instruction, and support teachers in developing third-grade students’ understanding of the relationship between area and perimeter. By comparing these two textbooks, researchers and educators can gain a comprehensive understanding of the affordances and limitations of different elementary mathematics curricula. The insights can guide teachers in making informed instructional decisions, adapting tasks, and using textbooks more effectively to support student learning and mathematical understanding. Specifically, we address the following overarching question: To what extent do the Bridges in Mathematics and Eureka Math curricula provide distinct or overlapping learning opportunities for third-grade students to develop a conceptual understanding of the relationship between area and perimeter?

3. Methods

Comparative analyses of curricula are well-established approach for examining the treatment of particular mathematical topics or domains, either cross-national or within a single context. Cai and Cirillo (2014) raised questions for curricula studies “what text in textbook(s) should we analyze and How much of that text should we analyze?” (p. 136). To investigate how the selected curricula address standards related to the relationship between area and perimeter, the two authors engaged in a careful selection process followed by iterative discussions to confirm the final data sources. The following section details the data sources and outlines the analytical schemes used in this study.

3.1. Data Source

This study examined two grade 3 U.S. mathematics curricula: Bridges in Mathematics, published by The Math Learning Center (2024), and Eureka Math, published by Great Minds (2015). The primary data source was teacher guides accompanying each curriculum.

Bridges in Mathematics is a widely used K–5 curriculum designed to foster conceptual understanding and problem solving while supporting procedural fluency. It emphasizes active, hands-on learning through the use of visual models and manipulatives to help students build mathematical understanding.

Eureka Math (formerly known as EngageNY) is a fully CCSSM-aligned K–12 curriculum originally created and maintained by the New York State Education Department. As of 2017, it had been downloaded more than 66 million times by educators across the country since the website launched in 2011 (Kaufman et al., 2017). The curriculum is available in multiple languages, including English, Spanish, and Chinese.

The selection of these two textbooks was not arbitrary. It was based on three key consideration: widespread use, accessibility for research, and conceptual similarity. First, these textbooks are widely used, and both strongly align with the CCSSM (EdReports, n.d.-a, n.d.-b). This popularity and alignment make them excellent subjects for a study aiming to provide relevant, broadly applicable findings. Additionally, both curricular materials are accessible for research purposes upon online requests via their publishers’ websites. Such accessibility allows for a thorough and replicable research process. Other researchers can easily verify our findings and conduct similar investigations, which is crucial for the transparency and reproducibility of academic research.

Finally, a quick look at their core student materials reveals they both consist of problem sets with dedicated space for student work (as shown in Figure 3); this initial resemblance is precisely what makes them good candidates for a comparative study. Both curricula officially state they prioritize the development of conceptual understanding and procedural fluency through problem-solving.

Our preliminary analysis, however, has unearthed numerous distinctions in their instructional approaches and design elements that are not immediately obvious. By delving into these specific differences, we can move beyond the “what” of their similar goals to investigate the “how” of their distinct methods. This comparative approach will provide crucial insights into how specific curricular design choices are structured. While linking these features directly to student learning outcomes is beyond the scope of this study, our findings will offer a foundational understanding of the curricular differences that may inform future research on that topic. Ultimately, this research will equip educators with the knowledge to make more discerning choices when selecting the most effective resources for their students.

3.2. Analyzed Lessons

Both curricula have three-tier hierarchy structures: Unit ⟶ Module ⟶ Session in Bridges in Mathematics and Module ⟶ Topic ⟶ Lesson in Eureka Math. For the purposes of this analysis, we refer to the smallest lesson units—sessions in Bridges and lessons in Eureka—as “lessons.” Both curricula recommend approximately 60 min of instruction per day.

Bridges in Mathematics dedicates five constructive lessons within a single module to the relationship between area and perimeter. Eureka Math addresses this relationship across two different “Topics.” The first Topic also includes five lessons, while the second Topic features additional lessons that involve creating a robot poster project, which reinforces understanding of the distinction between area and perimeter. However, as the teacher’s guide explicitly designates these robot poster lessons as optional, they are excluded from this study.

Both curricula introduce the definitions and application of area concepts earlier than perimeter concepts. For instance, Bridges in Mathematics introduces area in Unit 5 and perimeter in Unit 6, while Eureka Math presents area in Module 4 and perimeter in Module 7. A key difference, however, lies in when the formal definition of perimeter is introduced within the context of the analyzed lessons. Bridges in Mathematics presents this definition in the first analyzed lesson, whereas Eureka Math introduces it just prior to the analyzed lessons.

3.3. Data Analysis

We conducted a lesson-by-lesson textual analysis of each curriculum, focusing on the lessons on the relationship between area and perimeter using the Constant Comparisons Method (Stake, 2000). Our analytic framework was guided by four adapted dimensions of Mathematical Treatment and Emphasis: (1) overall lesson structures, (2) introductory lesson, (3) mathematical emphasis across the lesson sequence, and (4) mathematical representation.

The analytic process involved three phases. In the first stage, both authors jointly reviewed all relevant lessons from Bridges in Mathematics and Eureka Math via online meetings. During this phase, we coded lesson materials along the four dimensions, focusing especially on lesson structures (i.e., the placement of area–perimeter content within the larger unit and the overarching instructional flow) and introductory lessons (i.e., how the topic was launched through contextual tasks, manipulatives such as unit squares and tiles, or guided definitions). Because this phase was conducted collaboratively, we encountered only minimal disparities in our initial interpretations. Any differences in interpretation were discussed and resolved during meetings.

In the second stage, each author independently re-examined the selected lessons, focusing more closely on mathematical emphases across the sequence and representations. Detailed analytic notes captured the kinds of reasoning promoted (e.g., distinguishing between area and perimeter, or exploring shapes with equal perimeters but different areas), as well as the use of visual, symbolic, and manipulative models to support exploration, discussion, and formalization. We paid particular attention to the questions posed to students, the objectives stated, the activities designed, and the mathematical conclusions students were guided to draw, such as recognizing the non-direct relationship between area and perimeter.

In the third stage, we met repeatedly to compare interpretations and refine the coding scheme through iterative discussion until consensus was reached. This collaborative reliability check confirmed the consistency of our coding scheme and interpretations. Finally, all coded data were compiled into structured tables for each curriculum and synthesized into cross-curriculum matrices. This process enabled us to identify convergences and divergences in how Bridges in Mathematics and Eureka Math address the area–perimeter relationship, in both mathematical and pedagogical terms.

4. Results

In this section, we first describe the overall lesson structures, followed by an examination of the introductory lessons that open each curriculum’s treatment of the relationship between area and perimeter. These descriptions illustrate the lesson flow and the forms of student engagement emphasized in each program. We then compare the mathematical emphases, both explicit and implicit, across the lesson sequences. Finally, we analyze the use of mathematical representations in each curriculum.

4.1. Lesson Structures

The two curricula follow a consistent structure across their respective lessons. In Bridges in Mathematics, each lesson typically features one to two major “Problems and Investigations” as the core new learning experiences. Additional support is provided through “Daily Practice” and “Homework Connections.” A unique component is the “Work Place” station, where students engage in independent or collaborative activities using concrete or visual models.

Eureka Math lessons include five key components. They begin with Fluency Practice, which consists of quick exercises designed to build speed and accuracy with foundational skills. This is followed by an Application Problem, a real-world task that connects new concepts to prior learning. The core of the lesson is the Concept Development section, where new mathematical ideas are introduced and explored through guided discovery. Afterward, students participate in a Student Debrief, a reflective discussion to articulate their understanding and clarify misconceptions. Finally, each lesson concludes with an Exit Ticket, a brief formative assessment used to evaluate students’ grasp of the lesson objectives and to inform subsequent instruction.

Table 1. Comparison of typical lesson structures in Bridges in Mathematics and Eureka Math.

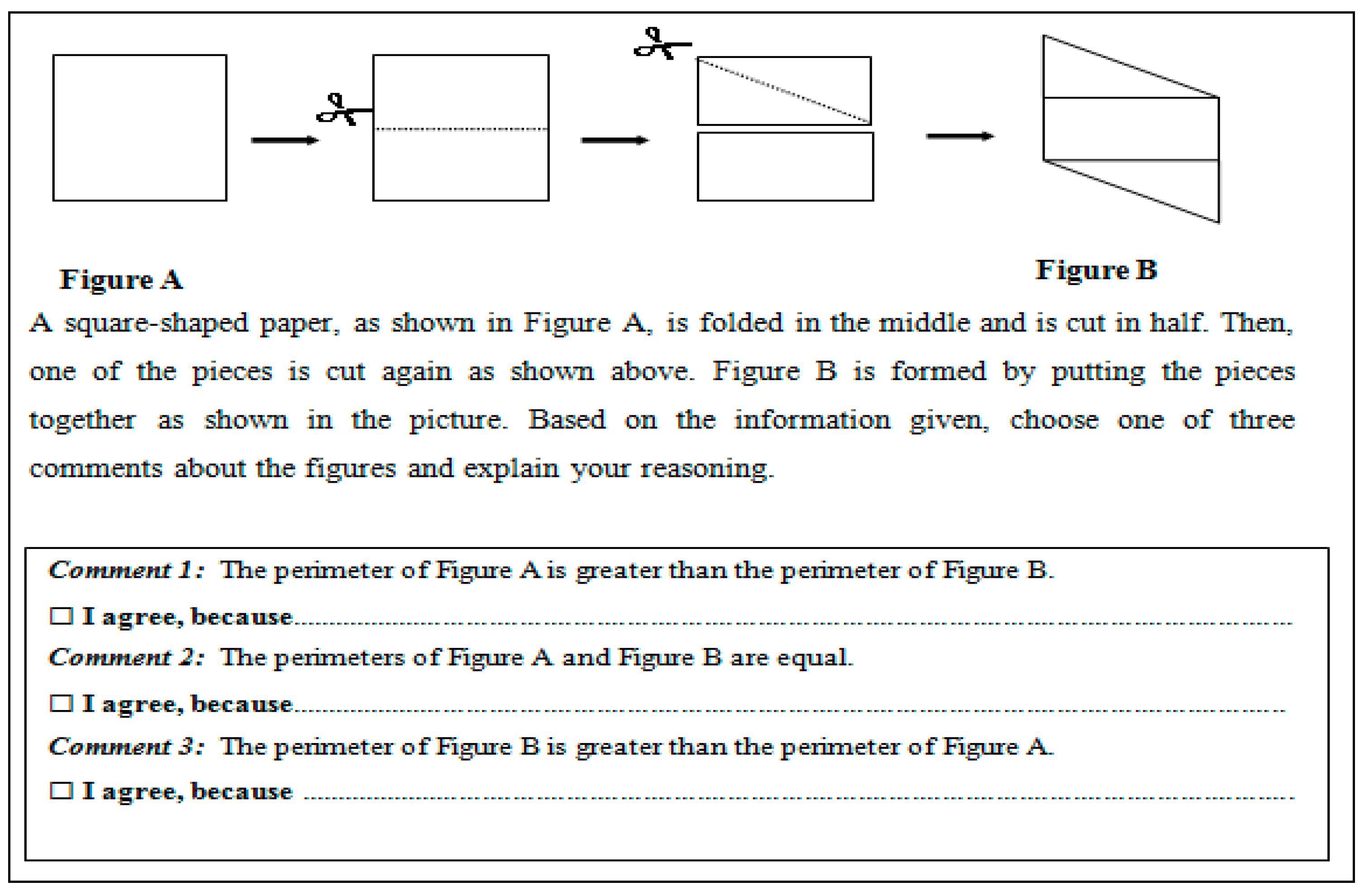
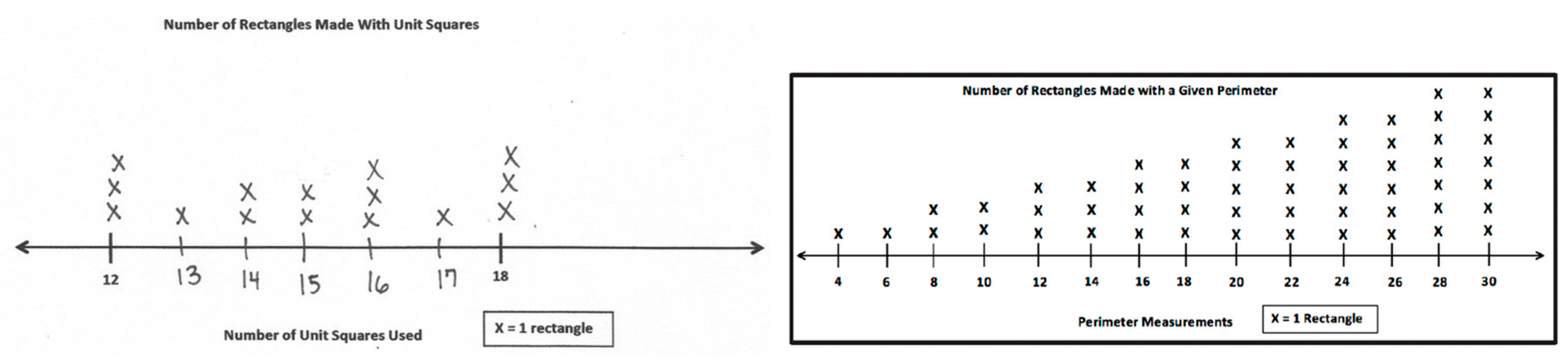
Feature/Curriculum	Bridges in Mathematics	Eureka Math
Core Learning	“Problems and Investigations”—1–2 major tasks serving as the core new learning experiences	“Concept Development”—main instructional portion with guided discovery and discussion
Practice/Review	“Daily Practice” and “Homework Connections” for reinforcement	“Fluency Practice”—quick and targeted exercises designed to build fluency with foundational skills
Reflection/Closure	Not a distinct component, but teachers’ guides include reflection prompts	“Student Debrief”—closing discussion for reflection and clarification
Unique Feature	“Work Place”—activity and game-based learning stations with concrete and visual models	“Application Problem”—connecting new concepts to real world context “Exit Ticket”—daily formative assessment

summarizes the structural components of each curriculum’s typical lesson.

In our primary analysis, we focused on the Core Learning and Reflection/Closure components. Routine Practice/Review activities were excluded, as they primarily reinforce procedural fluency. However, we included Work Place activities (Bridges) and Application Problems (Eureka) when they directly addressed the relationship between area and perimeter.

4.2. Introductory Lessons in the Two Curricula

4.2.1. Introduction Lesson in Bridges in Mathematics

In Bridges in Mathematics, the introduction of the relationship between area and perimeter in Unit 6, Module 3 begins with an open investigation using table arrangements to informally explore “same and different” in mathematical attributes. Prior to this, students had informal exposure to perimeter through tasks involving finding the total distance around shapes.

The lesson then transitions to a “Fundraiser” task, where students use square tables to create arrangements that seat exactly 10 guests. This leads students to think about how combining tables affects perimeter. Students are encouraged to manipulate tiles and line units to test their ideas and provide reasoning.

Later in the lesson, the concept of perimeter is formally introduced as the distance around the shape. A key pedagogical emphasis is to guide students to conclude that rectangles with different areas can have the same perimeter through constructing examples with tiles and line units. The lesson design promotes active student participation through hands-on modeling, problem solving, and collaborative discussion.

4.2.2. Introduction Lesson in Eureka Math

Eureka Math introduces the area–perimeter relationship in Module 7, Topics D and E, starting with teacher-led fluency practices that review multiplication facts and finding the area and perimeter of basic rectangles. This is followed by an application problem involving arrays to engage students to start thinking of different kinds of arrays associated with a specific number of dots.

The main activity involves students working in pairs to find all possible rectangles made from a fixed number of unit square tiles (e.g., 18 tiles), followed by a comparison of the perimeters of these area-equivalent rectangles. Through this process, students observe that rectangles with the same area can have different perimeters depending on their shape, with students noting that “long and skinny” rectangles tend to have greater perimeters.

To reinforce understanding, students complete a problem set in which they generate rectangles with a given area and compare their perimeters. The lesson concludes with a student debrief that encourages reflection, particularly through a prompt asking why squares tend to have the smallest perimeter for a fixed area, followed by an Exit Ticket that assesses students’ ability to determine missing side lengths and calculate perimeters for rectangles with a known area.

4.3. Lesson Sequence and Mathematical Emphasis

4.3.1. Bridges in Mathematics

In Bridges in Mathematics, the relationship between area and perimeter is developed over five lessons in Unit 6, Module 3, progressing from informal exploration to formalization and deeper investigation. The pedagogical approach emphasizes hands-on activities, systematic recording, and collaborative inquiry.

Table 2. Mathematical focus in Bridges in Mathematics.

	Main Activities	Main Emphases
U6M3S1	Table arrangement for 10 guests using different configurations	Define perimeter as the distance around a shape
U6M3S2	Build rectangular tables that seat exactly 20 guests	Rectangles of the same perimeter can have different areas
U6M3S3	Open investigation “Can rectangles have the same area but different perimeters?”	Rectangles with the same area can have different perimeters
U6M3S4	Explore table configurations including both rectangular and non-rectangle shapes of an area of 30 square units and a perimeter of 26 units.	Compare shapes with same area and same perimeter
U6M3S5	Estimate and reason about the area and perimeter various of rectangles; Work Place: build rectangles	Distinguish area vs. perimeter units; deepen understanding via comparative strategies

provides a lesson-by-lesson overview of how Bridges in Mathematics develops the relationship between area and perimeter across five sessions (labeled as U6M3S1 to U6M3S5, referring to Unit 6, Module 3, Sessions 1–5). Each session’s main activities are summarized alongside the corresponding mathematical emphases.

In Session 1, students explore the perimeter informally through table arrangements, where the number of “chairs” represents the perimeter and the number of “tables” represents the area. This foundational task introduces both concepts in a real-world context. Session 2 builds on this by having students construct rectangular tables to seat 20 guests. Through this, students discover that rectangles with the same perimeter can have different areas and begin identifying and recording patterns, such as the sum of the width and length equaling half the perimeter.

Session 3 transitions into an open investigation in which students are challenged to determine whether rectangles can have the same area but different perimeters. Using 24 square tables, they generate multiple configurations and reflect on why and how the perimeter changes. In Session 4, students revisit their findings and use equations to calculate area and perimeter. They also explore shapes with a given area (30 square units) and perimeter (26 units), extending their understanding beyond rectangles to include non-rectangular configurations.

Finally, Session 5 reinforces the distinction between area and perimeter by focusing on units of measurement (e.g., linear vs. square units) and invites students to compare strategies and reasoning through structured practice and a Work Place game. Across all five sessions, the curriculum systematically builds conceptual understanding, guiding students to explore, notice patterns, and articulate relationships between area and perimeter.

4.3.2. Eureka Math

In Eureka Math’s Module 7, Lessons 18 through 22 meticulously explore the relationship between area and perimeter, employing a pedagogical approach that blends guided discovery with systematic exploration and explicit reflection.

Table 3. Mathematical focus in Eureka Math.

	Main Activities	Main Emphases
M7TDL18	Application problem; Build rectangles with given unit squares (18, 24, 16, 15, 12)	Rectangles of the same area can have different perimeters.
M7TDL19	Application problem; build rectangles with areas 13–20; create line plots	The number of possible rectangles related to factor pairs of the area and recorded using line plots.
M7TDL20	Application problem; Build rectangles by using given perimeters (15, 12, 14, 8, 22)	Rectangles of the same perimeter can have different areas.
M7TDL21	Construct rectangles with specific perimeters (10, 14, 16, 20); identify square possibilities	Compare areas of rectangles with the same perimeter; squares tend to have the smallest perimeter.
M7TDL22	Create and compare line plots for area and perimeter; assess generalization	The same numerical values for area and perimeter can yield different numbers of possible rectangles.

outlines the mathematical focus of five lessons (labeled as M7TDL18 to M7TDL22, referring Module 7, Topic D, Lessons 18–22) in Eureka Math that explicitly address the relationship between area and perimeter.

Lesson 18 begins with an application problem involving arrays and guides students to construct rectangles using a fixed number of unit squares. This task emphasizes the connection between area and multiplication while prompting students to observe how the perimeter varies depending on how the squares are arranged. In Lesson 19, students build rectangles using given areas (13–20 square units) and represent their findings in line plots. This activity highlights the link between the number of rectangle configurations and the factor pairs of a number, noting that prime numbers (e.g., 13 or 17) yield fewer rectangles than composite numbers (e.g., 12, 16, or 18).

Lessons 20 and 21 shift the focus to the perimeter. Students use application problems and systematic strategies—such as halving the perimeter to find possible length–width combinations—to explore how different rectangles can share the same perimeter while differing in area. These lessons reinforce the idea that rectangles with the same perimeter can vary in shape and that squares tend to have the smallest perimeter for a given area.

Lesson 22 synthesizes these learnings by having students create and compare line plots representing the number of rectangles for given areas versus given perimeters. This comparison explicitly drives home the conclusion that there is no general direct relationship between area and perimeter, as the data do not consistently show a connection.

Eureka Math uses a carefully chosen range of numbers across the lessons to support exploration and generalization. For example, students work with values such as 8, 10, 12, 13, 14, 15, 16, 17, 18, 20, 22, and 24. These numbers are selected to highlight specific relationships—such as factorability, symmetry, and parity—that deepen students’ understanding of area and perimeter. The deliberate use of numerical variation allows students to make meaningful comparisons and notice patterns, further enriching the learning experience.

4.4. Mathematical Representation

4.4.1. Bridges in Mathematics

Modeling is a central pedagogical strength of Bridges in Mathematics, enabling students to transition between real-world situations and formal mathematical reasoning. The authentic task of arranging tables to seat guests is relatable, visual, and tangible. The curriculum begins to pose authentic mathematical questions: “How many guests can this arrangement seat? Will this arrangement fit in a given space?” These informal inquiries mark the entry point into mathematics.

Students start by physically modeling table configurations, using tile manipulatives to explore different arrangements to fit a given number of guests. As students explore these arrangements, they gradually shift from intuitive reasoning to explicit use of mathematical tools and concepts—counting unit squares, measuring side lengths, and calculating area and perimeter. Modeling thus becomes a method of mathematizing everyday experience: real-life configurations are translated into numerical representations, visual arrangement, and formal definitions. Students are supported in this transition through structured lesson steps.

Building on its use of modeling, Bridges in Mathematics further distinguishes itself by encouraging students to move beyond conventional shapes (i.e., rectangles in this context) and explore the broader world of rectilinear figures and irregular configurations. This openness is not an incidental feature, but a direct result of the curriculum’s commitment to contextualized modeling. As students work within the scenario of arranging tables to seat guests, they naturally encounter configurations that extend beyond simple rectangles, such as L-shapes or other composite figures.

4.4.2. Eureka Math

Eureka Math offers a sequenced progression that supports deep conceptual development. Each lesson builds on prior explorations, helping students gradually develop an understanding of the relationship between area and perimeter. Rather than introducing topics in isolation, the curriculum ties each new idea to previous learning, creating a coherent learning trajectory. This structure helps students make sense of mathematical ideas incrementally while reinforcing core understandings over time.

Throughout these lessons, Eureka Math uses application problems, systematic construction tasks, and reflective discussions to build students’ conceptual understanding of the independent nature of area and perimeter. Line plots are employed as a powerful visual tool to help students move beyond isolated examples and recognize broader patterns—and non-patterns—in mathematical relationships.

Specifically, in Lesson 22, Eureka Math has students create a new line plot showing the number of rectangles possible for a specific perimeter and then compare it to the area-based line plot. This direct comparison is critical for leading students to the conclusion that there is no general rule about a connection between perimeter and area. Figure 4 illustrates how students compared two line plots—one representing fixed areas (top) and one representing fixed perimeters (bottom)—to analyze whether a generalizable relationship exists between area and perimeter.

By visually contrasting the distributions and patterns on these two types of line plots, students can concretely grasp that these two measurements are independent, even if they might coincidentally share numerical values in some instances. This use of line plots transforms individual calculations into meaningful data sets, enabling students to engage in higher-level analysis and generalize about the complex relationship (or lack thereof) between area and perimeter.

5. Discussion

The compared lessons in Eureka Math and Bridges in Mathematics aim to address the following standards:

Solve real world and mathematical problems involving perimeters of polygons, including finding the perimeter given the side lengths, finding an unknown side length, and exhibiting rectangles with the same perimeter and different areas or with the same area and different perimeters (CCSS.MATH.CONTENT.3.MD.D.8).

Both curricula support students in understanding the inconsistency between area and perimeter and offer rich opportunities to observe these relationships across these lessons. This reflects long-standing arguments that curriculum materials are not neutral but embody particular ways of highlighting, sequencing, and representing mathematical ideas (Remillard, 2005).

The two textbooks describe the topic from different angles (Remillard & Kim, 2000; J. P. Smith & Barrett, 2017). Eureka Math begins with “same area, different perimeter,” then moves to “same perimeter, different area” and ultimately guides students to compare whether having the same numerical value for area and perimeter results in the same number of possible rectangles. While Bridges in Mathematics does not limit shapes to rectangles and also includes rectilinear figures, it begins with “same perimeter, different areas,” then moves to “same area, different perimeter,” followed by “same area and same perimeter can still result in different shapes.” Finally, it highlights that even for the same rectangle, the numerical values of area and perimeter can be different. These differences illustrate how curricular representations shape the pathways through which students encounter core mathematical relationships (Schmidt et al., 2005; Stein et al., 2007).

5.1. Shared Learning Opportunities Across Two Textbooks

Both curricula emphasize hands-on, visual representations to support sense-making (Ma, 2010; Valverde et al., 2002). Whether students are building configurations with tiles or drawing on grid paper, the materials and tasks are designed to make mathematical ideas tangible. Prior research underscores that visual and tactile models are critical mediators between intuitive reasoning and formal abstraction. This visual and tactile engagement helps students identify patterns, make comparisons, and explore the consequences of changing dimensions (e.g., Livy et al., 2012).

Another key similarity lies in both curricula’s use of real-world contexts to situate learning. In Bridges in Mathematics, students engage with table arrangements for seating guests across all five lessons, while Eureka Math, although less anchored in a single narrative context, also presents authentic problem settings. Embedding tasks in meaningful contexts has been shown to promote student engagement and transfer of mathematical ideas. These real-life scenarios help students connect abstract measurements to meaningful situations, supporting intuitive thinking as a foundation for formal mathematical reasoning.

Both programs incorporate scaffolded learning sequences—beginning with simpler tasks and gradually increasing in complexity. Students might start with counting units or constructing simple rectangles, then move toward more advanced reasoning, such as identifying patterns in factor pairs or comparing different configurations with the same perimeter. This progression supports students in developing fluency and flexibility in their thinking.

Finally, both Bridges in Mathematics and Eureka Math are attentive to student reasoning and discourse. They provide teachers with prompts, side notes, and suggested questions to encourage explanation, justification, and peer discussion. These practices align with the Standards for Mathematical Practice, particularly “construct viable arguments and critique the reasoning of others,” and help foster a classroom culture where mathematical thinking is made visible and valued. Prior studies confirm that curriculum guidance around discourse strongly influences whether teachers position students as sense-makers or passive learners (Remillard, 2005; M. S. Smith & Stein, 1998).

5.2. Distinct Learning Opportunities in Each Textbook

As discussed earlier, both curricula did not deliver abstract insights of the relationship between area and perimeter as facts but constructed through hands-on engagement, guided reflection, and repeated exposure across multiple lessons. Bridges in Mathematics emphasizes concrete and visual modeling, using manipulatives like tiles, diagrams, and hands-on arrangements to help students physically and visually grasp the meaning of space and boundary. In contrast, Eureka Math emphasizes symbolic and numerical reasoning, guiding students to connect area with multiplication and perimeter with addition. For example, students use factor pairs to determine rectangle dimensions for a given area and apply addition to calculate the perimeter. These distinct approaches reflect different entry points into the same core ideas, providing multiple pathways for students to build meaningful and transferable understanding. These different emphases reflect what Schmidt et al. (2005) describe as curricular “coherence”—the degree to which mathematical ideas are linked and developed systematically. Bridges highlights horizontal coherence across representations and contexts, while Eureka emphasizes vertical coherence through progressive formalization. Furthermore, they each has unique features that will be discussed further.

5.2.1. Modeling as a Bridge Between Real Life and Mathematics in Bridges in Mathematics

The Bridges in Mathematics curriculum leverages modeling as a central process for developing mathematical understanding, guiding students from real-life contexts to abstract mathematical reasoning. Instead of presenting abstract problems, the curriculum initiates learning through authentic tasks, such as arranging tables for guests, which are relatable and tangible. Students begin by physically manipulating tiles to represent different table configurations, naturally leading them to explore and solve problems related to seating, space, area, and perimeter. This process supports students in translating real-life situations into visual arrangements and numerical representations. Through structured lessons, students gradually transition from intuitive reasoning to explicit use of mathematical tools, such as counting unit squares and measuring side lengths. Ultimately, this approach helps students abstract mathematical relationships from concrete experiences.

A key strength of the Bridges in Mathematics is its openness to non-rectangular shapes, which is a direct outcome of its focus on contextualized modeling. As students model real-life scenarios, they naturally encounter irregular, composite shapes, such as L-shapes. This approach is significant because it reflects the complexity of the real world and challenges students to think beyond idealized, textbook-perfect figures. By working with these non-standard shapes, students deepen their conceptual understanding of area and perimeter as attributes of all two-dimensional shapes, not just rectangles. This requires them to develop more nuanced strategies, such as calculating area in parts and carefully considering all boundaries when determining perimeter. Unlike curricula that might guide students toward finding all factors for a given area, Bridges in Mathematics poses open-ended tasks, inviting students to discover multiple solutions. This approach validates diverse problem-solving strategies and ensures that students see irregular shapes as meaningful mathematical objects rooted in everyday logic.

5.2.2. Developing Strategic Thinking Through Cross-Domain Connections in Eureka Math

Eureka Math fosters strategic reasoning by creating a coherent learning trajectory that connects geometry with other mathematical domains. The curriculum goes beyond introducing concepts in isolation, instead building upon students’ prior knowledge of topics like multiplication, factors, and odd and even numbers to deepen their understanding of area and perimeter. This integration allows students to apply familiar ideas in new contexts, strengthening their ability to reason mathematically. For example, students are guided to recognize how the commutative property of multiplication relates to rectangles, understanding that a 1 × 18 rectangle has the same area as an 18 × 1 rectangle. This approach is further exemplified by the curriculum’s use of line plots, which serve as a bridge between measurement and statistics. Students organize and display data about the rectangles they have created, enabling them to visualize patterns, identify extremal values, and engage in data interpretation. This not only enhances their understanding of geometry but also subtly introduces them to early statistical concepts, fostering a deeper, cross-domain understanding of mathematics.

Finally, Eureka Math emphasizes the development of flexible and transferable problem-solving skills. The curriculum prompts students to reflect on the strategies they’ve used in previous lessons and adapt them for new situations. For instance, when transitioning from problems with a given area to those with a given perimeter, the curriculum poses reflective questions that guide students to connect known strategies (e.g., using factor pairs) to new contexts (e.g., addition facts). This strategic continuity reinforces prior learning and prepares students to develop and apply flexible strategies across different mathematical contexts. The curriculum also encourages reasoning about optimization by asking students to explore which rectangle with a fixed area has the smallest perimeter or vice versa, laying the groundwork for more advanced concepts related to efficiency and extremal values.

6. Conclusions

This comparative analysis of Bridges in Mathematics and Eureka Math reveals that both curricula offer valuable, yet distinct, opportunities for students to develop a conceptual understanding of area and perimeter. Each curriculum embodies a particular pedagogical orientation: Bridges in Mathematics encourages open-ended exploration, student-generated strategies, and learning through intuitive, real-world contexts; Eureka Math emphasizes mathematical precision, logical progression, and structured reasoning. This echoes prior analyses showing that different curricula encode distinct visions of mathematical learning and teacher enactment (Remillard & Kim, 2000; Valverde et al., 2002).

Bridges in Mathematics is structured around discrete activities, with step-by-step instructions provided for each session. The numbered steps offer a clear sequence of activities and questions, which supports teachers in implementing the lesson in an organized manner. This structure can be particularly helpful for novice teachers, as it provides a clear roadmap for pacing, instructional moves, and transitions between activities. For teachers who are still developing their confidence, this level of guidance offers structure and pedagogical routines. However, consistent with Davis and Krajcik (2005), such guided routines may also constrain teacher adaptation and limit opportunities for deep conceptual coherence.

However, this linear structure also presents some limitations. It may obscure the conceptual coherence or the interconnected development of mathematical ideas within and across lessons. While the activity sequence often reflects a progression in format or engagement, it does not always make the progression in mathematical depth or abstraction explicit. As a result, while the structure supports smooth lesson delivery, it may underemphasize the kind of intentional scaffolding necessary for fostering deep and connected mathematical understanding.

Eureka Math integrates teacher guidance directly into the lesson flow. Each lesson unfolds through a consistent and visibly tiered structure—Fluency Practice, Concept Development, Application Problem, and Student Debrief—creating a tight alignment between instructional goals and task design. This structure not only provides clarity around the intended learning trajectory but also makes the progression of mathematical ideas more transparent for both teachers and students (Schmidt et al., 2005). The design supports the gradual development of understanding, moving from foundational skills to new concept exploration, and then applying those concepts in varied contexts.

This coherence also places greater demands on the teacher. To implement the curriculum effectively, educators must have a clear vision of the broader mathematical landscape, including how each lesson fits into the larger learning arc (Lo et al., 2024). Teachers are expected to be familiar with the curriculum’s long-term progression and recognize the conceptual thread development through lessons, anticipate student thinking, and facilitate discourse that highlights underlying structures. This resonates with research showing that teacher expertise mediates how curricular materials are enacted in classrooms (Remillard, 2005; Stein et al., 2007). While classroom implementation was beyond the scope of the present study, future research could investigate how teachers interpret and enact these curricular structures in practice, and what forms of implementation best support student understanding.

Understanding these curricular design rationales is essential for teachers. When educators recognize how tasks are sequenced, how mathematical ideas are developed, and what mathematical thinking is highlighted, they are better positioned to make informed instructional decisions during teaching (Zhou et al., 2023). Rather than prescribing which curriculum teachers should adopt, we recommend that educators develop a deep familiarity with the structure, mathematical approaches, and pedagogical emphases of the curriculum they are using.

This comparative analysis contributes to broader curriculum research by illustrating how different design choices create distinctive learning opportunities. By examining these diverse pedagogical models, this study offers rich opportunities to investigate the trade-offs and benefits of each approach, which could then inform the development of more intentional and effective educational programs. Building on these findings, future research could investigate how students from each curriculum program respond to specific, non-standard problems that test their conceptual understanding beyond rote procedures. For example, a study could present students with the task in Figure 2 used by Tan Sisman and Aksu’s study, discussed earlier. Analyzing student responses to this question would reveal how each curriculum’s approach to modeling and strategic thinking influences a student’s ability to reason about the relationship between area and perimeter.