Design and Development of a Teaching–Learning Sequence about Deterministic Chaos Using Tracker Software
Abstract
1. Introduction
- What are the secondary school students’ spontaneous models when interpreting simple physical phenomena that show a deterministic chaotic behavior?
- How are secondary school students’ models of deterministic chaotic systems affected by their models of classical deterministic systems?
- To what extent is a computer-based TLS effective in familiarizing secondary school students with the key concepts of deterministic chaos?
2. Description of the Teaching–Learning Sequence
- Key Idea 1: Slight variations in the initial conditions affect the motion of chaotic deterministic systems.
- Key Idea 2: Representation of the unpredictability of chaotic deterministic systems.
2.1. Phase 1: Review of Classical Oscillating Systems and Introduction to the Double Pendulum Mechanics (3 h)
2.2. Phase 2: Analysis of the Double Pendulum Motion Using Tracker Software (3 h)
3. Educational Context and Sample
4. Educational Context and Sample
I1. When do we say that a system does not follow deterministic laws? Explain by discussing some examples.
I2. What does the term chaos make you think of?
P1. Describe in words the role of initial conditions in the temporal evolution of the motion of oscillating systems as a spring–mass system or a simple pendulum.
P2. Describe in words the role of the initial conditions in the temporal evolution of the motion of the double pendulum.
P3. What are the main similarities and differences between the motion of a simple pendulum and that of a double pendulum for small oscillations? And for ample ones?
P4. Qualitatively describe the motion of the double pendulum.
P5. Using the tracking function of Tracker, describe how the motion of the double pendulum evolves over time choosing a suitable graphical representation.
P6. What happens when the oscillations of the double pendulum become small?
5. Results
5.1. Pretest Analysis
5.2. Analysis of Students’ Responses to Worksheet Prompts
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Pretest
- What does it mean to study and/or know the temporal evolution of a phenomenon? Explain by giving concrete examples.
- What is necessary to know in order to be able to predict the temporal evolution of a phenomenon?
- When do we say that an event is predictable and when unpredictable? Explain using examples from everyday life.
- When do we say that a system does not follow deterministic laws? Explain by discussing some examples.
- When do we say that a body is subject to linear stress and when it is not? Explain this by giving studied examples.
- Do you think the terms random and chaotic have a similar meaning or not? Can you find similarities and differences between the two terms through concrete examples?
- Have you ever heard of random natural phenomena? Explain with concrete examples.
- Have you ever heard of chaotic natural phenomena? Explain with concrete examples.
- What does the term chaos make you think of? How would you explain the term deterministic chaos? Can a chaotic event be deterministic? Explain by giving concrete examples.
- Have you ever heard on television that, for example, a rainy and cold day is forecasted and then, instead, there is a beautiful day with bright sunshine and blue skies? Have you ever wondered why? Why do weather conditions not really seem ‘predictable’?
Appendix B. Interactive Worksheets
Phase 1
- Consider the following two systems: a body of mass m resting on a frictionless surface and attached to the free end of a spring and a simple pendulum in the absence of friction. Identify the forces at play in the two systems by drawing the force diagram in correspondence with at least four points of the trajectory of your choice. Finally, trace the acceleration vector at the previously chosen points. Import the available image in the team in Microsoft PowerPoint to draw the force diagram.
- What do you expect if we slightly vary the initial position? Briefly explain.
- If friction is considered, would it still be possible to determine the time evolution of the systems?
- Observe the “myPhysicsLab Single Spring” simulation of the motion of a simple harmonic oscillator. Vary slightly the initial conditions several times and observe the corresponding motions. Observe how the x coordinate varies as a function of time, x(t) and how the velocity of the mass varies as a function of the x coordinate, v(x). Briefly explain the trends observed.
- Observe the “myPhysicsLab Simple Pendulum” simulation of the motion of a simple pendulum. Vary slightly the initial conditions several times and observe the corresponding motions. Observe the x(t) and v(x) graphs. Briefly explain the observed trends.
- Based on the previous observations, describe in words the role of initial conditions in the temporal evolution of the motion of oscillating systems as a spring-mass system or a simple pendulum.
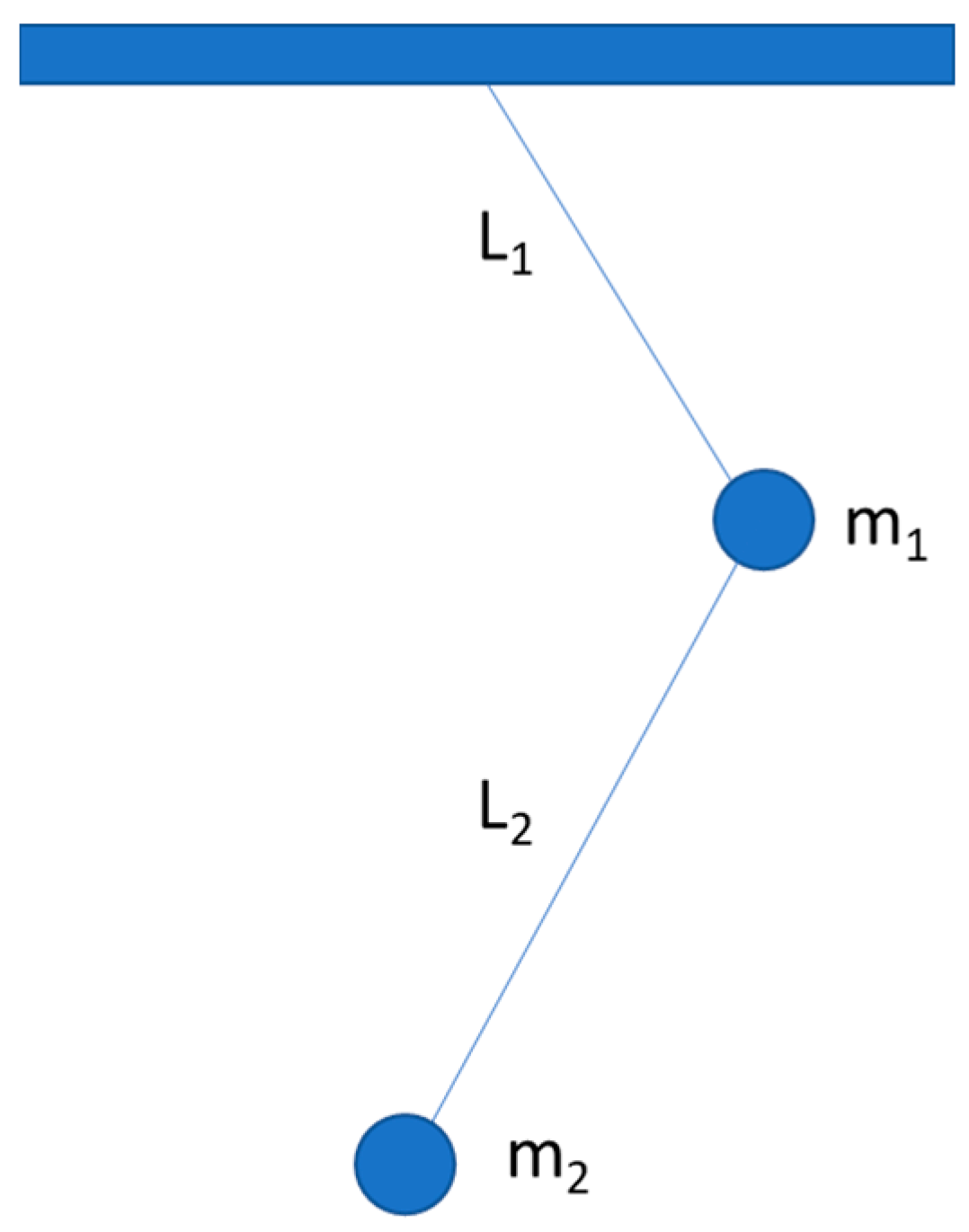
- Look at the double pendulum in the figure. Predict the motion of the system when it is released from a generic configuration of the two masses.
- Identify the forces at play in the system under examination by tracing the force diagram in the figure shown on this sheet. Import the available image in the team in PowerPoint to draw the force diagram.
- Qualitatively describe the motion of the double pendulum.
- Describe the motion of the system in the following two cases: m2 ≪m1; l_2≪ l1
- What are the main similarities and differences between the motion of a simple pendulum and that of a double pendulum for small oscillations? And for ample ones?
- Suppose you repeatedly start the system consisting of the two pendulums from rest varying slightly the initial positions ϑ1 and ϑ2. What do you expect to happen? Justify your reasoning.
Phase 2
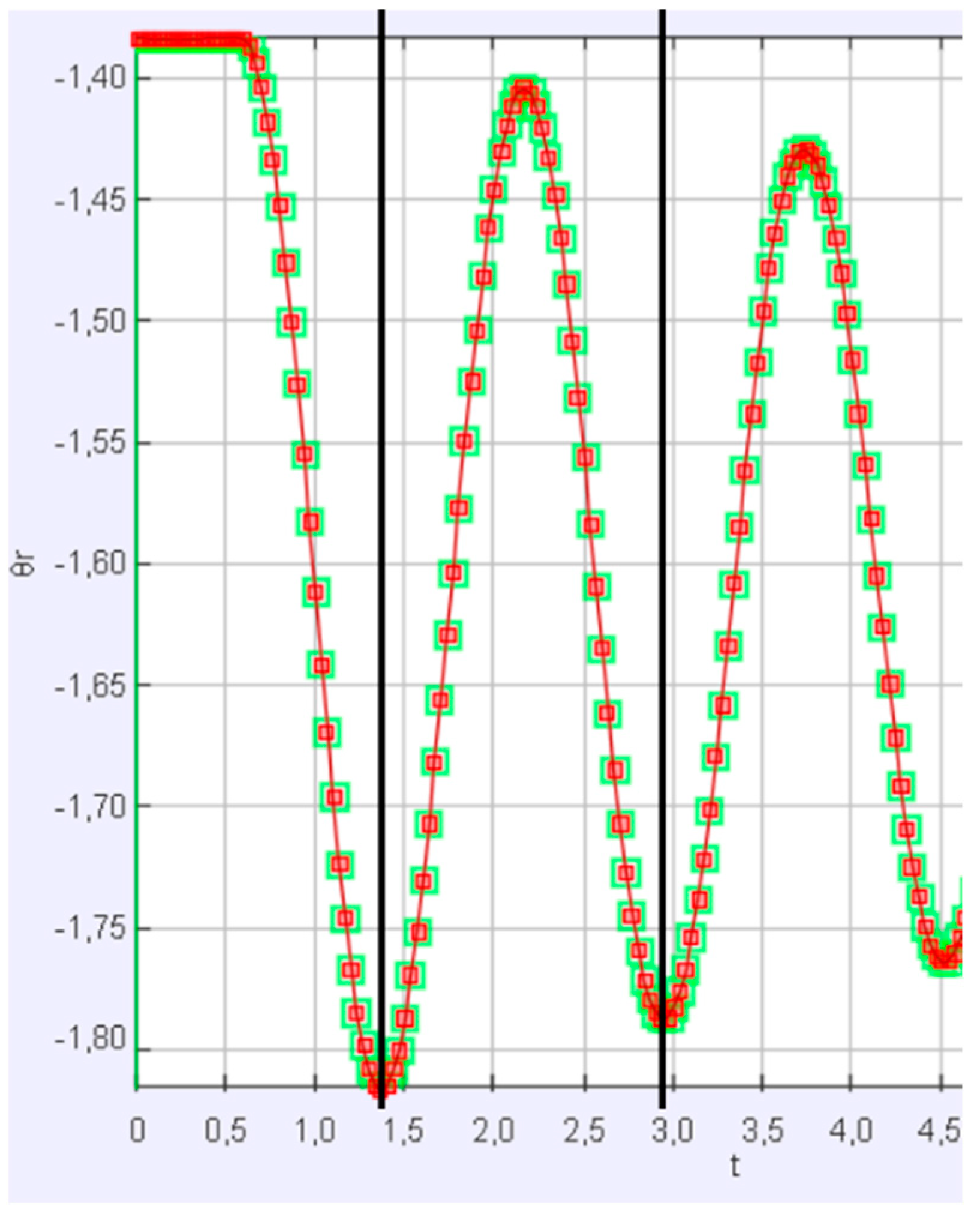
- Watch the Video S1 available on YouTube and compare it with your predictions. What are the main differences and similarities? In particular, how does the amplitude of the angles ϑ1(t) and ϑ2(t) change with time?
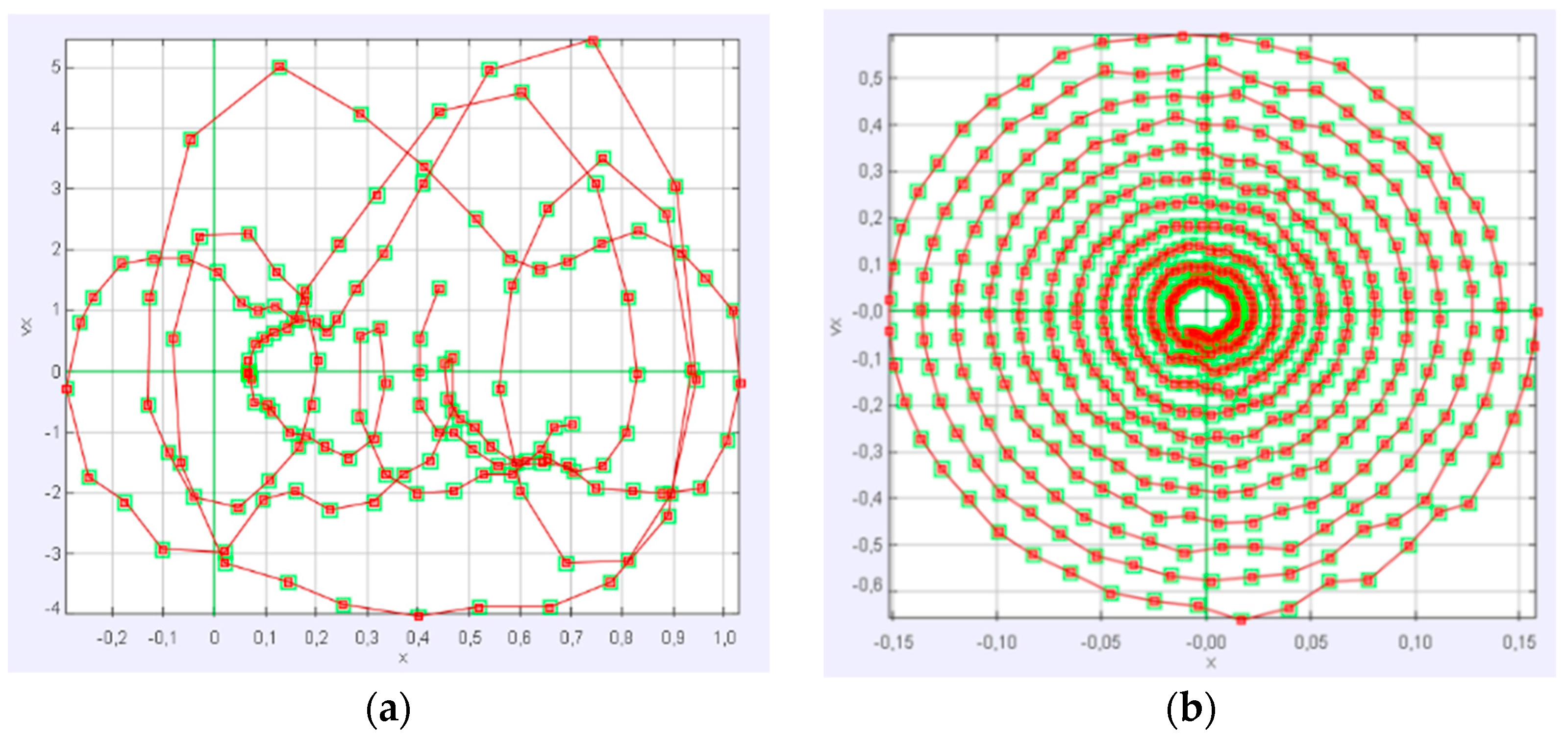
- The Tracker software functionalities allow to import a video, in our case the oscillations of the double pendulum, and to quantitatively measure those quantities that are difficult to measure with “traditional” instrumentation. Import the two Videos S1 and S2 provided to you (also available on YouTube) into the software, in which we have reproduced the same initial conditions (position and speed) as accurately as possible. By labeling the free end of the double pendulum, it is possible to reconstruct its trajectory. What do you observe when comparing the trajectories of the pendulum in the two videos?
- Using the tracking function of the Tracker software, describe how the motion of the double pendulum evolves over time choosing a suitable graphical representation.
- Import the Video S3 (also available on YouTube) that shows the small oscillations of the double pendulum. What happens when the oscillations of the double pendulum become small?
- Try to model the double pendulum as a physical pendulum (i.e., a rigid body) with mass M = 3 Kg and length L = 1 m and verify with the Tracker software that the period of the small oscillations is in agreement with the theoretical model of a physical pendulum.
- Observe the “myPhysicsLab Double Pendulum” simulation and change the masses and length of the two pendulums. Compare the behavior of the double pendulum in the simulation with what you observed in the previous videos. What are the main similarities and differences?
References
- Laws, W.P. A unit on oscillations, determinism and chaos for introductory physics students. Am. J. Phys. 2004, 72, 446–452. [Google Scholar] [CrossRef]
- Kraftmakher, Y. Experiments with a magnetically controlled pendulum. Eur. J. Phys. 2007, 28, 1007–1020. [Google Scholar] [CrossRef]
- Cuerno, R.; Rañada, A.F.; Ruiz-Lorenzo, J.J. Deterministic chaos in the elastic pendulum: A simple laboratory for nonlinear dynamics. Am. J. Phys. 1992, 60, 73–79. [Google Scholar] [CrossRef]
- Silva, P.H.O.; Nardo, L.G.; Martins, S.A.M.; Nepomuceno, E.G.; Perc, M. Graphical interface as a teaching aid for nonlinear dynamical systems. Eur. J. Phys. 2018, 39, 065105. [Google Scholar] [CrossRef]
- Sharpe, J.P.; Sungar, N. Supercritical bifurcation in a simple mechanical system: An undergraduate experiment. Am. J. Phys. 2010, 78, 5–520. [Google Scholar] [CrossRef]
- Sungar, N.; Sharpe, J.P.; Moelter, M.J.; Fleishon, N.; Morrison, K.; McDill, J.; Schoonover, R. A laboratory-based nonlinear dynamics course for science and engineering students. Am. J. Phys. 2001, 65, 591–597. [Google Scholar] [CrossRef]
- Raviola, L.A.; Véliz, M.E.; Salomone, H.D.; Olivieri, N.A.; Rodríguez, E.E. The bead on a rotating hoop revisited: An unexpected resonance. Eur. J. Phys. 2017, 38, 015005. [Google Scholar] [CrossRef]
- Nemirovsky, R. Students making sense of chaotic behaviour. Inter. Learn. Environ. 1993, 3, 151–175. [Google Scholar] [CrossRef]
- Chacon, R.; Batres, Y.; Cuadros, F. Teaching deterministic chaos through music. Phys. Educ. 1992, 27, 151–154. [Google Scholar] [CrossRef]
- Shore, L.S.; Garik, M.J.; Garik, P.; Hickman, P.; Stanley, H.E.; Taylor, E.F.; Trunfio, P.A. Learning fractals by «doing science»: Applying cognitive apprenticeship strategies to curriculum design and instruction. Inter. Learn. Environ. 1992, 2, 205–226. [Google Scholar] [CrossRef]
- Adams, H.M.; Russ, J.C. Exposing gifted elementary school children to chaos and fractals. J. Sci. Educ. Technol. 1992, 1, 191–209. [Google Scholar] [CrossRef]
- Komorek, M.; Duit, R. The teaching experiment as a powerful method to develop and evaluate teaching and learning sequences in the domain of non-linear systems. Int. J. Sci. Educ. 2004, 26, 619–634. [Google Scholar] [CrossRef]
- Stavrou, D.; Duit, R.; Komorek, M. A teaching and learning sequence about the interplay of chance and determinism in nonlinear systems. Phys. Ed. 2008, 43, 417–422. [Google Scholar] [CrossRef]
- Jones, N.A.; Ross, H.; Lynam, T.; Perez, P.; Leitch, A. Mental models: An interdisciplinary synthesis of theory and methods. Ecol. Soc. 2011, 16, 46. [Google Scholar] [CrossRef]
- Cantoral, R.; Moreno-Durazo, A.; Caballero-Pérez, M. Socio-epistemological research on mathematical modeling: An empirical approach to teaching and learning. ZDM 2018, 50, 77–89. [Google Scholar] [CrossRef]
- Deleanu, D. The dynamics of a double pendulum: Classic and modern approach. Ann. Dunarea Jos Univ. Galati 2011, 34, 203–211. [Google Scholar]
- Brown, D. Tracker Software. Available online: https://physlets.org/tracker/ (accessed on 1 August 2024).
- Goldstein, H.; Poole, C.; Safko, J. Classical Mechanics, 3rd ed.; TBS: Atlanta, GA, USA, 2001. [Google Scholar]
- La Fata, L. Progettazione e sperimentazione di un percorso di insegnamento/apprendimento per la scuola superiore: Il Caos Deterministico. Ph.D. Thesis, University of Palermo, Palermo, Italy, 2010. [Google Scholar]
- Strauss, A.; Corbin, J. Basics of Qualitative Research: Grounded Theory Procedures and Techniques, 2nd ed.; Sage: Newcastle upon Tyne, UK, 1998. [Google Scholar]
- Hernández-Zavaleta, J.E.; Preciado Babb, A.P.; Cantoral, R. Comparison as a Social Practice in the Analysis of Chaotic Phenomena: The Case of the Double Pendulum. Int. J. Sci. Math. Educ. 2024, 22, 101–112. [Google Scholar] [CrossRef]


| Phase of the TLS | Time | Description of Students’ Activities |
|---|---|---|
| 1 | 2 h | Review of classical oscillating systems: initial conditions in spring-mass system and simple pendulum |
| 1 | 1 h | Introduction to the double pendulum: qualitative description of its motion, role of initial conditions |
| 2 | 3 h | Analysis of the double pendulum motion using Tracker software: construction of position vs. time, trajectory, and momentum vs. position graphs |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parlati, A.; Giuliana, G.; Testa, I. Design and Development of a Teaching–Learning Sequence about Deterministic Chaos Using Tracker Software. Educ. Sci. 2024, 14, 842. https://doi.org/10.3390/educsci14080842
Parlati A, Giuliana G, Testa I. Design and Development of a Teaching–Learning Sequence about Deterministic Chaos Using Tracker Software. Education Sciences. 2024; 14(8):842. https://doi.org/10.3390/educsci14080842
Chicago/Turabian StyleParlati, Alessio, Giovanni Giuliana, and Italo Testa. 2024. "Design and Development of a Teaching–Learning Sequence about Deterministic Chaos Using Tracker Software" Education Sciences 14, no. 8: 842. https://doi.org/10.3390/educsci14080842
APA StyleParlati, A., Giuliana, G., & Testa, I. (2024). Design and Development of a Teaching–Learning Sequence about Deterministic Chaos Using Tracker Software. Education Sciences, 14(8), 842. https://doi.org/10.3390/educsci14080842







