Embodied Learning in Early Mathematics Education: Translating Research into Principles to Inform Teaching

Abstract

There exists a substantial body of research evidence that embodied learning modes can enhance children’s mathematics learning, yet implementation of the research findings in classrooms has so far been limited. This paper argues the need for translational research to bridge the gap between psychological, neuroscientific, and narrow-focused educational research and teaching practice in schools. As a foundation for such research, and with a focus on early year mathematics education (4 to 8 years), we derive a set of 12 principles of embodied learning from the research literature by applying an integrative literature review method. Based on the findings from the literature, we offer some advice on how these principles might be put into practice with young students.

1. Introduction

Over the past two decades, research evidence has rapidly accumulated for the value of utilising embodied modes of learning, such as body movement, gesture, or tracing, to benefit the mathematical development of children. Much of this research has been within the fields of philosophy, psychology, and neuroscience. Though less numerous, educational studies in classroom settings have confirmed the potential of specific embodied modes to improve learning outcomes for specific aspects of mathematics—for example, Alibali, Elia and Evangelou or Goldin-Meadow [1,2,3]. Although there is still much research to carry out, embodied cognition research has already produced significant recommendations for teaching practice to support student learning of specific concepts, using a single embodied mode, in specific contexts [4,5]. However, missing from the body of research in mathematics education are classroom-based studies that collaborate with teachers to broadly explore the connections between all the embodied modes, the mathematics curriculum, their own daily practice, and the learning needs of their students. One logical approach to designing such translational studies is to first distil the existing research findings into key ideas, or ‘principles’, to inform teaching practices. This article draws upon our previously published conference paper in which we first suggested the need for the study reported here [6].

The call for education to attend to the role of the body in learning rather than only the function of the mind is not new. The prominent scholar, John Dewey, declared in 1928 that ‘...the question of the integration of mind–body in action is the most practical of all questions we can ask of our civilization’ [7] (p. 8) and advocated for experiential learning in schools. Almost a century later, embodied cognition theory and research in psychology and neuroscience have advanced explanations of the mind–body relationship in learning, but similar advances in educational practice have been much slower. Sensorimotor learning is widely accepted as an essential source of development for infants and toddlers [8,9], yet it continues to be largely ignored as an important ingredient in the teaching of school-age children, despite the fact that embodied learning continues across our lifespan [10]. The notion of ‘losing’ an embodied approach to learning in the transition to formal schooling, in part, motivated our focus on the 4-to-8-year age range. One likely reason for the slow uptake of embodied learning approaches in education is the lack of practical advice for teachers on how to develop their pedagogy to make use of the research evidence. Therefore, the aim of the study reported in this paper is to derive a set of principles of embodied learning that could guide the practice of teachers and provide a foundation for further translational research, situated in schools and working with teachers.

In the next section, a theoretical perspective that combines embodied cognition theory with representation theory in mathematics is presented as the conceptual structuring for an integrative review of the literature. The reasoning behind selecting and conducting an integrative review is explained in the Methodology section. The findings for this study are presented as a set of 12 themes that emerged from the analysis of the literature. The final section of this paper proposes how the findings may support further translational research in this topic.

2. Theoretical Stance

2.1. Embodied Cognition

Embodied cognition theory captures enactive types of knowing and learning that cannot be well explained in terms of the ‘within brain’ processing of sensory inputs as information, as advocated by traditional Cognitivism. Over the past few decades, growth in the field of embodied cognition research has led to a broader acceptance of closer relationships between the roles of the mind and body in learning [11,12]. However, the field is still young, and no universally accepted definition of embodied cognition yet exists [6]. For a discussion of various views of embodied cognition theory, see Wilson and Golonka for a psychology perspective [13]; Shapiro and Stoltz, as well as Spackman and Yanchar, for an education perspective [5,14]; and Harpaintner et al. for a neuroscientific perspective [15]. Cognitive neuroscience research contributes to explanations of the interaction of the mind and body through the theory of the mirror neuron system [16] the mapping of module activation in the brain [17], and implications for education [18,19].

A key feature of embodied cognition theory is the importance of the body’s interaction with the external environment. A rapidly developing branch of embodied cognition theory focuses on human interaction with digital technologies and their dynamic representational affordances, particularly in education contexts and learning design in mathematics [20,21]. While more radical views of embodied cognition discount the role of representations of abstract ideas, the most common view integrates embodied representation with the traditional Cognitivist position on the key role of internal representation systems for knowledge development.

In this paper, we take an inclusive view of embodied cognition, grounded in Wilson’s [22] discussion of six claims about embodied cognition, ‘three of which outline the importance of considering cognition as a situated process, and the other three focus on the importance of the body as a tool for cognition’ [23] (p. 3). This view of embodied cognition emphasises ‘the role of sensory and motor functions in cognition itself’, and models ‘cognitive skills as the product of a dynamic interplay between neural and non-neural processes’ [24] (p. 319). Such a view incorporates the role of both internal (mind) representation and external (body and environment) representation and their inter-relationships in knowledge creation.

2.2. Representation Theory in Mathematics

One of the major philosophical stances in the discipline of mathematics is that mathematics exists as an organised collection of abstract ideas, and that external representations of these ideas are needed for manipulation and comprehension. In an education context, it is important to note that, as stated by Gérard Vergnaud, ‘mathematical concepts have their first roots in the action on, and in the representation of, the physical and social world; even though there may be a great distance today between that pragmatical and empirical source, and the sophisticated concepts of contemporary mathematics’ [25] (p. 168).

The authors are strongly influenced by the works of Gerald Goldin and James Kaput [26,27], whose representational view of knowledge and learning allows researchers to describe variation in children’s current achievement levels in terms of the development of each child’s sets of interrelated internal representational systems, such as language, imagery and symbols, and touch/kinaesthetic visualisations [26]. To some extent, researchers (and teachers) can infer the development of particular internal representation systems through a child’s self-created external representations (e.g., spoken words, drawings, modelling, and body actions) and their interactions with more formal representations created by others (e.g., symbols, diagrams) [28]. While this study focuses on the external embodied modes of representation, the relationships between such modes and the development of other representation systems such as language and visualisation are critical to learning.

Goldin and Shteingold propose that under-developed representational systems, or mismatches between internal representations and externally imposed representations, potentially create barriers to learning [26]. Incomplete representational systems are particularly noticeable in the discipline of mathematics, which places high demand on the formation and connection of multiple representation systems. Representational ‘thinking’ requires the learner to create, interpret, and communicate using both internal and external representations [26,29]. The interplay between internal and external representations should, therefore, be of primary concern to teachers [26]. This view of representation theory acknowledges that the internal–external ‘interplay’ is dynamic and two-way, meaning that external representations are not only communication tools but are also thinking tools that can cause cognitive change [27], hence the need to consider ‘representation’ as an act or process, not just a product or reflection of existing internal mental images [30]. The potential for embodied modes of representation of concepts and processes to enhance learning is therefore of primary interest when interrogating the literature in this study and when presenting the findings. 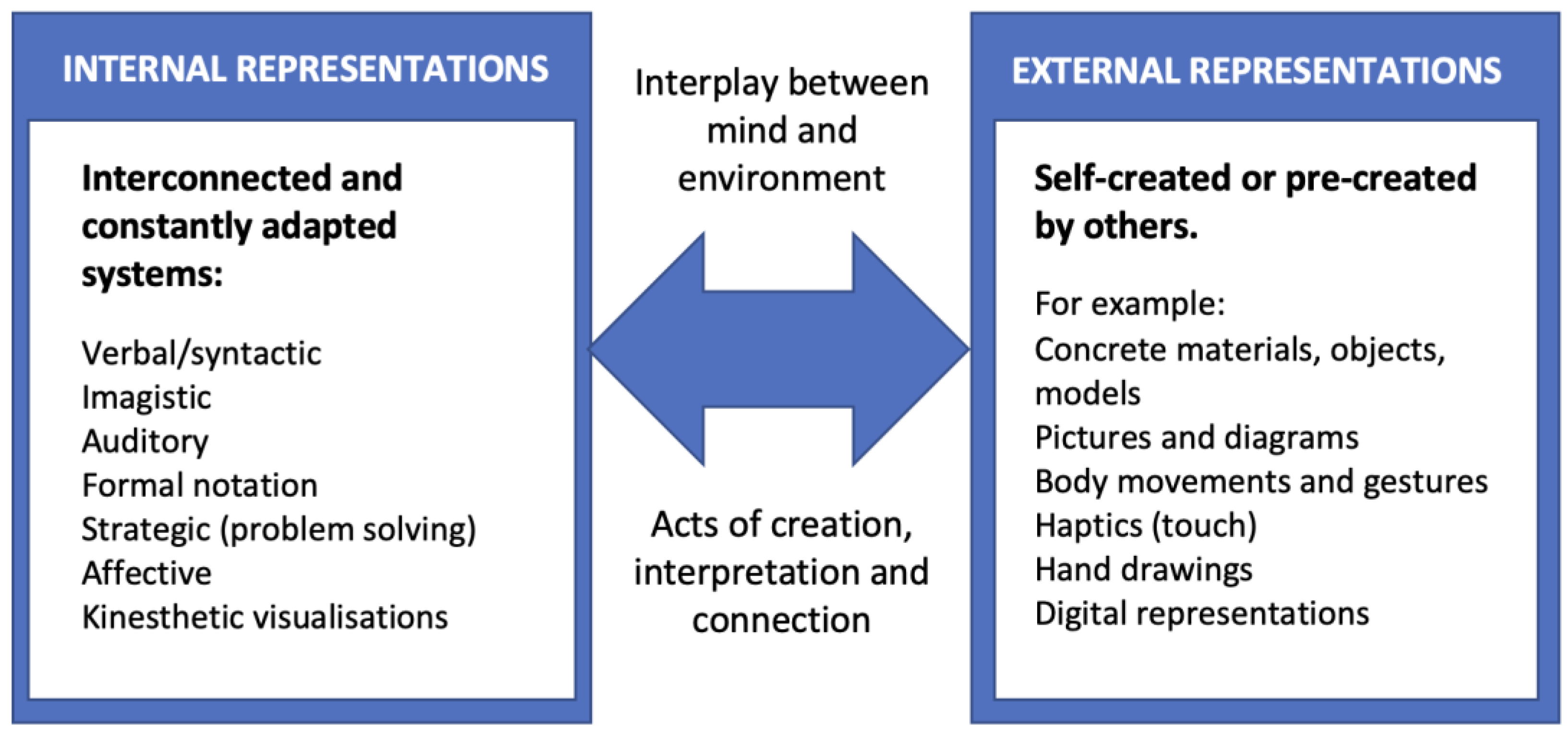Figure 1 (created by the authors) presents a summary of the described version of representation theory as situated in early mathematics education through a simple model depicting the interplay between internal (mind) and external (environment) representations, incorporating the role of the body and movement.

2.3. Embodied Learning and Mathematical Representation

In the field of education, the term ‘embodied learning’ is often preferred, rather than ‘embodied cognition’, as it better reflects the learning intention behind applying embodied cognition theory in educational settings [31]. Embodied learning in mathematics education places emphasis on representation through embodied modes (gesture, pointing, touching, tracing, drawing, and larger body movements), and so, the embodiments are necessarily linked to mathematical concepts or processes. An important point is that the origins of embodied representation lie in the movement of the body itself and/or in the interactions between the body and the external environment [11]. Combining embodied cognition theory and representation theory in mathematics explains the conceptual structuring for conducting this study. The elements composing Figure 1 provide a frame of reference for expressing the themes that resulted from the literature analysis in this study and for describing the ways in which various embodied modes interact with other representational systems.

3. Methodology

Integrative review was selected as the methodological vehicle for achieving the aim of this study, which was to derive a set of principles of embodied learning that could guide the practice of teachers and provide a foundation for further translational research, situated in schools and working with teachers. Our research question is the following: What pedagogical guidance for teachers of children aged 4 to 8 years can be derived from the research literature on embodied learning in mathematics?

Integrative review is well suited to the purposes of this study for the following reasons:

• An integrative review collects literature from across fields or communities of practice and can capture both empirical and theoretical publications [32].
• An integrative review differs from systematic review and meta-analysis in its capacity to capture both quantitative and qualitative data, thereby enabling a more thorough investigation of the chosen phenomenon [33].
• ‘It reviews, critiques, and synthesizes representative literature on a topic in an integrated way such that new frameworks and perspectives on the topic are generated’ [34] (p. 404).
• Having emerged from the evidence-based practice movement in the health professions, it produces a synthesis of knowledge with an emphasis on the applicability of results from reviewed studies to relevant practice [35].

As outlined by Lubbe et al. [33], the steps for conducting the review may parallel those of a classic primary study, as follows: 1. Composing the research question, 2. Sampling of the literature (searching, screening, selecting), 3. Data collection from the literature, 4. Analysis and synthesis of data, and 5. Presentation and discussion of findings. In addition, Toracco [36] emphasises the importance of establishing conceptual structuring for the review to frame its progress towards the intended outcome. The conceptual structuring for this study has been achieved in the preceding section of this paper through the explication of our theoretical stance on embodied cognition and mathematical representation.

Sampling, Data Collection and Analysis

Defining strategies for the selection of the literature is essential for integrative reviews, yet the sampling criteria need not be entirely rigid, and the relationship between selecting the literature and its analysis may be more flexible [36], depending on the context and purpose of the review. The four main strategies used in this study (outlined below) reflect such flexibility while attempting to maintain a relatively objective selection process to gather a representative sample of the available literature. We combined an initial phase of criteria-defined selection (Steps 1 and 2), with some subsequent investigative techniques in response to questions arising during the preparation of the material for analysis (Steps 3 and 4). We justify the ‘supplementary sampling’ as being a method for substantiating the level of inference required to interpret some of the ‘circumstantial evidence’ [32] provided in some qualitative studies.

• Steps for sampling the literature are as follows:
  • Data bases were selected to capture journal articles primarily in the fields of education, mathematics education, and educational psychology, namely ERIC, ProQuest Central, and Informit.
  • Primary search terms were used to shape the focus, including theoretical terms (embodied cognition), representation types/embodied modes (gesture, tracing, movement, drawing), and age group (early years, young children, preschool).
  • The preferred time period was after 2005, but older articles were not necessarily excluded if they were seminal or helped to address questions arising during analysis.
  • A post initial search was performed; as analysis began, additional ‘leads’ were investigated through open-ended searches via Google Scholar (e.g., 1, to seek further explanation from cognitive psychology or neuroscience research for findings reported in an education study, or, e.g., 2, applying the additional search term of ‘finger counting’ to ensure a representative sample of research on that topic). Specific journals that were found to be a rich source of relevant material, in terms of search criteria, were more carefully searched for articles that may not have been captured by the original search terms (e.g., The Journal of Mathematical Behaviour).

Data collection involves screening the accumulated literature against the criteria for final inclusion, logically organising the material, and extracting key information. Articles that did not meet the search criteria and scope of the research question were excluded, resulting in 72 documents. As most of the studies focused on a specific embodied mode (e.g., gesture, drawing, tracing), these modes provided a logical categorization for the annotated bibliography. A small number of articles dealt with embodied cognition/learning in general, so they were considered in the review of more than one category. The three categories were conceptual body movement (13 documents), gesture and tracing (34 documents), and mathematical drawing (25 documents). The initial entries for each paper included keywords and the abstract. Within each category, each paper was read, and notes were added about the key findings. These notes were then subjected to a thematic analysis process [37], resulting in statements of themes.

4. Findings: Synthesis of the Literature

Three broad categories—conceptual body movement, gesture and tracing, and mathematical drawing—are used to structure the presentation of findings. Within each category, the themes that emerged from the analysis of literature form the key findings of the study. At the end of each category, a summary is provided that renames the themes as teaching ‘principles’, with the implication that they can provide a basis for designing classroom pedagogy. The summary table also gathers examples of pedagogical practice inferred from the literature for each principle to create a basic framework for guiding the use of embodied learning in classroom practice.

4.1. Conceptual Body Movement

In keeping with our theoretical stance on embodied mathematical representations, we use the term ‘conceptual body movement’ to differentiate between movement and actions connected to mathematical concepts and processes and other forms of body movement for different purposes, such as physical health. By their traditional definition, concepts are mental constructs, and body movement manifests outside the mind; however, in the context of embodied learning, we believe the term aptly emphasises the purposeful use of movement to support the development of mathematical understanding—that is, movement can embody a concept. Analysis of the literature categorised as pertaining to conceptual body movement revealed three themes, and these are used to structure the synthesis of that literature.

4.1.1. Conceptual Body Movement Theme 1: Body Movement Experiences Involving Egocentric and Allocentric Spatial Frames of Reference Benefit Learning

In most situations, body movement involves spatial awareness, that is, the awareness of our own body in space and of the objects in the surrounding space. Early learning about aspects of the physical environment such as perspective, structures, measurable attributes, sequence, and position may be more effectively achieved through experiences that facilitate spatial exploration relative to the positioning of a child’s own body; that is, utilising egocentric spatial frames of reference [38]. Experiences that require making sense of relationships between objects external to the child or from the visual perspectives of others (allocentric frames of reference) are more strongly related to visual stimuli and support the memory of coherent scene representations and the planning of movement or navigation [39]. The implication is that both frames of reference should be considered when planning or interpreting children’s body movement experiences, with emphasis placed on the inclusion of egocentric experiences to support early years of development [40,41].

Conceptual body movement not only relates to spatial learning but can serve to link space and number concepts through active mapping processes to construct spatial–numerical representations, leading to relational knowledge about numbers [38]. For example, imagine a large-scale number track marked out on the floor, with numerals 1 to 20 placed ‘upright’ relative to a child standing on 1, facing the number sequence (Figure 2).

A child might experience starting at one to take equal-length steps along the number track while saying the matching counting numbers or stepping backwards to count down. The experience could be described as utilising an egocentric frame of reference, with forward and backward movements associated with increasing or decreasing number magnitude. Alternatively, the child might stand with a floor number line in front of them (zero to their left) and indicate visualised (or planned) movement to the right or left along the number line, which utilises an allocentric frame of reference (Figure 3). In this case, enacting their planned movement might make more sense to the child if they stepped sideways to the right (away from zero) or left (towards zero), rather than turning their bodies to step forward/back [42].

Once the child begins stepping along the number line, they activate an egocentric frame of reference. Integrating these spatial frames of reference are considered important for a functional understanding of the number line [38]. However, we note that the phenomenon of switching spatial perspectives and the role it might play in children’s learning is an under-researched area.

A range of studies with young children have established the benefits of body movement in developing skills in number sequencing and magnitude, number line estimation, and equidistant spacing, for example Dackermann et al., Link et al., or Fischer [38,43,44]—all of which are components of the ‘mental number line’, which is systematically related to arithmetic competencies, e.g., Booth and Seigler or Mavilidi et al. [45,46]. The learning benefits in spatial–numerical studies have been attributed to concept-linked embodied actions rather than just increased motivation or attention of the learners [42], often mentioned as an additional benefit of body movement approaches.

4.1.2. Conceptual Body Movement Theme 2: Co-Operative Action and Re-Enactment to Explore Physical Phenomena Can Enhance Learning

Body movement has the potential to reflect the dynamic nature of some mathematical representations, processes, or relationships. When exploring a phenomenon or physical representation, learning can also be enhanced through co-operative action and re-enactment using students’ bodies, often in conjunction with the materials that model the phenomenon. For example, a small group of children might explore creating triangles by jointly manipulating a loop of string held in their hands, watch other groups carry out the exploration, then use their arms or bodies to demonstrate what they discovered. The socio-kinaesthetic interaction of performing movements with others, joint contact with the physical objects, and watching re-enactments by others has been found to be a factor in maximising the learning benefits by supporting the memory of movements and making connections between concepts, processes, and movements [47]. A partial explanation for the value of combining co-operative action and re-enactment comes from neurophysiological mechanism of the mirror neuron system that enables humans to learn through imitating the behaviours of others [16].

4.1.3. Conceptual Body Movement Theme 3: Touch and Hand Movement (Sensory and Kinesthetics) in Exploratory and ‘Thinking’ Mode Can Create New Knowledge

This theme differs from the other body movement themes in the scale of the movements, yet also differs from other hand movements that have been categorised as gesture. Hand movement that also uses the sense of touch in an exploratory way can support conceptualisation—for example, when a child uses their hands to explore the surfaces and structure of a cylindrical object, curling fingers around the curved surface and placing a flat hand on each base [48].

Exploratory hand movement is different from gesture, which often has its origin in the brain, because the ‘ideation’ with touching originates in the hands [49]. The role of hand movements and touch is accentuated when the object the child is feeling is hidden from sight (perhaps inside a bag or under a tabletop) while they explore its characteristics. Such a situation triggers a different learning mechanism than visual or verbal stimuli [49]. The focus instead is on the sense of touch and the movement memory of the hands, rather than concrete and visual representation. The sense-making and image-building of the object under investigation resides in the hands [49]. The movement memory often becomes visible in the form of grounded gestures [50]—a repetition of the exploratory hand movements—when communicating the experience.

4.1.4. Conceptual Body Movement Summary and Teaching Advice

The analysis of the literature revealed the potential of using various forms of body movement and positioning to experience and represent mathematics concepts and processes, as well as support children’s learning. As a further step in addressing the study’s research question,

Table 1. Principles and teaching advice for conceptual body movement.

Principles	Teaching Practice Advice
M1: Body movement experiences involving egocentric and allocentric spatial frames of reference benefit learning.	Activities in which the child: Positions themselves in the environment, experiencing the space from their own perspective. Becomes part of a larger mathematical representation and considers the viewpoints of others (e.g., children become ‘counters’ on a ten-frame floor). Builds mental maps of objects in relation to other objects (scene layouts maps, navigation).
M2: Co-operative action and re-enactment to explore physical phenomena can enhance learning.	Activities in which: Small groups co-operate to explore spatial concepts or physical phenomena through play and modelling with objects and materials. Follow-up with the joint acting-out of what they have experienced using their bodies occurs. Children observe other groups acting out their similar experiences.
M3: Touch and hand movement (sensory and kinesthetics) in exploratory and ‘thinking’ modes can create new knowledge.	Activities in which the child: Without looking, explores objects with two hands to better notice features, structures, and relationships. Recounts the experience with hand movements (and spoken words) to consolidate the ideation process.

re-labels each theme as a ‘principle’ and provides examples of the types of learning activities inferred by previous research that teachers might design by implementing each principle.

4.2. Gesture and Tracing

Humans are genetically predisposed to attend to nonverbal behaviours, including gestures [51], and so, gestures can be used to focus student attention and enhance engagement [52]. While basic gestures come naturally and do not need to be taught (e.g., pointing, [53]), mathematics knowledge that requires explicit instruction can be supported by using planned accompanying gestures [54]. The use of all types of gestures, by children and/or teachers, has been shown to increase student understanding, recall, and performance (for meta-analyses, see Dargue et al. or Hostetter [55,56]), including in studies focused on mathematics teaching and learning.

In our analysis of the literature, we go beyond the encompassing term ‘gesture’ to distinguish (a) using a single finger to point and trace in the air, (b) touch pointing and tracing, where the finger contacts with a surface, and (c) in-air gesturing with one or two hands.

4.2.1. Gesture and Tracing Theme 1: Co-Speech Gestures Can Enhance Learning, Communication, and Vocabulary Development

Co-speech gestures are naturally produced while talking but can be deliberately planned to help connect concepts and mental images to the words that are spoken by the teacher [50,57]. Such gestures can take the form of non-representational gestures (beat gestures and pointing gestures) or representational gestures (iconic or metaphoric gestures). Non-representational gestures do not actually depict a concept, object, or process but are used to direct attention while talking; beat gestures are rhythmic movements of the hand referring to a particular element of speech or adding emphasis to key parts of a spoken message, while deictic gestures (including pointing, typically with the index finger) are used to indicate objects, locations, or directions. Pointing gestures physically link speech and associated mental processes to the physical environment.

Representational gestures depict a tangible object or dynamic scenario [58] and can be iconic or metaphoric in type. Iconic gestures correspond closely with the relevant speech through the shape of the hand and the trajectory it describes and tend to model a physical phenomenon (e.g., a rocking hand gesture used while verbally describing an equal-arm balance), while metaphoric gestures aim to convey abstract concepts through a concrete, visual–spatial representation (e.g., a rocking hand gesture used while talking about balancing the sides of an equation). However, gesture is not always directly connected to speech or words.

4.2.2. Gesture and Tracing Theme 2: Gesture Can Be a Thinking Tool

Co-thought gestures are produced while silently thinking, visualising, and problem-solving [59] and may enhance learning because of their ability to represent imagistic, spatial, and/or motor information that is difficult or even impossible to represent in speech [1,60,61], thus leading to new mathematical concepts or problem-solving strategies. Therefore, encouraging children to ‘think with their hands’ and attending carefully to their gestures may be beneficial. However, children’s spontaneous gestures may not always directly match their spoken words, and the gesture may represent an emerging idea or additional thinking that the words do not express [62]. Goldin-Meadow [3] suggests that such a mismatch may signal that a cognitive change is imminent. Noticing such a mismatch can alert a teacher to a ‘teachable moment’ so that they can assist the child in the further development of the idea.

4.2.3. Gesture and Tracing Theme 3: Deliberate Use of Iconic Gestures by the Teacher Can Enhance Learning and Support Vocabulary Development

A teacher’s deliberate use of co-speech, iconic gestures during mathematics instruction with young children has been found to be more effective in promoting learning than speech alone (e.g.,Valenzeno et al. [50]). The representational nature of iconic gestures (e.g., moving hands apart horizontally while saying ‘width’) offers an embodied bridge between speech and the physical world, whether the physical object is visible at the time or not [63]. The use of gestures in a pantomime-style way can assist young second-language learners in the acquisition of new vocabulary [46] and so may support the acquisition of key terms and concepts and meaning-making during learning experiences.

While children’s learning can be enhanced by observing various types of teacher gesturing, their own spontaneous or prompted gesturing can create more robust memories because gesturing while verbally communicating simultaneously activates two different regions of the brain and increases the likelihood of retrieval [64]. Reflecting the inherently social character of co-speech gestures, several studies have found that students will mirror, and sometimes extend, a teacher’s gestures when talking about the topic themselves [62]. Gestures will also co-emerge while children are interacting with their peers, particularly during spatial or geometric tasks [61].

4.2.4. Gesture and Tracing Theme 4: Using the Index Finger to Touch-Point or Touch-Trace Graphics Can Enhance Learning and Problem Solving

Touch-tracing and touch-pointing (our terms), with the finger contacting a surface, differs from ‘in-air’ gesturing, as it activates further sensorimotor learning opportunities [8,65,66]. Therefore, the child’s own pointing–tracing actions are likely to be more powerful than only seeing the teacher perform such actions. Unlike the physical manipulation of concrete materials, this form of touching usually involves interacting with graphics such as symbols, photos, drawings, or diagrams. Touching and tracing, when used by either the teacher or the child, serves to focus attention on specific features of the graphic, such as objects to be counted [67] or shape recognition [68]. This seems to be particularly useful when the quantity and/or complexity of the information presented in the graphic is difficult to process. The touch actions also appear to support ‘chunking’ of elements within the information, thus avoiding information overload and supporting comprehension. For example, one study [69] found that Year 2 students reported lower intrinsic and extraneous cognitive load, as well as higher rates of enjoyment of the lesson, when students mimicked the teacher’s tracing actions during a lesson on the empty number line.

Black et al. [70] argue that an additional stage of imagination, following embodied learning experiences based on action and gesture, can further enhance learning. More recently, Wang et al. [71] found that students (children in Experiment 1, adults in Experiment 2) who traced elements of mathematics by working through examples with their eyes first open and then with their eyes closed to encourage their imagination solved more practice problems than students who traced an equivalent number of worked examples with their eyes open. The ‘eyes-closed’ students reported lower intrinsic cognitive load and solved more transfer test questions than the ‘eyes-open’ students.

4.2.5. Gesture and Tracing Theme 5: Using Fingers to Represent Numbers Helps Number Knowledge, and Finger Counting Left to Right Supports Development of the Mental Number Line

The value of a child using pointing and touching gestures to support the counting process has been well established (e.g., Alibali and DiRusso [67]). However, the movement of hands as the learning resource rather than the tool that touches the resource provides a shift in focus. The association between finger use and numerical learning in children is of particular interest because of the discrepancy between the findings of neurocognition research that establishes the value of finger counting, a common practice in Western mathematics education that tends to discourage finger use after the age of 6 or 7 years in favour of abstract mental strategies [72].

Classroom-based research has shown that training 5/6-year-olds to use their fingers to represent numbers and for finger counting improves their mathematical problem-solving abilities [73,74]. Developing schema to physically represent numbers and relationships between numbers through finger movement seems to support working memory and facilitate problem-solving capacity [75]. The most beneficial period for teaching that promotes the purposeful use of fingers in this way appears to be 5 to 8 years old [76], although the benefits continue into adulthood [44]. Finger gnosis, the awareness of finger position, is processed by the same part of the brain as numerical thinking and visuo-spatial skills are, and its early development predicts future mathematics achievement and continues to be relevant in numerical thinking in adulthood [77,78,79]. Finger counting that moves sequentially from left to right (palms facing towards the person counting) provides a spatial representation of magnitude that supports the mental number line [48].

4.2.6. Gesture and Tracing Summary and Teaching Advice

The analysis of the literature revealed the value of using a finger, a hand, or combined hand movements to direct attention or increase the noticing of key features in mathematics-learning contexts.

Table 2. Principles and teaching advice for gesture and tracing.

Principles	Teaching Practice Advice
G1: Co-speech gestures can enhance learning, communication, and vocabulary development.	The teacher: Deliberately uses pointing gestures to draw attention to important features of mathematical representations. Encourages children to ‘talk with their hands’, as well as with words. ○ Observes children’s naturally occurring gestures to monitor comprehension.
G2: Gesture can be a thinking tool.	The teacher: Encourages children to gesture while thinking in problem-solving situations; to ‘think with their hands’. Watches for co-thought gestures, as they may reveal thinking beyond that which a child can express in words alone and so provide insights into a child’s problem-solving processes.
G3: Deliberate use of iconic gestures by the teacher can enhance learning and support vocabulary development.	The teacher: Repeatedly uses planned gestures to represent key concepts and matches them to vocabulary to clarify meanings. ○ Encourages air-tracing gestures by the students. ○ Observes whether the learners adopt or extend the teacher’s gestures.
G4: Using the index finger to touch-point or touch-trace graphics can enhance learning and problem solving.	Activities in which the child: Touch-points (to activate the sense of touch) to specific parts of graphics (e.g., corners of shapes, parts of a number sentence) in conjunction with spoken vocabulary. Touch-traces around graphics (e.g., shapes, numerals, diagrams), in a continuous movement (if relevant). Repeats touch-tracing with eyes closed to build memory of hand movements and touch sensations. Repeats tracing movements with the finger, leaving a visible trace (e.g., in sand, on a digital touch screen) to confirm reproduction of the graphic.
G5: Using fingers to represent numbers helps number knowledge, and finger counting left to right supports development of the mental number line.	Activities in which the child: Uses fingers to represent numbers and to count using finger movement (preferably from left to right). Represents numbers on fingers with eyes closed or fingers out-of-sight to increase finger awareness.

renames the themes that emerged from analysis of the gesture and tracing category of the literature as principles to guide teaching decisions and provides examples of the pedagogical messages contained in the discussion of the research findings.

4.3. Mathematical Drawing

The close relationship between drawing, gesture, and motor control supports the inclusion of drawing in discussions of embodied learning [80,81]. Like gestures, drawing typically involves the hand, is dynamic, and comes naturally to young humans, though drawing development is also socially and culturally contextualised [82]. In its early development, natural drawing, often referred to as mark making, is a form of graphic narrative play, often used in combination with gesture and movement, speech, dramatization, and expressive sound effects as part of meaning making [83]. Young children’s drawing develops in its purpose and forms over several years, moving in stages from playful scribble, to the exploration of movement and forms, and to pictorial and iconic representations of visualisations and real-world objects [84].

The literature analysed in this category focused on ‘drawing’ (used as verb) as an act of creating a mathematical representation, rather than ‘drawing’ (used as noun) to denote a completed artifact. Four themes were derived from the analysis.

4.3.1. Mathematical Drawing Theme 1: A Representational Level of Drawing Skill Is Needed as a Foundation for Mathematical Drawing

Most of the early research on children’s drawing development has been in relation to artistic development or meaning making as a prelude to writing language, and the need to provide children with frequent opportunities to draw has been highlighted [85,86]. Key to the mathematics context is the emergence of representational drawing around the age of four years [87]. Representational drawing is considered to indicate cognitive flexibility, as it requires the child to appreciate that a picture is itself an object as well as a representation of another object [88]. Further indicators of a child’s cognitive flexibility include the ability to adapt and change their drawing schemes to meet new demands, such as adapting their usual drawing of a human figure to draw a kangaroo [89,90]. The differing demands of perceptual and conceptual drawing can be problematic in school-based situations when the child is asked to represent a specific mathematical object. Creating a conceptual representation (e.g., drawing the solution to a contextualised subtraction problem) requires some previous experience and/or the ability to select and adapt an existing drawing procedure (schema). Creating a perceptual drawing (e.g., copy a specific type of triangle) requires the child to ‘draw what they see now’, rather than retrieve previous versions of the drawing subject (e.g., their generic representation of a triangle) [89,90].

The association between drawing development and cognitive flexibility continues as a child matures, as demonstrated by Ebersbach and Hagedorn [91] in their study of 7-to-11-year-old children’s ability to use depth cues when drawing three-dimensional objects. Indeed, spatial thinking is reflected in various aspects of drawing composition, such as positioning, orientation, shape, symmetry, perspective, and proportionality. As spatial ability has been consistently found to correlate with mathematical ability (e.g., Lowrie et al. [92]), the spatial nature of drawing may partially account for the connections found between children’s drawing development and their mathematical development (e.g., Poland and van Oers [93]). For example, Malanchini et al. studied the ‘longitudinal relationship between preschool drawing, school mathematics and general cognitive ability (measured at age 4 and 12)’ [87] (p. 12). Their findings indicate that drawing development at age 4 is somewhat predictive of mathematical ability at age 12 but is perhaps more strongly associated with general cognitive development than domain-specific abilities. Malanchini et al. [87] caution that other overlapping factors need to be considered, such as genetic factors, environmental influences, and motor skills such as finger function and upper limb control.

4.3.2. Mathematical Drawing Theme 2: Children’s Open-Ended Drawings and Verbalisation Can Reveal Levels of Conceptual Understanding and Contextualisation of That Understanding

Various studies have emphasised the value of engaging children in conversation about their drawings [83]. For example, children’s early drawings (4–5 years) are highly contextualised in prior social/cultural experiences, and asking children to tell the ‘story’ behind the drawing reveals more mathematical understanding than the drawing alone [94,95].

Although early drawing development comes naturally to children, applying drawing skills to self-created mathematical representations and to the production or interpretation of diagrams is not necessarily a natural extension of that development. Children need support to ‘mathematise’ their drawings [28,96]. Several studies have found that teaching interventions that focus on assisting children to gradually move from pictorial-type drawings to more schematised drawings can be successful in improving the depiction of mathematical ideas and improving problem-solving skills and later mathematics outcomes [93,97,98]. Social interactions between peers have also been found to assist. For example, drawings often represent dynamic events rather than static situations, so children invent, share, and borrow techniques and symbols (such as arrows) to express movement or the passage of time [85,99]. Indeed, collaborative drawing and peer dialogue has been shown to support the development of drawing as a communication tool [85,100].

4.3.3. Mathematical Drawing Theme 3: Drawing Is Both a Thinking Tool and a Communication Tool

The act of drawing is also part of thinking and of exploring emerging ideas, so the process is important, not just the finished representation [30]. Drawing can be a dynamic process that bridges mental images and physical representations and supports meaning making, problem solving, and higher-level thinking [30,98]. Research suggests that valuing drawing as a thinking tool in conjunction with other embodied modes can support the development of children’s mathematical drawing skills and enhance learning [101,102].

4.3.4. Mathematical Drawing Theme 4: There Is a Conceptual and Representational Distance between Children’s Own Drawings and the Conventions and Rules of Mathematical Diagrams

The representational mode of drawing is significant in mathematics because of the prevalence of diagrams to depict essential properties, structures, and relationships [103]. As children progress through school, the expectation to produce iconic drawings and to use symbols and mathematical drawing conventions increases. Of concern in education is the potential conceptual and representational distance between children’s own self-created drawings and the conventions and rules of mathematical diagrams, such as number lines, graphs, maps, and diagrams depicting interrelationships [104]. The interpretation of formal diagrams produced by more knowledgeable adults should not be considered self-evident to young students, and the comprehension of diagrams may be problematic for some [29].

4.3.5. Mathematical Drawing Summary and Teaching Advice

The analysis of this category of the literature revealed that the use of representational drawing in mathematics is problematic for many children and requires increased attention from teachers. Therefore, the teaching advice in

Table 3. Principles and teaching advice for drawing as a dynamic representation mode.

Principles	Teaching Practice Advice
D1: A representational level of drawing skill is needed as a foundation for mathematical drawing.	The teacher: Provides frequent (daily) drawing experiences to improve fluid hand movements and promote the natural development of drawing. Observes each child’s readiness to represent real objects they can see (perceptual drawing) and to create representations of mathematical ideas through drawing (conceptual drawing).
D2: Children’s open-ended drawings and verbalisation can reveal levels of conceptual understanding and contextualisation of that understanding.	The teacher: Uses drawing–telling approaches where the child explains what they have represented, rather than just relying on completed drawings as work samples for assessment purposes. Designs collaborative drawing tasks and encourages peer dialogue (including gesture) during and after drawing.
D3: Drawing is both a thinking tool and a communication tool.	The teacher: Expects and values drawing as a strategy during problem solving, as well as to communicate reasoning, processes, or solutions. Facilitates sharing and discussion of children’s drawings as representations of their thinking and highlights effective features of drawings.
D4: There is a conceptual and representational distance between children’s own drawings and the conventions and rules of mathematical diagrams.	The teacher: Shares and/or models both pictorial and schematic (more symbolic and structured) drawings of visualisations, problem solutions, or representations of external objects. Carefully introduces pre-made diagrams (ten-frames, number lines, etc.) to reveal their structure and purpose and build a shared understanding of their meaning. Supports children in noticing the parts of a diagram (e.g., through touch-tracing), how the parts fit together, and what they mean or how they are used. Explicitly teaches how to represent mathematical ideas in conventional ways when children are ready.

, summarised from the discussion of the literature, is dominated by strategies for developing and improving children’s drawing skills for the benefit of their mathematics learning.

5. Discussion and Conclusions

This study responded to a lack of pedagogical advice for teachers to enable them to translate the accumulated research evidence on embodied learning into productive experiences for children learning mathematics. A limitation of this study is that the literature is representative of the topic rather than exhaustive in its coverage. This limitation is somewhat mitigated by the convergence of research findings favouring the use of embodied learning approaches. Working through the theoretical lens of embodied cognition and representation theory in mathematics, the analysis of a representative sample of education and educational psychology research has shown that active engagement with a variety of embodied modes assists the child to notice and attend to the essential properties, structures, and relationships of the mathematical ideas, beyond what ‘looking’, ‘talking’, and retrieving mental images can achieve alone [57,65]. Such research provides glimpses of what the embodied modes ‘look like’ in practice in classrooms. Some indication of why embodied learning can support learning is offered by cognitive psychology studies (e.g., Gordon and Ramini or Dupont-Boime and Thevenot [23,75]). Another layer of insight is added through neuroscience and the mapping of brain activity that reveals overlapping patterns of neural activation for cognitive processing and physical movement (e.g., Harpainter et al. or Rizzolatti and Craighero [15,16]), providing further evidence for the interconnections between internal and external representations.

Although there is broad agreement that embodied approaches enhance learning, there is less agreement on how much engagement with embodied modes is needed to achieve additional learning gains. In the relatively small number of classroom-based studies completed so far, positive learning effects have been found with low, moderate, and high levels of engagement with embodied learning interventions, apparently depending on the type of embodiment and the type of engagement [31]. Different types of embodiment influence learning in different ways. Even less is known about the learning effects of an integrated approach to embodied learning, where, in practice, theoretical boundaries between embodied modes dissipate.

To further the idea of integrating embodied modes in practice, we note some ‘connecting threads’ across the embodied modes that may have significance in authentic classroom settings. One connecting thread is the involvement of spatial awareness and spatial reasoning, such as utilising spatial frames of reference in positioning the body, using gestures to represent spatial properties (e.g., shape or height), or drawing a map of a familiar environment. A second connecting thread is the promotion of social interaction, such as collaborative representation through body movement combined with watching others perform similar experiences, the communication power of gestures in conversation, or the benefit of collaborative drawing experiences. A third connecting thread is the support for language development, particularly mathematical vocabulary, afforded by the embodied modes. For example, stepping forwards and backwards on a number track gives meaning to the terms ‘counting forwards’ and ‘counting backwards’, and perhaps also to forward/back gestures made in relation to the body’s orientation. As another example, in-air tracing and touch-tracing of three-sided shapes connects the spoken label of ‘triangle’ to the figures and is also a rehearsal for drawing triangles. These three ‘connecting threads’ do not appear to have been previously investigated and could form the basis of studies designed to reveal more effective ways to teach/learn key concepts in mathematics.

The research question—‘What pedagogical guidance for teachers of children aged 4 to 8 years can be derived from the research literature on embodied learning in mathematics?’—has been addressed by the production of 12 embodied learning principles, accompanied by some teaching advice inferred from the research (Table 1, Table 2 and Table 3). The weight of evidence supports the implementation of an embodied learning approach in early year mathematics, yet there is still a lack of classroom-based studies that collaborate with teachers to broadly explore the connections between all the embodied modes, the mathematics curriculum, their own daily practice, and the learning needs of their students. This paper’s contribution to the literature on embodied learning in mathematics education is the distillation of the diverse research literature into a basic framework of multiple embodied modes as a starting point for further translational research in authentic classroom settings. Additionally, this paper proposes the potential value of exploring the connections between the embodied modes and the combined use of modes as a means of enhancing the learning benefits for students.