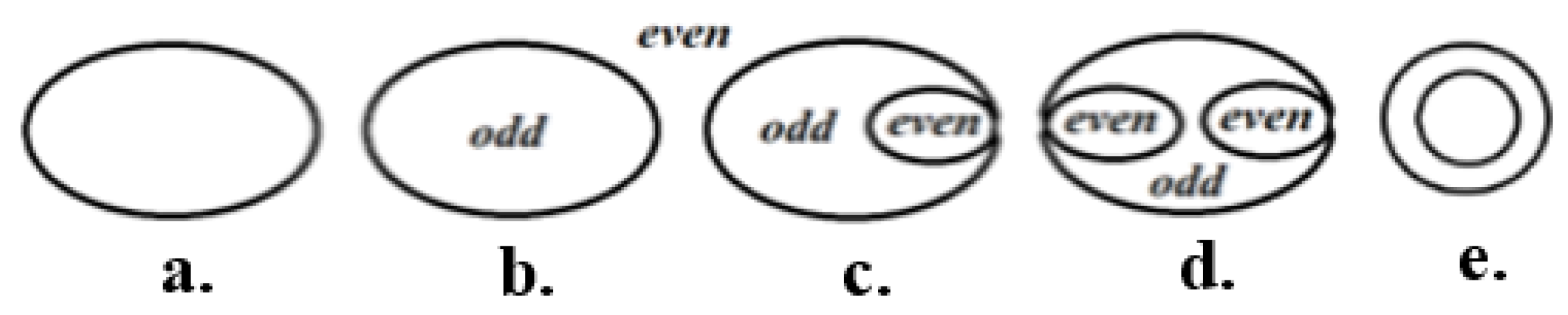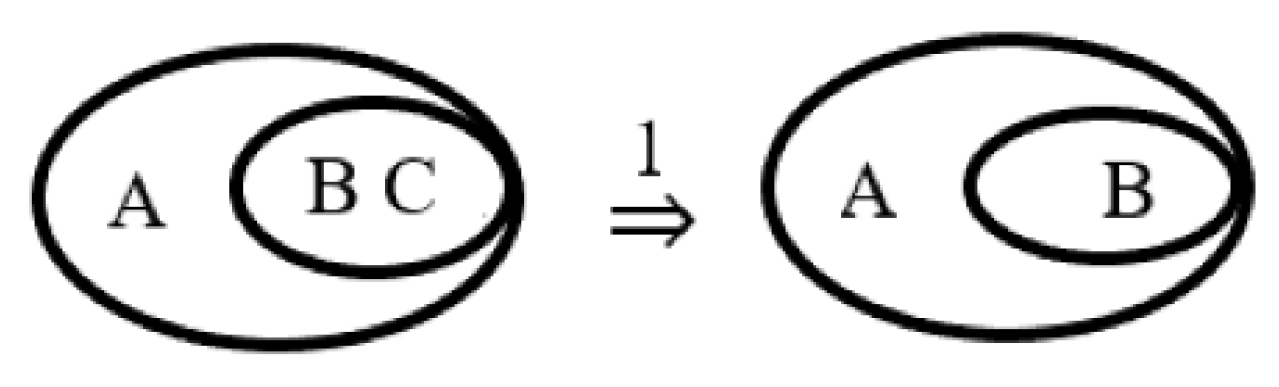Bridging the Gap: An Epistemic Logical Model for Analysing Students’ Argumentation and Proof in Mathematics Education Research ^†

Abstract

In this theoretical paper, an epistemic logical model for analysis of students’ argumentation and proof processes is presented. The model is conceived as a methodological tool addressed to the researcher in mathematics education that aims to shed light on the relations between argumentation and proof, highlighting the continuities and discontinuities within and between them. It reconciles the epistemic logic approach, which takes into account the exploratory phases of a statement, linked to argumentative processes, and the deductive logic approach, which takes into account the phases linked to proof in a classical sense. The model is based on Vergnaud’s concepts- and theorems-in-action, on Duval’s distinction between the epistemic and logical value of verbalised propositions, and on elements of Oostra’s intuitionistic existential graphs, a kind of graphical topological logic rooted in Peircean thought, adapted to mathematics education research by considering also shifts in the classical existential graphs. After exposing the theoretical grounding the model is based on, some examples taken from the literature are examined to exemplify how it works.

1. Introduction

While in mathematics education research (MER), it is taken for granted that logic taught in the mathematics classroom should consist of elements of classical propositional or first-order predicate logic (e.g., [1,2]), the situation may change when logic is intended as a means for analysis of students’ discursive productions. On the one hand, even if classical logic, being a bivalent truth-value logic, perfectly grasps the epistemological constraints of mathematical knowledge, it struggles to capture the purely epistemic aspects related to knowledge acquirement, such as knowing the appropriate properties or procedures. On the other hand, research shows that non-classical logical tools can produce different results in analysing students’ proof production concerning the proof structure [3], the validity of the involved arguments [4], or “updates” to students’ logical reasoning when new information is gained and the former reasoning needs to be reconstructed [5]. Furthermore, in MER, some scholars (e.g., [6,7]) state that there is a discontinuity between argumentation and mathematical proof due to their cognitive distance and the concomitant linguistic proximity, while other researchers are more oriented towards possible conditions of continuity and identify in some cases a kind of cognitive unity between a first conjecturing phase, where arguments are used to support the conjecture made by the students regarding a mathematical problem, and a second phase, where students are asked to prove their conjecture (e.g., [8,9]). For the second group of these researchers, argumentation is a kind of reasoning that supports knowledge acquisition during a conjecturing phase, while proof is a special, more logically strict kind of argumentation [2].

In MER, the Toulmin model [10] is the most frequently used and discussed in the context of the analysis of students’ argumentation and proof processes (e.g., [11,12], but see also [13] for a critical perspective on this model). The Toulmin model grasps some important epistemic aspects (e.g., What kinds of arguments are used? Are there rebuttals and counterexamples that restrict the domain of the argument?), but it does not provide technical logical tools for analysis and does not account for logical continuities or discontinuities in students’ reasoning. Neither does the model proposed by Duval [6,7], implicitly grounded in propositional logic, provide such tools, even if it accounts for the discontinuity between argumentation and proof. On the other hand, in MER, logical tools are often used to analyse students’ argumentation processes, but in these logical analyses, the epistemic considerations are made “from outside” the logical model and are not part of it (e.g., [14,15]). Also, natural deduction is used as a logical means for analysing students’ reasoning [1] since it is able to grasp the informal reasoning in mathematicians’ practice, where quantification is often not explicit, but this kind of logical model also does not take into account how the students know what they know and thus discuss the epistemic aspects not as belonging to the logical model itself but “from the outside”. Another model known from the literature is the nyaya scheme [3,4,16]. It rests on the logical investigation of an Ancient Indian philosophical school named nyaya that advocates for an argumentation scheme based on a kind of pragmatic logic, similar to the one used often by novices in mathematical reasoning. As D’Amore [3] shows, reasoning according to the nyaya scheme can be formalised within classical first-order logic, but it does not account for aspects related to the continuities/discontinuities in reasoning processes. Summing up, a model able to frame both the epistemic and logical aspects, in a way specific to MER, while also providing technical tools able to handle logical and epistemic continuity and discontinuity is still missing. This kind of model would represent a useful tool for researchers in ME and would represent a mathematical object specific to MER, as highlighted in [17]. Indeed, it is mathematical because it concerns mathematical knowledge, but it is specific to MER because it arises within this research context with its specific epistemic requirements, alien to mathematics as a research discipline.

The paper focuses on the following research question: Is the model presented in this paper a valuable tool for analysing students’ reasoning and highlighting the epistemic logical continuities/discontinuities that occur during reasoning processes? Hereafter, the epistemic logical model that forms the core of the paper is introduced; then, it is shown how it works, analysing and discussing three examples taken from the literature; finally, the answer to the research question is provided, conclusions are drawn, and some considerations on possible future research directions are made.

2. The Epistemic Logical Model

The model exposed here is composed of three parts: the first two are taken from MER [7,18] and are used to frame the epistemic logical aspect from a didactical viewpoint; the third part of the model is taken from mathematical logic [19] and provides a system of signs and transformation rules for Peircean intuitionistic existential graphs, as well as the interpretations needed to give meaning to them. This part of the model is presented after a preliminary introduction to classical existential graphs that should help the reader to better understand intuitionistic existential graphs, which can be understood as an extension of the classical ones. (In [20], intuitionistic existential graphs are introduced without a previous introduction to the classical existential graphs).

2.1. Concepts-in-Action and Theorems-in-Action

The first “ingredient” of the model consists of two elements of the theory of conceptual fields [18]: concepts-in-action and theorems-in-action. Concepts-in-action and theorems-in-action differ from “usual” concepts and theorems because they are not explicit and have to be inferred from the student’s behaviour. An important distinction to be made is the following: while theorems-in-action are propositional sentences, and thus are true or false, concepts-in-action cannot be classified as true or false but only as relevant or not relevant [18]. Furthermore, according to Vergnaud, even if one may think a sentence is true that in fact is false, it is still a theorem-in-action: “There is little difference, from the point of view of activity, between a true proposition and a false one considered as true” [18] (p. 88). What matters is that the subject behaves as if it were true. In this sense, Vergnaud’s point of view is truly epistemic because it concerns the student’s knowledge independently from its correspondence with normative aspects. This purely epistemic viewpoint cannot be captured using classical bivalent logic, which deals only with objective logical values (true/false/undecidable) of a proposition and not with subjective viewpoints.

2.2. The Meaning Space of a Verbalised Proposition

The second ingredient of the model is taken from Duval’s distinction between the content, value, and status of a verbalised proposition [7]. The content dimension refers to the objects of discourse and can be informative (provides information about objects or situations) or theoretical (provides information about the relations between the involved objects). The value dimension refers to the relation of the proposition to what it enunciates. It can be epistemic (obvious, absurd, possible, probable, etc.), logical (true, false, undecidable), or communicative (order, promise, question, assertion, etc.). The status dimension of a verbalised proposition refers to its relation to other propositions in the discourse. In the current version of the model, only the first two components of the value dimension are considered: the epistemic value fits the idea of theorem-in-action, based on concepts-in-action, because it is related to implicit, proposition-like knowledge, while the logical value fits the idea of theorem, based on explicit concepts.

2.3. The Graphical Topological Logic of Existential Graphs

The third ingredient of the model is provided by elements of a graphical topological logic based on Oostra’s intuitionistic version of Peircean existential graphs (EGs). Peirce [21] elaborated on a graphical logic corresponding to classical propositional logic (Alpha EGs), classical first-order logic (Beta EGs), and modal logic (Gamma EGs). Starting from Peirce’s work, Oostra proposed an intuitionistic version of EGs. Intuitionistic logic is, according to Hintikka [22], “truly epistemic” because the crucial notion in it “is not knowing that, but knowing what (which, who, where, …) (…) and this knowing-what-logic cannot be analysed in terms of knowing that plus the apparatus of received first order logic” (pp. 10–11). In this sense, intuitionistic logic refers to what a person actually knows and how, while a knowing-that logic, as classical logic, is based on objective combinatorial aspects and concerns truth values.

There are two main aspects that are connected through the presented model.

On the one hand, this conception of epistemic logic fits the idea of epistemic value as well as the idea of theorem-in-action and puts at the forefront aspects related to the way the student knows what he/she knows. As Oostra [19] states, quoting Brouwer, in the intuitionistic approach, “a mathematical proposition becomes true when the subject experiences or intuits its truth, after having carried out a suitable mental construction” (p. 123). It is misleading to talk here about truth in the classical sense, as to be true means that a suitable construction is known by the individuum. In this sense, intuitionistic logic postulates that constructions “stand over time”; that is, they are truth-preserving in a different way to that assumed in classical logic. Constructions are true in an intuitionistic sense if they hold “densely” in the future, meaning that if there is a moment in time at which a statement is considered true, there is always a subsequent moment in time at which it is true [23]. This concept of truth requires a different interpretation of logical connectives, e.g., the negation of a sentence means that something absurd may be constructed from it; the disjunction of two sentences is true if an effective construction of any of them is possible (or known); implication means that a construction of the consequent is possible (or known), provided a construction of the antecedent is possible (or known), etc.

On the other hand, it is important that mathematical knowledge is explicitly perceived as truth-functional, and students must accomplish a shift from an epistemic to a logical value and from theorems-in-action to theorems. To account for this shift, the model must be able to consider the switch from epistemic to classical logic.

In the following, the basic notions of the classical Alpha EG system are first introduced, according to Oostra [19]. Then, the Alpha intuitionistic EGs (Alph -IEGs) are introduced, which is the proper logical part of the model. The reader who is familiar with the classical EGs may proceed directly with Section 2.3.2, where the Alpha IEGs are presented. For more details on both kinds of EGs and on the formalisation of the classical EGs, the reader may refer to Oostra [19].

2.3.1. Introduction to the Classical EGs

The classical Alpha EG system is built of the following components: the sheet of assertion (the plane surface upon which the graphs are drawn, representing the universe of the possibilities of truth), propositional letters (capital letters, which represent propositions), and cuts (simple closed curves, like the one represented in Figure 1a). EGs, referred to in the following also simply as “graphs”, are thus diagrams composed of propositional letters or (inclusive disjunction) cuts, drawn upon the sheet of assertion. A region of the sheet of assertion limited by a certain number of cuts is called an area of the sheet of assertion. It does not matter where on the graph the sheet of assertion is drawn: “There may be repeated letters, but they all occupy different places. The cuts do not touch the letters, nor do they touch each other. We consider two graphs that can be continuously deformed into each other as equal. This reveals an underlying topology: the graphs can be seen as a part of ‘topological logic’” [19] (p. 106).

We can distinguish two types of areas: even or odd. An area is even if it is delimited by an even number of cuts (eventually zero); it is odd if it is limited by an odd number of cuts (Figure 1b–d, where the label “even” in Figure 1b,c concerns the empty sheet of assertion). A double cut is a graph made up of two nested cuts, one inside the other, without propositional letters or other cuts between them (Figure 1e).

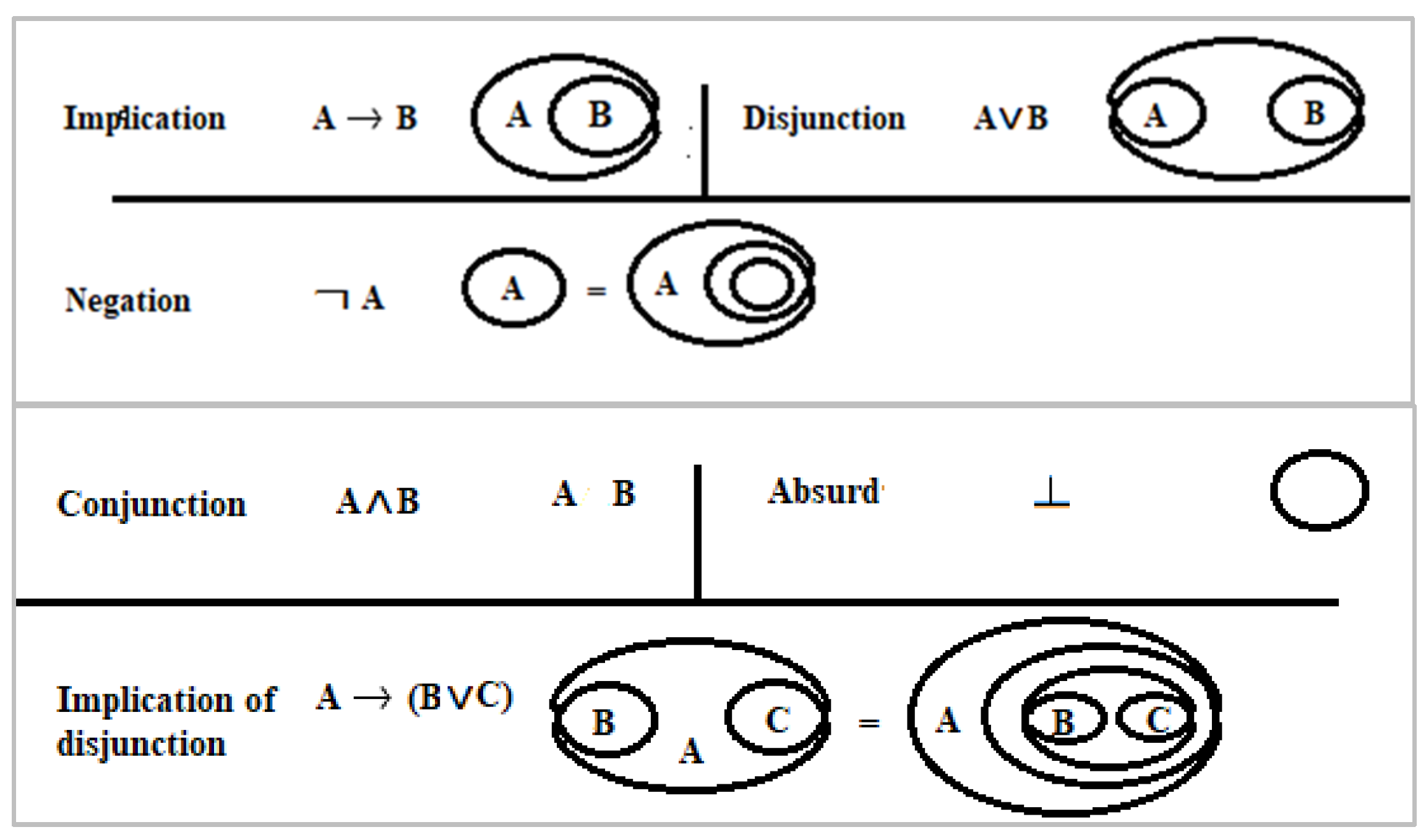
The semantic dimension is introduced, according to Oostra [19], by stating that drawing a cut on the sheet of assertion means asserting its interpretation, and writing a letter means asserting the proposition it represents. The interpretation of the four basic propositional connectives for classical Alpha EGs (negation, conjunction, disjunction, and implication) is represented in Figure 2, together with their “usual” notation in classical symbolic logic.

Starting from the basic graphs of the propositional connectives, one can build recursively a classical Alpha EG for any propositional formula.

In the following, the five classical transformation rules (CTRs) for the system of classical EGs are introduced: CTR1, Erasure; CTR2, Insertion; CTR3, Iteration; CTR4, Deiteration; CTR5, Double cut, and some examples of each of them are provided, according to Oostra [19]:

CTR1: Erasure. In an even area, any graph can be deleted.

Example. In Figure 3, the propositional letter C is written in an even area; indeed, there are an even number (two) of cuts around it. According to CTR1, it can thus be deleted.

CTR2: Insertion. In an odd area, any graph may be added.

Example. In Figure 4, the area between the two cuts is odd (there are an odd number of cuts (one) around it). According to CTR2, the propositional letter C can thus be scribed in this area.

CTR3: Iteration. Any graph may be iterated in its own area or in any area contained in it that is not part of the graph to be repeated.

Examples. In Figure 5a, starting from the graph on the left, the propositional letter A is added to the graph on the right. According to CTR3, this is allowed because A is iterated in its own area. In Figure 5b, starting from the graph on the left, the propositional letter A is inserted in the inner cut of the graph on the right. According to CTR3, this is allowed because A is iterated in an area contained in the area where A was written initially.

CTR4: Deiteration. Any graph may be erased if a copy of it persists in the same area or in any area around it.

Example. In Figure 6a, the propositional letter A is erased from the inner area of the cut. This is allowed according to CTR4 because a copy of it is present in the area around the cut. In Figure 6b, the propositional letter A is erased from the inner area of the cut. This is allowed according to CTR4 because a copy of it persists in the same area, i.e., in the inner area of the cut.

CTR5: Double cut. A double cut may be drawn around or removed from any graph on any area.

Example. In Figure 7a, the double cut around the propositional letter B is removed according to CTR5. In Figure 7b, a double cut is drawn around the propositional letter A, according to CTR5.

Adopting the five transformation rules and the connectives, it is possible to show that the system of classical EGs represents a sound logical system able to interpret all the propositions that can be expressed in classical logic [19]. As an example, in Figure 8, how the classical EGs work is shown by proving the law of the excluded middle, starting from the empty sheet of assertion.

In Figure 8, first, CTR5 is used (a double cut is drawn on the empty sheet of assertion). Then, CTR2 is applied (the graph composed of a cut with the propositional letter A is inserted into the odd area between the two cuts of the double cut). In the next step, CTR3 is applied (the same graph that was inserted in the previous step is iterated within an area contained in its area). The last step of the diagrammatic proof can be translated as follows into the symbolic language of classical propositional logic, starting from the outermost cut: $\neg \left(\left(\neg \mathrm{A}\right)˄\left(\neg \neg \mathrm{A}\right)\right)=\neg (\neg \mathrm{A}˄\mathrm{A})$. To arrive at this result, we used the law of double negation represented by the double cut introduced in the first step, which means that the law of the excluded middle needs the law of double negation, as is well known in classical logic.

Even if in this context we are not interested in formalising the logical tools used in the presented model, before moving to an introduction of intuitionistic EGs, some considerations on the foundations of EGs are necessary. It was only in the 1960s of the 20th century that scholars begun to formalise this graphical logic. An example in this sense is provided by Oostra [19]. Based on the previous results of Martinez [24], Oostra proposed considering a letter written on the sheet of assertion as a point on a plane, labelled with the corresponding propositional letter, and a cut drawn on the sheet as a simple closed curve, which can be considered the continuous injective image of the unit circle S1, with its usual topology, as a subspace of the plane. To combine different elements in a graph, Oostra defines an Alpha pre-graph as a continuous and injective map α that maps a topological sum of m copies of the unitary circle and a finite set of natural numbers with a discrete topology (that maps arbitrarily to a set of propositional letters) to the plane (ℝ²). In this way, the map is an embedding, the letters occupy different places, and the cuts do not touch the letters or touch each other. A graph can then be defined as a pre-graph-equivalence class, after having established a suitable equivalence relation in the set of pre-graphs.

Let us come now to the intuitionistic version of the EGs that represents the proper logical part of the model.

2.3.2. Intuitionistic EGs

The Alpha IEGs are here introduced with some additional elements with respect to the system exposed by Oostra, due to the specific needs of MER, as will be explained below.

According to Oostra [19], Alpha IEGs consist of the following elements: the sheet of assertion, propositional letters, two types of curves: cuts (Figure 9a) or scrolls (Figure 9b); each scroll is composed of a cut with one loop (single scroll, Figure 9b) or more loops (e.g., double scroll, Figure 9c) folded inside it.

In a scroll, the region limited by the cut and the loops is the outer area of the scroll, and the interior part of the loop is the inner area. The areas on the sheet of assertion can be even or odd, in the same way as in classical Alpha EGs (Figure 9d–f).

An Alpha IEG is a diagram consisting of a finite combination of propositional letters, cuts, and scrolls, represented upon the sheet of assertion.

The interpretation of the four basic and two derived connectives (the negation and implication of disjunction) for Alpha IEG are represented in Figure 10, where “=” stands for equivalence.

Before moving further with an introduction of the transformation rule for Alpha IEGs, to better contextualise this diagrammatic intuitionistic logical system, it is worth mentioning another topological interpretation of intuitionistic logic, discussed by van Dalen [25], that takes a cue from Tarski’s work, dating back to the 1930s. In this context, an open set of a topological space is assigned to each atomic proposition; the connectives of disjunction and conjunction are defined as union and intersection in open sets, while implication is defined as the interior (the interior of an open set is its largest open subset.) of the union of the complementary of the open set assigned to the antecedent and the open set assigned to the consequent; negation of a proposition is defined as the interior of the complement of the open set assigned to the proposition itself. As van Dalen [19] states, “Note that this looks very much like the traditional Venn diagrams, with the extra requirement that negation is interpreted by the interior of the complement” (p. 11). Considering that in the system of (I)EGs, drawing a cut around a graph means negating it and “that this simple cut enclosing a graph is an abbreviation of a scroll whose loop contains only an empty cut and whose outer area contains only the graph enclosed by the cut” [19] (p. 134), van Dalen’s quotation seems to recall the same representation described by Oostra. But van Dalen provides only hints to a symbolic version of the open set topological interpretation of intuitionistic logic. Conversely, Oostra goes beyond this and provides a graphical system where the cuts and the scrolls are curves (we could say that they are the closures of van Dalen’s open sets) with transformation rules that operationalise his diagrammatic system.

For the purposes of this paper, it is sufficient to introduce Alpha IEGs intuitively, as Peirce opted for when he devised this diagrammatic logic, considering Oostra’s results regarding the use of the scroll: “Our first successful experiments included a diagram for implication in which the inner cut meets the outer cut at one point:” [19] (p. 132). Peirce himself mentions in this regard a “node” when he refers to this point: “The node merely serves to aid the mind in the interpretation and will be used only when it can have this effect. (…) The scroll shall be a real curve of two closed branches (…) and these branches may or may not be joined at a node.” [21] (4.436).

Let us now introduce the transformation rules for the Alpha IEGs.

The transformation rules for the Alpha IEGs are an extension of the aforementioned transformation rules for the classical Alpha EGs. The intuitionistic TRs (ITRs) from 1 to 5 are taken from Oostra’s Alpha IEG presentation [19]. The ITRs from 1 to 4 (ITR1: Erasure, ITR2: Insertion, ITR3: Iteration, ITR4: Deiteration) contain both the CTRs for classical Alpha EGs (the first part, before the semicolon) and the intuitionist additions (the second part, after the semicolon), while ITR5 (ITR5: Scrolling) is purely intuitionistic. This system of IEGs represents a sound system of diagrammatic intuitionistic logic equivalent to the traditional intuitionistic logic [19]. In addition to the five necessary transformation rules, three transformation rules (ITR6: Increasing or decreasing loop, ITR7: Topological equivalence, ITR8: Detachment) that can be derived from the previous five are added to the model. These ITRs are not necessary, but their assumption as explicit transformation rules makes the model more concise and “user-friendly” for non-experts.

In the following, the abovementioned ITRs are presented.

ITR1: Erasure. In an even area, any graph may be deleted; any loop within an even area may be erased, together with its contents.

Example. In Figure 11, the propositional letter C is inserted into the inner area of the loop that is even.

ITR2. Insertion. In an odd area, any graph may be added; if the odd area is limited externally by a cut, a loop containing any graph may be added to the cut.

Example. In Figure 12, the propositional letter C is inserted into the outer area of the loop that is odd.

ITR3. Iteration. A graph can be repeated in its own area or in any area contained in it which is not part of the graph itself; any loop may be iterated, together with its contents, on its own cut.

Example. In Figure 13, the propositional letter A is present in the outer area of the loop, and the loop itself is contained in that area. Thus, the propositional letter A can be iterated in it.

ITR4. Deiteration. Any graph may be deleted if a copy of it persists in the same area or in any area around it; a loop, together with its contents, may be erased if another loop with the same contents is present on its cut.

Example. In Figure 14, the propositional letter A is present in the outer area of the loop and in the area around the scroll, so it can be deiterated from the outer area of the loop.

ITR5. Scrolling. A scroll with an empty outer area may be drawn around or removed from any graph on any area.

Example. In Figure 15, a scroll with an empty outer area is drawn around the propositional letter A, according to ITR5.

As stated above, in addition to the five Alpha ITRs according to Oostra, three further ITRs that can be derived from ITRs 1–5 are explicitly formulated as rules. ITRs 6 to 8 are added as rules specifically needed in the context of MER and express the constraints related to an increasing/decreasing epistemic value (ITR6), the relations between different concepts-in-action (ITR7), and shifts from an epistemic to a logical value and from theorems-in-action to theorems (ITR8). Since ITRs 6 to 8 can be derived from the system of ITRs 1 to 5, which represent a sound logical system [19], the added rules do not affect the soundness of the model.

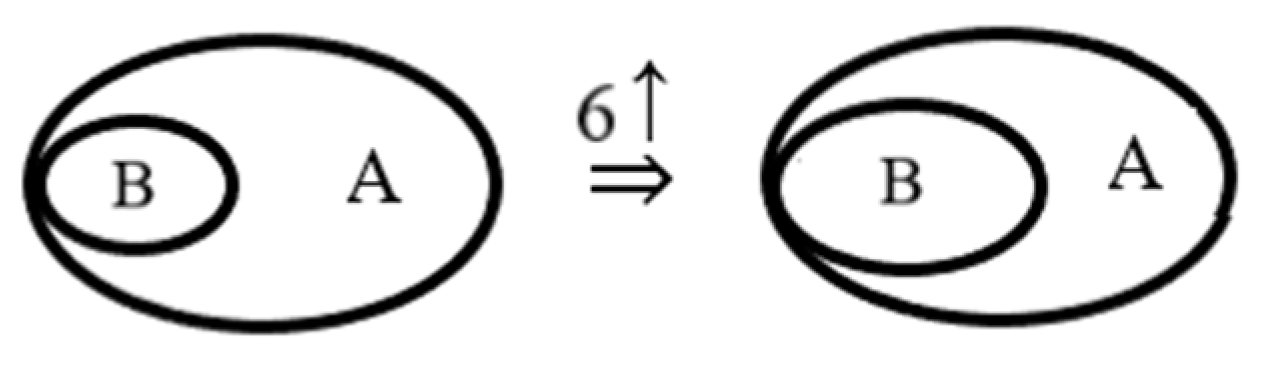
ITR6. Increasing or decreasing loop. In a scroll, the area enclosed by the loop can increase (↑) or decrease (↓).

Example. In Figure 16, the area enclosed by the loop increases (↑) within the scroll.

A scroll represents an implication intended as a theorem-in-action, where the antecedent (in this case expressed by the propositional letter A) is inserted within the area enclosed between the scroll and the loop, while the consequent (in this case expressed by the propositional letter B) is inserted into the inner area of the loop. In this sense, growing belief in the validity of the implication that acts as a theorem-in-action is expressed by the growth of the inner area of the loop. Vice versa, decreasing belief in the validity of the theorem-in-action is expressed by decreasing the area of the loop.

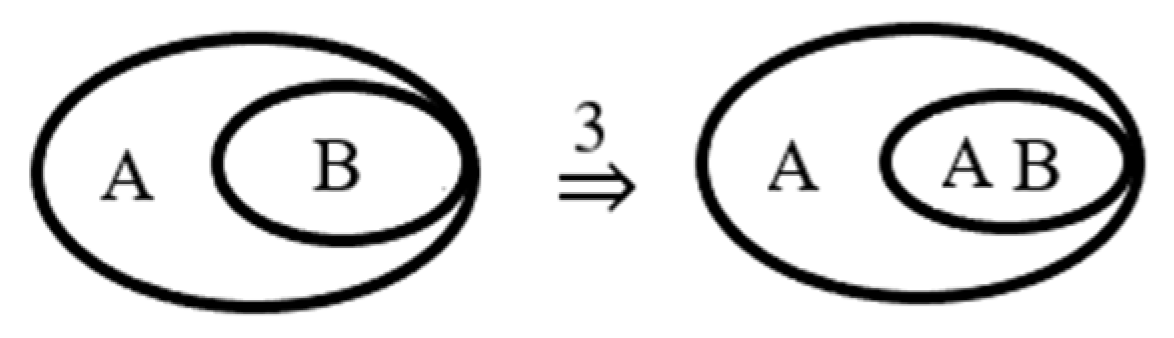
ITR7. Topological equivalence. A graph can be transformed into another equivalent of it by continuously transforming the curves it is composed of.

Example. The transformation in Figure 16 represents an example of ITR6 and ITR7.

ITR7 is a generalisation of ITR6. Indeed, EGs, both classical and intuitionistic, represent systems of topological logic according to which two graphs are equivalent if they can be transformed continuously in each other [19], i.e., without changing the characteristics of its areas by breaking or glueing their elements. This aspect justifies both ITR6 and ITR7.

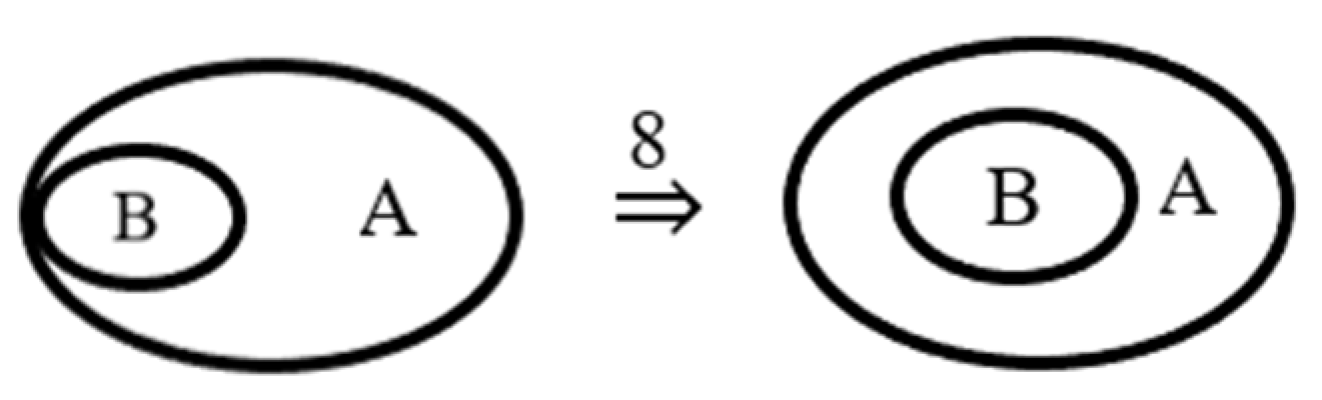
ITR8. Detachment. A loop of a scroll can be detached from the cut.

Example. In Figure 17, the loop of the scroll is first glued together with the loop, and than the loop is detached from it by applying ITR8.

ITR8 leads to a switch from intuitionistic to classical implication.

The idea of topological transformation anchored in ITR7 helps us to understand what could be meant by logical continuity. It is well known that insofar as a given figure is continuously deformed (i.e., previously connected points were not separated and previously separated points were not connected), the obtained figures are topologically equivalent to it. Starting from this idea of continuous transformation, a topological space (in this context, a bidimensional closed curve) associated with a connective (e.g., the implication A→B) can be transformed into another (e.g., A→(B˅C) through continuous transformations of the scroll that represents it. On the other hand, if one considers the topological equivalence of two connectives as based on the domain equivalence between the concepts-in-action they refer to, a relation of inclusion between domains corresponds to a continuous deformation of the corresponding curve. In this context, continuous transformations of the scroll curve of implication can be used to express an increasing or decreasing epistemic value, related to the increasing or decreasing number of different classes of objects that fall under the same concept-in-action (ITR6). In this sense, one could assume that shifts between graphs that are topologically equivalent could represent steps in the reasoning that are less challenging than steps between graphs that are not topologically equivalent because the former represent an elaboration on what was just stated before, while the latter represent the introduction of new elements into the graph.

As is well known, in intuitionistic logic, the law of the excluded middle does not hold in general, and ITR6 accounts for this characteristic, considering an increasing or decreasing epistemic value. As we have seen, classical Alpha EGs and Alpha IEGs differ from each other in representing implication and in the behaviour of negation. Indeed, in classical Alpha EGs, the implication is represented in a similar way to Alpha IEGs, but the “loop” and the cut do not touch each other, and the double negation corresponds to a double cut. Therefore, to frame the shift from the epistemic to the logical value of a proposition, and hence from theorems-in-action to theorems, one needs ITR8 (Detachment), which allows us to switch from an intuitionistic implication that “holds over time” to a classical implication that is true or false. This is in accordance with the Peircean intuitive conception of the scroll/double cut, just mentioned above: “The scroll shall be a real curve of two closed branches (…) and these branches may or may not be joined at a node” [21] (CP, 4.437).

As follows, in accordance with [20], the acronym Alpha IEGs-TRs* is used to denote the set of the eight previously presented transformation rules.

Finally, let us consider a transformation rule that cannot be part of the transformation rules for Alpha IEGs for reasons that will be explained below but which is needed for the purposes of the model. This transformation rule is the double cut classical TR (CTR5), which is recalled here for the reader’s convenience: A double cut may be drawn around or removed from any graph on any area.

The double cut is the diagrammatic equivalent of the classical double negation law that cannot be framed within the system of Alpha IEGs-TRs*. Indeed, it is a general law in classical logic but not in intuitionistic logic. Nevertheless, it can be used considering that through its use, one makes a shift to classical bivalent logic. (In [4], this transformation rule is present as TR5.1. within the system of transformation rules considered in the model, but adding it actually makes the logical system become classical instead of intuitionistic. Many thanks to Prof. Fernando Zalamea from the Universidad Nacional de Colombia for having pointed out this critical aspect in the model presented in [4]).

In the next section, three examples of analysis of excerpts taken from the literature, according to the epistemic logical model introduced above, are presented and discussed.

3. Example Analysis and Discussion

The examples discussed in this section were chosen for the following reasons: (1) they are particularly useful for making reasoning processes explicit, as they describe an evolution in students’ reasoning; (2) they are taken both from geometry and algebra to show that the model is able to account for students’ reasoning independently from the mathematical content involved in it; (3) they are examples discussed during recent CERME Conferences (CERME 11 and CERME 12) in Team Working Group 1, focused on argumentation and proof, and can thus be considered worth of attention by the researcher community working in this area. (As the reasoning described in the selected articles (partially mixed with the analysis made by the researchers) extends over several pages in the articles, it is not included in this paper but can be recovered from the sources quoted in the references. For the reader’s convenience, the most important excerpts are added as Supplementary Materials).

3.1. Example S1: Marie’s Cyclic Quadrilaterals

In MER, the so-called Lakatos-style proof approach is widely recounted in the literature (e.g., [26,27]). According to this approach, there are some techniques that can be used to improve “proofs” when they are invalidated by a counterexample. Two techniques are exception barring and lemma incorporation, both concerning an exploration of the domain under consideration that is restricted or enlarged to exclude counterexamples or to include further properties. Lada and Forbregd [27] discussed how prospective teachers (PTs) dealt with these two techniques while they were interviewed during an activity. The objective of the activity was to make the PTs discover the theorem A quadrilateral is cyclic if and only if its opposite angles are supplementary, but this was then judged too optimistic, and thus all the interviews ended once the necessary condition was conjectured by the participants: If a quadrilateral is cyclic, then its opposite angles are supplementary. The assignments were (a) to prove that the three perpendicular bisectors on the side of a triangle meet at one point and that this point is the centre of the circumscribed circle; (b) to investigate whether a similar result holds for quadrilaterals, to state a conjecture, and to try to prove it.

Marie is one of the PTs whose reasoning was exposed by Lada and Forbregd [27]. In the following, Marie’s reasoning is analysed using the tools provided by the presented epistemic logical model. Marie’s conjecturing and proving activity can be subdivided into nine steps. In the first part of the activity, which comprises steps 1 to 5, she explores the problem using the concept-in-action related to the intersection point of the bisectors. She implicitly uses theorem-in-action P: If a quadrilateral is cyclic (antecedent A), then the bisectors of its sides intersect at a point that is the centre of the circumscribed circle (consequent B). In Figure 18, the nine steps are represented by Alpha IEGs adopting the set of rules Alpha IEGs-TRs* as they were introduced in this paper.

Step 1: P as a general statement is negated because Marie believes there are no quadrilaterals with this property; Step 2: she discovers that a restricted version of P: A→B is true for squares; Step 3: Marie discovers that P is true for rectangles; Step 4: P is believed to be true by Marie for quadrilaterals with two parallel sides (overgeneralisation), which is then corrected later. Marie struggles to further explore the problem and is thus pushed by the researcher to use another concept-in-action, related to the supplementary angles in a quadrilateral. This implies the implicit use of another theorem-in-action, Q: If a quadrilateral is cyclic (antecedent A), then its opposite angles are supplementary (consequent C). In step 5, the shift to the supplementary angle property is expressed as the introduction of a second loop (C), which leads to the implication with disjunction A→(B˅C). In steps 6 and 7 in Figure 18, the “move” of loop C is represented, until it overlaps with loop B. The domain of the concept-in-action related to loop B is included in the domain of the concept-in-action related to loop C—quadrilaterals with bisectors that intersect at the same point have supplementary opposite angles—and thus loop C can be erased (ITR1). The shift from step 8 to step 9 represents the shift to truth-functional logic through detachment (ITR8).

The two conjectures (P and Q) are two theorems-in-action driven by two different concepts-in-action, and steps 2, 3, and 4 represent the increasing epistemic value of P experienced by Marie as she discovers new classes of quadrilaterals that satisfy it. Steps 5 to 9 are related to the (implicit) reasoning needed to finally shift to the theorem If a quadrilateral is cyclic, then its opposite angles are supplementary.

The analysis shows that the topological character of the employed logic allows us to highlight the distinction between the explorations based on the two different concepts-in-action. From a purely extensional viewpoint, the distinction between loop B and loop C (step 5), and thus between the concepts-in-action they are based on, does not make sense, but from an epistemic viewpoint, it does because the problem is explored by using two different properties. Indeed, Marie does not discover the usefulness of the second concept-in-action (the one related to the supplementary angles); she is pushed by the researchers to consider it. Furthermore, topological logic allows us to highlight in a diagrammatic manner the shift from an epistemic to a logical value (from step 8 to step 9). One can notice that steps 2 to 8 are performed by continuously deforming the initial curve. In this sense, the graphs in steps 2 to 8 are topologically equivalent and topologically different from the graph in step 9. This can be considered the representation of an epistemic continuity described by topological epistemic logic, joined to a logical discontinuity, which is presumably also epistemic, when shifting to step 9.

3.2. Example S2: Ale’s Tangent Circle

Boero and Turiano [28] discuss examples of 10th grade students’ reasoning on Euclidean geometry statements that make use of what the authors call a “continuity principle” (p. 139). A student, Ale, is working on a task, aiming to make him discover the construction of a circle inscribed in a triangle. He just knows how to construct a circle tangent to the two sides of an angle with the centre on the bisector. Ale’s behaviour is described in Figure 19.

The student seems to perform a mental transformation of the geometrical figure, supported by drawing some snapshots of it—a circle that moves while keeping its centre on the bisector of an angle and is tangent on two sides—with the purpose of “proving” the existence of a circle inscribed in the triangle, and seems to consider this as one proof of the existence of the required mathematical object: the circle S in Figure 19. How could Ale’s reasoning be framed within the model exposed in this paper? Ale first draws the circle near angle B of the triangle in Figure 19. As stated above, he just knows the Euclidean procedure for constructing a circle with its centre at the bisector and tangent to the sides of the angle. By drawing circle S, he exhibits the required object: a circle inscribed in the triangle. Let us consider two propositions: Proposition A—In a triangle, a circle with its centre at the bisector of an angle and tangent to the sides of the angle can be constructed—and Proposition B—A circle tangent to the three sides of a triangle can be constructed. The implication A→B can be considered in the intuitionistic sense: If I know how to construct the object in proposition A, then I am able to construct the object in proposition B. This knowledge is provided by the procedure that “transforms” the object in proposition A into the object in proposition B (see the drawing in Figure 19). Globally, the student seems to behave according to the modus ponens inferential rule (A and A→B, thus B), a rule that holds also in intuitionistic logic (Figure 20a).

The implication A→B can be considered a theorem-in-action based on a concept-in-action related to the property of tangency. The drawing of the intermediate circles represents the intermediate steps of this constructive “proof”, ending with the existence proof of the required object. In this sense, the epistemic value of the theorem-in-action increases by moving the centre of the circle at the bisector away from edge B of the triangle. Thus, an intermediate step in the modus ponens inference can be added that makes no sense from a classical logic viewpoint but does from an epistemic one. Indeed, the increasing epistemic value of the theorem-in-action A→B can be highlighted applying ITR6↑ to the loop of the first scroll (Figure 20b). Although the “proof” provided by the student is completely convincing for him, it requires further reasoning and validation to be considered as such by the researcher. Indeed, the researcher pushes the student to think about what would happen if the radius of the circle S increased further and then decreased again. In this sense, the student is induced to validate his “proof” by showing that S is really tangent to the side AC. For this purpose, the researcher introduces a new concept-in-action, linked to the property of being secant. Opposite to the case in Example S1, here, the new concept-in-action is related to the antecedent, not to the consequent, and thus there is no transformation rule that allows us to transform the A→B-graph into the C→B-graph. It could be conceived of as an application of modus ponens to the implication C→B, where C is the statement “The radius of the circle can be increased continuously, keeping the centre at the bisector until it has two distinct intersection points with a side, and then it can be decreased again continuously until these two points coincide at a unique point.” For the student, C→B becomes a theorem-in-action, in the same way that A→B was, although it does not seem to have a higher epistemic value for him than A→B. Indeed, he does not seem to feel the necessity of validating the “proof”, although he follows the researcher’s reasoning and agrees with it. To represent the shift to a logical value, as aimed for by the researcher, one must add a step of detachment (TR8) to the modus ponens proof based on the secant–tangent interplay (Figure 21).

Once validated by C→B, the former theorem-in-action A→B becomes a theorem within a truth-functional context.

In this example, three logical discontinuities can be recognised, which presumably are also epistemic: (1) in the shift from the first to the second modus ponens application (from Figure 20b to Figure 21); (2) in the shift to the validation, e.g., in analytical geometry (ITR8 in Figure 21, which represents the shift from argumentation to proof); (3) in the application of the double cut elimination rule, which is not part of the Alpha IEGs-TRs* and is represented in Figure 21 in the last step without the transformation rule.

3.3. Example S3: Numbers Ending with 1

The third example that is presented here concerns reasoning on numbers and their properties: a secondary school student is asked by the teacher to decide whether the following statement is true or false: If a number ends with the digit 1, then it is a prime number or is divisible by 3. The student argues as follows:

It is true. In fact, if we consider 11, 21, 31, 41, 51, 61, 71, etc., we see that they are all prime numbers or numbers divisible by 3. On the other hand, it is possible to reason also in general. If a number is prime and greater than 2, it ends with an odd digit (and 1 is just an odd digit). As for 3, among its multiples are 21, 51, 81, 111, 141, etc., all numbers ending on the right with the number 1. The thesis has been proven.

As discussed in [4], where this example was discussed within a different framework, the second part of the argumentation, where the student states that one could also reason “in general”, could be interpreted in two different ways. Firstly, it could be considered an inversion of the thesis with the hypothesis; secondly, the student might be giving generic examples of “suitable” objects, aiming to “prove” that he is reasoning about objects that actually exist, according to a pragmatic nyaya-style rationality [3,16]. In its current version, the epistemological model presented in this paper is not able to consider the second interpretation. Indeed, to this end, quantification according to the Beta IEGs would be needed. Therefore, hereafter, only the thesis–hypothesis inversion interpretation is discussed.

Let us formulate the statement at stake in the student’s argumentation using propositional letters: If a number ends with the digit 1 (antecedent A), then it is a prime number (consequent B) or a number divisible by 3 (consequent C). The proposition at stake can thus be expressed by the following implication: A→(B˅C), (The symbol “˅” stands for exclusive disjunction) where A is the antecedent and B˅C is the consequent expressed by a disjunction.

Let us now analyse the student’s argumentation and represent it according to the epistemic logical model presented above. At the beginning, the student states that A→(B˅C) is true; he seems to be sure about this, and in this sense, the statement appears epistemically undeniable. It is therefore represented as a classical implication (Figure 22a). In the first phase of the argumentation (Figure 22b,c), the student exposes his reasoning in support of what he stated previously. The general statement is treated as a hypothesis to be proven and is therefore represented as an intuitionistic implication (Figure 22b). There is no transformation rule that allows us to represent the shift from the reasoning in Figure 22a to the reasoning in Figure 22b. Following this, the student argues by exploring the domain of numbers ending with the digit 1 and first shows some of them being prime (B) and then others being divisible by 3 (C). This shows what is the first phase in the process that induces him to be convinced about the truth of the general statement at stake: there is a growing belief in the validity of the implication, expressed by the growth of the inner area of the loop (ITR6↑: Increasing loop) (Figure 22c), due to the discovery that each of the elements in the examined sequence of numbers ending with 1 is either prime or a multiple of 3. In the second phase of the argumentation (Figure 22d–g), the student shows awareness that the reasoning previously exposed is epistemically convincing but not general enough. Therefore, he tries to reason “in general.” Also, in this case, there is no transformation rule that allows us to represent the shift between the reasoning in Figure 22c and Figure 22d. During this second argumentative phase, it can be assumed that the student inverts the thesis and the hypothesis, arguing according to the two cases to be distinguished: B→A and C→A. In the first case (B→A), the student is actually referring to general properties (If a number is prime and greater than 2, it ends with an odd digit), pointing out that the case he is considering is a special case of this general propriety (and 1 is just an odd digit). This reasoning can be expressed by the implication represented in Figure 22d. In the second case (C→A), the student does not reason in general but by listing some examples of numbers that satisfy both properties, the one related to antecedent C (being a multiple of 3) and the one related to consequent A (being a number that ends with the number 1). This reasoning is expressed by switching from the graph represented in Figure 22d to the graph represented in Figure 22f via the one represented in Figure 22e. This can be described by applying ITR5 (Scrolling) and ITR2 (Insertion). Finally, the student asserts that “the thesis has been proven” (graph in Figure 22g), which is interpreted as an application of ITR8 (Detachment) and subsequent elimination of the cut around the propositional letter A (Figure 22h). There is no transformation rule that allows us to perform this last step (Figure 22g,h), and thus this step represents a break in the argumentation that is not supported by the logical system.

The analysis of this third example shows how the student relies on two theorems-in-action, A→(B˅C) and (B˅C)→A, and how the concepts-in-action related to the antecedents and the consequents act in support of the theorems-in-action.

Also, in this case, as just seen in the other two examples, topological logic allows us to highlight in a diagrammatic manner the shift from an epistemic to a logical value; in this case, there are two switches between them. Figure 22a,b represent a switch from a logical value (the statement is “true”) to an epistemic value (checking of examples); Figure 22f,g represent a switch from an epistemic (arguments in favour of (B˅C)→A) to a logical value (“the thesis has been proven”). While the second switch can be framed within the presented system Alpha IEGs-TRs*, the first one cannot be framed within it. Indeed, while in the second case, there is a transformation rule that can be applied to perform the switch from the graph in Figure 22f to the graph in Figure 22g (ITR8), there is no such transformation rule in switching from the graph in Figure 22a to the graph in Figure 22b. This means that there are two points of logical discontinuity in the student’s reasoning that are probably at the same time also epistemic discontinuities, as they require, at least implicitly, a change in the logical system of reference. Furthermore, one can notice that there are several epistemic, but not logical, discontinuities that are represented by switches between graphs that are not topologically equivalent (Figure 22c,d; Figure 22d,e; Figure 22f,g). Finally, even if there is no logical discontinuity between the graph in Figure 22c and the graph in Figure 22d, in the sense that there is no change between logical systems, there is an epistemic discontinuity, as there is no transformation rule that allows us to switch from one to the other. Indeed, this step represents a thesis–hypothesis inversion that is not a valid reasoning, as the statement at stake is not a logical equivalence.

This last example shows that due to the topological character of the implied logic, it is possible to highlight breaks in the student’s reasoning that would not be so easily representable using formal logic and that can be described as only epistemic, only logical, or as both.

4. Conclusive Remarks

The three examples discussed above show that the model proposed in this paper allows us to frame students’ argumentation within a “knowing-what and knowing-how” epistemic context, considering also the shift to proof in a classical “knowing-that” logical context. But even more importantly, especially the last example shows how reasoning during the argumentation phase is a kind of back and forth between different logical frames, between logical and epistemic values, and between theorems-in-action and theorems that needs a “hybrid” model able to account for such shifts between classical and non-classical contexts. Furthermore, the distinction between logical and epistemic discontinuities helps us to better understand the pitfalls in students’ reasoning. This could increase the possibility of effectively supporting learning processes by precisely recognising such difficulties.

Let us come back to the research question: Is the model presented in this paper a valuable tool for analysing students’ reasoning and highlighting the epistemic logical continuities/discontinuities that occur during reasoning processes? We can state that the model presented in this paper seems to be able to fulfil the role of an analytical tool for the researcher in mathematics education, even if there are several aspects that require further investigation. As just highlighted in [4], further research should be carried out to refine the model, considering also the use of quantification (Beta IEGs). Indeed, this would allow us to analyse also the second interpretation of the student’s reasoning in Example S3, which does not assume that the student is inverting the thesis and hypothesis. Furthermore, issues related to the concept of continuity (logical and epistemic) should be deepen and further exemplified in the future.