Abstract
Our mathematical thinking sheds light on how we see our world and what knowledge we have about it. In spite of this, mathematical performance is still mostly measured in calculation skills, and this also predestines the success of learning. So at school, what is important is how correctly we solved the task and not the way we got there. An internationally unique Hungarian-developed test (DPV—Pedagogical Examination of Dyscalculia/Diszkalkulia Pedagógiai Vizsgálata) draws our attention to the opposite of this. The special feature of the test is its criterion orientation, which emphasizes the correctness of mathematical thinking while examining the abilities necessary for learning mathematics. The aim of our study was to investigate, as a function of background variables (gender and socioeconomic status (SES)), (1) whether the abilities and thought processes required for learning mathematics function at an adequate level, (2) what effect these may have on mathematical performance, and (3) to what extent all of this is influenced by mathematical anxiety. Our background variables were gender and socioeconomic status. A total of 999 Hungarian students aged 10–15 participated in our study, including 483 boys and 516 girls. In general, we can say that the development of the skills necessary for learning mathematics is closely related to the students’ performance. Nevertheless, it happens that we encounter low performance despite good skills. In several cases, we can experience the presence of anxiety, especially math anxiety, which in most cases, regardless of the level of abilities, negatively affects the success of math learning processes. The findings confirm that socioeconomic status, gender, and performance are risk factors for mathematical anxiety. The following hypotheses have been formulated along the lines of the research objectives set out in the abstract: There are no differences in ability and mathematical performance between boys and girls. Girls are more anxious when they have to solve a mathematical problem. Socioeconomic status predicts ability level and the presence of math anxiety. Mathematical anxiety (MA) modifies the validity of mathematical ability (DPV).
1. Introduction
Cognitive processes and abilities facilitate intellectual functioning, encompassing mental functions such as perception, memory, and information processing, through which individuals gather information, formulate plans, and solve problems [1].
The highest level of cognitive activity is thinking. Thinking is necessary to solve problems that cannot be solved directly by perception, memory, or imagination. It is a high-level process because it relies on other low-level processes [2].
Childhood marks a pivotal stage in the evolution of cognitive processes [3].
The most important aim and task of teaching mathematics in upper secondary school is to familiarize students with the quantitative and spatial relations of their environment, to lay the foundations for their modern, applicable mathematical literacy, and to develop their thinking, and in secondary school, to further ensure the development of students’ independent, systematic thinking and their ability to apply mathematics [4].
Examining the development of counting skills, Szűcs and his colleagues found that the most significant change can be seen in the development of skills between the ages of 5 and 7. The older the child, the more the repertoire of counting strategies expands with the development of mathematical abilities, and with practice, the effectiveness of the strategies increases [5].
After extensive cognitive neuropsychological and neuroscientific investigations into mathematical abilities, two primary models have surfaced: McCloskey’s process-oriented model in 1992 and Dehaene’s “triple coding model” in 1995. McCloskey grounded his theory on the premise that mathematical tasks necessitate the integration of various sub-functions, each localized within distinct regions of the nervous system. Consequently, not all areas are necessarily compromised in the event of injury. McCloskey’s process-oriented model comprises three distinct components: (1) a number comprehension and perception unit; (2) a number-generation or production unit; and (3) a calculation unit. Dysfunction within any of these units manifests symptoms indicative of the source of the problem [6,7].
According to Dehaene’s triple coding model of number processing, an individual’s mathematical proficiency hinges on the concurrent utilization of three representations: (1) visual number form; (2) verbal number representation; and (3) analog magnitude representation. These numerical representations remain distinct from one another, operating independently and linking to different cerebral cortical areas. While each systems possesses unique inputs, outputs, and characteristics, they interact synergistically during mathematical problem solving. This interconnectivity renders the entire model flexible [8].
The development of numerical abilities, including performance, exhibits significant individual differences even among typically developing children. Performance denotes the qualitative application of knowledge, abilities, and skills. School math performance serves as an indicator of academic success and efficiency, often reflected in test scores. The benchmark for performance is determined by the requirements outlined in the school curriculum and within the specific grade-level mathematics subject [9].
Several factors can impede the effectiveness and efficiency of mathematical learning and performance [10].
Research findings demonstrate that stress significantly impacts higher-order cognitive processes, the learning process, working memory performance, and the retrieval of previously acquired knowledge [11].
The negative emotions experienced during stressful mathematical tasks can impair the effective execution of mathematical operations relying on higher cognitive abilities. It can be partly explained by general anxiety, but a specific form of anxiety is mathematical anxiety, which can occur when dealing with numbers and mathematical problems [12].
This can lead to emotional, physiological, cognitive, and behavioral symptoms of anxiety [13].
When math anxiety coincides with low self-esteem, it can hinder working memory, resulting in poorer mathematical performance [14]. In their study, focusing on 11–13-year-old upper elementary school students, Szűcs and Mammarella found that girls exhibited a higher level of math anxiety compared to boys, despite no significant difference in academic performance between the two genders. Among the primary causes contributing to girls’ higher math anxiety, Szűcs and Mammarella identified the influential role of math-related gender stereotypes, as well as girls’ tendency toward greater anxiety and their ability to accurately define and report anxious situations. To comprehend the impact of math anxiety on performance, it is essential to investigate its underlying factors. However, most research findings do not coalesce into a unified understanding of what triggers and sustains this specific form of anxiety [15].
Broadly, three major categories of causes are distinguished: (1) situational factors, such as mathematics assessments and class assignments; (2) social factors, including teacher attitudes and parental educational background and anxiety; and (3) structural factors, representing individual characteristics such as self-efficacy, self-image, and attitude [16].
Socioeconomic status (SES) refers to the social circumstances of families, encompassing factors like family income and parental education. While these metrics may have some correlation with mathematical performance, their impact tends to be less significant. Wealthier parents often have greater resources to support their children’s education and provide conducive learning environments [17].
Drawing upon these theoretical models, we present our research, aimed at elucidating the impact of anxiety and socioeconomic status on the outcomes of an internationally unique mathematical abilities test, as well as assessing the extent to which they predict performance.
2. Materials and Methods
2.1. Participants
The research participants were Hungarian secondary school students. The average age of the 999 students was 12.791 ± 2.28 years. A total of 483 boys and 516 girls took part in the research. In our research, we tried to follow the SAGER guidelines [18] and take gender into account when interpreting the results.
The tests took place in schools. The examinations were carried out with questionnaires and psychometric measuring instruments in group and individual form. The parents were informed about the course of the examination and the individual examination results. All institutions signed the research cooperation agreement. Both the parents and their children signed the consent form for the study. This study was approved by the ethics committee of ETT TUKEB (Medical Research Council, Scientific and Research Ethics Committee), license number: 35643-5/2017/EKU. We certify that this study was conducted in accordance with the ethical standards laid down in the 1964 Declaration of Helsinki and its subsequent amendments.
2.2. Survey
In the first phase of the study, the children were given a math test to assess their performance in math. The test was adapted to the grade level requirements set by the math teachers.
Then they filled out self-administered questionnaires under teacher supervision. The first was the Math Anxiety test (MA), then the General Anxiety (CBCL GA) test (Child Behavioral Check List (CBCL) anxious/depressed scale), and finally the students completed the Socioeconomic Questionnaire (SES—socioeconomic status). The Pedagogical Examination of Dyscalculia (DPV—Diszkalkulia Pedagógia Vizsgálata (Hungarian)) test of the skills necessary for learning mathematics was taken on another occasion by taking a personal test. We asked the schools for their end-of-term math grades.
In the first stage of the examination of the results, we performed descriptive statistics and frequency analysis for the main variables. The distribution of the data was analyzed using the Kolmogorov–Smirnov test.
We performed Spearman’s correlations in order to examine correlations between variables. We checked the multicollinearity in these variables by calculating the variance inflation Factor (VIF), because if it turned out that there was a too close correlation between two or more explanatory variables, it disturbed the estimation. As a result, we continued the analysis with a reduced number of variables.
We performed ANOVA analysis to determine whether the child’s socioeconomic status and gender influenced their development of abilities and math anxiety. We ran multivariate regression analyses to test the contribution of general anxiety, math anxiety, and ability to math achievement. We used IBM’s SPSS Statistics version 26.0 (IBM Corp., Armonk, NY, USA) for statistical analysis.
2.3. Test Materials
Several tests were included in the study, and their names and reliability indicators are listed in the following Table 1.

Table 1.
Tests used in the study.
The math knowledge test looked at a current level of knowledge according to the given grade. The students wrote this test in mathematics class under the supervision of specialist teachers.
The Math Anxiety test (MA) [19] is a measuring tool developed by the staff of the University of Debrecen to measure the components of math anxiety. The test contains 40 statements that the students rate on a 7-point Likert-scale, where 1 means “This is not typical of me at all”, while 7 means “This is completely typical of me”. The test is divided into two main factors: the first includes emotional and physiological symptoms, while the second includes cognitive symptoms—attitudes, attributions, and beliefs.
Emotional and physiological symptoms include fear, anxiety, restlessness when learning mathematics, and positive emotions such as joy or happiness. Physical symptoms such as nausea, abdominal pain, palpitations, tremors, or dizziness are also related to emotional factors. The cognitive factor encompasses content related to mathematical thinking and is not divided into further subfactors. The test was developed using the Mathematics Anxiety Rating Scale (MARS) [20], a questionnaire to measure feelings of tension and anxiety experienced when faced with math testing or problem solving.
The purpose of the test is to help educational professionals and psychologists better understand and manage math anxiety in the school setting [10].
In order to assess children’s behavioral and emotional problems, we used the Hungarian translation of the Child Behavior Check List (CBCL) [21].
This test was adapted for Hungarian children with high reliability scores (Cronbach’s alpha for the anxious/depressed scale was 0.81) [4]. We evaluated the anxious/depressed scale from the students’ answers. We call this generalized anxiety (GA) for the purpose of the study. The following answers can be given to the questions based on how typical it is of the student: 0 is not true, 1 is somewhat or sometimes true, and 2 is often true or very true. The corresponding score for each category is 0, 1, and 2 points. The total raw score of each scale was calculated by adding the scores of all items that could be assigned to it. The range of possible scores for the anxious/depressed subscale was 0–18. CBCL (GA) was measured here by the mean value of the anxious/depressed subscale (r = 0.72 ***).
The socioeconomic status was determined by answering the following questions: the educational level of the parents, whether the parents have a regular job, and whether the student has his/her own room, desk, and mobile phone.
Mathematical abilities were assessed using the Pedagogical Examination of Dyscalculia (DPV) developed in Hungary [22]. DPV not only measures numerical skills but also examines the child’s abilities necessary for learning mathematics, non-mathematic-specific cognitive functions, thinking strategies, and compensation mechanisms.
The test tries to separate the causes of underachievement in mathematics based upon their severity and whether we are dealing with a learning difficulty or a specific learning disorder. The measurement procedure examines the analog quantity system, the Arabic number format, the verbal system, and number processing, e.g., writing and reading numbers. The main basic functions are emphasized during the measurement procedure: the spatial–visual and central executive system, as well as working memory and language aspects. Scoring is criterion-oriented, and points are awarded if the child does not make mistakes. The task types of the measuring materials compiled according to age were constructed analogously. As the school grade goes up, the test consists of a different number of oral and written tasks, and their nature changes according to age characteristics [10].
2.4. Data Processing
Frequency Indicators
The following table (Table 2) shows the frequency indicators of our research. Minimum and maximum values, means, and standard deviations obtained in the tests are shown.

Table 2.
Mean and standard deviation of extreme values of variables.
The best grade is excellent (5), while the worst grade is unsatisfactory (1). The grades in mathematics are not normally distributed with respect to gender and grade (Table 3), and statistical calculations were therefore carried out using nonparametric tests.

Table 3.
Distributions between grades and grade by gender.
3. Results
3.1. Cross-Tables, Correlations
The DPV test results are classified into three categories according to the diagnostic criteria defined by the test editors; the test is divided into three broad classifications based on percentage points: symptom-free (86–100%), learning difficulty (41–85%), and specific learning disability (dyscalculia) (0–40%) (Table 4, Table 5 and Table 6). The tables illustrate the mathematical ability-based classification of our sample:

Table 4.
Gender distribution of DPV test results.

Table 5.
Distribution of DPV test results by grade.

Table 6.
DPV test classification and math school grade distribution.
These results are provided as background information, and the mathematical ability measured in the sample is grouped by gender, grade, and mathematics class, according to the diagnostic categories. This clearly shows the distribution of the ability of the students tested. The use of these categories in the analysis is no longer intended because we are not performing differential diagnostics but only measuring mathematical ability.
Table 4 clearly shows that there are more pupils with good mathematical ability among both boys and girls. Within the sample, 1.3% of pupils with a learning disability are boys and 1.4% are girls. The correlation analysis clearly shows that there is no significant difference between gender in terms of mathematical ability (Table 7).

Table 7.
Zero-order correlations of variables.
Similar distributions are also found for the year grouping (Table 2 and Table 5), with the difference being that the proportion of students with no problems and those with difficulties show less variation than in the gender grouping. In terms of grade, the existence of a straight proportionality is clearly visible here. The higher a pupil’s grade, the less the presence of a learning problem and its variation in severity (Table 6). As diagnostic tests require a combination of test scores, this information is only indicative and not diagnostic.
A positive significant correlation was found between gender and CBCL(GA) and MA. That is, girls are more anxious. Increases in age and grade are associated with decreases in general anxiety and also show a negative directional association with SES data, with a moderate degree of correlation.
Socioeconomic status and math achievement and ability show a medium-strong positive correlation, while SES data show a medium-strong negative correlation with CBCL(GA) and math anxiety. If students perform more poorly in mathematics, they are more anxious. If pupils are generally anxious, this is also reflected in high levels of MA.
One of the most relevant pieces of information for defining our research objective is the relationship between mathematical ability and other variables. The DPV test scores reflect students’ numeracy and reasoning abilities, which are independent of gender, age, and grade. Socioeconomic status is a clear determinant of the level of DPV (r = 0.654), while math grade (r = 0.818) and knowledge (r = 0.947) are based on DPV (Figure 1).
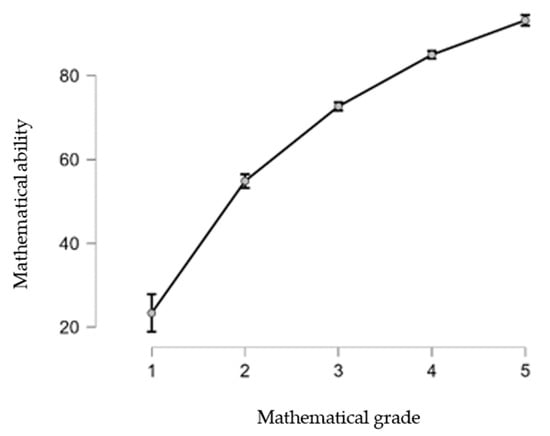
Figure 1.
Mathematical ability and grade correlation.
A negative significant correlation indicates that CBCL(GA) (r = −0.230) and MA (r = −0.338) are clearly mutually determinant, i.e., high levels of general and mathematical anxiety result in lower than expected ability levels.
No correlation was found between gender and age, grade, socioeconomic status, and mathematics grade. No association was found between age, math achievement (grade and math test), and MA, nor between grade, math grade, and MA (Table 3).
3.2. Variance Inflation Factor (VIF)
In the collinearity test, we controlled for VIF with gender, age, socioeconomic status (SES), math achievement (end-of-year grades and math test scores), general anxiety (CBCL GA), math anxiety (MA), and math ability (DPV). As a result, we found that general anxiety was strongly correlated with mathematics anxiety in terms of VIF and grade with mathematics test score, so we only continued analyses with these measures that were more relevant to the study, and general anxiety and mathematics test scores were excluded from the set of variables. Thus, based on the VIF indicator (VIF < 1.011–1.837), there is no multicollinearity between the variables.
3.3. Statistical Analysis
To answer the question of whether MA is affected by the gender of the child and the child’s SES, analysis of variance (ANOVA) was conducted. Girls have slightly higher anxiety scores than boys, so we can say that girls in our sample are more anxious when faced with a math problem (F = 26.473; df = 1; p < 0.001). Children with lower socioeconomic status are more anxious about math (F = 11.672; df = 9; p < 0.001), so SES data are predictive. Age, and thus grade, do not interact with MA.
We also conclude from the association between DPV and math grade (Table 6) that having the right ability is a predictor of achievement (R2 = 0.811; F = 1916.063; df = 1; p < 0.000), with 65.8% of this finding being confirmed.
The hypothesis that mathematical anxiety (MA) modifies the validity of mathematical ability (DPV) was confirmed in only 10.7% of our sample (R2 = 0.327; F = 119.224; df = 1; p < 0.000) (Figure 2).
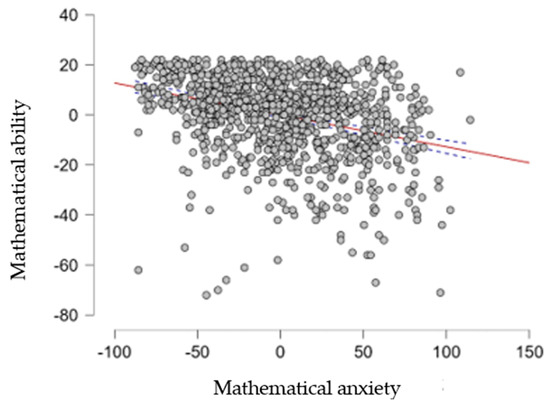
Figure 2.
The relationship between mathematical ability and the impact of mathematical anxiety.
To answer our main question, we fitted our main model of mathematical ability to normalized data. To explore the extent to which the validity of mathematical ability is jointly influenced by gender, age, grade, SES, and MA, we conducted multivariate linear regression analysis (Table 8).

Table 8.
Standardized Regression Coefficients for Main and Interaction Effects.
Our model explains 66.8% of our hypothesis (R2 = 0. 817; F = 397; 0.170; p < 0.000) that the validity of mathematical ability (DPV) is negatively influenced by gender, age, socioeconomic status, grade, and mathematical anxiety (MA).
4. Discussion
4.1. Measuring the Ability to Think
Thinking is the process of gaining indirect and in-depth knowledge of reality.
It is an ability that enables the imagination of objects and events, their mapping in memory, and the execution of operations on these representations. The capacity to think through logical relationships within problems in a systematic manner and to solve complex mathematical problems is significantly developed in children over the age of 12 [3]. The skills required for learning mathematics, from preschool to adulthood, play a crucial role in everyday life, and their proficiency level can significantly impact our performance. In our large-sample study, we utilized a unique test of mathematical ability, both in Hungary and internationally. What distinguishes this test is that it evaluates not only the correctness of the solution to a problem but also the methodology employed to arrive at the solution. Specifically, we examined whether the skills necessary to solve a given task are employed effectively. This approach allows for clear differentiation between various levels of mathematical ability, enabling proper definition of development levels and tasks. The DPV test is criterion-referenced, enabling prediction of other background factors that may influence the results.
4.2. Relationship between Performance and Ability
Significant individual differences exist in children’s development levels, often manifested in their academic grades. It is important to note that while grades serve as a measure of performance, they do not equate to performance itself. Performance entails the application of knowledge, ability, and skill to varying degrees and qualities in task execution [9]. In our studies, alongside ability tests, we also considered grades, which unsurprisingly showed a strong correlation with ability (r = 0.818; p < 0.05).
4.3. Gender Differences in the Prevalence of Mathematical Anxiety
Confident learners tend to exhibit more effective problem-solving skills as they employ efficient coping strategies and persevere in their efforts to succeed. Conversely, individuals with low self-confidence often respond to stressors by withdrawing, which may be compounded by feelings of shame if their performance falls short. Additionally, individuals prone to general anxiety often also experience heightened anxiety when confronted with mathematical tasks, which can significantly impact their performance [15]. Our research unequivocally demonstrates a strong correlation between high levels of CBCL(GA) and MA (r = 0.677; p < 0.05) and diminished problem-solving abilities in mathematics. Furthermore, our findings reveal that female students, despite displaying no significant disparity in mathematical academic achievement compared to boys (p > 0.05), frequently report lower math self-confidence. This discrepancy may be attributed to the higher prevalence of MA among girls (r = 0.153; p < 0.05), possibly stemming from entrenched gender stereotypes surrounding mathematics or from girls’ enhanced ability to accurately report and detect anxiety-inducing situations [23].
Szczygieł, on the other hand, reported that boys’ math performance is more closely associated with MA than girls’. He also observed a relationship between general anxiety and achievement. He concluded that lower levels of general anxiety in boys have a stronger effect on the impact of mathematics anxiety on performance than in girls [24].
4.4. The Impact of Socioeconomic Status and Anxiety on Performance
High levels of anxiety can precipitate learning difficulties, potentially leading to adverse life outcomes. Maladaptive coping mechanisms during learning may culminate in school dropout, juvenile delinquency, diminished labour market prospects, low socioeconomic status, and consequently, social isolation or even mental health issues for certain students [25]. Consistent with expectations, our results reveal robust associations across all socioeconomic status variables. We observed a negative directional relationship between CBCL(GA) (r = −0.150; p < 0.05) and MA (r = −0.284; p < 0.05) with socioeconomic (SES). Moreover, a positive and strong correlation emerged between ability (DPV) (r = 0.654; p < 0.05), math grade (r = 0.653; p < 0.05), and SES.
The negative impact of student socioeconomic status (SES) on academic performance is a major problem worldwide. A Finnish study investigated how socioeconomic status affects mathematics achievement among primary school pupils. They also concluded that lower socioeconomic status predicts lower ability. They also concluded that lower socioeconomic status predicts lower skills. In other words, lower SES implies lower mathematical competence, which reduces the likelihood of success [26].
The research of Guzmán and colleagues supports our results, showing a direct effect of SES on MA. This means that the lower the SES, the higher the MA level. Mathematical performance plays a mediating role in the SES–MA relationship [27].
Identifying students who experience MA is important. Immediate intervention is needed before the effects of anxiety take hold and their performance, and thus their mental health and subsequently their quality of life, deteriorates [7].
Executive control functions and emotion regulation processes interact, and both play a key role in mathematical anxiety. Exercises related to these theories could provide a good basis for intervention processes [28].
5. Limitations
Our study employed a cross-sectional design, which limits our ability to establish causal relationships between variables. Longitudinal studies could offer more comprehensive insight into the development of mathematical abilities, encompassing both performance and the anxiety influencing it.
We did not solicit information from parents or teachers regarding any anxiety they may experience. Research suggests that parents’ math anxiety could potentially impact their children’s performance when assisting them with math problems. Moreover, findings indicate that parents with high MA may better empathize with their children’s anxiety and consequently respond more effectively to it [29]. Future studies should incorporate considerations of gender stereotypes in mathematics and provide evidence-based statements to counter misconceptions, such as the notion that girls perform less effectively in mathematics. It would also be valuable to investigate other aspects of parental history, such as a family history of developmental disorders like learning disabilities or comorbidities with ADHD. Additionally, other dependent variables, such as environmental factors and spatial orientation difficulties, should be taken into account [9].
While our study focused on examining mathematical abilities, a more precise understanding of the role of other dependent variables could be achieved by assessing all students intellectually. This approach would enable us to accurately determine the influence of general intelligence on the mathematics learning process and facilitate targeted developmental interventions in the future.
6. Conclusions
In Hungary, large-scale studies utilizing mathematics ability tests and associated predictors have not yet been conducted. Our study contributes to filling this gap by demonstrating the significant impact of mathematical ability on performance. Lower levels of ability can result in poorer performance, leading to increased anxiety. Our model, adjusted for SES data and background variables, substantiates 66.8% of our assertions, suggesting that various factors may underlie different levels of mathematical ability.
Regardless of the influencing factor, teachers must be equipped to address these challenges effectively.
Author Contributions
Conceptualization, B.S. and S.Á.; Methodology, B.S. and S.Á.; Formal analysis, B.S.; Investigation, B.S.; Resources, B.S.; Data curation, B.S.; Writing—original draft, B.S.; Writing—review & editing, B.S. and S.Á.; Visualization, B.S.; Supervision, S.Á.; Funding acquisition, B.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Research Programme for Public Education Development of the Hungarian Academy of Sciences; National Laboratory for Social Innovation project (RRF-2.3.1-21-2022-00013), within the framework of Hungary's Recovery and Resilience Plan, with the support of the Recovery and Resilience Facility of the European Union.
Institutional Review Board Statement
This study was approved by the ethics committee of ETT TUKEB (Medical Research Council, Scientific and Research Ethics Committee), license number: 35643-5/2017/EKU.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Conflicts of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Atkinson, R.L.; Atkinson, R.C.; Smith, E.E.; Bem, D.J.; Nolen-Hoeksema, N. Pszichológia; Osiris Kiadó: Budapest, Hungary, 2003. [Google Scholar]
- Svraka, B. Az Észleléstől a Gondolkodásig—Kognitív Folyamatok a Tanítás Tanulás Folyamatában Iskoláskorban. In Szenzomotoros Információ-Feldolgozás, Mozgás, Nyelvi Képesség-A Frostig-Elven Alapuló Nevelési Terápia Elmélete és Gyakorlata; Gerebenné, V.K., Reményi, T., Rosta, K., Eds.; Gondolat Kiadó: Budapest, Hungary, 2021; pp. 397–410. ISBN 978 963 556 124 7. [Google Scholar]
- Cole, M.; és Cole, R.S. Fejlődéslélektan; Osiris Kiadó: Budapest, Hungary, 2001. [Google Scholar]
- Rózsa, S.; Kő, N. A Gyermekviselkedési Kérdőív (CBCL). Educatio Társadalmi Szolgáltató Nonprofit Kft., Budapest. 2015. Available online: https://docplayer.hu/7755914-A-gyermekviselkedesi-kerdoiv.html (accessed on 3 October 2023).
- Szűcs, D.; Devine, A.; Soltesz, F.; Nobes, A.; Gabriel, F. Cognitive components of a mathematical processing network in 9-year-old children. Dev. Sci. 2014, 17, 506–524. [Google Scholar] [CrossRef]
- Krajcsi, A. A numerikus képességek zavarai és diagnózisuk. Gyógypedagógiai Szle. 2010, 38, 1–21. [Google Scholar]
- Krzysztof, C.; Flavia, H.S.; Karin, K.; Ann, D. Mathematics anxiety—Where are we and where shall we go? Ann. N. Y. Acad. Sci. 2002, 1513, 10–20. [Google Scholar] [CrossRef]
- Polgárdi, V.; Csabáné, L.; Dékány, J. Alapismeretek a Diszkalkulia Pedagógiai Vizsgálatáról. Gyermeknevelés Tudományos Folyóirat 2018, 6, 24–54. [Google Scholar] [CrossRef]
- Ramirez, G.; Gunderson, E.A.; Levine, S.C.; and Beilock, S.L. Spatial Anxiety Relates to Spatial Abilities as a Function of Working Memory in Children. Q. J. Exp. Psychol. 2012, 65, 474–487. [Google Scholar] [CrossRef]
- Svraka, B.; Ádám, S. Prevalence of cognitive and affective factors influencing mathematical performance. Gyermeknevelés 2022, 10, 190–204. [Google Scholar] [CrossRef]
- Marin, M.F.; Lord, C.; Andrews, J.; Juster, R.P.; Sindi, S.; Arsenault-Lapierre, G.; Fiocco, A.J.; Lupien, S.J. Chronic stress, cognitive functioning and mental health. Neurobiol. Learn. Mem. 2011, 96, 583–595. [Google Scholar] [CrossRef]
- Caviola, S.; Carey, E.; Mammarella, I.C.; Szűcs, D. Stress, Time Pressure, Strategy Selection and Math Anxiety in Mathematics: A Review of the Literature. Front. Psychol. 2017, 8, 1488. [Google Scholar] [CrossRef]
- Krajcsi, A. A numerikus képességek sérülései és a diagnózis nehézségei. Pedagógusképzés A Nev. És Az Új Idegtudomány 2008, 101–125. [Google Scholar]
- Ashcraft, M.H. Math Anxiety: Personal, Educational, and Cognitive Consequences. Curr. Dir. Psychol. Sci. 2002, 11, 181–185. [Google Scholar] [CrossRef]
- Szűcs, D.; Mammarella, I.C. Math Anxiety. Educational Practice Series 31; UNESCO International Bureau of Education: Le Grand-Saconnex, Switzerland, 2020; Available online: https://www.cne.psychol.cam.ac.uk/files/maths_anxiety.pdf (accessed on 3 October 2023).
- Baloglu, M.; Kocak, R. Multivariate investigation of the differences in mathematics anxiety. Personal. Individ. Differ. 2006, 40, 1325–1335. [Google Scholar] [CrossRef]
- Marks, G.N. Cognitive ability has powerful, widespread and robust effects on social stratification: Evidence from the 1979 and 1997 US National Longitudinal Surveys of Youth. Intelligence 2022, 94, 101686. [Google Scholar] [CrossRef]
- Heidari, S.; Babor, T.F.; De Castro, P.; Tort, S.; Curno, M. Sex and gender equity in research: Rationale for the SAGER guidelines and recommended use. Res. Integr. Peer Rev. 2016, 1, 2. [Google Scholar] [CrossRef]
- Nótin, Á.; Páskuné Kiss, J.; Kurucz, G. A matematika szorongásmérő személyen belüli tényezőinek vizsgálata középiskolás tanulóknál. Budapest. Magy. Pedagógia 2012, 112, 221–241. [Google Scholar]
- Richardson, F.; Suinn, R.M. The Mathematics Anxiety Rating Scale Psychometric Data. J. Couns. Psychol. 1972, 9, 551–554. [Google Scholar] [CrossRef]
- Achenbach, T.M. Child Behavior Checklist. In Encyclopedia of Clinical Neuropsychology; Kreutzer, J.S., DeLuca, J., Caplan, B., Eds.; Springer: New York, NY, USA, 2011. [Google Scholar] [CrossRef]
- Dékány, J.; Polgárdi, V.; Láz, C. Matematikatanulási Problémák Hatékony és Preventív Mérése. A Diszkalkulia Pedagógiai Vizsgálata és Előszűrő Eljárása 1-4 (DPV; E-DPV); Logopédiai Kiadó: Budapest, Hungary, 2020; Available online: https://logopediakiado.hu/E-DPV-1-2-pendrive-es-urlapkollekcio (accessed on 3 October 2023).
- Devine, A.; Fawcett, K.; Szűcs, D.; Dowker, A. Gender differences in mathematics anxiety and the relation to mathematics performance while controlling for test anxiety. Behav. Brain Funct. 2012, 8, 33. [Google Scholar] [CrossRef]
- Szczygieł, M.; Hohol, M. The gender Gap in Math Anxiety (and in a Link between Math Anxiety and Math Performance too) Is Not So Salient When Other Anxieties Are Controlled for PsyArXiv Prepr. 2024. Available online: https://osf.io/preprints/psyarxiv/5trew (accessed on 3 October 2023).
- Firth, N.; Greaves, D.; Frydenberg, E. Coping styles and strategies: A comparison of adolescent students with and without learning disabilities. J. Learn. Disabil. 2010, 43, 77–85. [Google Scholar] [CrossRef]
- Haataja, E.S.H.; Niemivirta, M.; Holm, M.E.; Ilomanni, P.; Laine, A. Students’ socioeconomic status and teacher beliefs about learning as predictors of students’ mathematical competence. Eur. J. Psychol. Educ. 2024, 39, 1615–1636. [Google Scholar] [CrossRef]
- Guzmán, B.; Rodríguez, C.; Ferreira, R.A. Longitudinal Performance in Basic Numerical Skills Mediates the Relationship Between Socio-Economic Status and Mathematics Anxiety: Evidence From Chile. Front. Psychol. 2021, 11, 611395. [Google Scholar] [CrossRef]
- Cohen, L.D.; Rubinsten, O. Math anxiety and deficient executive control: Does reappraisal modulate this link? Ann. N. Y. Acad. Sci. 2022, 1513, 108–120. [Google Scholar] [CrossRef]
- Guzmán, B.; Rodríguez, C.; Ferreira, R.A. Effect of parents’ mathematics anxiety and home numeracy activities on young children’s math performance-anxiety relationship. Contemp. Educ. Psychol. 2023, 72, 102140. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).