Abstract
Recognizing the omnipresence of mathematics across various contexts, this paper addresses the untapped potential of museums as rich venues for informal mathematics learning beyond traditional educational settings like classrooms. This paper presents the InformalMath program, designed for the professional development of primary and middle school teachers using integrating mathematics education within art and history museums through designing mathematics visit workshops. Specifically, the focus is placed on Phase 1 of the program, in which teachers participated in two informal mathematics education workshops at two museums in Turin, Italy, and were asked to reflect on their participation through a written essay. The analysis of the essays reveals significant engagement, appreciation of mathematics as a cultural artifact, and the emergence of creativity and inclusion among participating teachers. These findings highlight the benefits of such interdisciplinary approaches in enhancing mathematical understanding and pedagogical strategies. Conclusions emphasize the program’s success in not only enriching teachers’ instructional repertoire but also in promoting a more holistic, engaging, and contextualized approach to mathematics education, suggesting a promising avenue for future educational practices and research in informal learning environments.
1. Introduction
It is extremely easy to verify the widespread claim that ‘Math is everywhere’ on the Internet. A simple search with any search engine yields numerous results of various kinds: websites, books, video channels, blogs, podcasts, and social pages, among others. Browsing through these results, one quickly realizes that most of the content aims to popularize mathematics. With the same purpose—popularizing mathematics to the general public—exhibitions, museums, or mathematics houses have begun to emerge recently. Among many, some notable examples include the Mathematikum (Giessen, Germany); the Maison des Mathématiques et de l’Informatique (Lyon, France); the Mathematics House (Isfahan, Iran); and the Giardino di Archimede (Pistoia, Italy) (see [1]).
While research in science education has long exploited science museums for informal education experiences [2], mathematics education has received less attention in this regard. There are only a few instances where mathematics education, beyond popularization, has been addressed within science museums or exhibitions from an interdisciplinary perspective [3,4,5].
We believe that art museums also hold significant potential for mathematics education. Associating or even integrating the two domains can offer numerous stimulating elements for both students and teachers. Drawing from our experience as mathematics educators and our review of the relevant literature, we identified two key components to achieve this: designing informal mathematics education (IME) activities and providing dedicated teacher training.
The literature highlights both opportunities and limitations associated with the use of field trips in education. In their review of science field trips, Behrendt and Franklin [6] point out a widespread lack of teacher training in designing field trip activities. They also emphasize that the success of field trip activities depends largely on the teacher’s planning and engagement. Furthermore, a study on the engagement of preservice teachers in planning mathematics lessons at two museums in Ankara, Turkey [7], examined how museum resources are integrated into lesson planning. This study revealed that planned activities often focused solely on numbers, operations, and data analysis. The museum context was typically used for routine calculation procedures rather than exploring the more abstract mathematical concepts embedded in exhibits.
In a previous project called Next-Land ([8], https://www.next-level.it/progetti/next-land-2, accessed on 10 March 2024), we explored how art and history museums could offer opportunities for mathematics learning. In collaboration with two teacher-researchers from our research group and museum educators, we designed four mathematics workshops, each one integrated into one history or art museum in Turin (Italy). These workshops were tailored for sixth-grade students, available for school trips, and led by museum guides.
During the workshops, we observed that many accompanying teachers participated in a detached manner, mainly ensuring proper student behavior in the museums. This detachment could be attributed to various factors. Some were specific to the Next-Land project, such as being conducted in the early days of the school year when some teachers were new and unfamiliar with both the students and museums. Other limitations arose from COVID-19 containment measures, including the use of face masks, social distancing, and sanitization requirements. Consequently, many teachers spent significant time ensuring compliance with these measures during the museum visit workshop.
Our observation prompted us to question the relevance of teacher education for informal mathematics education (IME) activities. To our knowledge, no studies have investigated the training of mathematics teachers specifically for IME activities in ‘non-scientific’ museums. By the term ‘non-scientific museum’, we refer to museums other than science and technology museums, where connections to mathematical aspects might be less immediately apparent. In this context, ‘non-scientific museums’ primarily include art and history museums. This term also encompasses ethnographic or other kinds of museums that are not primarily focused on exhibiting products of science or technology.
To address this research gap, we conceived the idea of developing a teacher education program tailored for primary and middle school teachers (first to eighth grade), focusing on designing mathematics workshops in history and art museums. This program, named ‘InformalMath’, will be detailed in Section 3.
In this paper, we concentrate on the first phase of the InformalMath program, which centers on the teachers’ first encounter with a structured IME program through the workshops we designed in two museums in Turin (Italy). We aim to amplify the voices of the participating teachers, offering insights from their perspectives.
The following section will situate the IME research within the broader literature.
2. Informal Mathematics Education
Let us consider two different scenarios where mathematics learning occurs.
In the first scenario, a class group is actively engaged in solving a problem. The classroom, typical of many, is furnished with desks, chairs, a teacher’s desk, and a blackboard displaying the assigned problem. Students, whether working alone or in groups, are focused on solving the given problem.
In contrast, the second scenario unfolds amidst the lively stalls of a market. A fruit and vegetable seller supervises their helper assisting a customer with math calculations. This scene is set against the backdrop of chatter from colleagues and other shoppers.
We can conceptualize these two scenarios as being at opposite ends of a spectrum. On one end, we have the classroom—a formal context for mathematics education. On the other end, we find the market—an informal setting.
Research in mathematics education has been extensively studying the formal context of the classroom for many decades. The informal scenario, and the market context in particular, has been explored in the studies conducted by Terezinha Nunes and colleagues. Their research focused on the calculation processes of young street vendors in Recife, Brazil [9], which belong to the strand of so-called ‘street mathematics’. Their findings reveal that these children can easily perform calculations and solve problems in the informal context of the market, whereas they often struggle with the same problems when presented in a school-like environment [9] (p. 23).
Between these two extremes lie numerous scenarios where mathematical activities are structured informally but explicitly designed to support participants’ learning. Nemirovsky, Kelton, and Civil discuss these scenarios within the ‘Futuristic Issues’ section of a Compendium for Research in Mathematics Education [10]. They address these contexts as informal mathematics education environments, emphasizing that, unlike everyday mathematics, informal mathematics education environments are intentionally designed to foster learning. On the other hand, IME activities differ from typical mathematics classroom activities in the following aspects:
- (IME-1).
- The learners’ free choice: “for the most part, learners volunteer to participate in them or are relatively free to pursue their own interests once they are in the environment”.
- (IME-2).
- The fluidity of the boundaries between disciplines: “activities may drift from mathematics to art, literature, science, games, technology, and so forth”.
- (IME-3).
- The absence of traditional forms of academic assessment: “Informal mathematics education needs to be documented for the purposes of professional development and collective exchange, but learners are not individually graded with scores” [10] (p. 970).
The chapter examines various experiences of informal mathematics education, with a particular focus on activities within museums. Specifically, it describes four research experiences related to mathematics exhibitions in science museums. These experiences raise questions about the learning of mathematics in such contexts and the nature of mathematics presented in the exhibitions. Toward the end of the chapter, the authors highlight key aspects that should be included in a research agenda for IME. One of the highlighted aspects is the importance of investigating the training of informal mathematics educators. These educators can include teachers, museum educators, or other agents involved in delivering informal mathematics education:
“To the extent that informal education practices differ qualitatively from formal education ones, it is clear that the education of informal mathematics educators needs to follow approaches different from prevalent ones in mathematics teacher education.”[10] (p. 977)
The InformalMath program has been developed in line with this research perspective and agenda.
3. The InformalMath Program
InformalMath [11] (www.informalmath.unito.it, accessed on 10 March 2024) is a project with a two-fold nature. It is a two-year teacher education program aimed at introducing teachers to informal mathematics education and engaging them as active protagonists therein. At the same time, it is a research project aimed at studying the development of teacher education processes within the training program. In this section, we will describe and account for the teacher education nature of the project.
The program started in December 2021 and is ongoing at the time of writing this paper. As researchers in mathematics education and teacher educators, we designed and managed the program. Jaworski [12,13] uses the term ‘didacticians’ to describe individuals who simultaneously fulfill roles as teacher educators and researchers, along with the associated tasks. This entails the responsibility to implement a teacher education program, select appropriate content and methods, as well as the commitment to contribute scientifically to the advancement of knowledge in teacher education. Given these roles and responsibilities, we identify ourselves as didacticians within the InformalMath program.
The program is structured into three phases (see Figure 1):
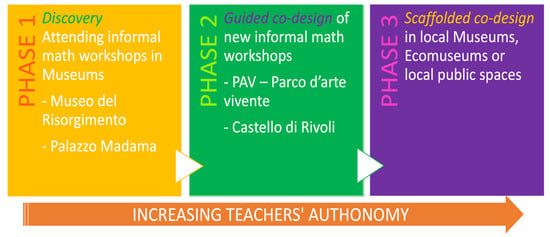
Figure 1.
Outline of the InformalMath training program.
In total, 27 teachers (13 from primary school and 14 from middle school) volunteered to participate and their participation was offered free of charge (according to Italian legislation on teachers’ professional development, in-service teacher education is mandatory, permanent, and structured for teachers working in public schools (L. 107/2015, comma 124: https://www.gazzettaufficiale.it/eli/id/2015/07/15/15G00122/sg, accessed on 10 March 2024). Teachers have the flexibility to choose the areas and duration of training initiatives they wish to participate in. InformalMath was offered to teachers free of charge, with the only cost being the entrance fee to the museum. The program received no external funding.). In the first phase, which took place between January and March 2022, the teachers were given the opportunity to participate in IME workshops designed for two museums: the National Museum of the Italian Risorgimento in Palazzo Carignano, and the City Museum of Ancient Art in Palazzo Madama. Each workshop allowed teachers to experience it as it was intended for students. Following each visit workshop, which lasted approximately 2 h, the teachers engaged in a critical reflection on the activities conducted, delving into the mathematical content encountered in the visit workshop and exploring related themes in mathematics education.
During the second and third phases, teachers were actively involved in co-designing new visit workshops. The activities for the second phase took place in two different museums selected for the teachers. In the third phase, the teachers, organized into groups, chose the museums for designing their educational activities. The teachers’ voices regarding Phase 2 were gathered and analyzed. The findings were presented at the CERME 13 conference [14].
The teacher education program operates on the premise that first-hand experience is essential for teachers to familiarize themselves with new approaches and that engaging in dialogue with researchers can support their development or enhancement as reflective practitioners [15]. The focus was placed on a critical element of teaching practices—the design of tasks for students [16,17].
The design and progression of the entire program through its three phases were informed by the cognitive apprenticeship model [18]. This approach foresaw a significant initial involvement of didacticians, paired with a lower degree of teacher autonomy, evolving gradually into greater teacher autonomy and a reduced presence of didacticians. Indeed, teachers’ participation evolved from directly experiencing visit workshops in Phase 1 to engaging in guided design work in museums selected by didacticians for Phase 2, culminating in full autonomy over museum and content selection in Phase 3. Correspondingly, the didacticians’ role transitioned from being central—designing workshops and leading reflective discussion post-visit workshops in Phase 1—to selecting museums and providing design support in Phase 2, and, finally, serving merely as consultants to the teachers’ design of informal mathematics education workshops in Phase 3.
4. Research Focus and Methods
In Section 3, we presented InformalMath as a teacher education program. Nonetheless, it is important to note that InformalMath also functions as a research initiative aimed at studying the development of teacher education processes within the context of the training program. To this end, each phase was accompanied by a structured research framework, targeting the exploration of whether and how an informal mathematics setting can serve as an effective tool in teacher education processes. In this paper, our focus is on Phase 1, specifically investigating the teachers’ perspectives.
We report that in the first phase of the InformalMath program, 27 teachers participated: 13 from primary schools and 14 from middle schools. We were involved as teacher educators (‘didacticians’, as discussed above). The teachers volunteered to join the program in response to an announcement circulated among all primary and middle schools in the Piedmont region and after attending an online informational meeting in which the program methods and schedule were described. Participation was not incentivized with any financial compensation.
To give voice to the teachers and collect data for our research at the conclusion of the first phase, we invited the teachers to compose brief personal essays. This gave them an opportunity to reflect on and articulate their own experience. Specifically, we provided them with the following prompt for the assignment (we present here both the English and the original Italian versions):
Write down your reflections following the two museum experiences. To do this, we invite you to revisit the experiences through your own eyes as a teacher, trying to bring out critical issues and opportunities of informal mathematics education experiences in a museum setting. (Scrivi le tue riflessioni a seguito delle due esperienze nei musei. Per fare questo, ti invitiamo a rileggere le esperienze con i tuoi occhi da insegnante, provando a far emergere criticità e opportunità delle occasioni di educazione matematica informale in un contesto museale.)
This assignment is part and parcel of the teacher education program, serving as a tool to elucidate the participants’ points of view. Subsequently, the essays were summarized and then discussed during an InformalMath meeting to encourage the teachers to take a further reflective stance.
We regard the responses from the teachers as valuable research data to understand the perceived opportunities and challenges associated with IME in non-scientific museum settings by the teachers involved in the InformalMath teacher education program.
To this end, we have formulated the following research questions:
- RQ1: Which opportunities have the participating teachers identified within informal mathematics education activities in museums?
- RQ2: What are the critical issues that need addressing within informal mathematics education activities in museums, according to the participating teachers?
Eighteen teachers—eight from primary schools and ten from middle schools—submitted the personal essay required, written in Italian. These essays underwent a qualitative content analysis [19], employing inductive category formation. Initially, individual words served as the unit of analysis. We selected sentences within the essays containing words from the following semantic domains: informal, mathematics, museum, criticality, and opportunity. Subsequently, sentences featuring these domain-specific words were analyzed as units, with each being assigned a label summarizing the teacher’s intended message. These labels were then grouped into categories based on their content (refer to Table in Section 6). Prior to engaging with the data analysis, and in order to account for the teachers’ reflections, it is pertinent to describe the two visit workshops that constituted the core experience in Phase 1.
5. The Informal Mathematics Education Workshops in the Museums
To initiate the discussion of the two visit workshops, we will first outline the theoretical principles underpinning their design. This will be followed by a succinct description of each workshop.
5.1. Design Principles
The design of the workshops carefully considered the historical and artistic content specific to each museum, as well as the distinctive architectural features of each location. To incorporate these artistic and historical elements into the activities, we conducted site visits and worked closely with the museum’s scientific advisors and guides.
Regarding the mathematical dimension of the workshop, three design principles have been identified.
5.1.1. Principle P1: History and Art Museums as Spaces for Bewilderment
The goal is to immerse students in an experience of aesthetic bewilderment (from the Italian “spaesamento”), acting as a catalyst for exploration, including mathematical exploration. This concept is inspired by outdoor education [20] and relates to the educational potential that arises from the state of being in an “elsewhere”—an unfamiliar environment, like a forest.
The notion of “dépaysement”—which, lacking a direct English equivalent, can be translated as “disorientation” or “bewilderment”—also finds relevance in mathematics education. Barbin discussed this notion, noting it as a benefit of incorporating the history of mathematics into teaching [21,22]. Barbin argues that encountering ancient mathematical texts can induce a kind of ‘cultural shock’ when they are not properly contextualized. It is thus imperative to situate these readings within the specific scientific, philosophical, and social milieu of their authors. This contextualization aids in comprehending the author’s intent. Moreover, it allows one to perceive mathematics not only as a finished product but as an evolving historical process. Experiencing “dépaysement” can allow both teachers and students to view mathematics in a new light, understanding that it has not always existed in its current form and acknowledging it as a result of human efforts across various cultural and historical landscapes.
In our view, a similar kind of dépaysement can be encountered by students (and indeed, their teachers as well) when they engage in mathematics activities within a museum setting that is not explicitly related to the realm of science.
5.1.2. Principle P2: Students Actively Involved in Laboratory Activities
This principle pertains to engaging students in inquiry-based mathematics activities. In particular, it refers to the concept of the “mathematics laboratory” as a teaching methodology [23,24], which has been taken up in the current Italian curriculum for primary and middle school [25]. The curriculum describes the laboratory “both as a physical space and as a moment in which the pupil is active, formulates his own hypotheses and checks their consequences, plans and experiments, discusses and argues his choices, learns to collect data, negotiates and constructs meanings, brings to temporary conclusions and new openings the construction of personal and collective knowledge” [25] (p. 49, translated by the authors).
Previous research has investigated the pivotal role of artifacts within the mathematical laboratory methodology [26]. This methodology shares several aspects with inquiry-based learning [27], a teaching–learning approach that rests on four foundational pillars: “student engagement in meaningful mathematics, student collaboration for sense making, instructor inquiry into student thinking, and equitable instructional practice to include all in rigorous mathematical learning and mathematical identity-building” [27] (p. 14).
5.1.3. Principle P3: Developing a Vision of Mathematics as a Cultural Product
This principle recognizes mathematics as a product of history and culture, in constant evolution, rather than as an inherent characteristic of nature itself. This perspective is strongly highlighted within the so-called ethnomathematics strand (e.g., [28], but also [29]) and among researchers who draw from the cultural–historical philosophical tradition (e.g., [26]).
5.2. Freedom Shall Decrypt
The workshop titled ‘Freedom Shall Decrypt’ (‘Libertà va’ decrittando’, in Italian), designed for the National Museum of the Italian Risorgimento in Palazzo Carignano stems from ideas suggested by the museum. From a mathematical standpoint, the detail around which the visit workshop focuses is the ‘cipher of Vittorio Emanuele,’ an artifact used for encrypted communications between the first King of Italy, Vittorio Emanuele II di Savoia (1820–1878) and his Prime Minister, Camillo Benso, Count of Cavour (1810–1861). This artifact serves as a catalyst for the workshop, which delves into the history of cryptography. Participants actively engage in a visit workshop, decoding encrypted messages through various methods to uncover the narratives within the museum exhibits. They employ substitution codes (like the ‘Carbonaro Code’, Caesar’s code, and Leon Battista Alberti’s disk), alongside steganography and transposition codes (such as the Spartan scytale). As each message is decoded, the pivotal events leading to the birth of the Italian state are sequentially unveiled (for more on the history of ‘Freedom Shall Decrypt’, see [8]).
Immediately following the visit workshop, the teachers engaged in an exploration of cryptographic topics and their integration into classroom curricula, with a particular emphasis on the relevance of problem posing and problem solving in mathematics education. They reviewed the coding and decoding activities experienced during the visit workshop, analyzing how the substitution codes they encountered exhibited distinct properties. The initial code, the Carbonaro Code, is a symmetrical monoalphabetic substitution code. It replaces letters in a message in a fixed pattern reflecting the phonetic characteristics of the sounds—for example, A with E and E with A, B with P and P with B, C with G and G with C, D with T and T with D, and so on. Consequently, for example, the word ‘BREAD’ encodes to ‘PLAET’, and, when re-encoded using the same encoding function, it decodes back to ‘BREAD’. In contrast, Ceasar’s Code, an asymmetrical monoalphabetic substitution code, shifts each letter to the one three positions further in the alphabet, and thus ‘BREAD’ becomes ‘EUHDG’. Decoding is possible by applying the reverse function, namely a backward shift of three positions in the alphabet.
This activity led to contemplation on inverse functions and biunivocal correspondences, especially noting that applying the Carbonaro Code twice yields the original word (BREAD → PLAET → BREAD), while Ceasar’s Code does not follow this pattern (BREAD → EUHDG → HXKGJ). Decoding messages encrypted with monoalphabetic substitution codes, without prior knowledge of the key, poses a fascinating problem. Teachers delved into basic cryptanalysis by scrutinizing letter frequencies in a message. For instance, in Italian the letter ‘E’ is the most frequent letter, leading to the deduction that in encrypted messages it is possible to assume that the letter that appears most often is indeed the equivalent of ‘E’. Moreover, since in Italian most words end with a vowel, one can assume that the final letters in the coded words are the equivalent of a vowel. These insights provide a foundation for a trial-and-error approach to decryption. Addressing these elements allowed for a deeper understanding of cryptanalysis challenges and the educational use of problems, precisely from the engagement that teachers experienced in facing not a simple exercise, but rather a challenging situation.
5.3. Swirl of Ideas
The ‘Swirls of Ideas’ workshop (‘Vortici di idee’, in Italian) takes place at the Museum of Ancient Art in Palazzo Madama. Drawing inspiration from the architectural splendor of this historic edifice, the workshop is a reflection of the building’s storied past. Palazzo Madama, a UNESCO World Heritage site situated in the heart of Turin, was the ancient eastern gate of the Roman settlement Julia Augusta Taurinorum. It served as a fortified house in the medieval period before becoming the residence of the Madama Reale in the early 17th century. The building received a majestic Baroque façade and monumental staircase from the architect Filippo Juvarra (1678–1736) in the 18th century, adorned with seashell and spiral motifs.
The spiral serves as a focal motif of the visit workshop. Participants are encouraged to seek out these curves in plane and space within the decorations and the numerous spiral staircases. Additionally, they have the opportunity to recreate these patterns using two custom-built mathematical machines: the spiralograph and the helicograph. As illustrated in Figure 2, these machines can be used to compose rotational and translational motions to trace out spirals on a plane or helices on a cylindrical surface (the reader can find more about ‘Swirls of Ideas’ in [8]).

Figure 2.
The mathematical machines used in ‘Swirl of Ideas: (a) spiralograph; (b) helicograph.
In the latter part of the session, the discussion centered on the construction of spirals as a composition of translations and rotations, along with an in-depth examination of the mathematics laboratory and the use of artifacts in mathematics education. Archimedes of Syracuse (3rd cent. BCE) was among the first to deal with spirals. In his treatise ‘On Spirals’, he characterizes this curve as the trajectory of a point moving on a line as it rotates. The mathematical machines used during the visit workshop enabled the teacher to investigate this feature firsthand. Further in-depth study provided an opportunity to discuss how such an artifact can be exploited didactically to delve into the mathematical properties it incorporates.
6. Data Analysis and Results

Table 1.
List of the categories.
For each category, we provide the corresponding code, the total occurrences observed in the 18 teachers’ essays, and the total number of documents containing each category. Only categories appearing in at least 2 essays are reported.
Below, we present annotated excerpts from the teachers’ essays, organized by categories. These examples were selected to represent each identified label as described in Section 4. This ensures that we include and briefly discuss the opinions of each teacher mentioned in this section. Teachers’ names have been anonymized using abbreviations, from T1 to T18, which precede the excerpts in parentheses. All of the excerpts have been translated into English by the authors.
6.1. Category C1: Engagement
Many teachers mentioned engagement in their essays. Specifically, this category appears in 11 of the 18 essays delivered, totaling 26 occurrences. This high frequency is not surprising, as engagement is a central principle in the design of the informal mathematics workshops. This suggests that the principle was effectively represented in the workshops, at least from the teachers’ perspective. Upon closer examination of the data, we can gain insights into how teachers perceive engagement within the proposed workshops.
Some teachers describe engagement as a holistic process that involves the student’s entire experience during their museum visit. For instance, T9 emphasizes the depth of this engagement and links it to emotions and feelings:
(T9) The engagement is not superficial but rather deep, requiring introspection. It stems from an inner reading prompt, such as the invitation to give a name, to express with words and signs their own emotions and feelings at the entrance of Palazzo Madama, or to re-experience the state of mind of those who fought at their own risk for freedom at the Museum of Risorgimento.
T10 acknowledges that this characteristic pertains to “the way of doing mathematics” that characterizes the designed workshops. They emphasize this as a difference between the experience of informal mathematics education workshops in museums and typical classroom teaching:
(T10) This way of doing mathematics is not just about the head, but engages the whole person. At the Museum of Risorgimento, one is asked to start by translating not just any word into code, but each person must translate their own name. One feels named, important, unique, from the very beginning. And then you go on, observing, feeling, moving, touching… all the senses, the whole person is engaged in doing mathematics. This aspect is so different from the math that is usually offered in the classroom!
When the essays delve into specifics about mathematics, engagement is often contrasted with fear and anxiety, highlighting the range of emotions that mathematics can evoke in students:
(T8) I believe that many students feel fascination and fear for Mathematics. Here, we need to focus on fascination. Fear and anxiety are the enemy of reasoning and creativity. The two paths we have experienced carry fascination, strong individual and group engagement, creativity, delight in research and success, and leave little room for fear.
Some teachers link students’ engagement to the use of artifacts; for example:
(T4) The use of the machines and the mathematical decoding of their operation, in my opinion, engage students by tickling their wits and allow them to understand to the roots the underlying mathematical concept.
T4 highlights how the use of artifacts in the two labs can foster engagement, allowing students to immerse themselves in the proposed situation, and thereby gain a deeper understanding of the mathematical concepts explored.
In summary, teachers view engagement in museums as a holistic process that deeply involves students emotionally and intellectually with mathematics. Using artifacts may foster a deeper understanding. This contrasts with the fear often associated with the subject in traditional classrooms.
6.2. Category C2: The Experience of Beauty Expanding from the Museum to Mathematics
Out of the 18 essays, 12 essays teachers shared reflections on the experience of beauty, which can be encountered in museums and further extended to mathematics through participation in informal mathematics education workshops. Of the 22 total occurrences related to this category, we present some examples to explore different aspects.
Many teachers point out that museums can demonstrate to children that beauty is all around us and takes various forms, including mathematical ones. For example:
(T9) Truly appreciable is the idea of doing mathematics within such a beautiful artistic, architectural, historical and cultural setting. It is important for our children to experience beauty, to be almost stunned by it, to be able to recognize and appreciate it, developing the ability to see beauty in everything around them, even in mathematics.
In T9, there is a connection drawn between the aesthetic experience of art and the beauty found in mathematical thought.
Teachers also discuss the connection between mathematics and other subjects through the lens of beauty:
(T5) These activities at museums would show children, through visiting, discovering and playing, that we are surrounded by beauty and that it can take various forms, nuances and artistic modes that are closely related to history, geography, human needs, and also to mathematics.
Finally, teachers often associate the experience of beauty with the playful nature of the workshops, seeing it as a catalyst for exploration processes. For instance:
(T8) [In the workshops] Research and investigation requests are always carried out in the form of a game. A game that takes place in a unique setting of fascinating beauty. This allows the student to relax, to have fun: the necessary conditions for speculating, exploring, finding answers and solutions without fear or performance anxiety.
By framing the learning experience within a game set in a beautiful environment, T8 suggests that this approach can alleviate the stress often linked with school performance.
In summary, teachers believe that museums can show children how beauty is intertwined with all of life, including mathematics. They advocate for merging aesthetic experiences with playful, stress-free learning in a rich cultural environment.
6.3. Category C3: Mathematics as Part of Reality
With 21 occurrences in 10 different essays, this category explores the transformative potential of informal mathematics workshops to change the students’ view of mathematics. As can be seen from the following excerpts, the view of mathematics fostered by museum experiences is considered different from that often perceived in the classroom:
(T8) I chose to participate [in the training course] because I was attracted above all by the idea of being able to offer my students engaging experiences within two realities, a museum and Mathematics, which are often mistakenly or metaphorically experienced as something static, outdated, difficult to understand.
T8 values the integration of mathematics learning within a museum environment, challenging the preconception that both museums and mathematics are static and outdated. The idea is to animate mathematics by situating it within engaging contexts, which can potentially shift student perception of mathematics from being arduous and irrelevant to something lively and engaging.
(T16) Experimenting with new ways of learning has been and is, in my opinion, even more crucial for a discipline, such as mathematics, often referred to as ‘abstract, hostile and difficult to understand’ by our students. [...] Museum workshops provide an opportunity to show to our students how mathematics has always been part of our reality, thus making it less abstract and more real, being able to touch it with their hands.
The statement made by T16 underscores the relevance of innovation in teaching methods, especially for subjects like mathematics, which are often perceived negatively. Through informal mathematics education workshops, teachers have the opportunity to reshape the perception of mathematics from an abstract and elusive discipline to a more tangible one. Such hands-on experiences serve to demystify mathematics, showing students that it is not solely a collection of abstract concepts but a field with concrete applications and is embedded in the fabric of our daily reality.
(T11) Experimenting with a form of outdoor education: ‘doing mathematics not in school but outside’, and this outside is even more stimulating when represented by a cultural context rich in history and art that lends itself to being used as an environment for exploring aspects of mathematics in everyday life.
Starting from the concept of outdoor education, T11 underlines that situating mathematics within historical and cultural contexts vivifies mathematics, demonstrating its application in everyday settings. It adheres to the design principle of “Developing a vision of mathematics as cultural product” by linking mathematical understanding with cultural narratives. Consequently, it may enhance students’ engagement by offering experiential learning opportunities that are both intellectually stimulating and directly connected to the environment they interact with outside of the traditional classroom.
In summary, the view expressed is that mathematics, when encountered in a museum context, presents a dynamic and captivating experience. This disrupts the traditional misperception of mathematics as inherently difficult, instead showcasing its tangible presence in history and culture.
6.4. Category C4: Group Collaboration Fosters Inclusion and Creativity
This category, appearing 19 times across 12 essays, highlights the significance of group collaboration. Teachers discussed this significance in two contexts: reflecting on their own experience during the InformalMath program and considering the possible benefits for students in informal mathematics education workshops in museums. The analysis reveals that group activity fosters two key elements: inclusion and creativity.
T14 emphasizes the role of inclusion in her own experience within the InformalMath program:
(T14) I enjoyed the active collaboration between all course colleagues, none excluded, in solving problematic/enigmatic situations during the course of the workshop both in the morning and in the afternoon.
The collaborative dynamic described by T14 captures the core of group experimentation. By engaging all members in the process of problem solving, the workshop environment nurtures a sense of community and shared purpose.
(T3) I found inclusive the possibility of working in small groups, where everyone can contribute.
T3 comments on the power of small group dynamics in fostering an inclusive atmosphere, where each member feels valued. This inclusion is crucial for amplifying the variety of voices.
Inclusion ensures that diverse perspectives are considered, which can lead to more creative and effective solutions:
(T8) It is beautiful to link the mathematical activity with the need to create, to invent, even to make mistakes, and then to correct them together. All the proposed activities require creativity to find answers.
The relationship between mathematical engagement and the liberty for creative experimentation and error, as discussed by T8, is integral to nurturing creativity. Group experimentation within this context not only permits but encourages individuals to take risks and innovate.
In summary, group activities within the InformalMath program highlight the promotion of inclusion, ensuring all voices contribute, and creativity, encouraging innovation and problem solving through collective effort and the freedom to make and learn from mistakes.
6.5. Category C5: Experimenting a Non-Curricular Mathematical Content
This category, identified 18 times across 12 essays, pertains to the selection of spirals and cryptography as focal points for laboratory-based approaches in museum workshops. These topics are not included in the Italian school curriculum. Some teachers contrast them to “school mathematics”, such as T2:
(T2) The impression of movement connected to the figure of the spiral really struck me and I find it contrasts with the idea of geometry we have at school, which is always so ‘static’ and unchanging. The spiral is more stimulating: it gives the idea of becoming, of growth, and this connects us to living organisms, to the spectacle that nature offers us by reproducing this motif in the most varied ways.
T2 describes the spiral as a vibrant and tangible representation of geometry, diverging from the static concepts often taught in school. This approach resonates with the principle of P3 “Developing a vision of mathematics as cultural product”, linking geometric shapes to growth patterns in nature, art, and history. This link offers a broader context that is often missing in school curricula. It aligns with the overarching aim of this project: to engage students by portraying mathematics as a dynamic discipline that mirrors the patterns of life, thereby making the content not only challenging but also pertinent to their everyday experiences.
Considering another excerpt from T3, we see that she addresses the stimulating challenges provided by topics that are not immediately identified as part of mathematics:
(T3) The most challenging part in my opinion is the decryption of the cryptography, which requires no prerequisites and brings logic and intuition into play. Basically, you do math without realizing it.
T3 mentions how the process of decrypting, with its reliance on logic and intuition, incorporates the design principle aimed at enhancing student engagement by making mathematics both challenging and relevant to everyday life. By engaging in cryptography, students might practice mathematics through a form of puzzle solving distinct from traditional classroom mathematics. This approach boosts engagement through real-world applications and critical thinking.
In the following excerpt, T3 points out the omnipresence of Archimedes’ spiral in daily life, evident in architecture, art, and nature, despite its absence in primary school curricula:
(T3) The subject of Archimedes’ spiral is fascinating. It is not reflected in what we do in the classroom, at least in primary school, but it is reflected in what surrounds us in everyday life, as an architectural, decorative, natural element, etc.
This notion reinforces the principle of P3 “Developing a vision of mathematics as cultural product” by linking a mathematical idea to its numerous real-world manifestations.
In summary, each excerpt presents ways in which mathematical concepts can be woven into cultural and everyday contexts, rendering the learning experience both challenging and engaging. By acknowledging mathematics as a cultural product and focusing on strategies that might increase student engagement, these approaches emphasize the importance of connecting classroom learning with the outside world, thereby enhancing students’ ability to relate to and understand mathematical content.
6.6. Category C6: Mathematics for the Benefit of History and Art
When designing the InformalMath program, one of our underlying assumptions was that the art and history encapsulated within museums could serve as vehicles to enhance the learning of mathematics. What emerges from the C3 category described above supports this working hypothesis. Yet, the reflections from the teachers indicate an additional, emergent synergy between mathematics and museums. Notably, the concept of the mathematical workshop as a medium for enhancing the museum visit experience, and by extension, the appreciation of art itself, has come to light. This concept suggests that IME activities can invigorate the learning environment, making the exploration of art and history more accessible and enjoyable. An example is as follows:
(T18) I discovered how a visit to the museum, which could sometimes be boring, especially for children, in this way can become engaging, playful and fun; it can definitely become an opportunity for learning and also for discovering and appreciating art.
In the following excerpt, T8 illustrates the role of mathematics as an enriching tool:
(T8) In both cases, at the Risorgimento Museum and at Palazzo Madama, Mathematics entered on tiptoe, almost as a service, however indispensable, to History, Art, Humanity, and Beauty. And it did not enter on its own, as a subject in itself, but in synergy with the context and with other disciplines. I believe it is very important that a discipline does not impose itself with impetuosity or technicality but enters naturally into the life of the student, of all students, through accessible and successful experiences.
Mathematics, in this context, is repositioned—not as the focal point but rather as an integrative facilitator within the learning experience. This approach aligns with the concept that mathematics can serve history and art by providing a framework to understand patterns, symmetry, and structure. Consequently, it enhances the engagement with a comprehension of cultural and historical artifacts, deepening the overall narrative and experiential journey.
T3 identifies the role of mathematics in deeper engagement:
(T3) I find mathematics to be a positive pretext to make children appreciate the beauty of Palazzo Madama and to lead them to a less superficial observation of artistic events.
In this case scenario, mathematics becomes a tool for unveiling deeper aspects of art, offering a unique perspective that might be overlooked during a superficial examination.
While some teachers emphasize the contribution of mathematics in examining or appreciating the artistic facets of museums, others highlight the added value brought into museum visits by the laboratorial nature of the workshops. For instance, T9 emphasizes how blending mathematics with museum experiences through laboratory activities can transform students’ perception of historical museums from being uninteresting to dynamic:
(T9) This kind of experience [...] leads students to perceive the reality of the historical museum differently. There is often the feeling that it is a boring and unattractive place to visit. By including activities of this kind, attention is captured by the mathematics, and thus the museum is transformed into a ‘living’ and interesting place, allowing students to assimilate even the most complicated and boring information related to Italian history.
Viewed in this way, mathematics serves as a bridge connecting students to history and art, capturing their interest, and fostering a lively environment where intricate historical details become more accessible.
The mathematics laboratory experience within the museum context can even suggest new ways of exploring art itself, as in the following excerpt:
(T6) Perhaps we really should start from here, from the idea that visiting a collection of works of art or objects that have historical value should become a natural gesture. Stopping and then perhaps going back to look at something more carefully, rather than going from one room to another as in the performance of a ritual that allows no choices or breaks. As in mathematics: arriving at the solution to a problem by traveling along intricate paths, being guided by what you gradually discover.
T6 draws an analogy between the liberty of exploring art and historical artifacts and the exploratory process of mathematical problem solving. The experience of solving mathematics problems through deep analysis of the various solution paths (“intricate paths”), guided by progressive results in the solving process, paves the way for a fresh approach to experiencing art. According to T6, this methodological approach should evolve into a “natural” way of interacting with artistic work.
To summarize, the discussed excerpts collectively converge on the idea that mathematics should not solely be an end in itself, but also a means to enrich the experience and deepen the understanding and appreciation of history and art. Mathematics introduces an additional layer to the engagement with cultural products. Teachers believe that this approach can allow students to engage with historical and artistic concepts in a manner that is both educational and captivating. The idea is not for mathematics to overshadow art and history but to serve as a complementary tool that enriches and enhances the learning experience.
6.7. Category C7: Bewilderment as a Tool for Active Engagement
This category, similar to C5, intersects with two foundational design principles: the museum as a space for inducing bewilderment in both teachers and students and the crucial role of student engagement in learning. C7 has been identified six times in five essays.
T7 captures the essence of aesthetic bewilderment as an educational tool:
(T7) The artistic beauty of Palazzo Madama confronts students with an aesthetic bewilderment that sets in motion the exploration of the surrounding space and the activation of cognitive resources.
Confronted with the artistic beauty of Palazzo Madama, students are invited to navigate and connect with the space in a manner that stimulates their cognitive faculties. This aligns with the design principle of the “History and art museums as spaces for bewilderment,” suggesting that the initial disorientation or bewilderment can serve as a powerful catalyst for learning. It showcases how such experiences can deepen engagement, compelling students to orient themselves within, and make sense of, the new and unexpected.
In T14’s excerpt, the experience of bewilderment is triggered by the “Carbonaro Code” encryption activity:
(T14) The video we started with, which involved encrypting our name on the basis of the ‘carbonaro code’, had left me bewildered. It was an experience that then actively engaged me.
The initial sense of bewilderment is acknowledged as a gateway to active engagement, affirming the idea that bewilderment can indeed be a precursor to engagement. The excerpt exemplifies how an initial challenge or confusion can pique someone’s curiosity and motivation to comprehend, leading to a more immersive and participative learning experience.
T16 emphasizes the dual perspective of experiencing the museum as both a student and a teacher, noting the amazement that accompanies new educational activities:
(T16) The two experiences I took part in, one at the Museo del Risorgimento and the other at Palazzo Madama, were interesting and engaging, but above all instructive: they allowed me to observe and experience the workshop activities with the eyes first of a student, then of a teacher, allowing me to fully experience the amazement that should be inherent in any way of proposing new educational activities.
Indeed, this sense of amazement or bewilderment is a fundamental element in the learning process, as per the design principles mentioned. The excerpt suggests that by embracing the unfamiliar, both teachers and students can engage more deeply with the material, cultivating a shared experience of discovery that is both educational and engaging.
The narrative from T17, which traces the shift from initial bewilderment to active engagement, exemplifies the transformative process that the design principles seek to cultivate:
(T17) On the first day, at the Museo del Risorgimento, I admit that I felt bewildered, a little bored perhaps: it may be that I had never had such an experience, but the initial activity did not excite me. Perhaps my expectations were different. Then, as the day progressed and we engaged in finding solutions to the questions asked, I felt engaged, and I realized that I was even enjoying myself.
The initial boredom and disorientation faced at the Museo del Risorgimento dissolve into engagement and enjoyment as the activities unfold. This metamorphosis showcases the utility of bewilderment in sparking curiosity and fostering active engagement. It suggests that the museum, despite its potential to initially disorient, offers an opportunity to break away from expectations and enter a state of open-minded engagement that is both educational and enjoyable.
In essence, these excerpts suggest that bewilderment can be a transformative force within educational contexts. Rather than hindering learning, it can stimulate deeper involvement and exploration. The museum, a space that can initially disorient both teachers and students, provides a fertile ground to challenge preconceived notions and expectations. This process, rich in curiosity and problem solving, unfolds as a journey of discovery that is immersive and emotionally resonant.
6.8. Category C8: Documentation as a Necessary Tool for Students’ Active Role
This category encompasses two kinds of teacher feedback. The first type pertains to the lived experience, asked, particularly in the workshop at Palazzo Madama, where teachers were asked to document their search for spirals. The second type reflects on the possible classroom reprise of the activities carried out during the workshop. The excerpts we bring here as examples well describe these two facets. In the first two, references are made to the lived experience, while in the latter ones, the emphasis is placed on the opportunities for continuing the activities in the school context:
(T13) During the workshop, participants work like mathematical investigators: they document and collect clues, with a productive role and not just a re-productive or executive one.
In this excerpt, T13 conveys that documentation is a key component of active learning. By stepping into the role of mathematical investigators, students can engage in a process of exploration and discovery. They are not passively receiving information but actively gathering, documenting, and interpreting data. This transition from a re-productive role, where students might simply replicate information, to a productive one, in which they analyze and synthesize new knowledge, underscores the importance of documentation as a tool for active learning. This was the ultimate aim of the project, to enable students to take ownership of their learning process and foster a deeper understanding of the material.
The process of documenting the search for spiral elements and representing these findings in drawings is highlighted as a valuable component of the learning process:
(T3) I really appreciated the activity on Juvarra’s staircase to search for spiral elements and the representation of this with drawings: the possibility of documenting the process was offered, so as to have a starting point for a possible reworking activity at school.
The act of recording the quest for spiral patterns and depicting them through drawings not only marks the steps of students’ investigative journey but also serves as a valuable resource for later reflection and discussion in a more traditional classroom setting. By creating a physical record of their experiences, students are able to engage more profoundly with the content, connecting the museum’s interactive environment to ongoing educational discourse. This documentation is key to fostering enduring engagement with the subject matter, ensuring a seamless and active learning continuum.
T11 suggests equipping students with the means to document their findings during a museum visit as a way to enhance their role from passive observers to active participants:
(T11) In a hypothetical field trip to the museum in search of mathematical aspects with my students, I would like to make sure that they are equipped ad hoc to ‘document’ the path they have taken and what they observe with their ‘new gaze’, like real investigators who pick up elements and record them.
Encouraged to adopt a “new gaze” for documenting their experiences, students learn to interact with their surroundings in a critical and purposeful manner. This practice does more than just enhance their learning; it also empowers them as contributors to the knowledge-gathering process, reinforcing the critical role of documentation in fostering an active role in education.
Moreover, T11 discusses the need for follow-up work in the classroom to synthesize and reflect on the museum experience:
(T11) I believe there is a need for a follow-up work in classroom ex-post, in which conclusions are drawn from the experience carried out, and possibly a final (collective or personal) check-up, which could be declined in various ways (group report, creation of a leaflet to invite other class groups to carry out the experience, a drawing, ….).
The extension of learning through various forms of documentation, such as reports, leaflets, or drawings, emphasizes the significance of processing and presenting the knowledge acquired. This approach ensures that the learning experience transcends the temporal boundaries of the museum visit, becoming part of a comprehensive educational journey. This form of documentation serves also as a tool for both personal and collective assessment of the experience, thereby reinforcing the student’s engaged and participatory role in their own learning process.
In conclusion, these excerpts collectively advocate for the use of documentation as a crucial tool in transforming the student experience from a passive intake of information to an active, exploratory, and engaging quest for knowledge. Documentation not only serves as a record of learning but also as a means for students to process and express their understanding in creative and individual ways. Furthermore, this focus on documentation underlines the need to bridge experiences inside and outside the school environment. By creating records of their encounters with mathematics in environments such as museums, students can carry the spark of discovery back into the classroom, allowing for a seamless integration of real-world experiences with formal education. This continuity is essential for fostering a holistic educational experience where learning transcends the confines of the classroom to become a continuous, interconnected process that resonates with students in various spheres of their lives.
7. Discussion and Conclusions
In this paper, we presented a research study concerning the implementation of the first phase of the teacher education program called InformalMath, which aims to integrate mathematics education into non-scientific museums, such as art and history museums. Initially, we established the groundwork for the research by exploring the concept of informal mathematics education (IME) and highlighting the necessity for innovative teacher training programs in non-scientific museum settings. Subsequently, we investigated the perspectives of teachers, focusing specifically on (i) the opportunities perceived by participating teachers in engaging with informal mathematics education activities within museums, and (ii) the critical issues that participating teachers believe need to be addressed in informal mathematics education activities within museums.
The first question seeks to understand the potential benefits or advantages that teachers associate with utilizing museum settings for mathematics education. The data analysis, conducted using the qualitative content analysis method, revealed eight categories, which were discussed and exemplified in the preceding section.
As expected, six categories (C1, C2, C4, C5, C6, and C7) are specific to the museum context. More precisely, they are all specific to the informal mathematics workshop experience in museums, which was shaped by the specific features of the mathematical laboratory methodology. In other words, as T6 described in category C6, encountering mathematics in a museum leads to a change in teachers not solely due to the experience but rather through the laboratory approach to mathematics The mathematics laboratory methodology is underpinned by a rigorous epistemological analysis of what it means to engage with mathematics and aims to involve students in genuine mathematical processes, such as formulating hypotheses, testing them, and drawing inferences and deductions. From our perspective, the distinction between simply encountering mathematics in a museum and actively engaging in the practice of “doing mathematics” within it (for example, through appropriately designed workshops) is what differentiates between an experience of “mathematics dissemination” and “mathematics education”.
However, two categories, C3 and C8, are not specifically related to the museum site; they are universal. These categories pertain to specific methodological choices made by teachers that can also be adopted in mathematical laboratory activities within school classrooms. These choices represent what we have previously referred to as “the double continuity” between school and out-of-school mathematics activities in IME [30]. Double continuity refers to the continuity of both content and methodology operated in the integration of a visit workshop within a broader classroom program. This double continuity is intended to prevent participating students from perceiving the out-of-school activity as disconnected from what concerns their own learning in mathematics.
Overall, the results of the data analysis validate the design framework of Phase 1. From the perspective of the training program, these results enable us to progress to Phase 2 with an awareness of the participating teachers’ point of view on the main principles of the teacher education program, which we believe is essential for advancing the design of new informal mathematics education workshops. Indeed, within the essays, we identified the three design principles, P1–P3, refined and redefined through the teachers’ experiences and reflections. Specifically, upon comparing the emerged categories with the theoretical design principles of informal mathematics workshops, categories C2 and C7 can be linked to P1: the use of history and art museums as venues for creating a sense of wonderment; categories C1, C4, and C9 align with P2: the active involvement of students in laboratory activities; and categories C3 and C6 relate to P3: fostering a vision of mathematics as a cultural product.
Within the aims of this project, we emphasize that the concept of bewilderment is addressed in relation to both mathematics itself and the teaching and learning of mathematics. This aligns with the concept of dépaysement as expressed by Barbin. According to Barbin [22], integrating the history of mathematics into teacher education enhances teaching approaches, emphasizing the complexity, diversity, and cultural aspects of mathematics, thereby fostering curiosity and deep understanding in learners. Our data appear to support the notion that a certain level of complexity (albeit different from that driven by the history of mathematics) can also be found when utilizing informal mathematics for teacher education purposes.
Additionally, two categories, C5 and C7, intertwine more than one principle: C5 relates to both Principle P2 and Principle P3, while C7 intertwines Principles P1 and P2. A graphical representation of these relationships can be summarized in Figure 3.
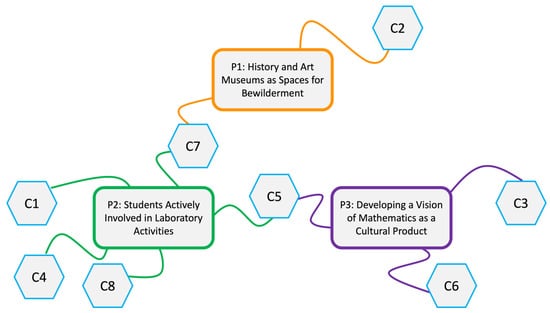
Figure 3.
Outline of the relationship of the identified categories with the workshop’s design principles.
Furthermore, a deeper analysis of the results reveals a greater richness within the teachers’ essays. In addition to reworking the three previously identified design principles, teachers have identified two new themes. The first theme, included in category C6 (mathematics for the benefit of history and art), highlights the role of mathematics workshops in enhancing museum visits and, by extension, the appreciation of art and history. The second theme emphasizes the dual function of documentation: as a record of learning, embodying the IME-3 aspect delineated in [10], and as a medium for connecting experiences within and beyond the school environment. From a research perspective, these new themes expand our understanding of the opportunities presented by designing informal mathematics education activities within the context of art and history museums. They will inform the development of future teacher education programs with components focused on informal mathematics.
Specifically, category C6 offers a fresh perspective on the relationship between museums and mathematics education. Initially, we, as educators, utilized museums as a setting for mathematics teacher education processes, hypothesizing that the experience of bewilderment in the museum could catalyze a reevaluation of mathematics and mathematics education, as evidenced by category C7. However, teachers also suggest another dimension in the relationship between museums and mathematics, one in which mathematics serves humanity through its artistic expression and historical development.
This perspective prompts reflection on the risks inherent in viewing a multifaceted reality, rich in social, cultural, and historical connotations, solely as a context for conducting mathematical activities. There is a risk of approaching this reality with a cultural colonialist mindset, entering a museum only with a mathematician’s eye, and interpreting everything only in mathematical terms. We think that such a risk can be lowered by engaging in genuine dialogue with other agents, like, for instance, museum experts.
On the teacher education aspect of the project, categories C6 and C8 can be interpreted in terms of “emerging learning”, a type of learning associated with informal mathematics education at the student level [31]. In essence, these results demonstrate that the InformalMath program exhibits characteristics of informal learning not only at the student level but also at a meta-level, specifically within teacher education. From a practical standpoint, this analysis has enabled us as teacher educators to consider the new categories when refining the design of Phases 2 and 3 of InformalMath.
The second research question aimed to pinpoint and address any challenges or concerns that teachers identified as significant barriers to effective mathematics education in museum contexts. We note that the few critical issues that surfaced from the data were consistently framed by teachers as challenges, accompanied by suggestions for transforming them into opportunities. Consequently, we were unable to gather sufficient data to discuss these issues except in these terms, which were integrated into the discussion of RQ1. We recognize that this limitation could be attributed not only to the teachers’ eagerness to engage in the later stages of the training program but also to the rapport that they developed with the authors, who served in the dual role of trainer and researcher.
As a final note, we offer a methodological reflection. To some extent, the research associated with the InformalMath teacher education program follows the paradigm of design-based research [32], wherein the design is rooted in chosen principles and the results of each phase inform the design of subsequent phases. However, given the innovative nature of the program, our research focus is essentially exploratory and may only be partly defined at the outset or parceled into a series of focused research questions. While we acknowledge the importance of clearly outlining the research focus and expressing it through specific research questions for communication purposes, we believe it is crucial—particularly in new domains of mathematics education—to move away from positivist methodologies that dictate the framing of every aspect of research within hypotheses and predetermined research focuses before empirical research is conducted. Instead, we advocate for a more open approach to research implementation. Building upon theoretical principles, we encourage openness to emerging (even unexpected) results, focus areas, and methodologies. We recognize the importance of fostering a dialectical relationship between theory and practice within the research process. The research study presented in this article reflects this tension between structured design-based research and open exploration.
Author Contributions
Conceptualization, R.C. and C.S.; methodology, R.C. and C.S.; validation, R.C. and C.S.; formal analysis, R.C. and C.S.; writing—original draft preparation, R.C. and C.S.; writing—review and editing, R.C. and C.S.; supervision, R.C. and C.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
This research was conducted and the resulting data were stored in accordance with international and local legislation, as well as institutional requirements, including the Declaration of Helsinki and the GDPR. In accordance with these requirements, the explicit approval of an ethics commission was not required for our research.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Data are unavailable due to privacy restrictions.
Acknowledgments
We would like to thank the teachers participating in this study for their enthusiasm and generosity in their collaboration.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Rejali, A.; Taylor, P.; Tabesh, Y.; Germoni, J.; Rafiepour, A. Mathematics Houses and Their Impact on Mathematics Education. In Proceedings of the 13th International Congress on Mathematical Education, Hamburg, Germany, 24–31 July 2016; Kaiser, G., Ed.; ICME-13 Monographs. Springer: Cham, Switzerland, 2017; pp. 679–680. [Google Scholar] [CrossRef]
- Phillips, M.; Finkelstein, D.; Wever-Frerichs, S. School site to museum floor: How informal science institutions work with schools. Int. J. Sci. Educ. 2007, 29, 1489–1507. [Google Scholar] [CrossRef]
- de Freitas, E.; Bentley, S.J. Material Encounters with Mathematics: The Case for Museum Based Cross-Curricular Integration. Int. J. Educ. Res. 2012, 55, 36–47. [Google Scholar] [CrossRef]
- Kelton, M.L. Mathematics Learning Pathways on a School Fieldtrip: Interactional Practices Linking School and Museum Activity. Visit. Stud. 2021, 24, 220–242. [Google Scholar] [CrossRef]
- El Bedewi, S.; Lavicza, Z.; Lyublinskaya, I. STEAM practices connecting mathematics, arts, architecture, culture and history in a non-formal learning environment of a museum. J. Math. Arts 2024, 1–34. [Google Scholar] [CrossRef]
- Behrendt, M.; Franklin, T. A review of research on school field trips and their value in education. Int. J. Environ. Sci. Educ. 2014, 9, 235–245. [Google Scholar] [CrossRef]
- Kayhan Altay, M.; Özdemir, E.Y. The use of museum resources in mathematics education: A study with preservice middle-school mathematics teachers. J. Educ. Teach. 2022, 49, 616–629. [Google Scholar] [CrossRef]
- Casi, R.; Leo, V.; Pizzarelli, C.; Sabena, C. La matematica nei musei con il progetto Next-Land. In Atti dell’Associazione Subalpina Mathesis 2020–22; Luciano, E., Oggero, M., Sabena, C., Eds.; L’Artistica Editrice: Savigliano, Italy, 2022; pp. 105–116. [Google Scholar]
- Nunes, T.; Schliemann, A.; Carraher, D. Street Mathematics and School Mathematics; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Casi, R.; Sabena, C. Informal mathematics experiences in museums: What potential for teacher professional development? In Proceedings of the Twelfth Congress of European Research in Mathematics Education (CERME12), Bolzano, Italy, 2–5 February 2022; Hodgen, J., Geraniou, E., Bolondi, G., Ferretti, F., Eds.; ERME/Free University of Bolzano-Bozen: Bolzano-Bozen, Italy, 2022; pp. 3065–3066. [Google Scholar]
- Nemirovsky, R.; Kelton, M.L.; Civil, M. Toward a vibrant and socially significant informal mathematics education. In Compendium for Research in Mathematics Education; Cai, J., Ed.; National Council of Teachers of Mathematics: Reston, VA, USA, 2017; pp. 90–101. [Google Scholar]
- Jaworski, B. Tensions in teachers’ conceptualizations of mathematics and of teaching. In Learning Mathematics: From Hierarchies to Networks; Burton, L., Ed.; Falmer Press: London, UK, 1999; pp. 153–172. [Google Scholar]
- Casi, R.; Sabena, C. Informal Mathematics in teacher’s education. The teachers’ voice. In Proceedings of the Thirteenth Congress of the European Society for Research in Mathematics Education (CERME13), Budapest, Hungary, 10–14 July 2023; Drijvers, P., Csapodi, C., Palmér, H., Gosztonyi, K., Kónya, E., Eds.; ERME/Alfréd Rényi Institute of Mathematics: Budapest, Hungary, 2023; pp. 3353–3360. [Google Scholar]
- Jaworski, B. Theory and practice in mathematics teaching development: Critical inquiry as a mode of learning in teaching. J. Math. Teach. Educ. 2006, 9, 187–211. [Google Scholar] [CrossRef]
- Schön, D.A. Educating the Reflective Practitioner: Toward a New Design for Teaching and Learning in the Professions; Jossey-Bass: Hoboken, NJ, USA, 1987. [Google Scholar]
- Sullivan, P.; Knott, L.; Yang, Y. The Relationships Between Task Design, Anticipated Pedagogies, and Student Learning. In Task Design In Mathematics Education: An ICMI Study 22, 1st ed.; Watson, A., Ohtani, M., Eds.; New ICMI Study Series; Springer: Cham, Switzerland, 2015; pp. 83–114. [Google Scholar] [CrossRef]
- Leung, A.Y.L.; Bolite-Frant, J. Designing Mathematics Tasks: The Role of Tools. In Task Design In Mathematics Education: An ICMI Study 22, 1st ed.; Watson, A., Ohtani, M., Eds.; New ICMI Study Series; Springer: Cham, Switzerland, 2015; pp. 191–225. [Google Scholar] [CrossRef]
- Collins, A.; Brown, J.S.; Newman, S.E. Cognitive apprenticeship: Teaching the crafts of reading, writing, and mathematics. In Knowing, Learning, and Instruction: Essays in Honor of Robert Glaser; Resnick, L.B., Ed.; Lawrence Erlbaum Associates, Inc.: Mahwah, NJ, USA, 1989; pp. 453–494. [Google Scholar]
- Mayring, P. Qualitative Content Analysis: Theoretical Background and Procedures. In Approaches to Qualitative Research in Mathematics Education; Bikner-Ahsbahs, A., Knipping, C., Presmeg, N., Eds.; Advances in Mathematics Education; Springer: Dordrecht, The Netherlands, 2015; pp. 365–380. [Google Scholar] [CrossRef]
- Farnè, R.; Bortolotti, A.; Terrrusi, M. Outdoor Education: Prospettive Teoriche e Buone Pratiche; Carocci Editore: Roma, Italy, 2018. [Google Scholar]
- Barbin, E. Histoire et enseignement des mathématiques: Pourquoi? Comment? Bull. AMQ 1997, 37, 20–25. [Google Scholar]
- Barbin, E. L’histoire des mathématiques dans la formation:une perspective historique (1975–2010). In Actes du Colloque EMF 2012. Enseignement des Mathématiques et Contrat Social: Enjeux et Défis Pour le 21e Siècle; Dorier, J.-L., Coutat, S., Eds.; Université de Genève: Geneve, Switzerland, 2012; pp. 546–554. [Google Scholar]
- Anichini, G.; Arzarello, F.; Ciarrapico, L.; Robutti, O. Matematica 2003. Attività Didattiche e Prove di Verifica per un Nuovo Curricolo di Matematica (Ciclo Secondario); Matteoni Stampatore: Lucca, Italy, 2004. [Google Scholar]
- Arzarello, F.; Robutti, O. Framing the embodied mind approach within a multimodal paradigm. In Handbook of International Research in Mathematics Education; English, L.D., Kirshner, D., Eds.; Routledge: New York, NY, USA, 2008; pp. 716–745. [Google Scholar] [CrossRef]
- Ministero dell’Istruzione dell’Università e Della Ricerca (MIUR). Indicazioni nazionali per il curricolo della scuola dell’infanzia e del primo ciclo d’istruzione. Ann. Pubblica Istr. 2012, 1, 1–88. [Google Scholar]
- Bartolini Bussi, M.G.; Mariotti, M.A. Semiotic Mediation in the Mathematics Classroom: Artefacts and Signs after a Vygotskian Perspective. In Handbook of International Research in Mathematics Education, 2nd ed.; English, L., Bartolini Bussi, M.G., Jones, G., Lesh, R., Tirosh, D., Eds.; Lawrence Erlbaum Associated Inc.: Mahwah, NJ, USA, 2008; pp. 746–783. [Google Scholar]
- Laursen, S.L.; Rasmussen, C. I on the prize: Inquiry approaches in undergraduate mathematics. Int. J. Res. Undergrad. Math. Educ. 2019, 5, 129–146. [Google Scholar] [CrossRef]
- Bishop, A.J. Mathematical Enculturation. A Cultural Perspective on Mathematics Education; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1988. [Google Scholar] [CrossRef]
- Barton, B. The Language of Mathematics: Telling Mathematical Tales; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
- Casi, R.; Sabena, C.; Borsero, M.; Pizzarelli, C. Circonferenze e spirali in un percorso di educazione matematica informale tra scuola e museo. DDM Ricerca Pratiche D’aula 2023, 14, 30–58. [Google Scholar] [CrossRef]
- Nemirovsky, R. Pedagogies of Emergent Learning. In Invited Lectures from the 13th International Congress on Mathematical Education; Kaiser, G., Ed.; ICME-13 Monographs; Springer: Cham, Switzerland, 2018; pp. 401–421. [Google Scholar] [CrossRef]
- DBRC—The Design Based Research Collective. Design-Based Research: An Emerging Paradigm for Educational Inquiry. Educ. Res. 2003, 32, 5–8. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).