Abstract
According to contemporary research, there exists an imbalance within the disciplines of Science, Technology, Engineering, and Mathematics (STEM), wherein certain subjects are lacking representation due to the neglect or omission of mathematical elements. The purpose of this study is to address this issue through the analysis of an established learning sequence that has been well-tested to promote mathematical skills. We adapted the selected biology-based learning sequence to foster mathematical problem solving and conducted it with a school class. The qualitative analysis of the recorded video footage of this adapted learning sequence revealed that the modified task effectively stimulated mathematical problem-solving skills. This successful adaptation demonstrates one approach through which mathematics can be strengthened and effectively utilized in STEM subjects.
1. Introduction
There are various perspectives on STEM education, with recent research focusing on an integrated approach [1,2]. This approach aims to establish connections and interactions between the four disciplines—science, technology, engineering, and mathematics—by integrating them into relevant contexts and applying the working methods of science, technology, engineering, and mathematics to real-world situations [3]. While publications involving all four disciplines are abundant [2], mathematics is often under-represented in student activities (e.g., [4,5]).
By neglecting the role of mathematics in STEM activities, we fail to address the challenge that many students face when applying mathematical knowledge and skills in scientific contexts. However, this requirement and obstacle are crucial in science education [6,7,8]. This is particularly significant because mathematical knowledge contributes to understanding complex scientific phenomena [9,10].
To counteract this, solely applying mathematics as a tool is not sufficient for acquiring mathematical knowledge and skills [11]. To work mathematically in a meaningful manner, various theoretical approaches have been proposed (e.g., [12,13]). However, when examining current teaching situations and teaching materials, it becomes evident that this goal has only been partially achieved. Mathematics continues to be underrepresented and lacks a focus on comprehension within the realm of STEM activities [4,5,14].
The issue at hand is not that mathematics is unnecessary for addressing STEM problems; rather, it is the lack of explicit consideration of mathematics or the complete omission of mathematical engagement [5,10]. The omission or trivializing simplification of mathematical activities is given if a mathematical model is presented without validation. This also occurs even if teachers explicitly consider mathematical activities, e.g., problem solving, but are unable to realize this and instead resort to superficial strategies and operational activities [15].
As a result, the potential for a holistic examination and integration of mathematics is left untapped [5,8]. This further underscores the challenges and obstacles that math teachers face in regards to integrating mathematics into STEM education, as the use of mathematics as a mere tool does not necessarily result in the acquisition of comprehensive mathematical knowledge and skills [16].
We aim to address this concern by presenting an alternative perspective alongside various theoretical approaches to strengthen the role of mathematics in STEM (e.g., [12,13]).
Instead of developing a new task, we utilize a well-tested and published learning activity from biology classrooms that focuses on enhancing metamodeling knowledge in biology [17]. Although the task does not explicitly refer to mathematical work, it provides an opportunity to promote mathematics, specifically mathematical problem solving. To expand this potential, we thoroughly analyzed the task and solution approaches and subsequently redesigned them with the goal of emphasizing mathematical work, particularly mathematical problem solving.
The purpose of this study is to demonstrate, using this specific example, how this potential can be meaningfully utilized. Through this approach, we showcase how even subtle modifications can enrich mathematical learning, foster mathematical problem solving, and alter perspectives on mathematics.
The objective of redesigning the biology learning unit is to promote mathematical problem solving, not only because it is crucial for mathematics but also because problem solving is an important interdisciplinary skill, particularly in STEM.
2. Theoretical Frameworks as the Basis for the Research Questions and Analysis
The revision is grounded in two theoretical frameworks. Firstly, it is based on current research on mathematical problem solving, which includes support strategies for problem solving. Second, it builds upon the original sequence: black box, specifically the Water Black Box utilized in the example, along with the specified task. Additionally, we introduce the Descriptive Phase Model of Problem Solving by Rott et al. [18] as the framework for evaluating the revision.
2.1. Problem Solving
Problem solving can be viewed as a multi-disciplinary challenge, with STEM offering a variety of complex real-world problems. In the field of mathematics, mathematical problems and problem solving are considered integral to the teaching and learning of mathematics [19,20]. Teaching mathematics through problem solving helps students develop increasingly interconnected and complex knowledge systems rather than isolated ideas and knowledge (e.g., [21,22,23]).
Before delving further into the theory of problem solving, we establish the definitions of problem and problem solving based on the literature used in this article. A problem refers to a task or question that does not have an obvious solution method, i.e., it cannot be solved through straightforward effort [19,24]. Problem solving is the cognitive process of dealing with a task or question without an apparent solution method [25]. In this process, the problem solver needs to refine, combine, and modify pre-existing knowledge [26]. If a direct solution path is available through prior knowledge, there is no longer a problem, so the designation of a problem depends on the solver [27].
2.1.1. Problem Solving Process
The problem-solving process can be described by an outer structure, i.e., the phases of the problem solving process, and an inner structure that refers to meta-cognitive processes [28]. Polya [29] proposes a normative phase model that structures problem solving in four phases: understanding the problem, devising a plan, carrying out the plan, and looking back. Schoenfeld [30] refined and renamed the phases of Pólya: reading, analysis, exploration, planning, implementation, and verification.
The first phase is reading the task, including the identification of the problem conditions. This is followed by the analysis, which involves attempting to understand the problem. These first two phases can be compared to Pólya’s first phase of “understanding the problem”. This also includes selecting specific perspectives and reformulating the problem, for example by simplifying it. The following three phases are related to Pólya’s second and third phases, devising a plan and carrying out the plan. Schoenfeld [30] distinguishes between exploration, planning, and implementation. Exploration is defined as a rather unstructured approach, while planning involves a more structured approach to the problem [30]. During exploration, students explore the problem space with the aim of finding relevant information. According to Schoenfeld [30], heuristics can be found in this phase. The final phase of the problem-solving process is verification, which is self-explanatory and is comparable to Pólya’s last phase “looking back” [18,30]. Although the phases of these two normative phase models build upon each other, they do not follow a linear sequence in the problem-solving process; instead, the problem solver shifts between phases, takes detours, and moves back and forth between the phases [18,31].
2.1.2. Aspects of Problem Solving
Schoenfeld [31] outlines five major aspects of cognition for problem solving based on existing literature, that persist in problem-solving research (e.g., [32]): “the knowledge base, problem solving strategies, monitoring and control, beliefs and affects, and practices” (p. 16).
The first aspect is the knowledge base, which encompasses not only the problem solvers’ prior knowledge but also their ability to access and apply this knowledge to address specific problem situations that require the application of the knowledge. The mathematics domain-specific prior knowledge significantly affects the success of solving the problem [33].
The second aspect refers to problem-solving strategies, which consist of general rules that serve as tools for approaching various non-routine problems [31,34]. Examples of heuristics include working forward, working backwards, using diagrams and/or models to describe or visualize the problem, organizing data and seeking patterns, and simplifying the problem [31].
The third aspect is monitoring and controlling, which, like problem-solving strategies, falls under the domain of metacognition. This involves observing and continuously reflecting on the problem-solving process, such as scrutinizing solution approaches, following up on promising approaches, and revisiting the initial question if the chosen approach does not seem to lead to the desired goal. This can result in shifts between the problem-solving phases. Schoenfeld [31] showed that more than half of the high school students in the study attempted to solve problems using their initial approach without questioning it, leading to unsolved problems if the approach was incorrect.
The fourth aspect encompasses beliefs and affects. Associating mathematics with certainty or quick solutions contradicts the nature of problem solving and can have negative impacts, such as a tendency to give up quickly [31].
The inquiry into how we educate students to become proficient problem solvers leads to the fifth aspect: mathematical practice and the promotion of problem solving.
2.1.3. Fostering (Mathematical) Problem Solving
Fostering problem solving is very complex and should incorporate the aforementioned aspects. In the following sections, we present different approaches to foster problem solving that have been employed in the redesign of the task and the learning environment.
- Learning problem solving through problem solving
- Reflecting on the problem-solving process
- Teaching problem-solving strategies (heuristics)
- Collaboration
One of the initial approaches traces back to Pólya, who emphasized learning problem solving through problem solving. This involves observing how problems are solved and independently solving problems oneself [29].
It is important to demonstrate the existence of various approaches and to adequately justify the steps taken and solutions derived [26]. Two main points must be considered: the role of the teacher and the nature of the tasks. According to Polya [29], if the teacher provides no assistance, the student may not make any progress. Conversely, excessive help may result in the student no longer needing to solve a problem, as the task is no longer a problem. Similar implications are drawn by Schoenfeld [31] when routine problems are given, as algorithmic solving does not involve problem solving, since a solution path or algorithm is readily available.
Studies support the connection between the nature of the task and the learning outcome in problem solving [32,35]. Cognitively demanding tasks have shown the greatest effects [26]. Conversely, focusing primarily on routine problems can have a negative impact on problem-solving abilities, as the solution method is obvious. For example, in chapters on exponential functions, students must use exponential functions to solve the problem. These tasks emphasize executing algorithmic calculations, which may create the perception that mathematics is simply a collection of facts and procedures centered around numbers and formulas [11]. Consequently, students fail to question or reconsider their problem-solving approach. This can lead to failure if their initial decision was incorrect and can foster debilitating beliefs about mathematics [31]. As a result, students may not critically evaluate their problem-solving approach but instead persist with it, even if it does not yield a solution. This inclination can hinder their ability to solve problems effectively [31].
However, it is possible to learn how to reflect on the problem-solving process, which gives rise to the second approach: metacognition [31]. Schoenfeld [31] prompts learners to reflect on their solution process through targeted questions, such as “What are you currently working on?” and “What goal are you trying to achieve with your current actions?”. This approach encourages learners to think about their problem-solving process and its contribution to finding a solution. Koichu et al. [36] also demonstrated this in their study. The inclusion of explicit prompts such as “Why is this one right?” and “Am I right?” resulted in an increased level of verification, akin to Pólya’s concept of looking back.
This leads to another approach that addresses metacognition: heuristics. Heuristics are an important aspect of problem solving, but simply teaching them does not enhance problem-solving abilities [31]. The impact of heuristics depends on their implementation and embedding [11,34]. This can be achieved, for example, by explicitly addressing them [37].
2.1.4. Analysis Tool—Descriptive Phase Model of the Problem-Solving Process
Models can serve as a tool for describing and analyzing problem-solving processes. Rott et al. [18] propose a descriptive model of problem solving, which is shown in Figure 1. This model considers the errors, detours, and cycles that occur in real collaborative problem solving. It offers the possibility of capturing the unique sequence of real problem-solving processes and allows for the comparison of different processes through accumulation. Furthermore, this model enables the differentiation between problem solving and routine processes [18].
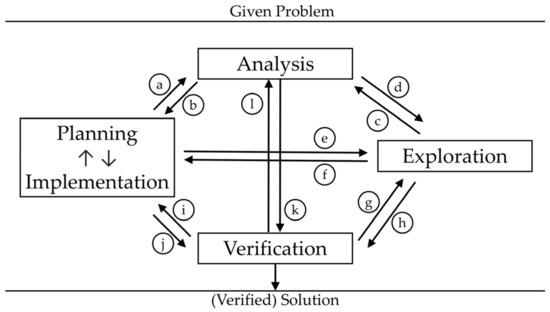
Figure 1.
Representation of the descriptive phase model of problem-solving processes according to Rott et al. [18] (p. 746).
The model is divided into three main categories: the given problem, the problem-solving process, and the (verified) solution. The first part of the model is the given problem, followed by the problem-solving process, which includes four sub-categories of problem-solving processes: analysis, exploration, planning and implementation, and verification. These phases are elaborated upon in the problem-solving processes.
Rott [38] operationalized these phases, providing the foundation for the coding in this study. The first sub-category is analysis, followed by exploration, and planning and implementation. Within the model, planning and implementation are differentiated and can be further categorized as implicit planning (planning) and execution (implementation). However, both are coded together in the model. The final subcategory of the model is verification. The last part of the model is the (verified) solution.
In addition to the phases, the model describes the transitions between the phases, represented by the arrows in Figure 1. The direction of the arrows indicates the directions of transitions from one phase to another. The letters within the circles represent the frequency of transitions between the categories.
In routine tasks, Rott et al. [18] identified a linear process. In contrast, problem tasks involved cyclical processes. Furthermore, exploration episodes were absent in routine tasks, as most students proceeded directly to planning and/or execution, justifying this approach by not needing to analyze the task.
We utilize this model as a categorization system to analyze students’ problem-solving processes and, consequently, evaluate the revision of the redesigned task: Water Black Box.
2.2. Black Box
The expression ‘black box’ is usually used for something unknown but without a precise definition [39,40,41]. The unknown can take various forms, such as a (mental) model, a physical object, a phenomenon, or a perspective. For the purpose of this article, the term ‘black box; will be used to refer to a (mental) object or phenomenon that possesses the following characteristics: “(a) being believed to be distinct, (b) having observable (and relatable) inputs and outputs, (c) being black (that is, opaque to the observer)” [42] (p. 1).
Using and working with a black box can have different objectives, such as structuring modeling processes [43]. Because of its opaqueness, the black box has a puzzle character that can be motivating for students (e.g., [17]). Furthermore, the question about the inside of a black box can pose a problem as there is no easily accessible procedure or strategy for opening the black box and thus answering the question.
2.2.1. The Water Black Box and Its Simulation
The Water Black Box utilized in the classroom activity is depicted in Figure 2a. It is a tangible enclosure that meets Glanville’s definition of a black box [42]. The so-called Water Black Box was initially designed by Ruebush et al. [44] and further developed by Koch et al. [45].
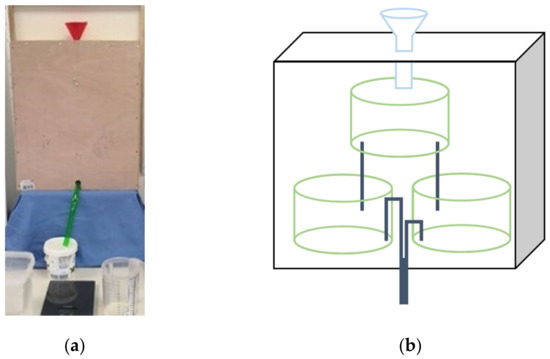
Figure 2.
(a) Photo of the physical Water Black Box; (b) schematic representation of the interior of the Water Black Box based on [17].
There is a funnel at the top of the box, through which the students pour water into the box in measured quantities (input). At the bottom of the box, there is a hose that leads to a measuring cylinder. The water flows through the box and into the measuring cylinder via the hose (output). Therefore, the input and output are observable and distinct. The students are unable to see the internal construction of the box or how the water flows within it, rendering it opaque to the observer.
Figure 2b provides a schematic representation of the interior of the black box. Inside the box, there are three water containers with different capacities and drainage systems. Once water is poured in, it flows directly into the upper container. This container has two holes at the bottom, which evenly distribute the water to the two containers below. Both containers are equipped with a siphon to drain the water, which is activated at different fill levels.
The left container empties when the water level exceeds 550 mL, while the right container empties when the water level exceeds 350 mL. When the siphon is triggered, the water flows through the hose into the measuring cylinder until the container is completely empty. If water is refilled in the meantime, it also flows into the measuring cylinder. Once the container is empty, the fill level required for activation must be reached again before water can be collected in the measuring cylinder.
During the learning unit, the students utilize a digital, dynamic replica of the model for experimentation to draw conclusions about the black box that can be applied to the real model. Therefore, the digital app can be considered as a simulation [46]. The user interface of the simulation is depicted in Figure 3. While any quantity can be poured into the actual black box, the students can only use the drag-and-drop method to fill the digital box with 100 mL, 200 mL, 300 mL, or 400 mL using the containers on the right side. It is not possible to simultaneously combine quantities, such as adding 100 mL and 400 mL of water at the same time. Students can repeat this process until the water runs out of the box. At this point, unlike in the real object, no water can be added. Only when the water has completely drained out can the students add water again.
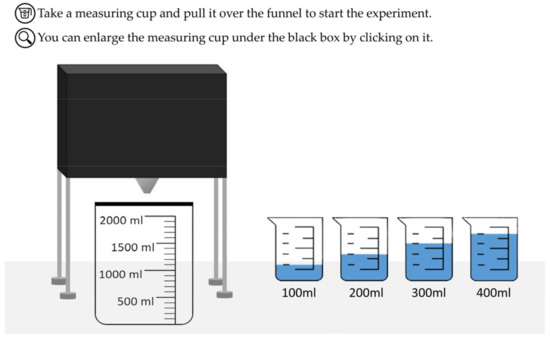
Figure 3.
Simulation of the Water Black Box (translated by the authors). The simulation is available at https://www.didaktik.mathematik.uni-wuerzburg.de/mathe-labor/hp2/tmp/Blackbox/top/blackbox.html (accessed on 25 April 2024).
2.2.2. STEM-Task—Description of the Original Biology Task
Krell and Hergert [17] conducted a study in which they investigated the opening of the black box in two different settings, once with university students and again with 11th and 12th-grade students. The task assigned to the university students was to develop a model of the inner structure of the box, using only the simulation.
In contrast, the students in the school classes worked in pairs and followed a set of instructions. The instructions, presented in Figure 4, consisted of six steps. The students were required to complete three specific tasks: (1) inputting 400 mL into the black box, (2) drawing a model of the inside of the black box, and (3) based on their model, formulating a hypothesis regarding the output if 400 mL were input again. The aim of these tasks was to guide the students towards a cyclical modeling process [17]. Lastly, the modeling process is reflected on.

Figure 4.
Assignment of the original task [45] (p. 99, translated by the authors).
3. Aims and Research Questions
There are various theoretical approaches to enhance the role of mathematics in STEM (e.g., [12,13]). This study aims to contribute to the inquiry as to how mathematics can be profitably strengthened in STEM activities through their redesign. By “profitably strengthened”, we mean that the objective is not solely focused on mathematics alone, but rather ensures that mathematical activities play a valuable role in the STEM task. This implies that students actively engage in mathematical thinking and problem solving within the STEM activity, rather than merely using mathematics as a tool for basic calculations. Building upon the theoretical foundation, we present an illustrative approach that demonstrates how a STEM task, which does not explicitly address mathematics, can be redesigned to promote mathematical problem solving and, consequently, mathematics itself. In this paper, we address the following research question based on the scientific task, Water Black Box: To what extent can the science (biology) activity, Water Black Box, be profitably transferred to a mathematical problem-solving task?
We answer this question by means of an exemplary redesign process and an evaluation of the redesigned task. To assess whether this revision results in a mathematical problem-solving task, we address the following two sub-questions:
- What structures of students’ problem solving are identified in the (redesigned) task?
- What sub-processes, such as routine or non-routine, of problem-solving are realized in working on the (redesigned) task?
4. Research Design
The specific improvement goal of the redesign process was to enhance the mathematical aspects of the Water Black Box activity. To accomplish this, the activity was analyzed from a mathematical perspective and potential mathematical opportunities were identified. The task was then redesigned with minimal changes, considering theoretical aspects of mathematical problem solving. The authors iteratively specified the task(s) and support cards. A pre-pilot of the learning unit was conducted with five pre-service teachers, four of them working in groups of two and one working independently. Based on observations and feedback from the pre-service teachers, improvements were made to the tasks. The improved tasks were then piloted during an enrichment course, which is a regular school event that caters to interested and gifted students in a specific subject, in this case mathematics. Following the implementation, the tasks and support cards were refined based on observations and feedback collected through semi-structured interviews.
The main objective of the study is to assess the extent to which the redesigned science (biology) activity, Water Black Box, can be effectively applied to mathematical problem solving. To address this objective, the redesigned task was carried out with a tenth-grade class and the implementation was analyzed through qualitative analysis using the theoretical categories of the descriptive phase model of problem-solving processes developed by Rott et al. [18].
4.1. Redesigning the Water Black Box Activity
In the original task, students are initially asked to develop a model without first understanding the problem and the (functional) relationships between input and output. To solve this task, several mathematical skills are required. The students must identify and process mathematical information to recognize, for example, that the black box dispenses water when more than 800 mL have been filled into it. The specification that 400 mL should always be added in the original task reduces the possible quantities generated, thus reducing the requirements in the documentation and analysis. On the other hand, certain input and output properties cannot be identified. For example, the correlation between input and output, that half the amount of water is always dispensed when the black box is triggered for the first time, is difficult to identify due to the specified addition of 400 ml at a time.
In the original task, students are instructed to follow a strict cyclical process. This contradicts the non-cyclical process of problem solving and mathematical modeling. In mathematical modeling, the cyclical process is seen as idealized. On the one hand, students are provided with an approach to solve the problem. On the other hand, they are expected to immediately execute a problem-solving method without analyzing the problem first. Schoenfeld [31] highlights this approach as a hindrance to problem solving.
In the redesigned task, the overall objective for the students is to determine how much water would flow into the measuring cylinder in the real Water Black Box if 900 mL of water were poured into the funnel in one step. This task represents a problem that can be solved in various ways. As there is no 900 mL vessel in the simulation, the amount of water cannot be explicitly determined through the simulation.
We provided the students with assistance in the form of support cards to enable them to work as independently as possible. In the preparation of the support, we structured the solution process according to Pólya’s four phases of problem solving. We then incorporated this structure into developed support cards that include heuristics, structuring questions, and reflective questions. These cards contain more detailed explanations of the problem on the one hand, and questions and tasks that support and reflect the problem-solving process on the other hand, such as:
- Look for regularities in the properties of the water box!
- What is the minimum amount of water that must be put into the empty box for water to flow out again?
- Does the partition of the water quantity influence how much water is in the measuring cylinder at the end?
- Check all the series of measurements!
In the pre-pilot, the university students exclusively solved the problem by analyzing patterns and regularities of the outer properties of the black box. They then drew conclusions regarding the desired output for a given input. As our main goal was to adapt the task to promote additional mathematical problem solving, it was imperative to adapt the task in such a way that students need to create a model of the internal structure of the black box as they progressed through the task.
To this end, the task was divided into two parts: analysis of the outer and the inner structure of the black box. The tasks structure the problem-solving process and prompt students to engage in reflecting the process. Specifically, students are asked to provide justifications for their solutions and to verify their solutions. The tasks are shown in Table 1. The first task serves as an introductory exercise to acquaint students with the simulation of the Water Black Box, while also urging them to analyze patterns and regularities of the outer properties of the black box. At the end of the first task, the students verify their assumptions using the replica Water Black Box. In the second task, the students must create a model for the inside of the black box.

Table 1.
Translated tasks of the Black Box Activity.
To solve the first task, it is not necessary to find the solution for the first task using a model of the internal structure of the black box. Since a maximum of 400 mL can be added at once, it remains unclear what result can be expected for other quantities, such as 246 mL or, in the present scenario, 900 mL. Although it is possible to combine the four different quantities to obtain a total of 900 mL, the resulting output varies depending on the specific combination due to the internal structure of the box (Table 2).

Table 2.
Comparison of inputs and resulting outputs with a total addition of 900 mL in two different splits.
The distribution and order of the input water quantity have an impact on the resulting output. This phenomenon can be explained by the fact that the container only produces an output when the input water quantity reaches a minimum threshold of 800 mL.
This implies that the addition of 900 mL can be simulated by first adding any quantity of water, distributed in any manner, if it is less than 800 mL. In this case, no output occurs. Subsequently, the remaining amount needed to reach a total of 900 mL is added all at once to the Water Black Box. This results in an output as the threshold of 800 mL is surpassed. In the simulation, only 100 mL, 200 mL, 300 mL, and 400 mL are available, allowing for combinations such as 500 mL/400 mL, 600 mL/300 mL, and 700 mL/200 mL. The solution is an output of 450 mL. Students can verify their result using the replica of the black box.
An alternative approach is to establish the connection between the input and the output. Up to a water addition of less than 1200 mL, half of the input is outputted. Therefore, when 900 mL of water are added, 450 mL must be dispensed.
To ascertain potential challenges in developing the model of the internal structure of the Water Black Box during the pre-piloting phase, we explicitly instructed the students to construct a model of the interior after determining the water output for 900 mL. In this process, the participants lacked guidance on structuring during the creation of the model. It became evident in this step that the participants lacked guidance on how to structure the model during its creation. As a result, participants primarily drew objects aimlessly, paying less attention to the previously identified behavior of the black box.
To address this, the work assignment was supplemented with an intermediate step (task 2.1). The students were first asked to create a list of possible components of the black box (e.g., tube, container with a hole, etc.). In this context, it was not necessary for the actual use of an element to be realistic, as the list served as a collection of ideas to facilitate model creation in the next task. This step serves as a prompt for exploration.
In task 2.2, students created a sketch model of the inner structure of the black box, using their results from the previous tasks. The prompt to use the previously obtained results was used to identify objects that, e.g., collect the water or halve the amount of input.
Additionally, we included a third sub-task aimed at formulating and testing hypotheses, as well as mathematizing the flow of input based on the model. For example, this could be achieved by using a term to calculate the output quantity of water. In task 2.3, students were asked to verify their solution by predicting the amount of water output three times using their model of the inner structure and comparing the results with the simulation.
If their hypothesis was incorrect, students were instructed to check the assumptions in their model and make improvements. Afterwards, they could compare their model with the actual set-up using the real black box. Formulating and testing hypotheses and thereby verifying or improving the created model was explicitly required in Task 2.3.
The improved task was piloted with nine students in an enrichment course. The implementation involved eight boys and one girl, with two male students from grade 9 and the remaining participants from grade 8. The nine participants were divided into three groups, each consisting of three students. Group one consisted of two ninth graders and one eighth grader. Group two and three each consisted of three eighth graders, with the female student in group three. Group three was not included in the study due to a lack of consent to use the students’ results for scientific purposes. The activity took place in the mathematics laboratory at the University of Wuerzburg (https://www.didaktik.mathematik.uni-wuerzburg.de/mathe-labor/hp2/?page=introduction (accessed on 25 April 2024)) over the course of two days, totaling six hours.
Subsequently, we made improvements to the task based on observations, student results, and feedback. Difficulties were encountered when implementing the simulation. To overcome these challenges, we updated the simulation to provide clear instructions on how to fill the black box with water. In task 1, students struggled to understand the simulation and therefore could not identify or solve the problem.
The students failed to identify characteristics of the black box in the simulation and proceeded to pour 900 mL into the black box as a solution to the task, without considering the distribution of water amounts. Unlike the pre-pilot participants, who answered the question by identifying attributes of the Water Black Box, the students attempted to make a sketch without comprehending how the black box behaved. As part of an intervention, we instructed the students to closely observe the behavior of the box. Additionally, they were asked to explain their reasoning to the supervisors and verify their results using the actual black box. This intervention was integrated into the redesigned task: “NOTE: The task can be solved without knowing the internal structure of the water box”.
When working on the first task, the students employed both aforementioned approaches to ascertain the output.
In task 2.1, the students generated highly imaginative ideas for the interior components, such as a “floor that detonates at a specific time”. The challenge of identifying the elements within the black box was addressed by utilizing help cards that contained queries such as “How does the water flow from top to bottom?” and more specific inquiries like “Is there a single vessel or multiple vessels?”.
During task 2.2, the students extrapolated the interior of the black box. To validate their models, all students employed the same approach: mentally introducing water into their model and sequentially tracing its path by proceeding step by step. The output of their model was then compared with that of the black box simulation. In cases where discrepancies arose, adjustments were made to the model.
The groups involved in the pilot project each produced a model at the conclusion, which they subsequently validated through simulation based on the hypotheses derived from their model. Figure 5 illustrates the temporal progression of the models developed by one group. Moreover, given that none of the groups had a direct approach to constructing a model of the inner structure of the black box, and taking into consideration the students’ emphasis on the task’s puzzle-like characteristics, we assume that the redesigned activity can be classified as a problem-solving task for the students. Consequently, we did not make further adjustments to the task. In the following section, we outline the process of verifying our assumption.
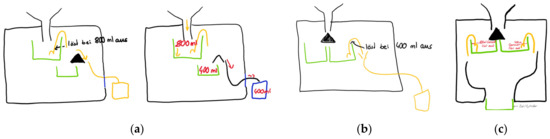
Figure 5.
Progression of the developed model of the inner structure of the black box. The green objects represent containers, the yellow lines represent siphons, and the black triangle splits the water in half. (a) First model and its validation of an input of 800 mL, translation: triggers at 800 mL; (b) second model of the inner structure with description of what is contained in the second panel; translation: triggers at 400 mL; (c) final model of the inner structure, translations: 600 mL limit (triggers) [left]; 400 mL limit (triggers) [right]; target/barrel [bottom].
4.2. Evaluation of the Redesigned Learning Sequence according to Mathematical Problem Solving
4.2.1. Data Collection—Sample
The research was conducted in the mathematics laboratory at the [affiliation of the author] over a two-day period with 24 tenth-grade students. The students were divided into groups of three, with four groups in each room. Video recordings were made of each group. However, due to student illnesses, only six out of the eight groups were able to complete the task. Specifically, Groups 1 and 2 consisted of three male students each, Groups 3 and 4 consisted of three female students each, and Groups 5 and 6 were mixed, Group 5 with two male and one non-binary student and Group 6 with two female and one male student.
The students were supervised by two teachers and pre-service teachers. For the analysis, one recording from each of the three group types was transcribed and coded. Conversations that were unrelated to the problem and problem-solving process, such as discussions about homework, were not transcribed or considered any further.
During the activity, the students received written assistance in the form of support cards and additional support from the teachers. Interventions were allowed during the data collection process. This decision was made because our primary objective was not to analyze problem-solving processes in general, but rather to focus on the specific process within this setting, which intentionally included interventions. The teachers and pre-service teachers were instructed to provide help only in the form of reflection questions or references to the help booklet. Examples of these types of questions included: What are you currently working on? What is your goal? How does your work contribute to solving the problem? Can you explain your model to me? What happens when x ml are filled into the box?
4.2.2. Data Analysis—Categorization System
The videos of three groups were transcribed and subsequently analyzed through qualitative content analysis [47]. Conversations of considerable length that were unrelated to problem solving, such as discussions about homework or leisure activities, were not transcribed and were marked with the symbol #Time# in the transcript.
To address the first sub-question, we conducted a qualitative content analysis using deductive categories in the MAXQDA 2022 software program.
The deductive categories align with the categories identified by Rott et al. [18] in the coding of the problem-solving process. These categories consist of the problem-solving phases outlined in the descriptive phase model, as well as three additional categories that are not directly related to solving the task: digression, organization, and writing.
Digressions are activities that are unrelated to the task at hand, such as discussing homework. Activities that are not directly associated with solving the problem but related to the task are classified as organization. These activities may include, for instance, the functionality of the simulation interface. Writing is an episode where students document their findings, and the process of writing took longer than 30 s [48].
Additionally, we coded the insight that the box is triggered at 800 mL and then dispenses half of the water as interim results of the students during the solution process of the first task.
The changes between the episodes are labelled transitions. Transitions can represent a phase in the problem-solving process but can also consist of zero lines in the transcript.
A description of the codes pertaining to the episodes in the problem-solving process, along with illustrative examples extracted from the transcripts, are listed in Appendix A in Table A1. A detailed description of the codes can be found in the coding manual of Rott [48]. To categorize the episodes, the complete problem-solving process of the student group was first viewed and then coded in a second run. The categorization of the episodes is a macro-level framework; a single sentence within an episode is not considered as another distinct episode.
In addition to the problem-solving phases, we coded the interventions in the implementation, including support cards and teacher–student discussions.
The changes between the phases over time correspond to the transitions between the phases according to the described phase model. Following this, the coded processes were analyzed to discern whether they constituted problem-solving processes or routine processes, to address the second sub-question.
Based on these findings, we address the overarching research question regarding the success of transferring the original learning activity to mathematics teaching.
5. Results
In the following section, the results of the qualitative analysis of the transcripts and videos are presented. Figure 6 displays the problem-solving process of student group 1, including the interventions. The group completed the task within the first day. It should be noted that one pre-service teacher mistakenly informed the group that their model was incorrect, although this was not the case. The students had created an equivalent model, albeit without the use of siphons. In Figure 6, this specific area is highlighted in gray.
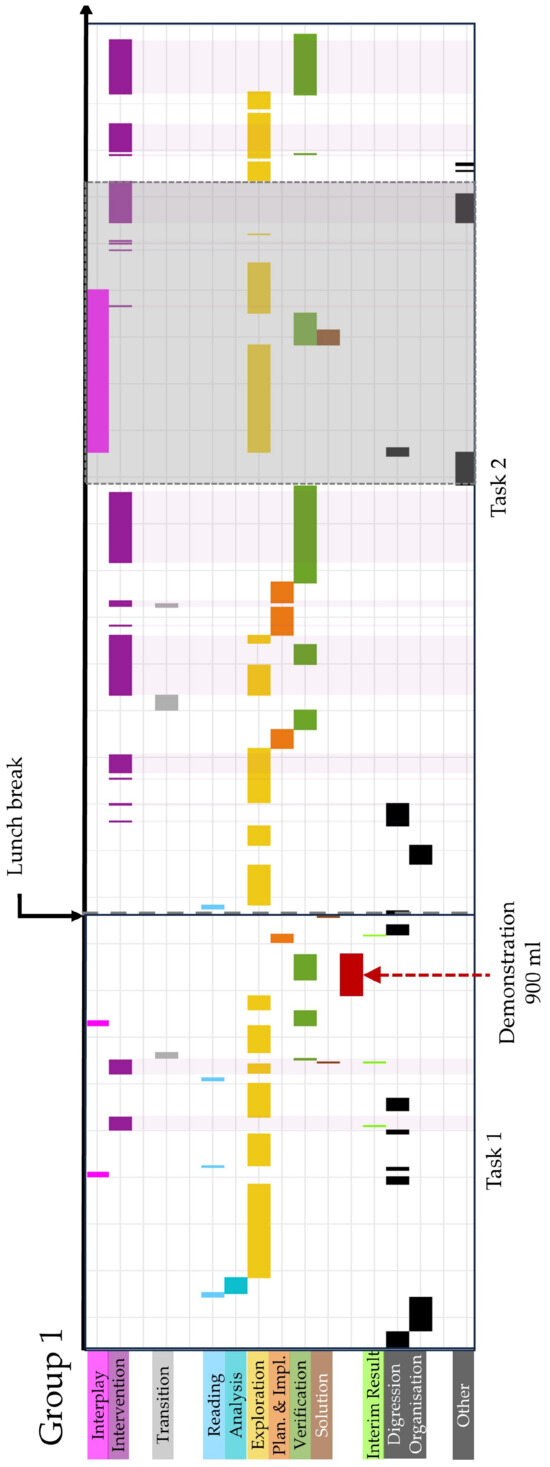
Figure 6.
Process coding of group one.
Group two and three continued working on the tasks on day 2. The process coding of Group two is illustrated in Figure A1, and the process coding of group three in Figure A2.
In all three groups, the most dominant episode type is exploration. While working on the first task, the episode planning and implementation take place in groups two and three, while group one continues with an exploratory approach. At the end of the first task, all three groups then switch between these phases and verification.
In the second task, all three groups start with episodes of exploration. Then the focus shifts to the planning and implementing and exploration phases. During this stage, episodes of verification occur, and initial solution proposals are also discussed. All groups conclude with the episode verification.
When transferring the process coding to the descriptive phase model according to Rott et al. [18], the gray shaded part was not included in the phase model. This is because including it would require additional transitions that the students would not have performed otherwise. In total, group one underwent 15 transitions, group two had 16 translations, and group three had 17 translations. The cumulated descriptive phase models of each of the three groups are shown in Figure 7a–c.
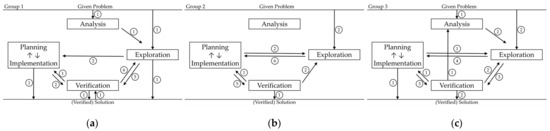
Figure 7.
Description of the problem-solving process using the descriptive phase model. (a) Group one; (b) group two; (c) group three.
The descriptive phase models also show similar patterns in terms of the frequency of transitions between the different phases. In all three groups, the most frequent translations occur regarding the episode exploration. Transitions between verification and exploration are the most dominant.
6. Discussion
We have demonstrated through both the descriptive phase model and the chronological sequence of the process that the problem-solving process of the redesigned task is not a linear process. Likewise, based on the process model and the descriptive phase model, it can be inferred that it is not a cyclical process either, as the translations would need to be more evenly distributed.
In addition, with dominance of the exploration phase, we conclude with the descriptive phase model of Rott et al. [18] that this task is a problem-solving task and not a routine task or a routine problem. Therefore, by making small adjustments to the task based on theory, it was possible to redesign the science activity into a mathematical problem-solving task that emphasizes structures and patterns.
Thus, this demonstrates the potential of this approach for incorporation of mathematics meaningfully within the broader field of STEM, as problem solving constitutes an integral component of mathematics [19,20]. Nevertheless, it is important to note that other disciplines within STEM are not neglected, as problem-solving skills hold comparable significance across all STEM domains [49]. Although only minor adjustments were made, these changes are not trivial in any way as the redesign process demonstrates:
The first step of the redesign process is to acknowledge and develop the mathematical potential. Specifically, recognizing the mathematical potential, or even mathematical activities themselves, can be challenging [5,10]. For instance, teachers and even researchers often assign primarily operational activities rather than other mathematical activities that took place in the activity to mathematics, or do not work out the potential [5,10]. One could argue that the tasks analyzed in the review were also designed by non-math teachers. However, the study of Ortiz-Laso et al. [50] provides evidence that even math teachers struggle with identifying mathematical potential.
The second step in the redesign process corresponds to the elaboration of the mathematical potential. This is challenging for teachers within all grade levels [15,50], as it requires specialized mathematical knowledge for teaching STEM and a holistic perspective on mathematics learning. To address this challenge, Ortiz-Laso et al. [50] showed that it requires long-term interventions.
Overall, our study demonstrates that mathematics can be successfully integrated into STEM education. This meaningful integration has the potential to address the barriers and challenges faced by mathematics teachers in terms of the marginalized position of mathematics within STEM. This evidence-based teaching unit does not negate the necessity for comprehensive teacher training but contributes to strengthening the role of mathematics in STEM.
Furthermore, the study emphasizes the practicality of using an established STEM learning unit as a foundation for identifying mathematical potential. This approach enables the utilization of numerous existing STEM learning resources, which currently lack substantial mathematical content, as a valuable resource for the creation of learning units that incorporate mathematics in a meaningful way.
7. Limitations
The results of our study are limited by several constraints within the study method and their implications. One limitation that should be acknowledged is the selection of the task. In the study, we used a biology task that was designed to enhance understanding of models and the cognitive process of modeling. A biology task is generally not a STEM task. However, we considered this unit as a STEM task due to its contribution to the field of science and the incorporation of engineering elements in the development of the model. The only aspect not explicitly covered is technology, which is limited to the simulation.
Another constraint is that we did not verify whether the revised task continues to promote model understanding. However, we made minimal changes to the closed tasks, so we assume that metamodeling knowledge is still promoted. Furthermore, the students stated that they learned during the learning unit that a simulation, particularly the simulation of the black box of water, is a model that cannot fully depict reality. This represents an aspect of metamodeling knowledge, as mentioned by Krell and Hergert [17]. The only adjustments made were to the additional tasks that have been moved upstream.
8. Conclusions
The role of mathematics in the field of science, technology, engineering, and mathematics (STEM) is often perceived as subordinate, with insufficient emphasis on comprehension within the realm of STEM activities [4,5,14]. The issue at hand is not that mathematics is unnecessary for addressing STEM problems; rather, it is the lack of explicit consideration for mathematics or the complete omission of mathematical engagement [10,43]. As a result, the potential for a holistic examination and integration of mathematics is left untapped [4,5]. To address this issue, we redesigned a science activity from a biology class that originally did not explicitly address mathematics. In this process, we explored the mathematical potentials and redesigned the activity into a problem-solving task that still fosters the original objective in science.
Through a qualitative content analysis of the videotaped implementation based on the descriptive phase model of Rott et al. [18], we demonstrate that the redesigned task is a problem-solving one, thereby confirming the success of the redesign.
Since problem solving is an integral component of mathematics and an important (mathematical) competence in STEM, we conclude that our approach demonstrates a meaningful incorporation of mathematics in STEM [8,19].
However, the redesign process also reveals the complex demands for teachers when planning an integrated STEM sequence, highlighting the need to address these skills in teacher training. At the same time, this approach might reduce inhibition regarding the planning of a STEM unit, as teachers can utilize a pre-existing task instead of developing one from scratch.
Based on these findings, we conclude that this approach of revising STEM tasks in the demonstrated way can contribute to strengthening mathematics in STEM.
Author Contributions
Conceptualization, J.J. and H.-S.S.; methodology, J.J. and H.-S.S.; formal analysis, J.J.; investigation, J.J.; resources, J.J. and H.-S.S.; writing—original draft preparation, J.J.; writing—review and editing, J.J. and H.-S.S.; visualization, J.J.; supervision, H.-S.S.; All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
The study was conducted, and the resulting date were stored in accordance with international and local legislation, as well as the Declaration of Helsinki, and the GDPR. In accordance with these requirements, the explicit approval of an ethics commission was not required for our research.
Informed Consent Statement
All participants, and in the case of underage individuals their legal guardians, were informed about the details of the study. Participation in the study was voluntary, and students could withdraw from the study without any consequences. Written informed consent has been obtained from the patient(s) or their legal guardians to publish this paper.
Data Availability Statement
The data presented in this study are not publicly available due to ethical reasons.
Acknowledgments
We would like to thank Julia Leisten for her assistance in developing the task and collecting data, as well as the participants of this study.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Details on the Qualitative Analysis

Table A1.
Description of the coding and example of the coding *.
Table A1.
Description of the coding and example of the coding *.
| Phase/Code | Description of the Code ** | Example of the Coding (Extracts of Episodes) |
|---|---|---|
| Analysis | Understanding the problem, including selecting certain perspectives and reformulating the problem | S5: What is our task actually? S6: Yes, okay. Determine how much water would flow into the measuring cylinder in the real water box if a-No, no, I can’t do that now (laughs) S5: Determine how much- S6: S5, that’s asking too much. S5: Determine how much water would flow in the real water box- S5: I don’t understand. S6: Determine how much water would flow into the measuring cylinder in the real water box if 900 milliliters were added in one step. Huh? Ah, we’re supposed to find out now if we put 900 milliliters into this funnel? S5: Yes. S6: How much then somehow- S5: It flows in there. S6: Exactly. 100 milliliters maybe. |
| Exploration | Unstructured approach to solve the problem, including exploration of the problem space and gathering relevant information. | S4: Okay, and on we go. S5: Guys, 400 are in. 400 is in, 400 is not out. Another 400 is 800. What runs out? S6: OK, eh? S5: 400 runs out when 800 is in. S4: That means there are 400 left. S5: There’s 400 left, now I‘ll add another 400. S6: That’s 1600 now. S5: Oh no. S6: Yes. No, it can’t be. S4: Wait a minute, yes, yes, yes. S6: No, we have 400. |
| Planning and Implementation | Structured approach to planning to solve the problem and its implementation to the problem | S8: Then step 2. 200 milliliters remain in the box. S7: Now we just have to do step 3 and step 4, I think, right? S8: Exactly, you can start at step-Okay, but we have to check that again. |
| Verification | Verification and testing of the solution or solution assumptions. | S1: Let’s see if our pattern is correct, that at least 800 are needed the first time. S2: Yes, wait a minute. S3: That was the case. That was already here- S1: Yes, yes, but we need more than 2. S2: Shall I do it with 200? S3: Yes. S1: Then 300. S1: Then 400. S3: No, then we’re at 900. S1: Yes? S3: Yes, but—yes, okay. S2: Yes, but then we can’t say #00:32:10# S1: Although, yes, yes, then do another 300. S3: That should be 400 now. (6 sec.) Yes. S1: Yes, that fits. |
| Solution | Students’ solutions to tasks, including solutions that the students have named as the final solution, regardless of whether the students have further engaged with the task after an intervention. | Solution followed by this conversation. S9: So, we have to contact the teacher now. So, no. S8: Let’s just say: We’re done. […] H1: Have you finished yet? S8: Yes. |
| Organization | Task-related work, but no content-related work | S8: No, but you’d better not take my sketch, I scribbled on it a bit. S9: Yes, otherwise I would have copied it in now and put #00:21:59# on it again. S8: Oh, we still have a bit of time. S9: I can draw it again. That’s not bad. |
| Digression | Conversations that are not related to problem solving | S5: Wait a minute (.) Let’s chill. |
* The examples were translated by the author. Conversations that are not related to problem processing are marked with #Time#. The students are referred to as S, the teachers as L, the pre-service teachers as H, and the task designer as B. ** For a detailed description of the codes see Rott [48].
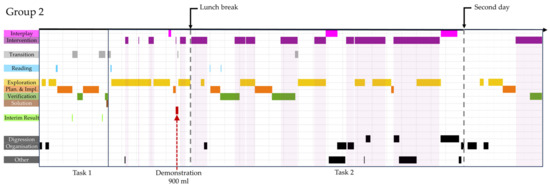
Figure A1.
Process coding of group 2.
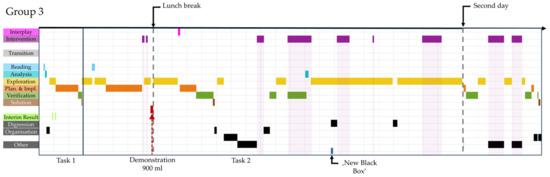
Figure A2.
Process coding of group 3.
References
- Martín-Páez, T.; Aguilera, D.; Perales-Palacios, F.J.; Vílchez-González, J.M. What are we talking about when we talk about STEM education? A review of literature. Sci. Ed. 2019, 103, 799–822. [Google Scholar] [CrossRef]
- Li, Y.; Wang, K.; Xiao, Y.; Froyd, J.E. Research and trends in STEM education: A systematic review of journal publications. Int. J. STEM Educ. 2020, 7, 11. [Google Scholar] [CrossRef]
- Kelley, T.R.; Knowles, J.G. A conceptual framework for integrated STEM education. Int. J. STEM Educ. 2016, 3, 11. [Google Scholar] [CrossRef]
- Aydin Gunbatar, S.; Ekiz Kiran, B.; Boz, Y.; Roehrig, G.H. A closer examination of the STEM characteristics of the STEM activities published in NSTA journals. Res. Sci. Technol. Educ. 2022, 1–26. [Google Scholar] [CrossRef]
- Just, J.; Siller, H.-S. The Role of Mathematics in STEM Secondary Classrooms: A Systematic Literature Review. Educ. Sci. 2022, 12, 629. [Google Scholar] [CrossRef]
- Galili, I. Physics and Mathematics as Interwoven Disciplines in Science Education. Sci. Educ. 2018, 27, 7–37. [Google Scholar] [CrossRef]
- van den Eynde, S.; van Kampen, P.; van Dooren, W.; de Cock, M. Translating between graphs and equations: The influence of context, direction of translation, and function type. Phys. Rev. Phys. Educ. Res. 2019, 15, 020113. [Google Scholar] [CrossRef]
- Siller, H.-S.; Günster, S.M.; Geiger, V. Mathematics as a Central Focus in STEM—Theoretical and Practical Insights from a Special Study Program Within Pre-service (Prospective) Teacher Education. In Disciplinary and Interdisciplinary Education in STEM; Li, Y., Zeng, Z., Song, N., Eds.; Springer Nature: Cham, Switzerland, 2024; pp. 317–343. ISBN 978-3-031-52923-8. [Google Scholar]
- Fitzallen, N. STEM Education: What Does Mathematics Have to Offer? In Mathematics education in the margins. In Proceedings of the 38th Annual Conference of the Mathematics Education Research Group of Australasia, Sunshine Coast, Australia, 13–18 July 2015; pp. 237–244. [Google Scholar]
- Braber, N.; Krüger, J.; Mazereeuw, M.; Kuiper, W. Reflecting on the Value of Mathematics in an Interdisciplinary STEM Course. In Proceedings of the Eleventh Congress of the European Society for Research in Mathematics Education, Utrecht, The Netherlands, 5–10 February 2019. [Google Scholar]
- Li, Y.; Schoenfeld, A.H. Problematizing teaching and learning mathematics as “given” in STEM education. Int. J. STEM Educ. 2019, 6, 44. [Google Scholar] [CrossRef]
- Stohlmann, M. Three modes of STEM integration for middle school mathematics teachers. Sch. Sci. Math. 2019, 119, 287–296. [Google Scholar] [CrossRef]
- Maass, K.; Geiger, V.; Ariza, M.R.; Goos, M. The Role of Mathematics in interdisciplinary STEM education. ZDM Math. Educ. 2019, 51, 869–884. [Google Scholar] [CrossRef]
- Forde, E.N.; Robinson, L.; Ellis, J.A.; Dare, E.A. Investigating the presence of mathematics and the levels of cognitively demanding mathematical tasks in integrated STEM units. Discip. Interdiscip. Sci. Educ. Res. 2023, 5, 3. [Google Scholar] [CrossRef]
- Arnone, K.A.; Hanuscin, D. An Exploratory Cross-Sectional Survey Study of Elementary Teachers’ Conceptions and Methods of STEM Integration. J.-STEM 2018, 4, 159–178. [Google Scholar] [CrossRef]
- Shriki, A.; Lavy, I. Mathematics and sciences teachers collaboratively design interdisciplinary lesson plans: A possible reality or wishful thinking? In Proceedings of the 41st Conference of the International Group for the Psychology of Mathematics Education, Singapore, 17–22 July 2017; pp. 201–208. [Google Scholar]
- Krell, M.; Hergert, S. The Black Box Approach: Analyzing Modeling Strategies. In Towards a Competence-Based View on Models and Modeling in Science Education; Upmeier zu Belzen, A., Krüger, D., van Driel, J., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 147–160. ISBN 978-3-030-30254-2. [Google Scholar]
- Rott, B.; Specht, B.; Knipping, C. A descriptive phase model of problem-solving processes. ZDM Math. Educ. 2021, 53, 737–752. [Google Scholar] [CrossRef]
- Liljedahl, P.; Santos-Trigo, M.; Malaspina, U.; Bruder, R. Problem Solving in Mathematics Education; Springer International Publishing: Cham, Switzerland, 2016; ISBN 978-3-319-40729-6. [Google Scholar]
- OECD. PISA 2022 Assessment and Analytical Framework; PISA, OECD Publishing: Paris, France, 2023. [Google Scholar] [CrossRef]
- Lambdin, D.V. Benefits of teaching through problem solving. Teach. Math. Through Probl. Solving Grades PreK 2003, 6, 3–14. [Google Scholar]
- Cai, J.; Hall, E.; Cifarelli, V.; Hiebert, J.; Lester, F.; Zawojewski, J. What research tells us about teaching mathematics through problem solving. Teach. Math. Through Probl. Solving PreK 2003, 6, 241–254. [Google Scholar]
- Hiebert, J.; Carpenter, T.P.; Fennema, E.; Fuson, K.; Human, P.; Murray, H.; Olivier, A.; Wearne, D. Problem Solving as a Basis for Reform in Curriculum and Instruction: The Case of Mathematics. Educ. Res. 1996, 25, 12. [Google Scholar] [CrossRef]
- Rott, B. Rethinking heuristics—Characterizations and vignettes. LUMAT 2015, 3, 122–126. [Google Scholar] [CrossRef][Green Version]
- Mayer, R.E.; Wittrock, M.C. Problem solving. Handb. Educ. Psychol. 2006, 2, 287–303. [Google Scholar]
- Lester, F.K.; Cai, J. Can Mathematical Problem Solving Be Taught? Preliminary Answers from 30 Years of Research. In Posing and Solving Mathematical Problems; Felmer, P., Pehkonen, E., Kilpatrick, J., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 117–135. ISBN 978-3-319-28021-9. [Google Scholar]
- Santos-Trigo, M. Problem Solving in Mathematics Education. In Encyclopedia of Mathematics Education; Lerman, S., Ed.; Springer: Dordrecht, The Netherlands, 2014; pp. 496–501. ISBN 978-94-007-4978-8. [Google Scholar]
- Philipp, K. Experimentelles Denken: Theoretische und Empirische Konkretisierung einer Mathematischen Kompetenz; [Experimental Thinking: Theoretical and Empirical Concretization of a Mathematical Competence]; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2013; ISBN 978-3-658-01119-2. [Google Scholar]
- Polya, G. How to Solve It: A New Aspect of Mathematical Method, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 2004; ISBN 978-0-691-11966-3. First published 1945. [Google Scholar]
- Schoenfeld, A.H. Mathematical Problem Solving; Academic Press: London, UK, 1985; ISBN 978-012-628-870-4. [Google Scholar]
- Schoenfeld, A.H. Learning to Think Mathematically: Problem Solving, Metacognition, and Sense Making in Mathematics (Reprint). J. Educ. 2016, 196, 1–38. [Google Scholar] [CrossRef]
- Liljedahl, P.; Cai, J. Empirical research on problem solving and problem posing: A look at the state of the art. ZDM Math. Educ. 2021, 53, 723–735. [Google Scholar] [CrossRef]
- Amalina, I.K.; Vidákovich, T. Cognitive and socioeconomic factors that influence the mathematical problem-solving skills of students. Heliyon 2023, 9, e19539. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Gong, T.; Saldivia, L.E.; Cayton-Hodges, G.; Agard, C. Using process data to understand problem-solving strategies and processes for drag-and-drop items in a large-scale mathematics assessment. Large-Scale Assess. Educ. 2021, 9, 2. [Google Scholar] [CrossRef]
- Tian, J.; Braithwaite, D.W.; Siegler, R.S. Distributions of textbook problems predict student learning: Data from decimal arithmetic. J. Educ. Psychol. 2021, 113, 516–529. [Google Scholar] [CrossRef]
- Koichu, B.; Parasha, R.; Tabach, M. Who-Is-Right tasks as a means for supporting collective looking-back practices. ZDM Math. Educ. 2021, 53, 831–846. [Google Scholar] [CrossRef]
- Bruder, R.; Collet, C. Problemlösen Lernen im Mathematikunterricht: [mit Kopiervorlagen]; [Learning to solve problems in math lessons, 1st ed.]; Cornelsen Scriptor: Berlin, Germany, 2011; ISBN 978-3589230747. [Google Scholar]
- Rott, B. Mathematische Problembearbeitungsprozesse von Fünftklässlern—Entwicklung eines deskriptiven Phasenmodells. [Problem Solving Processes of Fifth Graders: Developing a Descriptive Phase Model]. J. Math.-Didakt. 2014, 35, 251–282. [Google Scholar] [CrossRef]
- Williams, J.; Wake, G. Black Boxes in Workplace Mathematics. Educ. Stud. Math. 2007, 64, 317–343. [Google Scholar] [CrossRef]
- Bissell, C. Models and «black boxes»: Mathematics as an enabling technology in the history of communications and control engineering. Evue D’histoire Sci. 2004, 57, 305–338. [Google Scholar]
- Straesser, R. Didactics of mathematics: More than mathematics and school! Zent. Didakt. Math. 2007, 39, 165–171. [Google Scholar] [CrossRef]
- Glanville, R. Inside every white box there are two black boxes trying to get out. Behav. Sci. 1982, 27, 1–11. [Google Scholar] [CrossRef]
- Just, J.; Siller, H.-S. Towards implementing Black Boxes in Mathematical Modeling an epistemological Approach Adapting models from science and science education. In Proceedings of the Twelfth Congress of the European Society for Research in Mathematics Education (CERME12), Bolzano, Italy, 2–6 February 2022; pp. 4605–4612. [Google Scholar]
- Ruebush, L.; Sulikowski, M.; North, S. A Simple Exercise Reveals the Way Students Think about Scientific Modeling. J. Coll. Sci. Teach. 2009, 38, 18. [Google Scholar]
- Koch, S.; Krell, M.; Krüger, D. Förderung von Modellkompetenz durch den Einsatz einer Blackbox. [Promotion of model competence through the use of a black box]. Erkenn. Biol. 2015, 14, 93–108. [Google Scholar]
- Greefrath, G.; Siller, H.-S. Digitale Werkzeuge, Simulationen und Mathematisches Modellieren; [Digital Tools, Simulations and Mathematical Modeling]; Springer: Wiesbaden, Germany, 2018; ISBN 978-3-658-21939-0. [Google Scholar]
- Kuckartz, U. Qualitative Text Analysis: A Systematic Approach. In Compendium for Early Career Researchers in Mathematics Education; Kaiser, G., Presmeg, N., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 181–197. ISBN 978-3-030-15635-0. [Google Scholar]
- Rott, B. Mathematisches Problemlösen: Ergebnisse Einer Empirischen Studie; Mathematical Problem Solving: Results of an Empirical Study; WTM-STEIN: Münster, Germany, 2015; ISBN 978-3-942197-67-0. [Google Scholar]
- Johnson, C.C. Handbook of Research on STEM Education; Taylor & Francis Group: Milton, UK, 2020; ISBN 978-0-367-07560-6. [Google Scholar]
- Ortiz-Laso, Z.; Diego-Mantecón, J.-M.; Lavicza, Z.; Blanco, T.F. Teacher growth in exploiting mathematics competencies through STEAM projects. ZDM Math. Educ. 2023, 55, 1283–1297. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).