Feedforward Enhanced Control System to Pursue Mathematical Competencies Achievement in Engineering Education

Abstract

The learning process can be conceptualized as a dynamic system constantly evolving and adapting in response to a variety of stimuli and inputs. This paper presents a novel approach to competency-based assessment that integrates a dynamic assignment design of personalized activities with the aid of a 3D matrix array structure. This structure, named Topic, Activity, and Competency (TAC) cuboid, provides a detailed view of the student’s progress, enabling the design of tailored curricular strategies to facilitate the development of competencies. Personalized activities serve as control inputs that adapt to each learner’s state, driving a feedforward that promotes proactive improvement. An automation process becomes necessary to cope with the increased data volume from the TAC cuboid and the information complexity. The concept model registers TAC cuboid information, enabling a dynamic analysis to forward an adequate workload when required to facilitate students’ achievement of their expected mathematical competencies. Additionally, the paper discusses the initial application of these models in an educational role-playing game, demonstrating their effectiveness in a gamified learning environment.

1. Introduction

Competency-based, also known as proficiency-based, education is a framework where a continuous benchmark should be kept on some predetermined competencies that are to be achieved by the learners, and where focus is placed on outcomes and real-world performance [1]. The European Higher Education Area (EHEA) embraces this setting, with competencies and learning outcomes becoming a keystone in engineering education, which has to deal with rapid digital advances and job market requirements [2,3,4,5,6].

A thorough reflection of the competency-based initiatives in engineering education was developed by Edwards et al. [7] where the authors point out the problem that arises when the focus is placed on the method of how to teach competencies rather than what competencies our students should learn, leaving out the key issue of how to secure its achievement. When students are assessed in a competency-based learning framework, they are required to show their learned knowledge and skills at some given moments of assessment in order to prove they have achieved specific predetermined competencies [8].

Under a continuous assessment environment, the students are generally assessed at different moments during a course and usually have the opportunity to show achievement of a given competency multiple times. Very recently this idea has been taken further trying to reflect at each moment the level of achievement of competencies already assessed by the so-called Dynamic Continuous Discrete Assessment DCDA [9] as well as to take this continuous assessment to provide a feedforward input, (cf. [10,11,12]), to the student to improve or achieve their demonstrated competencies [13].

Indeed, a competency-based education framework requires that a basic double question is addressed, which is related to controlling the achievement of competencies, its level of achievement, and if and how they may be improved.

RQ: What type of activities and assessments are to be selected to determine if students are mastering or progressing adequately in the achievement of their expected competencies?

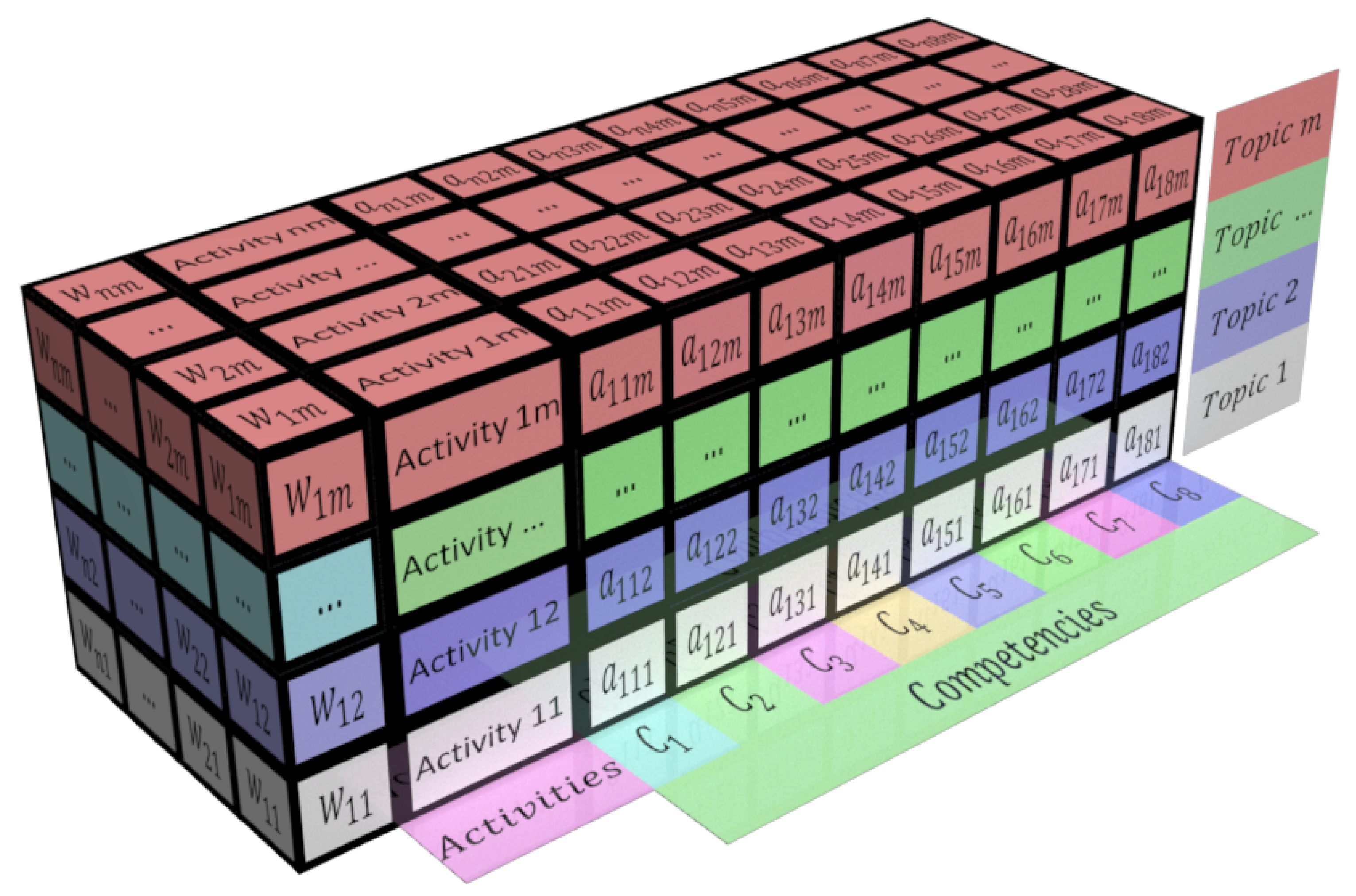
This paper provides insight into the above research question by exploiting the 3D matrix structure that considers the Topics, Activities, and Competencies (TAC) of the students, conforming a TAC cuboid for each student.

We further explore the innovative application of Game-Based Learning (GBL) strategies through the development and implementation of an educational Role-Playing Game (RPG) [14,15,16,17] in the Mathematics I course at School of Design Engineering ETSID, Universitat Politècnica de València in Spain.

The RPG developed serves as a practical case study, demonstrating the effective integration of the TAC and FECS models within a gamified context, thereby enhancing student engagement and learning outcomes in a STEM subject.

This paper is organized as follows. Section 2 revisits the concept of the TAC cuboid, and its significance in elaborating the data collected for the student assessment.

Section 3 and Section 4 analyze the relevance of designing appropriate activities to facilitate the achievement of individual and group objectives through the Feedforward Enhanced Control System (FECS).

Section 5 showcases how specific activities are organized for students, underlining the role of the educational RPG in enriching the learning process of each student.

Section 6 discusses how FECS supports the pursuit of mathematical competencies, highlighting its dynamic nature in competency-based education.

Finally, Section 7 and Section 8, respectively, synthesize the conclusions drawn from this study, and outline potential avenues for future research, particularly focusing on the expansion of FECS and GBL methodologies to broader educational contexts.

2. The Topics, Activities, Competencies Cuboid Setting

The level of competency achievement evolves after the performance of the different activities that take place throughout a course (on-site class, virtual class, MOOCs, lab sessions, personal tasks, flipped class, tests, …) covering the different topics of any given subject.

This evolution in the mastery of each competency requires a meaningful tracking of the assessment of the activities performed by each student [18], which led to the emergence of the Topics, Activities, Competencies (TAC) cuboid in [13].

This cuboid is represented in Figure 1, a 3D matrix that demonstrates the relationship within the aforementioned TAC and quantifies, as depicted in Figure 1, in each knot of the cuboid, the impact $a_{ijk}$ that the activity $A_{ik}$ has on the competency $C_j$ within the topic $T_k$, each activity $A_{ik}$ having a weight $w_{ik}$ on the topic $T_k$.

Moreover, each student has a personal TAC cuboid (pTAC) in [13] that registered each activity on a given topic via a binary evaluation of whether the competencies involved have been achieved, in which case the binary components corresponding to those competencies are multiplied by the subclass-activity weights at the moment of assessment and pushed into the pTAC cuboid. At each moment of assessment, one or several activities of different types may be carried out. TAC cuboids were tested in op. cit to assess the mathematical competencies of engineering students in a technological university, [19]. Here, the competencies considered were aligned with the criteria of the Mathematics Working Group, now called Mathematics Special Interest Group, of the European Society for Engineering Education SEFI [20,21], to assess the mathematical competencies, which are clustered in two basic groups. One is related to the use of mathematical language and tools, and the other is related to mathematical thinking, reasoning, posing and solving problems, and modeling.

Building upon the foundational concepts of the TAC cuboid setting, we now delve into the practical application of this framework in pursuing the achievement of mathematical competencies in engineering education. This approach not only conceptualizes the theoretical underpinnings of the TAC model but also illustrates its real-world implications and effectiveness in enhancing student learning outcomes.

At any educational level, the learning process outcomes are to be defined along with the aims and objectives of each degree, course, and subject. Once reached the mathematics subject level, we will build up an objective TAC cuboid, hereafter referred as an oTAC, with a scoring distribution guided by a pre-determined final objective.

However, as each student’s pTAC score evolves, it may evidence the fact that in a competency-based learning methodology, some learners find some individual skills or competencies achievement more difficult than others. For this reason, the learning process should allow different paces to different students, [22]. For this reason, each student’s oTAC likewise modifies, correlating with the number of activities, yet it remains consistent with a predefined objective profile.

From a computational perspective, this means that each activity execution conveys an evaluation vector input into the oTAC, maintaining alignment with the determined objective profile. Subsequently, the oTAC evolves with each activity.

In addition, a master TAC cuboid, henceforth referred to as mTAC, accurately evaluates the pTAC binary by considering the weight of each topic and activity within the subject. It is crucial to construct an mTAC that accurately represents the contribution of each activity execution. Selecting weights for each topic is relatively straightforward for any experienced instructor by considering its relevance, timing, and effort allocation within the subject. However, fixing the weight for all types and sub-types of activities is a more delicate issue due to the wide variations in their complexity.

Constructing an mTAC is indeed an uneasy task for which we propose a working methodology as follows:

• Create a pilot mTAC founded on the previous experience and the probable impact of each activity class on the expected competencies.
• Turn each evaluated work into individual activities, e.g., each question in each exam is considered an activity, and the same applies to each question/exercise in a lab session.
• Categorize activities in types or classes of activities, and sub-types or subclasses.
• Apply the mTAC to the sequence of activities.
• Compare the results obtained with the oTAC and test its validity. If required, make the corresponding necessary adjustment in the mTAC weight.
• Recalculate the model with the new mTAC.
• Validity of the model must be tested until we get an acceptable model to achieve the expected competencies.

As we have explored the foundational concepts and practical implications of the TAC cuboid in engineering education, it is also essential to highlight its innovative application in contemporary educational tools. One such application is the digital RPG designed to enhance student engagement, as mentioned in the introduction. This RPG incorporates various academic challenges including quizzes and problem-solving tasks, in line with the TAC model goals.

The game’s role-playing elements are utilized primarily to boost motivation and engagement. As students progress through the game, their interactions, including responses, number of attempts, time spent on each task, and accuracy, are meticulously recorded. These data contribute to conforming the pTAC for each student, providing a detailed picture of their learning progress, as well as areas where there is room for improvement.

3. The Keystone of Learning: The Activities

Organizing a degree in general and each subject, in particular, should have in mind the CDIO™ educational framework, which stresses an engineering fundamentals set in the context of Conceiving–Designing–Implementing–Operating (CDIO) real-world systems and products. The learning process is a real-world process and consequently, some instructors have assumed within this framework their curricular planning and outcome-based assessment [23]. In the final leg of this framework, when a course program is run, the activities developed in, or out of, the classroom correspond to the last slot and may be of very diverse natures: attending master classes, preparing classes and solving doubts with flipped teaching methodologies, seeing and working on some MOOCs, problem-solving, modeling and solving some particular physical phenomena, and even the exams are to be considered one of the activities that almost all courses consider in their planning, [9,13].

On some occasions, these activities may be considered learning objects, which are units meant for the students learning and acquiring skills, which usually are managed, stored, and on some occasions exchangeable irrespective of the delivery medium used, which might be even an external education platform, [24,25]. From this perspective, these objects may be handled independently and rearranged, [26,27].

As far as possible, having an activity bank comprising all activities is desirable. If this is the case, the activity bank will act as a repository housing references to all executable types of activities, the essential components that fuel the binary assessment model based on TAC cuboids. Subsequently, it is important to maintain a reference model allowing easy access to the activities.

Taking into account that performing activities helps to achieve mathematical competencies, the idea of generating an activity bank arises as a readily accessible collection of academically characterized activities, linked to the topics of the subject and to influence the development of competencies.

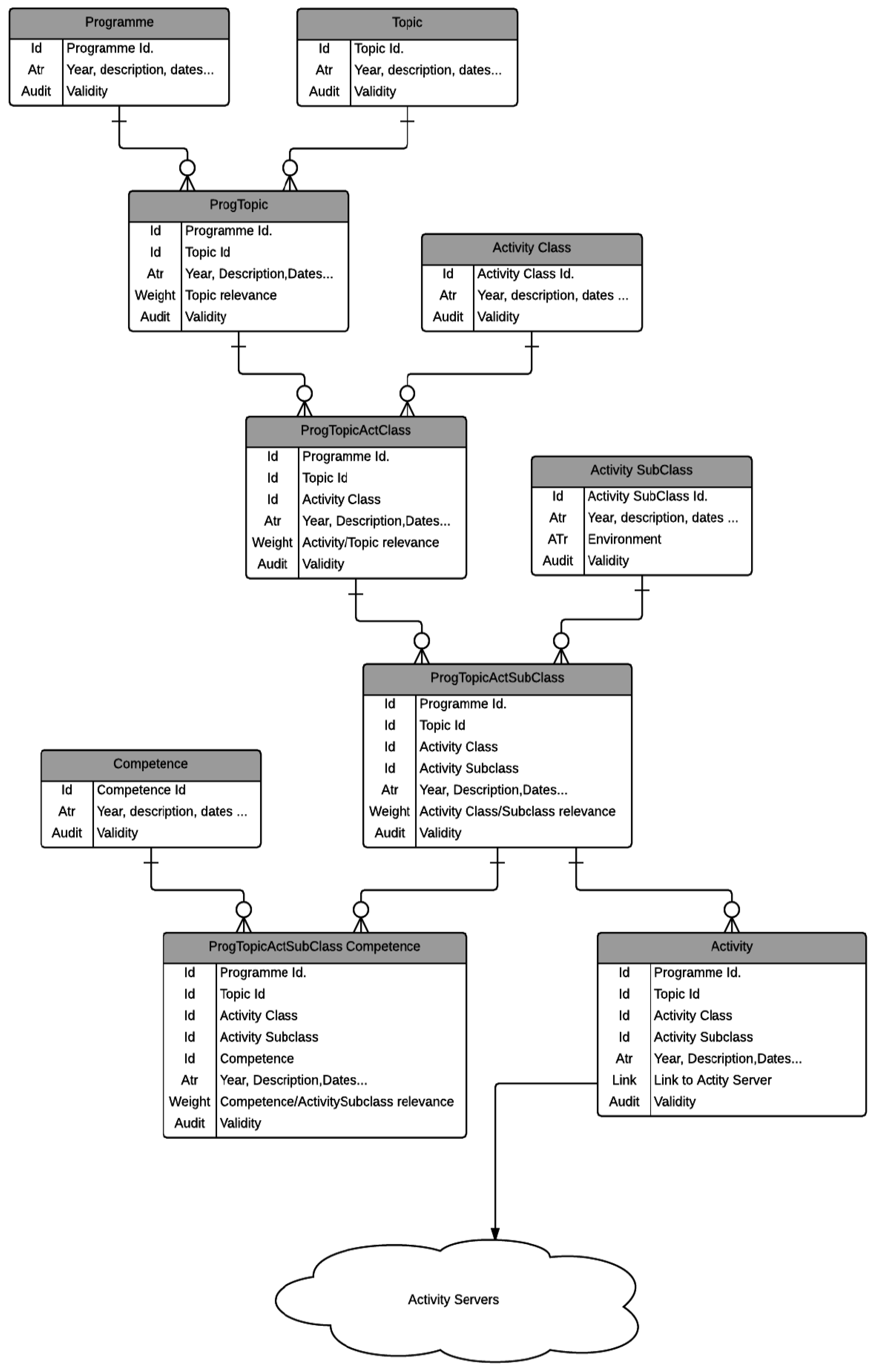
Figure 2 illustrates a conceptual model designed to record the identifiers of the activities, allowing them to be assigned to students depending on their performance. It is worth noting that this model is not a closed structure, as other attributes might be considered.

This collection of activities varies widely in terms of nature and accessibility, encompassing mostly digital activities, e.g., digital escape rooms, MOOCs, and lab software. However, some non-digital activities take place when requested or considered adequate, for instance, with some tutorial classes, textbook activities, or group work. Once an activity is assigned to a student, it is assumed that there will be digital access to it either at the university facilities or at home.

4. Feedforward Enhanced Control System

A Feedforward Enhanced Control System (FECS) arises when an activities assignment process is settled by selecting some, or a set, of activities that each student should perform as feedback of his/her personalized pTAC and oTAC, with the aim that each learner enjoys an attainable pathway with the expected competencies.

For this purpose, an activity backlog of each student is settled, gathering the data of all the activities assigned and executed by each student.

Answering RQ, the type of assessment and structure of activities to be performed must be aligned to provide an adequate feedforward to each student on his/her competencies achievement and development at any given moment of the learning process and not only when the relevant moments of the evaluation approach.

According to the type of assignment, these rely on one of the following categories:

• Compulsory assignment: Activities to be performed by all students that cover the whole course programme. These include all traditional exams where students must show competencies development and mastery.
• Reinforcement assignment: Throughout the course, some reinforcement activities are suggested, which the students voluntarily undertake.
• Recovery assignment: When low scores are obtained by some students in some moments of evaluation, some recovery activities are suggested so that the students may redeem their lacks. Its mode of implementation may be voluntary or mandatory.
• Personal assignment: Some students select their own reinforcement activities by themselves to improve their competencies at any time
• Dynamic assignment: By using adequate algorithms based on the students’ performance, some adequate activities are suggested so that the students may reach predetermined objectives.

The essence of FECS is fixing the dynamic assignment of activities based on student performance. For it, several tasks are to be taken at the beginning of the course related to developing the TAC model on which it relies. TAC data are essential to demonstrate FECS:

• To fix the topics and the contents of the subject, as well as the main moments of evaluation. Although any activity might be regarded as a moment of evaluation, emphasis is placed on the relevant ones. These relevant activities are conformed by a set of activities on one or several topics that have a major impact on the final grade.
• To settle the compulsory activities to encourage the students’ attendance and update tracking of the course.
• To draw the partially ordered set of topics as developed in [9] and its moments of evaluation to have retroactive feedback on the development of previously assessed competencies.
• To publish the mTAC so that all students know the course plan.
• Build the oTACs that enable each student to know the minimum objectives to be achieved to pass the course or to reach different levels of achievement.

After setting up the above data structure, and the bank of activities, we are ready to implement the FECS of the dynamic assignment of activities based on students’ performance.

The TAC model compares at determined time intervals the state of the pTAC of the students with their respective oTAC to detect deviations and the possibility of promoting the objective level to be reached, The system selects adequate activities from the activities bank for each student to pursue the achievement of the expected mathematical competencies.

Building upon the FECS framework, the aforementioned educational RPG’s design serves as an exemplary practical application. The data gathered from the personalized TAC cuboids (pTAC) of each student are meticulously analyzed within the FECS to discern patterns in student learning and performance. This analysis is instrumental for educators, enabling them to adapt the game’s content in real time, thus ensuring it remains in alignment with the educational objectives.

The game is enriched with a diverse array of learning materials, spanning from interactive tutorials to comprehensive problem-solving exercises, all tailored to reinforce and exemplify the principles of the TAC framework engagingly and interactively.

A particularly noteworthy feature of this RPG is its adaptive learning approach. The system dynamically adapts to the students’ prior interactions and performances, offering more personalized activities designed to meet their individual learning needs. For instance, if a student demonstrates difficulty with a specific concept, the game intuitively provides additional resources or alternative explanations, thereby enhancing the student’s understanding and engagement with the material.

5. Initial Application of TAC and FECS in an Educational RPG

The implementation of the TAC framework and FECS in an educational setting was innovatively and initially demonstrated through the development of an RPG, specifically designed for the Mathematics I course, with a focus on Algebra, at ETSID, Universitat Politècnica de Valéncia, Spain. The RPG, developed using RPG Maker MZ, was integrated into the curriculum to facilitate the development of crucial competencies in Problem-Solving and Critical-Thinking—key competencies essential for mastering Algebra and foundational mathematical concepts.

This implementation involved volunteer students from the Aerospace Engineering degree, engaging them in an interactive learning environments where their proficiency in these competencies was paramount. The RPG design was aligned with the course objectives, offering a practical and engaging approach to applying Algebraic principles.

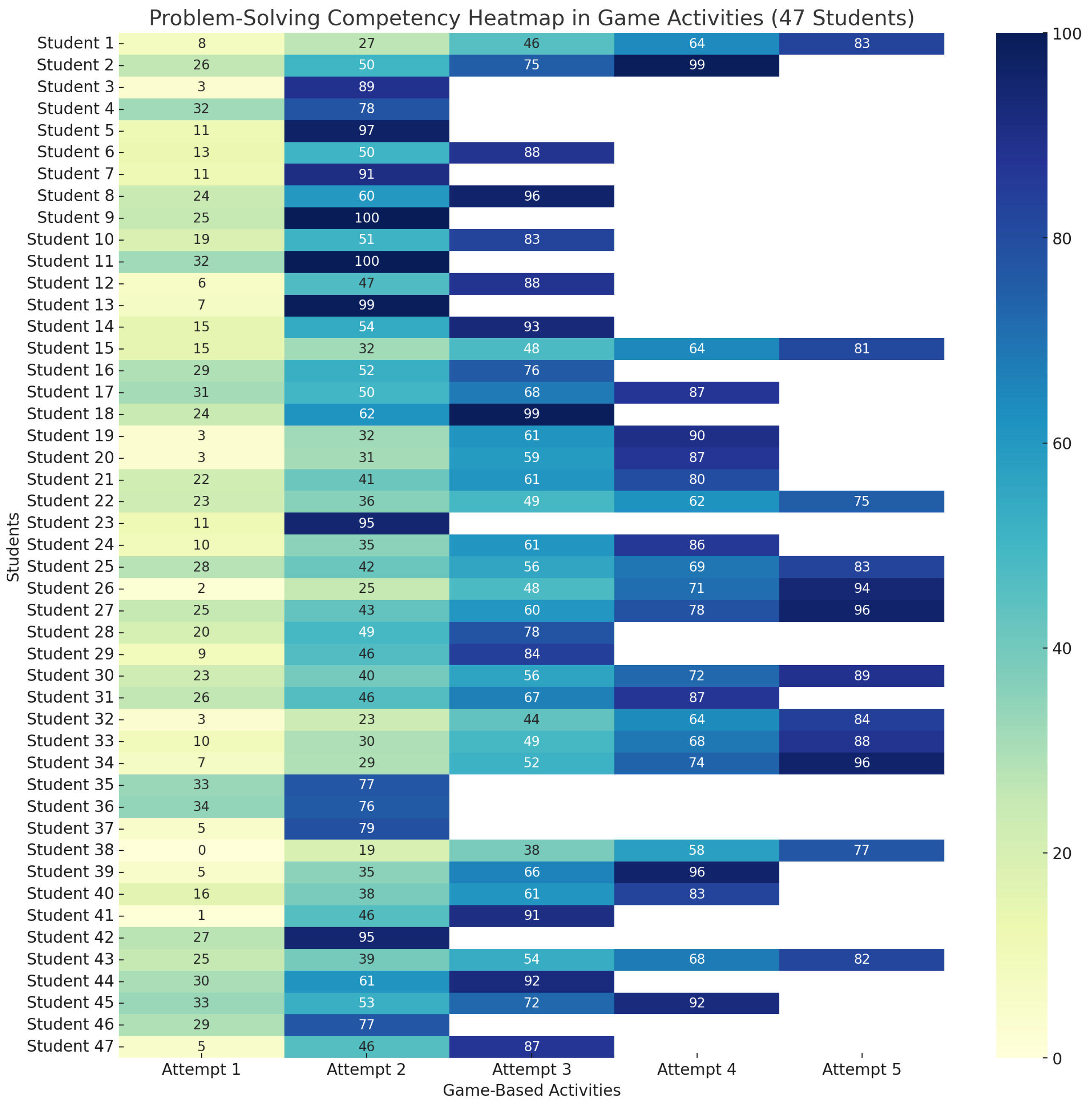
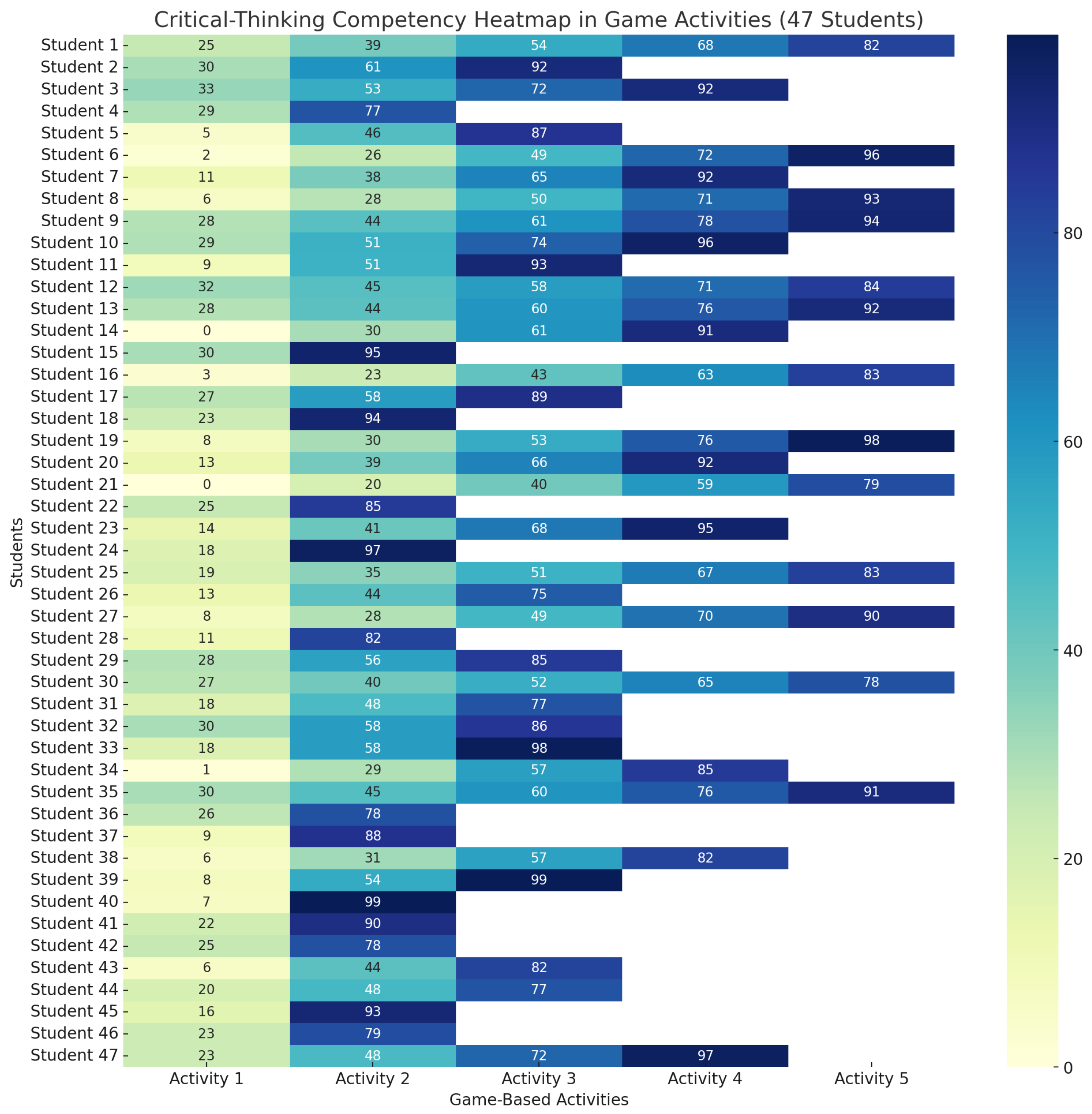
The students’ competency development was tracked using a scoring system ranging from 0 to 100, with their performance in the game directly influencing their scores. Heatmaps (Figure 3 and Figure 4) provide visual representations of their progression, where students initially scoring below 35 received targeted activities, derived from the game’s data, to aid their improvement. These activities, recommended by the FECS, were based on the students’ Personal TAC cuboid (pTAC) evaluations, reflecting their current competency levels. Adjustments and recommendations were also informed by the Objective TAC cuboid (oTAC), which set predefined competency targets, and the Master TAC cuboid (mTAC), which accounted for the overall course objectives and the weightage of different activities. As students interacted with the RPG, their pTACs evolved, capturing their real-time progress and aligning it with the oTAC goals. This dynamic interaction between the pTAC, oTAC, and mTAC ensured that each student received a customized learning experience, tailored to their individual progress and needs.

The successful integration of the TAC and FECS models within this educational RPG not only enhanced student engagement and learning in Algebra but also showcased the effectiveness of gamified learning in achieving specific educational outcomes. The positive results from this initial application suggest a significant potential for employing similar models in other areas of STEM education. Future research could focus on extending this approach to various digital platforms, thereby broadening the scope and impact of gamified learning methodologies in modern educational settings.

Students’ Opinion and Attitudes

To assess the impact of the TAC and FECS models on students’ learning experiences, we surveyed 47 students using the Typeform platform, adhering to strict data privacy and ethical considerations. The survey aimed to capture students’ perceptions across several dimensions, including the usefulness of the learning models, motivation, learning outcomes, understanding, comfort with the platform, skills improvement, and confidence levels.

The statistical results of this survey are presented in

Table 1. Statistic information on the survey.

Item	Mean	Median	Mode	SD	Q1	Q2	Q3
Usefulness	3.80	4.00	4.00	1.06	3.00	4.00	5.00
Motivation	3.72	4.00	4.00	1.07	3.00	4.00	5.00
Learning	3.80	4.00	4.00	0.92	3.00	4.00	5.00
Understanding	3.91	4.00	4.00	0.87	3.00	4.00	5.00
Comfortable	4.00	4.00	4.00	0.97	3.00	4.00	5.00
Improved Skills	3.77	4.00	4.00	0.91	3.00	4.00	4.00
Confidence	3.56	4.00	3.00	0.80	3.00	4.00	4.00

, summarizing the students’ feedback on the usefulness, motivation, learning improvement, understanding of the material, comfort with the technology, skill improvement, and confidence levels.

The survey data indicated positive student attitudes across multiple dimensions of their learning experience. For instance, the item ’Comfortable’, evaluating how at ease students feel with the technology and methodology used in the RPG, scored an average of 4.00, with a mode of 4.00, suggesting that most students found the integration of the TAC and FECS models into their learning environment to be user-friendly and accessible. Similarly, ’Understanding’, the item measuring students’ perception of clarity regarding the subject matter and the extent to which the models have helped in comprehending complex concepts, received a high mean score of 3.91, indicating that the models effectively facilitated a deeper comprehension of the course material. These findings reinforce the notion that the TAC and FECS models, along with the educational RPG, not only enhance students’ engagement and motivation but also contribute significantly to their academic success.

However, the item ’Confidence’, assessing the impact of the educational models on students’ confidence in their knowledge and competencies, had a slightly lower mean score of 3.56, indicating an area for improvement. This feedback suggests that while the educational models positively impact learning, there may be opportunities to further boost students’ confidence in their abilities through additional support and personalized feedback mechanisms.

Based on these insights, we have initiated several enhancements aimed at improving student confidence and ensuring that our models and tools are even more aligned with student needs and expectations. These adjustments include more interactive tutorial sessions, enhanced real-time feedback on competency development, and increased opportunities for students to engage in reflective practices regarding their learning progress.

6. Discussion

The execution of assigned activities following the proposed FECS model presents several significant advantages, each contributing to a more effective and personalized learning experience:

• FECS distributes the workload along the course reporting and responding at any time the possible final grade of each student.
• It allows to correct any discrepancy in the expected achievement and development of mathematical competencies in advance.
• It assigns the work to be completed in a personalized way by each student according to his/her personal needs.
• By performing the activities assigned to each student from the backlog of activities, the mTAC and the binary evaluation of each activity, a set of evaluation vectors are implemented into the pTAC that evolves over time
• The oTAC is recalculated taking into account the level of the achievement of objectives

A dynamic assignment algorithm of activities can be implemented related to the competencies achieved. A key issue is to restrain the number of selected activities so that it is respectful and sensitive to the other activities in other subjects.

The integration of data collected via digital tools and e-learning platforms can enhance the effectiveness of the FECS model. These data can provide real-time insights into student performance and engagement, facilitating dynamic adjustments within the mTAC and pTAC. This continuous optimization of learning pathways will be tailored to each student’s needs. Moreover, the use of predictive analytics will allow for the anticipation of student challenges, enabling proactive adjustments in teaching strategies and resource allocation. This data-driven approach is key to ensuring that the TAC framework remains agile and responsive to the evolving educational landscape and student requirements.

In the context of the digital RPG, the application of TAC and FECS has further demonstrated the potential of these models in a gamified learning environment. This approach has shown how game-based learning can be strategically used to enhance engagement and motivation, while also providing a rich source of data for the FECS model. The game’s interactive nature allows for a more engaging and immersive learning experience, which is particularly effective in capturing and maintaining student interest. The game’s ability to record detailed interactions provides valuable data that feed into the TAC and FECS model, ensuring a responsive and adaptive learning experience. This symbiotic relationship between the educational RPG and the FECS model exemplifies the future potential of integrating advanced pedagogical frameworks with digital gaming platforms.

7. Conclusions

The implementation of the Topics, Activities, Competencies (TAC) cuboid presents a transformative approach in the educational landscape, particularly in the assessment of mathematical competencies. This model offers a robust framework for the Dynamic Continuous Discrete Assessment (DCDA), enabling a comprehensive and nuanced understanding of students’ competency development over time.

Central to the success of this approach is the Feedforward Enhanced Control System (FECS), a dynamic model that complements the TAC cuboid by facilitating the tailored assignment of activities. The FECS model excels in providing timely, individualized feedforward, assisting each student in reaching their targeted competency levels effectively. This personalized approach ensures that students are not only assessed but also guided toward the mastery of competencies through a series of well-chosen and relevant activities.

Moreover, the integration of the TAC cuboid with the FECS model in a gamified learning environment, as exemplified in the educational RPG developed using RPG Maker MZ, suggests a potential for innovative, technology-driven educational strategies. This integration promises not only to improve student engagement and motivation but also to offer a practical and effective method for skills and competency development.

Continuing from this perspective, the evolving landscape of technology in education opens new horizons for applying the TAC framework. The advent of advanced digital tools and methodologies, such as Artificial Intelligence (AI), Virtual Reality (VR)/Augmented Reality (AR), and Big Data Analytics, heralds a new era of possibilities for transforming the TAC model. These emerging technologies are poised to enable more personalized learning experiences, create immersive educational environments, and provide deeper, data-driven insights, all crucial to the potential success of the TAC framework in a digitally enhanced educational setting.

AI’s ability to tailor learning experiences based on individual student data can significantly augment the precision and effectiveness of the TAC model. Similarly, the use of VR and AR technologies promises to transform learning spaces, making complex concepts more tangible and engaging. The application of Big Data Analytics in education can offer unprecedented insights into teaching methodologies and activity weightings, further refining the TAC framework.

Additionally, the potential integration of e-learning platforms and digital tools within the TAC framework could streamline the tracking and assessment processes significantly. Platforms like Moodle, Blackboard, or bespoke Learning Management Systems (LMS) could serve as hubs for TAC-related activities, facilitating the efficient collection and analysis of data on student engagement and performance. Such platforms could also become central to fostering collaborative and flipped classroom environments, integral aspects of the envisioned TAC model.

In acknowledging the transformative potential of the TAC cuboid and FECS model within digital age education, it is crucial to address the technological barriers that could impede widespread adoption. These barriers, ranging from unequal access to digital tools and high-speed internet to varying levels of digital literacy among students and educators, present significant challenges. To eliminate or mitigate these obstacles, it is essential to develop inclusive strategies that ensure equitable access to technology and foster a supportive learning environment. This might include the deployment of technology-enhanced learning materials that are accessible offline or designed for low-bandwidth environments, alongside initiatives aimed at enhancing digital literacy and competencies. Furthermore, recognizing the importance of a tailored approach, future iterations of the TAC framework should consider these barriers in their design and implementation, striving for a model that is not only innovative but also accessible and equitable.

In conclusion, while the TAC cuboid and FECS model represent a significant step forward in educational assessment and instruction, their integration with cutting-edge technologies suggests a bright future for educational tools and methodologies. The potential application of these models, augmented by the latest technological advancements, could lead to more personalized, effective, and engaging learning experiences. This prospect sets a new standard for competency-based education, especially in the digital era, and offers a promising blueprint for transforming teaching and learning processes through innovative, technology-driven strategies.

8. Future Work

The DCDA and TAC model has been developed in a STEM subject looking at the level of competencies achieved at each moment of evaluation. Personal features of learners should be tested at the beginning of the course to register personalized information so that adequate types of activities might be performed by each learner according to their competencies and way of learning. This approach ensures that achieving the target level of competencies is not unnecessarily difficult for learners who may feel uncomfortable or dislike certain types of activities. Instead, learners can engage in activities that they prefer while still achieving or developing the desired competencies. This line of research may be interesting for researchers in other fields of education.

However, the integration of technology in the TAC framework, while opening numerous possibilities, also introduces significant challenges. A primary concern is the digital gap, which can lead to disparities in educational outcomes due to unequal access to technology. To address this issue, educational institutions must work towards ensuring equitable access to necessary technologies for all students. This effort should be complemented by providing support for students who may lack digital literacy, ensuring that no student is left behind in the digital learning landscape.

Another challenge lies in the realm of data privacy. The collection and analysis of student data, essential for the effective implementation of the TAC model, must be handled with utmost care. Establishing robust data governance policies is vital to safeguarding student privacy and maintaining trust. Adherence to regulations and ethical standards in data handling will be critical in the sustainable and responsible use of student data.

In terms of capitalizing on the opportunities presented by digital advancements, there is a pressing need for educational institutions to invest in the training of educators. This training should focus on effectively integrating these technologies into teaching methodologies, ensuring that educators are well-equipped to leverage the benefits of digital tools in enhancing learning experiences. Moreover, adopting a collaborative approach that involves educators, technologists, and students will be instrumental in developing more effective and inclusive TAC models. Such collaboration can lead to innovative solutions that cater to diverse learning needs and preferences.

In addition to these considerations, applying TAC and FECS models in gamified contexts, such as the educational RPG, should be further explored. Research into how these models can be adapted and applied in different educational settings and across various disciplines will be valuable. The potential of these models to revolutionize learning experiences by making them more engaging, personalized, and effective presents a promising avenue for future educational innovations.

Our survey of 47 students provided valuable insights into the effectiveness of the TAC and FECS models in a restricted game environment, highlighting their positive impact on motivation, understanding, and overall learning experience. Future iterations of our models will focus on areas identified for improvement, such as increasing student confidence, by integrating more supportive and personalized feedback mechanisms.

Addressing the digital divide will be paramount in realizing the full potential of the TAC and FECS models in a global educational context. Future research should prioritize the exploration of technologies and methodologies that lower the entry barriers for all students, regardless of their socio-economic background. This includes the development of adaptive learning platforms that can function across a spectrum of technological infrastructures, from high-speed internet settings to areas where learners may only have access to basic digital resources. Moreover, future efforts must also explore the pedagogical implications of these models in diverse educational settings, including those with limited access to current technological advancements. By focusing on these areas, the next phase of research and development can ensure that the benefits of personalized and competency-based education are accessible to all learners, bridging the gap between educational innovation and equitable access.