Abstract
This study aimed to examine the collaborative design of an interdisciplinary STEAM activity conducted by lower-secondary school teachers of different disciplines. We adopted an approach based on a case study involving four teachers (art, music, technology, and mathematics/science teachers) designing an activity focused on the concept of symmetry. We gathered data through oral, semi-structured interviews with the teachers and through schematic representations of resource systems provided by the teachers themselves. Data analysis aimed to identify the different kinds of resources the teachers relied on, their utilization schemes, and the overarching meta-didactical praxeology adopted by the teachers for their collaborative design work. The theoretical model adopted for data analysis was a combination of the Documentational Approach to Didactics and the Meta-Didactical Transposition frameworks, originally introduced to study the work of researchers in the context of teacher professional development. An application of this model to the collaborative design work of teachers can provide a fresh insight into the relationship between teachers’ documentation work for the design of a STEAM activity, the practices that they adopt to address this shared task (praxis), and the shared justifying discourses (logos) for their praxis.
1. Introduction
In today’s rapidly evolving world, embracing an interdisciplinary approach to education is more vital than ever. Traditional subject boundaries no longer capture the complexities of real-world challenges. Interdisciplinary learning encourages students to explore connections between different fields, fostering critical thinking. By breaking down academic silos, we empower students to navigate the complexities of our interconnected world and cultivate the adaptability needed to address the multifaceted issues of the 21st century. Interdisciplinarity in STEAM teaching calls for the seamless integration of subject matters (science, technology, engineering, arts, and mathematics) stimulating creativity, problem-solving, and project- or problem-based learning [1]. The interdisciplinary approach in STEAM education aims to foster students’ analytical, intuitive, logical, and aesthetic modes of thinking [1]. In this context, presenting mathematics as a potent tool for understanding the world emerges as a fundamental objective of STEAM education [2].
Ref. [3] describes interdisciplinarity as an approach that brings together the skills of different scientific areas to give us a better understanding of a common topic. This collaborative endeavor finds its roots over 50 years ago, when scholars convened at the Seminar on Interdisciplinarity in Universities in Nice, France. After attending this seminar, Apostel [4] recognized the role of interdisciplinarity in helping students navigate the complexities of the contemporary world, enabling them to comprehend and critically evaluate the constant flow of information they encounter daily. Today, in an era where the demand for intertwined skills to understand the intricacies of our world is more pronounced than ever, the relevance of interdisciplinarity has only intensified. This is particularly evident in the realms of mathematics education [5] and STEAM (science, technology, engineering, arts, and mathematics) education [1,6], where the integration of diverse disciplines has become paramount.
In the literature, two other terms are employed with slightly varying meanings to denote the effort to establish connections between disciplines: multidisciplinarity and transdisciplinarity. While multidisciplinary teaching presents various disciplines simultaneously without explicit connections, interdisciplinary teaching emphasizes the explicit exploration of connections between different disciplines [3]. Transdisciplinary teaching takes a step further, advocating for a holistic understanding that transcends traditional disciplinary boundaries [7]. Each of these approaches necessitates an examination of the roles assumed by the different disciplines, each characterized by its own distinct epistemology. Our focus, in particular, centers on understanding the role of mathematics within the context of an interdisciplinary STEAM activity [8].
Researchers in mathematics education worldwide are actively exploring diverse conjunctions of mathematics with other knowledge domains [9]. In these explorations, the role of mathematics varies—it is sometimes perceived as a computational tool for solving scientific and technological problems, while in other instances, it serves as a means to model phenomena observed in different disciplines [10]. Despite the increasingly numerous school experiments in this field, the integration of STEAM activities, encompassing all subjects in the acronym, remains a challenge for many teachers, who often lack clear guidelines for implementation [11,12]. Notably, the prevailing lack of training among teachers in designing and implementing interdisciplinary activities poses a considerable challenge [4]. The authors have been engaging in interdisciplinary endeavors in the last few years (e.g., [13]), spanning various levels such as research, teacher PD, national and international projects, and educational experiments. Consequently, there is a natural need to delve deeper into these experiences, prompting further inquiry and reflection.
This study aimed to examine the collaborative design of a STEAM activity conducted by lower-secondary school teachers of different disciplines working in the same school in the context of the European Erasmus+ project STEAM-Connect, led by researchers in mathematics education from different countries. Our research focused on examining the resources that teachers utilized and how each teacher interacted with these resources in the design of an interdisciplinary STEAM activity for students. An additional central objective of the study was to elucidate the theoretical discourses (logos) that guide teachers in introducing their practices (praxes) throughout the design and implementation phases of this activity. To undertake this analysis, we turned to the Documentational Approach to Didactics framework to investigate how teachers create teaching materials starting from different kinds of resources. Additionally, we required a framework that would enable us to study teachers’ praxes and logos when working collaboratively with researchers towards a shared objective. In this regard, the Meta-Didactical Transposition framework [14] aligned seamlessly with our research goals. Our approach involved a combination [15] of these two theoretical frameworks to achieve a comprehensive and profound understanding of the intricate phenomenon under investigation. This kind of combination has already been adopted by the authors [16] to study the work of researchers in mathematics education who have the role of teacher educators when they design teaching materials for a teacher professional development (PD) program.
2. Theoretical Frameworks
2.1. Documentational Approach to Didactics
The DAD framework, introduced by Gueudet and Trouche in various studies [17,18,19], serves as a comprehensive tool for investigating the professional work and development of teachers as they interact with diverse resources. The intersection of teachers and resources in the creation of teaching materials has been a central focus in mathematics education research for decades. The DAD framework is grounded in a definition of a document that involves a fusion of resources and utilization schemes. Teachers generate documents by leveraging a set of resources and developing specific schemes of utilization tailored to the situations in which the documents will be employed. This dynamic process is termed documentational genesis.
The representation capturing the process of documentational genesis [17] is expressed as follows: Document = Resources + Utilization schemes. Utilization schemes consist of classes of situations (where resources are employed), rules of action (establishing stable patterns in resource utilization), and operational invariants (integral elements within the teacher’s beliefs and knowledge, serving as both motivators and results of their activity). Gueudet and Trouche assert that through the examination of teachers’ documentational genesis, one can effectively describe their professional work and trace their PD throughout a PD program. The methodology proposed by Gueudet and Trouche [19] for studying teachers’ documentational genesis is referred to as the “reflective investigation method” (p. 25). The data collection in this method adheres to four key principles:
- Active involvement of the teacher in the reflective collection of resources.
- Observation of the teacher’s activities both in and out of the classroom.
- Collection of the resources utilized and produced by the teacher.
- Organization of follow-up observations over an extended period to discern stabilities and evolutions.
Gueudet and Trouche ([19]) also propose to ask the teacher to draw a schematic representation of the structure of the utilized resources. They called it a schematic representation of the resource system (SRRS) (p. 28).
2.2. Meta-Didactical Transposition
MDT, as outlined in many studies (e.g., [14,20,21,22,23,24]), serves as a model for studying the collaborative work of a community of researchers with the role of teacher educators and a community of teachers involved in teacher professional development (PD).
The MDT model finds its theoretical foundation in the Anthropological Theory of Didactics (ATD) by Y. Chevallard [21], based on the notion of didactical transposition [21,22]. ATD, functioning as an epistemological model for describing the teaching of mathematics inside institutions, considers mathematics as a human activity aimed at addressing specific tasks within social institutions. The central theoretical tool is the concept of praxeology, which operates at two main levels: the “know-how” (praxis) level, encompassing a family of similar tasks and their solving techniques, and the “knowledge” (logos) level, comprising discourses that describe, explain, and justify these techniques.
In the MDT model, the praxeologies under examination, labeled as meta-didactical praxeologies, are not referred to as didactic activities in the classroom but as practices and theoretical reflections developed by teachers and researchers in teacher PD programs. The term “meta-didactical” denotes that crucial issues related to the didactical transposition of knowledge are addressed at a meta-level, taking a step further in respect to ATD because they involve a metacognitive layer where researchers and teachers critically reflect on and adapt the didactical transposition process.
MDT, with respect to ADT, introduces additional elements, including the dynamic interplay between diverse communities involved in teacher PD; institutional constraints imposed by participant affiliations; and other institutional factors, such as school traditions, curricula, and textbooks. A notable feature of MDT is its dynamic approach to teacher PD, viewing it as a process rather than merely a product. This dynamic perspective enables the description of the intertwined evolution of meta-didactical praxeologies within the communities involved in the PD program, considering the possible convergence towards shared components of meta-didactical praxeologies [23,24].
2.3. A model Combining DAD and MDT
In a previous paper [16], the authors introduced a model that combines, through networking principles [15], researchers’ documentational genesis conducted during a teacher PD program [25] within their overarching meta-didactical praxeology for the design and implementation of the PD program itself. This model, illustrated in Figure 1, designates the researchers as didacticians, employing Jaworski’s [26] terminology, as they undertake the role of teacher educators within the context of the PD program.
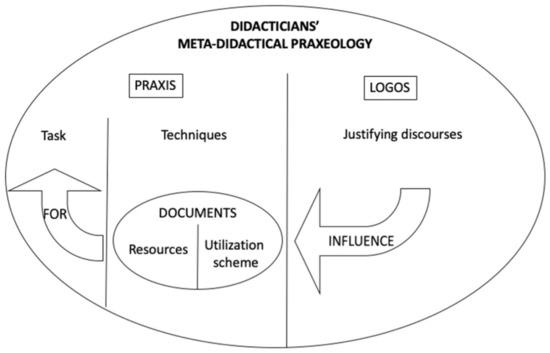
Figure 1.
A combined model for didacticians’ work ([16] p. 20).
In the networked model presented in [16], the DAD and MDT frameworks are, for the first time, integrated and mutually interpreted. Indeed, the documentational genesis is viewed as an integral component of the techniques employed by didacticians to execute their praxeology task, which involves designing and implementing the PD program. The utilization schemes of the didacticians’ documents encompass both the consistent elements in their actions and the motivating factors guiding their actions, revealing a profound influence from the overarching discourse (logos) that justifies the didacticians’ practices (praxes) within the PD program context.
3. Methodology
3.1. Institutional and Experimental Context
Our research unfolds within the context of the Erasmus+ Project STEAM-Connect. This collaborative initiative brings together researchers from diverse countries—Austria, Finland, Italy, Luxembourg, and Slovakia—along with secondary school teachers representing various subjects, such as arts, mathematics, music, science, and technology. The collaborative effort aims to collectively devise STEAM activities tailored for all school grades.
The STEAM-Connect project started in November 2021, with researchers collaboratively crafting a common template (Figure 2) for teachers involved in designing STEAM activities, ensuring a shared structure for organizing their creations. From the project’s onset, a consensus was reached that the scope of the letter A in the STEAM acronym should extend beyond art in the traditional sense to encompass music and the humanities at large, including philosophy.
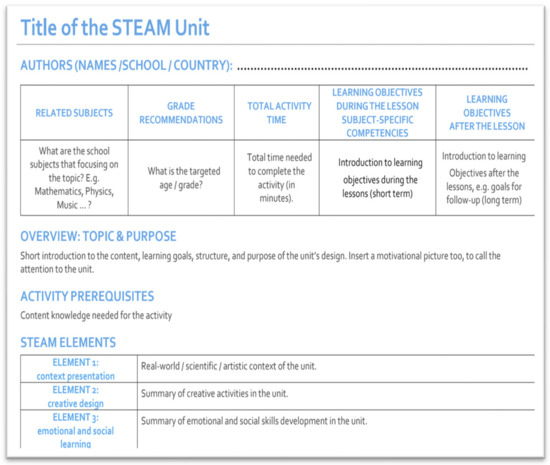
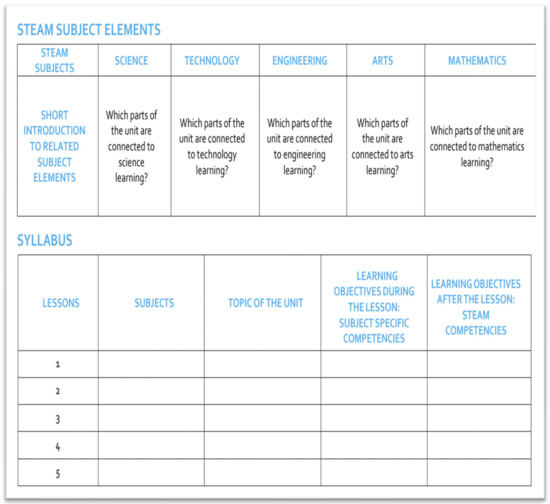

Figure 2.
Template for the activities designed in the context of the STEAM-Connect project.
The study presented in this paper was focused, in particular, on four teachers working together in a lower-secondary school in Northern Italy, teaching art, music, technology, and mathematics, respectively. The mathematics teacher actively participated in all project meetings alongside Italian and international researchers. This active involvement stemmed from her longstanding collaboration with the Mathematics Department at the University of Turin, which serves as the promoter of the Italian branch of the project.
3.2. Data Collection
We collected data from the following:
- -
- The activity template developed within the project (Figure 2), filled out by the teachers;
- -
- Oral interviews with the four teachers, conducted in four different sessions by the third author. The questions related to the teachers’ previous experiences and backgrounds, their relationship with teachers of different disciplines in the context of the STEAM-Connect project, the resources they rely on to design the STEAM activity in their school, and the role that they attribute to mathematics in the context of the STEAM activity;
- -
- A schematic representation of the resource system (SRRS) provided by each of the four teachers.
3.3. Data Analysis
The model presented in [16], as illustrated in Figure 1, served as a guiding framework for our data analysis methods. In light of this, our research delved into both the teachers’ individual documentation work and their shared meta-didactical praxeology guiding the STEAM activity design. We operated under the assumption that the logos of this praxeology play a pivotal role in steering the documentational genesis process, which is integral to the praxis component of the praxeology itself.
From the activity template filled out by the teachers, we gained an overview and a general understanding of the characteristics of the STEAM activity designed in their school, namely, the subjects involved in the activity and the focal topic for each subject, the time plan of the activity, the short-term and long-term learning objectives, etc.
From interviews with the teachers and from their SRRS, we derived information about the resources utilized by each teacher for the design of the STEAM activity of her responsibility and the utilization schemes of these resources. We produced a visual summary like the one below (Table 1), wherein “situation” represents the classroom situation in which the resources are employed, “resources” represent the different kinds of resources utilized by the teacher in that situation, “rules of action” represent the specific way in which the teacher utilizes these resources in the classroom, and “operational invariants” encapsulate the guiding principles that underlie these rules of action.

Table 1.
A visual summary employed for the analysis of teachers’ documents.
From the same data, we also obtained an insight into the teachers’ praxeology to address interdisciplinarity in the context of the design of the STEAM activity, and we could investigate if it was shared among all the teachers participating in the activity. In particular, we inferred the role that they attributed to mathematics throughout the different phases of the design and implementation of the STEAM activity. With the term “praxeology”, we mean “meta-didactical praxeology” because it refers to meta-level reflections on the design of a STEAM activity undertaken by a community of teachers in collaboration with a community of researchers participating in the same international project. More specifically, the praxis component encompasses the task of the meta-didactical praxeology—in this case, the design of the STEAM activity—and the techniques adopted by the teachers to accomplish this task. The logos component is the justifying discourse, which constitutes the overarching principles guiding the teachers’ collective design process.
4. Results
4.1. Overview of the STEAM Activity
From the analysis of the activity template filled out by the teachers, we understood that the STEAM activity designed in their school is based on the topic of symmetries and translations, explored across the various involved disciplines. The topic is a typical mathematics topic, as is evident from the title of the activity, “Let’s move symmetrically”. The time plan starts with the part of the activity conducted by the art teacher, aiming to introduce the concept of module and modular composition through the use of colored plastic caps and cardboard. The second part of the activity is still guided by the art teacher and aims to introduce the concepts of axis of symmetry and symmetric figures. The technology teacher is in charge of the third part, which involves the reproduction and juxtaposition of tiles depicting geometric patterns that can be arranged in different ways. The fourth part of the activity is guided by the music teacher and is focused on singing in canon. In the end, the concluding part of the activity relates to mathematics, where symmetries and translations are formalized with the aid of the Cartesian plane.
4.2. Teachers’ Documentation Work
4.2.1. Art Teacher
The first part of the activity, occurring within a two-hour art lesson, was dedicated to crafting a modular composition using plastic bottle caps of various colors. The art teacher divided the students into four groups and provided each of these groups with the necessary resources to carry out the activity: a specific number of yellow, white, and blue plastic bottle caps; a cardboard sheet; a gridded sheet where the length of each square corresponds to the diameter of the bottle caps; and glue. A brief explanatory video and the image that the different groups were supposed to reproduce on the cardboard were projected onto the interactive multimedia whiteboard (IWB). The colors of the module were chosen to recall the colors of the Ishtar Gate, which the students had recently learned about in art history. When all the groups had finished the module (an example is shown in Figure 3a), the teacher asked the students to arrange them in different patterns to create different modular compositions, aiming to grasp their differences (an example is shown in Figure 3b). The goal of this initial activity was to envision the repetition of the module as a “shift” and, thus, a translation. Furthermore, the properties of the geometric figure depicted allowed students to reflect on the concept of symmetry.

Figure 3.
(a) Module obtained with bottle caps. (b) Modular composition with 4 modules.
The art teacher included the following resources in her SRRS (Figure 4):
- -
- Technological resources, like the IWB for the reproduction of videos, projection of the image of the module, and projection of the YouTube video with instructions for students;
- -
- Material resources, like caps, sheets, glue, and the art textbook;
- -
- Human resources, like previous professional experiences as well as exchanges and sharing with colleagues.
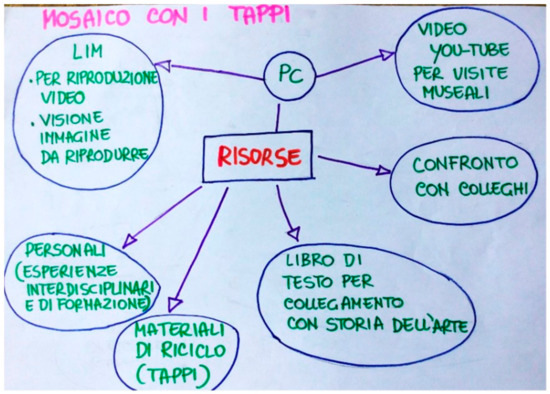
Figure 4.
SRRS created by the art teacher for the first part of the STEAM activity.
Based on the interview with the art teacher and her SRRS, we derived a visual summary of the document that she created for the first part of the activity, with indications about the situation in which it applies, the utilized resources, the rules of action, and the operational invariants (Table 2).

Table 2.
A visual summary of the document created by the art teacher for the first part of the activity.
The second part of the activity took place during the subsequent two-hour art lesson and involved the creation of a symmetric figure with tempera colors. The teacher started the lesson by playing a video that addressed a fundamental geometric concept within the context of the STEAM activity, namely, the axis of symmetry. In fact, if one were to imagine folding any symmetrical object along its axis of symmetry, two mirror-image sections would result that could perfectly overlap. For a better understanding of the concept, the video presented concrete examples, such as a monarch butterfly flapping its wings, overlapping its two sides. Subsequently, the students were given a blank sheet from a sketchbook, which they folded in half parallel to the longer side. The teacher then filled three separate containers, each with tempera paint of one of the three primary colors (red, blue, and yellow), and asked each student in the classroom to choose two out of the three colors. Finally, the teacher poured a small amount of the color chosen by the student into the fold of their sheet, instructing them to close the sheet by applying pressure along the fold in order to spread the color as much as possible (Figure 5).

Figure 5.
Symmetric colored blotches obtained with tempera.
The art teacher included the following resources in her SRRS (Figure 6):
- -
- Technological resources, like the IWB and the YouTube video on symmetries in nature;
- -
- Material resources, like tempera colors and drawing sheets;
- -
- Human resources, like previous professional experiences and acquired skills as well as exchanges and sharing with colleagues.
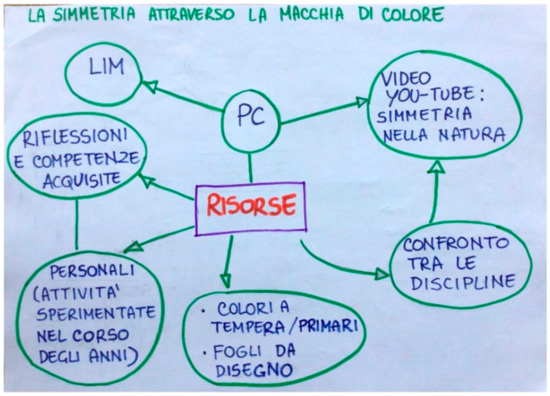
Figure 6.
SRRS created by the art teacher for the second part of the STEAM activity.
Following the interview with the art teacher and her SRRS, we developed a visual summary of the document she formulated for the second part of the activity. This table (Table 3) encompasses details regarding the situation, the resources employed, the rules of action, and the operational invariants.

Table 3.
A visual summary of the document created by the art teacher for the second part of the activity.
4.2.2. Technology Teacher
The third part of the activity took place during a two-hour technology lesson and focused on the creation of tiles and compositions with geometric patterns. As an introduction, the teacher presented one of the most significant figures in post-World War I architecture: the renowned designer and architect Giovanni Ponti. The teacher drew the students’ attention to the project of the Hotel Parco dei Principi in Sorrento from 1962, in which 27 tiles with different geometric combinations were used. The design featured a bicolor scheme of white and ultramarine blue, with an explicit reference to the colors of water. In Figure 7, one of these tiles is shown, with its geometric structure reproduced. In Figure 8, three possible compositions, each made with four of these, are presented.

Figure 7.
Example of tile designed by Giovanni Ponti.

Figure 8.
Different examples of compositions made with the same tiles.
After sharing the file containing the presentation of all the tiles on the classroom Google platform, the teacher asked each student to reproduce one of the tiles four times on a sheet of graph paper of specific dimensions. After drawing and coloring the four tiles, the students cut them out and placed them side by side as they pleased, observing the visual effects obtained as a result of the mutual arrangement of the tiles.
The technology teacher included the following resources in her SRRS (Figure 9):
- -
- Technological resources, like the IWB, the Internet, Google Workspace, and a slideshow about the work of Giovanni Ponti;
- -
- Material resources, like pencils, colored pencils, scissors, adhesive tape, and graph paper;
- -
- Human resources, like exchanges and sharing with colleagues.
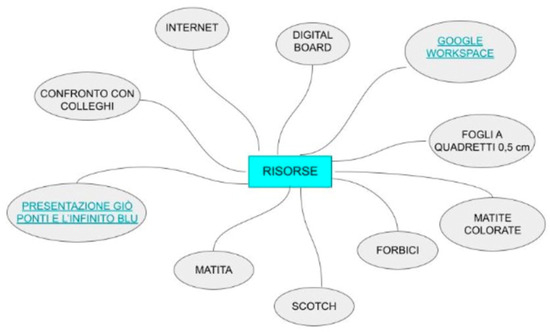
Figure 9.
SRRS created by the technology teacher for the third part of the STEAM activity.
Based on the interview with the technology teacher and her SRRS, we derived a visual summary of the document that she created for the third part of the activity, with indications about the situation in which it applies, the utilized resources, the rules of action, and the operational invariants (Table 4).

Table 4.
A visual summary of the document created by the technology teacher for the third part of the activity.
4.2.3. Music Teacher
The fourth part of the activity was conducted during a two-hour music lesson and consisted of a performance of a canon song.
Because the art teacher had introduced the concept of the axis of symmetry in a previous part of the activity, the music teacher began her session by projecting some images of very generic objects onto the interactive whiteboard and asking students to identify any symmetric figures within them, along with their corresponding axes of symmetry. Subsequently, to delve further into the discipline of music, the teacher showed the students a guitar, asking them if they could identify any symmetries within it. The students were then divided into two groups, and the teacher handed each group a small keyboard. Each group was required to observe the keyboard and identify any symmetries, marking a pencil on the key that could represent the axis of symmetry, as shown in the following figure.
Upon completion of this initial preparatory activity, the teacher explained the meaning of a canon song. The canon is a polyphonic musical form that originated around the 13th century and is based on the concept of imitation, i.e., the same melodic line is presented by multiple voices or instruments, progressively overlapping each other. A classic example of a melody with a canon structure is the famous “Frère Jacques”, known in Italian as “Fra’ Martino” or “Fra’ Martino campanaro”, a nursery rhyme and popular French song dating back to the 18th century. It is a simple and easily performable song, which is why the music teacher used it in her activity.
The teacher asked the students to sing the melody of “Fra’ Martino” in unison, reading from a score projected on the IWB. From a mathematical perspective, this unison singing activity can be likened to activities in art using mosaics and in technology using tiles.
Subsequently, the students were divided into two groups with the aim of singing the canon in two voices. The first group represented the first voice, and the second group represented the second voice. Students in the second group were instructed to imitate the singing of the first group after a two-beat delay, creating a “shift” or translation of the melody.
Following this, with the assistance of the math and support teachers present, the students were challenged to sing the canon in four voices. Two additional groups were introduced, each representing a third or fourth voice. Before replicating, or imitating, the song sung by the first group, the second group had to wait for two beats, the third group for four beats, and the fourth group for six beats, as shown in Figure 10. At the conclusion, the teacher presented two videos to the students: the first featured an instrumental canon, and the second featured the same piece but with dance, with dancers reproducing the same choreography.

Figure 10.
Example of the canon in the song “Fra’ Martino”.
Afterward, the teacher continued by projecting an image of a natural landscape on the IWB. Students were once again asked to identify symmetries and, if present, to indicate the corresponding axis that divides the figure into two equal parts. After sharing some observations and considerations about the concepts of reflection and distance, the teacher reintroduced the song “Fra Martino”, asking the students to try imagining the “reflected” melodic line. The teacher highlighted, in red lines, the “trajectory” of the notes in the “Fra Martino” melody. This way, students could more easily identify the direction of the reflected melody, i.e., an ascending line in the upper staff corresponded to a descending line in the lower staff, and vice versa. The figure below represents the reflected “Fra’ Martino” song (Figure 11).

Figure 11.
Reflected “Fra’ Martino” melody.
The axis of symmetry corresponded to the G note on the second musical staff. The teacher then asked all the students to sing the obtained melody in unison.
The music teacher included the following resources in her SRRS (Figure 12):
- -
- Technological resources, like the IWB, PC, YouTube videos, slideshows about unconventional music scores, and digital materials retrieved from the Web;
- -
- Material resources, like musical instruments and pencils;
- -
- Human resources, like students’ voices.
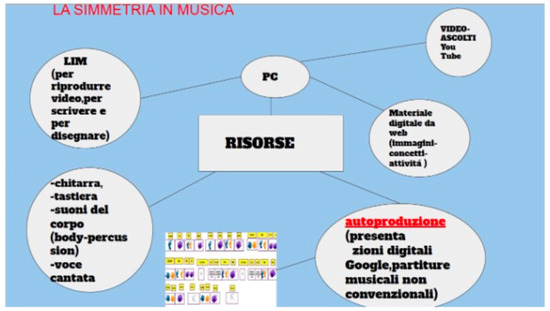
Figure 12.
SRRS created by the music teacher for the fourth part of the STEAM activity.
From the interview with the music teacher and her SRRS, we generated a visual summary of the document she designed for the fourth segment of the activity (Table 5). It includes details about the situation, the resources employed, the rules of action, and the operational invariants.

Table 5.
A visual summary of the document created by the music teacher for the fourth part of the activity.
The music teacher did not explicitly include a reference to collaboration with colleagues in her SRRS. However, throughout the entire interview, there were constant references to connections with other disciplines, demonstrating that the planning of the entire activity was conducted in collaboration with colleagues, agreeing on the connections among the different disciplines. For this reason, we inserted exchanges with colleagues as a resource on which the music teacher’s document is based.
4.2.4. Mathematics Teacher
The last part of the activity took place during a two-hour mathematics lesson focused on the construction on the Cartesian plane of geometric figures translated and symmetric with respect to the Cartesian axes. The teacher started by using the pattern of a tile design, the subject of the technology activity, as depicted in the following figure (Figure 13).
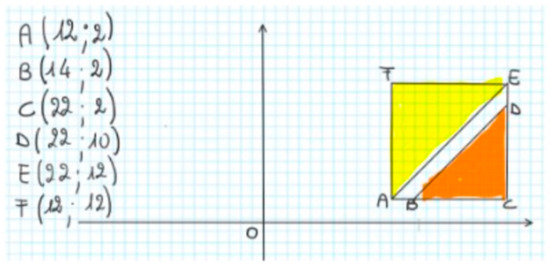
Figure 13.
Pattern of a tile in the Cartesian plane, with the Cartesian coordinates of the points in brackets.
She explained the concept of translation, prompting students to reflect on the Cartesian coordinates of the translated images and on the translation vector. The movements of the figures could occur horizontally, vertically, or diagonally, as shown in the following images (Figure 14).
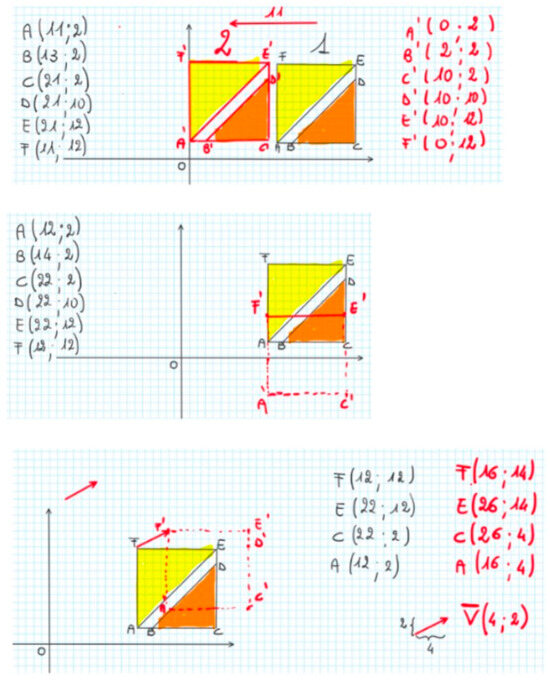
Figure 14.
Cartesian coordinates in figures translated in different directions, with the Cartesian coordinates of the points in brackets.
To conclude the explanation regarding translations, the teacher used the tiles already created in the technology activity. Initially, the teacher asked each student to reproduce their tile on the Cartesian plane, identifying the coordinates of the most important points. Subsequently, she asked to translate the obtained figure to the right, to the left, and diagonally, always identifying the coordinates of the points. All the rules related to translations were developed together with the students, noting reflections and considerations on the whiteboard. At various points in the activity, students were able to identify connections with modules previously constructed in the art activity and with the canon proposed in the music activity.
Regarding symmetry, the same process occurred. The teacher explained in detail the reflection of an image with respect to the x-axis, y-axis, and origin, always emphasizing the value of Cartesian coordinates. In this case as well, according to the mathematics teacher, students made interesting references to the art and music activities, particularly to the butterflies created with tempera colors.
The mathematics teacher included the following resources in her SRRS (Figure 15):
- -
- Technological resources, like the Internet and Google Drive;
- -
- Material resources, like textbooks;
- -
- Human resources, like previous professional experiences and exchanges with colleagues.
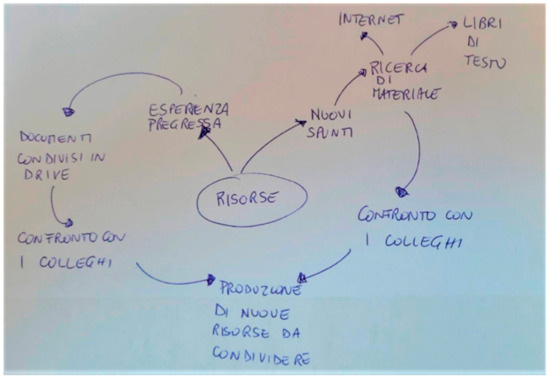
Figure 15.
SRRS created by the mathematics teacher for the last part of the STEAM activity.
Following the interview with the music teacher and her SRRS, we created a visual summary of the document she formulated for the last part of the activity (Table 6).

Table 6.
A visual summary of the document created by the mathematics teacher for the last part of the activity.
Notably, from the interview with the mathematics teacher, many resources emerged that were not enlisted in her SRRS, such as students’ comments and questions and the artifacts created in the previous parts of the activity.
4.3. Teachers’ Shared Meta-Didactical Praxeology
From the interviews with all the teachers, we could understand that they shared a common meta-didactical praxeology for the design of the STEAM activity to be implemented in their school, which guided their documentation work. This shared praxeology (Table 7) was a result of the collaborative work among the teachers and the researchers involved in the STEAM-Connect project. It entailed a significant effort as it was not natural for teachers to collaboratively design an activity centered around a common theme. Indeed, this type of collaborative work is not typically carried out in our schools in Italy, where disciplines are institutionally separated and opportunities for teachers to collaborate are few.

Table 7.
Teachers’ shared meta-didactical praxeology for the design of a STEAM activity.
The techniques to address the task of praxeology entail the proposal of embodied and hands-on activities, where the students create material artifacts or sing a song following specific instructions and can observe and experience different aspects of symmetries. The mathematics formalization of what students observe is left at the end of the activity, and the mathematics teacher is in charge of it.
The logos underlying this praxis constitute the shared conviction that engaging students in practical, hands-on activities enhances both their involvement and understanding and that these activities should be introduced prior to formalizing mathematical concepts.
In particular, from the words of the mathematics teacher, Diana, we can understand the role attributed to mathematics in the STEAM activity, which is a key for interpreting the world.
Diana: At the core of the project, there is the exploration of a path that leads students to understand that mathematics models the underlying reality. The intention is to convey the message that mathematics becomes a key to interpreting reality.
Therefore, the choice of symmetries and translations in the plane as the topic to address has been made recognizing how easily these geometric transformations can be observed in reality.
Diana: If I look around in a room or in any context, I see symmetries and translations everywhere.Diana: Mathematics serves as a unifying force in everything, it is a perspective on reality seen through mathematical eyes, but at the end of the activity.Diana: To try to describe with a metaphor the design of this activity, one can see mathematics at the center, like the largest gear of a clock, and the other disciplines as the other little gears that turn independently, not connected to each other. In the following, it happens that the central gear of mathematics shrinks, and the lateral gears enlarge, causing the other disciplines to connect with each other. In this way, the gear no longer has gaps, but it self-feeds each other.
We created the following figure (Figure 16) to illustrate the metaphor proposed by Diana for the evolution of the role of mathematics during the design process of the STEAM activity.
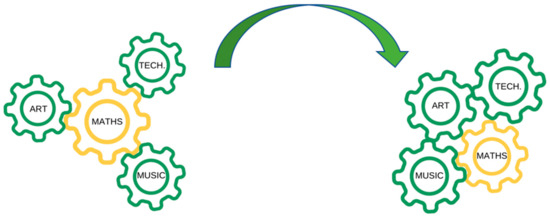
Figure 16.
Metaphor for the evolution of the role of mathematics in the design of the STEAM activity.
In the initial phases of teachers’ collaborative work for the design of the STEAM activity, mathematics had a central and predominant role, so the other disciplines did not interact with each other but only with mathematics, as if they were in service to it. In the final design of the activity, all disciplines assumed equal importance and interacted with each other, despite the original idea for the activity coming from the mathematics teacher and being centered around a mathematical topic.
5. Discussion and Conclusions
This study focused on investigating the collaborative design of a STEAM activity carried out by lower-secondary school teachers of various disciplines who collaborated within the same school in the context of the European project STEAM-Connect. Our research concentrated on analyzing the resources employed by the teachers and the utilization schemes of these resources created by the teachers themselves. Another key aim of the study was to clarify the meta-didactical praxeology adopted by the teachers for the design of the whole STEAM activity, with a specific focus on the role recognized in mathematics. We assumed that teachers’ meta-didactical praxeology guided their documentational genesis process according to the theoretical framework that we adopted, and we investigated if this praxeology was shared among all the teachers participating in the design of the STEAM activity. We delved into the teachers’ documentation work for the design of the STEAM activity through the SRRS produced by each of them and the individual interviews conducted by one of the authors with all the teachers.
We obtained two intertwined levels of results: one regarding teachers’ documentation work and one regarding their praxeology. The documentation work of each teacher was developed according to their expertise and goals, was connected to the taught discipline, and was based on a great variety of resources of diverse nature—material, technological, or human—combined with specific utilization schemes for each resource. This result is coherent with the studies by Gueudet and Trouche [17,18,19], deepening our insight into the collaborative work of teachers of different disciplines in designing a STEAM activity.
In the second level of results, we observed an emerging shared praxeology that guided all the teachers’ documentation works, thanks to a long, cohesive effort among the teachers themselves and with the researchers, re-creating the spirit of an inquiry community [26,27,28]. This praxeology was based on an overarching logos that ascribes a specific role to mathematics, that is, a lens to describe and interpret the world, as also described by [5]. These two levels of results were intertwined because the emerging praxeology was shared among the teachers from the different disciplines conducting different documentation works, giving coherence to the whole design of the STEAM activity. Indeed, the activity was designed foreseeing embodied experiences and hands-on activities related to art, technology, and music, leaving the mathematical formalization of the topic at the end to interpret what has been done before.
Our two levels of results confirm those by [11,29,30] according to which incorporating arts into STEAM not only unites the various disciplines under a broader umbrella and identity but also encapsulates the essential traits of the whole to mirror real-world challenges.
The peculiarity of this study is that interdisciplinarity was achieved by selecting a mathematical topic that has various real-world manifestations and by approaching it starting from the applications in various school disciplines. We acknowledge that there are many different ways to understand interdisciplinary approaches in the STEAM field (see, for example, [9,10]). This peculiarity is likely influenced by the fact that the mathematics teacher was the one most directly involved in the project, interacting with researchers who were, in most cases, experts in mathematics education. Despite this peculiarity, according to the mathematics teacher, the role of mathematics has evolved from the initial stages of collaboration among teachers, where other disciplines were in service to mathematics, to the final phase of the design work, where disciplines assume a more equitable role, finding spaces of mutual interaction [28].
To broaden the scope of our study as a pathway for further research, we aim to conduct a similar analysis in a case where the central topic of the STEAM activity is external to all disciplines, for example, a real-world problem, and is approached from the complementary perspectives of all the different disciplines, including the arts. This would involve studying the potential role of mathematics in such a scenario. We also aim to investigate the potential of the approach developed during the STEAM-Connect project to be adopted in diverse teacher PD programs [28] involving teachers of different disciplines with the common goal of designing interdisciplinary or transdisciplinary [3] activities for their students.
Author Contributions
Conceptualization: G.P. and O.R.; methodology: G.P. and O.R.; investigation: G.P., and E.C.; data curation: G.P. and E.C.; writing—original draft preparation: G.P.; writing—review and editing: G.P. and O.R.; supervision: O.R.; funding acquisition: O.R. All authors have read and agreed to the published version of the manuscript.
Funding
The research is partially funded by the STEAM-Connect Erasmus+ project (2021-1-LU01-KA220-SCH-000034433).
Institutional Review Board Statement
Ethical review and approval were waived for this study because the subjects who participated in the study were all adults who agreed on a voluntary basis.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Data is unavailable due to privacy restrictions.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Henriksen, D.; Mehta, R.; Mehta, S. Design Thinking Gives STEAM to Teaching: A Framework That Breaks Disciplinary Boundaries. In STEAM Education: Theory and Practice; Khine, M.S., Areepattamannil, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2019; pp. 57–78. [Google Scholar] [CrossRef]
- Maass, K.; Geiger, V.; Ariza, M.R.; Goos, M. The Role of Mathematics in interdisciplinary STEM education. ZDM Math. Educ. 2019, 51, 869–884. [Google Scholar] [CrossRef]
- Capone, R. Interdisciplinarity in Mathematics Education: From Semiotic to Educational Processes. EURASIA J. Math. Sci. Technol. Educ. 2022, 18, em2071. [Google Scholar] [CrossRef] [PubMed]
- Apostel, L.; Berger, G.; Briggs, A. (Eds.) Interdisciplinarity: Problems of Teaching and Research in Universities; OECD Publishing: Washington, DC, USA, 1972. [Google Scholar]
- Doig, B.; Williams, J.; Swanson, D.; Borromeo Ferri, R.; Drake, P. (Eds.) Interdisciplinary Mathematics Education. In ICME-13 Monographs; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Khine, M.S.; Areepattamannil, S. (Eds.) STEAM Education: Theory and Practice; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar] [CrossRef]
- Piaget, J. L’ épistémologie des relations interdisciplinaires. In Band 1 Wissenschaft als Interdisziplinäres Problem, Teil 1; Foundation Jean Piaget: Geneva, Switzerland, 2020; pp. 154–171. [Google Scholar] [CrossRef]
- Diego-Mantecon, J.M.; Prodromou, T.; Lavicza, Z.; Blanco, T.F.; Ortiz-Laso, Z. An attempt to evaluate STEAM project-based instruction from a school mathematics perspective. ZDM Math. Educ. 2021, 53, 1137–1148. [Google Scholar] [CrossRef] [PubMed]
- Williams, J.S.; Roth, W.M. Theoretical Perspectives on Interdisciplinary Mathematics Education. In Interdisciplinary Mathematics Education. ICME-13 Monographs; Doig, B., Williams, J., Swanson, D., Borromeo Ferri, R., Drake, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Williams, J.S.; Wake, G.D. Metaphors and models in translation between college and workplace mathematics. Educ. Stud. Math. 2007, 64, 345–371. [Google Scholar] [CrossRef]
- Breiner, J.M.; Harkness, S.S.; Johnson, C.C.; Koehler, C.M. What is STEM? A discussion about conceptions of STEM in education and partnerships. Sch. Sci. Math. 2012, 112, 3–11. [Google Scholar] [CrossRef]
- Wang, H.; Charoenmuang, M.; Knobloch, N.A.; Tormoehlen, R.L. Defining interdisciplinary collaboration based on high school teachers’ beliefs and practices of STEM integration using a complex designed system. Int. J. STEM Educ. 2020, 7, 3. [Google Scholar] [CrossRef]
- Pocalana, G.; Bini, G.; Robutti, O. A meta-disciplinary reflection on a STEAM school activity: The role of mathematics. In Proceedings of the 46th Conference of the International Group for the Psychology of Mathematics Education (Vol. 4), Haifa, Israel, 16–21 July 2023; Ayalon, M., Koichu, B., Leikin, R., Rubel, L., Eds.; PME: Haifa, Israel, 2023. [Google Scholar]
- Cusi, A.; Robutti, O.; Panero, M.; Taranto, E.; Aldon, G. Meta-didactical transposition.2: The evolution of a framework to analyse teachers’ collaborative work with researchers in technological settings. In Mathematics Teacher in the Digital Era, 2nd ed.; Clark-Wilson, A., Robutti, O., Eds.; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Prediger, S.; Bikner-Ahsbahs, A.; Arzarello, F. Networking strategies and methods for connecting theoretical approaches: First steps towards a conceptual framework. ZDM Math. Educ. 2008, 40, 165–178. [Google Scholar] [CrossRef]
- Pocalana, G.; Robutti, O. Evolution of didacticians’ meta- didactical praxeologies and documentation work. Int. J. Sci. Math. Educ. 2023, 22, 211–233. [Google Scholar] [CrossRef] [PubMed]
- Gueudet, G.; Trouche, L. Towards new documentation systems for mathematics teachers? Educ. Stud. Math. 2009, 71, 199–218. [Google Scholar] [CrossRef]
- Gueudet, G.; Trouche, L. (Eds.) Resources vives. In Le Travail Documentaire des Professeurs en Mathématiques; Presses Universitaires de Rennes/INRP, Paideia: Rennes, France, 2010. [Google Scholar]
- Gueudet, G.; Trouche, L. Teachers’ work with resources: Documentational geneses and professional geneses. In From Text to ‘Lived’ Resources: Mathematics Curriculum Materials and Teacher Development; Gueudet, G., Pepin, B., Trouche, L., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 23–41. [Google Scholar] [CrossRef]
- Arzarello, F.; Robutti, O.; Sabena, C.; Cusi, A.; Garuti, R.; Malara, N.; Martignone, F. Meta-didactical transposition: A theore-tical model for teacher education programmes. In The Mathematics Teacher in the Digital Era; Clark-Wilson, A., Robutti, O., Sinclair, N., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 347–372. [Google Scholar] [CrossRef]
- Chevallard, Y. La transposition didactique du savoir savant au savoir enseigné; La Pensée Sauvage: Grenoble, France, 1985. [Google Scholar]
- Chevallard, Y. L’analyse des pratiques enseignantes en théorie anthropologique du didactique. Rech. Didact. Math. 1999, 19, 221–266. [Google Scholar]
- Aldon, G.; Arzarello, F.; Cusi, A.; Garuti, R.; Martignone, F.; Robutti, O.; Soury- Lavergne, S. The meta-didactical transposition: A model for analysing teachers education programs. In Proceedings of the 37th Conference of the International Group for the Psychology of Mathematics Education—Mathematics Learning across the Life Span, Haifa, Israel, 28 July–2 August 2013; Lindmeier, A.M., Heinz, A., Eds.; PME: Haifa, Israel, 2013; Volume 1, pp. 97–124. [Google Scholar]
- Pocalana, G.; Robutti, O. Evolution of teachers’ and researchers’ praxeologies for designing inquiry mathematics tasks: The role of teachers’ beliefs. J. Math. Teach. Educ. 2024. [Google Scholar] [CrossRef]
- Pocalana, G.; Robutti, O.; Liljedahl, P. Inquiry activities are not for everyone: Teachers’ beliefs and professional development. Int. J. Math. Educ. Sci. Technol. 2023, 54, 1557–1580. [Google Scholar] [CrossRef]
- Jaworski, B. Theory and practice in mathematics teaching development: Critical inquiry as a mode of learning in teaching. J. Math. Teach. Educ. 2006, 9, 187–211. [Google Scholar] [CrossRef]
- Pocalana, G.; Robutti, O. Mathematics teacher educators work to foster an inquiry community. In Proceedings of the 45th Conference of the International Group for the Psychology of Mathematics Education, Alicante, Spain, 18–23 July 2022; Fernández, C., Llinares, S., Gutiérrez, A., Planas, N., Eds.; PME: Haifa, Israel, 2022; Volume 3, pp. 323–330. [Google Scholar]
- Falls, Z. Beyond boundaries: Pre-service teachers’ experiences of transdisciplinary education via STEAM making projects. In Proceedings of the Society for Information Technology & Teacher Education International Conference, Las Vegas, NV, USA, 18 March 2019; Graziano, K., Ed.; Association for the Advancement of Computing in Education (AACE): Waynesville, NC, USA, 2019; pp. 1556–1562. [Google Scholar]
- Quigley, C.F.; Herro, D. An Educator’s Guide to STEAM: Engaging Students Using Real-World Problems; Teachers College Press: New York, NY, USA, 2019. [Google Scholar]
- Shashidhar, B.; Bhesh Raj, M.; Wandee, K.; Hassan, T.; Munkhjargal, G.; Adeeb, J. At the dawn of science, technology, engineer-ing, arts, and mathematics (STEAM) education: Prospects, priorities, processes, and problems. Int. J. Math. Educ. Sci. Technol. 2022, 53, 2919–2955. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).