Cognitive Control among Primary- and Middle-School Students and Their Associations with Math Achievement

Abstract

Background: Math achievement is an important predictor of academic success. While many studies have examined math achievement in young children, studies with older children are scarce. This study focused on primary- and middle-school students, examining math achievements and cognitive control. Cognitive control was assessed referring to both domain-specific and domain-general cognitive control mechanisms and eliciting both simple and complex levels of conflict, and their association with math achievements. Methods: One-hundred-and-twenty-two participants performed two versions of a cognitive control task: a numerical Stroop task (NST; manipulating the numerical and physical size of Arabic numerals) and a perceptual Stroop task (PST; manipulating the location and direction of an arrow). For math achievements, participants performed math fluency and math curriculum tests. Results: Overall, the congruency effect was smaller in older students than in younger ones. Moreover, all participants demonstrated a similar congruency effect in the simple conflict task, whereas younger students showed a larger congruency effect in the complex conflict task. In addition, performance on the basic math fluency task was predicted by both Stroop tasks. However, performance on the comprehensive math achievement test was predicted only by the PST. Conclusions: Our results demonstrated enhanced cognitive control abilities of middle-school students and suggest that they can contribute to math achievements. We call for considering the implementation of both domain-specific and domain-general cognitive control activities as a potential approach to support math achievements.

1. Introduction

Mathematical performance is important for everyday life in modern society. Math performance impacts academic success from primary school, specifically in STEM (science, technology, engineering, and mathematics) subjects, to higher education [1], paving the way to better employment options and quality of life, decision making [2], and health [3]. Researchers have highlighted the developmental changes in mathematics since acquiring mathematical skills requires attaining knowledge, which is absorbed step by step during the individual’s schooling over the years [4]. For example, the capacity to solve math exercises automatically comprises a significant foundation for performing more complex calculations and forms the basis of higher mathematical comprehension [5,6,7].

Numerical representations among children are established and developed by their experience, with the development of formal mathematical knowledge. Moreover, the individual’s neuro-cognitive development of numerical representations and calculation abilities is related to the development of specific and general cognitive mechanisms, such as attention, cognitive control, working memory, and one’s experience and environment [8].

Many studies have examined math performance in primary school (e.g., [9,10,11]), suggesting that domain-specific alongside domain-general factors predict math achievement. Domain-specific factors in the context of math achievement are related to basic numerical cognitive abilities, including the approximate number system [12,13], mental number line [14,15,16], subitizing [17,18], ordinal processing [11], and automatic processing of Arabic numerals [19,20].

Other studies have emphasized the importance of domain-general factors significant for mathematical functioning, such as working memory (e.g., [21,22,23,24]), attention and executive abilities (e.g., [25,26,27]).

One of the critical domain-general factors is executive functions (EFs). EFs comprise a range of high-level skills, such as inhibition, planning, organization, and conflict resolution [28,29]. EFs develop during childhood and adolescence [30], enabling the individual to control their behavior and thoughts, contributing to the ability to make coherent plans for fulfilling internal goals [31].

A recent meta-analysis found that EF had a significant impact on academic outcomes in elementary school [32]. Specifically, previous studies have demonstrated a strong relationship between children’s EFs and their academic performance in math, suggesting that mathematical development and EF development are intertwined [25,27,33,34,35,36,37,38]. EFs were found to be a strong predictor to math achievement even when controlling for IQ and childhood socioeconomic status [27]. However, most studies examined children only up to the sixth grade. Indeed, it is possible that the role of EF components in math performance increases during adolescence [39]. Thus, a deeper examination of the complex relationship between EF and math is needed [25], especially among adolescents. Investigating this relationship among adolescents is critical due to the increased complexity of math in middle school.

One of the central components of EFs is the individual’s ability to navigate conflicting situations that trigger competing responses, necessitating the suppression of responses to irrelevant information (henceforth, termed cognitive control, and specifically conflict resolution). A common task for evaluating cognitive control is the Stroop task, presenting two conflicting dimensions of a stimulus, thus activating conflicting responses. In this task, faster reaction times (RTs) are expected in congruent conditions (i.e., where both dimensions converge, presenting no conflict between the dimensions) than in incongruent conditions (i.e., when the two dimensions conflict) [36], known as the congruency effect. A larger congruency effect indicates a lower cognitive control ability.

The Stroop task comprises two subtasks. In the simple-conflict level subtask, participants are instructed to respond to the more salient aspect. In the complex-conflict level subtask, participants need to suppress responses to the more salient irrelevant aspect of the stimuli. Thus, higher cognitive control is critical for performing the complex-level conflict subtask. Faster reaction times (RTs) are expected in simple level conditions than in complex level conditions. However, previous research has not focused on comparing congruency effects at different levels of conflict tasks [40,41].

Various conflict resolution tasks have been developed in the design of the Stroop task. The numerical Stroop-like task (NST) manipulates an Arabic numeral’s physical size and numerical value. In the NST, participants are presented with two digits side by side and are instructed to respond to the larger digit. In the congruent condition, the physically larger digit has a higher numerical value than the other digit (e.g., $3$ 5); see Figure 1A. In the incongruent condition, the physically larger digit has a lower numerical value (e.g., 3 $5$); see Figure 1C. The task includes two subtasks. In the physical subtask (the simple-conflict level), participants are instructed to respond to the physical dimension, and in the numerical subtask (the complex-conflict level), participants are instructed to respond to the numerical dimension [42]. Previous studies have examined the developmental trajectory of automatic numerical processing among primary-school children, applying the NST (e.g., [40,43]). The findings revealed that the congruency effect appeared at the end of first grade and continued to develop until fifth grade. Importantly, the congruency effect emerges in the beginning of primary school, but with age, it decreases, indicating the maturation of cognitive control abilities, which in turn attenuates the processing of the numerical value of the digit, when it is the irrelevant dimension of the stimulus. Further, NST studies found a decrease in the efficacy of the congruency effect among participants with developmental [20] and acquired [44,45] arithmetic disabilities. Nevertheless, it remains unclear whether Arabic number processing continues to develop beyond the fifth grade and whether it predicts mathematics performance in middle school.

Numerous Stroop-like tasks involve the processing of domain specific notation as letter (as in the classical Stroop task) or digit recognition, as in the NST. Another conflict resolution task, which minimizes the involvement of semantic processing, is the perceptual Stroop task (PST), which manipulates basic features such as the location (position) and pointing direction of an arrow. The position of the arrow on the screen (above/below the center of the screen) is perceived intuitively, independent of reading or numeracy acquisition or language.

In the PST, a single arrow is presented above or below a fixation mark (i.e., the arrow’s location), which can point up or down (i.e., the arrow’s direction). Here, too, the task comprised a congruent condition (e.g., an arrow located above the fixation mark, pointing up) (see Figure 1B) and an incongruent condition (e.g., an arrow located above the fixation mark, pointing down) conditions (see Figure 1D). In the location subtask (the simple-conflict level), participants were required to judge the arrow’s location, ignoring its direction, and in the direction subtask (the complex conflict level), vice versa, participants were required to judge the arrow’s direction, ignoring its location. Previous studies have shown that children in primary schools and middle schools presented a congruency effect in the PST task [41,46].

Importantly, both the NST and the PST examine conflict between different dimensions, but only the NST includes numerical processing. Thus, incorporating both tasks in a single study enabled us to examine the respective contributions of the domain-specific cognitive control mechanism (i.e., involving numerical processing in the NST) and the domain-general cognitive control mechanism (i.e., involving non-semantic processing in the PST) as predictors of math achievement for children and adolescents.

The current study is a cross-sectional study examining math achievement in sixth graders (end of primary school) and eighth/ninth graders (beginning of middle school) and their associations with cognitive control mechanisms.

Importantly, participants’ age groups in the present study were chosen due to several considerations: first, it was important to compare between primary and middle schools. The primary-school math curriculum emphasizes basic mathematical operations and procedures, while the middle-school math curriculum places greater cognitive demands on students. We focused on the end of primary school to examine children who already acquired basic mathematical skills [9]. Second, EF development continues throughout childhood and adolescence [30]. Thus, comparing between primary- and middle-school students can shed light on the role of EF in math achievements across two separate time points, including when EF is more mature.

In addition, whereas most studies examined measurements of math achievement using mostly math facts tests [47,48], we assessed math achievement with a math fact test in addition to a comprehensive curriculum-based math test for each grade level.

Our research questions were:

• What are the changes in cognitive control abilities with age? We hypothesized that middle-school students would present better conflict resolution (i.e., a smaller congruency effect) in both the NST and the PST than sixth graders.
• Is there a difference between the two types of conflict tasks (i.e., NST vs. PST) and between levels of conflict (i.e., simple vs. complex), and how does this difference change with age? We hypothesized that PST would be easier than NST, resulting in a smaller congruency effect in PST compared to NST. Moreover, we hypothesized that a simple level would be easier than a complex level, resulting in a smaller congruency effect in location compared to direction, and in physical compared to numerical comparisons. However, the difference between tasks may be reduced with age.
• Most importantly, our main research question aims to investigate the association between cognitive control and math achievement, and whether this association changes when dealing with basic vs. comprehensive math achievements. We hypothesized that the domain-specific cognitive control task (i.e., NST) would predict basic performance of math achievement (i.e., math fluency). In addition, we hypothesized that both the domain-general (i.e., PST) and domain-specific (i.e., NST) cognitive control factors would predict math performance as manifested in the comprehensive math achievement task (i.e., curriculum test).

Note, however, that due to a lack of previous relevant studies with adolescents, our hypotheses for research questions 2 and 3 were partially explorative.

2. Materials and Methods

2.1. Participants

Sixty-two sixth graders (in the current study, as in most schools in Israel, sixth grade is the final grade in primary schools, and eighth and ninth grades are part of middle schools) (29 females, mean age 11.6, SD = 0.3) and sixty eighth and ninth graders (34 females, mean age 14.1, SD = 0.5) participated in the study. Chi-square analysis revealed no difference in gender distribution between the two age groups, t = 1.2, p = 0.3.

2.2. Procedure

The research protocol was approved by the Chief Scientist of the Ministry of Education in Israel and the Ethics Committee of Tel-Aviv University. Participants were recruited from eight public schools in Israel—four primary and four middle schools. Approval was obtained from the school principal, and all parents and students signed an informed consent form. Each student participated in two sessions, administered on separate days. The order of the Stroop tasks (NST and PST) was counterbalanced. All sessions were performed in a quiet room during the school day, and students used noise-cancelling headphones during the tasks.

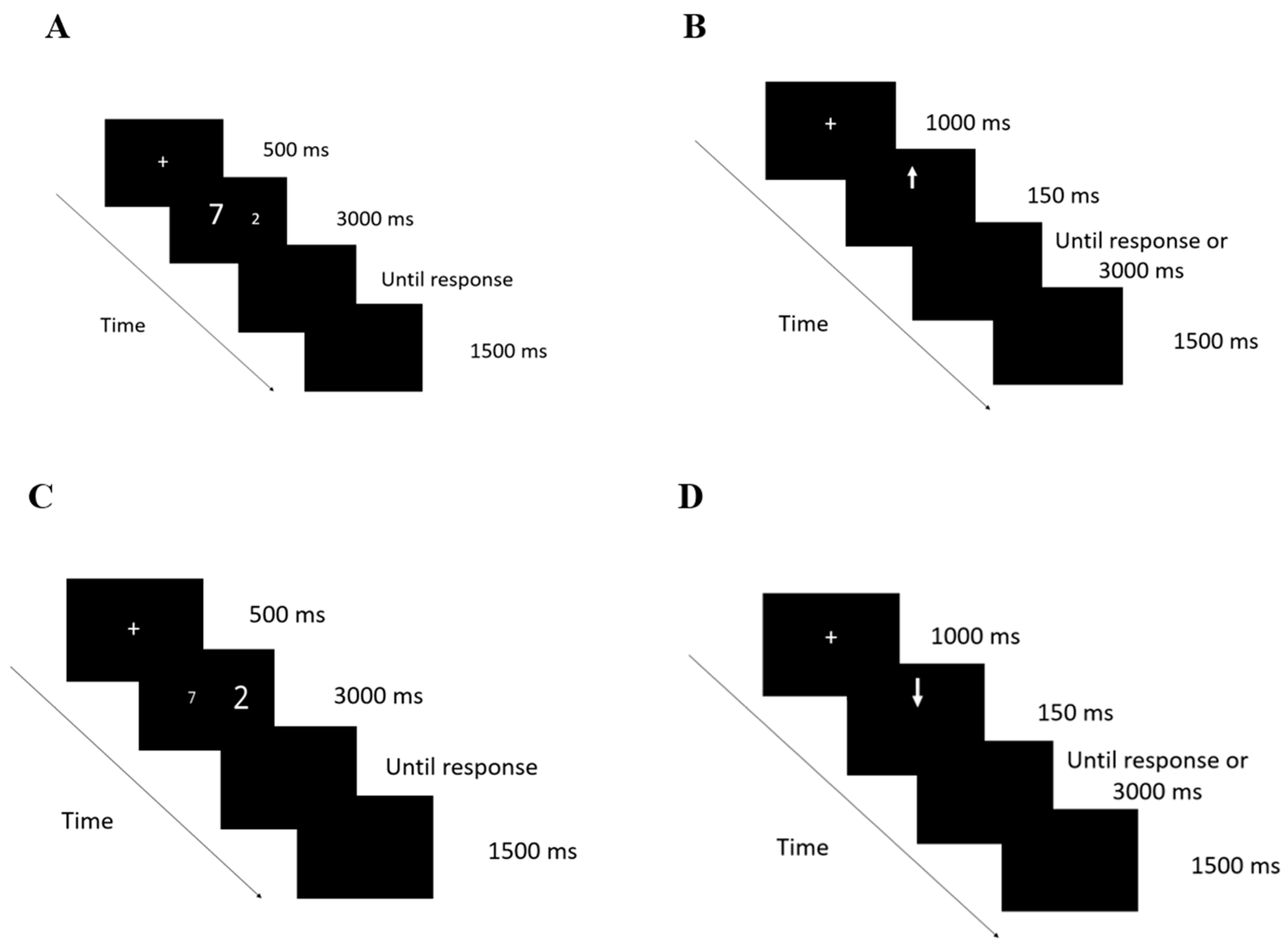
2.3. Tasks

2.3.1. Computerized Tasks

Participants completed two computerized tasks: the perceptual Stroop task (PST) and the numerical Stroop task (NST). Participants were instructed to press the QWERTY keyboard as accurately and quickly as possible on a 15.6-inch laptop screen. Both tasks included 10–15 practice trials with feedback before administering the task.

Numerical Stroop Task (NST)

The NST stimuli consisted of two single digits, displayed side by side in the center of the screen. The two digits differed in physical size and numerical value. In two different blocks, participants were instructed to indicate by a keypress which digit was numerically or physically larger. The stimuli were presented in two conditions: a congruent condition (e.g., the physically larger digit has a larger numerical value, $3$ 5) and an incongruent condition (e.g., the physically larger digit has a smaller numerical value, 3 $5$). Two numeric distances between the presented digits were used: distance 1 (with pairs: 1 2, 3 4, 6 7, 8 9) and distance 5 (with pairs 1 6, 2 7, 3 8, 4 9). The digit sizes corresponded to font sizes 30 and 58, for smaller and larger physical sizes. The numbers were displayed in the center of the screen in an area of 8.5 × 11 cm. Both subtasks (physical and numerical) consisted of two blocks with a break in the middle. They included 64 trials in each block: 2 congruent conditions × 2 numeric distances × 4 different pairs of digits per distance × 2 sides (large number left/right) × 2 repetitions. Each trial began with a fixation cross presented for 500 ms, followed by two digits in the center of the screen. The pair of digits was presented until the participant’s response, up to 3000 ms. The next trial began 1500 ms after the participant’s response (see Figure 1A). Response keys were ‘L’ (larger right) and ‘A’ (larger left) on the computer keyboard. Both accuracy and RT were recorded. RT was measured in milliseconds from target onset to the participant’s keypress. The reported split-half reliabilities (mean of 288 split-half estimates) of the NST were 0.56 for RT and 0.42 for accuracy data [49]. An inverse efficacy score (IES) was calculated for each participant; see further description in Section 2.4 below. All participants began with the physical subtask and then performed the numerical subtask.

Perceptual Stroop Task (PST)

In the PST, a white arrow (1.7 cm high and 0.8 wide) was briefly presented 1.5 cm above or below a white fixation cross point. In the location subtask, participants were instructed to indicate by a keypress whether the arrow was presented above or below the center of the screen. In the direction subtask, participants were requested to judge whether the arrow was pointed up or down. Each subtask had two conditions: the congruent condition (e.g., an arrow located above the fixation point and pointing upward) and an incongruent condition (e.g., an arrow located above the fixation point and pointing downward). Each subtask (location and direction) consisted of two blocks with a break in the middle and included 80 trials: 2 congruent conditions × 2 locations (up and down) × 20 repetitions. Each trial began with a fixation cross that lasted for 1000 ms, followed by the arrow for 150 ms. The brief presentation duration in the PST was essential to refrain from eye movements. A black screen appeared until the participant responded. The subsequent trial began 1500 ms after the response (see Figure 1B). The keyboard response keys were ‘L’ (above/up) and ‘A’ (below/down). Both accuracy and RTs were recorded. RT was measured from the target’s onset to the participant’s keypress. The reported split-half reliabilities (mean of 100,000 split-half estimates) of the PST were 0.95–0.96 for RT data and 0.75–0.83 for accuracy data [46]. An IES was calculated for each participant. For all participants, the location subtask preceded the direction subtask.

2.3.2. Math Achievement Measures

Math achievement was assessed by two tests: a math fluency test, examining performance on simple math exercises, and a curriculum-based math test, aligning with Ansari [50]. The tests were conducted in a paper-and-pencil format.

Math Fluency

The math fluency test was taken from the Woodcock–Johnson III Test of Achievement [51]. The test includes 160 simple single-digit arithmetic exercises, tapping addition, subtraction, and multiplication skills. Participants were given three minutes to solve as many problems as possible without skipping. Performance scores were derived from participants’ accuracy rate and number of solved exercises.

Curriculum-Based Math Test

Committees of professional experts developed the country-wide curriculum math tests under the supervision of The Ministry of Education of MASKED. The tests included the knowledge and skills as defined in the math curriculum. One-hundred-and-six students performed the 90 min test. The test was administered and scored by the participating schools’ math teachers. The tests included verbal questions, close-ended questions, and open-ended questions. For sixth graders, the test included simple and decimal fractions, calculating natural numbers including zero, data analysis, probability calculations, geometry, and measurements. For eighth and ninth graders, the test included algebra (e.g., an equation with two variables, functions), numerical (e.g., calculation rules, verbal question of power, square roots, adjusted numbers), and geometry (e.g., calculation of area and volume of geometrical shapes). As the tests differed for each grade, Z-scores were calculated for each age group.

2.3.3. Non-Verbal Intelligence

Non-verbal intelligence was assessed using Raven’s Progressive Matrices, applied in two versions due to different age norms. A colored version, Colored Progressive Matrices (CPM [52]), was administered to the sixth graders, and the Standard Progressive Matrices (SPM [53]) was administered to the eighth and ninth graders. No differences were found between groups in the Z-score of the Raven, t(120) < 1.

2.4. Statistical Analyses

In both Stroop tasks, trials that were slower or faster than 2 SD from the participant’s average RT were excluded from the analysis. NST and PST performance was assessed using a combined single dependent variable called the inverse efficiency score (IES). The IES variable derives from the mean RT on accurate responses and accuracy rates (i.e., (Mean RT_Correct/Accuracy Rates) for each condition). IES is expressed in milliseconds. However, it indicates the time spent for correct responses. When there is a trade-off between speed and accuracy, the IES effect will compensate for the differences in the percentage of incorrect responses [54]. A congruency effect in each Stroop task was calculated as the difference between IESs of congruent and incongruent trials. A lower IES score means a more efficient performance. All reported planned comparisons were conducted according to the Bonferroni correction.

3. Results

Descriptive statistics of accuracy rates and RTs for each condition in each age group presented in the Supplementary Materials.

First, we present the effects of age on performance in the domain-specific and domain-general cognitive control tasks. Then, we present their relation to math achievement.

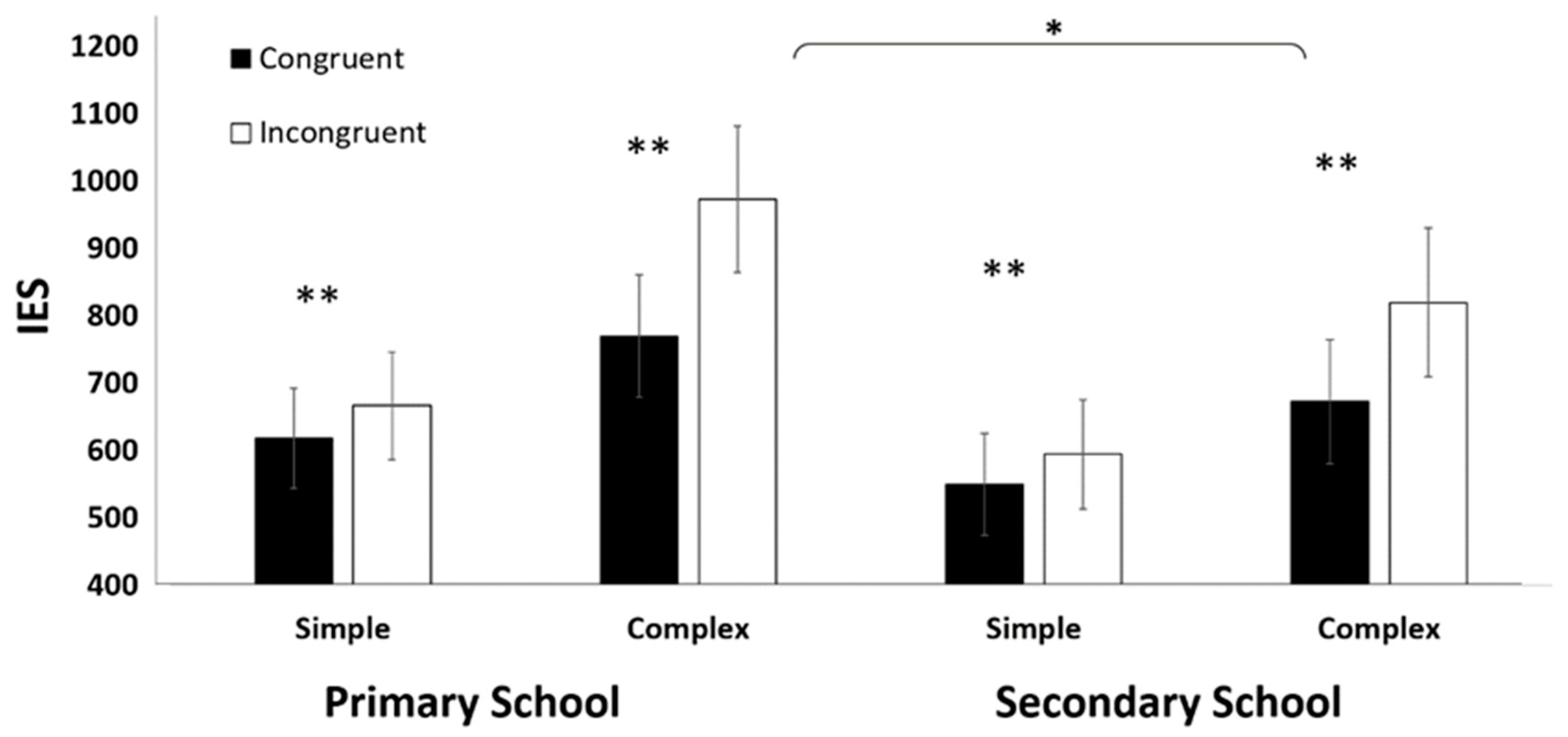
3.1. Cognitive Control by Task Type and Age Group

An ANOVA using inverse efficiency scores (IES) was carried out on the following variables: 2 (task: NST vs. PST) × 2 (conflict level: simple conflict, NST-physical and PST-location; and complex conflict, NST-numerical and PST-direction) × 2 (congruency: congruent vs. incongruent) × 2 (age group: primary vs. middle school).

A significant main effect for age group was found, showing that the middle-school students were more efficient (M = 659.03, SD = 127.04) than the primary-school students (M = 757.75, SD = 169.15), F(1,120) = 19.66, p < 0.001, p_η² = 0.14. Furthermore, a significant main effect for task was found, as PST performance was more efficient (M = 685.36, SD = 149.01) than NST performance (M = 732.56, SD = 163.64), F(1,120) = 31.20, p < 0.001, p_η² = 0.2. Also, a significant main effect for congruency was found, with a more efficient performance in the congruent condition (M = 653.03, SD =130.14) than in the incongruent condition (M = 764.40, SD = 162.57), F(1,120) = 384.00, p < 0.001, p_η² = 0.8. Finally, a significant main effect for conflict level was found, as the IES in the simple-conflict conditions was smaller (M = 607.91, SD = 94.86) than in the complex-conflict conditions (M = 809.51, SD = 97.91), F(1,120) = 401.05, p < 0.001, p_η² = 0.8.

Among the interactions between all independent variables of this analysis, those involving age groups were the most critical and relevant for our study, of which four were significant. First, the task × age group interaction was significant (see Figure 2A), F(1,120) = 17.67, p < 0.001, p_η² = 0.13. Planned comparisons revealed a significant difference between tasks among primary-school students (t = 6.98, p < 0.001) but not among middle-school students (t < 1, n.s.).

Second, the congruency × age group interaction was significant (see Figure 2B), F(1,120) = 7.49, p = 0.007, p_η² = 0.06. Planned comparisons revealed that both age groups demonstrated a congruency effect (t = −15.92, p < 0.001; t = −11.89, p < 0.001, for primary- and middle-school students, respectively). Most importantly, the congruency effect was larger for primary-school students than for middle-school students (t = 4.3, p < 0.001, d = 0.4). See Figure 2. This result suggests that primary-school students presented lower cognitive control abilities.

Third, the conflict level × age group interaction was significant (see Figure 2C), F(1,120) = 7.3, p = 0.008, p_η² = 0.06. Planned comparisons revealed that the performance difference between conflict levels was larger for primary-school students than for middle-school students (t = −4.2, p < 0.001, d = 1.6).

Fourth, the triple interaction of age group × conflict level × congruency was significant (see Figure 3), F(1,120) = 5.9, p = 0.02, p_η² = 0.05. Planned comparisons revealed significant congruency effects on all levels (primary school simple: t = −4.41, p < 0.001, d = −0.3; primary school complex: t = −18.29, p < 0.001, d = −1.29; middle school simple: t = −4.6, p < 0.001, d = −0.71; middle school complex: t = −11.77, p < 0.001, d = −1.89. In addition, performance differences between age groups in congruency effect appeared on the complex-conflict level, (t = 8.1, p = 0.005, d = 0.7), but not on the simple-conflict level (t < 1, n.s.).

In addition, the congruency × conflict level interaction was significant, F(1,120) = 131.08, p < 0.001, p_η² = 0.52. The congruency effect was larger in the complex conflict than in the simple conflict (t = −27.12, p < 0.001). This finding confirmed that the conflict resolution tasks used in the present study comprised two difficulty levels, as planned.

The task × congruency interaction was significant, F(1,120) = 8.08, p = 0.005, p_η² = 0.063. As expected, significant congruency effects were obtained in both tasks (t = −17.14, p < 0.001; t = −13.62, p < 0.001, for NST and PST, respectively), but the congruency effect was larger for the NST than the PST (t = 4.52, p < 0.001).

The task × conflict level interaction was significant, F(1,120) = 106.34, p < 0.001, p_η² = 0.47. In both tasks, performance in the simple-conflict subtask was better than in the complex-conflict subtask for NST (t = −22.1, p < 0.001) and for PST (t = −9.5, p < 0.001), with a greater difference for the NST than the PST (t = −2.8, p = 0.005).

The task × conflict level × congruency interaction was significant, F(1,120) = 25.76, p < 0.001, p_η² = 0.18. Planned comparisons revealed that the complex subtasks revealed larger congruency effects than the simple subtasks, t = 6.8, p < 0.001. Moreover, in the simple subtasks, IES was more efficient for the NST than for the PST (t = −4.3, p < 0.001), whereas in the complex subtasks, IES was more efficient for the PST than for the NST (t = 15.6, p < 0.001).

The following three-way interactions did not yield significance (all Fs < 1): age group × task × congruency, age group × task × level, and age group × task × congruency × level.

Note, since the interaction of age group × task × congruency was a specific research question in our study, and aligning with the a priori hypotheses, a follow-up analysis comparing congruency effect in each task separately for each age-group.

Planned comparisons revealed that primary-school students presented a difference in the congruency effect between PST and NST (F = 5.55, p = 0.02), but middle-school students did not (t = 2.78, p = 0.12). Moreover, the differences between age groups in congruency effects were presented in both tasks, F = 4.44, p = 0.037; and F = 4.87, p = 0.029; for PST and NST, respectively.

See further figures of all the reported effects in the Supplementary Materials.

3.2. Correlations between the Cognitive Control Tasks

We calculated a general congruency effect for each task (i.e., PST, NST). The correlations between the IES in the two cognitive control tasks were significant among middle-school participants (r = 0.41, p = 0.001) but not for primary-school students (r = 0.14, p = 0.3).

3.3. Math Achievement Measures and Their Associations with Cognitive Control Tasks

3.3.1. Math Fluency Test

The test was uniform for both grade levels. Middle-school students were more accurate in math fluency (M = 98.7%, SD = 1.9) and solved more exercises (M = 64.7, SD = 14.0) than primary-school students (M = 97.9%, SD = 2.1; M = 60.5, SD = 12.9; accuracy: t(120) = 2.1, p = 0.04; d = −0.38), number of exercises: t(120) = 1.7, p = 0.08, d = −0.3.

3.3.2. Curriculum-Based Math Test

The test differed between grade levels, as each grade had a test according to their curriculum. Both primary-school (M = 78.69, SD = 16.44) and middle-school (M = 78.02, SD = 16.47) students performed similarly on the tests, t(104) < 1. No differences were found between groups in the Z-score of the test, t(105) < 1.

3.3.3. Correlations and Regressions

We estimated the contribution of each cognitive control predictor to math achievement measures (i.e., math fluency and curriculum math tests), using correlations and linear regressions. See

Table 1. Correlations between cognitive control and math achievement measures by age group.

	Primary Students		Middle Students
	Math Fluency	Math Curriculum	Math Fluency	Math Curriculum
Raven Z-score	0.22	0.49 **	0.14	0.40 *
PST
Location-congruency effect	−0.27 *	−0.27 *	−0.25 *	−0.31 *
Direction-congruency effect	−0.16	−0.18	−0.14	0.11
NST
Physical-congruency effect	0.03	−0.22	−0.03	−0.21
Numerical-congruency effect	−0.33 *	−0.10	−0.25 *	−0.13

Note. *—p < 0.05, **—p < 0.01. Curriculum math performance was reported as Z-scores.

.

Findings revealed differences between the basic and comprehensive math achievement tests and their relation to cognitive control tasks. The basic math fluency test correlated negatively with location and numerical congruency effects. The comprehensive math curriculum test correlated positively with the Raven and with the location congruency effect but did not distinguish between the two age groups. Fisher’s r to z transformation revealed no differences between primary- and middle-school students. See further correlations and scatter plots in the Supplementary Materials.

The model that was tested by regression analysis was derived from the correlation coefficients; thus, it was an explorative analysis. We aimed to estimate the contribution of each cognitive control predictor (i.e., PST, NST) to math achievement measures using linear regressions. The predictors were the location congruency effect, numerical congruency effect, and Z Raven score.

Table 2. Summary of the predictors in the regression analysis for predicting performance in math achievement measures.

	Math Fluency			Curriculum-Based Test
Predictors	Estimates	CI	p	Estimates	CI	p
(Intercept)	62.58	60.33–64.83	<0.001	−0.00	0.17–0.17	0.995
Location Congruency Effect	−3.21	−5.51–−0.90	0.007	−0.21	−0.37 –0.04	0.015
Numerical Congruency Effect	−3.95	−6.23–−1.67	0.001	−0.08	0.24–0.09	0.378
Z Raven Score	1.21	−1.13–3.54	0.307	0.40	0.23–0.57	<0.001
Observations	122			106
R2/R2 adjusted	0.166/0.144			0.249/0.227

presents models of main predictors.

For math fluency, the regression model was significant, F(3,118) = 7.81, p < 0.001, for the main effects model with the predictors of PST and NST, but in with the interactions. For the curriculum math test, the regression model was significant, F(3,102) = 11.29, p < 0.001, for the main effects model with the predictors of Raven and PST, but in with the interactions. The predictors of each model and their β value and significance are reports in Table 2.

A regression model that included the interactions between age group and congruency effects revealed that these interactions were non-significant. See the full report in the Supplementary Materials. In the next section, we further discuss these results.

4. Discussion

The current study examined math achievement in primary- and middle-school students using domain-specific and domain-general cognitive control tasks (i.e., numerical and perceptual Stroop-like tasks), with two levels of complexity (i.e., simple vs. complex conflict level) in each one. Administering two types of conflict resolution tasks in a single experimental design provided compelling evidence regarding the involvement of domain-specific and domain-general cognitive control mechanisms in math achievement in different age groups.

In conflict tasks, the congruency effect was measured. A larger congruency effect indicates a lower executive function ability. In each conflict task, we used the IES measure of performance, which combined both RTs and accuracy rates. Lower IES indicates more efficient performance. We found that sixth graders’ performances were less efficient in the NST than in the PST. Moreover, sixth graders demonstrated larger congruency effects than the eighth and ninth graders in both cognitive control tasks. Importantly, a significant triple interaction between age group, conflict level and congruency was found, as sixth graders demonstrated a larger difference between congruency effects in simple-conflict and complex-conflict levels of the examined cognitive control tasks compared to middle-school students, suggesting that the cognitive control is more efficient in middle school than in primary school, beyond the stimuli type in each Stroop task. This interaction demonstrated that older participants were less prone to being affected by a more salient aspect of the stimulus when it was irrelevant compared to the younger participants. This is an important indication of the enhanced cognitive control abilities of middle-school students, in line with previous research [39].

Note that our hypothesis regarding the differences between age group, task and congruency was not supported, as this interaction did not reach significant. However, planned comparisons did indicate that only for sixth graders did the notation (i.e., type of stimuli, arrow vs. Arabic numerals) of the Stroop task impact their performance. The primary-school students exhibited differences in congruency effects between the NST and the PST, with a larger congruency effect in the NST than in the PST. However, among the middle-school students, the congruency effect was similar in both Stroop tasks. Thus, our results hint that processing notation in the context of conflict tasks changes with age, yet further research is needed.

The classical conflict Stroop task involves information conflict, namely the conflict between the information conveyed by each stimulus dimension (e.g., word ink color vs. word meaning in the classical Stroop task, number’s physical size vs. number’s value in the NST, arrow’s location vs. arrow’s direction in the PST). The information effect was calculated as the difference in IES between congruent vs. incongruent conditions. However, previous research has suggested that the Stroop task also incorporates exposure to task conflict (e.g., [55]).

Task conflict relates to the need to respond to the different stimulus dimensions (e.g., color naming vs. reading, the number’s physical size vs. value, and the arrow’s location vs. direction). Thus, task conflict is also incorporated into the congruent condition. Importantly, task conflict occurs since stimuli are strongly associated with a specific task. Our findings suggest that for primary-school students, the nature of the stimuli in conflict resolution tasks might impact their performance. Younger students appear to be more affected by the nature of the stimulus, whereas older students are more affected by the comparison between congruent and incongruent conditions. Thus, the current research sheds light on the development of the response to information conflict and task conflict, though further research is needed.

The present findings align with the seminal model of EFs suggested by Friedman and Miyake [56], who examined several EF tasks that relate to different EF components. They found that different tasks assessing the same EF have shared and distinct aspects. Our results elaborate on Friedman and Miyake’s findings, suggesting that the shared and distinct task aspects change with age. Specifically, our results may suggest that sixth graders process conflicts involving numerical information less efficiently than perceptual conflicts, whereas eighth and ninth graders perform equally well in conflicts involving numerical and perceptual stimuli. However, this suggestion should be considered carefully, as this difference appeared only in a planned comparison analysis. Importantly, we suggest that the saliency of the information plays a crucial role in responding to conflict tasks, specifically on a complex level. Taken together, we suggest that inhibitory control, a major component of EFs, consolidates during adolescence, paving the way for developing advanced controlled behaviors, especially when suppressing salient irrelevant information is required. One possible path that may allow adolescents to achieve that is through reducing contextual biases, which, in turn, leads to improved adjustment of their responses to the task requirements [56,57].

Interestingly, lower IES congruency performance presented by sixth graders in the current study was also reported for children with ADHD (Attention Deficit–Hyperactivity Disorder) in primary and middle school [41,46]. Consequently, lower performance was observed in less developed populations.

Does cognitive control contribute to math achievements? Our findings indicated that the math fluency scores correlated with cognitive control as measured by the NST and the PST in both age groups, whereas the curriculum test scores correlated only with the PST. In the correlation analysis, the easy conflict condition (i.e., the location level) was correlated with both math-fluency- and math-curriculum-based tests. Since it seems that the location level in the PST is not too difficult for all participants, including the younger age group, it may be a relatively sensitive measure of cognitive control. Consistent with this explanation is the finding that there was no significant difference between the two age groups on simple conflict tasks. However, as the Fisher r to Z analysis did not yield significant difference, we conclude that the association between cognitive control and math achievements is similar across both age groups.

Note that in the regression analysis, we included only one measure of congruency from each task. The fact that the PST contributed to the prediction of performance on the curriculum test above and beyond the prediction of general intellectual ability (measured by the Raven) strengthens its unique role. Taken together, we suggest that domain-general cognitive ability contributes to both basic (i.e., math fluency test) and comprehensive (i.e., curriculum test) math achievements among both 6th and 8th–9th students. Our findings are consistent with a previous study conducted with undergraduate students, where congruency effect in the PST was associated with the ability to resolve semantic conflicts between metaphoric and literal meanings of words [58].

Our results emphasize that studying cognitive control mechanisms in the context of math achievements holds promise. EFs are important to math as they are responsible for inhibiting incorrect responses and actions. Specifically, they may play a vital role in inhibiting inappropriate mathematical operations, for example, when carrying or borrowing numbers, and may secure the correct use of common denominators in fraction addition or subtraction. Additionally, EFs can inhibit the use of unsuitable problem-solving strategies, can aid in suppressing related but incorrect number facts, and can prevent the retrieval of irrelevant prepotent number representations. Understanding and enhancing these cognitive control mechanisms are essential for improving math achievements [59,60]. Importantly, math demands increase from primary to middle school and become more complex. Thus, the involvement of EFs in math achievements can be even more significant with age.

The central role of domain-general factors in math achievement has been reported in previous research. Students with developmental dyscalculia (DD), who suffer from poor numerical processing, also presented deficits in aspects of attention [44,45] and, specifically, in executive functions (i.e., conflict resolution [61]). Also, EFs (switching ability) contributed uniquely to symbolic numerical skills among children [62]. However, whereas most studies have focused on early childhood (e.g., [26,63]), a recent study examining EFs across the life span (from age 10 to 86) highlighted their development [64], underscoring the value of incorporating adolescents and middle-aged adults in these studies. EF skills develop relatively rapidly during the preschool and early adolescent period [39]. Thus, our study enabled a glimpse into more mature children and adolescents, neglected in previous research. Specifically, the current study explored the end of elementary school and early middle school, extending the associations between math achievement and domain-general cognitive factors in this age range.

A second explanation for the association between cognitive control and math achievement relates to the two levels of the math task demands. For the simple math fluency task, requiring recall of math facts, cognitive control alone predicted performance in both age groups. It has been suggested that recall of math facts relates to verbal phonological abilities [65]. However, in the math curriculum test, requiring more high-level math skills and abilities, other predictors, such as non-verbal intelligence (e.g., as measured by the Raven test), play a role in performance. Our findings, aligning with previous reports (e.g., [50]), highlight the importance of measuring multiple components of math achievement, specifically when examining middle-school students. Note, however, that both of our math achievement measures were paper-and-pencil tests. Future studies may use computerized math tests to increase the accuracy of RTs and duration measures of math performance.

Some limitations should be considered in the current study. First, we conducted a cross-sectional study, which limited our ability to examine developmental changes regarding the association between cognitive control abilities and math achievement. Future studies may conduct longitudinal designs to address the issue. Second, the current study focused on cognitive control mechanisms and math achievements and did not consider other factors that may influence math achievements, such as motivation, interest, socio-economic status, etc. Specifically, math anxiety, which also related to EFs and to math achievements [66], should be addressed in future studies. Note that our results indicate an associative relation between EFs and math achievements. However, only a direct intervention study may conclude of causal relationship between them. Another limitation in our study is that the durations of the fixation and the stimuli presentation in the two Stroop tasks were different. Future studies should examine whether similar presentation duration will influence congruency effects. Finally, while IES measures take into account the speed–accuracy trade-off, future studies also need to examine the influence of developmental changes in RT and control them.

The current results have important educational implications for teaching techniques. The 21st century educational skills set emphasizes applying metacognitive skills [67]. Thus, education policymakers should consider the implementation of cognitive control activities in mathematical education programs. Moreover, our results highlight the potential contribution of EF in math intervention programs. Nowadays, intervention programs for low math achievers focus mostly on young children and numerical domain-specific training (e.g., [68,69]). However, some difficulties may persist or even begin to appear in middle school due to the increased complexity of the material in math. Considering the involvement of cognitive control mechanisms in math achievement among adolescents, intervention programs in math may also incorporate EF training (e.g., [70,71,72]). It is crucial to recognize that math challenges may stem from cognitive sources beyond math itself, allowing for cognitive interventions, including cognitive control training, to improve math performance in certain cases. Hence, intervention designs should consider the student’s cognitive profile to provide personalized effective support. Further studies are needed to assess the effectiveness of interventions combining general cognitive abilities with math-specific training for different age groups. Interventions targeting EF skills have shown significant improvements not only in EF but also extended benefits in math and notable changes in brain function. By emphasizing metacognitive reflection and integrating EF training into math curricula, these interventions offer promising avenues to enhance math achievements [39]. Taken together, we call for strengthening the collaboration between researchers and educators. These thinktanks can yield theory-driven practical recommendations for teaching math and personalized support for both typical and low achievers.

5. Conclusions

Our study investigated the relationship between cognitive control mechanisms and math achievement in sixth-grade students vs. eighth- and ninth-grade students. The findings demonstrate that cognitive control mechanisms develop during the examined time window and are associated with both simple and comprehensive math achievements. These findings suggest that implementing cognitive control activities may enhance the development of math achievements in both primary- and middle-school students.