Abstract
Professional learning communities (PLCs) support the growth of educators to improve learning outcomes for all students. Guided by social constructivist and social cognitive theories, this longitudinal participatory action research study explored the implementation of an interdepartmental PLC across Hord’s five dimensions of a successful PLC—supportive and shared leadership, shared beliefs values and vision, collective learning and its application, shared personal practice, and supportive conditions. Additionally, this study explored how engaging with an interdepartmental PLC influenced participants’ collective efficacy. During the PLC, the collective expertise of mathematics teachers, administrators, and additional educational specialists (such as occupational therapists and speech and language pathologists) (n = 13) were leveraged to develop strategies for the improvement of mathematical problem solving among elementary and middle school students with disabilities. Our findings indicate statistically significant increases in the five dimensions of the PLC over time, with qualitative evidence supporting the PLC’s effectiveness. However, our findings revealed no significant increase in participants’ overall collective efficacy, a group’s shared belief that together they can achieve a desired result. Implications for practice and research are discussed.
1. Introduction
Despite years of mathematics teaching reform, the levels of mathematics achievement among students with disabilities have remained below those of their neurotypical peers, with limited progress being made []. According to the most recent NAEP [,,] results, high percentages of students with disabilities in Grades 4, 8, and 12 are continuing to score at or below the basic level in mathematics, with 93% of students with a disability being below proficient by the 12th grade []. NAEP [] testing data also show that the achievement gap between students with disabilities and their neurotypical peers is considered significant at all three tested grade levels. However, when considering achievement gaps, it is also important to look at the instruction or opportunity gaps that students may be facing. Research indicates that achievement gaps can be a manifestation of the opportunity gap in high-quality instruction provided for neurotypical students and students with identified disabilities []. Moreover, students from historically minoritized groups, such as individuals of diverse racial backgrounds and those with documented disabilities, frequently encounter fewer chances to engage in effective mathematics teaching and learning experiences [,,,]. We believe that the opportunity gap is where our attention should lie; i.e., how can we ensure that all students are provided with equitable and high-quality instruction in mathematics?
The literature focusing on enhancing the ability of educators to cultivate effective mathematics instruction for students with disabilities is limited []. Insufficient teacher preparation or limited effective professional development can result in inequities in student learning opportunities [,,]. Moreover, the backgrounds of educators teaching mathematics to students with disabilities often vary from general education to special education [,]. These diverse backgrounds and levels of expertise can contribute to divergent and fragmented instructional approaches in mathematics classrooms [,], contributing to the achievement and opportunity gaps faced by students with disabilities [,]. Removing the silos between educational areas of expertise to employ best practices in mathematics and special education together can enhance and provide more appropriate student support [,,]. An effective way to improve mathematics teaching practices is to support the needs of both general and special education teachers in a collaborative professional development model []. However, due to their differing backgrounds and levels of expertise, educators may sometimes find themselves unsure about the most effective approaches for teaching mathematics to students with disabilities [,]. Uniting educational experts from diverse backgrounds and areas of expertise not only forges a community driven by a common objective but also leads to the enhancement of teaching practices. The implementation of cross-departmental professional development has led to improvements in teaching practices for students with disabilities [,]. Expanding beyond general and special educators, collaboration with speech and language pathologists, occupational therapists, administration professionals, mathematics specialists, and reading specialists regarding teaching approaches for students with disabilities can bring in additional expertise and insights across different educational fields. As such, the present study explored the implementation of an eight-month professional learning community (PLC) that extended beyond special and general educators to include administration professionals and additional specialists, such as speech and language pathologists, occupational therapists, mathematics specialists, and reading specialists to focus on improving outcomes for elementary and middle school students with disabilities related to mathematical problem-solving strategies for word problems.
1.1. Professional Learning Communities
Teacher professional development is intended to help teachers develop new and improved skills and improve student outcomes []. From an analysis of 36 studies, Darling-Hammond et al. [] determined seven principles of effective teacher professional development: (1) being content-focused, (2) including active teacher learning, (3) being collaborative and often job-embedded, (4) modeling effective teaching practices, (5) including coaching and expert support, (6) providing teachers with feedback and reflection time, and (7) occurring over a sustained period. One successful model of professional development that makes use of the effective professional development principles is the PLC [,,].
A PLC “is an ongoing process in which educators work collaboratively in recurring cycles of collective inquiry and action research to achieve better results for the students they serve” [] (p. 10). The use of PLCs eliminates the isolation of teachers from their silos in schools and classrooms through the development of collaborative groups, with a primary focus on student learning [,,]. Following Du Four and colleagues’ [] model, PLC collaborative groups focus on student work and outcomes related to four central questions: (1) “What is it we want our students to know and be able to do?; (2) How will we know if each student has learned it?; (3) How will we respond when some students do not learn it?; and (4) How will we extend the learning for students who have demonstrated proficiency?” (p. 59). When PLCs are implemented as active, collaborative, and reflective communities of educators with the goal of improving student learning, they result in improved teaching practices and student outcomes [,,,,,,,,,,,,,,].
For nearly five decades, PLCs have led to an improvement in student learning within schools []. Research has indicated a relationship between PLCs, teacher professional growth, and student learning [,]. Historically, studies have primarily focused on PLCs solely aimed at either mathematics education or special education. For example, ndunda and colleagues [] conducted a study that showed forming university–school partnerships and including a university mathematics or science professor in a content-area PLC improved teacher practices and student achievement in general mathematics and science education classrooms. Studies conducted by Huggins and colleagues [] and Park and Bvun [] concluded that the presence of strong, supportive school leadership in mathematics PLCs resulted in a positive and collective school learning culture and improved teaching practices, with gains in student achievement. Cavanaugh and Garvey [] found that the participation of pre-service mathematics teachers in a PLC improved problem-solving pedagogy and resulted in greater links between theory and practice for pre-service teachers.
Research focused on improving special education practices through PLCs has revealed mixed results of their effectiveness, where the support of school or university leadership and the collaboration among PLC participants have been cited as primary reasons for the level of success of the PLC [,,,]. For example, Hardman [] developed web-based PLCs for special education teachers and found that most teachers passively participated by reading the posts of a few members which was attributed to a lack of school leadership encouraging participation. In this case, the teachers did not experience the collaborative nature of a PLC, and there was very little, if any, impact on student and teacher learning []. On the contrary, Courtade and colleagues [] conducted a web-based PLC study that determined an interactive online PLC decreased feelings of isolation in special education teachers and improved learning in classrooms. These studies demonstrate the importance of an intentional design that promotes meaningful collaboration resulting in productive PLCs. Additionally, the effectiveness of PLCs in a school for students on the autism spectrum revealed similar mixed results to a web-based PLC, which was largely influenced by the strength and support of school leadership []. Supportive administrative leadership who share the goal of the PLC is crucial for its success.
1.2. Cross-Departmental Professional Learning Communities
As we move to think about how to best support all students, the inclusion of both mathematics and special education teachers in common professional development opportunities seems pertinent, with research pointing to the promise of collaborative professional development. Harbour and colleagues [] implemented a two-year professional development project that focused on co-teaching between special and general educators related to high-quality mathematics for inclusive elementary classrooms, including students with disabilities. The results of the study showed not only statistically significant changes in the mathematical and pedagogical content knowledge of participants but also significant improvements in observed teacher facilitation, student engagement, and co-teaching practices.
Interdepartmental PLCs have also served as models of collaborative professional development by bringing together educators from different departments within a school to share expertise [,,]. While the available research is limited, recent studies have focused on using interdepartmental PLCs as a means of improving the practices of teachers and the outcomes for students with disabilities [,,]. Asher and Nichols [] and Feldman and Schechter [] conducted studies exploring interdepartmental PLCs of educators serving students on the autism spectrum. Asher and Nichols [] found a collaborative team that included a special educator, a general educator, an occupational therapist, and a speech and language pathologist had positive effects on teaching practices, student learning, and classroom functioning for an elementary student on the autism spectrum []. Feldman and Schecter [] explored an existing PLC made up of content-area teachers, special educators, and specialists, such as speech and language pathologists and occupational therapists, to gain insight on the factors influencing a PLC in a school for secondary students on the autism spectrum. Feldman and Schecter [] found that judgmental relationships between educators in the PLC impeded group collaboration. However, during this study, the members of the PLC and school administrators also recognized the importance of working as a collaborative team to support student learning, and identified factors needed for PLC success, such as supportive leadership, a shared common goal, dedicated time, and supportive relationships between group members [].
In an interdepartmental PLC drawing upon the expertise of mathematics education and special education, Tan and Thorius [] worked with six teachers (two general educators and four special educators) to identify ways to improve access to high-quality mathematics education for students with disabilities. Through the use of a PLC, Tan and Thorius [] found that professional identity and power tensions among the teachers in the PLC greatly impacted how the teachers implemented equitable mathematics teaching practices for their students with disabilities. During the PLC, special education teachers felt marginalized because of a perceived lack of content knowledge of mathematics, a lack of accessibility to teaching resources, exclusion from mathematics curricular decisions, and teacher mathematics anxiety. Throughout the study, the PLC became the mechanism through which power and identity tensions were addressed. The desire of teachers for shared practice and the need for systemic change were recognized, and avenues for future development in the teaching and learning of mathematics for students with disabilities were provided []. The findings of this study emphasize the need to build a community with a shared goal in which all members contribute and play a role.
2. Theoretical and Conceptual Frameworks
The framework for this study is grounded in social constructivism, specifically the social network of a PLC. This study explored how a social system for change can promote collective and collaborative inquiry and efficacy. By grounding the PLC in active participation and engagement in the learning process and by leveraging the five characteristics of effective PLCs, this study examined how interdepartmental PLCs can influence collective efficacy and classroom practices to promote access and equity in the teaching and learning of mathematical problem solving for students with disabilities.
2.1. Social Constructivist Theory and PLCs
Social constructivism, as developed by Vygotsky [], served as the primary guiding theoretical framework for this study. Within the framework of social constructivism, the learning process is often facilitated through a community of learners who collaborate to generate new knowledge [,]. Vygotsky [] emphasized that knowledge is constructed externally through social interactions and contexts and is vital to the learning process. Through a social constructivist lens, learning occurs through shared experiences among learners, aided by scaffolding and knowledge development through peer interactions and collaboration [].
Social constructivism also addresses the concept of a learner’s Zone of Proximal Development (ZPD), which represents the gap between what an individual knows or can learn independently and what they can achieve with the support of others, particularly through collaborative problem solving []. Groups of learners with diverse levels of comprehension and expertise allow for scaffolding and the opportunity to learn from more knowledgeable peers within the group []. The inclusion of diverse perspectives and expertise within these groups enables learners to develop in the learning process, achieve shared objectives, and attain a deeper understanding that may be challenging to reach individually []. Learning both with and from peers who bring additional insights and experience can enable the learner to challenge preconceived notions and construct new knowledge. This process aligns with the fundamental principles of both social constructivism and PLCs [].
2.2. Social Cognitive Theory and PLCs
In a PLC, a social network is formed from common behaviors and understandings of content, pedagogy, student needs, goals, and methods of student support []. The learning that occurs in a PLC through interactions and collaboration can be viewed through the lens of social cognitive theory [,,]. Social cognitivism supports the use of PLCs by emphasizing the importance of active participation and engagement in the learning process []. Social cognitive theory encourages learners to critically analyze and interpret new knowledge and engage in meaningful dialogues []. Through discussions and collaborative activities, learners are exposed to diverse viewpoints. Diverse opinions help facilitate learners to question prior approaches, challenge prior knowledge, and construct new understandings. Social cognitive theory has been used to examine the relationship between the communal nature of PLCs and the teacher learning that occurs in PLCs [,,]. Additionally, according to social cognitive theory, teaching is concerned with learning that occurs in a social context that is influenced by the people in that domain and the environment itself [,,]. Rooted in social cognitive theory is collective efficacy, “a group’s shared belief in its conjoint capability to organize and execute the courses of action required to produce given levels of attainment” [] (p. 477). In a learning organization, collective teacher efficacy refers to “the perceptions of teachers in a school that the efforts of the faculty as a whole will have a positive effect on students” [] (p. 480), namely, significantly higher levels of academic achievement [].
Due to the collaborative nature of PLCs, studies have been conducted to determine whether there is a relationship between collective teacher efficacy and PLCs [,,,]. High-functioning PLCs, especially with the presence of strong, supportive leadership, have been found to lead to improved teacher efficacy [,,,]. The reverse was also identified in a study by Gray and Summers [], where, in international private schools in Central and South America, collective efficacy was found to be among four factors contributing to successful PLCs. The other factors were enabling school structures, trusting in leadership, and trusting in colleagues [].
2.3. Conceptual Framework
Hord’s [,] extensive research on PLCs provides the structure used to examine the PLC in this study. Hord [] describes PLCs as “communities of continuous inquiry and improvement” (p. 9) that provide a mechanism through which educators individually and collectively change educational approaches to improve student learning. Hord [] identified five interrelated characteristics of successful PLCs and, in a later publication, refined them to be as follows: (a) shared beliefs, values, and vision; (b) supportive and shared leadership; (c) collective learning and its application; (d) supportive conditions—physical and structural factors and relational factors and human capacities; and (e) shared personal practice (see Table 1) []. Hord’s [] characteristics of PLCs have been used to evaluate the effectiveness of PLCs [,], to develop new conceptual frameworks for PLCs [,], and to design instruments that measure the effectiveness of a PLC [].

Table 1.
Characteristics of successful PLCs according to Hord and Somers [].
3. Purpose and Research Question
This study is part of a larger project that explores the relationships among an interdepartmental PLC, mathematics teacher practices, and the mathematics growth and achievement of Grade 5 and Grade 6 students with disabilities. The purpose of this study is to explore the functioning and development of an interdepartmental PLC as a social constructivist approach to learning to answer the following research questions: (1) How does an interdepartmental PLC on mathematical problem-solving strategies for students with disabilities develop across the dimensions of a PLC? (2) What is the relationship between participation in an interdepartmental PLC on mathematical problem-solving strategies for students with disabilities and the collective efficacy of PLC participants?
4. Methodology
4.1. Participants and Settings
The PLC participants consisted of five mathematics teachers and a mathematic specialist who teach Grade 5 and Grade 6, an administrator/reading specialist, two occupational therapists (OTs), two speech language pathologists (SLPs), and two reading specialists, resulting in a total of thirteen participants (see Table 2). All participants worked at a southeastern K-12, research-based independent school for students with learning differences, The Academy at Oak Grove (pseudonym), and self-selected to join the PLC and study following a recruitment meeting. All Grade 5 and Grade 6 mathematics teachers and middle school OTs and SLPs were included in the recruitment meeting. Administrators and reading specialists were invited to attend the recruitment meeting based on interest. The Academy at Oak Grove served 361 students, with approximately 95% of the students having a diagnosed disability; 70% of students having a diagnosed language-based learning disability; and many students having coexisting disabilities and needs.

Table 2.
Characteristics of PLC participants at The Academy at Oak Grove during 2022–2023.
4.2. Research Design
A participatory action research approach was used to explore the implementation of an interdisciplinary PLC focused on the mathematical problem-solving strategies of Grade 5 and Grade 6 students across the five dimensions of effective PLCs. The participatory action research approach was selected for this study because it has a social justice orientation that includes researchers and school practitioners to address problems in a school with the goal of school improvement [,,]. Action research makes use of a systematic inquiry process to gather, analyze, and report information to inform local practice or solve a local problem []. The researcher is the practitioner [], and the study takes place in the researchers’ own context, where they are “change agents who use inquiry to guide their work” [] (p. 198).
The present study, focused on forming PLCs to improve mathematics teaching practices around problem-solving strategies for word problems at an independent school for students with learning disabilities, lends itself to participatory action research. In the primary researcher’s position as the faculty chair of mathematics at The Academy at Oak Grove, supporting teachers to use and implement effective mathematical teaching practices for students with disabilities is a priority. As such, providing professional development opportunities on teaching mathematics to students with disabilities and collecting data to evaluate the effectiveness of such practices in classrooms are essential duties of the primary researcher at the school. Because problem solving was identified as an area needing improvement based on standardized test scores, designing professional development centered around mathematical problem-solving strategies for word problems was a way to impact local change. Through an interdepartmental PLC, this study sought ways to improve the mathematical thinking and reasoning skills of students with disabilities.
4.3. PLC Intervention
The interdepartmental PLC met twice per month for 40 min from October to May (see Table 3). The PLC focused on mathematical problem-solving strategies for students with disabilities using the four central questions of a PLC:

Table 3.
Overview of study timeline, 2022–2023.
- What is it we want our students to know and be able to do?
- How will we know if each student has learned it?
- How will we respond when some students do not learn it?
- How will we extend the learning for students who have demonstrated proficiency? [] (p. 59)
To answer the questions that drive a PLC [], teachers and specialists evaluated student problem-solving work samples, discussed the student work according to the four questions of a PLC, and determined possible next steps for instructional practices. Student problem-solving work samples came from student-worked examples from the school-provided curricular materials of Sadlier Math [], Progress Mathematics [], IM K-5 Math [], and IM 6–8 Math [], which correlated with the concepts covered in class throughout the school year. The mathematics specialist, administrator/reading specialist, reading specialists, OTs, and SLPs provided guidance and support to teachers in the evaluation of student work and offered suggestions for the possible next steps to take to support students in further developing the mathematical thinking and reasoning skills needed to solve word problems.
The initial four PLC meetings (see Table 3) were professional development sessions that aligned with existing research on approaches to support students with disabilities in mathematical problem-solving strategies for word problems [,,,,,,,,,,,,,,,,,,]. The areas of focus for the PD sessions were cognitive strategies, supporting language in mathematics, and evidence-based approaches for mathematical problem solving. The first PD session provided an overview of the organizational structure of a PLC [] and included cognitive strategies for solving word problems [,,,,]. The second PD session continued with cognitive strategy instruction using the Solve It! program methods []. The third PD session focused on supporting language in mathematics using Principles for the Design of Mathematics Curricula: Promoting Language and Content Development [] and Assisting Students Struggling with Mathematics: Intervention in the Elementary Grades []. The fourth PD session focused on evidence-based teaching practices using Improving Mathematical Problem Solving in Grades 4 Through 8 from the Institute of Educational Sciences [] and Assisting Students Struggling with Mathematics: Intervention in the Elementary Grades []. The principal researcher, who was also the faculty chair of mathematics, led the four professional development sessions with support from an administrator/reading specialist, SLP, and OT. The research-based and evidence-based methods of the PD sessions were used to inform subsequent PLC discussions around student work and instructional practices to support students with disabilities in using problem-solving strategies for word problems.
After the four PD sessions, the PLC sessions throughout the course of the school year focused on student work and the methods of instruction (successful and unsuccessful) used in Grade 5 and Grade 6 mathematics classrooms. The teachers of students in Grade 5 and Grade 6 brought to the PLC sessions student problem-solving work samples that aligned with the mathematics standards taught in class. As a collaborative group, the teachers, mathematics specialist, administrator/reading specialist, SLPs, OTs, and reading specialists reviewed the student work samples for evidence of understanding mathematics, language, structure, and strategies using the four central questions of a PLC. The student work was analyzed by the members of the PLC team to explore the students’ abilities to (a) make sense of the mathematics word problems, (b) work through the thinking and reasoning needed to solve a word problem, and (c) organize the work to solve a word problem. The PLC team of teachers, administrators, and specialists offered suggestions to support students in making sense of the mathematics word problems, working through the thinking and reasoning needed to solve a word problem, and organizing the work to solve a word problem, and to create extension activities for students who demonstrated mastery of problem-solving strategies for word problems. The mathematics specialist, administrator/reading specialist, OTs, SLPs, and reading specialists provided guidance and support to teachers in the evaluation of student work and the possible next steps to take to support students in further developing the mathematical thinking and reasoning skills needed to solve word problems. By looking at student work and pooling expertise and resources, the PLC of teachers, specialists, and school leadership established cohesive and comprehensive methods to support students with disabilities in mathematics classes.
4.4. Measures
4.4.1. Professional Learning Community Assessment—Revised
The Professional Learning Community Assessment—Revised (PLCA-R) [] assesses classroom and school practices as they apply to the five dimensions of a PLC—shared and supportive leadership; shared values and vision; collective learning and application; shared personal practice; and supportive conditions, which is broken into two sub-dimensions, supportive conditions–relationships and supportive conditions–structures. The PLCA-R has 52 items that are measured using a 4-point Likert scale rated from 1 to 4, with the average of scores reported in each of the five dimensions, with 1 meaning strongly disagree, 2 meaning disagree, 3 meaning agree, and 4 meaning strongly agree. The PLCA-R is an instrument with high reliability, with Cronbach’s alpha reliability ranging from 0.82 to 0.94 across the five dimensions [].
All participants of the PLC completed the PLCA-R [] before (Dec) and after (May) the collaborative portion of the PLC. From the PLCA-R, the outcomes of interest were six different scales across the dimensions of shared and supportive leadership, shared values and vision, collective learning and application, shared personal practice, and supportive conditions–relationships and supportive conditions–structures. These six total scores were created by summing the relevant individual items from each 4-point Likert scale at two time points—the beginning and end of the year—to explore potential differences between the two time points. To access sample items and scoring information, please visit https://www.plcassociates.org/assessments/formal/plca-r/ (website: accessed on 12 December 2023).
4.4.2. Teacher Collaboration Assessment Rubric
The Teacher Collaboration Assessment Rubric (TCAR) [] assesses the functioning of a PLC in four domains, namely, dialogue, decision making, action, and evaluation, and it is used as a developmental, formative, or outcome assessment of a PLC. The TCAR has 27 items organized by domain that are rated on a 3-point scale from 0 to 2, with 0 reflecting a practice that was not present, 1 reflecting a practice that was somewhat present, and 2 meaning a practice that was present. The TCAR is high in face validity, as it has undergone extensive field testing across multiple stakeholders [].
The TCAR [] was completed during observations by an external evaluator at three time points (beginning, middle, and end of the collaborative PLC intervention). The outcomes of interest were the four total scores created by summing the relevant individual items from each 3-point Likert scale at three time points—the beginning, middle, and end of the year. Additionally, a total score for PLC functioning was created by summing the 27 items across the four domains from each 3-point Likert scale. An example item for dialogue is “Team members participate equally in group dialogue; there are no hibernators or dominators” [], (p. 7). An example item for decision making is “All team decisions are informed by full group dialogue” [] (p. 7). An example item for action is “The group has clear, continuous, and accessible documentation of the instructional practices that they have stopped, started and/or changed over time” [] (p. 8). An example item for evaluation is “The team regularly analyzes the quality of their students’ actual work (i.e., work completed by their students in response to their instruction) [] (p. 8).
4.4.3. PLC Observation Notes
Anecdotal notes were taken by an outside observer during the collaborative PLC sessions that occurred from January to May. The notes provided information on activities, discussions, and experiences in the PLC. The notes were coded sentence by sentence using a priori coding to examine the development and functioning of the PLC. The a priori codes used correlated with the five dimensions of a PLC on the PLCA-R [] to align with the conceptual framework used for this study []. The notes were coded a second time to identify patterns throughout the progression of the PLC, which were then mapped and written as analytic memos to provide descriptive summaries of the data []. The analytic memos were laterally aligned with the quantitative analysis of the PLCA-R to develop, when possible, a deeper understanding of the progress and performance of each of the five dimensions of a PLC for the interdepartmental PLC.
4.4.4. Collective Efficacy Scale
The Collective Efficacy Scale (CE scale; []) measures collective teacher efficacy in a group within a school. The CE scale has 21 items that are measured using a 6-point Likert scale, with 1 meaning strongly disagree, 2 meaning disagree, 3 meaning somewhat disagree, 4 meaning somewhat agree, 5 meaning agree, and 6 meaning strongly agree. The measure has a high internal reliability Cronbach’s alpha of 0.96. Due to the collective and collaborative nature of a PLC and the highly positive effects of collective teacher efficacy on student learning [,], it was important to include collective efficacy with respect to the PLC. The CE scale 21-item long form [], completed by teachers before starting the PLC and at the conclusion of the study, was used to evaluate changes in the collective teacher efficacy of the PLC. From the CE scale, the outcome of interest was the difference between the pre- and post-intervention total scores, which were created by summing the 21 items from each 6-point Likert scale. An average of the individual teacher scores was calculated to determine a collective efficacy score for the PLC.
5. Results
5.1. Research Question 1
To answer our initial research question (how does an interdepartmental PLC on mathematical problem-solving strategies for students with disabilities develop across the dimensions of a PLC?), we considered evidence from the PLCA-R measure [], the TCAR measure [], and the PLC observation notes.
PLCA-R data, which assessed practices across the five dimensions of a PLC (i.e., shared and supportive leadership, shared values and vision, collective learning and application, shared personal practice, supportive conditions–relationships, and supportive conditions–structures), were analyzed using a Wilcoxon signed-rank test on the six scaled scores to identify the progress and growth of the PLC. The Wilcoxon signed-rank test [] is a non-parametric statistical test, and it was used to determine whether there were significant differences between the paired participant ratings of items before and after the collaborative PLC. This was carried out by testing for a non-zero median of the pre–post differences using rankings, after excluding pairs with differences of zero. Many of the pre–post differences were not normally distributed, and the sample size was small (n = 13), precluding use of the paired t-test. Data were analyzed using SPSS Statistics v29.
The median and interquartile ranges (IQRs) of the PLCA-R dimension are presented in Table 4 before the PLC collaboration component and after the PLC concluded, with the p-values calculated from the Wilcoxon signed-rank test. Because the dimensions have different numbers of items, the magnitude of each could not be compared across dimensions. Shared and supportive leadership, which consists of 11 items, increased from a median of 29 to a median of 32 (p = 0.002), while supportive conditions–structures, with only 4 items, increased from a median of 12 to 13 (p = 0.034). Shared personal practice showed the largest absolute gains in median scores from 17 to 21 (p = 0.012). The only dimension that did not show a statistically significant increase at the 0.05 level (p = 0.072) in median scores was supportive conditions–relationships; however, the growth was consistent in directionality (from 14 to 15) with the positive improvement across the other PLCA-R dimensions.

Table 4.
Medians, interquartile ranges, and Wilcoxon signed-rank p-values by dimension for PLCA-R.
To better understand which items contributed the most significance to each dimension, the median and IQRs of every item are presented in the online supplement. For shared and supportive leadership, at the end of the PLC, the participants felt that (a) they had more accessibility to key information (p = 0.003); (b) their advice was incorporated into the principal’s decisions (p = 0.014); (c) the principal proactively addressed areas where support was needed (p = 0.038); and (d) they were consistently involved in discussion and making decisions about most school issues (p = 0.039).
The TCAR measure, which assessed the functioning of the PLC in four domains (i.e., dialogue, decision making, action, and evaluation), provided additional evidence to answer Research Question 1. Descriptive statistics (see Table 5) and a visual analysis (Figure 1) were used to compare scores on each domain and the overall score. Specifically, the descriptive TCAR results are presented in Figure 1 according to the domains of dialogue, decision making, action, and evaluation, with total growth represented in blue.

Table 5.
TCAR descriptive statistics.
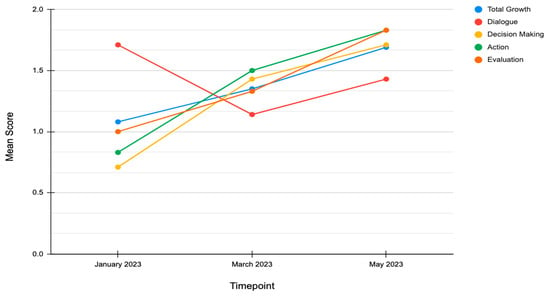
Figure 1.
Mean scores from the TCAR across three timepoints.
No statistical testing was performed using the TCAR data because only one PLC was measured at three timepoints; therefore, means and standard deviations are reported for general, non-statistical comparisons (see Table 5). Through a visual analysis and descriptive statistics, we observed approximate linear increases over the three timepoints across the overall mean TCAR measure, as well as the domains of decision making, action, and evaluation (from approximately 0.8 to 1.8). The dialogue domain, indicated in red (Figure 1), presented a unique pattern across time, with a high starting value (M = 1.71, SD = 0.49), a decrease at the midpoint (M = 1.14, SD = 0.38), and an increase by the end point (M = 1.43, SD = 0.53), although the highest value was at the start of the intervention.
To provide additional evidence to answer Research Question 1, qualitative statements and summary statements from the PLC observation notes (see Table 6) were explored, and they showed that the dimensions of the PLC, as measured using the PLCA-R, increased meaningfully throughout the collaborative portion of the PLC. For example, in the Shared and Supportive Leadership dimension, the specialists and administrators initially responded independently of each other when analyzing student work in the PLC. An example statement is [Mathematics Specialist] “What would a student need to have written to demonstrate he/she understood the standard?”. By the midpoint of the PLC, the specialists and administrators started to collaborate in their responses when analyzing student work and in their responses to mathematics teacher questions. For instance: [Speech and Language Pathologist and Mathematics Specialist] “Read it as is and then you can paraphrase”. By the end of the PLC, all members of the PLC were collaborating to analyze student work, respond to mathematics teacher questions, problem solve, and develop plans for students. An example statement is [Reading Specialist, Occupational Therapist, Mathematics Specialist, Speech and Language Pathologist] “All in agreement. Students have to answer the full question”.

Table 6.
PLC observation notes—codes aligned with PLCA-R dimensions [].
5.2. Research Question 2
To answer our second research question (what is the relationship between participation in an interdepartmental PLC on mathematical problem-solving strategies for students with disabilities and PLC participants’ collective efficacy?), we performed the Wilcoxon signed-rank test on the differences between the pre- and post-collaborative PLC CE scale measure []. Table 7 provides the medians and interquartile ranges at baseline and follow-up for the 21 items of the CE scale. The baseline median total CE score was 96 (IQR 83–107.5), out of a total possible score of 126, and the follow-up median score was 101 (IQR 84.5–106.5), showing no statistical change over the course of the PLC (p = 0.373). This high level of baseline CE is represented by the fact that the median rating was ≥4 for 90% of the items (i.e., 19 out of 21 items). The median rating was at the highest level of agreement for twenty-four percent (i.e., 5 out of 21 items) of the items, while the medians for forty-three percent (i.e., 9 out of 21 items) of the items were at the second highest level of agreement. For two individual items, there was statistically significant growth from baseline to follow-up. Item 6 states that, “If a child doesn’t want to learn teachers here give up”, showing a shift in medians from agree to strongly agree (p = 0.046). Similarly, item 1, “Teachers in this school have what it takes to get children to learn”, also shows a similar increase in medians (p = 0.008). For all but two of the items, the median score was in the average range.

Table 7.
Baseline and follow-up percentiles of the CE scale [] by item number with Wilcoxon signed-rank p-values.
6. Discussion
The National Council of Teachers of Mathematics [] calls for all students to have access to high-quality mathematics instruction. However, research shows that students with disabilities typically receive less opportunities to engage in high-quality mathematics learning, with instruction primarily based on procedures while de-emphasizing mathematical thinking and reasoning [,,]. Contributing factors to the inequities in learning opportunities often arise due to insufficient teacher preparation or limited effective professional development [,,]. Additionally, when considering those who serve students with disabilities, teachers often have varying levels of expertise in mathematics education and special education [,]. As such, it is critical to focus on the ways in which teachers are supported in meeting the needs of all students and closing the persistent opportunity gap experienced by many students with disabilities in mathematics classrooms.
Effective professional development models, such as PLCs, are one way to support mathematics educators in improving the methods of instruction [,,,]. Using social constructivist theory, social cognitive theory, and Hord’s conceptual framework for a PLC [,], the present study explored the growth of a PLC as a model of professional development for mathematics teachers of students with disabilities in terms of mathematical problem-solving strategies for word problems. A unique aspect of the present study is the interdepartmental nature of the PLC participants, where all experts serving students with disabilities collaborated and learned collectively. The goals of this study were (a) to explore the development of an interdepartmental PLC focused on improving outcomes for Grade 5 and Grade 6 students with disabilities related to mathematical problem-solving strategies for word problems and (b) to explore the influence of PLCs on collective efficacy. The findings have important implications for research and practice.
The results for Research Question 1, regarding the development of a PLC across the various dimensions [], showed significant improvements over time, as measured using the PLCA-R, in shared and supportive leadership, shared values and vision, collective learning and its application, and supportive conditions–structures. While the dimension of supportive conditions–relationships did not show significant improvements over time, it trended in the same direction as the other dimensions of a PLC. Qualitative data in the form of observation notes taken during the PLC and the quantitative data from the TCAR support the observed growth across the dimensions.
The development of the PLC was a gradual process over the course of eight months. During the beginning of the PLC, the participants primarily worked and responded independently of each other in siloed practices. Conversations were guided by a mathematics specialist with minimal sharing of teaching practices. While there was a lot of discussion, statements about student work were primarily deficits-based. Decisions regarding the teaching practices to use, the actions to take in the classroom, and the evaluation of practices, student work, and data primarily happened independently. Formal professional development in the form of presentations on cognitive strategies, language support, and evidence-based practices took place during the nascent period of the PLC and was conducted by the specialists.
Midway through the PLC, growth was seen in all dimensions, as reflected in the qualitative observation notes and the TCAR measures []. The specialists began collaborating with each other and offered joint responses. An OT gave a presentation on fine motor, visual perceptual, and visual motor skills, as they relate to mathematics, and a problem-solving template [] (p. 93) was given to teachers to use with their students. The mathematics teachers began to have conversations with the specialists and with each other about the structures that were provided, primarily the problem-solving template used for student work. The mathematics specialist provided student work samples to the group for analysis, and discussions moved from being deficits-based to being solution-based. Using the four questions of a PLC [], the members of the PLC began to evaluate students’ work and teaching practices. While the TCAR showed a mid-study increase in decision making, action, and evaluation, a decline occurred in the domain of discussion in the TCAR measure areas of an agenda for dialogue, protocols used to guide team dialogue, professional disagreements going unaddressed, and the presence of hibernators and dominators in discussion. The observational notes from the PLC indicate that a possible reason for the decline was the introduction of new structures and protocols, as teachers were becoming accustomed to them.
By the end of the PLC, structures were in place, and collaborative conversations about how to improve student learning occurred between the mathematics teachers, specialists, and the administrator in the PLC. The mathematics teachers asked questions, voluntarily brought student work to the meetings, and shared practices that did and did not work with their students, indicating a sense of trust between the members of the PLC. Practices that had been learned throughout the PLC from the specialists and from other mathematics teachers were used in classrooms. The teachers visited each other’s classrooms to observe one another. The PLC team began to look at longitudinal case studies of students who had not made progress over the course of 6–7 months to collaborate, pool expertise, and develop plans of action to support the students. The TCAR showed increases in all four domains. While dialogue increased, it did not increase to the pre-study level due to the presence of hibernators/dominators in conversations and an agenda for dialogue. An explanation for this may be due to the time of year, since observation 3 of the PLC took place in May during the final month of the school year.
Evaluating the interdepartmental PLC with the framework of the five dimensions of a PLC [] showed that the five dimensions of the PLC are complex and intertwined, developing together in stages over time. The first stage of development was learning, when participants took part in formal professional development presentation sessions and acted independently. The second stage of development was structural, when systems for PLC dialogue, student problem solving, and OT support were given. The final stage of development was collaborative, when members of the PLC worked together using their expertise to problem solve around student work samples and data in order to improve learning outcomes for students with disabilities.
The findings indicate that, by leveraging the expertise of all PLC participants, community learning was successful across the five dimensions of a PLC [,]. The PLC improved the collaboration of educators through shared and supportive leadership, shared values and vision, collective learning and its application, supportive conditions–structures, and shared personal practice with a common goal of improving outcomes for elementary and middle school students with disabilities related to mathematical problem-solving strategies for word problems. Our findings for Research Question 1 suggest that communal supportive structures can help teachers build a sense of trust that allows them to openly learn from and with others to best serve the needs of the students in their school. These positive results parallel the findings in previous research [,,,], where collaborative forms of professional development among members of a school community contributed to positive outcomes for educators and students. Similar to the findings of this study, Park and Byun [] and ndunda and colleagues [] found that supportive leadership contributed to a successful PLC. Likewise, Trahan and colleagues [] found that it is important to foster supportive conditions in communities of practice. Our findings also align with those of Harbour and colleagues [], in which the collaboration between general educators and special educators improved outcomes for mathematics educators.
The results for Research Question 2, exploring the relationship between participating in an interdepartmental PLC community and participants’ collective efficacy, showed no significant changes in overall collective efficacy over time, as measured using the CE Scale. However, collective efficacy was high at the beginning of the PLC and was also high at the end of the PLC. A possible explanation for the high collective efficacy at pre–post timepoints is that all of the participants who self-selected into the study were licensed educators or specialists, most had earned a graduate-level degree, and many had years of experience in education and in teaching at The Academy at Oak Grove. Therefore, the group of participants reported a high level of collective efficacy, with limited room for additional gains at the upper end of the CE Scale, representing a ceiling effect []. The ceiling effect may explain why no significant changes in the overall collective efficacy of the group of participants of the PLC were observed over time [,]. Even so, 2 individual items out of 21 items on the CE scale showed significant improvements. The first item was about teachers not giving up on students, and the second item was about belief in the ability of teachers at the school to get students to learn. A positive relationship between participation in a high-functioning PLC and collective efficacy has been found in prior research [,,,,]. The findings of the present study are similar to those of Gray and Summers [], where a high collective efficacy contributed to a successful PLC. With respect to the two individual items about teacher ability, the findings compare favorably to findings in prior research [,,,], where participation in a PLC contributed to an increase in collective efficacy over time.
Limitations and Future Research
As with all educational studies, the present study has limitations, which should be considered when interpreting the findings. Specifically, the limitations of the present study include the study taking place in a unique setting, influencing generalizability; the self-selection of participants and engagement in the PLC; the study sample size; and the participant demographics’ impact on collective efficacy. This study took place in an independent school for students with learning differences, and this school has a variety of professionals in place to support students. As such, the PLC was able to leverage a variety of expertise within the PLC, which may limit the generalizability of the findings in settings where students do not have access to these professionals or schools that are not specialized to support students with learning differences. Additionally, the small sample size of 13 participants limited the statistical tests that could be used [] due to the statistical assumptions underlying the test, like normality. A small sample size may affect the validity and the reliability of the results in two ways. First, the sample may not reflect the whole population of educators at schools with learning differences. Second, extreme observations may unduly influence the values of the statistical test, although this is minimized with non-parametric testing. Finally, the participants in the PLC self-selected into the study, likely leading to high collective efficacy and collaboration. Likewise, the existence of a high collective efficacy at the onset of the PLC intervention could have impacted the positive development of the PLC over time. As an action research study meant to address a local problem of practice, individual contexts and settings should be considered when transferring the results of the present study to other contexts [,].
Directions for future research include expanding the interdepartmental PLC model to different settings to determine whether similar findings occur, conducting the study in school districts that require participation in the PLC as a part of their professional development, and having a larger sample size to allow for parametric statistical analyses. Additionally, conducting the study with a group of educators whose collective efficacy has room for growth pre-intervention would provide information about the relationship between collective efficacy and an interdepartmental PLC on mathematical problem-solving strategies for word problems. Moreover, to test the generalizability of the findings of the present study, future research considerations should include public and private schools that have a more typical setting and population of students and educators. Conducting the present study in different settings with a larger and more diverse population of educators would provide a better understanding of the growth of interdepartmental PLCs over time. This may allow for the creation of a professional development model that improves outcomes for elementary and middle school students with disabilities related to mathematical problem-solving strategies for word problems and that can be used in multiple contexts and on a greater scale. Recommendations for practice are for schools to develop interdepartmental PLCs of general educators, mathematics educators, special educators, administrators, and specialists (such as speech and language pathologists and occupational therapists) to support the mathematical learning needs of their school population. The interdepartmental PLCs should have a structure around which educators can build trusting, collaborative relationships with a unified goal of improving learning outcomes in mathematical problem solving for students with disabilities.
Author Contributions
Conceptualization, D.M.P., K.E.H. and B.T.M.; methodology, D.M.P. and K.E.H.; software, D.M.P. and E.K.L.; validation, D.M.P. and E.K.L.; formal analysis D.M.P., K.E.H. and E.K.L.; investigation, D.M.P.; resources D.M.P., K.E.H. and B.T.M., data curation D.M.P. and E.K.L.; writing—original draft preparation D.M.P., K.E.H., B.T.M. and E.K.L.; writing—review and editing D.M.P., K.E.H., B.T.M. and E.K.L.; visualization D.M.P. and E.K.L.; supervision K.E.H. and B.T.M.; project administration D.M.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
This study was approved by the University of South Carolina Institutional Review Board (ID #Pro00124450).
Informed Consent Statement
Applicable consent was obtained for this study.
Data Availability Statement
The data presented in this study are available upon request from the corresponding author. The data are not publicly available due to privacy reasons.
Acknowledgments
We thank the evaluator, outside notetaker, and participants of the PLC for their dedication and contributions to the study.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Collective Efficacy Scale Descriptions [] (p. 492)
| Item | Description |
| CTE1 | Teachers in this school have what it takes to get the children to learn. |
| CTE2 | Teachers in this school are able to get through to difficult students. |
| CTE3 | If a child doesn’t learn something the first time teachers will try another way. |
| CTE4 | Teachers here are confident they will be able to motivate their students. |
| CTE5 | Teachers in this school really believe every child can learn. |
| CTE6 | If a child doesn’t want to learn, teachers here give up. |
| CTE7 | Teachers here need more training to know how to deal with these students. |
| CTE8 | Teachers in this school think there are some students that no one can reach. |
| CTE9 | Teachers here don’t have the skills needed to produce meaningful student learning. |
| CTE10 | Teachers here fail to reach some students because of poor teaching methods. |
| CTE11 | These students come to school ready to learn. |
| CTE12 | Homelife provides so many advantages the students here are bound to learn. |
| CTE13 | The lack of instructional materials and supplies makes teaching very difficult. |
| CTE14 | Students here just aren’t motivated to learn. |
| CTE15 | The quality of school facilities here really facilitates the teaching and learning process. |
| CTE16 | The opportunities in this community help ensure that these students will learn. |
| CTE17 | Teachers here are well-prepared to teach the subjects they are assigned to teach. |
| CTE18 | Teachers in this school are skilled in various methods of teaching. |
| CTE19 | Learning is more difficult at this school because students are worried about their safety. |
| CTE20 | Drug and alcohol abuse in the community make learning difficult for students here. |
| CTE21 | Teachers in this school do not have the skills to deal with student disciplinary problems. |
References
- U.S. Department of Education. Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress [NAEP]. Achievement Gap Results Mathematics (0–500 at Grades 4 and 8 0–300 at Grade 12), Students with Disabilities-Not Students with Disabilities Score Gap. U.S. Department of Education: Washington, DC, USA, 2023. Available online: https://www.nationsreportcard.gov/dashboards/achievement_gaps.aspx (accessed on 12 December 2023).
- U.S. Department of Education. Institute of Education Sciences, National Center for Education Statistics [NAEP]. Mathematics 2022. National Student Group Scores and Score Gaps, Grade 4, U.S. Department of Education: Washington, DC, USA, 2023. Available online: https://www.nationsreportcard.gov/mathematics/nation/groups/?grade=4 (accessed on 12 December 2023).
- U.S. Department of Education. Institute of Education Sciences, National Center for Education Statistics [NAEP]. Mathematics 2022. National Student Group Scores and Score Gaps, Grade 8, U.S. Department of Education: Washington, DC, USA, 2023. Available online: https://www.nationsreportcard.gov/mathematics/nation/groups/?grade=8 (accessed on 12 December 2023).
- U.S. Department of Education. Institute of Education Sciences, National Center for Education Statistics [NAEP]. Mathematics 2019. National Student Group Scores and Score Gaps, Grade 12, U.S. Department of Education: Washington, DC, USA, 2023. Available online: https://www.nationsreportcard.gov/mathematics/nation/groups/?grade=12 (accessed on 12 December 2023).
- U.S. Department of Education. Institute of Education Sciences, National Center for Education Statistics [NAEP]. Mathematics 2019. National Achievement-Level Results, Grade 12, U.S. Department of Education: Washington, DC, USA, 2019. Available online: https://www.nationsreportcard.gov/mathematics/nation/achievement/?grade=12 (accessed on 12 December 2023).
- Lambert, R.; Tan, P. Conceptualizations of students with and without disabilities as mathematical problem solvers in educational research: A critical review. Educ. Sci. 2017, 7, 51. [Google Scholar] [CrossRef]
- Tan, P. Developing mathematical understanding and students with emotional and behavioral disorders: A review of the literature. Emot. Behav. Diffic. 2016, 21, 361–376. [Google Scholar] [CrossRef]
- Tan, P.; Lambert, R.; Padilla, A.; Wieman, R. A disability studies in mathematics education review of intellectual disabilities: Directions for future inquiry and practice. J. Math. Behav. 2019, 54, 1–13. [Google Scholar] [CrossRef]
- Tan, P.; Thorius, K.K. Toward equity in mathematics education for students with dis/abilities: A case study of professional learning. Am. Educ. Res. J. 2019, 56, 995–1032. [Google Scholar] [CrossRef]
- Lambert, R.; Tan, P. Does disability matter in mathematics educational research? A critical comparison of research on students with and without disabilities. Math. Educ. Res. J. 2020, 32, 5–35. [Google Scholar] [CrossRef]
- Duchaine, E.L.; Reynosa, R.J.; Garza, R. Secondary math and science teachers prepared for inclusion. Learn. Disabil. Contemp. J. 2021, 19, 103–126. [Google Scholar]
- Hunt, J.H.; Martin, K.; Patterson, B.; Khounmeuang. Special educators’ knowledge of student mathematical thinking. J. Math Teach. Educ. 2021, 25, 581–598. [Google Scholar] [CrossRef]
- Maccini, P.; Gagnon, J.C. Perceptions and applications of NCTM standards by special and general teachers. Except. Child. 2002, 68, 325–344. [Google Scholar] [CrossRef]
- Maccini, P.; Gagnon, J.C. Mathematics instructional practices and assessment accommodations by secondary special and general educators. Except. Child. 2006, 72, 217–234. [Google Scholar] [CrossRef]
- McGatha, M.G.; Bay-Williams, J.M.; Kobett, B.M.; Wray, J.A. Everything You Need for Mathematics Coaching; Corwin: Thousand Oaks, CA, USA, 2018. [Google Scholar]
- Van de Walle, J.A.; Karp, K.S.; Bay-Williams, J.M. Elementary and Middle School Mathematics: Teaching Developmentally, 11th ed.; Pearson: Bloomington, MN, USA, 2023. [Google Scholar]
- Fuchs, L.S.; Newman-Gonchar, R.; Schumacher, R.; Dougherty, B.; Bucka, N.; Karp, K.S.; Woodward, J.; Clarke, B.; Jordan, N.C.; Gersten, R.; et al. Assisting Students Struggling with Mathematics: Intervention in the Elementary Grades (WWC 2021006); National Center for Education Evaluation and Regional Assistance (NCEE), Institute of Education Sciences, U.S. Department of Education: Washington, DC, USA, 2021. [Google Scholar]
- Harbour, K.E.; Livers, S.D.; McDaniel, S.C.; Gleason, J.; Barth, J.M. Professional development to support elementary mathematics and co-teaching practices: Collaborations between general and special education. Math. Teach. Educ. Dev. 2022, 24, 33–56. [Google Scholar]
- Asher, A.; Nichols, J.D. Collaboration around facilitating emergent literacy: Role of occupational therapy. J. Occup. Ther. Sch. Early Interv. 2016, 9, 51–73. [Google Scholar] [CrossRef]
- Darling-Hammond, L.; Hyler, M.E.; Gardner, M. Effective Teacher Professional Development; Learning Policy Institute: Palo Alto, CA, USA, 2017. [Google Scholar]
- DuFour, R.; DuFour, R.; Eaker, R.; Many, T.W.; Mattos, M. Learning by Doing: A Handbook for Professional Learning Communities at Work; Solution Tree Press: Bloomington, IN, USA, 2016. [Google Scholar]
- Hord, S.M. Professional Learning Communities: Communities of Continuous Inquiry and Improvement; Southwest Educational Development Laboratory: Austin, TX, USA, 1997. [Google Scholar]
- Hord, S.M.; Sommers, W.A. Leading Professional Learning Communities: Voices from Research and Practice; Corwin: Thousand Oaks, CA, USA, 2008. [Google Scholar]
- History of PLC|ALLTHINGSPLC|Powered by Solution Tree. (n.d.) Allthingsplc.info; Solution Tree. Available online: https://www.allthingsplc.info/about/history-of-plc (accessed on 20 November 2022).
- Cavanagh, M.S.; Garvey, T. A Professional Experience Learning Community for Pre-service Secondary Mathematics Teachers. Aust. J. Teach. Educ. 2012, 37, 56–75. [Google Scholar] [CrossRef]
- Courtade, G.R.; Shipman, S.D.; Williams, R. Increasing Academic Rigor Through Comprehensive, Ongoing Professional Development in Rural Special Education: A Description of the SPLASH Program. Rural Spéc. Educ. Q. 2017, 36, 191–202. [Google Scholar] [CrossRef]
- Hamos, J.E.; Bergin, K.B.; Maki, D.P.; Perez, L.C.; Prival, J.T.; Rainey, D.Y.; Rowell, G.H.; VanderPutten, E. Opening the classroom door: Professional learning communities in the Math and Science Partnership Program. Sci. Educ. 2009, 18, 14–24. Available online: http://www.nsela.org/images/stories/scienceeducator/18article5.pdf (accessed on 12 December 2023).
- Hardman, E.L. Supporting professional development in special education with web-based professional learning communities: New possibilities with web 2.0. J. Spec. Educ. Technol. 2012, 27, 17–31. Available online: http://www.tamcec.org/jset-index/supporting-professional-development-in-special-education-with-web-based-professional-learning-communities-new-possibilities-with-web-2-0 (accessed on 12 December 2023). [CrossRef]
- Huggins, K.S.; Scheurich, J.J.; Morgan, J.R. Professional Learning Communities as a Leadership Strategy to Drive Math Success in an Urban High School Serving Diverse, Low-Income Students: A Case Study. J. Educ. Stud. Placed Risk 2011, 16, 67–88. [Google Scholar] [CrossRef]
- Ndunda, M.; Van Sickle, M.; Perry, L.; Capelloni, A. University−Urban High School Partnership: Math and Science Professional Learning Communities. Sch. Sci. Math. 2017, 117, 137–145. [Google Scholar] [CrossRef]
- Park, J.-H.; Byun, S. Principal support, professional learning community, and group-level teacher expectations. Sch. Eff. Sch. Improv. 2021, 32, 1–23. [Google Scholar] [CrossRef]
- Schechter, C.; Feldman, N. The principal’s role in professional learning community in a special education school serving pupils with autism. J. Spec. Educ. Leadersh. 2019, 32, 17–28. Available online: https://www.casecec.org/journal (accessed on 12 December 2023).
- Trahan, M.P.; Olivier, D.F.; Wadsworth, D.E. Fostering special education certification through professional development, learning communities and mentorship. J. Am. Acad. Spec. Educ. Prof. 2015, 142–157. [Google Scholar]
- Feldman, N.; Schechter, C. Exploring the professional learning community in a special education school serving pupils with autism. Int. J. Spec. Educ. 2017, 32, 2–36. [Google Scholar]
- Vygotsky, L.S. Mind in Society: The Development of Higher Psychological Processes; Harvard University Press: Cambridge, MA, USA, 1978. [Google Scholar]
- Thapa, R.; Dahal, N.; Pant, B.P. GeoGebra integration in high school mathematics: An experiential exploration on concepts of circle. Math. Teach. Res. J. 2022, 14, 32. [Google Scholar]
- Vaičiūnienė, A.; Kazlauskienė, A. Manifestation of Social Constructionism in the Process of Teaching and Learning. Tech. Soc. Sci. J. 2022, 33, 217–226. [Google Scholar] [CrossRef]
- Rosales, J.J.; Sulaiman, F. The Development of integrated STEM-PBL Physics Module for Learning Classical Mechanics in Secondary Education. Solid State Technol. 2020, 63, 19410–19433. [Google Scholar]
- Amineh, R.J.; Asl, H.D. Review of constructivism and social constructivism. J. Soc. Sci. Lit. Lang. 2015, 1, 9–16. [Google Scholar]
- Anderson, S.G.; Olivier, D.F. A quantitative study of schools as learning organizations: An examination of professional learning communities, teacher self-efficacy, and collective efficacy. Res. Issues Contemp. Educ. 2022, 7, 26–51. [Google Scholar]
- Voelkel, R.H., Jr. Causal relationship among transformational leadership, professional learning communities, and teacher collective efficacy. Int. J. Leadersh. Educ. 2022, 25, 345–366. [Google Scholar] [CrossRef]
- Zhang, J.; Yin, H.; Wang, T. Exploring the effects of professional learning communities on teacher’s self-efficacy and job satisfaction in Shanghai, China. Educ. Stud. 2023, 49, 17–34. [Google Scholar] [CrossRef]
- Francis-Baldesari, C.; Pope, C. Using a social constructivist model of teaching to create a learning community. J. Nurs. Educ. 2008, 47, 143–144. [Google Scholar] [CrossRef]
- Bandura, A. Self-efficacy: Toward a unifying theory of behavioral change. Psychol. Rev. 1977, 84, 191–215. [Google Scholar] [CrossRef]
- Bandura, A. Social Foundations of Thought and Action: A Social Cognitive Theory; Prentice-Hall: Hoboken, NJ, USA, 1986. [Google Scholar]
- Bandura, A. Self-Efficacy: The Exercise of Control; Freeman and Company: Singapore, 1997. [Google Scholar]
- Goddard, R.; Hoy, W.K.; Hoy, A.W. Collective teacher efficacy: Its meaning, measure, and impact on student achievement. Am. Educ. Res. J. 2000, 37, 479–507. [Google Scholar] [CrossRef]
- Bandura, A. Perceived self-efficacy in cognitive development and functioning. Educ. Psychol. 1993, 28, 117–148. [Google Scholar] [CrossRef]
- Gray, J.A.; Summers, R. International professional learning communities: The role of enabling school structures, trust, and collective efficacy. Int. Educ. J. Comp. Perspect. 2015, 14, 61–75. [Google Scholar]
- Olivier, D.F.; Hipp, K.K. Leadership capacity and collective efficacy: Interacting to sustain student learning in a professional learning community. J. Sch. Leadersh. 2006, 16, 505–519. [Google Scholar] [CrossRef]
- Voelkel, R.H., Jr.; Chrispeels, J.H. Understanding the link between professional learning communities and teacher collective efficacy. Sch. Eff. Sch. Improv. 2017, 28, 505–526. [Google Scholar] [CrossRef]
- Hord, S.M. Learning Together, Leading Together: Changing Schools through Professional Learning Communities; Teachers College Press & NSDC: New York, NY, USA, 2004. [Google Scholar]
- Bond, N. Developing a professional learning community among preservice teachers. Curr. Issues Educ. (Tempe Ariz.) 2013, 16, 1–15. [Google Scholar]
- Wilson, A. From professional practice to practical leader: Teacher leadership in professional learning communities. Int. J. Teach. Leadersh. 2016, 7, 45–62. [Google Scholar]
- Hudson, C. A conceptual framework for understanding effective professional learning community (PLC) operation in schools. J. Educ. 2023. [CrossRef]
- Meeuwen, P.; Huijboom, F.; Rusman, E.; Vermeulen, M.; Imants, J. Towards a comprehensive and dynamic conceptual framework to research and enact professional learning communities in the context of secondary education. Eur. J. Teach. Educ. 2020, 43, 405–427. [Google Scholar] [CrossRef]
- Olivier, D.F.; Hipp, K.K. Assessing and analyzing schools as professional learning communities. In Demystifying Professional Learning Communities. School Leadership at Its Best; Hipp, K.K., Huffman, J.B., Eds.; Rowman & Littlefield Education: New York, NY, USA, 2010. [Google Scholar]
- Creswell, J.; Plano Clark, V. Designing and Conducting Mixed Methods Research, 3rd ed.; Sage: Newcastle upon Tyne, UK, 2018. [Google Scholar]
- Efron, S.E.; Ravid, R. Action Research in Education: A Practical Guide; Guilford Press: New York, NY, USA, 2020. [Google Scholar]
- Kemmis, S.; McTaggart, R.; Nixon, R. The Action Research Planner: Doing Critical Participatory Action Research; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Herr, K.; Anderson, G.L. The Action Research Dissertation: A Guide for Students and Faculty, 2nd ed.; Sage: Newcastle upon Tyne, UK, 2015. [Google Scholar]
- Belzer, A.; Ryan, S. Defining the problem of practice dissertation: Where’s the practice, what’s the problem? Plan. Chang. 2013, 44, 195–207. [Google Scholar]
- Sadlier Math; William H. Sadlier: New York, NY, USA, 2017.
- Progress Mathematics; William H. Sadlier: New York, NY, USA, 2014.
- Illustrative Mathematics. IM K-5 Math; Kendall-Hunt: Dubuque, IA, USA, 2021; Available online: https://im.kendallhunt.com/k5/curriculum.html (accessed on 12 December 2023).
- Illustrative Mathematics. IM 6–8 Math Version 3.14.15; Kendall Hunt: Dubuque, IA, USA, 2017. [Google Scholar]
- Case, L.P.; Harris, K.R.; Graham, S. Improving the mathematical problem-solving skills of students with learning disabilities: Self-regulated strategy development. J. Spec. Educ. 1992, 26, 1–19. [Google Scholar] [CrossRef]
- Fletcher, J.M.; Lyon, G.R.; Fuchs, L.S.; Barnes, M.A. Learning Disabilities: From Identification to Intervention; Guilford Press: New York, NY, USA, 2019. [Google Scholar]
- Fuchs, L.S.; Powell, S.R.; Cirino, P.T.; Schumacher, R.F.; Marrin, S.; Hamlett, C.L.; Fuchs, D.; Compton, D.L.; Changas, P.C. Does calculation or word-problem instruction provide a stronger route to prealgebraic knowledge? J. Educ. Psychol. 2014, 106, 990–1006. [Google Scholar] [CrossRef]
- Fuchs, L.S.; Fuchs, D.; Seethaler, P.M.; Cutting, L.E.; Mancilla-Martinez, J. Connections between reading comprehension and word-problem solving via oral language comprehension: Implications for comorbid learning disabilities. In Models for Innovation: Advancing Approaches to Higher-Risk and Higher-Impact Learning Disabilities Science. New Directions for Child and Adolescent Development; Fuchs, L.S., Compton, D.L., Eds.; Wiley: Hoboken, NJ, USA, 2019; Volume 165, pp. 73–90. [Google Scholar]
- Fuchs, L.S.; Fuchs, D.; Sterba, S.K.; Barnes, M.A.; Seethaler, P.M.; Changas, P. Building word-problem solving and working memory capacity: A randomized controlled trial comparing three intervention approaches. J. Educ. Psychol. 2022, 114, 1633–1653. [Google Scholar] [CrossRef]
- Griffin, C.C.; Jitendra, A.K. Word problem-solving instruction in inclusive third-grade mathematics classrooms. J. Educ. Res. 2009, 102, 187–201. [Google Scholar] [CrossRef]
- Jitendra, A.K.; Star, J.R.; Starosta, K.; Leh, J.M.; Sood, S.; Caskie, G.; Hughes, C.L.; Mack, T.R. Improving seventh grade students’ learning of ratio and proportion: The role of schema-based instruction. Contemp. Educ. Psychol. 2009, 34, 250–264. [Google Scholar] [CrossRef]
- Krawec, J.; Warger, C. Solve It! Teaching Mathematical Problem Solving in Inclusive Classrooms—Grades 5–6; Exceptional Innovations: Westerville, OH, USA, 2015. [Google Scholar]
- Krawec, J.; Huang, J. Modifying a research-based problem-solving intervention to improve the problem-solving performance of fifth and sixth graders with and without learning disabilities. J. Learn. Disabil. 2017, 50, 468–480. [Google Scholar] [CrossRef]
- Menon, V. Working memory in children’s math learning and its disruption in dyscalculia. Curr. Opin. Behav. Sci. 2016, 10, 125–132. [Google Scholar] [CrossRef]
- Montague, M.; Jitendra, A.K. Teaching Mathematics to Middle School Students with Learning Difficulties; Guilford Press: New York, NY, USA, 2006. [Google Scholar]
- Montague, M.; Enders, C.; Dietz, S. Effects of cognitive strategy instruction on math problem solving of middle school students with learning disabilities. Learn. Disabil. Q. 2011, 34, 262–272. [Google Scholar] [CrossRef]
- Powell, S.R.; Fuchs, L.S. Effective word-problem instruction: Using schemas to facilitate mathematical reasoning. Teach. Except. Child. 2018, 51, 31–42. [Google Scholar] [CrossRef]
- Montague, M. Self-regulation strategies to improve mathematical problem solving for students with learning disabilities. Learn. Disabil. Q. 2008, 31, 37–44. [Google Scholar] [CrossRef]
- Montague, M.; Krawec, J.; Enders, C.; Dietz, S. The effects of cognitive strategy instruction on math problem solving of middle-school students of varying ability. J. Educ. Psychol. 2014, 106, 469–481. [Google Scholar] [CrossRef]
- Zwiers, J.; Dieckmann, J.; Rutherford-Quach, S.; Daro, V.; Skarin, R.; Weiss, S.; Malamut, J. Principles for the Design of Mathematics Curricula: Promoting Language and Content Development; Stanford University, UL/SCALE: Stanford, CA, USA, 2017; Available online: http://ell.stanford.edu/content/mathematics-resources-additional-resource (accessed on 12 December 2023).
- Woodward, J.; Beckmann, S.; Driscoll, M.; Franke, M.; Herzig, P.; Jitendra, A.; Koedinger, K.R.; Ogbuehi, P. Improving Mathematical Problem Solving in Grades 4 through 8: A Practice Guide (NCEE 2012-4055); National Center for Education Evaluation and Regional Assistance, Institute of Education Sciences, U.S. Department of Education: Washington, DC, USA, 2012. Available online: http://ies.ed.gov/ncee/wwc/publications_reviews.aspx#pubsearch/ (accessed on 12 December 2023).
- Woodland, R. Evaluating PK-12 Professional Learning Communities: An Improvement Science Perspective. Am. J. Eval. 2016, 37, 1–17. [Google Scholar] [CrossRef]
- Miles, M.B.; Saldaña, J.; Huberman, A.M. Qualitative Data Analysis: A Methods Sourcebook; SAGE: Newcastle upon Tyne, UK, 2020. [Google Scholar]
- Hattie, J. Global Research Database: Influences; Visible Learning Metax; Corwin: Thousand Oaks, CA, USA, 2023; Available online: https://www.visiblelearningmetax.com/Influences (accessed on 2 June 2023).
- Wilcoxon, F. Individual comparisons by ranking methods. Biom. Bull. 1945, 1, 80–83. [Google Scholar] [CrossRef]
- National Council of Teachers of Mathematics [NCTM]. Access and Equity in Mathematics Education: A Position of the National Council of Teachers of Mathematics. 2014. Available online: https://www.nctm.org/Standards-and-Positions/Position-Statements/Access-and-Equity-in-Mathematics-Education/ (accessed on 12 December 2023).
- Tan, P.; Kastberg, S. Calling for research collaborations and the use of dis/ability studies in education. J. Urban Math. Educ. 2017, 10, 26–38. [Google Scholar] [CrossRef]
- Cramer, D.; Howitt, D.L. The SAGE Dictionary of Statistics: A Practical Resource for Students in the Social Sciences; Sage: Newcastle upon Tyne, UK, 2004. [Google Scholar]
- Chyung, S.Y.; Hutchinson, D.; Shamsy, J.A. Evidence-based survey design: Ceiling effects associated with response scales. Perform. Improv. 2020, 59, 6–13. [Google Scholar] [CrossRef]
- Tashakkori, A.; Teddlie, C. SAGE Handbook of Mixed Methods in Social and Behavioral Research; Sage: Newcastle upon Tyne, UK, 2010. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).