Abstract
Families have largely been excluded from the implementation of the Common Core State Standards in Mathematics (CCSSM), reducing their ability to extend their child’s mathematics learning. CCSSM emphasizes different instructional elements (e.g., pictorial representations, problem solving, multiple strategies for solving) that may differ greatly from how parents learned mathematics. In addition, many school officials have ineffectively engaged parents in the changes, further diminishing their capacity to participate in their child’s learning. This case study examined parent mathematics self-efficacy and parent mathematics knowledge for teaching, factors that influence the effectiveness of their engagement in their child’s mathematics learning. This study was also implemented to identify elements that the parent participant found helpful for their child’s mathematics learning. A thematic analysis was performed on the data sources, the interactive homework assignments, a survey, observations, a researcher’s journal, and an interview to conclude that the interactive homework assignments improved parent mathematics self-efficacy and parent mathematics knowledge for teaching. The parent participant also identified the assignments’ side-by-side examples, additional practice, and the easy access of the assignments as features of the intervention that enhanced her ability to support her child.
1. Introduction
Mathematics achievement is considered critical for social mobility, career opportunities, and full enjoyment of the world [1,2,3,4,5,6]. As a discipline, mathematics is also an important economic driver for countries [7,8,9]. Despite the recognized importance of learning mathematics to their children’s future, parents in school settings struggled to support them in learning mathematics [10,11,12]. The content, as well as the ways in which elementary mathematics was taught, changed with the implementation of the Common Core State Standards for Mathematics (CCSSM) [13]. For example, CCSSM focused on helping students develop a conceptual understanding of mathematics through physical and pictorial representations while also ramping up the mathematics content at each grade level. Furthermore, teachers with limited mathematics understanding required additional learning to use conceptual strategies; however, that notion was not always embraced by teachers, resulting in sometimes dated and ineffective mathematics explanations and instruction [14,15].
This study addresses how parents faced multiple barriers to helping their children with mathematics such as: the onslaught of the COVID-19 pandemic, the accompanying closing of schools, and the hasty implementation of remote instruction, which required more home support than ever before. This study was designed to support learning at home by helping parents move past traditional mathematics strategies such as algorithms and rote learning into science-based teaching methods that promote conceptual understanding of mathematics constructs. Based on Hatano and Inagaki’s [16] framework on conceptual development, conceptual strategies promote a deeper understanding that is transferable and generalizable in which students can reason about mathematics by identifying relationships and patterns. In contrast, those wedded to rote memorization and traditional strategies often struggle to apply different approaches when solving novel problems and can be challenged to judge the reasonableness of their answers [17]. This study also examines ways to effectively support families experiencing barriers associated with the pandemic and remote instruction (e.g., technological challenges, delivering lessons intended for face-to-face instruction, and reduction in teacher capacity and accessibility). Additionally, this study aims to help parents engage in dialogue that more closely resembles classroom discussion that supports their child’s critical thinking about mathematics.
There were two parts to the study: the needs assessment and the intervention. Prior to the development of the intervention study, a needs assessment was conducted to better understand what parents needed to help their children in learning mathematics. This needs assessment served as a preliminary tool to determine whether the school population’s needs were consistent with the parent needs highlighted by Goldman and Booker [10], Jackson and Remillard [11], and Remillard and Jackson [12]. The assessment was distributed to 67 parents of third-, fourth-, and fifth-grade students from an affluent and diverse suburban elementary school. Approximately 93% of the online parent participants had a bachelor’s degree (n = 21), a master’s degree (n = 24), or a doctorate (n = 12) as their highest level of educational attainment.
The online survey of open-ended questions (n = 7) and close-ended Likert-scale items (n = 19) and follow-up interviews with six in-person interviews indicated that parents had lower levels of mathematics self-efficacy regarding supporting their students’ mathematics learning of conceptual strategies and desired more instructional support in the form of textbooks and more homework that they could use with their children. Mathematics self-efficacy is the belief that one will be successful in mathematics and in performing mathematics tasks in general [18], and low mathematics self-efficacy is linked to low self-concept and high mathematics anxiety [19]. Parent responses also suggested misunderstandings about pictorial mathematics representations and their purpose. For example, one parent stated how he wished students learned useful mathematics such as percentages. This parent did not know that percentages are introduced in later grades after they have learned pictorial representations that support their understanding of percentages. Other parent participants emphasized the sole importance of arriving at the correct answer without understanding that pictorial representations help students develop a conceptual understanding so they can more accurately and more meaningfully use abstract algorithms. Additionally, parents were unaware that algorithms are taught after students developed an understanding of the meaning of the operations of addition, subtraction, division, and multiplication through physical and pictorial strategies. For example, in kindergarten, students are introduced to addition and subtraction through sets of physical objects (e.g., base-10 blocks, counters, and snap cubes) and pictures of various objects. Through a series of experiences comparing differences between two groups of these objects (e.g., visually, counting, and using balance beams), students begin to develop an understanding of addition and subtraction. The same materials serve to help students develop the meaning of place value. Understanding the concept of place value and the ideas behind the mathematical operations of addition and subtraction provides students with the understanding to use them in new settings and manage algorithms in subsequent grades.
An interactive homework intervention was shown to be effective for improving parent mathematics self-efficacy and parent mathematics knowledge for teaching. Interventions that resulted in improved parent mathematics self-efficacy included self-guiding tools [20,21,22] and emotional supports [23,24]. Interventions that included collaborative learning [25,26], engaging mathematics tasks [27,28], and guidance on the development of mathematics knowledge of content and mathematics knowledge of teaching [29,30] were also effective in developing parent mathematics knowledge for teaching. From the needs assessment and extant research, the following research questions served as the guide for the study: “In what ways does a homework intervention change perceived parent participant mathematics self-efficacy?”; In what ways does a homework intervention change perceived parent participant mathematics knowledge for teaching?”; and “What components of an interactive homework assignment program do parent participants identify as useful in helping them support their children with mathematics learning at home?” The interactive homework intervention addressed these questions through a focus on parent mathematics self-efficacy and parent mathematics knowledge for teaching by addressing misunderstandings and improving their understanding of the purpose of pictorial representations to support conceptual understandings.
2. Study Design
Due to the COVID-19 pandemic, the sample consisted of a parent and child partnership, which required a design change from a quasi-experimental concurrent mixed methods study to a descriptive, single-case holistic case study. This specific case study design is appropriate for examining one unit of analysis (e.g., parent participants) that is influenced by real world contexts [30]. This six-week case study began when parent participants were recruited with surveys about their experiences and backgrounds with traditional and conceptual mathematics strategies. Only one parent, Linda, was interested in participating in this project with her daughter, Laura Jean, a nine-year-old enrolled in a fourth-grade mathematics class. Linda and Laura Jean completed the required consent and assent documents. Then from February to March 2021, each week, Linda was emailed one interactive homework assignment, the first containing addition and subtraction problems, for completion at the end of each week. Six interactive homework assignments were sent in total. Zoom observations of the homework sessions, five in total and approximately 30 min in length, were conducted with the two participants using the interactive homework assignments. The researcher’s observations of the participants occurred after the first week to clarify homework assignment directions and provide guidance when necessary. All observed sessions were recorded. A final Zoom session was used to interview Linda about her reported experiences with the interactive homework assignments. In addition, a reflective journal was kept by the researcher to capture the changes over time in the parent and child’s interactions using the interactive homework assignments during the Zoom sessions. The researcher primarily served as a passive observer to gain an understanding of the assignment’s effectiveness in guiding participant interactions and parent learning. She occasionally intervened to maintain fidelity by encouraging the parent participant’s faithful adherence to assignment directions. All data sources—parent comments on the survey and interactive homework assignments, transcripts of observations, the researcher’s journal, and the interview transcript—were analyzed. A thematic analysis was performed in which all data sources were reviewed to identify patterns which were then grouped, coded, and analyzed. Member-checking occurred with the final parent interview, and peer debriefing between the researcher and her advisor occurred at various stages of the study: homework assignment modifications, review of participant transcripts, and coding and analysis processes. Lastly, the researcher’s weekly observations of the participants discussing and collaboratively solving their problems over Zoom further created a comprehensive understanding of parent mathematics self-efficacy and mathematics knowledge for teaching.
2.1. Participants
Linda is a White parent of two children, and Laura Jean, one of her daughters, was enrolled in a fourth-grade-level mathematics class in an affluent, suburban elementary school in Maryland. Linda has a master’s degree in social work, and her mathematics background is extensive, having minored in mathematics in college. She was well-versed in traditional mathematics strategies focused on procedural knowledge but struggled with the conceptually focused activities her children brought home. She chose to participate in this study to learn conceptual mathematics strategies as the parent who primarily helps her children with mathematics at home. School district initiatives led to the rapid transition from in-class instruction to remote instruction due to the pandemic. These changes resulted in additional challenges (e.g., limitations to differentiating classroom instruction, limitations in student collaboration, and technical difficulties) in supporting Laura Jean’s learning.
2.2. Researcher Identity
This study was conducted by Laura Moore, a National Board Certified educator with eight years of teaching experience. She is African American from a southern family and is third-generation college-educated. She would be considered middle class. Although Laura differs in race from the participants, similarities in social class and formal education reduced power imbalances between the researcher and parent participant. Given these factors, trust was quickly established between the researcher and the parent participant.
2.3. Interactive Homework
Interactive homework activities were used to address parents’ mathematics knowledge for teaching and self-efficacy. These two constructs are important in helping parents with their children’s homework. Ball et al.’s [31] mathematics knowledge for teaching (MKT) theory describes the mathematics understanding educators need for school instruction. Mathematics competence influences the role parents play in reinforcing mathematics instruction, and De Corte et al. [32] identified five necessary elements of mathematics competence: (a) positive mathematic beliefs, (b) specific mathematical knowledge, (c) heuristic methods, (d) metacognition, and (e) self-regulatory skills. De Corte et al. [32] reported that positive mathematics beliefs include high levels of self-concept and self-efficacy. Specific mathematical knowledge involves an understanding of mathematical constructs (e.g., symbols, procedures, and concepts) and the ability to make generalizations and use heuristic methods to make problem solving more meaningful.
Mathematics knowledge for teaching is divided between subject matter knowledge and pedagogical content knowledge, two dimensions originating from Ball et al.’s [31] MKT framework, which is based on Shulman’s [33] pedagogical content knowledge (PCK) construct, which emphasizes the connection between knowledge of a subject and the ability to teach that subject. Within these dimensions are six domains: (a) common content knowledge (CCK), (b) horizon content knowledge (HCK), (c) specialized content knowledge (SCK), (d) knowledge of content and students (KCS), (e) knowledge of content and curriculum (KCC), and (f) knowledge of content and teaching (KCT). CCK, HCK, and SCK fall under subject matter knowledge, and KCS, KCC, and KCT fall under pedagogical content knowledge.
Self-efficacy plays a significant role in guiding one’s motivation and engagement in specific behaviors described by Bandura [34]. Specifically, those with high levels of mathematics self-efficacy are more inclined to (a) create challenging goals, (b) view challenges as learning opportunities, (c) increase the effort required to master goals, and (d) associate failure with insufficient effort [28]. Thus, mathematics self-efficacy’s connection to overcoming educational obstacles [19] likely explains why high levels of mathematics self-efficacy correlate with higher mathematics achievement [28].
Bandura’s [34] triadic reciprocal determinism theory, coupled with his self-efficacy theory, demonstrates how environmental factors, personal factors, and behavioral factors interact to influence an individual’s life and was used to construct the themes in the self-efficacy data. The interactive homework assignments (environmental factors), collaboration (a behavioral factor), and mathematics knowledge for teaching (a personal factor) appeared to mutually reinforce each other to improve parent mathematics self-efficacy.
The interactive homework assignments (Appendix A) consisted of four components: the problem-solving section, the discussion section, the writing section, and the parent feedback section. The first three sections (e.g., problem solving, discussion, and writing) served to promote parent mathematics knowledge for teaching and parent mathematics self-efficacy for teaching. The feedback section promoted parent mathematics self-efficacy for teaching by allowing the parent participant to direct the content of the next session to further support their learning of the strategies. Each section was created for the express purpose of promoting dialogue and joint problem solving between parent and child. These assignments were designed as a template for parents to guide instruction without the researcher’s regular input.
The problem-solving section contained (a) a word problem or prompt, (b) side-by-side examples of strategies, (c) a list of problems to solve using the strategies, and (d) two areas designated for the parent and student to problem solve using their strategies. Each participant had to solve at least two problems, and this section’s three probing questions were used to help the parent and child observe the strategies in greater detail in preparation for deciding which strategies would be more suitable for solving specific problems (Figure 1). Figure 1 contains side-by-side examples of two mathematics representations of subtraction: base-10 blocks and the traditional algorithm. Figure 1 demonstrates the process of regrouping with subtraction using base-10 blocks, which are physical objects arranged in singular pieces and in groups of 10, 100, and 1000 to represent the base-10 numerical system. This section provided participants with images of the strategies employed, demonstrated connections between those strategies and word problems (and prompts), and highlighted how different strategies could be employed to solve problems. Choosing a problem and defending their reasoning for strategy choice served to boost interactions, and the separate writing sections designated for the parent and child participants also served to promote their interactions through joint problem solving on the same paper.
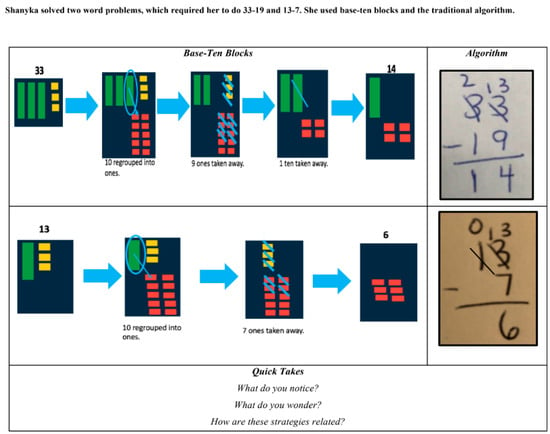
Figure 1.
Problem-solving section: Side-by-side examples of subtraction.
The discussion and writing sections encouraged participants to reflect on and discuss their engagement with the problems to deepen their mathematics knowledge about the strategies and to reflect on the effectiveness of their partnering. The discussion section contained two questions that the participants answered aloud to gain more insight into the relationship between their strategies and problems to determine which strategies were more effective for specific problems (Table 1).

Table 1.
Discussion section questions.
Additionally, the writing section contained questions (two to three) that encouraged the adult participant to compare strategies and form predictions about which strategies work best with different problems, strengthening their understanding of conceptual strategies’ purposes and advantages (Table 2). The number of questions would vary depending on whether the homework assignment contained a word problem or a prompt (Appendix A). If a homework assignment contained a prompt, Questions 1 and 2, were used. If a homework assignment contained a word problem Questions 1, 2, and 3 were used. The parent participant recorded her thinking in this section.

Table 2.
Writing section questions.
The feedback section also contained three statements in which the adult participant could describe student progress on the assignment. This section also encouraged the adult to provide recommendations for future assignments. Goldman and Booker’s [10] and Jackson and Remillard’s [11] studies aligned with this study’s needs assessment responses, which indicated that parents wanted more instructional resources on these strategies. Specifically, parent participants from the needs assessment desired supports that were prescriptive, such as textbook resources containing examples of how to use the strategies. The feedback section was created to empower the parent participant to request additional support on strategies to further aid their understanding of conceptual mathematics strategies. The researcher, also a fourth-grade teacher, was familiar with the strategies that the child participant had learned. Moreover, the researcher’s observations of parent–child interactions guided her construction of subsequent homework activities as she inserted and changed the pictorial representations to support the parent’s growing understanding of the strategies.
3. Results
This study was developed to examine the effectiveness of an interactive homework program for elementary mathematics students and their parents. Three research questions were designed to guide the study. Specifically, two research questions were designed to capture the intervention’s impact on Linda’s perceived mathematics self-efficacy and mathematics knowledge for teaching. The third research question involved her identifying helpful interactive homework program components. Many study results were unanticipated, and the emerging themes may prove helpful in guiding future studies regarding parent and child mathematics engagement.
3.1. Research Question One
Research Question One is “In what ways does the homework intervention change perceived parent participant mathematics self-efficacy?” Linda appeared to demonstrate greater confidence in teaching Laura Jean conceptual mathematics strategies, as indicated by the survey, interactive homework assignments, observations of the homework sessions, journal entries, and the interview, which yielded four themes: beliefs, autonomy, modification, and motivation. Beliefs is a theme in this study, referring to the parent participant’s reactions to new teaching methods and how her beliefs evolved throughout the intervention. Autonomy represents the participants’ capacity to direct the problem-solving process and collaboratively problem solve. Modification represents how the interactive homework sheets were changed based on participant interactions during the problem-solving process and parent requests. Motivation is the participants’ willingness to engage in pictorial mathematics strategies and extend their learning outside the interactive homework sessions.
With respect to the theme of beliefs, Linda was initially frustrated by conceptual strategies (Interactive Homework One; Interactive Homework Two; Sessions One through Three; Survey). During the first two observed sessions, Linda’s frustration appeared to stem from how she struggled to help Laura Jean realize success in mathematics when she had minored in mathematics (Survey and Session Two) and had extensive mathematics experiences with her own parents (Session Three). Linda shared, “Yeah, we [family] get pretty confused. My dad’s an engineer, my mom’s an accountant. So… numbers, we know them” (Session Three). Linda also believed that conceptual strategies were more complicated than necessary, as indicated by her response to the use of number lines, a strategy used to demonstrate the difference between whole numbers serving as endpoints:
I don’t like number lines. I really… I’m not asking you to make me do this again. But some of them seem, some problems are way harder to do with the number line because it’s much more complicated math. And I feel like they should just leave that behind now [and] move on.(Session Three)
Upon debriefing with Linda at the end of the first observed session featuring Interactive Homework Two, her disapproval of conceptual strategies appeared to be another source of concern, evidenced by her discussion of adjustment, a compensation strategy, in which the minuend, the top number, and subtrahend, the second number, in a subtraction problem, are modified by an equal amount. Figure 2, from the first interactive homework assignment, shows both reduced by 1. Linda expressed relief upon reviewing Interactive Homework Two, which did not contain a side-by-side example of the adjustment strategy, “Yeah, I don’t think I like adjustment. When I saw that… she [Laura Jean] started doing that, I’m like, I just…don’t want to change the number. I want to work [with] the number I have” (Session One). Her dislike of the conceptual strategies also led to her resistance to using them. For example, as referenced earlier, Linda’s comment regarding number lines, “I don’t like number lines… I’m not asking you to make me do this again” (Interactive Homework Four; Session Three). Because she did not feel comfortable using the conceptual strategies, she expressed satisfaction when she checked her answers using the traditional algorithm, “And that’s when you can use the algorithm and check against like…Oh, look at it” (Session Three).

Figure 2.
The adjustment strategy from the first assignment.
By the fourth session, Linda’s concerns about the conceptual strategies began to rapidly subside as she embraced conceptual strategies to help Laura Jean understand fractions, concepts Laura Jean struggled with more than whole numbers. As Laura Jean began to arrive at the correct answers and grasp adding fractions using number lines and area models, a region that is partitioned into equal areas, Linda praised the number line strategy for adding fractions, “Hey, Laura Jean. That makes sense on the number line” (Session Four). Linda also appeared to value how the area model helped Laura Jean visualize adding fractions, “Like having this the area model of your picture. She could do that and see what it is” (Session Four).
Linda began to demonstrate greater autonomy as the sessions continued (Researcher’s Journal, p. 4), and she became hopeful for what the assignments would bring, “Hopefully it’ll help me… make me more confident with my younger one [her youngest daughter] when she’s doing this stuff [conceptual strategies]” (Session Four). In the first session, Laura Jean selected the two problems (500-345, 400-289) that would have been appropriate for solving with the adjustment strategy. As a result, she left Linda with the remaining problems that were too difficult to solve with this strategy. As Linda conveyed in the assignment’s writing section, she could not complete her last problem. This incident reflected her limited authority in redirecting Laura Jean’s selection of problems as she did in later sessions, three through five, when Linda became more confident using conceptual strategies.
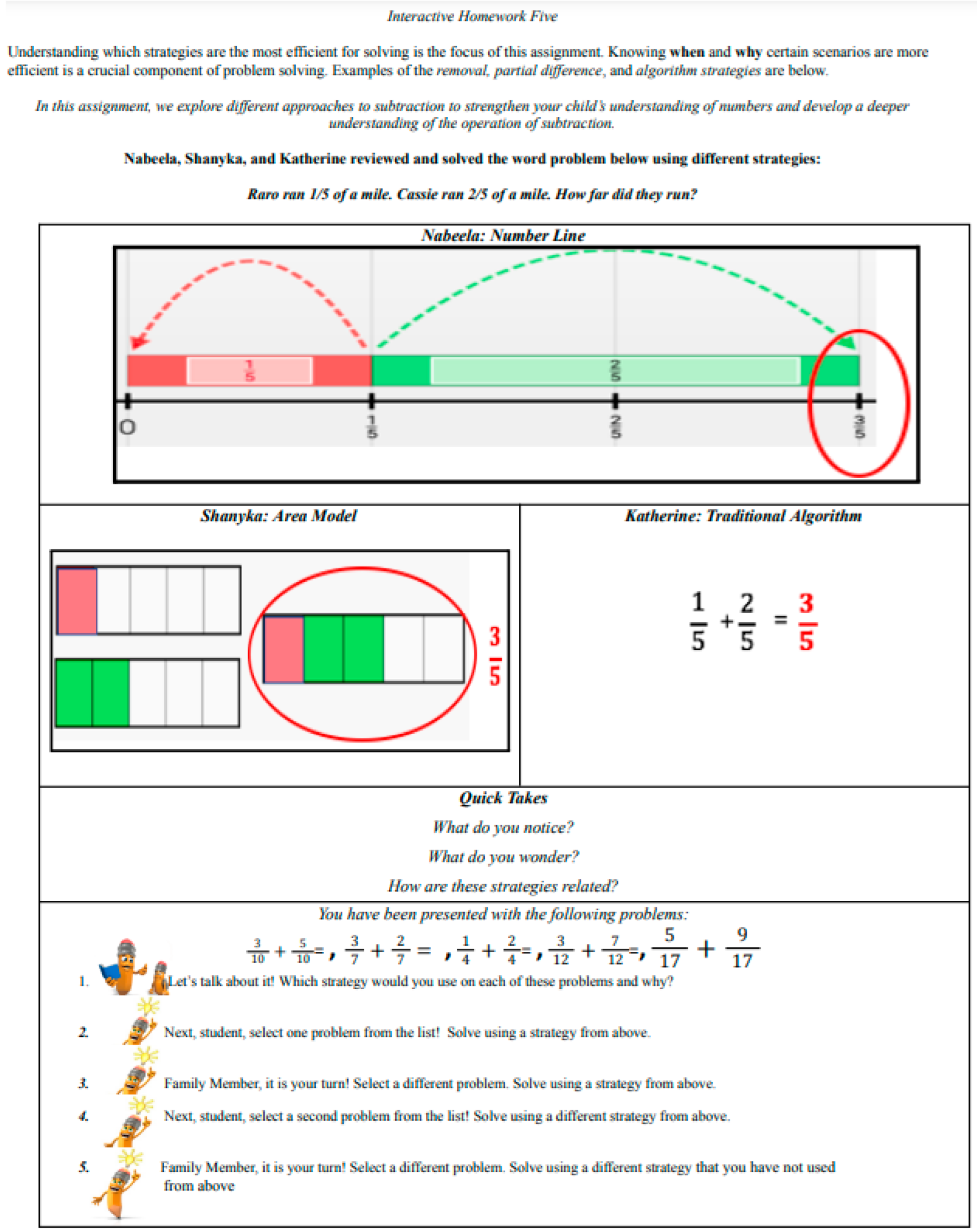
By the fourth observed session, when Laura Jean struggled to generate a number line for adding and , Linda skillfully directed her to the interactive homework’s pictorial representations and modeled creating a number line for the new problem. Linda’s reliance on the conceptual models to rectify Laura Jean’s confusion was apparent in her (a) highlighting features of the conceptual strategies; (b) creating her own model as a demonstration; and (c) asking follow-up questions to deepen and assess Laura Jean’s understanding of computing with fractions: “Okay. So, you know that one of these. We only need one for the tenths, and we cut [it] into 10 pieces. Three of the 10 pieces, right? Okay, but where [what] does this one represent? Do you still need these?” Linda’s techniques were based firmly on pictorial representations (Figure 3), demonstrating greater confidence in using conceptual strategies (Researcher’s Journal, p. 5)

Figure 3.
Video screenshot of parent work during session four using interactive homework five.
Each interactive homework assignment underwent modifications based on researcher observations and parent feedback on the assignments, effectively conforming the assignments to participant need to improve their confidence using the conceptual strategies. Linda was disincentivized from using conceptual strategies, believing that they were less useful after Laura Jean selected all the problems for solving that were appropriate for the adjustment strategy on the first assignment, leaving Linda with problems that were only suitable for solving with the traditional algorithm. Thus, the directions on the second interactive homework were modified to ensure that participants alternated turns when choosing problems to facilitate discussion and improve their opportunities for selecting strategies that correspond to the problems. The second assignment was also modified to include three strategies instead of two, as in Interactive Homework Assignment One, to facilitate Linda’s understanding and use of conceptual strategies (Figure 4 and Figure 5). Figure 4 shows side-by-side examples of the adjustment strategy (discussed above) and the traditional subtraction algorithm. Figure 5 illustrates three strategies. Removal is a number line strategy in which the total quantity is positioned at the right endpoint of the number line and the second number is removed through repeated subtraction in segments; the answer is the most left or last point on the number line. The partial difference strategy involves subtracting the minuend incrementally, often by place value. At the end of Session Three, Linda requested help with teaching fractions. In response, Interactive Homework Assignments Five and Six were modified to include ways to conceptually develop an understanding of fractions and fraction operations. Her request reflects improved confidence in using conceptual strategies to support Laura Jean’s understanding of the subtraction of whole numbers (Researcher’s Journal, p. 4).

Figure 4.
Interactive homework assignment one.
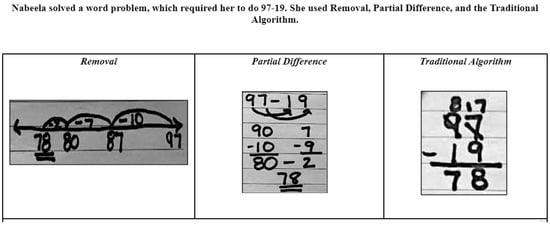
Figure 5.
Interactive homework assignment two.
The interactive homework assignments contributed to Laura Jean’s motivation to engage in mathematics activities. According to Linda, Laura Jean began to enjoy mathematics because she could practice and master concepts for which she had previously struggled (Interview; Sessions Three through Five). The assignments were tailored to her areas of development. As a result, Laura Jean experienced even greater success on more challenging problems, which also improved her motivation to participate in the intervention (Researcher’s Journal, p. 4). Her enjoyment of the interactive homework assignments and mathematics was evident when she opted to solve most of the problems instead of sharing the responsibility equally with her mother (Researcher’s Journal, pp. 3–5; Sessions Three through Five).
Linda credited the interactive homework’s collaborative nature to Laura Jean’s newly found interest in mathematics, which in turn motivated Linda to find additional problems for Laura Jean to practice:
But it was helpful for me to work with Laura Jean and for her to have somebody else… we have the assignment to go along, but we had to do [it] together and she actually enjoyed it. So, I think seeing her getting interested to study math, I think it helped, and gave us a reason to do more math. And we just said, hey, let’s just do some extra, like homework or sheets I found online. And so, it kind of gave us [a] purpose to do more math and work on some of the stuff that she’s been working on.(Interview)
3.2. Research Question Two
Research Question Two is “In what ways does the homework intervention change perceived parent participant mathematics knowledge for teaching?” An examination of participant comments on the survey and assignments, observations, researcher’s journal entries, and the interview indicated Linda’s greater proficiency in identifying and using conceptual strategies to support Laura Jean’s mathematics learning. For the second research question, understanding and functionality were identified themes that characterized improved parent mathematics knowledge for teaching. Understanding was defined as the participant’s growing knowledge of the pictorial representations or conceptual mathematics strategies and how and when to use them, and functionality was the parent participant’s growing understanding of the purposes of each set of strategies.
Linda’s limited understanding of conceptual mathematics strategies contributed to her challenges with helping Laura Jean. Due to these past struggles, she revealed in her interview that she joined the study to learn more about them. Because Linda did not know the conceptual strategies for computing with fractions, helping her daughter with fractions was particularly difficult:
… I don’t actually remember how to, like, do them, like subtract fractions and everything. … I can visually and I know what the number is like, and I could do it. But I’m like actually showing her… the traditional algorithm kind of way. I’m like, I don’t know that I know it [a conceptual strategy].(Session Three)
Linda’s unfamiliarity with these mathematics concepts also influenced her ability to identify connections between conceptual strategies and the traditional algorithm, “I don’t know. Do you see? … The algorithm next to the example … looks totally different to me. Like it doesn’t. I don’t see [the] relation” (Session Three). Yet, as the sessions progressed, Linda used the support from the side-by-side examples of how to solve the problem to connect her mathematics background to what Laura Jean was learning in school. In her interview she elaborated:
So, I guess it [the side-by-side example of the conceptual strategy] just informed me of what it is and kind of showed me compared to… how I learned in school. [It] kind of gave me a comparison so I can see what… I was doing compared to what I needed to be doing to show her [Laura Jean].
Learning more about the conceptual strategies led to Linda developing more positive beliefs about the use of conceptual strategies. She initially expressed dissatisfaction with the adjustment strategy (Interactive Homework One; Researcher’s Journal, pp. 1, 3; Session One), but by the third session, she conveyed that the addition of the number line on the fourth interactive homework assignment helped her learn the adjustment strategy, “Adjustment with the number line helped [me] to see how adjustment work[s].” Linda’s understanding improved with the combination of two conceptual strategies she initially disliked and did not understand. Linda’s greater familiarity with conceptual strategies and resulting improvements in her mathematics knowledge for teaching were illustrated when she relied on pictorial representations to help her daughter. For example, in the third session on Interactive Homework Four, Linda used the side-by-side examples of the base-10 model and traditional algorithm for subtraction to help Laura Jean understand regrouping:
…when you look at just this number like that, then you don’t have to borrow. Right? Right. So, if you did traditional, you’d have to like this, right? Cross that off, make that a seven, this would become 10. Right? Yes.
By the fourth session, Linda’s improved mathematics knowledge for teaching was illustrated by her complete reliance on or full use of pictorial representations. She was then asking questions of Laura Jean such as,” How does your picture represent three times? What part of your picture? Can you shade it?” These comments and resulting behaviors, reflective of Sessions Four and Five, directly contrast with her dependency on the traditional algorithm in Sessions One, Two, and Three.
Linda’s understanding and mathematics knowledge for teaching were also demonstrated in her correct assessment of Laura Jean’s abilities. By the end of the third session, which featured the fourth assignment, Linda desired a change in content because her daughter felt comfortable subtracting whole numbers in various ways, “Like she’s comfortable with this stuff. Now she fully understands it. But… She’s already [on] fractions [in class].” Her assessment matched that of the researcher, who had eight years of instructional experience. Moreover, although the intervention was initially created to develop a conceptual understanding of whole number operations, Linda requested practice computing with fractions once she observed that Laura Jean mastered subtracting whole numbers. The flexibility of the intervention was partially based on Linda’s input, allowing the researcher to use the intervention to target additional areas of need. Thus, the fifth and sixth assignments were adjusted to include fractions (Researcher’s Journal, pp. 5–6).
Linda’s improved understanding of conceptual strategies was also indicated by how she recognized these strategies in other parts of her daughters’ learning. She identified Interactive Homework Five’s models in Laura Jean’s DreamBox program, an online mathematics resource that teachers assigned as homework and classwork to reinforce mathematics learning. Linda also used this connection to help Laura Jean solve problems, “…these fractions are kind of like your square units that you were doing [on] that DreamBox. Remember how you’re doing it yourself?” (Session Five). She also recognized the homework assignment’s number line strategies in her younger daughter’s class work (Session Three).
Initially, Linda’s limited exposure to and understanding of conceptual strategies influenced her beliefs about them, as indicated by her concerns about their functionality, the second theme of Research Question Two. For example, when Laura Jean selected all the problems that corresponded to the adjustment strategy on the first assignment, Linda wrote, “Guess there are less steps in adjustment, but it can’t be used in every problem and requires extra thinking.” This observation demonstrated how she defined functionality by a strategy’s versatility. Linda also defined a strategy’s utility by the amount of effort required to use it, as indicated by her comments on the first assignment, which acknowledged advantages of the traditional algorithm for subtraction, “Traditional [algorithm] = straight forward and no extra thinking if it could work.” The concept of the traditional algorithm’s efficiency was reiterated in the third session, in which she discussed how the conceptual strategies “Force you to think about solving,” thereby reducing their efficiency in the process.
The assignments were adjusted weekly to help Linda redefine functionality and change her mindset and develop confidence using conceptual mathematics strategies (Researcher’s Journal, pp. 2–6). As a result, Linda began to understand that conceptual strategies promote understanding instead of achieving an immediate answer, the traditional algorithm’s purpose (Interactive Homework Assignments Three through Six; Sessions Three through Five). For example, before the intervention, Laura Jean spent at least two months learning the traditional algorithm for subtracting whole numbers, and she developed the habit of reversing minuends and subtrahends. After completing Interactive Homework Assignments Three and Four, which featured the base-10 model for subtraction, Linda observed the visual representation’s effectiveness when Laura Jean stopped reversing minuends and subtrahends for problems that required regrouping. This change in performance illustrates how visual representations remedied Laura Jean’s misunderstandings, transitioning her to the correct use of the traditional algorithm (Interactive Homework Four; Session Three; Researcher’s Journal, p. 4). Witnessing how learning conceptual strategies improved Laura Jean’s understanding of the traditional algorithm was an eye-opener for Linda, “Yeah, I mean, I think the base-10 blocks actually make the most sense to me visually” (Session Three).
3.3. Research Question Three
Research Question Three is “What components of the interactive homework assignment program do parent participants identify as useful in helping them support their children with mathematics learning at home?” The themes of repetition, convenience, and side-by-side examples were identified as effective intervention components for developing mathematics knowledge. Repetition was defined as the participants’ opportunities for repeated exposure to and practice with mathematics concepts. The side-by-side examples are about the diagrams of the pictorial strategies located in the interactive homework worksheets, and convenience is defined by the parent participant’s noted ease of using the interactive homework assignments.
Linda discussed the importance of repetition, requiring additional practice on mathematics concepts. Laura Jean struggled to recall what she learned in school because she took notes on white boards and rarely had homework in previous grades (Session Two; Session Five). Linda appreciated the additional practice she received with the homework assignments, “I always wanted more stuff from the school. I’m just trying to help [with] the math because I didn’t get it. And I took this opportunity as a chance to do that” (Session Four). Linda discussed how these additional resources and practice at home helped Laura Jean master concepts, “So it was helpful for her to have some extra math that wasn’t too hard to kind of talk about and stuff to see” (Interview).
Repetition and Laura Jean’s subsequent successes in mathematics led to her enjoyment of mathematics (Interview; Sessions Three through Five). This change in Laura Jean’s mindset inspired Linda to provide more opportunities for mathematics engagement:
But it was helpful for me to work with Laura Jean and for her to have somebody else kind of, I mean, we have the assignment to go along, but we had to do together and she actually enjoyed it. So, I think seeing her getting interested in studying math, I think it helped, and gave us a reason to do more math. And we just said, hey, let’s just do some extra, like homework or sheets I found online. And so, it kind of gave us purpose to do more math and work on some of the stuff that she’s been working on”.(Interview)
Laura Jean’s enjoyment of the interactive homework assignments and mathematics were also illustrated when she opted to do most of the assignments’ problems instead of sharing the responsibility with Linda (Researcher’s Journal, pp. 3–5; Sessions Two through Five). Linda appreciated how the side-by-side examples of the interactive homework assignments helped her understand the conceptual strategies. Linda was unfamiliar with these strategies and discussed the importance of using these examples to support Laura Jean:
And so, I think having that sample like above and explaining the different forms to do it helps at least a parent that knows some bit about math and doesn’t know the math isn’t, you know, going to figure it out unless they’re learning along with their kid. But yeah, I think the hardest thing was always that she was expected to do these different models. And I didn’t know what they were.(Session Four)
Linda discussed how she did not receive sufficient resources from Laura Jean’s teachers and how she appreciated how the side-by-side examples helped her compare conceptual strategies and the traditional algorithm to learn conceptual strategies:
So, I didn’t have any of the side-by-side stuff to show the different ways in what they’re supposed to be doing and how they were learning and stuff because none of it ever came … home where she was explaining, I don’t know what she was saying. So, so I guess [the examples] just informed me of what it is and kind of showed me compared to what how I learned in school kind of gave me a comparison so I can see what I was, what I was doing compared to what I needed to be doing to show her.(Interview)
The side-by-side strategies, serving as informative guides during remote instruction when access to teachers was more limited, and the resulting available problems informed Linda’s understanding of efficiency. She emphasized the importance of these samples, “So I think having a sample of what the kids are supposed to be working on, I think, helps” (Session Five).
Linda praised the convenience of the interactive homework assignments, stating how prior inconvenient resources and tools detracted from Laura Jean’s learning. She specifically cited the challenges of remote instruction that required students to complete assignments on the computer and Laura Jean’s difficulties writing on the touch screen of her school-district-provided Chromebook. Her screen was too small to write on and a stylus had not been provided:
It’s like if the screen is bigger, it would be easy to work on but their computer screens are [too small and] it’s like this big pain, and their little fingers are fat. And I guess if you had like little, like the pencils that write on screens…Yeah, that would make it easier. And I don’t know if they even work with these things. But um, but yeah, it makes it really hard to write on there and then to erase and then you need to go back and take. Yeah, it’s just a pain.(Session Three)
Linda believed that the typing feature of Pear Deck, an interactive app for student learning, posed additional challenges for setting up problems for solving:
And if you just type and use the type part…trying to get it to like [to] type the problem and then line it up and hit their space and that ends up, it doesn’t line up right.(Session Three)
She continued discussing challenges with Chromebooks in the fourth session, when she experienced difficulty locating Laura Jean’s school assignments to print out (Researcher’s Journal, p. 4). Given Linda’s difficulties with technology, she was grateful for the easy access to the interactive homework assignments and the ability to write directly on them for problem solving (Session Three).
4. Conclusions
In alignment with existing literature, this study’s findings revealed a need for providing parents with sufficient mathematics support to aid their child’s learning [10,11,12]. Although Linda had an extensive mathematics content background, she did not have extensive pedagogical content knowledge. Therefore, she initially struggled to help her daughter learn mathematics concepts and strategies for which she had limited experience. Linda began to demonstrate improvements in mathematics self-efficacy in her ready use of conceptual strategies to support Laura Jean. Improvements in parent mathematics self-efficacy appear to stem from greater exposure to and practice with conceptual mathematics strategies and modifications to the intervention to suit participant needs [23,24,28,35]. Specifically, participants solved problems together using various strategies, and their understanding of these strategies improved through repeated practice and the use of question prompts and examples to evaluate and reflect on the strategies’ effectiveness. As a result of practice and evaluation, their arsenal of strategies improved, leading to a deeper understanding of the nature of subtraction, addition, and the part-to-whole relationship of fractions. Moreover, participant learning and self-efficacy also progressed due to conditions that were controlled (e.g., the nature of parent–child discussion and opportunities for selecting different strategies) through weekly homework modifications based on participant feedback and need. Problem-solving tasks, collaboratively problem solving, direct instruction on instructional methods, self-guiding instruction, and emotional supports (e.g., a discussion question that asked participants to highlight each other’s contributions and prompts that promoted positive interactions among participants) were contributing factors to improved parent mathematics self-efficacy and parent mathematics knowledge for teaching.
A bilateral relationship between the parent–child partnership in their understanding of conceptual strategies and confidence using the conceptual strategies was postulated to affect the intervention’s outcomes. The improvement in Laura Jean’s learning was remarkable. Although Linda was the participant of primary focus of this study, the interactions between Linda and Laura Jean propelled their progress during the intervention. Specifically, as Linda’s mathematics self-efficacy and mathematics knowledge for teaching improved, Laura Jean’s mathematics skills also improved, resulting in Linda’s improved approach to her mathematics engagement with Laura Jean.
Additional themes that emerged from the intervention were initiative and ability. Initiative is defined as one’s willingness to take charge of the learning process, and ability refers to levels of mathematics proficiency. Laura Jean’s transformation was signaled by her willingness to take the initiative in solving problems in the homework. Session One was characterized by Laura Jean following Linda’s directions on completing the problems (Researcher’s Journal, p. 2). As Linda repeated the strategies’ procedures, Laura Jean quietly obeyed. As Linda attempted to engage Laura Jean, she initially responded with one to three words, grunts, and shrugs. Moreover, Linda did not answer the second homework’s discussion section question, “How did your partner help you learn about the strategies (e.g., encouragement, providing a great explanation)?”, reinforcing the researcher’s observations of how Laura Jean had not initially facilitated Linda’s learning (Researcher’s Journal, p. 2; Session One).
Their improved interactions mutually reinforced each other’s growth, leading to Laura Jean’s improved initiative to engage in mathematics tasks by the last session. At the beginning of the second session, Laura Jean maintained her passivity; however, after the base-10 strategy was explained, she volunteered to complete the rest of the interactive homework problems (Researcher’s Journal, p. 3). By Session Three, as Linda began to follow the discussion prompts to examine the side-by-side examples more closely, facilitate productive dialogue, and encourage Laura Jean, Laura Jean volunteered to do most of the homework problems and complete problems outside of the intervention and schoolwork (Interview; Researcher’s Journal, pp. 4–6; Sessions Three through Five). Linda’s guidance and encouragement, facilitated by the assignment’s prompts and questions, improved Laura Jean’s understanding. As a result, she experienced success in mathematics, leading to more positive reinforcement and, thus, a greater desire to engage in mathematics. By the last session, Laura Jean created models for solving and articulated her problem-solving process using mathematical language without Linda’s prompting. (Researcher’s Journal, p. 6; Session Five).
Laura Jean’s improved ability and rapid mathematics success appeared to be the linchpins that ignited improvements in Linda’s mathematics knowledge for teaching and mathematics self-efficacy as she observed the effectiveness of conceptual strategies. Before the intervention, Laura Jean struggled for at least two months using the traditional standard algorithm for subtraction with regrouping. After two sessions using the base-10 block strategy led to her accurate use of the traditional algorithm, Linda requested additional practice with conceptual strategies to improve Laura Jean’s understanding of fractions (Researcher’s Journal, p. 4; Session Three). By Session Four, Linda guided Laura Jean’s understanding of fractions through questioning and pictorial representations of the part-to-whole relationship. Linda had to correct Laura Jean’s area models for subtracting fractions less than one; however, by Session Five, Laura Jean adroitly created number lines with equivalent fractions greater than one to regroup with subtraction while correcting her mistakes and explaining her process for solving. Laura Jean’s self-corrections, articulation of her problem-solving process, and her adaptations of a conceptual strategy without prompting (e.g., placing equivalent fractions on the same number line to subtract) with more advanced concepts like fractions represent a marked departure from her mathematics engagement in the initial sessions. The parent participant’s knowledge and confidence in using conceptual development strategies translated to the child participant’s full embrace of mathematics as she began to experience success. As a result, the parent participant, initially resistant to using conceptual strategies, actively sought additional opportunities to work with her child to use conceptual strategies. Additional practice led to greater improvement in mathematics knowledge and confidence. Each participant fueled the other’s progress, likely resulting in the relatively rapid growth in their overall conceptual knowledge and self-efficacy. The dynamic between parent and child collaborations cannot be underestimated as a factor in future mathematics interventions.
Implications for the Future
While the results of the intervention appear promising, there are many questions that future studies should examine. The parent participant had a strong mathematics background that she used to catapult her understanding of conceptual mathematics strategies. Furthermore, she was confident in her general mathematics abilities. How effective would the interactive homework assignments be for parent participants with less mathematics experience and confidence? These participants were also affluent, and what would the impact of this intervention be with participants from various SES or a much more diverse set of participants in general? This intervention involved two participants, but what could be its impact on a larger sample size of participants? Given the small sample size, the assignments could be tailored based on specific needs. How could this intervention be scaled up to meet the varying needs of several more participants?
As schools in the United States continue to grapple with the aftermath of the COVID pandemic’s effects on student learning, new approaches must be taken to improve parent mathematics engagement. This study highlighted the impact of a parent participant, who, when appropriately supported, developed a new mindset and skills for helping her child overcome significant mathematics challenges and gaps in understanding. This study also revealed the importance of respecting parent perspectives; how valuing their needs, skills, and insight can work to accelerate their child’s progress. Schools should provide resources to families that help them learn new mathematics concepts and approaches to teaching mathematics different from ways that they may have learned. Specifically, these resources should be embedded with question prompts that promote positive mathematics engagement between family member and child, as the study revealed that guided collaboration enhanced the participant understanding of the strategies and their motivation to continue learning. Moreover, schools should focus on gathering feedback from families about the resources they need to support their children. As the participants grew in their knowledge of pictorial mathematics strategies, the parent participant better advocated for additional materials to meet her daughter’s needs. Improving the bridge between home and school through interactive tools that mirror classroom instruction and communication could be instrumental in improving this nation’s mathematics trajectory for the future.
Author Contributions
L.M. designed the study, carried out the study with the participants, organized and analyzed the data, and prepared the initial manuscript. R.N.R. oversaw the development and implementation of the study, assisted with the data analysis and the preparation of the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki, and approved by Homewood Institutional Review Board (protocol code HIRB00012604, date of approval: 20 October 2020).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Data will be stored in a secure facility for seven years.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Interactive Homework Examples.



References
- Gravemeijer, K.; Stephan, M.; Lin, F.; Julie, C.; Ohtani, M. What mathematics education may prepare students for the society of the future? Int. J. Sci. Math. Educ. 2017, 15, 105–123. [Google Scholar] [CrossRef]
- Kang, H.; Cogan, L. The differential role of socioeconomic status in the relationship between curriculum-based mathematics and mathematics literacy: The link between TIMSS and PISA. Int. J. Sci. Math. Educ. 2022, 20, 133–148. [Google Scholar] [CrossRef]
- Lawson, M.A. School-family relations in context: Parent and teacher perceptions of parent involvement. Urban Educ. 2003, 38, 77–133. [Google Scholar] [CrossRef]
- National Council of Teachers of Mathematics. Principles and Standards for School Mathematics; National Council Teachers Mathematics: Reston, VA, USA, 2000. [Google Scholar]
- Su, F. Mathematics for Human Flourishing; Yale University Press: New Haven, CT, USA, 2021. [Google Scholar]
- United States Department of Education. Mathematics Equals Opportunity. 20 October 1997. Available online: https://files.eric.ed.gov/fulltext/ED415119.pdf (accessed on 20 June 2020).
- Burrus, J.; Moore, R. The incremental validity of beliefs and attitudes for predicting mathematics achievement. Learn. Individ. Differ. 2016, 50, 246–251. [Google Scholar] [CrossRef]
- Carnevale, A.P.; Desrochers, D.M. The Democratization of Mathematics; Semantic Scholar: Seattle, WA, USA, 2003. [Google Scholar]
- National and Economic Importance of Improved Math-Science Education and H.R. 4272, the National Science Education Enhancement Act, 116th Cong. 2000. Available online: https://congressional-proquest-com.proxy1.library.jhu.edu/congressional/docview/t29.d30.hrg-2000-hew-0045?accountid=11752 (accessed on 14 November 2020).
- Goldman, S.; Booker, A. Making math a definition of the situation: Families as sites for mathematical practices. Anthropol. Educ. Q. 2009, 40, 369–387. [Google Scholar] [CrossRef]
- Jackson, K.; Remillard, J.T. Rethinking parent involvement: African American mothers construct their roles in the mathematics education of their children. Sch. Community J. 2005, 15, 51–73. Available online: http://www.adi.org/journalsearch/ (accessed on 5 December 2020).
- Remillard, J.T.; Jackson, K. Old math, new math: Parents’ experiences with standards-based reform. Math. Think. Learn. 2006, 8, 231–259. [Google Scholar] [CrossRef]
- National Governors Association Center for Best Practices & Council of Chief State School Officers. Common Core State Standards for Mathematics; National Governors Association Center for Best Practices & Council of Chief State School Officers: Washington, DC, USA, 2010. [Google Scholar]
- Silver, E.A.; Ghousseini, H.; Gosen, D.; Charalambous, C.; Strawhun, B. Moving from rhetoric to praxis: Issues faced by teachers in having students consider multiple solutions for problems in the mathematics classroom. J. Math. Behav. 2005, 24, 287–301. [Google Scholar] [CrossRef]
- Wei, R.C.; Darling-Hammond, L.; Andree, A.; Richardson, N.; Orphanos, S. Professional Learning in the Learning Profession: A Status Report on Teacher Development in the U.S. & Abroad (Technical Report); Learning Forward: Oxford, OH, USA; Stanford Center for Opportunity Policy in Education: Stanford, CA, USA, 2009. [Google Scholar]
- Hatano, G.; Inagaki, K. Two courses of expertise. In Child Development and Education in Japan; Stevenson, H., Azuma, H., Hakuta, K., Eds.; Freeman: New York, NY, USA, 1986; pp. 262–272. [Google Scholar]
- Givvin, K.B.; Stigler, J.W.; Thompson, B.J. What community college developmental mathematics students understand about mathematics, Part II: The interviews. MathAMATYC Educ. 2011, 2, 4–18. [Google Scholar]
- Hackett, G. The role of mathematics self-efficacy in the choice of mathematics related majors of college women and men. A path analysis. J. Couns. Psychol. 1985, 32, 47–56. [Google Scholar] [CrossRef]
- Jameson, M.M.; Fusco, B.R. Math anxiety, math self-concept, and math self-efficacy in adult learners compared to traditional undergraduate students. Adult Educ. Q. 2014, 64, 306–332. [Google Scholar] [CrossRef]
- Berkowitz, T.; Schaeffer, M.W.; Maloney, E.A.; Peterson, L.; Gregor, C.; Levine, S.C.; Beilock, S.L. Math at home adds up to achievement in school. Science 2015, 350, 196–198. [Google Scholar] [CrossRef]
- Berkowitz, T.; Schaeffer, M.W.; Rozek, C.S.; Maloney, E.A.; Levine, S.; Beilock, S.L. Response to comment on “Math at home adds up to achievement in school”. Science 2016, 351, 1161. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Schaeffer, M.W.; Rozek, C.S.; Berkowitz, T.; Levine, S.C.; Beilock, S.L. Disassociating the relation between parents with math anxiety and children’s math achievement: Long-term effects of a math app intervention. J. Exp. Psychol. 2018, 147, 1782–1790. [Google Scholar] [CrossRef] [PubMed]
- Jay, T.; Rose, J.; Simmons, B. Finding “mathematics”: Parents questioning school-centered approaches to involvement in children’s mathematics learning. Sch. Community J. 2017, 27, 201–230. [Google Scholar]
- Tobon, G.; Hughes, T.M. Engaging Latino families as mathematicians. Math. Teach. 2020, 113, 201–208. Available online: https://www-jstor-org.proxy1.library.jhu.edu/stable/10.5951/mtlt.2019.0001?seq=1#metadata_info_tab_conconte (accessed on 4 December 2020). [CrossRef]
- Mangram, C.; Metz, M.T.S. Partnering for improved parent mathematics engagement. Sch. Community J. 2018, 28, 273–294. [Google Scholar]
- Papadopoulos, I. Opening inquiry mathematics to parents: Can they be engaged as teachers’ partners in mathematical work? J. Pedagog. Res. 2017, 1, 1–20. Available online: https://search-proquest-com.proxy1.library.jhu.edu/docview/2265809190?accountid=11752 (accessed on 12 December 2020).
- Mistretta, R.M. Conversations with family members about math. Sch. Community J. 2017, 27, 181–201. Available online: http://www.schoolcommunitynetwork.org/SCJ.aspx (accessed on 4 December 2020).
- Williams, K.; Williams, H. Mathematics problem-solving homework as a conduit for parental involvement in learning. Evaluation of a pilot study. Educ. Rev. 2019, 73, 209–228. [Google Scholar] [CrossRef]
- Panaoura, A. Parental involvement in developing students’ perseverance in solving mathematical problems through the use of social media. Int. J. Technol. Educ. Sci. (IJTES) 2017, 1, 36–47. Available online: https://www.ijtes.net/index.php/ijtes/article/download/5/4 (accessed on 4 January 2020).
- Westenskow, A.; Boyer-Thurgood, J.; Moyer-Packham, P.S. A window into mathematical support: How parents’ perceptions change following observations of mathematics tutoring. J. Res. Child. Educ. 2015, 29, 258–475. [Google Scholar] [CrossRef]
- Ball, D.L.; Thames, H.; Phelps, G. Content knowledge for teaching: What makes it special? J. Teach. Educ. 2008, 59, 389–407. [Google Scholar] [CrossRef]
- De Corte, E.; Verschaffel, L.; Depaepe, F. Unraveling the relationship between students’ mathematics-related beliefs and classroom culture. Eur. Psychol. 2008, 13, 24–36. [Google Scholar] [CrossRef]
- Shulman, L.S. Those who understand: Knowledge growth in teaching. Educ. Res. 1986, 15, 4–14. [Google Scholar] [CrossRef]
- Bandura, A. Social Foundations of Thought and Action: A Social Cognitive Theory; Prentice-Hall: Englewood Cliffs, NJ, USA, 1986. [Google Scholar]
- Van Voorhis, F.L. Costs and benefits of family involvement in homework. J. Adv. Acad. 2011, 22, 220–249. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).