Abstract
This study investigates the effectiveness of an instructional approach called “Worked-out Examples Involving 4 Stages” (WEI4S) for enhancing middle school students’ algebraic problem-solving skills and reducing CL. Based on cognitive load theory (CLT), WEI4S combines four stages (analyse, explain, investigate, and apply) to facilitate deep comprehension. This study involved 36 novice seventh-grade students identified as having challenges solving algebraic word problems. Participants were randomly assigned to different groups, including the experimental group that received the WEI4S intervention and a control group that participated in problem-solving activities. Pre- and post-tests, as well as a transfer test, were administered to measure algebra performance and CL, and students’ opinions about the intervention were collected. The findings revealed that students exposed to WEI4S showed significant improvements in algebra performance, decreased intrinsic CL, and no negative changes in terms of extrinsic and germane load compared to the control group. Overall, the WEI4S approach offers a promising avenue for effective mathematics instruction by providing a structured framework that encourages active engagement and problem-solving skills.
1. Introduction
The field of algebra is a vital connection between mathematics and advanced mathematical concepts or other fields of study. By learning algebra, students move from a culture of numbers and operations with numbers to a culture in which letters are substituted for numbers and operations are performed with letters. This transition, as described by Lee [1], can be likened to a “cultural shock” as students shift from working with concrete numbers to manipulating abstract symbols. Algebra empowers students to translate numerical computations into broad, overarching relationships. The development of algebraic ways of thinking is supported by the elementary and middle school curriculum, and the basic concepts in algebra can be learned by the end of middle school [2,3].
Studies examining students’ algebra learning processes have shown that students have difficulties learning algebraic relations and the basic concepts of algebra, so they make many mistakes and have misconceptions [4,5,6]. Learning about the concepts of variables and equality is the basis of these difficulties experienced by students [7,8,9]. Although students learn to solve simple equations, students with previous arithmetic experience have trouble solving algebraic word problems when they need to apply these equations, and this situation sometimes causes students to drop out of mathematics [10]. Khng and Lee [11] reviewed the impact of previous arithmetic experiences among secondary school students in Singapore on their ability to solve word problems; algebra word problems were taught in primary school with arithmetic methods such as counting techniques, estimation and testing, backward working, grouping, and model methods. This led students to use these strategies derived from primary school mathematics instead of algebraic equation formulation when presented with word problems that demand problem-solving skills in secondary school.
Problem-solving has a wide range of meanings, from simple exercises to professional mathematical activities [12]. Problem-solving offers students the opportunity to understand abstract mathematical concepts, develop critical thinking skills, and strengthen their mathematical abilities [13]. Historically, problem-solving emerged as a process that shapes and develops mathematical thinking. For example, analysis of the strategies used by ancient mathematicians to solve complex problems provides important insights into the evolution of mathematical knowledge [14]. Importantly, the literature often divides problems into two main types: routine and non-routine [15]. Routine problems, which can also be called exercises and test the student’s knowledge of a recently learned topic, can be difficult but not surprising [16]; such problems are similar to problems that students have solved before. In contrast, non-routine problems cannot be answered immediately [17] and are not similar to problems that students have encountered before [15].
Generally, mathematical problems, whether they are routine or non-routine, are verbally presented challenges that necessitate arithmetic solutions [18]. Within the scope of this study, mathematical problem-solving is conceptualized as the process of applying pre-existing knowledge to address novel situations [12,13]. Secondary school educators often observe a lack of motivation among students for the acquisition of the skills necessary to solve algebraic word problems [19]. This can be partly attributed to the tendency of students to steer clear of activities that require representation, transformation, generalization, and verification. They do so by relying on concrete and visual representations of unknowns and employing predetermined arithmetic procedures for solving them [2]. A highly effective approach to mastering the solution process for such problems may be through the study of worked-out examples [20,21,22,23,24]. This study investigated the impact of worked-out examples on the performance of middle school students when solving first-order linear equation problems.
The acquisition of proficient problem-solving skills in algebraic contexts is crucial for students’ academic success and their ability to apply mathematical principles to practical situations. Although worked-out examples have been extensively employed as pedagogical tools, this research takes a step further by introducing a structured approach that integrates cognitive load theory (CLT), instructional design principles, and metacognitive strategies through self-explanation. This approach, anchored in a three-stage model (analyse, explain, apply) [25], extends the existing framework by adding an “examine” stage, which emphasizes error analysis and self-explanation.
2. Literature Review
Worked-out examples are based on CLT, which suggests that the amount of information that a person can process at one time is limited and that this limit can affect their ability to learn new information effectively [26]. The human brain’s limited working memory capacity can be overloaded by too much information, which makes it difficult to learn new information effectively [26,27,28]. According to CLT, CL can be categorized into three types: intrinsic, extraneous, and germane. Intrinsic load (IL) refers to the inherent difficulty of the task. Extraneous load (EL) refers to the additional cognitive demands created by how the task is presented or organized, and germane load (GL) refers to the cognitive demands associated with forming new mental representations of the information being learned [28,29].
Learners have a limited capacity for processing information in their working memory, and when the demands on working memory exceed its capacity, the CL is too high, and learning may be impaired [30]. Worked-out examples can help reduce CL by providing learners with preprocessed information that is easier to understand and requires less mental effort [20,31,32]. The fully worked out and explained example allows learners to focus their attention on the key concepts and principles without having to process the mechanics of solving the problem simultaneously.
Worked-out examples can also help learners develop schemas and mental representations of patterns that can be applied to new problems [33]. By studying and analysing worked-out examples, learners can gain insight into the underlying principles and strategies used to solve problems, and this insight can then be applied to new, similar problems, thus reducing the CL needed for problem-solving [33,34]. Worked-out examples are often used in mathematics education to support students’ learning and comprehension [35,36]. By seeing how a problem is solved, students can see the connections between different mathematical concepts and develop their problem-solving skills [34]. Worked-out examples can also help students build their procedural fluency and automaticity—that is, the ability to perform mathematical operations quickly and accurately. A recent meta-analysis of 43 articles reporting on 81 effect sizes showed that worked examples exhibit a favourable and moderate impact on students’ mathematical learning throughout their academic journey. The results showed that engaging with worked-out examples enables learners to allocate their cognitive efforts towards comprehending the pertinent elements and procedures involved in problem-solving. This, in turn, leads to the formation of mental frameworks specific to that type of problem, which then enhances subsequent performance on similar problems [22].
Worked-out examples encompass various instructional formats designed to facilitate understanding and learning. These examples can be classified into distinct types, each of which serves a specific purpose in enhancing comprehension. For example, whereas traditional worked-out examples offer step-by-step solutions to problems, providing learners with a clear model to follow, faded worked-out examples (backward or forward) gradually reduce the level of guidance, thus enabling students to transition from guided problem-solving to independent mastery, as recommended in the literature [37,38,39,40,41]. Worked-out examples that include self-explanation incorporate questions that encourage learners to articulate the reasoning behind each step, which promotes metacognitive awareness. Correct and incorrect worked-out examples [40,42] juxtapose correct and incorrect solutions, which aids in the identification of common misconceptions. These diverse types of worked-out examples cater to learners’ varying needs and cognitive capacities, offering an array of strategies to enhance their problem-solving skills and understanding of complex concepts. In the present study, different aspects of correct–incorrect worked-out examples with self-explanation were taken into account.
Research has shown that incorporating incorrectly worked examples, either alone or in combination with correct examples, is a form of instructional practice that enhances mathematics learning [7,41,42,43,44]. Incorrect worked-out examples involve solving a problem and intentionally displaying a common error made by a fictional student. When students encounter these incorrect examples, they are typically tasked with studying and explaining the error and sometimes even correcting it before proceeding to solve a similar practice problem. In studies involving erroneous examples, incorrect examples are presented either before [44] or after [41] correct examples. In the incorrect solution steps, students are prompted to identify errors in the solution and asked to explain the reasons for these errors and correct them. This typically involves self-explanation prompts in the worked-out examples to facilitate comparisons.
When students themselves analyse their mistakes, it facilitates learning [45]; in this study, instead of using incorrect worked-out examples conducted by fictitious students, students’ own mistakes were used as the incorrect solutions. By engaging in error analysis, teachers can gain valuable insight into what their students know and do not know, as well as identifying areas where they need additional support and instruction. This information can then be used to differentiate instruction and provide targeted feedback that addresses specific misunderstandings and misconceptions.
Another type of worked-out example included in the current study is the incorporation of self-explanation prompts [39]. Self-explanation is “the process of explaining text or material to oneself either orally or in writing” [46]; it entails learners explaining educational content to themselves, thus facilitating comprehension. Research has indicated that students who integrate self-explanation into their learning process exhibit enhanced performance in problem-solving tasks [47]. Notably, as some students—particularly novices—might not inherently use this strategy [48], the use of self-explanation prompts has been proposed. These prompts are external cues that illuminate the process of self-explanation. Typically embedded within the learning material, self-explanation prompts have been employed in studies related to worked-out examples [49]. It has frequently been observed that when students interact with an expository text, they may read each sentence in isolation and fail to establish links between new information and their existing knowledge, which leads them to overlook the potential implications arising from the new information. In both cases, the absence or ineffectiveness of metacognition becomes evident as learners struggle to identify (i.e., engage in metacognitive monitoring) and control gaps (i.e., demonstrate metacognitive control) in their comprehension [50]. The self-explanation questions strategically placed within the intervention foster metacognitive awareness by encouraging students to reflect on their problem-solving strategies and cognitive processes [46]. This metacognitive approach aligns with contemporary educational theories and promotes higher-order thinking skills. Barbieri et al. [22] examined different types of worked-out examples in their meta-analysis, from elementary levels to post-university settings. According to their findings, the inclusion of self-explanation prompts significantly influenced the effect of the examples. Studies that employed only correct worked-out examples yielded greater effect sizes than those using only incorrect examples or a combination of both correct and incorrect examples. Correct examples are generally particularly beneficial for learning, and the design modification of pairing examples with self-explanation prompts might not be efficient. Considering the results of this meta-analysis, the present research aimed to integrate the examination of students’ own mistakes into the examples worked rather than using incorrect solutions.
In Teaching Math with Examples, Pershan [25] expounds upon a pedagogical project denominated “Math by Example”, which is an illustrative instance of the practical application of worked-out examples in the domain of mathematics education. This project is a collaborative effort between researchers and a school district to enhance algebra learning for students. Researchers curated worked-out examples based on research literature, tested them in classrooms, and confirmed their effectiveness through experiments. These materials were then made accessible online for teachers’ use. The success extended to elementary students (“Math by Example”) and ongoing middle school work. The project demonstrates a research model that aligns with classroom needs. Upon reviewing the materials, Pershan [25] realized that instead of just presenting worked-out examples, the materials engage students in activities that encourage profound thinking. A complete mathematical strategy is presented through worked-out examples, which prompts student explanation. Students then apply this strategy to solve related problems, which results in a dynamic activity that resonates with students. According to Pershan [25], “The Algebra by Example” materials guide students through three stages: analysing solutions, explaining why they work, and applying them to new problems. The analysis stage involves careful reading of solutions to engage with new mathematical ideas; the second stage prompts self-explanation, while drawing attention to crucial solution aspects; and the third stage requires application to new problems, thus fostering generalizations. These stages collectively encourage active engagement and deeper understanding among students.
Current Study
This study combines Pershan’s [25] three-stage model (analyse, explain, and apply) with correct–incorrect worked-out examples and introduces a new stage called “examine” between the explain and apply stages. This “examine” stage involves students reviewing their own incorrect answers in response to self-explanation questions. Consequently, the model comprises four stages—analyse, explain, examine, and apply—and is referred to as Worked-Out Examples Including Four Stages (WEI4S) in this study. The “analyse” stage commences with questions and answers with explanations. In this stage, students thoroughly examine worked-out solutions that introduce them to new mathematical concepts and ideas. In the “explain” step, a similar problem is presented with a solution but without an explanation. Students are guided by questions to provide explanations, which is referred to as self-explanation in the literature. In the “examine” stage, students are given incorrect solutions, along with self-explanation questions to facilitate the examination of their mistakes. Students are directed to perform an error analysis of their incorrect solutions. Finally, in the “apply” stage, students are asked to apply their knowledge to a new, similar problem.
Studying worked-out examples is a valuable activity in the early stages of cognitive skill acquisition. However, it becomes inefficient in the later stages of learning as students develop a sufficient knowledge base [51,52]. At this point, students are better served by transitioning to independent problem-solving. In light of this, novice seventh-grade students who had not acquired sufficient cognitive skills to solve first-order equations with one unknown were included in this study. The purpose of this study was thus to examine the effect of WEI4S on seventh-grade novice students’ performance in solving word problems requiring algebraic equations and their CL. We thus propose our first hypothesis:
Hypothesis 1.
A significant improvement in near-transfer (similar problems; [53,54]) algebra performance (AAT) among the novice students in the experimental group will be observed as a result of the completion of WEI4S compared to the novice students in the control group.
This hypothesis is based on the expectation that the integration in the WEI4S model, which emphasizes self-explanation and error analysis, will enhance students’ ability to solve algebraic word problems. Learners’ active participation in WEI4S may lead not only to enhanced near transfer but also to better far transfer (dissimilar problems; [53,54]). Hypothesis 2 extends the investigation to include far transfers, building upon the near transfers explored in Hypothesis 1.
Hypothesis 2.
A significant improvement in far-transfer algebra performance will be achieved as a result of the completion of WEI4S among the students in the experimental group in comparison to the students in the control group.
Worked-out questions are based on CLT [31,39,55]. The differences in performance observed between the experimental and control groups in controlled experimental learning environments has been attributed to variations in CL in the literature [56]. Corroborating the results with other measures of CL to obtain more valid information can, however, provide convergent validity [56]. To assess the CL experienced by students in both the experimental and control groups during their performance of the Algebra Achievement Test–Procedural Knowledge (AAT-PK) and Algebra Achievement Test–Conceptual Knowledge (AAT-CK), a CL scale was administered to the students after both the pre-test and post-test sessions. In this context, Hypothesis 3 is based on the assumption that a reduction in CL components, such as IL and EL, will be brought about by the WEI4S model due to its emphasis on guided self-explanation and error analysis, ultimately resulting in an improvement in the efficiency of learning and problem-solving. Therefore:
Hypothesis 3.
The completion of WEI4S results in a significant decrease in the IL, EL, and CL of students related to the Algebra Achievement Tests (AAT-CK and AAT-PK) in the students of the experimental group compared to those in the control group.
Hypothesis 4 is related to the implementation of a worksheet based on WEI4S. In accordance with CLT, instructional materials can impose three distinct forms of CL on learners: intrinsic load, extraneous load, and germane load. Accurate measurement of these various CL types is instrumental in gaining insights into why the effectiveness and efficiency of learning environments might vary based on instructional formats and learner attributes [57]. Hypothesis 4 anticipates that the WEI4S model presented in the worksheet will be superior in optimizing CL, leading to a better allocation of cognitive resources and a deeper understanding of algebraic problem-solving.
Hypothesis 4.
The WEI4S intervention through worksheets is effective in reducing intrinsic load (IL) and extraneous load (EL) and enhancing germane load (GL).
Student feedback can also reveal challenges or difficulties, guiding improvements and tailoring instruction to cater to diverse learning needs. The thoughts and perceptions of students regarding the WEI4S intervention were collected through open-ended survey questions, and these responses hold great importance, as they provide valuable insights into the intervention’s effectiveness and its impact on the learning experience. Ultimately, students’ thoughts play a central role in evaluating, enhancing, and communicating the benefits of the WEI4S model in educational settings. Therefore we suggest:
Hypothesis 5.
Positive perceptions and thoughts regarding the WEI4S intervention will be held by students in the experimental group.
The purpose of this study was to examine the effect of the WEI4S intervention on students’ performance in solving word problems requiring algebraic equations and their CL. In this respect, the following research questions were answered.
- Does the completion of WEI4S lead to a significant improvement in the algebra performance of the experimental group students compared to the control group?
- Does the completion of WEI4S lead to a significant decrease in the IL, EL, and CL scores related to AAT in the experimental group students compared to the control group?
- What is the effectiveness of WEI4S intervention in terms of three types of CL (IL, EL, GL)?
- What are thoughts of students in the experimental group regarding their experience of the WEI4S intervention?
3. Materials and Methods
3.1. Participants
To examine the effect of the WEI4S intervention on novice seventh-grade students’ algebra performance and CL, an experimental research study using a pre-test–post-test control group was designed. The participants of this study were selected from 120 seventh-grade students in a public school in Istanbul, Turkey. Because participation in this study was voluntary and parental consent was obtained, the selection of participants continued with 86 volunteer students whose parents signed the consent form. If the learners have the cognitive schemata to solve the problem, the information presented in the worked-out examples is redundant [51]. For this reason, in order to include students who could not solve algebra problems, the Algebra Achievement Test (AAT) was administered to the students. The 36 novice students who encountered difficulties solving the algebra questions included in the pre-test (AAT-PK and AAT-CK) were chosen as participants for this study. These students had either been unable to solve the questions or had obtained three or fewer points out of ten on each question. Participants were assigned randomly to different groups, including the experimental group, which received the WEI4S intervention, and the control group, which did not. Out of these students, 19 (8 [42.1%] male and 11 [57.9%] female) were randomly assigned to the experimental group, and 17 (11 [64.7%] male and 6 [35.3%] female) were assigned to the control group. The mean age of the students was 11.7 years. These students had been taught to solve linear equations and algebraic word problems that can be solved by equations with one unknown one month before the WEI4S intervention.
3.2. Instruments
The data collection tool consisted of an AAT, a worksheet including the WEI4S intervention, a CL scale for intervention, a CL scale for pre- and post-AAT, transfer questions, and open-ended questions related to students’ opinions about the intervention.
3.2.1. Algebra Achievement Test
To assess students’ algebraic performance on problems with a first-order unknown, an AAT with eight questions was prepared by four mathematics teachers based on the questions in the students’ school textbooks. The first question was related to the solution of a first-order equation with one unknown, and the other seven questions consisted of problems solved using an equation with one unknown. The test was applied to all 86 participants during one lesson period (40 min) by the researcher. This test was used both to select novice participants and to select questions for the pre-test. The use of this test to choose participants was explained in the Section 3.1. The questions that were difficult for the students were determined by calculating item difficulty indices. Four questions (1, 5, 6, and 8) exhibiting low difficulty indices were chosen for the pre-test. Item difficulty indices were calculated by the ratio of the arithmetic mean of the item scores to the maximum score that could be obtained from the item. The item difficulty indices of these four questions were 0.40, 0.22, 0.19, and 0.14, respectively. The choice of questions with low difficulty indices for the pre-test was intentional. These questions were selected to ensure that the pre-test adequately measured students’ baseline knowledge. By including less challenging questions, it aims to establish a solid foundation for later comparisons with the post-test results. The selection of specific items was based on their alignment with this study’s research objectives and the desire to avoid redundancy for students who were already proficient in the subject matter.
The first question, the AAT-PK, was related to solving algebraic equations with one unknown required procedural knowledge. This question required the use of the distributive property. A scoring system was established for the answers to assess score reliability. Combined elements of both analytical and holistic scoring systems were used. The scoring was broken down into specific criteria, such as applying the distributive property and simplifying algebraic expressions. The response was assessed as a whole and received a single, cumulative score based on the overall correctness of the response. The question was finding x for the equation 3 (2x + 8)—4 (3x—5) = 2x—4. The scoring of the example for the first question was as follows: if the distribution property has been applied when answering the question, 2 points; if the distribution property has been applied correctly when answering the question, 5 points; after the simplified distribution property has actually been implemented by adding terms to algebraic expressions, 7 points; and if the answer to the question was completely correct, 10 points.
The other three questions, the AAT-CK, required conceptual knowledge and could be solved by first-order linear equations with one unknown. One of the questions (the eighth) is presented below (See Figure 1). The holistic scoring of the other three questions was as follows: no solution and solving without an algebraic expression, 0 points; writing the correct algebraic expression, 5 points; and solving a true algebraic expression completely, 10 points.
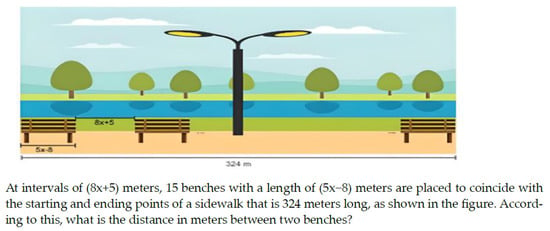
Figure 1.
One of the questions from pre-AAT-CK.
The objectives and the scoring system for the post-AAT for both PK and CK were the same as those for the pre-tests. The types of questions asked in the pre-test and post-test were similar. The post-test was given to students three weeks after the WEI4S intervention.
3.2.2. Worksheet including WEI4S (Analyse, Explain, Examine, and Apply)
While preparing the worked-out example worksheet, the WEI4S model was used. The model consisted of four stages: analyse, explain, examine, and apply. The analysis stage began with a similar question to that used in the pre-test, in addition to its answer with explanations (see Figure 2). In this stage, students carefully examined worked-out solutions that exposed them to new mathematical concepts and ideas. An example from WEI4S: The first stage (analysis) is provided below.

Figure 2.
An example from WEI4S: the first stage (analysis).
In the explain stage, a similar problem with a solution—but without an explanation—was presented to the student. Students were directed by questions to self-explain the solution. Students wrote their explanations about the solution in the spaces left under the questions. An example from WEI4S: the second stage (explain) is provided below (see Figure 3).

Figure 3.
An example from WEI4S: the second stage (explain).
In the examination stage, students were given their answers with self-explanation questions that made it easier to examine their incorrect solution. Students were directed to conduct an error analysis of their own incorrect solution. An example from WEI4S: the third stage (examine) is provided below (See Figure 4).

Figure 4.
An example from WEI4S: the third stage (examine).
In the fourth stage (apply), students were asked to apply what they knew to a new but similar problem. WEI4S was prepared for each question of the AAT-PK and AAT-CK.
3.2.3. CL Scale for Intervention
To assess the impact of WEI4S on learning processes, a CL scale developed by Leppink et al. [57] was used. This scale evaluated the complexity and comprehensibility of the learning materials, the level of effort students invested in understanding and processing those materials, and the extent to which they experienced CL based on their efforts. This original scale consisted of 10 items; in this study, 8 items representing three types of CL were used. The first three items (e.g., “The algebra questions in this worksheet were very complex”) were related to IL, which pertains to the inherent complexity of the task itself. The other two items (e.g., “The instructions and/or explanations for the questions given in this worksheet were ineffective”) were related to EL, which pertains to the supplementary cognitive demands stemming from how the task is structured or presented. The last three items (“This worksheet has truly improved my knowledge and understanding of algebra problems”) were related to GL, which encompasses the cognitive requirements for constructing novel mental models of the information being acquired. Students needed to choose the category that applied to them. Students responded to each of the questions on an 11-point Likert scale (0 meaning “not at all the case” and 10 meaning “completely the case”). In this study, the Cronbach’s alpha coefficient was calculated as 0.98 for IL, 0.95 for EL, and 0.99 for GL. Four additional items for data collection, as recommended by Leppink et al. [57] to measure CL [58], IL [59], EL [60], and GL [61], were added to investigate the intervention effectiveness in terms of CL. Detailed information about these items is provided in the Section 3.4.
3.2.4. CL Scale for Pre- and Post-AAT
The CL scale in this study was adapted from Leppink et al. [57] and was used to measure the cognitive challenges and mental effort experienced by students while performing the AAT-PK and AAT-CK. The scale comprises two subscales: intrinsic load (IL) and extrinsic load (EL). For the IL assessment, three statements, such as “The algebra questions in this test were very complex”, were utilized, whereas two statements, for example, “The instructions and/or explanations for the questions given in this test were insufficient”, were employed to measure EL. Students provided their responses using an 11-point Likert scale, with 0 indicating “not at all the case” and 10 representing “completely the case”. In addition to IL and EL, Paas’s [58] subjective rating scale was used to allow students to self-assess their overall CL, selecting from nine categories, ranging from “very, very low mental effort” to “very, very high mental effort”. The Cronbach’s alpha coefficients were computed for the IL subscale (0.82) and the EL subscale (0.96) in this study, which indicated good internal consistency for both measures. These coefficients demonstrate the reliability of the scales used in assessing CL.
3.2.5. Transfer Question (TQ)
Three weeks after the WEI4S intervention, a transfer question that included a dissimilar question (i.e., a far transfer question [53,54]) was conducted with a post-test. The objective of the transfer question was the same as that of the post-test. However, this problem was not similar to the questions previously solved. The maximum score that could be achieved was 10. The scoring of the question was the same as for the AAT-CK tests (pre and post). The problem is given below. According to the teachers of the participants, the problem requires highly demanding setting up of an equation.
Ahmet has bought two televisions for his home. The price of the A-brand television he bought is TRY 400 more than twice the price of the B-brand television. The total amount Ahmet paid for the two televisions is TRY 2800 less than four times the price of the B-brand television. In this case, how many Turkish Lira did Ahmet pay for these two televisions in total?
3.2.6. Open-Ended Questions Related to the Implementation of WEI4S
After implementing this study, students from the experimental group were given the following survey questions to evaluate the intervention: (1) What do you think about the worked-out example worksheets? (2) Did the worked-out example worksheet contribute to your learning? If so, how? (3) Would you like a worksheet like this to be prepared for you for the questions you could not answer? Why?
3.3. Experimental Process
This study commenced by administering the AAT one week before the WEI4S application to a group of 86 students. The purpose of the AAT was to identify novice students and to choose challenging questions for the pre-test. This administration session took approximately one and a half class hours (equivalent to 60 min). Subsequently, four questions with low item difficulty indices were selected from this test for inclusion in the pre-test for the AAT. Of these, one question assessed procedural knowledge (AAT-PK), whereas the remaining three focused on conceptual knowledge (AAT-CK). Both the CL pre-test and the ATT pre-test were administered to both the experimental and control groups as part of this study.
Following this, the main intervention, WEI4S, was administered by the researcher to the experimental group using worksheets for 80 min (2 class hours). The effectiveness of WEI4S was assessed using the CL scale for the intervention, and students’ perspectives on the intervention were gathered through open-ended survey questions. During the intervention period, instead of WEI4S, the control group focused on problem-solving activities facilitated by the researcher. In the control group, the same questions used in the experimental group were solved through lecturing.
Following this, both the experimental group and the control group underwent the AAT-PK, AAT-CK, and CL post-tests to evaluate their progress, along with a TQ to measure knowledge transfer three weeks after the WEI4S intervention. All details regarding the experimental procedures are outlined in Table 1. The researcher, with the assistance of two math teachers working with the participants, conducted all aspects of this study. During and after the intervention, the students in both the experimental and control groups did not receive any additional instruction about this subject.

Table 1.
Experimental process of this study.
3.4. Data Analysis
After the preparation of data for analysis, the mean, standard deviation, skewness, and kurtosis values of the dependent variables were calculated as descriptive statistics. An independent sample t-test was used to determine the differences among the groups in terms of pre-tests of AAT-PK, AAT-CK, IL, EL, and CL. Pre- and post-test comparisons of dependent variables were made by a paired sample t-test. Independent sample t-tests (when the assumptions of analysis of covariance [ANCOVA] were not satisfied) and ANCOVA tests (when the assumptions were satisfied) were used to determine the differences among the groups in terms of post-tests of AAT-PK, AAT-CK, TQ, IL, EL, and CL. The significance level was defined as at least 0.05. To analyse the opinions of the experimental group about the intervention, the content analysis method was used. The effectiveness of instruction in terms of three types of CL was analysed by calculating the mean score of each item of the CL scale for the intervention; this allowed for a comprehensive assessment of the three types of CL.
3.5. Validity and Reliability of the Experimental Process
In terms of validity, this study exhibits internal validity due to its controlled experimental design, grounded in CLT, and the use of standardized tests to measure outcomes. However, external validity is somewhat limited by the small sample size and the specific focus on seventh-grade students with algebraic problem-solving challenges, which potentially limits the generalizability of the findings to a broader population, although the normal distribution of data and the relatively large number of cases in each group, exceeding 15, mitigate this limitation. Even in non-normal distributions, a sample size of 15 cases per group might be sufficiently large to yield fairly accurate p-values [62]. Nevertheless, the subjective nature of student opinions and the lack of interrater reliability in their analysis present potential sources of variability.
3.6. Ethics Approval
Ethics approval was obtained from the relevant local ethics committees (Protocol no. 2021/03-10).
4. Results
Before the quantitative analysis of the data obtained in this study, descriptive and preliminary analyses were conducted for the dependent variables and are presented in Table 2. In addition, before the intervention, the pre-test scores of the dependent variables for the experimental and control groups were compared using the independent sample t-test. According to the results, there were no significant differences between the experimental and control groups on the pre-AAT-PK (t = 0.26, p > 0.05), pre-AAT-CK (t = −1.01, p > 0.05), pre-IL (t = 0.14, p > 0.05), pre-EL (t = 0.13, p > 0.05), and pre-CL (t = 0.31, p > 0.05). As seen in Table 2, considering that the calculated skewness values are between +2 and −2, the distribution can be accepted as normal [63].

Table 2.
Descriptive statistics for the dependent variables.
Hypotheses 1 and 2 suggested that a significant improvement in near- and far-transfer algebra performance would be achieved as a result of the completion of WEI4S among the students in the experimental group in comparison to the students in the control group. To test these hypotheses first, pre- and post-test comparisons related to AAT-PK and AAT-CK were made on both the experimental and control groups. According to the results of the paired sampled t-test, there were no significant differences between pre- and post-test scores for the AAT-PK (t = −1.99; p > 0.01) in the control group. On the other hand, there was a significant difference between the pre- and post-test scores for the AAT-CK in favour of the post-test (t = −3.99; p < 0.01). In the experimental group, there were significant differences between the pre- and post-test scores for both the AAT-PK (t = −3.37; p < 0.01) and the AAT-CK (t = −10.88; p < 0.01) in favour of post-tests.
To detect the effectiveness of the intervention, post-test scores were compared in terms of control and experimental groups using the ANCOVA test. First, we examined whether the assumption of “homogeneity of regression slopes”, which is an important assumption of ANCOVA, was fulfilled for the AAT-PK, AAT-CK, and TQ. For this purpose, the F-values for the interaction between group type, which is the independent variable, and the pre-test of dependent variables were determined. F-values were calculated as 1.24 for AAT-PK, 2.74 for AAT-CK, and 2.60 for TQ, and p-values were gauged as 0.30, 0.15, and 0.12, respectively. This result can be interpreted as fulfilling the condition of matching regression slopes needed for ANCOVA. To examine another important assumption of ANCOVA, Levene’s test was performed; the result (F = 2.5, p > 0.05 for AAT-PK, F = 0.69, p > 0.05 for AAT-CK, and F = 0.29, p > 0.05 for TQ) of Levene’s test for equality of variances specified that the assumption of the homogeneity of variances in the groups was satisfied. After these assumptions were satisfied, the ANCOVA test was conducted. When AAT-PK pre-test scores were controlled, there was a significant difference between the groups in terms of AAT-PK post-test scores (F (1.36) = 4.47, p < 0.05). The AAT-PK post-test scores of students in the experimental group were significantly higher than the scores of students in the control group. Partial eta-squared values, independent of pre-test scores from different groups (experimental and control), explained 12% of the variance in the AAT-PK post-test scores. When AAT-CK pre-test scores were controlled, there was a significant difference between the groups in terms of AAT-CK post-test scores (F (1.36) = 36.95, p < 0.001). The AAT post-test scores of students in the experimental group were significantly higher than the scores of students in the control group. Partial eta-squared values, independent of pre-test scores from different groups (experimental and control), explained 53% of the variance in the AAT-CK post-test scores. When AAT-CK pre-test scores were controlled, there was a significant difference between the groups in terms of TQ scores (F (1.36) = 6.38, p < 0.05). The TQ scores of students in the experimental group were significantly higher than the scores of students in the control group. Partial eta-squared values, independent of pre-test scores from different groups (experimental and control), explained 16% of the variance in the TQ scores. Thus, Hypotheses 1 and 2 of this study were confirmed.
Hypothesis 3 asserted that the completion of WEI4S would result in a significant decrease in the IL, EL, and CL experienced by students in relation to the AAT-PK and AAT-CK in the experimental group compared to those in the control group. To test Hypothesis 3, first, pre- and post-test comparisons related to IL, EL, and CL were made for both the experimental and control groups. According to the results of the paired sampled t-test, in the experimental group, there were no significant differences between pre- and post-test scores for both EL (t = 1.92; p > 0.01) and CL (t = 2.04; p > 0.06), but there was a significant difference between the pre- and post-test scores for IL (t = −2.92; p < 0.01). The post-test IL scores were significantly lower than the pre-test IL scores. In the control group, there were no significant differences between pre- and post-test scores for CL (t = −0.16; p > 0.01); however, there was a significant difference between the pre- and post-test scores for both IL (t = 3.04; p < 0.01) and EL (t = 2.82; p < 0.05). In both cases, post-test scores were significantly higher than pre-test scores. In addition, to detect the effectiveness of the intervention, an independent sample t-test was conducted to compare the post-test scores for IL, EL, and CL in the experimental and control groups, because the assumptions of the ANCOVA test were not satisfied. There was no significant difference between the experimental and control groups’ CL scores (t = −0.16, p > 0.05). The control group’s IL and EL post-test scores were significantly higher than the experimental group’s post-test scores (t = −5.14, p < 0.001 and t = −4.83, p < 0.001).
Hypothesis 4 suggested that the WEI4S intervention, implemented through the use of worksheets, would be effective in decreasing intrinsic load (IL) and extraneous load (EL), while enhancing germane load (GL). This hypothesis posited that the WEI4S model, as presented in the worksheet, would outperform other methods in optimizing CL. The effectiveness of the WEI4S intervention through worksheets in terms of three types of CL was investigated by the CL scale for the intervention; the means scores for the experimental groups are given in Table 3.

Table 3.
Mean scores for items on the CL scale for intervention.
The mean scores indicate the average response to each statement. Higher mean scores suggest greater agreement with the statement. Statements 1, 2, and 3 received moderate mean scores, which suggests that students found the questions in the worksheet, including the WEI4S model, moderately complicated. For both the 4th and 5th statements, the mean scores were quite low, which indicates a general disagreement with the statements. Participants gave low scores, on average, which suggests that they found the explanations clear and considered the instructions and explanations effective for learning. On the other hand, Statements 6, 7, and 8 received high mean scores, which indicates that the worksheet positively impacted understanding and knowledge of algebra problems.
In addition to this scale, data for four additional items were collected as recommended by Leppink et al. (2013) to measure CL [58]; IL [59], EL [60], and GL [61] were added to investigate the effectiveness of the intervention in terms of CL. Different aspects of CL were measured using specific scales. To gauge CL [58], participants selected the relevant category for the statement “In the worksheet that just finished, I invested” on a scale ranging from “very low mental effort” to “very high mental effort”. The mean score for this item was 4.68, which indicates a response near the middle of the scale—neither low nor high mental effort. IL [59] was assessed by having the participants select the appropriate category for the statement “The worksheet that I just finished was” on a scale ranging from very easy to very difficult. The mean score for this item was 3.79, which suggests a response near the scale’s “rather easy” point. EL [60] was evaluated using the statement “To learn from the worksheet was”, and participants indicated their perceptions on a scale from very easy to very difficult. The mean score for this item was 3.65, which indicates a response near the scale’s “rather easy” point. GL [61] was measured using the statement “How much did you concentrate while doing the worksheet?” Participants chose from a scale ranging from very little concentration to very great concentration. The mean score for this item was 6.37, which suggests a response near the scale’s “rather great” point.
Hypothesis 5 postulated that students in the experimental group would hold positive perceptions of and thoughts about the WEI4S intervention. To examine this hypothesis, written responses to open-ended questions related to the implementation of WEI4S were analysed. Students’ perspectives on the effectiveness of the intervention revealed that all of the students agreed that the WEI4S contributed to their learning; 73.7% of them stated that they were able to set up equations after the intervention, while 94.7% of them declared that they wanted to do worksheets, including WEI4S, for other mathematics subjects. Although these results were not sufficient to support Hypothesis 5, they were useful in obtaining information about the students’ thoughts about the implementation. More in-depth information is needed to confirm this hypothesis.
5. Discussions
5.1. Worked-Out Examples and Algebra Performance
The acquisition of proficient problem-solving skills in algebraic contexts is crucial for students’ academic success and their ability to apply mathematical principles to practical situations. Although worked-out examples have been extensively employed as pedagogical tools, this research endeavoured to take a step further by introducing a structured approach that integrates a three-stage model [25]—analyse, explain, apply—and extends the existing framework by adding an “examine” stage between explain and apply to emphasize the viewing of students’ own errors and knowledge gaps with self-explanation.
To determine the effectiveness of the WEI4S, pre- and post-test comparisons were conducted for both the experimental and control groups, focusing on the AAT-PK and AAT-CK scores. In the control group, no significant difference was observed for the AAT-PK scores, whereas the AAT-CK scores showed a significant improvement. The experimental group showed significant improvements in both the AAT-PK and AAT-CK scores. To further explore the intervention’s effectiveness, an ANCOVA test was performed to compare the post-test scores of the experimental and control groups. The ANCOVA results revealed significant differences between the groups’ post-test scores when controlling for pre-test scores. Specifically, the AAT-PK, AAT-CK, and TQ scores were all significantly higher in the experimental group.
The results of this study indicated that the use of the WEI4S intervention significantly affected the participants’ performance in solving both procedural and conceptual algebraic questions. The principle of CL, as highlighted by Chandler and Sweller [51], underscores that worked examples could be less effective when learners already possess the cognitive schemata to solve problems independently [31,55]. However, in the context of this study, the worked-out examples seemed to cater effectively to the learning needs of students who faced difficulties in solving complex algebraic problems.
To fully capitalize on the advantages of worked-out examples, students should be encouraged to deeply engage with the examples [25]. Among the examples, correct–incorrect worked-out examples and those with self-explanation were among the types of examples that have proven to be more effective in the literature. A recent meta-analysis study addressed these two types of worked-out examples and analysed their effect sizes. This meta-analysis revealed that the inclusion of self-explanation prompts significantly affected the effects of worked-out example. They determined that the use of only correct examples yielded greater effect sizes than those using only incorrect examples or a combination of correct and incorrect examples. From the results of this study, it can be concluded that self-explanation should be an integral part of worked-out examples [21]. The results of this study highlight the importance of self-explanation, because providing self-explanations boosts cognitive engagement [64], leading to the enhanced formation of knowledge and consequent improvement of the learner’s performance [65].
Self-explanation is not only an important part of the worked-out examples but can also be used in curriculum designs and books. A recent study examined the effectiveness of using worked-out examples with self-explanation prompts in a curriculum designed to enhance prealgebra students’ understanding of rational numbers. The study aimed to improve fraction number line estimation skills, rational number concepts, and procedural knowledge; it also examined whether individual variations in prior knowledge of rational numbers influenced the impact of the textbooks. The results showed that experimental textbooks that included worked examples and self-explanation prompts significantly improved fraction number line estimation skills compared to control textbooks. Moreover, example-supplemented textbooks were particularly effective in enhancing students’ understanding of rational number concepts. The effectiveness of both textbook sets in improving procedural skills was similar [21].
In the examination component of the current study, students studied their erroneous solutions, such as incorrectly worked examples, that usually represented the solutions of fictitious students. As a form of instruction, the use of incorrectly worked-out examples with or without correct examples enhances mathematics learning [7,41,42,43,44]. Adams et al. [7] investigated whether students benefit more from critiquing incorrect solutions to decimal problems rooted in common misconceptions than from solving these problems and receiving feedback. In a web-based tutoring system, 208 middle school students were assigned to either identify, explain, and correct errors made by a fictional student (erroneous examples group) or solve similar problems with feedback (problem-solving group). Although there was no significant difference between the two groups on an immediate post-test, students in the erroneous examples group performed significantly better on a delayed post-test administered one week later (effect size = 0.62). Additionally, the erroneous examples group displayed better accuracy in judging the correctness of their post-test answers (effect size = 0.49). Interestingly, students in the problem-solving group reported higher satisfaction with the instructional materials than those in the erroneous examples group. This suggests that students’ liking for instructional materials does not necessarily correlate with their effectiveness in promoting learning.
In their study, Durkin and Rittle-Johnson [42] introduced students to common misconceptions and errors, which students then compared to accurate solutions in a short tutoring session. According to the results of their study, this method was more effective in enhancing students’ understanding of decimal concepts and improving their conceptual and procedural knowledge than simply comparing correct solution methods. On the other hand, the advantages of the incorrect condition were not as robust as anticipated, and they did not show significant improvement in certain outcomes during either assessment period.
Considering the results of the meta-analysis study [22], although including erroneous examples is an important issue, the use of incorrect examples still raises questions. As indicated in the previous sections in the current study, many studies indicate that using incorrectly worked-out examples alone or in combination with correct examples enhances mathematics learning. The way incorrect examples are presented may also be important. If students’ mistakes, misconceptions, and deficiencies about the subject or the question are similar to those of the fictitious student, the student may benefit more from the incorrectly presented solution. In the current study, it may have been more beneficial to present the students’ own incorrect answers to the students after the correctly solved questions rather than those of a fictitious student.
In the current study, the students in the experimental group analysed their own incorrect answers to the questions during the intervention. As a result of these analyses, which are not included in the findings because they are not related to the research questions of this study, the students mostly stated that they were not able to construct the equation necessary for the solution of the problem before the instruction, that they did not understand the subject well, but that they learned to construct equations after the intervention. In addition, the findings from the students’ perspectives regarding the effectiveness of the intervention indicated unanimous agreement among all of the participants that WEI4S significantly enhanced their learning. Specifically, 73.7% of the students reported an improved ability to set up equations after the intervention. Furthermore, an overwhelming 94.7% expressed a strong desire to use worksheets incorporating WEI4S for other mathematics subjects.
5.2. Worked-Out Examples and CL
This study also examined the impact of worked-out examples on CL for pre-test and post-test and for implementation. In the pre-test–post-test comparisons, no significant difference was found between pre-test and post-test scores for both EL and CL in the experimental group. However, the post-test IL scores were significantly lower than the pre-test IL scores. Although there were no significant differences between the pre- and post-test scores for CL in the control group, remarkably, post-test scores of IL and EL were significantly higher than pre-test scores.
Furthermore, to assess the effectiveness of the intervention, independent sample t-tests were conducted to compare post-test scores for IL, EL, and CL between the experimental and control groups. There was no significant difference between the experimental and control groups’ CL scores. The control group’s IL and EL post-test scores were significantly higher than the experimental group’s post-test scores.
These findings suggest that, although the completion of WEI4S had no significant impact on EL and CL in the experimental group, it did lead to a significant reduction in IL. Additionally, the control group exhibited increases in IL and EL compared to the experimental group, although there was no significant difference in CL between the two groups. The completion of the WEI4S thus had a positive effect on reducing IL load and preventing the rise of EL for students preparing for an AAT. In this study, students also evaluated the implementation of WEI4S in terms of CL. Students found the WEI4S moderately complex (IL), the explanations clear (EL), and said that it positively affected their understanding (EL). According to them, the overall CL was moderate, they found the material quite easy, and they showed a lot of concentration on WEI4S. This outcome resonates with the broader theoretical framework of the CLT, which posits that well-designed instructional interventions, such as the worked-out examples in this study, can aid in optimizing CL management [26,29,66,67].
5.3. Implications for Teaching and Learning
The outcomes of this research hold profound implications for mathematics educators, curriculum designers, and instructional practitioners. The staged worked-out example intervention introduces a structured learning pathway that caters to students with varying levels of prior knowledge and cognitive capacities. The integration of an “examine” stage, focusing on error analysis and metacognition, aligns with contemporary pedagogical theories that underscore the value of self-regulation and deep cognitive processing. By delving into the impact of this intervention on CL, metacognitive awareness, and problem-solving efficacy, this research contributes valuable insights to the broader discourse on effective instructional strategies in mathematics education.
The staged worked-out examples proved beneficial in enhancing students’ algebraic problem-solving skills. This suggests that careful selection and presentation of instructional materials can effectively cater to learners with varying levels of prior knowledge and expertise. Additionally, the observed decrease in CL further underscores the significance of well-structured instructional materials that alleviate cognitive burdens, thus promoting more efficient and effective learning.
The staged approach in the intervention offers a personalized learning trajectory, catering to students with varying levels of prior knowledge and skills. By providing stages for analysing, explaining, examining errors, and applying knowledge, this research acknowledges the diversity in students’ learning styles and promotes a deeper understanding of algebraic concepts.
Although this study provides valuable insights, certain limitations should be acknowledged. One of the most significant limitations of the research is the presence of 19 individuals in the experimental group and 17 individuals in the control group. This limitation, due to the small sample size, may restrict the generalizability of the obtained results. Future research conducted with a larger sample group could contribute to making the results more reliable and widely applicable. In addition, this study was conducted within a specific timeframe and involved a limited set of questions and problems. Future research could explore the long-term impact of staged worked-out examples on students’ retention of algebraic concepts and problem-solving skills. Additionally, investigating the transferability of these findings to other mathematical domains and exploring the preferences of students with varying learning styles could enrich our understanding of the instructional potential of worked-out examples.
Funding
This research received no external funding.
Institutional Review Board Statement
Ethics approval was obtained from the İstanbul Medeniyet University Ethics Commitee (Protocol no. 2021/03-10)).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The datasets generated and analysed during the current study are not publicly available due to privacy but may be available from the corresponding author upon reasonable request.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Lee, L. An initiation into algebraic culture through generalization activities. In Approaches to Algebra: Perspectives for Research and Teaching; Bednarz, N., Kieran, C., Lee, L., Eds.; Kluwer: Dordrecht, The Netherlands, 1996; pp. 87–106. [Google Scholar]
- Kilpatrick, J.; Swafford, J.; Findell, B. Adding It Up: Helping Children Learn Mathematics; The National Academies Press: Washington, DC, USA, 2001; ISBN 978-0-309-21895-5. [Google Scholar]
- Kieran, C. Algebra teaching and learning. In Encyclopedia of Mathematics Education; Springer: Dordrecht, The Netherlands, 2020; pp. 36–44. [Google Scholar]
- Hall, R.D.G. An analysis of errors made in the solution of simple linear equations. Philos. Math. Educ. 2002, 1, 49–65. [Google Scholar]
- Kieran, C. The learning and teaching of school algebra. In Handbook of Research on Mathematics Teaching and Learning; Grouws, S.D.A., Ed.; National Council of Teachers of Mathematics: Reston, VA, USA, 1992; pp. 706–762. [Google Scholar]
- Kshetree, M.P.; Acharya, B.R.; Khanal, B.; Panthi, R.K.; Belbase, S. Eighth Grade Students’ Misconceptions and Errors in Mathematics Learning in Nepal. Eur. J. Educ. Res. 2021, 10, 1101–1121. [Google Scholar]
- Barbieri, C.A.; Booth, J.L. Mistakes on display: Incorrect examples refine equation solving and algebraic feature knowledge. Appl. Cogn. Psychol. 2020, 34, 862–878. [Google Scholar] [CrossRef]
- Kieran, C. Learning and teaching algebra at the middle school through college levels: Building meaning for symbols and their manipulation. Second Handb. Res. Math. Teach. Learn. 2007, 2, 707–762. [Google Scholar]
- Usiskin, Z. Algebra and calculus for all? J. Math. Sci. Collab. Explor. 1999, 2, 1–18. [Google Scholar]
- Cai, J. Why do US and Chinese students think differently in mathematical problem-solving? Impact of early algebra learning and teachers’ beliefs. J. Math. Behav. 2004, 23, 135–167. [Google Scholar]
- Khng, K.H.; Lee, K. Inhibiting interference from prior knowledge: Arithmetic intrusions in algebra word problem solving. Learn. Individ. Differ. 2009, 19, 262–268. [Google Scholar] [CrossRef]
- Shoenfeld, A.H. Learning to think mathematically: Problem solving, metacognition, and sense making in mathematics. In Handbook for Research in Mathematics Teaching and Learning; Grows, D., Ed.; Macmillan: New York, NY, USA, 1992; pp. 334–370. [Google Scholar]
- Mamona-Downs, J.; Downs, M. Problem Solving and its elements in forming proof. Math. Enthus. 2013, 10, 137–162. [Google Scholar] [CrossRef]
- Rizos, I.; Gkrekas, N. Incorporating history of mathematics in open-ended problem solving: An empirical study. Eurasia J. Math. Sci. Technol. Educ. 2023, 19, em2242. [Google Scholar] [CrossRef]
- Mayer, R.E. Cognitive, metacognitive, and motivational aspects of problem solving. Instr. Sci. 1998, 26, 49–63. [Google Scholar] [CrossRef]
- Vargas-Alejo, V.; Cristóbal-Escalante, C. Teacher’s ways of thinking about students’ mathematical learning when they implement problem solving activities. J. Math. Model. Appl. 2014, 1, 41–48. [Google Scholar]
- Zeitz, P. The Art and Craft of Problem Solving, 2nd ed.; John Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- Fuchs, L.S.; Fuchs, D.; Prentice, K.; Karin, P.; Mindy, B.; Hamlett, C.L.; Rhoda, O.; Kati, S. Enhancing third-grade students’ mathematical problem solving with self-regulated learning strategies. J. Educ. Psychol. 2003, 95, 306–315. [Google Scholar] [CrossRef]
- Ng, S.F.; Lee, K. The model method: Singapore children’s tool for representing and solving algebraic word problems. J. Res. Math. Educ. 2009, 40, 282–313. [Google Scholar] [CrossRef]
- Atkinson, R.K.; Derry, S.J.; Renkl, A.; Wortham, D.W. Learning from examples: Instructional principles from the worked examples research. Rev. Educ. Res. 2000, 70, 181–214. [Google Scholar] [CrossRef]
- Barbieri, C.A.; Booth, J.L.; Chawla, K. Let’s be rational: Worked examples supplemented textbooks improve conceptual and fraction knowledge. Educ. Psychol. 2023, 43, 1–21. [Google Scholar] [CrossRef]
- Barbieri, C.A.; Miller-Cotto, D.; Clerjuste, S.N.; Chawla, K. A meta-analysis of the worked examples’ effect on mathematics performance. Educ. Psychol. Rev. 2023, 35, 11. [Google Scholar] [CrossRef]
- Sweller, J.; van Merriënboer, J.J.G.; Paas, F.G. Cognitive architecture and instructional design. Educ. Psychol. Rev. 1998, 10, 251–296. [Google Scholar] [CrossRef]
- Van Gog, T.; Rummel, N. Example-based learning: Integrating cognitive and social-cognitive research perspectives. Educ. Psychol. Rev. 2010, 22, 155–174. [Google Scholar] [CrossRef]
- Pershan, M. Teaching Math with Examples. In The Edu-Book Club: Making CPD Resources Work in the Classroom; Tushingham, D., Rainbow, R., Eds.; Routledge: London, UK, 2023. [Google Scholar]
- Sweller, J.; Ayres, P.; Kalyuga, S. Intrinsic and extraneous cognitive load. In Cognitive Load Theory, Explorations in the Learning Sciences, Instructional Systems and Performance Technologies; Springer: New York, NY, USA, 2011; pp. 57–69. [Google Scholar]
- Paas, F.; Van Gog, T.; Sweller, J. Cognitive load theory: New conceptualizations, specifications, and integrated research perspectives. Educ. Psychol. Rev. 2010, 22, 115–121. [Google Scholar] [CrossRef]
- Sweller, J. Cognitive load during problem solving: Effects on learning. Cogn. Sci. 1988, 12, 257–285. [Google Scholar] [CrossRef]
- Sweller, J. Cognitive load theory: Recent theoretical advances. In Cognitive Load Theory; Plass, J.L., Moreno, R., Brünken, R., Eds.; Cambridge University Press: Cambridge, UK, 2010; pp. 29–47. [Google Scholar]
- Kirschner, F.; Kester, L.; Corbalan, G. Cognitive load theory and multimedia learning, task characteristics and learning engagement: The current state of the art. Comput. Hum. Behav. 2011, 27, 1–4. [Google Scholar] [CrossRef]
- Bokosmaty, S.; Sweller, J.; Kalyuga, S. Learning geometry problem solving by studying worked examples: Effects of learner guidance and expertise. Am. Educ. Res. J. 2015, 52, 307–333. [Google Scholar] [CrossRef]
- Kalyuga, S.; Ayres, P.L.; Chandler, P.A.; Sweller, J. The expertise reversal effect. Educ. Psychol. 2003, 38, 23–31. [Google Scholar] [CrossRef]
- Plass, J.L.; Moreno, R.; Brünken, R. (Eds.) Cognitive Load Theory; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Cooper, G.; Sweller, J. Effects of schema acquisition and rule automation on mathematical problem-solving transfer. J. Educ. Psychol. 1987, 79, 347. [Google Scholar] [CrossRef]
- Cattaneo, A.A.; Boldrini, E. Learning from errors in dual vocational education: Video-enhanced instructional strategies. J. Workplace Learn. 2017, 29, 357–373. [Google Scholar] [CrossRef]
- Du, X.; Zhang, Q. Tracing worked examples: Effects on learning in geometry. Educ. Psychol. 2019, 39, 169–187. [Google Scholar] [CrossRef]
- Hesser, T.L.; Gregory, J.L. Exploring the Use of Faded Worked Examples as a Problem-Solving Approach for Underprepared Students. High. Educ. Stud. 2015, 5, 36–46. [Google Scholar] [CrossRef]
- Renkl, A.; Atkinson, R.K.; Maier, U.H.; Staley, R. From example study to problem solving: Smooth transitions help learning. J. Exp. Educ. 2002, 70, 293–315. [Google Scholar] [CrossRef]
- Renkl, A.; Atkinson, R.K. Structuring the transition from example study to problem solving in cognitive skill acquisition: A cognitive load perspective. Educ. Psychol. 2003, 38, 15–22. [Google Scholar] [CrossRef]
- Özcan, Z.Ç. The effect of self-explanation prompts and fading steps in worked-out examples on students’ fraction problems performance. Kalem Int. J. Educ. Hum. Sci. 2018, 8, 39–62. [Google Scholar]
- Özcan, Z.Ç.; Kılıç, Ç.; Obalar, S. Öğrencilerin matematikteki hatalarını belirleme ve gidermede açıklayıcı ipuçlarıyla desteklenmiş çözümlü örnekler. Mehmet Akif Ersoy Üniv. Eğitim Fak. Derg. 2018, 45, 1–22. [Google Scholar]
- Durkin, K.; Rittle-Johnson, B. The effectiveness of using incorrect examples to support learning about decimal magnitude. Learn. Instr. 2012, 22, 206–214. [Google Scholar] [CrossRef]
- Adams, D.M.; McLaren, B.M.; Durkin, K.; Mayer, R.E.; Rittle-Johnson, B.; Isotani, S.; Van Velsen, M. Using erroneous examples to improve mathematics learning with a web-based tutoring system. Comput. Hum. Behav. 2014, 36, 401–411. [Google Scholar] [CrossRef]
- Booth, J.L.; Lange, K.E.; Koedinger, K.R.; Newton, K.J. Using example problems to improve student learning in algebra: Differentiating between correct and incorrect examples. Learn. Instr. 2013, 25, 24–34. [Google Scholar] [CrossRef]
- Zrebiec Uberti, H.; Mastropieri, M.A.; Scruggs, T.E. Check it off: Individualizing a math algorithm for students with disabilities via self-monitoring checklists. Interv. Sch. Clin. 2004, 39, 269–275. [Google Scholar] [CrossRef]
- McNamara, D.S.; Magliano, J.P. Self-explanation and metacognition: The dynamics of reading. In Handbook of Metacognition in Education; Hacker, D.J., Dunlosky, J., Graesser, A.C., Eds.; Routledge/Taylor & Francis Group: Abingdon, UK, 2009; pp. 60–81. [Google Scholar]
- Chi, M.T.H.; DeLeeuw, N.; Chiu, M.H.; LaVancher, C. Eliciting self-explanations improves understanding. Cogn. Sci. 1994, 18, 439–477. [Google Scholar] [CrossRef]
- Renkl, A. Learning from worked-out examples: A study on individual differences. Cogn. Sci. 1997, 21, 1–29. [Google Scholar] [CrossRef]
- Berthold, K.; Eysink, T.H.; Renkl, A. Assisting self-explanation prompts are more effective than open prompts when learning with multiple representations. Instr. Sci. 2009, 37, 345–363. [Google Scholar] [CrossRef]
- Bisra, K.; Liu, Q.; Nesbit, J.C.; Salimi, F.; Winne, P.H. Inducing self-explanation: A meta-analysis. Educ. Psychol. Rev. 2018, 30, 703–725. [Google Scholar] [CrossRef]
- Chandler, P.; Sweller, J. Cognitive load theory and the format of instruction. Cogn. Instr. 1991, 8, 293–332. [Google Scholar] [CrossRef]
- Renkl, A.; Atkinson, R.K. Learning from worked-out examples and problem solving. In Cognitive Load Theory; Plass, J.L., Moreno, R., Brünken, R., Eds.; Cambridge University Press: Cambridge, UK, 2010; pp. 91–108. [Google Scholar] [CrossRef]
- Atkinson, R.K.; Renkl, A.; Merrill, M. Transitioning from studying examples to solving problems: Effects of self-explanation prompts and fading worked-out steps. J. Educ. Psychol. 2003, 95, 774–783. [Google Scholar] [CrossRef]
- Renkl, A.; Stark, R.; Gruber, H.; Mandl, H. Learning from worked-out examples: The effects of example variability and elicited self-explanations. Contemp. Educ. Psychol. 1998, 23, 90–108. [Google Scholar] [CrossRef]
- van Loon-Hillen, N.; Van Gog, T.; Brand-Gruwel, S. Effects of worked examples in a primary school mathematics curriculum. Interact. Learn. Environ. 2012, 20, 89–99. [Google Scholar] [CrossRef]
- Brünken, R.; Plass, J.L.; Moreno, R. Current issues and open questions in cognitive load research. In Cognitive Load Theory; Plass, J.L., Moreno, R., Brünken, R., Eds.; Cambridge University Press: Cambridge, UK, 2010; pp. 253–272. [Google Scholar] [CrossRef]
- Leppink, J.; Paas, F.; Van der Vleuten, C.P.; Van Gog, T.; Van Merriënboer, J.J. Development of an instrument for measuring different types of cognitive load. Behav. Res. Methods 2013, 45, 1058–1072. [Google Scholar] [CrossRef] [PubMed]
- Paas, F. Training strategies for attaining transfer of problem-solving skills in statistics: A cognitive load approach. J. Educ. Psychol. 1992, 84, 429–434. [Google Scholar] [CrossRef]
- Ayres, P. Using subjective measures to detect variations of intrinsic load within problems. Learn. Instr. 2006, 16, 389–400. [Google Scholar] [CrossRef]
- Cierniak, G.; Scheiter, K.; Gerjets, P. Explaining the split attention effect: Is the reduction of extraneous cognitive load accompanied by an increase in germane cognitive load? Comput. Hum. Behav. 2009, 25, 315–324. [Google Scholar] [CrossRef]
- Salomon, G. Television is “easy” and print is “tough”: The differential investment of mental effort in learning as a function of perceptions and attributes. J. Educ. Psychol. 1984, 78, 647–658. [Google Scholar] [CrossRef]
- Green, S.B.; Salkind, N. Using SPSS for Windows and Macintosh: Analyzing and Understanding Data; Prentice Hall Press: Saddle River, NJ, USA, 2009. [Google Scholar]
- DeCarlo, L.T. On the meaning and use of kurtosis. Psychol. Methods 1997, 2, 292. [Google Scholar] [CrossRef]
- Bude, L.; Van de Wiel, M.W.J.; Imbos, T.; Berger, M.P.F. The effect of guiding questions on students’ performance and attitude towards statistics. Br. J. Educ. Psychol. 2012, 82, 340–359. [Google Scholar] [CrossRef]
- Chia, R. The problem of reflexitivity in organizational research: Towards a postmodern science of organization. Organization 1996, 3, 31–59. [Google Scholar] [CrossRef]
- Chen, O.; Retnowati, E.; Chan, B.K.Y.; Kalyuga, S. The effect of worked examples on learning solution steps and knowledge transfer. Educ. Psychol. 2023, 43, 914–928. [Google Scholar] [CrossRef]
- Tuovinen, J.E.; Sweller, J. A comparison of cognitive load associated with discovery learning and worked examples. J. Educ. Psychol. 1999, 91, 334. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).