Building Mathematics Learning through Inquiry Using Student-Generated Data: Lessons Learned from Plan-Do-Study-Act Cycles
Abstract
:1. Introduction
- How do PDSA cycles support pedagogical innovation in the classroom?
- How can reform-based teaching be transferred from theoretical ideas to classroom practice during full-time student teaching?
2. Background
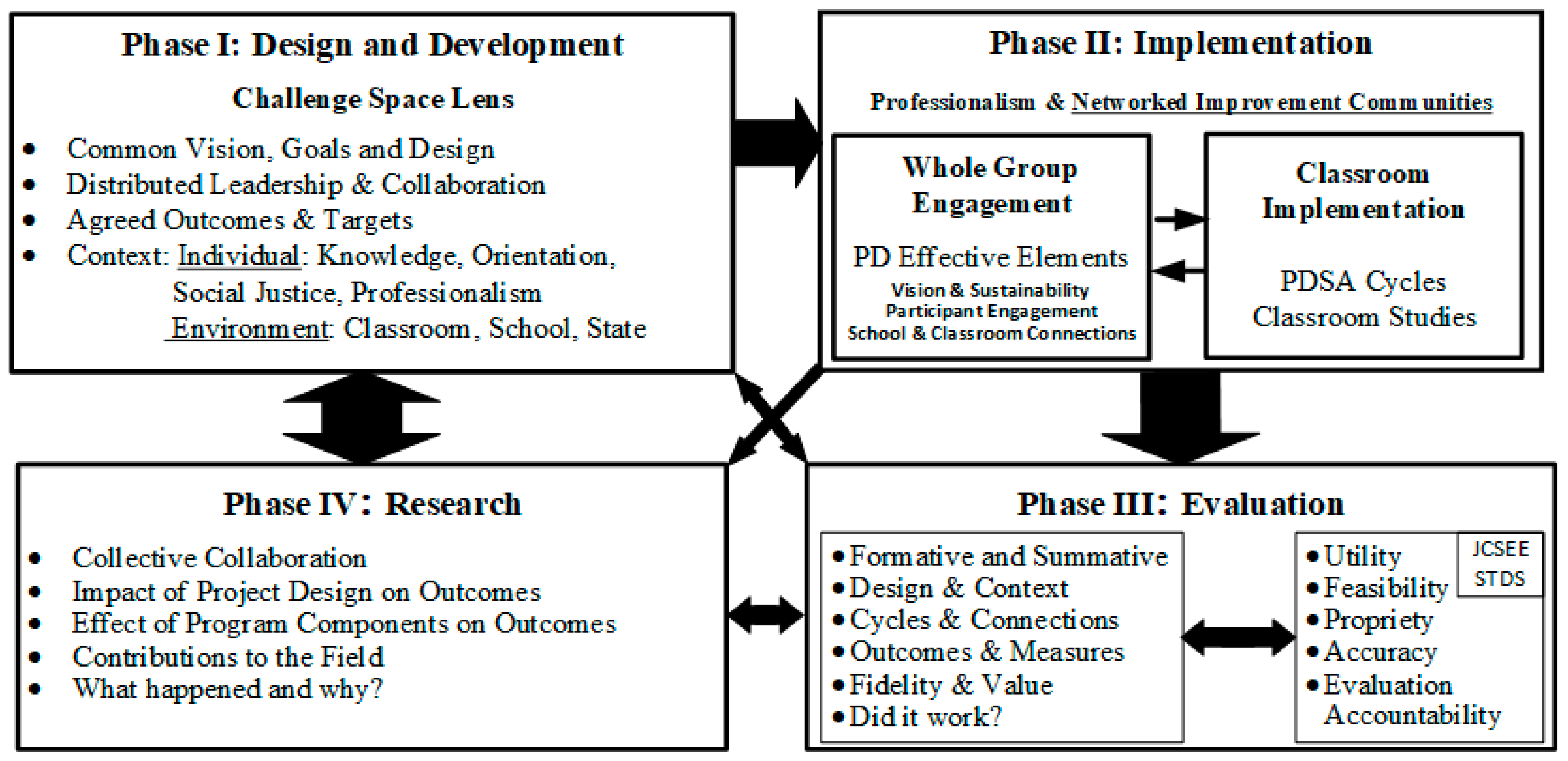
2.1. The PrimeD Framework: A PD Framework for Teacher Preparation
2.1.1. Phase I Design and Development
2.1.2. Phase II Implementation
The fundamental difference between an amateur and a professional in any field is not one of intelligence or willingness to work hard. Rather, it is that professionals are trained at accessing their own research field, and therefore are much less likely to spend time repeating the others’ prior mistakes. Educational reforms seem to have a less-than-glorious tradition of replicating major aspects of previous failed efforts.(p. 197)
2.1.3. Phase III Evaluation
2.1.4. Phase IV Research
2.2. Reformed Teaching, Inquiry, and Constructivism
3. Methods
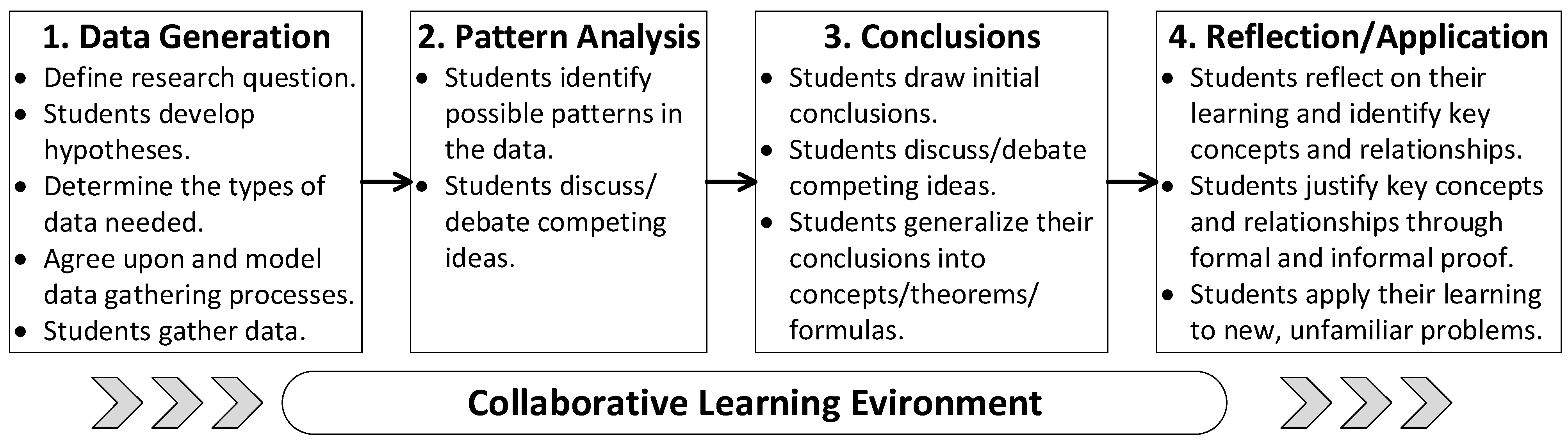
3.1. PDSA Cycles in the NIC
3.2. Data and Measures
4. Results
4.1. Teaching Mathematics through Inquiry
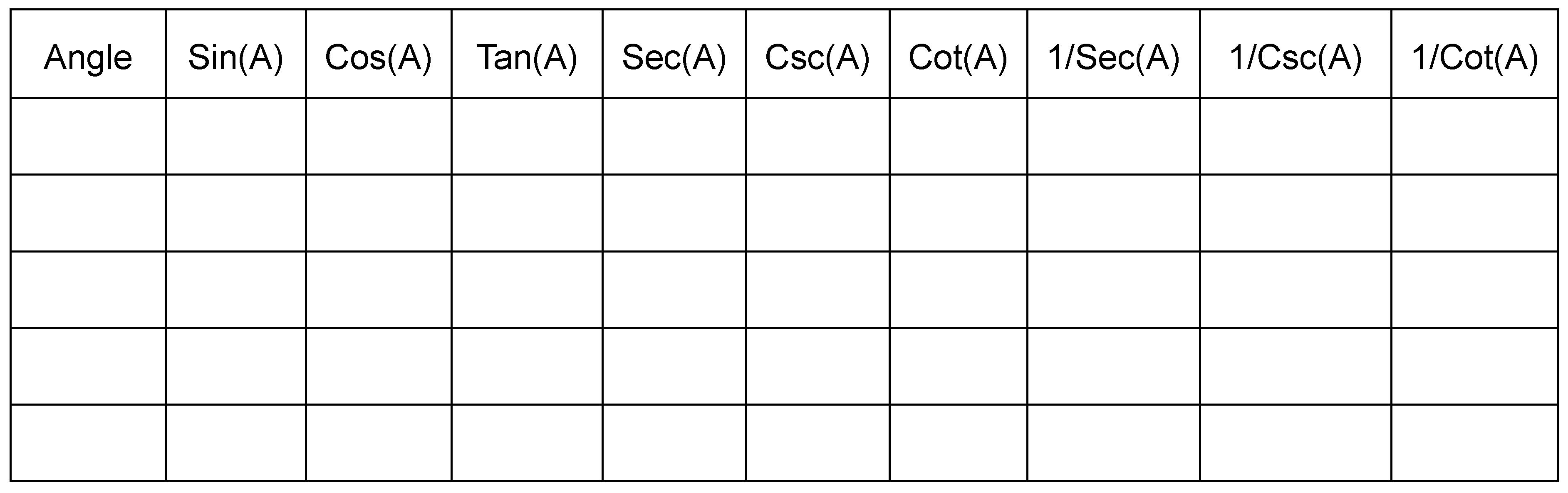
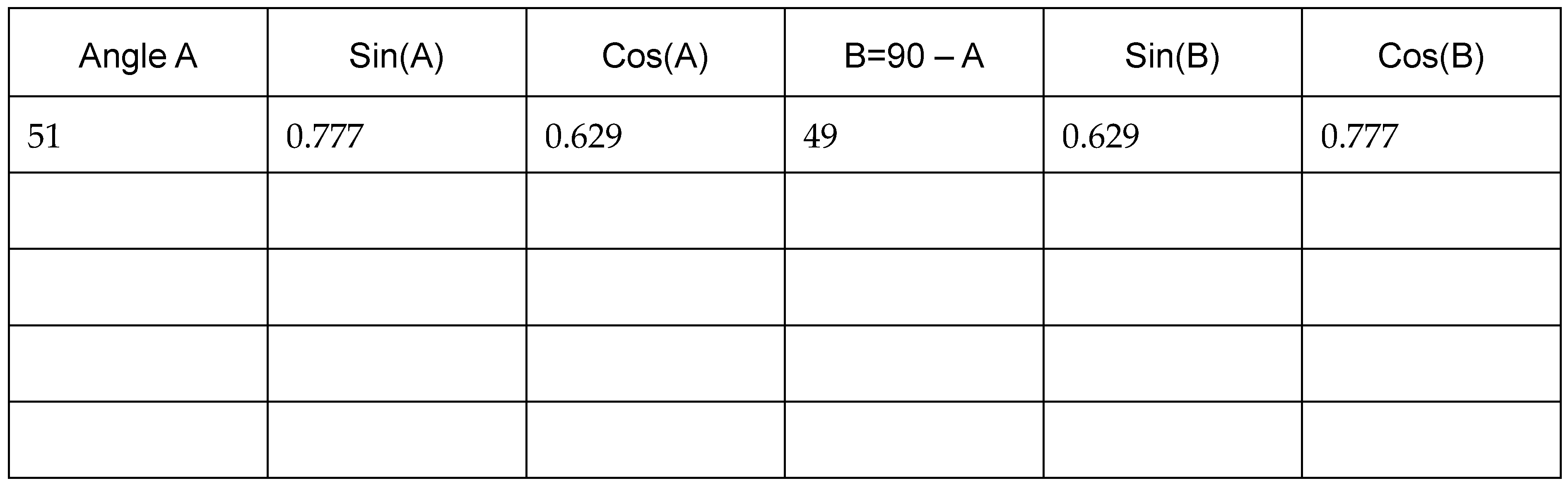
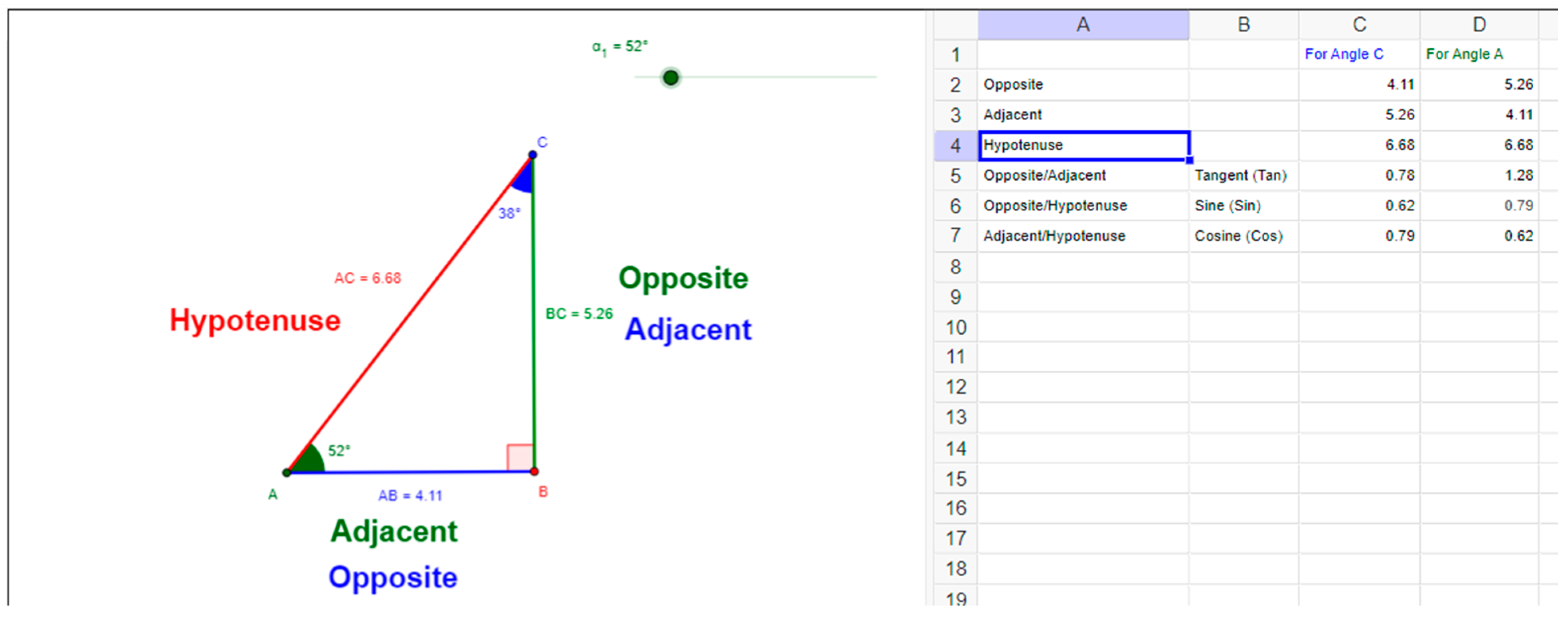
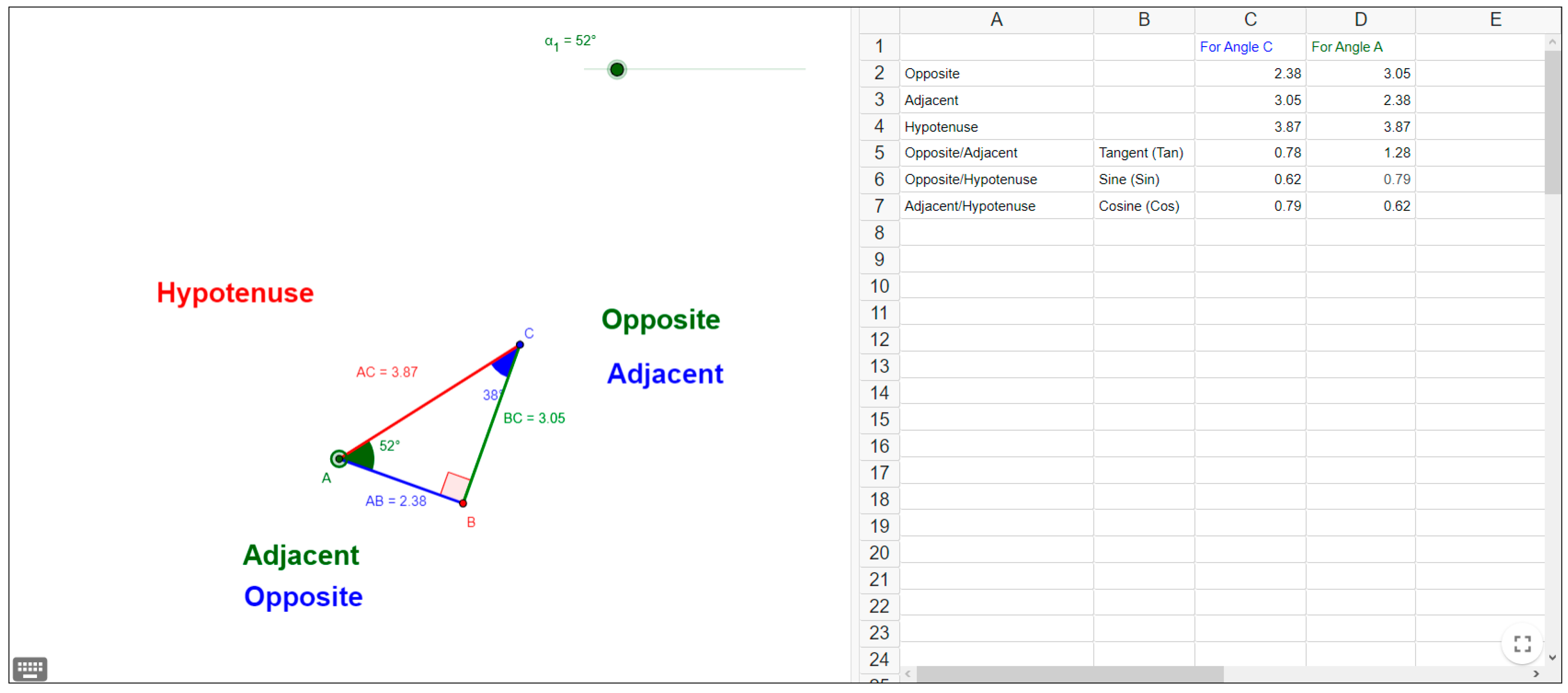
4.1.1. Example PDSA Lesson 1: Inquiry into Trigonometric Ratios
4.1.2. Example PDSA Lesson 2: Exploration of Population Density
4.2. Participation in Lessons Affected by PDSA Change Ideas
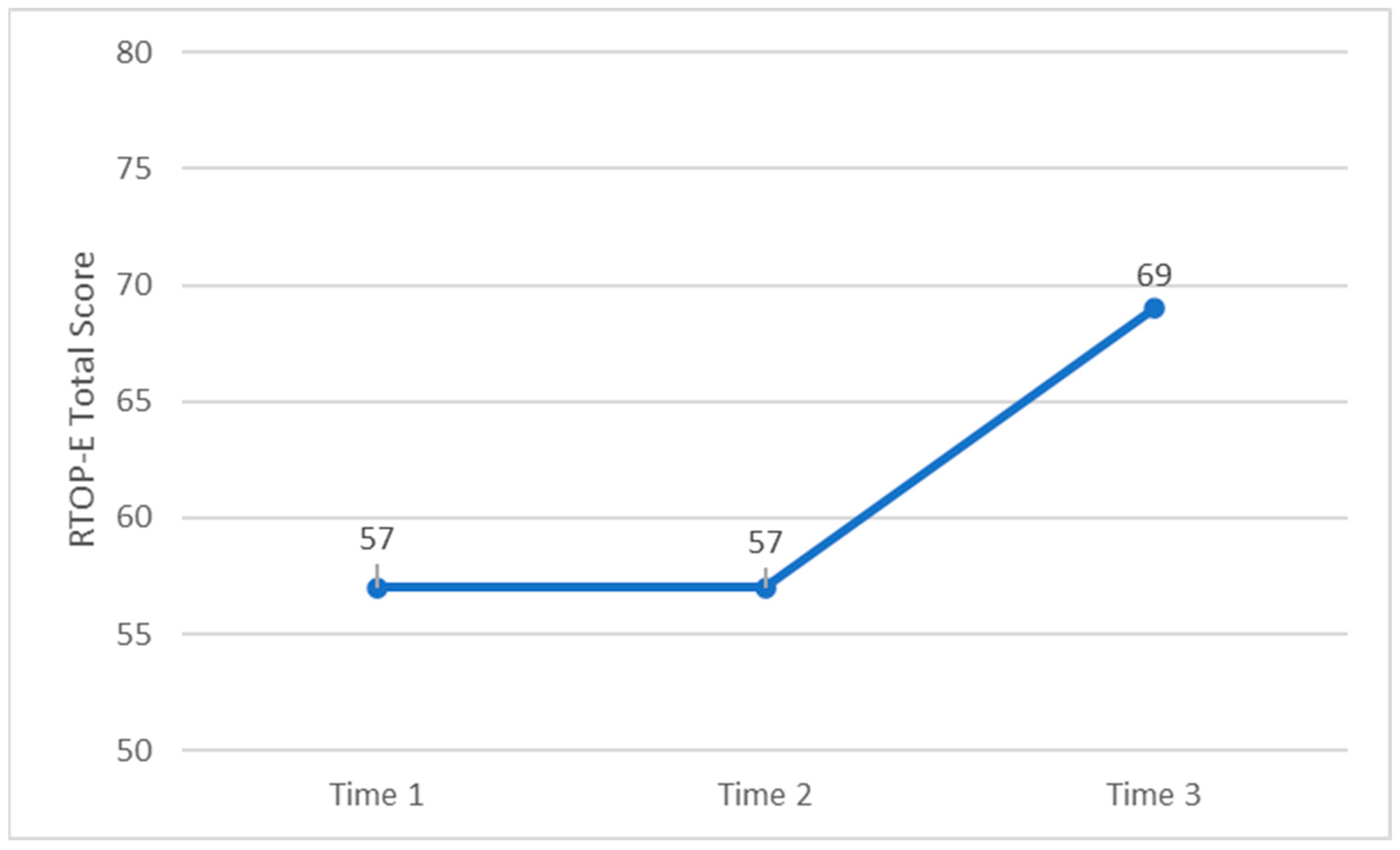
4.3. Teacher Candidate Growth in Reformed Teaching
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Secondary Mathematics Challenge Space
Appendix A.2. Vision
Appendix A.3. Goals
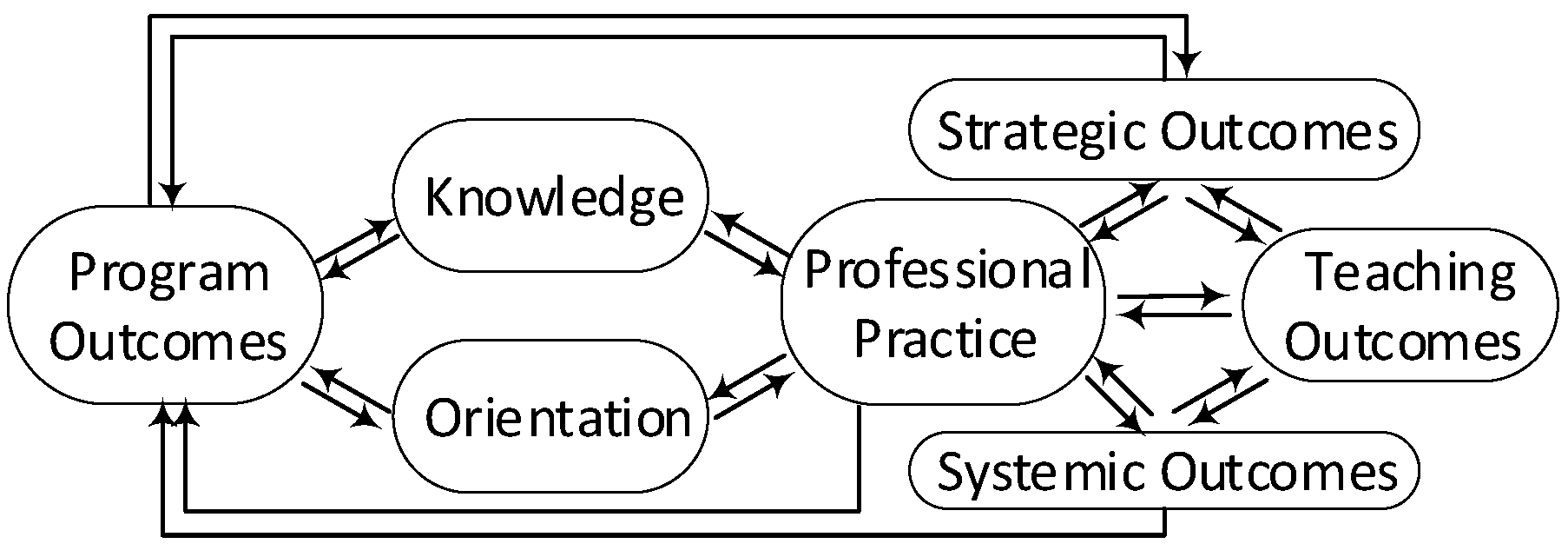
- Subject Matter Knowledge. Teachers have a robust knowledge of mathematics, understanding how concepts and procedures are interrelated and how to frame mathematics knowledge in a meaningful way to help students learn (Mathematics Knowledge for Teaching).
- Pedagogical Content Knowledge. Teachers develop robust pedagogical knowledge to support deep mathematics learning in their classrooms, including the use of tools for teaching mathematics (Knowledge for Teaching Mathematics).
- Knowledge of Orientation. Teachers understand and respect the relevance of the affect of each member of a learning community (e.g., attitudes, culture, beliefs, values, confidence, and anxiety) in learning mathematics.
- Knowledge of Discernment. Teachers understand that discernment encompasses the connections between cognition, metacognition, and learning and decision-making processes. Knowledge of discernment includes understanding developmental processes and the socio-emotional and sociocultural components of learning.
- Knowledge of Individual Context. Teachers understand that learning and decision-making processes take place within the context of the intersectionality of social categories.
- Knowledge of Environmental Context. Teachers understand the importance of building an inclusive and equitable environment to support a robust learning community.
Appendix A.4. Teacher Orientation
Appendix A.5. Teacher Practice
- Culture. Teachers establish a culture of access and equity through classroom structures and culturally relevant pedagogy to support each and every student in learning and participating in mathematics deeply. These classroom structures empower students to value diverse perspectives by elevating their voices, providing leadership opportunities, and developing a strong learning community. Teachers model vulnerability, viewing mistakes as learning opportunities. Varied approaches are visible and valued.
- Active Engagement. Teachers actively engage students in learning mathematics and/or science with meaning.
- Conceptual Understanding. Teachers explicitly foster, model, and insist upon conceptual understanding and coherence for all learners at all levels as a primary means for promoting procedural understanding in mathematics. Teachers insist that all teaching activities and learning experiences embrace the development of conceptual understanding as the fundamental core of learning and form the foundation for peer discussions.
- Connections. Teachers structure lessons through a phenomena-first approach, recognizing that authentic contexts are the foundation of the lesson and frame the content to be learned. Contexts are not simply enrichment that happens after the “real” lesson if at all.
- Reasoning. Inquiry-based projects are incorporated in every unit. Quantitative reasoning is modeled as scientific inquiry (claim, evidence, rationale).
- Questioning. Questioning is purposefully crafted to foster higher-order thinking and alternative modes of thinking about mathematics. Teachers pose questions of their students and encourage their students to ask deep, rich questions about their mathematical reasoning and that of their peers.
- Assessment. The ability to provide students feedback through formative (ongoing) and summative (reflective) assessment is differentiated from and valued more than grades. Assessments are ongoing, are aligned to standards, and (in)form teacher practice. Teachers understand that assessment can take many forms including formative (ongoing) and summative (reflective) assessment. Teachers incorporate a variety of assessments to ensure that each and every student has an opportunity to express their current understanding, including, but not limited to, observations, student-to-student and student-to-teacher dialogue, projects, performance tasks, interviews, portfolios, presentations, exit slips, and dynamic technology-based activities. Teachers recognize that understanding develops over time and leverage opportunities to reassess throughout the learning process.
Appendix A.6. Student Outcomes
References
- Darling-Hammond, L. Teacher quality and student achievement: A review of state policy evidence. Educ. Policy Anal. Arch. 2000, 8, 1. Available online: http://epaa.asu.edu/ojs/article/view/392/515 (accessed on 1 June 2023). [CrossRef]
- Ginsberg, R.; Rhodes, L.K. University faculty in partner schools. J. Teach. Educ. 2003, 54, 150–162. [Google Scholar] [CrossRef]
- U.S. Department of Education. Teacher Professional and Career Development; U.S. Department of Education: Washington, DC, USA, 2018. Available online: https://oese.ed.gov/archived/oii/teacher-professional-and-career-development/ (accessed on 15 July 2023).
- Gainsburg, J. Why new mathematics teachers do or don’t use practices emphasized in their credential program. J. Math. Teach. Educ. 2012, 15, 359–379. [Google Scholar] [CrossRef]
- Morris, A.K.; Hiebert, J. Effects of teacher preparation courses: Do graduates use what they learned to plan mathematics lessons? Am. Educ. Res. J. 2017, 54, 524–567. [Google Scholar] [CrossRef]
- Taylor, P.M.; Ronau, R. Syllabus study: A structured look at mathematics methods courses. AMTE Connect. 2006, 16, 12–15. Available online: https://amte.net/sites/all/themes/amte/resources/newsletters/AMTENewsletter_Vol16-1_Fall2006.pdf (accessed on 14 January 2023).
- Desimone, L.M. Improving impact studies of teachers’ professional development: Toward better conceptualizations and measures. Educ. Res. 2009, 38, 181–199. [Google Scholar] [CrossRef]
- Loucks-Horsley, S.; Stiles, E.; Mundry, S.; Love, N.; Hewson, P. Designing Professional Development for Teachers of Science and Mathematics, 3rd ed.; Corwin: Thousand Oaks, CA, USA, 2010. [Google Scholar]
- Bangel, N.J.; Enersen, D.; Capobianco, B.; Moon, S.M. Professional development of preservice teachers: Teaching in the super Saturday program. J. Educ. Gift. 2006, 29, 339–361. Available online: https://files.eric.ed.gov/fulltext/EJ746288.pdf (accessed on 14 January 2023). [CrossRef]
- Pollock, M.; Bocala, C.; Deckman, S.L.; Dickstein-Staub, S. Caricature and hyperbole in preservice teacher professional development for diversity. Urban Educ. 2016, 51, 629–658. [Google Scholar] [CrossRef]
- Garet, M.S.; Porter, A.C.; Desimone, L.; Birman, B.F.; Yoon, K.S. What makes professional development effective? Results from a national sample of teachers. Am. Educ. Res. J. 2001, 38, 915–945. [Google Scholar] [CrossRef]
- Putnam, R.T.; Borko, H. What do new views of knowledge and thinking have to say about research on teacher learning? Educ. Res. 2000, 29, 4–15. [Google Scholar] [CrossRef]
- Jones, K.; O’Brien, J. Introduction: Professional development in teacher education: European perspectives. In European Perspectives on Professional Development in Teacher Education; Jones, K., O’Brien, J., Eds.; Routledge: New York, NY, USA, 2014; pp. 1–6. [Google Scholar]
- Philippou, S.; Papademetri-Kachrimani, C.; Louca, L. ‘The exchange of ideas was mutual, I have to say’: Negotiating researcher and teacher ‘roles’ in an early years educators’ professional development programme on inquiry-based mathematics and science learning. Prof. Dev. Educ. 2015, 41, 382–400. [Google Scholar] [CrossRef]
- Sztajn, P. Research commentary: Standards for reporting mathematics professional development in research studies. J. Res. Math. Educ. 2011, 42, 220–236. [Google Scholar] [CrossRef]
- Rakes, C.R.; Bush, S.B.; Mohr-Schroeder, M.J.; Ronau, R.N.; Saderholm, J. Making teacher PD effective using the PrimeD framework. New Engl. Math. J. 2017, 50, 52–63. Available online: http://hdl.handle.net/11603/14416 (accessed on 15 June 2023).
- Saderholm, J.; Ronau, R.N.; Rakes, C.R.; Bush, S.B.; Mohr-Schroeder, M. The critical role of a well-articulated conceptual framework to guide professional development: An evaluation of a state-wide two-week program for mathematics and science teachers. Prof. Dev. Educ. 2017, 43, 789–818. [Google Scholar] [CrossRef]
- Martin, W.G.; Gobstein, H. Generating a networked improvement community to improve secondary mathematics teacher preparation: Network leadership, organization, and operation. J. Teach. Educ. 2015, 66, 482–493. [Google Scholar] [CrossRef]
- Wilson, S.M.; Floden, R.E.; Ferrini-Mundy, J. Teacher Preparation Research: Current Knowledge, Gaps, and Recommendations. A Research Report Prepared for the U.S. Department of Education; Document R-01-3; Center for the Study of Teaching and Policy, University of Washington: Seattle, WA, USA, 2001; Available online: https://www.education.uw.edu/ctp/sites/default/files/ctpmail/PDFs/TeacherPrep-WFFM-02-2001.pdf (accessed on 15 January 2023).
- Driskell, S.O.; Bush, S.B.; Ronau, R.N.; Niess, M.L.; Rakes, C.R.; Pugalee, D. Mathematics education technology professional development: Changes over several decades. In Handbook of Research on Transforming Mathematics Teacher Education in the Digital Age; Niess, M.L., Driskell, S.O., Hollebrands, K.F., Eds.; IGI Global: Hershey, PA, USA, 2016; pp. 107–136. [Google Scholar]
- Bryk, A.S.; Gomez, L.M.; Grunow, A. Getting ideas into action: Building networked improvement communities in education. In Frontiers in Sociology in Education; Hallinan, M.T., Ed.; Springer: Dordrecht, The Netherlands, 2011; pp. 127–162. Available online: https://link.springer.com/chapter/10.1007/978-94-007-1576-9_7 (accessed on 14 January 2023).
- Bryk, A.S.; Gomez, L.M.; Grunow, A.; LeMahieu, P. Learning to Improve. How America’s Schools Can Get Better at Getting Better; Harvard Educational Publishing: Cambridge, MA, USA, 2015. [Google Scholar]
- Yeager, D.; Bryk, A.; Muhich, J.; Hausman, H.; Morales, L. Practical Measurement; Carnegie Foundation for the Advancement of Teaching: Stanford, CA, USA, 2013. [Google Scholar]
- Datnow, A.; Stringfield, S. Working together for reliable school reform. J. Educ. Stud. Placed Risk 2000, 5, 183–204. [Google Scholar] [CrossRef]
- Shulman, L.S. The Wisdom of Practice: Essays on Teaching, Learning, and Learning to Teach, 1st ed.; Jossey-Bass: San Francisco, CA, USA, 2004. [Google Scholar]
- Anderson, T.; Shattuck, J. Design-based research: A decade of progress in education research? Educ. Res. 2012, 41, 16–25. [Google Scholar] [CrossRef]
- Drill, K.; Miller, S.; Behrstock, E. Teachers’ Perspectives on Educational Research (EJ1057457). Brock Educ. 2012, 23, 3–17. Available online: https://files.eric.ed.gov/fulltext/EJ1057457.pdf (accessed on 14 January 2023).
- Atay, D. Teacher research for professional development. ELT J. 2008, 62, 139–147. [Google Scholar] [CrossRef]
- Elliott, J. Teachers as researchers: Implications for supervision and for teacher education (ED293831). Teach. Teach. Educ. 1990, 6, 1–26. Available online: https://files.eric.ed.gov/fulltext/ED293831.pdf (accessed on 14 January 2023). [CrossRef]
- Savoie-Zajc, L.; Descamps-Bednarz, N. Action research and collaborative research: Their specific contributions to professional development. Educ. Action Res. 2007, 15, 577–596. [Google Scholar] [CrossRef]
- Zeichner, K.M. Teacher research as professional development for P–12 educators in the USA. Educ. Action Res. 2003, 11, 301–326. [Google Scholar] [CrossRef]
- Kirkwood, M.; Christie, D. The role of teacher research in continuing professional development. Br. J. Educ. Stud. 2006, 54, 429–448. [Google Scholar] [CrossRef]
- Brownell, W.A. Psychological considerations in the learning and the teaching of arithmetic. In The Teaching of Arithmetic; Yearbook 10; Reeve, W.D., Ed.; National Council of Teachers of Mathematics: Washington, DC, USA, 1935; pp. 1–31. Available online: https://files.eric.ed.gov/fulltext/ED096171.pdf (accessed on 15 January 2023).
- Colburn, W. First Lessons: Intellectual Arithmetic, upon the Inductive Method of Instruction; W. J. Reynolds & Co.: Boston, MA, USA, 1847; Available online: https://archive.org/details/colburnsfirstle00colbgoog/mode/2up (accessed on 15 January 2023).
- Fey, J.T. Mathematics teaching today: Perspectives from three national surveys. Math. Teach. 1979, 72, 490–504. [Google Scholar] [CrossRef]
- Hiebert, J.; Stigler, J.W.; Jacobs, J.K.; Givvin, K.B.; Garnier, H.; Smith, M.; Hollingsworth, H.; Manaster, A.; Wearne, D.; Gallimore, R. Mathematics teaching in the United States today (and tomorrow): Results from the TIMSS 1999 video study. Educ. Eval. Policy Anal. 2005, 27, 111–132. [Google Scholar] [CrossRef]
- Ültanir, E. An epistemological glance at the constructivist approach: Constructivist learning in Dewey, Piaget, and Montessori. Int. J. Instr. 2012, 5, 195–212. [Google Scholar]
- Bybee, R.W.; Sund, R.B. Piaget for Educators, 2nd ed.; Charles E. Merrill: Columbus, OH, USA, 1982. [Google Scholar]
- Sawada, D.; Piburn, M.D.; Judson, E.; Turley, J.; Falconer, K. Measuring reform practices in science and mathematics classrooms: The Reformed Teaching Observation Protocol. Sch. Sci. Math. 2002, 102, 245–253. [Google Scholar] [CrossRef]
- National Research Council. A Framework for K-12 Science Education: Practices, Crosscutting Concepts, and Core Ideas; Committee on a Conceptual Framework for New K-12 Science Education Standards; Board on Science Education, Division of Behavioral and Social Sciences and Education; The National Academies Press: Washington, DC, USA, 2012. [CrossRef]
- 41. Williams, T.H.; Singer, J.E.; Krikorian, J.G.; Rakes, C.R.; Ross, J.M. Measuring pedagogy and the integration of engineering design in STEM classrooms. J. Sci. Educ. Technol. 2019, 28, 179–194. [Google Scholar] [CrossRef]
- Rakes, C.R.; Saderholm, J.; Bush, S.B.; Mohr-Schroeder, M.J.; Ronau, R.N.; Stites, M.L. Structuring secondary mathematics teacher preparation through a professional development framework. Int. J. Res. Sci. Eng. 2022, 10, 194–208. Available online: https://ijres.org/papers/Volume-10/Issue-12/1012194208.pdf (accessed on 15 July 2023).
- National Council of Teachers of Mathematics. Catalyzing Change in High School Mathematics. Initiating Critical Conversations; National Council of Teachers of Mathematics: Reston, VA, USA, 2018. [Google Scholar]
- Cicchetti, D.V. Guidelines, criteria, and rules of thumb for evaluation normed and standardized assessment instruments in psychology. Psychol. Assess. 1994, 6, 284–290. [Google Scholar] [CrossRef]
- Watson, J.M. Statistics in context. Math. Teach. 2000, 93, 54–58. [Google Scholar]
- Lamar, T.; Boaler, J. The importance and emergence of K12 data science. Phi Delta Kappan 2021, 103, 49–53. [Google Scholar] [CrossRef]
- Anderson, R.D.; Anderson, B.L.; Varanka-Martin, M.A.; Romagnano, L.; Bielenberg, J.; Flory, M.; Mieras, B.; Whitworth, J. Issues of Curriculum Reform in Science, Mathematics and Higher Order Thinking across the Discipline (ED368064); U.S. Department of Education, Office of Educational Research and Improvement, ERIC: Washington, DC, USA, 1994. Available online: https://ia802607.us.archive.org/13/items/ERIC_ED368064/ERIC_ED368064.pdf (accessed on 14 January 2023).
- Engle, R.A.; Conant, F.R. Guiding principles for fostering productive disciplinary engagement: Explaining an emergent argument in a community of learners classroom. Cogn. Instr. 2002, 20, 399–483. [Google Scholar] [CrossRef]
- National Council of Teachers of Mathematics. Catalyzing Change in Middle School Mathematics; National Council of Teachers of Mathematics: Reston, VA, USA, 2020. [Google Scholar]
- Stigler, J.W.; Hiebert, J. Understanding and improving classroom mathematics instructions: An overview of the TIMSS video study. Phi Delta Kappan 1997, 79, 14–21. [Google Scholar]
- Council of Chief State School Officers (CCSSO). Common Core State Standards Initiative: Standards for Mathematical Practice. 2010. Available online: http://www.corestandards.org/Math/Practice/ (accessed on 1 June 2022).
- Desmos Studio. Desmos Online Calculator. 2022. Available online: https://www.desmos.com (accessed on 12 July 2023).
- National Council of Teachers of Mathematics. Notice and Wonder. 2023. Available online: https://www.nctm.org/noticeandwonder/ (accessed on 1 August 2023).
- Rakes, C.R. Trigonometric ratios Geogebra applet. 2021. Available online: https://www.geogebra.org/m/rhs38edz (accessed on 15 August 2023).
- Blair, A. Planning and unplanning mathematical inquiry. Math. Teach. 2020, 271, 40–41. [Google Scholar]
- Imagine Learning. ImagineMath. 2023. Available online: https://math.imaginelearning.com (accessed on 10 July 2023).
- Niesser, J.; Abreu, G.; Drane, D.L.; Pedersen, N.P.; Parsons, T.D.; Cleary, A.M. Opening a conceptual space for metamemory experience. New Ideas Psychol. 2023, 69, 100995. [Google Scholar] [CrossRef]
- Sreenivasulu, B.; Subramaniam, R. Mapping the conceptual space formed by students’ understaning of coordination number of a transition metal complex: An exploratory study. Chem. Educ. Res. Pract. 2019, 20, 468–483. [Google Scholar] [CrossRef]


| Prompt | Response |
|---|---|
| Challenge or goal of this PDSA cycle. | Collaboration with data collection |
| Context (e.g., grade level, course, topic) | 10th grade, geometry, density |
| Expected duration of this PDSA cycle. (e.g., 10/15 min). | One lesson, modeling data collection will be at the beginning of the lesson |
| Change idea or strategy for meeting your challenge | Model data collection before the students collect their own data |
| Prediction(s)/hypotheses (What you think the change idea/strategy will accomplish?) | Modeling the data collection will show students how to complete procedures. Avoid confusion when starting the collaboration and data collection |
| Evidence to collect | Student work and student ability to complete data collection on their own/with minimal help from the teacher |
| PDSA Lesson (Inquiry through Trigonometric Ratios) | Comparison Lessons: No (and Percent) That Engaged in Any Work (at Least One Question) | |||||
|---|---|---|---|---|---|---|
| Class | No. Students | No. (and Percent) That Completed Independent Work | No. (and Percent) That Engaged in Any Work (at Least One Question) | Lesson 1 before PDSA Lessons | Lesson 2 after PDSA Lessons | Lesson 3 after PDSA Lessons |
| 1 | 22 | 8 (36.4) | 13 (59.1) | 2 (9.1) | 2 (9.1) | 3 (13.6) |
| 2 | 27 | 18 (66.7) | 21 (77.8) | 9 (33.3) | 12 (44.4) | 18 (66.7) |
| 3 | 29 | 15 (51.7) | 16 (55.2) | 3 (10.3) | 10 (34.5) | 5 (17.2) |
| 4 | 31 | 19 (61.3) | 20 (64.5) | 3 (9.7) | 12 (38.7) | 15 (48.4) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rakes, C.R.; Wesneski, A.; Laws, R. Building Mathematics Learning through Inquiry Using Student-Generated Data: Lessons Learned from Plan-Do-Study-Act Cycles. Educ. Sci. 2023, 13, 919. https://doi.org/10.3390/educsci13090919
Rakes CR, Wesneski A, Laws R. Building Mathematics Learning through Inquiry Using Student-Generated Data: Lessons Learned from Plan-Do-Study-Act Cycles. Education Sciences. 2023; 13(9):919. https://doi.org/10.3390/educsci13090919
Chicago/Turabian StyleRakes, Christopher R., Angela Wesneski, and Rebecca Laws. 2023. "Building Mathematics Learning through Inquiry Using Student-Generated Data: Lessons Learned from Plan-Do-Study-Act Cycles" Education Sciences 13, no. 9: 919. https://doi.org/10.3390/educsci13090919
APA StyleRakes, C. R., Wesneski, A., & Laws, R. (2023). Building Mathematics Learning through Inquiry Using Student-Generated Data: Lessons Learned from Plan-Do-Study-Act Cycles. Education Sciences, 13(9), 919. https://doi.org/10.3390/educsci13090919







