Exploring the Interplay between Conceptualizing and Realizing Inquiry—The Case of One Mathematics Teacher’s Trajectory
Abstract
:1. Introduction
What characterizes Alex’s inquiry trajectory, interpreted through the interplay between his conceptualizations and realizations of inquiry?
What are the connections between Alex’s inquiry trajectory and the authority relationships in the mathematics classroom?
2. Theoretical Background
2.1. Inquiry in Mathematics Teaching
2.2. Teachers’ Conceptualizations and Realizations of Inquiry
2.3. Inquiry and Shared Authority
3. Methods
3.1. Alex
3.2. The PD Course
3.3. Data Collection
3.4. Analysis of Data
4. Results
4.1. Pre-PD Interview
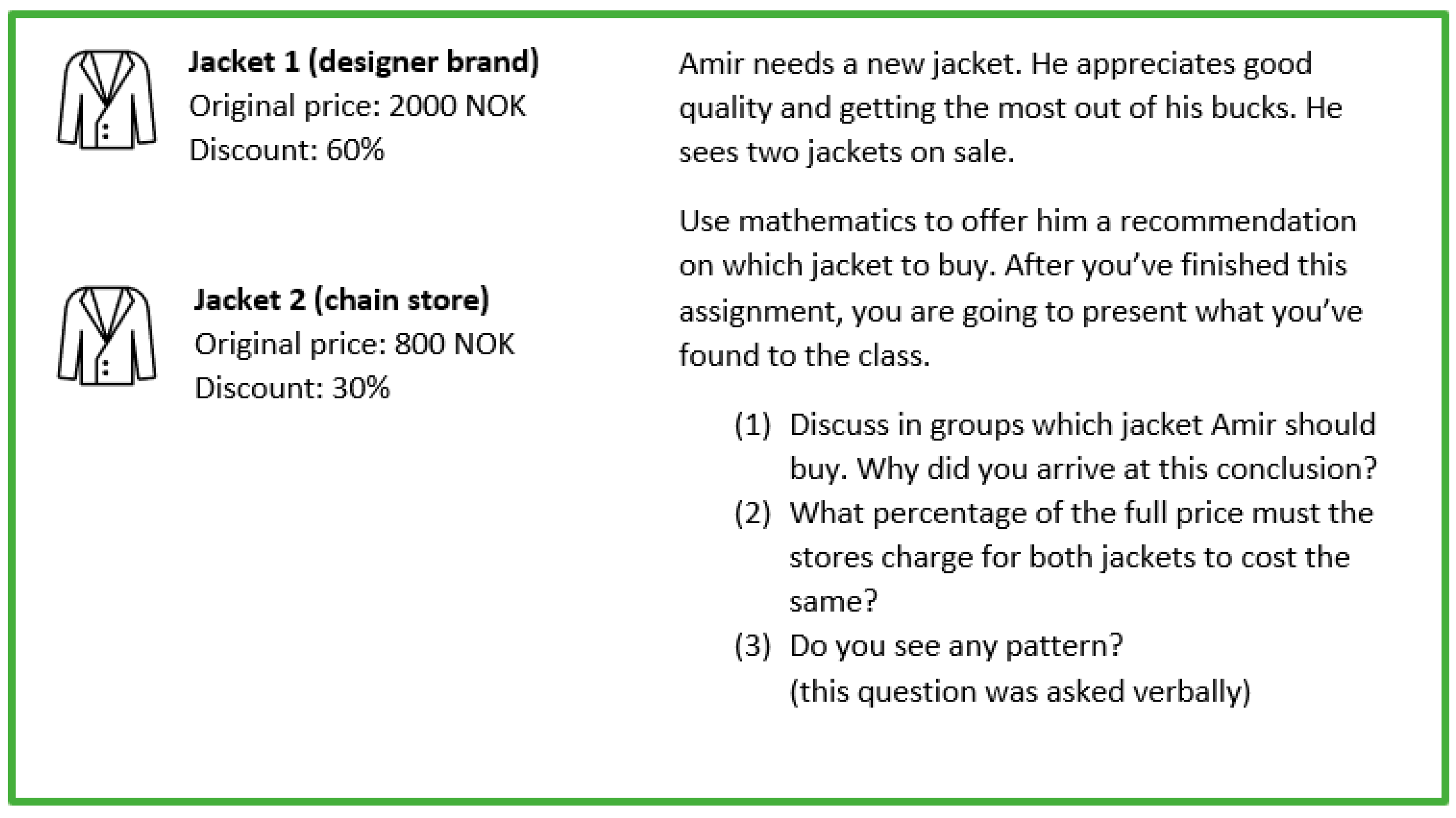
4.2. Lesson 1
4.2.1. Observation Lesson 1
4.2.2. Interview Proceeding Lesson 1
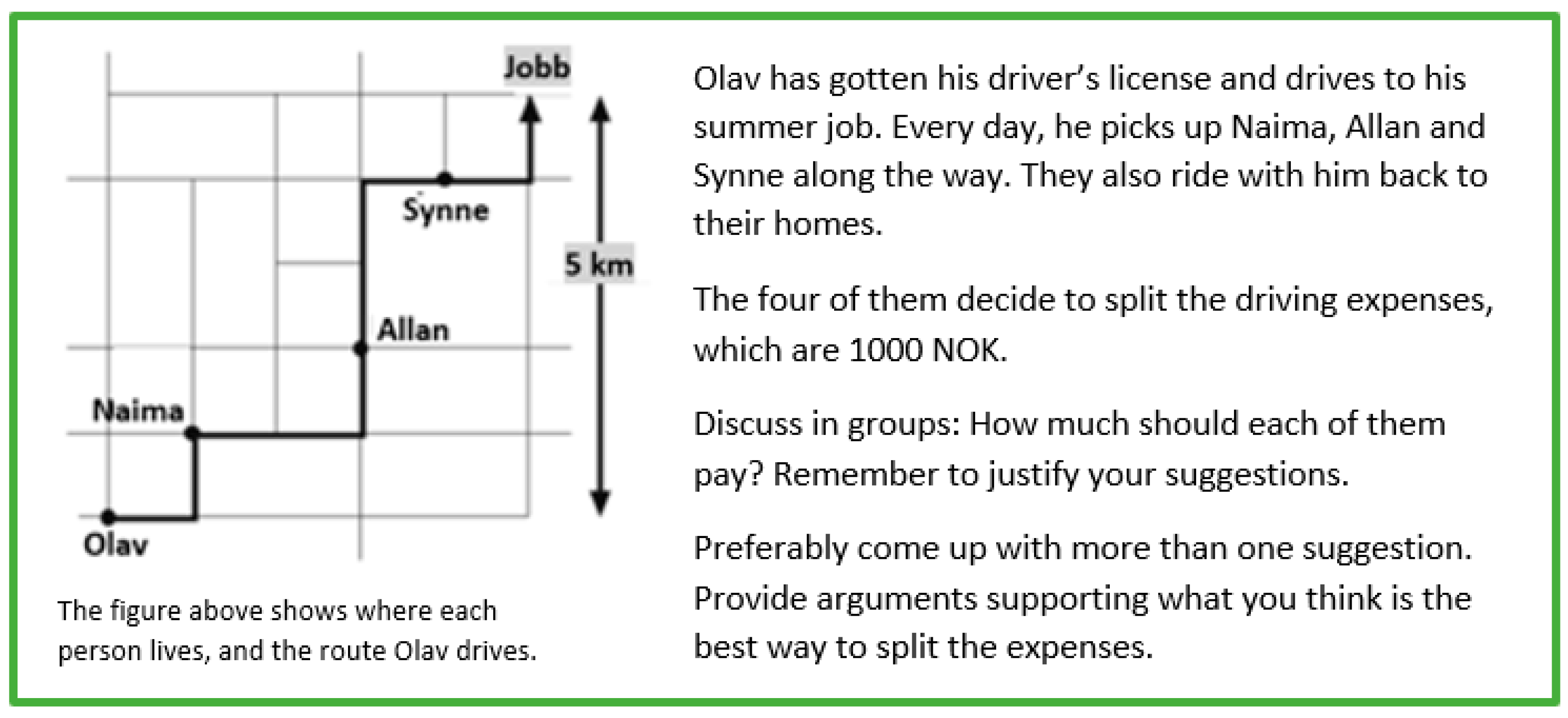
4.3. Lesson 2
4.3.1. Observation Lesson 2
4.3.2. Interview Proceeding Lesson 2
5. Discussion
5.1. Alex’s Inquiry Trajectory in Three Paths
| Pre-PD | Observation Lesson 1 | Interview Lesson 1 | Observation Lesson 2 | Interview Lesson 2 | |
|---|---|---|---|---|---|
| The teacher’s role | The “woodwork teacher” handing out tools | Removing himself from the inquiry (or directing it) | Acknowledging the importance of teacher questioning and preparation | Polya-inspired inquiry into students’ work | Purposeful questioning as an essential element of inquiry in mathematics |
| Growing idea of inquiry | Inquiry in mathematics equals (individual) discovery | Finding multiple solutions and strategies Touching upon communication and argumentation | “How and why”—supplementing exploration with argumentation | Students exploring, explaining, and sharing ideas | Exploration and argumentation. Students as active communicators |
| Orchestrating whole-class situations | Whole-class situations not mentioned | Show-and-tell Teacher directing students towards right answers | The importance of good teacher summaries to connect student ideas | Selecting and sequencing students’ contributions to display multiple solutions and strategies | Whole-class summaries as dialogues between students and teacher |
5.1.1. The Teacher Role in Inquiry Interactions—From the “Woodwork Teacher” to the Curious Questioner
5.1.2. A Growing Idea of Inquiry—Inquiry Is More Than Exploration
5.1.3. Orchestrating Whole-Class Situations
5.2. Alex’s Inquiry Trajectory in Light of Shared Authority
- Prior to PD, he believed that during inquiry, authority should be distributed between himself and the students (as a group) in separate agentic spaces. He was concerned with whether the students would play their roles, but he did not appear to see this problem as actionable and had no clear goals for his learning.
- In Lesson 1, he developed actionable ways of following up on his concern: reminding students of their roles and keeping quiet. After push-back from students, Alex revised his agenda to foster—through questioning—shared authority during groupwork and distributed authority during whole-class episodes.
- In Lesson 2, he experienced partial success in sharing authority during groupwork, through his more responsive questioning. Perhaps encouraged by this or overwhelmed by the burden on him in the distributed authority of whole-class discussion, he revised his agenda to sharing authority both in groupwork and in whole-class episodes.
6. Final Reflections
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dorier, J.-L.; Maaß, K. Inquiry-based mathematics education. In Encyclopedia of Mathematics Education; Lerman, S., Ed.; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar] [CrossRef]
- Laursen, S.; Rasmussen, C. I on the prize: Inquiry approaches in undergraduate mathematics. Int. J. Res. Undergrad. Math. Educ. 2019, 5, 129–146. [Google Scholar] [CrossRef]
- Maaß, K.; Artigue, M. Implementation of inquiry-based learning in day-to-day teaching: A synthesis. ZDM Math. Educ. 2013, 45, 779–795. [Google Scholar] [CrossRef]
- Bruder, R.; Prescott, A. Research evidence on the benefits of IBL. ZDM Math. Educ. 2013, 45, 811–822. [Google Scholar] [CrossRef]
- Hassi, M.-L.; Laursen, S.L. Transformative Learning: Personal Empowerment in Learning Mathematics. J. Transform. Educ. 2015, 13, 316–340. [Google Scholar] [CrossRef]
- Makar, K. The pedagogy of mathematics inquiry. In Pedagogy: New Developments in the Learning Sciences; Gillies, R.M., Ed.; Nova Science Publishers: New York, NY, USA, 2012; pp. 371–397. [Google Scholar]
- Ernest, P. Empowerment In Mathematics Education. Philos. Math. Educ. J. 2002, 15, 1–16. [Google Scholar]
- Artigue, M.; Bosch, M.; Doorman, M.; Juhász, P.; Kvasz, L.; Maaß, K. Inquiry based mathematics education and the development of learning trajectories. Teach. Math. Comput. Sci. 2020, 18, 63–89. [Google Scholar] [CrossRef]
- Romero-Ariza, M.; Quesada, A.; Abril, A.M.; Sorensen, P.; Oliver, M.C. Highly recommended and poorly used: English and Spanish science teachers’ views of inquiry-based learning (IBL) and its enactment. Eurasia J. Math. Sci. Technol. Educ. 2020, 16, em1793. [Google Scholar] [CrossRef]
- Capps, D.K.; Crawford, B.A.; Constas, M.A. A review of empirical literature on inquiry professional development: Alignment with best practices and a critique of the findings. J. Sci. Teach. Educ. 2012, 23, 291–318. [Google Scholar] [CrossRef]
- Capps, D.K.; Shemwell, J.T.; Young, A.M. Over reported and misunderstood? A study of teachers’ reported enactment and knowledge of inquiry-based science teaching. Int. J. Sci. Educ. 2016, 38, 934–959. [Google Scholar] [CrossRef]
- Ozel, M.; Luft, J.A. Beginning secondary science teachers’ conceptualization and enactment of inquiry-based instruction. Sch. Sci. Math. 2013, 113, 308–316. [Google Scholar] [CrossRef]
- Wee, B.; Shepardson, D.; Fast, J.; Harbor, J. Teaching and Learning About Inquiry: Insights and Challenges in Professional Development. J. Sci. Teach. Educ. 2007, 18, 63–89. [Google Scholar] [CrossRef]
- Maaß, K.; Swan, M.; Aldorf, A.-M. Mathematics teachers’ beliefs about inquiry-based learning after a professional development course—An International study. J. Educ. Train. Stud. 2017, 5, 1–17. [Google Scholar] [CrossRef]
- Stein, M.K.; Engle, R.A.; Smith, M.S.; Hughes, E.K. Orchestrating productive mathematical discussions: Five practices for helping teachers move beyond show and tell. Math. Think. Learn. 2008, 10, 313–340. [Google Scholar] [CrossRef]
- Engeln, K.; Euler, M.; Maaß, K. Inquiry-based learning in mathematics and science: A comparative baseline study of teachers’ beliefs and practices across 12 European countries. ZDM Math. Educ. 2013, 45, 823–836. [Google Scholar] [CrossRef]
- Stahnke, R.; Schueler, S.; Roesken-Winter, B. Teachers’ perception, interpretation, and decision-making: A systematic review of empirical mathematics education research. ZDM Math. Educ. 2016, 48, 1–27. [Google Scholar] [CrossRef]
- Damrau, M.; Barton, D.; Huget, J.; Chan, M.C.E.; Roche, A.; Wang, C.; Clarke, D.M.; Cao, Y.; Liu, B.; Zhang, S.; et al. Investigating teacher noticing and learning in Australia, China, and Germany: A tale of three teachers. ZDM Math. Educ. 2022, 54, 257–271. [Google Scholar] [CrossRef]
- Chan, M.C.E.; Roche, A.; Clarke, D.J.; Clarke, D.M. How Do Teachers Learn? Different Mechanisms of Teacher In-Class Learning. In Mathematics Education Research: Impacting Practice, Proceedings of the 42nd Annual Conference of the Mathematics Education Research Group of Australasia, Perth, Australia, 30 June–4 July 2019; Hines, G., Blackley, S., Cooke, A., Eds.; MERGA: Adelaide, Australia, 2019; pp. 164–171. [Google Scholar]
- Hayward, C.N.; Kogan, M.; Laursen, S.L. Facilitating instructor adoption of inquiry-based learning in college mathematics. Int. J. Res. Undergrad. Math. Educ. 2016, 2, 59–82. [Google Scholar] [CrossRef]
- Artigue, M.; Blomhøj, M. Conceptualizing inquiry-based education in mathematics. ZDM Math. Educ. 2013, 45, 797–810. [Google Scholar] [CrossRef]
- Goldsmith, L.T.; Doerr, H.M.; Lewis, C.C. Mathematics teachers’ learning: A conceptual framework and synthesis of research. J. Math. Teach. Educ. 2014, 17, 5–36. [Google Scholar] [CrossRef]
- Amit, M.; Fried, M.N. Authority and Authority Relations in Mathematics Education: A View from an 8th Grade Classroom. Educ. Stud. Math. 2005, 58, 145–168. [Google Scholar] [CrossRef]
- Artigue, M.; Blomhøj, M. Examples of inquiry-based activities with reference to different theoretical frameworks in mathematics education research. ZDM Math. Educ. 2013, 45. [Google Scholar]
- Kuster, G.; Johnson, E.; Keene, K.; Andrews-Larson, C. Inquiry-oriented instruction: A conceptualization of the instructional principles. Primus 2018, 28, 13–30. [Google Scholar] [CrossRef]
- Bråtalien, M.; Skogholt, J.; Naalsund, M. Designing problems introducing the concept of numerical integration in an inquiry-based setting. In Proceedings of the 45th Conference of the International Group for the Psychology of Mathematics Education, Alicante, Spain, 18–23 July 2022; Fernández, C., Llinares, S., Gutiérrez, Á., Planas, N., Eds.; PME: Alicante, Spain, 2022; Volume 2, pp. 91–98. [Google Scholar]
- Naalsund, M.; Bråtalien, M.; Skogholt, J. On the value of interthinking for mathematical learning. In Bringing Nordic Mathematics Education into the Future, Proceedings of Norma 20 the Ninth Nordic Conference on Mathematics Education, Oslo, Norway, 1–4 June 2021; Nortvedt, G.A., Buchholtz, N.F., Fauskanger, J., Hähkiöniemi, M., Jessen, B.E., Naalsund, M., Nilsen, H.K., Pálsdóttir, G., Portaankorva-Koivisto, P., Radišić, J., et al., Eds.; Swedish Society for Research in Mathematics Education: Gøteborg, Sweden, 2022; pp. 185–192. [Google Scholar]
- Hansen, E.K.S. Students’ agency, creative reasoning, and collaboration in mathematical problem solving. Math. Educ. Res. J. 2022, 34, 813–834. [Google Scholar] [CrossRef]
- Drageset, O.G. Redirecting, progressing, and focusing actions—A framework for describing how teachers use students’ comments to work with mathematics. Educ. Stud. Math. 2014, 85, 281–304. [Google Scholar] [CrossRef]
- Wood, T. Alternative patterns of communication in mathematics classes: Funneling or focusing. In Language and Communication in the Mathematics Classroom; Steinbring, H., Bussi, M.G.B., Sierpinska, A., Eds.; National Council of Teachers of Mathematics: Reston, VA, USA, 1998; pp. 167–178. [Google Scholar]
- Makar, K.; Bakker, A.; Ben-Zvi, D. Scaffolding norms of argumentation-based inquiry in a primary mathematics classroom. ZDM 2015, 47, 1107–1120. [Google Scholar] [CrossRef]
- Menezes, L.; Oliveira, H.; Canavarro, A.P. Inquiry-Based Mathematics Teaching: The Case of Célia. In Educational Paths to Mathematics: A C.I.E.A.E.M. Sourcebook; Gellert, U., Giménez Rodríguez, J., Hahn, C., Kafoussi, S., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2015; pp. 305–321. [Google Scholar] [CrossRef]
- Ensor, P. From Preservice Mathematics Teacher Education to Beginning Teaching: A Study in Recontextualizing. J. Res. Math. Educ. 2001, 32, 296–320. [Google Scholar] [CrossRef]
- Whitehead, A.N. The Aims of Education and Other Essays; Macmillan: New York, NY, USA, 1967. [Google Scholar]
- Buehl, M.M.; Beck, J.S. The relationship between teachers’ beliefs and teachers’ practices. In International Handbook of Research on Teachers’ Beliefs; Fives, H., Gill, M.G., Eds.; Routledge: London, UK, 2015; Volume 1, pp. 66–84. [Google Scholar]
- Kennedy, M.M. How does professional development improve teaching? Rev. Educ. Res. 2016, 86, 945–980. [Google Scholar] [CrossRef]
- Calleja, J. Changes in mathematics teachers’ self-reported beliefs and practices over the course of a blended continuing professional development programme. Math. Educ. Res. J. 2022, 34, 835–861. [Google Scholar] [CrossRef]
- Heyd-Metzuyanim, E.; Munter, C.; Greeno, J. Conflicting frames: A case of misalignment between professional development efforts and a teacher’s practice in a high school mathematics classroom. Educ. Stud. Math. 2018, 97, 21–37. [Google Scholar] [CrossRef]
- Towers, J. Learning to teach mathematics through inquiry: A focus on the relationship between describing and enacting inquiry-oriented teaching. J. Math. Teach. Educ. 2010, 13, 243–263. [Google Scholar] [CrossRef]
- Lotter, C.; Harwood, W.S.; Bonner, J.J. The influence of core teaching conceptions on teachers’ use of inquiry teaching practices. J. Res. Sci. Teach. 2007, 44, 1318–1347. [Google Scholar] [CrossRef]
- Chin, E.-T.; Lin, Y.-C.; Tuan, H.-L. Analyzing Changes in Four Teachers’ Knowledge and Practice of Inquiry-Based Mathematics Teaching. Asia-Pac. Educ. Res. 2016, 25, 845–862. [Google Scholar] [CrossRef]
- Kang, N.-H.; Orgill, M.; Crippen, K.J. Understanding Teachers’ Conceptions of Classroom Inquiry With a Teaching Scenario Survey Instrument. J. Sci. Teach. Educ. 2008, 19, 337–354. [Google Scholar] [CrossRef]
- National Research Council. Inquiry and the National Science Education Standards: A Guide for Teaching and Learning; National Academies Press: Washington, DC, USA, 2000. [Google Scholar]
- Horn, I.S.; Garner, B. Teacher Learning of Ambitious and Equitable Mathematics Instruction: A Sociocultural Approach; Routledge: London, UK, 2022. [Google Scholar]
- Staples, M.E. Promoting student collaboration in a detracked, heterogeneous secondary mathematics classroom. J. Math. Teach. Educ. 2008, 11, 349–371. [Google Scholar] [CrossRef]
- Wilkie, K.J. Rise or Resist: Exploring Senior Secondary Students’ Reactions to Challenging Mathematics Tasks Incorporating Multiple Strategies. Eurasia J. Math. Sci. Technol. Educ. 2016, 12, 2061–2083. [Google Scholar] [CrossRef]
- Wagner, D.; Herbel-Eisenmann, B. Mathematics teachers’ representations of authority. J. Math. Teach. Educ. 2014, 17, 201–225. [Google Scholar] [CrossRef]
- Wilson, M.; Lloyd, G.M. Sharing mathematical authority with students: The challenge for high school teachers. J. Curric. Superv. 2000, 15, 146–169. [Google Scholar]
- Ng, O.-L.; Cheng, W.K.; Ni, Y.; Shi, L. How linguistic features and patterns of discourse moves influence authority structures in the mathematics classroom. J. Math. Teach. Educ. 2021, 24, 587–612. [Google Scholar] [CrossRef]
- Arnesen, K.K.; Rø, K. The complexity of supporting reasoning in a mathematics classroom of shared authority. Math. Think. Learn. 2022, 1–26. [Google Scholar] [CrossRef]
- Kinser-Traut, J.Y.; Turner, E.E. Shared authority in the mathematics classroom: Successes and challenges throughout one teacher’s trajectory implementing ambitious practices. J. Math. Teach. Educ. 2020, 23, 5–34. [Google Scholar] [CrossRef]
- Bråtalien, M.; Naalsund, M. In-service teachers’ conceptualizations of inquiry in teaching and learning mathematics. Math. Educ. Res. J. Unpublished manuscript.
- Bråtalien, M. Inquiry to me: Four mathematics teachers’ conceptualizations of inquiry preceding a professional development course. In Proceedings of the Thirteenth Congress of the European Society for Research in Mathematics Education (CERME13), Budapest, Hungary, 10–14 July 2023. Unpublished manuscript. [Google Scholar]
- Tafoya, E.; Sunal, D.W.; Knecht, P. Assessing inquiry potential: A tool for curriculum decision makers. Sch. Sci. Math. 1980, 80, 43–48. [Google Scholar] [CrossRef]
- Lithner, J. Principles for designing mathematical tasks that enhance imitative and creative reasoning. ZDM Math. Educ. 2017, 49, 937–949. [Google Scholar] [CrossRef]
- Horn, I.S. Supporting the Development of Pedagogical Judgment: Connecting Instruction to Contexts through Classroom Video with Experienced Mathematics Teachers. In International Handbook of Mathematics Teacher Education: Volume 3; Lloyd, G.M., Chapman, O., Eds.; Brill: Leiden, The Netherlands, 2019; pp. 321–342. [Google Scholar] [CrossRef]
- Oppong-Nuako, J.; Shore, B.M.; Saunders-Stewart, K.S.; Gyles, P.D.T. Using Brief Teacher Interviews to Assess the Extent of Inquiry in Classrooms. J. Adv. Acad. 2015, 26, 197–226. [Google Scholar] [CrossRef]
- Kuster, G.; Johnson, E.; Rupnow, R.; Wilhelm, A.G. The inquiry-oriented instructional measure. Int. J. Res. Undergrad. Math. Educ. 2019, 5, 183–204. [Google Scholar] [CrossRef]
- Braun, V.; Clarke, V. One size fits all? What counts as quality practice in (reflexive) thematic analysis? Qual. Res. Psychol. 2021, 18, 328–352. [Google Scholar] [CrossRef]
- Powell, A.B.; Francisco, J.M.; Maher, C.A. An analytical model for studying the development of learners’ mathematical ideas and reasoning using videotape data. J. Math. Behav. 2003, 22, 405–435. [Google Scholar] [CrossRef]
- Polya, G. How To Solve It; Doubleday & Company, Inc.: New York, NY, USA, 1957. [Google Scholar]
- Swan, M.; Swain, J. The impact of a professional development programme on the practices and beliefs of numeracy teachers. J. Furth. High. Educ. 2010, 34, 165–177. [Google Scholar] [CrossRef]
- Watson, A.; Mason, J. Taken-as-shared: A review of common assumptions about mathematical tasks in teacher education. J. Math. Teach. Educ. 2007, 10, 205–215. [Google Scholar] [CrossRef]
- Maaß, K. How can teachers’ beliefs affect their professional development? ZDM 2011, 43, 573–586. [Google Scholar] [CrossRef]


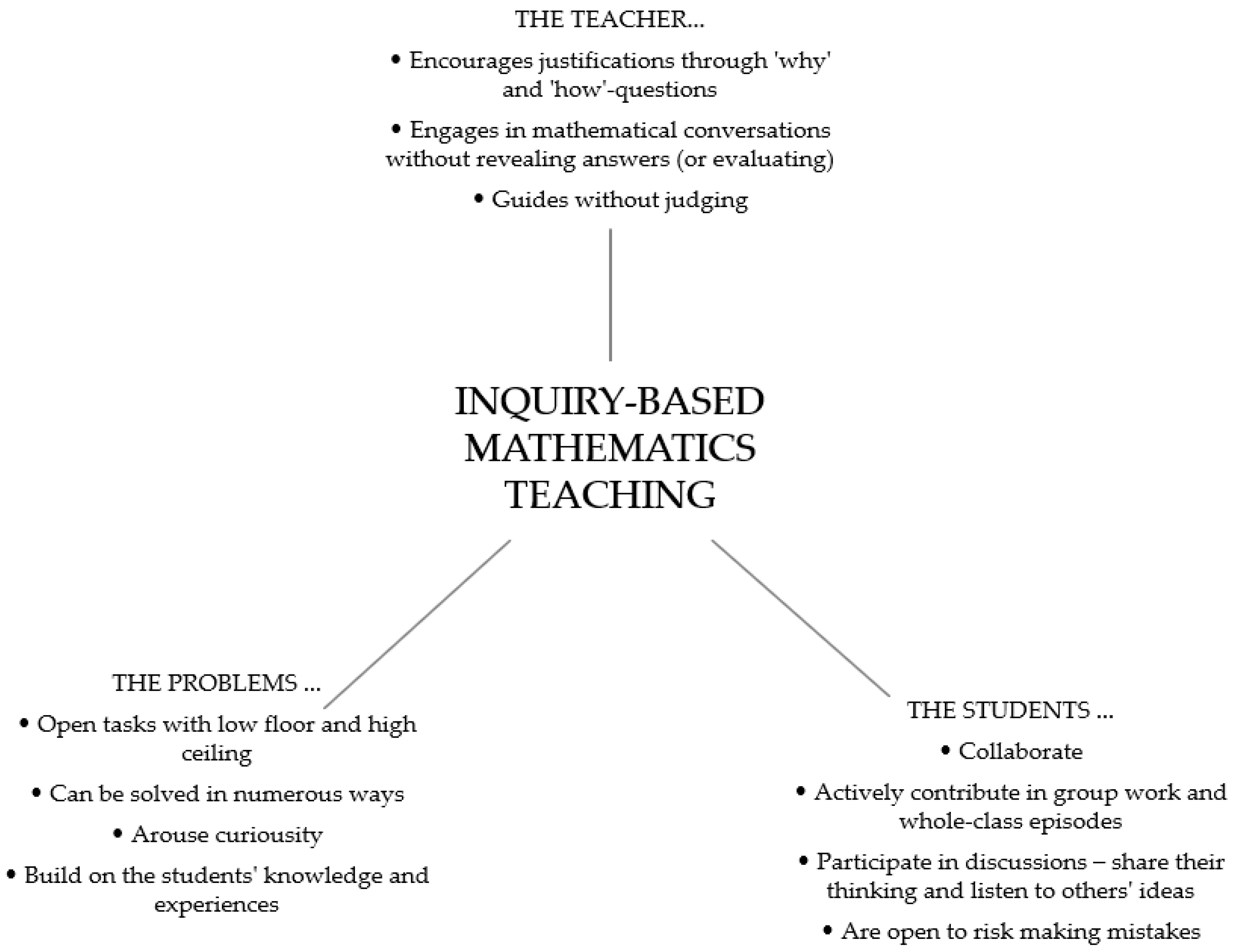
| Essential Elements of Inquiry in Teaching and Learning Mathematics. | |
|---|---|
| Students | Build on what they know to engage deeply with unfamiliar problems Collaboratively grapple with mathematical ideas Take on mathematical authority and responsibility |
| Teachers | Encourage and inquire into student reasoning Use student contributions to develop shared understandings and connections to formal mathematics Foster student empowerment through design, structure, and facilitation |
| Problems | Foster student engagement Are meaningful and relevant for students’ daily lives Are related to mathematical ideas and concepts |
| Inquiry Facet | Category (Codes in Parentheses) |
|---|---|
| Students | Collaborative and communicative processes (argue and challenge; build on ideas; discuss; evaluate; explain; share and listen to ideas; shared understanding) Student thinking (connect existing knowledge; explore; find strategies and solutions; see that there are multiple strategies and solutions *; use knowledge in new situations) Authority and accountability (actively engage; responsibility and ownership) |
| Teachers | Interactions with student reasoning (ask for justifications; challenge student thinking; direct *; encourage new solution or path; few prescriptions; foster collaboration; guide and support; inquire into student thinking; purposeful questioning *) Brokering (bridge student ideas and formal mathematics; connect students’ thinking with each other) Structure and planning (anticipate student thinking; plan activity; select and sequence; summarize) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bråtalien, M.; Naalsund, M.; Eriksen, E. Exploring the Interplay between Conceptualizing and Realizing Inquiry—The Case of One Mathematics Teacher’s Trajectory. Educ. Sci. 2023, 13, 843. https://doi.org/10.3390/educsci13080843
Bråtalien M, Naalsund M, Eriksen E. Exploring the Interplay between Conceptualizing and Realizing Inquiry—The Case of One Mathematics Teacher’s Trajectory. Education Sciences. 2023; 13(8):843. https://doi.org/10.3390/educsci13080843
Chicago/Turabian StyleBråtalien, Marte, Margrethe Naalsund, and Elisabeta Eriksen. 2023. "Exploring the Interplay between Conceptualizing and Realizing Inquiry—The Case of One Mathematics Teacher’s Trajectory" Education Sciences 13, no. 8: 843. https://doi.org/10.3390/educsci13080843
APA StyleBråtalien, M., Naalsund, M., & Eriksen, E. (2023). Exploring the Interplay between Conceptualizing and Realizing Inquiry—The Case of One Mathematics Teacher’s Trajectory. Education Sciences, 13(8), 843. https://doi.org/10.3390/educsci13080843







