Top Achievers in Mathematics in the End of Upper Secondary School
Abstract
1. Introduction
2. Mathematically Gifted Students
3. Individual and Environmental Factors behind Mathematical Competence
3.1. Individual Factors
3.2. Environmental Factors
4. Research Questions
- At which stage of basic education can the top achievers in mathematics be identified?
- 2.
- What kinds of factors predict students’ development into a top achiever in mathematics?
- 2.1
- What kinds of mathematical tasks predict development into a top achiever in mathematics?
- 2.2
- What background factors predict development into a top achiever in mathematics?
5. Methodological Solutions
5.1. The Data Set and Participants
5.2. Measurements
5.3. Statistical Analysis
6. Results
6.1. Top Achievers’ Mathematical Competence during Basic Education
6.2. Tasks That Predict Future Achievement in Mathematics
6.3. Attitudes That Predict Future Achievement in Mathematics
6.4. Gender Differences among Top Achievers
6.5. Differences in Parents’ Education and Support among Top Achievers
7. Discussion and Limitations
7.1. Implications of the Results
7.2. Limitations
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sriraman, B.; Leikin, R. Commentary on interdisciplinary perspectives to creativity and giftedness. In Creativity and Giftedness—Interdisciplinary Perspectives from Mathematics and Beyond; Leikin, R., Sriraman, B., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 259–264. [Google Scholar]
- Sternberg, R.J.; Davidson, J.E. (Eds.) Conceptions of Giftedness; Cambridge University Press: New York, NY, USA, 2005. [Google Scholar]
- Szabo, A. Mathematical Abilities and Mathematical Memory during Problem Solving and Some Aspects of Mathematics Education for Gifted Pupils. Ph.D. Thesis, Stockholm University, Stockholm, Sweden, 2017. Available online: https://www.diva-portal.org/smash/get/diva2:1143981/FULLTEXT01.pdf (accessed on 2 July 2023).
- Dai, D.Y. The Nature and Nurture of Giftedness: A New Framework for Understanding Gifted Education; Teachers College Press: New York, NY, USA, 2010. [Google Scholar]
- Leikin, R. Exploring mathematical creativity using multiple solution tasks. In Creativity in Mathematics and the Education of Gifted Students; Leikin, R., Berman, A., Koichu, B., Eds.; Sense Publisher: Rotterdam, The Netherlands, 2009; pp. 129–145. [Google Scholar]
- Leikin, R. Giftedness and High Ability in Mathematics. In Encyclopedia of Mathematics Education; Lerman, S., Ed.; Springer: Cham, Switzerland, 2018; pp. 1–11. [Google Scholar] [CrossRef]
- Bandura, A. Social Foundations of Thought and Action: A Social Cognitive Theory; Prentice Hall: Englewood Cliffs, NJ, USA, 1986. [Google Scholar]
- Niemi, E.K.; Metsämuuronen, J. (Eds.) Miten Matematiikan Taidot Kehittyvät? Matematiikan Oppimistulokset Peruskoulun Viidennen Vuosiluokan Jälkeen Vuonna 2008; Koulutuksen Seurantaraportti; Opetushallitus: Helsinki, Finland, 2010; Volume 2. [Google Scholar]
- Metsämuuronen, J. Perusopetuksen Matematiikan Oppimistulosten Pitkittäisarviointi Vuosina 2005–2012; Koulutuksen Seurantaraportit; Opetushallitus: Helsinki, Finland, 2013; Volume 4. [Google Scholar]
- Metsämuuronen, J. Oppia Ikä Kaikki—Matemaattinen Osaaminen Toisen Asteen Koulutuksen Lopussa 2015; Kansallinen Koulutuksen Arviointikeskus: Helsinki, Finland, 2017; Volume 1. [Google Scholar]
- Metsämuuronen, J.; Tuohilampi, J. Matemaattinen Osaaminen Lukiokoulutuksen Lopulla 2015; Kansallinen Koulutuksen Arviointikeskus: Helsinki, Finland, 2017; Volume 3. [Google Scholar]
- Ministry of Education and Culture. Finnish Education System, N.D.-D. Available online: https://okm.fi/en/education-system (accessed on 26 July 2023).
- Niemi, L.; Metsämuuronen, J.; Hannula, M.; Laine, A. Matematiikan parhaaksi osaajaksi kehittyminen perusopetuksen aikana. Ainedidaktiikka 2020, 4, 2–33. [Google Scholar] [CrossRef]
- Niemi, L.; Metsämuuronen, J.; Hannula, M.S.; Laine, A. Matematiikan parhaiden osaajien siirtyminen toiselle asteelle: Koulutusvalinnat ja matematiikan osaamisen kehittyminen. LUMAT Int. J. Math Sci. Technol. Educ. 2021, 9, 457–494. [Google Scholar] [CrossRef]
- Niemi, L.; Metsämuuronen, J.; Hannula, M.S.; Laine, A. Matematiikan parhaat osaajat lukion lopussa ja heidän matematiikka-asenteissaan tapahtuneet muutokset. LUMAT Int. J. Math Sci. Technol. Educ. 2021, 9, 804–843. [Google Scholar] [CrossRef]
- Brandl, M.; Barthel, C. A comparative profile of high attaining and gifted students in mathematics. In Proceedings of the ICME-12 Pre-Proceedings, Seoul, China, 8–15 July 2012; pp. 1429–1438. [Google Scholar]
- Szabo, A. Mathematical problem-solving by high achieving students: Interaction of mathematical abilities and the role of the mathematical memory. In Proceedings of the CERME 9-Ninth Congress of the European Society for Research in Mathematics, Prague, Czech Republic, 4–8 February 2015; Charles University and ERME: Prague, Czech Republic, 2015; pp. 1087–1093. [Google Scholar]
- Dweck, C. Mindset: The New Psychology of Success; Ballantine Books: New York, NY, USA, 2006. [Google Scholar]
- Roe, A. A psychological study of physical scientists. Genet. Psychol. Monogr. 1951, 43, 121–235. [Google Scholar]
- Bloom, B. Developing Talent in Young People; Ballantine Books: New York, NY, USA, 1985. [Google Scholar]
- Krutetskii, V.A. The Psychology of Mathematical Abilities in Schoolchildren; University of Chicago Press: Chicago, IL, USA, 1976. [Google Scholar]
- Mönks, F.; Katzko, M. Giftedness and Gifted Education. In Conceptions of Giftedness; Sternberg, R., Davidson, J.E., Eds.; Cambridge University Press: New York, NY, USA, 2005; pp. 187–200. [Google Scholar] [CrossRef]
- Sheffield, L.J.; Bennett, J.; Berriozabal, M.; DeArmond, M.; Wertheimer, R. Report of the NCTM task force on the mathematically promising. In Developing Mathematically Promising Students; Sheffield, L.J., Ed.; NCTM: Washington, DC, USA, 1999; pp. 309–316. [Google Scholar]
- Niemi, L.H.L. Matematiikan Parhaat Osaajat Perusopetuksessa ja Toisella Asteella: Pitkittäistutkimus Matematiikan Osaamisen ja Asenteiden Kehittymisestä Vuosina 2005–2015. Ph.D. Thesis, University of Helsinki, Helsinki, Finland, 2022. Available online: http://hdl.handle.net/10138/346768 (accessed on 2 July 2023).
- Niederer, K.; Irwin, R.J.; Irwin, K.C.; Reilly, I.L. Identification of Mathematically Gifted Children in New Zealand. High Abil. Stud. 2003, 14, 71–84. [Google Scholar] [CrossRef]
- McBee, M.T.; Peters, S.J.; Miller, E.M. The Impact of the Nomination Stage on Gifted Program Identification: A Comprehensive Psychometric nalysis. Gift. Child Q. 2016, 60, 258–278. [Google Scholar] [CrossRef]
- Lubinski, D.; Benbow, C.P. Study of mathematically precocious youth after 35 years: Uncovering antecedents for the development of math-science expertise. Perspect. Psychol. Sci. 2006, 1, 316–345. [Google Scholar] [CrossRef]
- Ruokamo, H. Matemaattinen Lahjakkuus ja Matemaattisten Sanallisten Ongelmanratkaisutaitojen Kehittäminen Teknologiaperustaisessa Oppimisympäristössä. Ph.D. Thesis, Helsingin Yliopiston Opettajankoulutuslaitos, Helsinki, Finland, 2000. [Google Scholar]
- Koshy, V.; Ernest, P.; Casey, R. Mathematically gifted and talented learners: Theory and practice. Int. J. Math. Educ. Sci. Technol. 2009, 40, 213–228. [Google Scholar] [CrossRef][Green Version]
- Leikin, R.; Leikin, M.; Paz-Baruch, N.; Waisman, I.; Lev, M. On the four types of characteristics of super mathematically gifted students. High Abil. Stud. 2017, 28, 107–125. [Google Scholar] [CrossRef]
- Reed, C.F. Mathematically gifted in the heterogeneously grouped mathematics classroom: What is a teacher to do? J. Second. Gift. Educ. 2004, 15, 89–95. [Google Scholar] [CrossRef]
- Brody, L.E.; Stanley, J.C. Youths who reason exceptionally well mathematically and/or verbally: Using the MVT:D4 model to develop their talents. In Conception of Giftedness; Sternberg, R.J., Davidson, J.E., Eds.; Cambridge University Press: New York, NY, USA, 2005; pp. 20–37. [Google Scholar]
- Brody, L.E. The John Hopkins talent search model for identifying and developing exceptional mathematical and verbal abilities. In International Handbook of Giftedness; Shavinina, L.V., Ed.; Springer: Dordrecht, The Netherlands, 2009; pp. 999–1016. [Google Scholar] [CrossRef]
- Elia, I.; van den Heuvel-Panhuizen, M.; Kolovou, A. Exploring strategy use and strategy flexibility in non-routine problem solving by primary school high achievers in mathematics. ZDM—Math. Educ. 2009, 41, 605–618. [Google Scholar] [CrossRef]
- Pólya, G. How Will I Solve the Mathematical Task; Školskaknjiga: Zagreb, Croatia, 1966. [Google Scholar]
- Boesen, J.; Lithner, J.; Palm, T. The relation between types of assessment tasks and the mathematical reasoning students use. Educ. Stud. Math. 2010, 75, 89–105. [Google Scholar] [CrossRef]
- Kablan, Z.; Ugur, S.S. The relationship between routine and non-routine problem solving and learning styles. Educ. Stud. 2020, 47, 328–343. [Google Scholar] [CrossRef]
- Siegler, R.S.; Duncan, G.J.; Davis-Kean, P.E.; Duckworth, K.; Claessens, A.; Engel, M.; Susperreguy, M.I.; Chen, M. Early Predictors of High School Mathematics Achievement. Psychol. Sci. 2012, 23, 691–697. [Google Scholar] [CrossRef]
- Metsämuuronen, J.; Nousiainen, S. Matematiikkaa COVID-19-Pandemian Varjossa II. Matematiikan Osaaminen 9. Luokan Lopussa Keväällä 2021; Kansallinen Koulutuksen Arviointikeskus: Helsinki, Finland, 2021; Available online: https://karvi.fi/wp-content/uploads/2021/12/KARVI_2721.pdf (accessed on 2 July 2023).
- Kell, H.J.; Lubinski, D.; Benbow, C.P. Who Rises to the Top? Early Indicators. Psychol. Sci. 2013, 24, 648–659. [Google Scholar] [CrossRef]
- Lubinski, D.; Benbow, C.P.; Kell, H.J. Life Paths and Accomplishments of Mathematically Precocious Males and Females Four Decades Later. Psychol. Sci. 2014, 25, 2217–2232. [Google Scholar] [CrossRef]
- Hannula, M.S.; Laakso, J. The structure of mathematics related beliefs, attitudes and motivation among Finnish grade 4 and grade 8 students. In Proceedings of the 35th Conference of the International Group for the Psychology of Mathematics Education, Ankara, Turkey, 10–15 July 2011; PME: Ankara, Turkey, 2011; Volume 1, pp. 9–16. [Google Scholar]
- Bhowmik, M.; Roy, B.B. A study on the relationship between achievement in mathematics and attitude towards mathematics of secondary school students. Scholar 2016, 1, 49–55. [Google Scholar] [CrossRef]
- Chen, L.; Bae, S.R.; Battista, C.; Qin, S.; Chen, T.; Evans, T.M.; Menon, V. Positive attitude toward math supports early academic success: Behavioral evidence and neurocognitive mechanisms. Psychol. Sci. 2018, 29, 390–402. [Google Scholar] [CrossRef]
- Dowker, A.; Cheriton, O.; Horton, R.; Mark, W. Relationships between attitudes and performance in young children’s mathematics. Educ. Stud. Math. 2019, 100, 211–230. [Google Scholar] [CrossRef]
- Pajares, F.; Miller, M.D. Role of self-efficacy and self-concept beliefs in mathematical problem solving: A path analysis. J. Educ. Psychol. 1994, 86, 193–203. [Google Scholar] [CrossRef]
- Bryan, R.R.; Glynn, S.M.; Kittleson, J.M. Motivation, achievement, and advanced placement intent of high school students learning science. Sci. Educ. 2011, 95, 1049–1065. [Google Scholar] [CrossRef]
- Jiang, Y.; Song, J.; Lee, M.; Bong, M. Self-efficacy and achievement goals as motivational links between perceived contexts and achievement. Educ. Psychol. 2014, 34, 92–117. [Google Scholar] [CrossRef]
- Suárez-Álvarez, J.; Fernández-Alonso, R.; Muñiz, J. Self-concept, motivation, expectations and socioeconomic level as predictors of academic performance in mathematics. Learn. Individ. Differ. 2014, 30, 118–123. [Google Scholar] [CrossRef]
- Kupari, P.; Nissinen, K. Matematiikan osaamisen taustatekijät. In Millä Eväillä Osaaminen Uuteen Nousuun? PISA 2012 Tutkimustuloksia; Välijärvi, J., Kupari, P., Eds.; Opetus- ja Kulttuuriministeriön Julkaisuja: Helsinki, Finland, 2015; Volume 6, pp. 10–27. Available online: http://julkaisut.valtioneuvosto.fi/bitstream/handle/10024/75126/okm6.pdf (accessed on 2 July 2023).
- Williams, T.; Williams, K. Self-efficacy and performance in mathematics: Reciprocal determinism in 33 nations. J. Educ. Psychol. 2010, 102, 453–466. [Google Scholar] [CrossRef]
- Tuohilampi, L.; Hannula, M. Matematiikkaan liittyvien asenteiden kehitys sekä asenteiden ja osaamisen välinen vuorovaikutus 3, 6. ja 9. luokalla. In Perusopetuksen Matematiikan Oppimistulosten Pitkittäisarviointi Vuosina 2005–2012; Metsämuuronen, J., Ed.; Koulutuksen Seurantaraportit; Opetushallitus: Helsinki, Finland, 2013; Volume 4. [Google Scholar]
- Hannula, M.S.; Bofah, E.; Tuohilampi, L.; Metsämuuronen, J. A longitudinal analysis of the relationship between mathematics-related affect, and achievement in Finland. In Proceedings of the Joint Meeting of PME 28 and PME-NA 36, Vancouver, BC, Canada, 15–20 July 2014; PME: Vancouver, BC, Canada, 2014; Volume 3, pp. 249–256. [Google Scholar]
- Beede, D.; Julian, T.; Langdon, D.; McKittrick, G.; Khan, B.; Doms, M. Women in STEM: A gender gap to innovation. Econ. Stat. Adm. Issue Brief 2011, 4, 1–22. [Google Scholar] [CrossRef]
- Ceci, S.J.; Ginther, D.K.; Kahn, S.; Williams, W.M. Women in academic science: A changing landscape. Psychol. Sci. Public Interest 2014, 15, 75–141. [Google Scholar] [CrossRef]
- Pääkkönen, J. Sukupuolten väliset erot matematiikan ja luonnontieteiden osaamisessa lukiossa. Yhteiskuntapolitiikka 2013, 78, 447–456. Available online: https://core.ac.uk/download/pdf/18618614.pdf (accessed on 2 July 2023).
- Hyde, J.S.; Mertz, J.E. Gender, culture, and mathematics performance. Proc. Natl. Acad. Sci. USA 2009, 106, 8801–8807. [Google Scholar] [CrossRef]
- Zhou, Y.; Fan, X.; Wei, X.; Tai, R.H. Gender Gap Among High Achievers in Math and Implications for STEM Pipeline. Asia-Pac. Educ. Res. 2017, 26, 259–269. [Google Scholar] [CrossRef]
- Vettenranta, J.; Hiltunen, J.; Kotila, J.; Lehtola, P.; Nissinen, K.; Puhakka, E.; Pulkkinen, J.; Ström, A. Perustaidoista Vauhtia Koulutielle. Neljännen Luokan Oppilaiden Matematiikan ja Luonnontieteiden Osaaminen. Kansainvälinen Timss 2019-Tutkimus Suomessa. Koulutuksen Tutkimuslaitos. 2020. Available online: https://jyx.jyu.fi/handle/123456789/73016 (accessed on 26 July 2023).
- Vettenranta, J.; Välijärvi, J.; Ahonen, A.; Hautamäki, J.; Hiltunen, J.; Leino, K.; Lähteinen, S.; Nissinen, K.; Nissinen, V.; Puhakka, E.; et al. PISA15 Ensituloksia. Huipulla Pudotuksesta Huolimatta; Opetus- ja Kulttuuriministeriön Julkaisuja: Helsinki, Finland, 2016; Volume 41, Available online: http://www.urn.fi/URN:ISBN:978-952-263-436-8 (accessed on 2 July 2023).
- O’Dea, R.E.; Lagisz, M.; Jennions, M.D.; Nakagawa, S. Gender differences in individual variation in academic grades fail to fit expected patterns for STEM. Nat. Commun. 2018, 9, 3777. [Google Scholar] [CrossRef]
- Johnson, W.; Carothers, A.; Deary, I.J. Sex differences in variability in general intelligence: A new look at the old question. Perspect. Psychol. Sci. 2008, 3, 518–531. [Google Scholar] [CrossRef]
- Ko, H.K.; Choi, S.; Kaji, S. Who has given up on mathematics? A data analysis. Asia Pac. Educ. Rev. 2021, 22, 699–714. [Google Scholar] [CrossRef]
- Metsämuuronen, J.; Lehikko, A. Challenges and possibilities of educational equity and equality in the post-COVID-19 realm in the Nordic countries. Scand. J. Educ. Res. 2022, 1–22. [Google Scholar] [CrossRef]
- Cvencek, D.; Meltzoff, A.N.; Greenwald, A.G. Math-gender stereotypes in elementary school children. Child Dev. 2011, 82, 766–779. [Google Scholar] [CrossRef]
- Lindberg, S.; Linkersdörfer, J.; Ehm, J.-H.; Hasselhorn, M.; Lonnemann, J. Gender differences in children’s math self-concept in the first years of elementary school. J. Educ. Learn. 2013, 2, 1–8. [Google Scholar] [CrossRef]
- Oppermann, E.; Vinni-Laakso, J.; Juuti, K.; Loukomies, A.; Salmela-Aro, K. Elementary school students’ motivational profiles across Finnish language, mathematics and science: Longitudinal trajectories, gender differences and STEM aspirations. Contemp. Educ. Psychol. 2021, 64, 101927. [Google Scholar] [CrossRef]
- Hannula, M.S.; Holm, M.E. Oppilaan matematiikkakuva oppimistuloksena ja oppimisen taustatekijänä. In Matematiikan Opetus ja Oppiminen; Joutsenlahti, J., Silfverberg, H., Räsänen, P., Eds.; Niilo Mäki Instituutti: Jyväskylä, Finland, 2018; pp. 132–155. [Google Scholar]
- Kaleva, S.; Pursiainen, J.; Hakola, M.; Rusanen, J.; Muukkonen, H. Students’ reasons for STEM choices and the relationship of mathematics choice to university admission. Int. J. STEM Educ. 2019, 6, 43. [Google Scholar] [CrossRef]
- Kupari, P.; Nissinen, K. Background factors behind mathematics achievement in Finnish education context: Explanatory models based on TIMSS 1999 and TIMSS 2011 data. In Proceedings of the 5th IEA international research Conference, Singapore, 26–28 June 2013; Available online: www.iea.nl/irc-2013.html (accessed on 2 July 2023).
- Marks, G.N.; Cresswell, J.; Ainley, J. Explaining Socioeconomic inequalities in student achievement. The role of home and school factors. Educ. Res. Eval. 2006, 12, 105–128. [Google Scholar] [CrossRef]
- Leino, K.; Ahonen, A.; Hienonen, N.; Hiltunen, J.; Lintuvuori, M.; Lähteinen, S.; Lämsä, J.; Nissinen, K.; Nissinen, V.; Puhakka, E.; et al. PISA18 Ensituloksia. Suomi Parhaiden Joukossa; Opetus- ja Kulttuuriministeriön Julkaisuja: Helsinki, Finland, 2019; Volume 40, Available online: http://urn.fi/URN:ISBN:978-952-263-678-2 (accessed on 2 July 2023).
- Salmela-Aro, K.; Chmielewski, A.K. Socioeconomic Inequality and Student Outcomes in Finnish Schools. In Socioeconomic Inequality and Student Outcomes; Education Policy & Social Inequality; Volante, L., Schnepf, S., Jerrim, J., Klinger, D., Eds.; Springer: Singapore, 2019; Volume 4. [Google Scholar] [CrossRef]
- Lehti, H.; Laaninen, M. Perhetaustan yhteys oppimistuloksiin Suomessa PISA-ja rekisteriaineistojen valossa. Yhteiskuntapolitiikka 2021, 86, 520–532. Available online: https://urn.fi/URN:NBN:fi-fe2021112456889 (accessed on 2 July 2023).
- Rautopuro, J.; Nissinen, K. Näkökulmia Perusopetuksen Tasa-Arvoon. Statement Issued for Clarification. 2021. Available online: https://api.hankeikkuna.fi/asiakirjat/e57d8e02-1729-464d-8610-6178679904f8/79558e04-1ee4-4d84-bb63-90e6b7466c10/KIRJE_20210128093639.PDF (accessed on 2 July 2023).
- Marks, G.N. Education, Social Background and Cognitive Ability: The Decline of the Social; Routledge: New York, NY, USA, 2015. [Google Scholar]
- Hattie, J. Visible Learning: A Synthesis of over 800 Meta-Analyses Relating to Achievement, 1st ed.; Routledge: New York, NY, USA, 2008. [Google Scholar] [CrossRef]
- APA. Report of the APA Task Force on Socioeconomic Status; American Psychological Association: Washington, DC, USA, 2007; Available online: https://www.apa.org/pi/ses/resources/publications/task-force2006.pdf (accessed on 2 July 2023).
- Bradley, R.H.; Corwyn, R.F. Socioeconomic Status and Child Development. Annu. Rev. Psychol. 2002, 53, 371–399. [Google Scholar] [CrossRef]
- Ouakrim-Soivio, N.; Kuusela, J. Historian ja Yhteiskuntaopin Oppimistulokset Perusopetuksen Päättövaiheessa 2011; Koulutuksen Seurantaraportit; Opetushallitus: Helsinki, Finland, 2012; Volume 3. [Google Scholar]
- Hildén, R.; Rautopuro, J. Ruotsin Kielen a-Oppimäärän Oppimistulokset Perusopetuksen Päättövaiheessa 2013; Kansallinen Koulutuksen Arviointikeskus: Helsinki, Finland, 2014; Volume 1. [Google Scholar]
- Robinson, K.; Harris, A. The Broken Compass: Parental Involvement with Children’s Education; Harvard University Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Salminen, J.; Lehti, H. Parental background and daughters’ and sons’ educational outcomes—Application of the Trivers-Willard hypothesis. J. Biosoc. Sci. 2023, 6, 1–20. [Google Scholar] [CrossRef] [PubMed]
- Lakin, J.M.; Wai, J. Spatially gifted, academically inconvenienced: Spatially talented students experience less academic engagement and more behavioural issues than other talented students. Br. J. Educ. Psychol. 2020, 90, 1015–1038. [Google Scholar] [CrossRef] [PubMed]
- Tran, B.T.N.; Wai, J.; McKenzie, S.; Mills, J.; Seaton, D. Expanding Gifted Identification to Capture Academically Advanced, Low-Income, or Other Disadvantaged Students: The Case of Arkansas. J. Educ. Gift. 2022, 45, 64–83. [Google Scholar] [CrossRef]
- Wai, J.; Putallaz, M.; Makel, M.C. Studying intellectual outliers: Are there sex differences, and are the smart getting smarter? Curr. Dir. Psychol. Sci. 2012, 21, 382–390. [Google Scholar] [CrossRef]
- Heller, K.A. Findings from the Munich longitudinal study of giftedness and their impact on identification, gifted education and counseling. Talent. Dev. Excell. 2013, 5, 51–64. Available online: https://gwern.net/doc/iq/high/munich/2013-heller.pdf (accessed on 26 July 2023).
- Opetushallitus. Lukion Opetussuunnitelman Perusteet 2003. Nuorille Tarkoitetun Lukiokoulutuksen Opetussuunnitelman Perusteet; Määräys 33/011/2003; Opetushallitus: Helsinki, Finland, 2003. [Google Scholar]
- Opetushallitus. Perusopetuksen Opetussuunnitelman Perusteet 2004; Opetushallitus: Helsinki, Finland, 2004. [Google Scholar]
- Opetushallitus. Ammatillisen Perustutkinnon Perusteet. Lapsi- ja Perhetyön Koulutusohjelma/Osaamisala; Määräys 18/011/2009; Opetushallitus: Helsinki, Finland, 2009. [Google Scholar]
- Jakku-Sihvonen, R. Oppimistulosten arviointijärjestelmästä ja niiden kehittämishaasteista. In Oppimisen Arvioinnin Kontekstit ja Käytännöt; Räisänen, A., Ed.; Raportit ja Selvitykset; Opetushallitus: Helsinki, Finland, 2013; Volume 3, pp. 13–36. [Google Scholar]
- Metsämuuronen, J. Metodit Arvioinnin Apuna. Perusopetuksen Oppimistulos-Arviointien ja-Seurantojen Menetelmäratkaisut Opetushallituksessa; Oppimistulosten arviointi 1/2009; Opetushallitus: Helsinki, Finland, 2009. [Google Scholar]
- Rasch, G. Probabilistic Models for Some Intelligence and Attainment Tests; Studies in Mathematic Psychology, I. Nielsen & Lydiche; Danmarks Pædagogishe Institut: Copenhagen, Denmark, 1960. [Google Scholar]
- Lord, F.M.; Novick, M.R. Statistical Theories of Mental Test Scores; Addison-Wesley: Boston, MA, USA, 1968. [Google Scholar]
- Fennema, E.; Sherman, J. Fennema-Sherman Mathematics Attitudes Scales: Instruments designed to measure attitudes toward the learning of mathematics. J. Res. Math. Educ. 1976, 7, 324–326. [Google Scholar] [CrossRef]
- Metsämuuronen, J. Challenges of the Fennema-Sherman Test in the International Comparisons. Int. J. Psychol. Stud. 2012, 4, 1. [Google Scholar] [CrossRef]
- Pedhazur, E. Multiple Regression Analysis in Behavioral Research; Holt, Rinehart and Winston: New York, NY, USA, 1982. [Google Scholar]
- Metsämuuronen, J. Tutkimuksen Tekemisen Perusteet Ihmistieteissä: Tutkijalaitos, 1st ed.; International Methelp: San Francisco, CA, USA, 2011. [Google Scholar]
- Tabachnick, B.G.; Fidell, L.S. Using Multivariate Statistics, 5th ed.; Pearson: Boston, MA, USA, 2007. [Google Scholar]
- Hosmer, D.W.; Lemenshow, S.; Sturdivant, R.X. Applied Logistic Regression, 3rd ed.; Wiley: New York, NY, USA, 2013. [Google Scholar]
- Nagelkerke, N.J.D. A note on a general definition of the coefficient of determination. Biometrika 1991, 78, 691–692. [Google Scholar] [CrossRef]
- Rita, H. Vetosuhde (odds ratio) ei ole todennäköisyyksien suhde. Metsätieteen Aikakauskirja 2004, 2, 207–212. [Google Scholar] [CrossRef]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences, 2nd ed.; Erlbaum: Hillsdale, NJ, USA, 1988. [Google Scholar]

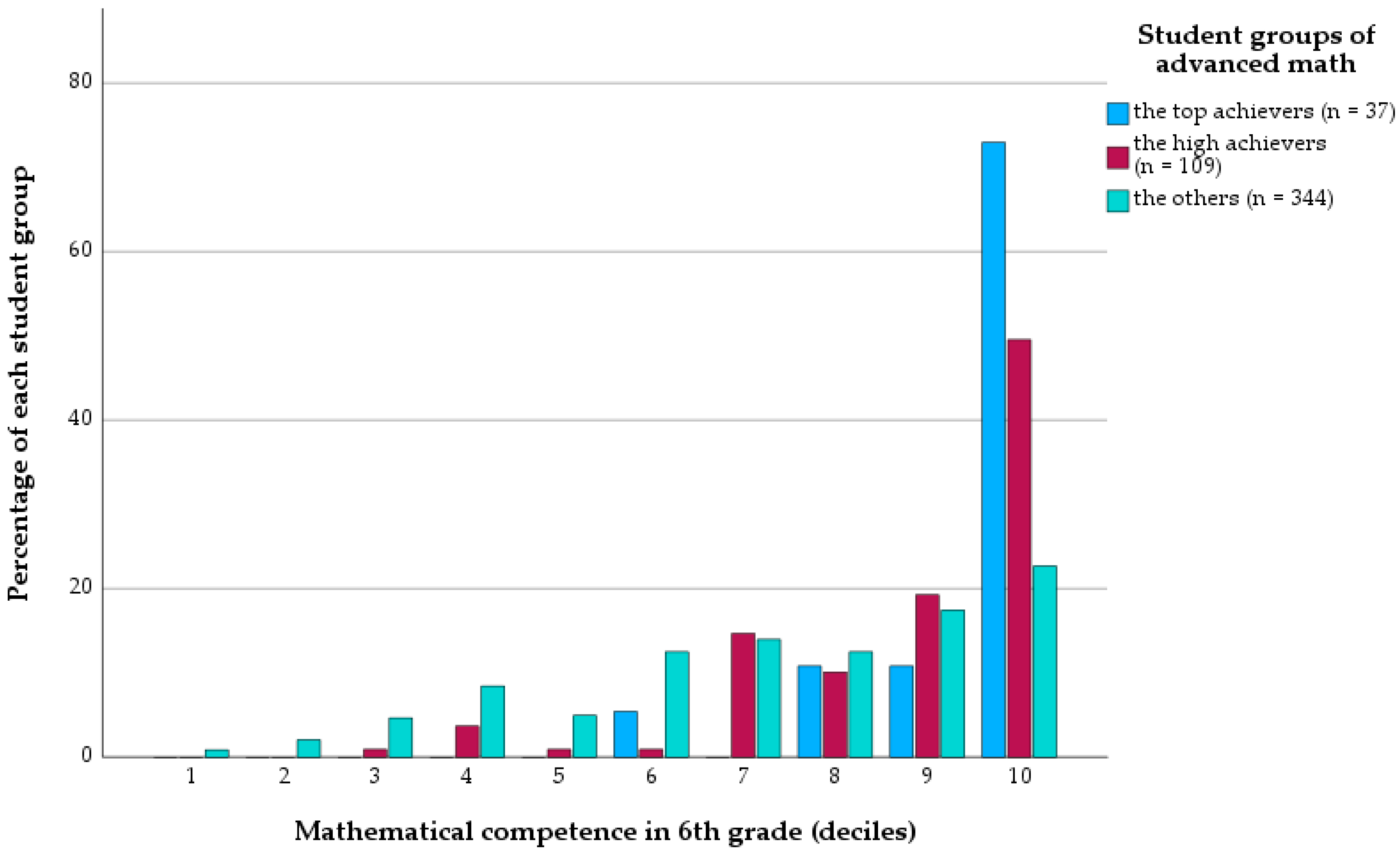
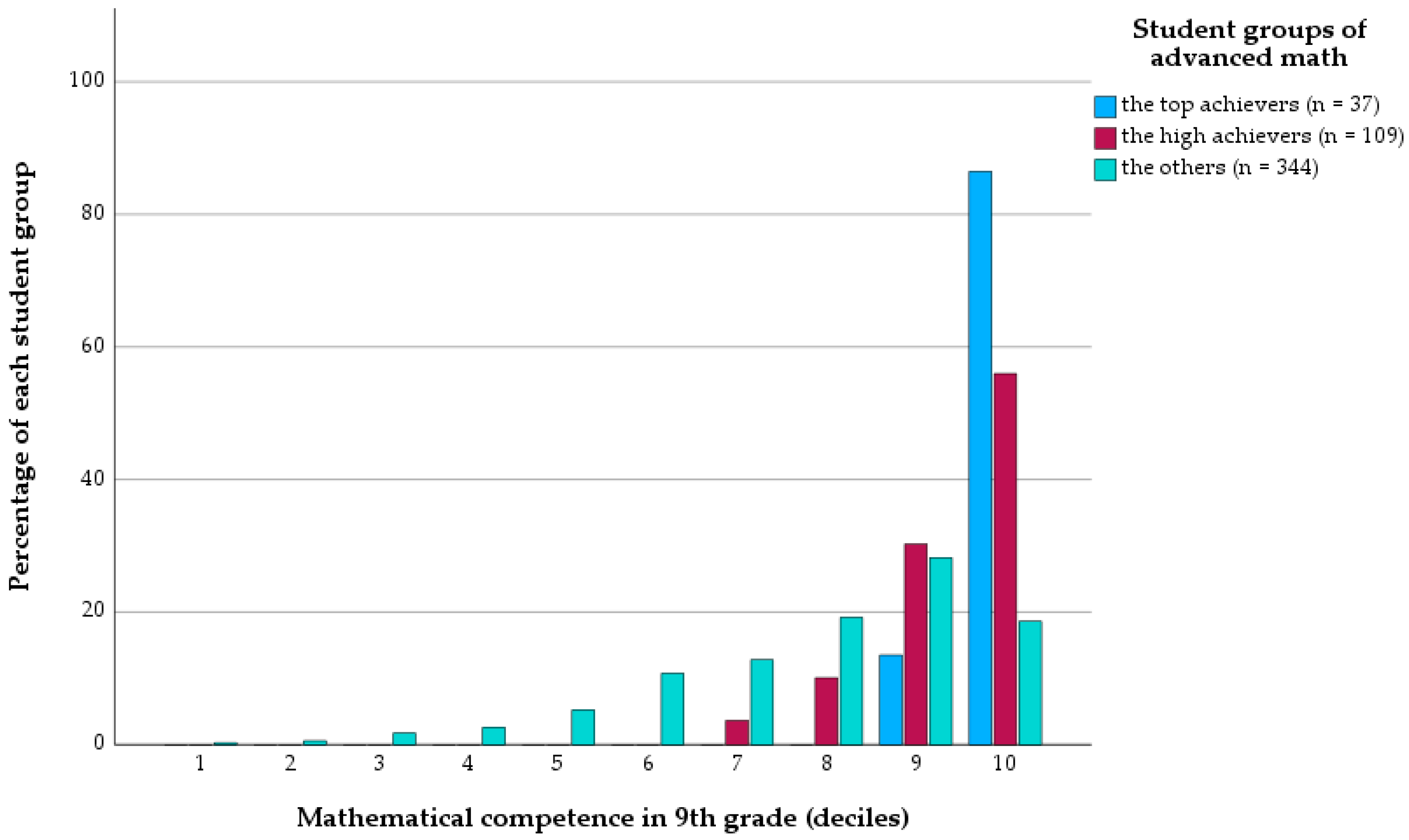
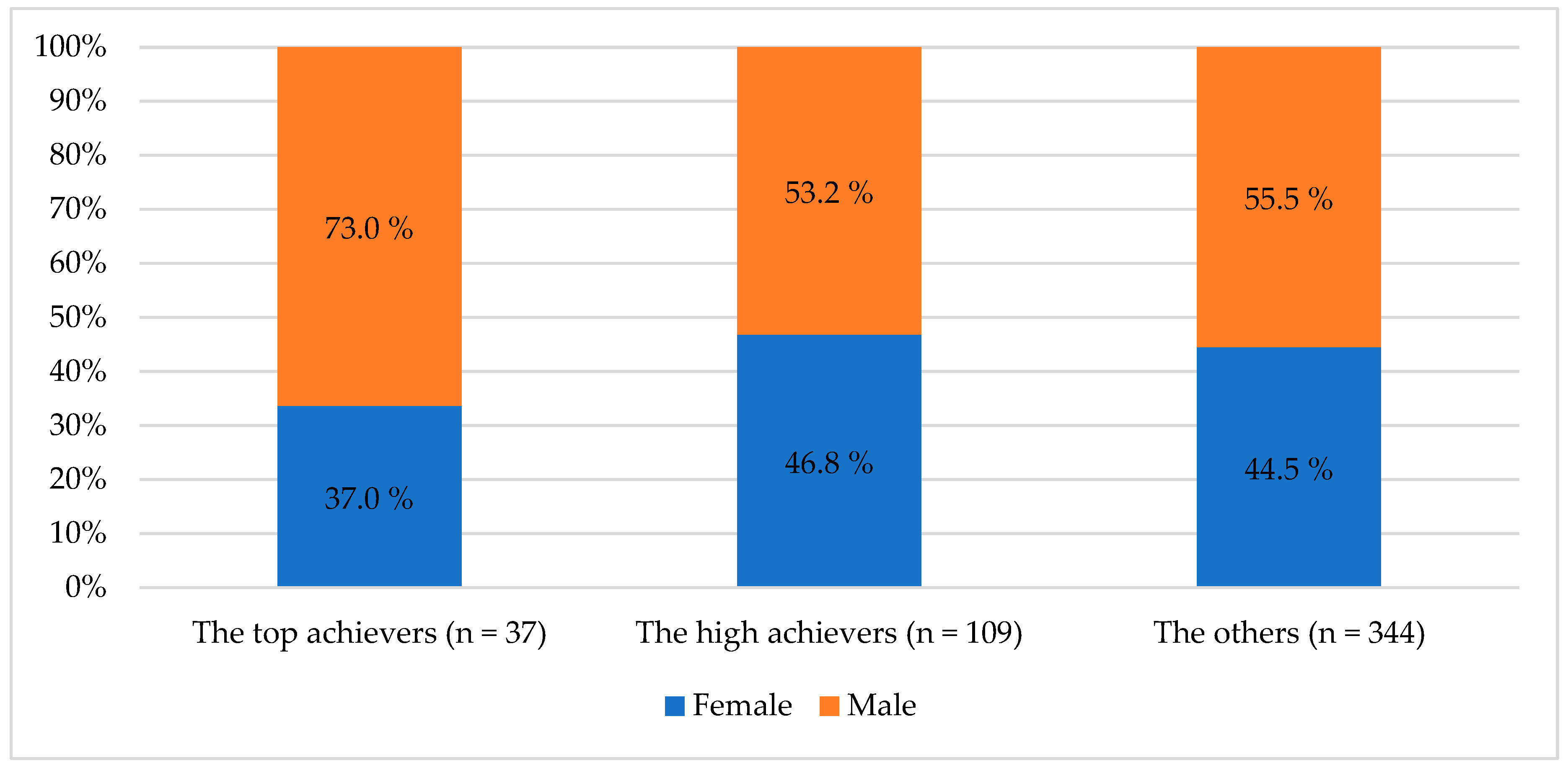
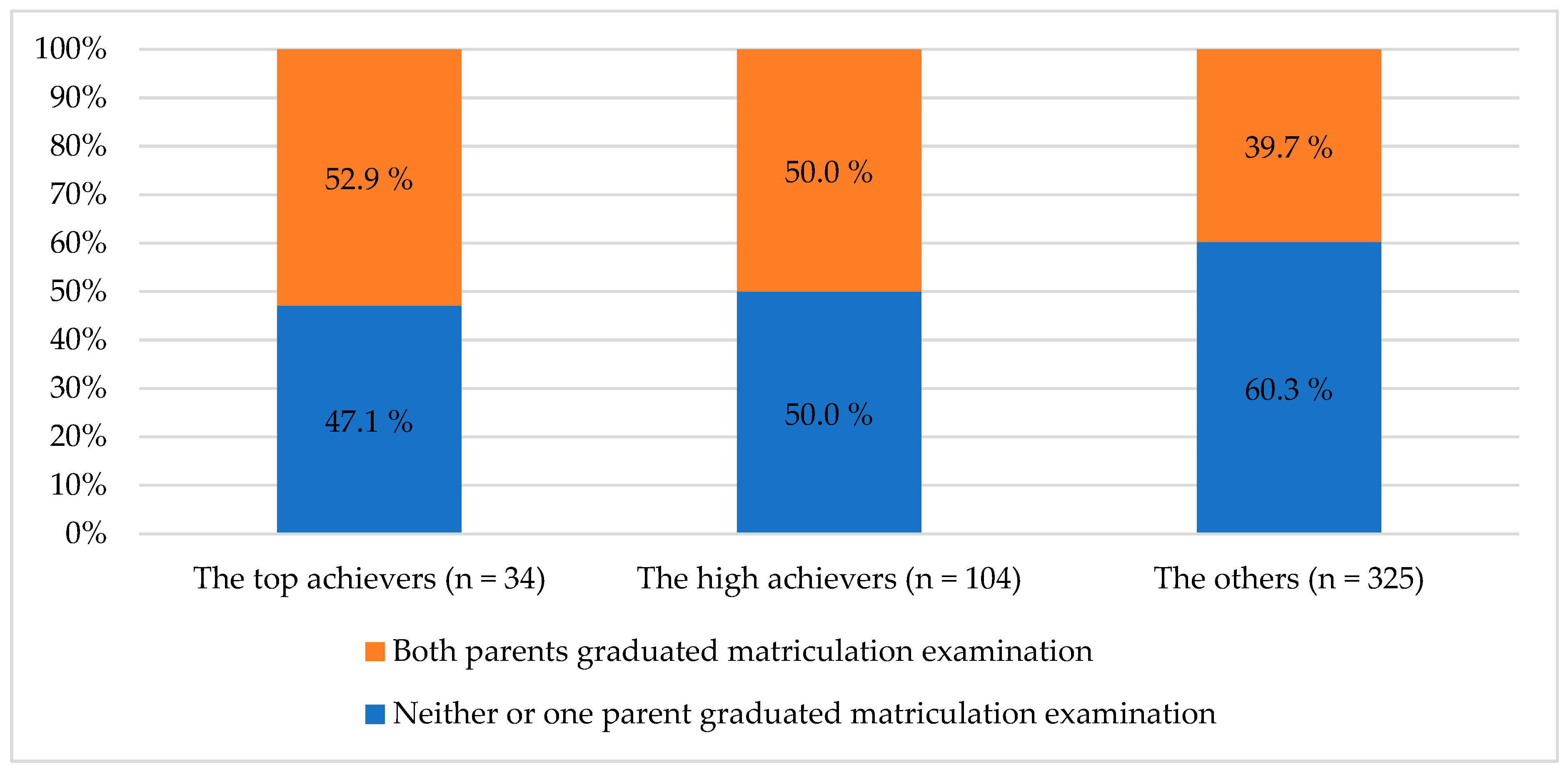
| Grade | Number of Items | Maximum Raw Score | Reliability (α) | |
|---|---|---|---|---|
| Overall mathematical competence | 3rd | 38 | 44 | 0.86 |
| 6th | 39 | 52 | 0.85 | |
| 9th | 68 1 | 84 1 | 0.94 | |
| General upper secondary school | 29 | 52 | 0.87 | |
| Vocational upper secondary school | 33 | 46 | 0.84 | |
| Numbers, calculations, and algebra | 3rd | 22 | 24 | 0.81 |
| 6th | 21 | 28 | 0.78 | |
| 9th | 36 | 40 | 0.88 | |
| General upper secondary school | 3 | 3 | 0.27 | |
| Vocational upper secondary school | 3 | 3 | 0.26 | |
| Geometry | 3rd | 10 | 14 | 0.67 |
| 6th | 10 | 14 | 0.66 | |
| 9th | 16 | 22 | 0.83 | |
| General upper secondary school | 7 | 14 | 0.73 | |
| Vocational upper secondary school | 7 | 14 | 0.65 | |
| Data processing, statistics, and probability | 3rd | 6 | 6 | 0.55 |
| 6th | 8 | 10 | 0.47 | |
| 9th | 7 | 9 | 0.61 | |
| General upper secondary school | 2 | 2 | 0.34 | |
| Vocational upper secondary school | 5 | 5 | 0.56 | |
| Algebra | General upper secondary school | 6 | 8 | 0.71 |
| Vocational upper secondary school | 6 | 8 | 0.71 | |
| Functions | General upper secondary school | 11 | 31 | 0.82 |
| Vocational upper secondary school | 12 | 22 | 0.66 |
| Grade | Number of Items | Maximum Score | Reliability (α) | |
|---|---|---|---|---|
| Overall attitude toward mathematics 1 | 3rd | 8 | 32 | 0.86 |
| 6th | 15 | 60 | 0.88 | |
| 9th | 15 | 60 | 0.91 | |
| General upper secondary school | 15 | 60 | 0.92 | |
| Vocational upper secondary school | 15 | 60 | 0.91 | |
| Self-concept | 3rd | 4 | 16 | 0.79 |
| 6th | 5 | 20 | 0.82 | |
| 9th | 5 | 20 | 0.88 | |
| General upper secondary school | 5 | 20 | 0.86 | |
| Vocational upper secondary school | 5 | 20 | 0.87 | |
| Liking mathematics | 3rd | 4 | 16 | 0.88 |
| 6th | 5 | 20 | 0.89 | |
| 9th | 5 | 20 | 0.90 | |
| General upper secondary school | 5 | 20 | 0.92 | |
| Vocational upper secondary school | 5 | 20 | 0.91 | |
| Usefulness of mathematics | 6th | 5 | 20 | 0.81 |
| 9th | 5 | 20 | 0.53 | |
| General upper secondary school | 5 | 20 | 0.83 | |
| Vocational upper secondary school | 5 | 20 | 0.83 |
| Variable | B | S.E. | Exp(B) | p | Percentage of Correct Answers (Top Achievers/High Achiever/Others) |
|---|---|---|---|---|---|
| Addition task with crossing hundreds | 1.61 | 0.76 | 4.98 | 0.034 | 93.5%/76.5%/79.0% |
| Conceptual and abstract understanding of geometric concepts: line segment and infinite | 1.55 | 0.51 | 4.73 | 0.002 | 83.9%/55.1%/50.9% |
| Pre-algebra, missing number task (a · b = c +__) | 1.32 | 0.51 | 3.72 | 0.010 | 83.9%/68.4%/49.5% |
| Conceptual and visual understanding of geometry | 1.07 | 0.40 | 2.92 | 0.007 | 61.3%/45.9%/27.5% |
| Constant | −6.44 | 0.98 | 0.002 | <0.001 |
| Variable | B | S.E. | Exp(B) | p | Percentage of Correct Answers (Top Achievers/High Achiever/Others) |
|---|---|---|---|---|---|
| Understanding of mean, multiple choice | 2.01 | 1.03 | 7.46 | 0.05 | 97.3%/84.4%/70.0% |
| Understanding of complementary event in probability, multiple choice | 2.01 | 1.03 | 7.46 | 0.05 | 97.3%/80.7%/70.8% |
| Choosing the correct unit of measure | 1.11 | 0.50 | 3.05 | 0.03 | 86.5%/71.6%/53.9% |
| Conceptual and visual understanding of geometry (same task as in the 3rd grade test) | 1.09 | 0.55 | 2.97 | 0.05 | 89.2%/78.0%/62.5% |
| Quotative division task, mental math | 0.76 | 0.38 | 2.13 | 0.05 | 67.6%/54.1%/32.7% |
| Constant | −8.21 | 1.51 | 0.00 | <0.001 |
| Variable | B | S.E. | Exp(B) | p | Percentage of Correct Answers (Top Achievers/High Achiever/Others) |
|---|---|---|---|---|---|
| Area of trapezium | 2.45 | 1.04 | 11.53 | 0.02 | 97.1%/76.4%/51.4% |
| Estimating and computing powers | 2.12 | 0.75 | 8.32 | 0.01 | 94.1%/59.4%/53.8% |
| Problem solving with equations and multiple steps | 2.03 | 0.48 | 7.63 | <0.001 | 83.8%/41.3%/24.1% |
| Geometric task with volume (problem solving) | 1.56 | 0.77 | 4.77 | 0.04 | 94.6%/78.0%/59.3% |
| Constant | −8.75 | 1.41 | 0.00 | <0.001 |
| Variable | B | S.E. | Exp(B) | p | Mean of Attitude (1–5) (Top Achievers/High Achievers/Others) |
|---|---|---|---|---|---|
| Self-concept | 0.07 | 0.02 | 1.07 | <0.001 | 4.6/4.3/4.1 |
| Constant | −8.30 | 1.50 | 0.00 | <0.001 |
| Variable | B | S.E. | Exp(B) | p | Mean of Attitude (1–5) (Top Achievers/High Achievers/Others) |
|---|---|---|---|---|---|
| “I can solve even difficult math tasks.” | 0.84 | 0.29 | 2.32 | 0.004 | 4.5/4.0/3.9 |
| “Math is one of my favorite subjects.” | 0.38 | 0.16 | 1.39 | 0.037 | 4.1/3.5/3.2 |
| Constant | −7.29 | 1.31 | 0.001 | <0.001 |
| Variable | B | S.E. | Exp(B) | p | Mean of Attitude (1–5) (Top Achievers/High Achievers/Others) |
|---|---|---|---|---|---|
| Self-concept | 0.03 | 0.01 | 1.03 | 0.030 | 4.4/4.3/4.0 |
| Constant | −4.88 | 1.12 | 0.01 | <0.001 |
| Variable | B | S.E. | Exp(B) | p | Mean of Attitude (1–5) (Top Achievers/High Achievers/Others) |
|---|---|---|---|---|---|
| “I think I am good at math.” | 0.98 | 0.33 | 2.66 | 0.003 | 4.7/4.5/4.1 |
| Constant | −6.87 | 1.55 | 0.001 | <0.001 |
| Top-Achieving Boys/Girls | High-Achieving Boys/Girls | Other Boys/Girls | |
|---|---|---|---|
| The highest decile in 3rd grade (n = 135) | 10.4%/4.4% | 21.5%/11.9% | 31.1%/20.7% |
| The highest decile in 6th grade (n = 159) | 12.6%/4.4% | 21.4%/12.6% | 34.0%/15.1% |
| The highest decile in 9th grade (n = 157) | 14.6%/5.7% | 24.2%/14.6% | 27.4%/13.4% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niemi, L.; Metsämuuronen, J.; Hannula, M.S.; Laine, A. Top Achievers in Mathematics in the End of Upper Secondary School. Educ. Sci. 2023, 13, 775. https://doi.org/10.3390/educsci13080775
Niemi L, Metsämuuronen J, Hannula MS, Laine A. Top Achievers in Mathematics in the End of Upper Secondary School. Education Sciences. 2023; 13(8):775. https://doi.org/10.3390/educsci13080775
Chicago/Turabian StyleNiemi, Laura, Jari Metsämuuronen, Markku S. Hannula, and Anu Laine. 2023. "Top Achievers in Mathematics in the End of Upper Secondary School" Education Sciences 13, no. 8: 775. https://doi.org/10.3390/educsci13080775
APA StyleNiemi, L., Metsämuuronen, J., Hannula, M. S., & Laine, A. (2023). Top Achievers in Mathematics in the End of Upper Secondary School. Education Sciences, 13(8), 775. https://doi.org/10.3390/educsci13080775







