Abstract
Students with learning disabilities/difficulties in mathematics often apply ineffective procedures to solve word problems due to a lack of conceptual understanding of word problem solving, which results in poor mathematics performance and falling further behind the normal achievements of their peers. Current mathematics curriculum standards emphasize conceptual understanding in problem solving as well as higher-order thinking and reasoning, including all students. The purpose of this study was to evaluate the impact of a computer-assisted model-based problem-solving intervention program (MBPS) on elementary students’ word problem-solving performance by analyzing the error patterns. Results indicate that after the MBPS intervention, participants significantly improved their problem-solving performance and made fewer errors in solving problems across a range of additive word problem situations. Specifically, the participating students made their attempt to represent the mathematical relation, decontextualized from the word problem story, in the model equation before solving the problem, rather than blindly applying an operation or relying on the “keyword” strategy as they did during the preassessment. Implications of the study are discussed in the context of the National Council of Teachers of Mathematics’ calling for teaching big ideas to help students develop a deep understanding of mathematics knowledge.
1. Introduction
According to the Nation’s Report Card [1], the mathematics scores of all students declined when compared to 2020. Particularly, lower-performing students exhibited greater achievement decline than their average- or high-performing peers based on 2022 long-term trend mathematics assessments for age 9 students. Currently, the majority (84%) of American 4th graders with disabilities performed below the proficiency level. By 8th grade, 93% of the students with disabilities performed below the Proficiency level [1]. In fact, students with learning disabilities or difficulties in mathematics (LDM) lag well behind their peers from very early on in their educational trajectory; they often continue to fall further behind as they transition from elementary to secondary schools [2]. In this study, LDM is defined as students who were receiving Tier II or Tier III support in the context of the Multi-Tiered Systems of Support (MTSS, https://mtss4success.org, accessed on 30 May 2023). These findings present a pressing issue for all teachers and educators because legal mandates (e.g., Every Student Succeeds Act [3]) and current standards (e.g., Common Core State Standards Initiative [CCSSI] [4]; National Council of Teacher of Mathematics [NCTM] [1]) require that all students, including students with LDM, in the US be taught to high academic standards that will prepare them to succeed in college and careers. As mathematical problem solving is an important part of school mathematics [5], it is imperative that all students achieve proficiency in word problem solving.
Students with LDM often treat word problems mechanically and apply ineffective procedures, such as searching for keywords to identify the operation. That is, they focus on whether to add, subtract, multiply, or divide rather than whether or how the problem makes sense. When encountering a word problem, they often just grab the numbers in the problem and apply an operation without comprehending the problem and understanding the mathematical relations in the word problem [6]. In fact, research in mathematical education (e.g., [7]) has documented some pre-matured strategies many elementary students use. For instance, “look at the numbers; they will tell you which operations to use. Try all the operations and choose the most reasonable answer......” [8] (p. 285). For instance, if the students saw a big number and a small number in the problem (e.g., Emily has 15 marbles, the number of marbles she has is 3 less than Jen, how many marbles does Jen have?), the students would often apply a subtraction (subtract the small number from the big number) to get a “good-sized” number (12) as the answer. Plus, the keyword “less” in the problem would “cue” the operation of subtract. Clearly, this solution plan was not based on a holistic understanding of the word problem and the mathematical relations described in the problem. Rather, it was relying on “gambling” on the operational sign to solve the problem.
On the other hand, NCTM (2000) [9] and Common Core State Standards (CCSSI, 2012) [4] both emphasize mathematical thinking and reasoning. Specifically, NCTM is calling for teaching “big ideas”, defined as “mathematical statements of overarching concepts that are central to a mathematical topic and link numerous smaller mathematical ideas into a coherent whole” [10] (p. 9). Mathematical big ideas draw students’ attention to fundamental concepts, link small facts/ideas together, and connect previously learned ideas to new concepts. As such, teaching big ideas can help students develop a deep understanding of mathematics knowledge [10].
1.1. Theoretical Framework in Mathematical Word Problem Solving
According to the existing literature in mathematics education [11,12], the semantic structure of the word problem significantly influences problem solving strategies in young children. Children apply a range of addition and subtraction strategies even before formal education in elementary school. Therefore, it is suggested that early mathematics education pays attention to the selection or construction of elementary arithmetic word problems. That is, it is preferred that the problems present in the textbook would reinforce the use of children’s pre-existing knowledge or make that knowledge useful and necessary. As such, there is a significant amount of research in the psychology of mathematics education and, recently, in the field of special education promoting the instruction or intervention that focuses on semantic analyses of word problems [5].
One extreme example of the use of semantics or words in word problem stories to teach elementary mathematical problem solving was the “keyword” strategy. The “keyword” strategy specifically focused on finding the keyword and translating the keyword into an operation sign for the solution [13]. For instance, students were taught that if you see words such as “altogether” or “more” in the word problem, addition would be the choice of operation for the solution. Likewise, students were taught that if you see words such as “take away” or “less”, then subtraction should be the choice of operation for the solution. Consequently, the keyword strategy directs students’ attention toward isolated keywords (e.g., “Together”) for making a decision about the operation for the solution without first comprehending the entire word problem. This emphasis on the decision making of the operation sign in word problem solving corroborates the operational paradigm described by researchers in mathematics education (e.g., [14]).
On the other hand, scholars in mathematics education [15,16] pointed out that focusing on the operation (e.g., whether to “add” or “subtract”) relevant to the calculation is likely to distract learners from mathematical relations depicted in the word problem. In fact, it is the mathematical relation on which the mathematical model is conceptualized that contributes to generalized problem solving [17]. In contrast to the operational paradigm, the relational paradigm promotes the idea that it is the mathematical relationship that constitutes the conceptual basis for problem solving [14]. The focus is NOT on identifying isolated keywords in the problem; rather, the learners need to read the entire word problem story for comprehension and, more importantly, discover the mathematical relations in the word problem. Then, it is the mathematical relation that will drive the solution planning, including the decision-making on the choice of operation for solving for the answer. This is consistent with the National Council of Teachers of Mathematics (NCTM) emphasis on teaching mathematical big ideas through making connections between smaller, more specific, interconnected ideas [10].
1.2. Difficulties Experienced by Students with LDM in Solving Word Problems
Error analysis is an assessment tool to help understand student knowledge gaps and, therefore, design instructions that address student misconceptions and help build word problem solving based on conceptual understanding [18]. Back in 1993, Jaspers and Liehshout [19] conducted a study to determine the specific errors of elementary and middle school students with disabilities in word problem solving. A total of 66 students with learning disability from 4th grade to 7th grade who had sufficient reading and arithmetic computation performance determined by a pretest were selected to participate in the study. Ten alternative/equivalent tests, each had seven inconstant language [20] word problem situations (e.g., “Ellen ran 62 miles in one month. Ellen ran 29 fewer miles than her friend named Cooper. How many miles did Cooper run?” where the keyword “fewer” in the problem is not consistent with the operation, adding, required for accurate solution), including three change problem types (please refer to Table 2 under the section “Measures,” similar sample problems are marked as Change3, Change5, and Change6), one combine problem (marked as Combine2 in Table 2), and three additive compare problems (marked as Compare1, Commpare5, and Compare6 in Table 2) were used as the dependent measure for the repeated measure analysis. Student errors were classified into the following categories, (a) “one number” (take one of the numbers from the problem as the answer), (b) “add-all” (add all the numbers in the problem), (c) “subtract -all” (subtract small numbers from the larger number), (d) “wrong-operation” (used incorrect operation), (e) no answer or an answer of zero, (f) “irrelevant added” or “irrelevant subtracted” (irrelevant numbers were added to or subtracted from the relevant numbers, and (g) others (other unclassified answers) [19] (p. 12).
The results of a repeated measures ANOVA indicated that fourth-grade Dutch school students with disabilities mostly just picked the number from the problem as the answer, and children in the fifth grade mostly used irrelevant information in their operation for the answer. The sixth-grade students with disabilities committed a lot of reversal (incorrect) operation errors on Compare5 (comparison problems involving the phrase “more than” however required an operation of subtraction) and Compare6 problem types (comparison problems involving the phrase “less than” however required an operation of addition), so-called “inconsistent language” problem types [20] or referent unknown problem types (Author, 2007; see sample problems in Table 2). It seems that the students used keywords (“more” indicates “add,” “less” indicates “subtract”) in making the decision on the operation, resulting in incorrect answers. Because the items included in the test were purposefully designed to include only inconsistent language problems, the study was able to detect improper or premature strategies the participating students used in solving additive word problems.
More recently, Powell et al. [21] conducted an analysis of the strategies used or errors made by third graders with mathematics difficulties in solving additive word problems. The error analysis study was conducted in the context of a group comparison study, where an experimental group who received “PMEQ” intervention (a supplemental intervention program in addition to the regular mathematics instruction) was compared to the performance of the business as usual (BAU) group who only received regular mathematics instruction. The intervention program (PMEQ) was a combination of “Pirate Math” [PM]) and “Equation Quest” [EQ]. “Pirate Math” focused on students’ identification and differentiation of three different additive word problem schemata. The three problem schemata include (a) total problems (or combine problems) with a corresponding equation of “P1 + P2 = Total”, (b) difference problems (or compare problems) with a corresponding equation of “Amount that is greater -Amount that is less = Difference”, and (c) change problems (change–join or change–separate) with a corresponding equation of “Start amount +/− Change amount = End amount” (pp. 6–7). The “Equation Quest” [EQ] part of the intervention focused on students’ understanding of the equal sign and solving equations (p. 58). The PMEQ intervention lasted for 16 weeks (three times a week, with each session lasting for about 30 min). After the intervention, it was found that the PMEQ group outperformed the BAU group on a double-digit word problem-solving test.
The error analysis study [21] focused on the analysis of the strategies used or errors made by 15 students (randomly selected from 51 students) in the PMEQ group and 15 students (randomly selected from 60 students) in the BAU group. Following the PMEQ intervention, it was found that 10 out of 15 (66.7%) students solved the total problem correctly. Among the ten students who solved the problem correctly, eight students (out of 10) identified the problem as the total problem schema; however, the other two students who solved the problem correctly (by adding two numbers) identified the problem as the difference problem schema which would call for the subtraction of two numbers. The mismatch between the schema identification and the choice of operation seems to indicate that the solution plan, including the operation use, might not be associated with the schema defined by the researchers.
In addition, eight out of fifteen students (53.3%) solved the difference problem correctly, of which seven students (47%) correctly identified the problem schema. Four students misidentified the problem as a total problem and therefore solved the problem incorrectly. One student identified the problem as a change problem, which would call for an operation of subtraction, but solved the problem by adding the two numbers together. As for the change problem type, seven out of fifteen students (46.7%) solved the change problem correctly, of which six students (40%) correctly identified the problem schema. One student who correctly solved the problem by subtracting, however, identified the problem as the total problem schema, which would call for addition. Again, it seems that, for some students, correct problem solving or correct solution plan was not associated with the correct identification of the problem schema. The authors commented in their discussion that “we encouraged the use of another schema if the student could explain why he or she thought this problem was a Total problem” (p. 13). “In many cases, students were able to use another schema to solve a word problem.” (p. 11). Overall, the low rate of correct identification of the problem schema and the mismatch between the solution plan, including operation use and the identification of the schema, seems to indicate that (1) participating students had difficulty in identifying the schemata defined by the researchers, and (2) the identification of the specific schema (e.g., whether it is a total, difference, or change problem schema) may not be a necessary condition for accurate problem solving.
1.3. Model-Based Problem Solving That Empathizes Mathematical Relations
As the outcome of collaborative work from mathematics education and special education, we have developed, with the support from the National Science Foundation (NSF, [22]), a web-based computer tutor that emphasizes the teaching of big ideas in additive word problem solving. Specifically, the MBPS program emphasizes the nurturing of fundamental mathematical ideas, for instance, the conception of “number as a composite unit.” According to Steffe et al. [23], the concept of the composite unit is the primary cognitive structure that underlies a child’s conceptualization of all additive part–part–whole problem situations. When a number is conceived of as a composite unit, a child can join a unit of 3 and a unit of 4 to compose a larger unit of 7; they can also break or decompose 7 into 3 and 4 (or 1 and 6, 2 and 5, 4 and 3, 5 and 2, and 6 and 1). With this composing and decomposing scheme, the child will be able to understand the part–part–whole (PPW) conceptual model [24]. The MBPS computer tutor was designed to specifically support the development of number concepts such as the composite unit, which would naturally lead to the big idea in additive reasoning; that is, part and part makes up the whole (P + P = W). Students were not required to identify whether the problem fit a specific problem schema (e.g., combine, or change–join in, change–separate), and the decision on the operation was not determined by the identification of the specific problem schema. Rather it was determined by the mathematical model equation (P + P = W) and the correct representation of the mathematical relation in the model equation.
To facilitate students’ conceptual understanding of abstract mathematical ideas and their model expressions, the MBPS program integrates evidence-based practices that are consistent with the latest IES practice guide [25], including concrete, representational, and abstract instructional sequences, visual and linguistic support, and teaching of precise mathematical language. In the MBPS program, virtual manipulatives (such as unifix cubes and biscuits) were used for the counting activities. Linguistic and visual support was an integrated part of the MBPS program. For instance, Word Problem Story Grammar prompting questions [6,26] were used as a series of linguistic scaffolds to facilitate students’ representation of word problems in mathematical model equations (e.g., part + part = whole) for accurate problem solving. Visuals, including diagram equations anchored by specific “name tags”, were used to support student understanding of the part–part–whole (PPW) mathematical model equation and the representation of various word problem situations in the model equation. Empirical studies have shown the effectiveness of MBPS in improving students’ word problem solving performance [27,28,29,30].
Given the above empirical evidence of MBPS, there is a need to further understand the impact of the MBPS, which has a focus on mathematical relations rather than semantic analysis of word problem stories, on students’ conceptual understanding of additive mathematical relations and problem solving. Therefore, the purpose of this study was to analyze participating students’ error patterns when solving addition and subtraction word problems before and after the MBPS intervention. Error analysis is an assessment tool used to help provide more comprehensive data about learner misconceptions or knowledge gaps in mathematical learning, including basic skills, procedural knowledge, and conceptual understandings. Error analysis also assists in identifying areas of instructional needs [31]. In this study, we were trying to answer the following research questions:
- Is there any changes in the success rate and error pattern of third graders with LDM on solving a range of addition and subtraction word problems before and after the MBPS intervention program?
- Is there any differential pattern in students’ ability to solve consistent and inconstant language problems before and after the MBPS intervention program?
2. Method
2.1. Participants and Setting
This study was conducted within the larger context of the National Science Foundation funded projecti [22]. The participants included in this study were 13 third-graders with LDM from one elementary school in the mid-western United States. Table 1 presents the demographic information of the participants. Specifically, Table 1a presents demographic information of four students who were part of a multiple-baseline–across-participants design study (MB design, 2017–2018), who took multiple baseline tests (pretests) and multiple post-intervention tests following the MBPS intervention. Table 1b presents demographic information of nine students who were part of a group design study (2018–2019) and only took one pretest before the MBPS intervention and one posttest after the intervention.

Table 1.
Participant demographics.
2.2. Measures
To measure participating students’ performance before and after the intervention, we used a researcher-developed 14-item word problem-solving criterion test (Author et al., 2020). It involves eight part–part–whole problems (including combine, change/join-in, and change/separate story situations) with either the part or the whole as the unknown and six additive compare problems (including “more than…” or “less than…” story situations) with either the compared quantity, referent quantity, or the difference as the unknown. The criterion test was designed in alignment with the NCTM [9] and Common Core standards [4], which emphasize varying construction of word problems for assessing conceptual understanding of mathematics problem solving. Cronbach’s Alpha of the criterion test was 0.86, and the test–retest reliability was 0.93 [32]. Table 2 presents sample word problems included in the criterion Test.

Table 2.
Sample word problem situations in the criterion test.
As for scoring, one point was given if a correct answer was given to a problem. In the case that the answer to the problem was incorrect, however, the algorithm or model equation was correctly set up, half a point was awarded.
2.3. MBPS Intervention
MBPS is a web-based interactive tutoring program. Sessions were monitored by supervisors. The participants worked with the MBPS computer tutor “one-on-one” during the afterschool program, Monday through Thursday, for a total of about 18–20 sessions (varies across different individuals), with each session lasting for about 20 min. The session supervisor helped each of the participants log onto the MBPS computer tutor program at the beginning of each of the sessions. Then, the student followed the direction of the computer tutor and engaged in the activities in Modules A through C. Module A engaged students in a series of activities involving the use of virtual manipulatives, such as unfix cubes, to nurture fundamental mathematical ideas that are crucial for the development of additive reasoning and problem solving [33]. It focuses on students’ conception of “number as the composite unit” and conceptual understanding of part–part–whole relation. Module B engaged students in representing and solving various combine and change problem types (see Table 2 for problem types) using one cohesive mathematical model equation (part and part makes up the whole, or P + P = W). Module C engaged students in representing and solving a range of additive compare problems using the same model equation; however, the denotations of each of the elements in the PPW diagram equation were adapted to the problem situations accordingly. Name tags were used to help students anchor “who has more?” which would be the “bigger” quantity or the “whole,” and “who has less?” which would be the “smaller” quantity or the “part.” After solving the comparison problems, students were given opportunities to represent and solve mixed additive word problems to further strengthen students’ construction of the mathematical model, P + P = W, for generalized problem solving. Figure 1 presents sample screenshot of Module C. It should be noted that participants were not taught/required to code or sort problems to different schema types (i.e., change, combine, etc.).
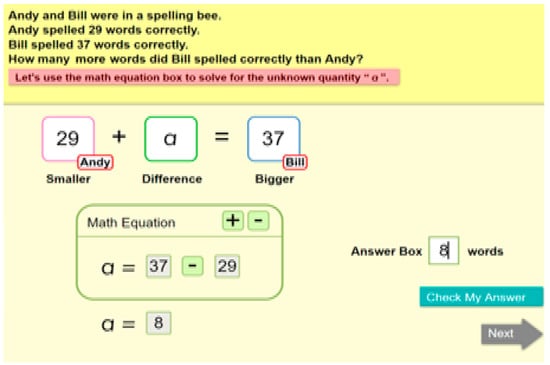
Figure 1.
Sample screenshot of Module C of the MBPS Tutor (© [22]). ©The screenshots presented in Figure 1 are copyrighted by the COMPS-RtI project (Xin et al., 2015). All rights reserved. Therefore, reproduction, modification, storage, in any form or by any means, is strictly prohibited without prior written permission from the Project Director Dr. Xin @yxin@purdue.edu.
3. Results
The purpose of this study was to explore the impact of the web-based MBPS computer tutor on students’ success rate or error patterns when solving a range of additive word problems. Specifically, we want to know what the changes were pertaining to student success rate or error pattern when solving a range of addition and subtraction word problems before and after MBPS instruction.
Due to the exploratory nature of the study and the small number of participants involved we used descriptive statistics supported by qualitative data to analyze the data and report the findings. To answer research question 1, “Is there any changes in the success rate and error pattern of third graders with LDM on solving a range of addition and subtraction word problems before and after the MBPS intervention program?”, we calculated the percentage of students who solved a specific problem correctly (i.e., item difficulty) using the group design study data involving nine students. We present students’ error patterns before and after the intervention across the 14 additive problem types in a bar graph. To answer research question 2, “Is there any differential patten in students’ ability to solve consistent and inconstant language problems before and after the MBPS intervention program?”, we calculated the percentage of problems solved correctly by each of the students using the data from both the MB design study involving four students as well as the group design study involving nine students. We present students’ performance, before and after the intervention, on solving consistent language problems or inconsistent language problems separately in line graphs. The next two sections report the findings answering each of the two research questions.
3.1. Success Rate and Error Pattern on Solving a Range of Additive Word Problems
Based on the data from the group design study [22], the participating students significantly improved their performance from an average of solving 5 (out of 14) problems correctly during the pretest to an average of solving about 10 problems correct on posttest. As the purpose of this specific study was on the error pattern or success rate of participating students in solving a range of additive word problems (a total of 14 variously constructed problems as shown in Table 2), Figure 2 presents the percentage of students who solved each of the problems correctly before and after the intervention (the problem type is noted at the bottom of the bars; please refer to Table 2 for the coding of each of the problem types).
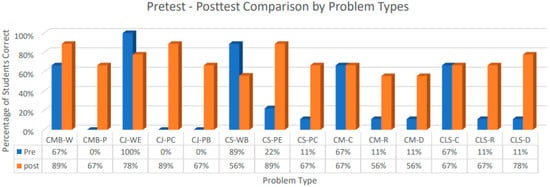
Figure 2.
Percentage of students correctly solved each of the problems before (in blue/dark color) and after (in orange/light color) the intervention.
As shown in Figure 2, after working with the MBPS tutor, participants made fewer errors in solving problems across a range of problem situations. Especially, students’ success rate dramatically improved in solving 10 out of 14 problems (71.4% of all problem situations). These problems are: combine with the whole or one of the parts as the unknown (CMB-W, CMB-P), change–join with the “change” amount as the unknown (CJ-PC), change–join with the beginning amount as the unknown (CJ-PB), change–separate with the ending amount or the change amount as the unmown (CS-PE, CS-PC), compare problems involving “more than” or “less than” with the “referent quantity” as the unknown (CM-R, CLS-R), compare problems with the “difference” as the unknown (CM-D, CLS-D).
Students’ success rates seemed to be kept the same when solving the two problem types. For one, the compare problem involves the phrase “...more than…” with the compared amount as the unknown (CM-C), and the correct operation for solving the problem is adding. The other problem situation is the compare problem involving the phrase “... less than …” with the compared amount as the unknown (CLS-C), and the correct operation for solving the problem is subtracting. Both are the “consistent language” problem type in which the keyword strategy would do the trick. In addition, it seems that the success rate declined in solving the following two problem situations: (a) change–join, ending total (whole) as the unknown (CJ-WE), and (b) change–separate, beginning amount (whole) as the unknown (CS-WB) (please refer to Table 2 for sample problems along with the coding). Both problem types require adding the two given numbers to get the answer, the total or “whole.”
3.2. Performance in Solving Consistent and Inconsistent Language Problems
We examined data from both the MB design study as well as the group design study concerning each student’s performance when solving consistent and inconsistent language problems before and after the MBPS intervention.
3.2.1. MB Design Study Data Analysis
Figure 3 presents four participants (Carmen, Gaby, Mary, and Sara, see Table 1b for their demographic information) from the MB design study, which shows students’ performance change from baseline to post-intervention phases. We calculated the percentage correct in solving seven consistent language problems (7 out of 14 problems, the line graph in blue color) separately from the percentage correct in solving inconsistent language problems (the other seven problems, the line graph in red color) to examine different potential patterns of participating students’ ability to solve these problems before and after the intervention. The black dash line represents the overall performance, percent correct on solving all 14 additive word problems.
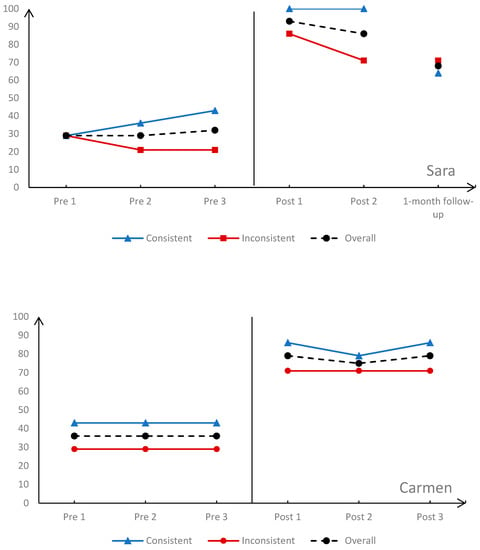
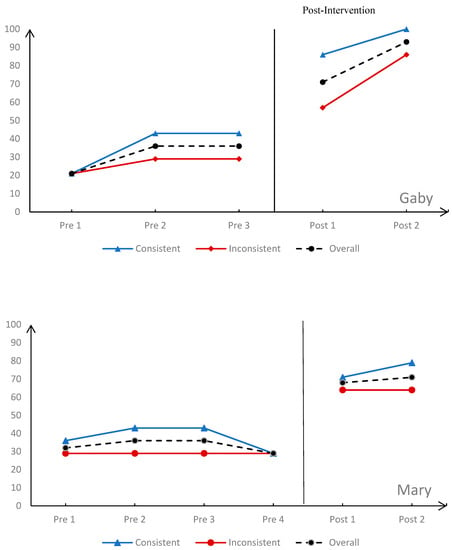
Figure 3.
Percentage correct in solving consistent (blue)/inconsistent language problems (red) from pre- to posttest phases.
Results indicate that after the MBPS intervention, participants improved their overall problem-solving performance from 36% to 79% (an increase of 43%) for Carmen, 36% to 82% (an increase of 46%) for Gabby, 36 to 68% (an increase of 32%) for Mary, and 29% to 89% (an increase of 60%) for Sara. One student, Sara, received a one-month follow-up probe, and she maintained her overall performance at 68% correct, a significant increase from her baseline performance, which is 29% correct.
As presented in Figure 3, across all four participants and across pretest and posttests, it seems that participating students had more difficulties in solving inconsistent language problems (as presented in the red color line graph) when compared to problems with consistent languages (as presented in the black color line graph). Following the MBPS intervention, it shows clearly that all participants improved their performance in solving both the consistent and inconsistent language problems because there is a clear level change from pretests to posttests.
3.2.2. Group Design Study Data Analysis
Figure 4 presents nine students in the group design study and their performance (% correct) in solving consistent and inconsistent language problems before and after the intervention. Again, we calculated the percent correct on solving consistent language problems (7 out of 14 problems, the line graph in blue color) separately from the percent correct when solving inconsistent language problems (the other seven problems, the line graph in red color) to examine potentially different patterns of participating students’ ability to solve these problems before and after the intervention. As shown in Figure 4 (left panel), it seems that there is a relatively clear patten/separation in terms of student performance in solving consistent and inconsistent language problems. Specifically, seven out of nine students (78%) performed better in solving consistent language problems when compared to inconsistent language problems. This finding is supported by existing literature in that students experience more challenges in solving inconsistent language problems [19]. However, after the intervention, it seems that the separation of the two lines becomes blurred or indistinct; in fact, there is an interaction between the two data paths.
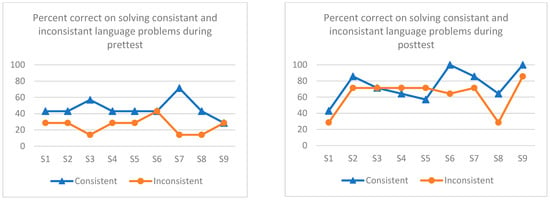
Figure 4.
Percentage correct in solving consistent (blue)/inconsistent language problems (orange) from pretest to posttest.
4. Discussion
The purpose of this study was to examine the impact of the MBPS intervention on students’ error patterns in solving a range of additive word problems. Error analyses help us understand whether students’ problem solving is based on their understanding of the word problems and their applications of strategies to solve the problems. Errors could be classified into the below categories: reading comprehension (read and understand the problem and what you are asked to solve for), transformation (represent the problem, form the equation or algorithm), process skills (come up with a solution plan including a decision on the operation sign), and encoding (give the answer including the unit of measurement) [34]. According to existing research, the most common error is pertinent to comprehension of the word problem [35]. Further, it was found that students tended to use keywords or fixation on other tricks to solve word problems [13]. The next two sections serve to answer each of the two research questions raised in this study.
4.1. Impact of MBPS on Students’ Success in Solving a Range of Additive Word Problems
The findings from this study seem to indicate that the MBPS intervention promoted students’ success in solving most of the problems except for the two problem situations, the change–join problem with the ending total (or whole) as the unknown (i.e., CJ-WE) and the change–separate with the beginning amount (whole) as the unknown (i.e., CS-WB). Upon careful examining students’ work in pretests, it was discovered that, during the pretest, most of the participating students simply took two numbers given in the problem and applied the same operation (e.g., adding) to achieve the answer, regardless of how the word problem was constructed and/or the mathematical relations described in the problem. This is supported by previous research in that students added all the numbers in the problem to solve problems (i.e., the “add-all” strategy, [19]). Figure 5 presents examples of how the participating students applied “adding the given two numbers in sequence” to solve all the problems.

Figure 5.
Sample student work showing the “Add-All” strategy applied by the participants during the pretests.
As shown in Figure 5, although the student achieved the correct answer for solving the combine problem with the total as the unknown (#6 in Figure 5), that does not necessarily mean that the student conceptually understood the problem if the student solved all the problems by adding the two numbers given regardless how they were presented. Regarding the change–join problems with the ending total (or “whole”) as the unknown (CJ-WE, see sample problem #8 in Figure 5), this type of problem is perhaps one of the easiest problem situations, as students could either rely on the keyword (“more” or “total” signifies an operation of addition) to solve the problem or the “add-all” strategy used by the participating students would help “win” through luck. As shown in Figure 2, 100% of the students solved this problem correctly during the pretest. In contrast, after the MBPS intervention, students made an effort to apply the newly learned strategy. That is, they attempted to first represent the information in the PPW diagram equation based on their understanding of the problem and then solve the problem. As a result, seven out of nine students represented and solved the problems correctly. This perhaps explains the decline in the number of students who solved this problem (CJ-WE) correctly following the intervention (see Figure 2).
Similarly, for the change–separate problems with the beginning amount (the “total” or “whole”) as the unknown (CS-WB, see sample problem #2 in Figure 5), most participating students (89%) got the correct answer during the pretest because adding the two given numbers would “win them the luck” although the “beginning amount unknown” problems were considered rather challenging for many students (Parmar et al.,1996). After the intervention, it seems that the participating students have yet to master the newly learned strategy (56% of the students solved this problem correctly). Figure 6 shows participating students’ work on solving this problem during the posttest. As shown in Figure 6 (left panel), the student did not engage in representing information in the PPW diagram equation; rather, they just applied an operation for the answer. It seems that the student reverted to the old strategies they had (e.g., the keyword strategy, “books checked out”—subtract!), resulting in an incorrect answer. In contrast, as shown in Figure 6 (right panel), this participating student used labels to anchor the representation of the three essential elements (i.e., P, P, W) in the PPW diagram equation and then solved the problem correctly.
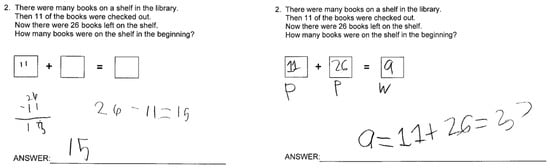
Figure 6.
Participating students’ use of labels to anchor representation (right panel) vs. no representation (left panel).
For the rest of the problem types, particularly those with missing part or missing addend problems (e.g., CMB-P, CJ-PC), problems with the beginning amount as the unknown (CJ-PB), comparison problems with the referent quantity as the unknown (e.g., CM-R, and the so-called “inconsistent language” problems, e.g., Sam was very hungry one day and ordered 41 hamburgers. Sam ordered 20 more hamburgers than Darryl. How many hamburgers did Darry order? [Problem #10 in Figure 5]), it seems that the MBPS strategy benefited the students in solving these problems as evidenced by a significantly improved percentage of students who solved the problem correctly (see Figure 2).
4.2. Impact of MBPS on Students’ Ability to Solve Consistent/Inconstant Language Problems
For comparison problems with “consistent languages” (e.g., CM-C, see sample problem #9 in Figure 5; CLS-C, see sample problem #14 in Figure 5), students’ performance stayed the same after the intervention (see Figure 2). It should be noted that to solve compare problems with “consistent language,” the use of the “keyword” strategy (e.g., the word “more” signifies the operation of “adding,” the word “less” cues the operation of “subtract”) would result in the correct answer. Therefore, we would not know whether the student solved the problem based on their conceptual understanding of the mathematical relations described in the problem or simply used the keyword strategy. Figure 7 presents a contrast of the participating student’s performance during pretest in solving a consistent language problem vs. an inconstant language problem that involves comparing one quantity to the other.

Figure 7.
Contrast of student’s work in solving consistent (left) vs. inconsistent language problems (right) during pretest.
As shown in Figure 7, either using the keyword strategy (i.e., the word “more” signifies an operation of addition) or blindly adding the two given numbers in sequence would result in the correct answer (left panel) for solving the consistent language problems with the context of compare-more; however, it would not work for the inconsistent language problem type (right panel). As such, we would not be able to simply conclude that the participating students did not improve on solving the consistent language problems because we would not know whether students’ problem solving during the pretest was based on their conceptual understanding due to the fact that the “add-all” strategy or the keyword strategy would serve them well in obtaining the correct answer. To exclude this confounding variable, future research should present only inconstant language problems, as Jaspers and van Lieshout [19] did in their study so that random luck would not become a confounding variable as researchers evaluate the impact of an intervention on conceptual understanding of problem solving.
Following the intervention, as shown in Figure 8, students used labels or “name tags” to anchor their representation of the information in the mathematical model equation based on their understanding of the three elements (“part, part, whole”, or “smaller, bigger, difference”) and the mathematical relations between the three quantities in the problem, rather than relying on the keywords for the decision making on the operation sign. Eventually, it is the model equation that drove the solution plan, the creation of the math sentence, for solving for an unknown quantity in the solution.

Figure 8.
Students’ use of “Labels” or “Name Tags” to anchor the representation process during posttest.
In summary, combing both the MB study data as well as the group study data, it seems that the MBPS intervention enhanced students’ performance in solving both the consistent and inconsistent language problems, as evidenced by elevated performance in solving both problem types (see Figure 3). It also seems that the MBPS intervention helped ease the difficulty level of solving the inconsistent language problems, at least for some students, which is evidenced by the interaction of the two data paths, as shown in Figure 4.
4.3. Limitations and Future Research
When considering the findings of this study, please take into consideration several limitations of this preliminary error analysis study. First, there was a dilemma in the decision making pertaining to whether the PPW diagram equation (i.e., P + P = W) should be present on the assessment sheets. As we were collecting multiple data points throughout the experiment studies, particularly in the MB design study, the PPW diagram equation was presented on the test sheets with the intention of evaluating whether the participating students were able to correctly represent the information in the diagram equation, a critical component of the MBPS approach. To ensure equality, we included the PPW diagram equation on both the pretest and posttest forms. Nevertheless, participating students were told to show whatever strategies they would use to solve the problem. In fact, many students were using the vertical forms to solve the problems, particularly during the pretests, ignoring the box diagram presented. Of course, we might not know how the box diagram impacted participating students’ performance. However, at least we kept this variable consistent across pretests and posttests.
To this end, future research could include a generalization test that removes the PPW diagram equation on all test sheets. Regardless, our previous research did find similar results as we found in this study in that students blindly grabbed the numbers given in the problem and applied the same operation to solve all the problems, even with no printing of the PPW diagram equation on the pretest sheets [6]. Therefore, we would not consider the presentation of diagram equations during the pretests as a serious confounding variable.
Second, a relatively small number of participants were included in this error analysis study. When large data sets are available, future research should conduct more comprehensive error analyses building upon this preliminary study and therefore gain more insight into how the MBPS interventions impact students’ word problem solving. Third, due to the real constraints of the school semester at the participating school, the participants in this study only received about 18–20 sessions of the MBPS intervention (varied from individual to individual) following the preset sequence of the lessons in the MBPS tutoring program. Given that the MBPS program involves the instruction on teaching students to solve all 14 problem types and limited lessons included in the prototype version of the MBPS tutoring program, participants’ mastery of each subskill was not secured due to the limited training sessions the participating students received within a school semester. As demonstrated in the findings of this study, not all participants achieved mastery of the MBPS strategy, which was demonstrated by some students’ returning to the use of premature strategies. Future research should continue the evaluation of the MBPS program once an enhanced version of the MBPS is developed and more field-test studies are conducted.
4.4. Implications for Practice
Existing research has shown that schema-based instruction is effective in teaching word problem solving to students with LDM [36]. According to research in the field of psychology, successful problem solvers possess problem schemata that guide the encoding and retrieval of problem information (e.g., [37]). Above and beyond, the problem solvers need to generate mathematical models or expressions [38] to successfully solve the problem. In fact, mathematical modeling is an essential part of all areas of mathematics, including arithmetic, and it should be introduced to all age groups, including elementary school students. A large volume of special education research in elementary mathematics problem solving has emphasized the semantic analyses of word problem stories and the coding of problems into various types (e.g., combine or group, change–increasee, change–decrease, compare, etc.). Yet, not enough attention has been paid to mathematical modeling and mathematical models. Existing research pertaining to word problem solving error analysis of students with LDM has shown that students might not correctly identify the problem schema defined by the researchers; however, they still solved the problem correctly [21] as long as they were able to generate the mathematical model (or “math sentence”) for the solution. While it is important to connect to children’s pre-existing knowledge pertaining to word problem story situations, ultimately, it is the mathematical model, decontextualized from the word problem story, which describes the mathematical relation between quantities and drives the solution plan.
The MBPS intended to help students construct the mathematical model (e.g., “part and part makes up the whole”) in additive word problem solving to promote generalized problem-solving skills. The error analyses of students’ work show that participating students improved in solving most of the problems after the MBPS intervention. Qualitative analysis of students’ work demonstrated that participating students no longer just grabbed the numbers gambling on the operation sign. They were making efforts to read/comprehend the problem and represent the mathematical relations in the model equation before applying an operation for the solution.
Finally, it should be noted that when teaching a new strategy, perhaps it will not be like switching a light bulb, “turning on” the new strategy and “turning off” the old strategy. Often there might be a delay in the use of the newly learned strategy or a mix-up in the use of the newly learned strategy and the old strategy [39]. As teachers/educators make efforts to promote students’ conceptual understanding of word problem solving and make connections between mathematical ideas, it is important to connect the new strategy/concept to learners’ existing strategies/knowledge. Students should be provided with abundant learning opportunities through strategically designed learning tasks [40] so that they can experience the advantages and/or the power of the new strategy. Specifically, when applying the MBPS program to teaching word problem solving, students should be exposed to variations in additive word problem situations so that they will eventually “construct” the PPW mathematical model themselves and be able to apply the model to solve a range of additive word problems.
5. Conclusions
Both the quantitative and qualitative data from this study seem to indicate that the MBPS intervention program helped the participating students solve variously constructed additive word problems through their understanding of the big idea in additive reasoning. That is, part and part make up the whole. Rather than “gambling” on the operation sign without reading/comprehending the problem first as they did during the preassessment, it seems that the participating students made an effort to identify the three essential elements (i.e., part, part, and whole), decontextualized from the cover story, and representing the quantitative relation in the PPW model equation, as demonstrated in their work during the post-intervention assessment. Finally, it was the mathematical model equation that drove their solution process.
Author Contributions
Conceptualization, Y.P.X.; methodology, Y.P.X.; software/tutoring program design, Y.P.X., S.J.K.; validation, Y.P.X.; formal analysis, Y.P.X.; investigation, Y.P.X., S.J.K., Q.L.; resources, Y.P.X., J.Z., X.M.; data curation, Y.P.X., J.Z., B.Y.Y., S.Y.; writing—original draft preparation, Y.P.X.; writing—review and editing, Y.P.X., S.J.K.; visualization, S.Y., B.Y.Y., Y.P.X., J.Z.; supervision, Y.P.X.; project administration, Y.P.X.; funding acquisition, Y.P.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially supported by the U. S. National Science Foundation, under grant #1503451.
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki, and the protocol was approved by the Institutional Review Board of Purdue University (Protocol #: 1503015877; date of approval: 27 July 2017.
Informed Consent Statement
All subjects gave their informed consent for inclusion before they participated in the study.
Data Availability Statement
Research data supporting reported results in this study can be accessed by contacting the first author Yan Ping Xin at yxin@purdue.
Acknowledgments
This research was partially supported by the National Science Foundation, under grant #1503451. The opinions expressed do not necessarily reflect the views of the Foundation. We would like to thank the administrators, teachers, and students in the Lafayette School Corporation as well as the COMPS-RtI research team at Purdue University who facilitated this study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- National Assessment of Educational Progress Result (NAEP). 2022. Available online: https://www.nationsreportcard.gov/highlights/ltt/2022/ (accessed on 30 May 2023).
- Carcoba Falomir, G.A. Diagramming and Algebraic Word Problem Solving for Secondary Students with Learning Disabilities. Interv. Sch. Clin. 2019, 54, 212–218. [Google Scholar] [CrossRef]
- U.S. Department of Education. Every Student Succeeds Act. Pub. L. No. 114-95 § 114 Stat. 2015. Available online: https://congress.gov/114/plaws/publ95/PLAW-114publ95.pdf (accessed on 28 June 2023).
- Common Core State Standards Initiative. Introduction: Standards for Mathematical Practice. 2012. Available online: http://www.corestandards.org/the-standards/mathematics (accessed on 30 May 2023).
- Verschaffel, L.; Schukajlow, S.; Star, J.; Van Dooren, W. Word Problems in Mathematics Education: A Survey. ZDM 2020, 52, 1–16. [Google Scholar] [CrossRef]
- Xin, Y.P.; Wiles, B.; Lin, Y. Teaching Conceptual Model-Based Word-Problem Story Grammar to Enhance Mathematics Problem Solving. J. Spec. Educ. 2008, 42, 163–178. [Google Scholar] [CrossRef]
- Sowder, L. Children’s Solutions of Story Problems. J. Math. Behav. 1988, 7, 227–238. [Google Scholar]
- Greer, B. Multiplication and Division as Models of Situations. In Handbook of Research on Mathematics Teaching and Learning; Grouws, D., Ed.; MacMillan: New York, NY, USA, 1992; pp. 276–295. [Google Scholar]
- National Council of Teachers of Mathematics (NCTM). Principles and Standards for School Mathematics; National Council of Teachers of Mathematics: Reston, VA, USA, 2000. [Google Scholar]
- Caldwell, J.H.; Karp, K.; Bay-Williams, J.M. Developing Essential Understanding of Addition and Subtraction for Teaching Mathematics in Prekindergarten–Grade 2 (Essential Understanding Series); National Council of Teachers of Mathematics: Reston, VA, USA, 2011. [Google Scholar]
- de Corte, E.; Verschaffel, L. The Effect of Semantic Structure on First Graders’ Strategies for Solving Addition and Subtraction Word Problems. J. Res. Math. Educ. 1987, 18, 363–381. [Google Scholar] [CrossRef]
- Carpenter, T.P.; Moser, J.M. The Acquisition of Addition and Subtraction Concepts in Grades One Through Three. J. Res. Math. Educ. 1984, 15, 179–202. [Google Scholar] [CrossRef]
- Nortvedt, G.A. Coping Strategies Applied to Comprehend Multistep Arithmetic Word Problems by Students with Above-average Numeracy Skills and Below-average Reading Skills. J. Math. Behav. 2011, 30, 255–269. [Google Scholar] [CrossRef]
- Polotskaia, E.; Savard, A. Using the Relational Paradigm: Effects on Pupils’ Reasoning in Solving Additive Word Problems. Res. Math. Educ. 2018, 20, 70–90. [Google Scholar] [CrossRef]
- Davydov, V.V. Psychological Characteristics of the Formation of Mathematical Operations in Children. In Addition and Subtraction: Cognitive Perspective; Carpenter, T.P., Moser, J.M., Romberg, T.A., Eds.; Lawrence Erlbaum Associates: Hillsdale, NJ, USA, 1982; pp. 225–238. [Google Scholar]
- Thompson, P.W. Quantitative Reasoning, Complexity, and Additive structures. Educ. Stud. Math 1993, 25, 165–208. [Google Scholar] [CrossRef]
- Jonassen, D.H. Designing Research-based Instruction for Story Problems. Educ. Psychol. Rev. 2003, 15, 267–296. [Google Scholar] [CrossRef]
- Fleischner, J.E.; Manheimer, M.A. Math Interventions for Students with Learning Disabilities: Myths and Realities. Sch. Psychol. Rev. 1997, 26, 397–413. [Google Scholar] [CrossRef]
- Jaspers, M.W.M.; van Lieshout, E.C.D.M. Diagnosing Wrong Answers of Children with Learning Disorders Solving Arithmetic Word Problems. Comput. Hum. Behav. 1994, 10, 7–19. [Google Scholar] [CrossRef]
- Lewis, A.B.; Mayer, R.E. Students’ Miscomprehension of Relational Statements in Arithmetic Word Problems. J. Educ. Psychol. 1987, 79, 361–371. [Google Scholar] [CrossRef]
- Powell, S.R.; Katherine, A.B.; Benz, S.A. Analyzing the Word-problem Performance and Strategies of Students Experiencing Mathematics Difficulty. J. Math. Behav. 2020, 58, 100759. [Google Scholar] [CrossRef]
- Xin, Y.P.; Kastberg, S.; Chen, V. Conceptual Model-Based Problem Solving: A Response to Intervention Program for Students with Learning Difficulties in Mathematics (COMPS-RtI). National Science Foundation (NSF) Funded Project. 2015. Available online: https://www.nsf.gov/awardsearch/showAward?AWD_ID=1503451 (accessed on 28 June 2023).
- Steffe, L.P.; von Glasersfeld, E.; Richards, J.; Cobb, P. Children’s Counting Types; Praeger: New York, NY, USA, 1983. [Google Scholar]
- Fuson, K.C.; Willis, G.B. Subtracting by Counting Up: More Evidence. J. Res. Math. Educ. 1988, 19, 402–420. [Google Scholar] [CrossRef]
- Fuchs, L.S.; Newman-Gonchar, R.; Schumacher, R.; Dougherty, B.; Bucka, N.; Karp, K.S.; Woodward, J.; Clarke, B.; Jordan, N.C.; Gersten, R.; et al. Assisting Students Struggling with Math: Intervention in the Elementary Grades (WWC 2021006). National Center for Education Evaluation and Regional Assistance (NCEE), Institute of Education Sciences, U.S. Department of Education: Washington, DC, USA, 2021. Available online: http://whatworks.ed.gov/ (accessed on 30 May 2023).
- Xin, Y.P. Conceptual Model-Based Problem Solving: Teach Students with Learning Difficulties to Solve Math Problems; Sense: Rotterdam, The Netherlands, 2012. [Google Scholar] [CrossRef]
- Witzel, B.S.; Myers, J.A.; Xin, Y.P. Conceptually Intensifying Word Problem Solving for Students with Math Difficulties. Interv. Sch. Clin. 2021, 58, 9–14. [Google Scholar] [CrossRef]
- Xin, Y.P.; Zhang, D.; Park, J.Y.; Tom, K.; Whipple, A.; Si, L. A Comparison of Two Mathematics Problem-Solving Strategies: Facilitate Algebra-Readiness. J. Educ. Res. 2011, 104, 381–395. [Google Scholar] [CrossRef]
- Xin, Y.P.; Tzur, S.L.; Hord, C.; Liu, J.; Park, J.Y. An Intelligent Tutor-assisted Math Problem-solving Intervention Program for Students with Learning Difficulties. Learn. Disabil. Q. 2017, 40, 4–16. [Google Scholar] [CrossRef]
- Xin, Y.P.; Kim, S.J.; Lei, Q.; Liu, B.; Wei, S.; Kastberg, S.E.; Chen, Y.-J. The Effect of Model-based Problem Solving on the Performance of Students Who are Struggling in Mathematics. J. Spec. Educ. 2023. [Google Scholar] [CrossRef]
- Kingsdorf, S.; Krawec, J. Error Analysis of Mathematical Word Problem Solving Across Students with and without Learning Disabilities. Learn. Disabil. Res. Pract. 2014, 29, 66–74. [Google Scholar] [CrossRef]
- Xin, Y.P.; Kim, S.J.; Lei, Q.; Wei, S.; Liu, B.; Wang, W.; Kastberg, S.; Chen, Y.; Yang, X.; Ma, X.; et al. The Impact of a Conceptual Model-based Intervention Program on Math Problem-solving Performance of At-risk English learners. Read. Writ. Q. 2020, 36, 104–123. [Google Scholar] [CrossRef]
- Kim, S.J.; Kastberg, S.E.; Xin, Y.P.; Lei, Q.; Liu, B.; Wei, S.; Chen, Y. Counting strategies of students struggling in mathematics in a computer-based learning environment. J. Math. Behav. 2022, 68, 101007. [Google Scholar] [CrossRef]
- Newman, M.A. An analysis of sixth-grade pupils’ errors on written mathematical tasks. In Research in Mathematics Education in Australia; Clements, M.A., Foyster, J., Eds.; Swinburne College Press: Melbourne, Australia, 1977; Volume 34, pp. 269–287. [Google Scholar]
- Rosli, S.; Shahrill, M.; Yusof, J. Applying the Hybrid Strategy in Solving Mathematical Word Problems at the Elementary School Level. J. Technol. Sci. Educ. 2020, 10, 216–230. [Google Scholar] [CrossRef]
- Peltier, C.; Vannest, K.J. A Meta-Analysis of Schema Instruction on the Problem-Solving Performance of Elementary School Students. Rev. Educ. Res. 2017, 87, 899–920. [Google Scholar] [CrossRef]
- Mayer, R.E. Memory for algebra story problems. J. Educ. Psychol. 1982, 74, 199–216. [Google Scholar] [CrossRef]
- Hamson. The place of mathematical modeling in mathematics education. In Mathematical Modeling: A Way of life; Lamon, S.J., Parker, W.A., Houston, K., Eds.; Horwood Publishing: Chichester, UK, 2003; pp. 215–255. [Google Scholar]
- Zhang, D.; Xin, Y.P.; Si, L. Transition from Intuitive to Advanced Strategies in Multiplicative Reasoning for Students with Math Difficulties. J. Spec. Educ. 2013, 47, 50–64. [Google Scholar] [CrossRef]
- Hunt, J.; Tzur, R. Connecting Theory to Concept Building: Designing Instruction for Learning. In Enabling Mathematics Learning of Struggling Students: International Perspectives; Xin, Y.P., Tzur, R., Thouless, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2022; pp. 83–100. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).