Teaching and Learning of Geometry—A Literature Review on Current Developments in Theory and Practice

Abstract

Geometry is part of the core of mathematics. It has been relevant ever since people have interacted with nature and its phenomena. Geometry’s relevance to the teaching and learning of mathematics can be emphasized, too. Nevertheless, a current potential shift in the topics of mathematics education to the detriment of geometry might be emerging. That is, other topics related to mathematics are seeming to grow in importance in comparison to geometry. Despite this, or perhaps because of it, geometry is an important component of current research in mathematics education. In the literature review, we elaborate relevant foci on the basis of current conference proceedings. By means of about 50 journal articles, five main topics are elaborated in more detail: geometric thinking and practices, geometric contents and topics, teacher education in geometry, argumentation and proof in geometry, as well as the use of digital tools for the teaching and learning of geometry. Conclusions and limitations for current and future research on geometry are formulated at the end of the article. In particular, the transfer to the practices of geometric teaching is explored on the basis of the elaborated research findings in order to combine both aspects of the teaching and learning of geometry.

1. Introduction

Geometry has been an indispensable subject of mathematics for thousands of years. What is more, “for a long time mathematics has been synonymous with geometry” [1] (p. 401). The word geometry comes from the Greek and originally meant earth measurement. Due to recurring natural events, such as the Egyptian field measurement after the Nile flood 4.000 years ago, the science of geometry developed. It is a branch of mathematics that is illustrative. Thus, it provides the possibility to learn from reality. Due to its historical relevance and its relation to reality, geometry plays a role in the learning and teaching of mathematics, and thus also in mathematics education research.

Both practical and theoretical influences condition ongoing innovations in the learning and teaching of mathematics. In recent years and decades, there have been educational policy decisions and reforms, as well as influences of new achievements and inventions that affect mathematics education. The question arises for all areas, but especially for the area of geometry, which is rich in history and culture, how the roots of the sub-discipline can be united with new trends and innovations. This review article aims to contribute to this question.

Therefore, the present review article focuses on current developments in the research area of teaching and learning geometry. It covers the period from 2017 until 2022, following up the geometry research review by [2], and presents recent research findings in an international context. The goal of this article is to highlight current trends and lines of research in geometry and to clarify future research concerns.

2. Methods and Materials

To achieve this goal, a multi-stage process was chosen (see Figure 1). For the purpose of linking theory and practice throughout the article, five European experts (Italy, Slovakia, Spain, France, and Portugal) in the field of mathematics education were first interviewed about their assessment of the role of geometry (a) in the national mathematics curricula as well as (b) in research on mathematics education. We chose university professors and members that are teaching in mathematics education and have been taken part in international projects linked to practical implementations of teaching and learning of geometry. Some of them, like Spain and France, have reported a shift in their curriculum of geometry, losing relevance in comparison to earlier curriculum versions. For example, the Spanish expert, a university professor of mathematics and mathematics education, assumed that geometry averages only about 20% of mathematics in school. In the French curriculum, a tendency for geometry to be replaced by algorithmics was reported. The French interview partner, a university professor engaged in the professional development of mathematics teachers, states that most teachers do not support this evolution since geometric fundamentals are missing in other topics as well. This impression is strengthened through the role of geometry in [3], addressing the question What may mathematics education prepare students for in the society of the future? Within the article’s text (excluding references), the word “Geometry” appears only four times, namely by describing the link between the different domains of mathematics, the role of space geometry in the specific context of 3D printing technology, and the idea of proof not being limited to geometry, but supported through dynamic geometry tools.

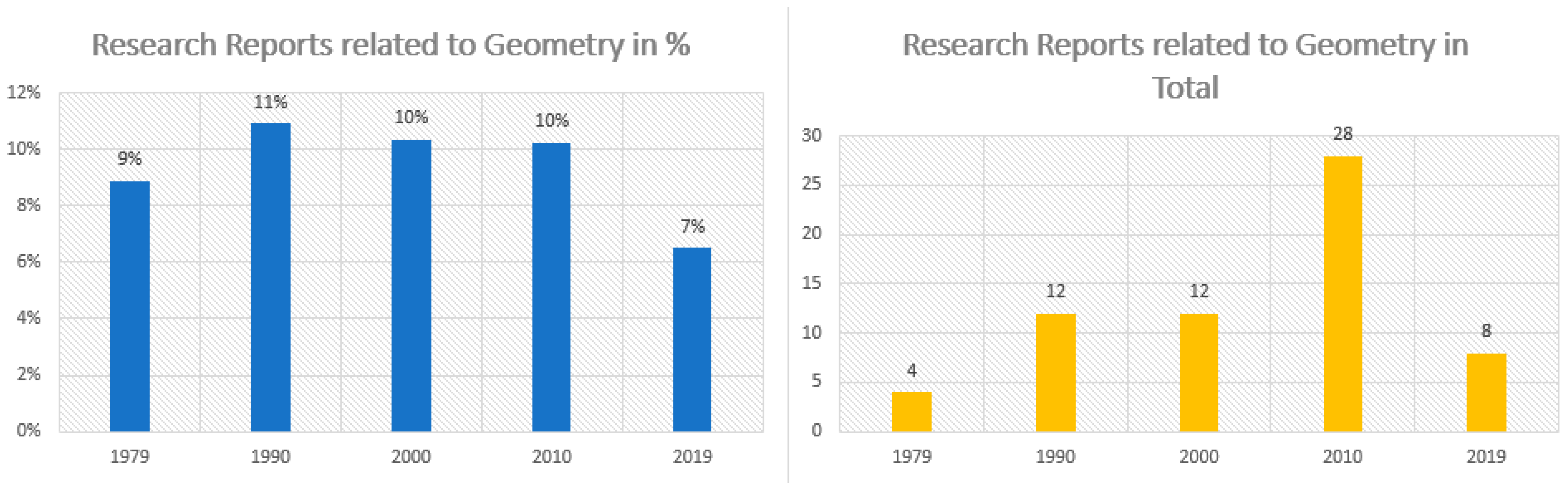
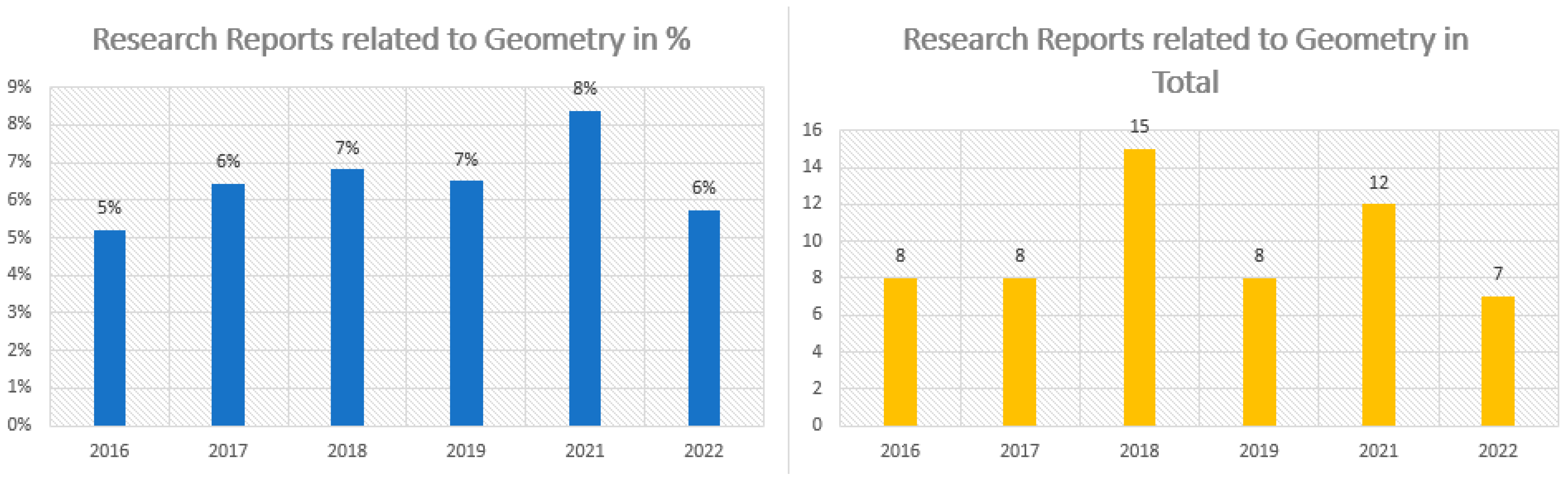
Based on these observations, we want to present an impression on the development of research activities linked to geometry in a second step. Since geometry is a topic relevant to different perspectives on mathematics education, the impression is narrowed down to the example of a psychological one. The results should not be limited to this perspective but provide a more detailed and international insight into the long-term development of one perspective on geometry. To do so, the Research Reports of the Psychology of Mathematics Education (PME) conferences for different years were analyzed to determine whether they contain a geometry-related topic. This analysis was carried out by means of the papers’ titles, abstracts, and keywords, within which we searched for the terms “geometry” and “geometric”. Deliberately, only these two umbrella terms were used at this point in order to obtain an unrestricted overview and not to unconsciously influence the focus by selecting further, more specific keywords. Thus, it can be assumed that further research reports could possibly be assigned to the field of geometry. Nevertheless, the uniform procedure for all years can guarantee that potential trends and changes can be described on the basis of the two keywords. Through the comparison of geometry-related papers and the total number of papers, we want to illustrate a general overview of geometry in mathematics education research. The results of our analysis of Research Reports from PME conferences are shown in Figure 2 and Figure 3 and reinforce the impressions gathered earlier about the declining relevance of geometry in mathematics education and related research on the long-term level. Still, with a focus on the research activities during the last five years, a generally falling trend cannot be observed. As a second intermediate result, geometry still seems to be of current relevance in mathematics education research.

In order to gain insight into the actual research activities linked to geometry, an iterative process was started to identify geometry-related research topics. Step 3 of the iterative process started with an analysis of the keywords in conference papers in the period from 2017 to 2022. The context of a conference was chosen to get a near-term impression of current research activities in the field of geometry. We chose the Conference of European Society for Research in Mathematics Education (CERME) for two reasons. Firstly, the conference has an international impact which goes beyond the European research community. Secondly, the CERME structure, organized in working groups, makes the identification of geometry-related papers clear through their association to the Geometry Working Group. With the goal of finding relevant trends in the research field of geometry, some keywords were grouped into larger topics. With 53 articles and 191 linked keywords, the following topics were identified (see

Table 1. Keyword analysis concerning topics in geometry.

Topic	Number of Related Keywords
Geometric thinking and practices (e.g., Shape Recognition, Construction, Strategies, Visualization)	53
Geometric contents, topics, and approaches to teaching (e.g., Definition, Area, Trigonometry, Space, Angle)	21
Teacher education in geometry (e.g., Training, In-service Teachers, Teaching, Task Design)	28
Argumentation and proof in geometry (e.g., Reasoning, Justification, Generalization)	15
Digital tools for the teaching and learning of geometry (e.g., DGS, GeoGebra)	12

). Hereby, the keywords were exclusively related to one of the topics. Still, each of the 53 articles could contribute to more than one of the topics if the respective keywords were listed.

Using these keywords as indicators for their importance in the current research on and with geometry, we identified relevant research articles by mainly analyzing four international journals with contributions to geometry: ZDM—Mathematics Education, International Journal of Science and Mathematics Education, Journal for Research in Mathematics Education, and Educational Studies in Mathematics. In these journals, all articles published since 2017 were classified as relevant or irrelevant to geometry based on their title and abstract (as of year-end 2022). 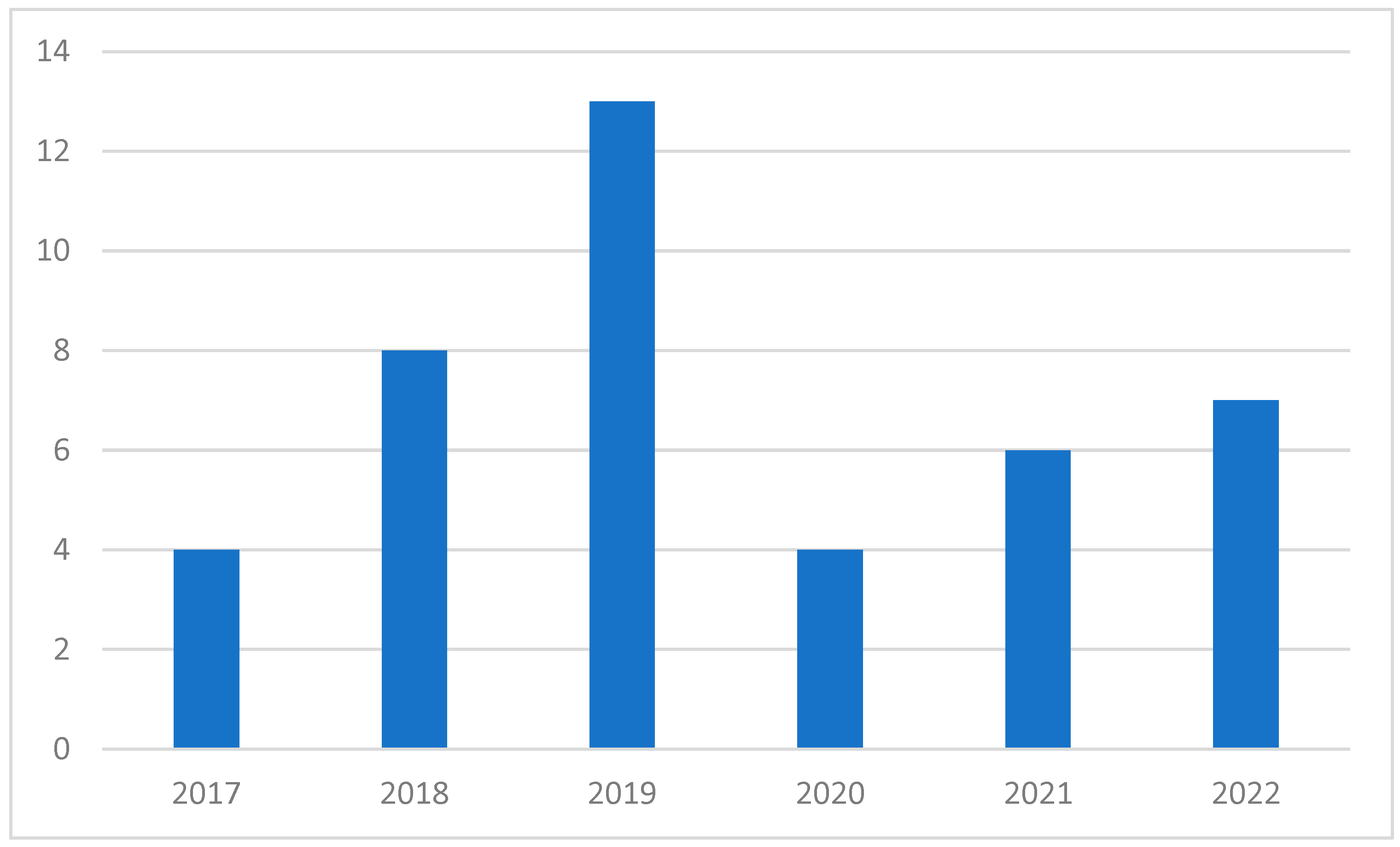If the relevance of the article was determined, it was assigned to one of the topics in Table 1. Furthermore, national journals, e.g., Quadrante and Journal für Mathematikdidaktik, were systematically searched using the previously used generic terms “geometry” and “geometric”. If articles were found and identified as relevant for the literature review, they were added to one of the topics in order to deepen the view on geometry teaching and learning. By following this procedure, 42 articles were selected. On average, each article was downloaded 2800 and cited 9 times. Figure 4 gives an insight into the range of their publication dates.

In the following chapters, each of the topics from Table 1 will be presented by means of the selected articles.

3. Geometric Thinking and Practices

In the first section, we focus on research that goes beyond geometric contents. When teaching and learning geometry, a certain way of thinking and working has to be transmitted. We call it geometric thinking and refer to different (cognitive) practices, such as spatial orientation, shape recognition, and (meta-)cognitive strategies. The report’s basis is the identified research articles as described in the introduction. Their contents are meant to give an insight into recent developments in geometric thinking and practices. Our review related to this category results in the report of current developments concerning spatial reasoning and object structure perspective taking from the perspective of young children. In addition, the use of oral and written language, as well as sketches and drawings, is reported in this chapter. Based hereon, a methodological development in the usage of eye-tracking technology can be observed.

3.1. Spatial Reasoning and Object Structure Perspective Taking in Elementary School

In a meta study, Ref. [4] highlight the lack of geometric thought and spatial reasoning in the curriculum for young children. Therefore, recent initiatives and interventions focus on the early abilities of students in spatial reasoning and structuring. The authors in [5] take up the role of understanding geometry and spatial reasoning to integrate both aspects in early education through designing an instructional activity in the children’s environment related to shapes, e.g., recognizing shapes in their surroundings. The results gained show a potential of the activity to help children to connect their experience about various types of forms in their life with mathematical knowledge (i.e., geometry and spatial reasoning) that allows them to reinvent and reinforce the geometry concept. In a related context, Ref. [6] introduces elementary school children’s object structure perspective taking (OSPT) from an assessment and training perspective. The authors take into account different objects as well as different spatial abilities, e.g., the ability to identify a view seen by an observer. Their results show that short training can significantly affect children’s OSPT abilities as well as a significant correlation between OSPT and mathematical scores for geometric objects.

3.2. The Role of Sketches and Drawings for Geometric Understanding

The authors in [7] examine the effect of interventions concerning the students’ measuring skills of rectangular areas in different ways. The strongest improvements could be observed when organized rows and columns of equal-sized unit squares were drawn—an intervention that highlights the importance of drawings as a geometric practice.

The obstacles in two-dimensional sketches, representing 3D objects, are identified by [8]. By including either misleading geometrical or helpful geometrical information in cube-related sketches, the authors propose a theoretical and empirical measure of visual difficulty. In the context of geometry modeling problems, Ref. [9] investigates the students’ strategic knowledge about drawing on a qualitative and quantitative level. Results show that intermediate-achieving students have less elaborated strategic knowledge about drawing than their high-achieving peers. In addition, the authors find a relationship between strategic knowledge about drawing and drawing accuracy as well as modeling performance. Also, in the study of [10], drawings are taken into consideration for geometry-related research from a still more methodological point of view. The authors use drawing production to measure the students’ creativity. The results show that creativity is a significant predictor of the students’ performance on geometrical problems. Since they compare closed-ended and open-ended problems, as well as non-routine and routine problems, the authors can specify that a high level of creativity influences the performance in geometry problems in general, but especially in open-ended non-routine problems asking for multiple solutions. Also, Ref. [11] examines the students’ creativity in geometric work in the sense of the influence of figure apprehension and auxiliary line construction on the ability to create multiple solutions as variables for creativity.

3.3. Written and Oral Language in Geometry

Recent studies with a focus on geometry highlight the connection to language development and geometric understanding. On the one hand, the role of language is taken into consideration in collaborative learning settings. Hereby, the role of conceptual and language development is fostered by the authors in [12]. With a focus on Vygotskian and Bakhtinian perspective on language, a learning environment involving the measurement of angles is developed, investigating its potential for mathematics language learning. In particular, discussions about controversies between different voices concerning measurements—in the senses of approximation and precision—are highlighted as opportunities for language development in geometry classes. Following a more narrow view on the understanding of the teaching and learning of definitions, Ref. [13] focuses on defining and classifying quadrilaterals. Taking a semiotic, dialogic approach, the authors qualitatively analyze the students’ collaborative decision-making processes while classifying quadrilaterals. The results show that the students’ decision-making processes are interpreted as transforming their informal or personal semiotic representations of an object to more institutional object representations.

On the other hand, written language in the sense of reading comprehension for geometric (construction) texts is investigated. The authors in [14] formulate two dimensions of a framework for its assessment, namely the reading comprehension of geometry construction texts and the mathematical essence of geometric construction texts. For the first of these, the authors used different categories related to PISA’s definition of reading and mathematical literacy, i.e., retrieving or recognizing (basic level), interpreting or connecting, as well as reflecting or reasoning. For the second dimension, the authors distinguished the required outcome, geometric properties, and basic geometric constructions. Also, Ref. [15] focuses on geometric texts in combination with pictorial representations. They investigate the reading scan paths of adult readers providing textual and figural representations. The authors report a strong majority for initially reading the text before inspecting the figure and conclude that the text mainly affects the processing of the participants and the integration of the figure through its word ordering.

3.4. Eye-Tracking Technology as a Method to Research Geometric Thinking

For the processing analysis, the authors in [14] use eye-tracking technology, a methodological possibility that has grown in importance for mathematics education research. As a basis, Ref. [16] introduces the eye–mind hypothesis (EMH) from reading research and adapt it to geometry. EMH follows the assumption that a person’s fixation is related to the person’s process. Their results from a case study show that in certain situations, the eye fixations relate to the student’s process, e.g., when the eye movement focuses on entities such as the corners given in the geometry task. In other situations, the EMH cannot be maintained, e.g., when the student fixates on a point in a diagram while calculating something else or identifying a mistake. The authors conclude that a certain ambiguity will remain in analyzing eye-tracking data in geometry.

3.5. Summary

To summarize the developments in the area of geometric thinking and practices, we formulate the following foci and innovations:

(1)

During recent research activities, the development, design principles, and evaluation of learning environments fostering geometric thinking and practices happen already with young children. This extension highlights the general significance of geometric thinking and practices that can be acquired spirally.

(2)

In terms of visualization, the usefulness of drawing and sketches during geometric practices is shown and can be seen as a support of geometric applications. Despite a general trend to use digital tools for visualization (cf. Section 7), the manual creation of sketches still seems to give an advantage.

(3)

We can further see that the role of written and oral language for the teaching and learning of geometry in terms of geometric thinking (e.g., classification), as well as practices (e.g., work with pictures), is relevant.

(4)

Finally, from a methodological point of view, the use of eye-tracking technology in the context of the teaching and learning of geometry can be highlighted. Also, a relation to the topic of “Digital Tools” (cf. Section 7) can be assumed here.

4. Geometric Contents, Topics, and Approaches to Teaching

The second topic focuses on geometric contents, topics, and approaches to teaching involved with its teaching and learning. On the one hand, we refer to recent research that takes principles of geometry into account. On the other hand, this chapter consists of research on the teaching and learning of concrete geometric topics. Since geometry is relevant at all school levels, we order the recent research chronologically from the primary to the upper secondary level.

4.1. Geometric Contents, Topics, and Approaches at Primary Age

Current studies that focus on geometry contents at primary age take the students’ understanding of certain geometric topics into deeper account. Based on our literature review, we identified studies that focus on such an understanding of geometric shapes and their classification in general, as well as the understanding of the area measurement of rectangles and polygons and volume in more detail.

The authors in [17] focus on the students’ classification of geometric shapes, too, and propose an extension of the concept definition, that is, theconcept image by Tall and Vinner, on the basis of the students’ concept image of parallelograms. Based on a case study, the authors suggest adding two constructs to the theory, namely the missing concept image (i.e., an example is wrongly classified as a non-example) and the mis-in concept image (i.e., a non-example is wrongly classified as an example). The author in [18] focuses on the students’ understanding in a related context, namely area measurement. In a comparison of three different classroom investigations, he emphasizes the effectiveness of an enriched curriculum that focuses on two-dimensional geometry in enhancing the understanding of area measurement. In addition, he observed facilitated reasoning concerning the relationship between the area and the perimeter of a rectangle. The authors in [19] conduct research on students’ understanding of polygons. In particular, the authors investigated the students’ understanding of recognition and classification of polygons. The results show that the students’ recognition of attributes is relevant for both achievements. In addition, a progressive complexity is seen from the recognition of a polygon to the transformation of a non-polygon to a polygon. Moving from the students’ understanding of plane figures to three-dimensional objects, Ref. [20] reports on the students’ understanding of volume. Hereby, the authors follow the engineering design in STEM education. The authors conclude with an intuitive understanding of volume that is usually associated with the students’ experiences from reality. Through engineering design, it is possible that students understand the concept of volume gradually, which the authors take up for future implications.

4.2. Geometric Contents and Topics in Upper Secondary Education

Whereas Section 4.1. focuses on the understanding of basic topics related to primary education, we can observe research with a more detailed focus on topics from secondary education, i.e., the understanding of formulas, the Cosine theorem, as well as a general overview of linear algebra.

The authors in [21] focus their research on geometric formulas in upper secondary education. In particular, the authors take up students’ problems in using formulas. To take a deeper insight into these problems, the students’ mathematical behavior is analyzed in order to understand the students’ “view on formula”. This term is described through ideal types of patterns in mathematical behavior in the handling of formulas. The authors point out that missing or inflexible views on formulas can lead to problems in their understanding and application. Vice versa, the students’ view on formulas can indicate missing mathematical knowledge in its usage. With a special focus on the Cosine theorem, the authors in [22] investigate an approach of Realistic Mathematics Education (RME) in secondary education. RME was developed by Freudenthal following the idea that the teaching of mathematics should start with a realistic situation. In their case study, the authors analyzed the students’ learning of the Cosine theorem following the idea of RME. For higher secondary education, Ref. [23] focuses on the ways in which geometry is used in the teaching of linear algebra. Following the approach of a textbook analysis, he identifies seven varieties, namely generalization, reduction, application, metaphorical representation, literal representation, self-contained investigation, and spatially based terminology. Additionally, he investigates the possible impact of the varieties on the students’ learning that are the basis for ongoing discussions about the role of geometry in linear algebra.

4.3. Summary

The findings in the area of geometric contents, topics, and approaches can be categorized concerning the following topics and investigations:

(1)

Researchers investigate different uses of geometry with elementary school children (e.g., classification) and upper secondary students (e.g., linear algebra). The spiral, long-term learning of geometry that was already assumed in Section 3 becomes even more obvious when regarding current research on geometric contents, topics, and approaches.

(2)

Also, with a focus on contents, topics, and approaches, researcher take “young learners” into their focus, i.e., primary school students’ understanding (also intuitive) of basic geometric contents such as area measurement, polygons, and volume. In combination with Section 3, we can see a general trend of involving geometric understanding at an early education stage.

(3)

For secondary school students, the described research focuses on problems when working with formulas and the involvement of RME in theoretical geometric contents. It can be assumed that a general trend focuses on their difficulties in working with abstract geometry concepts (i.e., formula). In particular, the idea of involving reality in geometry education suits the general origin of geometric concepts in the own nature and environment.

5. Teacher Education in Geometry

The following studies focus on the teaching of geometry from an educator’s perspective. Again, the choice of references derives from the literature research as described in the introduction. This review results in three main research perspectives: the teachers’ theories about teaching as well as their understanding of geometrical procedures and the role of geometry education in the transition from kindergarten to primary school, on the one hand, and in the transition from higher secondary school to advanced mathematics being taught at university.

5.1. Teachers’ Theories about Teaching

In the context of the first point, the authors in [24] focus on the theory of Mathematical Working Space. The theory links the mathematical work being produced when working on mathematical tasks in a specific educational setting. In an empirical study with 85 students solving a task from plane geometry, the authors outlined three criteria for evaluating the work, namely the completeness of the work, its compliance with a geometrical paradigm or interacting paradigms, and the correctness of the results achieved from a mathematical point of view. Based on this, the authors identify five geometric work forms derived from the Mathematical Working Space Theory: Dissector (decomposition into subfigures), Surveyor (area calculations with measurements), Explorer (construct several figures), Constructor (sole construction), and Calculator (development of a formula).

Focusing on a theory-driven approach, too, the authors in [25] investigate the plausibility of organizing the mathematical knowledge used in teaching according to the tasks of teaching in which knowledge is used. Focusing on the theory of Subject Matter Knowledge, the authors investigate its measurement in the field of high school geometry. The authors suggest that experience in teaching geometry has a significant effect on the general and geometric knowledge dimensions. Concerning the latter, the components of understanding the students’ work and choosing givens for a problem could be distinguished and differently related to experience in teaching high school geometry.

5.2. Teachers’ Understanding of Geometrical Procedures

The authors in [26] investigate the processes involved in coping with mental rotation tasks. Motivated by the absence of a theoretical framework, the authors aim at the investigation of a teacher training program. A total of 122 pre-service teachers responded to a questionnaire with tasks that required mental rotation. From the analysis of the strategies used, the authors conclude a benefit of implementing holistic over analytical strategies. Still, the authors observe that a certain strategy does not necessarily lead to a correct result. The authors hypothesize that a mechanism works in the interface of the strategy used and the conclusion drawn, a hypothesis that the authors suggest should be investigated further.

In their study, the authors in [27] focus on the meaning attributed by future teachers linked to mathematical modeling processes. In addition, the variation in the meanings is investigated when involved in different modeling activities. In the framework of the study, the researchers design a proposal for teaching mathematical modeling that is implemented by the teacher in charge of a three-dimensional geometry course.

5.3. The Role of Geometry in the Transitions from Kindergarten to School and from School to Advanced Mathematics

A special focus on early mathematics teaching, in particular pre-service kindergarten teachers, is laid down in the study of [28]. In the context of a training program, the authors analyze the use of a Hypothetical Learning Trajectory on length measurements by 64 teachers. The analysis results in different profiles of the teachers based on the use of the Hypothetical Learning Trajectory and the identified mathematical elements: mathematical elements related to the magnitude; mathematical elements related to the measurement of length; or both elements. Based on this, the authors suggest learning opportunities and activities in order to learn the specialized knowledge for teaching length and its measurement as well as for the student’s mathematical thinking.

The study of [29] focuses on the value of advanced mathematics for secondary mathematics teachers. The value is measured from a mathematicians’ view. From the findings taken from 24 interviews with mathematicians, the authors see a potential of advanced mathematics in the connection of mathematical domains, the problem-solving abilities of teachers, and an increased epistemological awareness of mathematics. The results are further examined by presenting examples of connecting advanced and school mathematicians.

5.4. Summary

In terms of teacher education in geometry, we can summarize the following topics as being relevant in recent research activities:

(1)

Researchers connect theories (e.g., Subject Matter Knowledge) relevant in research and professional development initiatives for teachers with a focus on geometry. It seems that a link and probably a rapprochement between theory and practice is wishful and started from the teachers’ perspective.

(2)

This first focus is enriched by investigations of teachers’ understanding of relevant geometric procedures (e.g., mental rotation).

(3)

Finally, we see a focus on the support of the transitions from kindergarten to school and from school to university in terms of a long-term and holistic geometric education. Again, this trend can be seen in the context of the foci given in Section 3 and Section 4 concerning an early start of geometry education.

6. Argumentation and Proof in Geometry

Argumentation and proof have always been relevant for the teaching and learning of mathematics and particularly geometry [2]. Also, in our literature review, we found different research topics that combine argumentation, proof, and geometry. The main topics are the role of argumentation and proof in textbooks, geometric proofs from a student’s perspective, and geometric proofs from a teacher’s perspective.

6.1. The Nature of Proof and Its Role in Textbooks

With a focus on its nature, the authors in [30] discuss an extension of the definition of proof. Hereby, they propose to include so-called recipe proofs as a sequence of instructions to perform mathematical actions. Appearing in the form of imperatives, recipe proofs can recently be found in textbooks. Their work results in a model on recipe proof. In addition, Ref. [31] proposes on the basis of a textbook analysis the use of alternative approaches to teach proof that are linked to two components of its nature: the geometrical theory and the function of the proof.

6.2. Student’s Perspective on Argumentation and Proof

Despite these fundamental studies on the nature of proof, we can observe two different perspectives: a student’s and a teacher’s perspective on the argumentation and proof in geometry. Starting from a student’s perspective, Ref. [32] focuses on the intuitive acceptance of proof by contradiction in geometry aiming at investigating the gap between the logical correctness of a proof and the feeling of a proven statement. By means of task-based interviews, the author compares the acceptance of proof by contradiction and of indirect argumentation. Using Fischbein’s theoretical framework, he can observe differences in the formal knowledge and intuitive acceptance of proof by contradiction, for example, students producing a proof by contradiction without realizing its completeness. He suggests indirect argumentation as a compromise between a proof by contradiction and the request of more evident proof. The authors in [33] take advantage of the theory of conceptual blending when focusing on the students’ reasoning concerning the Sierpinski triangle. The authors focus on the work and understanding of ten students in terms of the triangle’s area and perimeter, especially in terms of the paradox of infinite perimeter and zero area. They could observe the following blending processes: composition, completion, and elaboration.

6.3. Teacher’s Perspective on Argumentation and Proof

The authors in [34] take a teachers’ perspective and focus on their evaluation of students’ proofs in geometry. Involving 44 teachers, the authors analyzed their expectations and their rating of instructions. The results show that participants rated lower instruction that deviated from their expectations. The author in [35] focuses in particular on the role of examples to validate a statement empirically and highlights two different teaching interventions to foster this idea of empirical examination after the proof construction. On a more general level, Ref. [36] investigates the opportunities for discussions that teachers create for their students when engaging with proof. The results show that teachers frequently encourage discussion in their classrooms. Still, the reasons why they encourage discussion vary according to their teaching experience in geometry.

6.4. Summary

For the topic of argumentation and proof in the context of geometry, the following main foci can be summarized:

(1)

A focus is on the (already traditional) question of the nature of proof, with a focus on its appearance and use in textbooks. We can see that besides new trends in geometry education, more traditional discussions are still part of current research initiatives.

(2)

Within the focus on students’ acceptance of proof by contradiction as well as their reasoning in paradoxical geometric situations, we can in addition see that these traditional questions are at least partly linked and enriched by the involvement of digital tools (cf. Section 7). The focus therefore describes an “old” question being raised in the context of “new” approaches.

(3)

In the context of teachers’ evaluation of proof, the use of empirical examinations, and initiatives for encouraging discussions about proofs, a strong link between this chapter and the foci of Section 5 (teacher education) emerges.

7. Digital Tools for the Teaching and Learning of Geometry

With current developments in the use of digital tools for education in general, the topic has gained significance in geometry as well. Most of the articles that we put in the category of Digital Tools describe the use of dynamic geometry systems (DGSs) or dynamic geometry environments (DGEs) in different research contexts. In addition, current research involves digital tools in terms of space geometry and geometry in the environment.

7.1. Dynamic Geometry Systems

The authors in [37] relate their research to the teacher’s professional development and take advantage of professional instrumental genesis to describe the classroom practices of teachers when using DGS and potential problems. The author in [38] uses a DGE in the context of argumentation and proof in the sense that the manipulation of figures can be the basis for conjectures. In her paper, she reports on the abduction process supported by dragging processes. The authors in [39] describe the potential of DGS for the process of reasoning after observing high school students when using GeoGebra in the context of minima and maxima geometric problems. The authors in [40] aim at a link between manipulation and deduction in 3D DGEs in the context of proof. As a basis, the authors refer to the former finding of a gap between students being able to formulate arguments from a drawing on the one hand and proving on the other. Analyzing the data gained in a case study, the authors conclude that the instrumental work in 3D DGEs can contribute positively to this aim. In similar research, Ref. [41] describes an inquiry-based learning environment for eighth graders to learn about 3D shapes and surfaces by means of GeoGebra. As in the previous research, the authors describe the results in the context of the students’ argumentation. The authors in [42] examine the role of an inquiry-based activity, too, designed as a game in a DGE. The aim of the game is to discover Euclidian geometry theorems for ninth graders, whereby students play against each other in a first version and against the computer in a second. The authors observe positive impacts on the students’ reasoning in terms of conjectures and if–then statements concerning the game’s winning configuration.

7.2. Space Geometry

As a consequence of the growing role of 3D imaging and 3D printing, the role of space geometry is gaining new significance [3]. Despite the previously reported use of 3D DGEs, [43] describe the use of 3D printing pens in the context of learning as making. With students of grades 5 and 6, the authors conduct lessons in which the students create their own artefacts immediately with a 3D printing pen. By comparing the students’ interactions with the material to students working without the 3D printing pen, the authors emphasize the role of the pens in co-constructing meaning, mathematizing, use of technology, and inventing.

7.3. Geometry in the Environment

The role of mathematizing in the context of 3D objects in the real world and digital tools is particularly relevant in the studies of [44,45]. Both research articles focus on the idea of outdoor mathematics, in particular math trails, by means of digital tools, i.e., MathCityMap and Actionbound. With a focus on geometry objects in the environment, the authors in [44] describe in a case study that formulated hints in the MathCityMap app can help students in modeling activities, i.e., simplifying and structuring as well as mathematizing. In addition, the authors assume that the automatic answer validation supports the students’ own validation of the result achieved.

7.4. Summary

The role of digital tools can be seen for geometry in the following aspects:

(1)

Researchers aim at integrating GDSs and GDEs in professional development, argumentation, and proof, as well as inquiry-based learning of geometry. Its usage therefore shows links to nearly all other topics linked to geometry.

(2)

The use of 3D DGEs and 3D printing pens brings new significance to space geometry. Whereas sketches (cf Section 3) were assessed as being helpful in terms of two-dimensional tasks, we can see a strong influence of digital tools in the context of visualizing three-dimensional problems.

(3)

Finally, we see the trend of using the digital support of geometric learning and modelling in the environment. Again, the role of geometry in its core is highlighted. If the origin of geometry—as described in the introduction—lies in the environment, it is obvious to use this also for geometric questions and to create an awareness of their connection.

8. Discussion and Future Directions

This review shows that the teaching and learning of geometry are significant in current mathematics education research. We have identified five different main topics. The first two topics address the specifics of geometry. It becomes apparent that the current research continues to refer to geometric ways of thinking and concepts, e.g., spatial reasoning, and likewise material didactic topics and contents of geometry, e.g., definitions and formulas. In the other identified subject areas, geometry tends to be a topic that is treated there alongside others; teacher education, argumentation and proof, and digital tools are not exclusively relevant to geometric content. Nevertheless, numerous geometry-related studies could be found here.

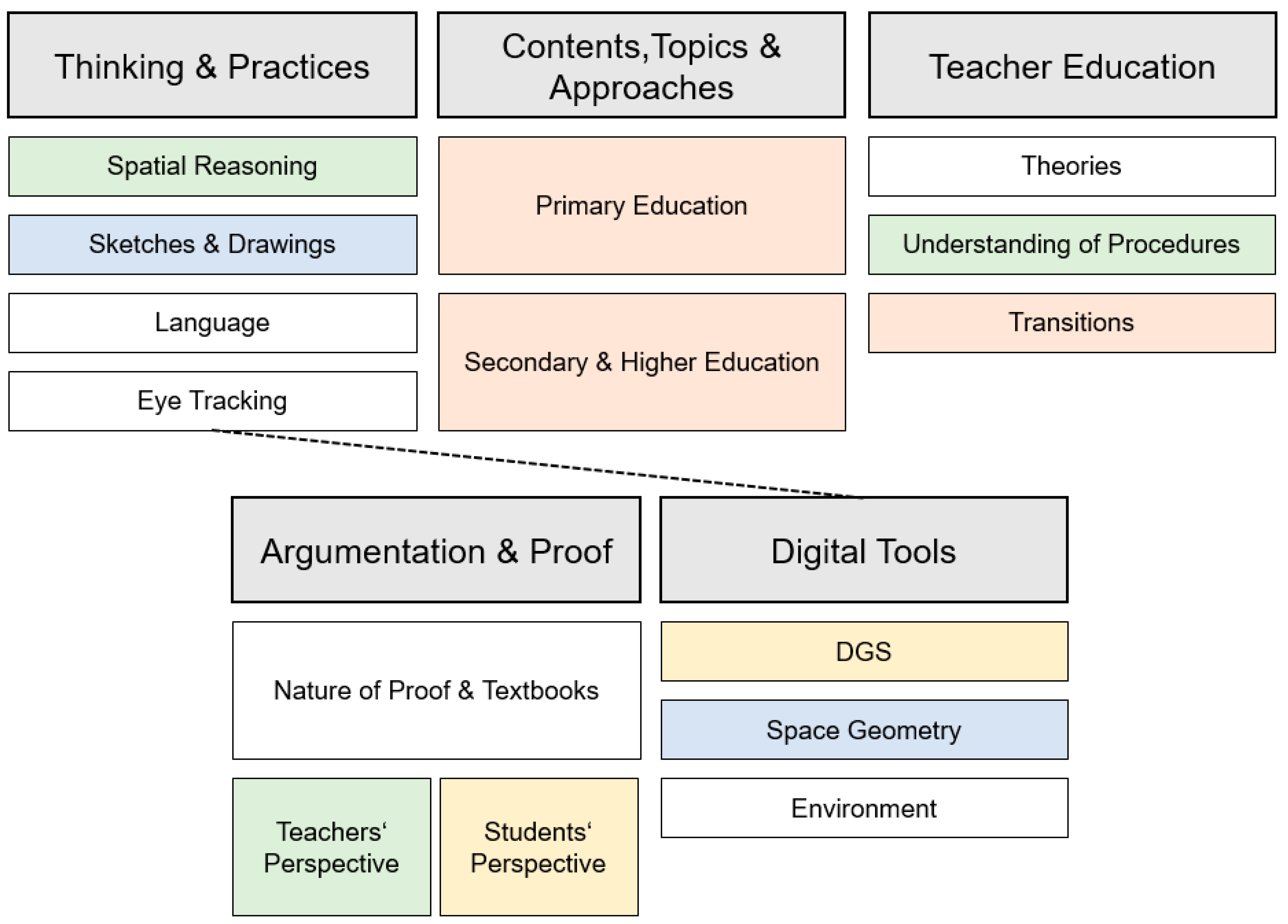
Furthermore, we can see several connections that arise implicitly and explicitly from the topics’ summaries. Our impression of the most important connections is highlighted in Figure 5. The four different colors (green, blue, red, and yellow) visualize interrelations of subdomains in the five identified topics. In particular, a strong connection seems to emerge between argumentation in geometry (especially from a students’ perspective) and the role of DGSs (yellow color), which, as with the first two topics, may represent a specificity of geometry. Symbolized by means of the dashed line, the use of eye tracking in geometry is linked to the role of digital tools, even though its purpose is more a methodological point of view instead of a usage by students. In addition, we can observe links between contents, topics, and approaches for primary/secondary education and the transitions from kindergarten to primary education and from secondary to advanced mathematics education that are addressed in teacher education (red color). Also, the role of sketches and drawings in the context of thinking and practices is linked to the subtopic of space geometry related to digital tools (blue color). Finally, the foci spatial reasoning, teachers’ perspective on argumentation and proof, as well as teachers’ understanding of geometric procedures combine three of the article’s main topics (green color).

Through these relations, the relevance of geometry in current research can be explained. It is a mathematical topic with long historical relevance. While the topics and ways of thinking are not alone in being the focus of current research, geometry shows that it is suitable as a topic for the study of current trends in general mathematics education. Vice versa, these current trends, e.g., in the area of digital tools, create new opportunities for geometry. For example, the topic of argumentation and proof has as long a history as geometry itself, yet the possibility of visualization, 3D animation, and discovery-based learning opens up new possibilities for the classroom. In addition to these connections, the inclusion of geometric content in the geometry learning of young children—before and from elementary school—can be reported in particular. It seems to be a main focus of research on various topics in relation to geometry that long-term and holistic learning is made possible. These results can be seen as a basis for further research activities with and through geometry.

However, limitations of the current research should be highlighted. First, a strong focus on case studies is evident. Even though important observations can be noted here, there still seems to be a lack of quantitative and representative studies in the field of geometry.

Perhaps this circumstance is a factor for the second, the potential discrepancy between the role of geometry in practice and the role of geometry in research mentioned in the introduction. Even if survey methods can be located empirically in principle, there still seems to be a lack of studies that make this discrepancy the object of their research. Questions such as What is the role of geometry in the current mathematics classroom? are addressed sporadically; however, more research seems to be needed here to reflect the significant research findings on the teaching and learning of geometry in the classroom and beyond.