Abstract
The adoption of the active learning paradigm presents a series of challenges and uncertainties. However, its adoption may result in better academic results and a more engaging attitude towards learning. In this sense, this paper presents a case scenario in which such a change of paradigm has been deployed, where escape rooms have been introduced as an assessment tool in an active learning context. The way to move through those escape rooms is by taking a series of questionnaires based on the knowledge acquired, such that failing a test keeps the group in the same position and passing it makes them move according to the grades obtained. Surveys and comments offered by students show they were more motivated and engaged after this task, and an improvement in academic performance has been detected.
1. Introduction
The use of gamification to drive active learning in on-site classes has been widely spread in recent years as a way to enhance learners’ engagement [1]. The introduction of game design elements within nongame contexts makes possible to enhance motivation in education, which leads to better performance according to what is appreciated by learning analytics [2]. Furthermore, gamification may be seen as a driving force to achieve the Sustainability Development Goal 4, sponsored by United Nations, related to ensuring inclusive and equitable quality education [3].
Focusing on the setup of gamification techniques into active learning deployments may boost students’ interest, improving the digital skills development expected at the workplace within the digital society. This leads to better academic achievements and an overall more satisfying learning process for learners [4]. In other words, gamification definitely facilitates active learning, which helps shrink the gap associated with education disparities and lack of motivation, specially in STEM-related subjects [5].
It may be said that the COVID-19 pandemic was the main catalyst for transformation in education in recent years, which led teachers to be more oriented towards the use of innovative teaching methods and tools [6]. On the other hand, students had to quickly become familiar with innovative e-learning tools and online classes, which opened up the door to apply diverse learning strategies once the pandemic emergency was over, such as e-learning, in both a traditional and hybrid form, where the first one implies purely online classes, the second one involves purely on-site classes and the third one allows blended learning, also known as extended learning, where part of the students are on-site and the rest are online, in such a way that all students may interact with each other and with the teacher [7].
Regarding the relationship between traditions and innovations in the pedagogical process, it appears that innovations enhance the educational process, although significant positive results are only achieved if pedagogical traditions are preserved, which means that pedagogical innovation must include traditionally oriented elements [8]. Apart from that, a good learning environment is widely related to different attributes according to diverse conceptual spaces in the educational process, such as variation and flexibility regarding the physical space, as well as active and self-directed learning with respect to the pedagogical space, and also safety with regards to the social space [9].
On the other hand, it is to be noted that there is a gap between research and practice when it comes to innovative education, as the impact of educational research knowledge is not being implemented in classrooms on a regular basis, as researchers’ works are often considered to be too theoretical, irrelevant and inaccessible and time consuming by practitioners [10]. In order to cope, researchers and practitioners should be connected together by policy makers, also referred to as knowledge brokers, whose role should be key in bridging educational research to educational practice [11].
Regardless, active learning may be seen as a generalized instructional process being characterized along two dimensions, such as for constructing knowledge and for deepening engagement, where the former may be viewed as antithetical to passive learning and the latter as antithetical to lecture [12]. This way, acquiring specific competences and skills is more engaging for scholars [13], whereas tutors act more as dynamizers and facilitators of the whole learning process by assisting and guiding in the process of scholars gaining knowledge and self-development [14].
There are different approaches to applying active learning in the classroom; thus, diverse strategies in designing in-class activities may be taken so as to engage scholars with both the material and each other, such as self-directed learning (SDL), student-centered learning (SCL) and flipped classrooms (FC) [15]. All three types move out of traditional-based passive learning, where the teacher takes responsibility for the learning process, thus passing such a responsibility of learning on to students, and hence moving information transmission out of the classroom [16], leading teachers to also take the role of brokers of both curricular knowledge and transversal competences [17].
Focusing on the flipped classroom paradigm, a common approach is the use of videos to convey information to scholars, which should be watched beforehand, making students contributors to the learning process. This allows them to make better use of time with their peers, as well as with the teacher [18]. Some of the benefits of this approach are the increased motivation and involvement of scholars both outside and inside the classroom, the improvement of comprehension and retention of the subjects taught, the enhanced development of competences and skills and the increase in satisfaction of both teachers and students [19].
Active learning activities are often linked to gamification, which may be seen as the application of game elements, not a fully fledged game, into a nongame environment, such as in a classroom [20]. On the other hand, such activities are frequently tied to game-based learning, which may be viewed as fully fledged games developed to provide new concepts and skills through the use of digital or nondigital games [21].
Within game-based learning, escape rooms are one of the most popular instances. Commercial escape rooms paved the way to educational escape rooms, where students make use of their skills to solve problems, which eventually will let them “escape” a room in a certain way [22]. This way, escape rooms are employed in educational contexts, aiming to promote cooperation, motivation and engagement [23].
In this paper, we expose our experience in the transition from a traditional passive learning environment to an active learning paradigm in a college subject devoted to teaching the basics of networking. We swapped from a teacher-taught paradigm to learner-led paradigm by converting the previous master classes into flipped classroom classes and transforming the previous written exams into both computer-based exams and escape rooms, which are taken by the students in a sequential manner at the end of each didactic unit for them to prove the knowledge acquired.
The rest of the paper is organized as follows: first, Section 2 is devoted to related work concerning escape rooms in educational environments; then, Section 3 exposes the contextualization of the subject being selected to implement the aforementioned active learning tools. After that, Section 4 explains the methodology employed. Next, Section 5 exhibits the fundamentals of the escape rooms being deployed. In turn, Section 6 presents the specifications of the escape rooms proposed. Afterwards, Section 7 presents a discussion about the results being obtained with the new paradigm, and eventually, Section 8 draws the final conclusions.
2. Related Work
Escape rooms are used in educational contexts as a didactic tool for both teaching and learning [24]. Such escape rooms are gameful experiences where participants form part of a compelling narrative, which gets them immersed into a collaborative and motivating adventure [25]. In order to complete the plot, players have to achieve the final objective of the game, given at the beginning by the game master, which may only be reached by solving a series of puzzles, missions and challenges related to the content of the curriculum within a given time limit [26].
Educational escape rooms may be completed live in the classroom or online, and they may use physical or digital tools and techniques to achieve the expected target [27]. One of the most commonly adopted descriptions of a escape room for education was coined by Nicholson, who defined it as a “live-action team-based game where players discover clues, solve puzzles, and accomplish tasks in one or more rooms in order to accomplish a specific goal (usually escaping from the room) in a limited amount of time” [28].
Therefore, an educational escape room presents the chance to engage the scholars in game-based learning because, as cited by Monaghan, “this offers a non-traditional, experiential, peer-group learning opportunity that fosters constructive interactions, leading to observations of one’s own and others’ unique leadership skills and styles” [29]. This way, one of the main targets is for students to feel that harnessing their individual talents makes them stronger as a team, whilst improving team-based learning [30].
Educational escape rooms may be applied to any educational degree and any subject within that scope, as a positive outcome is not only achieved by gaining basic curricular knowledge, but also transversal contents such as the development of social skills and attitudes, such as strong communication skills and team work ability [31]. It has to be said that gamification in general provides benefits focusing on four main areas: cognitive, emotional, social and motivational. In this sense, the pleasure and enjoyment experienced through the escape room increase the engagement in work and learning [32].
It is to be remarked that the skill and the challenge score should both be high, in such a way that the task becomes motivating for the player, where a flow state is achieved, according to the quadrant model of flow, established by Csikszentmihalyi’s flow theory [33]. Hence, any other combination of both factors may lead to unwanted results, such that low skill and high challenge results in anxiety, whilst low skill and low challenge leads to apathy, whereas high skill and low challenge cause boredom [34].
All activities found within an escape room are called puzzles. Basically, these puzzles use a simple game loop, such as a challenge to overcome, a solution which may be concealed and a reward for overcoming the challenge. This way, the puzzle keeps the solution hidden and it is up to the team to solve the puzzle to pass the challenge so as to achieve the prize [35]. Analogously, the challenge could be seen as a locked box, the solution as the combination and the reward as the content of the box.
Puzzles may be categorized as cognitive ones, which require thinking skills and logic; physical ones, which require the manipulation of artifacts; and meta-puzzles, which labels the last puzzle in a game, where the final solution is derived from the previous puzzles [36]. On the other hand, there are basically four ways to organize puzzles, where there is always a meta-puzzle to conclude the game. The first one is open path, where puzzles may be resolved in any sequence; the second one is a sequential or linear path, where solving a puzzle provides a clue for the next puzzle to be solved; the third one is path based, where there may be several paths of puzzles; and the fourth one is the combination of the previous structures, forming a hybrid structure [37].
Many studies have been carried out to assess the usefulness of escape rooms as active learning tools in higher education. For instance, some bachelor’s degree final projects have been devoted to escape rooms, such as that of [38], who proposed an instance called “fits and tolerances” devoted to the metrology part related to mechanical engineering and aerospace engineering, or [39], who designed an instance in the form of a video game entitled “laboratory 93” consisting of a 2D escape room with the use of BLE beacons for interacting with different rooms in the real world.
Likewise, some master’s degree final projects have also been dedicated to escape rooms, such as [40], who developed an escape room to evaluate the skills of a candidate applying for a vacant position, or [41], who designed a mobile application so as to keep record of all games performed. Additionally, some dissertations or PhDs have also focused on escape rooms, such as [42], who described an instance exploring the effects on perceptions of team processes and perceived team effectiveness, or [43], who presented an instance to deliver effective leadership training.
On the other hand, some master’s degree theses in secondary school teaching have been devoted to escape rooms to be applied to teenage scholars, such as [44], who proposed a breakout activity for students to get to know each other at the beginning of their first year of high school, as well as an escape room for the technology subject in that course in order to consolidate all knowledge acquired during the whole year. Additionally, ref. [45] designed an escape room to consolidate the basics of chemistry, focusing on the periodic table, as well as to formulate and name inorganic compounds, which are studied during the third year of high school. Additionally, ref. [46] plotted an escape room so as to retrieve the knowledge learnt in geometry classes during the third year of high school.
Moreover, ref. [47] proposes an escape room to review the concept of algebraic equation of the first and second degree, as well as different strategies of problem solving, which are taught during the second year of high school. Meanwhile, ref. [48] exposes an escape room devoted to auditing the knowledge acquired in the subject of English as a Foreign Language (EFL) for students in their third year of high school. Furthermore, Ref. [49] exhibits an escape room prepared for a range of Dutch secondary education students aged 16 to 20 related to consolidating their knowledge acquired in the biology lessons.
Focusing on higher education, specifically in medical science, ref. [50] proposes an escape room combining vascular surgery objectives, knowledge-based problems and technical skills to undertake the activity designed with time constraints. Meanwhile, Ref. [51] presents an immersive escape room to help resident trainees identify reportable patient safety priorities, where instructions for the game and clues to solve the puzzles are provided by means of quick response (QR) codes. Moreover, ref. [52] exhibits an escape room for nursery students for them to not only show their knowledge but demonstrate how to put it into practice, as well as showing transversal skills such as working under pressure, leadership or ability to work as a team.
Keeping to higher education, specifically in mathematics-related subjects, ref. [53] exposes an escape room initiative for math subjects in the degree of Pharmacy and Nursing during the pandemic lockdown and later restrictions to be performed in hybrid mode, e.g., online and in person at the same time. Meanwhile, ref. [54] presents an escape room to consolidate the knowledge of linear algebra in engineering, whilst [55] conducts a similar approach, although its target is focused on calculus.
As a matter of fact, existing literature about escape rooms in education comprises all levels, from primary school to higher education, and all fields, such physics or computing science, where students report high engagement, which implies they acquire new knowledge and skills by playing [56]. It is to be remarked that gamification and game-based learning have the same goal, as this also happens with serious educational games, even though they are all different in practice [57]. Regarding the latter, it may be seen as a custom-built game with a specific learning target; thus it need not be entertaining.
It is to be noted that gamification is commonly applied as an extra layer within existing environments, training or learning programs, whilst game-based learning is commonly conducted using existing games which may be repurposed for the learning target, whereas serious games are usually created from scratch for a specific objective. However, all of them usually share some design elements to enhance learning, such as rapid feedback, immersion, flow, clear goals, freedom to fail, collaboration, reflection and iteration [58].
At the end of the day, interactive classes start substituting master classes by means of gamification, game-based learning, serious educational games and other active learning techniques, where students become motivated to carry out their own learning process whilst having fun [59]. In this sense, active learning through a learning management system may be a centralized point for scholars to obtain study materials, as well as discussion forums and questionnaires, which may be further extended by including active learning activities such as digital escape rooms.
Furthermore, such systems may be also employed to obtain descriptive statistics out of quizzes or inductive statistics out of feedback provided by students. Additionally, motivation may be boosted by awarding digital badges to students for reaching some targets or for their performance in class, whereas leaderboards may motivate them to take a more active role during in class. Therefore, it may be said that a learning management system is definitely a tool that increases students’ involvement during active learning [60].
3. Contextualization
To start with, it is to be noted that the networking field may be considered as being located in the border of computing and telecommunication domains, as knowledge of both areas is mainly included in such a field. Hence, learning networking subjects at a higher education level implies a solid background not only in computer architecture and programming, but also on electronics, electromagnetism and optics.
We, the authors of this paper, are members of the Computing Engineering Department in the Miguel Hernández University (UMH), in Elche (Spain), where we teach subjects related to computing and networking fields in different degrees within the Polytechnic School of Elche at UMH, such as the degree in telecommunication engineering and the degree in information technology engineering.
In both degrees, the first course (composed of semesters 1 and 2) is devoted to common subjects geared towards learning the basics of mathematics, such as algebra and calculus, the background of physics, such as classical mechanics and electromagnetism, and the foundations of computer science, such as abstract data types and algorithmics.
Afterwards, the second course (composed of semesters 3 and 4) starts focusing on specific subjects within each degree, although the networking background at this stage is basically common in both cases, as that is the first contact with such a field within each degree, although they may both focus on different aspects of networking in other subjects taught in further courses.
This way, there is a networking fundamentals subject being taught in the fall semester dedicated to the lower layers of the OSI model, which range from 1 to 3, whose scope is how network traffic flows move through across the network. Furthermore, there is a twin subject being trained in the spring semester committed to the higher layers of the OSI model, namely those ranging from 4 to 7, whose scope is how network traffic flows are dealt with inside the end hosts.
In this context, we implemented an active learning methodology in the first of the aforementioned subjects in order to teach the networking principles related to layers 1, 2 and 3 of the OSI model. We think this is a crucial moment for the students when it comes to understanding the basics of networking, as it is the first time they encounter a network-related subject in college and the way they assimilate the foundational concepts of networking may make a difference to how they face further subjects in higher courses. Therefore, it is the ideal point to implement educational innovation techniques so as to both enhance students comprehension and boost students’ results related to the subjects belonging to the networking field.
4. Methodology
It is to be noted that the research question in this article is how we implemented an active learning paradigm in our classes in the aforementioned subject related to introduction to computer networks, where the methods applied to achieve that goal are going to be described in detail.
The previous paradigm being applied up until the last academic year was the so-called passive learning approach, where the teacher took all responsibility for the learning process in the classroom. However, we decided to undertake a paradigm change for this current academic year in order to embrace an active learning approach.
That change of paradigm implied a lot of work for us, the teachers, to get it ready. This work may be divided into three domains: theory sessions, practical sessions and evaluation sessions. Centering on the theory sessions, we already had the slides employed in our classes during the previous years, as well as a collection of problems related to such slides. However, we had to redesign many of those slides so as to adapt them to video recordings of each section within each chapter contained in the subject.
Most of that redesigning process was related to including more visual items in the slides, such as encircling key facts, overlapping elements or adding some extra text to further explain some important concepts. Furthermore, we had to include some slides with problem resolution activities, where a bunch of relevant problems are solved on a step-by-step basis.
Focusing on practical sessions, it just happened that the previous software we were using to carry out lab activities became unsupported; thus, we had to look for a different tool to undertake practical activities. Hence, as we were obliged to redesign all lab scripts to adapt them to such a new software tool, we did so by incorporating a more collaborative vision where students had to solve tasks in groups, where breakout rooms were encouraged.
Regarding the evaluation sessions, student tests used to be taken on paper, such that at the end of each didactic unit, a test was rendered. Afterwards, a final exam was taken at the end of the semester, even though scholars need not do it provided they had passed all previous chapter exams. However, a new evaluation strategy has been adopted, where computer-based tests have substituted pen and paper exams.
An evaluation session is held at the end of each didactic unit, where an individual test is taken first, followed by a group test in the form of an escape room environment. It is to be said that a specific scenario is built up for each instance of escape room in order to enhance motivation and engagement for the scholars, although in the end, the target is to present a series of group tests to them, which is going to be a part of their evaluation.
With respect to the motivation to undertake an active learning paradigm in our classes of the aforementioned subject, this is something that we had in mind for a long time, which eventually we decided to carry on for the current academic year. The main point was to try to implicate scholars more into the learning process, pushing them to become more responsible about the whole proceeding.
We were inspired by the proposals made in the references exposed in the bibliography, such that we drew the conclusion that all three domains stated above should be updated in order to properly follow an active learning perspective. In this sense, a flipped classroom was decided to be the approach for theory lessons, whereas practical lessons were geared toward collaborative activities.
Furthermore, evaluation procedures were moved from paper tests into computer-based testing, where individual tests are obviously taken by the student on their own, whilst group tests are presented in the form of an escape room. Focusing on the latter, their structures are all sequential paths, where the grades obtained in a given puzzle allow them to move forward a certain number of stages, rewarding the groups achieving better marks, as they will travel along in a faster way. Furthermore, each escape room was developed with a different theme in order to surprise students and get them more excited about the escape room.
In order to properly orchestrate the different contents of a subject, we are using Moodle as the Learning Management System (LMS), such that all the different syllabus needed in that subject are presented herein in an organized fashion. This way, Moodle may be seen as the hub where the subject is arranged, comprising theory materials, problems proposed, lab scripts, online exams and also escape rooms.
Focusing on the curriculum of the first one of the aforementioned subjects related to network foundations, it has been divided into five different chapters, where the first one presents an introduction to the OSI model, then the second one sticks to the physical layer, also known as layer 1. After that, the third one exposes the data link layer, also labeled as layer 2. Afterwards, the fourth one goes deeper into the media access control techniques carried out in layer 2, and finally, the fifth one undertakes the study of the network layer, also branded as layer 3.
Prior to implementing active learning strategies in this subject, the didactic approach was that of a frontal class for theoretical sessions, which is featured by the interactivity between teacher and students, where the active role is taken by the former. It is in charge of providing all contents through frontal lessons with the help of blackboards or slideshows. The students take a more passive role, as they basically listen to the explanations, although they also ask and answer questions posed by the teacher.
On the other hand, the didactic approach for the practical session was that of an interactive class, which is characterized by a higher level of interactivity between teacher and students, where the former provides part of the content with frontal lessons and design interactions, whereas the latter listen, even though they also participate in the activities by discussing and interacting with each other.
However, the implementation of active learning schemes turn both theoretical and practical sessions into hands-on classes, as they result in the co-creation of knowledge involving both the teacher and the students. In this case, the former has the role of designing and guiding the learning process, whereas the latter has the role of building content through an inductive process during their interactions with peers and the teacher.
In order to implement the hands-on learning framework for students to become an active player in the learning process, two different strategies have been followed when designing the theoretical and practical sessions. Regarding this theory, the flipped classroom approach has been deployed, where a video has been produced for each section of the chapters which are part of the subject.
This way, students may watch the corresponding video for a given session, allowing the teacher to dedicate the class time to solve questions about the videos, and in turn, being able to propose problems for students to be resolved in small groups, permitting them to apply the concepts learned. With respect to practical activities, a set of lab activities based on the mininet application run on Linux hosts are to be resolved in groups by the students in order to empower them to practice and experiment with the lessons previously learnt.
Evaluation of each chapter is carried out after completing the theory and lab sessions devoted to it. The proposed evaluation system consists of two parts to be completed in the same session, where the first one involves a computer-based quiz with a number of questions randomly extracted from a pool stored in Moodle for each individual chapter. Such questions may have different formats, such as filling in the blanks, choosing the right answer out of a group, selecting the right answers out of a bunch, or solving calculated operations with random inputs. Regarding the second part of the evaluation, it involves a escape room, resulting in five different escape rooms proposed for each of the didactic units, which are exposed in the following section.
Eventually, the conditions required to clear each chapter are to both pass the quiz and the escape room. This is the way each chapter is evaluated, which results in students passing the subject without a final exam if all chapters have been cleared. Otherwise, if any of the chapters have not been cleared, then students must take the final exam composed of a quiz and some problems to be resolved, although they only need complete the activities related to the chapters that had not been cleared before. This way, students get motivated to study for the chapter quizzes and for the escape rooms, as they may avoid taking the final exam if they achieve a good performance in all chapter quizzes and escape rooms.
Specifically, quizzes are composed of 30 questions to be resolved in 30 min. Quizzes are taken at the beginning of a session; thus, the rest of such a session may be devoted to undertaking a escape room, whose aim is not only amuse the students, but also to further test them on the knowledge acquired during the corresponding didactic unit, as the way to get through the escape room is to solve different quizzes about it. The questions for both the quizzes and the escape rooms are taken from the same bank, composed of some hundred questions for a given chapter. This way, students not only thoroughly prepare for a quiz, but they may take advantage of that preparation to perform better in the escape room, which seems to further motivate them to study.
5. Escape Room Representation
In this section, the structure of escape rooms is detailed from different points of view. To begin with, some details about its schematic representation are given, that being a diagram of states and transitions for the proposed escape room, which is fit for the Spanish grading system.
Additionally, a mathematical representation is proposed with two alternative views, with an arithmetic one presenting an expression for transitioning to a new state from a previous one according to the grades obtained in the quizzes, along with an algorithmic one displaying snippets of pseudocode so as to portray the dynamics of the escape room.
5.1. Schematic Representation
In order to present a schematic diagram related to this kind of escape room, it is necessary to state some previous considerations. Let us suppose that level j has an initial spot and a final spot , where the states within that level are all connected between both ends in a daisy chain form. Each state is defined as , with j showing the level it belongs to and k identifying the different states within that level in a sequential order.
The transition from the initial spot within level j, namely , and the first stage of that level, namely , is labeled as , meaning that it is an internal transition, resulting in an automatic movement from the former to the latter. Likewise, the transition from the last stage of a level j and the final stop of that level, namely , is also branded as , accounting for an automatic movement, which in turn leads to the initial spot of the next level, namely . As exposed before, it moves to the first state of that next level, meaning , in an automatic fashion as well.
According to these indications, it is to be noted that reaching the last stage of the last level will automatically lead to the final spot of that level, which in turn will lead to the end of the escape room, which will be depicted as getting the winner’s cup.
Furthermore, it is to be noted that according to the Spanish evaluation system, the minimum mark to pass an exam is 5, whereas the maximum mark is 10. Hence, considering only integer marks to keep it simple, there are six stages between 5 and 10, with the same number of states considered within each level. Additionally, if four levels are considered in a escape room, which account for four different contexts to be traversed during each escape room, then it will be over after clearing the fourth level.
Therefore, a schematic representation of the behavior of the proposed escape room with the Spanish grading system is depicted in Figure 1. The nomenclature will be explained in detail in further subsections, although three types of transition may be distinguished therein. On the one hand, there are transitions represented by , which happen when any end involved in a transition is either an initial spot, namely , or a final spot, namely , or even both of them. Those stands for internal transitions, which are supposed to be automatic, meaning they are transparent to the students.
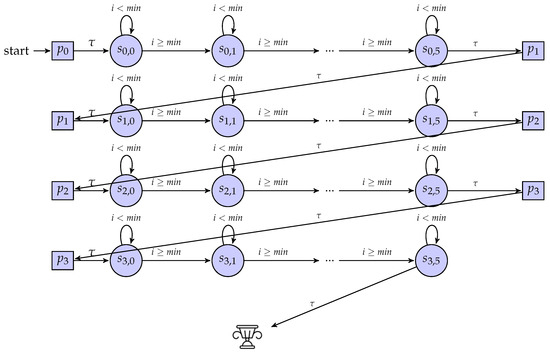
Figure 1.
Flow chart for the behavior of the proposed escape room with spanish grading system.
On the other hand, there are loop transition on each state, namely , which take place if students fail to pass a test, namely , such that the previous state is kept if no movement occurs. On the contrary, there are other transitions labeled as , which occur if students do pass a test, and in that case, a new state will be reached within the same level, where the magnitude of that movement will be exposed in the subsection dedicated to mathematical representation.
5.2. Mathematical Representation
As stated above, the escape room structure may be seen as a collection of rows, with each of those referred to as level j. Moreover, every level is composed of a number of states, each of those referred to as state k. The path to traverse the escape room has been decided to be sequential, such that each level needs to be cleared before moving to the following one. This implies taking the path from left to right across the states within a level, where the magnitude of each movement depends on the grade obtained in a particular test about the didactic unit the escape room is based on.
Centering on the Spanish way of evaluating, where grades range from 0 to 10 and 5 is the minimum mark to pass, it is proposed to have six states per level, such that being at the first state of a level and obtaining the top mark in a test will head for the last state of such a level, which in turn will lead to the first state of the next level. Sticking to the Spanish version, each test contains 10 questions, where each of those is graded as either correct or otherwise, thus earning 1 point in the former and 0 points in the latter, whilst the overall mark will account for the addition of the points obtained in all 10 questions.
On the other hand, the number of levels proposed for each escape room is four. Each of those is related to a different subtheme within the overall theme of one particular escape room. This way, a group of students getting top marks in the tests four times in a row may end the escape room, although this perfect situation may hardly happen.
The mathematical foundation behind the movement throughout the proposed escape room may be expressed in an arithmetic fashion by means of an expression to calculate the movement related to a certain grade in a test, which may further be employed to find out the new state attained due to that movement, considering the specific conditions of the structure of the escape room described above. Alternatively, the new state achieved may also be expressed in an algorithmic manner, which may help a main algorithm to describe the movement throughout the escape room.
First of all, let us present a generic case to calculate the movement linked to a certain mark achieved in a given test, which is expressed as the variable i. This generic scheme could be applied to the evaluation system of any country by particularizing the specific digits of the constant values related to and for that given country. In this sense, the constant value is referred to as the minimum grade to pass and the constant value is taken as the maximum grade. Moreover, variable represents the actual state within a given level, that being the state before taking the test, and variable represents the next state within the same level, that being the state after taking the test.
In this context, Equation (1) exhibits the expression for the movement assigned to the grade obtained in a given test, whereas Equation (2) depicts the expression of the new state actually assigned to such a grade, composed of the addition of the previous state and the movement calculated, along with a correction factor which might be applied in order not to overpass the last state within a level.
As a side note, it is to be noted that the symbol represents the quotient of the integer division of x by y, whereas the symbol represents the remainder of the integer division of x by n, also known as congruence modulo n.
Focusing on the Spanish evaluation scheme, the constant value is the minimum grade to pass a test and constant value is the maximum grade in a test, whereas grades lead to failing a test. Hence, expression (3) exposes the movement assigned to a certain mark in a test, whereas expression (4) displays the new state actually associated with that mark.
Hence, failing the test implies that the student will remain in the same state, where , whilst passing the test facilitates moving forward within the current level, where , taking into consideration that reaching the last state within the current level will lead to promotion to the next level. This, in turn, will bring them to the first state within such a level. Furthermore, getting to the last state of the last level will take them to the end of the escape room, which is represented by the winner’s cup.
Regarding the expression for movement for the Spanish evaluation system cited above, as quoted in (3), it is composed of three factors. The first one zeros marks below the threshold to pass, which is expressed by , because of applying the integer division by just that amount. This way, the integer division of a lower figure than the threshold yields zero, whilst it yields one for the threshold or above for the range of grades managed herein. However, there is an issue with the top mark, as it simply doubles the threshold for being twice as that amount, because .
However, the second factor solves this issue by halving only the top mark, whilst leaving the rest of the grades as they are. This is achieved by applying the properties of powers, such as in the former and in the latter, although that is taken with a negative exponent, such that , which results in .
Furthermore, the third factor carries out the real movement for the marks above or equal to the threshold, as the lower ones have already been canceled by the first factor, where such a movement is one hop away for the threshold, two hops away for the successive of the threshold, and so on, all the way to the top mark, which is six hops away.
With respect to the expression to find the next state for the Spanish evaluation system cited above, as quoted in (4), it is to be noted that it takes the expression for movement as its foundation, which is added up to the current state. This acts as an offset, and it is further subtracted to a correction factor to avoid overpassing the last stage within a given level. Such a correction factor contains two factors itself, where the former detects the cases where the last stage within a level is overcome and the latter applies the precise offset to stick to the aforementioned last stage.
In order to prove the aforementioned expressions for movement and new state in the Spanish evaluation system, namely (3) and (4), the following tests have been undertaken for the different scenarios available at a given level. In fact, the case is shown in Table 1, is portrayed in Table 2, is displayed in Table 3, is depicted in Table 4, is viewed in Table 5 and is appreciated in Table 6. Furthermore, the case , that being the last state within a level, does not apply, as it automatically gets forwarded to the first state of the next level, so it becomes the case .

Table 1.
New state when current state .

Table 2.
New state when current state .

Table 3.
New state when current state .

Table 4.
New state when current state .

Table 5.
New state when current state .

Table 6.
New state when current state .
An alternative way to represent the dynamics of the proposed escape room is by using snippets of pseudocode. This approach helps display the sequence of events happening according to the rules set in the structure of the proposed escape room in the form of flow diagram coded in pseudocode. The first algorithm proposed aims to find the new state, namely , considering the grade obtained in a given test, namely i, and the current state, namely . The latter are included as the input of the algorithm, whilst the former is the output, which is in fact returned after running it.
Looking at Algorithm 1, it may be seen that variables and are defined for the Spanish evaluation system, although when those lines are deleted, the algorithm becomes generic and could further be particularized for other grading systems. Additionally, this algorithm offers the same result as its arithmetic counterparts to calculate the new state, although it takes a logical approach, which allows us to declare conditions in order to distinguish the three different cases that are available. Moreover, this versatility permits the calculation of the new state without the need to determine the movement beforehand.
| Algorithm 1 Find New State |
Input: i, Output:
return |
Regarding the cases exposed, the first one exhibits the case where the grade in a test is lower than the threshold to pass it, which is determined by the condition and results in no movement whatsoever. The second one exposes the case in which a test is passed, which generates a movement that overlaps the last state within a level. This is expressed by the condition and results in moving until the last state of such a level, which in turn will lead to the first state of the following level. The third one includes the rest of the cases, such that a test is passed and the movement generated does not overlap the last state within a level.
Additionally, a main algorithm is presented in order to describe the sequence of events occurring when staring out in one of the proposed escape rooms. First of all, the initial value of the level is established, namely , as well as the initial state within that level, namely . Additionally, the number of levels within a escape room is defined in the variable , which in this case is set to fpur.
Afterwards, there is a loop represented by the clause , whose exit condition is that all levels of the escape room have been cleared. This does happen once the current level j equals variable , as the first level in the escape room is considered to be zero; thus, the last one will be . Hence, when such a level is cleared, the the variable j will reach the value of .
The actions to be repeated over and over again in the loop, until the exit condition is met, meaning the escape room is over, are as follows. First of all, a 10-question test is taken by a group of students, whose score is stored in variable i. Then, the procedure is called with the arguments i and , namely the current state, which will be taken as parameters by such a procedure, and after its execution, the appropriate value of is returned, namely the new state.
After that, it is checked whether the new state is the last state within a level. On the one hand, if this is the case, then the level is incremented, whilst the current state is set to 0, implying the first state of the new level. On the other hand, if that is not the case, then the value of the new state is assigned to the current state .
At this point, the actions within the loop have all been executed, which means that the exit condition of the loop is checked out again and the cycle is restarted again if the exit condition is not met. However, once such a condition is met, the loop is over and so is the main algorithm, as there is no more code to be executed, meaning that the escape room is over as the escape room is finished for that group of students.
5.3. Model Verification
From the point of view of usability, the model proposed is that of an escape room with a linear path, where puzzles are organized in a sequential way. However, the magnitude of the steps to traverse the model depends on the grades obtained during the group tests, which opens the door for student groups to apply different strategies, such as trying to achieve top marks and taking more time to take a test, or trying to get lower marks so as to speed up test taking.
A potential improvement in the design of the proposed escape room may be to change the sequential path with a hybrid structure, where shortcuts along the path may be found in order to move faster, as at the end of the day, the ultimate target is to reach the end of the path while investing the shortest time so as to get higher marks.
Otherwise, from a more formal point of view, the proposed model representations may be formally verified by applying logic. In this sense, let us start out with the schematic one, which constitutes the backbone of the proposed model. Figure 1 depicts a sequential path composed of four levels, with six stages per level. It is easily seen that the only way to traverse the path from beginning to the end is to go forward, whereas the magnitude of the hops within the path depends on the marks obtained in the diverse group tests. In this context, the sole manner not to move ahead is to fail all tests.
However, by applying the fairness condition, which is a common tool used to verify formal representations, it may be said that at some point in time, a test will be passed, and if there are no time constraints, then we may conclude that any team will eventually finish the proposed sequential path, as they will eventually pass enough tests to travel along the whole path. Nonetheless, it is to be pointed out that we do have a limited time in our classes to dedicate to escape rooms; hence, it might happen that a number of groups of students are unable to finish a given escape room, even though that fact does not invalidate the aforesaid premise.
Moving on to the mathematical representation, Algorithm 1 provides the new state in relation to the previous state and the grade obtained in a test. In this case, Table 1, Table 2, Table 3, Table 4, Table 5 and Table 6 display all possible combinations of the antecedents, which happens to offer a coherent consequent in all cases, according to the rules exposed above. With respect to Algorithm 2, it exhibits the flow diagram of the escape room, where a loop describes the movement within the path and the loop condition is to reach the end of that path, thus indicating the moment at which the escape room is complete.
| Algorithm 2 Main |
|
6. Designs for the Escape Rooms Proposed
Here, we discuss the make up of the five proposed escape rooms in order to help assess the five didactic units exposed above. It is to be reminded that there is a question bank in the LMS for each didactic unit, containing more than a hundred questions. Many of them are calculated activities with randomized inputs, which effectively extends the size of each question bank a great deal, thus minimizing the risk of cheating during the tests.
As stated above, there is an evaluation session after finishing up each didactic unit, where an individual test is first taken, and the rest of the session is dedicated to carrying out the corresponding escape room in groups of students; hence, each group may take advantage of the knowledge attained by all of its members so as to keep passing the different 10-question tests they may encounter during their journey to clear the escape room in the fastest possible way in order to get higher marks.
It is to be reminded that we consider a escape room as an incentive to encourage students to take tests in groups. In other words, the escape room is just a form of scenery provided in order to motivate them to take a series of group tests related to a didactic unit. Therefore, the escape rooms implemented for each didactic unit have no direct relation to the syllabus of each chapter, although their target is to get the students into the right mood for each of the proposed scenarios.
6.1. Zombie Apocalypse at University
Chapter 1 is branded as “Introduction to Networking” and its aim is to outline the OSI model, which is the theoretical framework of protocols governing all networking communications. Meanwhile, the TCP/IP model is also presented as the practical implementation of the OSI model, such that all network communications make use of this.
The escape room developed for chapter 1 is based on the concept of a zombie apocalypse at university, where a short debriefing is given at the beginning, stating that zombies have taken control of the university and they are turning all personnel therein into zombies. In this context, the mission is to go through different buildings throughout the college campus in a sequential order to try to find the vaccine to revert the zombification process.
The four levels prepared for this escape room are defined as the buildings to be traversed in a sequential manner:
- Faculty
- Administration
- Laboratories
- Rectory
6.2. Star Wars: A New Hope
Chapter 2 is entitled “Physical Layer”, also known as layer 1 of the OSI model, which is dedicated to exposing how data transmission takes place, mostly in digital format. Moreover, the main features of the most commonly used transmission media are exhibited, along with other concepts as multiplexing or data encoding schemes.
The escape room undertaken for chapter 2 is based on the film “Star Wars: a New Hope”, where a short speech is given initially, sketching the plot of the film, such that students are taken throughout its most significant events. In this context, the mission is to follow the adventures of the main characters of the film in a sequential order to try to eventually face the imperial space station called the Death Star.
The four levels proposed in this escape room are stated as parts of the film plot to be swept in a sequential fashion:
- The Rebel Alliance.
- Tatooine.
- Galaxy Chase.
- Death Star.
6.3. Lord of the Rings
Chapter 3 is named “Data Link Layer”, also known as layer 2 of the OSI model, which is devoted to explaining how communications between two end points take place within a local network. Its main features are depicted; these include physical addressing, error control through specific encoding systems and flow control.
The escape room carried out for chapter 3 is based on the film “Lord of the Rings”, where a brief speech is offered at the outset, sketching the storyboard of the three films within that trilogy, such that students are drawn into the plot if they do not know about it, or they can brush up on their knowledge of it. In this context, the mission is to go along with the main characters through the story plot of each film within the trilogy.
The four levels exposed in this escape room are dedicated to first presenting the background, followed by each of the plots of the three films displayed sequentially:
- The Adventure Begins.
- The Fellowship of the Ring.
- The Two Towers.
- The Return of the King.
6.4. History of Computing
Chapter 4 is labeled “Media Access Control”, which is an extension of the previous chapter devoted to layer 2 of the OSI model, where multiaccess protocols to local networks are reviewed. The journey starts out with random access and control access, followed by the most typically used nowadays, which are Ethernet and Wi-Fi.
The escape room designed for chapter 4 is based on the history of computing, where a small debrief is conducted to start with, exposing the main steppingstones of computing throughout human history until it reaches the point where we are in this day and age. In this context, the mission is to go along the different stages proposed, moving from the first historical traces of writing and math, the construction of mechanical devices, turned into electronic ones and the current state of the art.
The four levels exhibited in this escape room are devoted to the relevant periods, measured in centuries, for computing history in a sequential way:
- Ancient Times
- 17th–19th Centuries
- 20th Century
- 21th Century
6.5. The Movies of My Life
Chapter 5 is tagged as the “Network Layer”, also known as layer 3 of the OSI model, which is committed to explaining how communications between two end points take place regardless of the network on which they are located. Moreover, its main features are displayed, which include packet switching, logical addressing and the basics of routing.
The escape room designed for chapter 5 is based on the history of cinematography in recent years, where a little debrief is given at the outset, highlighting some of the most significant films from the last decades up until now. In this context, the mission is to go along the selected films in the different decades proposed, starting out in the 1980s and moving forward to the following decades all the way to the current times.
The four levels presented in this escape room are committed to showing some blockbusters produced in recent decades in a sequential order:
- 80s Decade: 1980–1989.
- 90s Decade: 1990–1999.
- 00s Decade: 2000–2009.
- 10s–20s Decades: 2010–now.
7. Discussion
It is to be noted that the swap from traditional learning to active learning has boosted the motivation and engagement in the attitude of students, as well as their academic performance, and it appears that the main factor responsible for such a change is the introduction of escape rooms as an assessment tool.
To start with, comments provided by students state that they are more motivated to watch the videos provided for the flipped classrooms, as they have become more competitive thanks to escape rooms. That competitiveness induce them to perform better by achieving better marks during the tests, and that point encourages them to review the theoretical materials more carefully in order to better understand the concepts exposed in the didactic unit. As an extra point, this will also allow them to perform better in the individual tests, as they are more prepared when taking their exams. This causes their overall performance in the assessments to rise, resulting in better marks.
On the other hand, some comments addressed the engagement of the scholars when it comes to the escape room, as they became absorbed into the mood of the escape room, which brought them into a flow state. Other comments go about pointing out the fun students have during escape room tasks, as opposed to the tension they experience during traditional exams.
Furthermore, surveys were passed to scholars, where they reiterated their support of the active learning context. The results of those surveys reveal that computer-based exams had a good acceptation rate, whilst the flipped classroom approach had a better acceptation mark. However, the use of escape rooms as an evaluation tool received the highest acceptation rate with a significant difference, as most of the students cited the motivation and the engagement they feel in relation to escape rooms.
Additionally, students’ academic performances improved since the introduction of the active learning paradigm. It appears that the reason for the increment in their grades is because they more thoroughly studied the materials provided in order to become more competitive in the escape rooms, as well as to enjoy the overall experience more and to be more collaborative with their team peers, all of which has all been corroborated by the students’ comments and surveys.
The measure of academic performance has been carried out by comparing the average grades obtained by scholars in previous academic years, where a traditional learning paradigm was employed, with the average marks attained by students in the current academic year, where an active learning paradigm has been undertaken.
This resulted in both more students passing the subject and an increase in marks overall, as we saw nearly a 15% rise in the former and nearly a 20% rise in the latter. Those figures are pretty similar to the rates quoted in the literature for STEM education when it comes to adopting an active learning approach in a subject.
Specifically, regarding the former, ref. [61] reported a 16% increment, whereas with respect to the latter, ref. [62] observed a 21.4% increase. Consequently, a better academic performance implies a better understanding of the content of the subject, which will help students consolidate knowledge, as well as helping them to better follow more advanced subjects relevant to their field of study.
In order to measure the level of engagement of students, the ISA engagement scale has been used. According to this scale, engagement may be seen as a positive state of mind relating to three different dimensions: intellectual, social and affective. Hence, taking all three together gives an overall level of engagement for each person [63].
The scoring has been obtained through a series of nine questions measured from 1 to 7, where the former stands for strong disagreement, whilst the latter stands for strongly agreement. There are three questions aimed at each of the three facets of engagement, where the average of each facet is calculated, and in turn, the average score overall is found out. The top score is obviously seven in each facet and overall, whereas the expected score is above six.
In this context, intellectual engagement measures the degree to which students are intellectually absorbed in a task, whilst social engagement measures the extent to which scholars feel socially connected during a task. Meanwhile, affective engagement measures the degree to which students experience positive feelings when doing a task.
The final item set of questions is presented in Table 7, which is cited from the original paper where the ISA engagement scale is defined [64].

Table 7.
The ISA Engagement Scale.
Regarding the feedback collected from students, this may be divided into two types: comments and surveys. On the one hand, the former were comprised by means of oral suggestions made by the students during the classes and the escape room, where they basically reinforced our decision to adopt an active learning paradigm, especially by embracing escape rooms as part of the evaluation process.
On the other hand, the latter were composed of standard surveys and the ISA engagement scale. With respect to the first one, they are standardized for all subjects at our college and they basically ask students several questions which encourage them to rate what they think about the subject contents and how the teachers performed. In this case, the results attained overlapped those achieved in previous academic years.
With regard to the second one, the scores obtained in the different domains which were part of the ISA engagement scale were 6.2 for the intellectual one, 6.5 for the social one and 6.5 for the affective one, resulting in an overall score of 6.4. We are happy about the outcome achieved, even though we expect to improve in the coming academic years.
From our point of view, the adoption of active learning techniques supposed some hard work at the beginning in order to get the contents of each didactic unit recorded, as well as preparing all the escape room scenarios. However, we really appreciate the change of dynamics in the classes thanks to this new approach in terms of motivation and participation. With respect to the flipped classroom paradigm, we acknowledge the contribution to getting scholars more involved in their classes by asking more questions and responding better to practical exercises.
Regarding the escape rooms, we noted the engagement and the good mood of the students in every session, providing them with a remarkable experience, whilst we noted an increase in their marks with respect to the master class paradigm. Therefore, we must say that the effort to swap to the active learning paradigm was worth it.
8. Conclusions
In this paper, the change of paradigm from traditional learning to active learning in the context of higher education has been described. Prior to that point, master classes were carried out, where teachers played an active role, whereas students played a passive one. However, a flipped classroom has been put in place, swapping the students role into an active role, whilst teachers adopt more of a dynamizer role. This promotes participation and collaboration among students.
This assumption of an active learning paradigm also affects how assessments are conducted. Previously, written exams used, although computer-based activities are now used instead. Two evaluation activities are carried out, where the first one is an individual questionnaire to assess each didactic unit out of a bank of theoretical questions with several possible answers, allowing students to choose one or more correct answers, as well as calculated activities with randomized input so as to avoid cheating.
Regarding the second assessment activity, a escape room has been developed to be undertaken right after each individual quiz. Students get together in groups with the purpose of solving a series of sequential puzzles, each of those consisting of a number of questions selected from the aforementioned bank of questions, until they may reach the end of the game, which is represented by the winner’s cup.
Hence, five escape rooms have been designed in order to cover five didactic units, each of them with different themes. The first one involves a zombie apocalypse at university, the second one follows the plot a Star Wars film, the third one involves the Lord of Rings trilogy, the fourth one is based on the history of computing and the fifth one concerns some famous films released in the last few decades.
With respect to the students’ opinions about the active learning paradigm adopted, most of them agree with it and the activity they like the most is the implementation of escape rooms. Their comments demonstrate the increase in motivation and engagement when the exam day comes, as they now consider it the escape room day. This motivation makes them study more; hence, they are better prepared for their exams, as the questions come from the same bank as those posed in the escape room.
Likewise, the possibility of clearing a didactic unit by performing well in both the individual exam and the escape room gets them further motivated, as they associate escape room day with engagement and fun, as opposed to the final exam day, which is perceived with anxiety and pressure. Therefore, it seems that the adoption of active learning offers interesting benefits for the students in terms of motivation and engagement, as well as better academic performance.
In summary, the research question in this paper is about how to implement the active learning paradigm in the sessions of our subject devoted to network fundamentals for the current academic year in order to boost performance, taking into consideration that traditional learning has been in place for many years. In order to deploy an active learning approach, a combination of methods have been put in place, such as swapping traditional master classes for theory with a flipped classroom strategy and changing our lab scripts for practice so as to encourage more collaboration.
Furthermore, the evaluation system substituted a paper-based exam to be fulfilled on an individual basis with a double computer-based exam, where one is taken individually and the other one is taken in groups in the form of a escape room in order to be more appealing to scholars. It is to be said that after analyzing the students’ outcomes, along with their comments and surveys, it seems clear that embracing the active learning paradigm has led to a whole range of benefits, such as a higher rate of passing students, higher average grades and an increase in engagement and motivation towards this subject due to the escape rooms.
Additionally, it is to be considered that the whole active learning paradigm have been implemented in this current academic year. Therefore, some improvements may be carried out in the near future in order to achieve better results from the students, such as achieving a better quality in the video recordings for the flipped classrooms, adding more problem-solving scenarios to those recordings or designing more collaborative lab scripts.
Focusing on the escape rooms, some enhancements may be geared to come up with other plots for escape rooms to be more surprising for the students, increase the questions within each question bank so as to avoid cheating or prepare new calculated operations with random inputs so as to avoid students memorizing the answers.
Moreover, a new twist in escape rooms could be incorporated by changing the sequential path of the escape room to a design with shortcuts. This way, students may try to apply some strategies related to obtaining not the highest possible mark in group tests, but the most interesting mark according to their current position in order to advance the most. This will minimize the time taken to traverse the whole escape room path, although the students might or might not get the desired mark in each test. Regardless, all these enhancements are geared for students to keep improving both students’ grades and their engagement.
Author Contributions
Conceptualization, P.J.R.; Formal analysis, P.J.R.; Supervision, P.J.R., S.A., K.G., C.B. and C.J.; Validation, P.J.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing is not applicable to this article as no new data were created or analyzed in this study.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DBR | Design Based Research. |
| FC | Flipped Classroom. |
| OSI | Open Systems Interconnection. |
| SCL | Student-centered learning. |
| SDL | Self-directed learning. |
| SEG | Serious Educational Games. |
| STEM | Science, Technology, Engineering, Mathematics. |
| TCP/IP | Transmission Control Protocol/Internet Protocol. |
References
- Reyssier, S.; Hallifax, S.; Serna, A.; Marty, J.C.; Simonian, S.; Lavoué, E. The Impact of Game Elements on Learner Motivation: Influence of Initial Motivation and Player Profile. IEEE Trans. Learn. Technol. 2022, 15, 42–54. [Google Scholar] [CrossRef]
- Okubo, F.; Shiino, T.; Minematsu, T.; Taniguchi, Y.; Shimada, A. Adaptive Learning Support System Based on Automatic Recommendation of Personalized Review Materials. IEEE Trans. Learn. Technol. 2023, 16, 92–105. [Google Scholar] [CrossRef]
- Park, S.; Kim, S. Is Sustainable Online Learning Possible with Gamification?—The Effect of Gamified Online Learning on Student Learning. Sustainability 2021, 13, 4267. [Google Scholar] [CrossRef]
- Murillo-Zamorano, L.R.; López-Sánchez, J.A.; Godoy-Caballero, A.L.; Bueno-Muñoz, C. Gamification and active learning in higher education: Is it possible to match digital society, academia and students’ interests? Int. J. Educ. Technol. High. Educ. 2021, 18, 15. [Google Scholar] [CrossRef]
- Marin, S.; Lee, V.; Landers, R.N. Gamified Active Learning and Its Potential for Social Change. In Transforming Society and Organizations through Gamification, 1st ed.; Palgrave-MacMillan: Cham, Switzerland, 2021; pp. 205–223. [Google Scholar]
- Lin, P.H.; Huang, L.R.; Lin, S.H. Why teaching innovation matters: Evidence from a pre- versus peri-COVID-19 pandemic comparison of student evaluation data. Front. Psychol. 2022, 13, 963953. [Google Scholar] [CrossRef]
- Stecula, K.; Wolniak, R. Influence of COVID-19 Pandemic on Dissemination of Innovative E-Learning Tools in Higher Education in Poland. J. Open Innov. Technol. Mark. Complex. 2022, 8, 89. [Google Scholar] [CrossRef]
- Korneiko, Y.; Tarangul, L.; Dovzhuk, V. Traditions and innovations: Two poles of education of the future. Futur. Educ. 2023, 3, 5–14. [Google Scholar] [CrossRef]
- Rönnlund, M.; Bergström, P.; Tieva, Å. Tradition and innovation. Representations of a “good” learning environment among Swedish stakeholders involved in planning, (re)construction and renovation of school buildings. Educ. Inq. 2021, 12, 249–265. [Google Scholar] [CrossRef]
- Chi, M.T.H. Translating a Theory of Active Learning: An Attempt to Close the Research-Practice Gap in Education. Top. Cogn. Sci. 2021, 13, 441–463. [Google Scholar] [CrossRef]
- Rycroft-Smith, L. Knowledge brokering to bridge the research-practice gap in education: Where are we now? Rev. Educ. 2022, 10, e3341. [Google Scholar] [CrossRef]
- Lombardi, D.; Shipley, T.F. The Curious Construct of Active Learning. Psychol. Sci. Public Interest 2021, 22, 8–43. [Google Scholar] [CrossRef]
- Benítez-Hernández, M.M.; Rodríguez-Testal, J.F.; Torrado-Herrera, M. Eficacia de un Programa de Innovación Docente en el Rendimiento, la Adquisición de Competencias Específicas y la Autoevaluación del Alumnado. Rev. Iberoam. Eval. Educ. 2021, 14, 191–208. [Google Scholar] [CrossRef]
- Fernández-Sánchez, M.R.; Valverde-Berrocoso, J. A community of practice: An intervention model based on computer supported collaborative learning. Comunicar 2014, 42, 97–105. [Google Scholar] [CrossRef]
- Smith, A.; Legaki, N.Z.; Hamari, J. Games and gamification in flipped classrooms: A systematic review. In Proceedings of the 6th International GamiFIN Conference 2022 (GamiFIN 2022), Tampere, Finland, 26–29 April 2022; pp. 33–43. [Google Scholar]
- Bond, M.; Buntins, K.; Bedenlier, S.; Zawacki-Richter, O.; Kerres, M. Mapping research in student engagement and educational technology in higher education: A systematic evidence map. Int. J. Educ. Technol. High. Educ. 2020, 17, 1–30. [Google Scholar] [CrossRef]
- Oonk, C.; Gulikers, J.T.M.; den Brok, P.J.; Wesselink, R.; Beers, P.J.; Mulder, M. Teachers as brokers: Adding a university-society perspective to higher education teacher competence profiles. High. Educ. 2020, 80, 701–718. [Google Scholar] [CrossRef]
- Akçayir, G.; Akçayir, M. The flipped classroom: A review of its advantages and challenges. Comput. Educ. 2018, 126, 334–345. [Google Scholar] [CrossRef]
- Prieto, A.; Barbarroja, J.; Álvarez, S.; Corell, A. Effectiveness of the flipped classroom model in university education: A synthesis of the best evidence. Rev. Educ. 2021, 391, 149–177. [Google Scholar]
- Al Fatta, H.; Maksom, Z.; Zakaria, M.H. Game-based Learning and Gamification: Searching for Definitions. Int. J. Simul. Syst. Sci. Technol. 2019, 19, 41. [Google Scholar] [CrossRef]
- Adipat, S.; Laksana, K.; Busayanon, K.; Asawasowan, A.; Adipat, B. Engaging students in the learning process with game-based learning: The fundamental concepts. Int. J. Technol. Educ. (IJTE) 2021, 4, 542–552. [Google Scholar] [CrossRef]
- Järveläinen, J.; Paalivainen-Mäntymäki, E. Escape Room as Game-Based Learning Process: Causation—Effectuation Perspective. In Proceedings of the 52nd Hawaii International Conference on System Sciences (HICSS-52), Grand Wailea, HI, USA, 8–11 January 2019. [Google Scholar]
- Yllana, F.; González-Gómez, D.; Jeong, J.S. The escape room and breakout as an aid to learning STEM contents in primary schools: An examination of the development of pre-service teachers in Spain. Education 2023, 3, 1–17. [Google Scholar]
- Taraldsen, L.H.; Haara, F.O.; Lysne, M.S.; Jensen, P.R.; Jensen, E.S. A review on use of escape rooms in education—Touching the void. Educ. Inq. 2022, 13, 169–184. [Google Scholar] [CrossRef]
- Manzano-León, A.; Rodríguez-Ferrer, J.M.; Aguilar-Parra, J.M.; Martínez-Martínez, A.M.; Luque-de-la-Rosa, A.; Salguero-García, D.; Fernández-Campoy, J.M. Escape Rooms as a Learning Strategy for Special Education Master’s Degree Students. Int. J. Environ. Res. Public Health 2021, 18, 7304. [Google Scholar] [CrossRef] [PubMed]
- Bellés-Calvera, L.; Martínez-Hernández, A.I. Slave away or get away: Escape rooms as a motivational tool for the CLIL history classroom in higher education. Lat. Am. J. Content Lang. Integr. Learn. 2022, 15, e1511. [Google Scholar]
- Ang, J.W.J.; Ng, Y.N.A.; Liew, R.S. Physical and digital ed-ucational escape room for teaching chemical bonding. J. Chem. Educ. 2020, 97, 2849–2856. [Google Scholar] [CrossRef]
- Nicholson, S. Peeking Behind the Locked Door: A Survey of Escape Room Facilities. White Paper. Available online: https://scottnicholson.com/pubs/erfacwhite.pdf (accessed on 3 May 2023).
- Monaghan, S.R.; Nicholson, S. Bringing escape room concepts to pathophysiology case studies. J. Hum. Anat. Physiol. Soc. 2017, 21, 49–65. [Google Scholar] [CrossRef]
- Gordon, S.K.; Trovinger, S.; DeLellis, T. Escape from the usual: Development and implementation of an ‘escape room’ activity to assess team dynamics. Curr. Pharm. Teach. Learn. 2019, 11, 818–824. [Google Scholar] [CrossRef]
- Dugnol-Menéndez, J.; Jiménez-Arberas, E.; Ruiz-Fernández, M.L.; Fernández-Valera, D.; Mok, A.; Merayo-Lloves, J. A collaborative escape room as gamifcation strategy to increase learning motivation and develop curricular skills of occupational therapy students. BCM Med. Educ. 2021, 21, 544. [Google Scholar] [CrossRef]
- Bilbao-Quintana, N.; Romero-Andonegui, A.; Portillo-Berasaluce, J.; López-de-la-Serna, A. Digital Escape Room for the Development of Collaborative Learning in Higher Education. Educ. Knowl. Soc. 2022, 23, 229–242. [Google Scholar]
- Abuhamdeh, S. Investigating the “Flow” Experience: Key Conceptual and Operational Issues. Front. Psychol. 2020, 11, 158. [Google Scholar] [CrossRef]
- Salvador-Gómez, A.; Escrig-Tena, A.B.; Beltrán-Martín, I.; García-Juan, B. El escape room virtual: Herramienta docente universitaria para el desarrollo de competencias transversales y para la retención del conocimiento. Tecnol. Cienc. Educ. 2022, 21, 7–48. [Google Scholar] [CrossRef]
- Wiemker, M.; Elumir, E.; Clare, A. Escape Room Games: “Can you transform an unpleasant situation into a pleasant one?”. In Game Based Learning—Dialogorientierung & Spielerisches Lernen Digital and Analog; Fachhochschule: St. Pölten, Austria, 15 October 2015; pp. 55–68. [Google Scholar]
- Veldkamp, A.; van de Grint, L.; Knippels, M.C.; van Joolingen, W. Escape education: A systematic review on escape rooms in education. Educ. Res. Rev. 2020, 31, 100364. [Google Scholar] [CrossRef]
- Nicholson, S. The State of Escape: Escape Room Design and Facilities. In Proceedings of the International Conference Meaningful Play, East Lansing, MI, USA, 20–22 October 2016. [Google Scholar]
- Mitre-Pérez, E. Gamification in Manufacturing Processes: An Educational Escape Room. Bachelor’s Thesis, Universidad de León, León, Spain, 2020. [Google Scholar]
- Seguí-Rodrigo, O. Escape Room Oriented to Awareness of the Problems and Solutions of a Pandemic. Bachelor’s Thesis, Universitat Jaume I, Castelló de la Plana, Spain, 2021. [Google Scholar]
- Barrientos-Jiménez, O. Escape Room: Herramienta de Selection. Master’s Thesis, Organizations and Human Resources, Universitat Jaume I, Castelló de la Plana, Spain, 2019. [Google Scholar]
- Díaz-Sandoval, D. Desarrollo de Aplicaciones Sobre Dispositivos Móviles: EscapeManager. Master’s Thesis, Universitat Oberta de Catalunya, Barcelona, Spain, 2019. [Google Scholar]
- Griggs, A.C. It’s Not Just a Game: Exploring the Effects of an Escape Room Team Building Intervention. Ph.D. Thesis, Embry-Riddle Aeronautical University, Daytona Beach, FL, USA, 2021. [Google Scholar]
- Arpin, R. The Effectiveness of Digital Escape Room Games to Deliver Leadership Training: A Mixed-Methods Study. Ph.D. Thesis, Franklin University, Columbus, OH, USA, 2021. [Google Scholar]
- Ayuso-Tapia, G. Creación de un Escape Room Educativo para Educación Secundaria Obligatoria. Master’s Thesis, Universidad de Valladolid, Valladolid, Spain, 2019. [Google Scholar]
- Dasca-Beneito, A. Especialitat Ciències Naturals: Física i Química. Master’s Thesis, Universitat Rovira i Virgili, Tarragona, Spain, 2021. [Google Scholar]
- Landa-Cillero, E. Gamificación Educativa con Escape Room en el aula de Matemáticas. Master’s Thesis, Universidad San Jorge, Zaragoza, Spain, 2018. [Google Scholar]
- Cruset-Domènech, R. Un Escape Room: Despertemos El álgebra. Master’s Thesis, Universitat Abad Oliba, Barcelona, Spain, 2022. [Google Scholar]
- Merchán-Macías, G.R. The Gate School Escape Room: An Educational Proposal. Master’s Thesis, Universidad de Valladolid, Valladolid, Spain, 2017. [Google Scholar]
- Heuvelmans, M. The Contribution of Game Design Elements to the Educational Potential of Escape Rooms in Secondary Biology Education. Master’s Thesis, Utrecht University, Utrecht, The Netherlands, 2020. [Google Scholar]
- Kinio, A.E.; Dufresne, L.; Brandys, T.; Jetty, P. Break out of the Classroom: The Use of Escape Rooms as an Alternative Teaching Strategy in Surgical Education. J. Surg. Educ. 2019, 76, 134–139. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.C.; Diemer, G.; Lee, H.; Jaffe, R.; Papanagnou, D. Finding the ‘QR’ to Patient Safety: Applying Gamification to Incorporate Patient Safety Priorities Through a Simulated ‘Escape Room’ Experience. Cureus J. Med. Sci. 2019, 11, e4014. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Urquiza, J. Qué es y cómo plantear una habitación de escapismo o escape room con fines docentes en Ciencias de la Salud. Rev. ENE de Enferm. 2019, 13, 1042. [Google Scholar]
- Rosillo, N.; Montes, N. Escape Room Dual Mode Approach to Teach Maths during the COVID-19 Era. Mathematics 2021, 9, 2602. [Google Scholar] [CrossRef]
- Stohlmann, M.S. Mathematical digital escape rooms. Sch. Sci. Math. 2023, 123, 26–30. [Google Scholar] [CrossRef]
- Magreñan, A.A.; Jiménez, C.; Orcos, L.; Roca, S. Teaching calculus in the first year of an engineering degree using a Digital Escape Room in an online scenario. Comput. Appl. Eng. Educ. 2022. early view. [Google Scholar]
- López-Pernas, S.; Saqr, M.; Gordillo, A.; Barra, E. A learning analytics perspective on educational escape rooms. Interact. Learn. Environ. 2022, 1, 1–17. [Google Scholar] [CrossRef]
- Brackenbury, T.; Kopf, L. Serious Games and Gamification: Game-Based Learning in Communication Sciences and Disorders. Perspectives 2022, 7, 482–498. [Google Scholar] [CrossRef]
- Ullah, M.; Amin, S.U.; Munsif, M.; Safaev, U.; Khan, H.; Khan, S.; Ullah, H. Serious Games in Science Education. A Systematic Literature Review. Virtual Real. Intell. Hardw. 2022, 4, 189–209. [Google Scholar] [CrossRef]
- Francisco, V.; Moreno-Ger, P.; Hervás. Application of Competitive Activities to Improve Students’ Participation. IEEE Trans. Learn. Technol. 2022, 15, 2–14. [Google Scholar] [CrossRef]
- Raharjo, R.S.; Handayani, P.W.; Putra, P.O.H. Active Student Learning through Gamification in a Learning Management System. Electron. J. e-Learn. 2021, 19, 601–613. [Google Scholar]
- Hacisalihoglu, G.; Stephens, D.; Johnson, L.; Edington, M. The use of an active learning approach in a SCALE-UP learning space improves academic performance in undergraduate General Biology. PLoS ONE 2018, 13, e0197916. [Google Scholar] [CrossRef] [PubMed]
- Nurbavliyev, O.; Kaymak, S.; Sydykov, B. The Effect of Active Learning Method on Students’ Academic Success, Motivation and Attitude Towards Mathematics. J. Lang. Linguist. Stud. 2022, 18, 701–713. [Google Scholar]
- Afzali, Z.; Izadpanah, S. The effect of the flipped classroom model on Iranian English foreign language learners: Engagement and motivation in English language grammar. Cogent Educ. 2020, 8, 1870801. [Google Scholar] [CrossRef]
- Soane, E.; Truss, C.; Alfes, K.; Shantz, A.; Rees, C.; Gatenby, M. Development and application of a new measure of employee engagement: The ISA Engagement Scale. Hum. Resour. Dev. Int. 2012, 15, 529–547. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).